A perturbative approach to multireference equation-of-motion coupled cluster

Abstract

We introduce a variant of the multireference equation-of-motion coupled-cluster (MR-EOMCC) method where the amplitudes used for the similarity transformations are estimated from perturbation theory. Consequently, the new variant retains the many-body formalism, a reliance on at most two-body densities, and the state-universal character. As a non-iterative variant, computational costs are reduced, and no convergence difficulties with near-singular amplitudes can arise. Its performance was evaluated on several test sets covering transition metal atoms, small diatomics, and organic molecules against (near-)full CI quality reference data. We further highlight its efficacy on the weakly avoided crossing of LiF and place MR-EOMCC and the new variant into context with linear response theory. The accuracy of the variant was found to be at least on par with expectations for multireference perturbation theories, judging by the NEVPT2 method. The variant can be especially useful in multistate situations where the high accuracy of the iterative MR-EOMCC method is not required.

GRAPHICAL ABSTRACT

KEYWORDS:

• Multireference methods
• perturbation theory
• coupled-cluster
• transform-then-diagonalize
• excited states

Introduction

Electron correlation effects play a vital role in calculating molecular properties and taking them into account accurately is often inevitable even to obtain a merely qualitative description of a system. Apart from dynamical correlation effects that arise from the inadequate treatment of short-range electron repulsion at the single-reference (SR) level, static correlation effects must also be considered in many important chemical systems. Examples include long-range dissociation problems and situations with near electronic degeneracy. The standard treatment in these cases accounts for the static effects by a relatively small multiconfigurational expansion which also serves as a starting point for quantitatively accurate multireference (MR) methods [1] that may rely on perturbation (PT), configuration interaction (CI) or coupled-cluster (CC) theory. In contrast to current density functional theory (DFT) approaches, such treatment can be systematically improved upon, possibly until the point of reaching chemical accuracy [2].

Recently, the multireference equation-of-motion coupled-cluster (MR-EOMCC) method [3–5] was proposed for the accurate treatment of strongly correlated electronic states. While this method holds the promise of efficiently calculating multiple states at the same time, some of the transformation steps involved in it require a significant amount of computational effort to carry through. To address this problem, we propose in the present study a multireference perturbation theory (MRPT) approximation to MR-EOMCC, to be referred to as MR-EOMPT. At their core, both MR-EOMCC and its MRPT variant are ‘transform-then-diagonalize’ approaches, where a transformed Hamiltonian is diagonalized over a compact manifold to obtain the states of interest. However, where MR-EOMCC uses iteratively determined amplitudes, the MR-EOMPT method foregoes the iterations and uses estimates from MRPT to yield comparable results at a lower computational cost.

To place MR-EOMPT into a proper context, let us briefly review single-reference CC theory and its MR extensions, with special regard to excited states. The defining concept in coupled-cluster theory is the exponential parameterization of the wave function, $|\mathrm{\Psi }⟩={\text{e}}^{\hat{T}}|0⟩$, which also engenders the similarity-transformed Hamiltonian $\overline{H}={\text{e}}^{-\hat{T}}\hat{H}{\text{e}}^{\hat{T}}$. By truncating the cluster operator $\hat{T}$ after single and double excitations and adding perturbative triples, we arrive at the CCSD(T) method, which is recognized as the ‘gold standard’ for single-reference calculations due to its highly accurate and reliable results [6,7]. To some extent, single-reference CC approaches like the linear response CC (LR-CC) theory [8] and EOMCC [9–12] (which has specialized variants such as spin-flip (SF) [13], ionization potential (IP) [14,15], double ionization potential (DIP) [16], electron attachment (EA) [17,18], and similarity-transformed STEOM [19–21]) can describe states that otherwise would require a multireference method [22].

The same is true for another early approach that shares a close connection [23] to the EOMCC formalism, namely the valence-universal [24–26] Fock-space coupled-cluster (FSCC) method [27–29], which allows the computation of excited as well as ionized or electron-attached states from a single reference state. At its core, FSCC relies on the theory of effective Hamiltonians, where a similarity-transformed Hamiltonian is set up in a reduced model space to reproduce a few eigenvalues of the exact Hamiltonian once the former has been diagonalized. The model space must be judiciously chosen to avoid intruder states, which generally cause serious convergence issues in FSCC calculations [29], although developments such as variants based on the use of intermediate Hamiltonians [30–34] or Mukherjee and co-workers’ eigenvalue-independent partitioning technique [35–37] greatly alleviate these issues. This theory further requires a reference for the cluster operators, which is a fully occupied core determinant [29]. The concepts [38–41] introduced with FSCC theory are integral to all ‘transform-then-diagonalize’ methods, of which the single-reference STEOM method has already been mentioned and of which the MR-EOMCC method can be regarded as a multireference extension.

In contrast to the single-reference approaches, genuine multireference methods require a reference that is not just a single determinant or configuration state function (CSF). For example, bond dissociation in N₂ with its triple bond is notoriously difficult to describe with single-reference methods, unless higher-order cluster operators including full triples and quadruples are also considered. On the other hand, there is no consensus yet as to what the ‘best way’ to parameterize a genuine multireference coupled-cluster (MRCC) theory is. For an overview of the competing developments, we refer the reader to a review by Lyakh et al. [42]. Broadly speaking, MRCC approaches can be classified into ‘single-reference’ MRCC, Hilbert- and Fock-space CC methods, of which we will briefly discuss the methods specifically targeted at computing excited states. These are often multistate approaches, in which several states are obtained in one go, as opposed to state-specific approaches, in which each state requires a separate calculation. Many of these excited state methods are obtained by extending single-reference techniques to the genuine multireference regime. A linear response function has been derived and implemented for Mukherjee’s state-specific MRCC (LR-Mk-MRCC) [43,44] theory and for the internally contracted MRCC (LR-ic-MRCC) developed in the group of Köhn and co-workers [45]. As for the EOM ansatz, the group of Nooijen and co-workers have formulated several approaches, starting with the state-specific (SS-)EOMCC method [46,47] and partially internally contracted (pIC)-MRCC [48] theory, which eventually culminated in the MR-EOMCC [3–5] method.

As mentioned above, the MR-EOMCC method can be viewed as a multireference extension of the FSCC approach in that it uses a state-averaged (SA) complete active space self-consistent field (CASSCF) wave function as its reference state. Using such a multideterminantal reference became possible after the introduction of ‘generalized normal order’ by Kutzelnigg and Mukherjee [49,50], which allows the cluster operators of internally contracted approaches to be written directly with respect to the reference wave function [51]. Generalized normal order also allows the use of ‘many-body residuals’ [3,48,52] with multireference wave functions, which are generally less costly than projected residual conditions and do not require focus on a particular target state [3]. This many-body aspect of MR-EOMCC (as well as FSCC and STEOM) further removes the need for higher-rank density matrices [48]. Additionally, the many-body residuals can be viewed as the natural extension of FSCC to multireference reference states [52].

The final ingredient to the MR-EOMPT method proposed in this study is multireference perturbation theory. Arguments from MRPT have already been used in an orbital selection scheme for the MR-EOMCC method to reduce computational cost, which is nonetheless different from the novel MR-EOMPT method since the selection scheme retained its iterative nature [53]. In general, perturbation theory is a well-tested approach to improving results compared to self-consistent field (SCF) calculations, especially when the SCF solution is already close to the exact wave function of the desired state. This assumption can be expected to hold for many CASSCF-based reference wave functions, since CASSCF itself already recovers a large part of static and, to a lesser extent, dynamic electron correlation. To discuss the relation of MR-EOMPT to the other MRPT approaches, we will classify them according to the order of diagonalization or perturbation steps. In this scheme, the most popular methods, state-specific CASPT2 [54,55] and NEVPT2 [56–58], can be called ‘diagonalize-then-perturb’ methods, and generally yield good accuracy. Furthermore, they have been extensively applied to compute excitation energies [59–62], and also properties such as g-tensors of transition metal complexes [63,64]. CASPT2 was also studied in the extensive benchmark by Thiel and co-workers [65,66], with results from NEVPT2 reported later on [60]. A major drawback is that CASPT2 and NEVPT2, by construction, rely on the four-body density matrix, which causes compute and memory demands to grow as the eighth power of the size of the active space. To overcome this, both methods have been combined with approximations to enable larger active spaces, such as DMRG [67–69] or cumulant approximations [70–72]. Local correlation approaches to reduce their overall scaling with system size have also been successfully implemented [73–75].

From the viewpoint of MR-EOMPT, a more closely related approach is the ‘diagonalize-then-perturb-then-diagonalize’ scheme, which generally describes quasidegenerate (QD) perturbation theory. First, the degenerate subspace of the Hamiltonian is diagonalized to avoid diverging perturbation expressions, and the resulting eigenfunctions are then used in the following perturbative treatment and final diagonalization to obtain the states of interest. Examples of this school are multiconfigurational MC-QDPT [76–78], multistate (MS-)CASPT2 [79] and QD-NEVPT2 [80], which have been extensively applied in the investigation of conical intersections [81,82], among others. In contrast to these methods, however, MR-EOMPT only uses a single set of amplitudes for all the states obtained in the final diagonalization.

The conceptually closest approach to the ‘transform-then-diagonalize’ methods discussed above are the ‘perturb-then-diagonalize’ formulations consisting of a single perturbative step and a subsequent diagonalization step. More precisely, after the effective Hamiltonian is constructed using perturbation theory methods, the final diagonalization mixes the perturbed model space functions into the final states. This approach has benefits over diagonalize-then-perturb methods in which dynamic correlation would mix the CASCI functions significantly, for example in ionic-covalent curve crossings [83,84] (see also Sec. 4.3). Compared to the more popular methods discussed earlier, only relatively few approaches have been developed, including NOCI-MP2 [85,86] and DCD-CAS [87].

Ultimately, however, the MR-EOMPT method should be considered as a multistate ‘transform-then-diagonalize’ approach. The non-iterative amplitudes are estimated such that the transformed Hamiltonian only couples to few determinants outside of the CAS space, which is then accounted for by a diagonalization over the CAS and remaining first-order interacting space. As will be demonstrated in the following, the results are still satisfactory in terms of accuracy despite these approximations, while being cheaper to compute than fully iterative MR-EOMCC results.

The remainder of this paper is organized as follows. First, the basic ideas behind MR-EOMCC theory will be recapitulated, with particular focus on the sequential similarity transformations. Then, we go on to explain how perturbatively estimated amplitudes may be used instead of the iterated equations to obtain the final, transformed Hamiltonian that can be diagonalized over the manifold of holes and particles to obtain the states of interest. We then present benchmarks and test systems from several problem types to validate the performance of MR-EOMPT against accurate reference values, its parent method, MR-EOMCC, and fully internally contracted (fic-, also called ‘partially contracted’ [58]) NEVPT2.

Theory

General notation

Throughout the entire theory section, we assume that we have a (SA-)CASSCF reference wave function. To refer to its orbital ranges, we use the index labels i, j, k, l for the doubly occupied inactive, t, u, v, w for the active, and a, b, c, d for the unoccupied virtual orbitals. Orbitals that may belong to either of those ranges are generically referred to with p, q, r, s. We further use the chemist’s notation for the real-valued two-electron integrals, (11|22). Repeated indices that only appear on one side of an equation are implicitly assumed to be summed over.

MR-EOMCC and its perturbative variant, MR-EOMPT

The electronic structure method described in this paper is closely related to the MR-EOMCC approach in that it retains the sequential similarity transformations as well as the final, uncontracted multireference configuration interaction including singles (MRCIS) diagonalization over a compact manifold. We only recapitulate the relevant features in this section and refer the reader to the published articles [3–5,88] for further details, especially regarding technicalities of the normal-ordered expansions. Multiple variants of the similarity transformations and the final diagonalization step have been described, but in the following, ‘MR-EOMCC’ should be taken to mean the MR-EOM-T|T^†|SXD|U-h-v method using the notation of Ref. [88]. In brief, the vertical lines indicate the sequential transformation steps, and the suffix ‘h-v’ denotes that the final Hamiltonian is symmetrized (vide infra).

We start by briefly recapitulating the salient features of coupled-cluster theory, with particular emphasis on the similarity transformation. In single-reference CC theory, the wave function $|\mathrm{\Psi }⟩$ is parameterized with an exponential of the cluster operator $\hat{T}$ on top of the closed-shell reference $|{\mathrm{\Phi }}_0⟩$, (1) $|\mathrm{\Psi }⟩={\text{e}}^{\hat{T}}|{\mathrm{\Phi }}_0⟩.$(1) By inserting Eq. (1) into the time-independent Schrödinger equation with the Born-Oppenheimer Hamiltonian (clamped nuclei) $\hat{H}$ and pre-multiplying with the inverse exponential, we arrive at the similarity-transformed Hamiltonian, (2) $\overline{H}|{\mathrm{\Phi }}_0⟩={\text{e}}^{-\hat{T}}\hat{H}{\text{e}}^{\hat{T}}|{\mathrm{\Phi }}_0⟩=E|{\mathrm{\Phi }}_0⟩.$(2) The residual conditions are then normally defined through projection, (3) $r_P=⟨{\mathrm{\Phi }}_P|\overline{H}|{\mathrm{\Psi }}_0⟩\stackrel{!}{=}0,$(3) where the excited determinants $⟨{\mathrm{\Phi }}_P|$ are obtained through action of the individual components (singles, doubles, … ; enumerated by the index P) of the cluster operator on the reference $|{\mathrm{\Phi }}_0⟩$.

The similarity transformation, as shown in Eq. (2), also plays a vital role in MR-EOMCC theory. In fact, it uses four sequential similarity transformations, which has also been investigated in the context of internally contracted (ic-)MRCC [89]. Of course, since MR-EOMCC is a genuine MRCC method, the reference $|{\mathrm{\Phi }}_0⟩$ is no longer closed-shell, but rather a (SA-)CASSCF wave function. Furthermore, the similarity-transformed Hamiltonian is expanded using Kutzelnigg and Mukherjee’s generalized normal order (GNO) [49,50,90] in a many-body form, (4) $\begin{array}{rl}\overline{H}& ={\text{e}}^{-\hat{T}}\hat{H}{\text{e}}^{\hat{T}}\\ & ={\overline{h}}_0+{\overline{h}}_q^p\{{\hat{E}}_p^q\}+{\overline{h}}_{rs}^{pq}\{{\hat{E}}_{pq}^{rs}\}+\dots ,\end{array}$(4) where the cluster operator $\hat{T}$ is defined as (5) $\hat{T}=t_a^i{\hat{E}}_i^a+t_a^t{\hat{E}}_t^a+\frac{1}{2}{t}_{ab}^{ij}{\hat{E}}_{ij}^{ab}+\frac{1}{2}{t}_{ab}^{it}{\hat{E}}_{it}^{ab}+\frac{1}{2}{t}_{ab}^{tu}{\hat{E}}_{tu}^{ab}.$(5)

We note that the cluster operator $\hat{T}$ is normal ordered since the (de-)excitation orbital spaces are disjoint. Consequently, we did not use curly braces $\{{\hat{E}}_{\dots }^{\dots }\}$ around the spin-free excitation operators in Eq. (5) to indicate normal ordered operators.

In the fully iterative version, MR-EOMCC, the amplitudes for the cluster operator $\hat{T}$ would be obtained by requiring projective residual conditions for the singles and many-body residuals [48,52] for the doubles to be fulfilled. In the MR-EOMPT method described in this paper, most of the amplitudes are computed from many-body perturbation theory to second order (MBPT2). In the following, we will list the perturbative formulae in the relevant cases, while dedicating Sec. 2.3 to their theoretical justification. To begin with, the virtual-inactive block of $\hat{T}$ is obtained as (6) $t_{ab}^{ij}=\frac{(ia|jb)}{{ϵ}_i+{ϵ}_j-({ϵ}_a+{ϵ}_b)},$(6) where ${ϵ}_p$ denotes the orbital energies of the inactive and virtual orbitals of the CASSCF reference.

Amplitudes involving active orbitals are computed using extended Koopman’s theorem (EKT) [91–93], (7) $t_{ab}^{tu}=\sum _{\tilde{v}\tilde{w}}{c}_{t\tilde{v}}^{\text{IP}}{c}_{u\tilde{w}}^{\text{IP}}\frac{(\tilde{v}a|\tilde{w}b)}{{ϵ}_{\tilde{v}}^{\text{IP}}+{ϵ}_{\tilde{w}}^{\text{IP}}-({ϵ}_a+{ϵ}_b)},$(7) where $c_{t\tilde{v}}^{\text{IP}}$ are the EKT orbital coefficients and ${ϵ}_{\tilde{v}}^{\text{IP}}$ are the EKT orbital energies for ionization potentials (IP). We also defined the transformed integrals, (8) $(\tilde{v}a|\tilde{w}b)=\sum _{tu}{c}_{t\tilde{v}}^{\text{IP}}{c}_{u\tilde{w}}^{\text{IP}}(ta|ub),$(8) where a tilde indicates an orbital in the EKT-IP basis.

The $t_{ab}^{it}$ amplitudes are computed analogously to the $t_{ab}^{tu}$ amplitudes. Explicit equations can be found in the supplementary information.

The singles amplitudes $t_a^i$, $t_a^t$ are computed to second instead of first order because the Brillouin condition requires that the first order amplitudes $t{}_a^{i(1)}=0$ [53]. Hence, the singles amplitudes are initially set to zero and the doubles estimate is performed according to Eq. (6) and its analogs for the $t_{ab}^{it}$ and $t_{ab}^{tu}$ amplitudes. Subsequently, the doubles-only state is used to compute the singles residuals, (9) $r_a^i=⟨{\mathrm{\Phi }}_0|{\hat{E}}_a^i\overline{H}|{\mathrm{\Phi }}_0⟩,$(9) which are then employed to estimate the second order singles amplitudes, (10) $t{}_a^{i(2)}=\frac{r_a^i}{{ϵ}_i-{ϵ}_a},t{}_a^{t(2)}=\sum _{\tilde{v}}{c}_{t\tilde{v}}^{\text{IP}}\frac{r_a^{\tilde{v}}}{{ϵ}_{\tilde{v}}^{\text{IP}}-{ϵ}_a}.$(10) In Eqs. (10), the transformed residual matrix elements $r_a^{\tilde{v}}$ are defined analogously to the transformed integrals from Eq. (8), again in the EKT-IP basis.

At this point, the Hamiltonian $\overline{H}$ is transformed with the de-excitation operator ${\hat{T}}^{†}$ in complete analogy to Eq. (4) to give the Hamiltonian $\tilde{H}$. This non-iterative step approximates the de-excitation amplitudes by setting (11) $\begin{array}{rl}& t_i^a=t_a^i,t_t^a=t_a^t,\end{array}$(11) (12) $\begin{array}{rl}& t_{ij}^{ab}=t_{ab}^{ij},t_{it}^{ab}=t_{ab}^{it},t_{tu}^{ab}=t_{ab}^{tu}.\end{array}$(12) The ${\hat{T}}^{†}$ transformation is included to make the transformed Hamiltonian more Hermitian. For more details, we refer to Ref. [88].

We then proceed with a third similarity transformation on top of the previous transformed Hamiltonian, (13) $\begin{array}{rl}\overline{F}& =\{{\text{e}}^{\hat{S}+\hat{X}+\hat{D}}{\}}^{-1}{\tilde{H}}_2\{{\text{e}}^{\hat{S}+\hat{X}+\hat{D}}\}\\ & ={\overline{f}}_0+{\overline{f}}_q^p\{{\hat{E}}_p^q\}+{\overline{f}}_{rs}^{pq}\{{\hat{E}}_{pq}^{rs}\}+\dots ,\end{array}$(13) where ${\tilde{H}}_2$ is the Hamiltonian from after the $\hat{T}$, ${\hat{T}}^{†}$ transformations truncated at two-body terms. For details on how the inverse of the normal-ordered exponential $\{{\text{e}}^{\hat{S}+\hat{X}+\hat{D}}{\}}^{-1}$ is computed we refer to Ref. [94]. The individual cluster operators used in this transformation are defined as (14) $\begin{array}{c}\hat{S}=s_{at}^{ij}\{{\hat{E}}_{ij}^{at}\},\\ \hat{X}=x_{au}^{ti}\{{\hat{E}}_{ti}^{au}\},\\ \hat{D}=d_{au}^{it}\{{\hat{E}}_{it}^{au}\}.\end{array}$(14) The amplitudes of excitations into active orbitals are again obtained perturbatively in MR-EOMPT using the electron attachment (EA) results from EKT for the orbital energies, e.g. (15) $s_{at}^{ij}=\sum _{\tilde{v}}{c}_{t\tilde{v}}^{\text{EA}}\frac{(ia|j\tilde{v})}{{ϵ}_i+{ϵ}_j-({ϵ}_a+{ϵ}_{\tilde{v}}^{\text{EA}})},$(15) with the corresponding integral being defined here in the EKT-EA basis, (16) $(ia|j\tilde{v})=\sum _t{c}_{t\tilde{v}}^{\text{EA}}(ia|jt).$(16) The guess amplitudes for $\hat{X}$ and $\hat{D}$ are computed equivalently and may be found in the supplementary information.

The remaining amplitudes of the last similarity transformation are computed exactly as in MR-EOMCC theory. By replacing the first three similarity transformations of the $\hat{T}$, ${\hat{T}}^{†}$ and $\hat{S}+\hat{X}+\hat{D}$ blocks with perturbatively estimated amplitudes, the MR-EOMPT method will, naturally, be faster than its parent method, MR-EOMCC, although at the cost of accuracy. This tradeoff has already been partially attempted with an iterative orbital selection scheme, which we mention here since it used the same definition for the non-iterative amplitude estimates therein [53]. A main focus of this paper will be to investigate the time-accuracy tradeoff. Furthermore, it will be easier to perturbatively obtain the amplitudes for the aforementioned similarity transformations since the iterative MR-EOMCC method may face convergence difficulties in the case of nearly singular amplitudes [47, 48].

The last similarity transformation is described by (17) $\begin{array}{rl}\overline{G}& ={\text{e}}^{-\hat{U}}{\overline{F}}_2{\text{e}}^{\hat{U}}\\ & ={\overline{g}}_0+{\overline{g}}_q^p\{{\hat{E}}_p^q\}+{\overline{g}}_{rs}^{pq}\{{\hat{E}}_{pq}^{rs}\}+\dots ,\end{array}$(17) with the two-body operator (18) $\hat{U}=\frac{1}{2}{u}_{tu}^{ij}\{{\hat{E}}_{ij}^{tu}\}.$(18) Amplitudes for this transformation are not computed perturbatively, but are solved for iteratively by requiring that the corresponding elements of the many-body expanded Hamiltonian $\overline{G}$, ${\overline{g}}_{tu}^{ij}$, must be zero as in MR-EOMCC theory, (19) $r_{tu}^{ij}={\overline{g}}_{tu}^{ij}\stackrel{!}{=}0.$(19) Although these amplitudes could also be estimated from MBPT2, they are iterated because they are never the rate-limiting step of the entire calculation. Furthermore, we normally observe fast convergence within up to five iterations.

After symmetrizing the similarity-transformed Hamiltonian $\overline{G}$ according to Ref. [88], the only remaining step is the final diagonalization of $\overline{G}$ over a suitable manifold. This step will then give access to the total energies of the desired states as well as the transition energies between them. The optimal setup of this final diagonalization step has been investigated several times by one of the present authors [4, 5, 88, 95]. For this paper, we have chosen to diagonalize the transformed Hamiltonian $\overline{G}$ over the reference CAS space including single hole and particle excitations with respect to the reference space. In the case of MR-EOMPT theory, there is a strong argument to use the smallest reasonable diagonalization space to minimize the computational costs. Extending the final diagonalization manifold is usually very costly with limited benefits for accuracy [88].

Discussion of the perturbative approximations

In this section, we will further explore the theoretical background of the perturbative formulae given in Sec. 2.2, which make the current MR-EOMPT method a (lowest-order) perturbative approximation to the full MR-EOMCCSD method. Strictly speaking, one would expect this to involve a well-defined partitioning of the Hamiltonian $\hat{H}={\hat{H}}_0+\hat{V}$, but it is more illuminating to think of the scheme as a (lowest-order) iterative approximation.

In general, the full residuals equation for the parameters $t\in \mathit{T}$ can be written as $r_P(\mathit{T})=0$, as exemplified in Eq. (3). With this, an iterative sequence can be defined, (20) ${\mathit{T}}^{(n+1)}={\mathit{T}}^{(n)}+{\mathrm{\Delta }}_P{r}_P({\mathit{T}}^{(n)}),$(20) where $n$ indicates the order of iteration. In principle, this can define the $n^{\text{th}}$-order iteration in analogy to $n^{\text{th}}$-order perturbation theory. In this work, we use ${\mathit{T}}^{(0)}=0$, and need to find a suitable definition of the ‘denominators’ ${\mathrm{\Delta }}_P$, which would ideally lead to a smooth convergence of the iterative sequence, especially in the first iteration. Note that the denominators are not associated with a zeroth-order Hamiltonian. The denominators used to converge the MR-EOM equations have been discussed in detail in Ref. [47], although it may be good to reiterate this rationale here.

Given the creation operators ${\hat{a}}^{†}$, ${\hat{t}}^{†}$, which are associated with the electron-attached states ${\hat{p}}^{†}|{\mathrm{\Psi }}_0⟩$, we can find optimal ‘extended Koopmans’ states’ [91–93, 96, 97] where we remove the coupling between active and virtual orbitals. Likewise, the annihilation operators $\hat{i}$, $\hat{t}$ are associated with ionized states $\hat{q}|{\mathrm{\Psi }}_0⟩$, and we can find optimal singly detached states and ionization potentials by solving the respective extended Koopmans’ problem, again preventing the rotation between active and inactive core ‘orbitals.’

As a result, we have a different one-particle basis for the active creation operators ${\hat{t}}^{†}$ and the active annihilation operators $\hat{t}$. Hence, the residuals $r$ need to be transformed to a basis in which the denominators ${\mathrm{\Delta }}_P$ are diagonal, as shown, e.g. in Eq. (10). It is also pertinent to observe that the difference in orbital energy for attachment and ionization associated with the same active label $t$ is large (e.g. 10 eV).

For this reason, there are no small denominators in the current scheme. Let us now comment on the nature of the perturbation $\hat{V}$. In the lowest-order scheme, the first iteration just uses the full (simplified) MR-EOM equation with $\mathit{T}=0$, i.e. the leading term involves the full Hamiltonian $\hat{H}$. However, the nature of the equations is that only those parts of $\hat{H}$ are included that couple active space determinants to excitations out of the active space, and this can naturally be associated with a perturbation. To discuss higher-order perturbation theory, we would advise using the iterative sequence as there does not appear to be a good way to properly define the perturbation. Since we only discuss the lowest-order variant here, we prefer to use the name perturbation theory for our scheme as this is commonly used in the literature, and it captures the nature of the approximations.

Relations to other MRPT approaches

It seems appropriate to elaborate on the differences between the fic-NEVPT2 approach as an example of a state-specific, ‘diagonalize-then-perturb’ MRPT and the MR-EOMPT method, which is a state-universal, ‘transform-then-diagonalize’ approach. Both NEVPT2 and MR-EOMPT rely on the solution of the CASSCF problem, (21) $\begin{array}{rl}& {\hat{H}}_{\text{CAS}}={\hat{P}}_{\text{CAS}}\hat{H}{\hat{P}}_{\text{CAS}},{\hat{P}}_{\text{CAS}}=\sum _I|{\mathrm{\Phi }}_I⟩⟨{\mathrm{\Phi }}_I|,\end{array}$(21) (22) $\begin{array}{rl}& {\hat{H}}_{\text{CAS}}|{\mathrm{\Psi }}_m⟩=E_m|{\mathrm{\Psi }}_m⟩=E_m\sum _I{c}_{I,m}|{\mathrm{\Phi }}_I⟩,\end{array}$(22) where $|{\mathrm{\Phi }}_I⟩$ are individual CSFs from the CASCI space combined with coefficients $c_{I,m}$ into the solution for the mth state. For fic-NEVPT2, these solutions are then taken to define the internally contracted perturber functions for MRPT by applying the excitation operators from the perturbation operator $\hat{V}$ to the CASSCF solution. For example, the perturber function space for a two-hole, one-particle situation is given by [56,58] (23) ${\overline{S}}_{ija}^{+1}={\hat{E}}_i^a{\hat{E}}_j^t|{\mathrm{\Psi }}_m⟩,\text{dim}({\overline{S}}_{ija}^{+1})=n_a.$(23) Here, $n_a$ denotes the number of active orbitals. In a similar fashion for all the remaining seven excitation classes, these perturber functions are state-specific in that they already explicitly contain the state of interest. The perturber functions then enter the expressions for the energy correction to second order [58]. Another consequence of the state-specific, internally contracted perturbers is that they ensue the presence of four-body (active) densities in the working equations for the ${\overline{S}}_i^{(-1)}$ and ${\overline{S}}_a^{(-1)}$ spaces [58].

For MR-EOMPT, an equation like (23) is conspicuously missing. Instead, a similarity-transformed Hamiltonian is built in the CASCI model space using perturbatively estimated amplitudes (vide supra). The working equations depend on the reference state in two ways: First, the one- and two-body reduced density matrices (RDMs) enter through the EKT orbital energies, e.g. Eq. (7). Second, the one-body RDM is also required to construct the similarity-transformed Hamiltonians $\overline{H}$, $\overline{F}$, and $\overline{G}$. Hence, this method is state-universal in character for all states in the CASCI space, as opposed to the state-specific fic-NEVPT2 method. The purpose of the similarity transformations is to decouple the model space from the outer space, as thoroughly discussed in both ST-EOMCC [19–21] and MR-EOMCC [3–5] theory. Eventually, the MRCIS diagonalization gives access to the final states of the transformed Hamiltonian. We note that the diagonalization is not only over the model CASCI space, but rather over the CASCI space and all single-hole and single-particle excitations relative to it, which is the first-order interacting subspace based on the (large elements of the) transformed Hamiltonian. The rationale behind this choice is that any residual coupling to the outer space should be captured in such a fashion. It is, however, not intended to significantly change the character of the model space states, which is why MR-EOMCC calculations generally require that the weight of the CSFs from the CASCI space $|{\mathrm{\Phi }}_I⟩$ exceed 90% in the final states [53].

Computational details

All calculations presented in the Results and Discussion section use a (SA-)CASSCF reference wave function and were computed using a development version of the ORCA [98–100] program package. The detailed settings regarding the number of active electrons, number of active orbitals, or which roots were included in the reference state can be found in the supplementary information. We normally used a ‘standard choice’ of the active space, meaning that we included all (anti-)bonding partners, complete π-systems, and other orbitals involved in excited state transitions, e.g. the n-orbitals.

When comparing the results of the MR-EOMCC and MR-EOMPT methods to pure CASSCF or fic-NEVPT2 calculations (referred to in the following as CASSCF and NEVPT2, respectively), we note that the MR-EOM methods do generally not use the same reference wave function as the CASSCF/NEVPT2 calculations. For the CASSCF and NEVPT2 results, we often simply included all roots of interest with equal weights in the CASSCF reference, with possible splitting into separate blocks of different multiplicity and irrep.

The setup of the MR-EOMCC and MR-EOMPT calculations may be somewhat counterintuitive in that the aim of their SA-CASSCF reference is to decouple the active space by virtue of the similarity transformations; and then obtain the states of interest from the final MRCIS step, while also taking any residual coupling into account. In more practical terms, our general procedure was as follows. First, an initial CASCI or CASSCF calculation over a number $(\stackrel{<}{\sim \phantom{{}_x}}5)$ of low-lying singlet and triplet roots each is done to obtain a ‘spectrum’ of states from which the MR-EOM reference will be selected. In the second step, we choose all roots beneath a threshold of a few eV ($\stackrel{<}{\sim \phantom{{}_x}}3$ eV), while taking care that the selection does not break wave function symmetry. This will be the reference state used in the MR-EOMCC and -PT calculations. In case of convergence difficulties in the MR-EOMCC method or final roots with a too low contribution of the CASCI space (vide supra), the reference state may be modified to achieve convergence. While a detailed study regarding root selection is out of scope of this study, the MR-EOMCC method (as well as the MR-EOMPT variant in our testing) has been shown to be relatively invariant with respect to the choice of the reference state [88]. The exact setup is detailed in the supplementary information as well.

When it comes to comparing the MR-EOMCC and MR-EOMPT results, we emphasize that the reference as well as the calculation settings were strictly the same in both cases, the only difference being that perturbative amplitudes were used for the MR-EOMPT calculations. The convergence threshold for the iterative amplitude equations was always set to a maximum absolute residual of 10⁻⁶.

Results and Discussion

Diatomic systems

The first test set that we use to gauge the accuracy of the MR-EOMPT method is a set of small, diatomic molecules first published as a means to assess the contraction error of a fic-MRCI implementation [101]. These diatomic molecules are entirely from the second period and are computed in the def2-SVP [102] basis set. Hence, we are able to obtain near-full CI (FCI) results from the iterative configuration expansion (ICE-)CI method [103,104], a selected CI approach in the vein of CIPSI (configuration interaction by perturbation with multiconfigurational zeroth-order wavefunction selected by iterative process) [105], by including all electrons and orbitals in the active space (ICE-FCI). The iterative cutoffs that were used in the ICE-FCI reference calculations $(T_{\text{gen}}={10}^{-5},T_{\text{var}}={10}^{-12})$ are expected to yield average deviations of less than 0.1 mE_h when compared to the total energy of a corresponding FCI calculation [104]. Consequently, the aim for this test set is to demonstrate how closely the MR-EOMPT method can reproduce nearly exact, FCI-quality transition energies.

In all calculations, a full valence CASSCF reference was chosen. The primary reason for such a comparatively large active space is that some transitions, for example the $X{}^2{\mathrm{\Sigma }}^{+}\to 2{}^2{\mathrm{\Sigma }}^{+}$ transition on both CN and CO⁺, describe a $2{\sigma }^{\ast }\to 3\sigma$ excitation out of the antibonding orbital formed from the atomic 2s orbitals, and neither of these methods can describe excitations not contained in the active space. For CASSCF, it is immediately clear that states outside of the active space cannot be described, and therefore also state-specific fic-NEVPT2 cannot perturbatively improve upon such state. In the case of MR-EOMCC and MR-EOMPT, the similarity transformations also only account for the states contained in the active space, and the final MRCIS diagonalization evaluates the residual coupling to the outside space (see Sec. 2.4). The detailed setup is summarized in the supplementary information.

The results of the CASSCF, NEVPT2, MR-EOMPT, and MR-EOMCC calculations are presented in Table 1. Due to the large, full-valence active space, all methods report rather accurate results, with the largest deviation in the vertical transition energy (VTE) being 0.48 eV by the CASSCF method. As expected, the CASSCF method is outperformed by the remaining methods since it does not account for most of dynamic electron correlation, even despite the large active space. We wish to emphasize that these results may be of limited applicability to larger calculations, since the full valence active space comprises an exceptionally large fraction of the total number of orbitals in the systems, which therefore captures a larger than usual amount of dynamic correlation in the reference.

Table 1. Errors in vertical transition energies (VTEs) with respect to ICE-FCI results (reference values) on diatomic systems from the second period. The VTEs are given relative to the ground state (GS) in parentheses. All values given in eV.

			ΔVTE
		VTE			MR-EOM
System (GS)	Exc. State	ICE-FCI	CASSCF	NEVPT2	-PT	-CC
CH (^2Π)	^2Δ	3.04	0.07	−0.01	−0.02	0.00
	^2Σ^−	3.40	−0.10	−0.02	−0.02	−0.04
	^2Σ^+	4.15	−0.04	0.04	0.10	0.14
CN (^2Σ^+)	^2Π	1.46	0.09	0.02	0.06	0.01
	2 ^2Σ^+	3.03	0.07	0.04	0.05	0.02
CO (^1Σ^+)	^1Π	8.78	0.47	0.08	0.01	−0.12
	^1Σ^−	10.30	0.15	0.07	0.06	0.00
	^1Δ	10.42	0.09	0.07	0.05	−0.02
	^3Π	6.33	0.20	0.03	−0.01	−0.08
	^3Σ^+	8.62	0.12	0.09	0.15	0.12
	^3Δ	9.55	0.14	0.08	0.11	0.06
	^3Σ^−	10.04	0.04	0.08	0.10	0.04
CO^+ (^2Σ^+)	^2Π	3.59	0.24	0.05	0.01	0.01
	2 ^2Σ^+	5.83	0.31	0.08	0.02	0.02
N2 (^1Σ^+)	^1Π	9.65	0.44	0.07	0.06	0.06
	^1Σ^−	10.41	0.47	0.08	0.01	0.00
	^1Δ	10.80	0.39	0.09	0.06	0.06
	^3Σ^+	7.94	0.16	0.06	0.09	0.06
	^3Π	8.26	0.48	0.04	0.08	0.10
	^3Δ	9.26	0.32	0.07	0.05	0.04
	^3Σ^−	10.06	0.21	0.09	0.11	0.11
O2 (^3Σ^+)	^1Δ	1.07	−0.12	−0.04	−0.04	−0.06
	^1Σ^+	1.73	−0.26	−0.05	−0.03	−0.06
	^3Δ	6.34	−0.19	0.00	−0.01	−0.06
OH (^2Π)	^2Σ^+	4.29	0.34	0.02	−0.03	−0.09
Statistical Evaluation of Errors
Min.			−0.26	−0.05	−0.04	−0.12
Avg.			0.16	0.05	0.04	0.01
Max.			0.48	0.09	0.15	0.14
Std.			0.20	0.04	0.05	0.07
MAE			0.22	0.05	0.05	0.05
RMSD			0.26	0.06	0.07	0.07

The statistical analysis of the errors reported in Table 1 shows that the correlated methods NEVPT2, MR-EOMPT, and MR-EOMCC perform similarly across this test set, judging by the maximum absolute error (MAE) or the root-mean-square deviation (RMSD). Out of all methods, fic-NEVPT2 reports the lowest standard deviation. In combination with an average deviation of 0.05 eV, we can conclude that it yields the most consistent results, despite the MR-EOMCC method having an average deviation of only 0.01 eV from the ICE-FCI reference. Even so, the RMSD for all methods beyond CASSCF is below 0.1 eV, which is generally considered to be in excellent agreement.

We further report the total energies for all the states used in this section in the supplementary information, as well as a statistical analysis of the deviations compared to the ICE-FCI reference data in Table 2. While the MR-EOM methods are primarily targeted at computing transition energies on a single system, the total energies may, e.g. also be used to compute energy differences between different geometries (see also Sec. 4.4). Unsurprisingly, the iterative MR-EOMCC method is the closest to the ICE-FCI reference, with an RMSD of 0.15 eV. Next are the perturbative methods MR-EOMPT and NEVPT2 with RMSDs of 0.46 and 0.77 eV, respectively. Thus, MR-EOMPT outperforms NEVPT2 in this regard, despite the RMSD across the transition energies from Table 1 being slightly worse than that of NEVPT2. As usual, the CASSCF results are far off since even the large full-valence active spaces used in this section are not enough to recover a substantial amount of dynamic electron correlation.

Table 2. Statistical evaluation of the differences of the total energies compared to the ICE-FCI reference values (given in eV). The total energies of the 32 states can be found in the supplementary information.

			MR-EOM
	CASSCF	NEVPT2	-PT	-CC
Min.	2.03	0.43	0.09	−0.03
Avg.	5.04	0.76	0.43	0.13
Max.	7.56	1.05	0.64	0.32
Std.	1.44	0.16	0.16	0.07
MAE	5.04	0.76	0.43	0.13
RMSD	5.24	0.77	0.46	0.15

Thiel test set

Continuing to focus on excitation energies, Thiel’s extensive test set [65, 66, 106] lends itself to further benchmarking. This test set contains highly accurate reference data in the form of CC3 results with a high singles-excitation dominated character ($\mathrm{\%}{T}_1>90\mathrm{\%}$) [65]. In the case of the Thiel benchmark set, multireference methods are not per se required since the included molecules are of closed-shell type, at least in their respective ground states. Nevertheless, the reported CC3 values may be used as reference values against which the MR-EOMPT method can be benchmarked, provided that the same calculation settings and basis set are used. Note that CC3 is known to have MAEs of well below 0.1 eV for singles-dominated transitions [65].

The reason why this test set is suitable for benchmarking the MR-EOMPT method is that it contains reference data for accurate excitation energies, which is also what its parent method, MR-EOMCC, was designed to calculate. Thiel’s test set, or a subset thereof, has already been used to benchmark other variants of the MR-EOMCC approach [4, 88]. We note that our choice of the zeroth-order CASSCF reference for the MR-EOMCC and MR-EOMPT calculations in this paper is not necessarily identical to the references in the published literature. The choice of the reference was found to have only a minor impact on the calculations [88], which we were able to confirm in our testing with the MR-EOMPT and MR-EOMCC methods. The reference state(s) used were obtained through the procedure outlined in Sec. 3 and can be found in the supplementary information.

Our results are summarized in Table 3, where we report the reference values (CC3) from Ref. [65] along with the deviation of the CASSCF, fic-NEVPT2, MR-EOMPT, and MR-EOMCC methods from our calculations. In line with expectations, the CASSCF results again fail to reproduce the reference values accurately and consistently. If we turn our attention to the perturbational approaches, we see that the description is much improved over the CASSCF base results. Furthermore, extreme outliers are rare, although absolute deviations of up to 0.68 eV can be found for the MR-EOMPT method. The fully iterative results from MR-EOMCC theory are closer to the reference values than either perturbative method, as expected from the results reported in Ref. [88].

Table 3. Errors in transition energies (eV) with respect to CC3 results [65] on molecules from the Thiel test set, TZVP basis set.

			ΔVTE
		VTE			MR-EOM
Molecule	Transition	CC3 (Ref.)	CASSCF	NEVPT2	-PT	-CC
Ethene	1 ^1Ag → 1 ^1B1u	8.37	1.07	0.27	0.41	0.09
	1 ^1Ag → 1 ^3B1u	4.48	−0.20	0.13	−0.05	−0.01
Butadiene	1 ^1Ag → 1 ^1Bu	6.58	1.52	−0.31	0.61	0.24
	1 ^1Ag → 2 ^1Ag	6.77	−0.18	0.05	−0.10	−0.17
	1 ^1Ag → 1 ^3Bu	3.32	−0.14	0.12	0.02	0.01
	1 ^1Ag → 1 ^3Ag	5.17	−0.24	0.16	−0.02	−0.02
Cyclopropene	1 ^1A1 → 1 ^1B1	6.90	0.39	−0.06	0.01	−0.09
	1 ^1A1 → 1 ^1B2	7.10	1.52	−0.03	0.58	0.25
	1 ^1A1 → 1 ^3B2	4.34	−0.14	0.21	−0.03	−0.05
	1 ^1A1 → 1 ^3B1	6.62	0.22	−0.05	0.00	−0.07
Benzene	1 ^1A1g → 1 ^1B2u	5.07	−0.11	0.15	−0.02	−0.03
	1 ^1A1g → 1 ^1B1u	6.68	1.28	−0.26	0.40	0.13
	1 ^1A1g → 1 ^1E1u	7.45	1.92	−0.40	0.68	0.23
	1 ^1A1g → 2 ^1E2g	8.43	−0.28	−0.03	−0.13	−0.27
	1 ^1A1g → 1 ^3B1u	4.12	−0.27	0.20	−0.03	−0.02
	1 ^1A1g → 1 ^3E1u	4.90	0.11	0.06	0.05	0.00
	1 ^1A1g → 1 ^3B2u	6.04	1.19	−0.37	0.36	0.09
	1 ^1A1g → 1 ^3E2g	7.49	−0.32	0.11	−0.04	−0.17
Pyrrole	1 ^1A1 → 2 ^1A1	6.40	0.05	0.16	0.10	−0.01
	1 ^1A1 → 1 ^1B2	6.71	0.91	−0.11	0.46	0.16
	1 ^1A1 → 3 ^1A1	8.17	1.35	0.02	0.67	0.19
	1 ^1A1 → 1 ^3B2	4.48	−0.44	0.27	−0.02	−0.03
	1 ^1A1 → 1 ^3A1	5.51	−0.15	0.20	0.06	−0.03

The statistical summary of the results on the Thiel benchmark set is presented in Table 4. As in the previous publications [65, 88], we compute the statistics over singlets and triplets separately to see any systematic error in either of the subsets.

Table 4. Statistical evaluation of the errors on the subset of the Thiel benchmark reported in Table 3. All values are given in eV.

			MR-EOM
	CASSCF	fic-NEVPT2	-PT	-CC
ΔVTE, Singlets
Min.	−0.28	−0.40	−0.13	−0.27
Avg.	0.79	−0.05	0.31	0.06
Max.	1.92	0.27	0.68	0.25
Std.	0.74	0.19	0.30	0.17
MAE	0.88	0.16	0.35	0.16
RMSD	1.08	0.20	0.43	0.18
ΔVTE, Triplets
Min.	−0.44	−0.37	−0.05	−0.17
Avg.	−0.03	0.09	0.03	−0.03
Max.	1.19	0.27	0.36	0.09
Std.	0.42	0.17	0.11	0.06
MAE	0.31	0.17	0.06	0.05
RMSD	0.43	0.19	0.11	0.07

The statistical analysis shows that the MR-EOMPT method clearly performs better on the subset of transitions to triplet excited states, compared to singlet excited states. In the case of a triplet final state, the RMSD across all transitions is merely 0.11 eV and can be considered in excellent agreement with the reference values, whereas the RMSD for the singlet transitions is about four times as large at 0.43 eV. This contrasts with the results from the NEVPT2 method, which reports almost equal RMSDs for the singlet and triplet transitions. The same effect is also present in the MR-EOMCC results, albeit much less pronounced at RMSDs of 0.18 and 0.07 eV for the singlet and triplet transitions, respectively.

These results may seem surprising initially when they are not carefully compared to the correct variant of the MR-EOMCC approach in the published literature. The closest variant from Ref. [88] is called ‘MR-EOM-T|T^†|SXD-h-v,’ which is implemented in the ORCA program package [99] along with the variant used in this paper, which could be analogously called ‘MR-EOM-T|T^†|SXD|U-h-v’ (see Sec. 2.2). The published MR-EOM-T|T^†|SXD-h-v results lack the final $\hat{U}$ transformation and therefore use a larger MRCI diagonalization space that also includes 2 h excitations from the CASCI space. Nevertheless, the MR-EOM-T|T^†|SXD-h-v results are comparable to our own MR-EOMCC results. Furthermore, Ref. [88] shows that especially the ${\hat{T}}^{†}$ transformation step deteriorates the quality of the singlet transitions, while it has negligible impact on the triplet transitions. For the MR-EOMPT method, this effect is amplified, making these results less robust compared to the iterative MR-EOMCC method. In the future, other variants of the MR-EOMPT approach, e.g. without the ${\hat{T}}^{†}$ transformation, can be explored. We further remark that a previous study [4] also found that the MR-EOMCC results tend to perform favorably for the triplet over singlet transitions, at least when compared to CC3 reference values. Even with this caveat, the MR-EOMPT method compares well with the reference data for both singlet and triplet states.

LiF avoided crossing

In this section, we present how MR-EOMPT fares against the other multireference methods in situations with weakly avoided crossings, such as in the dissociation of the LiF system. In this system, two potential energy surfaces cross at about $d_{\text{LiF}}\approx 13a_0$. Close to its equilibrium geometry, the system can be best described as Li⁺F⁻, i.e. it is an ionic state. As the system is pulled apart, the electrostatic penalty of charge separation continues to grow, thus leading to a lower energy state of neutral Li and F atoms.

Weakly avoided crossings can be difficult to describe. For example, it is well known [83] that state-specific NEVPT2 theories lead to unphysical double crossings for the LiF system when employing a minimal CAS(2,2) reference wave function. In this case, the underlying reference (which is diagonalized before perturbational corrections are considered) is too far off the correct description of the electronic states such that the perturbational description cannot recover the correct behavior. The situation changes when we switch to multistate methods since the final diagonalization, which results in the final states of the system, already includes the perturbational description. In contrast to the previous section, where we compared the MR-EOMPT results to state-specific fic-NEVPT2, we here compare against (strongly contracted) QD-NEVPT2 [80], partly for the known failure of state-specific fic-NEVPT2 to describe the LiF dissociation and further because this system was also extensively discussed in Ref. [80].

The potential energy surfaces for MR-EOMCC, MR-EOMPT, QD-NEVPT2 (in the strongly contracted variant) and the reference, ICE-FCI, are shown in Figure 1. The underlying CAS(2,2) zeroth-order wave function, which included the lithium 2s and fluorine 2p_z orbitals, was shared among all correlation methods such that any difference must come from the correlation treatment. Furthermore, the same basis set was employed throughout, with cc-pVDZ on the lithium atom and aug-cc-pVDZ on the fluorine atom to account for its anionic nature in one of the potential energy surfaces.

Figure 1. Neutral and ionic potential energy surfaces of the two lowest ¹Σ⁺ states of LiF for several computational methods. The ICE-FCI solution can be considered nearly exact, and thus the reference, within the given basis set and settings. The inset is a magnification around the region of the avoided crossing, with a vertical gray line indicating its position for reference.

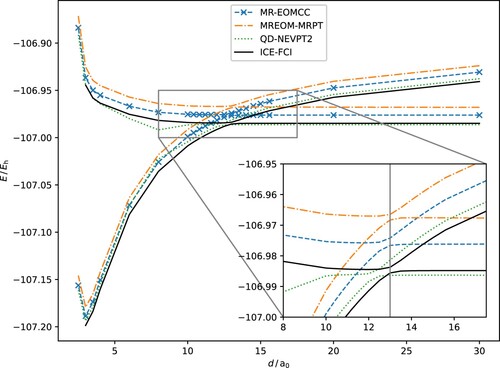
All presented methods accurately predict a single, weakly avoided crossing at about $d_{\text{LiF}}\approx 13a_0$ and correctly predict the shape of the PES, compared to the ICE-FCI reference. From Figure 1, it is obvious that the QD-NEVPT2 results are closest to the ICE-FCI reference in terms of total energy, apart from an artifact at about $d_{\text{LiF}}\approx 8a_0$. This artifact is located where state-specific fic-NEVPT2 would exhibit its first, spurious crossing, thus hinting that the QD-NEVPT2 approach also has difficulties in correcting the deficiencies in the underlying zeroth-order reference wave function. In contrast, MR-EOMCC and MR-EOMPT do not have this issue and are both highly parallel to the reference (Table 5). In fact, out of all methods, MR-EOMCC is most parallel to the ICE-FCI reference, with the non-parallelity error (NPE) [107] being 1.289 mE_h on the neutral state and even better on the ionic state.

Table 5. Non-parallelity errors across the PESs for the neutral and ionic states of ¹Σ⁺ LiF. All values are reported in mE_h.

State	QD-NEVPT2	MR-EOMPT	MR-EOMCC
Ionic	10.618	2.647	0.463
Neutral	10.051	2.213	1.289

A detailed look at the avoided crossing (inset of Figure 1) shows that both MR-EOMCC and MR-EOMPT accurately predict the location of the crossing, whereas QD-NEVPT2 slightly underestimates its location at $d_{\text{LiF}}\approx 12.5a_0$. We further realize that the energy difference between both ¹Σ⁺ states at any given separation $d_{\text{LiF}}$ is overestimated for separations larger than the avoided crossing in the QD-NEVPT2 results and underestimated for smaller separations. A statistical evaluation of the transition energies from the neutral to the ionic state, computed at every point of the PES scan, is shown in Table 6. It is noteworthy that due to fortuitous error cancellation, MR-EOMPT performs even better than MR-EOMCC, which slightly underestimates the transitions. QD-NEVPT2, also partly due to the artifact at $d_{\text{LiF}}\approx 8a_0$, underestimates the transitions and has the largest deviation.

Table 6. Statistical evaluation of the errors in the transition energies from the neutral to the ionic state on the LiF PES. All values are reported in mE_h.

	QD-NEVPT2	MR-EOMPT	MR-EOMCC
Min.	−22.916	−0.364	−2.217
Avg.	−6.285	0.178	−1.264
Max.	−3.152	0.501	−0.548
Std.	4.343	0.160	0.329
RMSD	7.640	0.239	1.306

CH₂ and SiH₂ singlet-triplet splitting

Singlet–Triplet splittings in organic diradicals (carbenes) have been historically challenging to compute [108, 109]. However, with the advent of highly correlated methods using large basis sets, the situation has greatly improved. Nowadays, these systems are also used to assess electronic structure methods, for example in the development of the NEVPT2 method [110].

In the context of benchmarking the MR-EOMPT method, the singlet–triplet splittings reported in this section differ from the results reported previously in this paper in that they are not transitions between different electronic states of a frozen geometry, but rather require computations on two distinct geometries since the ground-state geometries of singlet and triplet carbenes are not identical, especially when it comes to the bond angle on the atom carrying the two unpaired electrons. Generally speaking, singlet carbenes feature significantly smaller bond angles than do triplet carbenes [108]. Hence, the singlet–triplet splittings can be regarded as a test of the quality of the ground-state energy reported by various computational methods.

This test has already been used in Ref. [110] for the NEVPT2 method. In contrast to that publication, we use a larger basis set, def2-SVP, for our computations and use a FCI or ICE-FCI reference for methylene and silylene, respectively. The results are presented in Table 7.

Table 7. Singlet–triplet (¹A₁–³B₁) separation (kcal/mol) for methylene and silylene, computed at the equilibrium geometries from Ref. [110].

Method	CH2	SiH2
FCI*	14.46	−18.18
CASSCF	14.61	−16.51
fic-NEVPT2	15.75	−17.00
MR-EOMPT	15.10	−17.48
MR-EOMCC	14.54	−18.24

*Full CI for methylene, ICE-FCI $(T_{\text{gen}}={10}^{-5})$ for silylene.

We can see from Table 7 that the iterative MR-EOMCC outperforms all other methods, being off by $<0.1$ kcal/mol for both systems. MR-EOMPT betters fic-NEVPT2 on these systems, with errors of about 0.7 and 1.3 kcal/mol, respectively. Nonetheless, it must be emphasized that all these errors are small, being well below 0.05 eV in all cases.

Excited states of the Co and Cr atoms

In the development of the MR-EOMCC method, a benchmark paper on electronic transitions on bare metal atoms and ions has been published to demonstrate the accuracy of several variants of the MR-EOMCC approach [95]. These systems are well suited to illustrate the main benefit of transform-then-diagonalize methods such as the MR-EOM variants, since a small active space followed by a correlation treatment can give access to basically all states with d-d transitions. For the purposes of this publication, we will pick two atoms, cobalt and chromium, and compare the performance of the perturbative variant, MR-EOMPT, and the other methods to the experimental reference values from the NIST atomic spectra database (NIST ASD) [111]. It must, however, be emphasized that different electronic structure programs (ORCA [98, 99] vs. ACES II [112]) were used to compute the MR-EOMCC values. Furthermore, we note that what we denote as ‘MR-EOMCC’ most closely resembles ‘MREOM-T|SXD|U-min’ from Ref. [95], with an additional ${\hat{T}}^{†}$ transformation and the transformed Hamiltonian being symmetrized as discussed in Sec. 2.2.

All calculations in this section were done with Douglas–Kroll–Hess (DKH) scalar relativistic treatment [113, 114] and the def2-TZVPP basis set [102] with the exponents recontracted for the DKH procedure. Furthermore, the active space consisted of the 4s and 3d orbitals, with reference states being chosen such that the average occupation of the 4s orbital is 1.5, as described in Ref. [95]. In contrast to Ref. [95], we do not align the average energies of the calculated and experimental states prior to comparing the transition energies, but rather simply zero-align the lowest computed or experimental state and then compute the transition energies with respect to that state. We do, nonetheless, use the same J-averaging procedure to obtain a single energy for the non-degenerate sublevels of the experimental L-S multiplets [95], (24) $E_{LS}=\frac{{\sum }_J(2J+1)E_J}{{\sum }_J(2J+1)}.$(24) For both systems in this section, the setup of the CASSCF and NEVPT2 calculations differs from the general procedure described in Sec. 3. The other CASSCF and NEVPT2 calculations in this paper generally include all desired roots in the SA-CASSCF calculation (possibly split into different multiplicity and irrep blocks), which would lead to detrimental results as we would average over tens of states at the same time. Hence, we effectively report CASCI results, and NEVPT2 values computed on top of that, with the input orbitals from the MR-EOMPT and -CC reference states described below.

The transition energies for a neutral cobalt atom with a CASSCF reference of equal weights of the two lowest-lying ⁴F (4s¹3d⁸) and ⁴F (4s²3d⁷) states are summarized in Table 8. In the Co atom results, the ²D (4s²) state was possibly not well described by the either the MR-EOMCC or the MR-EOMPT method, as indicated by reference weights of 89% and 82%, respectively [88]. Consequently, this state is removed from the final statistical evaluation of the errors in the transition energies with respect to the experimental reference values. For consistency, it is also not included in the evaluation of the CASCI and NEVPT2 methods. However, we note that including the state in the statistical evaluation would have improved the accuracy of the methods.

Table 8. Transition energies (eV) between different states on neutral cobalt. Red values indicate unreliable results by a too low reference contribution. The errors were computed with respect to the NIST reference data [111], save for the unreliable ${}^4\text{F}(4s^2)\to {}^2\text{P}(4s^2)$ transition.

					MR-EOM
Config.	Term	NIST	CASSCF	NEVPT2	-PT	-CC
4s^2	^4F	0.00	0.00	0.00	0.00	0.00
4s^1	^4F	0.42	1.78	0.38	0.47	0.28
4s^1	^2F	0.88	2.43	0.88	0.46	0.71
4s^2	^4P	1.63	2.16	1.76	1.52	1.73
4s^1	^4P	1.83	3.94	1.86	2.22	1.77
4s^2	^2G	1.99	2.16	2.08	2.40	2.14
4s^1	^2D	1.97	3.11	1.94	1.60	1.88
4s^1	^2P	2.20	2.86	2.28	1.94	2.13
4s^2	^2P	2.47	4.62	2.48	3.06	2.62
4s^2	^2H	2.64	2.88	2.74	3.21	2.76
4s^2	^2D	2.68	3.79	2.84	2.55	2.83
4s^1	^2G	2.78	4.78	2.63	2.63	2.70
Statistical Evaluation of Errors
Min.			0.17	−0.15	−0.42	−0.17
Avg.			1.19	0.02	0.07	−0.01
Max.			2.14	0.13	0.59	0.15
Std.			0.72	0.08	0.37	0.12
MAE			1.19	0.07	0.33	0.11
RMSD			1.39	0.08	0.38	0.12

On the Co atom and with this particular CASSCF reference, fic-NEVPT2 and MR-EOMCC perform the best, with errors always below 0.17 eV for all transitions. The performance of the MR-EOMPT method is reasonable and certainly much better than the CASCI results, but nonetheless a bit disappointing with errors as large as 0.59 eV on the ${}^4\text{F}(4s^2)\to {}^2\text{P}(4s^2)$ transition. We suspect that the reason for this behavior lies in the fact that the CASSCF reference mixes the 4s and 3d orbitals among themselves in a detrimental way that cannot be corrected for as in the iterative MR-EOMCC method.

On a different note, we found that the current implementation of MR-EOMPT results in a slight degeneracy breaking of the L-S states of up to 3 meV, despite the SA-CASSCF reference being averaged over complete multiplets. However, due to the s-d mixing described above, the active orbitals differ in their energies depending on how much s-character they possess. Such a degeneracy breaking is not observed for the MR-EOMCC results.

Our second system is a neutral chromium atom with a CASSCF reference including equal root weights for the ${}^7\text{S}(4s^{1}3d^5)$, ${}^5\text{S}(4s^{1}3d^5)$ and ${}^5\text{D}(4s^{2}3d^4)$ states [95]. The individual transition energies are reported in Table 9, including the statistical evaluation of the errors with respect to the experimental reference values.

Table 9. Transition energies (eV) between different states on neutral chromium. The errors were computed with respect to the NIST reference data [111].

					MR-EOM
Config.	Term	NIST	CASSCF	NEVPT2	-PT	-CC
4s^1	^7S	0.00	0.00	0.00	0.00	0.00
4s^1	^5S	0.94	1.28	1.07	1.06	0.92
4s^2	^5D	1.00	1.10	1.15	1.20	1.05
4s^1	^5G	2.54	3.57	2.63	2.52	2.50
4s^1	^5P	2.71	4.09	2.94	2.81	2.81
4s^2	^3P	2.95	3.54	3.40	3.15	3.03
4s^2	^3H	2.99	3.31	3.27	3.09	2.95
4s^1	^5D	3.01	4.41	3.11	3.05	3.01
4s^1	^3G	3.09	4.47	3.42	3.13	3.03
4s^2	^3F	3.11	3.63	3.49	3.29	3.15
4s^1	^3P	3.37	4.95	3.66	3.56	3.47
4s^2	^3G	3.44	3.86	3.60	3.59	3.42
4s^1	^3D	3.55	5.30	3.91	3.63	3.52
4s^1	^3D	3.85	5.90	4.32	3.93	3.86
4s^1	^3I	3.85	5.21	3.94	3.75	3.73
4s^1	^5F	3.89	5.87	4.07	4.06	4.02
4s^2	^1G	3.97	4.57	4.31	3.99	3.87
4s^2	^1I	3.98	4.42	4.30	3.99	3.87
Statistical Evaluation of Errors
Min.			0.09	0.09	−0.10	−0.12
Avg.			1.01	0.25	0.09	0.00
Max.			2.06	0.47	0.20	0.13
Std.			0.61	0.12	0.08	0.07
MAE			1.01	0.25	0.11	0.06
RMSD			1.19	0.28	0.12	0.07

From the reported errors, MR-EOMCC outperforms all other methods on this system with an RMSD of 0.07 eV over 18 states (118 roots), as expected from Ref. [95]. In contrast to the Co atom system from above, MR-EOMPT does not perform much worse at an RMSD of 0.12 eV with respect to the NIST values. In fact, the roles are reversed with fic-NEVPT2, which has deviations of up to 0.47 eV on the $X{}^7\text{S}(4s^1)\to {}^3\text{D}(4s^1)$ transition. In combination with Ref. [95], we may again conclude that MR-EOMCC performs accurately on these systems, and that the MR-EOMPT method is less robust in terms of consistency, but still gives the expected accuracy of well-established perturbational approaches on these systems.

Comparison to LR-ic-MRCC

To show the differences between the approaches discussed in this paper and linear response methods, we now compare some results against the linear response internally contracted multireference coupled-cluster (LR-ic-MRCC) method developed in the group of Köhn and co-workers [45]. However, we must emphasize that the LR-ic-MRCC method is expected to yield results that are of superior accuracy to the perturbative MR-EOMPT method. A more fitting comparison would be against the MR-EOMCC results, which are also iterative in nature. Still, it is illuminating to understand in which situations either of the methods may be more applicable.

Response theory describes how a wave function behaves under an external, periodic influence, e.g. electromagnetic radiation using a series expansion in terms of response functions. From the response functions, the energies of the excited states can be determined as they correspond to poles of the response function. As such, the excited states and transition energies are not limited to lie within an active space, but rather require a satisfactory description of the ground-state wave function. It is also sufficient to consider only the linear response function if only excitation energies and transition moments between ground and excited states are desired. A more detailed exposition can be found in Refs. [8, 115], of which Ref. [8] also details the relation to EOM methods in the single-reference case.

Response theory is therefore in stark contrast to the other methods discussed in this paper, including the MR-EOMPT method. As discussed in Sec. 2.4, these methods require that all states of interest lie within the CASCI space spanned by the active electrons and orbitals. For example, given a full-valence active space, it is not possible to describe a valence-to-Rydberg transition, as the leading configurations of the final state would certainly lie outside the CASCI space. Hence, to compare to the LR-ic-MRCC results, we generally need to choose larger active spaces than the minimal spaces in the published reference [45].

We first present the singlet states of the methylene system. A full description of this test system has already been given in Refs. [45, 116]. Naturally, we use the same geometry and basis set in our calculations (see supplementary information). We must, however, remark that the reported [116] FCI transition energies $1{}^1{\text{A}}_1\to 2{}^1{\text{A}}_2$ and $1{}^1{\text{A}}_1\to 3{}^1{\text{B}}_1$ appear to be in error. While our own FCI calculation perfectly matched the other reported transition energies, these two transitions are in error of −0.627 eV and −0.104 eV, respectively. Using our corrected values also improves the statistics [45] of the LR-ic-MRCC method for this test system (Table 10).

Table 10. Transition energies (eV) between different states on singlet methylene, all with respect to the ground state 1 ¹A₁. Transitions may be either singles- or doubles-dominated, denoted s and d, respectively. We provide two reference values: the FCI results from Ref. [116], and our own FCI results. The LR-ic-MRCCSD values were sourced from Ref. [45] and use $N_{com}=2$, $\eta ={10}^{-5}$ and a CAS(6,6). For the statistical evaluation of the errors, our own FCI results were chosen as the reference.

						MR-EOM
Exc. State	Type	FCI (Pub.)	FCI	CASSCF	NEVPT2	-PT	-CC	LR-ic-MRCCSD
2 ^1A1	d	4.656	4.655	4.614	4.693	4.629	4.679	4.721
3 ^1A1	s	6.514	6.514	6.398	6.500	6.498	6.645	6.449
1 ^1B1	s	1.793	1.794	2.500	1.939	1.729	1.778	1.803
2 ^1B1	d	8.906	8.907	8.861	8.995	8.924	9.108	9.332
1 ^1B2	s	7.704	7.703	7.232	7.681	7.685	7.790	7.647
2 ^1B2	d	8.016	8.016	8.259	8.086	7.972	8.052	8.136
1 ^1A2	s	5.853	5.853	6.032	5.980	5.821	5.885	5.870
2 ^1A2	d	9.410^†	10.036	9.714	10.009	10.073	10.235	10.063
Statistical Evaluation of Errors
Min.				−0.471	−0.027	−0.064	−0.015	−0.065
Avg.				0.016	0.050	−0.019	0.087	0.068
Max.				0.707	0.146	0.037	0.201	0.425
Std.				0.341	0.064	0.030	0.077	0.146
MAE				0.266	0.067	0.032	0.090	0.098
RMSD				0.342	0.081	0.035	0.116	0.161

^† This appears to be an error in the original reference [116].

For our calculations (Table 10), we need to choose a larger active space than the minimal CAS(2,2) that may be used with the LR-ic-MRCC method (vide supra). For such a small system, a full valence active space is in order, which gives six active electrons in six active orbitals: all four carbon atomic orbitals from the second shell as well as two hydrogen 1s orbitals. The previous study [45] also reports calculations with a CAS(6,6) active space, including states outside of the CASCI space. We were forced to omit the $1{}^1{\text{A}}_1\to 3{}^1{\text{B}}_1$ and $1{}^1{\text{A}}_1\to 4{}^1{\text{A}}_1$ transitions in Table 10 since the leading configurations of the excited states lie outside of the CASCI space, and hence cannot be treated by our present methods. Otherwise, for the CASSCF and fic-NEVPT2 results, each of the four irreps of the C_2v point group were computed in a separate calculation, whereas in the MR-EOMCC and MR-EOMPT calculations, all singlet roots were obtained in a single run. The SA-CASSCF reference for the latter two methods consisted of the lowest seven singlet roots with equal weights, regardless of the irrep. This reference was necessary since otherwise the model space was not decoupled sufficiently from the outside space and nearly singular $\hat{T}$ amplitudes led to convergence difficulties.

All methods save for the CASSCF calculations show good accuracy and, somewhat surprisingly, the perturbative approaches perform best in this benchmark. In the case of the fic-NEVPT2 results, this has been aided by the fact that each irrep block was treated separately, as opposed to the MR-EOMCC and MR-EOMPT calculations, where all roots are obtained in one calculation from a single reference. Otherwise, we assume that fortuitous error cancellation is at work, especially since in the other benchmark sets discussed in this paper, non-perturbative methods generally show better performance.

All methods tend to overestimate transition energies, except MR-EOMPT, which underestimates them by −0.019 eV, on average. When comparing the iterative coupled-cluster methods, MR-EOMCC and LR-ic-MRCC, we find that the linear response theory is on average closer to the FCI results, but the larger standard deviation also leads to a higher overall RMSD. This is largely due to the $1{}^1{\text{A}}_1\to 2{}^1{\text{B}}_1$ transition, a high-lying doubles-dominated transition, which is in error of 0.423 eV compared to the FCI reference. Had this transition been left out of the evaluation, then the MR-EOMCC and LR-ic-MRCC results would have been of comparable accuracy. We further emphasize that, in contrast to single-reference CC theory [8], there is no simple relation between the multireference EOMCC and LR-CC theories.

We now present some additional calculations for the all-(E)-hexatriene molecule. The active space was chosen to be a CAS(6,6) of the π-system orbitals (three each of a_u and b_g symmetry). We focus on only two singlet transitions, which have already been discussed in Thiel’s benchmark set [65] and in the context of the LR-ic-MRCC method [45]. The transitions are the $1{}^1{\text{A}}_g\to 2{}^1{\text{A}}_g$ transition to the optically ‘dark’ state and the $1{}^1{\text{A}}_g\to 1{}^1{\text{B}}_u$ transition to the ‘bright’ state.

Although MR-EOMCC calculations have already been published for hexatriene, compared to the results reported in this paper, the calculation from Ref. [4] uses a different MR-EOMCC implementation that not only differs in the definitions of the cluster operators, but also uses a larger diagonalization space. Huntington et al. [88] have reported values for these transitions with a more similar implementation (vide supra), but again chose a different CASSCF reference with only five active orbitals and reference states of ³A_g and ³B_u symmetry. This choice was motivated by the fact that convergence with the MR-EOMCC method was problematic due to nearly singular amplitudes when exciting out of the 3-b_g orbital. Nonetheless, projecting out the offending amplitudes and choosing a reference of a single ³B_u state resulted in successful convergence of the many-body residual conditions. The same reference state was also chosen for the MR-EOMPT calculation.

Our results and the cited reference values are summarized in Table 11. Unfortunately, choosing the CC3 results [65] to be our reference values is not so simple since the $1{}^1{\text{A}}_g\to 2{}^1{\text{A}}_g$ is to a great extent a double excitation, $1a_u^{2}1b_g^{2}2a_u^2\to 1a_u^{2}1b_g^{2}2b_g^2$, which is also evidenced by the rather low %T₁ of 65.8%. When comparing the MR-EOMPT results to the MR-EOMCC and LR-ic-MRCC results, we find that the order of the excited states is the same, with the 2 ¹A_g state having lower total energy than the 1 ¹B_u state. This contrasts with CC3 results, in which the ordering of the states is the reverse. Furthermore, the MR-EOMPT method yields higher transition energies than both MR-EOMCC and LR-ic-MRCC. If we compare the transition energies of the singles-dominated $1{}^1{\text{A}}_g\to 1{}^1{\text{B}}_u$ transition to the CC3 values, we find that the MR-EOMPT method is in error of 0.55 eV, compared to only 0.22 and 0.08 eV for the MR-EOMCC and LR-ic-MRCC results, respectively. It does, however, outperform the fic-NEVPT2 result on this transition, which has an error of 1.19 eV.

Table 11. Bright and dark states of all-(E)-hexatriene (eV). The LR-ic-MRCC values were obtained from Ref. [45], and the CC3 values from Ref. [65].

Transition	CAS	NEVPT2	MR-EOMPT	MR-EOMCC	LR-ic-MRCC	CC3
$1{}^1{\text{A}}_g\to 2{}^1{\text{A}}_g$	5.45	5.59	5.52	5.43	5.44	5.72
$1{}^1{\text{A}}_g\to 1{}^1{\text{B}}_u$	6.59	6.77	6.13	5.80	5.66	5.58

Conclusion

In this paper, we presented a new multireference perturbation theory, called MR-EOMPT, which is based on the MR-EOMCC method. The approach is best classified as a ‘transform-then-diagonalize’ method in complete analogy to MR-EOMCC since the general theoretical structure is the same, except for the fact that perturbatively estimated amplitudes are used for the sequential similarity transformations. MR-EOMPT also shares the multistate character (which is closely related to their many-body aspect) with its parent method, and only requires a minimal MRCI diagonalization space due to the decoupling of the model CASCI space from the external space through the similarity transformations. Furthermore, MR-EOMPT and -CC only require one- and two-body RDMs of the CAS reference states, in stark contrast to other multireference perturbation theories, which formally require up to four-body RDMs. Our main goal was to show that using perturbative amplitudes in the MR-EOMPT method decreases computational cost while retaining at least the accuracy of other popular perturbational methods. Moreover, since the MR-EOMPT method foregoes the many-body residual equations, there are no convergence difficulties as in the MR-EOMCC method for nearly singular amplitudes.

The benchmarks presented mainly focus on vertical transition energies as calculating these is the major application of EOM methods in which the excited states can all be obtained from a single state-universal calculation. The first test set of small diatomic molecules in a double-ζ basis set shows that the MR-EOMPT method performs on par with fic-NEVPT2 at an RMSD of 0.07 eV over a set of 25 transition energies. This test set of small molecules with FCI-quality reference data is complemented by a subset from Thiel and co-workers’ benchmark [65] with larger molecules in a triple-ζ basis set. Compared to the published [65] CC3 reference values with a singles contribution of %T₁ > 90%, we found that the triplet transitions were treated more accurately than the transitions to singlet final states. For the triplet transitions, the RMSD across 12 transitions is 0.11 eV, about half of what was found for state-specific fic-NEVPT2 with an RMSD of 0.19 eV. The situation is the opposite for the singlets, where the RMSD across 11 transitions is 0.43 eV, about twice as much as for fic-NEVPT at 0.20 eV. The MR-EOMCC results with the same parent state are much more robust at an RMSD of only 0.18 eV for the singlet transitions, but still higher than for the triplet transitions (0.07 eV). For the MR-EOMCC results, this has already been found to be due to the ${\hat{T}}^{†}$ transformation in ORCA [88]. We should note that in the subset of Thiel’s benchmark, the fic-NEVPT2 calculations use orbitals optimized for each multiplicity and irrep, whereas the MREOM methods only use a single reference state.

The lithium fluoride PES scan was included to demonstrate the ability of the MR-EOMPT method to accurately reproduce weakly avoided crossings, which is straightforward with transform-then-diagonalize approaches as only the final step gives the states as combinations of the model space functions. When comparing the results to QD-NEVPT2, we found that the PES computed by the MR-EOMPT method is much more parallel to the FCI-quality reference without any artifacts located in the region of the avoided crossing. The MR-EOMPT method also performs better when it comes to the vertical transition energies between the neutral and ionic states of LiF at each point of the PES, with the results being effectively identical to the ICE-FCI reference data.

To assess the accuracy of ground-state energy calculation, we chose to compute the singlet–triplet gaps on methylene and silylene. Despite not being the focus of EOM-like methods, the ground state calculations on the singlet and triplet geometries demonstrate that the singlet–triplet gap is reproduced accurately to within 0.7 kcal/mol, an error comparable to that of the fic-NEVPT2 method at 1.3 kcal/mol. This finding is also supported by the quality of the total energies for the diatomic test systems, where the MR-EOMPT method reproduces the FCI-quality total energies better than fic-NEVPT2.

A paramount example of the MREOM methods are transition energies on transition metals, since most of the d-d transitions can be described from a single parent state in a reasonably small CAS(n,5) calculation. We computed a total of 190 state energies on the cobalt and chromium atom combined and found again that the perturbative approach is not as robust as the fully iterative MR-EOMCC at RMSDs of 0.38 and 0.12 eV versus 0.12 and 0.07 eV, respectively. The performance is, nonetheless, similar to that of fic-NEVPT2 on the transition metals. Also, since we used the same orbitals in these fic-NEVPT2 and MR-EOMPT calculations, the setup of the Co and Cr calculations was more similar than the setup of the Thiel benchmark calculations, where CASSCF and NEVPT2 used optimized orbitals for each multiplicity and irrep block.

Furthermore, we included a comparison against the LR-ic-MRCC method [45]. Linear response methods have the advantage that the states of interest need not lie in the CASCI space, which in turn allows smaller active spaces that only capture the necessary amount of static electron correlation. The MR-EOMPT method, as well as fic-NEVPT2, cannot treat states outside of the CASCI space. Hence, a larger active space is required to compare against the LR-ic-MRCC results on higher-lying singlet roots of methylene and hexatriene [45]. We found that the MR-EOMPT method outperforms even the MR-EOMCC method on the methylene singlet roots, which is attributed to fortuitous error cancellation since normally the MR-EOMCC method is more accurate. Conversely, on hexatriene, the iterative MR-EOMCC results are superior to the perturbative results, with MR-EOMPT and NEVPT2 performing similarly.

Overall, we have demonstrated that the accuracy of the MR-EOMPT approach is comparable to established multireference perturbation theories such as state-specific fic-NEVPT2. When benchmarked against its parent method, MR-EOMCC, we found that, despite sometimes even outperforming it, the MR-EOMPT method is less robust, i.e. less precisely reproduces the reference values. This comes at the benefit of lower computational cost and avoided convergence difficulties. The new method is especially useful in situations where dynamic electron correlation significantly mixes the model space functions among themselves, as showcased in the PES of the LiF system. We therefore recommend this new approach in these situations as well as for systems where the high accuracy of the MR-EOMCC method is not strictly required, but perturbational results of NEVPT2-like quality are sufficient.

Dedication: This paper is dedicated to the celebration of the 60^th birthday of Prof. John Stanton in recognition of his outstanding contributions to quantum chemistry and molecular spectroscopy.

Acknowledgments

Three of the authors (M.H.L., R.I., and F.N.) thank the Max Planck Society for financial support. M.H.L. gratefully acknowledges funding by the Fonds der Chemischen Industrie as well as by the Studienstiftung des deutschen Volkes. M.N. acknowledges funding through a discovery grant from NSERC (Natural Sciences and Engineering Research Council of Canada).

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

Funded by the Max Planck Society, the Fonds der Chemischen Industrie, the Studienstiftung des deutschen Volkes as well as through a discovery grant from NSERC (Natural Sciences and Engineering Research Council of Canada).