Predissociation spectroscopy of cold CN⁻H₂ and CN⁻D₂

Abstract

The vibrational predissociation spectra of the CN^–H₂ and CN^–D₂ complexes are measured in regions between 450 and 3100 cm${}^{-1}$ in an ion trap at different temperatures at the free electron lasers for infrared experiments (FELIX) Laboratory. Strong differences between the vibrational spectra of the two para and ortho nuclear spin isomers (CN^–(p-H₂) or CN^–(o-H₂) and CN^–(p-D₂) or CN^–(o-D₂)) are detected. In the case of CN^–H₂ we could assign the observed bands with the help of an accurate quantum calculation. The spectrum is dominated by the first overtone of the hindered H₂ rotation in combination with the hindered CN rotation of the CN^–(o-H₂) nuclear spin isomer. The energetically higher-lying CN^–(p-H₂) isomer was not observed due to efficient ortho-para ligand exchange. The C–N stretching mode was recorded at 2040(1) cm${}^{-1}$. For the CN^–D₂ system several vibrational modes of both spin isomers overlap in their low-lying intermonomer streching and bending region, but the main observed bands are attributed to the more stable CN^–(p-D₂) spin isomer. The D–D stretching vibration was found to be at 2898(1) cm${}^{-1}$.

GRAPHICAL ABSTRACT

Keywords:

• Molecular ions
• cryogenic ion trap
• vibrational spectra
• predissociation
• noncovalent interactions

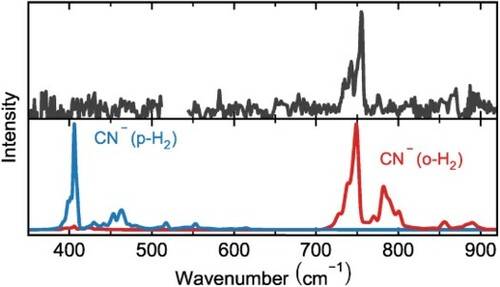
1. Introduction

Spectroscopic studies of weakly bound molecular complexes provide detailed information on their structure and intermolecular forces [1–3]. Ionic complexes play an important role in the chemistry of planetary atmospheres, including that of the Earth [4,5], plasmas [6], and have been discussed to exist in the interstellar medium (ISM) [7]. Vibrational spectroscopy of anion-neutral complexes allows for their structural characterisation and thus serves as a direct benchmark method to test ab initio potential energy surfaces (PESs) governing anion-neutral reactions and collisional excitation processes, e.g. of a molecular anion by H₂, the dominant collision partner in the ISM.

The CN^– molecular anion is the dominant negative ion observed in Titan's atmosphere [8,9], and one of the few anions so far identified in interstellar space, in a circumstellar shell around a late-type star [10]. The latter astronomical detection was based on high-resolution rotational spectroscopic data [11,12] and was later supported by calculations of the rate coefficients for the rotational excitation of CN^– by ortho and para H₂ based on a four-dimensional PES of the CN^–H₂ collisional system [13]. More recent work provides additional ro-vibrational collisional rates of CN^– with para H₂ [14].

To the best of our knowledge, there exist no theoretical or experimental data of the vibrational spectra of the CN^–H₂ and CN^–D₂ complexes, and only limited vibrational spectroscopic data exits for the bare CN^– ion. Forney et al. [15] assigned a vibrational band at 2053.1 cm${}^{-1}$ measured in a Ne-matrix to its fundamental CN^–stretching mode based on earlier ab initio calculations [16]. The only gas-phase data for this mode stems from photoelectron spectroscopic studies and provides a slightly lower value of 2035(40) cm${}^{-1}$ [17].

Infrared predissociation (IRPD) spectroscopy employing cryogenic multipole radio-frequency ion traps combined with buffer-gas cooling has emerged as a powerful action spectroscopic method to investigate weakly-bound ionic complexes experimentally [18–24]. Using this technique in combination with state-of-the-art calculations [25–27] we have recently shown that in the tri-atomic system Cl^–H₂ the linear complexes of Cl^–(o-H₂) and Cl^–(p-H₂) are energetically nearly degenerate in the vibrational ground state, but that the second overtones of their respective bending modes show an energy difference of about 260 cm${}^{-1}$ caused by the tunnelling splitting between the geometric structures of the hindered H₂ rotation along the bending coordinate.

In this work, we extend our study to the four-atomic CN^–H₂ and CN^–D₂ complexes. These systems have a linear structure and an electronic closed-shell ground state. Again, strong differences between the vibrational spectra of the para and ortho nuclear spin isomers are expected. The theoretical treatment of this system is more complex, due to the fact that the two nuclear spin isomers of the hydrogen molecule can attach to either the carbon or the nitrogen atom. This leads to formation of two nuclear spin isomers (CN^–(p-H₂) or CN^–(o-H₂) and CN^–(p-D₂) or CN^–(o-D₂)) and two stable conformers (CN^–H₂ or H₂CN^– and CN^–D₂ or D₂CN^–). We present and discuss vibrational predissociation spectra of CN^–H₂ and CN^–D₂ in the regions of their low-lying intermonomer stretching and bending modes, and their CN and D₂ stretching modes.

2. Methods

2.1. Experimental details

Experiments were performed at the FELion cryogenic ion trap beamline at the Free Electron Lasers for Infrared eXperiments (FELIX) Laboratory.¹ The FELion instrument and its use for vibrational spectroscopic studies employing infrared-predissociation (IRPD) action spectroscopy of rare-gas tagged molecular ions has been described in detail previously [22]. Here we only report the specific details related to the current investigation of the CN^–H₂ and CN^–D₂ systems.

CN^– anions were produced by dissociative electron attachment to acetonitrile CH₃CN (Sigma Aldrich, $>99.9$%) in a Gerlich-type storage ion source [28] using electrons with energies of 100 eV. Ions with $\mathrm{m}/\mathrm{z}=26$ were mass-selected in a quadrupole mass-filter and guided to the cryogenic 22-pole ion trap [29] held at a fixed temperature in the range of 8–40 K. At the beginning of the storage cycle a mixture of helium and hydrogen (or deuterium) with a mixing ratio H₂:He of 1:1 (D₂:He = 1:9 and 1:1) was pulsed into the trap for 100 ms leading to cooling of the ions and the formation of CN^–H₂ (or CN^–D₂) complexes. For the experiments described here normal H₂ and D₂ was used without para or ortho enrichment. The complexes were stored for 1.5–3.6 s in the trap where they were exposed to infrared radiation of the free-electron laser FEL-2 that delivers pulse energies in the interaction region varying from 20–35 mJ at 10 Hz repetition rate with a macropulse duration of $\sim 10\mu$s. The laser was scanned in regions between 250 and 3250 cm${}^{-1}$, and the depletion of the number of complex ions due to single-photon infrared predissociation (IRPD) was recorded as a function of the frequency. The FEL-2 was optimised for narrow bandwidth, reaching typical rms widths of about 0.2–0.4% of the centre value, [22] or about a FWHM of 4 cm${}^{-1}$ for the 350–850 cm${}^{-1}$ range and about 20 cm${}^{-1}$ for the 2000–3100 cm${}^{-1}$ range in the present experiment. To account for varying laser pulse energy E, pulse number n, baseline drifts due to varying source conditions and for saturation effects, the signal is normalised prior to averaging using $I=-\frac{ln(S/B)}{n\cdot E}$, with S the number of complexes as a function of laser frequency and B the number of baseline complexes. The trap temperature was varied (10, 17 or 40 K) to study the temperature dependence of the spectral bands. We assumed the complexes to be in their vibrational ground state.

2.2. Computational details

The predissociation spectra of the CN^–H₂ and CN^–D₂complexes were calculated using an accurate quantum approach, similar to that described in Lara-Moreno et al. [26], and using an existing four-dimensional potential energy surface [13] obtained by the following procedure. The H${}_2$ bond length was set to the value 1.44876 $a_0$ which is the vibrationally averaged internuclear distance in the ground vibrational state. With the latter H${}_2$ bond length, a 5D PES was computed [13] and then averaged with the ground vibrational state of the CN${}^{-}$ diatomic, finally providing a 4D PES. The basis set superposition error was corrected with the counterpoise procedure [13]. Briefly, the ro-vibrational energy levels are obtained by variationally solving the space-fixed rigid-monomer Schrödinger equation where the ro-vibrational wavefunctions are expanded over a product of a radial Discrete Variable Representation and symmetry-adapted angular functions [26]. Additionally, a complex absorbing potential was added to obtain the resonances [26]. This quantum approach allows then to calculate the inter-monomer vibrational motions, i.e. the low frequency motions, and the rotational motion. This is not an adiabatic approximation, but rather a reduced dimensionality approximation since the intra-monomer motions, i.e. the high frequency motions, are ignored.

Each of the linear complexes exists in a para and ortho nuclear spin isomeric form, corresponding to the symmetric and antisymmetric vibrational wave functions under permutation of the two identical nuclei (H or D). Let us recall that para and ortho forms of free H${}_2$ have respectively symmetric and antisymmetric wave functions under the nuclear permutation operator. Therefore the symmetric and antisymmetric vibrational wave functions of the CN^–H₂ complex correlate respectively with the dissociation products p–H${}_2$ and o–H${}_2$. According to their permutation parity, the vibrational wave functions are then assigned to the CN^–(p-H₂) or CN^–(o-H₂) species.

Each of these structures exhibits seven normal modes of vibration, the doubly degenerate hindered CN $({\nu }_1)$ and H₂ (D₂) $({\nu }_2)$ rotations/bendings, the intermonomer stretching $({\nu }_3)$, the CN $({\nu }_4)$ stretching, and the H₂ (D₂) stretching $({\nu }_5)$. In the following we will use the notation $({\nu }_1^{l_1},{\nu }_2^{l_2},{\nu }_3)$ to denote the low frequency bending and stretching modes, where $l_i$, $(i=1,2)$ is the quantum number associated with the projection of the vibrational angular momentum on the molecular axis. This notation implies ${\nu }_4={\nu }_5=0$. We computed the binding energies of the two geometric isomers CN^–H₂ and (H₂)CN^– using the same level of theory.

Besides the quantum calculations of the low frequency motions described above, we have also performed approximate quantum calculations of the high frequency motions, i.e. the monomers' stretching motions. The PES used for the accurate quantum approach calculations is based on a rigid-monomer approach for the CN^– and H₂ (D₂) diatomic subunits (monomers) and thus no information on the stretching modes of the diatoms $({\nu }_4,{\nu }_5)$ can be obtained. So far no 6D PES is available to calculate the higher energy stretching bands. As a consequence an approximate approach was used to calculate the CN^– and H₂ (D₂) stretching vibrational bands of the complexes. The 1D potential energy of the CN^– or H₂ monomers is calculated at the CCSD(T)-F12b/AV5Z level of theory using the MOLPRO program suite [30,31] for a set of values of the bond length of one monomer while other coordinates are kept constant at their equilibrium values. This means that we compute a 1D cut through the 6D PES. Then a 1D accurate discrete variable representation [32] is used to compute the fundamental frequencies of the monomers. This approach neglects most of the coupling between the vibrational motion of a monomer (CN^– or H₂, D₂) and all other modes of motion of the CN^–H₂ system.

3. Results and discussions

3.1. CN${}^{-}$H${}_2$

Our theoretical CCSD(T)-F12b/AV5Z results show that the CN^–H₂ conformer is the lower energy form of the complex, being 128 cm${}^{-1}$ more stable than the (H₂)CN^– conformer, in agreement with the calculated well-depth difference of 124 cm${}^{-1}$ on the PES [13]. In addition, substantial barriers of 222 and 94 cm${}^{-1}$ exist for the interconversion from CN^–(H₂) to (H₂)CN^– and vice versa. In the following discussion we thus focus on the lower-lying CN^–H₂ conformer, since the (H₂)CN^– conformer will only be formed in negligible amounts at the cold temperatures in the cryogenic ion trap. We would like to note here that while in the CN^–H₂ (and CN^–D₂) system the H₂ (D₂) prefers to bind to the N-site, the C-site shows a larger binding energy for longer chains of the form C${}_n$N${}^{-}$ [33–35].

In addition, the rigid-monomer accurate quantum calculations provide a dissociation energy $D_0$ of 336.7 and 442.3 cm${}^{-1}$ for CN^–(p-H₂) and CN^–(o-H₂), respectively. The energy difference $\mathrm{\Delta }E=105.6$ cm${}^{-1}$ is a combination of the ground state energy difference of the two spin isomers (12.8 cm${}^{-1}$) and the j = 1 rotational energy of o-H₂ (118.4 cm${}^{-1}$, [36]), the dissociation product of CN^–(o-H₂). The CN^–(o-H₂) is thus the more strongly bound nuclear spin isomer and thus the dominant nuclear spin isomer formed at the low temperatures used in the experiments.

The single photon infrared predissociation spectrum of CN^–H₂ is shown in the top panel of Figure 1, and compared to calculated values. The calculated ro-vibrational spectra (bottom panel) were convolved with a line width corresponding to the FEL-2 FWHM ($\sim 0.7$% of the respective frequency, middle panel).

Figure 1. Top panels: Experimental vibrational infrared predissociation spectra of CN^–H₂ recorded at 17 (a) and 8 K (c). The orange dotted line shows a Gaussian line-profile fit to the band at 2040(1) cm${}^{-1}$. Bottom panels: Theoretical predissociation spectra of CN^–H₂ simulated for 17 K using an accurate quantum approach shown as ro-vibrational stick spectra and convolved with the laser linewidth (0.7%) for better comparison (b). The dissociation energy $D_0$(o) of CN^–(o-H₂) is given by the dashed vertical line at 429.5 cm${}^{-1}$, whereas  the dissociation energy $D_0$(p) of CN^–(p-H₂) at 336.7 cm${}^{-1}$ is out of the plotted range. The calculated ortho and para transition intensities are scaled differently for better visibility. The calculated position of the C-N stretch fundamental at the CCSD(T)-F12b/AV5Z level of theory is shown in (d). The bare CN^– fundamental is shown as red vertical line [37].

The top right panel shows the IRPD spectrum (recorded at 8 K) of the CN stretching mode experimentally observed at 2040(1) cm${}^{-1}$, which is in close agreement with a theoretical fundamental frequency of 2045 cm${}^{-1}$, calculated at the CCSD(T)-F12b/AV5Z level of theory for the CN^–H₂ complex. A small shift is expected since we are dealing with a van der Waals system and negleting a part of the intermonomer couplings in the calculation for this band. The close agreement indicates that indeed the intramonomer motions are only weakly coupled to the intermonomer motions. This small influence on the stretching vibrations is also evident when we compare the experimental CN^– stretching mode of the complex (2040(1) cm${}^{-1}$) with that of the bare ion, measured previously by photoelectron spectroscopy at 2035(40) cm${}^{-1}$ , and to a recent high-level ab initio value of 2042(3) cm${}^{-1}$ [37]. The small influence of the tag on the CN stretching frequency is also in agreement with former studies on larger C${}_n$N${}^{-}$ systems, where D₂ was used as a tagging agent [34]. In this sense, the experimental data on the CN stretching mode of CN^–H₂ presented here can essentially be viewed as infrared predissociation data, where H₂ acts as a rather innocent spectator.

In the left panels we show the experimental and calculated spectra in the far-IR region between 350 and 850 cm${}^{-1}$. In the upper left panel the experimental spectrum at 17 K is shown, with maxima found at 735(1), 743(1), 755(1), 776(1), and 870(1) cm${}^{-1}$. Comparison with the calculated predissociation spectrum assuming an ion temperature of 17 K (lower left panel of Figure 1) shows that the experimental bands agree well with the calculated bands of the CN^–(o-H₂) nuclear spin isomer (shown in red). In contrast there are no features found in the region of the para nuclear spin isomer (shown in blue). Similar to he system of Cl^–H₂ [27], the para:ortho ratio is below the detection limit for the CN^–(p-H₂) bands due to efficient ligand exchange of CN^–(p-H₂) to CN^–(o-H₂) via collisions. We use a simple Boltzmann model to calculate the expected para:ortho ratio at different temperatures (1) $\frac{[(p{-\mathrm{H}}_2){\mathrm{CN}}^{-}]}{[(o{-\mathrm{H}}_2){\mathrm{CN}}^{-}]}=\frac{k_{L\leftarrow }}{k_{L\to }}\cdot \frac{[p{-\mathrm{H}}_2]}{[o-\mathrm{H}2]}={\mathrm{e}}^{-\frac{E_a}{k_{B}T}}\cdot \frac{[p{-\mathrm{H}}_2]}{[o{-\mathrm{H}}_2]}$(1) where $E_a=105.6$ cm${}^{-1}$ is the difference in dissociation energy, $k_L$ the forward and backward Langevin rates, $k_B$ the Boltzmann constant, and T the collisional temperature [38], giving us the expected ratio of $8\cdot {10}^{-8}$, $4\cdot {10}^{-5}$ and $8\cdot {10}^{-3}$ at 10, 17 and 40 K, respectively. At 17 K the expected strength of the predicted para band is about three orders of magnitude below the noise level.

Not only the transition frequencies agree well with the calculated spectra, also the line profile matches with the calculated bands for CN^–(o-H₂). When comparing the absolute frequency positions of the measured and calculated vibrational bands one finds a red shift of about 5 cm${}^{-1}$ for the strongest band. This is the same range as for the Cl^–H₂ system [27], and we attribute this to the overall accuracy of the potential energy surface.

Based on a partial assignment of resonances within the accurate quantum approach, the strong experimental features at 743(1) and 755(1) cm${}^{-1}$ may be assigned to unresolved P and R branch transitions, respectively, of the $(0,2^0,0)\leftarrow (0,0,0)$ vibrational transition, i.e. the second overtone of the hindered H₂ rotation. Several weaker features are detected in the recorded spectrum, albeit at very low signal-to-noise ratio. Based on their close match to the theoretical predictions, we provide in the following a tentative assignment. The feature at 776(1) cm${}^{-1}$ stems dominantly from the transition from the ground state to the combination mode $(1^1,2^0,0)$, where an additional quantum of the CN hindered rotation is excited. Similarly the band at 870(1) cm${}^{-1}$ is likely a combination mode involving the H₂ intermonomer stretching vibration. Surprisingly, the weak feature at 735(1) cm${}^{-1}$ might be assigned to the hot band transition $(1^1,2^0,0)\leftarrow (1^1,0,0)$. This assignment is strengthened by additional measurements at higher temperature, as discussed below.

As in the system of Cl^–H₂ the frequency difference for the para and ortho bands stems from the tunnelling splitting between the geometric structures of the hindered H₂ rotation along the bending coordinate. Whereas in the Cl^–H₂ system we calculated a frequency difference of 260 cm${}^{-1}$ for the $(0,2^0)\leftarrow (0,0)$ mode, we note here an even larger difference of 350 cm${}^{-1}$ for the corresponding $(0,2^0,0)\leftarrow (0,0,0)$ band. We assume that the larger shift between the two nuclear spin isomers is caused by the slightly different barrier height for the hindered H₂ rotation (836 cm${}^{-1}$ for Cl^–H₂ and 821 cm${}^{-1}$ for CN^–H₂  respectively) and most likely a different barrier width.

In order to quantify the nuclear spin isomer abundances we performed a saturation depletion measurement, as described previously [22,39], on the strongest observed band at around 755 cm${}^{-1}$, resulting in a maximum depletion of 93(5) %. We can thus infer that at 17 K we dominantly produce the CN^–(o-H₂) conformer, as expected.

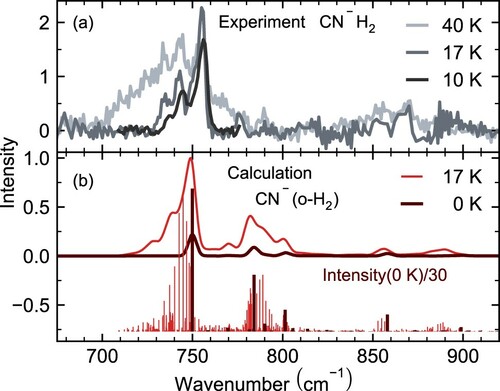
We subsequently repeated the IRPD experiments of the strong CN^–(o-H₂) bands at three different trap temperatures (10, 17, or 40 K) (see Figure 2). We clearly see a broadening of the band structure at the highest ion temperature, which we attribute to the higher rotational temperature leading to a more extended P and R branch substructure. The broadening is asymmetric towards lower photon energies, indicating a large anharmonicity resulting in a reduced rotational constant in the vibrationally excited states, and consequently an extended P and narrow R-branch. The same behaviour has also been observed for the Cl^–H₂ complex [25,27]. This reasoning is in agreement with additional calculations that we performed at a temperature of 0 K, which are also shown in Figure 2. At this temperature mainly the rotational ground state is populated, so that only the lowest R branch (or Q branch) transitions are simulated. This allows us to disentangle the vibrational from the rotational motion. It can be clearly seen that the calculated predissociation spectrum broadens when changing from 0 K to 17 K due to rotational population effects. An additional broadening of the 755 cm${}^{-1}$ band towards lower wavenumbers can be expected due to a stronger hot band transition $(1^1,2^0,0)\leftarrow (1^1,0,0)$ caused by a higher population in the low-lying ($\sim 21$ cm${}^{-1}$) CN hindered rotation mode of CN^–(o-H₂): the population of this mode relative to the vibrational ground state changes from $\sim 17$% to $\sim 47$% when increasing the temperature from 17 K to 40 K.

Figure 2. Experimental vibrational infrared predissociation spectra of CN^–H₂ recorded at 10 K (black), 17 K (grey) and 40 K (light grey) (a). Theoretical predissociation spectra of CN^–H₂ simulated for a complex temperature of 0 K (dark red) and 17 K (red) using an accurate quantum approach shown as ro-vibrational stick spectra and convolved with the laser linewidth (0.7%) for better comparision (b). The calculated transition intensities for 0 K are scaled for better visibility.

3.2. CN${}^{-}$D${}_2$

The single photon infrared predissociation spectrum of CN^–D₂ is shown in the upper panels of Figure 3. The D-D stretching vibration is measured to be at 2898(1) cm${}^{-1}$ at 17 K (see Figure 3 upper right panel). The calculated fundamental band position at the CCSD(T)-F12b/AV5Z level of theory is in close agreement to experiment, with 2873.3 cm${}^{-1}$ for the D-D stretch vibration of the complex. The calculated spectrum was convolved with a line width of 24 cm${}^{-1}$  the FWHM linewidth of FEL-2 in this range. Due to its large transition dipole moment the D-D stretch is much more intense than the bands in the lower energy range and is therefore scaled.

Figure 3. Top panels: Experimental vibrational infrared predissociation spectra of CN^–D₂ at 17 K (a). Orange dotted line shows a Gaussian line-profile fit to the band at 2897.9(1.4) cm${}^{-1}$ (c). Bottom panels: Theoretical predissociation spectrum of CN^–D₂ calculated with an accurate quantum approach at 17 K shown as ro-vibrational spectra and convolved with the laser line width (0.7%) for better comparison. The dissociation energy of CN^–(p-D₂) is given by the dashed vertical line at 512.5 cm${}^{-1}$ the dissociation energy of CN^–(o-D₂) at 452.1 cm${}^{-1}$. The calculated ortho and para transition intensities are scaled differently for better visibility. (b). The position of the D-D stretch vibration calculated at the CCSD(T)-F12b/AV5Z level of theory is shown in (d).

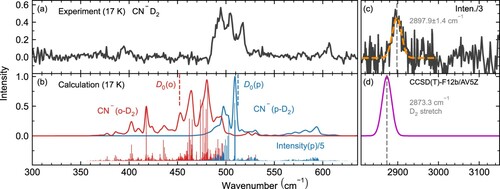
The experimental and calculated spectra between 300 and 640 cm${}^{-1}$ are shown in the left panel. Experimental band maxima are at 493(1), 505(1), 518(1), and 607(2) cm${}^{-1}$. In the system with D₂ the para spin isomer is more stable than the ortho one, since the former dissociates to p-D₂ with j = 1. The dissociation energies $D_0$ are 512.5 and 452.1 cm${}^{-1}$ for CN^–(p-D₂) and CN^–(o-D₂), respectively, using the calculated ground state energy difference of 0.6 cm${}^{-1}$ and the j = 1 rotational energy of p-D₂ (59.8 cm${}^{-1}$, [40]). The interconversion reaction between the spin isomer might be less effective due to a smaller energy difference of $\mathrm{\Delta }E=59.2$ cm${}^{-1}$. At 17 K we calculate an ortho:para ratio of about $3\cdot {10}^{-3}$ (see Equation (1(1) $\frac{[(p{-\mathrm{H}}_2){\mathrm{CN}}^{-}]}{[(o{-\mathrm{H}}_2){\mathrm{CN}}^{-}]}=\frac{k_{L\leftarrow }}{k_{L\to }}\cdot \frac{[p{-\mathrm{H}}_2]}{[o-\mathrm{H}2]}={\mathrm{e}}^{-\frac{E_a}{k_{B}T}}\cdot \frac{[p{-\mathrm{H}}_2]}{[o{-\mathrm{H}}_2]}$(1) )), meaning that the abundance of CN^–(o-D₂) is a factor of 300 less than that of CN^–(p-D₂). In the experimental spectrum we thus only expect contributions from the CN^–(p-D₂) nuclear spin isomer. As in the case of CN^–H₂ we expect only the more stable CN^–D₂ geometric isomer to be populated at 17 K. For comparison to the experimental data the rovibrational spectra are convolved with a line width corresponding to the FEL-2 FWHM (0.7% of the respective frequency).

We can tentatively match the strong experimental features at 505 and 518 cm${}^{-1}$ with unresolved ro-vibrational transitions of the predicted most prominent CN^–(p-D₂) features. Also the 607 cm${}^{-1}$ peak agrees with a calculated mode of this spin isomer. We would like to note here that the calculated ro-vibrational frequencies all belong to bound -- quasi-continuum transitions. The fact that they appear in the spectrum at frequencies below the dissociation energy means that they originate from energetically higher-lying rotational, or ro-vibrational, states. The remaining peak at 493 cm${}^{-1}$ and some lower intensity features at lower energy might be attributed to CN^–(o-D₂), indicating that the ligand exchange reaction is less efficient than calculated. Additional experiments performed at different temperatures and with an ortho-D₂ enriched sample could aid in assigning the spectrum and disentangling the contributions of the different spin isomers.

4. Conclusion

We present far-infrared and mid-infrared vibrational predissociation spectra of the weakly bound complexes CN^–H₂ and CN^–D₂. By using a cryogenic ion trap instrument coupled to the widely tunable free-electron lasers at the FELIX laboratory, we observed not only the CN and D₂ stretching modes of the diatomic subunits in the complexes, but could access the low-wavenumber region between 300 and 850 cm${}^{-1}$ where their low-lying bending (hindered rotation) and intermonomer stretching bands are located. In the case of CN^–H₂ we could assign the observed bands with the help of accurate quantum calculations. They are dominated by the first overtone of the hindered H₂ rotation in combination with the hindered CN rotation of the CN^–(o-H₂) nuclear spin isomer. The energetically higher-lying CN^–(p-H₂) isomer was not observed due to efficient ortho-para ligand exchange. Our calculations predict a large energy difference between corresponding bands in both spin isomers due to a strong tunnelling splitting of the hindered H₂ rotation along the bending coordinate, as was observed recently for the related triatomic Cl^–H₂ [26,27]. For the CN^–D₂ we mainly detected vibrational modes of the more strongly bound CN^–(p-D₂) system, but several vibrational modes of both spin isomers overlap, thus an unambigous assignment is difficult in this region. In-depth studies, if possible with enriched ortho-D₂, are necessary in order to unambiguously assign the individual bands.

Additional information

The ro-vibrational transition energies, scripts and raw data can be downloaded at https://doi.org/10.5281/zenodo.651682

Acknowledgments

We gratefully acknowledge the support of Radboud University and of NWO for providing the required beam time at the FELIX Laboratory, and the skilful assistance of the FELIX staff. We thank the Cologne Laboratory Astrophysics group for providing the FELion ion trap instrument for the current experiments and the Cologne Center for Terahertz Spectroscopy funded by the Deutsche Forschungsgemeinschaft (DFG, grant SCHL 341/15–1) for supporting its operation.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the Austrian Science Fund (FWF) through project No. I2920-N27 and through the Doctoral program Atoms, Light and Molecules, project number W1259-N27. The research leading to this result has been supported by the project CALIPSOplus under the Grant Agreement 730872 from the EU Framework program for Research and Innovation HORIZON 2020, by the Agence Nationale de la Recherche, project COLD HMINUS, by the research programme ROSAA with project number 740.018.010, which is (partly) financed by the Netherlands Organisation for Scientific Research (NWO), and by the Deutsche Forschungsgemeinschaft (DFG, grant SCHL 341/15–1).

Notes

1 https://www.ru.nl/felix