Molecular frames for a symmetry-adapted rotational basis set

Abstract

In molecular ro-vibrational calculations, it is desirable to build a symmetry-adapted basis set where both the rotational and vibrational functions are each separately symmetrised. Enabling rotational symmetrisation requires the use of body-fixed frames whose rotations under molecular symmetry operations are constant. The familiar Eckart and Sayvetz frames are examples of such frames, as are bisector frames for certain molecules. In this work, we introduce alternative frames for CH₃Cl-type molecules and C₂H₆ that can be used for rotational symmetrisation. These are defined by the vibrational coordinates without the need for a reference geometry. We also provide one method to find such frames. Finally, we state a straightforward transformation of the s-vectors when changing frames which facilitates the evaluation of kinetic energy operators in these non-standard frames.

GRAPHICAL ABSTRACT

1. Introduction

In ro-vibrational eigenfunction calculations, the choice of body-fixed (BF) frame is of great significance. A poorly chosen frame can result in large Coriolis coupling, leading to problems in the convergence of ro-vibrational energies. It is well known that the Eckart (for rigid molecules) and Sayvetz (for non-rigid molecules) frames [1] are designed to eliminate the first-order Coriolis coupling and as such are a typical choice [2–5]. Another common frame, defined by two vectors, has an axis parallel to one of the vectors and an axis perpendicular to the plane formed by the vectors (bond vector frames) [6–12]. For symmetric triatomic (ABA) molecules and some polyatomics, a frame which bisects two vectors or two planes is a standard choice [13–15].

A further consideration relates to the molecule's symmetry. It is often desirable to build a symmetry-adapted basis set as this reduces the corresponding Hamiltonian matrix to block diagonal form [16] and permits the labelling of the ro-vibrational eigenfunction as an irreducible representation (irrep) of the molecular symmetry (MS) group [17]. This label is crucial in intensity calculations because the eigenfunction has an associated nuclear spin weight dictated by its symmetry that in turn affects the transition intensity [18].

One approach to symmetrisation is to independently classify functions of the rotational and vibrational coordinates as irreps of the MS group so that the combined functions have the form (1) ${\psi }_a(\theta ,\varphi ,\chi {)}^{{\mathrm{\Gamma }}_{\mathrm{r}\mathrm{o}\mathrm{t}}^{i_a}}\times {\phi }_b(q_1,\dots ,q_n{)}^{{\mathrm{\Gamma }}_{\mathrm{v}\mathrm{i}\mathrm{b}}^{i_b}}$(1) where (θ, ϕ, χ) are the rotational coordinates, $(q_1,\dots ,q_n)$ are the vibrational coordinates, while a and b number the rotational and vibrational functions. The functions are the $i_a$th and $j_b$th components of the irreps ${\mathrm{\Gamma }}_{\mathrm{r}\mathrm{o}\mathrm{t}}$ and ${\mathrm{\Gamma }}_{\mathrm{v}\mathrm{i}\mathrm{b}}$, respectively. Multiplying all functions of irrep ${\mathrm{\Gamma }}_{\mathrm{r}\mathrm{o}\mathrm{t}}$ with all functions of irrep ${\mathrm{\Gamma }}_{\mathrm{v}\mathrm{i}\mathrm{b}}$ results in a list of functions which have a reducible representation ${\mathrm{\Gamma }}_{\mathrm{r}\mathrm{o}\mathrm{t}}\otimes {\mathrm{\Gamma }}_{\mathrm{v}\mathrm{i}\mathrm{b}}.$ This can be reduced to a sum of irreps through the equation (2) ${\mathrm{\Gamma }}_{\mathrm{r}\mathrm{o}\mathrm{t}}\otimes {\mathrm{\Gamma }}_{\mathrm{v}\mathrm{i}\mathrm{b}}=\underset{j}{⨁}{a}_j{\mathrm{\Gamma }}_j$(2) where $a_j$ are the coefficients and ${\mathrm{\Gamma }}_j$ are the irreps [18]. The result is a set of symmetrised functions of the form (3) ${\left(\sum _{ab}{c}_{ab}^k{\psi }_a\right(\varphi ,\theta ,\chi \left){\phi }_b\right(q_1,\dots ,q_n\left)\right)}^{{\mathrm{\Gamma }}_i^{i_k}}.$(3) where $c_{ab}^k$ is a coefficient and k numbers the combined function. It is the $i_k$th component of the irrep ${\mathrm{\Gamma }}_i$.

In this approach, to classify the rotational part, one needs to know how the Euler angles transform under the MS operation, or, in other words, how the BF-frame rotates under this operation. When the Eckart or Sayvetz frames are used, there are the so-called equivalent rotations [18] of the BF-frame which occur during an MS operation. This procedure has enabled the successful construction of the symmetry-adapted eigenfunctions of several molecules [19–25].

In general, however, the rotation associated with an MS operation depends on the vibrational coordinates. In particular, the χ Euler angle transforms as [18] (4) ${\chi }^{\prime }=\pm \chi +\gamma (q_1,\dots ,q_n).$(4) Because the rotational and vibrational coordinates are no longer separable, such a dependency will lead to a breakdown of the rotational basis set symmetrisation and prevent the construction of a symmetry-adapted rotational basis set [15].

There are two possible solutions to this problem. The first is to relax the rotational and vibrational separation in Equation (1(1) ${\psi }_a(\theta ,\varphi ,\chi {)}^{{\mathrm{\Gamma }}_{\mathrm{r}\mathrm{o}\mathrm{t}}^{i_a}}\times {\phi }_b(q_1,\dots ,q_n{)}^{{\mathrm{\Gamma }}_{\mathrm{v}\mathrm{i}\mathrm{b}}^{i_b}}$(1) ) and instead symmetrise the combined rotational and vibrational functions together, rather than separately [26]. This would essentially result in Equation (3(3) ${\left(\sum _{ab}{c}_{ab}^k{\psi }_a\right(\varphi ,\theta ,\chi \left){\phi }_b\right(q_1,\dots ,q_n\left)\right)}^{{\mathrm{\Gamma }}_i^{i_k}}.$(3) ) without Equation (1(1) ${\psi }_a(\theta ,\varphi ,\chi {)}^{{\mathrm{\Gamma }}_{\mathrm{r}\mathrm{o}\mathrm{t}}^{i_a}}\times {\phi }_b(q_1,\dots ,q_n{)}^{{\mathrm{\Gamma }}_{\mathrm{v}\mathrm{i}\mathrm{b}}^{i_b}}$(1) ) as an intermediate. This has the advantage of greatly increasing the possible frames that can be used, including ones that are easy to define such as the bond vector frame. The other option, the one explored in this publication, is to use BF-frames where γ is a constant for all MS operations and all vibrational geometries. The ensuing rotational and vibrational separation simplifies the process because subsets of the coordinates can be treated independently during symmetrisation [15].

As the Eckart and Sayvetz frames can only be solved analytically for triatomics [27] and planar molecules [28], and because they are suboptimal for molecules without a well-defined equilibrium, they are not always a suitable choice. Our goal is to find geometric frames – ones that can be expressed as an analytic function of the vibrational coordinates – for certain molecules where the frame's rotations are constants under symmetry operations.

The structure of this publication is as follows: Section 2 describes the action of the MS operations on the rotational and vibrational coordinates. The example of an ABA molecule illustrates frames where the rotation under MS operations depends on the vibrational coordinates. The transformation and invariance of the kinetic energy operator is stated and proved in Section 3. With the same ABA illustrative example, Section 4 demonstrates why rotational basis set symmetrisation is not possible for certain frames. Section 5 shows that the correct transformation of the kinetic energy operator was derived for an ABA molecule for both a bisector frame and a bond vector frame. It further proves that the rotations are constant under symmetry operations when using the Eckart frames. Section 6 largely follows the pattern of Section 5, but for the CH₃Cl molecule. It also provides a geometric frame for which the rotations are constant under symmetry operations. Section 7 uses C₂H₆ as an example of Section 3 for a Sayvetz and a geometric frame. Section 8 shows how one can find a geometric frame for CH₃Cl with which one can construct a symmetry-adapted rotational basis set and how to transform the kinetic energy operator between frames. Finally, Section 9 mentions the possible avenues for further research and Section 10 concludes the publication.

2. Coordinate transformations

To begin, some notation. The position vector of nucleus α from the centre of mass is denoted ${\mathit{R}}_{\alpha }$. Instead of a space-fixed (SF) frame, we use a ‘rotationally fixed’ (RF) frame whose origin is at the nuclear centre of mass but whose unit vectors are parallel to the unit vectors of the SF-frame. We will also partially follow Sørensen's [29] notation in denoting the RF and BF unit vectors by ${\hat{\mathit{e}}}_F$ and ${\hat{\mathit{e}}}_g$, that is, uppercase subscripts are RF unit vectors and lowercase are BF unit vectors. Then, the Cartesian coordinates of the position vectors in each frame are given by (5) $R_{\alpha F}={\mathit{R}}_{\alpha }\cdot {\hat{\mathit{e}}}_F,r_{\alpha g}={\mathit{R}}_{\alpha }\cdot {\hat{\mathit{e}}}_g.$(5) A list of coordinates $(R_{\alpha X},R_{\alpha Y},R_{\alpha Z})$ will be denoted by $R_{\alpha }$, i.e. unbolded but without the subscript indicating the specific component.

Finally, a transformed object under MS operations has an apostrophe. For example, the transformed Cartesian coordinates of $R_{\alpha }$ after a nuclear permutation is written as ${R_{\alpha }}^{\prime }$. These must be the Cartesian coordinates of another atom ${\alpha }^{\prime }$, thus ${R_{\alpha }}^{\prime }=R_{{\alpha }^{\prime }}$.

Typically, the Cartesian coordinates are expressed in terms of the vibrational and angular coordinates: e.g. ${\mathit{R}}_{\alpha }(q_1,\dots ,q_n,\varphi ,\theta ,\chi )$ where the latter three coordinates are the Euler angles which specify the orientation of the BF-frame with respect to the RF-frame [30]. We use the standard definition of the Euler angles which involves first rotating the BF-frame by ϕ about the z-axis of the BF-frame (which is also the z-axis of the RF-frame initially), then rotating the BF-frame by θ about the y-axis of the BF-frame, and finally by χ about the z-axis of the BF-frame. All rotations are counter-clockwise (right handed). See Figure 1. With this definition the coordinates $R_{\alpha }$ in the RF-frame are given by (6) $\begin{array}{rl}& R_{\alpha }(q_1,\dots ,q_n,\varphi ,\theta ,\chi )\\ & =M_z\left(\varphi \right)M_y\left(\theta \right)M_z\left(\chi \right)r_{\alpha }(q_1,\dots ,q_n)\\ & =M{r}_{\alpha }\end{array}$(6) where (7) $\begin{array}{rl}{M}_z\left(\varphi \right)& =\left(\begin{array}{ccc}\cos \varphi & -\sin \varphi & 0\\ \sin \varphi & \cos \varphi & 0\\ 0& 0& 1\end{array}\right),\\ M_y\left(\theta \right)& =\left(\begin{array}{ccc}\cos \theta & 0& \sin \theta \\ 0& 1& 0\\ -\sin \theta & 0& \cos \theta \end{array}\right),\\ M_z\left(\chi \right)& =\left(\begin{array}{ccc}\cos \chi & -\sin \chi & 0\\ \sin \chi & \cos \chi & 0\\ 0& 0& 1\end{array}\right)\end{array}$(7) and $r_{\alpha }$ are the coordinates of ${\mathit{R}}_{\alpha }$ in the BF-frame.

Figure 1. A visual representation of the Euler angles. (a) The first two Euler angles ϕ and θ which are essentially angles defining the spherical coordinates. The first rotation of ϕ is about the z-axis of both the RF- and BF-frame which initially coincide. The BF-frame is then rotated by θ about the y-axis of the BF-frame or the $y^{\prime }$-axis of the figure. (b) The final Euler angle χ is due to a rotation about the z-axis of the BF-frame or the $z^{\prime }$-axis of the figure.

The transformation of the RF Cartesian coordinates – the left-hand side of Equation (6(6) $\begin{array}{rl}& R_{\alpha }(q_1,\dots ,q_n,\varphi ,\theta ,\chi )\\ & =M_z\left(\varphi \right)M_y\left(\theta \right)M_z\left(\chi \right)r_{\alpha }(q_1,\dots ,q_n)\\ & =M{r}_{\alpha }\end{array}$(6) ) – under MS operations is well-defined and explained in [18]. For the transformation of the BF Cartesian coordinates, however, the definition is not so clear-cut as only the transformed Euler matrix multiplied by the transformed BF Cartesian coordinates – the right-hand side of Equation (6(6) $\begin{array}{rl}& R_{\alpha }(q_1,\dots ,q_n,\varphi ,\theta ,\chi )\\ & =M_z\left(\varphi \right)M_y\left(\theta \right)M_z\left(\chi \right)r_{\alpha }(q_1,\dots ,q_n)\\ & =M{r}_{\alpha }\end{array}$(6) ) – must equal the transformed RF Cartesian coordinates. There is thus an ambiguity for the transformation of the BF Cartesian coordinates as the rotation of the frame can be defined to compensate. See Appendix 2 of [31] for an example of this.

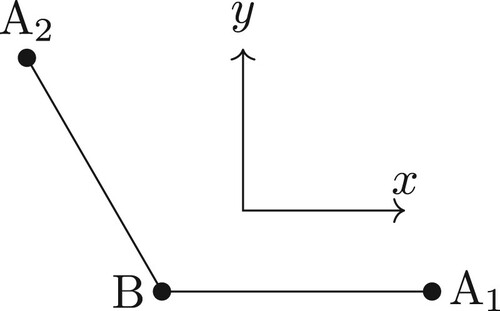
Figure 2. The bond vector BF-frame for the ABA molecule with the x-axis parallel to the A${}_1$–B bond and the y-axis in the plane of the three atoms. The axes are offset for clarity.

Our approach defines the transformation of the BF Cartesian coordinates $r_{\alpha }$ from the transformation of the vibrational coordinates. The latter can be determined if their definition in terms of the Cartesian coordinates is known. See Appendix 3 from [32]. Since the vibrational coordinates fully specify the BF Cartesian coordinates, their transformation encodes the transformation of the BF Cartesian coordinates. The change in the left-hand side of Equation (6(6) $\begin{array}{rl}& R_{\alpha }(q_1,\dots ,q_n,\varphi ,\theta ,\chi )\\ & =M_z\left(\varphi \right)M_y\left(\theta \right)M_z\left(\chi \right)r_{\alpha }(q_1,\dots ,q_n)\\ & =M{r}_{\alpha }\end{array}$(6) ) then can be used to find the Euler angle transformation.

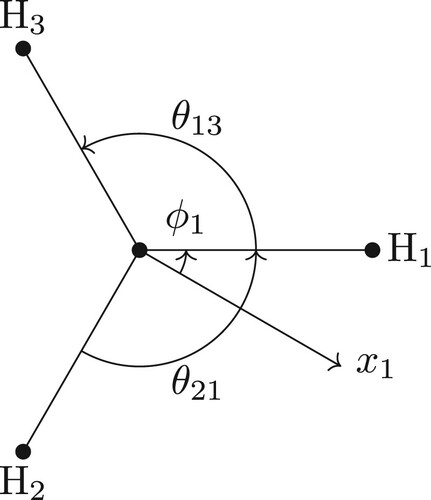
As an example, consider a triatomic molecule of type ABA and let the A-type atoms (called A₁ and A₂) have coordinates ${\mathit{R}}_{A1}(q_1,q_2,q_3,\varphi ,\theta ,\chi )$ and ${\mathit{R}}_{A2}(q_1,q_2,q_3,\varphi ,\theta ,\chi )$. In this representation, $q_1$ and $q_2$ are the AB bonds while $q_3$ is the ABA angle.

Throughout this work, the origin is chosen for convenience rather than at the centre of mass. Since the vector from the chosen origin to the centre of mass is the same for all atoms, the desired transformation properties will trivially be satisfied. In the case of the ABA molecule, the origin will be at the B atom.

For the BF-frame, one possible choice is with the x-axis parallel to the bond from atom B to A1 (i.e. parallel to the ${\mathit{R}}_{A1}-{\mathit{R}}_B$ vector) and the z-axis perpendicular to the plane of ABA (see Figure 2). With this choice, the BF Cartesian coordinates for the ABA molecule are (8) $\begin{array}{rl}{r}_{A1}& =(q_1,0,0)\\ r_{A2}& =(q_2\cos q_3,q_2\sin q_3,0)\\ r_B& =(0,0,0).\end{array}$(8) The operation (12) permutes $q_1$ and $q_2$ resulting in new BF Cartesian coordinates given by (9) $\begin{array}{rl}{\tilde{r}}_{A1}& =(q_2,0,0)\\ {\tilde{r}}_{A2}& =(q_1\cos q_3,q_1\sin q_3,0)\\ {\tilde{r}}_B& =(0,0,0)\end{array}$(9) where ${\tilde{r}}_{\alpha }$ is the result after transforming the vibrational coordinates in the expression for $r_{\alpha }$. In general, the Euler angles also change, and we call the Euler matrix with the transformed angles as $\tilde{M}$. As we have ${R_{\alpha }}^{\prime }=\tilde{M}{\tilde{r}}_{\alpha }$ and $\tilde{M}$ now defines a rotated BF-fame, we see that the transformed ${\tilde{r}}_{\alpha }$ are the BF Cartesian coordinates of $r_{\alpha }$ in the rotated BF-frame and after the transformation. The BF-frame is rotated in such a way so as to ensure that ${R_{A1}}^{\prime }=R_{A2}$ and vice versa. In this case, the new RF Cartesian coordinates are (10) $\begin{array}{rl}{R_{\alpha }}^{\prime }& =M_x(\varphi +\pi )M_y(\pi -\theta )M_z(2\pi -\chi -q_3){\tilde{r}}_{\alpha }\\ & =R_{{\alpha }^{\prime }}=\tilde{M}{\tilde{r}}_{\alpha }.\end{array}$(10) In performing this operation, we now have three frames: the RF-frame and the two BF-frames. Denoting the new BF-frame unit vectors as ${{\hat{\mathit{e}}}_g}^{\prime }$, i.e. with an asterisk, the components of ${\mathit{R}}_{\alpha }$ are then (11) ${\mathit{R}}_{\alpha }\cdot {{\hat{\mathit{e}}}_g}^{\prime }={\tilde{r}}_{\alpha ,g}.$(11) It is of interest to note what the transformed Cartesian coordinates in the original BF-frame are (denoted by ${r_{\alpha }}^{\prime }$). Since the Euler matrix of this frame is unchanged, if ${R_{\alpha }}^{\prime }=R_{{\alpha }^{\prime }}$, we have, (12) ${R_{\alpha }}^{\prime }=M{r_{\alpha }}^{\prime }=R_{{\alpha }^{\prime }}=M{r}_{{\alpha }^{\prime }}=\tilde{M}{\tilde{r}}_{\alpha }$(12) and so ${r_{\alpha }}^{\prime }=r_{{\alpha }^{\prime }}$. We also have (13) ${r_{\alpha }}^{\prime }=M^T\tilde{M}{\tilde{r}}_{\alpha }\equiv N{\tilde{r}}_{\alpha }$(13) where $N\equiv M^T\tilde{M}$ is the rotation matrix relating the coordinates of ${\mathit{R}}_{\alpha }$ in the new BF-frame to that of the old BF-frame. In this case, it is (14) $N_{\left(12\right)}=\left(\begin{array}{ccc}\cos q_3& \phantom{-}\sin q_3& 0\\ \sin q_3& -\cos q_3& 0\\ 0& 0& -1\end{array}\right).$(14)

3. Kinetic energy transformation

3.1. Kinetic energy operator

For completeness, we state the MS transformation properties of the objects used in constructing the kinetic energy operator (KEO), namely, the s and t vectors [29]. These are labelled as, for example, ${\mathit{s}}_{a,\alpha }$, which is the s-vector for atom α and vibrational or rotational coordinate a. The vibrational coordinates will be labelled by i, j and k, and their primed versions; the rotational coordinates by g and h, and their primed versions. The Hamiltonian $\hat{H}$ is then given by (15) $\hat{H}=\hat{T}+V$(15) where V is the potential energy while $\hat{T}$ is the KEO given by (16) $\begin{array}{rl}\hat{T}& =\frac{1}{2}\sum _{i,j}{\hat{\pi }}_i(\sum _{\alpha }\frac{1}{m_{\alpha }}{\mathit{s}}_{i,\alpha }\cdot {\mathit{s}}_{j,\alpha }){\hat{\pi }}_j\\ & +\frac{1}{2}\sum _{i,g}{\hat{\pi }}_i(\sum _{\alpha }\frac{1}{m_{\alpha }}{\mathit{s}}_{i,\alpha }\cdot {\mathit{s}}_{g,\alpha }){\hat{J}}_g\\ & +{\hat{J}}_g(\sum _{\alpha }\frac{1}{m_{\alpha }}{\mathit{s}}_{g,\alpha }\cdot {\mathit{s}}_{i,\alpha }){\hat{\pi }}_i\\ & +\frac{1}{2}\sum _{g,h}{\hat{J}}_g(\sum _{\alpha }\frac{1}{m_{\alpha }}{\mathit{s}}_{g,\alpha }\cdot {\mathit{s}}_{h,\alpha }){\hat{J}}_h+U\end{array}$(16) where $m_{\alpha }$ is the mass of atom α, ${\hat{\pi }}_i=-\mathrm{i}\hslash \mathrm{\partial }/\mathrm{\partial }{q}_i$ is the vibrational momentum operator for vibrational coordinate $q_i$, ${\hat{J}}_g$ is the g-axis BF component of the SF angular momentum operator, and U is the pseudo-potential. The generic terms in brackets are known as the G-matrix elements, defined by (17) $G_{ab}=\sum _{\alpha }\frac{1}{m_{\alpha }}{\mathit{s}}_{a,\alpha }\cdot {\mathit{s}}_{b,\alpha }.$(17) The terms of Equation (16(16) $\begin{array}{rl}\hat{T}& =\frac{1}{2}\sum _{i,j}{\hat{\pi }}_i(\sum _{\alpha }\frac{1}{m_{\alpha }}{\mathit{s}}_{i,\alpha }\cdot {\mathit{s}}_{j,\alpha }){\hat{\pi }}_j\\ & +\frac{1}{2}\sum _{i,g}{\hat{\pi }}_i(\sum _{\alpha }\frac{1}{m_{\alpha }}{\mathit{s}}_{i,\alpha }\cdot {\mathit{s}}_{g,\alpha }){\hat{J}}_g\\ & +{\hat{J}}_g(\sum _{\alpha }\frac{1}{m_{\alpha }}{\mathit{s}}_{g,\alpha }\cdot {\mathit{s}}_{i,\alpha }){\hat{\pi }}_i\\ & +\frac{1}{2}\sum _{g,h}{\hat{J}}_g(\sum _{\alpha }\frac{1}{m_{\alpha }}{\mathit{s}}_{g,\alpha }\cdot {\mathit{s}}_{h,\alpha }){\hat{J}}_h+U\end{array}$(16) ) contain both vibrational and rotational s-vectors, specified by their subscript, which are inverses of the rotational and vibrational t-vectors. We have the relations (18) $\sum _{\alpha }{\mathit{s}}_{a,\alpha }\cdot {\mathit{t}}_{b,\alpha }={\delta }_{ab}.$(18) We shall consider all four in turn and then evaluate the transformation of the KEO, demonstrating its invariance.

3.2. s and t vector transformations

In the so-called s-vector approach [33], one needs the vibrational and rotational s-vectors as well as the rotational t-vectors (to calculate the rotational s-vectors). For the transformation $R_{\alpha }\to R_{{\alpha }^{\prime }}$ and $q_k\to q_{k^{\prime }}$, the definition and transformation of the vectors and operators are summarised in Table 1. Table 2 shows the transformation for the vibrational s-vectors and vibrational momentum operators for more complex vibrational transformations. The transformation of the rotational s-vectors and angular momentum operators is unchanged.

Table 1. The transformation of the t and s vectors.

Object	Equation	Transformation
${\mathit{s}}_{k,\alpha }$	${\hat{\mathit{e}}}_F{\mathrm{\partial }}_{\alpha F}{q}_k$	${\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}$
${\mathit{s}}_{g,\alpha }$	[29]	$N_{hg}{\mathit{s}}_{h,{\alpha }^{\prime }}\mp \dot{\phantom{a}}{\gamma }_k{\mathit{s}}_{k,\alpha }{N}_{zg}$
${\mathit{t}}_{k,\alpha }$	${\mathrm{\partial }}_k{\mathit{R}}_{\alpha }$	${\mathit{t}}_{k^{\prime },{\alpha }^{\prime }}\pm \dot{\phantom{a}}{\gamma }_{k^{\prime }}{\mathit{t}}_{z,{\alpha }^{\prime }}$
${\mathit{t}}_{g,\alpha }$	${\hat{\mathit{e}}}_g\times {\mathit{R}}_{\alpha }$	$N_{hg}{\mathit{t}}_{h,{\alpha }^{\prime }}$
${\hat{J}}_g$	[34]	$N_{hg}{\hat{J}}_h$ [18]
${\hat{\pi }}_k$	$-i\hslash \mathrm{\partial }/\mathrm{\partial }{q}_k$	${\hat{\pi }}_{k^{\prime }}\pm \dot{\phantom{a}}{\gamma }_{k^{\prime }}{\hat{J}}_z$

Note: This assumes that ${R_{\alpha }}^{\prime }=R_{{\alpha }^{\prime }}$ and that ${q_k}^{\prime }=q_{k^{\prime }}$. The matrix is N is that of Equation (13(13) ${r_{\alpha }}^{\prime }=M^T\tilde{M}{\tilde{r}}_{\alpha }\equiv N{\tilde{r}}_{\alpha }$(13) ). The term ${\dot{\gamma }}_k={\mathrm{\partial }}_k\gamma$ where γ is the angle in the χ transformation ${\chi }^{\prime }=\pm \chi +\gamma$ of Table 3. The sign in front ${\dot{\gamma }}_k$ corresponds to the left and right transformations of Table 3. The definition of the rotational s-vector ${\mathit{s}}_{g,\alpha }$ and the BF angular momentum operator components ${\hat{J}}_g$ are given in [29] and [34], respectively. Summation over repeated indices is assumed.

Table 2. The transformation of $q_k$ in the left column and the corresponding transformed vibrational s-vector and vibrational momentum operator.

Coordinate	s-vector	Momentum operator
$q_k\to -q_{k^{\prime }}$	$-{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}$	$-({\hat{\pi }}_{k^{\prime }}\pm \dot{\phantom{a}}{\gamma }_{k^{\prime }}{\hat{J}}_z)$
$q_k\to a{q}_k+b{q}_{k^{\prime }}$	$a{\mathit{s}}_{k,{\alpha }^{\prime }}+b{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}$	$a({\hat{\pi }}_k\pm \dot{\phantom{a}}{\gamma }_k{\hat{J}}_z)+b({\hat{\pi }}_{k^{\prime }}\pm \dot{\phantom{a}}{\gamma }_{k^{\prime }}{\hat{J}}_z)$

Note: The transformations of the Cartesian coordinates, the rotational s-vectors and the angular momentum operators remain the same as Table  1.

Table 3. The change in the Euler angles for a given rotation of the BF-frame.

	$R_{\alpha }^{\pi }$	$R_z^{\text{β}}$
θ	$\pi -\theta$	θ
ϕ	$\varphi +\varphi$	ϕ
χ	$2\pi -2\alpha -\chi$	$\chi +\text{β}$

Note: $R_{\alpha }^{\pi }$ and $R_z^{\text{β}}$ are rotations of the BF-frame. $R_{\alpha }^{\pi }$ is a rotation of π radians about an axis in the xy plane making an angle α about with the x-axis (α is measured in the right-handed sense about the z-axis) and $R_z^{\text{β}}$ is a rotation of β radians about the z-axis (β measured in the right handed sense about the z-axis) [18].

The vibrational s-vector is defined (19) ${\mathit{s}}_{k,\alpha }={\hat{\mathit{e}}}_F{\mathrm{\partial }}_{\alpha F}{q}_k(R_1,\dots ,R_n)$(19) whose components are in the RF-frame. In practical applications, however, we would prefer to have the components of ${\mathit{s}}_{k,\alpha }$ in the BF-frame.

In Appendix 1, it is shown that to calculate the components of ${\mathit{s}}_{k,\alpha }$ in another frame one simply must evaluate ${\mathrm{\partial }}_{\alpha F}{q}_k$ at the Cartesian coordinates of that frame [35].

In the BF-frame, the Cartesian coordinates $r_{\alpha }$ are functions of the vibrational coordinates. In Appendix 1, it is also shown that the transformed vibrational s-vectors can also be expressed in the new BF-frame by performing the vibrational coordinate transformation (which we shall denote as ${\tilde{s}}_{k,\alpha g}$) on the original BF components $s_{k,\alpha g}$. The same procedure also applies to the other vectors.

3.3. G-matrix transformation

From the transformation properties of the s-vectors, we can obtain the transformation of the G-matrix. Assuming the vibrational coordinates $q_i$ and $q_{i^{\prime }}$ transform to $q_j$ and $q_{j^{\prime }}$, respectively, the vibrational, rotational and Coriolis components of the G-matrix transform as (20) $\begin{array}{rl}{G_{i{i}^{\prime }}}^{\prime }& =G_{j{j}^{\prime }}\\ {G_{g{g}^{\prime }}}^{\prime }& =N_{hg}{N}_{h^{\prime }{g}^{\prime }}{G}_{h{h}^{\prime }}+{\dot{\gamma }}_k{\dot{\gamma }}_{k^{\prime }}{G}_{k{k}^{\prime }}{N}_{zg}{N}_{z{g}^{\prime }}\\ & -{\dot{\gamma }}_k{G}_{kh}(N_{h{g}^{\prime }}{N}_{zg}+N_{hg}{N}_{z{g}^{\prime }})\\ {G_{gi}}^{\prime }& =N_{hg}{G}_{hj}-{\dot{\gamma }}_k{G}_{kj}{N}_{zg}\end{array}$(20) where the rotation matrix N is that of Equation (13(13) ${r_{\alpha }}^{\prime }=M^T\tilde{M}{\tilde{r}}_{\alpha }\equiv N{\tilde{r}}_{\alpha }$(13) ) and relates the directions of the original and rotated BF-frames and ${\dot{\gamma }}_k={\mathrm{\partial }}_k\gamma$ defined in Table  1. The left-hand side of the above equations are of the form $G_{ab}\circ P(q_1,\dots ,q_n)$, where P is the MS operation which transforms the coordinates first, after which the G matrix element $G_{ab}$ is applied to the transformed coordinates. The right-hand side is in terms of $G_{ab}(q_1,\dots ,q_n)$ which is the matrix element $G_{ab}$ applied to the un-transformed coordinates.

From the definition of the G matrix, we have (21) $\begin{array}{rl}{G}_{ab}& =\sum _{\alpha }\frac{1}{m_{\alpha }}{s}_{a,\alpha F}{s}_{b,\alpha F}=\sum _{\alpha }\frac{1}{m_{\alpha }}{s}_{a,\alpha g}{s}_{b,\alpha g}\\ & =\sum _{\alpha }\frac{1}{m_{\alpha }}{s}_{a,\alpha g^{\prime }}{s}_{b,\alpha g^{\prime }}\end{array}$(21) where the s-vector components are in the RF, old BF and new BF-frame, respectively. Since the new BF-frame components of the transformed s-vectors are given by ${\tilde{s}}_{a,\alpha }$, to transform the G matrix, one can also perform the vibrational coordinate transformation on the original G matrix.

Action of the full Hamiltonian on a function $\psi (q_1,\dots ,q_n,\varphi ,\theta ,\chi )$ is of the form (22) $\begin{array}{rl}\hat{H}\psi & =\frac{1}{2}{\hat{\pi }}_a{G}_{ab}{\hat{\pi }}_b\psi +U\psi +V\psi \\ & =\phantom{+}\frac{1}{2}{G}_{k{k}^{\prime }}{\hat{\pi }}_k{\hat{\pi }}_{k^{\prime }}\psi +\frac{1}{2}\left({\hat{\pi }}_k{G}_{k{k}^{\prime }}\right)\left({\hat{\pi }}_{k^{\prime }}\psi \right)\\ & +\frac{1}{2}{G}_{gh}{\hat{J}}_g{\hat{J}}_h\psi +\frac{1}{2}{G}_{gk}{\hat{J}}_g{\hat{\pi }}_k\psi +\frac{1}{2}\left({\hat{\pi }}_k{G}_{kg}\right){\hat{J}}_g\psi \\ & +\frac{1}{2}{G}_{kg}{\hat{\pi }}_k{\hat{J}}_g\psi +U\psi +V\psi .\end{array}$(22) where implicit summation of repeated indices is assumed. In Appendix 2, it is shown that the Hamiltonian is invariant under the transformations of Table 1.

4. Rotational symmetrisation

As described in the Introduction, typical eigenfunctions in ro-vibrational calculations have the form (23) $\sum _{ab}{c}_{ab}{\psi }_a(\theta ,\varphi ,\chi ){\phi }_b(q_1,\dots ,q_n).$(23) If one applies the full Hamiltonian to the function ${\phi }_b(q_1,\dots ,q_n)$, then the rotational and Coriolis parts drop out, and we can find the transformation of $\hat{H}\phi$ under MS operations. The vibrational operators then transform as ${\hat{\pi }}_k^{\prime }={\hat{\pi }}_{k^{\prime }}$, i.e. without the second term, and the Hamiltonian is invariant, showing the vibrational eigenfunctions also are irreps of the same group [18].

To symmetrise the rotational part, however, a standard choice of basis functions are the rigid rotors functions $|J,k,m〉$ [36]. These have definite transformation properties under the rotations defined in Table 3, given by (24) $R_z^{\text{β}}|J,k,m〉=e^{ik\text{β}}|J,k,m〉$(24) and (25) $R_{\alpha }^{\pi }|J,k,m〉=(-1{)}^J{e}^{-2ik\alpha }|J,-k,m〉.$(25) If we refer back to our ABA example and instead use the principal axis system at the vibrational equilibrium, shown in Figure 3, with the z-axis pointing out of the plane and the y-axis bisecting the ABA angle, then one can follow the prescription of Section. 12.1 of [18] and find the ‘equivalent rotations’ of the axes during an MS operation. There are four symmetry operations for the MS group ${\mathcal{C}}_{2\mathrm{v}}$(M): $\{E,E^{\ast },(12),(12{)}^{\ast }\}$, and they have the equivalent rotations of $R_z^0,R_z^{\pi },R_{\pi /2}^{\pi },R_0^{\pi }$, respectively. This results in the transformation properties of $(|J,k,m〉,|J,-k,m〉)$ being (26) $\begin{array}{rl}{R}^0\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)& =\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\\ R_z^{\pi }\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)& =(-1{)}^k\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\\ R_{\pi /2}^{\pi }\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)& =(-1{)}^{J+k}\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\\ R_0^{\pi }\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)& =(-1{)}^J\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\end{array}$(26) which is a representation of the MS group ${\mathcal{C}}_{2\mathrm{v}}$(M) of the ABA molecule. Irreducible representations can be formed through standard projection operator techniques [18]. The result is that the symmetrised functions $|J,|k|,m,p〉$ have the form (27) $|J,|k|,m,p〉=\frac{1}{\sqrt{2}}(|J,k,m〉+p(J,|k|\left)|J,-k,m〉\right)$(27) where $p(J,|k|)=\pm 1$. The values of p and the symmetry are summarised in Table 4.

Figure 3. The principal axis system for the ABA molecule in vibrational equilibrium with the z-axis pointing out of the plane and the y-axis bisecting the A1–B–A2 bond. The axes are offset for clarity.

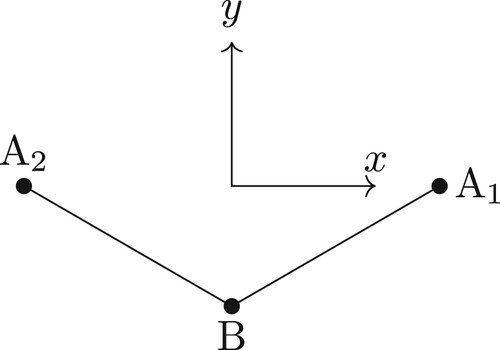
Table 4. The irrep of the function $|J,|k|,m,p〉$ for the MS group ${\mathcal{C}}_{2\mathrm{v}}$(M) depending on the values of J, $|k|$ and p.

J	k	$p(J,|k\left|\right)$	Γ
even	even	1	A${}_1$
even	even	$-1$	A${}_2$
odd	even	$-1$	A${}_1$
odd	even	1	A${}_2$
even	odd	$-1$	B${}_1$
even	odd	1	B${}_2$
odd	odd	1	B${}_1$
odd	odd	$-1$	B${}_2$

The key aspect of these transformations that enable this is that the transformation matrices are constant (up to J and k) which allow standard combinations of the rigid rotors (dependant on J and k) that transform irreducibly under the MS group transformations [15].

In our original example, however, we saw that the rotations associated with the MS group were not the equivalent rotations, nor were they constant. The operation (12), for example, included the rotations $R_0^{\pi }{R}_z^{q_3}$ whose effect on the rigid rotors is (28) $\begin{array}{rl}& R_0^{\pi }{R}_z^{q_3}\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\\ & =(-1{)}^J\left(\begin{array}{cc}0& e^{-ik{q}_3}\\ e^{ik{q}_3}& 0\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right).\end{array}$(28) With this transformation, the representation of the group now depends on the angle $q_3$, and one can no longer form $q_3$ independent combinations of the rigid rotors that transform as the irreps of the group. For example, if J and k are both even, the A${}_1$ irrep has the form (29) ${|J,|k|〉}^{{\mathrm{A}}_1}=\frac{1}{\sqrt{2}}(|J,k,m〉+e^{-ik{q}_3}|J,-k,m〉).$(29) Thus, one cannot have separate symmetry-adapted rotational functions used in Equation (1(1) ${\psi }_a(\theta ,\varphi ,\chi {)}^{{\mathrm{\Gamma }}_{\mathrm{r}\mathrm{o}\mathrm{t}}^{i_a}}\times {\phi }_b(q_1,\dots ,q_n{)}^{{\mathrm{\Gamma }}_{\mathrm{v}\mathrm{i}\mathrm{b}}^{i_b}}$(1) ) using this choice of BF-frame. A separate rotational basis set can still be used, but it cannot be assigned a symmetry label of the group in question. To do this, a different BF-frame is required. Alternatively, one could use the $q_3$ dependent symmetry-adapted rotational functions and take them into account when performing further calculations.

The upshot of this result is that to keep the rotational and vibrational coordinates separate, and thus for the rotational functions to transform with matrices that do not depend on the vibrational coordinates, the rotation angle must be constant and its axis of rotation relative to the BF-frame must also be constant. This will ensure N is constant and ${\dot{\gamma }}_k=0$. Whatever the rotation axis is, the angle must be $2\pi /n$ where n is the order of the MS operation.

5. ABA example

5.1. Bond vector frame

To demonstrate the MS transformation of the KEO and its invariance, we return to the ABA molecule in more detail. For our original BF-frame we know that matrix N for the operation (12) is Equation (14(14) $N_{\left(12\right)}=\left(\begin{array}{ccc}\cos q_3& \phantom{-}\sin q_3& 0\\ \sin q_3& -\cos q_3& 0\\ 0& 0& -1\end{array}\right).$(14) ). The components of the G matrix are as follows [37]: the rotational part is (30) $\begin{array}{rl}{G}_{\mathrm{r}\mathrm{o}\mathrm{t}}& =(\begin{array}{c}{\displaystyle \frac{\cot q_3^2}{{\mu }_{\mathrm{A}\mathrm{B}}{q}_1^2}}+{\displaystyle \frac{\csc q_3^2}{{\mu }_{\mathrm{A}\mathrm{B}}{q}_2^2}}-{\displaystyle \frac{2\cot q_3\csc q_3}{m_{\mathrm{B}}{q}_1{q}_2}}\\ {\displaystyle \frac{\cot q_3}{{\mu }_{\mathrm{A}\mathrm{B}}{q}_1^2}}-{\displaystyle \frac{\csc q_3}{m_{\mathrm{B}}{q}_1{q}_2}}\\ 0\end{array}\\ & \begin{array}{cc}{\displaystyle \frac{\cot q_3}{{\mu }_{\mathrm{A}\mathrm{B}}{q}_1^2}}-{\displaystyle \frac{\csc q_3}{m_{\mathrm{B}}{q}_1{q}_2}}& 0\\ {\displaystyle \frac{1}{{\mu }_{\mathrm{A}\mathrm{B}}{q}_1^2}}& 0\\ 0& {\displaystyle \frac{1}{{\mu }_{\mathrm{A}\mathrm{B}}{q}_1^2}}\end{array})\end{array}$(30) where ${\mu }_{\mathrm{A}\mathrm{B}}$ is the reduced mass (31) $\frac{1}{{\mu }_{\mathrm{A}\mathrm{B}}}=\frac{1}{m_{\mathrm{A}}}+\frac{1}{m_{\mathrm{B}}}$(31) and $m_{\mathrm{A}}$ and $m_{\mathrm{B}}$ are the masses of A and B, respectively; the Coriolis part is (32) $G_{\mathrm{c}\mathrm{o}\mathrm{r}}=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& {\displaystyle \frac{\sin q_3}{m_{\mathrm{B}}{q}_1}}\\ 0& 0& -{\displaystyle \frac{1}{{\mu }_{\mathrm{A}\mathrm{B}}{q}_1^2}}+{\displaystyle \frac{\cos q_3}{m_{\mathrm{B}}{q}_1{q}_2}}.\end{array}\right)$(32) where the rows correspond to the vibrational coordinates and the columns to the axes; the vibrational part of the G matrix (33) $\begin{array}{rl}{G}_{\mathrm{v}\mathrm{i}\mathrm{b}}& =(\begin{array}{cc}{\displaystyle \frac{1}{{\mu }_{\mathrm{A}\mathrm{B}}}}& {\displaystyle \frac{\cos q_3}{m_{\mathrm{B}}}}\\ {\displaystyle \frac{\cos q_3}{m_{\mathrm{B}}}}& {\displaystyle \frac{1}{{\mu }_{\mathrm{A}\mathrm{B}}}}\\ -{\displaystyle \frac{\sin q_3}{m_{\mathrm{B}}{q}_2}}& -{\displaystyle \frac{\sin q_3}{m_{\mathrm{B}}{q}_1}}\end{array}\\ & \begin{array}{c}-{\displaystyle \frac{\sin q_3}{m_{\mathrm{B}}{q}_2}}\\ -{\displaystyle \frac{\sin q_3}{m_{\mathrm{B}}{q}_1}}\\ {\displaystyle \frac{1}{{\mu }_{\mathrm{A}\mathrm{B}}}}({\displaystyle \frac{1}{q_1^2}}+{\displaystyle \frac{1}{q_2^2}})-{\displaystyle \frac{2\cos q_3}{M_B{q}_1{q}_2}}\end{array}).\end{array}$(33) If we list the vibrational momentum and angular momentum operators as (34) $\hat{\mathrm{\Pi }}=\left(\begin{array}{c}{\hat{\pi }}_1\\ {\hat{\pi }}_2\\ {\hat{\pi }}_3\end{array}\right),\hat{J}=\left(\begin{array}{c}{\hat{J}}_x\\ {\hat{J}}_y\\ {\hat{J}}_z\end{array}\right)$(34) then the full kinetic energy operator (besides the pseudo-potential) is given by $\frac{1}{2}{\hat{\mathrm{\Pi }}}^T{G}_{\mathrm{v}\mathrm{i}\mathrm{b}}\hat{\mathrm{\Pi }}+\frac{1}{2}{\hat{\mathrm{\Pi }}}^T{G}_{\mathrm{c}\mathrm{o}\mathrm{r}}\hat{J}+\frac{1}{2}{\hat{J}}^T{G}_{\mathrm{c}\mathrm{o}\mathrm{r}}^T\hat{\mathrm{\Pi }}+\frac{1}{2}{\hat{J}}^T{G}_{\mathrm{r}\mathrm{o}\mathrm{t}}\hat{J}.$During the MS operation, we transform $q_1\leftrightarrow q_2$ in each of the G matrix elements. The operator $\hat{\mathrm{\Pi }}$ transforms to (35) ${\hat{\mathrm{\Pi }}}^{\prime }=C\hat{\mathrm{\Pi }}-D\hat{J}$(35) where C and D are given by (36) $C=\left(\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right),D=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right).$(36) The rotational operators transform as ${\hat{J}}^{\prime }=N_{\left(12\right)}^T\hat{J}\equiv N^T\hat{J}$. The transformed kinetic energy operator is then (37) $\begin{array}{rl}& \phantom{+}\frac{1}{2}{\hat{\mathrm{\Pi }}}^T\underset{G_{\mathrm{v}\mathrm{i}\mathrm{b}}}{\underbrace{\left(C^T{\tilde{G}}_{\mathrm{v}\mathrm{i}\mathrm{b}}C\right)}}\hat{\mathrm{\Pi }}\\ & +\frac{1}{2}{\hat{\mathrm{\Pi }}}^T\underset{G_{\mathrm{c}\mathrm{o}\mathrm{r}}}{\underbrace{(C^T{\tilde{G}}_{\mathrm{c}\mathrm{o}\mathrm{r}}{N}^T-C^T{\tilde{G}}_{\mathrm{v}\mathrm{i}\mathrm{b}}D)}}\hat{J}\\ & +\frac{1}{2}{\hat{J}}^T\underset{G_{\mathrm{c}\mathrm{o}\mathrm{r}}^T}{\underbrace{(N{\tilde{G}}_{\mathrm{c}\mathrm{o}\mathrm{r}}^{T}C-D^T{\tilde{G}}_{\mathrm{v}\mathrm{i}\mathrm{b}}C)}}\hat{\mathrm{\Pi }}\\ & +\frac{1}{2}{\hat{J}}^T\underset{G_{\mathrm{r}\mathrm{o}\mathrm{t}}}{\underbrace{\begin{array}{c}(N{\tilde{G}}_{\mathrm{r}\mathrm{o}\mathrm{t}}{N}^T+D^T{\tilde{G}}_{\mathrm{v}\mathrm{i}\mathrm{b}}D\\ -D^T{\tilde{G}}_{\mathrm{c}\mathrm{o}\mathrm{r}}{N}^T-N{\tilde{G}}_{\mathrm{c}\mathrm{o}\mathrm{r}}^{T}D)\end{array}}}\hat{J}\end{array}$(37) where the expressions in brackets can be confirmed to be the original G matrix elements. The other generator for the MS group of the ABA molecule is $E^{\ast }$. For this operation, the vibrational coordinates are unchanged so that ${\tilde{r}}_{\alpha }=r_{\alpha }$. For ${R_{\alpha }}^{\prime }=-R_{\alpha }$ to be satisfied, the BF-frame rotates by π about the z-axis. The rotation $N_{E^{\ast }}$ is then (38) $N_{E^{\ast }}=M_z\left(\pi \right)=\left(\begin{array}{ccc}-1& 0& 0\\ 0& -1& 0\\ 0& 0& 1\end{array}\right)$(38) and we have ${R_{\alpha }}^{\prime }=M{N}_{E^{\ast }}{\tilde{r}}_{\alpha }=-R_{\alpha }$, as required. The corresponding operation $R_z^{\pi }$ changes the rigid rotors by the second line of Equation (26(26) $\begin{array}{rl}{R}^0\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)& =\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\\ R_z^{\pi }\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)& =(-1{)}^k\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\\ R_{\pi /2}^{\pi }\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)& =(-1{)}^{J+k}\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\\ R_0^{\pi }\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)& =(-1{)}^J\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\end{array}$(26) ) and thus an irreducible representation for the subgroup $\{E,E^{\ast }\}$ can be formed. In other words, we can use a product basis set with this BF-frame to symmetrise the rotation basis functions by parity (the subgroup $\{E,E^{\ast }\}$), but not of the full MS group ${\mathcal{C}}_{2\mathrm{v}}$(M).

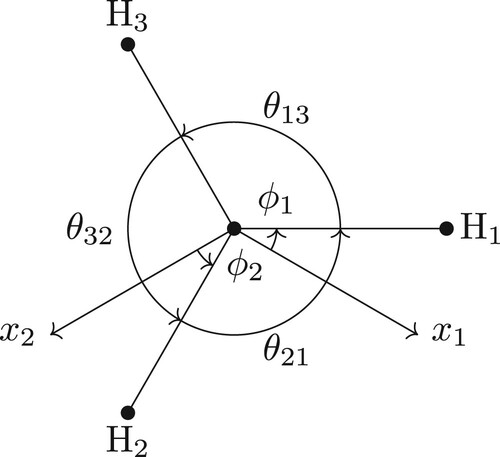
5.2. Bisector frame

Another obvious BF-frame choice for the ABA molecule is the y-axis bisecting the angle and the z-axis pointing out of the plane. The equivalent rotations for this frame were given in Equation (26(26) $\begin{array}{rl}{R}^0\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)& =\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\\ R_z^{\pi }\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)& =(-1{)}^k\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\\ R_{\pi /2}^{\pi }\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)& =(-1{)}^{J+k}\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\\ R_0^{\pi }\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)& =(-1{)}^J\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}|J,k,m〉\\ |J,-k,m〉\end{array}\right)\end{array}$(26) ). There is a subtle difference, however. In that frame, the y-axis bisects ABA angle as this is the orientation of the principal axis system at vibrational equilibrium. In this case, the y-axis bisects the ABA angle for all geometries. The BF Cartesian coordinates in this frame are given by (39) $\begin{array}{rl}{r}_{\mathrm{A}1}& =(q_1\sin (q_3/2),q_1\cos (q_3/2),0)\\ r_{\mathrm{A}2}& =(-q_2\sin (q_3/2),q_2\cos (q_3/2),0)\\ r_{\mathrm{B}}& =(0,0,0).\end{array}$(39) This time, when we apply the (12) operation, the matrix $N_{\left(12\right)}$ given by (40) $N_{\left(12\right)}=M_y\left(\pi \right)=\left(\begin{array}{ccc}-1& 0& 0\\ 0& 1& 0\\ 0& 0& -1\end{array}\right)$(40) has exactly the property that ${R_1}^{\prime }=M{N}_{\left(12\right)}{\tilde{r}}_1=R_2$, and likewise for $R_2$. In this case, we can build a symmetry adapted rotational basis set because the rotation angle is $\pi =2\pi /2$ and the axis of rotation is constant relative to the BF-frame for this operation.

For this frame, the vibrational G matrix is [37] Equation (33(33) $\begin{array}{rl}{G}_{\mathrm{v}\mathrm{i}\mathrm{b}}& =(\begin{array}{cc}{\displaystyle \frac{1}{{\mu }_{\mathrm{A}\mathrm{B}}}}& {\displaystyle \frac{\cos q_3}{m_{\mathrm{B}}}}\\ {\displaystyle \frac{\cos q_3}{m_{\mathrm{B}}}}& {\displaystyle \frac{1}{{\mu }_{\mathrm{A}\mathrm{B}}}}\\ -{\displaystyle \frac{\sin q_3}{m_{\mathrm{B}}{q}_2}}& -{\displaystyle \frac{\sin q_3}{m_{\mathrm{B}}{q}_1}}\end{array}\\ & \begin{array}{c}-{\displaystyle \frac{\sin q_3}{m_{\mathrm{B}}{q}_2}}\\ -{\displaystyle \frac{\sin q_3}{m_{\mathrm{B}}{q}_1}}\\ {\displaystyle \frac{1}{{\mu }_{\mathrm{A}\mathrm{B}}}}({\displaystyle \frac{1}{q_1^2}}+{\displaystyle \frac{1}{q_2^2}})-{\displaystyle \frac{2\cos q_3}{M_B{q}_1{q}_2}}\end{array}).\end{array}$(33) ).

The rotational G matrix is (41) $\begin{array}{rl}{G}_{\mathrm{r}\mathrm{o}\mathrm{t}}& =(\begin{array}{c}{\displaystyle \frac{{\sec }^2\left(q_3/2\right)}{4{\mu }_{\mathrm{A}\mathrm{B}}}}({\displaystyle \frac{1}{q_2^2}}+{\displaystyle \frac{1}{q_1^2}})+{\displaystyle \frac{{\sec }^2\left(q_3/2\right)}{2m_{\mathrm{B}}{q}_1{q}_2}}\\ {\displaystyle \frac{\csc q_3}{2{\mu }_{\mathrm{A}\mathrm{B}}}}({\displaystyle \frac{1}{q_2^2}}-{\displaystyle \frac{1}{q_1^2}})\\ 0\end{array}\\ & \begin{array}{c}{\displaystyle \frac{\csc q_3}{2{\mu }_{\mathrm{A}\mathrm{B}}}}({\displaystyle \frac{1}{q_2^2}}-{\displaystyle \frac{1}{q_1^2}})\\ {\displaystyle \frac{{\csc }^2\left(q_3/2\right)}{4{\mu }_{\mathrm{A}\mathrm{B}}}}({\displaystyle \frac{1}{q_2^2}}+{\displaystyle \frac{1}{q_1^2}})-{\displaystyle \frac{{\csc }^2\left(q_3/2\right)}{2m_{\mathrm{B}}{q}_1{q}_2}}\\ 0\end{array}\\ & \begin{array}{c}0\\ 0\\ {\displaystyle \frac{1}{4{\mu }_{\mathrm{A}\mathrm{B}}}}({\displaystyle \frac{1}{q_2^2}}+{\displaystyle \frac{1}{q_1^2}})+{\displaystyle \frac{\cos q_3}{4m_{\mathrm{B}}{q}_1{q}_2}}\end{array}).\end{array}$(41) The Coriolis G matrix is (42) $G_{\mathrm{c}\mathrm{o}\mathrm{r}}=\left(\begin{array}{ccc}0& 0& -{\displaystyle \frac{\sin q_3}{2m_{\mathrm{B}}{q}_2}}\\ 0& 0& {\displaystyle \frac{\sin q_3}{2m_{\mathrm{B}}{q}_1}}\\ 0& 0& {\displaystyle \frac{1}{2{\mu }_{\mathrm{A}\mathrm{B}}}}({\displaystyle \frac{1}{q_2^2}}-{\displaystyle \frac{1}{q_1^2}})\end{array}\right).$(42) In this BF-frame, D = 0 for operation (12). One can again use Equation (37(37) $\begin{array}{rl}& \phantom{+}\frac{1}{2}{\hat{\mathrm{\Pi }}}^T\underset{G_{\mathrm{v}\mathrm{i}\mathrm{b}}}{\underbrace{\left(C^T{\tilde{G}}_{\mathrm{v}\mathrm{i}\mathrm{b}}C\right)}}\hat{\mathrm{\Pi }}\\ & +\frac{1}{2}{\hat{\mathrm{\Pi }}}^T\underset{G_{\mathrm{c}\mathrm{o}\mathrm{r}}}{\underbrace{(C^T{\tilde{G}}_{\mathrm{c}\mathrm{o}\mathrm{r}}{N}^T-C^T{\tilde{G}}_{\mathrm{v}\mathrm{i}\mathrm{b}}D)}}\hat{J}\\ & +\frac{1}{2}{\hat{J}}^T\underset{G_{\mathrm{c}\mathrm{o}\mathrm{r}}^T}{\underbrace{(N{\tilde{G}}_{\mathrm{c}\mathrm{o}\mathrm{r}}^{T}C-D^T{\tilde{G}}_{\mathrm{v}\mathrm{i}\mathrm{b}}C)}}\hat{\mathrm{\Pi }}\\ & +\frac{1}{2}{\hat{J}}^T\underset{G_{\mathrm{r}\mathrm{o}\mathrm{t}}}{\underbrace{\begin{array}{c}(N{\tilde{G}}_{\mathrm{r}\mathrm{o}\mathrm{t}}{N}^T+D^T{\tilde{G}}_{\mathrm{v}\mathrm{i}\mathrm{b}}D\\ -D^T{\tilde{G}}_{\mathrm{c}\mathrm{o}\mathrm{r}}{N}^T-N{\tilde{G}}_{\mathrm{c}\mathrm{o}\mathrm{r}}^{T}D)\end{array}}}\hat{J}\end{array}$(37) ) to confirm the invariance of the G matrix.

5.3. Frame conditions

A more qualitative way to understand these results, which will prove important when studying the Eckart frames, is to examine the three conditions which define the BF-frame in the Sørensen approach. These conditions are, in general, functions of the BF Cartesian components $C^g(r_1,\dots ,r_n)$ which must be zero at all times. In the case of the bisector frame of the ABA molecule (43) $\begin{array}{rl}{C}^1& =z_{{\mathrm{A}}_1}-z_B=0\\ C^2& =z_{{\mathrm{A}}_2}-z_B=0\\ C^3& =(x_{{\mathrm{A}}_1}-x_B)(y_{{\mathrm{A}}_2}-y_B)\\ & +(x_{{\mathrm{A}}_2}-x_B)(y_{{\mathrm{A}}_1}-y_B)=0\end{array}$(43) where the subscript refers to the atom the coordinate refers to. The first two conditions specify that the z-axis is perpendicular to the A₁-B-A₂ plane and the last that the y-axis bisects A₁-B-A₂ angle. It should be pointed out that these do not totally define the BF-frame orientation, as we can rotate the BF-frame by π about any of the BF-frame axes and the conditions would still hold. One must supplement these conditions with the BF Cartesian coordinates defined in terms of the vibrational coordinates. These implicitly assume the BF-frame the conditions define. In general, the conditions also do not define the handedness of the axes as one can change all the BF Cartesian coordinates $r_i$ to $-r_i$ (i.e. make the axes left handed) and the conditions would still hold.

An MS operation applied to each condition relabels the BF Cartesian coordinates. The result is the transformed BF Cartesian coordinates in the original BF-frame. For example, for the (12) operation, they become (44) $\begin{array}{rl}{C^1}^{\prime }& =z_{{\mathrm{A}}_2}-z_B=0\\ {C^2}^{\prime }& =z_{{\mathrm{A}}_1}-z_B=0\\ {C^3}^{\prime }& =(x_{{\mathrm{A}}_2}-x_B)(y_{{\mathrm{A}}_1}-y_B)+(x_{{\mathrm{A}}_1}-x_B)(y_{{\mathrm{A}}_2}-y_B)=0\end{array}$(44) which are actually still zero, a manifestation of the possible choice we had in the BF-frame that satisfies these conditions. We know that we must apply a π rotation about the z-axis, after which they become (45) $\begin{array}{rl}{C^1}^{\prime }& =z_{{\mathrm{A}}_2}-z_B=0\\ {C^2}^{\prime }& =z_{{\mathrm{A}}_1}-z_B=0\\ {C^3}^{\prime }& =(x_{{\mathrm{A}}_2}-x_B)(y_{{\mathrm{A}}_1}-y_B)\\ & +(x_{{\mathrm{A}}_1}-x_B)(y_{{\mathrm{A}}_2}-y_B)=0\end{array}$(45) which are the original conditions and thus zero.

In the bond vector frame choice of the molecule, the conditions were (46) $\begin{array}{rl}{C}^1& =z_{{\mathrm{A}}_2}-z_B=0\\ C^2& =z_{{\mathrm{A}}_1}-z_B=0\\ C^3& =y_{{\mathrm{A}}_1}-y_B=0\end{array}$(46) which after a transformation of $\left(12\right)$ and a rotation by π are (47) $\begin{array}{rl}{C^1}^{\prime }& =z_{{\mathrm{A}}_1}-z_B=0\\ {C^2}^{\prime }& =z_{{\mathrm{A}}_2}-z_B=0\\ {C^3}^{\prime }& =-y_{{\mathrm{A}}_2}+y_B.\end{array}$(47) The last condition is in general not zero.

5.4. Eckart frame

Approaching the problem from this point of view provides us with an alternative way to check if the BF-frame undergoes a constant rotation under MS operations. This is especially useful when the BF Cartesian coordinates as functions of the vibrational coordinates are not available analytically. In particular, we can check that the Eckart frame also satisfies the aforementioned rotation condition.

The conditions for the Eckart frame are defined as [38] (48) $C=\sum _{\alpha }{m}_{\alpha }{a}_{\alpha }\times r_{\alpha }$(48) where the equilibrium frame is defined to be the principal axis system (PAS). The $a_{\alpha g}$ are the BF Cartesian components of the nuclei at equilibrium and enter the condition as constants. As stated above, the PAS for the ABA molecule in vibrational equilibrium is the bisector. We thus have (49) $\left(m_{\mathrm{A}}\right[a_{{\mathrm{A}}_1}\times r_{{\mathrm{A}}_1}+a_{{\mathrm{A}}_2}\times r_{{\mathrm{A}}_2}]+m_{\mathrm{B}}{a}_{\mathrm{B}}\times r_{\mathrm{B}})=0$(49) where $a_{{\mathrm{A}}_1}$, $a_{{\mathrm{A}}_2}$ and $a_{\mathrm{B}}$ are of the form (50) $a_{{\mathrm{A}}_1}=\left(\begin{array}{c}b\\ c\\ 0\end{array}\right),a_{{\mathrm{A}}_2}=\left(\begin{array}{c}-b\\ c\\ 0\end{array}\right),a_{\mathrm{B}}=\left(\begin{array}{c}0\\ d\\ 0\end{array}\right).$(50) In particular, if $N_{\left(12\right)}\equiv N=M_y\left(\pi \right)$, then $a_{{\mathrm{A}}_2}=N^T{a}_{{\mathrm{A}}_1}$ and $a_{\mathrm{B}}=N^T{a}_{\mathrm{B}}$. Once the operation (12) is applied, we have (51) $\left(m_{\mathrm{A}}\right[a_{{\mathrm{A}}_1}\times r_{{\mathrm{A}}_2}+a_{{\mathrm{A}}_2}\times r_{{\mathrm{A}}_1}]+m_{\mathrm{B}}{a}_{\mathrm{B}}\times r_{\mathrm{B}})$(51) where we reiterate that the components $r_{\alpha }$ are in the original BF-frame. If we then rotate the frame the new conditions are (52) $\begin{array}{rl}{C}^{\prime }& =\left(m_{\mathrm{A}}\right[a_{{\mathrm{A}}_1}\times N{r}_{{\mathrm{A}}_2}+a_{{\mathrm{A}}_2}\times N{r}_{{\mathrm{A}}_1}]+m_{\mathrm{B}}{a}_{\mathrm{B}}\times N{r}_{\mathrm{B}})\\ & =N{N}^T\left(m_{\mathrm{A}}\right[a_{{\mathrm{A}}_1}\times N{r}_{{\mathrm{A}}_2}+a_{{\mathrm{A}}_2}\times N{r}_{{\mathrm{A}}_1}]\\ & +m_{\mathrm{B}}{a}_{\mathrm{B}}\times N{r}_{\mathrm{B}})\\ & =N\left(m_{\mathrm{A}}\right[N^T{a}_{{\mathrm{A}}_1}\times r_{{\mathrm{A}}_2}+N^T{a}_{{\mathrm{A}}_2}\times r_{{\mathrm{A}}_1}]\\ & +m_{\mathrm{B}}{N}^T{a}_{\mathrm{B}}\times r_{\mathrm{B}})\\ & =N\left(m_{\mathrm{A}}\right[a_{{\mathrm{A}}_2}\times r_{{\mathrm{A}}_2}+a_{{\mathrm{A}}_1}\times r_{{\mathrm{A}}_1}]+m_{\mathrm{B}}{a}_{\mathrm{B}}\times r_{\mathrm{B}})=0\end{array}$(52) where in the second line we applied $I=N{N}^T$ to the conditions and in the third line used the property that, if N is a rotation, $N(a\times b)=Na\times Nb$. The last line is N applied to the original conditions and therefore zero.

The operation $E^{\ast }$ is even easier and can be trivially shown to work as the operation changes the $r_i$ to $-r_i$ while $M_z(\pi {)}^{T}a\equiv N^{T}a=-a$. We have therefore shown that the Eckart frames are applicable for ABA molecules if one desires a symmetry-adapted rotational basis set.

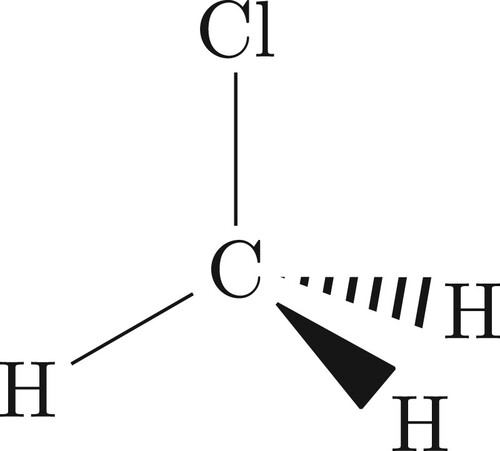
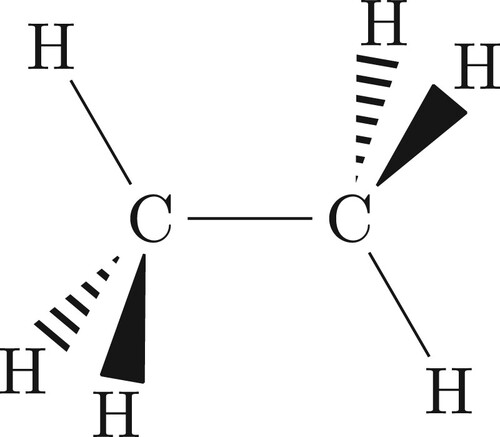
6. CH₃Cl example

6.1. Eckart frame

For ABA molecules, it was relatively straightforward to choose alternative (to Eckart) axes with which one could symmetrise the rotational basis functions. For other molecules the choice is not so simple. We introduce the example of CH₃Cl (shown in Figure 4) and again demonstrate the Eckart frame (whose equilibrium orientation is shown in Figure 5) can be employed to build a symmetry-adapted rotational basis set and also describe an alternative and geometric frame which one can also use.

Figure 4. The structure of the CH₃Cl molecule.

Figure 5. The equilibrium Eckart frame for CH₃Cl. The z-axis is along the C–Cl bond and the x-axis in the plane formed by Cl–C–H${}_1$.

The Eckart conditions for CH₃Cl are (53) $\begin{array}{rl}& \left(\right[m_C{a}_C\times r_C+m_{Cl}{a}_{Cl}\times r_{Cl}]+m_H[a_{H1}\times r_{H1}\\ & +a_{H2}\times r_{H2}+a_{H3}\times r_{H3}\left]\right)=0\end{array}$(53) where the PAS frame for the equilibrium geometry is shown in Figure 5. Because of this, both $a_{Cl}$ and $a_C$ only have a z component.

The MS group of CH₃Cl is ${\mathcal{C}}_{3\mathrm{v}}$(M) and can be constructed from two generating operations (123) and $(23{)}^{\ast }$ with equivalent rotations of $R_z^{2\pi /3}$ and $R_{\pi /2}^{\pi }$, respectively.

For the operation (123), we can relate the equilibrium coordinates as $a_{H2}=A^2{a}_{H1}$ and $a_{H3}=A{a}_{H1}$ where $A=M_z\left(2\pi /3\right)$ from Equation (7(7) $\begin{array}{rl}{M}_z\left(\varphi \right)& =\left(\begin{array}{ccc}\cos \varphi & -\sin \varphi & 0\\ \sin \varphi & \cos \varphi & 0\\ 0& 0& 1\end{array}\right),\\ M_y\left(\theta \right)& =\left(\begin{array}{ccc}\cos \theta & 0& \sin \theta \\ 0& 1& 0\\ -\sin \theta & 0& \cos \theta \end{array}\right),\\ M_z\left(\chi \right)& =\left(\begin{array}{ccc}\cos \chi & -\sin \chi & 0\\ \sin \chi & \cos \chi & 0\\ 0& 0& 1\end{array}\right)\end{array}$(7) ). The Eckart conditions can thus be can be expressed as (54) $\begin{array}{rl}& \left(\right[m_C{a}_C\times r_C+m_{Cl}{a}_{Cl}\times r_{Cl}]+m_H[a_{H1}\times r_{H1}\\ & +A^2{a}_{H1}\times r_{H2}+A{a}_{H1}\times r_{H3}\left]\right)=0.\end{array}$(54) Applying the operation (123), the Eckart conditions become (55) $\begin{array}{rl}& \left(\right[m_C{a}_C\times r_C+m_{Cl}{a}_{Cl}\times r_{Cl}]+m_H[a_{H1}\times r_{H3}\\ & +A^2{a}_{H1}\times r_{H1}+A{a}_{H1}\times r_{H2}\left]\right).\end{array}$(55) As usual, we rotate the frame, in this case by $R_z^{2\pi /3}$. This transforms $r_i$ to $A^T{r}_i$. Using the same procedure as for the ABA case we can rewrite this as (56) $\begin{array}{rl}& A^T\left(\right[m_C{a}_C\times r_C+m_{Cl}{a}_{Cl}\times r_{Cl}]+m_H[A{a}_{H1}\times r_{H3}\\ & +a_{H1}\times r_{H1}+A^2{a}_{H1}\times r_{H2}\left]\right)=0\end{array}$(56) where we used that A applied to the equilibrium coordinates of Cl or C does not change them. The final result is precisely the same as in the case of ABA.

For the operation $(23{)}^{\ast }$, the rotation matrix is $N=M_y\left(\pi \right)$. We can again relate the equilibrium coordinates by $N{a}_{H2}=-a_{H3}$ and vice versa. Also, $N{a}_{H1}=-a_{H1}$ and likewise for C and Cl. The Eckart conditions can thus be written (57) $\begin{array}{rl}& \left(\right[-m_{C}N{a}_C\times r_C-m_{Cl}N{a}_{Cl}\times r_{Cl}]\\ & -m_H[N{a}_{H1}\times r_{H1}-N{a}_{H3}\\ & \times r_{H2}-N{a}_{H2}\times r_{H3}\left]\right)=0.\end{array}$(57) The result after applying $(23{)}^{\ast }$ is (58) $\begin{array}{rl}& \left(\right[m_{C}N{a}_C\times r_C+m_{Cl}N{a}_{Cl}\times r_{Cl}]\\ & +m_H[N{a}_{H1}\times r_{H1}+N{a}_{H3}\times r_{H3}+N{a}_{H2}\times r_{H2}]).\end{array}$(58) Rotating the frame by N, multiplying the conditions by $N{N}^T$, and using the same steps as before, we have (59) $\begin{array}{rl}& N\left(\right[m_C{a}_C\times r_C+m_{Cl}{a}_{Cl}\times r_{Cl}]\\ & +m_H[a_{H1}\times r_{H1}+a_{H3}\times r_{H3}+a_{H3}\times r_{H3}])=0.\end{array}$(59) The technique used in this proof can be applied to many different molecules where the Eckart frame is used as it relied on relations between the equilibrium Cartesian coordinates of the molecule. In vibrational equilibrium, the Cartesian coordinates of the nuclei are related to each other by constant rotations. These rotations can be found, for example, through graphical means, which is the technique used to find the equivalent rotations explained in [18]. Alternatively, although the form of the BF Cartesian coordinates as a function of vibrational coordinates for all geometries is not known, their equilibrium ‘structure’ (à la Equation (50(50) $a_{{\mathrm{A}}_1}=\left(\begin{array}{c}b\\ c\\ 0\end{array}\right),a_{{\mathrm{A}}_2}=\left(\begin{array}{c}-b\\ c\\ 0\end{array}\right),a_{\mathrm{B}}=\left(\begin{array}{c}0\\ d\\ 0\end{array}\right).$(50) )) is. The required rotation for an MS operation can then be found by satisfying $a_{{\alpha }^{\prime }}=N{\tilde{a}}_{\alpha }=N{a}_{\alpha }$, where $a_{\alpha }$ are the equilibrium BF Cartesian coordinates. These do not change under the vibrational coordinate transformation because the vibrational coordinates are effectively frozen. Since the matrix N should be the same regardless of the geometry, if it is found in vibrational equilibrium, it is found in general. As demonstrated above, if one uses the PAS system at the vibrational equilibrium to define the reference geometry, then the equivalent rotations are the correct rotations of the BF-frame undergoing MS operations.

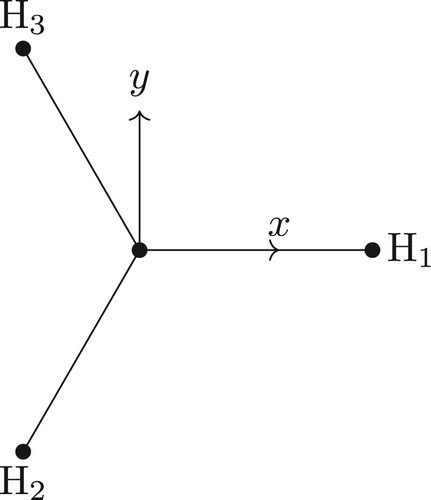
6.2. Geometric CH₃Cl frame

We introduce a frame definition which can be solved analytically. In this case, the z-axis always points parallel the C–Cl bond and the direction of the x-axis is defined by ϕ, given by (60) ${\varphi }_1=\frac{1}{3}({\theta }_{21}-{\theta }_{13})$(60) where ${\theta }_{21}$ is the dihedral angle from the plane formed by Cl–C–H${}_2$ to the plane Cl–C–H${}_1$ and likewise for ${\theta }_{13}$. This is illustrated in Figure 6. Had we decided to start from H₂, the choice of x-axis direction ($x_2$) would be determined by (61) ${\varphi }_2=\frac{1}{3}({\theta }_{32}-{\theta }_{31})$(61) where Figure 7 illustrates this choice. A feature of these choices is the angle between the x-axes, as illustrated in Figure 8, can be found as follows: (62) $\begin{array}{rl}{\theta }_{21}-{\varphi }_1+{\varphi }_2& ={\theta }_{21}-\frac{1}{3}({\theta }_{21}-{\theta }_{13})+\frac{1}{3}({\theta }_{32}-{\theta }_{21})\\ & =\frac{1}{3}({\theta }_{21}+{\theta }_{13}+{\theta }_{32})=\frac{2\pi }{3}.\end{array}$(62) Thus the angle between them is always $2\pi /3$, irrespective of the coordinates of the atoms. It is this property that allows the frame to be used when symmetrising the rotational basis set.

Figure 6. The dihedrals that determine the value of ${\varphi }_1=1/3({\theta }_{21}-{\theta }_{13})$.

Figure 7. The dihedrals that determine the value of ${\varphi }_2=1/3({\theta }_{32}-{\theta }_{21}).$

Figure 8. All the angles relevant angles to determine the angle between $x_1$ and $x_2$.

To demonstrate that, with this frame, the Cartesian coordinates transform correctly under MS operations if the BF-frame rotates by constant angles, let us first parametrise the vibrational coordinates by the Cl–C stretch ($q_1$), the 3 C–H stretches ($q_2$ to $q_4$), the three Cl–C–H bends ($q_5$ to $q_7$), and the symmetrised coordinates defined by (63) $\begin{array}{rl}{q}_8& =\frac{1}{\sqrt{6}}(2{\theta }_{32}-{\theta }_{21}-{\theta }_{13})\\ q_9& =\frac{1}{\sqrt{2}}({\theta }_{21}-{\theta }_{13}).\end{array}$(63) Note that $q_9$ is the angle $3/\sqrt{2}{\varphi }_1$.

The BF Cartesian coordinates in the bond vector frame are given by (with the origin at the C atom) (64) $\begin{array}{rl}{r}_C& =(0,0,0)\\ r_{Cl}& =(0,0,q_1)\\ r_{H1}& =(q_2\sin q_5,0,q_2\cos q_5)\\ r_{H2}& =(q_3\cos {\theta }_{21}\sin q_6,-q_3\sin {\theta }_{21}\sin q_6,q_3\cos q_6)\\ r_{H3}& =(q_4\cos {\theta }_{13}\sin q_7,q_4\sin {\theta }_{13}\sin q_7,q_4\cos q_7).\end{array}$(64) Solving Equation (63(63) $\begin{array}{rl}{q}_8& =\frac{1}{\sqrt{6}}(2{\theta }_{32}-{\theta }_{21}-{\theta }_{13})\\ q_9& =\frac{1}{\sqrt{2}}({\theta }_{21}-{\theta }_{13}).\end{array}$(63) ) for the angles ${\theta }_{21}$ and ${\theta }_{13}$ by using the substitution ${\theta }_{32}=2\pi -{\theta }_{21}-{\theta }_{13}$, we obtain (65) $\begin{array}{rl}{\theta }_{21}& =\frac{4\pi }{6}-\frac{q_8}{\sqrt{6}}+\frac{q_9}{\sqrt{2}}\\ {\theta }_{13}& =\frac{4\pi }{6}-\frac{q_8}{\sqrt{6}}-\frac{q_9}{\sqrt{2}}\end{array}$(65) which can be substituted into Equation (64(64) $\begin{array}{rl}{r}_C& =(0,0,0)\\ r_{Cl}& =(0,0,q_1)\\ r_{H1}& =(q_2\sin q_5,0,q_2\cos q_5)\\ r_{H2}& =(q_3\cos {\theta }_{21}\sin q_6,-q_3\sin {\theta }_{21}\sin q_6,q_3\cos q_6)\\ r_{H3}& =(q_4\cos {\theta }_{13}\sin q_7,q_4\sin {\theta }_{13}\sin q_7,q_4\cos q_7).\end{array}$(64) ). Applying the rotation matrix $M_z\left(\sqrt{2}{q}_9/3\right)$ (the matrix S of Equation (90(90) $N^{T}S{r}_{{\alpha }^{\prime }}=\tilde{S}{\tilde{r}}_{\alpha }$(90) )) to the BF Cartesian coordinates and using the relations $\cos (x+\pi /2)=-\sin x$ and $\sin (x+\pi /2)=\cos x$, the final result is (66) $\begin{array}{rl}{r}_C& =(0,0,0)\\ r_{Cl}& =(0,0,q_1)\\ r_{H1}& =(q_2\cos \left(\frac{\sqrt{2}{q}_9}{3}\right)\sin q_5,\\ & q_2\sin \left(\frac{\sqrt{2}{q}_9}{3}\right)\sin q_5,q_2\cos q_5)\\ r_{H2}& =(-q_3\sin ({\displaystyle \frac{\pi }{6}}-{\displaystyle \frac{q_8}{\sqrt{6}}}+{\displaystyle \frac{q_9}{3\sqrt{2}}})\sin q_6,\\ & -q_3\cos ({\displaystyle \frac{\pi }{6}}-{\displaystyle \frac{q_8}{\sqrt{6}}}+{\displaystyle \frac{q_9}{3\sqrt{2}}})\sin q_6,q_3\cos q_6)\\ r_{H3}& =(-q_4\sin ({\displaystyle \frac{\pi }{6}}-{\displaystyle \frac{q_8}{\sqrt{6}}}-{\displaystyle \frac{q_9}{3\sqrt{2}}})\sin q_7,\\ & q_4\cos ({\displaystyle \frac{\pi }{6}}-{\displaystyle \frac{q_8}{\sqrt{6}}}-{\displaystyle \frac{q_9}{3\sqrt{2}}})\sin q_7,q_4\cos q_7).\end{array}$(66) The operation (123) changes the stretches and angles in the usual manner and changes the dihedrals according to (67) $\begin{array}{rl}{q_8}^{\prime }& =\frac{1}{\sqrt{6}}(2{\theta }_{21}-{\theta }_{13}-{\theta }_{32})\\ {q_9}^{\prime }& =\frac{1}{\sqrt{2}}({\theta }_{13}-{\theta }_{32})\end{array}$(67) or (68) $\left(\begin{array}{c}{q_8}^{\prime }\\ {q_9}^{\prime }\end{array}\right)=\left(\begin{array}{cc}-1/2& \sqrt{3}/2\\ -\sqrt{3}/2& -1/2\end{array}\right)\left(\begin{array}{c}{q}_8\\ q_9\end{array}\right).$(68) The transformed coordinates are then (69) $\begin{array}{rl}{\tilde{r}}_C& =(0,0,0)\\ {\tilde{r}}_{Cl}& =(0,0,q_1)\\ {\tilde{r}}_{H1}& =(q_4\cos (-{\displaystyle \frac{q_8}{\sqrt{6}}}-{\displaystyle \frac{q_9}{3\sqrt{2}}})\sin q_7,\\ & q_4\sin (-{\displaystyle \frac{q_8}{\sqrt{6}}}-{\displaystyle \frac{q_9}{3\sqrt{2}}})\sin q_7,q_4\cos q_7)\\ {\tilde{r}}_{H2}& =(q_2\sin (-{\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{\sqrt{2}{q}_9}{3}})\sin q_5,\\ & -q_2\cos (-{\displaystyle \frac{\pi }{6}}+{\displaystyle \frac{\sqrt{2}{q}_9}{3}})\sin q_5,q_2\cos q_5)\\ {\tilde{r}}_{H3}& =(q_3\sin (-{\displaystyle \frac{\pi }{6}}-{\displaystyle \frac{q_8}{\sqrt{6}}}+{\displaystyle \frac{q_9}{3\sqrt{2}}})\sin q_6,\\ & q_3\cos (-{\displaystyle \frac{\pi }{6}}-{\displaystyle \frac{q_8}{\sqrt{6}}}+{\displaystyle \frac{q_9}{3\sqrt{2}}})\sin q_6,q_3\cos q_6).\end{array}$(69) These are in the new BF-frame. If we now consider them in the old BF-frame via the rotation matrix (70) $\begin{array}{rl}{N}_{\left(123\right)}& =\left(\begin{array}{ccc}-\sin \left(\pi /6\right)& -\cos \left(\pi /6\right)& 0\\ \cos \left(\pi /6\right)& -\sin \left(\pi /6\right)& 0\\ 0& 0& 1\end{array}\right)\\ & =\left(\begin{array}{ccc}-\cos \left(\pi /3\right)& -\sin \left(\pi /3\right)& 0\\ \sin \left(\pi /3\right)& -\cos \left(\pi /3\right)& 0\\ 0& 0& 1\end{array}\right)\end{array}$(70) and apply the first form to ${\tilde{r}}_{H1}$ and ${\tilde{r}}_{H2}$ and the second form to ${\tilde{r}}_{H3}$, we obtain the original coordinates but permuted by (123).

For the operation $(23{)}^{\ast }$, the stretches and angles transform in an obvious way while the dihedrals transform as (71) $\left(\begin{array}{c}{q_8}^{\prime }\\ {q_9}^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& \phantom{-}0\\ 0& -1\end{array}\right)\left(\begin{array}{c}{q}_8\\ q_9\end{array}\right).$(71) Performing this transformation and also applying the matrix $M_y\left(\pi \right)$ to the Cartesian coordinates, we obtain (72) $\begin{array}{rl}{M}_y\left(\pi \right){\tilde{r}}_C& =(0,0,0)=-r_C\\ M_y\left(\pi \right){\tilde{r}}_{Cl}& =(0,0,-q_1)=-r_{Cl}\\ M_y\left(\pi \right){\tilde{r}}_{H1}& =(-q_2\cos \left(\frac{\sqrt{2}{q}_9}{3}\right)\sin q_5,\\ & -q_2\sin \left(\frac{\sqrt{2}{q}_9}{3}\right)\sin q_5,\\ & -q_2\cos q_5\phantom{\left(\frac{\sqrt{2}{q}_9}{3}\right)})=-r_{H1}\\ M_y\left(\pi \right){\tilde{r}}_{H2}& =(q_3\sin ({\displaystyle \frac{\pi }{6}}-{\displaystyle \frac{q_8}{\sqrt{6}}}-{\displaystyle \frac{q_9}{3\sqrt{2}}})\sin q_6,\\ & -q_3\cos ({\displaystyle \frac{\pi }{6}}-{\displaystyle \frac{q_8}{\sqrt{6}}}-{\displaystyle \frac{q_9}{3\sqrt{2}}})\sin q_6,\\ & -q_3\cos q_6\phantom{\left(\frac{\sqrt{2}{q}_9}{3}\right)})=-r_{H3}\\ M_y\left(\pi \right){\tilde{r}}_{H3}& =(q_4\sin ({\displaystyle \frac{\pi }{6}}-{\displaystyle \frac{q_8}{\sqrt{6}}}+{\displaystyle \frac{q_9}{3\sqrt{2}}})\sin q_7,\\ & q_4\cos ({\displaystyle \frac{\pi }{6}}-{\displaystyle \frac{q_8}{\sqrt{6}}}+{\displaystyle \frac{q_9}{3\sqrt{2}}})\sin q_7,\\ & -q_4\cos q_7\phantom{\left(\frac{\sqrt{2}{q}_9}{3}\right)})=-r_{H2}\end{array}$(72) which are the original Cartesian coordinates with 2 and 3 permuted and then inverted.

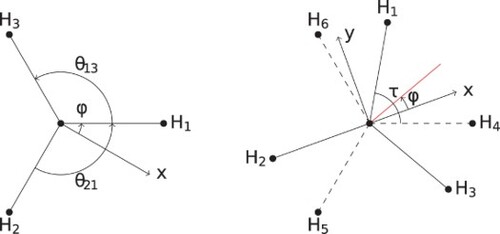
7. C₂H₆ example

7.1. Sayvetz frame

The Sayvetz condition [39] is an addition to the Eckart conditions for non-rigid molecules, defined by (73) $\sum _{\alpha }{m}_{\alpha }{a}_{\alpha }^{\prime }\left(\tau \right)\cdot r_{\alpha }=0$(73) where now the equilibrium Cartesian coordinates $a\left(\tau \right)$ are functions of a non-rigid vibrational coordinate τ where the BF-frame is set to the PAS frame for every value of τ while all other coordinates are in equilibrium. The prime on $a^{\prime }\left(\tau \right)$ signifies that it is a derivative.

We shall prove these conditions work for the C₂H₆ molecule, shown in Figure 9. In the PAS (shown in Figure 10), the x-axis bisects the dihedral formed by H${}_1$–C–C and H${}_4$–C–C while the z-axis is parallel to the C–C bond. The origin is the middle of the C–C bond. The PAS coordinates of H₁ and H₄ are given by (74) $a_{H1}\left(\tau \right)=\left(\begin{array}{c}c\cos \left(\tau /2\right)\\ c\sin \left(\tau /2\right)\\ d\end{array}\right),a_{H4}\left(\tau \right)=\left(\begin{array}{c}\phantom{-}c\cos \left(\tau /2\right)\\ -c\sin \left(\tau /2\right)\\ -d\end{array}\right)$(74) for some c and d. The coordinates of the other atoms are (75) $\begin{array}{rl}& a_{H2}=A{a}_{H1},a_{H3}=A^2{a}_{H1},a_{H6}=A{a}_{H4},\\ & a_{H5}=A^2{a}_{H4},a_{C_b}=-a_{C_a}\end{array}$(75) where $A=M_z\left(2\pi /3\right)$. The carbons only have a z-component and are constants. The Eckart conditions are thus given by (76) $\begin{array}{rl}C& =m_C(a_{C_a}\times r_{C_a}-a_{C_a}\times r_{C_b})\\ & +m_H(a_{H1}\times r_{H1}+A{a}_{H1}\times r_{H2}+A^2{a}_{H1}\times r_{H3}\\ & +a_{H4}\times r_{H4}+A^2{a}_{H4}\times r_{H5}+A{a}_{H4}\times r_{H4})=0.\end{array}$(76) and the Sayvetz condition is given by (77) $\begin{array}{rl}S& =m_C(a_{C_a}^{\prime }\cdot r_{C_a}-a_{C_a}^{\prime }\cdot r_{C_b})\\ & +m_H(a_{H1}^{\prime }\cdot r_{H1}+A{a}_{H1}^{\prime }\cdot r_{H2}+A^2{a}_{H1}^{\prime }\cdot r_{H1}\\ & +a_{H4}^{\prime }\cdot r_{H4}+A^2{a}_{H4}^{\prime }\cdot r_{H5}+a_{H4}^{\prime }\cdot r_{H6}=0.\end{array}$(77) The MS group of C₂H₆ is ${\mathcal{G}}_{36}$(EM) which has generators given by Table 5.

Figure 9. The structure of the C₂H₆ molecule.

Figure 10. The equilibrium Sayvetz frame for C₂H₆. The z-axis is parallel to the C–C bond and the x-axis bisects the dihedral between the planes formed by C–C–H${}_1$ and C–C–H${}_4$.

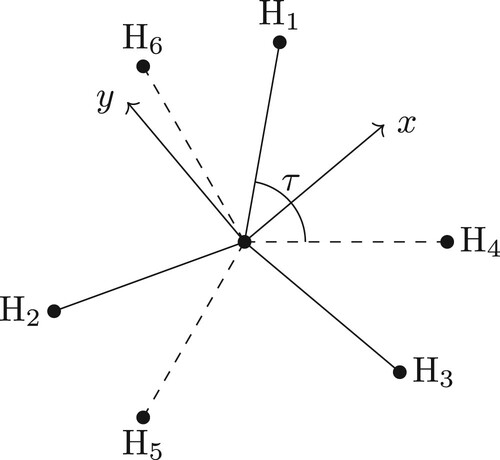
Table 5. The generators of the extended group ${\mathcal{G}}_{36}$(EM) of C₂H₆ and their effect on the torsional angle (τ) and the equivalent rotation of the generator [32].

Transformed τ	Equivalent rotation	${\mathcal{G}}_{36}($EM) generator
$\tau -4\pi /3$	E	(123)(456)
τ	$R_z^{2\pi /3}$	(132)(456)
$2\pi -\tau$	E	$\left(14\right)\left(26\right)\left(35\right)(ab{)}^{\ast }$
τ	$R_0^{\pi }$	$\left(14\right)\left(25\right)\left(36\right)\left(ab\right)$
$\tau +2\pi$	$R_z^{\pi }$	$E^{\prime }$

The operation (123)(456) changes the hydrogen labels in the usual way. However, due to the change in the τ angle, the PAS equilibrium coordinates change according to $a\to A^{2}a$ for hydrogens 1, 2 and 3 and $a\to Aa$ for hydrogens 4, 5 and 6. The carbons are unchanged. We thus have (78) $\begin{array}{rl}{C}^{\prime }& =m_C(a_{C_a}\times r_{C_a}-a_{C_a}\times r_{C_b})\\ & +m_H(A^2{a}_{H1}\times r_{H3}+a_{H1}\times r_{H1}+A{a}_{H1}\times r_{H2}\\ & +A{a}_{H4}\times r_{H6}+a_{H4}\times r_{H4}+A^2{a}_{H4}\times r_{H5})=0.\end{array}$(78) which is the original equation. The derivatives of the PAS equilibrium coordinates transform the same way under a change in τ and thus the Sayvetz condition is trivially satisfied.

For the operation (132)(456), the angle τ does not change, but the rotation $R_z^{2\pi /3}$ is applied and thus the instantaneous Cartesian coordinates change by $r\to A^{T}r=A^{2}r$. We thus have (79) $\begin{array}{rl}{C}^{\prime }& =m_C(a_{C_a}\times A^2{r}_{C_a}-a_{C_a}\times A^2{r}_{C_b})\\ & +m_H(a_{H1}\times A^2{r}_{H2}+A{a}_{H1}\times A^2{r}_{H3}+A^2{a}_{H1}\\ & \times A^2{r}_{H1}+a_{H4}\times A^2{r}_{H6}+A^2{a}_{H4}\times A^2{r}_{H4}\\ & +A{a}_{H4}\times A^2{r}_{H5}).\end{array}$(79) We apply $A^{T}A$ to the conditions and using the same technique as before, the result is $A^T$ applied to the original conditions, and this is zero. For the Sayvetz condition, we use that $Aa\cdot Ab=a\cdot b$ and pre-apply A to both terms of all dot products. The original condition is re-obtained.

The operation $\left(14\right)\left(26\right)\left(35\right)(ab{)}^{\ast }$ has no rotation and changes $a_{H1}\to -a_{H4}$ and vice versa. The result is (80) $\begin{array}{rl}{C}^{\prime }& =-m_C(a_{C_a}\times r_{C_b}-a_{C_a}\times r_{C_a})\\ & m_H(a_{H1}\times r_{H1}+A{a}_{H4}\times r_{H6}+A^2{a}_{H4}\times r_{H5}\\ & +a_{H1}\times r_{H1}+A^2{a}_{H1}\times r_{H3}+A{a}_{H1}\times r_{H2}\left)\right).\end{array}$(80) which is the original set of conditions and thus is zero. The Sayvetz condition is satisfied in the same way.

The element $\left(14\right)\left(25\right)\left(36\right)\left(ab\right)$ does not transform τ but has the equivalent rotation $R_0^{\pi }$. Thus, it transforms the instantaneous coordinates to $r\to Nr$, where $N=M_x\left(\pi \right)$, and changes the conditions to (81) $\begin{array}{rl}{C}^{\prime }& =m_C(a_{C_a}\times N{r}_{C_b}-a_{C_a}\times N{r}_{C_a})\\ & +m_H(a_{H1}\times N{r}_{H4}+A{a}_{H1}\times N{r}_{H5}+A^2{a}_{H1}\\ & \times N{r}_{H6}+a_{H4}\times N{r}_{H1}+A^2{a}_{H4}\times N{r}_{H2}\\ & +A{a}_{H4}\times N{r}_{H1}).\end{array}$(81) The matrix N changes the equilibrium Cartesian coordinates of the carbons by Na = −a and H₁'s by $N{a}_{H1}=a_{H4}$. Also, $NA=A^{2}N$ and $N{A}^2=AN$. Thus, in applying I = NN to the transformed condition, we have (82) $\begin{array}{rl}{C}^{\prime }& =N\left(m_C\right(-a_{C_a}\times r_{C_b}+a_{C_a}\times r_{C_a})\\ & +m_H(a_{H4}\times r_{H4}+A^2{a}_{H4}\times r_{H5}+A{a}_{H4}\times r_{H6}\\ & +a_{H1}\times r_{H1}+A{a}_{H1}\times r_{H2}+A^2{a}_{H1}\times r_{H1}\left)\right)=0.\end{array}$(82) which is zero. The Sayvetz condition works the same way as in the previous operations.

Finally, the operation $E^{\prime }$ is peculiar. It is defined to change the torsional coordinate τ by $\tau \to \tau +2\pi$ through a rotation of only one of the CH₃ groups, ensuring the Cartesian coordinates in a non-rotating frame do not change. The Euler angle χ changes by $\chi \to \chi +\pi$ with an associated equivalent rotation $R_z^{\pi }$. Due to the τ change, the equilibrium as transform as $a\to M_z\left(\pi \right)a$; the frame rotation changes the $r_{\alpha }$s by $r_{\alpha }\to M_z\left(\pi \right)r_{\alpha }$. Applying I = NN, where $N=M_z\left(\pi \right)$, to the transformed condition then results in $M_z\left(\pi \right)$ applied to the original condition and is thus zero. The Sayvetz condition again works the same way.

7.2. Geometric C₂H₆ frame

As with the case of CH₃Cl, we define a geometric frame which can be used to produce a symmetry-adapted rotational basis set. The valence coordinates used are $q_1$ for the C–C bond, $q_2$ to $q_7$ for the C–H bonds, $q_8$ to $q_{13}$ for the H–C–C angles, and the symmetrised dihedrals given by (83) $\begin{array}{rl}{q}_{14}& =\frac{1}{\sqrt{6}}(2{\theta }_{23}-{\theta }_{31}-{\theta }_{12})\\ q_{15}& =\frac{1}{\sqrt{2}}({\theta }_{31}-{\theta }_{12})\\ q_{16}& =\frac{1}{\sqrt{6}}(2{\theta }_{65}-{\theta }_{54}-{\theta }_{46})\\ q_{17}& =\frac{1}{\sqrt{2}}({\theta }_{54}-{\theta }_{46})\end{array}$(83) and, finally, the symmetrised torsional angle given by (84) $q_{18}=\frac{1}{3}({\theta }_{14}+{\theta }_{26}+{\theta }_{35}).$(84)

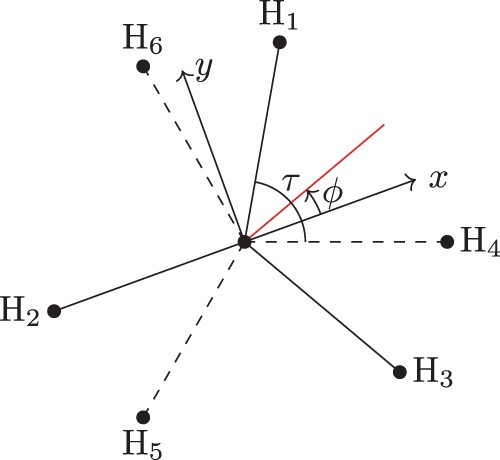
The geometric frame has the x-axis pointing at an angle (85) $\varphi =\frac{(q_{15}+q_{17})}{3\sqrt{2}}$(85) from the bisector between H${}_1$ and H${}_4$. See Figure 11.

Figure 11. The geometric frame for C₂H₆. The z-axis is parallel to the C–C bond. The x-axis is at an angle $\varphi =(q_{15}+q_{17})/\left(3\sqrt{2}\right)$ from the bisector of the dihedral angle between the planes formed by C–C–H${}_1$ and C–C–H${}_4$ (colour online).

The geometric frame fro C2H6. The z-axis is parallel to the C-C bond. The x-axis is at an angle φ = (q15 + q17)/32) from the bisector of the dihedral angle between the planes formed by C-C-H1 and C-C-H4. The bisector is the line which the φ angle points to in the figure (the red line in the web version of this article).

In the bisector frame, the Cartesian coordinates are given by, with the origin between $C_a$ and $C_b,$ (86) $\begin{array}{rl}{r}_{C_a}& =(0,0,\frac{q_1}{2})\\ r_{C_b}& =(0,0,-\frac{q_1}{2})\\ r_{H1}& =(q_2\cos \left(\frac{{\theta }_{14}}{2}\right)\sin q_8,\\ & q_2\sin \left(\frac{{\theta }_{14}}{2}\right)\sin q_8,\frac{q_1}{2}-q_2\cos q_8)\\ r_{H2}& =(q_3\cos (-\frac{{\theta }_{14}}{2}+{\theta }_{42})\sin q_9,\\ & q_3\sin (-\frac{{\theta }_{14}}{2}+{\theta }_{42})\sin q_9,\frac{q_1}{2}-q_3\cos q_9)\\ r_{H3}& =(q_4\sin (-\frac{{\theta }_{14}}{2}+{\theta }_{42}-{\theta }_{26}+{\theta }_{63})\sin q_{10},\\ & q_4\cos (-\frac{{\theta }_{14}}{2}+{\theta }_{42}-{\theta }_{26}+{\theta }_{63})\sin q_{10},\\ & \frac{q_1}{2}-q_4\cos q_{10}\phantom{\left(\frac{\sqrt{2}{q}_9}{3}\right)})\\ r_{H4}& =(q_5\cos (-\frac{{\theta }_{14}}{2})\sin q_{11},\\ & q_5\sin (-\frac{{\theta }_{14}}{2})\sin q_{11},-\frac{q_1}{2}+q_5\cos q_{11})\\ r_{H5}& =(-q_6\sin (-\frac{{\theta }_{14}}{2}+{\theta }_{42}-{\theta }_{26}+{\theta }_{63}\\ & -{\theta }_{35}\phantom{\frac{{\theta }_{14}}{2}})\sin q_{12},\\ & q_6\cos (-\frac{{\theta }_{14}}{2}+{\theta }_{42}-{\theta }_{26}+{\theta }_{63}-{\theta }_{35})\sin q_{12},\\ & -\frac{q_1}{2}+q_6\cos q_{12}\phantom{\left(\frac{\sqrt{2}{q}_9}{3}\right)})\\ r_{H6}& =(-q_7\sin (-\frac{{\theta }_{14}}{2}+{\theta }_{42}-{\theta }_{26})\sin q_{13},\\ & -q_7\cos (-\frac{{\theta }_{14}}{2}+{\theta }_{42}-{\theta }_{26}+)\sin q_{13},\\ & -\frac{q_1}{2}+q_7\cos q_{13}\phantom{\left(\frac{\sqrt{2}{q}_9}{3}\right)})\end{array}$(86) where the dihedral angle combination results from the Z-matrix definition of the Coordinates. The atoms of the Z-matrix are, in turn, a, b, 1, 4, 2, 6, 3 and 5. The un-symmetrised dihedral angles are defined by (87) $\begin{array}{rl}{\theta }_{12}& ={\theta }_{42}-{\theta }_{14}\\ {\theta }_{23}& ={\theta }_{63}-{\theta }_{26}\\ {\theta }_{31}& =2\pi -{\theta }_{12}-{\theta }_{23}\\ {\theta }_{65}& ={\theta }_{63}-{\theta }_{35}\\ {\theta }_{46}& ={\theta }_{42}-{\theta }_{26}\\ {\theta }_{54}& =2\pi -{\theta }_{65}-{\theta }_{46}.\end{array}$(87) Solving the symmetrised Coordinates for the dihedrals in a manner similar to CH₃Cl, we get (88) $\begin{array}{rl}{\theta }_{14}& =\frac{q_{15}}{3\sqrt{2}}-\frac{q_{17}}{3\sqrt{2}}+q_{18}\\ {\theta }_{42}& =\frac{2\pi }{3}-\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}-\frac{\sqrt{2}{q}_{17}}{3}+q_{18}\\ {\theta }_{26}& =-\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}+\frac{q_{16}}{\sqrt{6}}+\frac{q_{17}}{3\sqrt{2}}+q_{18}\\ {\theta }_{63}& =\frac{2\pi }{3}+\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}+\frac{q_{16}}{\sqrt{6}}+\frac{q_{17}}{3\sqrt{2}}+q_{18}\\ {\theta }_{35}& =\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}-\frac{q_{16}}{\sqrt{6}}-\frac{q_{17}}{3\sqrt{2}}+q_{18}.\end{array}$(88) Substituting this into Equation (86(86) $\begin{array}{rl}{r}_{C_a}& =(0,0,\frac{q_1}{2})\\ r_{C_b}& =(0,0,-\frac{q_1}{2})\\ r_{H1}& =(q_2\cos \left(\frac{{\theta }_{14}}{2}\right)\sin q_8,\\ & q_2\sin \left(\frac{{\theta }_{14}}{2}\right)\sin q_8,\frac{q_1}{2}-q_2\cos q_8)\\ r_{H2}& =(q_3\cos (-\frac{{\theta }_{14}}{2}+{\theta }_{42})\sin q_9,\\ & q_3\sin (-\frac{{\theta }_{14}}{2}+{\theta }_{42})\sin q_9,\frac{q_1}{2}-q_3\cos q_9)\\ r_{H3}& =(q_4\sin (-\frac{{\theta }_{14}}{2}+{\theta }_{42}-{\theta }_{26}+{\theta }_{63})\sin q_{10},\\ & q_4\cos (-\frac{{\theta }_{14}}{2}+{\theta }_{42}-{\theta }_{26}+{\theta }_{63})\sin q_{10},\\ & \frac{q_1}{2}-q_4\cos q_{10}\phantom{\left(\frac{\sqrt{2}{q}_9}{3}\right)})\\ r_{H4}& =(q_5\cos (-\frac{{\theta }_{14}}{2})\sin q_{11},\\ & q_5\sin (-\frac{{\theta }_{14}}{2})\sin q_{11},-\frac{q_1}{2}+q_5\cos q_{11})\\ r_{H5}& =(-q_6\sin (-\frac{{\theta }_{14}}{2}+{\theta }_{42}-{\theta }_{26}+{\theta }_{63}\\ & -{\theta }_{35}\phantom{\frac{{\theta }_{14}}{2}})\sin q_{12},\\ & q_6\cos (-\frac{{\theta }_{14}}{2}+{\theta }_{42}-{\theta }_{26}+{\theta }_{63}-{\theta }_{35})\sin q_{12},\\ & -\frac{q_1}{2}+q_6\cos q_{12}\phantom{\left(\frac{\sqrt{2}{q}_9}{3}\right)})\\ r_{H6}& =(-q_7\sin (-\frac{{\theta }_{14}}{2}+{\theta }_{42}-{\theta }_{26})\sin q_{13},\\ & -q_7\cos (-\frac{{\theta }_{14}}{2}+{\theta }_{42}-{\theta }_{26}+)\sin q_{13},\\ & -\frac{q_1}{2}+q_7\cos q_{13}\phantom{\left(\frac{\sqrt{2}{q}_9}{3}\right)})\end{array}$(86) ) and applying the rotation $M_z\left(\right(q_{15}+q_{17}\left)/\right(3\sqrt{2}\left)\right)$, we obtain (89) $\begin{array}{rl}{r}_{C_a}& =(0,0,\frac{q_1}{2})\\ r_{C_b}& =(0,0,-\frac{q_1}{2})\\ r_{H1}& =(q_2\cos (\frac{\sqrt{2}{q}_{15}}{3}+\frac{q_{18}}{2})\sin q_8,\\ & q_2\sin (\frac{\sqrt{2}{q}_{15}}{3}+\frac{q_{18}}{2})\sin q_8,\frac{q_1}{2}-q_2\cos q_8)\\ r_{H2}& =(-q_3\sin (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}+\frac{q_{18}}{2})\sin q_9,\\ & q_3\cos (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}+\frac{q_{18}}{2})\sin q_9,\\ & \frac{q_1}{2}-q_3\cos q_9\phantom{\frac{\pi }{6}})\\ r_{H3}& =(-q_4\sin (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}+\frac{q_{15}}{3\sqrt{2}}-\frac{q_{18}}{2})\sin q_{10},\\ & -q_4\cos (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}+\frac{q_{15}}{3\sqrt{2}}-\frac{q_{18}}{2})\sin q_{10},\\ & \frac{q_1}{2}-q_4\cos q_{10}\phantom{\frac{\pi }{6}})\\ r_{H4}& =(q_5\cos (\frac{\sqrt{2}{q}_{17}}{3}-\frac{q_{18}}{2})\sin q_{11},\\ & q_5\sin (\frac{\sqrt{2}{q}_{17}}{3}-\frac{q_{18}}{2})\sin q_{11},\\ & -\frac{q_1}{2}+q_5\cos q_{11}\phantom{\frac{\pi }{6}})\\ r_{H5}& =(-q_6\sin (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}+\frac{q_{17}}{3\sqrt{2}}+\frac{q_{18}}{2})\sin q_{12},\\ & -q_6\cos (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}+\frac{q_{17}}{3\sqrt{2}}+\frac{q_{18}}{2})\sin q_{12},\\ & -\frac{q_1}{2}+q_6\cos q_{12}\phantom{\frac{\pi }{6}})\\ r_{H6}& =(-q_7\sin (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}-\frac{q_{17}}{3\sqrt{2}}-\frac{q_{18}}{2})\sin q_{13},\\ & q_7\cos (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}-\frac{q_{17}}{3\sqrt{2}}-\frac{q_{18}}{2})\sin q_{13},\\ & -\frac{q_1}{2}+q_7\cos q_{13}\phantom{\frac{\pi }{6}}\phantom{\frac{{\theta }_{14}}{2}}).\end{array}$(89) In Appendix 3 it is demonstrated that this frame can be used for rotational symmetrisation.

8. Transforming between BF-frames

As explored above, a bond vector BF-frame is not always suitable if one requires a symmetry-adapted rotational basis set. However, the KEO is quite straightforward to define and compute in this frame. In the Sørensen approach, for example, the three rotational conditions of Equation (46(46) $\begin{array}{rl}{C}^1& =z_{{\mathrm{A}}_2}-z_B=0\\ C^2& =z_{{\mathrm{A}}_1}-z_B=0\\ C^3& =y_{{\mathrm{A}}_1}-y_B=0\end{array}$(46) ) are very simple. In contrast, defining a condition in terms of ${\varphi }_1$ of Equation (60(60) ${\varphi }_1=\frac{1}{3}({\theta }_{21}-{\theta }_{13})$(60) ) is trickier and involves using trigonometric functions of the Cartesian coordinates rather than simple differences.

In this section, we shall explain how to find the angle ${\varphi }_1$ in the case of CH₃Cl and also how to transform the s-vector components defined in a bond vector BF-frame to the desired frame.

For a general symmetry operation, if $R_{\alpha }\to R_{{\alpha }^{\prime }}$, we required that $r_{{\alpha }^{\prime }}=N{\tilde{r}}_{\alpha }$ or $N^T{r}_{{\alpha }^{\prime }}={\tilde{r}}_{\alpha }$. We then stipulate that N is a constant matrix, for example $N_{\left(123\right)}=M_z\left(2\pi /3\right)$ for CH₃Cl. The Cartesian coordinates $r_{\alpha }$ are in the old BF-frame. In the new BF-frame, they will be of the form $S(q_1,\dots ,q_n)r_{\alpha }$ for some rotation matrix S which is a function of the vibrational coordinates. We thus want (90) $N^{T}S{r}_{{\alpha }^{\prime }}=\tilde{S}{\tilde{r}}_{\alpha }$(90) for every operation. In the case of CH₃Cl we see that the z-axis along the Cl–C bond should be maintained. Only a rotation about the z-axis is required. Since motion of the atoms in this plane is parametrised by the dihedral angles, we will assume the simplest rotation of the form $M_z(a{q}_8+b{q}_9)$ where a and b are constants. The position of H₁ in this, yet, undetermined frame is given by (91) $\begin{array}{rl}{r}_{H1}& =(q_2\cos (a{q}_8+b{q}_9)\sin q_5,\\ & q_2\sin (a{q}_8+b{q}_9)\sin q_5,q_2\cos q_5)\end{array}$(91) while $N^T{r}_{H3}$ is given by (92) $\begin{array}{rl}{N}^T{r}_{H3}& =(q_4\cos (-\frac{q_8}{\sqrt{6}}-\frac{q_9}{\sqrt{2}}+a{q}_8+b{q}_9)\\ & \sin q_7,q_4\sin (-\frac{q_8}{\sqrt{6}}-\frac{q_9}{\sqrt{2}}+a{q}_8+b{q}_9),\\ & q_4\cos q_7\phantom{\frac{q_9}{\sqrt{2}}}).\end{array}$(92) Thus we want to equate the transformed $a{q}_8+b{q}_9$ to $-\frac{q_8}{\sqrt{6}}-\frac{q_9}{\sqrt{2}}+a{q}_8+b{q}_9$, or (93) $\begin{array}{rl}& -a\frac{q_8}{2}+a\frac{\sqrt{3}{q}_9}{2}-b\frac{\sqrt{3}}{2}{q}_8-b\frac{q_9}{2}\\ & =-\frac{q_8}{\sqrt{6}}-\frac{q_9}{\sqrt{2}}+a{q}_8+b{q}_9\end{array}$(93) from which we obtain (94) $\begin{array}{r}b=\frac{\sqrt{2}}{3}+\frac{(-3q_8+\sqrt{3}{q}_9)a}{\sqrt{3}{q}_8+3q_9}.\end{array}$(94) For the operation $(23{)}^{\ast }$, $r_{H2}$ in this frame is given by (95) $\begin{array}{rl}{r}_{H2}& =(q_3\cos (\frac{4\pi }{6}-\frac{q_8}{\sqrt{6}}+\frac{q_9}{\sqrt{2}}-a{q}_8-b{q}_9)\sin q_6,\\ & -q_3\sin (\frac{4\pi }{6}-\frac{q_8}{\sqrt{6}}+\frac{q_9}{\sqrt{2}}-a{q}_8-b{q}_9)\sin q_6,\\ & q_3\cos q_6\frac{q_9}{\sqrt{2}})\end{array}$(95) and $-M_y\left(\pi \right)r_{H3}=-N{r}_{H3}$ is (96) $\begin{array}{rl}{r}_{H3}& =(q_3\cos (\frac{4\pi }{6}-\frac{q_8}{\sqrt{6}}-\frac{q_9}{\sqrt{2}}+a{q}_8+b{q}_9)\sin q_6,\\ & -q_3\sin (\frac{4\pi }{6}-\frac{q_8}{\sqrt{6}}+\frac{q_9}{\sqrt{2}}+a{q}_8+b{q}_9)\sin q_6,\\ & q_3\cos q_6\frac{q_9}{\sqrt{2}}).\end{array}$(96) Equating the transformed Equation (95(95) $\begin{array}{rl}{r}_{H2}& =(q_3\cos (\frac{4\pi }{6}-\frac{q_8}{\sqrt{6}}+\frac{q_9}{\sqrt{2}}-a{q}_8-b{q}_9)\sin q_6,\\ & -q_3\sin (\frac{4\pi }{6}-\frac{q_8}{\sqrt{6}}+\frac{q_9}{\sqrt{2}}-a{q}_8-b{q}_9)\sin q_6,\\ & q_3\cos q_6\frac{q_9}{\sqrt{2}})\end{array}$(95) ) to Equation (96(96) $\begin{array}{rl}{r}_{H3}& =(q_3\cos (\frac{4\pi }{6}-\frac{q_8}{\sqrt{6}}-\frac{q_9}{\sqrt{2}}+a{q}_8+b{q}_9)\sin q_6,\\ & -q_3\sin (\frac{4\pi }{6}-\frac{q_8}{\sqrt{6}}+\frac{q_9}{\sqrt{2}}+a{q}_8+b{q}_9)\sin q_6,\\ & q_3\cos q_6\frac{q_9}{\sqrt{2}}).\end{array}$(96) ), we have (97) $\begin{array}{rl}& \frac{4\pi }{6}-\frac{q_8}{\sqrt{6}}-\frac{q_9}{\sqrt{2}}-a{q}_8+b{q}_9\\ & =\frac{4\pi }{6}-\frac{q_8}{\sqrt{6}}-\frac{q_9}{\sqrt{2}}+a{q}_8+b{q}_9.\end{array}$(97) From these we obtain a = 0 and $b=\sqrt{2}/3$ as stated previously.

For the second step, that of transforming the s-vectors to the new BF-frame, first one starts with the original BF vibrational and rotational s-vector components $s_{k,\alpha }$ and $s_{g,\alpha }$, respectively. It can be shown that the vibrational s-vector components transform to (98) $s_{k,\alpha }\to S{s}_{k,\alpha }$(98) where S is the matrix which transformed the Cartesian coordinates.

The rotational s-vector components $s_{g,\alpha }$ can be written as a matrix $s_{\mathrm{r},\alpha }$ where g signifies the row. It then transforms as (99) $s_{\mathrm{r},\alpha }\to S(s_{\mathrm{r},\alpha }-\sum _k{\omega }_k{s}_{k,\alpha }^T)S^T$(99) where ${\omega }_k$ is defined by (100) $S^T\frac{\mathrm{\partial }S}{\mathrm{\partial }{q}_k}=\left(\begin{array}{ccc}0& -{\omega }_{k,z}& {\omega }_{k,y}\\ {\omega }_{k,z}& 0& -{\omega }_{k,x}\\ -{\omega }_{k,y}& {\omega }_{k,x}& 0\end{array}\right).$(100) For multiple rotations, these steps are applied sequentially.

These results are a generalisation of the results [40] for rotations which are not linear functions of the vibrational coordinates, and also a transform of the s-vectors rather than the G matrix. This enables their form to be simplified further with software which performs analytic computations on the smaller s-vectors compared to the G matrix. It is ideal to calculate the vibrational G matrix and the pseudo-potential with the original s-vectors as these do not depend on the choice of frame. The Coriolis and rotational G matrix must be calculated with the new frame.

For the t-vector approach, if $t_{k,\alpha }$ and $t_{g,\alpha }$ are the original BF vibrational and rotational t-vector components, respectively, then the transformed vibrational t-vector components in the new BF-frame are (101) $t_{k,\alpha }\to S(t_{k,\alpha }+\sum _g{\omega }_{k,g}{t}_{g,\alpha })$(101) and the transformed rotational t-vectors are (102) $t_{\mathrm{r},\alpha }\to S{t}_{\mathrm{r},\alpha }{S}^T$(102) where $t_{\mathrm{r},\alpha }$ is the matrix formed from $t_{g,\alpha }$, where g signifies the column.

9. Further applications

In the above sections, the focus was on valence coordinates as these are the simplest to define and use to determine the appropriate frames. However, this does not preclude the use of other coordinates. For example, the Jacobi [41] and Radau [42] coordinates offer alternative parametrisations. These have advantages due to the simplification of the Hamiltonian.

It is feasible that a similar procedure could be applied for these coordinates for rotational basis symmetrisation. Indeed, the s-vector approach stipulates that the vibrational coordinates are independent of the translation and rotation of the molecule. It does not specify the form of the coordinates. For CH₃F, for example, the kinetic energy operator was derived in [43] where the canonical point was the centre of mass of the CH₃ group and the vectors were the distances from that point to the hydrogen and fluorine nuclei. The frame chosen was the bond vector using vectors from the canonical point to two of the hydrogens. Using vibrational coordinates analogous to the valence ones for CH₃Cl of Section 6.2, it is clear that the structure of the Cartesian coordinates as a function of the vibrational is identical, and hence the same process should work.

The size of the Coriolis coupling was not considered in this work and was beyond its scope, but it is arguably the most important factor when comparing these frames. Previously research into this has been undertaken; see, for example, Sarka et al.[44] who compared the Radau bisector, the valence bisector, and the Eckart frame for symmetric triatomics and found that the Radau bisector is superior in reducing this coupling and should lead to better ro-vibrational separation. Comparing the frames described in this publication is a possible avenue for further research.

Moving beyond the molecules chosen, the question of the possibility of finding non-Eckart/Sayvetz frames where rotational symmetrisation is possible still remains. For certain molecules, such as ammonia, a trisector can define the z-axis. Then, once again, two symmetrised coordinates based on the dihedrals could be used to rotate about this z-axis as the structure is the same as the CH₃Cl molecule. For other molecules, such as CH₄, it is remarkably more challenging. For Equation (90(90) $N^{T}S{r}_{{\alpha }^{\prime }}=\tilde{S}{\tilde{r}}_{\alpha }$(90) ), one can replace $r_{{\alpha }^{\prime }}$ with $B{\tilde{r}}_{\alpha }$, where B is the rotation matrix relating the old and rotated bond vector frame (i.e. it is the matrix N of Equation (13(13) ${r_{\alpha }}^{\prime }=M^T\tilde{M}{\tilde{r}}_{\alpha }\equiv N{\tilde{r}}_{\alpha }$(13) ) for the bond vector frame rather than the desired frame). Then, the equation that must be solved is (103) $N\tilde{S}=SB$(103) for each generator. For CH₄, the matrix S would be parametrised by five symmetrised angles and the coefficient values could only be found numerically, if they could be found at all. In general, finding the frame for a given molecular structure and coordinate choice would have to be done on a case-by-case basis.

We aim to use the results in this study on the ro-vibrational calculations of C₂H₆. An analytic KEO in valence coordinates and using this frame has been derived. Moreover, we have a Taylor expanded KEO based on linearised coordinates in the Sayvetz frame. A comparison of the two approaches would be instructive.

10. Conclusion

The main result in this study was the determination of geometric BF-frames for a certain classes of molecules – with the CH₃Cl and C₂H₆ molecules used as defining examples – where rotational symmetrisation is possible. The Eckart and Sayvetz frame were also shown to be suitable for these molecules, with the form of the proofs extendable to other molecules as they relied on the correspondence between the MS group of the molecule and the point group of the molecule when in vibrational equilibrium.

Furthermore, one approach to find such frames is described for CH₃Cl, and a method to check frames is also given, provided one has the BF Cartesian coordinates as a function of the vibrational coordinates. Finally, a simple transformation of the s-vectors due to a change of frame is stated, allowing them to be calculated in a straightforwardly defined frame first and then transformed to another, more appropriate, frame.

Acknowledgments

T. Mellor would like to thank S. Yurchenko and J. Buldyvera for their suggested improvements in the structure of the manuscript.

Disclosure statement

No potential conflict of interest was reported by the author.

Appendices

Appendix 1 Vibrational s-vector components

In this section we demonstrate that the components of the vibrational s-vectors in any frame are found by evaluating ${\mathrm{\partial }}_{\alpha i}{q}_k$ in the Cartesian coordinates of that frame. To show this, we use the property that the value of $q_k$ does not depend on which frame it is evaluated in, i.e. (A1) $q_k(M{R}_1+d,\dots ,M{R}_n+d)=q_k(R_1,\dots ,R_n).$(A1) where $M{R}_{\alpha }+d$ are the coordinates of ${\mathit{R}}_{\alpha }$ when the frame is rotated and translated. Calling $T\left(R\right)=MR+d$, we want to determine ${\mathrm{\partial }}_{\alpha i}\left(q_k\right)\left(T\right(R_1),\dots ,T(R_n\left)\right)$ in terms of ${\mathrm{\partial }}_{\alpha i}\left(q_k\right)(R_1,\dots ,R_n)$. Let us define the function $\tilde{T}$ as (A2) $\tilde{T}(R_1,\dots R_n)=\left(T\right(R_1),\dots ,T(R_n\left)\right).$(A2) Then, the translational and rotational invariance can be expressed as (A3) $q_k\circ \tilde{T}(R_1,\dots ,R_n)=q_k(R_1,\dots ,R_n).$(A3) Differentiating both sides, and using the chain rule, we obtain (A4) $\begin{array}{rl}& {\mathrm{\partial }}_{\alpha F}\left(q_k\right)(R_1,\dots ,R_n)={\mathrm{\partial }}_{\alpha F}(q_k\circ \tilde{T})(R_1,\dots ,R_n)\end{array}$(A4) (A5) $\begin{array}{rl}& =\sum _{\text{β}}{\mathrm{\partial }}_{\alpha F}\left(\tilde{T}{)}^{\text{β}G}\right(R_1,\dots ,R_n\left){\mathrm{\partial }}_{\text{β}G}\right(q_k\left)\right(\tilde{T}(R_1,\dots ,R_N))\end{array}$(A5) Here ${\mathrm{\partial }}_{\alpha F}(\tilde{T}{)}^{\text{β}G}$ is the $\text{β}G$ component of the derivative of $\tilde{T}$, which is non-zero only when $\text{β}=\alpha$ and is given by $M_{GF}$. We thus have (A6) ${\mathrm{\partial }}_{\alpha F}\left(q_k\right)(R_1,\dots ,R_N)=M_{GF}{\mathrm{\partial }}_{\alpha G}\left(q_k\right)\left(T\right(R_1),\dots ,T(R_n\left)\right).$(A6) Thus (A7) $\begin{array}{rl}{\mathit{s}}_{k,\alpha }& ={\hat{\mathit{e}}}_F{\mathrm{\partial }}_{\alpha F}\left(q_k\right)(R_1,\dots ,R_N)\\ & =M_{GF}{\hat{\mathit{e}}}_F{\mathrm{\partial }}_{\alpha G}\left(q_k\right)\left(T\right(R_1),\dots ,T(R_n\left)\right)\\ & ={\hat{\mathit{e}}}_G{\mathrm{\partial }}_{\alpha G}\left(q_k\right)\left(T\right(R_1),\dots ,T(R_n\left)\right)\end{array}$(A7) where ${\hat{\mathit{e}}}_G=M_{GF}{\hat{\mathit{e}}}_F$. Since the Cartesian components in the new frame are given by $M_{GF}{R}_{\alpha F}+d$, ${\hat{\mathit{e}}}_G$ are the unit vectors in the same frame, which tells us the component of ${\mathit{s}}_{k,\alpha }$ is the derivative of $q_k$ evaluated at the Cartesian coordinates of that frame. This gives a computational way to determine the components of ${\mathit{s}}_{k,\alpha }$ in any frame that does not involve first evaluating the components in the RF-frame and applying the rotation matrix.

For the transformed s-vector, we have that (A8) $\begin{array}{rl}{{\mathit{s}}_{k,\alpha }}^{\prime }& ={\mathrm{\partial }}_{\alpha I}{q}_k\left(P\right(R_1,\dots ,R_n\left)\right){\hat{\mathit{e}}}_I\\ & ={\mathrm{\partial }}_{\alpha I}{q}_k(R_{p_1},\dots ,R_{p_n})){\hat{\mathit{e}}}_I\\ & ={\mathrm{\partial }}_{\alpha g}{q}_k\left(T\right(R_{p_1}),\dots ,T(R_{p_n}\left)\right){\hat{\mathit{e}}}_g\\ & ={\mathrm{\partial }}_{\alpha g}{q}_k({\tilde{r}}_1,\dots ,{\tilde{r}}_n){\hat{\mathit{e}}}_g\end{array}$(A8) as $T\left(R_{p_{\alpha }}\right)$ are the coordinates of atom α after the MS operation is performed and in the new BF-frame. As we have seen, this is given by ${\tilde{r}}_{\alpha }$, so that to transform the BF components $s_{k,\alpha g}$ we simply perform the vibrational coordinate transformation (which we shall denote as ${\tilde{s}}_{k,\alpha g}$). This will give us the transformed s-vector components in the new BF-frame.

Appendix 2

Kinetic energy operator invariance

If ${q_i}^{\prime }=q_j$ and ${q_{i^{\prime }}}^{\prime }=q_{j^{\prime }}$ then the KEO (without the pseudo-potential) transforms as (A9) $\begin{array}{rl}{{\hat{\pi }}_i}^{\prime }{G_{i{i}^{\prime }}}^{\prime }{{\hat{\pi }}_{i^{\prime }}}^{\prime }& =({\hat{\pi }}_j+{\dot{\gamma }}_j{J}_z)G_{j{j}^{\prime }}({\hat{\pi }}_{j^{\prime }}+{\dot{\gamma }}_{j^{\prime }}{J}_z)\\ & ={\hat{\pi }}_j{G}_{j{j}^{\prime }}{\hat{\pi }}_{j^{\prime }}+\underset{\text{172}}{\underbrace{{\hat{\pi }}_j{\dot{\gamma }}_{j^{\prime }}{G}_{j{j}^{\prime }}{\hat{J}}_z}}+\underset{\text{173}}{\underbrace{{\dot{\gamma }}_j{\hat{J}}_z{G}_{j{j}^{\prime }}{\hat{\pi }}_{j^{\prime }}}}+\underset{\text{174}}{\underbrace{{\dot{\gamma }}_j{\dot{\gamma }}_{j^{\prime }}{\hat{J}}_z{G}_{j{j}^{\prime }}{\hat{J}}_z}}\\ {{\hat{\pi }}_i}^{\prime }{G_{ig}}^{\prime }{{\hat{J}}_g}^{\prime }& =({\hat{\pi }}_j+{\dot{\gamma }}_j{J}_z)(N_{hg}{G}_{jh}-{\dot{\gamma }}_k{G}_{jk}{N}_{zg})N_{lg}{\hat{J}}_l\\ & ={\hat{\pi }}_j{G}_{jl}{\hat{J}}_l+\underset{\text{175}}{\underbrace{{\dot{\gamma }}_j{\hat{J}}_z{G}_{jl}{\hat{J}}_l}}-\underset{\text{172}}{\underbrace{{\hat{\pi }}_j{\dot{\gamma }}_k{G}_{jk}{\hat{J}}_z}}-\underset{\text{174}}{\underbrace{{\dot{\gamma }}_k{\dot{\gamma }}_j{\hat{J}}_z{G}_{jk}{\hat{J}}_z}}\\ {{\hat{J}}_g}^{\prime }{G_{gi}}^{\prime }{{\hat{\pi }}_i}^{\prime }& =N_{lg}{\hat{J}}_l(N_{hg}{G}_{hj}-{\dot{\gamma }}_k{G}_{kj}{N}_{zg})({\hat{\pi }}_j+{\dot{\gamma }}_j{J}_z)\\ & ={\hat{J}}_l{G}_{lj}{\hat{\pi }}_j+\underset{\text{176}}{\underbrace{{\dot{\gamma }}_j{\hat{J}}_l{G}_{lj}{\hat{J}}_z}}-\underset{\text{173}}{\underbrace{{\dot{\gamma }}_k{\hat{J}}_z{G}_{kj}{\hat{\pi }}_j}}-\underset{\text{177}}{\underbrace{{\dot{\gamma }}_k{\dot{\gamma }}_j{\hat{J}}_z{G}_{kj}{\hat{J}}_z}}\\ {{\hat{J}}_g}^{\prime }{G_{g{g}^{\prime }}}^{\prime }{{\hat{J}}_{g^{\prime }}}^{\prime }& =N_{lg}{\hat{J}}_l[N_{hg}{N}_{h^{\prime }{g}^{\prime }}{G}_{h{h}^{\prime }}+{\dot{\gamma }}_k{\dot{\gamma }}_{k^{\prime }}{G}_{k{k}^{\prime }}{N}_{z{g}^{\prime }}{N}_{zg}\\ & -{\dot{\gamma }}_k{G}_{kh}(N_{h{g}^{\prime }}{N}_{zg}+N_{hg}{N}_{z{g}^{\prime }})]N_{l^{\prime }{g}^{\prime }}{\hat{J}}_{l^{\prime }}\\ & ={\hat{J}}_h{G}_{h{h}^{\prime }}{\hat{J}}_{h^{\prime }}+\underset{\text{177}}{\underbrace{{\dot{\gamma }}_k{\dot{\gamma }}_{k^{\prime }}{\hat{J}}_z{G}_{k{k}^{\prime }}{\hat{J}}_z}}-\underset{\text{175}}{\underbrace{{\dot{\gamma }}_k{\hat{J}}_z{G}_{kh}{\hat{J}}_h}}-\underset{\text{176}}{\underbrace{{\dot{\gamma }}_k{\hat{J}}_h{G}_{hk}{\hat{J}}_z}}\end{array}$(A9) Terms under-braced with the same number cancel. What remains when all is summed together is the original Hamiltonian, showing invariance.

The pseudo-potential U consists of the four terms (A10) $\begin{array}{rl}{U}_1& =\frac{1}{8}\sum _{\alpha ,g,g^{\prime }}\frac{1}{m_{\alpha }}({\hat{\mathit{e}}}_g\times {\mathit{s}}_{g,\alpha })\cdot ({\hat{\mathit{e}}}_{g^{\prime }}\times {\mathit{s}}_{g^{\prime },\alpha })\\ U_2& =\frac{1}{4}\sum _{\alpha ,g,i}\frac{1}{m_{\alpha }}({\hat{\mathit{e}}}_g\times {\mathit{s}}_{i,\alpha })\cdot {\mathrm{\partial }}_i{\mathit{s}}_{g,\alpha }\\ U_3& =-\frac{1}{4}\sum _{\alpha ,i,j}\frac{1}{m_{\alpha }}{\mathit{s}}_{i,\alpha }\cdot {\mathrm{\partial }}_i{\mathrm{\partial }}_j{\mathit{s}}_{j,\alpha }\\ U_4& =-\frac{1}{8}\sum _{\alpha ,i,j}\frac{1}{m_{\alpha }}{\mathrm{\partial }}_i{\mathit{s}}_{i,\alpha }\cdot {\mathrm{\partial }}_j{\mathit{s}}_{j,\alpha }\end{array}$(A10) Table 1 provides the s-vector transforms. One can show that the BF-frame unit vectors transform as ${\hat{\mathit{e}}}_g^{\prime }=N_{hg}{\hat{\mathit{e}}}_h$ while the derivatives of the s-vectors transform as, if $q_i\to q_{i^{\prime }}$ and $q_j\to q_{j^{\prime }}$, (A11) $\begin{array}{rl}{{\mathrm{\partial }}_i{\mathit{s}}_{g,\alpha }}^{\prime }& ={\mathrm{\partial }}_{i^{\prime }}(N_{hg}{\mathit{s}}_{h,{\alpha }^{\prime }}-{\dot{\gamma }}_{k^{\prime }}{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}{N}_{zg})+{\dot{\gamma }}_{i^{\prime }}{\hat{\mathit{e}}}_z\\ & \times (N_{hg}{\mathit{s}}_{h,{\alpha }^{\prime }}-{\dot{\gamma }}_{k^{\prime }}{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}{N}_{zg})\\ & =\left({\mathrm{\partial }}_{i^{\prime }}{N}_{hg}\right){\mathit{s}}_{h,{\alpha }^{\prime }}+N_{hg}{\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{h,{\alpha }^{\prime }}\\ & -{\ddot{\gamma }}_{i^{\prime }{k}^{\prime }}{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}{N}_{zg}-{\dot{\gamma }}_{k^{\prime }}{\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}{N}_{zg}\\ & +{\dot{\gamma }}_{i^{\prime }}{\hat{\mathit{e}}}_z\times N_{hg}{\mathit{s}}_{h,{\alpha }^{\prime }}-{\dot{\gamma }}_{i^{\prime }}{\dot{\gamma }}_{k^{\prime }}{\hat{\mathit{e}}}_z\times {\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}{N}_{zg},\\ {{\mathrm{\partial }}_j{\mathit{s}}_{j,\alpha }}^{\prime }& ={\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}+{\dot{\gamma }}_{j^{\prime }}{\hat{\mathit{e}}}_z\times {\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}\\ {{\mathrm{\partial }}_i{\mathrm{\partial }}_j{\mathit{s}}_{j,\alpha }}^{\prime }& ={\mathrm{\partial }}_{i^{\prime }}{\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}+{\dot{\gamma }}_{i^{\prime }}{\hat{\mathit{e}}}_z\times ({\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}\\ & +{\dot{\gamma }}_{j^{\prime }}{\hat{\mathit{e}}}_z\times {\mathit{s}}_{j^{\prime },{\alpha }^{\prime }})+{\hat{\mathit{e}}}_z\times ({\ddot{\gamma }}_{j^{\prime }{i}^{\prime }}{\mathit{s}}_{j^{\prime },\alpha }+{\dot{\gamma }}_{j^{\prime }}{\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }})\\ & ={\mathrm{\partial }}_{i^{\prime }}{\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}+{\dot{\gamma }}_{i^{\prime }}{\hat{\mathit{e}}}_z\times {\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}+{\dot{\gamma }}_{i^{\prime }}{\dot{\gamma }}_{j^{\prime }}{\hat{\mathit{e}}}_z\\ & \times ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{j^{\prime },{\alpha }^{\prime }})+{\ddot{\gamma }}_{i^{\prime }{j}^{\prime }}{\hat{\mathit{e}}}_z\times {\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}+{\dot{\gamma }}_{j^{\prime }}{\hat{\mathit{e}}}_z\times {\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{i^{\prime },{\alpha }^{\prime }}\end{array}$(A11) where ${\ddot{\gamma }}_{i^{\prime }{j}^{\prime }}={\mathrm{\partial }}_{i^{\prime }}{\mathrm{\partial }}_{j^{\prime }}\gamma$ and ${\hat{\mathit{e}}}_z$ is z-axis vector of the BF-frame. We assume a rotation N of the first column of Table 3. Due to this, the term containing ${\mathrm{\partial }}_{i^{\prime }}{N}_{zg}=0$.

With these expressions, we shall express the transformation of the pseudo-potential terms (temporarily ignoring the summation over the masses) by subscripting each U term with the atom it corresponds to. For $U_{1,\alpha }$, it is given by (A12) $\begin{array}{rl}{U_{1,\alpha }}^{\prime }& =N_{hg}{\hat{\mathit{e}}}_h\times (N_{lg}{\mathit{s}}_{l,{\alpha }^{\prime }}-{\dot{\gamma }}_k{\mathit{s}}_{k,{\alpha }^{\prime }}{N}_{zg})\\ & \cdot N_{h^{\prime }{g}^{\prime }}{\hat{\mathit{e}}}_{h^{\prime }}\times (N_{l^{\prime }{g}^{\prime }}{\mathit{s}}_{l^{\prime },{\alpha }^{\prime }}-{\dot{\gamma }}_{k^{\prime }}{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}{N}_{z{g}^{\prime }})\\ & =({\mathit{e}}_h\times {\mathit{s}}_{h,{\alpha }^{\prime }}-{\dot{\gamma }}_k{\hat{\mathit{e}}}_z\times {\mathit{s}}_{k,{\alpha }^{\prime }})\\ & \cdot ({\mathit{e}}_{h^{\prime }}\times {\mathit{s}}_{h^{\prime },{\alpha }^{\prime }}-{\dot{\gamma }}_{k^{\prime }}{\hat{\mathit{e}}}_z\times {\mathit{s}}_{k^{\prime },{\alpha }^{\prime }})\\ & =({\hat{\mathit{e}}}_h\times {\mathit{s}}_{h,{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_{h^{\prime }}\times {\mathit{s}}_{h^{\prime },{\alpha }^{\prime }})\\ & -2{\dot{\gamma }}_k({\hat{\mathit{e}}}_z\times {\mathit{s}}_{k,{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_h\times {\mathit{s}}_{h,{\alpha }^{\prime }})\\ & +{\dot{\gamma }}_k{\dot{\gamma }}_{k^{\prime }}({\hat{\mathit{e}}}_z\times {\mathit{s}}_{k,{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}).\end{array}$(A12) For $U_{2,\alpha }$, it is (A13) $\begin{array}{rl}{U_{2,\alpha }}^{\prime }& =(N_{hg}{\hat{\mathit{e}}}_h\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\\ & \cdot \left[\right({\mathrm{\partial }}_{i^{\prime }}{N}_{lg}){\mathit{s}}_{l,{\alpha }^{\prime }}+N_{lg}{\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{l,{\alpha }^{\prime }}-{\ddot{\gamma }}_{i^{\prime }{k}^{\prime }}{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}{N}_{zg}\\ & -{\dot{\gamma }}_{k^{\prime }}{\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}{N}_{zg}+{\dot{\gamma }}_{i^{\prime }}{\hat{\mathit{e}}}_z\times N_{lg}{\mathit{s}}_{l,{\alpha }^{\prime }}\\ & -{\dot{\gamma }}_{i^{\prime }}{\dot{\gamma }}_{k^{\prime }}{\hat{\mathit{e}}}_z\times {\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}{N}_{zg}]\\ & =({\hat{\mathit{e}}}_h\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot ({\dot{\gamma }}_{i^{\prime }}{\delta }_{hy}{\mathit{s}}_{x,{\alpha }^{\prime }}-{\dot{\gamma }}_{i^{\prime }}{\delta }_{hx}{\mathit{s}}_{y,{\alpha }^{\prime }}+{\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{h,{\alpha }^{\prime }}\\ & -{\ddot{\gamma }}_{i^{\prime }{k}^{\prime }}{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}{\delta }_{hz}-{\dot{\gamma }}_{k^{\prime }}{\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}{\delta }_{hz}+{\dot{\gamma }}_{i^{\prime }}{\hat{\mathit{e}}}_z\times {\mathit{s}}_{h,{\alpha }^{\prime }}\\ & -{\dot{\gamma }}_{i^{\prime }}{\dot{\gamma }}_{k^{\prime }}{\delta }_{hz}{\hat{\mathit{e}}}_z\times {\mathit{s}}_{k^{\prime },{\alpha }^{\prime }})\\ & =({\hat{\mathit{e}}}_h\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot {\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{h,{\alpha }^{\prime }}+{\dot{\gamma }}_{i^{\prime }}({\hat{\mathit{e}}}_y\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\\ & \cdot {\mathit{s}}_{x,{\alpha }^{\prime }}-{\dot{\gamma }}_{i^{\prime }}({\hat{\mathit{e}}}_x\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot {\mathit{s}}_{y,{\alpha }^{\prime }}-{\dot{\gamma }}_{k^{\prime }}({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot {\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}\\ & +{\dot{\gamma }}_{i^{\prime }}({\hat{\mathit{e}}}_h\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{h,{\alpha }^{\prime }})\\ & -{\ddot{\gamma }}_{i^{\prime }{k}^{\prime }}({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot {\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}\\ & -{\dot{\gamma }}_{i^{\prime }}{\dot{\gamma }}_{k^{\prime }}({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot ({\mathit{e}}_z\times {\mathit{s}}_{k^{\prime },{\alpha }^{\prime }})\end{array}$(A13) where in the second line we use $N_{hg}\left({\mathrm{\partial }}_{i^{\prime }}{N}_{lg}\right){\mathit{s}}_{l,{\alpha }^{\prime }}={\dot{\gamma }}_{i^{\prime }}({\delta }_{hy}{\mathit{s}}_{x,{\alpha }^{\prime }}-{\delta }_{hx}{\mathit{s}}_{y,{\alpha }^{\prime }})$. For $U_{3,\alpha }$, we have (A14) $\begin{array}{rl}{U_{3,\alpha }}^{\prime }& ={\mathit{s}}_{i^{\prime },{\alpha }^{\prime }}\cdot ({\mathrm{\partial }}_{i^{\prime }}{\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}+{\dot{\gamma }}_{i^{\prime }}{\hat{\mathit{e}}}_z\times {\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}\\ & +{\dot{\gamma }}_{i^{\prime }}{\dot{\gamma }}_{j^{\prime }}{\hat{\mathit{e}}}_z\times ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{j^{\prime },{\alpha }^{\prime }})+{\ddot{\gamma }}_{i^{\prime }{j}^{\prime }}{\hat{\mathit{e}}}_z\\ & \times {\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}+{\dot{\gamma }}_{j^{\prime }}{\hat{\mathit{e}}}_z\times {\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\\ & ={\mathit{s}}_{i^{\prime },{\alpha }^{\prime }}\cdot {\mathrm{\partial }}_{i^{\prime }}{\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}\\ & -{\dot{\gamma }}_{i^{\prime }}{\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})-{\dot{\gamma }}_{i^{\prime }}{\dot{\gamma }}_{j^{\prime }}({\hat{\mathit{e}}}_z\\ & \times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{j^{\prime },{\alpha }^{\prime }})-{\ddot{\gamma }}_{i^{\prime }{j}^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\\ & -{\dot{\gamma }}_{j^{\prime }}{\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\end{array}$(A14) Finally, for $U_{4,\alpha }$, we have (A15) $\begin{array}{rl}{U_{4,\alpha }}^{\prime }& =({\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{i^{\prime },{\alpha }^{\prime }}+{\dot{\gamma }}_{i^{\prime }}{\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot ({\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}+{\dot{\gamma }}_{j^{\prime }}{\hat{\mathit{e}}}_z\times {\mathit{s}}_{j^{\prime },{\alpha }^{\prime }})\\ & ={\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{i^{\prime },{\alpha }^{\prime }}\cdot {\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}+2{\dot{\gamma }}_{i^{\prime }}{\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\\ & +{\dot{\gamma }}_{i^{\prime }}{\dot{\gamma }}_{j^{\prime }}({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{j^{\prime },{\alpha }^{\prime }})\end{array}$(A15) The first term of each of these corresponds to the original U elements, so summing over them as in Equation (A10(A10) $\begin{array}{rl}{U}_1& =\frac{1}{8}\sum _{\alpha ,g,g^{\prime }}\frac{1}{m_{\alpha }}({\hat{\mathit{e}}}_g\times {\mathit{s}}_{g,\alpha })\cdot ({\hat{\mathit{e}}}_{g^{\prime }}\times {\mathit{s}}_{g^{\prime },\alpha })\\ U_2& =\frac{1}{4}\sum _{\alpha ,g,i}\frac{1}{m_{\alpha }}({\hat{\mathit{e}}}_g\times {\mathit{s}}_{i,\alpha })\cdot {\mathrm{\partial }}_i{\mathit{s}}_{g,\alpha }\\ U_3& =-\frac{1}{4}\sum _{\alpha ,i,j}\frac{1}{m_{\alpha }}{\mathit{s}}_{i,\alpha }\cdot {\mathrm{\partial }}_i{\mathrm{\partial }}_j{\mathit{s}}_{j,\alpha }\\ U_4& =-\frac{1}{8}\sum _{\alpha ,i,j}\frac{1}{m_{\alpha }}{\mathrm{\partial }}_i{\mathit{s}}_{i,\alpha }\cdot {\mathrm{\partial }}_j{\mathit{s}}_{j,\alpha }\end{array}$(A10) ), we obtain the original U. Thus we must show the other terms sum to zero. The difference between the transformed and original terms, $\mathrm{\Delta }{U}_{i,\alpha }={U_{i,\alpha }}^{\prime }-U_{i,\alpha }$, are given by (A16) $\begin{array}{rl}\mathrm{\Delta }{U}_{1,\alpha }& =-2{\dot{\gamma }}_k({\hat{\mathit{e}}}_z\times {\mathit{s}}_{k,{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_h\times {\mathit{s}}_{h,{\alpha }^{\prime }})\\ & +\underset{\text{174}}{\underbrace{{\dot{\gamma }}_k{\dot{\gamma }}_{k^{\prime }}({\hat{\mathit{e}}}_z\times {\mathit{s}}_{k,{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{k^{\prime },{\alpha }^{\prime }})}}\\ \mathrm{\Delta }{U}_{2,\alpha }& ={\dot{\gamma }}_{i^{\prime }}({\hat{\mathit{e}}}_y\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot {\mathit{s}}_{x,{\alpha }^{\prime }}-{\dot{\gamma }}_{i^{\prime }}({\hat{\mathit{e}}}_x\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot {\mathit{s}}_{y,{\alpha }^{\prime }}\\ & -\underset{\text{176}}{\underbrace{{\dot{\gamma }}_{k^{\prime }}{\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})}}\\ & +{\dot{\gamma }}_{i^{\prime }}({\hat{\mathit{e}}}_h\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{h,{\alpha }^{\prime }})\\ & -\underset{\text{175}}{\underbrace{{\ddot{\gamma }}_{i^{\prime }{k}^{\prime }}({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot {\mathit{s}}_{k^{\prime },{\alpha }^{\prime }}}}\\ & -\underset{\text{173}}{\underbrace{{\dot{\gamma }}_{i^{\prime }}{\dot{\gamma }}_{k^{\prime }}({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot ({\mathit{e}}_z\times {\mathit{s}}_{k^{\prime },{\alpha }^{\prime }})}}\\ \mathrm{\Delta }{U}_{3,\alpha }& =-\underset{\text{172}}{\underbrace{{\dot{\gamma }}_{i^{\prime }}{\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})}}\\ & \times \underset{\text{173}}{\underbrace{-{\dot{\gamma }}_{i^{\prime }}{\dot{\gamma }}_{j^{\prime }}({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{j^{\prime },{\alpha }^{\prime }})}}\\ & -\underset{\text{175}}{\underbrace{{\ddot{\gamma }}_{i^{\prime }{j}^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})}}-\underset{\text{176}}{\underbrace{{\dot{\gamma }}_{j^{\prime }}{\mathrm{\partial }}_{i^{\prime }}{\mathit{s}}_{j^{\prime },\alpha }\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },\alpha })}}\\ \mathrm{\Delta }{U}_{4,\alpha }& =\underset{\text{172}}{\underbrace{2{\dot{\gamma }}_{i^{\prime }}{\mathrm{\partial }}_{j^{\prime }}{\mathit{s}}_{j^{\prime },{\alpha }^{\prime }}\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})}}\\ & +\underset{\text{174}}{\underbrace{{\dot{\gamma }}_{i^{\prime }}{\dot{\gamma }}_{j^{\prime }}({\hat{\mathit{e}}}_z\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{j^{\prime },{\alpha }^{\prime }})}}\end{array}$(A16) The terms under-braced by the same number cancel each other. Thus we must show the remaining terms cancel. We have (A17) $\begin{array}{rl}& {\dot{\gamma }}_{i^{\prime }}({\hat{\mathit{e}}}_h\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_z\times {\mathit{s}}_{h,{\alpha }^{\prime }})-{\dot{\gamma }}_k({\hat{\mathit{e}}}_z\times {\mathit{s}}_{k,{\alpha }^{\prime }})\cdot ({\hat{\mathit{e}}}_h\times {\mathit{s}}_{h,{\alpha }^{\prime }})\\ & ={\dot{\gamma }}_{i^{\prime }}({\mathit{s}}_{i^{\prime },{\alpha }^{\prime }}\cdot {\mathit{s}}_{z,{\alpha }^{\prime }}-s_{h,\alpha h}{s}_{i^{\prime },\alpha z})-{\dot{\gamma }}_k({\mathit{s}}_{z,{\alpha }^{\prime }}\cdot {\mathit{s}}_{k,{\alpha }^{\prime }}-s_{h,{\alpha }^{\prime }z}{s}_{k,{\alpha }^{\prime }h})\\ & ={\dot{\gamma }}_k{s}_{h,{\alpha }^{\prime }z}{s}_{k,{\alpha }^{\prime }h}-{\dot{\gamma }}_{i^{\prime }}{s}_{h,\alpha h}{s}_{i^{\prime },\alpha z}\\ & ={\dot{\gamma }}_k(s_{x,{\alpha }^{\prime }z}{s}_{k,{\alpha }^{\prime }x}+s_{y,{\alpha }^{\prime }z}{s}_{k,{\alpha }^{\prime }y})-{\dot{\gamma }}_{i^{\prime }}(s_{x,{\alpha }^{\prime }x}{s}_{i^{\prime }\alpha z}+s_{y,{\alpha }^{\prime }y}{s}_{i^{\prime },\alpha z})\\ & ={\dot{\gamma }}_{i^{\prime }}(s_{x,{\alpha }^{\prime }z}{s}_{i^{\prime },{\alpha }^{\prime }x}-s_{x,{\alpha }^{\prime }x}{s}_{i^{\prime },{\alpha }^{\prime }z})-{\dot{\gamma }}_{i^{\prime }}(s_{y,{\alpha }^{\prime }y}{s}_{i^{\prime },\alpha z}-s_{y,{\alpha }^{\prime }z}{s}_{i^{\prime },{\alpha }^{\prime }y})\\ & ={\dot{\gamma }}_{i^{\prime }}{\mathit{s}}_{x,{\alpha }^{\prime }}\cdot (s_{i^{\prime },{\alpha }^{\prime }x}{\hat{\mathit{e}}}_z-s_{i^{\prime },{\alpha }^{\prime }z}{\mathit{e}}_x)-{\dot{\gamma }}_{i^{\prime }}{\mathit{s}}_{y,{\alpha }^{\prime }}\cdot (s_{i^{\prime },{\alpha }^{\prime }z}{\hat{\mathit{e}}}_y-s_{i^{\prime },{\alpha }^{\prime }y}{\mathit{e}}_z)\\ & =-{\dot{\gamma }}_{i^{\prime }}{\mathit{s}}_{x,{\alpha }^{\prime }}\cdot ({\hat{\mathit{e}}}_y\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }})+{\dot{\gamma }}_{i^{\prime }}{\mathit{s}}_{y,{\alpha }^{\prime }}\cdot ({\hat{\mathit{e}}}_x\times {\mathit{s}}_{i^{\prime },{\alpha }^{\prime }}).\end{array}$(A17) The last line exactly cancels the remaining two terms.

Appendix 3

Geometric C₂H₆ frame proof

For simplicity we shall drop the bond and angle contributions of the hydrogens since they transform trivially.

The first operation (123)(456) transforms the dihedrals as (A18) $\left(\begin{array}{c}{q}_k\\ q_{k^{\prime }}\end{array}\right)\to \left(\begin{array}{cc}-\frac{1}{2}& -\frac{\sqrt{3}}{2}\\ \frac{\sqrt{3}}{2}& -\frac{1}{2}\end{array}\right)\left(\begin{array}{c}{q}_k\\ q_{k^{\prime }}\end{array}\right)$(A18) where $(q_k,q_{k^{\prime }})$ represents the pairs $(q_{14},q_{15})$ and $(q_{17},q_{16})$. The torsional angle transforms as Table 5. With these transformations, the (abridged) transformed BF Cartesian coordinates are (A19) $\begin{array}{rl}{\tilde{r}}_{C_a}& =(0,0,\frac{q_1}{2})\\ {\tilde{r}}_{C_b}& =(0,0,-\frac{q_1}{2})\\ {\tilde{r}}_{H1}& =(-\sin (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}+\frac{q_{15}}{3\sqrt{2}}-\frac{q_{18}}{2}),\\ & -\cos (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}+\frac{q_{15}}{3\sqrt{2}}-\frac{q_{18}}{2},),\frac{q_1}{2}-q_4\cos q_{10})\\ {\tilde{r}}_{H2}& =(\cos (\frac{\sqrt{2}{q}_{15}}{3}+\frac{q_{18}}{2}),\sin (\frac{\sqrt{2}{q}_{15}}{3}+\frac{q_{18}}{2}),\\ & \frac{q_1}{2}-q_2\cos q_8\phantom{\frac{\sqrt{2}{q}_{15}}{3}})\\ {\tilde{r}}_{H3}& =(-\sin (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}+\frac{q_{18}}{2}),\\ & \cos (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}+\frac{q_{18}}{2}),\frac{q_1}{2}-q_3\cos q_9)\\ {\tilde{r}}_{H4}& =(-\sin (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}-\frac{q_{17}}{3\sqrt{2}}-\frac{q_{18}}{2}),\\ & \cos (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}-\frac{q_{17}}{3\sqrt{2}}-\frac{q_{18}}{2}),-\frac{q_1}{2}+q_7\cos q_{13}).\\ {\tilde{r}}_{H5}& =(\cos (\frac{\sqrt{2}{q}_{17}}{3}-\frac{q_{18}}{2}),\\ & \sin (\frac{\sqrt{2}{q}_{17}}{3}-\frac{q_{18}}{2}),-\frac{q_1}{2}+q_5\cos q_{11})\\ {\tilde{r}}_{H6}& =(-\sin (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}+\frac{q_{17}}{3\sqrt{2}}+\frac{q_{18}}{2}),\\ & -\cos (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}+\frac{q_{17}}{3\sqrt{2}}+\frac{q_{18}}{2}),-\frac{q_1}{2}+q_6\cos q_{12})\end{array}$(A19) which are precisely the original BF Cartesian coordinates permuted according to (123)(456). There is no rotation.

For the operation (132)(456), the dihedrals $(q_{14},q_{15})$ transform as the transpose of Equation (A18(A18) $\left(\begin{array}{c}{q}_k\\ q_{k^{\prime }}\end{array}\right)\to \left(\begin{array}{cc}-\frac{1}{2}& -\frac{\sqrt{3}}{2}\\ \frac{\sqrt{3}}{2}& -\frac{1}{2}\end{array}\right)\left(\begin{array}{c}{q}_k\\ q_{k^{\prime }}\end{array}\right)$(A18) ) and the torsional angle does not change. The transformed Cartesian coordinates are (A20) $\begin{array}{rl}{\tilde{r}}_{H1}& =(\cos (\frac{q_{14}}{\sqrt{6}}+\frac{q_{15}}{3\sqrt{2}}-\frac{q_{18}}{2}),\\ & -\sin (\frac{q_{14}}{\sqrt{6}}+\frac{q_{15}}{3\sqrt{2}}-\frac{q_{18}}{2}),\frac{q_1}{2}-q_3\cos q_9)\\ {\tilde{r}}_{H2}& =(-\sin (\frac{\pi }{6}+\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}+\frac{q_{18}}{2}),\\ & \cos (\frac{\pi }{6}+\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}+\frac{q_{18}}{2}),\frac{q_1}{2}-q_4\cos q_{10})\\ {\tilde{r}}_{H3}& =(-\sin (\frac{\pi }{6}-\frac{\sqrt{2}{q}_{15}}{3}-\frac{q_{18}}{2}),\\ & -\cos (\frac{\pi }{6}-\frac{\sqrt{2}{q}_{15}}{3}-\frac{q_{18}}{2}),\frac{q_1}{2}-q_2\cos q_8)\\ {\tilde{r}}_{H4}& =(\cos (\frac{q_{16}}{\sqrt{6}}+\frac{q_{17}}{3\sqrt{2}}+\frac{q_{18}}{2}),\\ & -\sin (\frac{q_{16}}{\sqrt{6}}+\frac{q_{17}}{3\sqrt{2}}+\frac{q_{18}}{2}),-\frac{q_1}{2}+q_7\cos q_{13}).\\ {\tilde{r}}_{H5}& =(-\sin (\frac{\pi }{6}-\frac{\sqrt{2}{q}_{17}}{3}+\frac{q_{18}}{2}),\\ & -\cos (\frac{\pi }{6}-\frac{\sqrt{2}{q}_{17}}{3}+\frac{q_{18}}{2}),-\frac{q_1}{2}+q_5\cos q_{11})\\ {\tilde{r}}_{H6}& =(-\sin (\frac{\pi }{6}+\frac{q_{16}}{\sqrt{6}}-\frac{q_{17}}{3\sqrt{2}}-\frac{q_{18}}{2}),\\ & \cos (\frac{\pi }{6}+\frac{q_{16}}{\sqrt{6}}-\frac{q_{17}}{3\sqrt{2}}-\frac{q_{18}}{2}),-\frac{q_1}{2}+q_6\cos q_{12}).\end{array}$(A20) With this construction of the Cartesian coordinates, the corresponding BF-frame rotation is $M_z\left(2\pi /3\right)$. Thus we have (A21) $\begin{array}{rl}{N}_{\left(132\right)\left(456\right)}& =\left(\begin{array}{ccc}-\sin \left(\pi /6\right)& -\cos \left(\pi /6\right)& 0\\ \phantom{-}\cos \left(\pi /6\right)& -\sin \left(\pi /6\right)& 0\\ 0& 0& 1\end{array}\right)\\ & =\left(\begin{array}{ccc}-\cos \left(\pi /3\right)& \phantom{-}\sin \left(\pi /3\right)& 0\\ -\sin \left(\pi /3\right)& -\cos \left(\pi /3\right)& 0\\ 0& 0& 1\end{array}\right)\end{array}$(A21) Applying the first form to H₁, H₃, H₄, and H₅, and the second form to H₂ and H₆, we recover the transformed Cartesian coordinates in the original BF-frame.

The operation $\left(14\right)\left(26\right)\left(35\right)(ab{)}^{\ast }$ changes the dihedrals according to (A22) $\left(\begin{array}{c}{q}_{14}\\ q_{15}\end{array}\right)\to \left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}{q}_{16}\\ q_{17}\end{array}\right)$(A22) and likewise for $(q_{16},q_{17})$. The torsional angle changes as $q_{18}\to 2\pi -q_{18}$. The result is (A23) $\begin{array}{rl}{\tilde{r}}_{C_a}& =(0,0,\frac{q_1}{2})\\ {\tilde{r}}_{C_b}& =(0,0,-\frac{q_1}{2})\\ {\tilde{r}}_{H1}& =(-\cos (\frac{\sqrt{2}{q}_{17}}{3}-\frac{q_{18}}{2}),-\sin (\frac{\sqrt{2}{q}_{17}}{3}-\frac{q_{18}}{2}),\\ & \frac{q_1}{2}-q_5\cos q_{11})=-r_{H4}\\ {\tilde{r}}_{H2}& =(\sin (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}-\frac{q_{17}}{3\sqrt{2}}-\frac{q_{18}}{2}),\\ & -\cos (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}-\frac{q_{17}}{3\sqrt{2}}-\frac{q_{18}}{2}),\\ & \frac{q_1}{2}-q_7\cos q_{13}\phantom{\frac{\sqrt{2}{q}_{15}}{3}})\\ & =-r_{H6}\\ {\tilde{r}}_{H3}& =(\sin (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}+\frac{q_{17}}{3\sqrt{2}}+\frac{q_{18}}{2})\sin q_{12},\\ & \cos (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}+\frac{q_{17}}{3\sqrt{2}}+\frac{q_{18}}{2})\sin q_{12},\\ & -\frac{q_1}{2}+q_6\cos q_{12}\phantom{\frac{\sqrt{2}{q}_{15}}{3}})=-r_{H5}\\ {\tilde{r}}_{H4}& =(-\cos (\frac{\sqrt{2}{q}_{15}}{3}+\frac{q_{18}}{2}),-\sin (\frac{\sqrt{2}{q}_{15}}{3}+\frac{q_{18}}{2}),\\ & -\frac{q_1}{2}+q_2\cos q_8\phantom{\frac{\sqrt{2}{q}_{15}}{3}})=-r_{H1}\\ {\tilde{r}}_{H5}& =(\sin (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}+\frac{q_{15}}{3\sqrt{2}}-\frac{q_{18}}{2}),\\ & \cos (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}+\frac{q_{15}}{3\sqrt{2}}-\frac{q_{18}}{2}),-\frac{q_1}{2}+q_4\cos q_{10})\\ & =-r_{H3}\\ {\tilde{r}}_{H6}& =(\sin (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}+\frac{q_{18}}{2}),\\ & -\cos (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}+\frac{q_{18}}{2}),-\frac{q_1}{2}+q_3\cos q_9)\\ & =-r_{H2}\end{array}$(A23) which are exactly the original BF Cartesian coordinates after the operation $\left(14\right)\left(26\right)\left(35\right)(ab{)}^{\ast }$ is applied, which means no rotation is required.

Next, the operation $\left(14\right)\left(25\right)\left(36\right)\left(ab\right)$ transforms the dihedrals as (A24) $\left(\begin{array}{c}{q}_{14}\\ q_{15}\end{array}\right)\to \left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}{q}_{16}\\ q_{17}\end{array}\right)$(A24) and likewise for $(q_{16},q_{17})$ and does not change the torsional angle. With the BF-frame rotation of $N_{\left(14\right)\left(25\right)\left(36\right)\left(ab\right)}\equiv N=M_x\left(\pi \right)$ applied, the transformed Cartesian coordinates in the original frame are (A25) $\begin{array}{rl}N{\tilde{r}}_{C_a}& =(0,0,-\frac{q_1}{2})\\ N{\tilde{r}}_{C_b}& =(0,0,\frac{q_1}{2})\\ N{\tilde{r}}_{H1}& =(\cos (\frac{\sqrt{2}{q}_{17}}{3}-\frac{q_{18}}{2}),\sin (\frac{\sqrt{2}{q}_{17}}{3}-\frac{q_{18}}{2}),\\ & -\frac{q_1}{2}+q_5\cos q_{11}\phantom{\frac{\sqrt{2}{q}_{15}}{3}})\\ N{\tilde{r}}_{H2}& =(-\sin (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}-\frac{q_{17}}{3\sqrt{2}}+\frac{q_{18}}{2})\sin q_{12},\\ & -\cos (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}+\frac{q_{17}}{3\sqrt{2}}+\frac{q_{18}}{2})\sin q_{12},\\ & -\frac{q_1}{2}-q_6\cos q_{12}\phantom{\frac{\sqrt{2}{q}_{15}}{3}})\\ N{\tilde{r}}_{H3}& =(-\sin (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}-\frac{q_{17}}{3\sqrt{2}}-\frac{q_{18}}{2}),\\ & \cos (\frac{\pi }{6}-\frac{q_{16}}{\sqrt{6}}-\frac{q_{17}}{3\sqrt{2}}-\frac{q_{18}}{2}),-\frac{q_1}{2}+q_7\cos q_{13}).\\ N{\tilde{r}}_{H4}& =(\cos (\frac{\sqrt{2}{q}_{15}}{3}+\frac{q_{18}}{2}),\sin (\frac{\sqrt{2}{q}_{15}}{3}+\frac{q_{18}}{2}),\\ & \frac{q_1}{2}-q_2\cos q_8\phantom{\frac{\sqrt{2}{q}_{15}}{3}})\\ N{\tilde{r}}_{H5}& =(-\sin (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}+\frac{q_{18}}{2}),\\ & \cos (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}-\frac{q_{15}}{3\sqrt{2}}+\frac{q_{18}}{2}),\frac{q_1}{2}-q_3\cos q_9)\\ N{\tilde{r}}_{H6}& =(-\sin (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}+\frac{q_{15}}{3\sqrt{2}}-\frac{q_{18}}{2}),\\ & -\cos (\frac{\pi }{6}-\frac{q_{14}}{\sqrt{6}}+\frac{q_{15}}{3\sqrt{2}}-\frac{q_{18}}{2}),\frac{q_1}{2}-q_4\cos q_{10})\end{array}$(A25) which is the desired permutation.

Finally, the operation $E^{\prime }$ is not an MS operation. The nuclei should not be permuted or inverted. With $q_{18}\to 2\pi +q_{18}$, the x and y components of all the nuclei become negative, while the rotation $M_z\left(\pi \right)$ transforms them back, so the operation has no effect on the Cartesian coordinates, as desired.