Transport Corrections and Sensitivities in the Discrete-Ordinates Method

Abstract

Methods for approximately accounting for the terms neglected in a finite (L’th-order) Legendre expansion of the scattering source in the transport equation are called transport corrections. This paper derives adjoint-based sensitivities of a neutron or gamma-ray transport response for problems that use diagonal, Bell-Hansen-Sandmeier (BHS), or n’th-Cesàro-mean-of-order-2 (Cesàro) transport corrections in the discrete-ordinates method. For diagonal and BHS transport corrections, there is a sensitivity to the L + 1ʹth scattering cross-section moment, and the sensitivity to nuclide and material densities requires this contribution. For the Cesàro transport correction, the sensitivities to the scattering cross section for the l’th moment are multiplied by a simple function of l and the scattering expansion order L. Numerical results for a k_eff problem and a fixed-source problem verify the derivation and implementation of the sensitivity equations into the SENSMG multigroup sensitivity code. The Cesàro transport correction yields inaccurate responses for both problems.

Keywords:

• Transport correction
• discrete ordinates
• sensitivity theory
• PARTISN, SENSMG

I. INTRODUCTION

Truncating the spherical harmonics expansion of the scattering source in the Boltzmann transport equation leads to truncation error. Methods for approximately accounting for the neglected terms are called transport corrections.¹ This paper deals with three widely used transport corrections in the discrete-ordinates method: diagonal,² Bell-Hansen-Sandmeier³ (BHS), and n’th-Cesàro-mean-of-order-2 (Cesàro).⁴ These transport corrections modify the scattering cross sections and (except for Cesàro) the total cross sections used in the transport calculation. Another transport correction for several applications, including discrete ordinates, was derived by Stacey⁵ from a variational principle for the quantity of interest. Transport corrections are also used in nuclear reactor physics.^6–8

Transport corrections were developed in a time when including even one scattering cross-section moment beyond isotropic (i.e., a linearly anisotropic expansion) was challenging, both in terms of computation time and memory. As fast and large as modern computers are, modern multigroup discrete-ordinates transport codes still have transport correction options. PARTISN (Ref. 9) has diagonal, BHS, Cesàro, and the default of none. These options, including the coding, were inherited from PARTISN’s predecessor, ONEDANT (Ref. 10). Denovo (Ref. 11) has diagonal, Cesàro, and none, with diagonal being the default. ARDRA (Ref. 12) has diagonal and none, with none being the default. Attila (Ref. 13) has diagonal, BHS, and none, with diagonal being the default. (ARDRA has historically offered two additional transport corrections that have not been published.¹⁴ Attila also offers an “optimized diagonal” transport correction.^15,16) Of course, users who supply their own nuclear data to the deterministic transport code can apply a transport correction in the nuclear data preparation process. The nuclear data formatting utility code¹⁷ TRANSX offers the diagonal and BHS transport corrections as well as the consistent-P approximation³ (and two other approximations described only briefly in Ref. 1 and the various versions of the TRANSX and NJOY code manuals^17,18). ARDRA relies on data processing and formatting codes for its transport corrections.¹⁴

Transport corrections are well known, but to this author’s knowledge, the adjoint-based sensitivity of a computed response to the transport-corrected scattering and total cross sections and nuclide densities has never been presented. Calculating adjoint-based sensitivities is enormously efficient compared to using direct perturbations. This paper discusses the issues associated with computing sensitivities with adjoint methods when transport corrections are used. The three transport correction options available in PARTISN have been implemented in the SENSMG multigroup neutron sensitivity code.^19,20 SENSMG has a similar role as the old SWANLAKE (Ref. 21), FORSS (Ref. 22), and SENSIT (Ref. 23) codes. It has capabilities similar to those of SUSD3D (Refs. 24 and 25), which also uses PARTISN. SUSD3D relies on TRANSX for its nuclear data, and its transport corrections are applied in TRANSX rather than the transport code.

This paper is organized as follows. The diagonal, BHS, and Cesàro transport corrections are presented in Sec. II. Transport-corrected adjoint sensitivities are derived in Sec. III. Section IV presents numerical results for a k_eff test problem, and Sec. V presents numerical results for an inhomogeneous (fixed-source) test problem. Section VI is a summary and conclusions. The Appendix provides a corrigendum for Ref. 19.

II. TRANSPORT CORRECTIONS

The forward Boltzmann transport equation for neutral particles is

(1) $A\psi =\lambda F\psi +q,$(1)

where

ψ = ${\psi }^g(r,\hat{\mathbf{\Omega }})$ =	=	the angular flux of particles at position r, direction $\hat{\mathbf{\Omega }}$, and energy group g
q = $q=g(r,\widehat{\Omega })$ =	=	the source rate density at position r, direction $\hat{\mathrm{\Omega }}$, and energy group g
λ =	=	multiplication factor; λ = 1 if q ≠ 0 and $\lambda =1/k_{eff}$ is the eigenvalue if q = 0
F =	=	the fission production operator, which will not be discussed in this paper
A =	=	the loss operator, defined by

(2) $\begin{array}{r}A\psi =\hat{\mathbf{\Omega }}\cdot \mathrm{\nabla }{\psi }^g(r,\hat{\mathbf{\Omega }})+{\mathrm{\Sigma }}_t^g(r){\psi }^g(r,\hat{\mathbf{\Omega }})\\ -\sum _{l=0}^L\sum _{g{ }^{\mathrm{\prime }}=1}^G(2l+1){\mathrm{\Sigma }}_{s,l}^{g{ }^{\mathrm{\prime }}\to g}(r){\varphi }_l^{g{ }^{\mathrm{\prime }}}(r)\text{.}\end{array}$(2)

In Eq. (2(2) $\begin{array}{r}A\psi =\hat{\mathbf{\Omega }}\cdot \mathrm{\nabla }{\psi }^g(r,\hat{\mathbf{\Omega }})+{\mathrm{\Sigma }}_t^g(r){\psi }^g(r,\hat{\mathbf{\Omega }})\\ -\sum _{l=0}^L\sum _{g{ }^{\mathrm{\prime }}=1}^G(2l+1){\mathrm{\Sigma }}_{s,l}^{g{ }^{\mathrm{\prime }}\to g}(r){\varphi }_l^{g{ }^{\mathrm{\prime }}}(r)\text{.}\end{array}$(2) ),

${\mathrm{\Sigma }}_t^g(r)$ =	=	the total macroscopic cross section at position r and energy group g
${\mathrm{\Sigma }}_{s,l}^{g{ }^{\mathrm{\prime }}\to g}(r)$ =	=	the l’th Legendre moment of the macroscopic scattering cross section from energy group g′ to g at position r
${\varphi }_l^{g{ }^{\mathrm{\prime }}}(r)$ =	=	the l’th Legendre moment of the angular flux in energy group g′ at position r
G =	=	the number of energy groups
L =	=	the scattering expansion order.

Equation (1)(1) $A\psi =\lambda F\psi +q,$(1) has appropriate boundary conditions such as vacuum (appropriate forward boundary conditions are any that, with the adjoint boundary conditions mentioned in Sec. III, cause the bilinear concomitant to vanish²⁶). The macroscopic cross section ${\mathrm{\Sigma }}_x^g(r)$ for reaction x in group g at position r is

(3) ${\mathrm{\Sigma }}_x^g(r)=\sum _{i=1}^I{N}_i(x){\sigma }_x^g,$(3)

where

${\sigma }_x^g$ =	=	the microscopic cross section for nuclide i
$N_i(x)$ =	=	the atom density of nuclide i at position r
I =	=	the number of nuclides in the material at position r.

The diagonal transport correction² corrects the macroscopic total and self-scattering cross sections using

(4) ${\tilde{\mathrm{\Sigma }}}_t^g={\mathrm{\Sigma }}_t^g-{\mathrm{\Sigma }}_{s,L+1}^{g\to g},g=1,\dots ,G$(4)

and

(5) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g}={\mathrm{\Sigma }}_{s,l}^{g\to g}-{\mathrm{\Sigma }}_{s,L+1}^{g\to g},\\ g=1,\dots ,G,l=0,1,\dots ,L,\end{array}$(5)

where the tilde represents the transport-corrected cross section that is used in Eq. (2)(2) $\begin{array}{r}A\psi =\hat{\mathbf{\Omega }}\cdot \mathrm{\nabla }{\psi }^g(r,\hat{\mathbf{\Omega }})+{\mathrm{\Sigma }}_t^g(r){\psi }^g(r,\hat{\mathbf{\Omega }})\\ -\sum _{l=0}^L\sum _{g{ }^{\mathrm{\prime }}=1}^G(2l+1){\mathrm{\Sigma }}_{s,l}^{g{ }^{\mathrm{\prime }}\to g}(r){\varphi }_l^{g{ }^{\mathrm{\prime }}}(r)\text{.}\end{array}$(2) instead of the cross section without the tilde. (In this section, the translation from the original sources’ notation to that of this paper was facilitated by chapter 3 of the PARTISN manual.⁹) Strictly speaking, Pendlebury and Underhill² defined the diagonal transport correction only for L = 0. Bell et al.³ provided the natural extension to an arbitrary scattering expansion order. Pendlebury and Underhill wrote that the diagonal transport correction “can be expected to be fairly reliable as long as the major contribution to elastic scattering retains the neutrons in the same energy group.”²

The BHS transport correction³ corrects the macroscopic total and self-scattering cross sections using

(6) ${\tilde{\mathrm{\Sigma }}}_t^g={\mathrm{\Sigma }}_t^g-\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}},g=1,\dots ,G$(6)

and

(7) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g}={\mathrm{\Sigma }}_{s,l}^{g\to g}-\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}},\\ g=1,\dots ,G,l=0,1,\dots ,L.\end{array}$(7)

Following Lathrop,²⁷ Bell et al.³ called their method the “extended transport correction,” an appellation that MacFarlane¹ retained in addition to the more common one. Comparing the diagonal transport correction with the BHS (or extended) transport correction, Bell et al. wrote, “… [F]or a coarse group structure, this approximation [i.e., the diagonal transport correction] approaches the extended transport approximation, while for G → ∞, the ‘transport correction term’ … vanishes altogether.”³ Attila (Ref. 13) requires L ≥ 1 for use of the BHS correction.

The Cesàro transport correction⁴ corrects the macroscopic scattering cross sections using

(8) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g{ }^{\mathrm{\prime }}}=\frac{(L+2-l)(L+1-l)}{(L+2)(L+1)}{\mathrm{\Sigma }}_{s,l}^{g\to g{ }^{\mathrm{\prime }}},\\ g=1,\dots ,G,g{ }^{\mathrm{\prime }}=1,\dots ,G,l=0,\dots ,L.\end{array}$(8)

The Cesàro transport correction has no effect for l = 0 (isotropic scattering), and the modified scattering cross sections do not affect the total cross section ${\mathrm{\Sigma }}_t^g$. The n in the phrase “n’th Cesàro mean of order 2” is in our notation L, the order of the last term in the scattering expansion. While the diagonal and BHS transport corrections seek to make the S_N form of the transport equation as close as possible to the P_N form,¹ the Cesàro transport correction seeks to approximate the infinite sum

(9) ${\mathrm{\Sigma }}_s^{g\to g{ }^{\mathrm{\prime }}}({\mu }_0)=\sum _{l=0}^{\mathrm{\infty }}\frac{(2l+1)}{4\pi }{P}_l({\mu }_0){\mathrm{\Sigma }}_{s,l}^{g\to g{ }^{\mathrm{\prime }}}$(9)

with the partial sum^28,29

(10) ${\tilde{\mathrm{\Sigma }}}_s^{g\to g{ }^{\mathrm{\prime }}}({\mu }_0)=\sum _{l=0}^L\frac{(2l+1)}{4\pi }{P}_l({\mu }_0){\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g{ }^{\mathrm{\prime }}}.$(10)

In Eqs. (9)(9) ${\mathrm{\Sigma }}_s^{g\to g{ }^{\mathrm{\prime }}}({\mu }_0)=\sum _{l=0}^{\mathrm{\infty }}\frac{(2l+1)}{4\pi }{P}_l({\mu }_0){\mathrm{\Sigma }}_{s,l}^{g\to g{ }^{\mathrm{\prime }}}$(9) and (10(10) ${\tilde{\mathrm{\Sigma }}}_s^{g\to g{ }^{\mathrm{\prime }}}({\mu }_0)=\sum _{l=0}^L\frac{(2l+1)}{4\pi }{P}_l({\mu }_0){\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g{ }^{\mathrm{\prime }}}.$(10) ), μ₀ is the cosine of the scattering angle and P_l is the Legendre polynomial of order l. Albert and Nelson recognized that the Cesàro transport correction would only be accurate for relatively large degrees of anisotropy, whereas the usual partial sum,

(11) ${\mathrm{\Sigma }}_s^{g\to g{ }^{\mathrm{\prime }}}({\mu }_0)=\sum _{l=0}^L\frac{(2l+1)}{4\pi }{P}_l({\mu }_0){\mathrm{\Sigma }}_{s,l}^{g\to g{ }^{\mathrm{\prime }}}$(11)

“for relatively low degrees of anisotropy … tends to be much better than the [Cesàro transport correction],”⁴ but they sought to exploit the fact that ${\tilde{\mathrm{\Sigma }}}_s^{g\to g{ }^{\mathrm{\prime }}}({\mu }_0)$ is nonnegative. Denovo requires L ≥ 2 for use of the Cesàro correction.¹¹ The PARTISN manual⁹ advises this, but the code does not require it.

PARTISN applies the selected transport correction to the macroscopic material cross sections. The output cross-section file macrxs contains uncorrected cross sections. However, the cross sections output to the standard output file using xsectp > 0 in block 5 are transport corrected.

III. TRANSPORT-CORRECTED SENSITIVITIES

The relative sensitivity $S_{R,x}$ of a response R to input parameter x is defined to be

(12) $S_{R,x}\equiv \frac{x_0}{R_0}{\left.\frac{\mathrm{\partial }R}{\mathrm{\partial }x}\right|}_{x=x_0},$(12)

where subscript 0 indicates a specific state of the system. The sensitivity is evaluated at a particular system state. Henceforth, subscript 0 will be assumed.

Briefly, the adjoint-based relative sensitivity $S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}$ of a response R to the total cross section ${\sigma }_{t,i}^g$ of nuclide i in energy group g is obtained by multiplying Eq. (2)(2) $\begin{array}{r}A\psi =\hat{\mathbf{\Omega }}\cdot \mathrm{\nabla }{\psi }^g(r,\hat{\mathbf{\Omega }})+{\mathrm{\Sigma }}_t^g(r){\psi }^g(r,\hat{\mathbf{\Omega }})\\ -\sum _{l=0}^L\sum _{g{ }^{\mathrm{\prime }}=1}^G(2l+1){\mathrm{\Sigma }}_{s,l}^{g{ }^{\mathrm{\prime }}\to g}(r){\varphi }_l^{g{ }^{\mathrm{\prime }}}(r)\text{.}\end{array}$(2) by the adjoint angular flux ${\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})$ and integrating over volume and angle.³⁰ The adjoint flux satisfies

(13) $A^{\ast }{\mathrm{\Gamma }}^{\ast }=\lambda F^{\ast }{\mathrm{\Gamma }}^{\ast }+q^{\ast },$(13)

where

$q^{\ast }$ = $q^{\ast g}(r,\hat{\mathbf{\Omega }})$ =	=	the adjoint source rate density at position r, direction $\hat{\mathbf{\Omega }}$, and energy group g
λ =	=	the same multiplication factor as in Eq. (1(1) $A\psi =\lambda F\psi +q,$(1) )
$F^{\ast }$ =	=	the adjoint fission production operator, which will not be discussed in this paper
$A^{\ast }$ =	=	the adjoint loss operator, defined by

(14) $\begin{array}{r}{A}^{\ast }{\mathrm{\Gamma }}^{\ast }=-\hat{\mathbf{\Omega }}\cdot \mathrm{\nabla }{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})+{\mathrm{\Sigma }}_t^g(r){\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})\\ -\sum _{l=0}^L\sum _{g{ }^{\mathrm{\prime }}=1}^G(2l+1){\mathrm{\Sigma }}_{s,l}^{g\to g{ }^{\mathrm{\prime }}}(r){\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r),\end{array}$(14)

where ${\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)$ is the l’th Legendre moment of the adjoint angular flux in energy group g′ at position r. Equation (13)(13) $A^{\ast }{\mathrm{\Gamma }}^{\ast }=\lambda F^{\ast }{\mathrm{\Gamma }}^{\ast }+q^{\ast },$(13) has appropriate boundary conditions, such as vacuum (appropriate adjoint boundary conditions are any that, with the forward boundary conditions mentioned in Sec. II, cause the bilinear concomitant to vanish²⁶). The sensitivity is

(15) $S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}=-{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{t,i}^g{\psi }^g(r,\hat{\mathbf{\Omega }}).$(15)

The right side of Eq. (15)(15) $S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}=-{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{t,i}^g{\psi }^g(r,\hat{\mathbf{\Omega }}).$(15) may have a denominator, depending on the response and whether q = 0 in Eq. (1)(1) $A\psi =\lambda F\psi +q,$(1) . (For example, for an eigenvalue problem in which R = k_eff is the response, $S_{k_{eff},{\sigma }_{t,i}^g}$ is Eq. (15)(15) $S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}=-{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{t,i}^g{\psi }^g(r,\hat{\mathbf{\Omega }}).$(15) divided by $\sum _{g=1}^G{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}F{\psi }^g$.) Likewise, the relative sensitivity $S_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ of R to the scattering cross section ${\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}$ of nuclide i for expansion order l from energy group g to g′ is

(16) $\begin{array}{r}{S}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}={\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)\\ -{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}),\end{array}$(16)

where ${\delta }_{pq}$ is the Kronecker delta function (see Appendix). The second term on the right side appears because the isotropic scattering cross sections are addends in the total cross section ${\sigma }_{t,i}^g$.

The relative sensitivity $S_{R,N_i}^g$ in group g of R to the density of nuclide i is

(17) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}},$(17)

where the relative sensitivity $S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}$ to total scattering within and out of group g is

(18) $S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}=\sum _{l=0}^L{\int }_{V}dV\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)$(18)

(the effect of isotropic scattering on the total cross section is accounted for in $S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}$). $S_{R,{\nu }_i^g}^{\hspace{0.17em}}$ is the contribution from the fission terms and is not discussed further in this paper; see Ref. 20. The relative sensitivity $S_{R,\rho }^g$ in group g of R to the mass density ρ of the material is

(19) $S_{R,\rho }^g=\sum _{i=1}^I{S}_{R,N_i}^g,$(19)

where I is the number of nuclides in the material, as before.

When the BHS transport correction is used, Eqs. (6)(6) ${\tilde{\mathrm{\Sigma }}}_t^g={\mathrm{\Sigma }}_t^g-\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}},g=1,\dots ,G$(6) and (7)(7) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g}={\mathrm{\Sigma }}_{s,l}^{g\to g}-\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}},\\ g=1,\dots ,G,l=0,1,\dots ,L.\end{array}$(7) are used in Eq. (2)(2) $\begin{array}{r}A\psi =\hat{\mathbf{\Omega }}\cdot \mathrm{\nabla }{\psi }^g(r,\hat{\mathbf{\Omega }})+{\mathrm{\Sigma }}_t^g(r){\psi }^g(r,\hat{\mathbf{\Omega }})\\ -\sum _{l=0}^L\sum _{g{ }^{\mathrm{\prime }}=1}^G(2l+1){\mathrm{\Sigma }}_{s,l}^{g{ }^{\mathrm{\prime }}\to g}(r){\varphi }_l^{g{ }^{\mathrm{\prime }}}(r)\text{.}\end{array}$(2) to yield

(20) $\begin{array}{r}\tilde{A}\psi =\hat{\mathbf{\Omega }}\cdot \mathrm{\nabla }{\psi }^g(r,\hat{\mathbf{\Omega }})+\left({\mathrm{\Sigma }}_t^g(r)-\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}}(r)\right){\psi }^g(r,\hat{\mathbf{\Omega }})-\sum _{l=0}^L\sum _{g{ }^{\mathrm{\prime }}=1}^G(2l+1)\left({\mathrm{\Sigma }}_{s,l}^{g{ }^{\mathrm{\prime }}\to g}(r)-{\delta }_{gg{ }^{\mathrm{\prime }}}\sum _{g{ }^{\mathrm{\prime }\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }\mathrm{\prime }}}(r)\right){\varphi }_l^{g{ }^{\mathrm{\prime }}}(r)=A\psi -\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}}(r){\psi }^g(r,\hat{\mathbf{\Omega }})+\sum _{l=0}^L(2l+1)\left(\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}}(r)\right){\varphi }_l^g(r).\end{array}$(20)

The same derivation that leads to Eqs. (15)(15) $S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}=-{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{t,i}^g{\psi }^g(r,\hat{\mathbf{\Omega }}).$(15) and (16(16) $\begin{array}{r}{S}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}={\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)\\ -{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}),\end{array}$(16) ) yields the relative sensitivity $S_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ of R to the scattering cross section ${\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}$ of nuclide i for expansion order L + 1 from energy group g to g′:

(21) $\begin{array}{r}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=-\sum _{l=0}^L{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)+{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(21)

The first term on the right side of Eq. (21)(21) $\begin{array}{r}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=-\sum _{l=0}^L{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)+{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(21) appears because of Eq. (7(7) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g}={\mathrm{\Sigma }}_{s,l}^{g\to g}-\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}},\\ g=1,\dots ,G,l=0,1,\dots ,L.\end{array}$(7) ); the second term appears because of Eq. (6)(6) ${\tilde{\mathrm{\Sigma }}}_t^g={\mathrm{\Sigma }}_t^g-\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}},g=1,\dots ,G$(6) . Comparing Eqs. (4)(4) ${\tilde{\mathrm{\Sigma }}}_t^g={\mathrm{\Sigma }}_t^g-{\mathrm{\Sigma }}_{s,L+1}^{g\to g},g=1,\dots ,G$(4) and (5(5) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g}={\mathrm{\Sigma }}_{s,l}^{g\to g}-{\mathrm{\Sigma }}_{s,L+1}^{g\to g},\\ g=1,\dots ,G,l=0,1,\dots ,L,\end{array}$(5) ) with Eqs. (6)(6) ${\tilde{\mathrm{\Sigma }}}_t^g={\mathrm{\Sigma }}_t^g-\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}},g=1,\dots ,G$(6) and (7(7) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g}={\mathrm{\Sigma }}_{s,l}^{g\to g}-\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}},\\ g=1,\dots ,G,l=0,1,\dots ,L.\end{array}$(7) ), when diagonal transport correction is used, the relative sensitivity of R to the scattering cross section ${\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}$ is ${\delta }_{gg{ }^{\mathrm{\prime }}}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$, or just the diagonal elements of the scattering sensitivity matrix. Note that the index on the adjoint flux in the first term on the right side of Eq. (21)(21) $\begin{array}{r}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=-\sum _{l=0}^L{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)+{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(21) is g, not the usual g′ for scattering sensitivities—e.g., see the first term in Eq. (16)(16) $\begin{array}{r}{S}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}={\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)\\ -{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}),\end{array}$(16) —because only the within-group scattering cross section is transport corrected [Eq. (7)(7) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g}={\mathrm{\Sigma }}_{s,l}^{g\to g}-\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}},\\ g=1,\dots ,G,l=0,1,\dots ,L.\end{array}$(7) ].

When diagonal transport correction is used, the relative sensitivity $S_{R,N_i}^g$ in group g of R to the density of nuclide i is

(22) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,L+1,i}^{g\to g}}^{\hspace{0.17em}},$(22)

and when the BHS transport correction is used, the relative sensitivity $S_{R,N_i}^g$ in group g of R to the density of nuclide i is

(23) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}+\sum _{g{ }^{\mathrm{\prime }}=1}^G{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}.$(23)

When the Cesàro transport correction is used, Eq. (8)(8) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g{ }^{\mathrm{\prime }}}=\frac{(L+2-l)(L+1-l)}{(L+2)(L+1)}{\mathrm{\Sigma }}_{s,l}^{g\to g{ }^{\mathrm{\prime }}},\\ g=1,\dots ,G,g{ }^{\mathrm{\prime }}=1,\dots ,G,l=0,\dots ,L.\end{array}$(8) is used in Eq. (2)(2) $\begin{array}{r}A\psi =\hat{\mathbf{\Omega }}\cdot \mathrm{\nabla }{\psi }^g(r,\hat{\mathbf{\Omega }})+{\mathrm{\Sigma }}_t^g(r){\psi }^g(r,\hat{\mathbf{\Omega }})\\ -\sum _{l=0}^L\sum _{g{ }^{\mathrm{\prime }}=1}^G(2l+1){\mathrm{\Sigma }}_{s,l}^{g{ }^{\mathrm{\prime }}\to g}(r){\varphi }_l^{g{ }^{\mathrm{\prime }}}(r)\text{.}\end{array}$(2) to yield

(24) $\begin{array}{r}\tilde{A}\psi =\hat{\mathbf{\Omega }}\cdot \mathrm{\nabla }{\psi }^g(r,\hat{\mathbf{\Omega }})+{\mathrm{\Sigma }}_t^g(r){\psi }^g(r,\hat{\mathbf{\Omega }})-\sum _{l=0}^L\sum _{g{ }^{\prime }=1}^G(2l+1)\frac{(L+2-l)(L+1-l)}{(L+2)(L+1)}{\mathrm{\Sigma }}_{s,l}^{g\to g{ }^{\prime }}(r){\varphi }_l^{g{ }^{\prime }}(r).\end{array}$(24)

The same derivation that leads to Eqs. (15)(15) $S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}=-{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{t,i}^g{\psi }^g(r,\hat{\mathbf{\Omega }}).$(15) and (16)(16) $\begin{array}{r}{S}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}={\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)\\ -{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}),\end{array}$(16) yields the modified relative sensitivity ${\tilde{S}}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ of R to the scattering cross section ${\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}$ of nuclide i for expansion order l from energy group g to g′:

(25) $\begin{array}{r}{\tilde{S}}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=\frac{(L+2-l)(L+1-l)}{(L+2)(L+1)}{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)-{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(25)

Likewise, the modified relative sensitivity to total scattering within and out of group g is

(26) ${\tilde{S}}_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}=\sum _{l=0}^L\frac{(L+2-l)(L+1-l)}{(L+2)(L+1)}{\int }_{V}dV\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r).$(26)

Thus, when the Cesàro transport correction is used, the relative sensitivity $S_{R,N_i}^g$ in group g of R to the density of nuclide i is

(27) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+{\tilde{S}}_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}.$(27)

For diagonal and BHS transport corrections, the macroscopic total and self-scatter cross sections are modified [Eqs. (4)(4) ${\tilde{\mathrm{\Sigma }}}_t^g={\mathrm{\Sigma }}_t^g-{\mathrm{\Sigma }}_{s,L+1}^{g\to g},g=1,\dots ,G$(4) through (7(7) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g}={\mathrm{\Sigma }}_{s,l}^{g\to g}-\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}},\\ g=1,\dots ,G,l=0,1,\dots ,L.\end{array}$(7) )] for the transport, but the sensitivity of R to the microscopic total and self-scatter cross sections is unaffected by the transport correction, except insofar as the forward and adjoint fluxes are affected. In other words, Eqs. (15)(15) $S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}=-{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{t,i}^g{\psi }^g(r,\hat{\mathbf{\Omega }}).$(15) and (16(16) $\begin{array}{r}{S}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}={\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)\\ -{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}),\end{array}$(16) ) are still used for $S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}$ and $S_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$. The calculation of these sensitivities is unaffected by the transport correction.

For the diagonal and BHS transport corrections, Eq. (21)(21) $\begin{array}{r}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=-\sum _{l=0}^L{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)+{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(21) is used for $S_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$. For the diagonal transport correction, the sensitivity matrix is diagonal, ${\delta }_{gg{ }^{\mathrm{\prime }}}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$.

For the diagonal and BHS transport corrections, a new term is added to the nuclide and material density sensitivities, the last term on the right side of Eqs. (22)(22) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,L+1,i}^{g\to g}}^{\hspace{0.17em}},$(22) and (23(23) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}+\sum _{g{ }^{\mathrm{\prime }}=1}^G{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}.$(23) ). An analogous term is added to the interface- and boundary-location derivatives.^19,20

It is sometimes advantageous to approximate the second term on the right side of Eq. (21)(21) $\begin{array}{r}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=-\sum _{l=0}^L{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)+{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(21) using adjoint and forward flux moments instead of angular fluxes²⁵; i.e.,

(28) ${\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }})\approx \sum _{l=0}^L{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r).$(28)

Unfortunately, when this approximation is used, $S_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ is zero because the two terms on the right side of Eq. (21)(21) $\begin{array}{r}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=-\sum _{l=0}^L{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)+{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(21) cancel.

IV. TEST PROBLEM FOR k_eff

The test configuration for k_eff was Flattop-Pu, otherwise known as PU-MET-FAST-006 (Ref. 31), a 6.06-kg ball of δ-phase plutonium reflected by 19.6 cm of natural uranium (NU) (the evaluation³¹ and its antecedent report³² refer to this material as normal uranium). The geometry and materials are given in Table I. The density and composition were converted from the standard International Criticality Safety Benchmark Evaluation Project specification in atom density using modern values of physical constants. The problem was run with various scattering expansion orders and each of the transport corrections available in PARTISN (including none).

TABLE I Flattop-Pu Model

Region	Material	Outer Radius (cm)	Density (g/cm^3)	Composition (Weight Fraction)
1	Plutonium	4.5332	15.52990779	^239Pu, 9.380012881E−01 ^240Pu, 4.799879422E−02 ^241Pu, 2.999857897E−03 ^69Ga, 6.536531152E−03 ^71Ga, 4.463528618E−03
2	NU	24.142	18.99986673	^234U, 5.407778609E−05 ^235U, 7.109665361E−03 ^238U, 9.928362569E−01

An angular quadrature of S₂₅₆ and fine mesh spacing of 0.005 cm were used. Thirty-group ENDF/B-VIII.0 cross sections having upscattering in the bottom five groups were used. The maximum scattering expansion order available in this library is 4 (indexed from 0). PARTISN version 8.32.54 was used.

IV. A. k_eff

The k_eff’s are compared in Table II and Fig. 1. The k_eff’s for L = 4 (R₄) are identical for no transport correction, BHS, and diagonal transport correction because that is the highest expansion order in the cross-section library; there is no ${\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}}$ to use in Eqs. (4)(4) ${\tilde{\mathrm{\Sigma }}}_t^g={\mathrm{\Sigma }}_t^g-{\mathrm{\Sigma }}_{s,L+1}^{g\to g},g=1,\dots ,G$(4) through (7(7) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g}={\mathrm{\Sigma }}_{s,l}^{g\to g}-\sum _{g{ }^{\mathrm{\prime }}=1}^G{\mathrm{\Sigma }}_{s,L+1}^{g\to g{ }^{\mathrm{\prime }}},\\ g=1,\dots ,G,l=0,1,\dots ,L.\end{array}$(7) ). PARTISN writes the message “isct too large for transport correction” and solves the problem with no correction. SENSMG writes the message “no transport correction for nuclide [nuclide specified].” The k_eff’s for L = 0 are identical for no transport correction and Cesàro transport correction because ${\tilde{\mathrm{\Sigma }}}_{s,0}^{g\to g{ }^{\mathrm{\prime }}}={\mathrm{\Sigma }}_{s,0}^{g\to g{ }^{\mathrm{\prime }}}$ in Eq. (8)(8) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g{ }^{\mathrm{\prime }}}=\frac{(L+2-l)(L+1-l)}{(L+2)(L+1)}{\mathrm{\Sigma }}_{s,l}^{g\to g{ }^{\mathrm{\prime }}},\\ g=1,\dots ,G,g{ }^{\mathrm{\prime }}=1,\dots ,G,l=0,\dots ,L.\end{array}$(8) .

TABLE II Flattop-Pu k_eff

Transport Correction	Scattering Order (L)	R	(R – R4)/R4
No	0	1.149628	14.998%
	1	0.974799	−2.491%
	2	1.005704	0.601%
	3	0.997479	−0.222%
	4	0.999698	0.000%
Diagonal	0	1.010732	1.104%
	1	0.997655	−0.204%
	2	0.999657	−0.004%
	3	0.999066	−0.063%
	4	0.999698	0.000%
BHS	0	1.009837	1.014%
	1	0.997628	−0.207%
	2	0.999660	−0.004%
	3	0.999070	−0.063%
	4	0.999698	0.000%
Cesàro	0	1.149628	14.998%
	1	1.097266	9.760%
	2	1.072832	7.316%
	3	1.058075	5.839%
	4	1.048259	4.858%

Fig. 1. k_eff versus scattering expansion order for Flattop-Pu for four transport corrections (including none). The LANL standard 30-group structure was used. The PARTISN manual⁹ advises against using the Cesàro transport correction for L < 2.

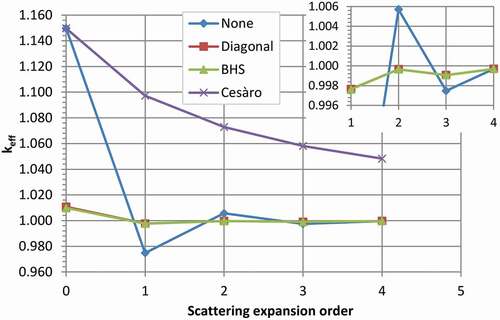
Assuming that R₄ with no transport correction (or diagonal or BHS) is the most accurate value, each of the k_eff’s is compared to R₄ in Table II. For L ≥ 1, diagonal and BHS results are essentially identical. Diagonal- and BHS-corrected P₁ calculations are slightly more accurate than a P₃ calculation with no transport correction.

The conventional wisdom that a P₁ scattering expansion is more accurate than P₂ is not true for this problem using these nuclear data, even without transport correction.

The Cesàro transport correction is wildly inaccurate for this problem, even for L ≥ 2.

IV.B. k_eff Sensitivities

In order to verify the derivations in Sec. III as well as the implementation in code, central-difference (CD) estimates of sensitivities were compared with adjoint-based calculations.

How important is it to account for the transport correction when using adjoint-based sensitivities? In other words, is it really necessary to use Eqs. (22)(22) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,L+1,i}^{g\to g}}^{\hspace{0.17em}},$(22) , (23(23) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}+\sum _{g{ }^{\mathrm{\prime }}=1}^G{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}.$(23) ), or (27) (depending on the transport correction) instead of Eq. (17(17) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}},$(17) )? The adjoint-based (SENSMG) relative sensitivity of each of the material densities, computed without accounting for the effect of the transport corrections on the sensitivities [i.e., using Eq. (17(17) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}},$(17) )], was compared with a CD estimate for various scattering expansion orders and each of the transport corrections (including none). The CD estimate of the relative sensitivity of response R when input parameter x is perturbed by $\pm \mathrm{\Delta }x$ is

$\begin{array}{rl}& {\left(S_{R,x}\right)}_{\mathrm{C}\mathrm{D}}=\frac{x_0}{R_0}\frac{R(x_0+\mathrm{\Delta }x)-R(x_0-\mathrm{\Delta }x)}{(x_0+\mathrm{\Delta }x)-(x_0-\mathrm{\Delta }x)}\\ & =\frac{x_0}{R_0}\frac{R(x_0+\mathrm{\Delta }x)-R(x_0-\mathrm{\Delta }x)}{2\mathrm{\Delta }x}\hspace{0.17em}\\ & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\frac{1}{R_0}\frac{R(x_0+\mathrm{\Delta }x)-R(x_0-\mathrm{\Delta }x)}{2p}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em},(29)\end{array}$

where p is the relative perturbation $\left|\mathrm{\Delta }x/x_0\right|$. For the CDs, each material mass density was perturbed ±0.1% (separately). The adjoint-based material density sensitivity is the sum of the nuclide density sensitivities $S_{R,N_i}^g$ over nuclide and energy group [Eq. (19)(19) $S_{R,\rho }^g=\sum _{i=1}^I{S}_{R,N_i}^g,$(19) ]. Results are shown in Table III. These results are shown for information only; SENSMG has no user option to disable the correct accounting for any transport correction. Again, the point of this comparison is to assess the importance of accounting for the transport correction when computing adjoint-based sensitivities.

TABLE III Relative Sensitivity (%/%) of Flattop-Pu k_eff to Material Density When SENSMG Does Not Account for Transport Correction

Transport Correction	L	Plutonium			NU
		SENSMG	CD	Difference^a	SENSMG	CD	Difference^a
No	0	0.65012	0.65012	0.000%	0.22134	0.22133	0.002%
	1	0.68385	0.68385	0.000%	0.23843	0.23842	0.002%
	2	0.67558	0.67555	0.004%	0.21800	0.21801	−0.003%
	3	0.67784	0.67783	0.000%	0.22813	0.22813	0.000%
	4	0.67736	0.67734	0.004%	0.22404	0.22404	0.000%
Diagonal	0	0.71552	0.67481	6.033%	0.33116	0.22083	49.960%
	1	0.67593	0.67789	−0.289%	0.20210	0.22661	−10.818%
	2	0.67733	0.67733	0.001%	0.23095	0.22444	2.901%
	3	0.67747	0.67748	−0.001%	0.22376	0.22544	−0.745%
	4	0.67736	0.67734	0.004%	0.22404	0.22404	0.000%
BHS	0	0.71598	0.67481	6.100%	0.33200	0.22083	50.343%
	1	0.67594	0.67790	−0.289%	0.20215	0.22664	−10.805%
	2	0.67733	0.67735	−0.002%	0.23095	0.22444	2.900%
	3	0.67747	0.67748	−0.001%	0.22374	0.22544	−0.750%
	4	0.67736	0.67734	0.004%	0.22404	0.22404	0.000%
Cesàro	0	0.65012	0.65012	0.000%	0.22134	0.22133	0.002%
	1	0.63646	0.66096	−3.707%	0.15210	0.22766	−33.188%
	2	0.64714	0.66539	−2.743%	0.18388	0.22809	−19.382%
	3	0.65298	0.66791	−2.235%	0.18839	0.22825	−17.462%
	4	0.65694	0.66959	−1.889%	0.19526	0.22805	−14.375%

^aRelative to CD.

Table III shows that adjoint sensitivities can be in error by several percent for low scattering orders if transport correction is not accounted for. Also, results for L = 4 for no transport correction, BHS, and diagonal transport correction are all identical, as in Table II, and for the same reason.

The proper adjoint-based (SENSMG) relative sensitivity of each of the material densities, which accounts for the effect of the transport corrections on the sensitivities, was also compared with the CD estimates. Results are shown in Table IV. Table IV verifies Eqs. (22)(22) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,L+1,i}^{g\to g}}^{\hspace{0.17em}},$(22) , (23(23) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}+\sum _{g{ }^{\mathrm{\prime }}=1}^G{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}.$(23) ), and (27(27) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+{\tilde{S}}_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}.$(27) ) for the diagonal, BHS, and Cesàro transport corrections, respectively.

TABLE IV Relative Sensitivity (%/%) of Flattop-Pu k_eff to Material Density When SENSMG Accounts for Transport Correction

Transport Correction	L	Plutonium			NU
		SENSMG	CD	Difference^a	SENSMG	CD	Difference^a
Diagonal	0	0.67480	0.67481	−0.001%	0.22084	0.22083	0.006%
	1	0.67789	0.67789	−0.001%	0.22662	0.22661	0.003%
	2	0.67734	0.67733	0.002%	0.22444	0.22444	0.000%
	3	0.67748	0.67748	−0.001%	0.22544	0.22544	0.003%
	4	0.67736	0.67734	0.004%	0.22404	0.22404	0.000%
BHS	0	0.67484	0.67481	0.004%	0.22083	0.22083	0.000%
	1	0.67790	0.67790	0.000%	0.22664	0.22664	0.002%
	2	0.67734	0.67735	−0.001%	0.22444	0.22444	0.000%
	3	0.67748	0.67748	0.000%	0.22544	0.22544	0.001%
	4	0.67736	0.67734	0.004%	0.22404	0.22404	0.000%
Cesàro	0	0.65012	0.65012	0.000%	0.22134	0.22133	0.002%
	1	0.66093	0.66096	−0.005%	0.22765	0.22766	−0.003%
	2	0.66534	0.66539	−0.007%	0.22813	0.22809	0.017%
	3	0.66791	0.66791	0.000%	0.22823	0.22825	−0.006%
	4	0.66958	0.66959	−0.001%	0.22808	0.22805	0.014%

^aRelative to CD.

Equation (21)(21) $\begin{array}{r}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=-\sum _{l=0}^L{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)+{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(21) for the relative sensitivity $S_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ of R to the L + 1’th scattering cross section for the BHS transport correction and the quantity ${\delta }_{gg{ }^{\mathrm{\prime }}}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ for the diagonal transport correction were verified using CDs. For each scattering expansion order L, all ²³⁸U L + 1 elastic scattering cross sections were perturbed by ±10%. The computed sensitivity is $\sum _{g=1}^G\sum _{g{ }^{\mathrm{\prime }}=1}^G{S}_{R,{\sigma }_{elastic,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ for BHS and $\sum _{g=1}^G{S}_{R,{\sigma }_{elastic,L+1,i}^{g\to g}}^{\hspace{0.17em}}$ for diagonal, with $S_{R,{\sigma }_{elastic,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ given by Eq. (21)(21) $\begin{array}{r}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=-\sum _{l=0}^L{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)+{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(21) . Results are shown in Table V. The adjoint sensitivities are in excellent agreement with the CDs. (Elastic, and later, inelastic scattering cross sections for use in SENSMG and in the CD were obtained from an output file written by the cross-section processing code³³ NJOY’s GROUPR module.)

TABLE V Relative Sensitivity (%/%) of Flattop-Pu k_eff to ²³⁸U Elastic Scattering Cross Section L + 1’th Moment*

Transport Correction	L	SENSMG	CD	Difference^a
Diagonal	0	−0.10663	−0.10663	−0.003%
	1	0.024510	0.024516	−0.025%
	2	−0.0064855	−0.0064869	−0.021%
	3	0.0016742	0.0016749	−0.042%
BHS	0	−0.10662	−0.10662	−0.003%
	1	0.024515	0.024521	−0.025%
	2	−0.0064894	−0.0064910	−0.024%
	3	0.0016791	0.0016798	−0.043%

*SENSMG accounts for transport correction. Sum of self-scattering and out-scattering.

^aRelative to CD.

Kodeli and Slavič²⁵ used this problem and computed the total relative sensitivity of k_eff to ²³⁸U elastic and inelastic scattering. They used ENDF/B-VII.0 nuclear data in a 33-group structure, so their results are not directly comparable with ours.

The total relative sensitivity $S_{R,{\sigma }_{x,i}^{\hspace{0.17em}}}^{\hspace{0.17em}}$ of R to scattering reaction x of nuclide i when the diagonal or BHS transport correction is used is

(30) $S_{R,{\sigma }_{x,i}^{\hspace{0.17em}}}^{\hspace{0.17em}}=\sum _{l=0}^{L+1}\sum _{g=1}^G\sum _{g{ }^{\mathrm{\prime }}=1}^G{S}_{R,{\sigma }_{x,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}},$(30)

where $S_{R,{\sigma }_{x,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ for 0 ≤ l ≤ L is from Eq. (16)(16) $\begin{array}{r}{S}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}={\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)\\ -{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}),\end{array}$(16) and $S_{R,{\sigma }_{x,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ is from Eq. (21)(21) $\begin{array}{r}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=-\sum _{l=0}^L{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)+{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(21) . The total relative sensitivity $S_{R,{\sigma }_{x,i}^{\hspace{0.17em}}}^{\hspace{0.17em}}$ of R to scattering reaction x of nuclide i when the Cesàro transport correction is used is

(31) $S_{R,{\sigma }_{x,i}^{\hspace{0.17em}}}^{\hspace{0.17em}}=\sum _{l=0}^L\sum _{g=1}^G\sum _{g{ }^{\mathrm{\prime }}=1}^G{\tilde{S}}_{R,{\sigma }_{x,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}},$(31)

where ${\tilde{S}}_{R,{\sigma }_{x,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ is from Eq. (25(25) $\begin{array}{r}{\tilde{S}}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=\frac{(L+2-l)(L+1-l)}{(L+2)(L+1)}{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)-{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(25) ) [but ${\tilde{S}}_{R,{\sigma }_{x,0,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ of Eq. (25)(25) $\begin{array}{r}{\tilde{S}}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=\frac{(L+2-l)(L+1-l)}{(L+2)(L+1)}{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)-{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(25) is equal to $S_{R,{\sigma }_{x,0,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ of Eq. (16)(16) $\begin{array}{r}{S}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}={\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)\\ -{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}),\end{array}$(16) ].

The adjoint formulas for the sensitivity of k_eff to ²³⁸U elastic scattering are compared with CDs in Table VI. All ²³⁸U elastic scattering cross sections were perturbed ±10%. The adjoint sensitivities are in excellent agreement with the CDs. It is noteworthy that for L ≥ 1, sensitivities are essentially identical when the diagonal and BHS corrections are used. Kodeli and Slavič²⁵ reported a sensitivity of 0.1431%/% for L = 3 and 0.1399%/% for L = 5.

TABLE VI Relative Sensitivity (%/%) of Flattop-Pu k_eff to ²³⁸U Total Elastic Scattering*

Transport Correction	L	SENSMG	CD	Difference^a
No	0	0.17814	0.17819	−0.030%
	1	0.12226	0.12227	−0.002%
	2	0.13164	0.13168	−0.031%
	3	0.13047	0.13049	−0.018%
	4	0.13024	0.13027	−0.023%
Diagonal	0	0.13159	0.13163	−0.026%
	1	0.13002	0.13005	−0.020%
	2	0.13037	0.13040	−0.023%
	3	0.13041	0.13043	−0.022%
	4	0.13024	0.13027	−0.023%
BHS	0	0.13191	0.13195	−0.027%
	1	0.13007	0.13010	−0.020%
	2	0.13036	0.13039	−0.023%
	3	0.13041	0.13043	−0.022%
	4	0.13024	0.13027	−0.023%
Cesàro	0	0.17814	0.17819	−0.030%
	1	0.16704	0.16707	−0.019%
	2	0.15949	0.15952	−0.019%
	3	0.15448	0.15451	−0.019%
	4	0.15090	0.15093	−0.019%

*SENSMG accounts for transport correction. Sum of self-scattering and out-scattering.

^aRelative to CD.

The adjoint formulas for the sensitivity of k_eff to ²³⁸U inelastic scattering are compared with CDs in Table VII. All ²³⁸U inelastic scattering cross sections were perturbed ±10%. The adjoint sensitivities are in excellent agreement with the CDs. Sensitivities when the diagonal and BHS corrections are used are similar but differ noticeably. Kodeli and Slavič²⁵ reported a sensitivity of 0.06776%/% for L = 3 and 0.06451%/% for L = 5.

TABLE VII Relative Sensitivity (%/%) of Flattop-Pu k_eff to ²³⁸U Total Inelastic Scattering*

Transport Correction	L	SENSMG	CD	Difference^a
No	0	0.032464	0.032382	0.253%
	1	0.083017	0.083034	−0.020%
	2	0.061841	0.061816	0.040%
	3	0.069775	0.069774	0.002%
	4	0.067132	0.067119	0.019%
Diagonal	0	0.064187	0.064174	0.020%
	1	0.069120	0.069113	0.009%
	2	0.067268	0.067257	0.016%
	3	0.067973	0.067965	0.012%
	4	0.067132	0.067119	0.019%
BHS	0	0.063824	0.063810	0.022%
	1	0.069093	0.069087	0.009%
	2	0.067273	0.067262	0.016%
	3	0.067968	0.067960	0.012%
	4	0.067132	0.067119	0.019%
Cesàro	0	0.032464	0.032382	0.253%
	1	0.044115	0.044049	0.150%
	2	0.049555	0.049500	0.111%
	3	0.053055	0.053008	0.089%
	4	0.055423	0.055382	0.075%

*SENSMG accounts for transport correction. Sum of self-scattering and out-scattering.

^aRelative to CD.

It should be noted that there is a longstanding bug in the publicly available version of PARTISN, version 8.29.32, that affects adjoint calculations that use the BHS transport correction. The BHS correction is made after the scattering matrix is transposed; it should be made before. This bug was inherited from ONEDANT (Ref. 10). It has been fixed as of PARTISN version 8.32.52.^a (A slightly newer version was used for this paper.)

V. TEST PROBLEM FOR INHOMOGENEOUS SOURCE

The test configuration for an inhomogeneous (fixed-source) transport problem was a 4.5-kg sphere of α-phase, weapons-grade plutonium (the BeRP ball³⁴) reflected by 38.1 mm of high-density polyethylene (HDPE). The geometry and materials (simplified from the compositions given in Ref. 34—in particular, all impurities in the plutonium were turned into gallium) are given in Table VIII. The response of interest was the total leakage of neutrons from the outer surface. The problem was run with various scattering expansion orders and each of the transport corrections (including none) available in PARTISN.

TABLE VIII Simplified BeRP Ball Model

Region	Material	Outer Radius (cm)	Density (g/cm^3)	Composition (Weight Fraction)
1	Plutonium	3.794	19.6	^239Pu, 9.38039E−01 ^240Pu, 5.94113E−02 Ga, 2.54981E−03
2	HDPE	7.604	0.95	^1H, 1.43701E−01 C, 8.56299E−01

An angular quadrature of S₂₅₆ and fine mesh spacing of 0.005 cm were used. The 79-group Kynea3 cross sections³⁵ having upscattering in the bottom 35 groups were used. The maximum scattering expansion order available in this library is 7 (indexed from 0). The ¹H cross sections include thermal scattering. PARTISN version 8.32.54 was used.

SOURCES4C (Ref. 36) was used to compute the neutron source rate density from spontaneous fission.

V.A. Neutron Leakage

The leakages are compared in Table IX and Fig. 2. Scattering order 0 (isotropic scattering only) is not shown because that causes the system to be supercritical for all transport corrections. Scattering orders 1 and 2 also cause the system to be supercritical with the Cesàro transport correction. The leakages for L = 7 (R₇) are identical for no transport correction, BHS, and diagonal transport correction because that is the highest expansion order in the cross-section library. The leakages for L = 0 are identical for no transport correction and the Cesàro transport correction because ${\tilde{\mathrm{\Sigma }}}_{s,0}^{g\to g{ }^{\mathrm{\prime }}}={\mathrm{\Sigma }}_{s,0}^{g\to g{ }^{\mathrm{\prime }}}$ in Eq. (8)(8) $\begin{array}{r}{\tilde{\mathrm{\Sigma }}}_{s,l}^{g\to g{ }^{\mathrm{\prime }}}=\frac{(L+2-l)(L+1-l)}{(L+2)(L+1)}{\mathrm{\Sigma }}_{s,l}^{g\to g{ }^{\mathrm{\prime }}},\\ g=1,\dots ,G,g{ }^{\mathrm{\prime }}=1,\dots ,G,l=0,\dots ,L.\end{array}$(8) .

TABLE IX BeRP Ball Leakage

Transport Correction	Scattering Order (L)^a	R (10^6 neutrons/s)	(R – R7)/R7
No	1	1.380973	−17.703%
	2	1.719439	2.467%
	3	1.675059	−0.178%
	4	1.677911	−0.008%
	5	1.678125	0.005%
	6	1.678039	0.000%
	7	1.678046	0.000%
Diagonal	1	1.475439	−12.074%
	2	1.692591	0.867%
	3	1.680865	0.168%
	4	1.676516	−0.091%
	5	1.678480	0.026%
	6	1.677936	−0.007%
	7	1.678046	0.000%
BHS	1	1.610892	−4.002%
	2	1.715937	2.258%
	3	1.671834	−0.370%
	4	1.677877	−0.010%
	5	1.678270	0.013%
	6	1.678037	−0.001%
	7	1.678046	0.000%
Cesàro	3	12.439907	641%
	4	5.957554	255%
	5	4.350959	159%
	6	3.622205	116%
	7	3.205996	91%

^aL = 0 for all transport corrections and L = 1 and 2 for Cesàro did not converge.

Fig. 2. Neutron leakage versus scattering expansion order for the simplified BeRP ball for four transport corrections (including none). The Kynea3 79-group structure³⁵ was used. The PARTISN manual⁹ advises against using the Cesàro transport correction for L < 2.

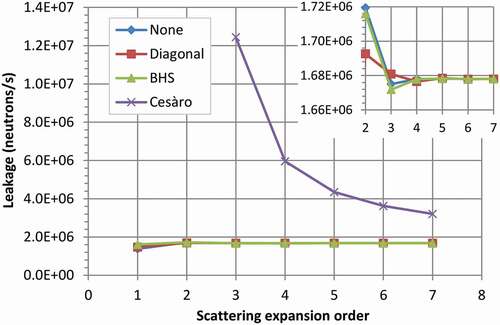
Assuming that R₇ with no transport correction (or diagonal or BHS) is the most accurate value, each of the leakages is compared to R₇ in Table IX. Whether the diagonal or BHS transport correction is more accurate depends on the scattering order. Interestingly, for L ≥ 4, using no transport correction is more accurate than using the diagonal or BHS transport correction.

The conventional wisdom that P₃ scattering is more accurate than P₄ is not true for this problem using these nuclear data.

For L > 2, the Cesàro transport correction is wildly inaccurate for this problem.

V.B. Neutron Leakage Sensitivities

Again, in order to verify the derivations in Sec. III as well as the implementation in code, CD estimates of sensitivities were compared with adjoint-based calculations. The adjoint-based (SENSMG) relative sensitivity of each of the material densities, computed without accounting for the effect of the transport corrections on the sensitivities, was compared with a CD estimate for various scattering expansion orders and each of the transport corrections (including none). For the CDs, each material mass density was perturbed ±0.1% (separately). The adjoint-based material density sensitivity is the sum of the nuclide density sensitivities $S_{R,N_i}^g$ over nuclide and energy group [Eq. (19)(19) $S_{R,\rho }^g=\sum _{i=1}^I{S}_{R,N_i}^g,$(19) ]. Results are shown in Table X. These results are shown for information only; SENSMG has no user option to disable the correct accounting for any transport correction. Again, the point of this comparison is to assess the importance of accounting for the transport correction when computing adjoint-based sensitivities.

TABLE X Relative Sensitivity (%/%) of BeRP Ball Leakage to Material Density When SENSMG Does Not Account for Transport Correction

Transport Correction	L^a	Plutonium			HDPE
		SENSMG	CD	Difference^b	SENSMG	CD	Difference^b
No	1	5.67597	5.67502	0.017%	1.02083	1.02091	−0.008%
	2	7.10436	7.10325	0.016%	1.35770	1.35803	−0.024%
	3	6.91909	6.91841	0.010%	1.32045	1.32043	0.001%
	4	6.93067	6.92945	0.018%	1.32370	1.32313	0.043%
	5	6.93157	6.93033	0.018%	1.32351	1.32276	0.057%
	6	6.93124	6.93002	0.018%	1.32346	1.32273	0.055%
	7	6.93127	6.92991	0.020%	1.32348	1.32291	0.044%
Diagonal	1	6.07378	6.08883	−0.247%	1.05099	1.10892	−5.225%
	2	6.99099	6.98967	0.019%	1.35225	1.33532	1.268%
	3	6.94359	6.94256	0.015%	1.32011	1.32360	−0.264%
	4	6.92485	6.92361	0.018%	1.32404	1.32316	0.066%
	5	6.93302	6.93202	0.014%	1.32344	1.32385	−0.031%
	6	6.93085	6.92929	0.023%	1.32348	1.32255	0.070%
	7	6.93127	6.92991	0.020%	1.32348	1.32291	0.044%
BHS	1	6.62953	6.64660	−0.257%	1.09946	1.26461	−13.059%
	2	7.08943	7.08799	0.020%	1.35580	1.35387	0.143%
	3	6.90550	6.90472	0.011%	1.32084	1.31912	0.130%
	4	6.93053	6.92920	0.019%	1.32369	1.32358	0.009%
	5	6.93216	6.93199	0.003%	1.32348	1.32383	−0.027%
	6	6.93124	6.92977	0.021%	1.32346	1.32339	0.005%
	7	6.93127	6.92991	0.020%	1.32348	1.32291	0.044%
Cesàro	3	51.4798	53.2008	−3.235%	10.9120	15.7975	−30.926%
	4	24.6345	25.2504	−2.439%	5.12752	7.07026	−27.478%
	5	17.9835	18.3638	−2.071%	3.69359	4.91125	−24.793%
	6	14.9671	15.2400	−1.791%	3.04391	3.93149	−22.576%
	7	13.2449	13.4573	−1.578%	2.67354	3.36780	−20.615%

^aL = 0 for all transport corrections (including none) and L = 1 and 2 for Cesàro did not converge.

^bRelative to CD.

Table X shows that adjoint sensitivities can be in error by several percent for low scattering orders if transport correction is not accounted for. Also, results for L = 7 for no transport correction, BHS, and diagonal transport correction are all identical, as in Table IX, and for the same reason.

The proper adjoint-based (SENSMG) relative sensitivity of each of the material densities, which accounts for the effect of the transport corrections on the sensitivities, was also compared with the CD estimates. Results are shown in Table XI. Table XI verifies Eqs. (22)(22) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,L+1,i}^{g\to g}}^{\hspace{0.17em}},$(22) , (23(23) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}+\sum _{g{ }^{\mathrm{\prime }}=1}^G{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}.$(23) ), and (27(27) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+{\tilde{S}}_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}}.$(27) ) for the diagonal, BHS, and Cesàro transport corrections, respectively.

TABLE XI Relative Sensitivity (%/%) of BeRP Ball Leakage to Material Density When SENSMG Accounts for Transport Correction

Transport Correction	L^a	Plutonium			HDPE
		SENSMG	CD	Difference^b	SENSMG	CD	Difference^b
Diagonal	1	6.08866	6.08883	−0.003%	1.10799	1.10892	−0.084%
	2	6.98995	6.98967	0.004%	1.33652	1.33532	0.090%
	3	6.94259	6.94256	0.000%	1.32361	1.32360	0.000%
	4	6.92385	6.92361	0.003%	1.32321	1.32316	0.004%
	5	6.93202	6.93202	0.000%	1.32365	1.32385	−0.015%
	6	6.92985	6.92929	0.008%	1.32342	1.32255	0.066%
	7	6.93027	6.92991	0.005%	1.32348	1.32291	0.044%
BHS	1	6.64668	6.64660	0.001%	1.26496	1.26461	0.028%
	2	7.08840	7.08799	0.006%	1.35380	1.35387	−0.005%
	3	6.90450	6.90472	−0.003%	1.31893	1.31912	−0.015%
	4	6.92953	6.92920	0.005%	1.32367	1.32358	0.007%
	5	6.93116	6.93199	−0.012%	1.32357	1.32383	−0.020%
	6	6.93024	6.92977	0.007%	1.32346	1.32339	0.005%
	7	6.93027	6.92991	0.005%	1.32348	1.32291	0.044%
Cesàro	3	53.0060	53.2008	−0.366%	15.7895	15.7975	−0.051%
	4	25.2359	25.2504	−0.057%	7.06522	7.07026	−0.071%
	5	18.3565	18.3638	−0.040%	4.90546	4.91125	−0.118%
	6	15.2367	15.2400	−0.021%	3.92665	3.93149	−0.123%
	7	13.4558	13.4573	−0.011%	3.36814	3.36780	0.010%

^aL = 0 for all transport corrections and L = 1 and 2 for Cesàro did not converge.

^bRelative to CD.

As stated in Sec. IV.B, there is a longstanding bug in the publicly available version of PARTISN, version 8.29.32, that affects adjoint calculations that use the BHS transport correction. It has been fixed as of PARTISN version 8.32.52. (A slightly newer version was used for this paper.)

VI. SUMMARY AND CONCLUSIONS

Sensitivities for neutron or gamma-ray transport responses have been derived for problems that use the diagonal, BHS, or Cesàro transport corrections in the discrete-ordinates method. For the BHS transport correction, the response is sensitive to the L + 1’th scattering cross sections ${\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}$ of all nuclides. For the diagonal transport correction, the response is sensitive to the within-group scattering cross sections ${\sigma }_{s,L+1,i}^{g\to g}$. For the BHS and diagonal transport corrections, the sensitivities to the total cross sections and to the scattering cross sections for l ≤ L have their usual formulas [Eqs. (15)(15) $S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}=-{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{t,i}^g{\psi }^g(r,\hat{\mathbf{\Omega }}).$(15) and (16(16) $\begin{array}{r}{S}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}={\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)\\ -{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}),\end{array}$(16) )]. Also for the BHS and diagonal transport corrections, the sensitivities to material and nuclide densities must account for the L + 1’th term separately. For the Cesàro transport correction, the sensitivities to the total cross sections and the isotropic scattering cross sections have their usual formulas [Eqs. (15)(15) $S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}=-{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{t,i}^g{\psi }^g(r,\hat{\mathbf{\Omega }}).$(15) and (16(16) $\begin{array}{r}{S}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}={\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)\\ -{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}),\end{array}$(16) )], and the sensitivities to the scattering cross sections for l ≥ 1 are the usual formulas [Eq. (16(16) $\begin{array}{r}{S}_{R,{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}={\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)\\ -{\delta }_{l0}{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}),\end{array}$(16) )] multiplied by a simple function of l and L. Also for the Cesàro transport correction, the sensitivities to nuclide and material densities have their usual formulas [Eqs. (17)(17) $S_{R,N_i}^g=S_{R,{\nu }_i^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{t,i}^g}^{\hspace{0.17em}}+S_{R,{\sigma }_{s,i}^g}^{\hspace{0.17em}},$(17) and (19(19) $S_{R,\rho }^g=\sum _{i=1}^I{S}_{R,N_i}^g,$(19) )].

It should be emphasized that in Eq. (21)(21) $\begin{array}{r}{S}_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}=-\sum _{l=0}^L{\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)+{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }}).\end{array}$(21) for the relative sensitivity $S_{R,{\sigma }_{s,L+1,i}^{g\to g{ }^{\mathrm{\prime }}}}^{\hspace{0.17em}}$ for the diagonal and BHS transport corrections, the index on the adjoint flux in the first term on the right side is g, the same as the forward flux, not g′ as usual for the scattering term.

These formulas have been implemented in the multigroup sensitivity code SENSMG, which uses PARTISN for the neutron transport. Numerical test results confirm the derivations and implementation.

While the intent of this paper is not necessarily to compare the performance of the transport corrections themselves, it was noteworthy that the Cesàro transport correction yielded extremely inaccurate results for k_eff and for the neutron leakage in a fixed-source problem. Caution is advised when using the Cesàro transport correction in PARTISN, Denovo, or any other transport code that offers it.

Acknowledgments

The author would like to thank D. K. Parsons (LANL) for providing the GROUPR file with the elastic and inelastic scattering cross sections for ²³⁸U. The author would like to thank the following people for discussions about the transport corrections used in their codes: M. A. Jessee (Oak Ridge National Laboratory), B. R. Beck and P. N. Brown (Lawrence Livermore National Laboratory), G. A. Failla (Silver Fir Software, Inc.), J. M. McGhee [Varian Medical Systems (retired)], and D. K. Parsons (LANL). This work was supported by the National Nuclear Security Administration.

Notes

^a M. I. Ortega and R. J. Zerr at Los Alamos National Laboratory (LANL) fixed this bug.

APPENDIX

CORRIGENDUM FOR REF. 19

In Table I of Ref. 19, the entries for isotropic scattering had typos, and the entries for anisotropic scattering had typesetting errors. The correct entries are given in Table A.I. The notation of Ref. 19 is retained.

TABLE A.I Reaction-Rate Ratio Sensitivities to Scattering for λ-Mode Flux,* Indirect Effect

Sensitivity	Label	Equation
In-scattering, P0	in-scat-0	$\begin{array}{r}{\left(S_{R,{\sigma }_{s,0,i}}^{g{ }^{\mathrm{\prime }}\to g}\right)}_{indirect}={\int }_{V}dV\sum _{\genfrac{}{}{0ex}{}{g{ }^{\mathrm{\prime }}=1}{g{ }^{\mathrm{\prime }}\ne g}}^G{\mathrm{\Gamma }}_0^{\ast g}(r)N_i{\sigma }_{s,0,i}^{g{ }^{\mathrm{\prime }}\to g}{\varphi }_0^{g{ }^{\mathrm{\prime }}}(r)\\ -{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}\sum _{\genfrac{}{}{0ex}{}{g{ }^{\mathrm{\prime }}=1}{g{ }^{\mathrm{\prime }}\ne g}}^G{\mathrm{\Gamma }}^{\ast g{ }^{\mathrm{\prime }}}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,0,i}^{g{ }^{\mathrm{\prime }}\to g}{\psi }^{g{ }^{\mathrm{\prime }}}(r,\hat{\mathbf{\Omega }})\end{array}$
Self-scattering, P0	self-scat-0	$\begin{array}{r}{\left(S_{R,{\sigma }_{s,0,i}}^{g\to g}\right)}_{indirect}={\int }_{V}dV{\mathrm{\Gamma }}_0^{\ast g}(r)N_i{\sigma }_{s,0,i}^{g\to g}{\varphi }_0^g(r)\\ -{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,0,i}^{g\to g}{\psi }^g(r,\hat{\mathbf{\Omega }})\end{array}$
Out-scattering, P0	out-scat-0	$\begin{array}{r}{\left(S_{R,{\sigma }_{s,0,i}}^{g\to g{ }^{\mathrm{\prime }}}\right)}_{indirect}={\int }_{V}dV\sum _{\genfrac{}{}{0ex}{}{g{ }^{\mathrm{\prime }}=1}{g{ }^{\mathrm{\prime }}\ne g}}^G{\mathrm{\Gamma }}_0^{\ast g{ }^{\mathrm{\prime }}}(r)N_i{\sigma }_{s,0,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_0^g(r)\\ -{\int }_{V}dV{\int }_{4\pi }d\hat{\mathbf{\Omega }}\sum _{\genfrac{}{}{0ex}{}{g{ }^{\mathrm{\prime }}=1}{g{ }^{\mathrm{\prime }}\ne g}}^G{\mathrm{\Gamma }}^{\ast g}(r,\hat{\mathbf{\Omega }})N_i{\sigma }_{s,0,i}^{g\to g{ }^{\mathrm{\prime }}}{\psi }^g(r,\hat{\mathbf{\Omega }})\end{array}$
In-scattering, Pl, 1 ≤ l ≤ L	in-scat-[l]	${\left(S_{R,{\sigma }_{s,l,i}}^{g{ }^{\mathrm{\prime }}\to g}\right)}_{indirect}={\int }_{V}dV\sum _{\genfrac{}{}{0ex}{}{g{ }^{\mathrm{\prime }}=1}{g{ }^{\mathrm{\prime }}\ne g}}^G{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,l,i}^{g{ }^{\mathrm{\prime }}\to g}{\varphi }_l^{g{ }^{\mathrm{\prime }}}(r)$
Self-scattering, Pl, 1 ≤ l ≤ L	self-scat-[l]	${\left(S_{R,{\sigma }_{s,l,i}}^{g\to g}\right)}_{indirect}={\int }_{V}dV{\mathrm{\Gamma }}_l^{\ast g}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g}{\varphi }_l^g(r)$
Out-scattering, Pl, 1 ≤ l ≤ L	out-scat-[l]	${\left(S_{R,{\sigma }_{s,l,i}}^{g\to g{ }^{\mathrm{\prime }}}\right)}_{indirect}={\int }_{V}dV\sum _{\genfrac{}{}{0ex}{}{g{ }^{\mathrm{\prime }}=1}{g{ }^{\mathrm{\prime }}\ne g}}^G{\mathrm{\Gamma }}_l^{\ast g{ }^{\mathrm{\prime }}}(r)N_i(2l+1){\sigma }_{s,l,i}^{g\to g{ }^{\mathrm{\prime }}}{\varphi }_l^g(r)$

* These equations are also used for α-mode and fixed-source flux, but $\lambda =1/k_{eff}$ is set to 1 and a divisor is used where needed.