An Inferentialist Perspective on How Note-taking can Constrain the Orchestration of Math-Talk

ABSTRACT

The aim of this study is to investigate relationships between note-taking and the orchestrating of math-talk in whole-class teaching. A lesson on (average) velocity in a Swedish Grade 6 has been observed. Taking an inferentialist stance on human understanding, the study conceptualizes teaching and learning from the perspective of how students come to be engaged in the language practice of giving and asking for reasons. The study shows how note-taking supports a teacher-student relationship where the teacher produces content and the students’ participation is reduced to consume content. It shows how note-taking can support descriptive math-talk of concepts and symbols and step-by-step procedural math-talk, connected to the goal of providing students examples of tasks, similar to the tasks in their textbook.

KEYWORDS:

• Note-taking
• math-talk
• inferentialism
• teacher control

Contemporary research calls attention to the importance of orchestration of math-talk, in the mathematics classroom (Brodie, 2013; Conner, Singletary, Smith, Wagner, & Francisco, 2014; Hufferd-Ackles, Fuson, & Sherin, 2004; Walshaw & Anthony, 2008). In math-talk students have the opportunity to listen to explanations (Hintz & Tyson, 2015), share insights and ideas (Barron, 2003), observe the strategies of other (Walshaw & Anthony, 2008), engage in collective argumentation (Conner et al., 2014) and explain one’s reasoning of a phenomenon (Jackson, Garrison, Wilson, Gibbons, & Shahan, 2013). However, research suggests that math-talk is usually relatively constrained (Brodie, 2011) and does not always allow for the development of and extending students’ mathematical understanding (Fraivillig, Murphy, & Fuson, 1999). A teacher needs to guide and help students in advancing and structuring the content of math-talk (Stein, Engle, Smith, & Hughes, 2008) and to zoom in the talk on important mathematical ideas (Charalambous & Hill, 2012). But, on the contrary, research suggests that a teacher should not be too dominant in talk-based mathematics teaching. Students opportunities to engage in mathematics can come to be constrained because teachers feel insecure to let go of control of how content should be introduced, expressed and dealt with in the classroom (Emanuelsson & Sahlström, 2008; Hoekstra, Brekelmans, Beijaard, & Korthagen, 2009; Walshaw & Anthony, 2008). This dilemma shows there are still many complicated relations to explore between students’ engagement in and a teacher’s ways of orchestrating math-talk (Ryve, Larsson, & Nilsson, 2013). The aim of the present study is to investigate such relations in a case where the teacher uses the whiteboard as a surface for structuring math-talk and where the students are asked to take notes during the talk.

The present study adopts the semantic and pragmatism theory of Inferentialism (Brandom, 1994, 2000) as an overall theoretical frame for conceptualizing talk in the mathematics classroom. Inferentialism gives pride to the social and interactive nature of language games (Wittgenstein, 1968) and particularly, to the game of giving and asking for reasons (GoGAR) in which understanding is conceptualized in terms of the practical mastery of “being able to distinguish, what follows from the applicability of a concept, and what it follows from” (Brandom, 2000, p. 48).

Aim of Study

Taking an inferentialist stance on teaching and learning, the aim of the present study is to explore how note-taking can influence on how students come to be engaged in games of giving and asking for reasons in math-talk in the mathematics classroom.

Theoretical Background

Note-Takings as a Tool for Learning in and From Teaching

Notes appear to serve two overall roles in students’ learning (Di Vesta & Gray, 1972). As an external storage mechanism notes can provide a resource for later study by the learner and as an encoding mechanism they allow the learner to “transcribe whatever subjective associations, inferences, and interpretations occurred to him while listening” (Di Vesta & Gray, 1972, p. 8). Specifying these roles, Applebee (1984) points to how notes are supposed to support learning according to: (a) the permanence of the written word, allowing the learner to recall, rethink and revise over an extended period, (b) the explicitness required in writing if meaning is to remain constant beyond the context in which it was originally written, (c) the resources provided by conventional forms of discourse for organizing and thinking through new ideas and experience and for explicating the relationship among them, and (d) the active nature in writing, providing a medium for exploring implications entailed within the otherwise unexamined assumptions.

Despite these promises of note-taking, research shows that note-taking does not always be the learning resource it is supposed to be (Hidi & Klaiman, 1983; Kobayashi, 2005). For instance, it has been shown how little appears in student’ notes that goes beyond the information on board (Stefanou, Hoffman, & Vielee, 2008). Note-taking often becomes an act of “copying,” with low mental activity involved. Students are merely copying information presented in verbatim form rather than reconstructing the meaning through paraphrasing, inferring, summarizing or reorganizing the information provided in the situation (Bereiter & Scardamalia, 1985). For teaching that emphasizes math-talk these issues are certainly problematic. In talk-based teaching of mathematics much of the content is expressed verbally so, obviously, if students only pay attention to the board in taking-notes, many of the main points will be left outside (Lew, Fukawa-Connelly, Mejía-Ramos, & Weber, 2016) and, consequently, students will have limited opportunities to recall, rethink and revise the content after the actual teaching situation (Applebee, 1984).

Mathematics Classroom Talk – An Inferentialist Perspective

Inferentialism is a sematic pragmatism theory, which builds on Sellar’s philosophical idea that meaning and understanding of concepts¹ are to be understood as a function of how well one can navigate and master the “space of reasons” (Sellars, Rorty, & Brandom, 1997). People decide “what to think and do in the relevant domain in light of what there is most reason to think or do” (Bakhurst, 2011, p. 136). Understanding involves having a grasp of reasons, driven by the peculiar force of striving for more acceptable and better reasons (Bakhurst, 2011).

To Brandom, the space of reasons is essentially inferentially structured. It is inferentially structured in that concepts, and claims in general, gains their meaning according to their positions to other concepts and claims. Consequently, and by necessity, inferentialism is resolutely holistic (Bakker & Derry, 2011; Bransen, 2002). One needs many concepts in order to have any, since the content of each concept is constituted by its inferential relationship to other concepts. Think of the situation of having practical mastery of the concept of “probability,” coming into articulation in the claim, “the probability of six is 1/6 when rolling a die.” Claiming this implies, among many things, to know that the claim is based on a perfectly symmetric die, that the relative frequencies of sixes stabilize around 1/6 as we increase the number of rolls and that the probability of not having a six is 5/6. This example involves a GoGAR of many reasons related to the concept of probability, of which only a few been made explicit here. The main point, however, is that these reasons are relevant and become contentful due to their inferential connections. Their bringing to bear in the learners’ understanding depends on the judgments of the learners, i.e., on their own responsiveness to reasons (Bakker & Derry, 2011), and on their ability to distinguish and make explicit what follows from the applicability of a claim and what it follows from (Brandom, 2000).

To Brandom, the space of reasons is socially articulated in that, rather than being articulated in the space in which thought moves, it is articulated in the space of a language game (Sellars et al., 1997; Wittgenstein, 1968) and, particularly, in the game of giving and asking for reasons (GoGAR) (Brandom, 1995, 2002). Putting together the inferential and the social, Brandom lets us understand that, getting to grips with the content of a concept (e.g., “Probability” in “the probability of six is 1/6 when rolling a die”) entails getting to grips with the conditions of its application in the GoGAR (Bakker & Derry, 2011; Bransen, 2002). It is “to have practical mastery over the inferences it is involved in—to know, in the practical sense of being able to distinguish, what follows from the applicability of a concept, and what it follows from” (Brandom, 2000, p. 48).

However, understanding, described in terms of the ability to navigate and master the GoGAR, is not a binary function. It is not that a knower either mastering the GoGAR completely or not mastering it at all, according to some topic. What is essential is to characterize the GoGARs that evolves; to distinguish how content and the understanding of content are constituted in relation to the quality of the GoGAR that is orchestrated in classroom talk. So, in order to increase the analytical power of GoGAR I distinguish between rich and limited GoGARs.

Rich mathematical GoGAR demands students’ mathematical talk (Walshaw & Anthony, 2008). In rich mathematical GoGARs, students are engaged in the production of mathematics in teaching. Students have the rights to be engaged in and feel obliged to take responsibility for their engagement (Meyer & Turner, 2002). Students should feel it is worth contributing to the talk. The teacher makes “everyone feel included by respecting and valuing the mathematics and the cultures that students bring to the classrooms” (Anthony & Walshaw, 2009, p. 150). In rich mathematical GoGARs, the content is holistic and reasons made explicit (Bakker & Derry, 2011). Rich mathematical GoGARs provides space for the students’ ideas and informal strategies and encourages mathematical activities such as analyzing, making connections, explaining, inferring and generalizing (Fraivillig et al., 1999).

Limited mathematical GoGARs, features the situation of high teacher control. The teacher dominates more or less the entire talking space and feels insecure to let go of control of how content should be introduced, expressed and dealt with in the classroom (Emanuelsson & Sahlström, 2008). The well-known IRE-model (Brodie, 2011) is a representative of limited mathematical GoGARs. In a pattern of IRE, a teacher tends to ask questions of a factual kind, to which she/he already has the answer (Panayiotou et al., 2014) and funnelling students towards the answer she/he wants (Bauersfeld, 1998). In limited mathematical GoGARS, content is atomistic and implicit, lacking relational structure. The meaning of content is of a referential, dictionary nature. That is, in limited mathematical GoGARs content is likely to be reduced merely to observational reports, naming of objects, concept definitions and descriptions of the step taken in a procedure (Hufferd-Ackles et al., 2004).

The construct of a didactical contract (Brousseau, 1997) can provide further insight to the distinction of limited and rich mathematical GoGARs. The didactical contract is based on the idea that teachers and students are engaged in the joint enterprise of succeeding with students’ learning (Brousseau, 1997). To this end, teacher and students develop certain patterns of obligations, responsibility and expectations. For instance, in teaching students expect of the teacher that she/he provides them with only solvable tasks. And, on the contrary, teachers expect of the students they will do their best in solving the tasks. Brousseau connects the didactical contract to the process of devolution, by which the teacher intends to have students taking responsibility for a task and accepting the consequences of this transfer of responsibility for him/herself. When the devolution does not succeed, i.e., the GoGAR is limited from an inferentialist perspective on learning, a possible consequence is that, rather than addressing problems in terms of the underlying concepts, students address them in terms of the didactical situation, which is controlled by the teacher and in which the students mainly focus on what they think that the teacher will expect them to say or do (Millar, Leach, & Osborne, 2001).

Method

The Classroom Scene and Data Collection

A 40-minute lesson on the teaching of the concept of velocity in a Grade 6 of a Swedish classroom was observed. After the class is seated, the teacher organizes a whole-class session combining talk and note-taking. In the following, I refer to this part of the lesson as the “note-taking activity,” or simply the “activity.” The note-taking activity lasted for 29 minutes. In the remaining time of the lesson, the students were working in their textbook. It is the note-taking activity that is the focus of the present analysis. The teacher, which is named Tara, is positioned at the whiteboard, in front of the classroom. None of the students are writing at the whiteboard during the lesson. Taking notes during whole-class sessions in mathematics is a teaching format the class is used to.

Tara uses an interactive whiteboard on which she write and upload definitions and work through examples of tasks, which she has prepared in advance to the lesson. All in all, the class works through eight tasks during the 29 minutes of note-taking activity. Tara tells the class that the tasks are similar to the tasks of the textbooks. She also sequences the tasks similar to how the tasks are sequenced in the students’ textbooks. Some of the tasks are also borrowed from the textbook. In the first half of the activity, the tasks ask for a distance. Here the time parameter changed between the tasks and the average velocity was kept constant. In the second half of the activity, the tasks ask for the average velocity, given distance and time. This time, both the distance and the time changed between the tasks.

The whole lesson was video-recorded by two cameras. One camera was placed at the back of the classroom, to cover the teacher and the whiteboard. The other camera was placed in front of the classroom, directed out in the class to cover student moves.

Method of Analysis

The study follows the methodology of qualitative case study research (Yin, 2013), in order to account for details in the relationship between note-taking and the orchestration of math-talk. The study is empirical in that the aim is not to illustrate the power of a new methodological tool. Instead, the distinction between limited and rich mathematical GoGAR and the concept of didactical contract are to be considered as means for providing sensitizing concept (Blumer, 1954), for organizing the analysis of the empirical material of the case in question.

In the first step of the analysis, I looked at the teacher’s and the students’ positions and roles during the activity. I focused on relational aspects, according to the social game between the teacher and the students.

Next, I looked more closely to how content was expressed. The data were coded according to if and how the content of the talk was inferentially expressed. For instance, if the teacher articulated, “The unit of velocity is kilometres per hour,” without any further elaboration, this expression was coded as an instance of limited mathematical GoGAR. The concept of velocity is given an atomistic, referential meaning, in terms of a one-to-one mapping to the symbol km/h. An instance, coded as an expression of rich mathematical GoGAR, is when the teacher articulates the inference from “the average velocity can be 80 kilometres per hour” to “one travels 80 kilometres in one hour.” The two claims are relationally combined; the first claim serves as a reason for the second claim.

The result of the two first analyses was that the math-talk of the activity was rather constrained. In order to account for the role that note-taking had in this, I analysed the situation again and, this time by means of the construct of didactical contract (Brousseau, 1997).

The entire note-taking activity (29 minutes) was analysed. I choose transcripts from a different episode of the whole note-taking activity. The episodes are chosen as they represent a variety of situations that enable me to analyse and show how note-taking came to influence on students’ opportunities to engage in math-talk.

Results and Analysis

The analysis shows how students’ obligations to take notes can come to support a teacher’s position and control of the content production in the mathematics classroom and, thereby, limiting students’ opportunities to engage in rich mathematical GoGARs. The analysis distinguishes two overall teaching formats – teacher presentations and IRE-interaction – where the teacher’s control of how content is introduced, expressed and dealt with is reinforced (Emanuelsson & Sahlström, 2008) and where students’ participation is basically reduced to listening and taking notes and to providing answers to closed, factual questions from the teacher. The mathematical GoGARs that occurs within these teaching formats are then primarily atomistically rather than relationally composed i.e., concepts and symbols are limited connected to other concepts and/or symbols. The language game is lacking connections between claims and explicit expressions of reasons for claims (Brandom, 2000). More concretely, the meaning of concepts and symbols is expressed in definitions, or in the direct referential (dictionary) meaning of what a symbol stands for, and the meaning of procedures is constituted in the step-by-step procedural talk.

Limited Mathematical GoGARs with High Teacher Control

Tara begins the lesson by presenting a set of speed signs on the whiteboard (Figure 1).

Tara:

You can write velocity as heading in your notebooks. Velocity! You have all seen this kind of signs along the road, which tell at what velocity cars should drive. Here we have 80, 40, 60, 120 and 100 [pointing to a set of signs presented on the smart-board]. Velocity/ … /Velocity is measured in kilometres per hour. And, you write out velocity in this way [pointing to and underlying km/h, presented on the board].

Sara:

Should we write this?

Tara:

You write down this [moving her hand over the whole screen]. Kilometres and then a slash, which means per [emphasizes the wording of “per”]. And then it is an h there.

Edwin:

That I know!

Tara:

What is h standing for now, Edwin?

Edwin:

hour!

Tara:

h is standing for hour [saying the English word “hour”] and that is “timme” [timme is the Swedish word for hour] in English. Hence, this is [pointing to the expression km/h on the board] kilometre per hour. And, another concept is average velocity. The average velocity tells how far one gets if one drives … 

Marc:

Should we write that?

Tara:

Yes. [Tara then immediately continues the prior sentence] … if one drives at the same velocity during one hour. So, the average velocity can be 80 kilometres per hour, then one travels 80 kilometres in one hour [Tara illustrates a constant distance by holding up her two hands in front of her. She then moves her hands, the distance, to the left when expressing “in one hour”]. If the average velocity is 120, you will travel 120 kilometres per hour.

Figure 1. Picture of the board with speed-signs and the unit “km/h” marked.

Tara owns the talking-space throughout the lesson. The teaching does not provide room for the students’ ideas. Instead, the ideas come from Tara. Generally speaking, it is the teacher’s role to produce content and the students’ role to consume content! When it comes to mathematics it is Tara who is asking questions. Students’ questions are almost exclusively about note-taking such as, “Should we write this?”. But, even though Tara’s question is about mathematics, they do not qualify as asking for reasons. They do not invite for extending and deepening a reasoning (Fraivillig et al., 1999). The questions are more of closed, fact-eliciting questions like, “what is h standing for now?”.

If the teaching does not provide students opportunities to produce reasoning, does it then provide them opportunities to follow reasoning, produced by the teacher? The answer is that the teaching shows limited instances of such opportunities as well. What is more evident is talk of a descriptive, referential nature. For instance, in the first act of teacher presentation above, Tara paints a story of velocity, by using speed signs as referential objects. She then tells that velocity is measured in km/h. Linking velocity to the concept of “measure,” may indicate that she describes a method for calculating velocity, i.e., how to measure it. However, Tara is not saying how velocity is measured, in terms of the ration between a distance (km) and time (h). What she expresses is that velocity is measured in km/h. This indicates that she is merely expressing a one-to-one mapping between the symbol “velocity” and the symbol km/h. This interpretation is strengthened in her subsequent claim, where she emphasizes how to write out velocity, and underlines the unit km/h on the board (Figure 1).

One of few occasions where Tara develops aspects of richer mathematical GoGAR in an act of presentation appears in the last sequence of the transcript above. Here she articulates inferentially composed claims and relationships between claims. For instance, Tara articulates the inference from “the average velocity can be 80 kilometres per hour” to “one travels 80 kilometres in one hour” and, similarly, the inference from “the average velocity is 120” to “you will travel 120 kilometres per hour.” So, in the change of numbers involved, these two conditionals are also inferentially linked in between them. Relationally speaking, Tara also accompanies these conditionals with gestures. So, in this situation the students are provided the opportunity to follow a reasoning, inferentially composed. However, again we see that the situation provide no room for students ideas, to contribute to and engage in the common content production in the activity. The situation confirms the teacher’s role in producing content and the students’ role in consuming content by listening and note-taking.

From time to time teacher presentations are interrupted with short patterns of IRE. In IRE-interactions, Tara frames and controls the content production of the talk by closed, factual questions to single students. How Tara and Edwin conclude on what h stands for follows the IRE-model. The IRE-model is most frequent when the talk comes to concern procedures. Overall, procedural talk is dominating the entire note-taking activity and, below I will return to how this focus works with the overall goal of the activity, to prepare the students for textbook work. The procedural talk then comes in the form of step-by-step procedural talk. Step-by-step procedural talk is lacking the explicit use of giving or asking for reasons for how and why a procedure works. Instead, it focuses on describing a solution procedure and following the steps in the execution of the solution procedure. What it is for students to do and to learn is learning to identify, follow and, to similar tasks, apply a procedure. Step-by-step procedural talk departures from the Tara describing a task and a solution method for solving the task:

Tara:

We are going to talk a bit about how we do to calculate a velocity. And, to calculate a velocity we need to know two things. We need to know how far we been driven [underlining “Distance” on the whiteboard (at the top of Figure 2)], how far we have come. And, we need to know, how long time did it take [underlining “Time” (at the top of Figure 2)]. And, the velocity [pointing to the word “Distance” on the board] should be in kilometres and time should be in hours.

 

One student, Alen, interrupts Tara, asking, “Shall we write this down?”

Tara:

Yes! This you need to write down, how you do to calculate a velocity [pointing to the formula on the board].

Alen:

Shall we also record “Calculating the velocity” [On the board in Swedish: “Räkna ut hastigheten”].

Tara:

[Nodding].

Alen:

Okay.

Tara:

“Calculating the velocity” is as a little heading. So, to calculate the velocity, we are taking the distance in kilometres and dividing this by the time, in hours.

Tara then introduces the task of calculating the velocity by which Adam drives if we know that Adam travels 180 kilometres in three hours.

Tara:

We know how far he gets in three hours. In three hours he reach 180 kilometres. We want to know how far he gets in one hour. [Several students want to answer] Philip you were first.

 

Philip You divide by three.

We see that Tara does not handing over much of the solution to the students. She goes through the steps of the procedure and, in line with funnelling (Bauersfeld, 1998) she leads the students to what calculation they are supposed to perform in order to reach the answer. Tara re-voices Philip’s answer and repeats the steps to take to reach 180 divided by three. Following the IRE-pattern, the step-by-step procedural talk continues towards the solution (Figure 2):

Tara:

And … , Renate?

Renate:

60.

Tara:

180 divided by three is 60 [add 60 to the board]. Should it just be 60? Wilda?

Wilda:

Kilometres!

Tara:

[Writing km after 60]. It is now an average velocity, a velocity we have, should it just be kilometres then?

Alen:

Hour!

Tara:

[Nodding and adding /h after 60 to complete the unit].

Figure 2. The solution to the calculation of Adam’s velocity. The English translations added to the left.

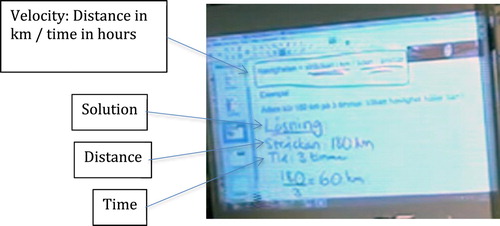
The episode provides further evidence of the large amount of talking-space the teacher receives in the note-taking activity and how the students are positioned as consumers of content. The episode discloses also that, when students were invited to contribute they did so by providing short, atomistic answers to factual-like questions. And, when a student gives the wrong answer, as is the case when Wilda responds kilometres instead of kilometres per hour, which is not the answer Tara wants, Tara does not use this answer as a source for or in need of elaborating or deepening the talk. Instead, following the IRE-model, she quickly asks for the correct answer. After Alen has provided the answer she wanted, the task is completed and she moves to the next task.

As is evident in the interaction between Tara and Alen, the note-taking activity did not only support descriptive math-talk and step-by-step procedural talk. What the activity did was to elicit also note-taking talk! We saw an instance of such talk also in the first transcript. Characteristic of the note-taking talk is that it focuses on form rather than content. It focuses on what and how notes should be taken. Typically is that students simply ask, “Should we write this?” On all such questions, Tara tell the students to do that. There is no instance where Tara tells the students not to record. It could also be that Tara provides directives from the beginning like, “You can write velocity as the heading in your notebooks.” It is also notable that the students’ note-taking and note-taking talk only came to concern what appeared on the whiteboard. The students did not record information any that was only orally expressed.

The Didactical Contract of the Note-Taking Activity

I use the construct of a didactical contract (Brousseau, 1997) to elaborate more on how note-taking can come to support high teacher control, where students’ participation basically become reduced to listening and taking notes and to providing answers to closed, factual questions.

The didactical contract expresses the idea that teachers and students are engaged in the common goal of succeeding with students’ learning (Brousseau, 1997). In the present study, the common, overall goal of the note-taking activity is to prepare the students for individual work in their textbooks. This is evident in that the activity is located at the beginning of the lesson and that Tara often emphasizes that the examples she has chosen are similar to the tasks in the students’ textbooks. How Tara is sequencing the tasks are also similar to how tasks are sequenced in the textbook and, at some occasions, Tara uses tasks from the textbook. Tara also makes the aim of the activity explicit in her introduction; “I know that some of you already has begun working on this [referring to the chapter on velocity in the book] but, we are going through it together first/ … /then you are working by your own.” Immediately after the note-taking activity the students then begin working in their textbooks.

The overall goal of the activity is the main reason that the teacher gains high control of the content production in the activity depends. According to this goal, it is Tara’s responsibility to equip the students with tools that they can use to solve textbook tasks. The tool she offers the students is examples of task, which are similar to the tasks of the students’ textbooks. By recording the solution of examples, the students can return to their note-books and imitate or compare the solution to the tasks they meet in their textbooks. From time to time, Tara makes this teaching strategy, teaching through examples (Bills et al., 2006), explicit by sayings like, “The examples that I will go through are similar to the tasks in the textbook but, with different numbers” and “We have this. Really good to remember [circling the formula of velocity on the board (see Figure 2)].” All at all, the class goes through eight examples during the 29 minutes the note-taking activity runs.

Tara has a clear idea of what content she aims for and would like to appear on the whiteboard. The content she aims for is descriptions of example tasks and well-structured and correct solutions to the tasks. The activity is well organized and structured and, Tara comes to control the content production throughout the entire activity by keeping to the task trajectory she has planned for in advance. All tasks have a clear starting point and a clear endpoint. What the episodes above show is that note-taking can come to be part of constituting highly structured, example-based teaching, which leaves limited room for students’ ideas or informal strategies. It can come to be part of a teaching, which does not invite for rich mathematical GoGAR. Instead, the present analysis shows how note-taking may support teaching that increases teacher’s control, descriptive math-talk and step-by-step procedural talk according to the presentation of example tasks.

Obviously, it is not enough that a teacher fulfils his/her responsibility if notes should be the tool it is supposed to be for students’ learning (Di Vesta & Gray, 1972). In the present case, it is not enough that Tara fulfils her responsibility in selecting and presenting the content in a form that is appropriate for note-taking. To be the external resource for the students’ learning, i.e., for students to learn to solve similar tasks on their own, the students have also a responsibility. What is notable though, is how students’ responsibility also contributes to increase Tara’s control in a producer-consumer relationship between the teacher and the students. The students’ part of the contract involves paying attention and listening (Nathan & Knuth, 2003; Wood, 2002) and keeping up with the pace of the activity and taking notes in a reliable way. Keeping up with the pace of the activity and taking notes in a reliable way are the main reasons for the appearance of note-taking talk. Avoiding not missing something important from the board, students sometimes felt the need to interrupt Tara, “Hey, I was not done!”, in order to make her slow down. In the transcripts above we also see how the students, at several occasions, are asking Tara for advice of what notes to take. However, by consulting Tara about what notes to take, the learning potential of note-taking decreases. In asking Tara for advice the students are bypassing their own responsibility by handing-over much of the responsibility to the teacher. Interpreted in the frame of a didactical contract (Brousseau, 1997), it is reasonable to assume that the students trust the teacher and do not expect her to recommend them recording anything that will not be important and useful for them. However, by handling-over the responsibility to the teacher, note-taking does not become the learning resource it is supposed to be (Kobayashi, 2005). Taking notes is reduced to an act of copying the board controlled by the teacher (Stefanou et al., 2008), with low mental activity from the students. The students are not taking an active part in reflecting on what and how they should take notes. In other words, taking notes becomes less an act of paraphrasing, inferring, summarizing or reorganizing the information provided in the situation (Bereiter & Scardamalia, 1985).

In teacher presentations, Tara presents, yet in a descriptive form, information that certainly would be important for students’ understanding of the relationship between velocity, distance and time. However, because the students are only expected to record information that is displayed on the board, many of the main points verbally expressed will certainly be left outside (Lew et al., 2016) and, consequently, students will have limited opportunities to recall, rethink and revise a fuller picture of the content after the actual teaching situation (Applebee, 1984). However, rethinking, reorganizing and revising speak to note-taking as being a learning resource for conceptual knowledge (Hiebert & Lefevre, 1986). Tara’s and the students’ joint enterprise is in the present situation to provide students with procedural tools for solving tasks, similar to the tasks presented on the whiteboard. It is in relation to this enterprise, to this overall goal, note-taking takes a position in the present context. In other words, it is as a learning resource for allowing students to recall representatives for imitative reasoning (Lithner, 2008) on task solutions that note-taking takes a position in the activity and, consequently, comes to work with limited mathematical GoGARs in terms of descriptive and step-by-step procedural math-talk and of note-taking talk in relation to copying the board.

Concluding Discussion

This study took departure in the observation that math-talk is usually relatively constrained (Brodie, 2011) and does not always allow for the development and extending of students’ mathematical understanding (Fraivillig et al., 1999). A dilemma was observed, between a teacher’s need to guide students in advancing and structuring the content of math-talk (Stein et al., 2008) and high teacher-control in the content production of math-talk (Emanuelsson & Sahlström, 2008). The present study not only confirms that math-talk can be constrained in teaching. In relation to the dilemma between teacher guiding and teacher control, the study also shows how note-taking (Di Vesta & Gray, 1973) can come to support such constrains. The study particularly shows how students’ obligations to take notes can reinforce high teacher control in the content production of math-talk and position students as consumers of content, in terms of listening, recording and answering factual questions. The analysis distinguishes two overall teaching formats – teacher presentations and IRE-interaction – where the teacher controlled the production of descriptive math-talk and step-by-step procedural math-talk by providing students with task examples, similar to the tasks in their textbook.

The analysis shows how Brandom’s inferentialism (Brandom, 1994) provides perspective and language that helps to account for details of math-talk (Hufferd-Ackles et al., 2004). The distinction between limited and rich mathematical GoGAR forces attention to the extent, and in what ways, a math-talk is relationally orchestrated, i.e., how participants of a talk produce and consume reasons, how they engage in navigating and mastering what follows from the application of a mathematical claim, what it follows from, and what is incompatible with it. It is how the distinction puts focus on inferential details in math-talk we come to understand that the math-talk of the current study is of a descriptive and procedural nature and so, providing students with only limited opportunities to learn mathematics from an inferential stance on learning. The practical implication of this inferential picture on learning is that, if a math-talk is to count as a talk for understanding mathematics, there is a need of socio-mathematical norms (Yackel & Cobb, 1996), which requires students and teacher being specific and accurate in what they refer to and in making explicit what is entailed by a claim, what would serve as evidence for it, and what is incompatible with it (Bakker & Derry, 2011; Brandom, 2002).

The study sheds further light on how note-taking can come to be a practice of copying the board (Stefanou et al., 2008). A teacher is supposed to guide and help students in advancing and structuring subject-matter (Stein et al., 2008). However, the present case shows how note-taking can lead to that a teacher’s help be over-structured. The teacher, Tara, is in high control of the teaching (Hoekstra et al., 2009) and teaching becomes more a question of a teacher producing and students consuming content, rather than students taking responsibility for their own learning and being actively engaged in co-producing the content of the activity. In this producer-consumer relationship, note-taking is meant to be used as a storage for the students; the overall aim of the note-taking activity is to prepare students with examples of tasks and task solutions that they can recall from the storage and use when working in their textbook. Hence, it is in how note-taking comes to work with example-driven teaching (Bills et al., 2006) we can further our understanding of how note-taking can turn into a practice of copying the board. On practical implications, these findings of the presents study suggest that teachers need to be sensitive to how note-taking can come to support high teacher control. Connected to how note-taking often becomes a question of copying the board, teacher need to be aware of if, and how, such a note-taking practice can come to support imitative reasoning strategies (Lithner, 2008) when, what is to be copied is examples of tasks and task-solutions, similar to the tasks of the students’ textbooks. Moreover, if much of content is expressed verbally, as is the case in the present study, but the norm is that it is only what is displayed on the board that counts for note-taking, many of the main points will be left outside (Lew et al., 2016). On this account, the present study stresses the need for a teacher to actively work with note-taking techniques, so the note-taking be the learning resource it has the potential to be, as a means for paraphrasing, inferring, summarizing or reorganizing the information provided in teaching (Bereiter & Scardamalia, 1985).

So, should the consequences of the present study be to recommend teachers to avoid combining discussion-based teaching with note-taking or, support structures in general? I would suggest that this is not how the results of the study should be interpreted. Following the methodology of qualitative case study research (Yin, 2013), the study has provided insights on how note-taking, as a certain support structure, can come to constrain the orchestration of math-talk in teaching. However, I do not claim that the study provides a complete picture of the relationship between note-taking and the orchestration of math-talk. Further research is needed to develop this picture. One methodological idea could be to compare how the same teacher, the same class, orchestrates math-talk when the teaching involves note-taking and when it does not. The insights from the study also challenges design research (McKenney & Reeves, 2012) in mathematics education to investigate the possibilities to develop a teaching practice that creates synergies between talk-based teaching of mathematics and note-taking, as a resource for paraphrasing, inferring, summarizing and reorganizing the information provided in such teaching (Bereiter & Scardamalia, 1985).

Disclosure statement

No potential conflict of interest was reported by the author.

Additional information

Funding

This work was supported by the Swedish Research Council (Vetenskapsrådet) (dnr. 721-2012-4811).

Notes

1 Brandom does not make any significant distinction between terms and concepts so in the rest of the paper I will use them interchangeably.