Different Learning Possibilities from the Same Activity—Swedish Preschool Teachers’ Enactment of a Number Relation Activity

ABSTRACT

In this paper, differences in the implementation of a number activity called the snake game are studied. Nine Swedish preschool teachers worked in collaboration with a research team, enacting the same activity with their groups of 5-year-old children over a 3-month period. Variation theory forms the basis for the analysis of 67 videorecorded enactments. The results suggest that an activity such as the snake game can bring various aspects of numbers to the fore through differences in enactment. The activity became mathematically richer when the teacher compared children’s different finger patterns and used systematically varied examples of number relations. This study’s results contribute knowledge about characteristics of teaching that foregrounds numbers’ part-whole relations.

KEYWORDS:

• Variation theory
• mathematical activity
• in-service preschool teachers
• early numbers
• part-whole relationship
• part-whole relations
• finger patterns

Introduction

In the early years mathematics education research field, knowledge of the additive part-whole relation of numbers¹ is seen as important for children’s development of arithmetic skills (e.g., Baroody, 2016; Neuman, 1987; Resnick, 1983). Understanding the part-whole relationships of numbers enables the understanding of mathematical principles such as commutativity, inverse relations between addition and subtraction, and equality (Clements & Sarama, 2009), in addition to the within relation of three numbers (Baroody, 2016; Schmittau, 2004). While some have argued that part-whole relations cannot be learned before primary school (Piaget, 1965; Resnick, 1983), interview studies show that children’s understanding of part-whole relations can develop before they enter primary school (Hunting, 2003; Sophian & McCorgray, 1994; Sophian & Vong, 1995). Whereas most researchers argue that counting is a prerequisite for understanding the part-whole relationship (e.g., Nesher et al., 1982; Resnick, 1983), others (Davydov, 1982; Neuman, 1987, 2013; Schmittau, 2004) accentuate the importance of discerning numbers as structured relations of parts and whole and instead of focusing on counting single units, they see the part-whole relationship as a fundamental base for children’s development of arithmetic skills.

While children’s learning of additive part-whole number relationships has been emphasised in the literature, few studies have investigated differences in teachers’ ways of conducting activities intended to foreground structured part-whole relations. In particular, investigation of instructions, explanations, gestures, and use of resources at a more detailed level is lacking. The current study seeks to fill this gap by analysing, in detail, one specific part-whole activity, and how this activity, in which fingers are used as a tool for structuring number relations, may promote learning of structured part-whole relations.

This paper reports on a study in five Swedish preschools²; the study involved working with nine in-service preschool teachers to implement one specific activity, called the snake game, with the teachers’ 5-year-old preschool children. The snake game is a decomposition activity in which a collection of items is decomposed into two parts, and one of these parts is hidden. The snake resource itself, in different designs, was familiar to the preschool teachers. However, the mathematical principles that can be foregrounded with the help of the snake game were not as well known. Through a collaborative process, the snake game was implemented during a 3-month period. Sixty-seven videorecorded observations of the implementation of the game were analysed.

Implementation of an activity can be investigated from the perspective of variation theory by analysing the object of learning—what is made possible to learn—in an actual learning situation (Marton, 2015; Runesson, 2005). In this paper, viewing the activity through the variation-theoretical lens reveals differences in the enactment of the object of learning and the learning possibilities afforded through these different enactments.

The overall aim of this study is to contribute knowledge about how the same part-whole activity, designed collectively, can be enacted differently. Through examining teachers’ enactment of the snake game in preschool groups, it is possible to identify the different opportunities the children are given to learn about number relations, mathematical principles, and finger patterns for representing compositions of parts and whole.

The research questions are the following:

• What objects of learning are constituted within the snake-game activity?

• What are the different learning possibilities of part-whole relationship offered within the different enactments of the activity?

Literature Review

To situate this study within the literature about research on part-whole relationships, an overview of the literature is provided here. This review looks at the research from a learning and teaching perspective, exploring what mathematical principles can be brought to the fore in the enactment of a part-whole activity and identifying what characterises a structural approach to part-whole relationships.

Key Features of Learning Part-Whole Relationships

The terms whole and parts describe the set-subset relationship of a collection of items, and this relationship can be represented by numbers (Fischer, 1990). When children are to learn that within a collection (set) there are smaller groups of items (subsets), they need to understand the cardinality principle (in counting items, each number word refers both to the last counted item and to all the items together) (Fuson, 1982). A whole collection can be decomposed into two subsets in different ways (e.g., five marbles in subsets of four and one or two and three), and it can be composed to form the same whole collection again (Payne & Rathmell, 1975). Comprehending various additive compositions of parts is a prerequisite for understanding the addition concept (Piaget, 1965), and the knowledge of the part-whole relationship of numbers is seen as important for the development of more effective counting strategies and viewed as a pathway to learning number facts (e.g., Baroody, 1987, 2016; Fuson, 1992). When children are asked to identify the total quantity in different collection of items, they may estimate, count the items one by one, or see them as composite sets of units. The ability to immediately discern the total quantity in small sets of units (three to four items) without counting them as single units is called subitising (Wynn, 1992) or perceptual subitising (Clements, 1999). Clements and Sarama (2009) differentiate perceptual subitising from conceptual subitising. They argue that conceptual subitising comes into play when the range of items perceived as a set is extended through patterns recognised as a composition of parts and wholes, for instance, six dots on a die seen as two columns of three, or four fingers on each hand seen as one 8, without each finger or dot having to be counted (Clements & Sarama, 2009).

Mathematical Principles Linked to Part-Whole Relationships

In preschool and early primary school, children’s knowledge about the part-whole relationship of numbers enables them to learn various mathematical principles (Baroody, 1987; Resnick, 1983). Knowing the within relation of three numbers (fact family; Schmittau, 2004) in a specific part-whole relation (e.g., the whole number 5 and its two parts, 4 and 1) enables solution of any additive relation problem involving this family with one missing value (e.g., $1+\mathrm{\_}=5;5-\mathrm{\_}=1$) in a context problem with manipulatives or symbols. The part-whole relationship also enables children to experience the complement principle (the inverse relation of addition and subtraction; $\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{a}+\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{b}=\mathrm{w}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{c},\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s}\mathrm{w}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{c}-\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{a}=\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{b}$) and the commutative principle. The commutative principle ($\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{a}+\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{b}=\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{b}+\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{a}$)—that is, the irrelevant order of the addends—is one of the essential properties of the part-whole relationship of numbers (Kilpatrick et al., 2001). In addition to facilitating learners’ computational fluency, the commutative principle is integral to part-whole reasoning (Ching & Nunes, 2017) such as understanding that the relation among three quantities, for example 5/4/1, can be expressed with symbols (e.g., $1+4=5;4+1=5$) and that both equations describe the same part-whole relation. Previous research has shown that children acquire informal knowledge of commutativity before entering school. For instance, Canobi et al.’s (2002) study showed that most 4-to-6-year-olds could understand that the order of physical objects in two sets did not matter; the total was the same. However, in another study conducted with the same age group, when formal symbolic examples were added, most children used repeated counting to check their answers, and they did not apply the commutative principle when solving related tasks (Baroody, 1987). These results suggest that not all children understand the commutative principle before they begin formal schooling.

Structured Approaches to Teaching Part-Whole and Finger Representations

The literature draws a distinction between counting-based and structural approaches to early numbers. From a structural approach, the part-whole relation is seen as a fundamental focus from the outset (Davydov, 1982; Neuman, 1987, 2013), enabling the simultaneous discernment of parts and whole. Some representations of numbers support this simultaneous perception of parts and whole and their relationship better than others. One such representation uses fingers. Finger counting is seen as important in the transition from perceptual counting to figural counting (Steffe et al., 1988). Finger representation makes it possible to see 10 as equal to 2 × 5 (the sub-base 5 system) and 5 as a benchmark by, for instance, representing 5 with a full opened hand and numbers larger than 5 by adding fingers on the other hand (Wasner et al., 2015). However, there are important differences in how children use their fingers. Using fingers for representing numbers through counting single units is different from structuring fingers into numbers as patterned part-whole relations. Brissiaud (1992) argued that young children’s numerical understanding can be developed if they are encouraged to use their fingers as “symbol sets” or structured patterns representing quantities. Using finger patterns for structuring numbers enables children to discern number relations as parts and whole. Knowing the whole number and one part makes it possible to identify the missing part without having to count fingers one by one. Neuman (1987) found that 7-year-olds who used structured finger patterns successfully solved additive relation problems with answers that did not exceed 10; by contrast, children who used single-unit finger counting failed to solve the problems. Similar results were found in a study with 4-to-5-year-olds (Björklund et al., 2019). Structured finger patterns unify numbers’ ordinal aspect (the experience of ordered fingers) and cardinal aspect (the experience of each number referring to a certain group of fingers) as well as the sense of how the parts within the whole number are related to each other (Bender & Beller, 2012; Davydov, 1982; Marton, 2015). Therefore, structured finger patterns function as a useful tool in additive relation problem solving.

Examining the Teaching of Part-Whole Relationships

Building on evidence both that understanding the part-whole relationship of numbers is fundamental for children’s development and that this understanding is possible among preschool-aged children (Fischer, 1990; Jung et al., 2013), some early mathematics intervention programmes implement number activities that emphasise part-whole relations (e.g., Clements & Sarama, 2009; Dyson et al., 2011). Some interventions have included a narrower focus on a structural approach to part-whole relations. One such example is an Australian study where structured spatial pattern and number activities were carefully implemented with 4-to-8-year-olds (Mulligan & Mitchelmore, 2009; Mulligan et al., 2013). The results indicated that children showing a higher awareness of structure more easily learned about properties of early numbers and tended to look at and explore new patterns in successful ways. However, few studies have more explicitly examined teaching part-whole relations of numbers. In a preschool intervention programme, 4-to-5-year-olds who received instruction in part-whole relationships developed a better understanding of numbers and of solving additive relation word problems than the group of children following the more common “counting” programme (Fischer, 1990). In a 2013 study by Jung et al. in which activities focusing on part-whole relationships, number relations, and subitising were implemented, similar positive effects were found in the group that received instruction which emphasised number relationships and subitising, whereas in the control group no such effects were seen.

In summary, the structural approach to part-whole relationships enables mathematical principles, subitising, and number relations to be foregrounded in teaching. As previous studies have shown, structured finger patterns also promote the simultaneous discernment of whole and parts. The findings of these studies can be used to guide the design and implementation of part-whole activities in preschool settings.

Theoretical Framework

In this study, variation theory was used as an analytical tool for studying, in detail, the teaching of part-whole relations, how the object of learning was enacted, and the learning opportunities afforded. Since the focus of this study is how the content was handled in the enactment, variation theory (Marton, 2015) was deemed appropriate. From a variation theory perspective, “there is no learning without something being learned, so learning always has an object” (Runesson, 2005, p. 70); that is, there must be something—specific content or a certain capability—that is to be learned. Learning is seen as experiencing the specific object of learning in a new and different way. In order for this to happen, aspects not previously discerned must be attended to. When new aspects are discerned, the way the object of learning is experienced changes. Thus, ways of experiencing are due to which aspects that come into the fore of attention and are discerned simultaneously. Variation theorists state that learning comes from experiencing differences rather than similarities: “new meanings are appropriated through contrast or differences” (Marton, 2015, p. 64). For instance, to understand the meaning of a specific number, one must also experience other numbers. The aspects that are essential for a particular way of experiencing have to be discerned as dimensions of variation; that is, something varies within the aspect in focus while other things are constant /invariant (Marton & Tsui, 2004). For instance, if a child does not know what 7 is, in a learning situation 7 can be contrasted with other numbers (e.g., by comparing a collection of seven marbles with a collection of five marbles), while the objects (marbles) are kept constant. The teacher can create learning opportunities and help children experience the object of learning in a new way by foregrounding essential aspects and opening them up as dimensions of variation. Variation theory assumes that a learner can discern an aspect if it is opened up as a dimension of variation since what varies against a stable background (invariant) is likely to be discerned (Marton & Pang, 2006). So, by analysing what aspects are opened up as dimensions of variation, variation theory allows one to describe the enacted object of learning—how the object of learning is handled by teachers. Hence, the aspects opened up as dimensions of variation constitute the enacted object of learning. When analysing how the same content is taught, different objects of learning might be found, depending on which dimensions of variation are opened up (or not) in different enactments (see, for instance, Runesson, 1999).

Method

Design of the Study

The current study is a part of a broader research project³ on teaching and learning early numbers in Swedish preschools. In this project, preschool teachers worked collaboratively with researchers in an iterative development process, designing activities and exploring and reflecting on learning activities in their own practice.

The preschool teachers met researchers from the project group every fortnight over a period of 3 months. In the meetings the teachers and the research group discussed aspects associated with structured part-whole relationships of numbers and planned how to implement the activity. The teachers themselves decided in which settings the snake game was to be implemented. Sometimes the teacher and children were sitting around a table or on the floor, and sometimes children were invited to join the activity in other indoor spaces used for play. Between each meeting, the preschool teachers videorecorded at least one implementation of the activity and uploaded the video to the project’s server. In preparation for the next meeting, the research team analysed the videorecorded observations and selected key episodes to be discussed. The selected episodes formed the basis for teachers’ reflections on both their handling of the activity and the children’s reactions. The teachers became increasingly familiar with principles that can be foregrounded in structured part-whole relations and that were embedded in the activity. The meetings usually culminated with the collective decision to repeat and refine the game and re-enact it in the teachers’ preschool groups. Each teacher enacted the snake game several times.

The Part-Whole Activity—The Snake Game

The snake game is a decomposition activity (no written numerals are used). The resource⁴ consists of two different “snakes”, one with five beads all of the same colour (the 5-snake), and one with 10 beads of two different colours (the 10-snake), grouped on a string as five of one colour and five of another colour (see Figure 1). This resource was matched in the activity with the use of finger patterns. The finger and bead representations support the simultaneous discernment of parts and whole and may also promote awereness of numbers as composite sets. In the enactment, some beads are hidden, and children are asked to show the same number on their fingers; by looking at their folded and unfolded fingers, they are able to say how many beads are hidden. For instance, if six beads of the 10-snake are visible and four beads are hidden, 6 can be represented with all fingers on the left hand and the thumb on the right hand. Now the hidden four might be identified by subitising, just by looking at the knuckles of the four folded fingers on the left hand (see Figure 2). The teachers usually led the activity, and sometimes the children took turns hiding beads of the snake and the teacher participated.

Figure 1. The 5-snake and 10-snake.

Figure 2. Six beads of the 10-snake are visible. The child shows the finger pattern (10/6/4).

The snake game can reify aspects that are central to the structural approach to part- whole relations, where the relations of parts and whole are in focus from the outset and are used as a foundation for addition and subtraction. Additionally, the commutative relationships can be discerned through simultaneously paying attention to parts and whole in a sequence of examples.

Participants and Data Collection

Nine preschool teachers working in two suburban districts close to a large Swedish city, along with their sixty-five 5-year-old preschool children, participated in this study. All the preschool teachers had a teacher certificate and between 2 and 32 years of work experience in Swedish preschools. The number of children participating on each teaching occasion varied between one and eight. The teachers and the parents of all 65 children had given their written consent to participate, according to the ethical guidelines of the Swedish Research Council (2011). In cases where the parents had not given permission to videorecording, the camera was directed towards the teacher and only the children’s voices and fingers were recorded. The data was comprised of 67 videorecorded observations of the nine teachers. The observations lasted between 2 and 16 min (films shorter than 2 min were excluded), and the mean time was 7.5 min. The teacher–child dialogues were transcribed verbatim and included teachers’ speech and gestures as well as children’s utterances and actions during the activity, in particular how they used their fingers. The children’s names were changed to pseudonyms.

Analysis

The aim of the study is to examine how the same part-whole activity can be enacted and what these different enactments enable preschool children to learn about part-whole relations.⁵ Thus, the purpose is not to compare individual teachers or to explore changes over time.

The data analysed were from transcripts of videorecordings. The method of analysis followed the principles of variation theory (Marton, 2015; Marton & Tsui, 2004). The following questions were used to support the process of analysis and to help maintain focus on the object of learning: What in the teacher–child dialogues emphasises the additive part-whole relationship (e.g., explanations, examples, questions, actions, gestures)? What aspects can be opened up as dimensions of variation? When a dimension of variation is opened up, what varies and what is kept invariant? Dimensions of variation that were opened up in the teachers’ enactments were identified. For instance, when a child counted the beads on the visible part of the snake one by one, and the teacher contrasted counting with seeing items as a composite set of units by saying: “Yes, 7. You can also see them as a 5 (circling the five beads) and two more”, the number (7) was kept constant and the way of identifying the beads varied (counting one by one vs. seeing them as composite sets). In this way, the aspect of numbers as composite sets was opened up as a dimension of variation.

Analysing teacher–child dialogues in this way made it possible to identify aspects which were opened up as dimensions of variation in the learning situations.

Watching the videorecordings and reading the transcripts repeatedly I, the author of this paper, identified the dimensions of variation that were opened up in each observation. I found that some dimensions were often opened up, whereas others were only opened occasionally. I then compared the identified dimensions of variation. This enabled me to see different ways of opening up the same dimension of variation and to identify what separated one opened-up dimension from another. For each observation, the dimensions of variation that were opened up were described. Then the observations were compared, and those with the same sets of dimensions of variation were grouped together. As an enacted object of learning is constituted of the dimensions of variation opened up (Marton, 2015), this step of the analysis enabled me to identify different enacted objects of learning (each with a set of opened-up dimensions of variation).

Since, according to variation theory, the dimensions of variation opened up is what is made possible for the learners to experience. The analysis also enabled me to describe what the children were offered to learn about part-whole relationships in relation to each of the identified enacted objects of learning.

Results

In the analysis, six dimensions of variation were identified as being opened up in the activity. These constituted the following four enacted objects of learning⁶:

• Enacted object of learning A – Numbers as countable units (three dimensions of variation opened up)

• Enacted object of learning B – Numbers as a structured composition of parts and wholes (three dimensions opened up, two of which were the same as in A, and another that was new)

• Enacted object of learning C – Numbers as decomposable parts (one further dimension of variation not seen thus far was opened up)

• Enacted object of learning D – Commutative number relations (one new dimension of variation opened up beyond the four dimensions of variation identified in C)

These enacted objects of learning, constituted in the implementation of the snake game, are reported in detail below, together with the learning opportunities afforded within each. Finally, a summary of the constitutions of the four enacted objects of learning and the different learning opportunities is provided.

Enacted Object of Learning A—Numbers as Countable Units

The enacted object of learning A is characterised as numbers as single-counted units. In Excerpt 1, the teacher introduced the 10-snake and presented two examples where the whole number 10 and its different parts are determined by counting one by one.

Table

Excerpt 1:
1	Teacher:	“How many on this snake?”
2	Peter counts the 10 beads by (touching each bead and saying the numbers).
3	In the first example (10/5/5), the teacher hides five beads and asks: “How many are hidden?”
4	Peter counts the five visible beads one by one and answers: “five.”
5	Teacher:	“Are you sure?” (opens her hand)
6	Peter counts, one by one, the beads that had been hidden.
7	In the next example (10/7/3), the teacher hides three beads in her hand and says “Now, I have hidden some beads again.”
8	Peter and Anna count the seven beads, (pointing to each one), then say: “seven.”
9	Teacher:	“How many in my hand?”
10	Anna:	“Three”
11	Peter:	“Four”
12	Teacher:	“You think it is four, and you think it is three; how do you know? Let’s check!” (opens her hand)
13	Children: “Three” (No more examples are presented)
		(Observation 2)

Across examples in this situation, where the whole number is 10 (constant) and the set sizes vary, the teacher repeatedly asked the children to determine the quantity of various collections of beads, using the single question “How many?” (Lines 1, 3, and 9). The children repeatedly counted the beads one by one. At no point were any alternatives to counting one by one given for determining collections of items larger than three; that is, no variation was provided. For instance, when the children identified seven beads and disagreed about how many were hidden, no strategy to figure out the hidden part was offered by the teacher (Line 12). The way the enacted object of learning A was constituted, in terms of dimensions of variation being opened up, gave the children the opportunity to experience numbers as countable units.

Enacted Object of Learning B—Numbers as a Structured Composition of Parts and Wholes

The enacted object of learning B was constituted differently than the enacted object of learning A. The way the activity was enacted made it possible to experience number relations as structured compositions of parts and wholes. In Excerpt 2, the teacher handled a sequence of examples where different part-whole relations were supposed to be structured on fingers.

Table

Excerpt 2:
1	Teacher:	“There are five beads, just like one hand. We are going to use it [holds up her hand] together with this snake.” In the first example (5/3/2), the teacher hides two beads.
2	Teacher:	“Show me with your hand how many you see! … How many are hidden?”
3	Children show three unfolded and two folded fingers in three different ways.
4	Teacher:	“What did you do with your fingers, Ali?” (thumb, index, and middle finger unfolded) “What about you, Elin?” (index, middle, and ring finger unfolded) “First there were three visible, then two hidden.” (points to her unfolded and folded fingers)
5	In the next example (5/1/4), the teacher hides four beads and says: “How many fingers do you see … how many hidden?”
6	Kim raises one finger and says, “five.”
7	Teacher discusses with Kim and models one and four on her own hand. Kim structures his finger pattern in the same way as the teacher.
8	Teacher:	“There are five on the whole snake, we can see one, just like you showed before.” (touches Kim’s knuckles) “How many are left?”
9	Kim turns his hand around and says, “four.”
	(Another four examples are presented.)
		(Observation 40)

Just as in the enacted object of learning A, variation was created by presenting a sequence of examples where the same whole number (constant) was decomposed into two parts and the set size of the parts varies. The dimension of variation related to representations of numbers (beads and fingers) was also opened up. The teacher emphasised the use of fingers to represent numbers, comparing the number of beads on the string with the same number of fingers (representation varies, the number is kept constant); thus, the same number relation was represented simultaneously with both fingers and groups of beads. Another aspect opened up as a dimension of variation is that a finger pattern simultaneously can represent two composite sets of units (folded and unfolded fingers), which makes the part-whole relationship visible. The teacher reinforced finger patterns for structuring various part-whole relations of 5 (Lines 2 and 5). Variation was offered when the same whole number (5) was decomposed into two parts in different ways (3 and 2; 1 and 4). It was thereby made possible for the children to experience that a specific whole number can be decomposed in different ways. In addition, when the teacher compared children’s different finger patterns (Lines 3 and 4), she offered variation of finger patterns representing the same part-whole relation when she directed the children’s attention to how the specific number relation 5/3/2 can be represented with finger patterns in different ways. When Kim had difficulty identifying the hidden four beads, the teacher offered an alternative to his way of using fingers, modelling the part-whole relation (5/1/4) on one hand herself (Lines 7–8), which enabled Kim to see the missing 4 on his fingers.

Later in the sequence, Elin used the fingers of both hands, showing 3 as the visible part. It then became hard for her to identify the hidden part of the whole 5. The teacher then offered variation to Elin’s 10 fingers by foregrounding the whole number 5, saying, “If you instead use one hand. On one hand we have 5”, which enabled Elin to discern the hidden part of 5. In the enactment, the visible part (3) was kept the same, and the whole number of fingers differed.

The way the enacted object of learning B was constituted, in terms of dimensions of variation being opened up, made it possible for the children to experience numbers as a structured composition of parts and wholes, both with beads and fingers. By structuring the whole number and one part on fingers, children can learn how to figure out the hidden part in a part-whole relationship without having to count their fingers as single units.

Enacted Object of Learning C—Numbers as Decomposable Parts

In the enacted object of learning C, an additional dimension of variation, which had not been opened up in the enacted objects of learning A and B, was present. This relates to the fact that parts within a specific part-whole relation can also be decomposed into smaller parts. For instance, if eight beads are visible and two are hidden, the 8 can be decomposed into two parts, the composite units 5 and 3. Alternatively, it is possible to decompose the 8 into the composite unit 5 and three single units (see Figure 3).

Figure 3 .#Ten beads on the whole snake, two hidden. The eight beads can be separated in two composite sets of units 5 and 3 or the composite unit of 5 and three single units.

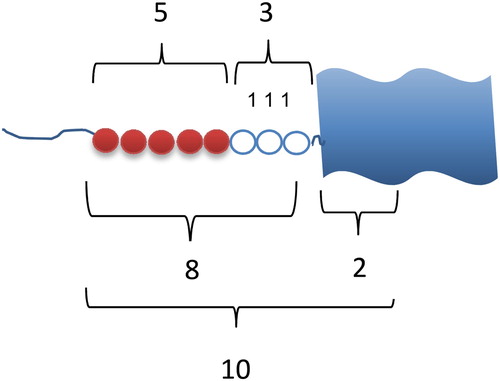
This way of handling the content, decomposing a part into smaller parts, as is demonstrated in Excerpt 3, enables children to extend their subitising range.

Table

Excerpt 3:
The teacher first shows five beads, then shows the other five beads and refers to 10 fingers on two hands. A sequence of examples of visible/hidden parts of the 10-snake is presented. Different finger patterns are shown by the children and the teacher.
1	After the children identify the missing part (7) in the relation 10/3/7 by looking at their finger pattern, Cleo spontaneously starts to count the seven beads one by one.
2	Teacher:	“Do you remember all those were 5?” (circles the five red beads on the string) “So, you do not have to count them … 6 and 7.” (pointing to two white beads)
3	In the next example (10/2/8), the children identify the missing part (8) by looking at their finger patterns.
4	When the teacher shows the hidden number of beads, Teo starts to count the eight beads one by one.
5	Teacher:	“Eight, exactly, do you remember … 5 [circles the five red beads, points to the three white beads] … 6, 7, 8. So, 8 and 2, altogether, makes 10.” (circles the two parts)
6	Later, when a child starts counting seven beads one by one, the teacher says: “Do you remember the ‘tip’, not needing to count all the beads?”
7	Bill points to the five beads, saying “5, 6, 7.”
		(Observation 63)

As with the enacted object of learning B, dimensions of variation related to part-whole relations, representations, and finger patterns were opened up. The teacher noticed that even if the children could see the parts within the whole number 10 as composite sets of units by structuring different part-whole relations on their fingers, some children spontaneously checked the identified part (beads) by counting one unit at a time (Lines 1, 4, and 6). The teacher then contrasted counting in ones, making use of the composite unit 5. She separated the undivided 5 from 7 and 8 by circling the beads in the same colour (Lines 2 and 5) and counted on in ones, “6, 7” and “6, 7, 8”, and later referred back to the “tip” (Line 6). Here, variation in the units added was offered, as the teacher drew the children’s attention to the undivided 5 (constant) and varied the units that were added (2 and 3, respectively). The teacher’s way of repeatedly underlining the 5 (by circling, pointing, and comparing beads and fingers) helped the children to see that the undivided 5 is helpful for identifying collections numbering slightly above 5.

The way the enacted object of learning C was constituted, in terms of dimensions of variation being opened up, enabled the children to experience numbers as decomposable parts. A part which exceeds the subitising range can be experienced as a composite set of units, as decomposed into two parts, or as a combination of a decomposed set of units and single counted units. Structured finger patterns facilitate the children’s discernment of the part-whole relationship and their seeing the parts as composite sets of units.

Enacted Object of Learning D—Commutative Number Relations

Compared to enacted objects of learning A, B, and C, where the examples were presented in a more or less randomly chosen order, the enacted object of learning D was constituted by using a systematic order of examples that can make a specific principle of part-whole relations visible. For instance, by choosing appropriate values of visible and hidden parts of the 10-snake and varying the order of the addends (e.g., 10/2/8; 10/8/2; 10/3/7; 10/7/3; 10/6/4; 10/4/6), a commutative pattern is shown.

Another way to emphasise the commutative principle was seen when the teacher offered the example 5/3/2 followed by 5/2/3. The children showed the part-whole relations with finger patterns. After presenting the second example (5/2/3), the teacher said, “This time 2 here [points to the two beads on the left side in her hand] and 3 here [points to the three beads on the right side], altogether … 5.” She then continued, “Before [moves one bead to the left] we had 3 there [points to three beads] and 2 there [points], that is also 5 [circles the parts]” (Observation 12). The differences and similarities between the two examples were highlighted by the teacher when she drew attention to the interchangeability of the parts that compose the whole by comparing 3 and 2 with 2 and 3, talking about the number of beads on the string and moving one bead from the part of the snake that had three beads to the part that had two.

In the enacted object of learning D, representations as well as sets of units structured with finger patterns were opened up as dimensions of variation. This offered the children an opportunity to experience the commutative principle, as well.

Summary

The results suggest that the snake-game activity consisted of four different objects of learning. The way the enacted object of learning A was constituted, no variation of representations or alternative to counting in ones was provided. In the enacted objects of learning B, C, and D, beads were connected to fingers and the variation of finger patterns was opened up. The enacted object of learning B provided variation of finger patterns for structuring the same part-whole relation. Enacted object of learning C was constituted differently than the others, as the teacher also contrasted counting single units with decomposing a part into smaller parts. The enacted object of learning D provided a systematic variation of examples, demonstrating the commutative principle in a sequence of two examples. The other enacted objects of learning did not offer this systematic pattern of variation.

The main differences identified in the opportunities afforded for learning about additive part-whole relationships are between the enacted object of learning A and the other enacted objects of learning (B, C, and D). In enactment A, the children were only given the opportunity to learn that collections of items can be determined by counting them as single units. By structuring the part-whole relations (beads and fingers), the other enacted objects of learning afforded the children the chance to experience numbers as a composition of parts and wholes. The children were given the opportunity to learn how to use finger patterns as a tool for structuring additive relations without having to count their fingers as single units (enacted object of learning B). The way the enacted object of learning C was constituted, the children could experience that one part (collections of beads) can be decomposed into smaller parts and that the undivided 5 can be used as a benchmark. The children were thus offered opportunities to see numbers as composite sets and parts as decomposable while still seeing that the parts—whether there are two or more—are composable into the same whole number. Only the enacted object of learning C afforded these learning opportunities. Finally, the enacted object of learning D gave the children an opportunity to learn the commutative principle.

Discussion

This study reports on the implementation of a part-whole activity which, at first sight, can be regarded as “non-complex”; however, the activity has a potential to teach important mathematical ideas, that are relevant in early childhood mathematics. The results show that although it was planned collectively, implemented several times, and reflected on in meetings, the same snake-game activity was enacted differently on the occasions observed. The variation theoretical analysis of nine teachers’ teaching with different groups of children made it possible to describe the various ways of enacting the part-whole activity. Even though the snake game was limited and simple, analysis of the activity allowed me to describe aspects that were focused on, variation and invariance being offered, and the different learning opportunities afforded. The activity became mathematically richer when the objects of learning were expanded and several aspects were thus opened up as dimensions of variation, and it became even richer when aspects related to commutativity were highlighted in the teaching.

The results of this study contribute with pedagogical knowledge about characteristics of teaching that foregrounds numbers’ part-whole relations. Young children’s developmental stages in whole number arithmetic learning are well documented (Fuson, 1992). It is, for instance, known that before entering primary school, many children have knowledge about the part-whole relations of numbers (Fischer, 1990; Hunting, 2003) and commutativity (Baroody, 1987; Canobi et al., 2002) in concrete situations. The literature also tells us what is significant in successful strategies for solving additive relations problems (Neuman, 1987; Steffe et al., 1988). However, this research base does not tell us so much about how teachers can specifically support children’s understanding of number relations. This study’s results show in detail how teachers, in their instructions, gestures, and ways of using resources, can promote children’s learning of structured part-whole relations.

By representing number with finger patterns and bead strings, the enactments observed in this study supported simultaneous discernment of parts and whole. When teachers directed children’s attention to the structure of finger patterns or organisation of the beads in two colours on the string, these representations also helped them see numbers as composite sets; the children were thereby offered an alternative to single-unit counting. The use of fingers has been highlighted as a potential way to represent numbers and number relations (Brissiaud, 1992; Neuman, 1987). In the current study, children were encouraged to use their fingers. The results show that representing numbers with finger patterns aided the children in modelling different part-whole relations of “5 – one hand” and “10 – two hands” and in experiencing numbers as structured compositions of parts and wholes. This demonstrates the power of using structured finger patterns as a tool for also solving addition and subtraction problems. Here it is important to clarify that finger representation is not a goal in itself. Some children were able to identify the missing part without representing the relation with finger patterns, but most children needed finger patterns to do so. The results suggest that the snake-game activity has the potential to support subitising (see, e.g., Clements, 1999) and to extend the subitising range by working in a limited number range. The structured finger patterns as well as the structured bead string—with 10 beads in two colours grouped in two sets of five—support the idea of “the undivided 5” and can make it easier to see quantities without counting them as single units. This was the case, for instance, in the enacted object of learning C, when the teacher offered an alternative to single counting units and emphasised the undivided 5 as a benchmark for determining collections numbering slightly above 5.

Repeated single-unit counting to determine the size of collections of items is well known (Baroody, 1987; Fuson, 1982), and teachers might be unfamiliar with possible alternatives. If no alternatives to counting single units are offered by teachers, the snake game might even reinforce counting one by one, and children might only experience numbers as countable items as was the case in enacted object of learning A. The current study, like the one conducted by Jung et al. (2013), suggests that there are alternatives to single unit counting that are important for pre-service and in-service preschool teachers to become familiar with so they can implement them in practice.

Providing one example of decomposing a whole number into two parts is not enough to foster the understanding that a number can be decomposed in different ways (Payne & Rathmell, 1975). In this study, the teachers presented several examples of hidden parts in a more or less randomly chosen order. Watson and Mason (2006) suggested that examples in a succession should be presented in a structured sequence in order to show systematicity. Thus, if the visible and hidden parts of the snake are presented in a structured sequence, it might provide children the opportunity to also see connections between different part-whole relations. Through choosing to show and hide appropriate numbers of beads on the snake, the teachers created systematic variation, and the enacted object of learning D thus afforded children the opportunity to perceive a commutative pattern. This understanding of the commutative principle has been shown to be important for developing arithmetic skills (Kilpatrick et al., 2001). The results of this study suggest two features that seem crucial for enabling learners to discern the commutative principle: Teachers’ use of systematically varied examples, and teachers’ directing learners’ attention to the interchangeability of the parts that compose the whole by comparing two examples.

Some limitations of this study need to be considered. Nine teachers’ enactments of the snake-game activity were analysed. It is possible that if other teachers or a greater number of teachers had conducted the activity, other ways of enacting it could have been identified. Another limitation may be that 5 and 10 were the only whole numbers emphasised in the snake-game activity. It would have been valuable, from a learning perspective, to conduct the snake game or alternative part-whole activities in combination with finger patterns for structuring part-whole relationships and to focus on other whole numbers (e.g., 7, 8 or 9). This could reveal whether structured finger patterns support children’s solving of problems such as $8-3$, where they need to understand that some fingers must be excluded (folded) when they show the number 8 with both hands.

Despite these limitations, this study contributes to the field of research on implementation of mathematical activities in preschool as well as to teachers’ professional development in early childhood mathematics teaching. It proposes that experiencing structured finger patterns can make visible the part-whole relationships of numbers and that whether children see quantities as composite sets of units depends on how the mathematical ideas are enacted by the teacher.

Acknowledgment

This work was supported by the Swedish Research Council under grant number 721-2014-1791.

Disclosure Statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by Swedish Research Council [grant number 721-2014-1791].

Notes

1 In this paper, the part-whole relationship of numbers concerns the additive relationship, not the multiplicative relationship.

2 Swedish preschool is part of the public education system and is voluntary. It is offered to children aged one to five years. The participating children in this study were attending their final year of preschool.

3 The FASETT project – The ability to discern the first ten numbers as a necessary ground for arithmetic skills.

4 Different versions of the snake resource are available in Swedish preschools.

5 A preliminary analysis was presented at the X conference in X, Sweden. X, (2018).

6 The four enacted objects of learning (labelled A-D) were given names in order to highlight their characteristics.