A graph-theoretic criterion for absolute irreducibility of integer-valued polynomials with square-free denominator

Abstract

An irreducible element of a commutative ring is absolutely irreducible if no power of it has more than one (essentially different) factorization into irreducibles. In the case of the ring $\text{Int}(D)=\{f\in K[x]|f(D)\subseteq D\},$ of integer-valued polynomials on a principal ideal domain D with quotient field K, we give an easy to verify graph-theoretic sufficient condition for an element to be absolutely irreducible and show a partial converse: the condition is necessary and sufficient for polynomials with square-free denominator.

Keywords and phrases:

• Factorization
• non-unique factorization
• irreducible elements
• absolutely irreducible elements
• atoms
• strong atoms
• atomic domains
• integer-valued polynomials
• simple graphs
• connected graphs

2010 Mathematics Subject Classification:

• 13A05
• 13B25
• 13F20
• 11R09
• 11C08
• 13P05

1. Introduction

An intriguing feature of non-unique factorization (of elements of an integral domain into irreducibles) is the existence of non-absolutely irreducible elements, that is, irreducible elements some of whose powers allow several essentially different factorizations into irreducibles [1, 6–8, 10].

For rings of integers in number fields, their existence actually characterizes non-unique factorization, as Chapman and Krause [4] have shown.

Here, we investigate absolutely and non-absolutely irreducible elements in the context of non-unique factorization into irreducibles in the ring of integer-valued polynomials on D $$\text{Int}(D)=\{f\in K[x\left]\right|f(D)\subseteq D\},$$ where D is a principal ideal domain and K its quotient field.

In an earlier paper [5, Remark 3.9] we already hinted at a graph-theoretic sufficient condition for $f\in \text{Int}(D)$ to be irreducible. We spell this out more fully in Theorem 1. This condition is not, however, necessary.

We formulate a similar graph-theoretic sufficient condition for $f\in \text{Int}(D)$ to be absolutely irreducible in Theorem 2, and show a partial converse. Namely, our criterion for absolute irreducibility is necessary and sufficient in the special case of polynomials with square-free denominator, cf. Theorem 3.

First, we recall some terminology. Let R be a commutative ring with identity.

1. $r\in R$ is called irreducible in R (or, an atom of R) if it is a non-zero non-unit that is not a product of two non-units of R.

2. A factorization (into irreducibles) of r in R is an expression (1) $$r=a_1\cdots a_n$$(1)

where $n\ge 1$ and a_i is irreducible in R for $1\le i\le n.$

1. $r,s\in R$ are associated in R if there exists a unit $u\in R$ such that r = us. We denote this by $r\sim s.$

2. Two factorizations into irreducibles of the same element, (2) $$r=a_1\cdots a_n=b_1\cdots b_m,$$(2)

are called essentially the same if n = m and, after a suitable re-indexing, $a_j\sim b_j$ for $1\le j\le m.$ Otherwise, the factorizations in (2(2) $$r=a_1\cdots a_n=b_1\cdots b_m,$$(2) ) are called essentially different.

Definition 1.1.

Let R be a commutative ring with identity. An irreducible element $c\in R$ is called absolutely irreducible (or, a strong atom), if for all natural numbers n, every factorization of cⁿ is essentially the same as $c^n=c\cdots c.$

Note the following fine distinction: an element of R that is called “not absolutely irreducible” might not be irreducible at all, whereas a “non-absolutely irreducible” element is assumed to be irreducible, but not absolutely irreducible.

We now concentrate on integer-valued polynomials over a principal ideal domain.

Recall that a polynomial in $D[x],$ where D is a principal ideal domain, is called primitive if the greatest common divisor of its coefficients is 1.

Definition 1.2.

Let D be a principal ideal domain with quotient field K, and $f\in K[x]$ a non-zero polynomial. We write f as $$f=\frac{a\prod _{i\in I}{g}_i}{b},$$ where $a,b\in D\setminus \left\{0\right\}$ with $\gcd (a,b)=1,$ I a finite (possibly empty) set, and each g_i primitive and irreducible in $D[x]$ and call this the standard form of f.

We refer to b as the denominator, to a as the constant factor, and to $a\prod _{i\in I}{g}_i$ as the numerator of f, keeping in mind that each of them is well-defined and unique only up to multiplication by units of D.

Definition 1.3.

For $f\in \text{Int}(D),$ the fixed divisor of f, denoted $\mathsf{d}(f),$ is the ideal of D generated by f(D).

An integer-valued polynomial $f\in \text{Int}(D)$ with $\mathsf{d}(f)=D$ is called image-primitive.

When D is a principal ideal domain, we may, by abuse of notation, write the generator for the ideal, as in $\mathsf{d}(f)=c$ meaning $\mathsf{d}(f)=cD.$

Remark 1.4.

Let D be a principal ideal domain with quotient field K, and $f\in K[x]$ written in standard form as in Definition 1.2. Then f is in $\text{Int}(D)$ if and only if b divides $\mathsf{d}(\prod _{i\in I}{g}_i).$

Remark 1.5.

Let D be a principal ideal domain with quotient field K. Then any non-constant irreducible element of $\text{Int}(D)$ is necessarily image-primitive. Otherwise, if a prime element $p\in D$ divides $\mathsf{d}(f),$ then $$f=p·\frac{f}{p}$$ is a non-trivial factorization of f.

Furthermore, $f\in K[x]\setminus \left\{0\right\}$ (written in standard form as in Definition 1.2) is an image-primitive element of $\text{Int}(D)$ if and only if (up to multiplication by units) a = 1 and $b=\mathsf{d}(\prod _{i\in I}{g}_i).$

Definition 1.6.

Let D be a principal ideal domain. For $f\in \text{Int}(D),$ and p a prime element in D, we let $${\mathsf{d}}_p(f)=v_p(\mathsf{d}(f))$$

Remark 1.7.

By the above definition, $$\mathsf{d}(f)=\prod _{p\in \mathbb{P}}{p}^{{\mathsf{d}}_p(f)}\hspace{1em}\text{and}\hspace{1em}{\mathsf{d}}_p(f)=\underset{c\in D}{\min }{v}_p(f(c))$$ where $\mathbb{P}$ is a set of representatives of the prime elements of D up to multiplication by units.

By the nature of the minimum function, the fixed divisor is not multiplicative: $${\mathsf{d}}_p(f)+{\mathsf{d}}_p(g)\le {\mathsf{d}}_p(fg),$$ but the inequality may be strict. Accordingly, $$\mathsf{d}(f)\mathsf{d}(g)|\mathsf{d}(fg),$$ but the division may be strict. Note, however, that $$\mathsf{d}(f^n)=\mathsf{d}{(f)}^n$$ for all $f\in \text{Int}(D)$ and $n\in \mathbb{N}.$

2. Graph-theoretic irreducibility criteria

We refer to, for instance, [2] for the graph theory terms we use in this section.

Definition 2.1.

Let D be a principal ideal domain, $I\ne \varnothing$ a finite set and for $i\in I,$ let $g_i\in D[x]$ be non-constant and primitive. Let $g(x)=\prod _{i\in I}{g}_i,$ and $p\in D$ a prime.

1. We say that g_i is essential for p among the g_j with $j\in I$ if $p|\mathsf{d}(g)$ and there exists a $w\in D$ such that $v_p(g_i(w))>0$ and $v_p(g_j(w))=0$ for all $j\in I\setminus \left\{i\right\}.$ Such a w is then called a witness for g_i being essential for p.

2. We say that g_i is quintessential for p among the g_j with $j\in I$ if $p|\mathsf{d}(g)$ and there exists $w\in D$ such that $v_p(g_i(w))=v_p(\mathsf{d}(g))$ and $v_p(g_j(w))=0$ for all $j\in I\setminus \left\{i\right\}.$ Such a w is called a witness for g_i being quintessential for p.

We will omit saying “among the g_j with $j\in I$” if the indexed set of polynomials is clear from the context.

Remark 2.2.

When we consider an indexed set of polynomials g_i with $i\in I,$ we are not, in general, requiring $g_i\ne g_j$ for $i\ne j.$ Note, however, that g_i being essential (among the g_j with $j\in I$) for some prime element $p\in D$ implies $g_i\cancel{\sim }{g}_j$ in $D[x]$ for all $j\in I\setminus \left\{i\right\}.$

Definition 2.3.

Let D be a principal ideal domain, $I\ne \varnothing$ a finite set and for each $i\in I,$ $g_i\in D[x]$ primitive and irreducible.

1. The essential graph of the indexed set of polynomials $(g_i|i\in I)$ is the simple undirected graph whose set of vertices is I, and in which (i, j) is an edge if and only if there exists a prime element p in D such that both g_i and g_j are essential for p among the g_k with $k\in I.$

2. The quintessential graph of the indexed set of polynomials $(g_i|i\in I)$ is the simple undirected graph whose set of vertices is I, and in which (i, j) is an edge if and only if there exists a prime element p in D such that both g_i and g_j are quintessential for p among the g_k with $k\in I.$

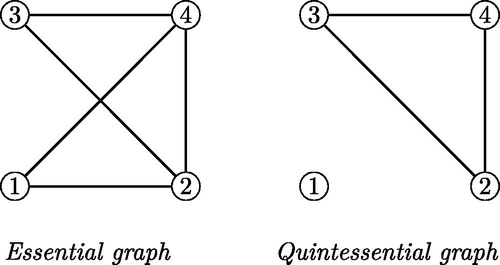
Example 2.4.

Let $I=\{1,2,3,4\}$ and for $i\in I,g_i\in \mathbb{Z}[x]$ as follows: $$g_1=x^3-19,\hspace{1em}{g}_2=x^2+9,\hspace{1em}{g}_3=x^2+1,\hspace{1em}{g}_4=x-5,$$

and set $$g=(x^3-19)(x^2+9)(x^2+1)(x-5).$$

A quick check shows that the fixed divisor of g is 15.

1. Taking w = 1, 2, 0, respectively, as witnesses, we see that $g_2,g_3,g_4$ are quintessential for 5. The polynomial g₁ is not essential for 5 because $v_5(g_1(a))>0$ only if $a\in 4+5\mathbb{Z}$ and for such a, also $v_5(g_2(a))>0.$

2. Taking w = 1, 0, 2 respectively, as witnesses, we see that $g_1,g_2,g_4$ are essential for 3. Only g₄ is quintessential for 3. The polynomial g₃ is not essential for 3.

Figure 1 shows the essential and quintessential graphs of $(g_1,g_2,g_3,g_4).$

Figure 1. Graphs for example 2.4.

Lemma 2.5.

Let D be a principal ideal domain and $f\in \text{Int}(D)$ a non-constant image-primitive integer-valued polynomial, written in standard form according to Definition 1.2 as $$f=\frac{\prod _{i\in I}{g}_i}{\prod _{p\in T}{p}^{e_p}},$$ where T is a finite set of pairwise non-associated primes of D, and let $n\in \mathbb{N}.$

Every $h\in \text{Int}(D)$ dividing fⁿ can be written as $$h(x)=\frac{\prod _{i\in I}{g}_i^{{\gamma }_i(h)}}{\prod _{p\in T}{p}^{{\beta }_p(h)}},$$ with ${\gamma }_i(h)\in {\mathbb{N}}_0$ for $i\in I$ and unique ${\beta }_p(h)\in {\mathbb{N}}_0$ for $p\in T$. Moreover, every such representation of h satisfies:

1. If $q\in T$ and $j\in I$ such that g_j is quintessential for q among the $i\in I$, then $${\beta }_q(h)=e_q{\gamma }_j(h).$$

2. In particular, whenever g_j and g_k are both quintessential for the same prime $q\in T$, then ${\gamma }_j(h)={\gamma }_k(h).$

Proof.

We know $\mathsf{d}(f^n)=\mathsf{d}{(f)}^n$ (cf. Remark 1.7). So, fⁿ is image-primitive, and, therefore, all polynomials in $\text{Int}(D)$ dividing fⁿ are image-primitive. Let $f^n=hk$ with $h,k\in \text{Int}(D).$ When h is written in standard form as in Definition 1.2, the fixed divisor of the numerator equals the denominator, and the constant factor is a unit. The same holds for k. This is so because h and k are image-primitive; see Remark 1.5.

Now let $q\in D$ be prime and $j\in I$ such that g_j is quintessential for q. Note that, by Remark 2.2 and unique factorization in $K[x],$ the exponent of g_j in the numerator of any factor of fⁿ is unique.

Writing $f^n=hk$ as $$\frac{\prod _{i\in I}{g}_i^n}{\prod _{p\in T}{p}^{n{e}_p}}=\frac{\prod _{i\in I}{g}_i^{{\gamma }_i(h)}}{\prod _{p\in T}{p}^{{\beta }_p(h)}}·\frac{\prod _{i\in I}{g}_i^{{\gamma }_i(k)}}{\prod _{p\in T}{p}^{{\beta }_p(k)}},$$ we observe the following equalities and inequalities of the exponents:

1. $n{e}_q={\beta }_q(h)+{\beta }_q(k)$

2. $n={\gamma }_j(h)+{\gamma }_j(k)$ and hence $n{e}_q=e_q{\gamma }_j(h)+e_q{\gamma }_j(k)$

3. $e_q{\gamma }_j(h)\ge {\beta }_q(h)$ and $e_q{\gamma }_j(k)\ge {\beta }_q(k).$

(i) follows from unique factorization in D.

(ii) follows from unique factorization in $K[x]$ and Remark 2.2.

To see (iii), consider a witness w for g_j being quintessential for q. Since f is image-primitive, $e_q=v_q(\mathsf{d}(\prod _{i\in I}{g}_i)),$ by Remark 1.5. From Definition 2.1 and Remark 1.4 we deduce $$e_q{\gamma }_j(h)=v_q(g_j(w)){\gamma }_j(h)=v_q(g_j^{{\gamma }_j(h)}(w))=v_q\left(\prod _{i\in I}{g}_i{(w)}^{{\gamma }_i(h)}\right)\ge {\beta }_q(h)$$

(and similarly for k instead of h).

Finally, (i)–(iii) together imply $e_q{\gamma }_j(h)={\beta }_q(h)$ and $e_q{\gamma }_j(k)={\beta }_q(k).$ □

Theorem 1.

Let D be a principal ideal domain with quotient field K. Let $f\in \text{Int}(D)$ be a non-constant image-primitive integer-valued polynomial, written in standard form as $f=g/b$ with $b\in D\setminus \left\{0\right\}$, and $g=\prod _{i\in I}{g}_i$, where each g_i is primitive and irreducible in $D[x].$

If the essential graph of $(g_i|i\in I)$ is connected, then f is irreducible in $\mathit{\text{Int}}(D).$

Proof.

If $\left|I\right|=1,$ then f is irreducible in $K[x],$ and, by being image-primitive, also irreducible in $\text{Int}(D).$

Now assume $\left|I\right|>1,$ and suppose f can be expressed as a product of m non-units $f=f_1\cdots f_m$ in $\text{Int}(D).$ Since $\mathsf{d}(f)=1,$ we see immediately that no f_i is a constant, and that $\mathsf{d}(f_k)=1$ for every $1\le k\le m.$

Write $f_k=h_k/b_k$ with $b_k\in D$ and h_k primitive in $D[x].$ Then $b=b_1\cdots b_m$ and there exists a partition of I into non-empty pairwise disjoint subsets $I={\cup }_{i=1}^m{I}_k,$ such that $h_k=\prod _{i\in I_k}{g}_i.$

Select $i\in I_1$ and $j\in I$ with $j\ne i.$ We show that also $j\in I_1.$ Let $i=i_0,i_1,\dots ,i_s=j$ be a path from i to j in the essential graph of $(g_i|i\in I).$ For some prime element p₀ in D dividing b, $g_{i_0}$ and $g_{i_1}$ are both essential for p₀. As g_i is essential for p₀, p₀ cannot divide any b_k with $k\ne 1$ and, hence, p₀ divides b₁. For any g_k essential for p₀ it follows that $k\in I_1,$ and, in particular, $i_1\in I_1.$ The same argument with reference to a prime p_k for which both $g_{i_k}$ and $g_{i_{k+1}}$ are essential, shows for any two adjacent vertices $i_k$ and $i_{k+1}$ in the path that they pertain to the same I_k, and, finally, that $j\in I_1.$

As $j\in I$ was arbitrary, $I_1=I$ and m = 1. □

Theorem 2.

Let D be a principal ideal domain and $f\in \text{Int}(D)$ be non-constant and image-primitive, written in standard form as $$f=\frac{\prod _{i\in I}{g}_i}{\prod _{p\in T}{p}^{e_p}},$$ where $I\ne \varnothing$ is a finite set and for $i\in I,$ $g_i\in D[x]$ is primitive and irreducible in $D[x].$

If the quintessential graph G of $(g_i|i\in I)$ is connected, then f is absolutely irreducible.

Proof.

Suppose $$f^n=\prod _{l=1}^s{f}_l,\hspace{1em}\text{where}\hspace{1em}{f}_l=\frac{\prod _{i\in I}{g}_i^{m_l(i)}}{\prod _{p\in T}{p}^{k_l(p)}}$$ and $0\le m_l(i)\le n,0\le k_l(p)\le n{e}_p$ and for all i, ${\sum }_{l=1}^s{m}_l(i)=n$ and for all p, ${\sum }_{l=1}^s{k}_l(p)=n{e}_p.$

Fix t with $1\le t\le s.$ We show that f_t is a power of f by showing that each g_i with $i\in I$ occurs in the numerator of f_t with the same exponent.

Let $i,j\in I.$ By the connectedness of the quintessential graph, there exists a sequence of indices in I, $i=i_0,i_1,i_2,\dots ,i_k=j$ and for each h, a prime element p_h in T such that $g_{i_h}$ and $g_{i_{h+1}}$ are both quintessential for p_h. By Lemma 2.5, $g_{i_h}$ and $g_{i_{h+1}}$ occur in the numerator of f_t with the same exponent. Eventually, g_i and g_j occur in the numerator of f_t with the same exponent, for arbitrary $i,j\in I.$ In an image-primitive polynomial, the numerator determines its denominator (as in Remark 1.5) and, hence, f_t is a power of f. Since f_t is irreducible, f_t = f. □

Example 2.6.

The binomial polynomial $$\left(\begin{array}{c}x\\ p\end{array}\right)=\frac{x(x-1)\cdots (x-p+1)}{p!}$$ where $p\in \mathbb{Z}$ is a prime, is absolutely irreducible in $\text{Int}(\mathbb{Z}),$ by Theorem 2.

The converse of Theorem 2 does not hold in general. For instance, the polynomial $$f=\frac{x^2(x^2+3)}{4}\in \text{Int}(\mathbb{Z})$$ is absolutely irreducible in $\text{Int}(\mathbb{Z})$ but the quintessential graph of $(x,x,x^2+3)$ is not connected.

There is, however, a converse to Theorem 2 in the special case where the denominator of f is square-free, as we now proceed to show, cf. Theorem 3.

3. Absolutely irreducible polynomials with square-free denominator

Let D be a principal ideal domain with quotient field K. When we talk of the denominator of a polynomial in $K[x],$ this refers to the standard form of a polynomial introduced in Definition 1.2.

Remark 3.1.

Let D be a principal ideal domain. Suppose the denominator of $f\in \text{Int}(D),$ written in standard form as in Definition 1.2, is square-free: $$f=\frac{\prod _{i\in I}{g}_i}{\prod _{p\in T}p}.$$

Then, if f is irreducible in $\text{Int}(D),$ it follows that each g_i is essential for some $p\in T.$ Otherwise, we can split off g_i. This further implies $g_i\cancel{\sim }{g}_j$ in $D[x]$ for $i\ne j,$ whenever $f\in \text{Int}(D)$ with square-free denominator is irreducible. A criterion for irreducibility of an integer-valued polynomial with square-free denominator has been given by Peruginelli [9].

Theorem 3.

Let D be a principal ideal domain and $f\in \text{Int}(D)$ be non-constant and image-primitive, with square-free denominator, written in standard form as $$f=\frac{\prod _{i\in I}{g}_i}{\prod _{p\in T}p},$$ where $I\ne \varnothing$ is a finite set and for $i\in I,$ $g_i\in D[x]$ is primitive and irreducible in $D[x].$

Let G be the quintessential graph of $(g_i|i\in I)$ as in Definition 2.3.

Then f is absolutely irreducible if and only if G is connected.

Proof.

In view of Theorem 2, we only need to show necessity. If $\left|I\right|=1,$ then G is connected. Now assume $\left|I\right|>1,$ and suppose G is not connected. We show that f is not absolutely irreducible. If f is not even irreducible, we are done. So suppose f is irreducible. This implies $g_i\cancel{\sim }{g}_j$ in $D[x]$ for $i\ne j,$ by Remark 3.1. Since G is not connected, I is a disjoint union of J₁ and J₂, both non-empty, such that there is no edge (i, j) with $i\in J_1$ and $j\in J_2.$

We express T as a disjoint union of T₁ and T₂ by assigning every $p\in T$ for which some $g_i\in J_1$ is quintessential to T₁, every $p\in T$ for which some $g_i\in J_2$ is quintessential to T₂, and assigning each $p\in T$ for which no g_i is quintessential to T₁ or T₂ arbitrarily. (It may happen that $T_1=\varnothing$ and $T_2=T$ or vice versa).

Then f ³ factors in $\text{Int}(D)$ as follows: $$f^3=\frac{{(\prod _{i\in J_1}{g}_i)}^2\prod _{j\in J_2}{g}_j}{{(\prod _{p\in T_1}p)}^2\prod _{q\in T_2}q}·\frac{{(\prod _{j\in J_2}{g}_j)}^2\prod _{i\in J_1}{g}_i}{{(\prod _{q\in T_2}q)}^2\prod _{p\in T_1}p}.$$

As $\text{Int}(D)$ is atomic (cf. [3]), each of the two factors above can further be factored into irreducibles. Since J₁ and J₂ are both non-empty and $g_i\cancel{\sim }{g}_j$ in $D[x]$ (and hence, $g_i\cancel{\sim }{g}_j$ in $K[x]$) for $i\ne j,$ it is clear that the resulting factorization of f³ into irreducibles is essentially different from $f·f·f.$ □

Remark 3.2.

Let D be a principal ideal domain. The proof of Theorem 3 shows that any non-absolutely irreducible element $f\in \text{Int}(D)$ with square-free denominator exhibits non-unique factorization of fⁿ already for n = 3.

If $f(x)=\prod _{i\in I}{g}_i(x)/p,$ where D is a principal ideal domain, p a prime of D and each $g_i\in D[x]$ primitive and irreducible in $D[x],$ then it is easy to see that f is an irreducible element of $\text{Int}(D)$ if and only if

1. $\mathsf{d}(\prod _{i\in I}{g}_i(x))=p$ and

2. each g_i is essential for p, that is, for each $i\in I$ there exists $w_i\in D$ such that $v_p(g_i(w_i))>0$ and $v_p(g_j(w_i))=0$ for all $j\in I\setminus \left\{i\right\}.$

An analogous statement relates absolutely irreducible integer-valued polynomials with prime denominator to quintessential irreducible factors of the numerator:

Corollary 3.3.

Let D be a principal ideal domain, $p\in D$ a prime, and $I\ne \varnothing$ a finite set. For $i\in I$, let $g_i\in D[x]$ be primitive and irreducible in $D[x]$. Let $$f(x)=\frac{\prod _{i\in I}{g}_i(x)}{p}.$$

Then f is an absolutely irreducible element of $\text{Int}(D)$ if and only if

1. $\mathsf{d}(\prod _{i\in I}{g}_i(x))=p$ and

2. each g_i is quintessential for p among the g_i with $i\in I$, that is, for each $i\in I$ there exists $w_i\in D$ such that $v_p(g_i(w_i))=1$ and $v_p(g_j(w_i))=0$ for all $j\in I\setminus \left\{i\right\}.$

Proof.

If $\mathsf{d}(\prod _{i\in I}{g}_i(x))=p,$ then $f\in \text{Int}(D)$ with $\mathsf{d}(f)=1,$ and Theorem 3 applies. If, on the other hand, f is in $\text{Int}(D)$ and is absolutely irreducible, then f is, in particular, irreducible and therefore $\mathsf{d}(f)=1,$ and, again, Theorem 3 applies. Now the statement follows from the fact that, whenever $\mathsf{d}(\prod _{i\in I}{g}_i(x))=p$ is prime, the quintessential graph of $(g_i|i\in I)$ is connected if and only if every g_i is quintessential for p. □

We conclude by an example of how to apply Theorem 3:

Example 3.4.

The following polynomial $f\in \text{Int}(\mathbb{Z})$ is irreducible, by Theorem 1; but not absolutely irreducible, by Theorem 3: $$f=\frac{(x^3-19)(x^2+9)(x^2+1)(x-5)}{15}$$

This is so because the essential graph of $(x^3-19,x^2+9,x^2+1,x-5)$ is connected, but the quintessential graph is not connected, see Example 2.4 and Figure 1.

Additional information

Funding

S. Frisch and S. Nakato are supported by the Austrian Science Fund (FWF): P 30934.