Centralisers of finite groups in locally finite simple groups

Abstract

We answer in the negative a question of Hartley about representations of finite groups, by constructing examples of finite simple groups with arbitrarily large representations whose endomorphism ring consists of just the scalars. We show as a consequence that there are finite simple groups of automorphisms of the locally finite simple group $SL(\infty ,{\mathbb{F}}_q)$ with trivial centralizer. The smallest of our examples is $A_6$ with $q=9$.

Keywords:

• Centralizer
• locally finite group
• representation theory

2020 Mathematics Subject Classification:

• Primary: 20F50
• Secondary: 20C20
• 16G20

1 Introduction

A group is said to be locally finite if every finitely generated subgroup is finite. A group is said to be linear if it has a faithful representation by matrices over a field.

In the introduction to [7], and Section 3 of [8], Brian Hartley mentioned the following problem.

Question 1.1.

Is it the case that in a nonlinear locally finite simple group, the centralizer of every finite subgroup is infinite?

Papers that have investigated Hartley’s Question 1.1 include Brescia and Russo [5], Ersoy and Kuzucuoğlu [6], Hartley and Kuzucuoğlu [10], Kuzucuoğlu [12–15]. In particular, it is shown in [10] that if the finite subgroup is cyclic then the answer is “yes.”

A closely related problem is Problem 3.15 of Hartley [9], which asks the following (with notation slightly altered to align with ours).

Question 1.2.

Let H be a finite simple group, or perhaps a finite group such that $O_p(H)=1$. Suppose that $H⩽\mathit{PSL}(n,{\mathbb{F}}_q)=K$, where q is a power of p and $C_K(H)=1$. Does it follow that n is bounded in terms of |H|? We are particularly interested in the case when H is also a projective special linear group over ${\mathbb{F}}_q$. What about the algebraic group situation, that is, say, $H\cong PS{L}_m({\overline{\mathbb{F}}}_p)$, $K\cong PS{L}_n({\overline{\mathbb{F}}}_p)$, with $C_K(H)=1$? Does it follow that n is bounded in terms of m?

An example of a non-linear simple locally finite group is $SL(\infty ,{\mathbb{F}}_q)$, the union of the groups $SL(n,{\mathbb{F}}_q)$ under the natural inclusions $SL(n,{\mathbb{F}}_q)\to SL(n+1,{\mathbb{F}}_q)$ fixing the new basis vector. It is simple because (except for $n=2$, $q=2$ or 3) every proper normal subgroup of $SL(n,{\mathbb{F}}_q)$ consists of scalar multiples of the identity, and are no longer scalar in $SL(n+1,{\mathbb{F}}_q)$ unless trivial. In this group, the centralizer of a finite subgroup is obviously infinite.

We do not succeed in answering Question 1.1, but we answer a closely related question with the following theorem.

Theorem 1.3.

Let $K_q$ be the locally finite group $SL(\infty ,{\mathbb{F}}_q)$. For every prime p, there exists a power q of p and a finite simple group of automorphisms $H⩽\mathsf{Aut}(K_q)$ such that the centralizer of H in $K_q$ is trivial.

We prove Theorem 1.3 as a consequence of the following theorem, together with some information about extensions between simple modules. This theorem gives a negative answer to Question 1.2, as is shown in Section 3. We restrict our attention to finite groups and linear algebraic groups in order to address Hartley’s question, but it should be clear from the methods that other situations are also covered.

Theorem 1.4.

Let k be a field of characteristic p. Let H be a finite group, or a linear algebraic group over k. Suppose that

1. H has non-isomorphic simple modules $S\cancel{\cong }T$ over k such that $\mathsf{En}{\mathsf{d}}_H(S)\cong \mathsf{En}{\mathsf{d}}_H(T)\cong k$, and ${\dim }_k\mathsf{Ex}{\mathsf{t}}_H^1(S,T)⩾3$, or

2. H has non-isomorphic simple modules R, S and T with $\mathsf{En}{\mathsf{d}}_H(R)\cong \mathsf{En}{\mathsf{d}}_H(S)\cong \mathsf{En}{\mathsf{d}}_H(T)\cong k$, ${\dim }_k\mathsf{Ex}{\mathsf{t}}_H^1(R,T)⩾1$ and ${\dim }_k\mathsf{Ex}{\mathsf{t}}_H^1(S,T)⩾2$, or

3. H has non-isomorphic simple modules R, $S_1,\dots ,S_r$, and $T_1,\dots ,T_r$ with endomorphism rings isomorphic to k, and such that the groups $\mathsf{Ex}{\mathsf{t}}_H^1(R,T_1)$, $\mathsf{Ex}{\mathsf{t}}_H^1(S_i,T_i)$, $\mathsf{Ex}{\mathsf{t}}_H^1(S_{i+1},T_i)$ and $\mathsf{Ex}{\mathsf{t}}_H^1(S_1,T_r)$ are all non-trivial.

Then there exists a sequence of indecomposable H-modules $M_m$ over k and embeddings $M_m\to M_{m+1}$ such that

1. The radical (i.e., the intersection of the maximal submodules) $\mathsf{Rad}(M_m)$ is isomorphic to a direct sum of m copies of T (respectively of a direct sum of the $T_i$ in case (iii)).

2. $M_m/\mathsf{Rad}(M_m)$ is isomorphic to a direct sum of m copies of S in case (i) and a direct sum of one copy of R and $m-1$ copies of S in case (ii).

3. The endomorphism ring $\mathsf{En}{\mathsf{d}}_H(M_m)$ consists just of scalar multiples of the identity map.

The three cases of Theorem 1.4 are proved in Sections 2, 4, and 6, and examples illustrating these three cases are given in Sections 3, 5, and 7. Theorem 1.3 is proved in Section 8.

2 Three dimensional $\mathsf{Ex}{\mathsf{t}}^1$ groups Three dimensional $\mathsf{Ex}{\mathsf{t}}^1$ groups

In this section, we deal with case (i) of Theorem 1.4. Let k be a field, and let Q be the quiver with two vertices and three arrows given by the following diagram.

A representation of Q over k consists of two k-vector spaces V and W together with three k-linear maps $X,Y,Z:V\to W$. We are interested in properties of a particular family of representations ${\mathsf{M}}_m$ of kQ for $m⩾1$ and embeddings ${\mathsf{M}}_m\to {\mathsf{M}}_{m+1}$.

For the representation ${\mathsf{M}}_m$, the spaces V and W have dimension m, and bases $v_1,\dots ,v_m$ and $w_1,\dots ,w_m$. The actions of X, Y, and Z on $v_i$ are given as follows.(2.1) $$\begin{array}{cccc}& X& Y& Z\\ i=1& w_1& 0& 0\\ 2\mathit{\text{⩽i⩽m}}& 0& w_i& w_{i-1}\\ & & & \end{array}$$(2.1)

This can be pictured as follows.

Here, the actions of X, Y, and Z are described by the single, double and triple downward edges respectively. The embedding ${\mathsf{M}}_m\to {\mathsf{M}}_{m+1}$ takes the basis vectors $v_i$ and $w_i$ of ${\mathsf{M}}_m$ to the basis elements of ${\mathsf{M}}_{m+1}$ with the same names.

Theorem 2.2.

The endomorphism ring of the kQ-module ${\mathsf{M}}_m$ is equal to k, acting as scalar multiples of the identity map.

Proof.

We have direct sum decompositions $V=\mathsf{Ker}(Y)\oplus \mathsf{Ker}(X)$ and $W=\mathsf{Im}(X)\oplus \mathsf{Im}(Y)$. Here, $\mathsf{Ker}(Y)$ is spanned by $v_1$ and $\mathsf{Ker}(X)$ is spanned by $v_2,\dots ,v_m$. Similarly, $\mathsf{Im}(X)$ is spanned by $w_1$ and $\mathsf{Im}(Y)$ is spanned by $w_2,\dots ,w_m$.

If $\alpha$ is an endomorphism of ${\mathsf{M}}_m$ then $X\alpha (v_1)=\alpha (X{v}_1)=\alpha (w_1)$, so $\alpha (w_1)$ is in the image of X. It is therefore a multiple of $w_1$. Subtracting off a multiple of the identity map, we can suppose that $\alpha (w_1)=0$. Then $\alpha (v_1)$ is in $\mathsf{Ker}(X)\cap \mathsf{Ker}(Y)$ and is hence also zero.

Suppose by induction on j that we have shown that we have $\alpha (v_i)=0$ and $\alpha (w_i)=0$ for $1⩽i<j$. Then $Y\alpha (v_j)=\alpha (Y{v}_j)=\alpha (w_{j-1})=0$ and $X\alpha (v_j)=\alpha (X{v}_j)=0$, so $\alpha (v_j)\in \mathsf{Ker}(Y)\cap \mathsf{Ker}(X)$ and hence $\alpha (v_j)=0$. Then $\alpha (w_j)=\alpha (Y{v}_j)=Y\alpha (v_j)=0$. It follows by induction that for $1\mathit{\text{⩽j⩽m}}$ we have $\alpha (v_j)=0$ and $\alpha (w_j)=0$, and hence $\alpha =0$. ▪

Proof of Theorem 1.4

in case (i).

Suppose that k is a field of characteristic p and H is a finite group, or a reductive algebraic group, with non-isomorphic simple (left) modules S and T satisfying $\mathsf{En}{\mathsf{d}}_H(S)=\mathsf{En}{\mathsf{d}}_H(T)=k$ and ${\dim }_k\mathsf{Ex}{\mathsf{t}}_H^1(S,T)⩾3$. Then there is an H-module $\Delta$ satisfying $\mathsf{Rad}(\Delta )\cong T\oplus T\oplus T$ and $\Delta /\mathsf{Rad}(\Delta )\cong S$. Setting $B=\Delta \oplus T$, the algebra $\mathsf{En}{\mathsf{d}}_H{(B)}^{\mathsf{op}}$ is isomorphic to the quiver algebra kQ described above. So B has a right action of kQ commuting with the left action of H. As a right kQ-module, B is a projective generator for $\mathsf{mod}$-kQ. Thus B is a H-kQ-bimodule with the property that the functor $B{\otimes }_{kQ}-:kQ$-$\mathsf{mod}\to H$-$\mathsf{mod}$ is fully faithful and exact. It sends the simple kQ-modules to S and T and the three arrows in $J(kQ)$ to three linearly independent elements of $\mathsf{Ex}{\mathsf{t}}_H^1(S,T)$. So $M_m=B{\otimes }_{kQ}{\mathsf{M}}_m$ is a module of the following form:where the three types of lines represent the three linearly independent extension classes chosen in the construction of U. By Theorem 2.2, we have $\mathsf{En}{\mathsf{d}}_H(M_m)\cong k$ and $M_m$ embeds in $M_{m+1}$. Setting $d={\dim }_{k}S+{\dim }_{k}T$, we have ${\dim }_k{M}_m=md$. This completes the proof of Theorem 1.4. ▪

3 Examples involving three dimensional $\mathsf{Ex}{\mathsf{t}}^1$ groups Examples involving three dimensional $\mathsf{Ex}{\mathsf{t}}^1$ groups

In this section, we indicate that there are many examples of absolutely irreducible modules S and T over reductive algebraic groups and over finite simple groups H, such that $\mathsf{Ex}{\mathsf{t}}_{kH}^1(S,T)$ is at least three dimensional, and sometimes much larger. The first such examples were discovered by Scott, and already, feeding these into Case (i) of Theorem 1.4 gives negative answers to both parts of Question 1.2.

Theorem 3.1.

Suppose that $n⩾6$. Then for all large enough primes p, there exist irreducible $\mathit{PSL}(n,{\overline{\mathbb{F}}}_p)$-modules S and T such that $${\dim }_{{\overline{\mathbb{F}}}_p}\mathsf{Ex}{\mathsf{t}}_{\mathit{PSL}(n,{\overline{\mathbb{F}}}_p)}^1(S,T)⩾4.$$

And for all large enough powers q of p, the restrictions of S and T are absolutely irreducible ${\mathbb{F}}_{q}PSL(n,{\mathbb{F}}_q)$-modules such that $${\dim }_{{\mathbb{F}}_q}\mathsf{Ex}{\mathsf{t}}_{{\mathbb{F}}_{q}PSL(n,{\mathbb{F}}_q)}^1(S,T)⩾4.$$

Proof.

This is proved in Section 2 of Scott [19], by computing coefficients of Kazhdan–Lusztig polynomials. The stabilisation of the dimensions of $\mathsf{Ex}{\mathsf{t}}^1$ for the finite groups to the dimension for the algebraic group comes from Theorem 2.8 of Andersen [1], see Remark (iii) at the end of that section. ▪

Remark 3.2.

It is shown in Section 4 of Lübeck [17] that for all large enough primes, taking S to be the trivial module ${\overline{\mathbb{F}}}_p$, there are simple modules T for $\mathit{PSL}(n,{\overline{\mathbb{F}}}_p)$ with$$H^1(\mathit{PSL}(n,{\overline{\mathbb{F}}}_p),T)\cong \mathsf{Ex}{\mathsf{t}}_{\mathit{PSL}(n,{\overline{\mathbb{F}}}_p)}^1({\overline{\mathbb{F}}}_p,T)$$having the following dimensions,$$\begin{array}{ccccc}n& 6& 7& 8& 9\\ {\dim }_{{\mathbb{F}}_q}{H}^1(\mathit{PSL}(n,{\overline{\mathbb{F}}}_p),T)& 3& 16& 469& 36672\\ & & & & \end{array}$$ and then for large enough powers q of p, the restriction of these T are irreducible modules for ${\mathbb{F}}_{q}PSL(n,{\mathbb{F}}_q)$ with these dimensions for $H^1(\mathit{PSL}(n,{\mathbb{F}}_q),T)$. It is not known whether these dimensions are unbounded for larger values of n, though that seems very likely. In the same paper, Lübeck proves similar results for the other classical groups of types $B_n$, $C_n$, and $D_n$, as well as groups of types $F_4$ and $E_6$. These groups could therefore also be used equally well as examples in Theorem 1.3. There are also cross characteristic examples of large dimensional $\mathsf{Ex}{\mathsf{t}}^1$ for simple modules over groups of Lie type, but the Lie rank in these cases needs to be a lot larger.

The problem with the theorems above is that the phrase “large enough” is difficult to quantify. Some more explicit examples of three dimensional $H^1(H,T)$ for T an absolutely irreducible module for a finite simple group H can be found in Bray and Wilson [4], for the group $\mathit{PSU}(4,{\mathbb{F}}_3)$ over ${\mathbb{F}}_3$ with ${\dim }_{{\mathbb{F}}_3}T=19$ (easily verified with Magma [3]), and for the group ${}^2{E}_6({\mathbb{F}}_2)$ over ${\mathbb{F}}_2$ with ${\dim }_{{\mathbb{F}}_2}T=1702$ (not so easily verified).

4 Two dimensional $\mathsf{Ex}{\mathsf{t}}^1$ groups Two dimensional $\mathsf{Ex}{\mathsf{t}}^1$ groups

In this section, we deal with case (ii) of Theorem 1.4. The proof is very much like that of case (i). We begin with the quiver Q with three vertices and three arrows as follows.

A representation of kQ over a field k consists of three vector spaces U, V, and W together with three k-linear maps

For the kQ-module ${\mathsf{M}}_m$, U is spanned by $v_1$, V is spanned by $v_2,\dots ,v_m$, and W is spanned by $w_1,\dots ,w_m$. The actions of X, Y, and Z are exactly the same as in Table (2.1).

Theorem 4.1.

The endomorphism ring of the kQ-module ${\mathsf{M}}_m$ is equal to k, acting as scalar multiples of the identity map.

Proof.

The proof is the same as for Theorem 2.2. ▪

Proof of Theorem 1.4

in case (ii).

Suppose that k is a field of characteristic p, and let H be a finite group with non-isomorphic simple modules R, S and T with $\mathsf{En}{\mathsf{d}}_{kH}(R)=\mathsf{En}{\mathsf{d}}_{kH}(S)=\mathsf{En}{\mathsf{d}}_{kH}(T)=k$, ${\dim }_k\mathsf{Ex}{\mathsf{t}}_{kH}^1(R,T)⩾1$, and ${\dim }_k\mathsf{Ex}{\mathsf{t}}_{kH}^1(S,T)⩾2$. Then there are kH-modules ${\Delta }_1$ and ${\Delta }_2$ with$$\mathsf{Rad}({\Delta }_1)\cong T,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\Delta }_1/\mathsf{Rad}({\Delta }_1)\cong R,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathsf{Rad}({\Delta }_2)\cong T\oplus T,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\Delta }_2/\mathsf{Rad}({\Delta }_2)\cong S.$$

Setting $B={\Delta }_1\oplus {\Delta }_2\oplus T$, the algebra $\mathsf{En}{\mathsf{d}}_{kH}{(B)}^{\mathsf{op}}$ is isomorphic to kQ. This makes B a kH-kQ-bimodule with the property that as a right kQ-module it is a projective generator for $\mathsf{mod}$-kQ. The functor $B{\otimes }_{kQ}-$ is fully faithful and exact. It sends the three simple kQ-modules to R, S and T. So this time, $M_m=B{\otimes }_{kQ}{\mathsf{M}}_m$ is a module of the following form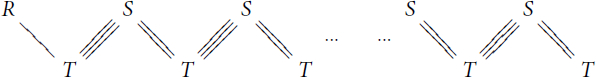whose endomorphism ring is k, acting by scalar multiples of the identity. ▪

5 Examples involving two dimensional $\mathsf{Ex}{\mathsf{t}}^1$ groups Examples involving two dimensional $\mathsf{Ex}{\mathsf{t}}^1$ groups

In this section, we give examples of finite simple groups H and simple modules R, S, and T satisfying the hypotheses of Case (ii) of Theorem 1.4.

Example 5.1.

Let H be the group $\mathit{PSL}(2,q)$ with $q=p^2$, p odd, and let $k={\mathbb{F}}_q$. Then by Corollary 4.5 of Andersen, Jørgensen and Landrock, there are exactly two simple modules S and T, of dimensions ${(\frac{p-1}{2})}^2$ and ${(\frac{p+1}{2})}^2$, such that $\mathsf{Ex}{\mathsf{t}}_{kH}^1(S,T)$ and $\mathsf{Ex}{\mathsf{t}}_{kH}^1(T,S)$ are two dimensional. All the other $\mathsf{Ex}{\mathsf{t}}^1$ groups between simple kH-modules are zero or one dimensional. In fact, the entire quiver with relations in this example may be found in Koshita [11]. Since S and T are in the principal block, and are not the only simples in the principal block, we can choose a simple module R not isomorphic to S or T, so that $\mathsf{Ex}{\mathsf{t}}_{kH}^1(R,T)⩾1$. For example, if $p=3$ then $\mathit{PSL}(2,9)\cong A_6$ has simples of dimensions 3, 1, and 4 for R, S, and T.

Example 5.2.

Another example is the sporadic group $M_{12}$ over ${\mathbb{F}}_2$. There are three simple modules R, S, and T in the principal block of ${\mathbb{F}}_2{M}_{12}$, of dimensions 44, 1, and 10. We have ${\dim }_{{\mathbb{F}}_2}\mathsf{Ex}{\mathsf{t}}_{{\mathbb{F}}_2{M}_{12}}^1(R,T)=1$ and ${\dim }_{{\mathbb{F}}_2}\mathsf{Ex}{\mathsf{t}}_{{\mathbb{F}}_2{M}_{12}}^1(S,T)=2$, see Schneider [18].

Example 5.3.

The following examples were computed using Magma [3]. For the group $\mathit{PSL}(3,{\mathbb{F}}_4)$ over ${\mathbb{F}}_4$, we can take for R, S, and T simple modules of dimensions 8, 9, and 1. For the group $\mathit{PSL}(4,{\mathbb{F}}_3)$ over ${\mathbb{F}}_3$, we can take for R, S, and T simple modules of dimensions 19, 1, and 44. For the Higman–Sims group HS over ${\mathbb{F}}_2$, we can take for R, S, and T the simple modules of dimensions 56, 20, and 1.

6 One dimensional $\mathsf{Ex}{\mathsf{t}}^1$ groups One dimensional $\mathsf{Ex}{\mathsf{t}}^1$ groups

In some circumstances, our method can be modified to deal with groups where all $\mathsf{Ex}{\mathsf{t}}^1$ groups between simple modules have dimension zero or one. This technique works whenever there is an even length cycle in the $\mathsf{Ex}{\mathsf{t}}^1$ quiver with alternating directions, and with some other arrow head meeting two of its arrow heads:

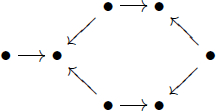
The method described in Section 4 is a degenerate case of this with a cycle of length two. This will lead to Case (iii) of Theorem 1.4.

Let Q be the quiver above, with even cycle length $2r⩾4$. Then a representation of Q over k consists of vector spaces U, $V_1,\dots ,V_r$ and $W_1,\dots ,W_r$ together with k-linear maps $X:U\to W_1$, $Y_i:V_i\to W_i$, $Z_{i+1}:V_{i+1}\to W_i$ and $Z_1:V_1\to W_r$. The case $r=3$ is illustrated as follows.

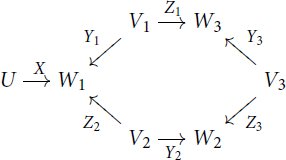
The module ${\mathsf{M}}_m$ has basis vectors $v_1,\dots ,v_m$ and $w_1,\dots ,w_m$. The space U is spanned by $v_1$, $V_i$ is spanned by the $v_j$ with $1<j\equiv i\hspace{1em}(\mathrm{mod}r)$, and $W_i$ is spanned by the $w_j$ with $1⩽j\equiv i\hspace{1em}(\mathrm{mod}r)$. The actions of the arrows are as in Table 2.1, with all $Y_i$ acting like Y and all $Z_i$ acting like Z.

Theorem 6.1.

The endomorphism ring of the kQ-module ${\mathsf{M}}_m$ is equal to k, acting as scalar multiples of the identity map.

Proof.

The proof is the same as for Theorem 2.2. ▪

Proof of Theorem 1.4

in case (iii).

We have kH-modules $\Delta ,{\Delta }_1,\dots ,{\Delta }_r$ with$$\mathsf{Rad}(\Delta )\cong T_1,\Delta /\mathsf{Rad}(\Delta )\cong R,\mathsf{Rad}({\Delta }_i)\cong T_i\oplus T_{i-1}(\text{or }{T}_1\oplus T_r\text{ if }i=1),{\Delta }_i/\mathsf{Rad}({\Delta }_i)\cong S_i.$$

The kH-module B is $\Delta \oplus {\oplus }_{i=1}^r{\Delta }_i\oplus {\oplus }_{i=1}^r{T}_i$, and $\mathsf{En}{\mathsf{d}}_{kH}(B)\cong kQ$. This makes B a kH-kQ-bimodule with the property that as a right kQ-module it is a projective generator for $\mathsf{mod}$-kQ. The functor $B{\otimes }_{kQ}-$ is fully faithful and exact. It sends the simple kQ-modules to the corresponding simple kH-modules. So this time, $M_m=B{\otimes }_{kQ}{\mathsf{M}}_m$ is a module of the following form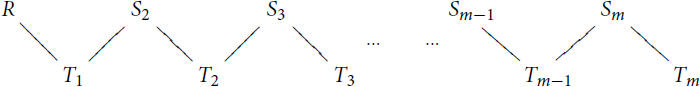where the indices are taken modulo r. ▪

7 Examples involving one dimensional $\mathsf{Ex}{\mathsf{t}}^1$ groups Examples involving one dimensional $\mathsf{Ex}{\mathsf{t}}^1$ groups

In this section, we give examples satisfying Case (iii) of Theorem 1.4.

Example 7.1.

The $\mathsf{Ex}{\mathsf{t}}^1$ quiver of the Higman–Sims group HS over a finite splitting field k of characteristic three is as follows.

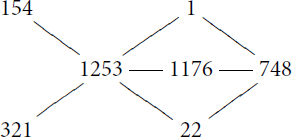
This information comes from Section 2 of Waki [20]. The numbers indicate the dimensions of the corresponding simple modules, and each edge denotes a single arrow in each direction. Choosing the 4-cycle $1\to 1253\leftarrow 22\to 748\leftarrow 1$ and incoming arrow $154\to 1253$, the modules $M_m$ take the following form.

Example 7.2.

Landrock and Michler [16] showed that the $\mathsf{Ex}{\mathsf{t}}^1$ quiver of the principal block of the sporadic Janko group $J_1$ over the splitting field ${\mathbb{F}}_4$ is as follows.

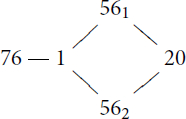
So we can take the 4-cycle ${56}_2\to 1\leftarrow {56}_1\to 20\leftarrow 1$ and incoming arrow $76\to 1$.

Example 7.3.

For $H=\mathit{PSL}(4,{\mathbb{F}}_2)$ and $k={\mathbb{F}}_2$, the $\mathsf{Ex}{\mathsf{t}}^1$ quiver was computed in Benson [2] to be as follows.

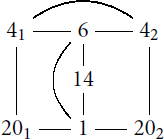
So for example we can take a 4-cycle $1\to 6\leftarrow 4_1\to {20}_1\leftarrow 1$ and incoming arrow $14\to 6$.

Example 7.4.

Computations using Magma [3] exhibit further examples. For the group $H=\mathit{PSL}(3,{\mathbb{F}}_5)$ and $k={\mathbb{F}}_5$, all the $\mathsf{Ex}{\mathsf{t}}^1$ groups are zero or one dimensional, but the $\mathsf{Ex}{\mathsf{t}}^1$ quiver has a 4-cycle of the form $19\to 6\leftarrow 18\to 8\leftarrow 19$ and an incoming arrow $35\to 6$.

8 The construction

In this section, we show how to pass from the constructions of Sections 2, 4, and 6 and groups satisfying the hypotheses of Theorem 1.4 to examples proving Theorem 1.3. For convenience, we assume that H is a finite simple group, though this could probably be weakened somewhat.

Let k and Q be as in Section 2, 4, or 6. We define the kQ-module ${\mathsf{M}}_{\infty }$ to be the colimit of the sequence of modules$${\mathsf{M}}_2\to {\mathsf{M}}_3\to {\mathsf{M}}_4\to \cdots .$$

This has a basis consisting of the $v_i$ and $w_i$ with $i⩾1$. Then there are submodules ${\mathsf{M}}_m^{\prime }$ of ${\mathsf{M}}_{\infty }$ such that ${\mathsf{M}}_m\cap {\mathsf{M}}_m^{\prime }=0$, and ${\mathsf{M}}_{\infty }/({\mathsf{M}}_m+{\mathsf{M}}_m^{\prime })$ is one dimensional, spanned by the image of $v_{i+1}$. Namely, we take ${\mathsf{M}}_m^{\prime }$ to be the submodule spanned by the basis vectors $v_i$ with $i⩾m+2$ and $w_i$ with $i⩾m+1$.

Let $M_{\infty }$ and $M_m^{\prime }$ be the kH-modules defined as the images of ${\mathsf{M}}_{\infty }$ and ${\mathsf{M}}_m^{\prime }$ under $B{\otimes }_{kQ}-$. Thus $M_{\infty }$ is the colimit of the sequence of modules$$M_2\to M_3\to M_4\to \cdots .$$

The submodules $M_m^{\prime }$ of $M_{\infty }$ satisfy $M_m\cap M_m^{\prime }=0$ and $M_{\infty }/(M_m+M_m^{\prime })\cong S$.

We define $G_m$ to be the group consisting of the vector space automorphisms $\alpha$ of $M_{\infty }$ such that $\alpha$ preserves and acts with determinant one on $M_m$, and there exists $h\in H$ such that $\alpha$ acts in the same way as h on both $M_{\infty }/M_m$ and $M_m^{\prime }$. It follows from these conditions that $\alpha (M_i)\subseteq M_i$ for all $i⩾m$. Then since $M_m\subseteq M_{m+1}$ and $M_{m+1}^{\prime }\subseteq M_m^{\prime }$, we have $G_m⩽G_{m+1}$. The action of H on $M_{\infty }$ gives an inclusion $i:H\to G_m$ for each m, compatible with these inclusions.

We have group homomorphisms $G_m\to H$ and $G_m\to SL(M_{m+1})$ given by the actions on $M_m^{\prime }$ and on $M_{m+1}$. Since $M_m^{\prime }$ and $M_{m+1}$ span $M_{\infty }$, the intersection of the kernels of the actions on these spaces is trivial, so we obtain an injective homomorphism$$G_m\to H\times SL(M_{m+1}).$$

This is not surjective, because the image of $G_m$ in $SL(M_{m+1})$ stabilises $M_m$ setwise; but it properly contains $SL(M_m)$. However, the image contains $H\times 1$, and is therefore the direct product of H and the image in $SL(M_{m+1})$. The subgroup mapping to $H\times 1$ consists of elements acting as $h\in H$ on $M_m^{\prime }$ and as the identity of $M_{\infty }/M_m^{\prime }$. This subgroup depends on m, and is not the same as the image of $i:H\to G_m$. Indeed, the composite $H\stackrel{i}{\to }{G}_m\to SL(M_{m+1})$ gives the action of H on the module $M_{m+1}$.

Lemma 8.1.

The centralizer of the image of $i:H\to G_m$ is trivial.

Proof.

Let z be an element of $C_{G_m}(i(H))$. Then z commutes with the action of H on $M_{\infty }$, and so z acts as a scalar multiple of the identity. But then z also acts on $M_{\infty }/M_m$ as a multiple of the identity. The action of $G_m$ on $M_{\infty }/M_m$ factors through $G_m\to H$, and $Z(H)$ is trivial, so $z=1$. ▪

We define $G_{\infty }$ to be the colimit of the inclusions$$G_2\to G_3\to G_4\to \cdots .$$

By Theorem 1.4 (3), we have $C_{G_m}(H)\subseteq Z(G_m)=1$ and $C_{G_{\infty }}(H)\subseteq Z(G_{\infty })=1$.

Theorem 8.2.

The group $G_{\infty }$ is isomorphic to a semidirect product $SL(\infty ,k)⋊H$.

Proof.

By the definition of $G_m$, there is a homomorphism $G_m\to H$, taking an element $\alpha$ to the element $h\in H$ that acts on $M_{\infty }/M_m$ and $M_m^{\prime }$ in the same way as $\alpha$. The composite $H\stackrel{i}{\to }{G}_m\to H$ is the identity. These homomorphisms are compatible with the inclusions $G_m\to G_{m+1}$, and therefore describe a homomorphism $G_{\infty }\to H$ with kernel $SL(\infty ,k)$a normal complement to the inclusion $i:H\to G_{\infty }$. ▪

Theorem 8.3.

Given a finite simple group H satisfying condition (i), (ii) or (iii) of Theorem 1.4, there is an action of H on $SL(\infty ,k)$ with trivial centralizer.

Proof.

This follows from Theorem 8.2 and Lemma 8.1. ▪

Proof of Theorem 1.3.

We set $k={\mathbb{F}}_q$ in Theorem 8.3. For p odd, we can use Example 5.1, and for $p=2$ we can use Example 5.2 for the choice of H; there are, of course, many other possible choices. ▪

Acknowledgments

I would like to thank Alexandre Zalesskii for introducing me to these problems at breakfast at the Møller Institute in Cambridge. This was while attending the post Covid-19 resumption of the programme ‘Groups, representations and applications: new perspectives’ in 2022, at the Isaac Newton Institute, supported by EPSRC grant EP/R014604/1. My thanks also go to the Isaac Newton Institute for their support and hospitality.