Arithmetic equivalence under isoclinism

Abstract

Two algebraic number fields are called arithmetically equivalent if the Dedekind zeta functions of the fields coincide. We show that if a G-extension contains non-conjugate arithmetically equivalent fields and there is an injection from G to another group H inducing an isoclinism between G and H, then there are non-conjugate arithmetically equivalent fields inside an H-extension.

KEYWORDS:

• Arithmetically equivalent fields
• Dedekind zeta function
• Gassmann equivalence
• isoclinism

2020 MATHEMATICS SUBJECT CLASSIFICATION:

• 11R42
• 20D60
• 20E45

1 Main theorem

In our previous paper [5], we considered coincidence of Hecke L-functions of abelian extensions of several different fields and observed that the coincidence is closely related to the isoclinism class of certain Galois groups associated to the L-functions. The aim of this paper is to study the relation between coincidence of Dedekind zeta functions and isoclinism.

Two number fields are called arithmetically equivalent if the Dedekind zeta functions of the fields coincide. If two fields are conjugate, then their Dedekind zeta functions coincide obviously and thus, non-conjugate arithmetically equivalent fields are of interest. Non-conjugate arithmetically equivalent fields still share many arithmetic invariants such as the discriminant, the signature, the Galois closure and so on.

Let K₁ and K₂ be number fields inside a Galois extension L over $\mathbb{Q}$ with Galois group G. Such a Galois extension $L/\mathbb{Q}$ is called a G-extension. Let $J_1=\text{Gal}(L/K_1)$ and $J_2=\text{Gal}(L/K_2)$.

In his paper [2], Gassmann reduced this arithmetic problem to a purely group-theoretic setting and proved that K₁ and K₂ are arithmetically equivalent if and only if the groups J₁ and J₂ are Gassmann equivalent in G, which is defined as follows.

Definition 1.1.

Let G be a finite group and J₁, J₂ subgroups of G. The subgroups J₁ and J₂ are said to be Gassmann equivalent in G if the permutation characters $1_{J_1}^G$ and $1_{J_2}^G$ coincide. Such a triple $(G,J_1,J_2)$ is called Gassmann triple.

In the arithmetic situation, we are mainly interested in the non-conjugate Gassmann triples as we mentioned above. Also for explicit construction of G-extensions, the smallest possible G containing J₁, J₂ is in demand. We thus make the following additional definition.

Definition 1.2.

Let G be a finite group and J₁, J₂ subgroups of G. Assume that J₁ and J₂ are Gassmann equivalent in G. The subgroups J₁ and J₂ are called properly Gassmann equivalent in G if they are not conjugate in G and also they are core-free in G. In this case, we call $(G,J_1,J_2)$a proper Gassmann triple.

The core-free condition means that the Galois closure of K₁ and K₂ coincides with L.

In this paper, we consider a method to generate new Gassmann triples from a given triple by means of isoclinism. More precisely, we prove the following theorem.

Theorem 1.3.

Let $(G,J_1,J_2)$ be a proper Gassmann triple. If there is an injective homomorphism ι from G to another group H inducing isoclinism, then $(H,\iota (J_1),\iota (J_2))$ is also a proper Gassmann triple.

An immediate corollary is the following.

Corollary 1.4.

Let $L/\mathbb{Q}$ be a G-extension. Assume that $L^{J_1}$ and $L^{J_2}$ are arithmetically equivalent for subgroups J₁ and J₂ in G. If there is an injection ι from G to another group H inducing isoclinism, then for any H-extension $K/\mathbb{Q}, K^{\iota (J_1)}$ and $K^{\iota (J_2)}$ are non-conjugate arithmetically equivalent fields.

Theorem 1.3 will be proved in Section 2. In Section 3, we give explicit examples of the application of the theorem. We will also notice that we obtain unexpectedly many Gassmann triples in some situation. In Section 4, we discuss another method to produce new Gassmann triples.

Throughout this paper, we use the following notation. For a finite group G, we denote by Z(G) the center of G and by $G\prime$ the commutator subgroup of G. Finite groups are often identified by the GAP ID. For example, we denote by (240, 191) the 191-st group of order 240. As we already used above, $1_H$ is the principal character of H, and if H is a subgroup of G, then $1_H^G$ is the induced character of $1_H$ to G.

2 Proof of the main theorem

The following lemma is similar to the statement of the main theorem, but without the assumption that the injection ι from G to H induces an isoclinism.

Lemma 2.1.

Let $(G,J_1,J_2)$ be a core-free Gassmann triple. If there is an injection ι from G to another group H, then $(H,\iota (J_1),\iota (J_2))$ is a core-free Gassmann triple.

Proof.

We first show that the subgroups $\iota (J_1)$ and $\iota (J_2)$ are core-free in H. Indeed, since J₁ is core-free in G, we have $${\text{Core}}_H(\iota (J_1))=\underset{h\in H}{\cap }h\iota (J_1)h^{-1}\subset \underset{\iota (g)\in \iota (G)}{\cap }\iota (g)\iota (J_1)\iota {(g)}^{-1}\cong \underset{g\in G}{\cap }g{J}_1{g}^{-1}=1.$$

The same holds for $\iota (J_2)$.

Since $(G,J_1,J_2)$ is a Gassmann triple, we have $1_{J_1}^G=1_{J_2}^G$. This implies $1_{\iota (J_1)}^{\iota (G)}=1_{\iota (J_2)}^{\iota (G)}$. Taking the induction from $\iota (G)$ to H, we obtain $$1_{\iota (J_1)}^H={\left(1_{\iota (J_1)}^{\iota (G)}\right)}^H={\left(1_{\iota (J_2)}^{\iota (G)}\right)}^H=1_{\iota (J_2)}^H.$$

This shows that $(H,\iota (J_1),\iota (J_2))$ is a Gassmann triple. □

Without the asumpution on ι inducing isoclinism, we cannot guarantee that the obtained triple is proper. Namely, even if J₁ and J₂ are non-conjugate in G, it can happen that $\iota (J_1)$ and $\iota (J_2)$ may be conjugate as seen in the following example.

Example 2.2.

Let $G=\text{Hol}(C_8)$ be the holomorph of C₈. The GAP ID of G is (32, 43). We identify it with a matrix group: $$\text{Hol}(C_8)=\left\{\left[\begin{array}{cc}a& b\\ 0& 1\end{array}\right]|a\in {(\mathbb{Z}/8\mathbb{Z})}^{\times }, b\in (\mathbb{Z}/8\mathbb{Z})\right\}=〈\left[\begin{array}{cc}7& 1\\ 0& 1\end{array}\right],\left[\begin{array}{cc}7& 2\\ 0& 1\end{array}\right],\left[\begin{array}{cc}5& 0\\ 0& 1\end{array}\right]〉.$$

For later use, let us call these generators A, B, and C in order. The group G has non-conjugate subgroups (2.1) $$J_1=〈\left[\begin{array}{cc}7& 2\\ 0& 1\end{array}\right],\left[\begin{array}{cc}5& 4\\ 0& 1\end{array}\right]〉,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{J}_2=〈\left[\begin{array}{cc}7& 2\\ 0& 1\end{array}\right],\left[\begin{array}{cc}5& 0\\ 0& 1\end{array}\right]〉$$(2.1) of order 4 which constitutes a non-conjugate Gassmann triple $(G,J_1,J_2)$. There is an injection ι from G to the central product with GAP ID. (64, 257): $$\begin{array}{c}{D}_4°D_8=〈a,b,c,d|a^4=b^2=d^2=1,c^4=a^2,\\ \mathit{\text{bab}}=a^{-1},\mathit{\text{ac}}=\mathit{\text{ca}},\mathit{\text{ad}}=\mathit{\text{da}},\mathit{\text{bc}}=\mathit{\text{cb}},\mathit{\text{bd}}=\mathit{\text{db}},\mathit{\text{dcd}}=a^2{c}^3〉\end{array}$$ sending $$A\mapsto \mathit{\text{dba}},\hspace{1em}B\mapsto \mathit{\text{dc}},\hspace{1em}C\mapsto b.$$

We have $$\iota (J_1)=〈\mathit{\text{dc}},b{d}^{-1}{c}^{-1}\mathit{\text{dc}}{d}^{-1}{c}^{-1}{d}^{-1}c{d}^2〉,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\iota (J_2)=〈\mathit{\text{dc}},b〉$$and they are conjugate: $(\mathit{\text{ba}})\iota (J_1){(\mathit{\text{ba}})}^{-1}=\iota (J_2)$.

This example and the examples of Section 3 below were produced using MAGMA [1].

Our theorem claims that if the injection ι induces an isoclinism, then $\iota (J_1)$ and $\iota (J_2)$ are always non-conjugate.

Before proceeding to the proof of the theorem, we recall the definition of isoclinism from [3].

Definition 2.3.

Let G and H be finite groups. The groups G and H are isoclinic if there exist isomorphisms $\phi :G/Z(G)\tilde{\to }H/Z(H)$ and $\psi :G\prime \tilde{\to }H\prime$ such that the commutator relation $$\psi (\mathit{\text{xZ}}(G),\mathit{\text{yZ}}(G))=(\phi (\mathit{\text{xZ}}(G)),\phi (\mathit{\text{yZ}}(G)))$$holds. If G and H are isoclinic, then we write $H\sim G$ and we call the pair $(\phi ,\psi )$ an isoclinism.

Therefore our assumption that “the injection $\iota :G\to H$ induces an isoclinism” means that ι induces $\phi$ and ψ. The condition for the induction is given by Hall in the same paper.

Lemma 2.4

(Hall [3]). The injection $\iota :G\to H$ induces the isoclinism if and only if $\iota (G)Z(H)=H$ holds.

If the condition of the lemma holds, then we have the following commutative diagram clarifying the situation.

Lemma 2.5.

If an injective homomorphism $\iota :G\to H$ induces an isoclinism $(\phi ,\psi )$, then we have the following commutative diagram with exact rows.

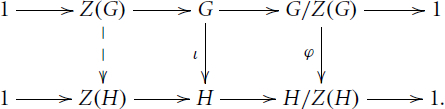
Proof.

Almost all assertions are obvious by our assumption. It remains to show that the restriction of ι to Z(G) induces a homomorphism into Z(H). If $z\in Z(G)$, then $[z,g]=1$ holds for all $g\in G$ and thus we have $[\iota (z),\iota (g)]=\iota ([z,g])=1$. This means that $\iota (z)$ is contained in the centralizer of $\iota (G)$. On the other hand, it follows from Lemma 2.4 that $\iota (G)Z(H)=H$. Hence every $h\in H$ can be written as $h=\iota (g)z\prime$ with $g\in G$ and $z\prime \in Z(H)$. We compute $[\iota (z),h]=[\iota (z),\iota (g)z\prime ]=[\iota (z),\iota (g)]=1$. Therefore we conclude $\iota (z)\in Z(H)$. □

We now prove Theorem 1.3.

Proof of Theorem 1.3.

We shall show that if the injection ι induces the isoclinism $(\phi ,\psi )$, then $(H,\iota (J_1),\iota (J_2))$ is a non-conjugate Gassmann triple.

Suppose to the contrary that $\iota (J_1)$ and $\iota (J_2)$ are conjugate. Namely there exists $h\in H$ such that $\iota (J_1)=h\iota (J_2)h^{-1}$. By Lemma 2.4, we can write $h=\iota (g)z$ with $g\in G$ and $z\in Z(H)$. This yields $$\iota (J_1)=\iota (g)z\iota (J_2)z^{-1}\iota {(g)}^{-1}=\iota (g{J}_2{g}^{-1}).$$

The injectivity of ι implies $J_1=g{J}_2{g}^{-1}$ and this is a contradiction. □

It is worth mentioning Hekster’s result here. In his paper [4, 4.2 Theorem], it is shown that $G_1\sim G_2$ if and only if there exists a group G containing subgroups isomorphic to G₁ and G₂ such that $G_1\sim G\sim G_2$. Therefore we can construct injections from both G₁ and G₂ to G inducing isoclinism.

Corollary 2.6.

If a G-extension contains a proper Gassmann triple, then for any abelian group A, the direct product G × A also contains a proper Gassmann triple.

Proof.

Let ι be the natural injection from G to G × A. Since $\iota (G)Z(G\times A)=\iota (G)(Z(G)\times A)=G\times A$, the map ι induces an isoclinism between G and G × A by Lemma 2.4. The corollary follows immediately from Theorem 1.3. □

In general, a group isoclinic to G is not necessarily of the form G × A with an abelian group A, but it is a quotient of G × A and hence, if a G-extension is given and $G\sim H$, then an H-extension can be obtained as a subfield of a $(G\times A)$-extension for some A. See [7, Theorem 4.2] for explicit description.

3 Explicit examples

The aim of this section is to give explicit examples of Theorem 1.3. For this purpose, additional study of injective homomorphisms is in order.

If there are several injective homomorphisms from G to H inducing isoclinism, then it is possible to construct several non-conjugate Gassmann triples inside H and they are sometimes mutually non-conjugate. If $(G,J_1,J_2)$ is a non-conjugate Gassmann triple and $g\in G$, then it is clear that $(G,g{J}_1{g}^{-1},g{J}_2{g}^{-1})$ is also a non-conjugate Gassmann triple. Such conjugate pairs of Gassmann triples are undesirable.

A necessary condition of being mutually non-conjugate is given by the following proposition.

Proposition 3.1.

Suppose that an injective homomorphism $\iota :G\to H$ induces an isoclinism $G\sim H$ and also that $(G,J_1,J_2)$ is a Gassmann triple. For any $u\in \text{Hom}(G/G\prime Z(G),Z(H))$, the following assertions hold.

1. The map $\mathit{ȷ}:g\mapsto \iota (g)u(\mathit{\text{gG}}\prime Z(G))$ is also an injective homomorphism inducing an isoclinism $G\sim H$.

2. If there exists an element $h\in H$ so that $u(\mathit{\text{gG}}\prime Z(G))=[\iota {(g)}^{-1},h]$ holds for all $g\in G$, then $(H,\iota (J_1),\iota (J_2))$ and $(H,\mathit{ȷ}(J_1),\mathit{ȷ}(J_2))$ are mutually conjugate Gassmann triples with $\mathit{ȷ}$ given in the assertion i.

Proof.

Since the image of u is contained in the center of G, it is easy to see that $\mathit{ȷ}$ is a homomorphism. In the below, we abbreviate $u(\mathit{\text{gG}}\prime Z(G))$ to u(g).

1. If $g\in \mathrm{\text{ker}}\mathit{ȷ}$, then $\iota (g)=u(g^{-1})$ and $\iota (g)\in Z(H)$. This implies that, for any $x\in G$, we have $\iota ([g,x])=[\iota (g),\iota (x)]=1$. Since ι is injective, it follows that $[g,x]=1$ and this yields $g\in Z(G)$. We thus conclude $\mathrm{\text{ker}}\mathit{ȷ}\subset Z(G)$. Since $\mathrm{\text{ker}}u\supset Z(G)$, we have $\mathit{ȷ}(z)=\iota (z)u(z)=\iota (z)$ for any $z\in Z(G)$ and hence if moreover $z\in \mathrm{\text{ker}}\mathit{ȷ}$, then z = 1. This shows that $\mathit{ȷ}$ is an injection.

   By Lemma 2.4, we have $\iota (G)Z(H)=H$ by assumption. Hence we have $\mathit{ȷ}(G)Z(H)=\iota (G)u(G)Z(H)=\iota (H)Z(H)=H$. This means that $\mathit{ȷ}$ also induces an isoclinism.

2. If $u(g)=[\iota {(g)}^{-1},h]$ for some $h\in H$, then we have $\mathit{ȷ}(g)=\iota (g)[\iota {(g)}^{-1},h]=h\iota (g)h^{-1}$ for any $g\in G$ from the assumption. This shows that $\iota (H_i)$ and $\mathit{ȷ}(H_i)$ are conjugate in H for i = 1, 2.

□

We note that the group $G/G\prime Z(G)$ is an isoclinism invariant and therefore Z(H) determines how many such homomorphisms u there are. But it seems difficult to tell exactly how many injections from G to H there are with the desired local behavior on J₁ and J₂. See [9] for related problems. The following examples reveal how our theorem produces new Gassmann triples in H, but also the difficulty to tell how many there are.

Example 3.2.

Let $G=\text{Hol}(C_8)$ as in Example 2.2. From G, there exist injective homomorphisms inducing isoclinisms to the following groups of relatively small orders:

Table

ID	Z(H)	$\#\text{Inj}.$	$\#\text{Gassmann triples}$
(64, 254)	[2, 2]	32	4
(64, 256)	[4]	16	2
(96, 183)	[6]	4	1
(128, 1676)	[2, 4]	32	4
(128, 1687)	[8]	16	2
(128, 2310)	[2, 2, 2]	256	16
(128, 2312)	[2, 4]	128	8
(160, 197)	[10]	4	3

In the first column, the GAP IDs of the groups are given. The abelian invariants of Z(H) are given in the second column. The numbers of injective homomorphisms up to inner automorphisms of H are in the third column. The fourth column shows the number of non-conjugate Gassmann triples obtained as the images of J₁ and J₂ in (2.1). Indeed, every Gassmann triple in H is an image of some injection from G in this example.

The groups $(64,254),(128,1676),(128,2310)$, and (128, 2312) are direct products of G and an abelian group and thus we can apply Corollary 2.6.

Here we make an explicit description for $$\begin{array}{c}H=(64,256)\\ =〈a,b,c,d|a^8=b^2=c^2=d^2=1,\mathit{\text{bab}}=a^{-1},\mathit{\text{cac}}=a^5,\mathit{\text{ad}}=\mathit{\text{da}},\mathit{\text{cbc}}=\mathit{\text{dbd}}=a^{4}b,\mathit{\text{cd}}=\mathit{\text{dc}}〉.\end{array}$$

Among the 16 injections from G to H, we consider the following two injections: $$\begin{array}{c}{\iota }_1:A\mapsto \mathit{\text{ba}},B\mapsto b,C\mapsto \mathit{\text{dc}}\\ {\iota }_2:A\mapsto \mathit{\text{dcb}},B\mapsto \mathit{\text{ba}},C\mapsto c.\end{array}$$

Let J₁ and J₂ be the subgroups of G as in (2.1). While the map ι₁ yields a Gassmann triple $$(H,〈b,\mathit{\text{dc}}{b}^{-1}{a}^{-1}\mathit{\text{ba}}{b}^{-1}{a}^{-1}{b}^{-1}a{b}^2〉,〈b,\mathit{\text{dc}}〉),$$ι₂ yields a mutually non-conjugate Gassmann triple $$(H,〈\mathit{\text{ba}},c{b}^{-1}{a}^{-1}\mathit{\text{ba}}{b}^{-1}{a}^{-1}{b}^{-1}a{b}^2〉,〈c,\mathit{\text{ba}}〉).$$

As for the construction of an H-extension from a G-extension, we proceed as follows. Theorem 4.2 in [7] tells us that an H-extension is contained in $G\times C_4$-extensions, where $G\times C_4\cong (128,1676)$. We have a surjective homomorphism ψ from $G\times C_4$ to H mapping $$A\mapsto \mathit{\text{dcb}},\hspace{1em}B\mapsto \mathit{\text{cab}},\hspace{1em}C\mapsto c{b}^{-1}{a}^{-1}\mathit{\text{ba}}{b}^{-1}{a}^{-1}a{b}^2,\hspace{1em}s\mapsto d{a}^{-1}{b}^{-1}\mathit{\text{ab}},$$where s is a generator of C₄. The kernel of ψ is a cyclic group of order 2 generated by the product of $\left[\begin{array}{cc}1& 4\\ 0& 1\end{array}\right]\in Z(G)$ and s².

Let k be the fixed subfield by Z(G) in a G-extension K. We can choose an element $\alpha \in k$ such that $K=k\left(\sqrt{\alpha }\right)$. Let $L/\mathbb{Q}$ be a C₄-extension and F the intermediate quadratic field in kL/k. We can choose $\gamma \in F$ such that $\mathit{\text{kL}}=F\left(\sqrt{\gamma }\right)$.

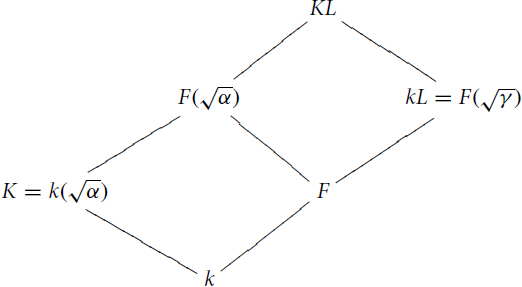
We can show that our H-extension coincides with $F\left(\sqrt{\alpha \gamma }\right)$.

Example 3.3.

Let ${\mathbb{F}}_{16}$ be a finite field of 16-elements. In this example, we consider the case with the Frobenius group $$G=F_{16}=\left\{\left[\begin{array}{cc}a& b\\ 0& 1\end{array}\right]|a\in {\mathbb{F}}_{16}^{\times },b\in {\mathbb{F}}_{16}\right\}=(240,191).$$

In the previous paper [6], it is proved that there are 3 non-conjugate subgroups of order 4 whose trivial characters induce the same character of G. We call the number of the non-conjugate subgroups the length of Gassmann multiple. In this terminology, G contains a non-conjugate Gassmann multiple of length 3.

Table

ID	Z(H)	#Inj.
(480, 1190)	[2]	4
(720, 786)	[3]	12
(960, 10909)	[4]	4
(960, 11365)	[2, 2]	4
(1200, 967)	[5]	20
(1440, 5892)	[6]	12
(1690, 938)	[7]	4
1920, 238132	[8]	4
(1920, 240054)	[2, 4]	4
1920, 240400	[2, 2, 2]	4

These groups in the table above are all direct products of G and abelian groups. In each case, the injections from G to H produce mutually conjugate Gassmann multiples of length 3. Although the group (480, 1190) has a Gassmann multiple of length 7, it does not consist of the images of the injective homomorphisms. This seems to be partly because $\text{Hom}(G/G\prime Z(G),Z(H))$ in Proposition 3.1 is trivial since $G/G\prime Z(G)\cong C_{15}$.

4 Further construction

In this section, we give another method to produce new Gassmann triples from a given one.

Proposition 4.1.

Let K₁ and K₂ be arithmetically equivalent fields with Galois closure L and Galois kernel F, which is, by definition, the common largest Galois subfield of K₁ and K₂. Let $G=\text{Gal}(L/\mathbb{Q}),J_1=\text{Gal}(L/K_1)$ and $J_2=\text{Gal}(L/K_2)$. Let $L\prime$ be a G-extension containing F and linearly disjoint over F. If $K_1^{\prime }$ and $K_2^{\prime }$ are subfields of $L\prime$ such that an isomorphism $G\cong \text{Gal}(L\prime /\mathbb{Q})$ induces $J_1\cong \text{Gal}(L\prime /K_1^{\prime })$ and $J_2\cong \text{Gal}(L\prime /K_2^{\prime })$, then the composite fields $K_1{K}_1^{\prime }$ and $K_2{K}_2^{\prime }$ are arithmetically equivalent.

Our situation is depicted in the following diagram: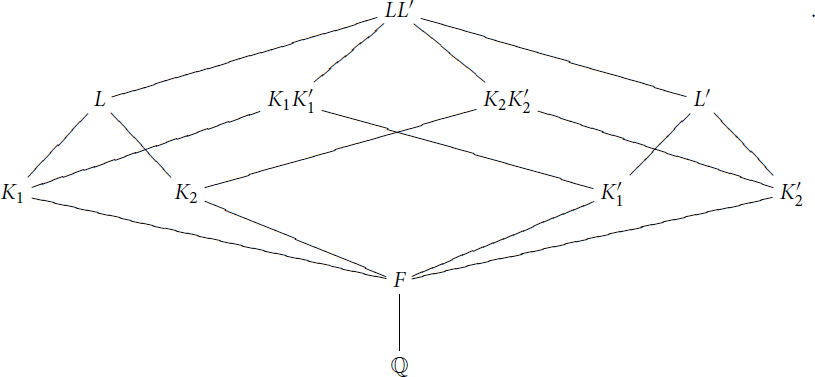

Proof.

Let us write $G^{*}=\text{Gal}(L\prime /\mathbb{Q}), J_1^{*}=\text{Gal}(L\prime /K_1^{\prime })$ and $J_2^{*}=\text{Gal}(L\prime /K_2^{\prime })$. We also write $$\mathcal{G}=\text{Gal}(\mathit{\text{LL}}\prime /\mathbb{Q}), {\mathcal{J}}_1=\text{Gal}(\mathit{\text{LL}}\prime /K_1{K}_1^{\prime }), {\mathcal{J}}_2=\text{Gal}(\mathit{\text{LL}}\prime /K_2{K}_2^{\prime }).$$

We shall show that $(\mathcal{G},{\mathcal{J}}_1,{\mathcal{J}}_2)$ is a Gassmann triple. Set $\mathcal{U}=\text{Gal}(\mathit{\text{LL}}\prime /L)$ and ${\mathcal{U}}^{*}=\text{Gal}(\mathit{\text{LL}}\prime /L\prime )$. Let ${\mathcal{V}}_i$ be the inverse image of H_i by the natural projection $\mathcal{G}\to G$ for i = 1, 2. The group ${\mathcal{V}}_i$ contains $\mathcal{U}$ and, by assumption, $(\mathcal{G}/\mathcal{U},{\mathcal{V}}_1/\mathcal{U},{\mathcal{V}}_2/\mathcal{U})$ is a Gassmann triple. Namely we have (4.1) $$1_{{\mathcal{V}}_1/\mathcal{U}}^{\mathcal{G}/\mathcal{U}}=1_{{\mathcal{V}}_2/\mathcal{U}}^{\mathcal{G}/\mathcal{U}}.$$(4.1)

The natural map between the left cosets $\mathcal{G}/{\mathcal{V}}_1\to (\mathcal{G}/\mathcal{U})/({\mathcal{V}}_1/\mathcal{U})$ induces a left $\mathcal{G}$-module isomorphism of free $\mathbb{C}$-modules over these coset spaces. The same holds for J₂ and hence (4.1) yields (4.2) $$1_{{\mathcal{V}}_1}^{\mathcal{G}}=1_{{\mathcal{V}}_2}^{\mathcal{G}}.$$(4.2)

Similarly we obtain (4.3) $$1_{{\mathcal{V}}_1^{*}}^{\mathcal{G}}=1_{{\mathcal{V}}_2^{*}}^{\mathcal{G}}$$(4.3) where ${\mathcal{V}}_i^{*}$ is defined as the inverse image of $H_i^{*}$ in $\mathcal{G}$. On the other hand, from a natural left $\mathcal{G}$-module isomorphism $\mathbb{C}[\mathcal{G}/{\mathcal{V}}_1\cap {\mathcal{V}}_1^{*}]\cong \mathbb{C}[\mathcal{G}/{\mathcal{V}}_1]\oplus \mathbb{C}[\mathcal{G}/{\mathcal{V}}_1^{*}]$, it follows $$1_{{\mathcal{V}}_1\cap {\mathcal{V}}_1^{*}}^{\mathcal{G}}=1_{{\mathcal{V}}_1}^{\mathcal{G}}{1}_{{\mathcal{V}}_1^{*}}^{\mathcal{G}}.$$

Interchanging the role of ${\mathcal{V}}_1$ and ${\mathcal{V}}_2$, we also have $$1_{{\mathcal{V}}_2\cap {\mathcal{V}}_2^{*}}^{\mathcal{G}}=1_{{\mathcal{V}}_2}^{\mathcal{G}}{1}_{{\mathcal{V}}_2^{*}}^{\mathcal{G}}.$$

By combining these with (4.2) and (4.3), we conclude $$1_{{\mathcal{V}}_1\cap {\mathcal{V}}_1^{*}}^{\mathcal{G}}=1_{{\mathcal{V}}_2\cap {\mathcal{V}}_2^{*}}^{\mathcal{G}}.$$

Since ${\mathcal{J}}_1={\mathcal{V}}_1\cap {\mathcal{V}}_1^{*}$ and ${\mathcal{J}}_2={\mathcal{V}}_2\cap {\mathcal{V}}_2^{*}$, the proof is now complete. □

We can interchange K₁ and $K_1^{\prime }$ and also K₂ and $K_2^{\prime }$ and we therefore obtain:

Corollary 4.2.

Under the same assumption as in Proposition 4.1, the four fields $K_1{K}_1^{\prime },K_1{K}_2^{\prime },K_2{K}_1^{\prime },K_2{K}_2^{\prime }$ are arithmetically equivalent.

It is classically known that the fields $\mathbb{Q}(\sqrt[8]{a})$ and $\mathbb{Q}(\sqrt[8]{16a})$ are arithmetically equivalent, if $X^8-a\in \mathbb{Q}[X]$ is irreducible. The Galois group of the Galois closure of these fields is isomorphic to $\text{Hol}(C_8)$. By recursive use of Proposition 4.1, the $2^r$ fields $$\mathbb{Q}\left(\sqrt[8]{{(16)}^{v_1}{a}_1},\dots ,\sqrt[8]{{(16)}^{v_r}{a}_r}\right),\hspace{1em}(v_1,\dots ,v_r)\in {\mathbb{F}}_2^r$$are arithmetically equivalent for suitable choice of $a_1,\dots ,a_r\in \mathbb{Z}$. This is the main result in [8] by K. Komatsu, although the proof is different. His result is the first explicit example of a large family of arithmetically equivalent fields preceding [6].

Proposition 4.1 is also applicable to the situation in Example 3.3 by taking the fixed field by the commutator subgroup of F₁₆ as the Galois kernel F.

Additional information

Funding

This work was supported by JSPS KAKENHI Grant Number 20K03521.