On the distribution of bids for construction contract auctions

Abstract

The statistical distribution representing bid values constitutes an essential part of many auction models and has involved a wide range of assumptions, including the Uniform, Normal, Lognormal and Weibull densities. From a modelling point of view, its goodness is defined by how well it enables the probability of a particular bid value to be estimated – a past bid for ex-post analysis and a future bid for ex-ante (forecasting) analysis. However, there is no agreement to date of what is the most appropriate form and empirical work is sparse. Twelve extant construction data-sets from four continents over different time periods are analysed in this paper for their fit to a variety of candidate statistical distributions assuming homogeneity of bidders (ID not known). The results show there is no one single fit-all distribution, but that the 3p Log-Normal, Fréchet/2p Log-Normal, Normal, Gamma and Gumbel generally rank the best ex-post and the 2p Log-Normal, Normal, Gamma and Gumbel the best ex-ante – with ex-ante having around three to four times worse fit than ex-post. Final comments focus on the results relating to the third and fourth standardized moments of the bids and a post hoc rationalization of the empirical outcome of the analysis.

Keywords:

• Modelling
• forecasting
• bidding
• tendering
• probability distribution
• Fréchet
• Log-Normal

Introduction

The uses of probabilistic models of bids are manifold. For economics, they provide the basis for the development of equilibrium theories (to identify optimal auction arrangements for example Klemperer 2004), while for business, they offer the potential for a sharpened competitive edge through the analysis of competitor bidding behaviour (e.g. Ballesteros-Pérez, Skitmore, Pellicer, Gutiérrez-Bahamondes 2016, Ballesteros-Pérez, Skitmore, Pellicer, Zhang 2016).

Many advanced theoretical studies obtain distribution-free results, which are invariant for a wide range of probability distributions with only mild restrictions (such as being twice differentiable) (e.g. Wilson 1977, Riley and Samuelson 1981, Milgrom and Weber 1982, McAfee and McMillan 1987, Hendricks and Porter 1992). In more practical applications, the approach is to simply assume bid values follow a standard distributional form, such as the Uniform (e.g. Vickrey 1961, Cauwelaert and Heynig 1978), Normal (e.g. Mitchell 1977, Morrison and Stevens 1980), Log-Normal (e.g. Klein 1976, Weverbergh 1982), Gamma (Friedman 1956) or Weibull (Oren and Rothkopf 1975), and proceed accordingly without further justification. Recent applications in which the bid distribution needs to be assumed are abnormal bid detection methods (Ishii 2009, Ballesteros-Pérez, Skitmore, Das et al. 2015), in order to identify a bid as extremely high or low according to its percentile placement in the distribution (Ballesteros-Pérez, Skitmore, Pellicer et al. 2015). Empirical studies to test these assumptions are rare, however, and the methods used to fit distributional forms uncertain.

This is particularly problematic for construction contract auctions, where the complex and non-repetitive nature of projects and scarcity of suitable data-sets available for analysis exacerbate the situation further (Ballesteros-Pérez et al. 2010). Different studies assume different distributions with no empirical support, making the economic models involved of questionable validity. Hence, the main purpose of this paper is to help establish the most appropriate distribution form, or forms, for construction contract bids in order to evaluate the validity of existing parametric studies and provide a more realistic basis for future work. This is undertaken through the analysis of several extant sets of construction contract auction bidding data gathered from different parts of the world at different time periods. All the probability distributions assumed to date for auction bids are tested for their goodness of fit to each data-set by an average measure of the three different kinds of errors expected from choosing a particular distribution. The results show that, assuming homogeneity of bidders (ID not known), there is no one single fit-all distribution, but that the 3p Log-Normal, Fréchet/2p Log-Normal, Normal, Gamma and Gumbel generally rank the best ex-post (fit with past data) and the 2p Log-Normal, Normal, Gamma, Gumbel, Weibull, 3p Log-Normal and Fréchet the best ex-ante (accuracy of forecasting future results) – with the ex-ante results having around three to four times worse fit than the ex-post results. Final comments focus on the results relating to the third and fourth standardized moments (skewness and kurtosis) of the bids and a post hoc rationalization of the empirical outcome of the analysis.

Literature review

Friedman’s (1956) seminal operations research (OR) paper is generally considered to contain the first in a long line of sealed-bid auction bidding models to emerge from the literature over the years. Although Friedman’s general approach provided the basis for much of what was to follow, his method of empirically estimating the individual statistical distributions needed for each bidder has been found wanting, especially for construction contract auctions, where (1) each contract is different (making the effects of data pooling unpredictable), (2) there are a small number of bidders for each contract (the statistical procedures for small samples are less well developed than for large samples), (3) different bidders bid for each contract (making the contract-bidder matrix usually over 90% redundant) and (4) the bidders may not be bidding independently of each other (Skitmore 2014). As a result, many researchers have resorted to the assumption that all bidders’ bids are independently and identically distributed (iid) – known as the symmetrical assumption in economics and the homogeneity assumption in construction (Skitmore 1991) – for the purposes of theory development. By disregarding the behaviour of individual bidders in this way, the estimation problem is reduced to one of determining, or assuming, the collective distributional form involved. Even this simplifying assumption, however, to do this empirically for sealed bid construction contract auctions presented an insurmountable task for many years, leaving researchers with no option but to make what they considered an appropriate assumption concerning the distribution form needed. As can be seen in Table 1, which represents just some examples from the first 25 years of the construction (OR) discipline, many such assumptions have been made.

Table 1. Early sample of statistical distributions implemented to model construction bids

Modeller	Data	Form
Alexander (1970)	USA oil and mineral tracts – source of data unknown	Normal
Arps (1965)	USA oil and mineral tracts – source of data unknown	Lognormal
Beeston (1982)	“Large sample” of UK PSA contracts	Pos. skewed
Brown (1986)	USA oil and mineral tracts – source of data unknown	Lognormal
Capen et al. (1971)	USA oil and mineral tracts – source of data unknown	Lognormal
Cauwelaert and Heynig (1978)	Assumed for theoretical purposes	Uniform
Cauwelaert and Heynig (1978)	“Consistent with work of other researchers”	Normal
Crawford (1970)	USA oil and mineral tracts – source of data unknown	Lognormal
Dougherty and Nozaki (1975)	USA oil and mineral tracts – source of data unknown	Gamma
Emond (1971)	USA oil and mineral tracts – source of data unknown	Normal
Fine and Hackemar (1970)	“Adequate sample” of UK construction contracts	Uniform
Friedman (1956)	“Frequently furnishes a good fit”	Gamma
Grinyer and Whittaker (1973)	153 UK government construction contracts	Uniform
Hossein (1977)	545 USA civil engineering and 63 mechanical engineering contracts	Gamma
Klein (1976)	Assumed for theoretical purposes	Lognormal
McCaffer (1976)	183 Belgian building contracts	Normal
McCaffer (1976)	16 Belgian bridge contracts	Normal
McCaffer (1976)	384 Belgian road contracts	Normal
McCaffer and Pettitt (1976)	384 Belgian road contracts	Normal
Mitchell (1977)	Assumed for theoretical purposes	Normal
Morrison and Stevens (1980)	Assumed for theoretical purposes	Normal
Oren and Rothkopf (1975)	Assumed for theoretical purposes	Weibull
Park (1966)	USA construction projects – source of data unknown	Pos. skewed
Pelto (1971)	USA oil and mineral tracts – source of data unknown	Lognormal
Weverbergh (1982)	Assumed for theoretical purposes	Lognormal
Whittaker (1970)	153 UK government construction contracts	Uniform

The recent situation has changed little, with current researchers assuming similar, or sometimes more advanced, statistical distributions for modelling the bid distribution of single bidders or groups of bidders, such as the Uniform (e.g. Ballesteros-Pérez, González-Cruz, Cañavate-Grimal 2013, Ballesteros-Pérez, González-Cruz, Cañavate-Grimal Pellicer 2013, Mohlin et al. 2015), Normal (e.g. Conti et al. 2012, Costantino et al. 2011, European Union 1999), Gamma (e.g. Skitmore 2014, Takano et al. 2014), Log-Normal (e.g. Campo 2012), three-parameter Log-Normal (Skitmore et al. 2001), Weibull (e.g. Skitmore et al. 2007) and Beta distributions (Ballesteros-Pérez, del Campo-Hitschfeld et al. 2015, 2014).

Among the few empirical comparative studies concerning construction bids, they almost without exception retain the iid assumption. Of these, McCaffer and Pettitt (1976) considered that the Normal distribution was superior to the Uniform, whereas Hossein’s (1977) results a year later indicated that the Gamma distribution offered a generally better fit compared to the Log-Normal and Normal distribution. Other work has considered the possibility of outliers and the potential use of truncated or censored probability distributions (Skitmore and Lo 2002, Skitmore 2001, 2002, 2004). Their empirical results suggest that a censored Normal/Log-Normal distribution is preferable to either a truncated Normal/Log-Normal distribution, or a truncated or censored Uniform distribution.

Although there is a substantial body of theoretical literature concerning asymmetric auctions that obviates the iid assumption (e.g. Maskin and Riley 2000), it is only relatively recently that Skitmore (1991) has managed to separate individual bidders and fit a probability distribution to each bidder, albeit of a composite nature (same distributional form, such as Uniform or Normal, but with different parameters for each bidder). From this, a three-parameter Log-Normal distribution (Skitmore 1991), and later also a two-parameter form of Gamma distribution (Skitmore 2014), were shown to be appropriate for the data involved. It was also shown that the parameter estimates were significantly different between bidders, hence challenging the tenability of the iid assumption, at least for the data used in that study (Skitmore 1991).

More recently still, Runeson and Skitmore (1999) have questioned the stability of the bidders’ probability functions – an assumption implied in the fitting procedure. Their main concern is that the bidders’ changing workload situation and the interrelated effects of market conditions are not accommodated in the models. Two lines of analyses have been used previously to test the significance of this. One, by McCaffer (1976), examined the changes in bidding patterns by individual bidders prior to winning a contract, based on the assumption that bidders are more likely to be “hungry” for work prior to winning than after winning, it is expected that bids tendered prior to winning will be lower than those made after winning. Empirical analysis by Skitmore and Runeson (2006), however, suggests that this may not be as significant as first thought and is unlikely to be a distorting factor in model building. The second line of analysis, by Skitmore (1981a, 1987), examined the changes in distributional shape of UK contract bids under the iid assumption in comparison with changing macroeconomic circumstances during the 1970s and found what appeared to be a general surge in bid range (coefficient of variation) and skewness immediately after the 1974 oil crisis, when oil prices quadrupled virtually overnight. Again, though, these results have been questioned in a repeat analysis over an extended period up to 1991 (Rawlinson and Raftery 1997).

Finally, a few multivariate models that include correlation between bidders have started to emerge quite recently (Yuan 2011, 2012) in which bidder heterogeneity can be considered, but where parameter estimation still represents a challenging issue.

In summary, while there is a large amount of theoretical work that has been conducted on the properties of auctions, there is little empirical support, especially relating to construction contract bids. Despite some reservations about their statistical nature and influencing factors, the general trend towards modelling over the last 25 years suggests that iid assumption may be an oversimplification for scenarios where bidder IDs are known. However, a much more common real-world situation is that either the identity of the bidder for each bid in a database of construction contract auction is not known or the identity of the bidders to take part in future action is not known, or both. In this case, there is little alternative to modelling the bidders as iid.

This paper therefore mostly focuses on identifying the statistical distribution(s) that best model all bids from the same auction as a whole. Of course, this may result in some “noise” being added to the bid distribution due to the heterogeneity of bidders (Skitmore 1988, Lan Oo et al. 2007, Oo et al. 2010). However, as is shown later, there is evidence of an overall satisfactory ex-post fit of simple and unimodal distributions, which rules out at least one objection to the iid assumption. The remainder of this paper is devoted to the task of analysing the 12 varied data-sets of construction contract bids from different countries in different time periods and, hence, different economic conditions. Firstly, a detailed summary of the data-sets is provided. The methods of analysis are then presented for the ex-post and ex-ante situations, followed by details of the results to show that, although there is no one single fit-all distribution, the Fréchet and Log-Normal are the closest in most cases. Therefore, despite there being no clear winning distribution, a small number of distributions provide a much better model than others, especially for forecasting purposes.

Data

Table 2 summarizes the 12 construction data-sets used in the analysis. For ease of notation, these data-sets are identified later as UK51, UK218, UK373, US62, US50, HK199, HK259, AU152, AU161, UK272, SP116 and SP51, as shown in the Table (the prefix denotes the country of origin whereas the suffix values are the number of contract auctions contained in the data-set). The values of all bids received for each contract are available in all the data-sets and, with the exception of AU152, AU161, UK272 and SP51, the identities of the associated bidders. All the values from the first 10 data-sets are converted to approximate pounds sterling equivalence and rebased to a common date (1980). This is approximate for UK218 and US50 as no dates of individual contracts are available. Data-sets SP116 and SP51, on the other hand, have been rebased to 2008 Euros. It is not to be expected that these two different rebased currencies condition the analyses in any way. Furthermore, data-sets SP116 and SP51 l comprise capped bids (auctions in which the bid is upper limited and all bidders can only underbid a previously known maximum price). The remaining data-sets comprise uncapped bids.

Table 2. Construction data-sets used for the analysis

Data-set	Source	Description	Period	N° bids	N° contracts	Avg N° bids/contract	Avg mean bid	Avg st. dev.	Avg skew.	Avg ex. kurt.
UK51	Skitmore (1991)	London building contracts	1981–82	318	51	6.24	1,770,351	86,753	0.417	0.049
UK218	Skitmore (1986)	North of England public works contracts	1979–82	1235	218	5.67	143,382	10,238	0.142	0.208
UK373	Skitmore (1986)	London building contracts	1976–77	1915	373	5.13	828,705	45,438	0.253	0.339
US62	Brown (1986)	USA Government agency building contracts	1976–84	417	62	6.73	914,019	71,863	0.686	1.142
US50	Shaffer and Micheau (1971)	USA building contracts	1965–69	235	50	4.70	921,970	62,652	0.185	−0.054
HK199	Drew (1995)	Primary, secondary schools, police, fire stations and hostels in Hong Kong	1981–90	2531	199	12.72	1,122,132	118,579	0.850	1.164
HK259	Fu (2004)	Hong Kong Administrative Services Department contracts	1991–96	3445	259	13.30	5,500,889	566,769	0.793	1.150
AU152	Runeson (1987)	General contractors’ bids for New South Wales Public Works and Housing	1972–82	1316	152	8.66	1,605,075	101,345	0.656	0.933
AU161	Runeson (1987)	Specialist contractors’ bids for New South Wales Public Works and Housing	1972–82	1010	161	6.27	230,346	27,515	0.432	0.579
UK272	Skitmore (1981b)	BCIS detailed analyses of UK contracts	1969–79	1670	272	6.14	835,921	46,048	0.134	0.223
SP116	Ballesteros-Pérez, González-Cruz et al. (2015)	Spanish High speed railway contracts	2008–14	3300	110	30.00	37,610,797	2,222,114	0.447	0.835
SP51	Ballesteros-Pérez et al. (2012)	Spanish waste water treatment plants and sewer systems	2007–08	761	51	14.93	3,236,328	226,291	−0.084	−0.377

Additional information of the source of the data-set, nature of contract work, time period, number of bids and number of contracts is provided in the first columns. Furthermore, unweighted averages are provided for the number of bids per contract, mean bid, sample standard deviation, skewness and (excess) kurtosis. Only auctions with four bids are considered in the analysis for two reasons: contracts with at least four bids are necessary to calculate the kurtosis values (an additional analysis undertaken later). Second, contracts with two or three bids provide a perfect or almost perfect fit, respectively, when working with two or more parameter statistical distributions, biasing the results.

As Table 2 indicates, SP116 has by far the highest average value contracts with an average mean bid of 37,610,797, while the UK218 is the smallest with an average mean bid of 143,382. Also, as expected, the Spanish data-sets (SP116 and SP51) followed by the Hong Kong data-sets (HK199 and HK259) have the highest average number of bidders per contract due to the predominant Spanish and Hong Kong practice of open tendering in an ongoing highly competitive environment. In terms of skewness, it is interesting to note that all data-sets except the last one have a positive coefficient on average, with the highest being the two Hong Kong data-sets and the lowest being SP51 which, although negative, is very close to zero. With the exception of US50 and SP51, all data-sets also have positive average kurtosis coefficients (a kurtosis value of zero is expected for the Normal distribution and −1.2 for the Uniform distribution), with the two Hong Kong data-sets again being the highest.

Overall, it appears that none of the data-sets stand out as being clearly different from the others, with the possible exception of the two Hong Kong data-sets with the extra numbers of bidders involved and fairly high average skewness and kurtosis coefficients. In terms of the moments of the bid distributions, the skewness values do not seem to denote significantly skewed distributions, whereas some excess kurtosis values appear to be rather high for the normal distribution to apply.

As can be seen, the data-sets comprise auctions from five countries over four continents, with different nature of works, economic sizes and time periods. Therefore, it is expected that any common trends will provide representative results transferrable to other countries not included here.

Transformations

Finally, for ease of calculation depending on the specific distribution to be fitted later, the original bid values x_ij (value of the bid by contractor i for contract j) are either used directly (natural values) (e.g. for the Normal and Uniform distributions), transformed to a natural logarithmic scale (ln x_ij) (e.g. for the Log-Uniform and the common two-parameter log-Normal distributions), or transformed according to the expression (in this case for the three-parameter log-Normal distribution only). The latter transformation follows Skitmore’s (1991) procedure when looking for the best composite distributional form for individual bidders, while the analysis in this paper concerns the composite distribution of bids for individual auctions assuming homogeneity among bidders, that is, IDs are not known. The expression x_(1)j in the latter case denotes the lowest bid entered for contract j, with m an arbitrary multiplier which Skitmore’s (1991) empirical analysis found to be relatively stable with a value generally equal to 0.82. However, this multiplier value has been replaced here by m = 0.812, since a preliminary ex-post analysis indicated that this small change could slightly improve (maximize) the overall fit by minimizing the average sum of the squared residuals per auction, that is, the squared differences between the actual bids and the respective 3p log-Normal estimations for each auction, in the 12 data-sets simultaneously.

Methods

The analysis follows two distinct approaches to fitting the probability distributions to the data – the ex-post fit (modelling past bids) and the ex-ante fit (forecasting future bids). The iid assumption is followed and no attempt is made here to examine censored or truncation distributions.

Ex-post distribution fit (modelling past bids)

Before undertaking a wide statistical distribution fit analysis such as this is, two major decisions must be made. First, to select the candidate statistical distributions to be tested and, second, decide how to measure the deviation errors between the actual distribution of bid values and each statistical distribution.

Concerning the candidate statistical distributions, the seemingly endless list of distributions is narrowed down to an initial list comprising the Uniform, Normal, 2-parameter (2p) and 3-parameter (3p) Log-Normal, Gamma and Weibull distributions, since they have been extensively used by researchers and practitioners alike. To these are added other similar distributions, not encountered in the literature but good candidates nevertheless, comprising the Gumbel and the Fréchet since, like the Weibull, they are also Extreme Value distributions. The log-versions of all (i.e. Log-Uniform, Log-Gamma, Log-Fréchet and Log-Gumbel, with the exception of the log-Weibull, which is equivalent to the Gumbel distribution) are also added since this might partially compensate for the data-sets evidencing positive skewness. With the exception of the 3p Log-Normal, no three or more-parameter distributions are included, as parameter estimation for those more complex distributions involves fitting procedures that are quite difficult and time-consuming to carry out (even requiring iterative calculations). For the massive analysis needed here, which involves fitting 13 distributions to nearly 2000 contract auctions, resorting to increasingly complex distributions would not be feasible. Also, as will be seen, the difference in fit between the 3p Log-Normal and best 2p distributions is surprisingly small.

Two obvious measures are available to compare the goodness of fit of the various distributions. The first, and classical, approach is to employ the p-value but, with most values ranging between 0.00 and 0.05, it is hard to distinguish between one small value and another. Moreover, p-values depend upon both the magnitude of association and the precision of the estimate (the sample size), and yet the sample size in most auctions is quite small (between 4 and 10 bids per auction). A better alternative is to use the measure from which the p-values are obtained − the sum of the squared errors (as in the χ² test). These are the sum of the squared deviations between the observed (actual) and estimated (fitted distribution) values, standardized to the mean square error (MSE) to remove the effect of the different number of bids in the auction.

One limitation of the MSE is the difficulty in interpreting the closeness of fit between the actual and fitted values, since they are expressed in squared terms. Two measures are used to counter this limitation. These are the mean absolute percentage error (MAPE), which gives the average deviation from the actual bid values divided by the estimated values expressed as a percentage; and the mean absolute error (MAE), which is analogous to the MAPE but is expressed as an average difference instead of a percentage.

The actual bid and model values for an auction can be represented by a graph, with the X- and Y-axes corresponding to the actual bid value and model cumulative probability values, respectively, the latter increasing from 0 to 1 when the bids have been ordered from lowest to highest. The MSE, MAPE and MAE errors are then calculated as a function of the differences between the Y-coordinates for each bid. Other methods are available, but the ones used here are simpler, more common and considered sufficiently fit for the purpose.

Ex-ante distribution fit (forecasting future bids)

Fitting a distribution when the bids are known is useful for many purposes, but making use of the statistical distribution of bids to anticipate their value in a future contract auction, as yet unknown, is also a very important application, although one seldom treated in the bidding literature.

The aim of this second subsection is to reverse the analysis and, instead of using the bid values to obtain the distribution parameter values, do this the other way around. That is, to estimate the distribution parameter values from another forecasting variable and then observe how closely the distribution defined by these parameters represents the actual bid values once they occur.

The first step in this is to choose a variable that can be known prior to the auction to derive the distribution parameters. By far, the most recurrent forecasting variable for construction contract auctions is the “cost estimate”, denoted by b_o (Ballesteros-Pérez, Skitmore, Pellicer et al. 2012, 2015). The cost estimate is usually calculated by each bidder before submitting a bid, but it is not normally shared with the other bidders – often for legal as well as commercial reasons – this being the main reason why data-sets containing cost estimates are very difficult to obtain. Fortunately, in 7 out of the 12 data-sets, cost estimates from either one bidder or the designer’s pre-auction estimate of bid prices are available, which allows its use as a forecasting parameter.

Most of the ex-post distribution parameters in the previous section were intentionally estimated by the Method of Moments, i.e. from the mean and standard deviation of the bids for each auction. For distributions such the Normal, both the sample mean and the standard deviation constitute the best estimates themselves, while for distributions such as the Gamma or Gumbel, it is quite easy to estimate their parameters once the mean bid and the bid standard deviation are known. For other distributions, such as the Log-Normal, the bid values have to be expressed in log values first. For ex-ante applications, therefore, all that is needed is the function that connects the cost estimate to the bid mean and standard deviation, a relationship that is already well researched in the literature and explained later in the Ex-ante prediction subsection of the Results.

Results

The results for the Log-Gamma, Log-Fréchet and Log-Gumbel are relatively poor and not presented here.

Ex-post fit

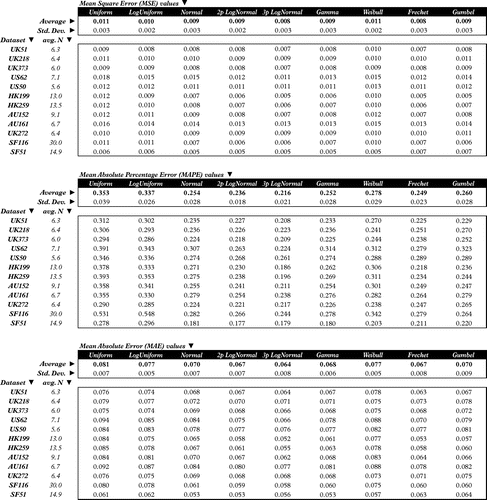
The results of the goodness of fit tests are presented in Figure 1. This contains a separate table for each of the three error measures. The columns in each table show the 9 distributions tested and the rows contain the 12 data-sets, including the average number of bidders (N) once the auctions containing less than 4 bids have been removed. The mean and standard deviation for each of the 9 distributions are given at the head of each column, with higher errors indicating a worse distribution fit. Therefore, the results with figures closer to zero are considered the best fit for each distribution.

Figure 1. Ex-post distribution fit

Several interpretations can be made from Figure 1. The first is that, as expected, the 3p Log-Normal provides the best fit (the phrase “on average” is assumed from this point). Immediately following are the Fréchet and the 2p Log-Normal, tying in second position for MAE and each occupying second or third position in their MSE and MAPE, respectively). Close behind are the Normal, Gamma and Gumbel distributions. Meanwhile, the clear losers are the Weibull, Log-Uniform and Uniform, with the Weibull result being the most surprising, since it is widely used for modelling bid variability (Skitmore et al. 2007).

The second interpretation is that, despite a tentative ranking of fit, a closer look reveals that the error values between the best (3p Log-Normal) and the worst (Uniform) distributions are not as wide as might be expected. For example, for the MAE measurements, the 3p Log-Normal errs by 6.4%, whereas the Uniform is just a little more at 8.1%. This is very little on a scale from 0 to 1 (0 to 100%) and also occurs with the MSE and MAPE measurements, although the basis of comparison is quite close to zero. A tentative conclusion, therefore, is that despite some distributions performing slightly better than others, their differences are not great. Another supporting argument is that the standard deviations (second row in each vertical block) are also generally high enough to anticipate a high degree of overlap between the distributions. That is, a statistical test such as ANOVA might not indicate any significant differences in means.

Ex-ante prediction

The relationship between the cost estimate (forecasting parameter) and each of the distribution parameters is summarized graphically in Figure 2 for the US50 data-set, where the auction cost estimates (noted as b_o) are available for the j auctions of each data-set.¹

Figure 2. Example of the linear regression relationships between the mean bid, minimum bid and bid standard deviation as a function of the cost estimate for US50 (in USD)

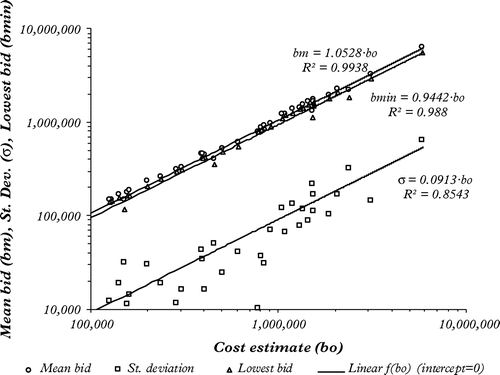
As can be seen, there is a strong linear correlation (R² values very close to 1) between the cost estimate (b_o) and both the mean bid (b_m) and lowest bid (b_min) for this data-set, with and , which means that, on average, the bid average and the minimum of the bids submitted to the auction within data-set US50 were, respectively, around 5.28% above and 5.58% below the cost estimate. This latter parameter b_min – previously noted as x_(1)j in Skitmore’s (1991) original notation – will be used for the 3p Log-Normal parameter estimation. Indeed, these two curves assume that the lines have a null intercept, something that greatly simplifies calculations in some Bid Tender Forecasting Models (BTFM). Also, there is a clear moderate linear correlation between b_o and the bid standard deviation (σ), with (which means an average Coefficient of Variation CV = σ/b_m = 0.0913/1.0528 = 8.67%) and a lower, but still moderately high, R² value of 0.8543. Using the known b_o values (either from a single bidder, before applying a mark-up, or project designer,) to estimate b_m, b_min and σ in this way for each auction enables the distribution fit to be assessed by the MSE, MAPE and MAE results in the same way as before except that cross validation (alternatively termed the “leave-one-out” or “deleted residual” method) is used to better simulate the forecasting situation. This involves estimating the b_m, b_min and σ for an auction using the data of all the other auctions in the database to construct the regression models. With this aim, Table 3 shows, for all the data-sets where the cost estimates are available, the regression coefficients (assuming a null intercept) between the cost estimate b_o and the mean bid (b_m), the lowest bid (b_min) and the bid standard deviation (σ), plus the Coefficient of Variation (CV) calculated as σ/b_m.

Table 3. Regression coefficient values between the cost estimate and the mean bid, minimum bid and bid standard deviation assuming null intercept, and the coefficient of variation, for seven data-sets

Data-set	Cost estimates (bo) provider	bm	bmin	σ	CV
K51	Single bidder	1.042	0.988	0.045	0.043
UK218	–	–	–	–	–
UK373	–	–	–	–	–
US62	Project designer	1.097	1.038	0.044	0.040
US50	Single bidder	1.053	0.944	0.091	0.087
HK199	–	–	–	–	–
HK259	Project designer	0.957	0.861	0.078	0.082
AU152	Project designer	1.030	0.943	0.064	0.062
AU161	Project designer	1.050	0.987	0.069	0.065
UK272	–	–	–	–	–
SP116	–	–	–	–	–
SP51	Single bidder	0.974	0.875	0.059	0.061

Interestingly, although the intentions of the bidders’ and designers’ cost estimates are quite different in principle, with bidders’ estimating their anticipated cost of performing the contract, while designers are estimating the value of the lowest bid, the results shown in Table 3 are surprisingly similar. Taken together, most minimum bids are below the cost estimate itself (as the coefficients are below 1 virtually without exception), which is understandable for the designers are known to prefer overestimating to underestimating (e.g. Cheung et al. 2008). For the bidders, however, this is less clear and highlights the difficulties faced by bidders in winning construction auctions. Moreover, countries such as Hong Kong (HK259) and Spain (SP51) even have average bids below the cost estimate, indicating very different levels of bidding aggressiveness between data-sets (and countries) as it is surprising how, even though most of the minimum bids are below the cost estimate itself countries like Hong Kong (HK259) and Spain (SP51) exacerbate this behaviour by exhibiting auction mean bids whose even the average bids are below the cost estimate too. Such evidence, despite worth pursuing, does not constitute the main aim of this piece of research and will be left for a separate paper on the subject.

Finally, Figure 3 shows the results of repeating this process for all the seven data-sets for which cost estimates are available.

Figure 3. Ex-ante distribution forecasts

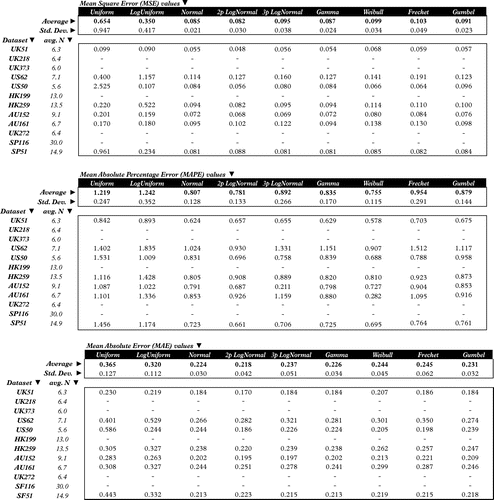
Comparing Figures 1 and 3, it is immediately obvious that the predictive ability is around 10 times worse for the MSE measurements, and from 3 to 4 times for the MAPE and MAE measurements, due to the estimating of b_m, b_min and σ indirectly from the b_o values instead of directly from the data. In contrast with the ex-post results, the best distribution is now the 2p Log-Normal, very closely followed by the Normal and then the Gamma and Gumbel distributions, Weibull, 3p Log-Normal and the Fréchet. The two worst fitting are again the Log-Uniform and Uniform distributions.

Third and fourth moments

To finish this Results section, one part of the analysis regarding the third and fourth moments (skewness and kurtosis) is worthy of comment. As noted earlier, for both the ex-post and ex-ante analyses, all the distributions are fitted by the Method of Moments. For the 2-parameter distributions used here, this implies the parameters are derived solely from the auction b_m and σ, i.e. the first and second moments. To fully assess the distribution fit with the actual data, the third and fourth moments of the actual data are compared with those of the fitted distributions.

In doing this, the first important consideration concerns two of the four special features of construction contract auctions, namely that (1) each contract is different (making the effects of data pooling unpredictable), and (2) there are a small number of bidders for each contract (the statistical procedures for small samples are less well developed than for large samples). The implication of (1) here is that each auction has to be treated as a separate entity, so it is necessary to consider the third and fourth moments for each auction, and for (2) the number of data points involved in calculating the moments are quite small (typically between 4 and 10). Therefore, as the small sampling distribution of the third and fourth moments are known to be highly variable, the best approach is to focus on their average, rather than individual, values.

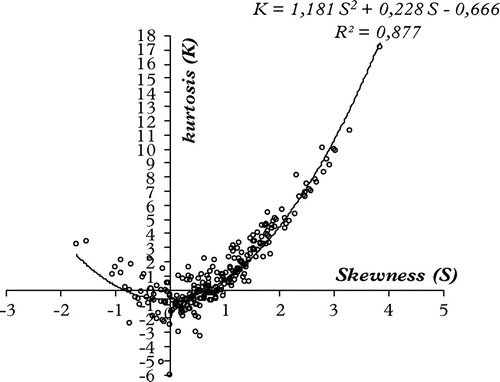
A second consideration is the known quadratic relationship between the third and the fourth moments, with (excess) Kurtosis = a·Skewness² + b·Skewness + c. Importantly, the combination of values of a, b and c are unique for each kind of statistical distribution. To utilize this property, a, b and c are first estimated for the actual bids by regression analysis, as shown in Figure 4.

Figure 4. Example of Skewness–Kurtosis quadratic regression line calculation for the HK259 data-set

Each round point in Figure 4 represents the skewness (X) and kurtosis (Y) values for each auction in the data-set (in this case HK259).

The next step replicates the same operation using each of the candidate distributions for generating simulated bid values. The skewness and kurtosis values are then calculated for each auction and the best regression quadratic curve for each statistical distribution is found for each data-set.

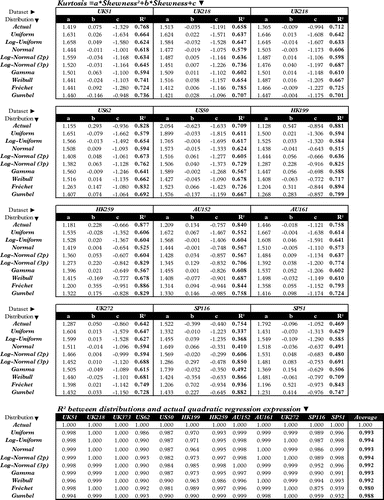
Clearly, if the S-K quadratic expression from a statistical distribution (defined by its a, b and c values) corresponds exactly with the quadratic expression from the actual data, that distribution would be modelling the actual situation perfectly. The regression coefficients obtained by doing this for the actual data and all nine distributions, along with their respective coefficients of determination (R²), are shown at the top of Figure 5.

Figure 5. Skewness–Kurtosis quadratic comparisons

However, with correlations of this nature (where the R² values generally vary between 0.60 and 0.85), directly comparing the coefficients a, b and c from each distribution with the actual a, b and c values seems impractical. That is why a Sub-Table is provided at the bottom of Figure 5 showing the direct correlation between the quadratic expressions from each distribution and the quadratic expression obtained from the actual bid values, i.e. comparing the quadratic expressions from the Sub-Tables above. These values are also numerically equivalent to obtaining the coefficient of determination of the actual S-K points when the quadratic expression from each of the statistical distribution is used, but have the advantage of being expressed on a 0–1 scale.

In interpreting the Sub-Table at the bottom of Figure 5, it is clear that all the distributions closely approximate the actual third and fourth moments, despite being fitted from only the first two moments. The only possible exceptions are the Fréchet and Gumbel distributions, although their average R² values are still above 0.98. However, a closer look indicates that this difference derives from SP116 and SP51, the only Capped Tender data-sets (i.e. with upper limited prices), which might be having a distorting effect on these Extreme Value distributions.

Furthermore, despite almost all distributions providing virtually identical results, the best (average) fit is again provided by the 2p Log-Normal distribution but also, surprisingly, by the Log-Uniform. Overall though, as stated, it can be considered that the four moments of all the distributions provide a close resemblance to those of the actual bid distribution, which reinforces the previous conclusion that, despite some distributions performing slightly better than others, the differences are very small.

Discussion

Ex-post and ex-ante compared

Returning to the differences between the ex-post and ex-ante results, the average deviations in the MAE values increase from 6 to 8% in the ex-post analysis, to 22 to 25% for the top performing distributions in the ex-ante analysis, due to having to forecast the distribution parameters indirectly from the cost estimate. Of interest in this is the difference in distribution ranking between the ex-post and ex-ante situations, with ex-post 3p Log-Normal, Fréchet/2p Log-Normal, Normal, Gamma and Gumbel, and ex-ante 2p Log-Normal, Normal, Gamma, Gumbel, Weibull, 3p Log-Normal and Fréchet.

One possibility relates to the accuracy of the expression for forecasting the bid moments and the consequent parameter estimation by the Method of Moments. The top-performing Normal and 2p Log-Normal distributions make direct use of the bid mean and standard deviation, the former and latter having a strong and moderate correlation, respectively, with the cost estimate. In contrast, the distribution parameters of the Gamma and Gumbel distributions have to be calculated indirectly from the mean and standard deviation, involving an extra layer of uncertainty, and hence they perform slightly worse. The 3p Log-Normal requires three parameters (the extra being the lowest bid, b_min), so the prospects of being more inaccurate are also higher. On other hand, both the Weibull and the Fréchet make use of two parameters. One, commonly termed the “scale” parameter, is quite similar to a “location” parameter. Therefore, this “scale/location” parameter also has a strong linear relationship with the cost estimate with a null intercept. However, the second parameter from these distributions (the “shape” parameter) has no known mathematical relationship connecting it with the cost estimate. Forcing the values to coincide with the average of all the highly variable shape parameter values within the same database, necessarily results in a significant loss of accuracy. The better performance of the Weibull distribution would then be because this variability was slightly lower than the Fréchet. Finally, the Uniform and Log-Uniform distributions make use of the lowest (b_min) and highest (b_max) bids, respectively. However, despite the cost estimate being highly correlated with b_min it is less so for b_max, which eventually increased the bid deviations.

The provisional conclusion, therefore, is that the Log-Normal and Normal distributions constitute a good alternative for bid forecasting purposes. They are certainly not as accurate as they can be when their parameters are calculated ex-post, but are still very useful. This raises the further question of how the forecasting accuracy of the distributions may be improved. For the method used here, this involves improving the expressions connecting the cost estimate (b_o) with the parameters with lower R² values, i.e. mainly the bid standard deviation (σ) and the highest bid (b_max); also, particularly for the Weibull and Fréchet distributions, by finding a mathematical expression for anticipating their shape parameters.

In short, each distribution makes use of a robust parameter that is highly correlated with the cost estimate and another that is weak or even does not have a known expression to be forecast. For BTFM to become widespread in the future for practical purposes in real auctions, more research is needed to improve these “weak” parameters.

The Fréchet and Log-Normal distributions

Reference to the Fréchet for modelling bids, although not new (e.g. Martinez 2013), is rare, making its good ex-post fit a surprising and important result. As noted earlier, the Fréchet distribution is an Extreme Value (EV) distribution. EV distributions are useful for modelling extreme events, that is, the distribution of maxima or minima from other distributions. Normally, the Weibull models the minima from semi-bounded distributions (e.g. ranging from 0 to +∞) and the Fréchet models the maxima from semi-bounded distributions, whereas the Gumbel can model the maxima or minima from unbounded distributions (those ranging from −∞ to +∞). Most interesting, however, is that the parameters from these distributions are somehow “conditioned” (sometimes directly “inherited”) from the original value-generating distribution.

The process for calculating the EV distribution parameters from the source distribution is not generally easy though, and this is reflected in the Fréchet’s low forecasting accuracy in the bidding context. Only a few cases have been studied properly. Nevertheless, among these, the distribution of maxima of the Pareto distribution is of particular interest. The Pareto distribution is a semi-bounded mono-parametric distribution, therefore its distribution of maxima is well modelled (under mild conditions) by the Fréchet distribution (David and Nagaraja 2003). For this particular distribution of maxima, it is known that the Frechet’s shape parameter has the same numerical value as the original Pareto’s shape parameter from which it comes (whenever the Fréchet’s scale parameter equals 1).

On the other hand, it is also well known that the budget items from any construction project follow a Pareto distribution once they are ordered from higher to lower values (Blackman and Chan 2013). So, the obvious speculation would be to “forecast” the Fréchet’s shape parameter by fitting a Pareto distribution to the project construction budget. The resulting Fréchet distribution is unlikely to have a unity scale parameter, which is why this statistical/mathematical problem is not easy to solve. However, this does seem an interesting lead to follow for future research, as well as also to improve the mathematical expression that connects the cost estimate with the bid standard deviation (as this would also benefit the Log-Normal, Normal, Gamma and Gumbel distributions alike).

Finally, concerning the Log-Normal distribution, the analysis of the skewness and kurtosis values indicates the top performing distribution to be the Log-Normal, despite all the other distributions (apart from the Fréchet and the Gumbel in capped tenders) having similarly high coefficients of determination. This confirms the robustness of the Log-Normal result as among the best options, irrespective of the approach. It is also known that the Log-Normal and the Pareto distributions are used interchangeably in many applications since they have relatively similar distribution shapes (Malevergne et al. 2011). The extreme order statistics of a Log-Normal distribution do not have a simple mathematical expression, but they can be closely approximated by another Log-Normal distribution (Munro and Wixley 1970). Overall then, assuming that any construction budget can be relatively well represented by a Pareto or Log-Normal distribution, whose order statistics can also be well modelled by a Fréchet or Log-Normal distribution, respectively. The parameters of the latter might be inferred in the (near?) future from the parameters from the former, bringing some hope for a definitive real breakthrough in Bid Tender Forecasting modelling.

Abnormal bid detection

Another practical application of the results concerns the development of methods for detecting abnormally high or low bids. Assuming that an abnormal bidder can distort the distribution parameters in an auction, the Log-normal distribution, which makes use of the two most relatively robust parameters (mean and standard deviation in log bids) identified so far might be the best option available for calculating the percentiles to which, especially the extremely highest and lowest bids, correspond. This analysis however, should not be directly made with the best-fitting ex-post Log-Normal itself, but through comparing the actual bids with the respective order statistics from that log-Normal distribution. For instance, the lowest bid in an auction with 10 bidders which has been modelled by a log-Normal distribution should be compared with the lowest order statistic of that log-normal distribution in order to fairly assess the chances that the lowest draw in a distribution with 10 iid draws (number of bids submitted) correspond with that (low bid) value.

Other distribution options, such as the three-parameter log-Normal (or even the (log-) Uniform with similar goodness-of-fit results), despite evidencing a better (or at least good) ex-post fit, requires the lowest bid to be used as a location parameter, while the lowest bid is highly susceptible to abnormally low bids, so it would not constitute a reliable distribution for abnormal bid detection purposes.

Overall, this just constitutes a first step in the suggested direction and clearly much more work needs to be developed before further conclusions can be drawn.

Conclusions

Selecting an appropriate statistical distribution for representing the variability of construction auction bids constitutes an essential pre-requisite for many bidding models. The applications of these models are varied in both theoretical (e.g. auction theory and auction design) and practical settings (e.g. bid tender forecasting and abnormal bid detection). However, no previous study has undertaken a thorough comparison of the goodness of fit of the most recurrent statistical distributions. This study has addressed this knowledge gap by comparing nine commonly found distributions, with three different goodness-of-fit measures, ex-post description and ex-ante forecasting for 12 construction data-sets around the world from different time periods and nature of works.

The most significant results, quite surprisingly, are the small differences in fit between the different distributions tested and, in many cases, not significant among the top performers. However, irrespective of the testing approach used, the Log-Normal distribution stands out as consistently offering the best fit, with its three-parameter version providing just a minimum ex-post improvement.

Another unexpected distribution which currently performs as well as the Log-Normal when describing past bids ex-post is the Fréchet distribution. Other distributions, such as the Gamma and Normal also offer a very good fit, whereas the Uniform and Log-Uniform seem to be consistently the worst options.

However, the study has demonstrated that, to develop more effective tools for forecasting future bids, further research is needed into the parameter estimation of the distributions involved – particularly bid standard deviation and the Fréchet shape parameter – as their ex-ante accuracy is around three to four times less than their ex-post accuracy. Some guidance connecting the Pareto-distributed construction budget and its Fréchet-distributed (or Log-Normal-distributed) order statistics has been provided. These connections deserve further attention for their potential to eventually help overcome the current main limitation in considering the economic cost estimate as the unique forecasting variable for determining the parameters of modelling the distribution of auction bids.

Also of note is that the comparisons made here take advantage of almost optimal conditions for fitting the distributions (bid values known for the ex-post analysis and all auctions known for ex-ante analysis), whereas the data may be much less complete in a real-world situation. As has been demonstrated in this paper, the most appropriate distribution depends on the data available. In the same vein, one of the early stated limitations of the present analysis is the iid assumption, making the results applicable to situations in which bidder IDs are not known. In this sense, new evidence has been found that there might be a relatively stable distribution type that is not expected to differ much among bidders. However, it is also acknowledged that the mechanisms for such stability are hard to explain when potentially heterogeneity among bidders’ bidding behaviour is neglected. Probably because of this, it has been in general difficult to establish a particular single fit-for-all distribution for modelling the iid bid distribution in an auction.

For situations where bidder IDs are known, on the other hand, the fact that bidders may behave significantly different to each other would need to be taken into account, or at least tested for significance. One thing that is clear from the analysis in this paper is that the evidence does not seem to be in favour of the existence of multimodal distributions (a possible sign of bidder heterogeneity). The generally high level of accuracy found in ex-post distribution fit suggests that the differences that do exist in bidding behaviours between bidders may not be significantly detrimental in the application of bidding models to construction contract auctions.

Disclosure statement

No potential conflict of interest was reported by the authors.

Notes

1. Note that, strickly speaking, we should use the notation b_o j, b_m j, b_min j and σ_j. However, for the sake of simplicity, we will just refer to them as b_o, b_m, b_min and σ as follows.