Preventing environmental disasters from grounding accidents: A case study of tugboat positioning along the Norwegian coast

Abstract

An important task of operators in Norwegian vessel traffic services (VTS) centres is to cleverly position tugboats before potential vessel distress calls. Here, we formulate a non-linear binary-integer program, integrated in a receding horizon control algorithm that minimises the expected cost of grounding accidents by positioning tugboats optimally under uncertainty about vessel incidents and environmental conditions. Linearisations of the model lead to easy-to-compute bounds on the optimal value. Numerical experiments with real-world data demonstrate significant reduction in the expected cost, suggesting that the model can be used as a decision-support tool at VTS centres.

Keywords:

• OR in maritime industry
• mixed integer programming
• search and rescue
• oil spill

1. Introduction

During the last decades marine transportation of crude oil and petroleum products has increased considerably as well as its associated risk to the environment. Although accidental oil spills from tankers are relatively rare (Goerlandt & Montewka, 2014), oil transport remains one of the main concerns for various stakeholders in the protection of the marine environment (Dalton & Jin, 2010). Indeed, oil spills can result in severe consequences to the marine ecosystem (Lecklin, Ryömä, & Kuikka, 2011). In addition, there are high socioeconomic costs, clean-up costs, and even possibility of loss of life. Most of the large oil spills are related to grounding and collision accidents of oil tankers (Vanem, Endresen, & Skjong, 2008). About one third of commercial ship accidents are caused by ship grounding accidents (ITOPF, 2013).

In Norway, several hundred oil tankers travel each year along the northern coastline. To monitor this traffic, the Norwegian Coastal Administration (NCA) operates a centre for vessel traffic services (VTS) in the town of Vardø in northeastern Norway. The VTS centre is responsible for the coastline from the Russian border in the Barents Sea to Rørvik near Trondheim, a distance of more than 600 nautical miles. The region is environmentally sensitive due to important fisheries and increasing tourism. About 200 vessels are monitored daily by the VTS centre of which 10–20 oil tankers receive special attention due to their size or risk of pollution (Eide et al., 2007). These tankers are required by law to sail along a predefined corridor about 27 nautical milesfrom the coast. The VTS centre operates a fleet of two tugboats with the purpose to intercept any vessel that lose steering, propulsion, or power, and drift towards land. Dynamic information (e.g., position, heading, speed over ground, rate of turn) and static information (e.g., identity, dimensions, cargo, flag) of the ships entering the region are obtained every 2 s on average through the Automatic Identification System (AIS). In addition to AIS information, weather forecast, real-time measurements of ocean currents, wave height, and wind are available to predict drift trajectories. At any time, an oil tanker moving in the region may lose its maneuverability, e.g., through steering or propulsion failure. Thus, the tugboats have to be sufficiently close to hook-up with any drifting oil tanker before it runs ashore.

The increasing oil tanker traffic in the High North makes it difficult for the VTS operators to dynamically position the tugboats to locations where they can be the most effective. In an effort to improve the positioning of tugboats, the authors were invited by the NCA to visit the VTS centre in Vardø and suggest improvements in the process. This paper reports models for the optimal tugboat positioning (OTP) problem as well as computational results obtained after the visit and subsequent meetings and exchanges of information with the VTS centre and the NCA representatives. NCA is currently evaluating the possibility to implement the models in a decision support system operating at the VTS. This paper is the first to formulate the OTP problem and demonstrate the benefits from its solution using historical events.

The remainder of the paper is organised as follows. In Section 2, we introduce the related literature on emergency response and safety organisation. In Section 3, formulate a non-linear binary integer program (BIP) for the OTP problem with two linearisations. Section 4 gives methods for obtaining input data to the models, and Section 5 presents computational experiments. The paper ends with conclusions and a discussion of further research in Section 6.

2. Related literature

We present a review on general resource location/allocation and patrol routing problems, where safety organisation and emergency response systems are the primary concern, followed by specific literature on the OTP problem.

The patrol routing problem consists of maximising the coverage of critical highway stretches subject to constraints on available resources and feasible routes. As in the vessel traffic service, ambulance emergency medical services (EMS), police districting problems (PDP), and freeway service patrol (FSP) problems are cases of emergency response systems, where resources are allocated to demand points in a short response time. The OTP problem, however, differs from other emergency response systems because of the high environmental consequences, human casualties and the possibility of extremely bad weather conditions, which require dynamic allocation and positioning of resources in a highly stochastic and dynamic environment.

The primary goal of the EMS is to save lives by ensuring quick response to emergencies of which the performance is affected by the ambulance locations and their deployment. Tavakoli and Lightner (2004) use a mathematical modelling approach to solve the locating/allocating of emergency vehicles and facilities. Moreover, preparedness is a way of assessing the ability to serve current and future potential patients with ambulances. Accordingly, Andersson and Värbrand (2007) propose new algorithms for the ambulance deployment and the dynamic ambulance relocation problems, with the primary goal of finding new locations for some of the ambulances that increases the preparedness in the area of interest. Their problem is similar to the one studied in *Gendreau2001, with the major difference of relocating ambulances to any zone in the region of interest, not just to vacant stations. The objective function of their dynamic relocation model minimises the maximum travel time for any of the relocated ambulances. Lee (2011) investigates the role of preparedness by developing a dispatching algorithm that takes into account future calls. It is found in their study that the consideration of preparedness in ambulance deployment considerably reduces the response time.Indeed, a greedy minimisation of each current call might increase the response time of future calls that have high call rates.

To account for uncertainty on the ambulance availability, the hypercube model is found to be useful in determining the EMS systems performance (Jarvis, 1985). However, it is computationally expensive as the number of simultaneous equations for m servers (ambulances) would be equal to $2^m$. To address this issue, approximations of the hypercube model have been developed with some assumptions on the distribution of the service time (Rajagopalan, Xiao & Saydam, 2008). A MIP model that finds best locations of highway incidents at a minimum cost is proposed by Pal and Bose (2009). Their approach consider fixed and variable costs of vehicles and depots, but they do not consider the deployment of the response segments as in *Iannoni2009. These authors develop a method to optimise the configuration and operation of EMS on Brazilian highways. The method considers the location of ambulance bases along the highway and the districting of the response segments. Their approach embeds a spatially distributed hypercube model into a hybrid genetic algorithm. Similarly, *ToroDiaz2013 propose a mathematical formulation that combines integer programming model representing location and dispatching decisions, with a hypercube model that represents the congestion phenomena and queuing elements. Their results, obtained with genetic algorithms, show that minimising the response time and maximising the coverage can be achieved using a common closest dispatching rule. *Majzoubi2012 consider the problem of dispatching and relocating EMS vehicles with possibility of rerouting a vehicle transporting a low-priority patient to pick-up one more patient. They propose a solution based on integer nonlinear and linear programming models with an approximation algorithm. Although the OTP problem is different from the EMS, they share a common goal of quick response to distress calls.

The PDP involves the design of patrol sectors in terms of performance attributes such as response time and workload that result in crime reduction and better service. Camacho-Collados and Liberatore (2015) develop a decision support system based on mathematical algorithms that incorporate predictive policing capabilities with patrolling districting model. The aim of their system is to reduce the probability of criminal acts. Similarly, *Miskovic2015 propose a mathematical model for the emergency service network of Police Special Forces Units (PSFUs) in the Republic of Serbia and solve the problem with a variable neighbourhood search (VNS) algorithm. In addition, *Camacho20151 investigate crime prevention by increasing the effectiveness of the deterrent effect of the agent’s presence on the territory. This is achieved by concentrating the agents in the areas with a higher risk of crime. Other approacher such as dynamic programming are also used to optimally deploy crime preventive police patrol teams to areas of higher risk of crime (Oghovese & Olaniyi, 2014). *DSPSSINQTEAmico2002 and Zhang and Brown (2013) on the other hand focus on the reaction to crime incidents with the objective of minimising the response to emergency calls.

Another related patrol problem studied in the literature is the FSP problem, which consists of deploying freeway service patrols to detect, respond to and clear traffic incidents. A network of freeways are divided into a set of patrol beats (connected freeway segments) and tow trucks are assigned to patrol each of these beats, moving back and forth to clear any possible incident, which consists of changing flat tires, offering gasoline and moving vehicles. *Lou2011 develop two non-linear mixed integer programming (MIP) models for deterministic and stochastic integrated beat design and fleet allocation of FSP. Their main objective is to minimise the expected total response time over the high-consequence scenarios.

The OTP problem closely relates to maritime search and rescue (SAR) operations. SAR operations consist of search for missing or distressed vessels followed by their rescue. Basdemir (2004) proposes a maximal covering location problem (MCLP) model that allocates SAR helicopters to candidate bases to satisfy predefined incidents regions. A combination of p -median problem ( p -MP) and p -centre problem ( p -CP) models are used in *Dawson2007 to determine the locations of security teams over a geographic area to maintain security for the United States air force intercontinental ballistic missile systems. The combined model minimises both the distance travelled and the maximum distance from any missile site to required security forces. An optimisation and simulation method is used in *Afshartous2009 to determine the locations of the United States coast guard air stations to respond to emergency distress calls. They model the problem as a p -Uncapacitated Facility Location Problem ( p -UFLP). The authors assume the demand for each client to be equal and served with a single resource. A similar problem is presented in Razi and Karatas (2016), but the demand for each incident varies and each demand can be covered from multiple resources. Radovilsky and Koermer (2007) develop an integer linear programming model to optimally allocate small boats to the United States coast guard (USCG) stations. Their objective function minimises the shortage or excess capacity at the stations. An improved formulation called boat allocation tool (BAT) is developed by Wagner and Radovilsky (2012), but do not consider actual locations of incidents and the corresponding response time. *Chircop2013 address the fleet sizing problem faced by the Royal Australian Navy (RAN) with a column generation algorithm incorporated into a branch-and-price framework. A fleet patrol boats should be able to provide complete coverage of a set of specified patrol regions. Moreover, Millar and Russell (2012) develop a binary integer programming model (BIP) for the fisheries surveillance patrol routing problem in the Canadian Atlantic offshore groundfish fishery. The primary goal of the fisheries patrol routing problem is to maximise the deterrent effect of a patrol vessel through routing over a network of fishing grounds. They are the first to formulate this problem, which relates to the selective travelling salesman problem, where the fishing grounds represent the cities, and all or a subset of grounds is visited on a given trip. Their model, however, focuses more on scheduling than boat positioning. Additionally, (Wang, Zhu, Kaku, Chen, and Wang, 2014), address the tugboat assignment problem under a hybrid scheduling rule and present an improved discrete particle swarm optimisation (IDPSO) algorithm to minimise the turnaround time of ships. *Pelot2015 categorise SAR boats based on their capabilities and use historical incident data to solve the allocation problem for the Canadian coast guard. In their study, incidents are classified based on their severity and a response time requirement is established for each type. Similarly, Eide et al. (2007) develop a dynamic risk model that prioritise oil tankers based on their potential oil spill volume in case of grounding accidents and subdivide the northern Norwegian coastline in segments, where each segment has an associated risk level. The model estimates the environmental risk of a drift grounding accident occurring with a specific tanker, at a given location, and under current weather conditions. Drift trajectories with high risk can then be prioritised in the planning of tugboat positions. Abi-Zeid and Frost (2005) develop a geographic decision support tool (SRAPlan) based on search theory to assist the Canadian forces in the planning of search missions for missing aircrafts. A similar system is also developed for the Polish SAR teams (Wysokiński, Robert, & Dajda, 2014).

All these tools and models, despites their importance, do not suggest how and where the fleet of tugboats should move in order to minimise risk. Razi and Karatas (2016) on the other hand develop a tactical model for determining the optimal placement of SAR boats, however, their model do not account for uncertainty related to vessel incidents and the dynamic nature of the SAR resources positioning, which are the primary concern of the OTP problem. To determine the optimal positions of tugboats in real time, researchers have developed methods both including genetic algorithms (Bye, 2012; Bye & Schaathun, 2014; Bye & Schaathun, 2015a, b) and an MIP model (Assimizele, Oppen, & Bye, 2013). Their algorithms and models assume oil tankers move along piecewise-linear corridors and approximately parallel to the coastline. Additionally, their proposed set of objective functions focuses mainly on the minimisation of distances between future tugboat positions and locations, where hook-up with a drifting vessel might be possible. However, in situations with multiple tugboats, sum of distances are not effective surrogates for the probability of successful hook-up between a tugboat and a vessel and the cost associated with failure to do so. In addition, a distance minimisation will not capture the different consequences associated with each vessel type and grounding location. Moreover, a one-dimensional modelling approach also has less flexibility in geographical positioning. All these weaknesses are addressed in this paper with a two-dimensional nonlinear binary integer programming model.

In contrast to the optimisation of SAR and related operations (see for example Alpern & Gal, 2002; Pietz & Royset, 2015; Royset & Sato, 2010; Shechter, Ghassemi, Gocgun, & Puterman, 2015; Stone, 2016 and references therein), where search for a vessel is a central aspect, operators in the present context know the location of vessels. In an OTP problem, a tanker in distress has a known current location due to the continuously transmitted AIS information. That is, the OTP problem is primarily a rescue mission. However, uncertainty about which vessel will need assistance and the subsequent drift trajectories and weather conditions add complexity to the process of planning current and future tugboat positions. Thus, our aim is to assist the VTS operators by developing a non-linear BIP model integrated in a receding horizon control algorithm that minimises the expected environmental cost associated with grounding vessels and utilises a two-dimensional discretisation of the coastal zone. Royset and Sato (2010) adopt a similar two-dimensional modelling approach by subdividing the region of interest into a finite set of cells in a discrete-time route-optimisation problem, where searchers seek to detect randomly moving targets.

3. Model formulation

We subdivide the High North region controlled by the VTS centre in Vardø into a finite number of cells $\mathcal{C}=\{1,...,C\}$ and discretise the planning horizon into a finite set of time periods $\mathcal{T}=\{0,1,...,T\}$. Each vessel (oil tanker) in the set $\mathcal{V}=\{1,...,V\}$ occupies one cell at each time period and can move to any reachable cell in a time period depending on its speed, which is influenced by the weather conditions.

Every vessel $v\in \mathcal{V}$ is associated with a family of possible paths and times when it might become in distress. A path $p=(c_1,c_2,...,c_T)$, $c_t\in \mathcal{C}$, is a sequence of cells representing the trajectory of the vessel over time. The pair ${\omega }_v=(t,p)$ gives a vessel scenario for vessel v , where p is the associated path and $t\in \mathcal{T}\cup \{T+1\}$ is the time the VTS centre is alerted to the distress of vessel v . Typically, the vessel reports steering failure, loss of propulsion, and other issues through AIS. However, sometimes incidents go unreported and the VTS centre might simply observe a change in heading and speed. We let ${\mathrm{\Omega }}_v$ be the set of scenarios for vessel v . Typically, each vessel has a scenario (t, p) , where the path p is the planned trajectory of the vessel in the absence of failure. In this case, there will be no distress call and the time t is set to $T+1$. In addition, we define $\overline{\omega }=({\omega }_1,...,{\omega }_V)\in \overline{\mathrm{\Omega }}$ , where $\overline{\mathrm{\Omega }}={\mathrm{\Omega }}_1\times ....\times {\mathrm{\Omega }}_V$ is the collection of all scenarios. Even though we consider a finite number of scenarios, the approach is general. In the case of a continuous probability distribution, one can always construct an approximation, for example, by sampling that approximates the actual distribution; see for example Shapiro and Darinka (2009) for details.

Let $\mathcal{G}=\{1,...,G\}$ be the set of tugboats operated by the VTS centre in Vardø. At the beginning of the planning horizon, each tugboat $g\in \mathcal{G}$ is positioned at cell $c_{0g}\in \mathcal{C}$. The tugboats can transit between reachable cells each time period. Specifically, let ${\mathcal{F}}_{\mathit{tg}}(c)\subset \mathcal{C}$ be the set of cells that are adjacent to $c\in \mathcal{C}$ in period t for tugboat g . That is, the set of cells reachable from cell c in one time period by tugboat g . The set ${\mathcal{F}}_{\mathit{tg}}(c)$ depends on the weather conditions in time period t and the maximum speed for tugboat g . Additionally, the fleet of tugboats is not allowed to move far away from the coastline because of a secondary escort mission; some of the ships in transit to ports located in the north of Norway need to be escorted by tugboats. This secondary task does not influence the model we develop as the available number of tugboats at each time period in the planning horizon is known well in advance.

A vessel might start drifting at any time period with a certain probability, which depends on internal factors of the vessel as well as the weather conditions (e.g., ocean current, wave height). Moreover, the path followed while drifting is also determined by environmental factors. In Section 4, we give details about how the specifics of a scenario can be computed. We let $R_{{\omega }_v}$ be the probability of scenario ${\omega }_v$ for vessel v . We assume that the probability of a scenario for a vessel is independent of the probability of a scenario for another vessel. Although this assumption might not always be reasonable, here we justify it by the fact that vessels in distress are usually spatially separated with few common environmental factors. Hence, the probability for a scenario $\overline{\omega }$ is given by $R_{\overline{\omega }}={\prod }_{v\in \mathcal{V}}{R}_{{\omega }_v}$. A critical component is a tugboat’s ability to hook-up with a vessel that is drifting next to it. We let the probability of successful hook-up by tugboat g with vessel v , given vessel v follows scenario ${\omega }_v=(t,p)$ and tugboat g is in cell c at time of distress call t , be denoted by $Q_{gc{\omega }_v}$.

The aim is to move tugboats between cells in such a way that the expected cost of ship grounding accidents is minimised. Let $K_{{\omega }_v}$ be the grounding cost associated with vessel scenario ${\omega }_v=(t,p)$, i.e., the cost for a vessel following path p and no tugboat manages to hook-up with the drifting vessel. We note that $K_{{\omega }_v}$ is a deterministic quantity, but it is trivial to account for uncertainty in the cost by defining additional vessel scenarios. The cost mostly depends on the grounding location as well as the type and volume of the oil spill. This cost is equal to zero for vessel scenarios having $t=T+1$, i.e., no failure occurs and the vessel follows a normal route in the corridor. We define $x_{\mathit{gct}}$ as a binary variable that takes the value 1 if tugboat g is in cell c at time t , and 0 otherwise. For a tugboat g in cell c at time of distress t , the probability of not being able to hook-up with vessel v following scenario ${\omega }_v=(t,p)$ is $1-Q_{gc{\omega }_v}$. Thus, the probability that no tugboat rescues vessel v if vessel scenario ${\omega }_v$ occurs equals$$\begin{array}{c}\hfill \prod _{g\in \mathcal{G},c\in \mathcal{C}}{(1-Q_{gc{\omega }_v})}^{x_{\mathit{gct}}}.\end{array}$$

Note that subscript t in the variable $x_{\mathit{gct}}$ is the time of distress in scenario ${\omega }_v=(t,p)$ and the probability of hook-up $Q_{gc{\omega }_v}$ is relative to that time. Then, the expected grounding cost for scenario $\overline{\omega }$ equal(1) $$\begin{array}{c}\hfill \sum _{v\in \mathcal{V}}{K}_{{\omega }_v}\prod _{g\in \mathcal{G},c\in \mathcal{C}}{(1-Q_{gc{\omega }_v})}^{x_{\mathit{gct}}}.\end{array}$$(1)

The expected total cost across all scenarios follows as(2) $$\begin{array}{c}\hfill \sum _{\overline{\omega }=({\omega }_1,....,{\omega }_V)\in \overline{\mathrm{\Omega }}}{R}_{\overline{\omega }}\sum _{v\in \mathcal{V}}{K}_{{\omega }_v}\prod _{g\in \mathcal{G},c\in \mathcal{C}}{(1-Q_{gc{\omega }_v})}^{x_{\mathit{gct}}},\end{array}$$(2)

which we denote by $f(\mathbf{x})$, where $\mathbf{x}$ is the vector with components $x_{\mathit{gct}}$. Let ${\alpha }_{gc{\omega }_v}=-ln(1-Q_{gc{\omega }_v})$ be the hook-up rate. The function f can be equivalently written as:(3) $$\begin{array}{cc}& f(\mathbf{x})=\sum _{\overline{\omega }=({\omega }_1,....,{\omega }_V)\in \overline{\mathrm{\Omega }}}{R}_{\overline{\omega }}\sum _{v\in \mathcal{V}}{K}_{{\omega }_v}\hfill \\ \hfill & \times exp\left(-\sum _{g\in \mathcal{G}}\sum _{c\in \mathcal{C}}{\alpha }_{gc{\omega }_v}{x}_{\mathit{gct}}\right).\hfill \end{array}$$(3)

Since costs are nonnegative, f is a convex function. In fact, the exponential function is convex and f is a sum of exponential functions. In the following subsections, we formulate the OTP problem as a non-linear BIP and give linear approximations.

3.1. OTP model

A nonlinear BIP model is developed next to minimise the objective function f in (3) subject to operational constraints.

OTP model:

Indices

t	=	time period
$c{c}^{\prime }{c}_t$	=	cells
v	=	vessel
g	=	tugboat
p	=	path $p=(c_1,...,c_T)$
${\omega }_v$	=	scenario for vessel v ; ${\omega }_v=(t,p)$
$\overline{\omega }$	=	scenario for all vessels $\overline{\omega }=({\omega }_1,...,{\omega }_V)$

Sets

$\mathcal{C}$	=	set of cells $\mathcal{C}=\{1,...,C\}$
${\mathcal{F}}_{\mathit{tg}}(c)\subseteq \mathcal{C}$	=	set of cells reachable from cell c in period t for tugboat g
$\mathcal{V}$	=	set of vessels $\mathcal{V}=\{1,...,V\}$
$\mathcal{G}$	=	set of tugboats $\mathcal{G}=\{1,...,G\}$
$\mathcal{T}$	=	set of time periods $\mathcal{T}=\{0,1,...,T\}$
${\mathrm{\Omega }}_v$	=	set of scenarios for vessel v
$\overline{\mathrm{\Omega }}$	=	set of all possible scenarios $\overline{\mathrm{\Omega }}={\mathrm{\Omega }}_1\times ....\times {\mathrm{\Omega }}_V$

Parameters

$K_{{\omega }_v}$	=	grounding cost for vessel v in scenario ${\omega }_v=(t,p)$
$R_{{\omega }_v}$	=	probability for vessel scenario ${\omega }_v=(t,p)$
$R_{\overline{\omega }}$	=	probability for scenario $\overline{\omega }=({\omega }_1,...,{\omega }_V)$, $R_{\overline{\omega }}={\prod }_{v\in \mathcal{V}}{R}_{{\omega }_v}$
$Q_{gc{\omega }_v}$	=	probability of successful hook-up by tugboat g with vessel v, given tugboat g is in cell c at time of distress call t and vessel v follows scenario ${\omega }_v=(t,p)$
${\alpha }_{gc{\omega }_v}$	=	hook-up rate with vessel v for tugboat g in cell c under scenario ${\omega }_v$, ${\alpha }_{gc{\omega }_v}=-ln(1-Q_{gc{\omega }_v})$

Variables

$x_{\mathit{gct}}$

=

binary variable taking the value 1 if tugboat g is in cell c at time t, 0 otherwise

Formulation$$\begin{array}{c}\hfill minf(\mathbf{x})\end{array}$$                        s.t.(4) $$\begin{array}{cc}\hfill \sum _{c\in {\mathcal{F}}_{\mathit{tg}}(c^{\prime })}{x}_{gct-1}& \ge x_{g{c}^{\prime }t}\forall g\in \mathcal{G},\forall c^{\prime }\in \mathcal{C},\forall t\in \mathcal{T}\backslash \{0\}\hfill \\ \hfill \sum _{c\in \mathcal{C}}{x}_{\mathit{gct}}& =1\forall g\in \mathcal{G},\forall t\in \mathcal{T}\hfill \\ \hfill x_{g,c_{0g},0}& =1\forall g\in \mathcal{G}\hfill \\ \hfill x_{\mathit{gct}}& \in \{0,1\}\forall g\in \mathcal{G},\forall c\in \mathcal{C},\forall t\in \mathcal{T}\hfill \end{array}$$(4)

Constraints (4) ensure tugboats move only between reachable cells. In addition, constraints (5) make sure tugboats are not located in more than one cell in any time period. Constraints (6) give initial positions of tugboats. That is, cell $c_{0g}$ is the position of tugboat g at the beginning of the planning horizon.

3.2. Linearisation of the objective function

The assignment of tugboats to vessels is done dynamically in a highly uncertain environment. Thus, the OTP problem is modelled as a multiple time periods dynamic and stochastic convex non-linear integer programs integrated in a receding horizon control framework to allow the change of information about vessels, probabilities of failure, drift trajectories and its associated expected environmental cost and probabilities of successful hook-up. This approach is a major contribution of the paper as it avoids the formulation of a multistage stochastic program and the associated high-computational cost. It is, however, important to note that the model formulations in this paper look similar to that of a multi-stage stochastic problem. We have done preliminary computations with non-linear solvers and the computational time is very high.

Since a direct solution of the OTP model might be computationally costly, we develop two approaches to linearise the objective function f and obtain two resulting mixed-integer linear programming models MIP-L and MIP-U. A viable alternative could be the continuous relaxation (Branch-and-bound) to the convex problem using standard mixed-integer nonlinear program (MINLP) solvers. However, Royset and Sato (2010) use a similar non-linear convex exponential function to address the discrete-time route-optimisation problem. They present two solutions approaches, one based on the cutting-plane (linearisation) method and the other on continuous relaxation of the objective function. In their study, standard MINLP solvers , Bonmin and DICOPT, have higher solution time compared to CPLEX with the linearised model. Moreover, the effective cut-building technology in mixed-integer linear program (MIP) are not available in the MINLP solvers.

3.2.1. Lower linearisation: MIP-L

New nonnegative variables $z_{{\omega }_v}$ are included to remove the nonlinearity in the objective function through the standard lower-bounding approximation (Ramos, 2007; Royset & Sato, 2010)$$\begin{array}{cc}& exp(-y)\ge \underset{k\in \mathcal{K}}{max}\{exp(-y_k)-exp(-y_k)(y-y_k)\}\hfill \\ \hfill & \forall y,y_k\in \mathbb{R},k\in \mathcal{K}.\hfill \end{array}$$

Accordingly, let $Y_{{\omega }_{v}k}\in \mathbb{R}$, $k\in \mathcal{K}$, where $\mathcal{K}$ represents the set of breakpoints. The resulting mixed-integer linear model (MIP-L) takes the following form.

Model MIP-L:

Additional Set

$\mathcal{K}$

=

set of breakpoints $\mathcal{K}=\{1,...,K\}$

Additional Parameters

$Y_{{\omega }_{v}k}$

=

breakpoint number k , $k\in \mathcal{K}$ for vessel scenario ${\omega }_v$

Additional Variables

$z_{{\omega }_v}$

=

nonnegative variable used for linearisation for vessel scenario ${\omega }_v$

Formulation$$\begin{array}{c}\hfill min\sum _{\overline{\omega }=({\omega }_1,....,{\omega }_V)\in \overline{\mathrm{\Omega }}}{R}_{\overline{\omega }}\sum _{v\in \mathcal{V}}{K}_{{\omega }_v}{z}_{{\omega }_v}\end{array}$$                        s.t.$$\begin{array}{c}\hfill (4)-(7)\text{and}\end{array}$$ Let ${\theta }_{\text{OPT}}$ and ${\theta }_{\text{MIP-L}}$ be the optimal value for the OTP and MIP-L models, respectively. Obviously, ${\theta }_{\text{MIP-L}}\le {\theta }_{\text{OPT}}$.

3.2.2. Upper linearisation: MIP-U

It is well known (Lin, Carlsson, Ge, Shi, & Tsai, 2013; Bazaraa, Sherali, & Shetty, 1995) that $exp(-y)$ can be bounded from above on $[0,y_{max}]$ by a piecewise linear function that coincides with $exp(-y_k)$ at points $y_k\in [0,y_{max}],k\in \mathcal{K}$. We apply this approach to the term $exp(-{\sum }_{g\in \mathcal{G}}{\sum }_{c\in \mathcal{C}}$${\alpha }_{gc{\omega }_v}{x}_{\mathit{gct}})$ and set $y_{max}={\sum }_{g\in \mathcal{G}}{max}_{c,{\omega }_v}{\alpha }_{gc{\omega }_v}$. The piecewise linear function is most easily represented by nonnegative auxiliary variables that sums to one. Specifically, ${\sum }_{k\in \mathcal{K}}{\lambda }_{k}exp(-y_k)\ge exp(-{\sum }_{k\in \mathcal{K}}{\lambda }_k{y}_k)$ for $0\le {\sum }_{k\in \mathcal{K}}{\lambda }_k{y}_k\le y_{max}$. Using these relations, we obtain the upper-bounding model MIP-U as follows:

Model MIP-U:

Additional Parameters

$Y_{{\omega }_{v}k}$, $F_{{\omega }_{v}k}=exp(-Y_{{\omega }_{v}k})$

=

function values at $k\in \mathcal{K}$

Additional Variables

${\lambda }_{{\omega }_{v}k}$

=

nonnegative variable used for linearisation

Formulation$$\begin{array}{c}\hfill min\sum _{\overline{\omega }=({\omega }_1,....,{\omega }_V)\in \overline{\mathrm{\Omega }}}{R}_{\overline{\omega }}\sum _{v\in \mathcal{V}}{K}_{{\omega }_v}\left(\sum _{k\in \mathcal{K}}{\lambda }_{{\omega }_{v}k}{F}_{{\omega }_{v}k}\right)\end{array}$$

s.t.$$\begin{array}{c}\hfill (4)-(7)\text{and}\end{array}$$$$\begin{array}{cc}& \sum _{g\in \mathcal{G}}\sum _{c\in \mathcal{C}}{\alpha }_{gc{\omega }_v}{x}_{\mathit{gct}}=\hfill \\ \hfill & \sum _{k\in \mathcal{K}}{\lambda }_{{\omega }_{v}k}{Y}_{{\omega }_{v}k}\forall {\omega }_v=(t,p)\in {\mathrm{\Omega }}_v,\forall v\in \mathcal{V}\hfill \\ \hfill & \sum _{k=1}^K{\lambda }_{{\omega }_{v}k}=1\forall {\omega }_v=(t,p)\in {\mathrm{\Omega }}_v,\forall v\in \mathcal{V}\hfill \\ \hfill & {\lambda }_{{\omega }_{v}k}\ge 0\forall {\omega }_v\in {\mathrm{\Omega }}_v,\forall v\in \mathcal{V},\forall k\in \mathcal{K}\hfill \\ \hfill \end{array}$$

The optimal value of MIP-U provides an upper bound for ${\theta }_{\text{OPT}}$. However, it is obviously better to use the true objective function value. Accordingly,$$\begin{array}{c}\hfill {\theta }_{\text{MIP-L}}\le {\theta }_{\text{OPT}}\le min\{f(\overline{\mathbf{x}}),f(\underline{\mathbf{x}})\},\end{array}$$

where $\overline{\mathbf{x}}$ and $\underline{\mathbf{x}}$ are the vectors of optimal $x_{\mathit{gct}}$ for MIP-U and MIP-L, respectively. We observe that MIP-L suffices to generate both upper and lower bounds on ${\theta }_{\text{OPT}}$, but we also include MIP-U as it solves much faster than MIP-L and sometimes yields better solutions.

4. Input parameters

In this section, we present preliminary methods to obtain accurate input parameter to the OTP model.

4.1. Hook-up probabilities

Each drifting vessel is detected by the VTS centre, which in turn informs the nearest tugboat. The time needed for a tugboat to reach the drifting vessel depends on the reaction and mobilisation time, sailing time from the initial tugboat position to the vessel and the time required to hook-up the vessel to the tugboat. It takes on average 2 h to hook-up the drifting vessel with the tugboat when they are next to each other, but this can increase in bad weather conditions (Eide et al., 2007). Once the vessel is reached by the tugboat, the time, $t_l$, left before it runs ashore will determine the probability of successful hook-up. Recall that $Q_{gc{\omega }_v}$ is the probability of successful hook-up by tugboat g to vessel v, given tugboat g is in cell c at time t and vessel v follows ${\omega }_v=(t,p)$. For every vessel scenario and tugboat position, we determine $t_l$ using the maximum speed of the tugboat and the location of c relative to p , and set$$Q_{gc{\omega }_v}={\displaystyle \frac{{\beta }_{{\omega }_v}exp({\delta }_{{\omega }_v}(t_l-t_{\text{min}}))}{1+exp({\delta }_{{\omega }_v}(t_l-t_{\text{min}}))}}.$$

The parameter $t_{\text{min}}$ represents the minimal remaining drift time required to attempt hook-up. If $t_l$ is less than $t_{\text{min}}$, $Q_{gc{\omega }_v}$ is set to 0 . In addition, ${\beta }_{{\omega }_v}\in \left[0,1\right]$ and ${\delta }_{{\omega }_v}\ge 0$ represent the influence of weather. This model is a preliminary attempt to estimate the hook-up probabilities. Further work is needed to fit the model using empirical data from field tests and actual accidents.

4.2. Drift trajectories

The motion of a drifting vessel is entirely determined by the sum of surface and body forces acting on it (Jankowski, 1992). The forces acting on the surface are caused by the buoyancy force, the sea surface current, surface wind and the waves. The gravitational force is the only body force acting on its centre of mass.

The drift caused by the wind alone is termed the object’s leeway (Hodgins & Mak, 1995). Because of the asymmetric shape of the vessel, the drag and lift component of the wind will cause the object to drift at an angle relative to the wind called “leeway angle.” The Norwegian Meteorological Institute (NMI) developed a LEEWAY model as part of its oceanic trajectory models suite for Search and Rescue, Vessel Traffic Service and Environmental Protection Agency (Breivik & Allen, 2008).

Uncertainty parameters such as leeway divergence angle is obtained through Monte Carlo simulation (Breivik & Allen, 2008) and field investigation (Allen & Plourde, 1999). (Ni, Qiu, & Su, 2010) present a theoretical drift prediction based on the law of physics and non-probabilistic analysis of uncertainty. Consider a vessel in steady drift with velocity $U_B$ subjected to a forcing field with constant wind velocity $U_W$ and a constant current velocity $U_C$. 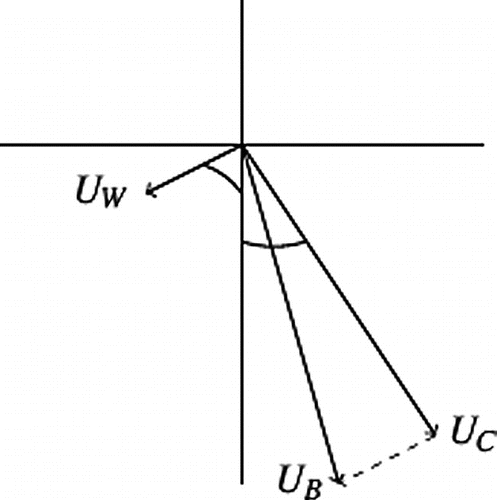The law of motion dictates that the relative wind force $U_W-U_B$ and the leeway force $U_B-U_C$ must be opposite to each other. In addition, the sum of the two forces is equal to zero for a steady drift. Thus, the drift velocity can be expressed as follow:$$\begin{array}{c}\hfill U_B={\displaystyle \frac{1}{1+\tau }}{U}_C+{\displaystyle \frac{\tau }{1+\tau }}{U}_W=U_C+\mu (U_W-U_C),\end{array}$$

where $\mu$ is the leeway rate and ${\tau }^2={(C_{D}A\rho )}_1/{(C_{D}A\rho )}_2$. The subscripts 1 and 2 refer to the in-air and in-water quantities, respectively, where $C_D$ is the drag coefficient, A is the cross-sectional area exposed, and $\rho$ is the fluid density. More details can be found in (Ni, Qiu, & Su, 2010). This formula does not consider the wave drift force which can be expressed by $F=\frac{1}{2}{\rho }_2{f}_{g}L{C}_{2W}{a}^2$. The wave amplitude is one-half of the wave height and is represented by a , $C_{2W}$ denotes the wave drift coefficient and L is the vessel length and $f_g$ is the gravitational force. Hence, the drift velocity with wave force included can be expressed as follow:(5) $$\begin{array}{c}\hfill U_B={\tilde{U}}_B-\frac{{\tilde{U}}_B-U_C}{1-\tau }+\sqrt{{\left(\frac{{\tilde{U}}_B-U_C}{1-\tau }\right)}^2+\frac{\chi }{1-{\tau }^2}},\end{array}$$(5)

where ${\tilde{U}}_B$ is the solution of the equation of motion in the absence of waves and the parameter$$\begin{array}{c}\hfill \chi ={\displaystyle \frac{f_{g}L{C}_{2W}{a}^2}{{(C_{D}A)}_2}}.\end{array}$$

As the region is discretised into cells, it is possible to estimate, for every time period, the next position of a drifting vessel given information on the local wind, surface current of the initial position, and the shape and buoyancy of the vessel. For every vessel and time step, we can estimate a potential drift trajectory using (13), which is represented by a sequence of cells (see Figure 1). Specifically, we compute a path for a vessel as follows.

Step 0:	Set $i:=0$ and $p:=(c_t)$, where $c_t$ represents the position of the vessel at the time of distress call $t\le T$.
Step 1:	Obtain the wind, current velocities and wave force as well as actual vessel velocity from the AIS for the current cell $c_{t+i}$ and set $i:=i+1$.
Step 2:	Determine the new actual vessel velocity, $U_B$, using the formula in (8) as illustrated in Figure 1.
Step 3:	Determine in which cell falls the new obtained vessel force $U_B$ and denote it by $c_{t+i}$; and set $p:=(c_t,...,c_{t+i})$.
Step 4:	Go back to Step 1 or stop if the current cell $c_{t+i}$ is ashore or outside the region of interest.

The algorithm above does not generate the whole path followed by the vessel, but only from the time of distress call at cell $c_t$ to shore. However, it is trivial to include the other parts of the path.

Figure 1. Drift velocity.

4.3. Environmental costs and drift probabilities

Vessel grounding accidents can result in severe pollution from oil spills and damage to the environment. In addition, the oil spill highly depend on vessel type (Talley, Yip, & Jin, 2012), capacity and grounding location. These consequences can be evaluated in terms of costs for a better classification of vessels and potential grounding locations.

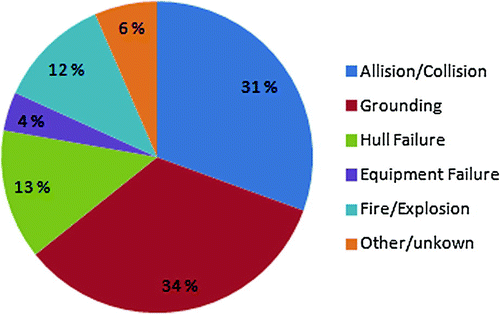
About 34% of oil spills in European seas are caused by vessel grounding accidents (see Figure 2). One of the best known grounding-related oil spill accident is that of the Sea Empress in 1996, which ran aground in the entrance to Milford Haven, in the southwestern United Kingdom. The vessel released a total of 72,360 tonnes of oil into the sea (ITOPF, 2013).

Figure 2. Volume of oil spilled per cause of accidents in European Seas for accidents above 7 tonnes per spill. Data Source: ITOPF 2013.

The main factors influencing the cost of oil spills include the type of oil, amount of oil spilled and spillage rate, the physical, biological, and economic characteristics of the spill location, and the weather and sea conditions at the time of the spill (Grey, 1999; Kontovas, Psaraftis, & Ventikos, 2010; Vanem, Endresen, & Skjong, 2008; White, 2003). The levels and types of cleanup capabilities to optimally respond to oil spills are outside of the scope of this paper (see Psaraftis, Tharakan, & Ceder, 1986 for related research in this area). Although a grounding vessel might not lose its entire cargo, the vessel size indicates the potential volume of oil spill. In addition, the amount of oil spill depends on the grounding location. A vessel running aground on hard rock will likely cause more oil spills than grounding on sand.

Vanem et al. (2008) develop a model that incorporates all costs of oil tanker spill accidents. They consider the spill amount as the major factor with a global average cleanup cost of USD 16, 000 / tonne. In addition to the cleanup cost, average environmental damage and socioeconomic costs are estimated to be around USD 24000/tonne. Research conducted about Norwegian waters assesses the environmental damage to be almost twice the cost associated with cleanup and rescue operations (Hansen, 2003). Kontovas et al. (2010) use a regression analysis of oil spill cost with data from the IOPCF (International Oil Pollution Compensation Federation) and obtain a total cost $K=51.432V^{0.728}$ in terms of V , the volume in tonne of oil spilled. The total cost, in USD, includes three cost categories: cleanup, socioeconomics losses and environmental costs. In this paper, the cost related to each vessel scenario in the OTP model are obtained from this total cost formula with V determined by the size of the vessel and the part of the coast it might hit as categorised by Eide et al. (2007).

In the model formulation, $R_{{\omega }_v}$, with ${\omega }_v=(t,p)$, is the probability for vessel v to start drifting along the path p at time $t\in \mathcal{T}$. The probability mainly depends on human factors (experience of nautical officers, excessive fatigue, stress and usage of alcohol), type of vessel (size, wind exposure area of the ship, flag state, age of the vessel), weather conditions, and the characteristics of the route (length, depth and width of the waterway). Sophisticated methods, such as fault tree analysis (Kum & Sahin, 2015; Mokhtari, Ren, Roberts, & Wang, 2011; Senol, Aydogdu, Sahin, & Kilic, 2015), for determining $R_{{\omega }_v}$ are beyond the scope of this paper. We simply generate these probabilities randomly in the simulation experiments based on historical information both about how often drifts actually occur on average, and also about how much the probabilities vary between vessels due to different characteristics, such as flag state, age, and previous incidents.

5. Case studies

In this section, we discuss the effectiveness, efficiency and performance of the models through three different case studies. First, we present the general settings common to all cases. Second, an illustrative example of the model and output is presented in Case 1. Third, we compare the MIP-L and MIP-U solutions and discuss the computational costs, the number of breakpoints, the effect of time horizon on the solution quality and the sensitivity analysis with larger scale problems in Case 2. Fourth, three real-world examples with historical data from the NCA are presented in Case 3.

5.1. Computational settings

We limit the set $\overline{\mathrm{\Omega }}$ to those scenarios with exactly one distress call and also only consider one possible drift trajectory for each vessel in distress. The first assumption is reasonable as distress calls are quite rare. The second assumption is a simplification that places focus on the main source of uncertainty: time of distress call (Ni et al., 2010). A richer set of scenarios are easily included but its generation is beyond the scope of the paper. In Cases 1 and 2, the drift trajectories are randomly generated using a Markov chain. Specifically, we subdivide the region into 20 zones, where the sum of the wind and current force direction ($U_w+U_C$) for each zone is either north-east, north-west or north-south. Each zone is randomly associated with one of these three directions. Additionally, every cell in the region is directly connected from below with three cells, which are named Left, Straight, and Right. The next cell in the path $p=(c_t,...,c_T)$ of a drifting vessel scenario is randomly determined based on the zone where the current cell falls (see Table 1). For instance, if the current cell is located in the zone where the vector $U_w+U_C$ has a north-east direction, then the Left cell will be chosen as next cell in the path with a probability equal to 0.25. In addition, the wave magnitude at each cell is randomly given a value of 0 or 1 with equal probabilities, where the value of 0 represents low wave height and 1 that of large wave magnitude. The drifting vessel will spend two time periods at cells with large wave magnitude and only one time period at cells with small wave height. In Case 3, historical wave height, current and wind forces are used to determine each drift trajectory; see further details in Subsection 5.4.

Table 1. Transition probabilities for path generation.

$U_w+U_C$	North-east			North-west			North-south
Cell	Left	Straight	Right	Left	Straight	Right	Left	Straight	Right
Prob	0.25	0.25	0.5	0.5	0.25	0.25	0.25	0.5	0.25

The probability $R_{{\omega }_v}$ is randomly generated according to a uniform random variable on [0.01, 0.09]. Furthermore, the grounding cost for each vessel scenario is computed using the formula $K=51.432V^{0.728}$, where the volume V is randomly generated according to a uniform random variable on [2187, 51,704] plus a normal random variable with mean 15,000 and standard deviation = 5000 (see Kontovas et al. (2010) for details on grounding costs and volume of oil spills). Moreover, the VTS centre in Vardø currently operates with two tugboats. We use this number of tugboats for experiments in all the three cases. These tugboats have a secondary function of escorting vessels that are in transit to Norwegian ports. Thus, they are required to move relatively close to shore as reflected in our discretisation of the area of interest and movement constraints. The problem of whether the resource capacity is optimal or not is out of the scope of this paper. We propose an optimal tugs policy based on the resource available. However, the fleet of tug was reduced from three to two a year ago by the NCA and could be justified by few main reasons. First, the accidents are very rare and most of the drift time are very long with 20–30 h (slow drift) and fast drift count for only 10 h Eide et al. (2007). Second, The NCA have acquired “ship arrestors,” which considerably reduce the vessel’s drifting speed and give more time to the tugs to hook-up with the vessel in time.

All computations are carried out on a personal computer with an Intel(R) Pentium(R) IV 3.0 CPU and 4.0 GB of RAM, running Windows 7. The optimisation solver is Gurobi 5.5.0.

5.2. Case 1: Illustrative example

We start by considering a corridor of length 40 kilometers and width 20 kilometers divided into 800 cells of 1-by-1 kilometer. Six vessels sail in the corridor 18 km off the coastline. These vessels are patrolled by two tugboats moving close to shore with a maximal speed of 10.7 knots ( 1 knot$=1.85$ km/h). Each vessel moves in the corridor with an average speed between 6.5 and 19.5 knots. Moreover, a planning horizon of 6 is used with a time step of 1 h. For this case, tugboats are constrained to move relatively slowly. 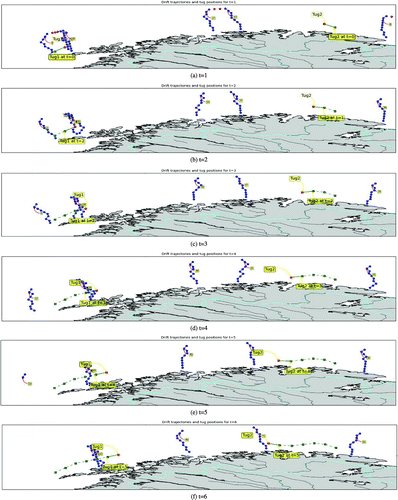Each cell c has a total of 15 reachable cells in ${\mathcal{F}}_{\mathit{tg}}(c)$, which represents the number of possible hops per time period. Figure 3 shows an optimal solution, where tugboats are represented by small squares and are allowed to move between shore and the green line. Tug2 is initially positioned 3 km off the coast and 15 km from the origin point with coordinate (0, 0) in the figure, while Tug1 is positioned 2 km away from the coast and 34 km from the origin point along the coast. The optimal positions of tugboats are also shown in Figure 3. In addition, the initial position of each vessel is represented by a red circle and the vessel scenarios for each time period as blue circles linked with blue sticks. Moreover, the corridor is delimited by a yellow line and the coast is shown by a red line. The cost, in million NOK, for each vessel scenario is labelled close to each drift trajectory. The number of scenarios, $|\overline{\mathrm{\Omega }}|$, is equal to 36 for six vessels and six time periods. For every time period, Figure 3 illustrates the optimal decision of the model and the potential drift trajectories. In the figure for time period t , we only show the six drift trajectories that are associated with a distress call at t .

Figure 3. Results for case1: Illustrative example.

Note: The green and blue solid lines represent the movement of tugboats and drift trajectories of vessels, respectively.

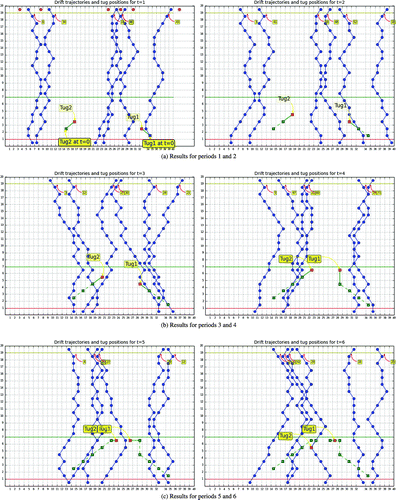
Both MIP-L and MIP-U give the same objective value of NOK 0.67 million as well as tugboat positions at each time period. This optimal solution is obtained in 15 s for MIP-U and 170 s for MIP-L. For this test instance, MIP-L model has a total number of 60, 765 constraints and 36 continuous variables, whereas MIP-U has a total number of 825 constraints and 36, 000 continuous variables. The two models have the same number of binary variables of 2, 880 . At each time period in the planning horizon, the optimal decisions are influenced by the vessel scenarios of the next time periods. This is well illustrated in period 2, where Tug2 moves slightly away from the path with high cost of NOK 41 million. In fact, there are more scenarios with considerable cost on the east side of Tug2 both in periods 2, 3 and 4. Additionally, if we consider only vessel scenarios at the fourth time period, it might not be optimal to move Tug2 east, which is actually optimal when considering vessel scenarios in the next time periods. As expected, the tugboats move towards the corridor until they reach the green line limit (see Figure 3). The closer the tugboats move away from the coastline, the greater the probability of successful hook-up of potential drifting vessels.

5.3. Case 2: Computational tests

To evaluate the performance and quality of the models developed, we present results for realistically sized test instances. The cells for this case are built with geographical positions from the region of interest for the VTS. Clearly, we collect the geographical coordinates of the centre position of each cell and transform them into Cartesian coordinates for calculations. Once the model is run, the optimal positions of tugboats as well as drift trajectories and vessels positions are transformed back to geographical coordinates. The region of interest covers about 1100 km of coastline and the corridor is on average 50 km off the coastline. We partition the area between the corridor and the coastline into cells of 5 by 5 km, which gives a total number of 2200 cells. In practice, the number of cells is slightly smaller than the number given above. This is explained by the fact that the corridor and the coastline are not straight lines and neither totally parallel to each other. Thus, we use few triangle cells with different sizes to better represent the region of interest. Vessels typically have an operating speed of 14–15 knots and tugboats about 12 knots (Eide et al., 2007). In addition, the operators have subdivided the region of interest into two zones. The first tugboat is assigned to the first zone, Zone A, spanning from the border to Russia to Torsvåg, and Zone B from Torsvåg to Røst is patrolled by the second tugboat.

5.3.1. Case 2A: Many breakpoints

In this subsection, we mainly compare the MIP-U and MIP-L models with regards to solution quality and run time, and present the gap between the optimal OTP value and optimal MIP-U or MIP-L values. Accordingly, a test set of 6 vessels and 2 tugboats over a period of 20 h with 1 h time steps are randomly generated. In this test set, the tugboats cannot move more than 25 km away from the shore. That is, the patrol zone accounts for about 1100 cells along the coastline. The test case constitutes 30 instances and the results for the two MIPs are presented in Table 2. The run time is in minutes and the objective function in million NOK.

Preliminary calculations indicate that $K=1000$ is the minimum number of breakpoints in MIP-L and MIP-U, that gives an optimal solution of OTP. Consequently, we use 2000 breakpoints in order to be highly confident that MIP-L and MIP-U give the optimal solutions of the OTP model. For each instance, the total number of binary variables for both MIPs is 22,974 with 120 and 240,000 continuous variables, respectively, for MIP-L and MIP-U. The total number of constraints for MIP-L is 261,924 and 22,045 for MIP-U.

As presented in Table 2, the MIP-U model is about 93 times faster than MIP-L. Additionally, the variability in run times for MIP-L is larger than that of MIP-U. The average solution value is NOK 0.5797 million for MIP-U and NOK 0.5792 for MIP-L. Although the objective values of the two MIPs are slightly different, the optimal decisions for the tugboat positions are the same for every test result. In addition, the relative optimality gap defined by $(min\{f(\overline{\mathbf{x}}),f(\underline{\mathbf{x}})\}-\text{MIP-L})/\text{MIP-L}$ is the negligible 0.03%, with a maximum of 0.05%.

Table 2. Case 2A. Test results for 30 instances GAP = $(min\{f(\overline{\mathbf{x}}),f(\underline{\mathbf{x}})\}-\text{MIP-L})/\text{MIP-L}$.

	MIP-U		MIP-L		$min\{f(\overline{\mathbf{x}}),f(\underline{\mathbf{x}})\}$	%GAP
	Obj.Val	Time (min)	Obj.Val	Time (min)
Avrg	0.5797	7.57	0.5792	707.07	0.5796	0.029
Std.dev	0.3955	10.43	0.3954	95.42	0.3955	0.019
Min	0.1251	1.49	0.1250	573.72	0.1251	0.006
Max	1.5497	52.18	1.5485	888.63	1.5493	0.052

5.3.2. Case 2B: Few breakpoints

The choice of 2000 breakpoints leads to optimal tugboat positions in all instances examined at the expense of high run times. As presented in Table 2, it takes between 1.5 and 52.2 min to obtain a solution of MIP-U, and even longer for MIP-L. In order to assess the solution quality with relatively few breakpoints, the two MIPs models are run with another set of 50 instances in the same manner as in Case 2A, with 500 breakpoints for MIP-U and 200 for MIP-L. This gives a total number of 82,974 variables and 22,045 constraints for MIP-U, and 23,094 variables with 45,924 constraints for MIP-L.

The average relative optimality gap is 0.51%, with a maximum of 5.4% (see Table 3). The solution is obtained in 1.99 and 13.17 min on average for MIP-U and MIP-L, respectively. Moreover, the runtime for MIP-U is less than 9 min for every test instance. The MIPs are able to obtain optimal decisions on tugboat positions for 15 instances out of 50. Although the number of vessels is the same for each instances, the initial vessel positions along the corridor are different for each test case. Consequently, the number of scenarios varies for every test instance. Clearly, some vessels might leave the region before the end of the planning horizon, and thus reduce the number of vessel scenarios. This explains the high standard deviation both on the objective values and runtime presented in Table 3. However, these results remain practically reasonable as one might run the model every hour within a receding horizon framework discussed in the next subsection. Additionally, the standard deviation is very high, 0.71 for an average value of 0.69, which indicate that the environmental factors (weather conditions, probability of failure) have a considerable effect on the average expected potential grounding costs. This raise the need for more than one drift trajectory for each vessel scenario as discussed in Section 6.

Table 3. Case 2B. Test results for 50 instances with small number of breakpoints GAP= $(min\{f(\overline{\mathbf{x}}),f(\underline{\mathbf{x}})\}-\text{MIP-L})/\text{MIP-L}$.

	MIP-U		MIP-L		$min\{f(\overline{\mathbf{x}}),f(\underline{\mathbf{x}})\}$	%GAP
	Obj.Val	Time (min)	Obj.Val	Time (min)
Avrg	0.6901	1.9958	0.6855	13.1669	0.6886	0.5152
Std.dev	0.7139	1.9709	0.7092	7.0475	0.7120	0.9421
Min	0.1762	0.1517	0.1746	2.4903	0.1757	0.0003
Max	2.0669	8.4818	2.0560	26.9707	2.0616	5.4455

Figure 4. Case 2C. Influence of the number of scenarios on the computational time.

Note: The blue solid line represents the performance of the MIP-L model and the green solid line is that of the MIP-U model.

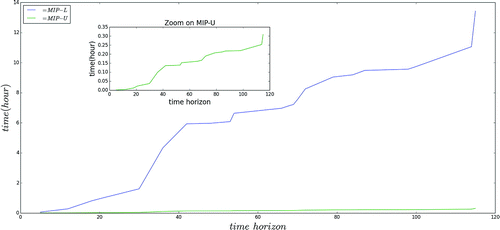
Figure 5. Case 2D. Influence of the number of tugboats and distributions of the drift trajectories on the expected environmental cost.

Note: The green solid line represents the optimal costs for the current distribution while the red and blue solid lines represent the variation in the costs with different distributions.

Figure 6. Case 3A. Illustration of the first six time periods.

Note: The dashed green lines represent tugboat movements at each time period and the blue solid lines represent vessel trajectories.

5.3.3. Case 2C: Effect of time horizon

The number of scenarios increases with the length of the planning horizon. We use one large test instance from Case 2A and run the MIP models for different planning horizons, ranging from 2 to 22 h. The result in Figure 4 shows how the computational time increases with the length of the time horizon and highlights the run times performance of MIP-U compared to that of MIP-L. Furthermore, it is clear from Figure 4 that MIP-U better copes with larger instance size than MIP-L. However, MIP-L is of course essential in computing a relative optimality gap.

The weather forecast is available in real time at the VTS centre and dynamic information from vessels are transmitted on average every 2 s (Eide et al., 2007). This information can be used for repeated updates of the model resulting in better predictions of future vessel scenarios; see for example *Park2009 and *Wang2007 for background on such receding horizon control. Accordingly, MIP-U could be run in real time, with parameters updated every time period. For instance, the model could be run for 20 h, while only the first hour is being implemented. Then we update the parameters and run the model again for the next 20 h and so forth.

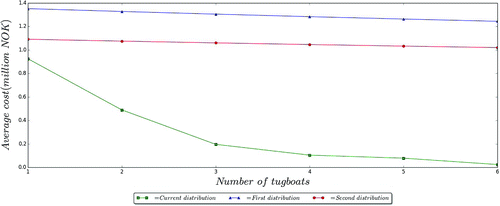
5.3.4. Case 2D: Sensitivity analysis with larger scale problems

To analyse the sensitivity of the MIP-U model as well as its scalability, we run different test instances with a total of 10 vessels for a number of tugboats ranging from one to six. For each number of tugboats and distribution of drift trajectories, we run the MIP-U model and compare its solution value with two different distributions for the same tugboat positions. These settings allow us to analyse the sensitivity of the solution value to different probabilities of failure $R_{{\omega }_v}$, grounding costs $K_{{\omega }_v}$ for each vessel scenario and fleet size.

In Figure 5, the green solid line represents the optimal cost distribution while the red and blue solid lines represent the variation of the expected cost for two different distribution of drift trajectories. Unsurprisingly, the solution values are very sensitive with changes in the failure probabilities and grounding costs. This is mainly due to the high uncertainty about weather conditions and ocean currents. Although the integration of the MIP-U model with the receding horizon control algorithm, described in Section 4.2, could considerably address this issue, more accurate parameters estimation are required. Additionally, the expected environmental cost obviously decreases with higher number of tugboats as shown in Figure 5. Increasing the fleet size will bring additional acquisition costs, which are strategic decisions not discussed in this paper. Our model, however, focuses on operational decision level by proposing optimal real-time allocation and positioning of tugboats based on the available fleet size. Nevertheless, the NCA has decided to reduce the speeds of drifting vessels by acquiring new “ship arrestors” and reduce its fleet size from three to two tugboats. Moreover, the maximum runtime for these larger scale instances is less than 45 min, which is sufficient to run the model every 1 or 2 h with the receding horizon control algorithm. Sophisticated heuristics algorithms might reduce this computing time further. For cases where larger fleet sizes are needed, this scalability issue can also be easily addressed by subdividing the region of interest into smaller zones and optimally assign tugboats to each zone. The new problem will then be very similar to that of the location/allocation and deployment of ambulances in the EMS systems.

Table 4. Case 3A. Initial vessel positions and speeds.

	Vessel 1	Vessel 2	Vessel 3	Vessel 4	Vessel 5	Vessel 6
Direction	North-west	West-north	West-north	North-west	West-north	North-west
Latitude	$N{68}^{o}02$	$N{68}^{o}15$	$N{68}^{o}21$	$N{71}^{o}07$	$N{71}^{o}22$	$N{70}^{o}38$
Longitude	$E{009}^{o}44$	$E{010}^{o}34$	$E{010}^{o}50$	$E{019}^{o}24$	$E{021}^{o}49$	$E{032}^{o}10$
SOG	12.4	10.5	13.7	13.2	11.5	13.3

Figure 7. Case 3B. Results for the first instance with grounded vessel.

Note: The dashed green lines represent the suggested movements of tugboats by the MIP-U model and the predicted drift trajectories in blue solid lines. In addition, the actual drift trajectory of the vessel that ran aground is represented by green solid lines. The paths in red are the actual positions of tugboats from the time of distress to the time of grounding.

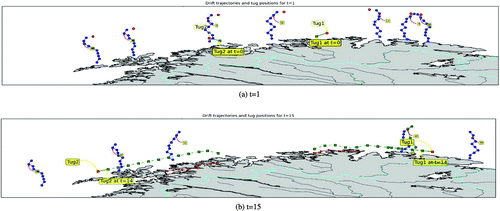
Figure 8. Zoom on the grounded vessel for case 3B.

Notes: The dashed green lines represent the suggested movements of the nearest tugboat by the MIP-U model and the predicted drift trajectories are represented in blue solid lines. In addition, the actual drift trajectory of the vessel that ran aground is represented in green solid lines. The path in red is the actual positions of the nearest tugboat from the time of distress to the time of grounding and the estimated grounding cost in million NOK for each drift trajectory is labelled in yellow.

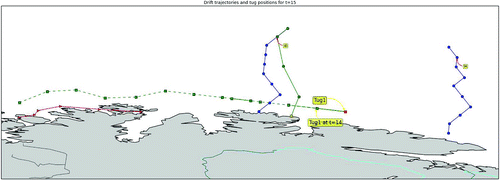
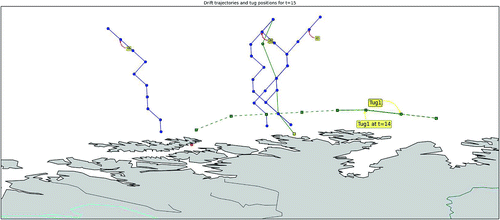
Figure 9. Results for Case 3C.

Notes: The dashed green lines represent the suggested movements of the tugboats by the MIP-U model and the predicted drift trajectories are represented in blue solid lines. In addition, the actual drift trajectory of the vessel that ran aground is represented in green solid lines. The two cycles in red are the actual static position of the tugboats from the time of distress to the time of grounding and the estimated grounding cost in million NOK for each drift trajectory is labelled in yellow.

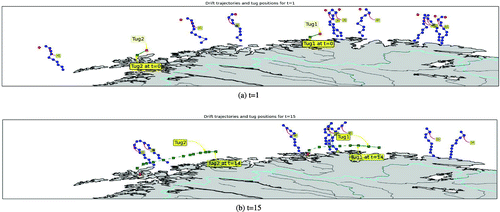
Figure 10. Zoom on the grounded vessel for case 3C.

Notes: The dashed green lines represent the suggested movements of the nearest tugboat by the MIP-U model and the predicted drift trajectories are represented in blue solid lines. In addition, the actual drift trajectory of the vessel that ran aground is represented in green solid lines. The cycle in red is the actual static position of the nearest tugboat from the time of distress to the time of grounding and the estimated grounding cost in million NOK for each drift trajectory is labelled in yellow.

5.4. Case 3: Historical events

In this subsection, we discuss three real-world cases with historical data from the NCA. Case 3A involves no grounding incident, but highlights the potential cost saving opportunities that could be gained by having solutions of the OTP problem guide decisions. In Cases 3B and 3C, we present two different instances where an accident actually occurred and run the model for 15 h prior to the time of distress.

A path $p=(c_1,...,c_T)$ for each vessel scenario ${\omega }_v$ is generated using AIS and NMI information with the algorithm presented in Section 4.2. Specifically, we collect the wind and current velocities, and wave force of the centre point of each cell at each time period of the planning horizon and use the algorithm described in Section 4.2. to generate a path for each vessel scenario ${\omega }_v$. In addition, the number of vessels in the region and their geographical positions for every time period, the time of distress and grounding locations are collected from AIS. Moreover, we use the basemap library in python to plot and draw the map with vessel scenarios and tugboat positions.

5.4.1. Case 3A: 7 May 2014

On the 7 May 2014, six vessels sailed along the coastline of the High North. Their initial positions, speed over the ground (SOG) and direction at 1:30am are given in Table 4. At each time period of 1 h, a potential vessel scenario is randomly generated, based on the historical wind and current directions and the model presented in Section 4.2, for every vessel. The problem size for this case is the same as Case 2A.

The optimal solution for MIP-U was found in 5.6 min with an objective value of NOK 0.34 million. The actual events had the first tug boat located at ${70}^o{58}^{\prime }N-{025}^o{51}^{\prime }E$ and the second one at ${69}^o{40}^{\prime }N-{018}^o{59}^{\prime }E$, and they were stationary during the whole planning horizon of 20 h in accordance with current VTS policy.

The optimal locations for the first six time periods are presented in Figure 6. The priority is given to vessel scenarios with high cost. In the first time period, Tug2 moves north because of the high costs located in that direction. Tug1 moves west towards a vessel with small cost of NOK 15 millions in period 4, leaving a vessel with higher cost of NOK 41 millions, but this is due to the high cost of NOK 82 and NOK 51 million that appear in periods 5 and 6, respectively.

In this instance where no accident happened, the real cost was of course equal to zero. However, the expected cost under this policy is actually NOK 0.75 million, significantly higher than the optimised of NOK 0.34 million.

5.4.2. Case 3B: 21 March 2014

On the 21 st of Mars 2014 at 11:10pm, a vessel ran aground at ${71}^{o}01.{06}^{\prime }N-{028}^{o}27.{46}^{\prime }E$ after about 15 h of drifting time. At the time of distress, 07:55am, the nearest tugboat was located at ${70}^o{40}^{\prime }N-{023}^o{40}^{\prime }E$, and was not able to reach the drifting vessel on time. The tugboat moved towards the vessel but was 142.8 km away at the time of grounding. We run the MIP-U model with this case for 15 h prior to the time of distress and present the results for the first and last time periods in Figure 7. The blue lines in Figure 7 represent the predicted drift trajectories for all the vessels that moved into the region in that time horizon, including the one that ran ashore, while the actual path followed by the drifting vessel is presented in green solid line. The two directed paths in red solid lines are the actual positions of tugboats from the time of distress to the time of grounding and the paths in dashed green line are suggested positions of tugboats by the model prior to the distress call. It is important to note that, in these green paths, the last positions represent the location of tugboats at time of distress of the vessel that ran ashore, not at the grounding time. A zoomed-in view of the grounding location of the drifting vessel as well as the nearest tugboat (Tug1) are presented in Figure 8, where the distance between the predicted and actual grounding location is about 17 km. Although this value is not large, further research as highlighted in the last section, needs to be done for accurate drift trajectories.

The probability of successful hook-up of the grounded vessel by Tug1 with the predicted drift trajectory and the MIP-U model is 0.79 and that of the actual drift trajectory is equal to 0.86. That is, the grounded vessel had 86% chance to be rescued if the MIP-U model was implemented at that time. Based on the actual position of Tug1 at time of distress from the current policy (see the first position of the red path in Figure 8) the vessel had only 0.22 probability to be hooked-up. For this real-world instance, the expected cost is equal to NOK 0.19 million if using the OTP model and NOK 0.28 million for the actual movement of tugboats.

5.4.3. Case 3C: 12 September 2014

In this case, a vessel ran ashore at ${71}^{o}02.{97}^{\prime }N-{023}^{o}53.{89}^{\prime }E$ on September 12 2014 at 2:25pm. The nearest tugboat, located at ${70}^{o}41.{58}^{\prime }N-{023}^{o}19.{21}^{\prime }E$, stayed static for the whole drifting time of about 9 h. As explained by the operators at the VTS centre, vessels are not given the same priority and sometimes vessels moving out of the corridor will “misinform” the VTS centre that they are not in trouble but merely fishing (or some other false message) while they are in fact drifting with the risk of grounding. This peculiar situation often stems from misunderstandings about the cost of rescue to the ship owner. The rescue is in fact free for the ship owner, but this is not widely known. The MIP-U model is also run for 15 h prior to the time of distress of the grounding vessel.

The results for the first and last time periods are presented in Figure 9 and the zoom on the grounding location is presented in Figure 10, where the red circle represents the position of the nearest tugboat. The predicted drift trajectory has a grounding position 43 km away from the location where the vessels actually run aground. For this particular case, the model and the current policy have a close probability of successful hook-up of 0.79 and 0.69, respectively. This is mainly due to the actual static position of the tugboat and the grounding location, which in this case is rather fortunate. In addition, the MIP-U model does not know which drift will occur in advance and thus, tries to minimise the overall expected cost. Indeed, there are two drift trajectories with high costs on the right side of the nearest tugboat. This is why the tugboat does not move closer to the drift trajectory that actually occurred. The expected cost for this real-world instance is equal to NOK 0.07 million if using the OTP model and NOK 0.24 million for the current policy.

6. Conclusions

In this article, we developed a nonlinear binary integer programming model to minimise the clean-up costs, socioeconomic losses and environmental costs associated with oil spill from grounding accidents. Two linearisations of the model lead to mixed integer models that bound the optimal value of the original problem with practically near zero optimality gaps. The paper also presents methods for obtaining input data to the model. Preliminary results for small and realistically sized instances indicate noteworthy features of our approach. Optimal tugboat positions are obtained in less than 2 min for realistic instances with a small number of breakpoints. A test with a real-world instance in Case 3A indicates a total clean-up and socio-economic costs saving opportunity of 45%. Moreover, tests with three representative historical data-sets highlight the importance and benefits of implementing the MIP-U model at the NCA. Specifically, we demonstrate that on a single day in 2014, decision support by the proposed model might have reduced the expected cost from grounding accidents that day from NOK 0.75 million to NOK 0.34 million. In two other studies of actual grounding incidents in 2014, we predict that adoption of the decision support tool in the hours prior of the grounding events might have increased the probability of avoiding those accidents from 22 to 86% in the first incident and from 69 to 79% in the second. The NCA finds these estimates exceptionally interesting and the proposed decision support tool highly promising as the basis for a real-time automated system that can assist the NCA’s VTS operators. Although the model is not yet implemented in practice, the examples use real data, which provide an indicate of what we can expect.

The current models and tools developed so far in maritime SAR (see Abi-Zeid and Frost (2005); Chircop et al. (2013); Millar and Russell (2012); Pelot et al. (2015); Radovilsky and Koermer (2007); Razi and Karatas (2016); Wagner and Radovilsky (2012)), despite their importance, do not suggest how and where the fleet of tugboats should move, while accounting for uncertainty related to vessel incidents and the dynamic nature of the SAR resources positioning, in order to minimise risk, which is the primary concern of the OTP problem addressed in this paper.

Maritime transportation is associated with various potential incidents that require effective and efficient emergency response actions. These incidents include vessel drifting or breakdown associated with illegal border crossing, collusion, fire and lost cargo or ISO containers at sea . In addition, the decision on tugboats location and allocation depend on a given problem that has different criteria, such as resource capabilities, environmental and geographical factors, and political rules. Thus, the models developed in this paper can be adapted or integrated to solve various maritime SAR resource location and allocation problems. For instance, the OTP model can be adapted and extended to address a maritime SAR planning problem that evaluate the overall SAR response system with the aim of obtaining a maximum coverage of a region of interest at sea with a minimum required fleet size.

It is recommended that further studies are initiated in order to obtain more accurate input for the model. First, the region should be partitioned into an “optimal” number of cells. A large cell size will reduce the precision on tugboat positions as well as vessel scenarios. Conversely, small cells size gives good precision at the expense of high model complexity. Second, more than one vessel scenario at each time period and scenario could be considered, which might lead to a need for Monte Carlo sampling techniques. Third, and most importantly, there is a need for better assessments of grounding costs at each coastline segment as well as estimates of probabilities of distress calls. Furthermore, the model can be extended and incorporate a receding horizon control algorithm to effectively address the uncertainty and dynamic environment of the problem. In fact, there might be new vessels entering and leaving the region during the planning horizon. In addition, one of the tugboats could be out of patrol because of several reasons such as escort of vessels and crew shift. All this information needs to be updated dynamically. Finally, different objective functions could be used for the OTP problem. For instance, minimising the superquantile instead of the expected cost could be of great interest to the NCA.

Acknowledgements

This work is carried out with partial funding from Aalesund University College and the Research Council of Norway through the project Dynamic Resource Allocation with Maritime Application (DRAMA), grant ES504913. We sincerely acknowledge Trond Ski at the Norwegian Coastal Administration (NCA) for his support and input during the work with this paper.

Additional information

Funding

This work was supported by the Norwegian University of Science and Technology; the Norwegian Research Council.

Notes

No potential conflict of interest was reported by the authors.