An interactive surrogate-based method for computationally expensive multiobjective optimisation

Abstract

Many disciplines involve computationally expensive multiobjective optimisation problems. Surrogate-based methods are commonly used in the literature to alleviate the computational cost. In this paper, we develop an interactive surrogate-based method called SURROGATE-ASF to solve computationally expensive multiobjective optimisation problems. This method employs preference information of a decision-maker. Numerical results demonstrate that SURROGATE-ASF efficiently provides preferred solutions for a decision-maker. It can handle different types of problems involving for example multimodal objective functions and nonconvex and/or disconnected Pareto frontiers.

Keywords:

• Multiple criteria decision-making (MCDM)
• interactive methods
• computational cost
• black-box functions
• metamodeling techniques
• achievement scalarising function

1. Introduction

Many multiobjective optimisation problems (MOPs), arising e.g., in engineering applications, often involve multiple incommensurable, highly nonlinear, black-box and/or multimodal objective functions. Function evaluations in such problems may be conducted through time-consuming experiments and/or simulators. In the literature, these problems are called computationally expensive multiobjective optimisation problems. MOPs typically have several (in many cases infinitely many) optimal solutions known as Pareto optimal solutions. The set of all Pareto optimal solutions in the objective space (called Pareto frontier) can be nonconvex and/or disconnected. From a mathematical point of view and without any preference consideration, Pareto optimal solutions are equally acceptable for an MOP. Therefore, when solving an MOP, a decision-maker (DM) is required to provide preference information and to choose his/her preferred solutions.

Multiobjective optimisation methods are often categorised according to a decision-maker’s role in the solution process, i.e., non-interactive and interactive methods (Miettinen, 1999). According to Miettinen (2008), in non-interactive methods, the DM either is not involved or provides preference information before or after the actual solution process. In interactive methods, the DM plays an essential role and the intention is to support him/her in the search for the most preferred solution. In such methods, steps of an iterative solution algorithm are repeated and the DM progressively specifies preference information so that the most preferred solution can be found. Examples of types of specifying preference information are reference points and classification of objective functions. What is noticeable is that the DM can determine and alter his/her preferences between each iteration and in the meantime learn about the interdependencies in the problem as well as about one’s own preferences. This is a significant advantage of interactive methods in light of the fact that becoming more acquainted with the problem, its possibilities and limitations is often very valuable for the DM. See Miettinen (2008), Miettinen, Ruiz, and Wierzbicki (2008) for details of non-interactive and interactive methods.

Surrogate-based methods are commonly used in the literature to alleviate computational cost (Jones, 2001; Regis & Shoemaker, 2012; Audet, 2014; Tan, 2015; Dengiz et al., 2009; Chih, 2013; Reis dos Santos & Reis dos Santos, 2011; Hurrion, 2000; Kleijnen & van Beers, 2013; Van Beers & Kleijnen, 2003; Yang & Tseng, 2002; Mehdad & Kleijnen, 2015; Park, Yum, Hung, Jeong, & Jeong, 2016). The basic idea in such methods is to introduce a computationally less expensive problem called a surrogate problem and to replace the original problem with the surrogate one. In the literature, methods have been developed in which surrogate problems are built independently of the type of the optimisation algorithms employed in them. In Messac and Mullur (2008), a non-interactive surrogate-based method is developed. This surrogate-based method does not consider the role of a DM and cannot handle multimodal functions or disconnected Pareto frontiers. The surrogate-based methods proposed in Yun, Yoon and Nakayama (2009), Kitayama, Srirat, Arakawa, and Yamazaki (2013) consider the role of a DM in the solution process. However, they are not interactive methods. This means that if a DM wishes to provide new preferences, the entire methods should be run again. Therefore, the DM should wait for a long time to get new solutions corresponding to his/her preferences. In (Hartikainen, Miettinen, & Wiecek, 2012; Hartikainen & Lovison, 2015; Ruiz, Sindhya, Miettinen, Ruiz, & Luque, 2015) methods have been developed by which the DM can find preferred solutions quickly. These methods require a set of approximated solutions a priori generated by some other surrogate-based methods.

In Tabatabaei, Hakanen, Hartikainen, Miettinen, and Sindhya (2015), we surveyed surrogate-based methods, and observed some shortcomings including inability to (1) involve a DM in the solution process, (2) deal with multimodal functions and (3) capture a nonconvex and disconnected Pareto frontier. To overcome these shortcomings, in this paper, we develop an interactive surrogate-based method. In our method, a DM provides his/her preferences in the form of a reference point containing aspiration levels representing desirable values for objective functions. According to Larichev (1992), the type of preference information in the form of a reference point has been regarded to be understandable for a DM.

The method proposed is called SURROGATE-ASF and involves two phases, i.e., initialisation and decision-making phases. In the initialisation phase, a set of non-dominated solutions in the decision and objective spaces are generated. Using these solutions, hyper-boxes are formed in the decision space. Corresponding to each hyper-box, a single objective surrogate function is built by approximating an achievement scalarising function (ASF) (Wierzbicki, 1986). In the literature, this function is used to compute the (weakly) Pareto optimal solution for a given reference point. In the decision-making phase, the single objective surrogate functions built in the initialisation phase are employed in generating solutions reflecting the preferences of the DM. One should note that the DM is only involved in the latter phase. Based on the comparison in Muller and Shoemaker (2014), a cubic radial basis function (RBF) with a linear tail is employed as the metamodeling technique in this paper, but SURROGATE-ASF is not limited to RBF.

SURROGATE-ASF has been developed for computationally expensive MOPs with box constraints. The novelty of SURROGATE-ASF can be summarised as follows: (1) the DM does not need to wait for a long time to obtain his/her solutions corresponding to his/her preferences, (2) SURROGATE-ASF utilises reference points given by a DM as input, (3) the DM can explore different regions, a particular interesting region or the entire Pareto frontier, (4) it provides approximated solutions in both the decision and objective spaces simultaneously.

The rest of this paper is organised as follows. In Section 2, the basic concepts used in this paper are addressed. The SURROGATE-ASF method is presented in Section 3. Numerical results of evaluating the performance of SURROGATE-ASF on a practical shape optimisation problem of designing an airfoil as well as some benchmark problems are presented in Section 4. Finally, in Section 5, we draw our conclusions and discuss paths for future research.

2. Basic concepts

In this section, we introduce the concepts and notations used in this paper. We consider multiobjective optimisation problems of the form:(1) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\{f_1(\mathbf{x}),\dots ,f_k(\mathbf{x})\},\end{array}$$(1)

where $f_i:S\to \mathbb{R}$ are k $(\ge 2)$ conflicting, computationally expensive objective functions, $S=\{\mathbf{x}\in {\mathbb{R}}^n:x_c^l\le x_c\le x_c^u,c=1,\dots ,n\}$ is a nonempty feasible decision set which is a subset of the decision space ${\mathbb{R}}^n$. A solution $\mathbf{x}={(x_1,\dots ,x_n)}^T\in S$ is called a feasible decision (variable) vector, where $x_c,$$c=1,\dots ,n,$ are decision variables and, $x_c^l$ and $x_c^u$ are the lower and upper bounds of $x_c$, respectively. The image of $\mathbf{x}$ in the objective space ${\mathbb{R}}^k$ is called a feasible objective vector denoted by $\mathbf{f}(\mathbf{x})$. The image of S in the objective space is called the feasible objective set denoted by $Z(=\mathbf{f}(S))$.

A feasible solution ${\mathbf{x}}^{\ast }\in S$ and the corresponding $\mathbf{f}({\mathbf{x}}^{\ast })\in Z$ are termed weakly Pareto optimal for problem (1(1) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\{f_1(\mathbf{x}),\dots ,f_k(\mathbf{x})\},\end{array}$$(1) ), if there does not exist another feasible solution $\mathbf{x}\in S$ such that $f_i(\mathbf{x})<f_i({\mathbf{x}}^{\ast })$ for all $i=1,\dots ,k$. Correspondingly, they are Pareto optimal for problem (1(1) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\{f_1(\mathbf{x}),\dots ,f_k(\mathbf{x})\},\end{array}$$(1) ), if there does not exist another feasible solution $\mathbf{x}\in S$ such that $f_i(\mathbf{x})\le f_i({\mathbf{x}}^{\ast })$ for all $i=1,\dots ,k,$ and $f_j(\mathbf{x})<f_j({\mathbf{x}}^{\ast })$ for at least one index $j\in \{1,\dots ,k\}$. The set of all Pareto optimal solutions in the objective space is called a Pareto frontier. Let the set $X^d=\{{\mathbf{x}}^1,\dots ,{\mathbf{x}}^d\}$ be an arbitrary subset of feasible solutions in S, and $F^d=\{\mathbf{f}({\mathbf{x}}^1),\dots ,\mathbf{f}({\mathbf{x}}^d)\}$, the corresponding objective vectors in Z. A solution ${\mathbf{x}}^i$ (or $\mathbf{f}({\mathbf{x}}^i)$), $i=1,\dots ,d,$ that satisfies the definition of Pareto optimality with respect to all solutions in $X^d$ (or $F^d$), is called a non-dominated solution in $X^d$ (or $F^d$). A solution ${\mathbf{x}}^{{}^{\prime }}$ (or $\mathbf{f}({\mathbf{x}}^{{}^{\prime }})$) is called a locally non-dominated solution if there exist a non-empty set $S^{{}^{\prime }}\subseteq S$ such that, ${\mathbf{x}}^{{}^{\prime }}$ (or $\mathbf{f}({\mathbf{x}}^{{}^{\prime }})$) satisfies the definition of Pareto optimality with respect to all points in $S^{\prime }$ (or $\mathbf{f}(S^{\prime })$). A Pareto optimal solution is a non-dominated solution, but a non-dominated one is not necessarily Pareto optimal.

We also define a feasible solution ${\mathbf{x}}_e^i\in {\text{argmin}}_{\mathbf{x}\in S}\{f_i(\mathbf{x})\}$ for $i=1,\dots ,k$. The $i^{\mathit{th}}$-pagination

extreme point (solution) for $i=1,\dots ,k,$ is defined as ${\mathbf{z}}_e^i=\mathbf{f}({\mathbf{x}}_e^i)$. These extreme points in the objective space are also extremes of the Pareto frontier. Based on the extreme points, a vector of lower bounds of the objective function values in the Pareto frontier is defined as the ideal (objective) vector and denoted by ${\mathbf{z}}^{\mathit{ideal}}={(z_1^{\mathit{ideal}},\dots ,z_k^{\mathit{ideal}})}^T$ where $z_i^{\mathit{ideal}}=f_i({\mathbf{x}}_e^i)$ for $i=1,\dots ,k$. The utopian (objective) vector ${\mathbf{z}}^{\mathit{utp}}$ is a vector in which its components are calculated by subtracting some small positive scalar (e.g., ${10}^{-6}$) from the components of ${\mathbf{z}}^{\mathit{ideal}}$. A vector of upper bounds of the objective function values in the Pareto frontier is defined as the nadir (objective) vector and denoted by ${\mathbf{z}}^{\mathit{nadir}}={(z_1^{\mathit{nadir}},\dots ,z_k^{\mathit{nadir}})}^T$. The components of the nadir vector can be approximated by e.g., a pay-off table using the extreme points. More information of the ideal, utopian and nadir vectors is given e.g., in Miettinen (1999). We define the difference operator $\mathbf{a}-\mathbf{b}=(a_1-b_1,\dots ,a_k-b_k),$ where $\mathbf{a}=(a_1,\dots ,a_k),\mathbf{b}=(b_1,\dots ,b_k)\in {\mathbb{R}}^k$.

In SURROGATE-ASF, the DM provides his/her preferences in the form of a reference point ${\overline{\mathbf{z}}}^{\ast }={({\overline{z}}_1^{\ast },\dots ,{\overline{z}}_k^{\ast })}^T$, where ${\overline{z}}_i^{\ast }$ is an aspiration level representing a desirable value for the objective function $f_i$. One can find a preferred solution for a reference point given by a DM by applying an appropriate scalarisation. Scalarising problem (1(1) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\{f_1(\mathbf{x}),\dots ,f_k(\mathbf{x})\},\end{array}$$(1) ) means formulating a single objective optimisation problem such that its (globally) optimal solution is a Pareto optimal solution for (1(1) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\{f_1(\mathbf{x}),\dots ,f_k(\mathbf{x})\},\end{array}$$(1) ). In this paper, we consider the following widely used achievement scalarising function (ASF) (Wierzbicki, 1986) as an important element of SURROGATE-ASF:(2) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \text{ASF:}& S\times {\mathbb{R}}^k\to \mathbb{R}\hfill \\ \hfill & (\mathbf{x},{\overline{\mathbf{z}}}^{\ast })\mapsto \underset{i=1,\dots ,k}{max}(w_i(f_i(\mathbf{x})-{\overline{z}}_i^{\ast })),\hfill \end{array}\end{array}$$(2)

where $w_i\ge 0,$ for $i=1,\dots ,k,$ are non-negative fixed weights which actually set a direction where ${\overline{\mathbf{z}}}^{\ast }$ is projected onto the Pareto frontier. In this paper we set $w_i=\frac{1}{z_i^{\mathit{nadir}}-z_i^{\mathit{utp}}}$, for $i=1,\dots ,k$, which are widely used (Wierzbicki, 1986). A new (but still computationally expensive) single objective optimisation problem is formulated as(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3)

The reference point in problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) can be feasible or infeasible, i.e., inside or outside of the feasible objective set. As proved in Wierzbicki (1986), theoretically by solving problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ), a (weakly) Pareto optimal solution corresponding to the reference point is obtained, regardless of the feasibility or infeasibility of the reference point. This does not hold for all other scalarising approaches (Miettinen, 1999 ). Different (weakly) Pareto optimal solutions can be obtained by changing the reference point in problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ). One can add an augmentation term to (2(2) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \text{ASF:}& S\times {\mathbb{R}}^k\to \mathbb{R}\hfill \\ \hfill & (\mathbf{x},{\overline{\mathbf{z}}}^{\ast })\mapsto \underset{i=1,\dots ,k}{max}(w_i(f_i(\mathbf{x})-{\overline{z}}_i^{\ast })),\hfill \end{array}\end{array}$$(2) ) to avoid weakly Pareto optimal solutions as discussed and proved in Miettinen (1999), Wierzbicki (1986).

Numerically, in cases with a limited number of function evaluations, the optimal solution of problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) is a locally non-dominated solution. In what follows, an optimal solution of problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) corresponding to a reference point given by a DM and a predetermined reference point is called a preferred solution and a reference solution, respectively. Moreover, problem (1(1) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\{f_1(\mathbf{x}),\dots ,f_k(\mathbf{x})\},\end{array}$$(1) ) is referred to as the original problem and its computationally expensive functions as original functions.

3. The SURROGATE-ASF method

In the SURROGATE-ASF method, a DM can provide preferred ranges of the objective functions. Then, they are considered as the utopian and the nadir vectors corresponding to the region which is interesting for the DM in the objective space. Alternatively, estimates of the utopian and nadir vectors can be incorporated into the method. In fact, if the utopian and nadir vectors are given, then the DM can explore the entire Pareto frontier by providing different reference points through multiple interactions in the decision-making phase to be discussed in Section 3.3. SURROGATE-ASF involves two phases, i.e., initialisation and decision-making phases. In the initialisation phase, a set of non-dominated solutions within the preferred ranges given by the DM is generated. Then, by calling Algorithm 1 to be discussed in the following subsection, a finite number of hyper-boxes is formed using the non-dominated solutions in the decision space. For each individual hyper-box, a single objective surrogate function is built by approximating the ASF (2(2) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \text{ASF:}& S\times {\mathbb{R}}^k\to \mathbb{R}\hfill \\ \hfill & (\mathbf{x},{\overline{\mathbf{z}}}^{\ast })\mapsto \underset{i=1,\dots ,k}{max}(w_i(f_i(\mathbf{x})-{\overline{z}}_i^{\ast })),\hfill \end{array}\end{array}$$(2) ) where the decision variables of problem (1(1) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\{f_1(\mathbf{x}),\dots ,f_k(\mathbf{x})\},\end{array}$$(1) ) and the aspiration levels appearing in the ASF are treated as variables of the surrogate function. In the decision-making phase to be discussed in Section 3.3, these computationally inexpensive surrogate functions are utilised to interact with the DM.

Figure 1. Projection of a given reference point onto the convex hull.

Figure 2. (a): A convex hull with 5 points for a bi-objective problem with $q=4$ divisions. (b): A convex hull with 15 points for a three-objective problem with $q=4$ divisions.

3.1. Surrogate building module

If the DM provides the preferred ranges, the extreme points of the corresponding region in the objective space must be calculated. To be more specific, the corresponding solutions in the decision space are found by solving problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) using the extreme points as reference points. One should note that if the extreme points are formed based on the estimates of the utopian and nadir vectors, then their corresponding solutions in the decision space are already available. The approximation of the ASF requires sample points for the aspiration levels and the decision variables. However, before discussing the procedure of selecting sample points, we first look at an interesting property regarding problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ). This property assists to identify regions in the decision and objective spaces where to select sample points.

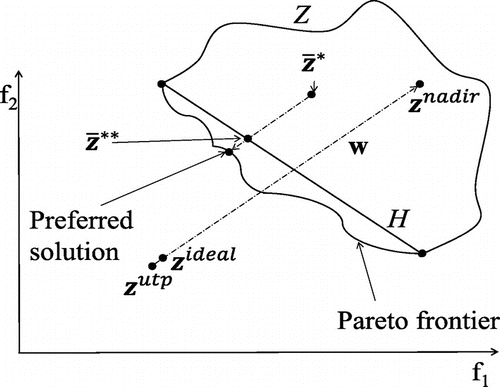
Suppose that H is the convex hull of all individual extreme points. This is constructed by a convex combination of all extreme points in the objective space. Moreover, let ${\overline{\mathbf{z}}}^{\ast }$ be a reference point given by a DM, and ${\mathbf{x}}^{\ast }$ be the corresponding optimal solution of problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ). Thus, ${\mathbf{x}}^{\ast }\in \underset{\mathbf{x}\in S}{\text{argmin}}[\underset{i=1,\dots ,k}{\text{max}}(w_i(f_i(\mathbf{x})-{\overline{z}}_i^{\ast }))]$. On the other hand, ${\mathbf{x}}^{\ast }\in \underset{\mathbf{x}\in S}{\text{argmin}}[\underset{i=1,\dots ,k}{\text{max}}(w_i(f_i(\mathbf{x})-{\overline{z}}_i^{\ast }))+t],$ for all $t\in \mathbb{R}$. Therefore, we have:$$\begin{array}{ccc}\hfill {\mathbf{x}}^{\ast }& \in \hfill & \hfill \underset{\mathbf{x}\in S}{\text{argmin}}\left[\underset{i=1,\dots ,k}{max}(w_i(f_i(\mathbf{x})-{\overline{z}}_i^{\ast }))+t\right]\\ \hfill & =\underset{\mathbf{x}\in S}{\text{argmin}}\left[\underset{i=1,\dots ,k}{max}(w_i(f_i(\mathbf{x})-{\overline{z}}_i^{\ast })+t)\right]\hfill \\ \hfill & =\underset{\mathbf{x}\in S}{\text{argmin}}\left[\underset{i=1,\dots ,k}{max}(w_i(f_i(\mathbf{x})-{\overline{z}}_i^{\ast }+\frac{t}{w_i}))\right]\hfill \\ \hfill & =\underset{\mathbf{x}\in S}{\text{argmin}}\left[\underset{i=1,\dots ,k}{max}(w_i(f_i(\mathbf{x})-({\overline{z}}_i^{\ast }-\frac{t}{w_i})))\right]\hfill \\ \hfill & =\underset{\mathbf{x}\in S}{\text{argmin}}\left[\underset{i=1,\dots ,k}{max}(w_i(f_i(\mathbf{x})-{\overline{z}}_i^{\ast \ast }))\right],\hfill \end{array}$$

where ${\overline{\mathbf{z}}}^{\ast \ast }$ is treated as an arbitrary reference point on the ray passing through ${\overline{\mathbf{z}}}^{\ast }$ in parallel with $\mathbf{w}={(w_1,\dots ,w_k)}^T$. It means that the optimal solution of problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) for a reference point ${\overline{\mathbf{z}}}^{\ast }$ given by a DM is also the optimal solution of problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) for any reference point on the ray passing though ${\overline{\mathbf{z}}}^{\ast }$ in parallel with $\mathbf{w}$ (see Figure 1). The following problem gives the projected reference point ${\overline{\mathbf{z}}}^{\ast \ast }$ in H:(4) $$\begin{array}{c}\hfill {\overline{\mathbf{z}}}^{\ast \ast }\in \underset{\mathbf{h}\in H}{\text{argmin}}∥\frac{\mathbf{h}-{\overline{\mathbf{z}}}^{\ast }}{\mathbf{w}}∥\end{array}$$(4)

where $\Vert .\Vert$ is the Euclidean norm. Problem (4(4) $$\begin{array}{c}\hfill {\overline{\mathbf{z}}}^{\ast \ast }\in \underset{\mathbf{h}\in H}{\text{argmin}}∥\frac{\mathbf{h}-{\overline{\mathbf{z}}}^{\ast }}{\mathbf{w}}∥\end{array}$$(4) ) applies if and only if there exists a real number $t\in \mathbb{R}$ such that ${\overline{\mathbf{z}}}^{\ast }=\mathbf{h}+t\mathbf{w}$ for some $\mathbf{h}\in H$.

Since any reference point within the preferred ranges of objective functions given by the DM can be projected onto the convex hull H (i.e., finding the closest point on H along the direction $\mathbf{w}$), sample points for the aspiration levels as reference sample points are selected on this convex hull. To do this, first, a set of evenly distributed predetermined reference points including the extreme points is generated on the convex hull H and denoted by ${\overline{Z}}^P$. The reference solutions (non-dominated solutions) in the decision space corresponding to these reference points are obtained by solving problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) for each individual predetermined reference point. This is conducted by employing a surrogate-based single objective optimisation method. The choice of this method has an impact on the performance of SURROGATE-ASF. One can use an appropriate state-of-the-art method to solve problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) efficiently. These reference solutions are evaluated with the original functions.

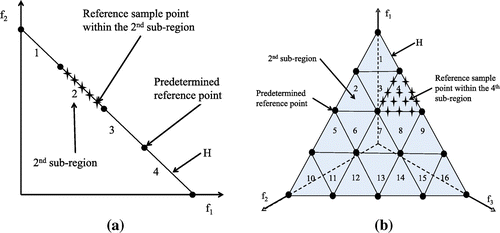
In order to generate the predetermined reference points (without involving any DM), we use the method presented in Das and Dennis (1998) that places points on a convex hull of all individual extreme points (a $(k-1)$- dimensional simplex). If $h_z$ predetermined reference points (including the extreme points in the objective space) are considered, the q divisions along each objective coordinate axis in the objective space of a k-objective problem can be calculated using:(5) $$\begin{array}{c}\hfill h_z=\left(\begin{array}{c}k+q-1\\ q\end{array}\right).\end{array}$$(5)

Figures 2 (a) and 2 (b) depict two convex hulls for bi- and three-objective problems with $q=4$ and $h_z=\left(\begin{array}{c}2+4-1\\ 4\end{array}\right)=5$ and $h_z=\left(\begin{array}{c}3+4-1\\ 4\end{array}\right)=15$ predetermined reference points (black circles), respectively.

The sets of reference solutions in the decision and the objective spaces are denoted by $X^P$ and $F^P$, respectively. By making use of the set of predetermined reference points ${\overline{Z}}^P$ and reference solutions $X^P$, the convex hull H and the decision space are decomposed into a finite number of sub-regions and hyper-boxes, respectively. In what follows, $a=1,\dots ,r$, represents the index corresponding to the $a^{\mathit{th}}$ hyper-box or sub-region where r is the number of hyper-boxes (sub-regions). For $k=$ 2 and 3, we have $r=q$ and $q^2$, respectively.

Algorithm 1 starts by constructing sub-regions on H using the predetermined reference points in ${\overline{Z}}^P$. Each sub-region is formed by selecting the k nearest neighbor points on H starting from one of the extreme points. Figures 2 (a) and 2 (b) represent one possible way of forming the sub-regions and numbering them where $k=2$ and $k=3$, respectively. Then, reference sample points (the stars in Figures 2 (a) and 2 (b)) are selected within these sub-regions. To select reference sample points, the predetermined reference points corresponding to the $a^{\mathit{th}}$ sub-region (i.e., ${\overline{Z}}^{P,a}=\{{\overline{\mathbf{z}}}^{P,a,1},\dots ,{\overline{\mathbf{z}}}^{P,a,k}\}$) are considered as the extreme points of this sub-region. Then, by using the method presented in Das and Dennis (1998), a set of evenly distributed reference sample points within this sub-region on the convex hull is generated. The larger the number of generated reference sample points, the higher is the accuracy of the surrogate function ${\widetilde{\text{ASF}}}^a$ corresponding to the $a^{\mathit{th}}$ sub-region. These reference sample points along with the reference points in ${\overline{Z}}^{P,a}$ are considered as sample points corresponding to this sub-region and denoted by ${\overline{Z}}^a$.

To decompose the decision space, hyper-boxes are built corresponding to sub-regions on the convex hull H. Considering the $a^{\mathit{th}}$ sub-region on H and the set of predetermined reference points forming this sub-region, i.e., ${\overline{Z}}^{P,a}=\{{\overline{\mathbf{z}}}^{P,a,1},\dots ,{\overline{\mathbf{z}}}^{P,a,k}\}$, the set of non-dominated solutions corresponding to these predetermined reference points in the decision and the objective spaces are denoted by $X^{P,a}=\{{\mathbf{x}}^{P,a,1},\dots ,{\mathbf{x}}^{P,a,k}\}$ and $F^{P,a}=\{\mathbf{f}({\mathbf{x}}^{P,a,1}),\dots ,\mathbf{f}({\mathbf{x}}^{P,a,k})\}$, respectively. Then, the lower and the upper bounds of the decision variable $x_c$, for $c=1,\dots ,n,$ within the $a^{\mathit{th}}$ hyper-box denoted by $S^a$ corresponding to this sub-region are calculated as follows:(6) $$\begin{array}{cc}\hfill min\{x_c^{P,a,1},\dots ,x_c^{P,a,k}\}& \le x_c\le max\{x_c^{P,a,1},\dots ,x_c^{P,a,k}\},\hfill \\ \hfill & \text{for all}c=1,\dots ,n.\hfill \end{array}$$(6)

Figure 3 shows a simple example of hyper-boxes for a problem with two decision variables. Once $S^a$ is formed, a small number of initial sample points within this hyper-box is selected using some sampling technique such as Latin hypercube sampling (LHS) (Helton, Johnson, Sallaberry, & Storlie, 2006) and evaluated with the original functions. These evaluated points along with the non-dominated solutions in $X^{P,a}$ are considered as the initial sample points in the decision space corresponding to $S^a$ and denoted by ${\overline{X}}^a$.

Figure 3. Hyper-boxes in the decision space corresponding to the sub-regions on the convex hull in Figure 2 (a). For example, reference solutions ${\mathbf{x}}^{P,1,1}$ and ${\mathbf{x}}^{P,1,2}$ form $S^1$.

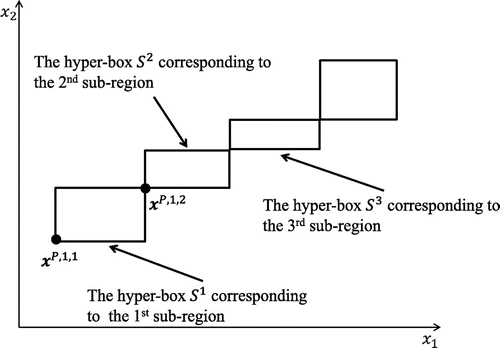
To build the surrogate function ${\widetilde{\text{ASF}}}^a$ corresponding to the hyper-box $S^a$, a cubic RBF with a linear tail is employed to approximate ASF (its description is given e.g., in Muller, Shoemaker, and Piche (2013)). To do this, the following Cartesian product of sets ${\overline{X}}^a$ and ${\overline{Z}}^a$ is formed as input data denoted by $T^a$ for RBF:(7) $$\begin{array}{cc}\hfill T^a& ={\overline{X}}^a\times {\overline{Z}}^a=\{(\overline{\mathbf{x}},\overline{\mathbf{z}})|\overline{\mathbf{x}}\in {\overline{X}}^a\text{and}\overline{\mathbf{z}}\in {\overline{Z}}^a\}.\hfill \end{array}$$(7)

The ASF values of all elements in $T^a$ are calculated. One should note that the objective function values of all sample points in ${\overline{X}}^a$ are available. Then, $T^a$ is divided into validation and training sets using the leave-one-out cross-validation (LOOCV) or the k-fold cross-validation method discussed in Muller and Shoemaker (2014) (note that it differs from the index k for the $k^{\mathit{th}}$ objective function). Let $\left|T^a\right|$ be the cardinality of $T^a$. According to Muller and Shoemaker (2014), if $\left|T^a\right|\le 50$, we use LOOCV. If $\left|T^a\right|>50$, then we use the k-fold cross-validation method where $k=10$, for $50<\left|T^a\right|\le 100$, $k=20$, for $100<\left|T^a\right|\le 150$ and $k=30$, for $150<\left|T^a\right|\le 200$. Having the elements in the training set and their corresponding ASF values as input data, RBF is employed to build ${\widetilde{\text{ASF}}}^a$. When using either LOOVC or the k-fold cross-validation method, the prediction accuracy of ${\widetilde{\text{ASF}}}^a$ is evaluated using standard error measures like Root Mean Squared Error (RMSE) (Giunta, Watson, & Koehler, 1998) and/or $R^2$ (Jin, Chen, & Simpson, 2001).

The steps of the decomposition procedure of the decision space into a finite number of hyper-boxes and building corresponding surrogate functions are shown in Algorithm 1. Note that the prediction accuracy of ${\widetilde{\text{ASF}}}^a$ may not be satisfactory after steps 1-10 of Algorithm 1 and, in that case, it needs to be improved. In the following subsection, we discuss an update strategy called Algorithm 2 by which new sample points within the hyper-box $S^a$ can be selected. The process of updating ${\widetilde{\text{ASF}}}^a$ is repeated until a desired accuracy is achieved.

The non-dominated solutions used to form hyper-boxes correspond to the predetermined reference points on the convex hull. It may happen that at least two predetermined reference points have the same corresponding non-dominated solution. In such cases, to form sub-regions and hyper-boxes, out of all predetermined reference points with the same non-dominated solution (i.e., the same objective values but different decision variable values), only one reference point (selected arbitrarily) and its corresponding non-dominated solution are considered along with other different predetermined reference points and non-dominated solutions. Then, sub-regions and hyper-boxes are formed. It may also occur that hyper-boxes overlap each other. In these cases, some sample points selected fall into more than one hyper-box. However, sub-regions and hyper-boxes are still formed as mentioned in Algorithm 1.

In practice, obtaining a desired accuracy may not be possible. In such a case, depending on the computational budget, one can consider a maximum number of function evaluations for each individual hyper-box. Then, either achieving a desired accuracy or reaching the maximum number of function evaluations can be considered as a stopping criterion.

3.2. Accuracy improvement module

To improve the accuracy prediction of ${\widetilde{\text{ASF}}}^a$ corresponding to $S^a$, we discuss Algorithm 2. When updating ${\widetilde{\text{ASF}}}^a$, two matters are considered, i.e, sampling non-dominated solutions within $S^a$ and having a good diversity among the sample points in ${\overline{X}}^a$.

In order to sample non-dominated solutions, we employ the sampling function discussed in Kitayama et al. (2013) to generate new sample points within $S^a$. The authors of Kitayama et al. (2013) modify the Pareto fitness function (Schaumann, Balling, & Day, 1998) and introduce a sampling function by using RBF such that by minimising this function, the optimal solution can be a non-dominated solution. See Kitayama et al. (2013) for details of building this sampling function. For the sake of simplicity, we refer to this sampling function as the modified Pareto fitness function (MPF).

By minimising the MPF iteratively, non-dominated solutions within $S^a$ can be generated. Nevertheless, the diversity of the points in ${\overline{X}}^a$ to cover the hyper-box should be considered. Thus, in some iteration of updating ${\widetilde{\mathit{ASF}}}^a$, some solution obtained by minimising the MPF is not evaluated with the original functions. This requires a criterion to assess whether the optimal solution of the MPF should be evaluated with the original functions and added into ${\overline{X}}^a$ or not. We discuss this criterion here.

Since some points are not evaluated with the original functions, we introduce ${\overline{\mathit{XP}}}^a$ and ${\overline{\mathit{FP}}}^a$ as sets of archived points generated during the updating process in the decision and the objective spaces, respectively. These sets include all points in ${\overline{X}}^a$ and ${\overline{F}}^a$ (the points evaluated with the original functions) and sample points which are not evaluated with the original functions. In what follows, a procedure is discussed to assign objective function values to the points not evaluated with the original functions.

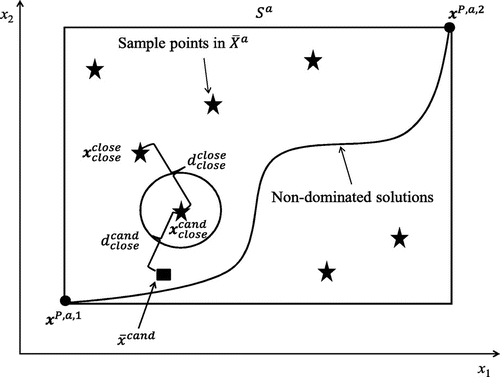
Building the MPF is based on the points in ${\overline{\mathit{XP}}}^a$ and ${\overline{\mathit{FP}}}^a$. To do this, all points in ${\overline{\mathit{XP}}}^a$ and their corresponding MPF values are considered as input data to train a cubic RBF with a linear tail. Once the MPF is built, it is minimised and the optimal solution ${\overline{\mathbf{x}}}^{\mathit{cand}}$ within $S^a$ is obtained. Then, as depicted in Figure 4, the closest point in ${\overline{X}}^a$ in terms of the Euclidean distance to ${\overline{\mathbf{x}}}^{\mathit{cand}}$ is found. This point is denoted by ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}$, the corresponding objective vector by ${\overline{\mathbf{f}}}_{\mathit{close}}^{\mathit{cand}}$ and the Euclidean distance between ${\overline{\mathbf{x}}}^{\mathit{cand}}$ and ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}$ by $d_{\mathit{close}}^{\mathit{cand}}$. The closest point in ${\overline{X}}^a\backslash \{{\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}\}$ to ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}$ is also found. We denote this point by ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{close}}$ and the Euclidean distance between ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{close}}$ and ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}$ by $d_{\mathit{close}}^{\mathit{close}}$.

Figure 4. Selecting sample points within $S^a$ to update ${\widetilde{\mathit{ASF}}}^a$.

To have diversity among sample points within ${\overline{X}}^a$, the criterion $d_{\mathit{close}}^{\mathit{cand}}>\frac{d_{\mathit{close}}^{\mathit{close}}}{2}$ is checked. This means that if ${\overline{\mathbf{x}}}^{\mathit{cand}}$ is outside the circle centered on ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}$ with radius $\frac{d_{\mathit{close}}^{\mathit{close}}}{2}$ (see Figure 4), then ${\overline{\mathbf{x}}}^{\mathit{cand}}$ is evaluated with the original functions and the objective vector ${\overline{\mathbf{f}}}^{\mathit{cand}}$ is calculated. Before adding ${\overline{\mathbf{x}}}^{\mathit{cand}}$ and ${\overline{\mathbf{f}}}^{\mathit{cand}}$ into ${\overline{X}}^a$ and ${\overline{F}}^a$, respectively, the prediction accuracy of ${\widetilde{\text{ASF}}}^a$ is assessed. To accomplish this, a test set as defined in $T^a$ (7(7) $$\begin{array}{cc}\hfill T^a& ={\overline{X}}^a\times {\overline{Z}}^a=\{(\overline{\mathbf{x}},\overline{\mathbf{z}})|\overline{\mathbf{x}}\in {\overline{X}}^a\text{and}\overline{\mathbf{z}}\in {\overline{Z}}^a\}.\hfill \end{array}$$(7) ) is formed where ${\overline{\mathbf{x}}}^{\mathit{cand}}$ and all reference sample points in ${\overline{Z}}^a$ are utilised to form the Cartesian product set. All elements in the test set are evaluated with ${\widetilde{\text{ASF}}}^a$ and ASF, and the prediction accuracy of ${\widetilde{\text{ASF}}}^a$ is checked. If the accuracy is not acceptable, ${\overline{\mathbf{x}}}^{\mathit{cand}}$ is added into ${\overline{X}}^a$ and ${\overline{\mathit{XP}}}^a$ and ${\overline{\mathbf{f}}}^{\mathit{cand}}$ into ${\overline{F}}^a$ and ${\overline{\mathit{FP}}}^a$, respectively. Then, the points in ${\overline{X}}^a$ are utilised to update ${\widetilde{\text{ASF}}}^a$ and the points in ${\overline{\mathit{XP}}}^a$ to update the MPF. The process of minimising the MPF and checking the diversity criterion is repeated. If the prediction accuracy is acceptable, then the process of updating ${\widetilde{\text{ASF}}}^a$ is terminated.

If $d_{\mathit{close}}^{\mathit{cand}}\le \frac{d_{\mathit{close}}^{\mathit{close}}}{2}$, ${\overline{\mathbf{x}}}^{\mathit{cand}}$ is inside the circle centered on ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}$ with radius $\frac{d_{\mathit{close}}^{\mathit{close}}}{2}$, then ${\overline{\mathbf{x}}}^{\mathit{cand}}$ is not evaluated with the original functions and is not added into ${\overline{X}}^a$. However, to generate new sample points by the MPF, the objective vector corresponding to ${\overline{\mathbf{x}}}^{\mathit{cand}}$ is required. In this case, to avoid generating ${\overline{\mathbf{x}}}^{\mathit{cand}}$ again, the objective vector corresponding to this point is artificially treated as a dominated point in the objective space by the objective vector ${\overline{\mathbf{f}}}_{\mathit{close}}^{\mathit{cand}}$. To do this, an artificial objective vector denoted by ${\overline{\mathbf{f}}}_{\mathit{artif}}^{\mathit{cand}}$ is considered for this point by adding a random vector with positive components to the objective vector ${\overline{\mathbf{f}}}_{\mathit{close}}^{\mathit{cand}}$. This random vector is a fraction of ${\mathbf{z}}^{\mathit{nadir}}-{\overline{\mathbf{f}}}_{\mathit{close}}^{\mathit{cand}}$, e.g., $\frac{{\mathbf{z}}^{\mathit{nadir}}-{\overline{\mathbf{f}}}_{\mathit{close}}^{\mathit{cand}}}{10}$. By this choice, ${\overline{\mathbf{f}}}_{\mathit{close}}^{\mathit{cand}}$ is non-dominated with respect to ${\overline{\mathbf{f}}}_{\mathit{artif}}^{\mathit{cand}}$, and is inside the feasible objective space. Then, ${\overline{\mathbf{x}}}^{\mathit{cand}}$ and ${\overline{\mathbf{f}}}_{\mathit{artif}}^{\mathit{cand}}$ are added into ${\overline{\mathit{XP}}}^a$ and ${\overline{\mathit{FP}}}^a$. Note that these points are not added into ${\overline{X}}^a$ and ${\overline{F}}^a$. Then, the MPF values of all points in ${\overline{\mathit{XP}}}^a$ are calculated and the MPF is updated. The updating process is repeated until the stopping criterion regarding the accuracy of ${\widetilde{\text{ASF}}}^a$ is met.

3.3. SURROGATE-ASF and decision-making

In this subsection, we present both the decision-making phase as well as the SURROGATE-ASF algorithm. As discussed in Section 3.1, in the initialisation phase, surrogate functions are built by calling Algorithm 1. These surrogate functions are employed to interact with the DM.

In the decision-making phase, if the DM did not provide any preferred ranges, the utopian and the nadir vectors are shown to him/her. The DM is supposed to specify reference points within the ranges. In any case, the DM provides a reference point ${\overline{\mathbf{z}}}^{\ast }$. The interaction with the DM in SURROGATE-ASF corresponds to that of the reference point method given in Wierzbicki (1982). The reference point ${\overline{\mathbf{z}}}^{\ast }$ is projected onto the convex hull H by solving problem (4(4) $$\begin{array}{c}\hfill {\overline{\mathbf{z}}}^{\ast \ast }\in \underset{\mathbf{h}\in H}{\text{argmin}}∥\frac{\mathbf{h}-{\overline{\mathbf{z}}}^{\ast }}{\mathbf{w}}∥\end{array}$$(4) ) as discussed in Section 3.1. In practice, to find the projected reference point denoted by ${\overline{\mathbf{z}}}^{\ast \ast }$, we do not solve problem (4(4) $$\begin{array}{c}\hfill {\overline{\mathbf{z}}}^{\ast \ast }\in \underset{\mathbf{h}\in H}{\text{argmin}}∥\frac{\mathbf{h}-{\overline{\mathbf{z}}}^{\ast }}{\mathbf{w}}∥\end{array}$$(4) ). A simple approach is to generate a large number of uniformly distributed points on H. Then, the point that minimise the objective function of problem (4(4) $$\begin{array}{c}\hfill {\overline{\mathbf{z}}}^{\ast \ast }\in \underset{\mathbf{h}\in H}{\text{argmin}}∥\frac{\mathbf{h}-{\overline{\mathbf{z}}}^{\ast }}{\mathbf{w}}∥\end{array}$$(4) ) is selected. Then, the sub-region and the hyper-box number corresponding to this projected reference point are identified and denoted by $\tilde{a}$ and the following surrogate problem is solved by using any appropriate single objective optimisation method:(8) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S^{\tilde{a}}}{\text{minimise}}{\widetilde{\text{ASF}}}^{\tilde{a}}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast \ast }),\end{array}$$(8)

where $S^{\tilde{a}}$ is the ${\tilde{a}}^{\mathit{th}}$ hyper-box. The optimal solution obtained is an approximation of the preferred solution in the decision space corresponding to the reference point ${\overline{\mathbf{z}}}^{\ast }$ given by the DM. This solution is evaluated with the original functions and shown to the decision-maker. The process of asking for a reference point from the DM, projecting it onto the convex hull and solving the corresponding surrogate problem is repeated until the most preferred solution satisfying the DM is obtained. An overview of the algorithm of SURROGATE-ASF including the initialisation and the decision-making phases is given in Algorithm 3.

4. Numerical results

In this section, we demonstrate the performance of SURROGATE-ASF through solving a shape optimisation problem of designing an airfoil. Since this problem contains objective functions with a practical meaning, it is easier to describe the decision-making process. Therefore, we discuss the decision-making phase comprehensively for this problem. In addition to this practical problem, we consider academic benchmark problems attributing different characteristics such as non-convex Pareto frontiers, connected or disconnected sets of Pareto optimal solutions and multimodal functions. Results involving the benchmark problems are given in Section 4.2. The decision-making phase for these academic benchmark problems is similar to the one in the shape optimisation problem.

We compare the performance of SURROGATE-ASF with the method (Yun et al., 2009) (henceforth called here the Yun method) and the PAINT method (Hartikainen, Miettinen, & Wiecek, 2012). According to the findings presented in Tabatabaei et al. (2015), the Yun method and PAINT are the most similar methods to SURROGATE-ASF because in all of them the DM provides preference information in the form of a reference point and, thus, these three methods are comparable.

The Yun method is non-interactive in which $\mu -\nu -$SVR (Yun et al., 2009) is applied as the metamodeling technique. Because it is not interactive by nature, for each individual reference point given by the DM, the entire method must be run for enabling interaction with the DM. In this method, first each objective function is approximated and a surrogate multiobjective optimisation problem is formulated. With the objective functions in the surrogate problem, problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) as a single objective computationally inexpensive problem is formulated to be solved. The solution of this problem as well as some sample points, selected based on the Lagrangian coefficients in $\mu -\nu -$SVR, are utilised to improve the accuracy of the surrogate problem. By comparing the performance of the Yun method and SURROGATE-ASF, we show the advantages of the approach of approximating the achievement scalarising function (2(2) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \text{ASF:}& S\times {\mathbb{R}}^k\to \mathbb{R}\hfill \\ \hfill & (\mathbf{x},{\overline{\mathbf{z}}}^{\ast })\mapsto \underset{i=1,\dots ,k}{max}(w_i(f_i(\mathbf{x})-{\overline{z}}_i^{\ast })),\hfill \end{array}\end{array}$$(2) ) as a computationally expensive objective function and then converting it to a computationally inexpensive one over the approach of first approximating each expensive function individually and then forming the achievement scalarising function. We implemented the Yun method in MATLAB 2015b.

Similar to SURROGATE-ASF, the PAINT method requires a set of non-dominated solutions being available to build a surrogate problem. In PAINT, a linear mixed integer multiobjective optimisation problem is introduced as a surrogate of the original problem. Then, this problem is scalarised using the achievement scalarising function including a reference point given by the DM. This scalarised problem is solved, and an approximated solution in the objective space is obtained. PAINT can only provide solutions in the objective space, i.e., decision variable values of the approximated solutions cannot be obtained. The approximated solution is shown to the DM. If the DM is not satisfied, (s)he provides another reference point. The interaction with the DM is conducted until the approximated solution obtained is acceptable for the DM. Then, this solution is considered as a reference point. Using this reference point and the original, computationally expensive functions, problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) is formulated as a computationally expensive single objective optimisation problem. This problem is solved by a (surrogate-based) single objective optimisation method. The optimal solution is the most preferred (approximated) solution and provided to the DM. One should note that, for any approximated solution generated in the intermediate iterations, it is possible to obtain the corresponding decision variable values by solving an expensive single objective optimisation problem. In this paper, we follow the steps given in Hartikainen et al. (2012) and do not calculate approximated solutions in the decision space until the last iteration.

At the end of the solution process by an interactive method, the most preferred solution (which is usually a single solution) is obtained. In this aspect, to the best of our knowledge, there is no established quality measure in the literature which is suitable for a reference point based interactive method. Therefore, we compare the closeness of approximated solutions in the objective space obtained by SURROGATE-ASF, the Yun method and PAINT with their corresponding solutions obtained by solving problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) in which the original functions are used. To do so, problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) (for the academic benchmark problems) is solved including reference points given by the DM. In what follows, we refer to these solutions as original solutions. The closeness of the approximated solution ${\tilde{\mathbf{f}}}^{j\ast }$ and the original solution ${\mathbf{f}}^{j\ast }$ for $j=1,\dots ,l,$ (where l is the number of reference points given by the DM) in the objective space is assessed based on the Euclidean distance. To do this, first normalised approximated solutions ${\tilde{\mathbf{f}}}_{\mathit{norm}}^{j\ast }=\frac{{\tilde{\mathbf{f}}}^{j\ast }-{\mathbf{z}}^{\mathit{ideal}}}{{\mathbf{z}}^{\mathit{nadir}}-{\mathbf{z}}^{\mathit{ideal}}}$ and normalised original solutions ${\mathbf{f}}_{\mathit{norm}}^{j\ast }=\frac{{\mathbf{f}}^{j\ast }-{\mathbf{z}}^{\mathit{ideal}}}{{\mathbf{z}}^{\mathit{nadir}}-{\mathbf{z}}^{\mathit{ideal}}}$ are calculated for $j=1,\dots ,l$. Then, the Euclidean distance between the normalised approximated and original solutions in the objective space is calculated as follows:(9) $$\begin{array}{c}\hfill E_j=\Vert {\widetilde{{\mathbf{f}}^{\ast }}}_{\mathit{norm}}^j-{{\mathbf{f}}^{\ast }}_{\mathit{norm}}^j\Vert \end{array}$$(9)

where $\Vert .\Vert$ is the Euclidean norm.

We also define(10a) $$\begin{array}{c}\hfill {\mu }_c=\frac{1}{l}\sum _{j=1}^l{E}_j,\end{array}$$(10a) (10b) $$\begin{array}{c}\hfill {\sigma }_c=\sqrt{\frac{1}{l-1}\sum _{j=1}^l{(E_j-{\mu }_c)}^2}.\end{array}$$(10b)

as mean and standard deviation of the $E_j$s, respectively, to be used for comparing the $E_j$s obtained by the methods.

4.1. Solving a shape optimisation problem

In this subsection, we demonstrate the performance of SURROGATE-ASF by solving a bi-objective airfoil shape optimisation problem(11) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\left\{\frac{C_d(\mathbf{x})}{C_l(\mathbf{x})},C_m^2(\mathbf{x})\right\},\end{array}$$(11)

where $C_d$, $C_l$ and $C_m$ are the drag, lift and pitching moment coefficients, respectively, and $S=\{\mathbf{x}\in {\mathbb{R}}^{12}:0.0085\le x_1\le 0.0126,0.0020\le x_2\le 0.0040,7.0000\le x_3\le 10.0000,10.0000\le x_4\le 14.0000,-0.0060\le x_5\le -0.0030,0.0025\le x_6\le 0.0050,0.4100\le x_7\le 0.4600$, $0.1100\le x_8\le 0.1300$, $-0.9000\le x_9\le -0.7000$, $0.2000\le x_{10}\le 0.2600$, $-0.0230\le x_{11}\le -0.0150,0.0500\le x_{12}\le 0.2000\}$ is the feasible decision set. The angle of attack, Reynolds and Mach numbers were $4.0^{\circ }$, $2.0\times {10}^6$ and 0.1, respectively. The CFD solver adopted in this problem was XFOIL (Drela, 1989). Problem (11(11) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\left\{\frac{C_d(\mathbf{x})}{C_l(\mathbf{x})},C_m^2(\mathbf{x})\right\},\end{array}$$(11) ) termed as $ASO-MOP2$ has been investigated with a non-interactive method in Arias-Montano, Coello Coello, and Mezura-Montes (2012) with a budget of 2000 function evaluations. In our paper, we also used the same budget to solve the problem. In Arias-Montano, Coello Coello, and Mezura-Montes (2012), the description of the decision variables and the geometry of the corresponding airfoil (see Figure 3 in Arias-Montano, Coello Coello, and Mezura-Montes (2012)) is provided. In this problem, the DM was interested in exploring the objective space for ranges $0.0043\le f_1\le 0.0064$ and $0.0076\le f_2\le 0.034$.

As said, the surrogate-based single objective optimisation method to solve problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) as a computationally expensive one has an impact on the performance of SURROGATE-ASF in terms of reducing the computational cost. In Muller and Shoemaker (2014), a toolbox implemented in MATLAB called MATSuMoTo (can be downloaded from https://courses.cit.cornell.edu/jmueller/) has been developed to solve computationally expensive global optimisation problems. We applied MATSuMoTo to solve problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ).

In the initialisation phase of SURROGATE-ASF, according to equation (5(5) $$\begin{array}{c}\hfill h_z=\left(\begin{array}{c}k+q-1\\ q\end{array}\right).\end{array}$$(5) ), $h_z=4$ ($q=3$) predetermined reference points for the bi-objective problem were considered. For each predetermined reference point, 350 function evaluations were used to find the corresponding reference solutions by solving problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ). In Algorithm 1, the criteria to check the accuracy of ${\widetilde{\text{ASF}}}^a$ corresponding to the $a^{\mathit{th}}$ hyper-box (sub-region) for $a=1,\dots ,r,$ were $R^2=0.95$ and $RMSE=0.005$ as they are commonly used in the literature. Since the accuracy of the initial surrogate functions was not satisfactory with these choices, we applied Algorithm 2 to update the surrogate functions with respect to a maximum number of 100 function evaluations within each hyper-box. Tables A.1 and A.2 in Appendix A summarise the parameter settings of SURROGATE-ASF and MATSuMoTo, respectively. In Table A.1, the number of reference sample points (i.e., $h_z$) within each sub-region was chosen heuristically according to (5(5) $$\begin{array}{c}\hfill h_z=\left(\begin{array}{c}k+q-1\\ q\end{array}\right).\end{array}$$(5) ). In the initialisation phase, we set 1400 function evaluations for MATSuMoTo to obtain the reference solutions $X^P$ and $F^P$ corresponding to the points in ${\overline{Z}}^P$. The number of function evaluations needed by SURROGATE-ASF to build all surrogate functions was 284. Therefore, the total number of function evaluations in the initialisation phase of SURROGATE-ASF using MATSuMoTo to build all surrogate functions was 1684.

In the decision-making phase, reference points given by the DM were projected onto the convex hull H according to (4(4) $$\begin{array}{c}\hfill {\overline{\mathbf{z}}}^{\ast \ast }\in \underset{\mathbf{h}\in H}{\text{argmin}}∥\frac{\mathbf{h}-{\overline{\mathbf{z}}}^{\ast }}{\mathbf{w}}∥\end{array}$$(4) ). Then, the corresponding surrogate problem (8(8) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S^{\tilde{a}}}{\text{minimise}}{\widetilde{\text{ASF}}}^{\tilde{a}}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast \ast }),\end{array}$$(8) ) was solved including the projected reference points. In this problem, while the computationally inexpensive surrogate problem (8(8) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S^{\tilde{a}}}{\text{minimise}}{\widetilde{\text{ASF}}}^{\tilde{a}}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast \ast }),\end{array}$$(8) ) can be solved by any appropriate method, we employed a single objective genetic algorithm with the parameter settings given in Goldberg (1989). As shown in Table 1, in the first iteration, the DM provided the first reference point ${\overline{\mathbf{z}}}^{{\ast }^1}$ within his preferred ranges. The corresponding surrogate problem was solved and the preferred solution was obtained. This solution was evaluated with the original functions and the corresponding objective vector ${\mathbf{f}}^1$ was shown to the DM. For ${\mathbf{f}}^1$, the DM was interested in improving the ratio of drag to lift coefficient while keeping the pitching moment coefficient the same. Then, the next reference point ${\overline{\mathbf{z}}}^{{\ast }^2}$ was given by the DM and the preferred solution ${\mathbf{f}}^2$ was presented to him. Comparing the ratio of drag to lift coefficient in ${\overline{\mathbf{z}}}^{{\ast }^2}$, ${\mathbf{f}}^1$ and ${\mathbf{f}}^2$, the DM realised that with this pitching moment coefficient, the improvement in the ratio of drag to lift coefficient is very small. Thus, the DM sacrificed the pitching moment coefficient to improve the ratio of drag to lift coefficient, and provided the reference point ${\overline{\mathbf{z}}}^{{\ast }^3}$. The preferred solution ${\mathbf{f}}^3$ was shown to the DM. The change in the pitching moment coefficient from ${\mathbf{f}}^2$ to ${\mathbf{f}}^3$ was acceptable for the DM. Based on the pitching moment coefficient in ${\mathbf{f}}^3$, the DM provided ${\overline{\mathbf{z}}}^{{\ast }^4}$ to improve the ratio of drag to lift coefficient. The corresponding preferred solution ${\mathbf{f}}^4$ was presented to the DM.

Table 1. Reference points given by the DM and corresponding preferred solutions in the objective space.

	Reference points	Preferred solutions (SUR.)	Solutions (PAINT.)	Solutions (Yun.)
1	${\overline{z}}^{\ast 1}=(6.50\times {10}^{-3},8.00\times {10}^{-3})$	${\mathbf{f}}^1=(6.32\times {10}^{-3},7.48\times {10}^{-3})$	${\mathbf{f}}^1=(6.44\times {10}^{-3},7.74\times {10}^{-3})$	${\mathbf{f}}^1=(7.63\times {10}^{-3},8.24\times {10}^{-3})$
2	${\overline{z}}^{\ast 2}=(5.50\times {10}^{-3},7.48\times {10}^{-3})$	${\mathbf{f}}^2=(6.13\times {10}^{-3},8.46\times {10}^{-3})$	${\mathbf{f}}^2=(7.41\times {10}^{-3},1.62\times {10}^{-2})$	${\mathbf{f}}^2=(6.24\times {10}^{-3},3.72\times {10}^{-2})$
3	${\overline{z}}^{\ast 3}=(5.00\times {10}^{-3},1.50\times {10}^{-2})$	${\mathbf{f}}^3=(5.10\times {10}^{-3},1.57\times {10}^{-2})$	${\mathbf{f}}^3=(5.54\times {10}^{-3},1.63\times {10}^{-2})$	${\mathbf{f}}^3=(7.34\times {10}^{-3},2.52\times {10}^{-2})$
4	${\overline{z}}^{\ast 4}=(5.00\times {10}^{-3},1.57\times {10}^{-2})$	${\mathbf{f}}^4=(5.07\times {10}^{-3},1.68\times {10}^{-2})$	${\mathbf{f}}^4=(9.34\times {10}^{-3},2.27\times {10}^{-2})$	${\mathbf{f}}^4=(7.20\times {10}^{-3},2.11\times {10}^{-2})$

Table 2. The Euclidean distance between approximated and original solutions in the objective space (biobjective problems, SUR. and PAINT with MAT.).

	$E_1$			$E_2$			$E_3$			${\mu }_c,{\sigma }_c$
	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun
ZDT1	0.16	0.24	1.91	0.25	0.27	4.66	0.26	0.28	1.73	0.23, 0.05	0.26, 0.01	2.76, 1.64
ZDT2	0.10	0.21	3.40	0.36	0.47	2.89	0.70	0.84	4.76	0.39, 0.30	0.51, 0.32	3.68, 0.96
ZDT3	0.40	0.54	0.56	0.72	0.82	0.81	1.13	1.34	2.80	0.75, 0.36	0.90, 0.40	1.39, 1.22
ZDT4	3.67	4.41	3.24	4.58	4.79	4.24	4.50	4.86	4.16	4.25, 0.50	4.69, 0.23	3.88, 0.55
ZDT6	0.59	0.67	0.67	0.71	0.89	7.67	1.46	1.64	7.70	0.92, 0.47	1.07, 0.50	5.35, 4.04

Note: Bold values indicates correct values.

Table 3. The Euclidean distance between approximated and original solutions in the objective space (biobjective problems, SUR. and PAINT with DIR.).

	$E_1$			$E_2$			$E_3$			${\mu }_c,{\sigma }_c$
	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun
ZDT1	2.18	2.29	1.91	5.10	5.38	4.66	2.14	2.79	1.73	3.14, 1.69	3.49, 1.65	2.76, 1.64
ZDT2	3.58	3.79	3.40	3.13	3.36	2.89	4.93	5.14	4.76	3.88, 0.93	4.10, 0.92	3.68, 0.96
ZDT3	1.31	1.46	0.56	1.58	1.73	0.81	2.90	3.17	2.80	1.93, 0.84	2.12, 0.91	1.39, 1.22
ZDT4	0.42	0.79	3.24	0.44	0.61	4.24	0.43	0.51	4.16	0.43, 0.01	0.64, 0.14	3.88, 0.55
ZDT6	6.90	6.92	0.67	7.83	7.94	7.67	7.93	8.04	7.70	7.56, 0.56	7.63, 0.62	5.35, 4.04

Note: Bold values indicates correct values.

Table 4. The Euclidean distance between approximated and original solutions in the objective space (3-objective problems, SUR. and PAINT with MAT.).

	$E_1$			$E_2$			$E_3$			$E_4$			${\mu }_c,{\sigma }_c$
	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun
DTLZ1	327.40	328.19	329.25	323.41	329.71	328.38	326.44	329.42	328.55	329.40	331.43	330.13	326.66, 2.49	329.6, 1.33	329.0, 0.79
DTLZ2	0.42	0.51	0.90	0.54	0.61	0.78	0.48	0.59	0.53	0.23	0.17	0.48	0.42, 0.13	0.47, 0.20	0.67, 0.20
DTLZ3	250.40	254.43	191.15	250.32	257.46	197.42	250.50	251.37	197.36	250.34	253.46	195.35	250.39, 0.08	254.1, 2.53	195.32, 2.94
DTLZ4	0.94	1.05	1.13	0.81	0.98	0.97	0.25	0.31	0.56	0.96	1.16	1.25	0.74, 0.33	0.88, 0.38	0.98, 0.30
DTLZ5	0.20	0.44	0.58	0.64	0.76	0.71	0.90	0.97	0.98	0.81	0.87	0.91	0.64, 0.31	0.76, 0.23	0.79, 0.18
DTLZ6	2.82	2.94	2.95	3.26	3.42	3.74	3.44	3.71	3.73	3.43	3.64	3.84	3.24, 0.29	3.43, 0.34	3.57, 0.41
DTLZ7	0.81	0.91	0.88	2.07	2.41	15.87	2.73	2.94	10.89	3.30	3.74	3.66	2.23, 1.06	2.50, 1.19	7.82, 6.82

Note: Bold values indicates correct values.

Figure 5. Geometric representation of the airfoils corresponding to each iteration.

Table 5. The Euclidean distance between approximated and original solutions in the objective space (3-objective problems, SUR. and PAINT with DIR.).

	$E_1$			$E_2$			$E_3$			$E_4$			${\mu }_c,{\sigma }_c$
	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun
DTLZ1	162.20	168.43	329.25	162.28	168.43	328.38	145.32	148.34	328.55	165.81	168.41	330.13	158.90, 9.20	163.41, 10.04	329.08, 0.79
DTLZ2	0.53	0.71	0.90	0.39	0.40	0.78	0.21	0.29	0.53	0.04	0.10	0.48	0.29, 0.21	0.38, 0.25	0.67, 0.20
DTLZ3	1.30	2.14	191.15	1.03	1.71	197.42	0.77	0.92	197.36	0.76	0.97	195.35	0.97, 0.25	1.44, 0.59	195.32, 2.94
DTLZ4	1.14	1.15	1.13	0.98	1.0	0.97	0.58	0.71	0.56	1.27	1.36	1.25	0.99, 0.30	1.06, 0.27	0.98, 0.30
DTLZ5	0.15	0.20	0.58	0.40	0.51	0.71	0.67	0.70	0.98	0.77	0.80	0.91	0.50, 0.28	0.55, 0.26	0.79, 0.18
DTLZ6	4.66	4.90	2.95	4.44	4.73	3.74	4.37	4.57	3.73	4.46	4.61	3.84	4.48, 0.12	4.70, 0.14	3.52, 0.41
DTLZ7	11.03	11.02	0.88	16.13	16.84	15.87	11.47	11.80	10.89	13.04	13.97	3.66	12.92, 2.30	13.41, 2.60	7.82, 6.82

Note: Bold values indicates correct values.

Table 6. The Euclidean distance between approximated and original solutions in the objective space (DTLZ2 problem, SUR. and PAINT with MAT.).

	$E_1$			$E_2$			$E_3$			$E_4$			$E_5$			${\mu }_c,{\sigma }_c$
	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun
k=4	0.15	0.21	0.39	0.13	0.38	0.43	0.21	0.37	0.49	0.12	0.36	0.91	0.16	0.55	0.56	0.15, 0.03	0.37, 0.11	0.56, 0.20
k=5	0.34	0.61	0.37	0.42	0.93	1.58	0.37	0.89	1.17	0.48	0.84	1.21	0.19	0.21	1.23	0.36, 0.11	0.70, 0.29	1.11, 0.44

Note: Bold values indicates correct values.

Table 7. The Euclidean distance between approximated and original solutions in the objective space (DTLZ2 problem, SUR. and PAINT with DIR.).

	$E_1$			$E_2$			$E_3$			$E_4$			$E_5$			${\mu }_c,{\sigma }_c$
	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun	SUR.	PAINT	Yun
k=4	0.18	0.19	0.39	0.15	0.42	0.43	0.18	0.43	0.49	0.17	0.46	0.91	0.15	0.57	0.56	0.17, 0.01	0.41, 0.13	0.56, 0.20
k=5	0.42	0.92	0.49	0.51	1.14	1.58	0.70	1.00	1.17	0.58	0.99	1.21	0.42	0.62	1.23	0.53, 0.11	0.93, 0.19	1.14, 0.39

Note: Bold values indicates correct values.

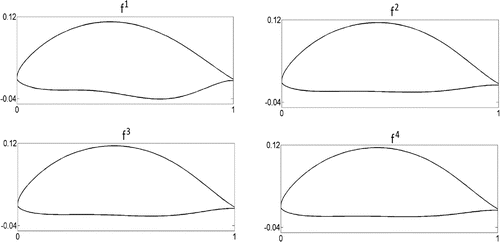
When comparing ${\overline{\mathbf{z}}}^{{\ast }^4}$ and ${\mathbf{f}}^4$, the DM figured out that the ratio of drag to lift coefficient is very close to his preferred value given in ${\overline{\mathbf{z}}}^{{\ast }^4}$. Since the pitching moment coefficient in ${\mathbf{f}}^4$ was acceptable for the DM, ${\mathbf{f}}^4$ satisfied him and the solution process was terminated. Table 1 summarises the reference points given and the corresponding preferred solutions in the objective space obtained by SURROGATE-ASF (SUR) with MATSuMoTo. Figure 5 depicts the geometric shape of the airfoils corresponding to the preferred solutions obtained in each iteration. In the decision-making phase, only four computationally expensive function evaluations were conducted, that is, one for each reference point. Because of this, the DM was able to find the most preferred solution fast. One should note that the total number of function evaluations in the initialisation and decision-making phases of SURROGATE-ASF using MATSuMoTo was 1688. We used this number for comparing with other methods.

For the reference points given by the DM, we also obtained the corresponding preferred solutions by the Yun method and PAINT. Since the Yun method is a non-interactive method, we ran the method for each individual reference point. The number of function evaluations used for each reference point was set as $⌊\frac{1688}{4}⌋=422$. Regarding PAINT, to build a surrogate problem, we employed the same reference solutions in $F^P$ used in SURROGATE-ASF. During the decision-making phase, we only obtained the approximated preferred solutions in the objective space. At the end of the decision-making by PAINT, we solved problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) for the last reference point given by the DM. The maximum number of function evaluations in this step was 288 function evaluations, since 1400 evaluations were already used in obtaining the reference solutions $F^P$.

Since the Pareto optimal set of this problem is not known, we cannot use the Euclidean distance (9(9) $$\begin{array}{c}\hfill E_j=\Vert {\widetilde{{\mathbf{f}}^{\ast }}}_{\mathit{norm}}^j-{{\mathbf{f}}^{\ast }}_{\mathit{norm}}^j\Vert \end{array}$$(9) ) and, instead, compare the solutions obtained in terms of dominance. As can be seen in Table 1, all solutions obtained by SURROGATE-ASF with MATSuMoTo dominate the corresponding solutions obtained by the Yun method and PAINT.

In terms of computational burden, SURROGATE-ASF with MATSuMoTo required 66 minutes to build surrogate functions in the initialisation phase. In the decision-making phase, the DM waited 2 seconds for each reference point to see the preferred solutions. In PAINT, the surrogate problem was built in 57 minutes. Then, for all reference point except the last once, the DM was able to see the preferred solutions after 2 seconds. However, to see the preferred solution corresponding to the last iteration, the DM had to wait for 9 minutes. In the Yun method, for each reference point, the DM had to wait for 27 minutes to see the corresponding solution. To summarise, the last preferred solution was obtained with SURROGATE-ASF, PAINT and the Yun method after 8 seconds, 546 seconds and 108 minutes, respectively. This comparison highlights the advantage of SURROGATE-ASF in which the DM was able to find the preferred solutions quickly. All this was done on a Dell Desktop with Intel(R) Core(TM) i7-3770 CPU @ 3.40GHz processor and 8.00 GB RAM.

4.2. Solving benchmark problems

In this subsection, we evaluate the performance of SURROGATE-ASF through solving ZDT (Zitzler, Deb, & Thiele, 2000) and DTLZ (Deb, Thiele, Laumanns and Zitzler, 2002) benchmark problems. The Pareto frontiers of ZDT1, ZDT4 and DTLZ1 are convex, of ZDT2, ZDT6, DTLZ2, DTLZ3, DTLZ4, DTLZ5 and DTLZ6 are nonconvex and of ZDT3 and DTLZ7 are nonconvex and disconnected. Moreover, ZDT4, ZDT6, DTLZ2, DTLZ3, DTLZ4 and DTLZ6 have many locally nondominated solutions. These benchmark problems also contain multimodal objective functions. For all benchmark problems, we considered $n=7$ decision variables. The number of objective functions in ZDT and DTLZ problems was $k=2$ and $k=3$, respectively. Additionally, to evaluate the performance of SURROGATE-ASF on problems with more than 3 objective functions, we considered DTLZ2 (with multimodal objective functions) with 4 and 5 objective functions. Although objective functions involved in the benchmark problems are known, we treat them as black-box functions. In order to demonstrate the performance of SURROGATE-ASF in computationally expensive problems where solution times may be limited, we set the maximum number of function evaluations for each benchmark problem as 300.

For the problems considered here, along with MATSuMoTo discussed in Section 4.1, we applied the derivative-free DIRECT method (Jones, Perttunen, & Stuckman, 1993) (can be downloaded from http://www4.ncsu.edu/~ctk/Finkel_Direct/) as the second method to solve problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) in the initialisation phase. Although DIRECT has not been developed for computationally expensive problems, we show how these different types of methods affect the performance of SURROGATE-ASF. Table A.3 in Appendix A summarises the parameter settings of DIRECT.

For each benchmark problem, we first applied MATSuMoTo and then DIRECT to solve problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) taking into account the preferences of the DM. In the initialisation phase of SURROGATE-ASF, according to equation (5(5) $$\begin{array}{c}\hfill h_z=\left(\begin{array}{c}k+q-1\\ q\end{array}\right).\end{array}$$(5) ), $h_z=4$ ($q=3$) predetermined reference points were considered for biobjective problems. For three-, four- and five-objective problems we set $h_z=6$ ($q=2$), $h_z=10$ ($q=2$) and $h_z=15$ ($q=2$), respectively.

By increasing the number of objective functions, the number of predetermined reference points is also increased. On the other hand, the computational budget was fixed. Therefore, in this phase, for two-, three-, four- and five-objective problems, we considered 230, 230, 200 and 150 function evaluations, respectively, to find the reference solutions (non-dominated solutions) corresponding to the predetermined reference points by solving problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ). In two-, three-, four- and five-objective problems, we considered $l=3,4,5$ and 5 reference points given by the DM. This means that in the decision-making phase, only l function evaluations were required. The remaining number of function evaluations was used in the initialisation phase to build a surrogate function for each sub-region. In the decision-making phase, while the computationally inexpensive surrogate problem (8(8) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S^{\tilde{a}}}{\text{minimise}}{\widetilde{\text{ASF}}}^{\tilde{a}}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast \ast }),\end{array}$$(8) ) can be solved by any appropriate global optimisation method, we employed DIRECT.

Similar to Section 4.1, we compare the performance of SURROGATE-ASF (with both MATSuMoTo and DIRECT) taking into account the preferences of a DM to that of the Yun method and PAINT. In this comparison, we find solutions corresponding to reference points given by the DM within the preferred ranges of the objective functions provided by the DM. These preferred ranges for all benchmark problems were set as ${[-50,50]}^k$. This demonstrates that the method is not too sensitive on the choice of the ranges. As before, the Yun method was run for each individual reference point given by the DM. The number of function evaluations used for each reference point in all benchmark problems was set as $⌊\frac{300}{l}⌋$ where l is the number of reference points given by the DM in the decision-making phase. Regarding PAINT to build a surrogate problem, we employed the same non-dominated solutions used in SURROGATE-ASF. During the decision-making phase, we only obtained the approximated preferred solutions in the objective space. At the end of the decision-making by PAINT, we solved problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) for the last reference point given by the DM. The maximum number of function evaluations in this step was the remaining budget out of 300 function evaluations.

Tables 2a summarises the Euclidean distances $E_j$, $j=1,\dots ,l,$ between the approximated solutions obtained with SURROGATE-ASF (with MATSuMoTo), PAINT (with MATSuMoTo) and the Yun method and the original solutions for biobjective problems. Similarly, these results for SURROGATE-ASF (with DIRECT), PAINT (with DIRECT) and the Yun method are summarised in Table 2b. The rightmost column represents mean and standard deviation defined in (10a(10a) $$\begin{array}{c}\hfill {\mu }_c=\frac{1}{l}\sum _{j=1}^l{E}_j,\end{array}$$(10a) ) and (10b(10b) $$\begin{array}{c}\hfill {\sigma }_c=\sqrt{\frac{1}{l-1}\sum _{j=1}^l{(E_j-{\mu }_c)}^2}.\end{array}$$(10b) ) for $E_j$, $j=1,\dots ,l,$ for the methods mentioned above. Corresponding results for three-, four- and five-objective problems with MATSuMoTo and DIRECT are summarised in Tables 3a, 3b, 4a and 4b, respectively. Bold figures show the smallest distance between the approximated solutions obtained and the original solutions for each reference point. In all tables, SUR, MAT and DIR stand for SURROGATE-ASF, MATSuMoTo and DIRECT, respectively.

As far as applying MATSuMoTo is concerned to solve problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) to obtain reference solutions corresponding to the predetermined reference points, SURROGATE-ASF outperformed PAINT and the Yun method on ZDT1, ZDT2, ZDT3, ZDT6 (highlighted distances in Table 2a), on DTLZ1, DTLZ4, DTLZ5, DTLZ7 (highlighted distances in Table 3a) and on DTLZ2 with 4 and 5 objective functions (highlighted distances in Table 4a).

Regarding problems with disconnected Pareto frontiers, SURROGATE-ASF with MATSuMoTo outperformed PAINT and Yun on ZDT3 and DTLZ7. As can be seen in Tables 2a, 2b, 3a and 3a, the Euclidean distances corresponding to solutions obtained by PAINT are larger than those by SURROGATE-ASF. This confirms the fact that PAINT does not perform well on problems with disconnected Pareto frontiers as mentioned in Hartikainen et al. (2012).

As can be seen in Table 3a, on DTLZ2 with 3 objective functions, SURROGATE-ASF performed better than the other methods expect on the last reference point. Due to the limited function evaluation budget for each hyper-box (sub-problem), Algorithm 2 stopped updating the surrogate function corresponding to this reference point before reaching the desirable accuracy $R^2=0.95$ and $RMSE=0.005$. As a result, for this reference point, the approximated solution obtained by PAINT was slightly closer to the original one. On DTLZ6, the Yun method performed slightly better than SURROGATE-ASF with MATSuMoTo. For other reference points, though, approximated solutions obtained by SURROGATE-ASF were closer to the original ones.

On ZDT4 (in Table 2a) and DTLZ3 (in Table 3a), the reference solutions obtained by DIRECT were closer to the Pareto frontier in comparison with those obtained by MATSuMoTo. As a result, SURROGATE-ASF with DIRECT performed better than PAINT and the Yun method (as show in Tables 2b and 3b). In particular, SURROGATE-ASF with DIRECT surpassed the Yun method significantly (in Table 3b). On the other hand, the Yun method outperformed SURROGATE-ASF with MATSuMoTo on these problems.

As can be seen in Tables 3a and 3b, MATSuMoTo and DIRECT solved problem (3(3) $$\begin{array}{c}\hfill \underset{\mathbf{x}\in S}{\text{minimise}}\text{ASF}(\mathbf{x},{\overline{\mathbf{z}}}^{\ast }).\end{array}$$(3) ) for DTLZ1 and DTLZ2. On DTLZ1, not only SURROGATE-ASF with DIRECT (Table 3b) outperformed PAINT and the Yun method, but also SURROGATE-ASF with MATSuMoTo. For DTLZ2, SURROGATE-ASF with MATSuMoTo (Table 3a) performed better than SURROGATE-ASF with DIRECT, PAINT and the Yun method.

Tables 4a and 4b summarise the results for the problems with four and five objective functions. By increasing the number of objective functions, the number of sub-problems is also increased. With a limited number of function evaluations for each hyper-box (sub-problem), Algorithm 2 terminated the updating process based on the computational budget allocated rather than reaching the desirable accuracy $R^2=0.95$ and $RMSE=0.005$. However, SURROGATE-ASF with MATSuMoTo and DIRECT surpassed both PAINT and the Yun method. Moreover, SURROGATE-ASF with MATSuMoTo performed better than SURROGATE-ASF with DIRECT.

Overall, considering ${\mu }_c$ and ${\sigma }_c$ given in Tables 2a, 3a, 3b, 4a and 4b, SURROGATE-ASF (based on both MATSuMoTo and DIRECT) performed very well in the numerical tests when compared to the two other methods. However, only in Table 2b, the Yun method outperformed SURROGATE-ASF based on DIRECT. In addition, SURROGATE-ASF based on MATSuMoTo performed better than SURROGATE-ASF based on DIRECT on the benchmark problems considered.

In terms of computational burden we only report the maximum CPU time among all CPU time taken by the methods to solve the benchmark problems. SURROGATE-ASF with MATSuMoTo and DIRECT required at most 22 and 18 seconds, respectively to build surrogate functions in the initialisation phase. In the decision-making phase, the DM found the preferred solution corresponding to each reference point in less than 1 second. In PAINT with MATSuMoTo and DIRECT, the surrogate problem was built in 183 and 169 seconds, respectively. Then, the DM was able to find the preferred solutions in less than 1 seconds for all reference point except the last once. In the last iteration, to see the corresponding preferred solution, the DM waited for 4 seconds. In the Yun method, the DM managed to see the preferred solution for each reference point in 255 seconds. As can be understood, SURROGATE-ASG with MATSuMoTo and DIRECT outperformed other methods in terms of CPU time to provide preferred solutions for the DM.

5. Conclusions and future research directions

In this paper, we developed an interactive surrogate-based method called SURROGATE-ASF to solve computationally expensive MOPs. This method consists of two phases: initialisation and decision-making phases. In the initialisation phase, the decision space is decomposed into a finite number of hyper-boxes. For each hyper-box, a single objective surrogate of the achievement scalarising function is built by using e.g., a cubic RBF with a linear tail. In the decision-making phase, iterations with a decision-maker are conducted in an interactive fashion. In this phase, at each iteration a reference point is specified by the decision-maker. Then, a surrogate single objective optimisation problem is formulated and solved by any appropriate single objective optimisation method. The optimal solution is an approximation of the preferred solution in the decision space. This solution is evaluated with the original functions and shown to the decision-maker. The interaction with the decision-maker is repeated until the most preferred solution for him/her is found.

In SURROGATE-ASF, the approach of building a computationally inexpensive surrogate of the achievement scalarising function is applied instead of a typical approach of building a surrogate of each individual computationally expensive objective function and then forming the achievement scalarising function as discussed in Yun et al. (2009). Therefore, when interacting with the DM, only a single objective optimisation problem is solved. The surrogate assists the DM to find his/her preferred solutions in both the decision and the objective spaces quickly. Numerical results confirmed that SURROGATE-ASF performed very well, in particular, on problems with multimodal objective functions, non-convex and/or disconnected Pareto frontier and it fills a gap in the selection of methods available for computationally expensive problems. Solving a real-world computationally expensive airfoil optimisation problem demonstrated that SURROGATE-ASF reduced the computational burden significantly in comparison with the typical approach by which the DM had to wait for a long time to find the most preferred solution. The speed can be further improved by applying parallel computing when building single objective surrogate functions.

By increasing the number of objective functions, the number of sub-problems is also increased. Therefore, with a fixed budget of function evaluations, the number of function evaluations for each sub-problem is decreased. This may lead to a sacrificed accuracy of the sub-problems. A possible idea is to merge hyper-boxes and sub-regions to reduce the number of sub-problems. This is a future research direction when SURROGATE-ASF is to be applied for problems with a large number of objective functions. SURROGATE-ASF with the current setting along with an appropriate single objective surrogate-based method can be employed for problem with a high-dimensional decision space. However, the accuracy of the surrogate functions for each hyper-box may not be satisfactory. A possible approach is to apply a dimensionality reduction method within each hyper-box to obtain a low-dimensional hyper-box. Then, SURROGATE-ASF with the current format can be applied for each new hyper-box. This is another future research direction.

6. Abbreviations and Notations

MOP	=	Multiobjective Optimization Problem
DM	=	Decision-Maker
ASF	=	Achievement Scalarising Function
RBF	=	Radial Basis Function
SVR	=	Support Vector Regression
LOOCV	=	The leave-one-out cross-validation
MPF	=	Modified Pareto Fitness
k	=	Number of (computationally expensive) objective functions
n	=	Number of decision variables
$f_i$	=	$i^{\mathit{th}}$ computationally expensive objective function
S	=	Feasible decision set
$\mathbf{x}$	=	Decision (variable) vector
$x_c$	=	$c^{\mathit{th}}$ decision variable
$x_c^l,x_c^u$	=	Lower and upper bounds of $x_c$
${\mathbb{R}}^k$	=	Objective space
$\mathbf{f}(\mathbf{x})$	=	Objective vector
$Z=\mathbf{f}(S)$	=	Feasible objective set
${\mathbf{z}}_e^i$	=	$i^{\mathit{th}}$ extreme point
${\mathbf{z}}^{\mathit{ideal}}$	=	Ideal (objective) vector
${\mathbf{z}}^{\mathit{utp}}$	=	Utopian (objective) vector
${\mathbf{z}}^{\mathit{nadir}}$	=	Nadir (objective) vector
${\overline{\mathbf{z}}}^{\ast }$	=	Reference point given by the decision-maker
H	=	Convex hull of all individual extreme points
${\mathbf{z}}^{\ast \ast }$	=	Projected reference point on H corresponding to ${\mathbf{z}}^{\ast }$
${\overline{Z}}^P$	=	Set of predetermined reference points generated on H
$X^P$	=	Set of reference solutions in the decision space
$F^P$	=	Set of reference solutions in the objective space
q	=	Number of divisions along each objective coordinate axis
r	=	Number of sub-regions (or hyper-boxes)
$S^a$	=	$a^{\mathit{th}}$ hyper-box
${\overline{z}}^{P,a,i}$	=	$i^{\mathit{th}}$ predetermined reference point forming the $a^{\mathit{th}}$ sub-region on H
${\overline{Z}}^a$	=	Set of reference sample points corresponding to the $a^{\mathit{th}}$ sub-region
$X^{P,a}$	=	Set of non-dominated solutions in the decision space corresponding to the predetermined reference points in ${\overline{Z}}^P$
$F^{P,a}$	=	Set of non-dominated solutions in the objective space corresponding to the predetermined reference points in ${\overline{Z}}^P$
${\mathbf{x}}^{P,a,i}$	=	$i^{\mathit{th}}$ of the non-dominated solutions defining $S^a$
${\overline{X}}^a$	=	Set of sample points in the decision space corresponding to $S^a$
${\widetilde{\text{ASF}}}^a$	=	Surrogate function corresponding to $S^a$
$T^a$	=	Cartesian product of sets ${\overline{X}}^a$ and ${\overline{Z}}^a$
${\overline{\mathit{XP}}}^a$	=	Set of archived points in the decision space generated during the updating process
${\overline{\mathit{FP}}}^a$	=	Set of archived points in the objective space generated during the updating process
${\overline{\mathbf{x}}}^{\mathit{cand}}$	=	Minimiser of MPF
${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}$	=	Closest point in ${\overline{X}}^a$ to ${\overline{\mathbf{x}}}^{\mathit{cand}}$
${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{close}}$	=	Closest point in ${\overline{X}}^a\backslash \{{\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}\}$ to ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}$
$d_{\mathit{close}}^{\mathit{cand}}$	=	Euclidean distance between ${\overline{\mathbf{x}}}^{\mathit{cand}}$ and ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}$
$d_{\mathit{close}}^{\mathit{close}}$	=	Euclidean distance between ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}$ and ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{close}}$
${\overline{\mathbf{f}}}_{\mathit{close}}^{\mathit{cand}}$	=	Objective vector corresponding to ${\overline{\mathbf{x}}}_{\mathit{close}}^{\mathit{cand}}$
${\overline{\mathbf{f}}}_{\mathit{artif}}^{\mathit{cand}}$	=	Artificial objective vector

Acknowledgements

This work was partly funded by the COMAS Doctoral Program at the University of Jyvaskyla, the Academy of Finland [project No. 287496], Early Career Scheme (ECS) sponsored by the Research Grants Council of Hong Kong [project No. 21201414 (Dr. Matthias Hwai Yong Tan)] and the KAUTE Foundation. Mohammad Tabatabaei thanks Dr. Alfredo Arias Montano for providing the airfoil optimisation problem code and Prof. Raino Mäkinen for fruitful discussions on this problem.

Appendix 1

Table A1. Parameter settings for SURROGATE-ASF.

Initial number of sample points within each hyperbox	$n+1$
Number of reference sample points within each sub-region	k=2	30 (q = 29)
	k=3	66 (q = 10)
	k=4	84 (q = 6)
	k=5	125 (q = 5)

Table A2. Parameter settings for MATSuMoTo.

Metamodeling technique	Cubic RBF
Sampling technique	Latin hypercube sampling
New candidate points to be evaluated with the computationally expensive functions	adding random perturbations to the best point found so far
Initial number of sample points	2(n+1)

Table A3. Parameter settings for DIRECT.

Maximum number of function evaluations	To solve problem (3) differs for each reference point and benchmark problem	To solve problem (8) 500
Maximum number of iterations	500	500
Maximum number of rectangle divisions	1000	1000