In Praise of Simplicity not Mathematistry! Ten Simple Powerful Ideas for the Statistical Scientist

Abstract

Ronald Fisher was by all accounts a first-rate mathematician, but he saw himself as a scientist, not a mathematician, and he railed against what George Box called (in his Fisher lecture) “mathematistry.” Mathematics is the indispensable foundation of statistics, but for me the real excitement and value of our subject lies in its application to other disciplines. We should not view statistics as another branch of mathematics and favor mathematical complexity over clarifying, formulating, and solving real-world problems. Valuing simplicity, I describe 10 simple and powerful ideas that have influenced my thinking about statistics, in my areas of research interest: missing data, causal inference, survey sampling, and statistical modeling in general. The overarching theme is that statistics is a missing data problem and the goal is to predict unknowns with appropriate measures of uncertainty.

KEY WORDS:

• Calibrated Bayes
• Causal inference
• Measurement error
• Missing data
• Penalized spline of propensity

1. INTRODUCTION: THE UNEASY RELATIONSHIP BETWEEN STATISTICS AND MATHEMATICS

American Statistical Association President, Sastry Pantula, recently proposed renaming the Division of Mathematical Sciences at the U.S. National Science Foundation as the Division of Mathematical and Statistical Sciences. Opponents, who viewed statistics as a branch of mathematics, questioned why statistics should be singled out for special treatment.

Data can be assembled in support of the argument that statistics is different—for example, the substantial number of academic departments of statistics and biostatistics, the rise of the statistics advanced placement examination, and the substantial number of undergraduate statistics majors. But the most important factor for me is that statistics is not just a branch of mathematics. It is an inductive method, defined by its applications to the sciences and other areas of human endeavor, where we try to glean information from data.

The relationship between mathematics and statistics is somewhat uneasy. Since the mathematics of statistics is often viewed as basically rather pedestrian, statistics is rather low on the totem pole of mathematical subdisciplines. Statistics needs its mathematical parent, since it is the indispensable underpinning of the subject. On the other hand, unruly statistics has ambitions to reach beyond the mathematics fold; it comes alive in applications to sciences and other fields. In a citation review (Science Watch 2002), 13 of the 20 researchers in mathematics who were most highly cited in science were statisticians. On this theme, Efron (1998) noted that

During the 20th century, statistical thinking and methodology have become the scientific framework for literally dozens of fields, including education, agriculture, economics, biology and medicine, and with increasing influence recently on the hard sciences such as astronomy, geology and physics.

The scientific theme of modern statistics fits the character of its most influential developer, the great geneticist, R. A. Fisher, who seemed to revolutionize the field of statistics in his spare time! Fisher's momentous move to Rothampsted Experimental Station rather than academia underlined his dedication to science. Though an excellent mathematician, Fisher viewed himself primarily as a scientist, and disparaged rivals like Neyman and Pearson as mere “mathematicians.”

George Box's engaging Fisher lecture focused on the links between statistics and science (Box 1976). He wrote:

My theme then will be first to show the part that [Fisher] being a good scientist played in his astonishing ingenuity, originality, inventiveness, and productivity as a statistician, and second to consider what message that has for us now.

Box attributed Fisher's hostility to mathematicians to distaste for what he called “mathematistry,” which he defined as

[…] the development of theory for theory's sake, which, since it seldom touches down with practice, has a tendency to redefine the problem rather than solve it. Typically, there has once been a statistical problem with scientific relevance but this has long since been lost sight of. (Box 1976)

I was a pure mathematics undergraduate (as it happens at Gonville and Caius College, Cambridge, which was Fisher's college); I loved pristine theorems on groups and rings more than messy applications of mathematics to the real world. We need clear-thinking mathematical statisticians to bring theory and rigor to our subject, so I am not denying their importance. However, like Box, I am not enthusiastic about the “mathematization” of statistics. There has undeniably been progress on the applications front, as evidenced by Efron's quote, but I still feel that too much of academic statistics values complex mathematics over elegant simplicity—it is necessary for a research article to be complicated in order to get it published. Mathematics strives for generality, but applied statistics seeks to solve a problem. Since applied statistics rarely involves theorems, a mathematician may see little worthy of academic publication in important or instructive applications of statistics.

In praise of simplicity over mathematistry, I offer here 10 simple ideas that have influenced my research and application of statistics. Not the 10 simple ideas, since they are focused on my research interests of missing data, survey sampling, and causal inference. To broaden the perspective, I asked friends in the statistics and biostatistics departments at the University of Michigan, on the American Statistical Association Board, and at the Australian Bureau of Statistics (which I happened to visit while finalizing my lecture) for their top three simple statistical ideas. They cannot be generalized, since my sample was not random (violating the simple idea in Section 2.7), but I like them anyway, so the 15 ideas mentioned more than once are listed in Table 1. Some are related to my own simple ideas, so at least mine are not totally idiosyncratic.

Table 1 Simple ideas mentioned more than once in an informal poll of statisticians. Number of times mentioned in parentheses. Those in italics are related to the ideas discussed in the text

Histograms/plot the data/exploratory analysis (12)

Random selection/random treatment assignment (7)

Skepticism/understanding assumptions/model checking (5)

Resampling—bootstrap, permutation, jackknife (5)

Regression/ANOVA (4)

Monte Carlo Simulation—Gibbs/Metropolis-Hastings etc. (4)

Prediction from models that reflects uncertainty (4)

Factorial/fractional factorial designs (3)

Likelihood/maximum likelihood/likelihood principle(3)

Parsimonious models (3)

Understand the question/what data are needed (3)

Confounding/mediation (2); Potential outcomes (2)

Hierarchical models (2)

Observed = Fit + Residual/Pearson chi-square (2)

Smooth density estimation, loess, additive models (2)

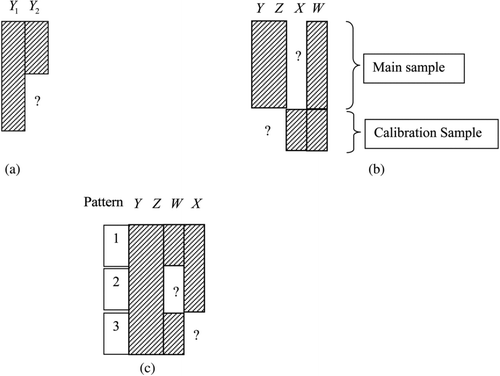
Figure 1 Missing-data patterns. (a) Bivariate monotone data (Exs 1,2,6,7). (b) External calibration data (Exs 3,5). (c) Regression with two missing covariates (Ex 8).

My focus here is on methodology rather than specific scientific applications, though the methods I discuss are highly relevant to applications. Also, I acknowledge that many problems tackled in modern statistics are inherently complex, and the search for simplicity may result in over-simplification. Box's (1976) coined the term “cookbookery” as the flip side of “mathematistry,” defined as

The tendency to force all problems into the molds of one or two routine techniques, insufficient thought being given to the real objectives of the investigation or to the relevance of the assumptions implied by the imposed methods.

Cookbookery is bad statistics, but I would still argue that conceptual simplicity, as in the calibrated Bayes perspective of Sections 2.2 and 2.3, can still aid in the solution of complex problems.

2. MY 10 SIMPLE IDEAS

2.1 Make Outcomes Univariate (When It Makes Sense to Do So)

When modeling, it can be useful to factor a multivariate distribution into sequence of conditional distributions. Univariate regression is easier to understand, and a sequence of univariate conditional regressions is more easily elaborated, for example, by including interactions, polynomials, or splines, or modeling heteroscedasticity. A delightfully simple four-page article by Anderson (1957) exploits this idea, and is the topic of my first example.

Example 1. Maximum likelihood estimation for monotone missing data. Anderson (1957) writes in the abstract:

Several authors recently have derived maximum likelihood estimates of parameters of multivariate normal distributions in cases where some observations are missing … [I] give an approach … that indicates the estimates with a minimum of mathematical manipulation; this approach can easily be applied to other cases … The method will be indicated by treating the simplest case involving a bivariate normal distribution.

The italics are mine and fit my theme of simplicity. The lack of mathematical manipulation not only saves calculation, which was challenging in 1957, but replaces it with added statistical insight. Anderson presents the idea in a simple case, leaving the generalizations to lesser lights in need of journal publications. Some of our modern-day statistical stars might benefit from that approach.

The data (Figure 1(a)) consist of r complete bivariate observations {y_i =(y _i1, y _i2), i=1, …, r} on Y=(Y ₁, Y ₂), and n − r observations {y _i1, i=r+1, …, n} on Y ₁ alone. Assuming data are normal and missingness of Y ₂ depends on Y ₁ so the mechanism is missing at random (MAR, Rubin 1976), the log-likelihood is given by

where μ and Σ are the mean and covariance matrix of Y. Maximum likelihood (ML) estimates of μ and Σ can be found by maximizing this function with respect to μ and Σ. The likelihood equations based on differentiating (1) do not have an obvious solution. However, Anderson (1957) factors the joint distribution of Y ₁ and Y ₂ into the marginal distribution of Y ₁ and the conditional distribution of Y ₂ given Y ₁. For the ith observation,

where f(y _i1|μ₁, σ₁₁) is the normal distribution with mean μ₁, and variance σ₁₁, and f(y _i2|y _i1, β_20.1, β_21.1, σ_22.1) is normal with mean β_20.1, β_21.1 y _i1 and variance σ_22.1. The loglikelihood (1) can then be expressed in the alternative factored form

where φ=(μ₁, σ₁₁, β_20.1, β_21.1, σ_22.1) ^T is a one–one function of the original parameters θ=(μ₁, μ₂, σ₁₁, σ₁₂, σ₂₂) _T of the joint distribution. If the parameter space for θ is the standard natural parameter space with no prior restrictions, (μ₁, σ₁₁) and (β_20.1, β_21.1, σ_22.1) are distinct, since knowledge of (μ₁, σ₁₁) does not yield any information about (β_20.1, β_21.1, σ_22.1). Hence, ML estimates of φ can be obtained by independently maximizing the likelihoods corresponding to these parameter subsets. This yields , where

the sample mean and sample variance of the n observations y _i1, y _n1, and

where for j, k=1, 2 and s _22.1=s ₂₂−s ² ₁₂/s ₁₁.

The ML estimates of functions of φ are simply the functions evaluated at the ML estimates . For example, the mean of Y ₂ is μ₂(φ)=β_20·1+β_21·1μ₁, so

ML estimates of the other parameters of the joint distribution also are simple (Anderson 1957; Little and Rubin 2002).

Anderson's idea of factoring the likelihood is an important feature of modern missing data programs such as SAS PROC MI (SAS 2010) or IVEware (Raghunathan et al. 2001), which relaxes the multivariate normal assumption. Specifically, multiple imputations (Rubin 1987) for monotone missing data are obtained by factoring the joint distribution into a sequence of regressions corresponding to conditional distributions. These regressions can be tailored to the dependent variable type and can include nonlinear terms and interactions between the regressors.

2.2 Bayes Rule, for Inference Under an Assumed Model

What could be simpler or more powerful than Bayes’ Rule? If U = unknown and K = known, the posterior distribution of U given K is

where p(U) is the prior distribution of U and p(K|U) is the probability of K given U. Freed from the shackles of prohibitive computation by Monte Carlo simulation methods, Bayesian methods have been applied to increasingly complex problems, as reflected in the substantial Bayesian representation by mathematicians who are most highly cited in science (Science Watch 2002).

There are (to me, compelling) theoretical arguments in favor of Bayesian statistics; I present here simple examples that illustrate two attractive properties in applications: the ability to achieve better frequentist confidence coverage by properly reflecting uncertainty about nuisance parameters, and clarity about conditioning.

Example 2 (Example 1 continued). Bayesian Computations for Monotone Normal Data. Adding a prior distribution and replacing the ML estimates in Equation (5) (with a hat) with draws (with a d) from the posterior distributions, we obtain draws from the posterior distribution of μ₂:

With conjugate prior distributions, the draws φ^(d) are simple functions of the sufficient statistics that make up the ML estimates in Equations (3) and (4), and draws of chi-squared and standard normal deviates—for details, see Section 7.3 of Little and Rubin (2002). The sample variances of draws provide estimates of uncertainty that are easier to compute than asymptotic variances based on the information matrix, and have better frequentist properties since (unlike ML) they incorporate “Student T” corrections for estimating the variances (Little 1988).

Example 3. Calibration Based on an External Calibration Sample. Figure 1(b) describes data from external calibration, a design that allows for adjustment of a variable X subject to measurement error. The main sample consists of values of W, the proxy for X subject to measurement error, an outcome variable Y, and a vector of other covariates Z. An external calibration sample contains values of X and W, for example, in a calibration study conducted by an assay manufacturer. The goal is to regress Y on X and Z.

In the calibration sample, the values of X are predetermined and hence fixed, and the measurement error is in W. Accordingly, the classical calibration (CA) method constructs a calibration curve by regressing the surrogate values of W in the calibration sample on the true values of X. Given a measured value W, an estimate of the true values of X is obtained from the calibration curve by inverse regression, and then treated as the true value in the main analysis.

The CA method is used extensively in practice, especially when dealing with assay data. However, the conditioning in CA is wrong: we need to predict missing values of X from the regression of X on W, but the regression estimated from the calibration sample was of W on X. As a result of this faulty conditioning, CA yields biased regression estimates when the measurement error is substantial (Freedman et al. 2008; Guo, Little, and McConnell 2011).

An alternative to CA is to formulate a prior distribution for X and model parameters, and apply Bayesian multiple imputation (MI), which creates multiple datasets with imputations drawn from the posterior predictive distribution of the missing values of X, given the known variables. Once MI datasets are created, standard analysis methods for complete data can be applied, with imputation uncertainty being addressed by simple MI combining rules.

For multivariate normal models, multiple imputation is extremely simple to implement, since the assumption of nondifferential measurement error—(Y, Z) is independent of W, given X—leads to a just-identified model, implying that the multiple imputations can be computed by direct (noniterative) simulation from their predictive distribution. For the simple computational details see Guo, Little, and McConnell (2011). The procedure only needs summary statistics from the calibration sample, a useful feature since in the external calibration setting the raw data from the calibration sample are often not available. Simulations summarized in Section 2.4 show that this approach, with dispersed prior distributions, yields superior frequentist properties to CA. The main reason for its success is that it gets the conditioning of unknown quantities U on known quantities K in Bayes’ rule correct.

2.3 Calibrated Bayes, to Keep Inferences Honest

If we knew the model, statistics would be simply a matter of computation. The problem of course is that models and prior distributions are not known, and a terrible model yields a terrible answer. All models are wrong, but some are useful, to paraphrase Box. The quest for useful models is what makes statistics interesting.

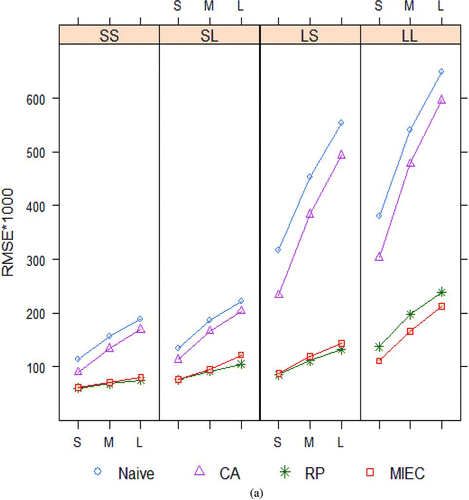
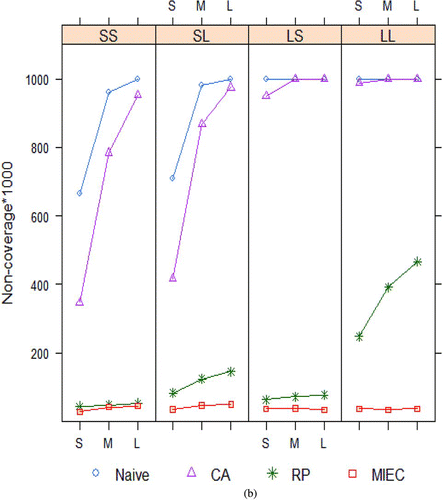
Figure 2 (a) Root mean squared errors of estimates and (b) Noncoverage of 1000 confidence intervals (nominal = 50) of coefficient of X from four methods for handling measurement error in a covariate X, for external calibration data displayed in Figure 1. Naïve = no adjustment, CA = classical calibration, RP = regression prediction, MIEC = multiple imputation for external calibration. The online version of this figure is in color. (Continued)

The idea of Calibrated Bayes is to seek models that yield Bayes inferences, such as posterior credibility intervals, with good frequentist properties, such as confidence coverage close to nominal levels. For posterior credibility intervals to be credible, Bayesians need to be frequentists, in that they should seek inferences that have good frequentist properties. Some key references on this viewpoint are Box (1980), Rubin (1984), and Rubin and Schenker (1986). For a recent nontechnical discussion, see Little (2006).

My example concerns the application of Calibrated Bayes to official statistics, though I think the idea is useful more generally.

Example 4. Calibrated Bayes as a Paradigm for Official Statistics. Statistics is fundamentally about prediction (Geisser 1993); for inference about finite population quantities from sample surveys, the goal is simply to predict survey variables for nonsampled or nonresponding units with appropriate measures of uncertainty. Sample surveys are a key tool for official statistics, and calibrated Bayes provides a flexible and unified paradigm for survey inference (Little 2012). To be reliably calibrated, models need to incorporate key design features like stratification and weighting (through covariates) and clustering (through hierarchical models with random effects) (Little 2004, 2012).

The current paradigm of survey inference is a combination of design-based and model-based ideas, which I call the “design/model compromise” (DMC) in Little (2012). for inference about descriptive statistics like means and totals in large samples, DMC applies randomization-based inference, where the population values are treated as fixed and inferences are based on the randomization distribution that governs sample statistics. For small area estimation, survey nonresponse, or some specialized areas like time series analysis, inferences are based on models for the data (e.g., Kalton 2002; Rao 2003, 2011). This application of disparate approaches is to me a form of inferential schizophrenia and leads to inconsistency and confusion. For small area modeling, where is the dividing line to be drawn between the model-based and design-based approach? Since small area models borrow strength across areas, confidence intervals based on models can be considerably narrower than design-based confidence intervals based on direct estimates. Hence, a model-based confidence interval can be narrower than a design-based inference based on more data, leading to inconsistencies near the threshold between the two inferential approaches. DMC also leads to controversy when design-based and model-based systems clash, as in the issue of whether to include sampling weights in inferences for regression models. In contrast, calibrated Bayes assigns unambiguous roles for models (for the inference) and design-based computations (to seek models that lead to well-calibrated inferences). Bayesian inference with relatively flat priors has been shown to yield excellent frequentist properties, if the sample design is incorporated in the model (Zheng and Little 2004, 2005; Yuan and Little 2007; Chen, Elliott, and Little 2010). In short, Calibrated Bayes is in my view a much more satisfying and coherent approach to survey inference than the current paradigm. See Little (2012) for more discussion.

2.4 Embrace Well-Designed Simulation Experiments

In most academic statistical journals, one needs a “real” data example to get a novel method or theory passed the referees (“Real” being in quotes since the reality is often superficial, in that key aspects of the real application are ignored). Illustrations on individual datasets provide a context, but are no basis for establishing statistical properties. The fact that a more plausible estimate or lower standard error is obtained on a single dataset says nothing about the general utility of the method.

On the other hand, thoughtfully designed frequentist simulation experiments can cast useful light on the properties of a method. Good simulation studies are not given the respect they deserve. Often the design is perfunctory and simplistic, neglecting to attempt a factorial experimental design to cover the relevant sample space, and results are over-generalized. Well-designed simulation studies with realistic sample sizes are an antidote to a fixation on asymptotics and a useful tool for assessing calibration. Establishing theoretical properties is important, but sometimes resorting to simulations to assess finite-sample performance is seen as a serious lapse in mathematistry, and grounds for rejecting an article! For a clear discussion of the link between Bayesian methods and simulation studies, see Rubin and Schenker (1986).

Example 5 (Example 3 continued). External Calibration Simulation Study. Figure 2 displays a subset of the results from a basic simulation study (Guo, Little, and McConnell 2011). It compares the mean-squared error of estimates (Figure 2(a)) and confidence coverage (Figure 2(b)) of four ways of estimating the coefficient of X in the regression of Y on X and Z, for the data discussed in Example 3 and depicted in Figure 1(b). One thousand datasets were generated for each simulation condition according to the model

where γ _x =0.4 (small)or1.2(large),   γ _z =0, 4, β₁=1.1, σ²=0.25 (small), 0.5 (moderate) or 0.75 (large), and the correlation of X and Z is small (0.3) or large (0.6). The sample sizes were 400 in the main sample and 100 in the calibration sample. The methods compared were:

	Multiple Imputation for External Calibration (MIEC): Multiple imputation assuming normal models for measurement error and the regression.
	Naïve: Assumes X = W, that is, ignoring the measurement error.
	Classical Calibration (CA): The classical calibration method, with X imputed by inverse regression.
	Regression Prediction (RP): Imputing the conditional mean of X given Z for the missing values of X. This method is the same as the method known as regression calibration when there are no Z variables.

The simulation results (including those for the coefficient of Z, not presented here) suggest that MIEC is much better than alternative existing methods, to adjust for covariate measurement error, eliminating bias, and providing confidence interval coverage close to nominal levels. Other simulations, where the true covariate X has a moderately skewed distribution or the covariate Z is binary, suggest that MIEC has a degree of robustness to lack of normality, continuing to perform better than the other methods. Guo and Little (2013) also reviewed the results on multiple imputation that allows for heteroskedastic measurement variance, for both the external calibration design of Figure 1(b) and for the internal calibration design, where Y and Z are also measured in the calibration sample.

2.5 Distinguish the Model/Estimand, the Principle of Estimation, and Computational Methods

It is often argued that a weakness of Bayesian methods is that they require assumptions (as if other methods do not!). On the contrary, a strength of Bayesian methods is that the assumptions are explicit, and hence out in the open, capable of criticism and refinement, and easily communicated to nonstatisticians.

A strong feature of Bayesian inference is that it distinguishes the target of inference (the estimand), the principle of estimation (Bayes’ rule), and computational methods (how to compute the posterior distribution). Sometimes these aspects get mixed up. An example is classical robustness (e.g., Huber 1981), where for asymmetric distributions, the choice of estimand changes depending on the choice of estimator. Areas of statistics such as data mining and genetics are often characterized by estimation by algorithm—assumptions are implicit and buried in the computations.

Another area where the estimand and the method of estimation are often confused is clinical trials subject to missing data. A recent National Research Council report on the topic (National Research Council 2010, p. 26) recommends:

The trial protocol should explicitly define (a) the objective(s) of the trial; (b) the associated primary outcome or outcomes; (c) how, when, and on whom the outcome or outcomes will be measured; and (d) the measures of intervention effects, that is, the causal estimands of primary interest. These measures should be meaningful for all study participants, and estimable with minimal assumptions. Concerning the latter, the protocol should address the potential impact and treatment of missing data.

As an example, the “per protocol estimand”—the treatment effect on all individuals who would comply with all of the compared treatments if assigned them—should be distinguished from the “per protocol estimate,” which is a particular choice of estimator of this estimand. The assumptions underlying various estimators are discussed in Example 9 below.

2.6 Parsimony—Seek a Good Simple Model, Not the “Right” Model

Much modern nonparametric and semiparametric statistical theory lives in the “land of asymptotia” (Figure 2 in Little 2006). However, “nonparametric” often means “infinite-parametric.” The mathematics of problems with infinite parameters is interesting, but with finite sample sizes, I would rather have a parametric model. “Mathematistrists” may eschew parametric models because the asymptotic theory is too simple, but they often work well in practice. Parametric models can also be flexible, as the following generalization of Examples 1 and 2 illustrates.

Example 6 (Examples 1 and 2 continued). Penalized Spline of Propensity Prediction for Univariate Missing Data. Let (Y ₁, X ₁, …, X_p ) be a vector of variables with Y observed for units i=1, …r and missing for i=r+1, …, n, and fully observed covariates X ₁, …, X_p . We assume that missingness of Y depends only on X ₁, …, X_p , so the missing data mechanism is MAR (Rubin 1976), and consider estimation and inference for the mean of Y, μ=E(Y). Let M denote an indicator variable with M=1 when Y is missing and M=0 when Y is observed.

We can multiply impute (MI) the missing values of Y with draws from their predictive distribution under a regression model for the distribution of Y given X ₁, …, X_p . Concerns with effects of model misspecification have motivated robust imputation methods based on nonparametric and semiparametric methods (Robins, Rotnitzky, and Zhao 1994; Rotnitzky, Robins, and Scharfstein 1998; Little and An 2004; Bang and Robins 2005). In this context, an estimator is doubly robust (DR) if it is consistent when either the regression of Y on X ₁, …, X_p is correctly specified or the model for the missing data mechanism is correctly specified.

The Penalized Spline of Propensity Prediction (PSPP) model is a flexible but parametric imputation model yielding estimates with a DR property. Define the logit of the propensity for Y to be observed as:

Imputations in PSPP are predictions from the following model:

where N(μ, σ²) denotes the normal distribution with mean μ and constant variance σ². The first component of the mean function in Equation (8), s(P*), is a penalized spline (e.g., Wahba 1990; Ruppert, Wand, and Carroll 2003) of the form

where 1, P*, (P*−κ₁)+, …, (P*−κ _k )₊ is the truncated linear basis; κ₁<⋅⋅⋅<κ _K are selected fixed knots and K is the total number of knots, and (γ₁, …, γ _K ) are random effects assumed normal with mean 0 and variance τ². The second component g(P*, X ₂, …X_p ; β) is a parametric function, which includes any covariates other than P* that predict Y. One of the predictors here, X ₁, is omitted from the g-function to avoid multicollinearity. This model can be fitted by mixed model maximum likelihood software (Ngo and Wand 2004), such as PROC MIXED in SAS (SAS 2010) and function linear mixed effects in S-plus (Pinheiro and Bates 2000). The first step of fitting a PSPP model estimates the propensity score, for example, by a logistic regression model or probit model of M on X ₁, …, X_p ; in the second step, the regression of Y on the estimate of P* is fit as a spline model with the other covariates included in the model parametrically in the g-function. We assume here a normal error distribution for Y with constant variance. For other types of data, extensions of the PSPP can be formulated allowing the variance to depend on covariates, or by using generalized linear models with different link functions. Bayesian implementations are also possible using Monte Carlo simulation methods.

By the balancing property of the propensity score (Rosenbaum and Rubin 1983), the average of the observed and imputed values of Y has a DR property, meaning that the predicted mean of Y is consistent if either (a) the mean of Y given (P*, X ₁, …, X_p ) in model (3) is correctly specified, or (b1) the propensity P* is correctly specified, and (b2) E(Y|P*)=s(P*). The robustness feature derives from the fact that s(P*) has a flexible form, and the regression function g does not have to be correctly specified (Little and An 2004; Zhang and Little 2008). Simulations in Zhang and Little (2011) suggest favorable frequentist properties of this method compared with other doubly robust methods.

2.7 Model the Inclusion/Assignment Mechanism, and Try to Make it Ignorable

Randomization is the gold standard for design of sample surveys and treatment comparisons—probability sampling for surveys, random treatment allocation for causal comparisons—but was once seen as unnecessary in the Bayesian paradigm, since the randomization distribution is not the basis of the inference. This poses a problem: either randomization is irrelevant (contradicting my intuition) or the Bayesian inferential approach is flawed.

The problem is resolved by including the distribution of selection, response, or treatment assignment as part of the model. Randomization then justifies ignoring the selection or assignment mechanism in the model, reducing dependence on the model assumptions. Rubin's (2005) Fisher lecture discusses this point in detail. From a Calibrated Bayes perspective, randomization justifies exchangeability and promotes calibrated inferences.

With sampling, the selection of units is under the control of the sampler, and probability sampling ensures that the sampling mechanism is ignorable. With missing data, there is no guarantee that the missing-data mechanism can be ignored. Rubin (1976) gave sufficient conditions under which the missing data mechanism can be ignored for likelihood inferences; the key condition is missing at random (MAR), where after conditioning on the observed data, missingness does not depend on missing values. In the context of Example 1, MAR means that P(Y ₂ mis|Y ₁, Y ₂) = fn(Y ₁), where fn is an arbitrary function.

For data missing not at random, I generally favor sensitivity analysis based on the pattern-mixture model factorization f(M, Y|θ, φ)=f(Y|M, θ)f(M|φ), on grounds of simplicity. The following gives a normal pattern-mixture model that generalizes Examples 1 and 2.

Example 7 (Examples 1 and 2 continued). Missing Not at Random Extensions of Anderson's method. For the data in Figure 1(a), the following pattern-mixture model for (M, Y ₁, Y ₂) leads to a simple generalization of Anderson's ML estimates (Little 1994):

Here N(μ^(j), Σ^(j)) denotes as distinct bivariate normal distribution for each missing-data pattern j, and Bern(π) is the Bernoulli distribution with . The three parameters of the normal regression of Y ₂ on Y ₁ for incomplete case (M = 1) are not identified for this model. However, if we assume

for known λ and arbitrary function g, then the distribution of (y _i1, y _i2|y* _i ) is independent of M_i , yielding three restrictions on the parameters that just identify the model. The resulting estimate of the mean of Y ₂ (combined over patterns) is

with similarly simple expressions for the other parameters. These reduce to Anderson's estimates (Example 1) when λ = 0 and the data are MAR.

The data provide no information about the value of λ; one possibility is to do a sensitivity analysis for various choices of this parameter (Little 1994). Andridge and Little (2011) develop an extension of this method to a set of covariates called proxy pattern-mixture analysis, to model the impact of survey nonresponse. West and Little (2012) apply an extension to handle measurement error in survey covariates used for nonresponse adjustments.

2.8 Consider Dropping Parts of the Likelihood to Reduce the Modeling Task

Section 2.2 argued for the conceptual clarity and simplicity of Bayesian inference. However, fully Bayes inference requires detailed probability modeling, which is often a daunting task (Efron 1986). It seems worth sacrificing some Bayesian inferential purity if the task can be simplified by eliminating nuisance parameters that are not the primary focus of interest. In particular, creating a partial likelihood (Cox 1975) to eliminate nuisance parameters seems worthwhile, and a partially Bayesian analysis that adds a prior distribution to this partial likelihood (Volinsky et al. 1997; Volinsky and Raftery 2000) seems a promising tactic that could be applied more often in practice. For example, the standard analysis of the proportional hazards model by partial likelihood is asymptotic, and is suspect in small samples. Adding a prior distribution and conducting a Bayesian analysis of the partial likelihood (Sinha, Ibrahim, and Chen 2003) avoids specifying the baseline hazard function, and might lead to better small-sample frequentist properties.

Here is another example, concerning regression with missing data in covariates.

Example 8. Regression with Missing Data in Two Covariates. Figure 1(c) displays data on four variables Y, Z, W, and X, where the objective is the regression of Y on X, W, and Z. Data are complete for Pattern 1, missing values of W for Pattern 2, and missing values of X for Pattern 3. Likelihood-based or Bayesian methods like multiple imputation that ignore the missing data mechanism assume MAR, which for this pattern implies that

Here is the indicator for whether w_i is missing, and is the indicator for whether x_i is missing. The MAR assumption is a little strange here, since it implies that the missingness of W depends on X (and perhaps Z and Y), and the missingness of X depends on W (and perhaps Z and Y). Suppose instead of Equation (10) we assume that

so, missingness of both W and X depends on the covariates, but not the outcome. This mechanism is missing not at random, so a full likelihood analysis requires modeling the missing-data mechanism. However, the regression analysis of Y on Z, X, and W, based on the complete units , is valid without modeling the mechanism, since Y is independent of (M_w , M_x ) given Z, X, and W (Little and Rubin 2002, Example 3.3). Complete-case analysis can be viewed as a partial likelihood method that discards contributions to the likelihood from the incomplete units.

A drawback of complete-case analysis in this setting is that the incomplete units may have useful information about the regression parameters. Little and Zhang (2011) proposed subsample ignorable likelihood (SSIL), which is a hybrid between a full likelihood analysis based on the all the data and an analysis based on the complete units. Suppose that missingness of W is assumed to depend on Z, W, X but not Y, and X is assumed MAR in the subsample of units with W observed. In symbols,

SSIL then applies an ignorable likelihood method to the subsample of units with W observed, that is patterns 1 and 3 in Figure 1(c). Under this mechanism, SSIL yields consistent estimates, but (a) CC analysis may yield inconsistent estimates since missingness of X may depend on the outcome Y, and (b) ignorable likelihood methods may yield inconsistent estimates, since missingness of W can depend on missing values of W (i.e., missing not at random). SSIL can be viewed as a partial likelihood method, ignoring the contribution to the likelihood from the omitted pattern. These units potentially have information for the regression of interest, but a model for the missing-data is needed to exploit this information, and the penalty from misspecifying this model may outweigh the gain in information.

From a practitioner's viewpoint, the main challenge in applying SSIL is deciding which covariates belong in the set W and which belong in the set X; that is, which covariates are used to create the subsample for the MAR analysis. The choice is guided by the basic assumptions in Equation (12) concerning which variables are considered covariate-dependent missing not at random and which are considered subsample MAR. This is a substantive choice that requires an understanding of the missing data mechanism in the particular context. It is aided by learning more about the missing data mechanism, for example, by recording reasons why particular values are missing. Although a challenge, we note that the same challenge is present in any missing data method. When faced with missing data, assumptions are inevitable, and they need to be as reasonable and well considered as possible. For elaborations of this example and more details, see Little and Zhang (2011).

2.9 Potential Outcomes and Principal Stratification for Causal Inference

Conceptual simplicity is particularly welcomed in the challenging world of causal inference. A favorite conceptual idea is the definition of the causal effect of a treatment for subject i as the difference in potential outcomes under active treatment and under control. Sometimes called “Rubin's causal model” (Rubin 1974; Holland 1986), Rubin attributes the initial idea to Jerzy Neyman. From this perspective, inference for causal effects is basically a missing data problem, since we only get to see the outcome from one treatment, the treatment actually received. We do not observe causal effects for individuals, but can estimate average effects in subpopulations. A related idea is principal stratification of posttreatment variables, where strata are created based on classifications of units by potential posttreatment values under both treatments (Frangakis and Rubin 2002).

These ideas are useful in clarifying effects of treatments in randomized clinical trials with noncompliance. The following example (Little, Long, and Lin 2009) illustrates the power of these ideas.

Example 9. Noncompliance in Randomized Trials. We consider studies involving random assignment to an active treatment (R = 1) and a control treatment (R = 0). We assume the treatments are subject to all-or-nothing compliance, so that the actual treatment received (say T(R)) can differ from the treatment assigned (R). Specifically, we assume that the population can then be divided into three groups: never-takers (C = n), who take the control treatment whether they are assigned to the control or active treatment (T(1)=T(0)=0); compliers, who take the treatment they are assigned (C = c) (T(R)=R); and always-takers (C = a), who take the active treatment whether assigned the active or control treatment (T(1)=T(0)=1). We make the monotonicity assumption that there are no defiers who take the opposite treatment to that assigned, and the stable unit-treatment value assumption, which implies that compliance and outcomes for individuals are not affected by the treatment assignments of other individuals in the sample (Angrist, Imbens, and Rubin 1996).

We call C principal compliance, since it is a special case of principal stratification (Frangakis and Rubin 2002). It differs from observed compliance, which concerns only whether a participant complied with the assigned treatment. Observed noncompliers in the treatment group are never-takers (C = n), observed compliers in the treatment group are compliers or always-takers (C = c or a), observed noncompliers in the control group are always-takers (C = a), and observed compliers in the control group are compliers or never-takers (C = c or n). Thus C is only partly observed. Since it is unaffected by the treatment assigned, C can be used as a stratification variable in treatment comparisons, if the missing data problem can be solved.

Table 2(a) shows a classification of the population by R and C, assuming a proportion α of the population is assigned to the treatment, and population proportions π _n , π _c , π _a of never takers, compliers, and always takers, respectively. The entries reflect independence of R and C, which is a consequence of random treatment assignment.

Let μ _rj denote the mean of an outcome Y when assigned R = r (r = 0, 1) for the subpopulation with C = j, ( j = n, c or a); let denote the corresponding sample mean, and m_rj the corresponding sample size. Table 2(b) displays population means of Y, with square parentheses when corresponding sample quantities are not observed. The observed sample counts and means are shown in Table 2(c). Since there are six cell means in Table 2(b), and only four observed means, two model restrictions on the means are needed to just identify the model. The complier-average causal effect (CACE) is the average treatment effect in the subpopulation of principal compliers:

The quantity estimates the CACE in Equation (13), but and are not observed, and additional assumptions are needed to identify the estimate. One possibility is to assume

which asserts that the mean outcome under the control treatment is the same for compliers and never-takers (“no compliance effect for controls,” or NCEC), and the mean outcome under the active treatment is the same for compliers and always-takers (“no compliance effect for treatment,” or NCET). Under NCEC_μ and NCET_μ, it is natural to estimate both μ_0c and μ_0n by and both μ_1c and μ_1a by , yielding the per-protocol (PP) estimate

of the CACE. The problem is that the underlying NCEC_μ and NCET_μ assumptions are strong and widely viewed as unacceptable, since compliers and never-takers may differ on various unobserved characteristics related to the outcome under the control treatment, and similarly compliers and always-takers may differ on characteristics related to the outcome under the active treatment. NCEC_μ and NCET_μ can be weakened by adjusting for known covariates, but they remain strong assumptions.

Table 2 Example 9. Classifications by treatment and principal compliance: (a) Population proportions; (b) Population mean outcomes; (c) Observed means (sample counts)

(a) Population proportions
	Principal compliance C
	a	c	n	ALL
Randomized treatment R
0	(1−α)π a	(1−α)π c	(1−α)π n	1−α
1	απ a	απ c	απ n	α
ALL	π a	π c	π n
(b) Population mean outcomes
	Principal compliance C
	a	c	n	ALL
Randomized treatment R
0	μ0a	[μ0c ]*	[μ0n ]	μ0+
1	[μ1a ]	[μ1c ]	μ1n	μ1+
ALL	[μ+a ]	[μ+c ]	[μ+n ]
(c) Observed means (Sample counts)
	Principal compliance C
	a	c	n	ALL
Randomized treatment R
0
1
ALL	?	?	?
*[.] = not identifiable from the observable random variables without additional assumptions.

A different, potentially more palatable way of identifying the CACE is to note that participants in the subpopulation of never-takers (C = n) are randomly assigned to treatment or control, and in both cases they receive T = 0. Similarly always-takers (C = a) receive T = 1 whether assigned to treatment or control. The exclusion restriction (ER) assumption implies that the means in Table 2(b) are such that:

The ER assumption is usually defined as equality of the distributions of outcomes under R for never-takers and always takers, but in fact it is sufficient to assume equality of the means as in Equation (16). This assumption may be more plausible than Equation (14), but it remains an assumption, since the outcome may be affected by whether treatment or control is assigned even though the resulting treatment remains the same, particularly in trials of behavioral interventions. Under ER_μ, is a consistent estimate of both μ_0n and μ_1n , and is a consistent estimate of both μ_0a and μ_1a . These estimates lead to the following estimate of the CACE, which is consistent under ER_μ because the numerator and denominator are consistent estimates of their respective estimands:

where and estimate the proportions of always-takers and never-takers. Equation (17) is sometimes termed the instrumental variable (IV) estimate (Baker and Lindeman 1994; Angrist, Imbens, and Rubin 1996), since it is has the form of an IV estimate with the randomization indicator as the instrument. Since under ER_μ the treatment effect is zero for the always-takers and never-takers, inflates the ITT estimate by the estimated proportion of compliers.

To summarize, the NCEC_μ and NCET_μ assumptions lead to , and the ER_μ assumption leads to . Combining these assumptions leads to another choice, the “as treated” estimator (Little, Long, and Lin 2009). The principal stratification framework clarifies the target of inference and the assumptions of the various methods.

3. THE LAST SIMPLE IDEA

My last simple idea is overarching: statistics is basically a missing data problem! Draw a picture of what's missing and find a good model to fill it in, along with a suitable (hopefully well calibrated) method to reflect uncertainty. All of the nine ideas in Section 2 followed this approach to problems concerning missing data, measurement error, survey inference and causal inference.

Box concludes his Fisher lecture with a warning about the serious consequence of mathematistry for the training of statisticians:

Although statistics departments in universities are now commonplace, there continues to be a severe shortage of statisticians competent to deal with real problems. But such are needed.

We still need more well-trained applied statisticians today. Mathematistrists see applications of statistics as basically straightforward, like applying mathematics to word problems, and a diversion from the study of mathematical properties of statistical procedures. But developing good statistical solutions to real applied problems, based on good science rather than “cookbookery,” is far from easy.

Statistics departments need to train their students on the nuances of applied statistical modeling. This task is aided by conceptually powerful but simple ideas such as those presented in this article.

Acknowledgments

This article is dedicated to the memory of George Box, a great and inspiring statistician. Thanks to the Fisher lectureship committee, for the invitation to deliver the Fisher lecture at the 2012 Joint Statistical Meetings; my mentors, including Martin Beale, David Cox, Maurice Kendall, Wilfred Dixon, David Wallace, Don Rubin; and my current and former students, including the following coauthors of articles mentioned here: Hyonggin An, Rebecca Andridge, Ying Guo, Qi Long, Qixuan Chen, Ying Yuan, Guangyu Zhang, Nanhua Zhang, and Hui Zheng. The profoundly simple aria that closed my Fisher lecture was by Handel (1747).