Speeding Up MCMC by Efficient Data Subsampling

ABSTRACT

We propose subsampling Markov chain Monte Carlo (MCMC), an MCMC framework where the likelihood function for n observations is estimated from a random subset of m observations. We introduce a highly efficient unbiased estimator of the log-likelihood based on control variates, such that the computing cost is much smaller than that of the full log-likelihood in standard MCMC. The likelihood estimate is bias-corrected and used in two dependent pseudo-marginal algorithms to sample from a perturbed posterior, for which we derive the asymptotic error with respect to n and m, respectively. We propose a practical estimator of the error and show that the error is negligible even for a very small m in our applications. We demonstrate that subsampling MCMC is substantially more efficient than standard MCMC in terms of sampling efficiency for a given computational budget, and that it outperforms other subsampling methods for MCMC proposed in the literature. Supplementary materials for this article are available online.

KEYWORDS:

• Bayesian inference
• Big Data
• Block pseudo-marginal
• Correlated pseudo-marginal
• Estimated likelihood
• Survey sampling

1. Introduction

Bayesian methods became much more popular after 1990 due to advances in computer technology and the introduction of powerful simulation algorithms such as Markov chain Monte Carlo (MCMC) (Gelfand and Smith, 1990). However, posterior sampling with MCMC is still time-consuming and there is an increasing awareness that new scalable algorithms are necessary for MCMC to remain an attractive choice for inference in datasets with a large number of observations.

1.1. Scalable MCMC

Current research on scalable MCMC algorithms belongs to two major groups. The first group employs parallelism through the typical MapReduce scheme (Dean and Ghemawat, 2008) by partitioning the data and computing separate subposteriors for each partition in a parallel and distributed manner, see, for example, Scott et al. (2013), Neiswanger, Wang, and Xing (2014), Wang and Dunson (2014), Minsker et al. (2014), and Nemeth and Sherlock (2018). Our approach belongs to the second group of methods that use a subsample of the data in each MCMC iteration to speed up the algorithm, which we refer to as subsampling MCMC; see Korattikara, Chen, and Welling (2014), Bardenet, Doucet, and Holmes (2014), Maclaurin and Adams (2014), Bardenet, Doucet, and Holmes (2017), and Liu, Mingas, and Bouganis (2015). Section 4.4 compares these approaches against our methods. See Bardenet, Doucet, and Holmes (2017) for an excellent review of these methods and a broad overview of the problem in general.

1.2. Pseudo-Marginal MCMC

For models where the likelihood cannot be computed analytically (intractable likelihood) Beaumont (2003) proposed estimating the likelihood unbiasedly and running a Metropolis-Hastings (MH) algorithm on an extended space, which also includes the auxiliary random variables used to form the likelihood estimate. Andrieu and Roberts (2009) called this a pseudo-marginal (PM) approach and prove that PM methods target the true posterior density if the likelihood estimator is unbiased and almost surely positive.

1.3. Our Contribution

Our article uses the PM framework where at each iteration the log-likelihood from n observations is estimated unbiasedly from a random subset with m ≪ n observations, and the resulting likelihood estimate is then bias corrected to obtain an approximately unbiased estimate of the likelihood. The reason for doing subsampling is because we consider problems where computing the full likelihood is feasible but inordinately expensive. This leads to a PM sampling scheme targeting a slightly perturbed posterior, which mixes well because we use control variates to significantly reduce the variability in the log-likelihood estimate and a correlated PM scheme to improve the acceptance probability in the MH as discussed below. The control variates are crucial for reducing the variance of the likelihood estimate, and we propose a mixed strategy involving two types of approximations of the log-likelihood contributions of individual data items: (i) Taylor expansion around a reference value in parameter space (parameter expanded control variates) (Bardenet, Doucet, and Holmes, 2017) and (ii) Taylor expansion around the nearest centroid in data space (data expanded control variates).

We show that by taking $m=O\left(n^{\frac{1}{2}}\right)$, the total variation norm of the error in the perturbed posterior is O(n^{− 2}) if we have access to the maximum likelihood estimate (MLE) based on all data for constructing the control variates, or $O\left(n^{-\frac{1}{2}}\right)$ if the MLE is based on a subset with $\tilde{n}=O\left(n^{\frac{1}{2}}\right)$ observations. We further show heuristically and also empirically that the proportional error in the perturbed posterior is considerably smaller in regions of high posterior concentration. We also provide feasible estimators of the proportional error in the perturbed posterior and show empirically that this error is extremely small in our examples. Finally, our PM scheme is straightforward to implement and tune.

1.4. Variance of the Log of the Likelihood Estimator and Scalability

The variance of the log of the estimated likelihood is crucial for the performance of PM algorithms: a large variance can easily produce extreme over-estimates of the likelihood and cause the Markov chain to get stuck for long periods. Conversely, a too precise likelihood estimator might be unnecessarily costly. Pitt et al. (2012), Doucet et al. (2015) and Sherlock et al. (2015) analyze the variance of the log of the likelihood estimator that maximizes the number of effective draws per unit of computing time. They conclude that the optimal number of particles m should be such that this variance is around 1. Moreover, m = O(n) is required to obtain the optimal value of the variance.

It is now recognized that it is the variance of the difference in the logs of the likelihood estimators at the current and proposed values of the parameters that must be controlled. In the standard PM, this is equivalent to controlling the variance of the log of the estimated likelihood. Recent advances in PM algorithms correlate or block the random numbers used to form the estimates of the likelihood in the MH ratio at the current and proposed values of the parameters (see Deligiannidis, Doucet, and Pitt, 2016; Tran et al. 2017, respectively). Deligiannidis, Doucet, and Pitt (2016) show that this makes it possible to target a variance of the log estimated likelihood that is much larger than one, and the optimal variance can be obtained with m = O(n^1/2). Dahlin et al. (2015) also introduces the correlated PM but their article does not contain any analytic nor optimality results. Tran et al. (2017) give an alternative derivation of this result and generalize it to the case where the likelihood is estimated by randomized quasi-Monte Carlo. Our article introduces both the correlated and block correlated PM approaches to data subsampling.

1.5. Related Approaches Using Our Subsampling Methods

The subsampling methods and theory proposed here have already found applications in several recently proposed algorithms.

Quiroz et al. (2018b) use the insights and methods of our article (control variates and correlated and block PM for subsampling) to obtain unbiased estimates of posterior expectations of functions of the parameters. The method uses a version of the unbiased, but possibly negative, Poisson estimator (Wagner 1988) of the likelihood and runs a PM algorithm based on the absolute value of this estimator. The resulting iterates are subsequently used in an importance sampling scheme following Lyne et al. (2015) to obtain simulation consistent posterior expectations of functions of the parameters. Although exact, this approach has some drawbacks compared to the approach proposed here. First, it does not automatically produce an estimate of the posterior distribution of a function of the parameters because it is not an MCMC approach, and hence it is infeasible in practice to obtain credible regions with it. Second, it results in a more expensive algorithm (as measured by the computational time (CT), which balances the number of subsamples and MCMC efficiency) than our approach since the possible negativity of the estimator adversely affects the variance of the importance sampling step.

Quiroz et al. (2018a) apply the framework, methodology and theory of a previous version of our article to propose a delayed acceptance subsampling scheme, which they implement using the data expanded control variates. Unlike Theorem 1 and Corollary 1 of our article, there are no theoretical or empirical results of how the parameter expanded control variates affect the error in the perturbed posterior.

1.6. Article Outline

The article is organized as follows. Section 2 introduces the general likelihood estimator and derives some important properties. Section 3 outlines the subsampling MCMC algorithm and its theoretical framework, including results on the accuracy of the perturbed posterior. Section 4 studies empirically our proposed methodology and shows that it outperforms both standard (non-subsampling) MCMC and other subsampling approaches. There is online supplementary material to the article. We refer to pages, sections, etc. in the supplement as Page S1, Section S1, etc. Section S1 contains implementation details, Section S2 contains some proofs, and Section S3 shows how our theory applies to generalized linear models.

2. Sampling-Based Log-Likelihood Estimators

2.1. A Log-Likelihood Estimator Based on Simple Random Sampling With Efficient Control Variates

Let {y_i, x_i}ⁿ_{i = 1} denote the data, where y is a response vector and x is a vector of covariates. Let θ ∈ Θ be a p-dimensional vector of parameters. Given conditionally independent observations, we have the usual decomposition of the log-likelihood (1) $${\ell }_{\left(n\right)}\left(\theta \right):=\sum _{i=\text{1}}^n{\ell }_i\left(\theta \right),\text{where}{\ell }_i\left(\theta \right):=logp\left(y_i\right|\theta ,x_i)$$(1) is the log-likelihood contribution of the ith observation. For any given θ, (1(1) $${\ell }_{\left(n\right)}\left(\theta \right):=\sum _{i=\text{1}}^n{\ell }_i\left(\theta \right),\text{where}{\ell }_i\left(\theta \right):=logp\left(y_i\right|\theta ,x_i)$$(1) ) is a sum of a finite number of elements and estimating it is equivalent to the classical survey sampling problem of estimating a population total. See Särndal, Swensson, and Wretman (2003) for an introduction. We assume in (1(1) $${\ell }_{\left(n\right)}\left(\theta \right):=\sum _{i=\text{1}}^n{\ell }_i\left(\theta \right),\text{where}{\ell }_i\left(\theta \right):=logp\left(y_i\right|\theta ,x_i)$$(1) ) that the log-likelihood decomposes as a sum of terms where each term depends on a unique piece of data information. This applies to longitudinal problems where ℓ_i(θ) is the log joint density of all measurements on the ith subject, and we sample subjects rather than individual observations. It also applies to certain time-series problems such as AR(l) processes, where the sample elements become (y_t, …, y_{t − l}), for t = l + 1, …, n. Our examples in Section 4 use independent identically distributed (iid) observations and time series data.

Estimating (1(1) $${\ell }_{\left(n\right)}\left(\theta \right):=\sum _{i=\text{1}}^n{\ell }_i\left(\theta \right),\text{where}{\ell }_i\left(\theta \right):=logp\left(y_i\right|\theta ,x_i)$$(1) ) using simple random sampling (SRS), where any ℓ_i(θ) is included with the same probability generally results in a very large variance. Intuitively, since some ℓ_i(θ) contribute significantly more to the sum in (1(1) $${\ell }_{\left(n\right)}\left(\theta \right):=\sum _{i=\text{1}}^n{\ell }_i\left(\theta \right),\text{where}{\ell }_i\left(\theta \right):=logp\left(y_i\right|\theta ,x_i)$$(1) ) they should be included in the sample with a larger probability, using so called probability proportional-to-size sampling. However, this requires each of the n sampling probabilities to be proportional to a measure of their size. Evaluating n size measures is likely to defeat the purpose of subsampling, except when there is a computationally cheaper proxy than ℓ_i(θ) that can be used instead. Alternatively, one can make the {ℓ_i(θ)}ⁿ_{i = 1} more homogeneous by using control variates so that the population elements are roughly of the same size and SRS is then expected to be efficient. Our article focuses on this case and proposes efficient control variates q_{i, n}(θ) such that the computational cost (CC) of the estimator is substantially less than O(n). The dependence on n is due to q_{i, n}(θ) being an approximation of ℓ_i(θ), which typically improves as more data is available as we will discuss in detail later.

Define the differences d_{i, n}(θ)  ≔  ℓ_i(θ) − q_{i, n}(θ) and let $$\begin{array}{ccc}\hfill {\mu }_{d,n}\left(\theta \right)& :=& \frac{1}{n}\sum _{i=1}^n{d}_{i,n}\left(\theta \right)\hfill \\ \hfill \text{and}{\sigma }_{d,n}^2\left(\theta \right)& :=& \frac{{\sum }_{i=1}^n{\left(d_{i,n}\left(\theta \right)-{\mu }_{d,n}\left(\theta \right)\right)}^2}{n}\hfill \end{array}$$be the mean and variance of the finite population {d_{i, n}(θ)}ⁿ_{i = 1}. Let u₁, …, u_m be iid random variables such that $Pr(u=k)=1/n$ for k = 1, …, n. The difference estimator (DE; Särndal, Swensson, and Wretman 2003) of ℓ_(n)(θ) in (1(1) $${\ell }_{\left(n\right)}\left(\theta \right):=\sum _{i=\text{1}}^n{\ell }_i\left(\theta \right),\text{where}{\ell }_i\left(\theta \right):=logp\left(y_i\right|\theta ,x_i)$$(1) ) is (2) $${\widehat{\ell }}_{(m,n)}\left(\theta \right):=q_{\left(n\right)}\left(\theta \right)+n{\widehat{\mu }}_{d,n}\left(\theta \right),{\widehat{\mu }}_{d,n}\left(\theta \right):=\frac{1}{m}\sum _{i=1}^m{d}_{u_i,n}\left(\theta \right),$$(2) with q_(n)(θ)  ≔  ∑ⁿ_{i = 1}q_{i, n}(θ). It is straightforward to use unequal sampling probabilities with the DE, but the sampling probabilities need to be evaluated for every observation, which can be costly. The following lemma gives some basic properties of the DE estimator. Its proof is in Section S2.

Lemma 1.

Suppose that ${\widehat{\ell }}_{(m,n)}\left(\theta \right)$ is the estimator of ℓ_(n)(θ) = ℓ(θ) given by (2(2) $${\widehat{\ell }}_{(m,n)}\left(\theta \right):=q_{\left(n\right)}\left(\theta \right)+n{\widehat{\mu }}_{d,n}\left(\theta \right),{\widehat{\mu }}_{d,n}\left(\theta \right):=\frac{1}{m}\sum _{i=1}^m{d}_{u_i,n}\left(\theta \right),$$(2) ). Then, for each θ,

(i)	$\mathrm{E}\left[{\widehat{\mu }}_{d,n}\left(\theta \right)\right]={\mu }_{d,n}\left(\theta \right)$.
(ii)	$$\begin{array}{c}\\ \hfill \mathrm{E}\left[{\widehat{\ell }}_{(m,n)}\left(\theta \right)\right]& =& {\ell }_{\left(n\right)}\left(\theta \right)\hfill \\ \hfill \text{and}{\sigma }_{LL,m,n}^2\left(\theta \right)& :=& \mathrm{var}\left[{\widehat{\ell }}_{(m,n)}\left(\theta \right)\right]=\frac{n^2{\sigma }_{d,n}^2\left(\theta \right)}{m}.\hfill \end{array}$$
(iii)	${\widehat{\ell }}_{(m,n)}\left(\theta \right)$ is asymptotically normal when m → ∞ for fixed n and σ2d, n(θ) < ∞, or when both m, n → ∞ with m = O(nα) for α > 0 and σ3d, n(θ) < ∞.

The assumptions of finite σ²_{d, n}(θ) and σ³_{d, n}(θ) in Lemma 1 part (iii) are nonrestrictive because the random variables are discrete with a finite sample space: they are satisfied for any control variates that are finite. We use the following estimate of σ²_{d, n}(θ) $$\widehat{\sigma }{}_{d,n}^2\left(\theta \right):=\frac{{\sum }_{i=1}^m{\left(d_{u_i,n}\left(\theta \right)-{\widehat{\mu }}_{d,n}\left(\theta \right)\right)}^2}{m}.$$We also define the higher order central moments $$\begin{array}{ccc}\hfill {\phi }_{d,n}^{\left(b\right)}\left(\theta \right)& :=& \mathrm{E}\left[{(d_{u_i,n}\left(\theta \right)-{\mu }_{d,n}\left(\theta \right))}^b\right]\hfill \\ & =& \sum _{i=1}^n{(d_{i,n}\left(\theta \right)-{\mu }_{d,n}\left(\theta \right))}^b/n\text{for}b\ge 1,\hfill \end{array}$$and the corresponding standardized quantities Ψ^(b)_{d, n}(θ)  ≔ ϕ_{d, n}^(b)(θ)/σ^b_{d, n}(θ).

2.2. Control Variates for Variance Reduction and Optimal Subsample Size

We will now show that the variance reduction from control variates has a dramatic effect on how the subsample size m relates to the sample size n. The theory on how to choose the number of particles in PM in Pitt et al. (2012) and Doucet et al. (2015) is based on minimization of the CC of obtaining a single posterior draw that corresponds to an iid draw. This theory assumes that the likelihood is estimated directly, rather than indirectly via a bias-corrected log-likelihood estimator as proposed here. The relevant cost for evaluating the likelihood estimator in Pitt et al. (2012) and Doucet et al. (2015) can therefore be argued to be inversely proportional to variance of the log of the likelihood estimator, and the optimal number of particles or subsampled units m targets a variance of the log of the likelihood estimator around one. In our approach, the estimation effort is instead spent on estimating the log-likelihood. The relevant CC is therefore inversely proportional to σ²_{LL, m, n} and the optimal m targets a σ²_{LL, m, n} of O(1). See Section 3.6 for more details.

Lemma 2 below details the asymptotic behavior of σ²_{LL, m, n} using the definition (3) $$a_n\left(\theta \right):=2\underset{i=1,\cdots ,n}{max}\left|d_{i,n}\left(\theta \right)\right|.$$(3)

The proof of the following lemma is straightforward and therefore omitted. All terms in the lemma depend on θ.

Lemma 2.

For each θ ∈ Θ,

(i)	σbd, n = O(anb) for b ⩾ 1. In particular, σ2d, n = O(an2).
(ii)	${\sigma }_{LL,m,n}^2=\frac{n^{2}O\left(a_n^2\right)}{m}$.
(iii)	ϕ(b)d, n = O(abn) and Ψ(b)d, n = O(1).

Part (ii) of Lemma 2 shows that keeping the variance of the log-likelihood estimate bounded as a function of n requires that $\frac{n^{2}O\left(a_n^2\right)}{m}=O\left(1\right)$. This highlights the importance of the variance reduction: SRS without control variates scales poorly because O(a²_n) = O(1) and so m = O(n²) is optimal. Conversely, with control variates that improve as, say d_{i, n} = O(n^{− α}) with α ⩾ 0, we have O(a²_n) = O(n^{− 2α}) and m = O(n^{2(1 − α)}) is optimal. Lemma 2 also shows the asymptotic properties of the central moments, which are useful for our derivation of the perturbed target in Section 3.3.

2.3. Computational Complexity

The difference estimator in (2(2) $${\widehat{\ell }}_{(m,n)}\left(\theta \right):=q_{\left(n\right)}\left(\theta \right)+n{\widehat{\mu }}_{d,n}\left(\theta \right),{\widehat{\mu }}_{d,n}\left(\theta \right):=\frac{1}{m}\sum _{i=1}^m{d}_{u_i,n}\left(\theta \right),$$(2) ) requires computing q_(n)(θ) = ∑ⁿ_{i = 1}q_{i, n}(θ) in every MCMC iteration, that is, it requires computing the control variates q_{i, n}(θ) for i = 1, …, n. We now explore specific choices of q_{i, n} that allow us to compute ∑ⁿ_{i = 1}q_{i, n}(θ) using substantially less evaluations than n. Denote the CC for the standard MH without subsampling that evaluates ℓ_(n)  ≔  ∑ⁿ_{i = 1}ℓ_i by CC[ℓ_(n)(θ)]  ≔  n · c_ℓ, where c_ℓ is the cost of evaluating a single log-likelihood contribution (assuming the cost is the same for all i). For the difference estimator in (2(2) $${\widehat{\ell }}_{(m,n)}\left(\theta \right):=q_{\left(n\right)}\left(\theta \right)+n{\widehat{\mu }}_{d,n}\left(\theta \right),{\widehat{\mu }}_{d,n}\left(\theta \right):=\frac{1}{m}\sum _{i=1}^m{d}_{u_i,n}\left(\theta \right),$$(2) ), we have $$\mathrm{CC}\left[{\widehat{\ell }}_{(m,n)}\left(\theta \right)\right]:=n·c_q+m·c_{\ell },$$where c_q is the cost of computing a control variate. We now briefly describe two particular control variates that reduce the first term n · c_q. Section S1 gives implementation details.

First, consider the control variates in Bardenet, Doucet, and Holmes (2017), who proposed using a second-order Taylor expansion of each ℓ_i(θ) around some reference value θ^⋆_n, for example, the MLE. This reduces the complexity from n evaluations to a single one (similar to sufficient statistics for a normal model because q_{i, n}(θ) is quadratic in θ). As noted by Bardenet, Doucet, and Holmes (2017), this control variate can be a poor approximation of ℓ_i(θ) whenever the algorithm proposes a θ that is not near to θ^⋆_n, or when there is no access to a reasonable θ^⋆_n.

Second, we propose a new control variate which is based on clustering the data {z_i = (y_i, x_i)}ⁿ_{i = 1} into K clusters that are kept fixed, and is independent of θ^⋆_n. At a given MCMC iteration, we compute the exact log-likelihood contributions at all K centroids and use a second-order Taylor expansion with respect to z_i at the centroid z^c as a local approximation of ℓ_i around each centroid. This allows us to compute ∑ⁿ_{i = 1}q_{i, n}(θ) by evaluating quantities computed at the K centroids (similar to sufficient statistics for a normal model because q_{i, n}(θ) is now quadratic in z). The cost of the resulting estimator is (4) $$\mathrm{CC}\left[{\widehat{\ell }}_{(m,n)}\left(\theta \right)\right]=K·c_q+m·c_{\ell },$$(4) where typically K ≪ n.

We refer to the control variate that uses a Taylor expansion with respect to θ as parameter expanded, and the control variate type that Taylor expands with respect to z as data expanded.

2.4. Asymptotic Properties of the Control Variates

2.4.1. Data Expanded Control Variates

To derive the asymptotic behavior of a_n(θ) in (3(3) $$a_n\left(\theta \right):=2\underset{i=1,\cdots ,n}{max}\left|d_{i,n}\left(\theta \right)\right|.$$(3) ) for data expanded control variates, we bound the remainder term (Hubbard and Hubbard, 1999, Appendix A.9) $$\left|d_{i,n}\left(\theta \right)\right|\le O\left({\left(\left|\right|z-z^c{\left|\right|}_1\right)}^3\right)=O\left({ϵ}^3\right),$$where || · ||₁ denotes the l₁-norm and ε is an input to Algorithm S1 in Section S1, which is proportional to the maximum l₁-distance between an observation z and its centroid z^c. If the number of clusters increases with n such that ε = O(n^{− ζ}) for some ζ > 0, then α = 3ζ in d_{i, n}(θ) = O(n^{− α}) and hence a_n(θ) = O(n^{− 3ζ}) for this control variate. Our simulations show that the numbers of clusters needs to increase rapidly with n to satisfy the error decay (ζ > 0) when the effective dimension of the data $\tilde{p}$ is large and data are independent across dimensions (not shown here); these empirical results are supported by Theorem 5.3b in Graf and Luschgy (2002), which states that the mean distance in k-means clustering between an observation to its nearest centroid decreases as $O\left(n^{-1/(\tilde{p}+2)}\right)$ if the number of centroids grows as $o\left(n^{\tilde{p}/(\tilde{p}+2)}\right)$ for any distribution with compact support. However, the performance on real data depends on the extent to which the observed data lies close to a lower-dimensional manifold, and we have observed good performance in our examples in Section 4, where $\tilde{p}\le 21$. Nevertheless, data expanded control variates will eventually suffer from the curse of dimensionality, and we now turn to the asymptotic properties of parameter expanded control variates.

2.4.2. Parameter Expanded Control Variates

Assumption 1.

Suppose that for each i, ℓ_i(θ) is three times differentiable with $$\underset{j,k,l\in \{1,\cdots ,p\}}{max}\underset{\theta \in \Theta }{sup}\left|\frac{{\partial }^3{\ell }_i\left(\theta \right)}{\partial {\theta }_j\partial {\theta }_k\partial {\theta }_l}\right|$$bounded.

We now have the following result, where || · || is the l₂ norm for the rest of the article unless stated otherwise. The proof of the lemma is immediate.

Lemma 3.

Suppose that Assumption 1 holds. Then, a_n(θ) = ||θ − θ^⋆_n||³O(1).

While the asymptotics for the data expanded covariates are interpreted in a nonstochastic sense (z is nonstochastic) our interpretation here also treats data as nonstochastic, but the parameter as stochastic so that we can use the Bernstein-von Mises theorem (BvM). The BvM theorem states that the posterior distribution converges to the normal distribution (in some sense) when the sample size n → ∞. There are probabilistic (stochastic data) and nonstochastic (nonstochastic data) versions of the BvM, and we use a version of the latter one due to Chen (1985). Treating the data as fixed leads to a better interpretation in our context and is also consistent with a Bayesian interpretation.

3. Subsampling MCMC Methodology

3.1. MCMC With Likelihood Estimators From Data Subsampling

We propose an efficient unbiased estimator ${\widehat{\ell }}_{(m,n)}\left(\theta \right)$ of the log-likelihood and then approximately bias-correct it following Ceperley and Dewing (1999) (see also Nicholls, Fox, and Watt 2012) to obtain the approximately bias-corrected likelihood estimator (5) $$\widehat{L}{}_{(m,n)}(\theta ,u):=exp\left({\widehat{\ell }}_{(m,n)}\left(\theta \right)-\frac{n^2}{2m}{\widehat{\sigma }}_{d,n}^2\left(\theta \right)\right),$$(5) where ${\widehat{\ell }}_{(m,n)}\left(\theta \right)$ and ${\widehat{\sigma }}_{d,n}^2\left(\theta \right)$ are the estimators presented in Section 2.1. The form of (5(5) $$\widehat{L}{}_{(m,n)}(\theta ,u):=exp\left({\widehat{\ell }}_{(m,n)}\left(\theta \right)-\frac{n^2}{2m}{\widehat{\sigma }}_{d,n}^2\left(\theta \right)\right),$$(5) ) is motivated by the case when ${\widehat{\ell }}_{(m,n)}\sim \mathcal{N}({\ell }_{\left(n\right)}\left(\theta \right),{\sigma }_{LL,m,n}^2\left(\theta \right))$, and σ²_{LL, m, n} is known, in which case all bias is removed. Normality holds asymptotically in both m and n by part (iii) of Lemma 1. However, the assumption of a known variance is unrealistic because the computation requires the entire dataset. The estimator in (5(5) $$\widehat{L}{}_{(m,n)}(\theta ,u):=exp\left({\widehat{\ell }}_{(m,n)}\left(\theta \right)-\frac{n^2}{2m}{\widehat{\sigma }}_{d,n}^2\left(\theta \right)\right),$$(5) ) is therefore expected to only be nearly unbiased.

There are four main differences between our approach and Ceperley and Dewing (1999) and Nicholls, Fox, and Watt (2012). First, our approach is PM and takes into account that the log-likelihood is estimated using a random subsample at each iteration and is therefore guaranteed to converge to the posterior distribution. Second, we use control variates to decrease the variance of the estimator of the log-likelihood and analyze the effect that these control variates have on the variance of the log of the estimate of the likelihood. Third, we use correlated PM schemes to also allow the log of the estimated likelihood to have a large variance. Finally, our convergence rate of the error (Theorem 1 below) is O(n^{− 1}m^{− 2}) as opposed to O(m^{− 1}) in Nicholls, Fox, and Watt (2012).

We now outline how to carry out a PM MH scheme with the approximately unbiased estimator in (5(5) $$\widehat{L}{}_{(m,n)}(\theta ,u):=exp\left({\widehat{\ell }}_{(m,n)}\left(\theta \right)-\frac{n^2}{2m}{\widehat{\sigma }}_{d,n}^2\left(\theta \right)\right),$$(5) ) and derive the asymptotic error in the stationary distribution. Denote the likelihood by L_(n)(θ)  ≔  p(y|θ), let p_Θ(θ) be the prior and define the marginal likelihood $\bar{L}{}_{\left(n\right)}:=\int L_{\left(n\right)}\left(\theta \right)p_{\Theta }\left(\theta \right)d\theta$. Then, the posterior is ${\pi }_{\left(n\right)}\left(\theta \right)=L_{\left(n\right)}\left(\theta \right)p_{\Theta }\left(\theta \right)/\bar{L}{}_{\left(n\right)}$. Let p_U(u) be the distribution of the vector u of auxiliary variables corresponding to the subset of observations to include when estimating L_(n)(θ). Let $\widehat{L}{}_{(m,n)}(\theta ,u)$, for fixed m and n, be a possibly biased estimator of L_(n)(θ) with expectation $$L_{(m,n)}\left(\theta \right)=\int \widehat{L}{}_{(m,n)}(\theta ,u)p_U\left(u\right)du.$$Define (6) $$\begin{array}{ccc}\hfill {\bar{\pi }}_{(m,n)}(\theta ,u)& :=& \widehat{L}{}_{(m,n)}(\theta ,u)p_U\left(u\right)p_{\Theta }\left(\theta \right)/{\bar{L}}_{(m,n)},\text{with}{\bar{L}}_{(m,n)}\hfill \\ & :=& \int L{}_{(m,n)}\left(\theta \right)p_{\Theta }\left(\theta \right)d\theta ,\hfill \end{array}$$(6) on the augmented space (θ, u). It is straightforward to show that ${\bar{\pi }}_{(m,n)}(\theta ,u)$ is a proper density with marginal $$\begin{array}{ccc}\hfill {\bar{\pi }}_{(m,n)}\left(\theta \right)& =& \int {\bar{\pi }}_{(m,n)}(\theta ,u)du=L_{(m,n)}\left(\theta \right)p_{\Theta }\left(\theta \right)/{\bar{L}}_{(m,n)}.\hfill \end{array}$$

The standard PM that targets (6(6) $$\begin{array}{ccc}\hfill {\bar{\pi }}_{(m,n)}(\theta ,u)& :=& \widehat{L}{}_{(m,n)}(\theta ,u)p_U\left(u\right)p_{\Theta }\left(\theta \right)/{\bar{L}}_{(m,n)},\text{with}{\bar{L}}_{(m,n)}\hfill \\ & :=& \int L{}_{(m,n)}\left(\theta \right)p_{\Theta }\left(\theta \right)d\theta ,\hfill \end{array}$$(6) ) uses a joint proposal for θ and u given by $$q_{\Theta ,U}(\theta ,u|{\theta }_c,u_c)=p_U\left(u\right)q_{\Theta }\left(\theta \right|{\theta }_c),$$where θ_c denotes the current state of the Markov chain. The PM acceptance probability becomes (7) $$\alpha =min\left(1,\frac{\widehat{L}{}_{(m,n)}({\theta }_p,u_p)p_{\Theta }\left({\theta }_p\right)/q_{\Theta }\left({\theta }_p\right|{\theta }_c)}{\widehat{L}{}_{(m,n)}({\theta }_c,u_c)p_{\Theta }\left({\theta }_c\right)/q_{\Theta }\left({\theta }_c\right|{\theta }_p)}\right).$$(7) This expression is similar to the standard MH acceptance probability, but with the true likelihood replaced by its estimate. By Andrieu and Roberts (2009), the draws of θ obtained by this MH algorithm have ${\bar{\pi }}_{(m,n)}\left(\theta \right)$ as invariant distribution. If $\widehat{L}{}_{(m,n)}(\theta ,u)$ is an unbiased estimator of L_(n)(θ), then the marginal of the augmented MCMC scheme above has ${\bar{\pi }}_{(m,n)}\left(\theta \right)={\pi }_{\left(n\right)}\left(\theta \right)$ (the true posterior) as invariant distribution. However, if $\widehat{L}{}_{(m,n)}(\theta ,u)$ is biased, the sampler is still valid but has a perturbed marginal ${\bar{\pi }}_{(m,n)}\left(\theta \right)$.

3.2. Perturbation Analysis – Asymptotics

The discussion in Section 2.4 argued that parameter expanded covariates have better asymptotic properties. We therefore state and prove our main theorem on the fractional error in the perturbed quantities under this choice of control variate. Let π_(n)(θ)∝exp (ℓ_(n)(θ))p_Θ(θ) be the density function of the posterior distribution of θ, where p_Θ is the prior density for θ. Let θ^⋆_n be a mode of π_(n), and $${\Delta }_n\left(\theta \right):=\frac{{\partial }^{2}log{\pi }_n\left(\theta \right)}{\partial \theta \partial {\theta }^T}.$$Denote by H(a, δ) = {θ ∈ Θ: ‖θ − a‖ ⩽ δ} a neighborhood of a. We follow Chen (1985) and make the following assumptions.

Assumption 2.

Assume that the following hold.

A1.	$\partial log{\pi }_n\left(\theta \right){/\partial \theta |}_{\theta ={\theta }_n^{★}}=0$.
A2.	Δn(θ⋆n) is negative definite.
A3.	‖Σn‖2 = O(n− 1), where Σn = ( − Δn(θ⋆n))− 1.
A4.	For any ε > 0, there exist a δε > 0 and an integer N1, ε such that for any n > N1, ε and θ ∈ H(θ⋆n, δε), Δn(θ) exists and satisfies $$-A\left(ϵ\right)\le {\Delta }_n\left(\theta \right)({\Delta }_n\left({\theta }_n^{★}\right){)}^{-1}-I\le A\left(ϵ\right)$$where A(ε) is a positive semidefinite matrix whose largest eigenvalue goes to 0 as ε → 0.
A5.	For any δ > 0, there exists a positive integer N2, δ and two positive numbers c and κ such that for n > N2, δ and $\theta \notin H({\theta }_n^{★},\delta )$$$\frac{{\pi }_{\left(n\right)}\left(\theta \right)}{{\pi }_{\left(n\right)}\left({\theta }_n^{★}\right)}<exp\left(-c[{(\theta -{\theta }_n^{★})}^T{\Sigma }_n^{-1}(\theta -{\theta }_n^{★}){]}^{\kappa }\right).$$

Chen (1985) showed that the conditions in Assumption 2 hold in regular exponential families with conjugate priors. His proof carries directly over to generalized linear models in the canonical parameterization, which includes the logistic regression used in the applications in Section 4. This result also generalizes in a straightforward way to the noncanonical case if the link function has continuous third derivative, see Section S3 for details.

Theorem 1.

Suppose that we use parameter expanded control variates and assume that the regularity conditions in Assumption 2 are satisfied. Then,

(i)	$${\int }_{\Theta }\left|{\bar{\pi }}_{(m,n)}\left(\theta \right)-{\pi }_{\left(n\right)}\left(\theta \right)\right|d\theta =O\left(\frac{1}{n{m}^2}\right).$$
(ii)	Suppose that h(θ) is a function such that $limsup{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left[h^2\left(\theta \right)\right]<\infty$. Then $$\left|{\mathrm{E}}_{{\bar{\pi }}_{(m,n)}}\left[h\left(\theta \right)\right]-{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left[h\left(\theta \right)\right]\right|=O\left(\frac{1}{n{m}^2}\right).$$

The proof is in Section S2.

Note first that for a fixed n the errors in Theorem 1 are of order O(m^{− 2}) in the subsample size. More importantly, the theorem shows that the perturbation error can decrease at a very rapid rate with respect to n. For example, $m=O\left(n^{\frac{1}{2}}\right)$ gives a perturbation error of order O(n^{− 2}). However, the accuracy of the control variates expanded around the posterior mode increases so extremely rapidly with the sample size n that the optimal subsample size m = O(n^{− 1}) actually decreases with n. This in turn leads to a perturbation error of O(n). Control variates based on expanding around the posterior mode therefore makes the two aims efficiency and accuracy incompatible.

However, it is not practical to use control variates based on the posterior mode as we wish to avoid handling all the observations. A way around this is to obtain the posterior mode using stochastic gradient descent based on an unbiased estimate of the gradient from a subsample. Alternatively, one can use the posterior mode from a fixed subsample. The following corollary shows the approximation rates in Theorem 1 and the asymptotic behavior of σ²_{LL, m, n} in Lemma 2 when the control variates are based on the posterior mode from a fixed subset of $\tilde{n}\ll n$ observations. Its proof is in Section S2.

Corollary 1.

Suppose that ${\theta }_{\tilde{n}}^{★}-{\theta }_n^{★}=O\left({\tilde{n}}^{-\frac{1}{2}}\right)$ and Assumptions 2 or 3 hold. Then,

(i)	$${\int }_{\Theta }\left|{\bar{\pi }}_{(m,n)}\left(\theta \right)-{\pi }_{\left(n\right)}\left(\theta \right)\right|d\theta =O\left(\frac{n^2}{m^2{\tilde{n}}^3}\right).$$
(ii)	Suppose that h(θ) is a function such that $limsup{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left[h^2\left(\theta \right)\right]<\infty$. Then, $$\left|{\mathrm{E}}_{{\bar{\pi }}_{(m,n)}}\left[h\left(\theta \right)\right]-{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left[h\left(\theta \right)\right]\right|=O\left(\frac{n^2}{m^2{\tilde{n}}^3}\right).$$
(iii)	${\sigma }_{LL,m,n}^2\left(\theta \right)=O\left(\frac{n^2}{m{\tilde{n}}^3}\right)$ for ${\Sigma }_n^{-\frac{1}{2}}(\theta -{\theta }_n^{★})=O\left(1\right)$.

To understand the implications of this result, suppose that $\tilde{n}=n^{\kappa },m=n^{\alpha }$ and we target σ²_{LL, m, n}(θ) = O(1). Then, Corollary 1 (iii) implies that the optimal subsample is obtained with α = 2 − 3κ. The errors in (i) and (ii) then decrease with n if only if κ < 2/3. If we for example take κ = 1/2, then α = 1/2 and the error in parts (i) and (ii) of Corollary 1 are $O\left(n^{-\frac{1}{2}}\right)$. If instead κ ⩾ 2/3 then α ⩽ 0, so the optimal m is decreasing in n, and the errors in parts (i) and (ii) therefore increase with n. So, for κ ⩾ 2/3 there is a tradeoff between efficiency and accuracy.

An interesting intermediate approach uses $\tilde{n}\ll n$ observations for the control variates initially and then updates ${\theta }_{\tilde{n}}^{★}$ after the sampler has reached a central region in the posterior. This would correspond to using a κ closer to one, with the approximation error rates being closer to those in Theorem 1.

Finally, we note that it is straightforward to show that Theorem 1 still holds if we construct the control variates using the MLE rather than a posterior mode. To do so we assume that

Assumption 3.

In Assumption 2, we replace π_(n)(θ) by L_(n)(θ), so that θ^⋆_n is now an MLE, Δ_n(θ) = ∂ℓ_(n)(θ)/∂θ∂θ^T, etc.

Then Theorem 1 holds under Assumption 3 and mild conditions on the prior, for example, that $p_{\Theta }\left(\theta \right)/p_{\Theta }\left({\theta }_n^{★}\right)$ is bounded.

3.3. Approximating the Perturbation Error

Theorem 1 and Corollary 1 are large sample results on the error in the perturbed posterior. In this section, we give sharper, but more heuristic, results on this proportional error in the perturbed posterior and show that it is a lot smaller that the proportional error in the perturbed likelihood. We then outline how these sharper bounds can be used to estimate the proportional error in practice.

Let ${\xi }_{m,n}\left(\theta \right)={\widehat{\ell }}_{(m,n)}\left(\theta \right)-\frac{1}{2}{\widehat{\sigma }}_{LL,m,n}^2\left(\theta \right)$. Then, we can show that for large m, $\mathrm{E}\left({\xi }_{m,n}\left(\theta \right)\right)={\ell }_{\left(n\right)}\left(\theta \right)-\frac{1}{2}{\sigma }_{LL,m,n}^2\left(\theta \right)$ and Λ_{(m, n)}(θ) = var(ξ_{m, n}(θ)) = σ²_{LL, m, n}(θ) + 2Γ_{(m, n)}(θ), where (8) $${\Gamma }_{(m,n)}\left(\theta \right)=\frac{{\sigma }_{LL,m,n}^4\left(\theta \right)}{8m}({\Psi }_{d,n}^{\left(4\right)}\left(\theta \right)-1)-\frac{{\sigma }_{LL,m,n}^3\left(\theta \right)}{2\sqrt{m}}{\Psi }_{d,n}^{\left(3\right)}\left(\theta \right),$$(8) where Ψ^(b)_{d, n}  ≔  ϕ_{d, n}^(b)/σ^b_{d, n} for b = 1, …, 4.

We now take m = m(n), for example, $m=O\left(\sqrt{n}\right)$ and suppose that as n → ∞, ${\sigma }_{LL,m,n}^2\left(\theta \right)\to {\bar{\sigma }}_{LL,m,n}^2\left(\theta \right)<\infty$ and ${\Psi }_{d,n}^{\left(b\right)}\left(\theta \right)\to {\bar{\Psi }}_{d,n}^{\left(b\right)}\left(\theta \right)$, with ${\bar{\Psi }}_{d,n}^{\left(b\right)}\left(\theta \right)$ bounded for all θ. Then, by a standard central limit argument we can show that ${\xi }_{m,n}\left(\theta \right)-({\ell }_{\left(n\right)}\left(\theta \right)-\frac{1}{2}{\sigma }_{LL,m,n}^2\left(\theta \right))$ tends to a normal density with mean 0 and variance ${\bar{\sigma }}_{LL,m,n}^2\left(\theta \right)$.

This central limit theorem result is driven by m becoming large. Hence, if n is fixed and $m\uparrow m\left(n\right)=\sqrt{n}$ we will have that ${\xi }_{m,n}\left(\theta \right)-{\ell }_{\left(n\right)}\left(\theta \right)-({\ell }_{\left(n\right)}\left(\theta \right)-\frac{1}{2}{\sigma }_{LL,m,n}^2\left(\theta \right))$ tends to a normal with variance Λ_{(m, n)}(θ). Now for fixed n, ${\xi }_{m,n}\left(\theta \right)-{\ell }_{\left(n\right)}\left(\theta \right)-({\ell }_{\left(n\right)}\left(\theta \right)-\frac{1}{2}{\sigma }_{LL,m,n}^2\left(\theta \right))$ is bounded so that (9) $$\begin{array}{ccc}& & \mathrm{E}\left[exp\left({\xi }_{m,n}\left(\theta \right)-{\ell }_{\left(n\right)}\left(\theta \right)-\left({\ell }_{\left(n\right)}\left(\theta \right)-\frac{1}{2}{\sigma }_{LL,m,n}^2\left(\theta \right)\right)\right)\right]\hfill \\ & & \to exp\left(\frac{1}{2}{\Lambda }_{(m,n)}\left(\theta \right)\right)\hfill \end{array}$$(9)

Lemma 4 gives analytical expression for the proportional errors in the perturbed likelihood L_{(m, n)}(θ) and the perturbed posterior. Its proof is straightforward and omitted. The normality assumption in the lemma assumes that n and m = m(n) are large and is based on (9(9) $$\begin{array}{ccc}& & \mathrm{E}\left[exp\left({\xi }_{m,n}\left(\theta \right)-{\ell }_{\left(n\right)}\left(\theta \right)-\left({\ell }_{\left(n\right)}\left(\theta \right)-\frac{1}{2}{\sigma }_{LL,m,n}^2\left(\theta \right)\right)\right)\right]\hfill \\ & & \to exp\left(\frac{1}{2}{\Lambda }_{(m,n)}\left(\theta \right)\right)\hfill \end{array}$$(9) ).

Lemma 4.

Suppose that ξ_{m, n}(θ) is normal with mean ${\ell }_{\left(n\right)}\left(\theta \right)-\frac{1}{2}{\sigma }_{LL,m,n}^2\left(\theta \right)$ and variance Λ_{(m, n)}(θ) Then, (10) $$\frac{L_{(m,n)}\left(\theta \right)-L_{\left(n\right)}\left(\theta \right)}{L_{\left(n\right)}\left(\theta \right)}=exp\left({\Gamma }_{(m,n)}\left(\theta \right)\right)-1,$$(10) is the proportional error in the perturbed likelihood and (11) $$\frac{{\pi }_{(m,n)}\left(\theta \right)-{\pi }_{\left(n\right)}\left(\theta \right)}{{\pi }_{\left(n\right)}\left(\theta \right)}=\frac{exp\left({\Gamma }_{(m,n)}\left(\theta \right)\right)}{{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left(exp\left({\Gamma }_{(m,n)}\right)\right)}-1$$(11) is the proportional error in the perturbed posterior.

From part (iii) of Lemma 2, Ψ^(b)_{d, n}(θ) = O(1) for any b ⩾ 1. Hence, it follows from Lemma 4 that the perturbation error (10(10) $$\frac{L_{(m,n)}\left(\theta \right)-L_{\left(n\right)}\left(\theta \right)}{L_{\left(n\right)}\left(\theta \right)}=exp\left({\Gamma }_{(m,n)}\left(\theta \right)\right)-1,$$(10) ) in the likelihood depends on σ²_{LL, m, n}(θ), whereas the error in the perturbed posterior (11(11) $$\frac{{\pi }_{(m,n)}\left(\theta \right)-{\pi }_{\left(n\right)}\left(\theta \right)}{{\pi }_{\left(n\right)}\left(\theta \right)}=\frac{exp\left({\Gamma }_{(m,n)}\left(\theta \right)\right)}{{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left(exp\left({\Gamma }_{(m,n)}\right)\right)}-1$$(11) ) will tend to be much smaller because the term $$\frac{exp\left({\Gamma }_{(m,n)}\left(\theta \right)\right)}{{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left(exp\left({\Gamma }_{(m,n)}\right)\right)}$$will be close to 1 for all θ in the region $\left|\right|{\Sigma }_n^{-\frac{1}{2}}(\theta -{\theta }_n^{★})\left|\right|\le k$ for a fixed k > 0 as the posterior becomes very concentrated around θ^⋆_n for n large. In particular, if we write Γ_{(m, n)}(θ) = C + γ_{(m, n)}(θ), where C is independent of θ and suppose that γ_{(m, n)}(θ) ≪ C. Then, the proportional error in the perturbed likelihood depends on C, whereas the error in the perturbed posterior $$\frac{exp\left({\Gamma }_{(m,n)}\left(\theta \right)\right)}{{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left(exp\left({\Gamma }_{(m,n)}\right)\right)}=\frac{exp\left({\gamma }_{(m,n)}\left(\theta \right)\right)}{{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left(exp\left({\gamma }_{(m,n)}\right)\right)}$$will be very small. If γ_{(m, n)}(θ) ≡ 0, then there is no approximation in the perturbed posterior even if C is large so that the error in the perturbed likelihood is large. Thus, the error in the perturbed posterior is likely to be much smaller than in the perturbed likelihood.

We can use Lemma 4 to estimate the perturbation error in the posterior for any given application. The term Γ_{(m, n)}(θ) can be evaluated or estimated from a subsample because the terms σ_{LL, m, n}(θ) and Ψ^(b)_{d, n}(θ) are easily evaluated for any θ at the cost of evaluating ℓ_i(θ) for all i = 1, ..., n, or estimated from a subsample. The term ${\mathrm{E}}_{{\pi }_{\left(n\right)}}(exp\left({\Gamma }_{(m,n)}\right))$ can be estimated from the MCMC output. Alternatively, we can use a Laplace approximation by taking π_(n)(θ) as approximately normal with mean θ^⋆_n and covariance matrix Σ_n and then approximate Γ_{(m, n)}(θ) by a quadratic centered at θ^⋆_n, where θ^⋆_n is obtained from the MCMC output.

Remark 1.

Similar results to the above can be obtained if ${\sigma }_{LL,m,n}^2\left(\theta \right)/m^{\beta }\to {\bar{\sigma }}_{LL,m,n}^2\left(\theta \right)$ as n → ∞, with 0 < β < 1.

3.4. Subsampling With Correlated Proposals of u

Deligiannidis, Doucet, and Pitt (2016) proposed a general method that correlates the current and proposed values of the u_i. The advantage of using this correlation is that it makes the variance of the difference in the logarithms of the estimated likelihoods in (7(7) $$\alpha =min\left(1,\frac{\widehat{L}{}_{(m,n)}({\theta }_p,u_p)p_{\Theta }\left({\theta }_p\right)/q_{\Theta }\left({\theta }_p\right|{\theta }_c)}{\widehat{L}{}_{(m,n)}({\theta }_c,u_c)p_{\Theta }\left({\theta }_c\right)/q_{\Theta }\left({\theta }_c\right|{\theta }_p)}\right).$$(7) ) much smaller than that of each of the terms themselves. This leads, in our context, to being able to target much higher values of σ²_{LL, m, n}(θ) than unity thus requiring much smaller values of m. In this section, we adapt the method of Deligiannidis, Doucet, and Pitt (2016) to our problem, and in the next we discuss a variant of the correlated PM, which we call the block correlated PM.

For the correlated PM approach to subsampling, we let u be a vector of length n with binary elements u_i that determine if observation i is included (u_i = 1) when estimating the log-likelihood. Note that this is different from above, where u contained the observation indices and was of length m. Moreover, here the sample size is random and we let m^⋆ be the expected sample size. The sampling probabilities become $Pr(u_i=1)=m^{★}/n$ for i = 1, …, n. We use the auxiliary variable (particle) v in Deligiannidis, Doucet, and Pitt (2016) to induce dependence at the current u^c_i and proposed u^p_i sampling indicator through a Gaussian copula as we now explain. The correlated PM method uses a Gaussian autoregressive kernel $\mathcal{K}(v_c,v_p)$ defined by $v_p=\varphi v_c+\sqrt{1-{\varphi }^2}\epsilon$, where $\epsilon \sim \mathcal{N}(0,1)$. We also have $v_c\sim p\left(v\right)=\mathcal{N}\left(v\right|0,1)$ and $\mathcal{K}(v_c,v_p)$ is reversible with respect to p(v). We sample the u_i’s by first generating v_c and v_p and set $u_i^c=\mathcal{I}[\Phi \left(v_c\right)\le \frac{m^{★}}{n}]$ and $u_i^p=\mathcal{I}[\Phi \left(v_p\right)\le \frac{m^{★}}{n}]$, where Φ denotes the standard normal cdf.

As noted above, in contrast to Section 2.1, u is a binary vector. We can instead use the Horvitz-Thompson (Horvitz and Thompson 1952) which (under SRS) is $${\widehat{d}}_{(m^{★},n)}=\sum _{i=1}^n\frac{d_{i,n}}{m^{★}/n}{u}_i,$$and is unbiased for d_(n). Note that we can write $$\begin{array}{ccc}\hfill {\widehat{d}}_{(m^{★},n)}& =& \frac{1}{m^{★}}\sum _{i=1}^{n}n{d}_{i,n}{u}_i,\text{with}{\sigma }_{LL,m^{★},n}^2=\frac{{\sigma }_{\xi ,m^{★},n}^2}{m^{★}},\hfill \\ \hfill \text{where}{\sigma }_{\xi ,m^{★},n}^2& =& n\left(1-\frac{m^{★}}{n}\right)\sum _{i=1}^n{(d_{i,n}-{\mu }_{d,n})}^2\hfill \end{array}$$can be unbiasedly estimated by $${\widehat{\sigma }}_{\xi ,m^{★},n}^2=n^2\left(1-\frac{m^{★}}{n}\right)\frac{1}{m^{★}}\sum _{i=1}^n{(d_{i,n}-{\mu }_{d,n})}^2{u}_i.$$

3.5. Subsampling With Block Proposals for u

Tran et al. (2017) proposed the block correlated PM algorithm and show that it is a natural way to correlate the logs of the likelihood estimates at the current and proposed value of the parameters in our subsampling problem. The method divides the vector of observation indices u = (u₁, …, u_m) into G blocks and then updates one block at a time jointly with θ. By setting a large G, a high correlation ρ between the estimates of the likelihoods at the proposed and current parameter values is induced, reducing the variability of the difference in the logs of the estimated likelihoods at the proposed and current values of θ. More precisely, they show that under certain assumptions ρ is close to 1 − 1/G.

3.6. Optimal Variance of the Estimator

Pitt et al. (2012), Doucet et al. (2015), and Sherlock et al. (2015) obtained the value of $\mathrm{var}(log\widehat{L})$, where $\widehat{L}$ is an unbiased likelihood estimator (e.g., based on importance sampling or a particle filter) that optimizes the tradeoff between MCMC sampling efficiency and CC in standard PM. The consensus is that $\mathrm{var}(log\widehat{L})$ should lie in the interval [1, 3.3], where the less efficient the proposal in the exact likelihood setting, the higher the optimal value of $\mathrm{var}(log\widehat{L})$. The optimal value is derived assuming that the cost of computing one MCMC sample is inversely proportional to $\mathrm{var}(log\widehat{L})$.

For our problem, the log of the estimated likelihood is $log\left({\widehat{L}}_{(m,n)}\left(\theta \right)\right)={\widehat{\ell }}_{(m,n)}\left(\theta \right)-\frac{1}{2}{\widehat{\sigma }}_{LL,m,n}^2\left(\theta \right)$, which has variance Λ_{(m, n)}(θ) = σ²_{LL, m, n}(θ) + 2Γ_{(m, n)}(θ), where Γ_{(m, n)}(θ) is defined in (8(8) $${\Gamma }_{(m,n)}\left(\theta \right)=\frac{{\sigma }_{LL,m,n}^4\left(\theta \right)}{8m}({\Psi }_{d,n}^{\left(4\right)}\left(\theta \right)-1)-\frac{{\sigma }_{LL,m,n}^3\left(\theta \right)}{2\sqrt{m}}{\Psi }_{d,n}^{\left(3\right)}\left(\theta \right),$$(8) ). We take the computing cost as inversely proportional to σ²_{LL, m, n}(θ) because our estimation effort is based on computing ${\widehat{\ell }}_{(m,n)}$, with the extra cost of computing ${\widehat{\sigma }}_{LL,m,n}^2$ being negligible in comparison.

Thus, for the parameter expanded control variates, we follow Pitt et al. (2012) and define the CT as (12) $$\begin{array}{ccc}\hfill \mathrm{CT}({\sigma }_{LL,m,n}^2,{\Lambda }_{(m,n)})& :=& \frac{\mathrm{IF}\left({\Lambda }_{(m,n)}\right)}{{\sigma }_{LL,m,n}^2},\hfill \\ \hfill \text{with}\mathrm{IF}\left({\Lambda }_{(m,n)}\right)& :=& 1+2\sum _{l=1}^{\infty }{\rho }_l,\hfill \end{array}$$(12) which is proportional to the time required to produce one sample equivalent to an iid draw from the posterior distribution. In (12(12) $$\begin{array}{ccc}\hfill \mathrm{CT}({\sigma }_{LL,m,n}^2,{\Lambda }_{(m,n)})& :=& \frac{\mathrm{IF}\left({\Lambda }_{(m,n)}\right)}{{\sigma }_{LL,m,n}^2},\hfill \\ \hfill \text{with}\mathrm{IF}\left({\Lambda }_{(m,n)}\right)& :=& 1+2\sum _{l=1}^{\infty }{\rho }_l,\hfill \end{array}$$(12) ), ρ_l is the l-lag autocorrelation of the chain and IF(Λ_{(m, n)}) is the inefficiency factor (IF), which we note depends on Λ_{(m, n)}. However, Λ_{(m, n)} ≈ σ²_{LL, m, n} for m large so that we will write IF(σ²_{LL, m, n}).

If we use the data expanded control variates, then it is necessary to select both m and the number of clusters K. The CC of each cluster involves computing ℓ_i, and its gradient and Hessian at the centroid. An approximate upper bound for the cost of a new cluster is therefore 3c_ℓ, where c_ℓ is the cost of a single ℓ_i-evaluation. However, in many models it is possible to reuse some terms when computing the gradient and Hessian, so the true cost is probably much closer to c_ℓ. For example, in the logistic regression model in Section 4, the gradient and Hessian will be functions of exp ( ± x^T_iθ) which is already computed when evaluating ℓ_i(θ). Assuming that the cost of a cluster is ωc_ℓ, for some ω > 0, a reasonable measure of CT is (13) $${\mathrm{CT}}_{(m,K)}\left({\sigma }_{LL,m,n}^2\left(K\right)\right):=\mathrm{IF}\left({\Lambda }_{(m,n)}^2\left(K\right)\right)\times (\omega K+m).$$(13) This expression is similar to Tran et al. (2016), who also take into account an overhead cost in their CT. We find m and K by standard numerical optimization using an expression for the IF (e.g., the ones derived in Pitt et al. 2012 for PM and the Tran et al. 2017 for block PM).

For the correlated PM, we can follow Deligiannidis, Doucet, and Pitt (2016) and show for our application that the variance of the log of the estimated likelihood at the proposed values of u and θ conditional on the estimated likelihood at the current values of u and θ is τ²_{m, n} = Λ_{(m, n)}(1 − ρ²) ≈ σ²_{LL, m, n}(1 − ρ²), where ρ is the correlation between the logs of the two estimates of the likelihood, with the optimal value of τ²_{m, n} around 4. Similarly, for the block correlated PM, Tran et al. (2017) show that the variance of the log of the likelihood estimator at the proposed values conditional on only updating one block of u, keeping the others fixed, is τ²_{m, n, G} = Λ_{(m, n)}(1 − ρ²_G) ≈ σ_{LL, m, n}²(1 − ρ²_G). Let G = G(m) = O(m^β). Using Corollary 1 and ρ_G(m) = 1 − 1/G(m), it follows using the same notation as in the discussion below that corollary that τ²_{m, n, G}(θ) = O(1) is achieved if we take $m=O\left(n^{\alpha }\right),\tilde{n}=n^{\kappa }$ with 2 = 3κ + α(1 + β). If κ = 1/2 and β = 0, that is G does not depend on m, then the approximations in parts (i) and (ii) of Corollary 1 are $O\left(n^{-\frac{1}{2}}\right)$. We can then ensure that τ²_{m, n, G}(θ) is around the optimal value of 4 while σ²_{LL, m, n} ≫ 1 by adapting G. In practice, we usually take G = 100 which gives us a correlation close to 0.99.

We emphasize that it is the combined effect of using both the control variates and correlating the logs of the estimated likelihoods at the current and proposed values that makes the method scale well.

3.7. Strategy for Subsampling MCMC

We have argued that the parameter expanded control variates have good asymptotic properties and that the data expanded control variates have the advantage of not requiring a central measure θ^⋆_n of θ. Data expanded control variates also have the advantage of working well over the whole parameter space since they are always evaluated at the proposed θ. Our proposed subsampling MCMC algorithm will therefore begin with the data expanded control variates during a training period and then switch to the parameter expanded control variates once we have learned a reasonable value of θ^⋆_n. This value is set at the end of the training period by computing the geometric median (Vardi and Zhang 2000) of the 10% preceding iterations, which requires evaluating the likelihood over the full dataset once. We include this in our CC.

Although we have argued that the data expanded control variates have poor asymptotic properties for large p, we can still use them with a reasonably small K as the error decreases at the fast rate O(m^{− 2}). Hence, there is no need to make the approximation very accurate by using a large K in relation to n, as this increases the computing cost.

4. Applications

4.1. Empirical Studies

This section performs a number of experiments to compare our proposed algorithms against both standard MCMC, which we call MH and other competing subsampling methods. To compare against other subsampling approaches, we follow Bardenet, Doucet, and Holmes (2017). We compare the standard (independent) PM, the correlated PM and the block correlated PM using the data expanded control variates, since, for our examples, the parameter expanded control variates will give a very small variance once we find a good θ^⋆_n, and hence there are no gains from implementing BPM or CPM compared to PM. However, note that correlating or blocking subsamples is especially useful in the training phase of our algorithm that combines both types of control variates as described in Section 3.7, when we are learning about an appropriate θ^⋆_n, because otherwise the algorithm is likely to get stuck.

4.2. Models and Datasets

We consider three models in our experiments. The first two, which are used for comparing against other subsampling approaches, are AR(1) models with Student-t iid errors ε_t ∼ t(5) with $\text{five}$-degrees of freedom $$\begin{array}{cc}\hfill {\mathrm{M}}_1:& y_t={\beta }_0+{\beta }_1{y}_{t-1}+{ϵ}_t\left[\theta =({\beta }_0=0.3,{\beta }_1=0.6)\right]\\ \hfill {\mathrm{M}}_2:& y_t=\mu +\varrho (y_{t-1}-\mu )+{ϵ}_t\left[\theta =(\mu =0.3,\varrho =0.99)\right]\end{array}$$with priors $$\begin{array}{ccc}\hfill p({\beta }_0,{\beta }_1)& \stackrel{\text{ind.}}{=}& \mathcal{U}\left({\beta }_0\right|-5,5)·\mathcal{U}\left({\beta }_1\right|0,1)\hfill \\ \hfill \text{and}p(\mu ,\varrho )& \stackrel{\text{ind.}}{=}& \mathcal{U}\left(\mu \right|-5,5)·\mathcal{U}(\varrho |0,1),\hfill \end{array}$$where^{Table 1Figure 1}$\mathcal{U}(·|a,b)$ is the uniform density on the interval [a, b]. Model ${\text{M}}_2$, the so called steady state AR, is interesting as ϱ close to 1 gives a weakly identified μ, with a posterior that concentrates very slowly as n increases (Villani 2009). We simulate n = 100, 000 observations from both models.

The third model is the logistic regression $$\begin{array}{ccc}\hfill p\left(y_i\right|x_i,\beta )& =& {\left(\frac{1}{1+exp\left(x_i^T\beta \right)}\right)}^{y_i}{\left(\frac{1}{1+exp(-x_i^T\beta )}\right)}^{1-y_i},\hfill \\ \hfill \text{with}p\left(\beta \right)& =& \mathcal{N}\left(\beta \right|0,10I),\hfill \end{array}$$which we fit to three datasets. The first dataset concerns firm bankruptcy with $n=4\text{,}748\text{,}089$ observations with firm default as the response variable and eight firm-specific and macroeconomic covariates (p = 9 with intercept); see Giordani et al. (2014) for details. We use this dataset to study the different proposals for u with two proposals for θ, the random walk MH and the independence MH. The second dataset is the well known HIGGS data (Baldi, Sadowski, and Whiteson 2014) with the response “detected particle” explained by 21 covariates consisting of kinematic properties measured by particle detectors (we exclude high-level features for simplicity). From the 11 million observations, we use a subset of n =1,100,000 observations. The third dataset is Cover Type (Covtype), which was originally a classification problem with seven classes. We follow Collobert et al. (2002) and Bardenet, Doucet, and Holmes (2017) and transform it into a binary classification problem. The dataset consists of $n=550\text{,}087$ observations and p = 11 variables, after removing the qualitative variables for simplicity. We use these three datasets to benchmark our proposed subsampling MCMC algorithm in Section 3.7 against standard MCMC using a random walk MH proposal.

4.3. Experiment 1: Comparing Different Proposals for u

The first comparison between the different proposals for u uses the logistic regression with the Bankruptcy dataset described in Section 4.2. Since there are relatively few observations corresponding to bankruptcy (y_i = 1) (41,566 defaults), we only subsample the observations with y_k = 0, that is, the first term in $$\begin{array}{ccc}\hfill \ell \left(\theta \right)& =& \sum _{i:y_i=1}{\ell }_i\left(\theta \right)+\sum _{i:y_i=0}{\ell }_i\left(\theta \right),\hfill \end{array}$$is always evaluated (and included in the CC).

The tuning parameters m and K are determined by optimizing the CT in (13(13) $${\mathrm{CT}}_{(m,K)}\left({\sigma }_{LL,m,n}^2\left(K\right)\right):=\mathrm{IF}\left({\Lambda }_{(m,n)}^2\left(K\right)\right)\times (\omega K+m).$$(13) ) with respect to m and K, with $${\sigma }_{LL,m,n}^2\left(K\right)=\frac{n^2{\sigma }_{d,n}^2\left(K\right)}{m}.$$We estimate the relation σ²_{d, n}(K) = C₀K^ν for each example by running the clustering algorithm on a grid of K and for each value of the grid we compute σ²_{d, n} at the MLE θ^⋆_n. Given C₀ and ν, it is straightforward to use the expression for the IF in Pitt et al. (2012) (PM) and Tran et al. (2017) (block PM) to minimize CT_{(m, K)} in (13(13) $${\mathrm{CT}}_{(m,K)}\left({\sigma }_{LL,m,n}^2\left(K\right)\right):=\mathrm{IF}\left({\Lambda }_{(m,n)}^2\left(K\right)\right)\times (\omega K+m).$$(13) ) and obtain m_opt and K_opt and the corresponding ${\sigma }_{\mathrm{opt}}^2={\sigma }_{LL,m_{\mathrm{opt}},n}^2\left(K_{\mathrm{opt}}\right)$. The correlated PM uses m_opt^⋆ = m_opt and the same value of K_opt as the block correlated PM. Table 1 summarizes the settings for comparing the proposals for u, including the settings for the AR example in Section 4.4. Finally, we set G = 100 (ρ_G = 0.99) for the block PM and φ = 0.9999 (κ = 0.9863) for the correlated PM.

Table 1. Experimental settings for comparing proposals for u in the applications.

Example	n	Proposal	100mopt/n	100Kopt/n	σLL, opt^2
Logistic	4.7 × 10^6	RWM/IMH
Uncorr			8.615	4.967	0.27
Block/Corr			1.286	0.485	56.89
AR(1): M1	10^5	RWM
Uncorr			1.896	2.464	0.11
Block/Corr			0.757	0.993	12.41
AR(1): M2	10^5	RWM
Uncorr			4.561	8.192	0.11
Block/Corr			2.151	3.176	12.40

n is the number of observation. The proposals are the random walk metropolis (RWM) $q\left(\theta \right|{\theta }_c)=\mathcal{N}\left(\theta \right|{\theta }_c,{\Sigma }_{{\theta }_n^{★}})$ and the Independent MH (IMH) $q\left(\theta \right)=t_{10}\left(\theta \right|{\theta }_n^{★},{\Sigma }_{{\theta }_n^{★}})$, where the location parameter is θ^⋆_n is the posterior mode and ${\Sigma }_{{\theta }_n^{★}}$ is the negative inverse Hessian of the log-posterior evaluated at θ^⋆_n, both obtained from an initial numerical optimization. We denote the optimal sample size and number of clusters by m_opt and K_opt, and ${\sigma }_{LL,\text{opt}}^2$ is the corresponding optimal variance of the log-likelihood estimate. We use $N=50\text{,}000$ iterates after discarding 5000 iterates as burn-in.

Figure 1 shows^{Figure 2Table 2}the sampling efficiency of the PM algorithms with the different proposals for u relative to that of the MH algorithm on the full dataset as measured by the relative computational time (RCT) defined, for any base sampler $\mathcal{A},$ as ${\mathrm{CT}}_{\mathrm{MH}}/{\mathrm{CT}}_{\mathcal{A}}$. The figure also shows the relative if (RIF) , which is defined as $\mathrm{IF}{}_{\mathcal{A}}/{\mathrm{IF}}_{\mathrm{MH}}$, where each IF is estimated using the $\mathtt{coda}$ package in R (Plummer et al. (2006). The figure shows that both the correlated and block PM schemes significantly outperform standard independent PM and also the MH algorithm applied to the full dataset with respect to RCT. Figure 2 plots the kernel density estimates (KDE) of the posterior densities of the parameters for the three PM schemes and the exact MH approach. The figure shows that targeting a large σ²_{LL, m, n} (≈ 56) for the block correlated and correlated PM samplers results in a very small bias in this application, with the proportional approximation error in (11(11) $$\frac{{\pi }_{(m,n)}\left(\theta \right)-{\pi }_{\left(n\right)}\left(\theta \right)}{{\pi }_{\left(n\right)}\left(\theta \right)}=\frac{exp\left({\Gamma }_{(m,n)}\left(\theta \right)\right)}{{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left(exp\left({\Gamma }_{(m,n)}\right)\right)}-1$$(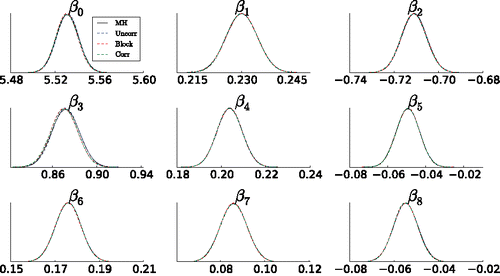11) ) being − 0.01 for both the block correlated and correlated PM and − 0.0001 for the standard PM.

Figure 1. Logistic regression for firm bankruptcy. For algorithm $\mathcal{A}$ (uncorrelated (Uncorr), block (Block) and correlated (Corr) PM) the figure shows the relative inefficiency factors (RIF) and relative computational time for RWM proposal (left panel) and IMH (right panel). For RCT, the filled (dashed) bar correspond to ω = 3 (ω = 1) in (13(13) $${\mathrm{CT}}_{(m,K)}\left({\sigma }_{LL,m,n}^2\left(K\right)\right):=\mathrm{IF}\left({\Lambda }_{(m,n)}^2\left(K\right)\right)\times (\omega K+m).$$(13) ).

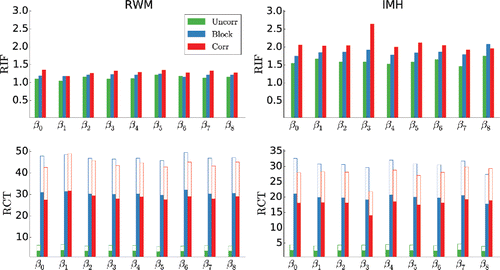
Figure 2. Logistic regression example. Kernel density estimates of marginal posteriors obtained by the IMH proposal. The figure shows the marginal posteriors obtained using the uncorrelated (Uncorr), block (Block) and correlated (Corr) PM (dashed blue, red, and green, respectively) and MH (solid black line).

4.4. Experiment 2: Comparison Against Other Subsampling Approaches

We compare our algorithm against the approximate algorithms austerity MH (Korattikara, Chen, and Welling 2014), the confidence sampler (Bardenet, Doucet, and Holmes 2014), the confidence sampler with control variates (Bardenet, Doucet, and Holmes 2017), and the exact algorithm Firefly Monte Carlo (Maclaurin and Adams 2014). See Bardenet, Doucet, and Holmes (2017) for an excellent discussion of these algorithms.

We follow Bardenet, Doucet, and Holmes (2017) in setting the tuning parameters of the competing algorithms, with the following exceptions. First, we adapt during the burn-in phase to reach an acceptance probability of α = 0.35 (instead of α = 0.50), which is optimal for RWM with two parameters (Gelman, Roberts, and Gilks 1996). For the PMs we use α = 0.15 as in the five-parameter example by Sherlock et al. (2015). Second, the p-value of the t-test in the Austerity MH algorithm is set to ε = 0.01 (instead of ε = 0.05) to put the approximation error of the method on par with the other methods. Setting ε = 0.05 gives an unusably poor approximation (and also produces a much lower RCT than our methods). Additionally, the confidence sampler with proxies (from a Taylor series approximation with respect to θ) requires that the third derivative can be bounded uniformly for every observation and any θ. This bound is achieved by computing on a θ-grid, where the posterior mass is located (this extra CC is not included in the total cost here).

Table 2 shows the mean of the sampling fraction over MCMC iterations. We note that both confidence samplers and the Austerity MH estimate the numerator and denominator in each iteration, and therefore require twice as many evaluations in a given iteration as MCMC (in some cases evaluations from the previous iteration can be reused). It is clear that our algorithms makes very efficient use of a small subsample, especially the block and correlated PM samplers.

Table 2. AR-process example.

	MH	Uncorr	Block	Corr	Conf	ConfProxy	AustMH	Firefly
M1	1.000	0.093	0.037	0.037	1.493	0.160	1.037	0.100
M2	1.000	0.291	0.117	0.116	1.490	1.500	1.019	0.137

Mean of sampling fraction f = m/n over MCMC iterations for models M₁ and M₂ with MH (using the full dataset), uncorrelated PM (Uncorr), block PM (Block) and correlated PM (Corr), confidence sampler (Conf), confidence sampler with proxies (ConfProxy), Austerity MH (AustMH), and Firefly Monte Carlo (Firefly).

Figures 3 and 4 show the marginal posteriors obtained by, respectively, alternative sampling approaches and the various PM approaches. Moreover, the figures show the sampling efficiency of the different subsampling MCMC algorithms relative to that of the MH algorithm as measured by the RCT. Figure 3 shows the striking result that many of these approaches are not more efficient than MH on the whole dataset. The PM algorithms (and also the confidence samplers) provide excellent approximations: indeed, the perturbation error in (11(11) $$\frac{{\pi }_{(m,n)}\left(\theta \right)-{\pi }_{\left(n\right)}\left(\theta \right)}{{\pi }_{\left(n\right)}\left(\theta \right)}=\frac{exp\left({\Gamma }_{(m,n)}\left(\theta \right)\right)}{{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left(exp\left({\Gamma }_{(m,n)}\right)\right)}-1$$(11) ) is less than 10^{− 6} for all our methods. Firefly Monte Carlo, although being an exact algorithm, is highly inefficient in this example, as also documented in Bardenet, Doucet, and Holmes (2017). In fact, for M₂, we were unable to obtain a single effective sample out of $55\text{,}000$ iterations, and hence it was impossible to construct a KDE in this case.

Figure 3. AR-process example: Results for other subsampling algorithms. The left and right panels, respectively, show the results for models M₁ and M₂. Each column shows the kernel density estimates of marginal posteriors (top two) and for algorithm $\mathcal{A}$ (confidence sampler (Conf), confidence sampler with proxies (ConfProxy), Austerity MH (AustMH), and Firefly Monte Carlo (Firefly)) the relative computational time (RCT) (bottom).

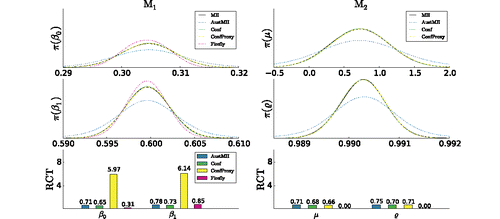
Figure 4. AR-process example: Results for subsampling PM algorithms. The left and right panels, respectively, show the results for models M₁ and M₂. Each column shows the kernel density estimates of marginal posteriors (top two) and for algorithm $\mathcal{A}$ (uncorrelated (Uncorr), block (Block) and correlated (Corr) PM) the relative computational time (RCT) (bottom). For RCT, the filled (dashed) bar correspond to ω = 3 (ω = 1) in (13(13) $${\mathrm{CT}}_{(m,K)}\left({\sigma }_{LL,m,n}^2\left(K\right)\right):=\mathrm{IF}\left({\Lambda }_{(m,n)}^2\left(K\right)\right)\times (\omega K+m).$$(13) ).

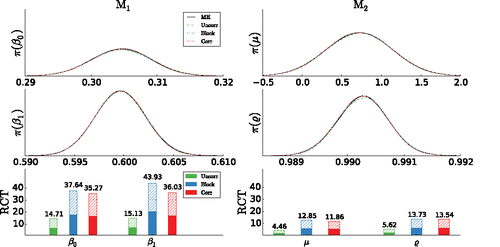
We conclude that the only viable subsampling MCMC approaches are the confidence sampler with proxies (Bardenet, Doucet, and Holmes 2017) and the PM approaches we propose. Moreover, a significant speed up is only obtained with the correlated PMs (both correlated and block).

4.5. Experiment 3: Subsampling MCMC versus MCMC

Our final experiment compares standard MCMC against our algorithm with a combination of control variates based on expanding θ and z as described in Section 3.7. We use a random walk proposal with a scaled covariance matrix evaluated at a θ^⋆_n obtained from optimizing the posterior based on 0.1% of the data. The same value is used as a starting value for the algorithms. The scaling factor is $2.38/\sqrt{p}$ for MCMC (Roberts, Gelman, and Gilks 1997) and $2.5/\sqrt{p}$ for subsampling MCMC (Sherlock et al. 2015). We set the training period (see Section 3.7) to 5000 iterations and sample $50\text{,}000$ draws thereafter. Our algorithm uses the block PM for updating u, where we set m and K following Section 4.3. After the training period, we reset m as the initial m is now too large (since the control variates based on θ now give an accurate approximation). We set the new value to m = 1000, which is sensible for block PM with G = 100.

Figure 5 shows the RCT for each of the datasets. Significant speed ups are achieved by switching to the parameter expanded control variates once a sensible value of θ^⋆_n is found. Finally, Table 3 shows some statistics of the absolute proportional error in the perturbed posterior in (11(11) $$\frac{{\pi }_{(m,n)}\left(\theta \right)-{\pi }_{\left(n\right)}\left(\theta \right)}{{\pi }_{\left(n\right)}\left(\theta \right)}=\frac{exp\left({\Gamma }_{(m,n)}\left(\theta \right)\right)}{{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left(exp\left({\Gamma }_{(m,n)}\right)\right)}-1$$(11) ) over 100 MCMC iterations. It is evident that the perturbed posterior is very accurate, a result that we also confirm graphically by inspecting KDE estimates of marginal posteriors (not shown here).

Figure 5. Subsampling MCMC versus MCMC. The figure shows relative computational time (RCT) for different datasets. The RCT over the parameters are summarized by the minimum (green), median (blue), and maximum (red). The PM algorithm combines the control variates based on expanding θ and z as described in Section 3.7 and use block proposals for u. The filled (dashed) bars correspond to the lower (upper) bound of the computational cost discussed in Section 2.3.

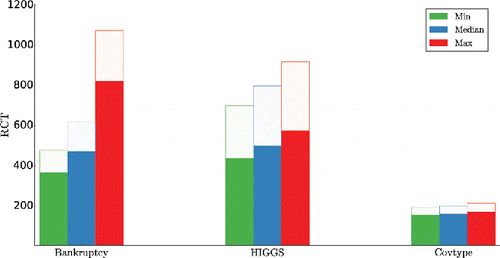
Table 3. Subsampling MCMC versus MCMC.

	Mean	Max	50%	75%	95%
Bankruptcy	1.418 × 10^− 6	1.243 × 10^− 5	1.246 × 10^− 6	1.255 × 10^− 6	2.284 × 10^− 6
HIGGS	8.594 × 10^− 8	7.104 × 10^− 7	7.730 × 10^− 8	7.823 × 10^− 8	9.072 × 10^− 8
Covtype	5.136 × 10^− 8	2.358 × 10^− 6	8.207 × 10^− 9	8.324 × 10^− 9	1.853 × 10^− 7

The table shows the mean, max, and 50, 75, 99% quantiles of the absolute error in (11(11) $$\frac{{\pi }_{(m,n)}\left(\theta \right)-{\pi }_{\left(n\right)}\left(\theta \right)}{{\pi }_{\left(n\right)}\left(\theta \right)}=\frac{exp\left({\Gamma }_{(m,n)}\left(\theta \right)\right)}{{\mathrm{E}}_{{\pi }_{\left(n\right)}}\left(exp\left({\Gamma }_{(m,n)}\right)\right)}-1$$(11) ) computed using 100 draws from the perturbed posterior distribution. The results are shown for the Bankruptcy, HIGGS, and Covtype datasets.

5. Conclusions and Future Research

We propose a framework for speeding up MCMC by data subsampling for datasets with many independent units. At each MCMC iteration, we use two types of control variates to estimate the log of the likelihood unbiasedly and efficiently using only a small random fraction of the data. This results in a PM sampling scheme with a slightly perturbed posterior. We also use two correlated sampling schemes to improve the mixing of the Markov chain. We show that by taking $m=O\left(n^{\frac{1}{2}}\right)$, the total variation norm of the error in the perturbed posterior is O(n^{− 2}) if we have access to the MLE based on all data for constructing the control variates, or $O\left(n^{-\frac{1}{2}}\right)$ if the MLE is based on a subset with $\tilde{n}=O\left(n^{\frac{1}{2}}\right)$ observations. We also show (more heuristically) as well as empirically that in regions of high concentration of the posterior the proportional perturbation error of the posterior is extremely small and much smaller than the corresponding error in the likelihood. Finally, we document large speed ups relative to MCMC using all the data and show that our method outperforms other recent subsampling approaches in the literature.

If we change the PM sampling scheme to a Metropolis-within-Gibbs one where we generate the u conditional on θ and then θ conditional on u, then we can obtain exact derivatives of the log of the estimated likelihood. That means that the subsampling approach can use efficient proposals such as those based on Gibbs sampling, Laplace approximations, and Langevin diffusions and so can readily scale up in terms of the number of unknown parameters. A recent example using Hamiltonian Monte Carlo (Dang et al. (2017) demonstrates that our approach can scale to larger dimensional problems.

One immediate application of our methods will be to problems where computing the density of each data unit is very expensive, although the number of data units is not necessarily large. This may be the case when latent variables are present so the density of each observation is an integral.

Supplementary Material

The online supplementary materials contain implementation details, proofs, and displaying how our theory applies to generalized linear models.

Acknowledgments

The authors thank the Reviewers and the Associate Editor for helping to improve both the content and the presentation of the article. We also thank the authors in Bardenet et al. (2017) for making their code publicly available, which facilitated the comparison against other subsampling approaches, and David Frazier for a useful discussion on the Bernstein-von Mises result.

Additional information

Funding

Matias Quiroz and Robert Kohn were partially supported by Australian Research Council Center of Excellence grant CE140100049. Quiroz was also partially supported by VINNOVA grant 2010-02635. Mattias Villani was partially financially supported by Swedish Foundation for Strategic Research (Smart Systems: RIT 15-0097). Minh-Ngoc Tran was partially supported by a Business School Pilot Research grant. Quiroz carried out part of the work while affiliated with Sveriges Riksbank, Linköping University and Stockholm University.