Simultaneous Inference for Empirical Best Predictors With a Poverty Study in Small Areas

Abstract

Today, generalized linear mixed models (GLMM) are broadly used in many fields. However, the development of tools for performing simultaneous inference has been largely neglected in this domain. A framework for joint inference is indispensable to carry out statistically valid multiple comparisons of parameters of interest between all or several clusters. We therefore develop simultaneous confidence intervals and multiple testing procedures for empirical best predictors under GLMM. In addition, we implement our methodology to study widely employed examples of mixed models, that is, the unit-level binomial, the area-level Poisson-gamma and the area-level Poisson-lognormal mixed models. The asymptotic results are accompanied by extensive simulations. A case study on predicting poverty rates illustrates applicability and advantages of our simultaneous inference tools.

Keywords:

• EBP
• Generalized mixed models
• Mixed parameters
• Small area estimation
• Uniform inference

1 Introduction

Generalized linear mixed models (GLMM) are suitable for modeling clustered and correlated data with categorical or count outcomes. They are ubiquitous in applied statistics, for example, in biometrics or small area estimation (SAE). In the latter, they serve to analyze surveys on a disaggregated level. Despite an increasing interest, for example, to guide resource allocation, the development of methods for simultaneous inference for predictors is missing. It is surprising as only those would make joint considerations of clusters valid. Available $(1-\alpha )$-confidence intervals (CI) for mixed parameters (except the credibility intervals of Ganesh 2009) are constructed such that for each study at least $\alpha 100\%$ of them do not contain the true value. Undoubtedly, practitioners do compare, but so far without valid statistical tools. We aim to close this distressing gap, not to improve any existing method.

Specifically, we introduce simultaneous confidence interval (SCI) and multiple test procedure (MTP) for the empirical best predictor (EBP) of Jiang (2003). They are based on max-type statistics combined with extreme value theory. We prove asymptotic convergence of SCI and MTP for nested (or hierarchical) GLMM within the exponential family. We study the numerical performance of our SCI and MTP for two area-level and one unit-level mixed models that are widely used, for example, for studying local poverty rates (Pratesi 2016). All introduced methods show a satisfactory performance within considered modeling frameworks. Even though our estimates under the area-level models appear to be less volatile, one can argue that EBPs are not directly comparable because different methods and model classes are used. Finally, under area-level Poisson-gamma model, we derive a new mean squared error (MSE) estimator which is of crucial interest in SAE.

The amount of literature on estimation and testing under GLMM is considerable, see, i.a., the review of Tuerlinckx et al. (2006), the monograph of Jiang (2007), and the article of Ghosh et al. (1998) which is particularly interesting within the context of SAE. Furthermore, researchers put forward several methodologies broadly used in the analysis of count data. Molina, Saei, and Lombardía (2007) and Scealy (2010) studied the estimation of labor force status using multinomial logistic models, whereas Saei and Taylor (2012) focused on the same target parameter, and examined the performance of a bivariate random components model. Chandra, Chambers, and Salvati (2012) and Franco and Bell (2015) provided extensions for modeling proportions using logistic unit- and area-level models. Hobza and Morales (2016) implemented the EBP for unit-level, and Boubeta, Lombardía, and Morales (2016) for area-level GLMM to study poverty in small areas. Chambers, Salvati, and Tzavidis (2012) and Tzavidis et al. (2015) extended the M-quantile inference for robust estimation and prediction of count data. Yet, to the best of our knowledge, no one addresses the issue of simultaneous inference for clusters-level parameters when applying GLMM. Likewise, little research has been carried out on simultaneous inference for cluster level parameters in linear mixed effects models (LMM). Ganesh (2009) developed credibility intervals for a mixed parameter in a particular area-level model. Reluga, Lombardía, and Sperlich (2019) proposed bootstrap SCI and MTP for mixed parameter under LMM, whereas Kramlinger, Krivobokova, and Sperlich (2018) developed a framework for marginal and conditional inference with quadratic forms.

After an introduction of a model and estimators in Section 2, we propose the construction of SCI and MTP for a general EBP, followed by the theoretical justifications in Section 3. Sections 4 and 5 present simulations and a case study. Conclusions are drawn in Section 6. More details are deferred to appendix and our supplementary material (SM).

2 Best Prediction for GLMM

Let D be the number of clusters or areas with $d\in [D]$, n_d the number of sampled units in each area $j\in [n_d]$ with $n={\sum }_{d=1}^D{n}_d$, N_d the known population sizes with $N={\sum }_{d=1}^D{N}_d,[A]=\{1,\dots ,A\}$. Since in our context the notion of cluster and area can be used synonymously, we proceed with the latter. Suppose that $\{v_d:d=1,\dots ,D\}$ is a set of independent and identically distributed (iid) random effects with unknown variance ${\delta }^2,\delta >0$, which is often parameterized as $v_d=\delta u_d$ with $u_d\sim N(0,1)$. The target variable y_dj represents the jth sample observation from the dth area. Furthermore, we consider nested data structures such that $y_{dj}\ne y_{d\prime j}$ for $d\ne d\prime$. In full generalization, we assume that random variables Y_dj, conditionally on a random effect u_d, are independent with a probability density function (pdf) from the exponential family $y_{dj}|u_d\sim \hspace{0.17em}\text{Exp}\hspace{0.17em}.\text{Family}(\mathit{\theta })$ $$\begin{array}{c}{y}_{dj}|u_d\sim \text{indep}.g_{Y_{dj}|u_d}(y_{dj}|u_d),\\ g_{dj}(y_{dj}|u_d,\mathit{\theta })=\hspace{0.17em}\text{exp}\hspace{0.17em}\{{\phi }^{-1}[y_{dj}{\gamma }_{dj}-b({\gamma }_{dj})]+c(y_{dj},\phi )\},\end{array}$$where $\mathit{\theta }={({\mathit{\beta }}^t,\delta ,\phi )}^t$ with δ the variability parameter, $\mathit{\beta }={({\beta }_1,\dots ,{\beta }_p)}^t$ regression parameters of auxiliary variables ${\mathit{x}}_{dj}={(x_{dj1},\dots ,x_{\mathit{djp}})}^t$ for which typically $x_{dj1}=1,\forall j\in [n_d] \forall d\in [D]$, and γ_dj, $\phi$ are canonical and scale parameters, respectively. Link function M relates $\mathbb{E}(Y_{dj}|u_d)$ to a linear mixed model such that ${\gamma }_{dj}=M\{\mathbb{E}(Y_{dj}|u_d)\}={\mathit{x}}_{dj}^t\mathit{\beta }+\delta u_d$.

2.1 Estimation and Computation

Let ${\mathit{y}}_d={(y_{d1},\dots ,y_{d{n}_d})}^t$ for all $d\in [D]$ be the vector of outcomes, and $\mathit{y}={({\mathit{y}}_1^t,\dots ,{\mathit{y}}_D^t)}^t$. A conditional pdf of y and the likelihood contribution from each area d are given by(1) $$\begin{array}{c}{\mathcal{L}}_d(\mathit{\theta }):=f_d({\mathit{y}}_d|\mathit{\theta })=\int g_d({\mathit{y}}_d|u_d,\mathit{\theta })h(u_d)\mathrm{d}{u}_d\\ =\int \prod _{j=1}^{n_d}{g}_{dj}(y_{dj}|u_d,\mathit{\theta })h(u_d)\mathrm{d}{u}_d,\end{array}$$(1) where $\mathit{\theta }$ can be derived from$$\mathcal{L}(\mathit{\theta }):=\prod _{d=1}^D{\mathcal{L}}_d(\mathit{\theta })=\prod _{d=1}^D\int \prod _{j=1}^{n_d}{g}_{dj}(y_{dj}|u_d,\mathit{\theta })h(u_d)\mathrm{d}{u}_d.$$

In case of area-level models, n_d = 1, and Equation (1)(1) $$\begin{array}{c}{\mathcal{L}}_d(\mathit{\theta }):=f_d({\mathit{y}}_d|\mathit{\theta })=\int g_d({\mathit{y}}_d|u_d,\mathit{\theta })h(u_d)\mathrm{d}{u}_d\\ =\int \prod _{j=1}^{n_d}{g}_{dj}(y_{dj}|u_d,\mathit{\theta })h(u_d)\mathrm{d}{u}_d,\end{array}$$(1) simplifies accordingly. For a concise presentation, we assume that there is a single random effect for each area such that the integral in Equation (1)(1) $$\begin{array}{c}{\mathcal{L}}_d(\mathit{\theta }):=f_d({\mathit{y}}_d|\mathit{\theta })=\int g_d({\mathit{y}}_d|u_d,\mathit{\theta })h(u_d)\mathrm{d}{u}_d\\ =\int \prod _{j=1}^{n_d}{g}_{dj}(y_{dj}|u_d,\mathit{\theta })h(u_d)\mathrm{d}{u}_d,\end{array}$$(1) is one-dimensional. Extensions to multidimensional random effects follow immediately with some changes of notations and more complicated computation. Finding an analytical solution to Equation (1)(1) $$\begin{array}{c}{\mathcal{L}}_d(\mathit{\theta }):=f_d({\mathit{y}}_d|\mathit{\theta })=\int g_d({\mathit{y}}_d|u_d,\mathit{\theta })h(u_d)\mathrm{d}{u}_d\\ =\int \prod _{j=1}^{n_d}{g}_{dj}(y_{dj}|u_d,\mathit{\theta })h(u_d)\mathrm{d}{u}_d,\end{array}$$(1) is difficult unless the integral can be simplified. Often one evaluates the integral numerically by Laplace approximation (LA) (De Bruijn 1981), Gaussian quadrature (GQ) (Naylor and Smith 1982) or adaptive GQ (AGQ) (Pinheiro and Bates 1995). In what follows, we proceed with AGQ as it is a higher order version of LA, that is, it gives smaller approximation errors (Bianconcini 2014). An alternative is the quasi-likelihood (Breslow and Clayton 1993) which suffers from a nondecreasing bias (Tuerlinckx et al. 2006), and the method of moments (Jiang 1998). In addition, researchers considerably advanced in developing methods to compute maximum likelihood (ML) estimators under GLMM. (Jiang 2007, sec. 4.1) proposed an expectation–maximization algorithm, whereas Lele, Nadeem, and Schmuland (2010) developed the so-called data cloning subsequently implemented by Torabi (2012).

Since we consider a prediction problem of possibly nonlinear mixed effects ${\zeta }_d={\zeta }_d(\mathit{\beta },u_d)$, we use the best predictor (BP) $\widetilde{{\zeta }_d}$ in the sense of minimizing the area-specific MSE in Equation (3)(3) $$\begin{array}{c}\text{MSE}({\widehat{\zeta }}_d)=\mathbb{E}\left[{\{{\tilde{\zeta }}_d(\widehat{\mathit{\theta }})-{\zeta }_d\}}^2\right]\\ =\mathbb{E}\left[{\{{\tilde{\zeta }}_d(\widehat{\mathit{\theta }})-{\tilde{\zeta }}_d(\mathit{\theta })\}}^2\right]+\mathbb{E}\left[{\{{\tilde{\zeta }}_d(\mathit{\theta })-{\zeta }_d\}}^2\right]\\ =:g_{2d}+g_{1d},\end{array}$$(3) which is actually the area-specific mean squared prediction error:(2) $$\begin{array}{c}{\tilde{\zeta }}_d=\widetilde{{\zeta }_d}(\mathit{\theta }):=\mathbb{E}\{{\zeta }_d(\mathit{\beta },u_d)|\mathit{y}\}=\mathbb{E}\{{\zeta }_d(\mathit{\beta },u_d)\left|{\mathit{y}}_d\right\}\\ =\frac{\int {\zeta }_d(\mathbf{\beta },u_d)g_d({\mathbf{y}}_d|u_d,\mathbf{\theta })h(u_d)\mathrm{d}{u}_d}{\int g_d({\mathbf{y}}_d|u_d,\mathbf{\theta })h(u_d)\mathrm{d}{u}_d}.\end{array}$$(2)

Simplification of Equation (2)(2) $$\begin{array}{c}{\tilde{\zeta }}_d=\widetilde{{\zeta }_d}(\mathit{\theta }):=\mathbb{E}\{{\zeta }_d(\mathit{\beta },u_d)|\mathit{y}\}=\mathbb{E}\{{\zeta }_d(\mathit{\beta },u_d)\left|{\mathit{y}}_d\right\}\\ =\frac{\int {\zeta }_d(\mathbf{\beta },u_d)g_d({\mathbf{y}}_d|u_d,\mathbf{\theta })h(u_d)\mathrm{d}{u}_d}{\int g_d({\mathbf{y}}_d|u_d,\mathbf{\theta })h(u_d)\mathrm{d}{u}_d}.\end{array}$$(2) is possible by choosing the pdf of u_d accordingly. If we replace $\mathit{\theta }$ by a consistent estimator, then we obtain EBP ${\widehat{\zeta }}_d:={\tilde{\zeta }}_d(\widehat{\mathit{\theta }})$. Note that in order to obtain the consistency for random effects, one needs to assume that $n_d\to \infty$ for each ${\widehat{\zeta }}_d,d=1,\dots ,D$ (Jiang and Lahiri 2001).

Regarding the estimation of the variability of the EBP ${\widehat{\zeta }}_d$, MSE is by far the most popular measure. Well known techniques to estimate MSE are the analytical approximation based on a Taylor expansion (Jiang 2003), and parametric bootstrap approaches (Boubeta, Lombardía, and Morales 2016; Hobza and Morales 2016). Consider the following MSE decomposition:(3) $$\begin{array}{c}\text{MSE}({\widehat{\zeta }}_d)=\mathbb{E}\left[{\{{\tilde{\zeta }}_d(\widehat{\mathit{\theta }})-{\zeta }_d\}}^2\right]\\ =\mathbb{E}\left[{\{{\tilde{\zeta }}_d(\widehat{\mathit{\theta }})-{\tilde{\zeta }}_d(\mathit{\theta })\}}^2\right]+\mathbb{E}\left[{\{{\tilde{\zeta }}_d(\mathit{\theta })-{\zeta }_d\}}^2\right]\\ =:g_{2d}+g_{1d},\end{array}$$(3) which can be derived applying the law of iterated expectations (for details, see Jiang 2003, and our SM). The analytical formulas of MSE estimators are model dependent. Bootstrapping permits to obtain estimators that do not vary with the model assumed. In what follows, we denote with ${\mathbb{E}}^{*}$, $\mathbb{V}{\text{ar}}^{*}$, and ${\text{MSE}}^{*}$, the corresponding bootstrap operators for expected value, variance and MSE and define(4) $$\begin{array}{c}{\text{MSE}}_B^{*}({\widehat{\zeta }}_d)={\mathbb{E}}^{*}\left\{{({\widehat{\zeta }}_d^{*}-{\zeta }_d^{*})}^2\right\}\\ \approx B_1^{-1}\sum _{b_1=1}^{B_1}{\left({\widehat{\zeta }}_d^{*(b_1)}-{\zeta }_d^{*(b_1)}\right)}^2=:{\text{mse}}_B({\widehat{\zeta }}_d),\end{array}$$(4) which is a bootstrap equivalent of Equation (3)(3) $$\begin{array}{c}\text{MSE}({\widehat{\zeta }}_d)=\mathbb{E}\left[{\{{\tilde{\zeta }}_d(\widehat{\mathit{\theta }})-{\zeta }_d\}}^2\right]\\ =\mathbb{E}\left[{\{{\tilde{\zeta }}_d(\widehat{\mathit{\theta }})-{\tilde{\zeta }}_d(\mathit{\theta })\}}^2\right]+\mathbb{E}\left[{\{{\tilde{\zeta }}_d(\mathit{\theta })-{\zeta }_d\}}^2\right]\\ =:g_{2d}+g_{1d},\end{array}$$(3) . In their article, Hall and Maiti (2006) pointed out that (4) tends to underestimate the MSE, and propose a double-bootstrap bias-correction(5) $$\begin{array}{c}{\text{MSE}}_{\text{BC}}^{*}({\widehat{\zeta }}_d)=2{\text{MSE}}_B^{*}({\widehat{\zeta }}_d)-{\text{MSE}}_{B2}^{*}({\widehat{\zeta }}_d)\\ \approx 2{\text{mse}}_B({\widehat{\zeta }}_d)-{\text{mse}}_{B2}({\widehat{\zeta }}_d),\end{array}$$(5) where ${\text{MSE}}_{B2}^{*}({\widehat{\zeta }}_d)$ is the second-stage bootstrap MSE estimator, that is$$\begin{array}{c}{\text{MSE}}_{B2}^{*}({\widehat{\zeta }}_d)={\mathbb{E}}^{**}\left\{{({\widehat{\zeta }}_d^{**}-{\zeta }_d^{**})}^2\right\}\\ \approx B_1^{-1}{B}_2^{-1}\sum _{b_1=1}^{B_1}\sum _{b_2=1}^{B_2}{\left({\widehat{\zeta }}_d^{**(b_1,b_2)}-{\zeta }_d^{**(b_1,b_2)}\right)}^2\\ =:{\text{mse}}_{B2}({\widehat{\zeta }}_d).\end{array}$$

The computation of ${\text{MSE}}_{B2}^{*}({\widehat{\zeta }}_d)$ involves selecting B₂ bootstrap replicates from each first-stage bootstrap sample. In this article we do not aim for a precise estimation of the variability of EBP, but the construction of narrow SCI and reliable MTPs. It turns out that for doing this, the use of an estimate of $g_{1d}$ as in Equation (3)(3) $$\begin{array}{c}\text{MSE}({\widehat{\zeta }}_d)=\mathbb{E}\left[{\{{\tilde{\zeta }}_d(\widehat{\mathit{\theta }})-{\zeta }_d\}}^2\right]\\ =\mathbb{E}\left[{\{{\tilde{\zeta }}_d(\widehat{\mathit{\theta }})-{\tilde{\zeta }}_d(\mathit{\theta })\}}^2\right]+\mathbb{E}\left[{\{{\tilde{\zeta }}_d(\mathit{\theta })-{\zeta }_d\}}^2\right]\\ =:g_{2d}+g_{1d},\end{array}$$(3) yields better results than using an estimate of the entire MSE (see Section 4), similarly as in Chatterjee, Lahiri, and Li (2008) under LMM.

2.2 Popular Examples of GLMM and Their Properties

2.2.1 Poisson-Gamma Area-Level Model

The Poisson-gamma model is widely applied for modeling counts in the presence of overdispersion (see Cameron and Trivedi 2013, Section 4.2.2). Within the SAE context, Chen, Jiang, and Nguyen (2015) investigated the observed best prediction and bootstrap MSE estimation for small area mean counts. Among others, they also consider a Poisson-gamma specification. We propose a different model formulation, focus on the EBP of ${\zeta }_d:={\mu }_d^{\text{PG}}$ and develop a plug-in MSE estimator. Let $y_d|u_d\sim \text{Poiss}({\mu }_d^{\text{PG}})$, $d=1,\dots ,D$, where ${\mu }_d^{\text{PG}}>0,n_d=1 \forall d\in [D]$, with canonical parameter $\text{log}\hspace{0.17em}{\mu }_d^{\text{PG}}={\mathit{x}}_d^t\mathit{\beta }+u_d$, and $w_d:=\hspace{0.17em}\text{exp}\hspace{0.17em}(u_d)\sim \text{Gamma}(\delta ,\delta )$ such that $\mathbb{E}(y_d|u_d)={\mu }_d^{\text{PG}}={\lambda }_d{w}_d=\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{x}}_d^t\mathit{\beta })w_d=\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{x}}_d^t\mathit{\beta }+u_d)$. Since Gamma pdf is conjugate to the Poisson, their mixture yields a negative binomial $y_d\sim NB({\lambda }_d,{\delta }^{-1})$ with likelihood(6) $$\begin{array}{c}{\mathcal{L}}^{\text{PG}}(\mathit{\theta }):=f^{\text{PG}}(\mathit{y}|\mathit{\theta })=\prod _{d=1}^D\frac{\Gamma (y_d+\delta )}{\Gamma (y_d+1)\Gamma (\delta )}\\ \times {\left(\frac{\delta }{\delta +{\lambda }_d}\right)}^{\delta }{\left(\frac{{\lambda }_d}{\delta +{\lambda }_d}\right)}^{y_d},\end{array}$$(6) where $\mathbb{E}(y_d)={\lambda }_d$ and $\mathbb{V}\text{ar}(y_d)={\lambda }_d+{\delta }^{-1}{\lambda }_d^2$. The marginal mean of y_d is the same as in the Poisson case, but the random effect increases the variance. Suppose that this model holds for all areas of population $\mathcal{P}$ of size N partitioned into subpopulations ${\mathcal{P}}_1,{\mathcal{P}}_2,\dots ,{\mathcal{P}}_D$ of sizes $N_1,N_2,\dots ,N_D$. We can show that the BP for counts ${\tilde{\mu }}_d^{\text{PG}}(\mathit{\theta }):=\mathbb{E}({\mu }_d^{\text{PG}}|y_d)$ is(7) $$\begin{array}{c}\mathbb{E}({\mu }_d^{\text{PG}}|y_d)=\frac{{\int }_0^{\infty }{\lambda }_d{w}_{d}g(y_d|w_d)h(w_d)d{w}_d}{{\int }_0^{\infty }g(y_d|w_d)h(w_d)d{w}_d}\\ =\frac{A_d^{\text{PG}}(y_d,\mathit{\theta })}{C_d^{\text{PG}}(y_d,\mathit{\theta })}=\frac{{\lambda }_d(y_d+\delta )}{({\lambda }_d+\delta )}\\ =:{\psi }_d^{\text{PG}}(y_d,\mathit{\theta }).\end{array}$$(7)

Equation (7)(7) $$\begin{array}{c}\mathbb{E}({\mu }_d^{\text{PG}}|y_d)=\frac{{\int }_0^{\infty }{\lambda }_d{w}_{d}g(y_d|w_d)h(w_d)d{w}_d}{{\int }_0^{\infty }g(y_d|w_d)h(w_d)d{w}_d}\\ =\frac{A_d^{\text{PG}}(y_d,\mathit{\theta })}{C_d^{\text{PG}}(y_d,\mathit{\theta })}=\frac{{\lambda }_d(y_d+\delta )}{({\lambda }_d+\delta )}\\ =:{\psi }_d^{\text{PG}}(y_d,\mathit{\theta }).\end{array}$$(7) follows from the conjugation of the Gamma pdf to the Poisson pdf, while$$\begin{array}{c}{A}_d^{\text{PG}}={\int }_0^{\infty }{\lambda }_d{w}_d\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}(-{\lambda }_d{w}_d){\lambda }_d^{y_d}{w}_d^{y_d}{\delta }^{\delta }{w}_d^{\delta -1}\hspace{0.17em}\text{exp}\hspace{0.17em}(-w_d\delta )}{y_d!\Gamma (\delta )}d{w}_d\\ =\frac{{\lambda }_d^{y_d+1}{\delta }^{\delta }\Gamma (y_d+1+\delta )}{\Gamma (\delta )y_d!{({\lambda }_d+\delta )}^{y_d+1+\delta }}.\end{array}$$

The EBP ${\widehat{\mu }}_d^{\text{PG}}$ is obtained by replacing the vector of unknown parameters $\mathit{\theta }$ in Equation (7)(7) $$\begin{array}{c}\mathbb{E}({\mu }_d^{\text{PG}}|y_d)=\frac{{\int }_0^{\infty }{\lambda }_d{w}_{d}g(y_d|w_d)h(w_d)d{w}_d}{{\int }_0^{\infty }g(y_d|w_d)h(w_d)d{w}_d}\\ =\frac{A_d^{\text{PG}}(y_d,\mathit{\theta })}{C_d^{\text{PG}}(y_d,\mathit{\theta })}=\frac{{\lambda }_d(y_d+\delta )}{({\lambda }_d+\delta )}\\ =:{\psi }_d^{\text{PG}}(y_d,\mathit{\theta }).\end{array}$$(7) with a consistent estimator $\widehat{\mathit{\theta }}$. Under the Poisson-gamma model $\phi =1$ and $\mathit{\theta }=(\mathit{\beta },\delta )$. We derive an analytical plug-in MSE estimator to measure the variability of our EBP.

Proposition 1.

Let $\mathbb{V}{\text{ar}}_d(\mathit{\theta })=D\mathbb{E}\{(\widehat{\mathit{\theta }}-\mathit{\theta }){(\widehat{\mathit{\theta }}-\mathit{\theta })}^t\}$. An analytical MSE decomposition with its corresponding practical plug-in estimator are given by(8) $$\begin{array}{c}{\text{MSE}}_{\text{PG}}({\tilde{\mu }}_d^{\text{PG}})=g_{\text{PG}1d}+\frac{1}{D}{c}_d(\mathit{\theta })+o(1/D)\hspace{1em}\text{and}\\ {\text{mse}}_{\text{PG}}({\widehat{\mu }}_d^{\text{PG}})={\widehat{g}}_{\text{PG}1d}+\frac{1}{D}{\widehat{c}}_d(\widehat{\mathit{\theta }}),\end{array}$$(8) (9) $$\begin{array}{c}{g}_{\text{PG}1d}={\kappa }_{1d}(\mathit{\theta })-{\kappa }_{2d}(\mathit{\theta }),\\ {\widehat{g}}_{\text{PG}1d}={\kappa }_{1d}(\widehat{\mathit{\theta }})-{\widehat{\kappa }}_{2d}(\widehat{\mathit{\theta }}),\hspace{1em}d\in \left[D\right],\\ \mathrm{ }\text{with}\mathrm{ }{\kappa }_{1d}(\mathit{\theta })=\frac{{\lambda }_d^2(\delta +1)}{\delta }\hspace{1em}\mathrm{ }\text{and}\mathrm{ }\\ {\kappa }_{2d}(\mathit{\theta })=\sum _{j=0}^{\infty }\frac{{\lambda }_d^2{(j+\delta )}^2}{{({\lambda }_d+\delta )}^2}P(y_d=j),\\ \mathrm{ }\text{as}\mathrm{ }\text{well}\mathrm{ }\text{as}\mathrm{ }{c}_d(\mathit{\theta })=\sum _{j=0}^{\infty }{\left\{\frac{\partial }{\partial \mathit{\theta }}{\psi }_d^{\text{PG}}(y_d,\mathit{\theta })\right\}}^t\\ \times \mathbb{V}{\text{ar}}_d(\mathit{\theta })\left\{\frac{\partial }{\partial \mathit{\theta }}{\psi }_d^{\text{PG}}(y_d,\mathit{\theta })\right\}P(y_d=j).\end{array}$$(9)

${\widehat{c}}_d(\mathit{\theta })$ is a Monte Carlo approximation of $c_d(\mathit{\theta }),{\widehat{\kappa }}_{2d}$ refers to ${\kappa }_{2d}$ with an infinite series truncated at a large term and $\mathit{\theta }$ replaced by $\widehat{\mathit{\theta }}$. To estimate ${\kappa }_{1d}$ we need only the latter.

One can estimate $\mathbb{V}{\text{ar}}_d(\mathit{\theta })$ using any reasonable method. In Section 4 we use bootstrap estimators defined in (24). Details on the derivation of Equations (6)(6) $$\begin{array}{c}{\mathcal{L}}^{\text{PG}}(\mathit{\theta }):=f^{\text{PG}}(\mathit{y}|\mathit{\theta })=\prod _{d=1}^D\frac{\Gamma (y_d+\delta )}{\Gamma (y_d+1)\Gamma (\delta )}\\ \times {\left(\frac{\delta }{\delta +{\lambda }_d}\right)}^{\delta }{\left(\frac{{\lambda }_d}{\delta +{\lambda }_d}\right)}^{y_d},\end{array}$$(6) and (8)(8) $$\begin{array}{c}{\text{MSE}}_{\text{PG}}({\tilde{\mu }}_d^{\text{PG}})=g_{\text{PG}1d}+\frac{1}{D}{c}_d(\mathit{\theta })+o(1/D)\hspace{1em}\text{and}\\ {\text{mse}}_{\text{PG}}({\widehat{\mu }}_d^{\text{PG}})={\widehat{g}}_{\text{PG}1d}+\frac{1}{D}{\widehat{c}}_d(\widehat{\mathit{\theta }}),\end{array}$$(8) are deferred to our SM.

2.2.2 Poisson-Lognormal Area-Level Model

The Poisson-lognormal model has been thoroughly examined by, among others, Cameron and Trivedi (2013), Section 4.2.4, Franco and Bell (2015) and Boubeta, Lombardía, and Morales (2016). For $u_d\sim N(0,1)$, let $y_d|u_d\sim \text{Poiss}({\mu }_d^{\text{PL}}),d=1,\dots ,D$, where ${\mu }_d^{\text{PL}}>0$, n_d = 1 for all $d\in [D]$. In addition, ${\mu }_d^{\text{PL}}={\nu }_d{\rho }_d$, where ν_d is a known size variable and ρ_d a binomial probability. The canonical parameter is $\text{log}\hspace{0.17em}{\mu }_d^{\text{PL}}=\hspace{0.17em}\text{log}\hspace{0.17em}{\nu }_d+{\mathit{x}}_d^t\mathit{\beta }+\delta u_d$ for all $d\in [D]$. Typically ${\zeta }_d:={\rho }_d$ for which we have ${\rho }_d=\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{x}}_d^t\mathit{\beta }+\delta u_d)$ with $\mathit{\theta }=({\mathit{\beta }}^t,\delta )$. In this case, the likelihood is$$\begin{array}{c}{\mathcal{L}}^{\text{PL}}(\mathit{\theta }):=f^{\text{PL}}(\mathit{y}|\mathit{\theta })={(2\pi )}^{-D/2}\\ \prod _{d=1}^D{\int }_{\mathbb{R}}^{}\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}(-{\nu }_d{\rho }_d){\nu }_d^{y_d}\hspace{0.17em}\text{exp}\hspace{0.17em}\{y_d({\mathit{x}}_d^t\mathit{\beta }+\delta u_d)\}}{y_d!}\hspace{0.17em}\text{exp}\hspace{0.17em}\left(\frac{-u_d^2}{2}\right)du.\end{array}$$

Once $\mathit{\theta }$ is estimated, we obtain BPs ${\tilde{\mu }}_d^{\text{PL}},{\tilde{\rho }}_d$, and EBPs ${\widehat{\mu }}_d^{\text{PL}},{\widehat{\rho }}_d$ using the formulas from Boubeta, Lombardía, and Morales (2016). In Section 4.1 we estimate their MSE by bootstrap.

2.2.3 Logit Unit-Level Model

The unit-level logit model is a popular choice for binary responses, comprehensively discussed by Hobza and Morales (2016). Under this setting, $y_{dj}|u_d\sim \text{Bin}(m_{dj},p_{dj}),u_d\sim N(0,1)$ with m_dj a known size parameter for a logistic regression. The natural parameter is $p_{dj}/(1-p_{dj})={\mathit{x}}_{dj}^t\mathit{\beta }+\delta u_d,d\in [D]$, $j\in [n_d]$ where $p_{dj}=\{\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{x}}_{dj}^t\mathit{\beta }+\delta u_d)\}/\{1+\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{x}}_{dj}^t\mathit{\beta }+\delta u_d)\}$. We assume that the unit-level logit model holds for all units of population $\mathcal{P}$ of size N, partitioned into D subpopulations ${\mathcal{P}}_d$ of sizes N_d, $d\in [D]$. Let ${\zeta }_d:={\mu }_d^U={\sum }_{j=1}^{N_d}{p}_{dj}$. As for the Poisson models, we have $\phi =1$ and therefore $\mathit{\theta }=({\mathit{\beta }}^t,\delta )$. The likelihood is given by(10) $$\begin{array}{c}{\mathcal{L}}^U(\mathit{\theta }):=f^U(\mathit{y}|\mathit{\beta },\delta )\\ ={(2\pi )}^{-D/2}\prod _{d=1}^D{\int }_{\mathbb{R}}^{}\hspace{0.17em}\text{exp}\hspace{0.17em}[\sum _{j=1}^{n_d}\hspace{0.17em}\text{log}\hspace{0.17em}\left(\begin{array}{c}{m}_{dj}\\ y_{dj}\end{array}\right)+\sum _{j=1}^{n_d}{y}_{dj}({\mathit{x}}_{dj}^t\mathit{\beta }+\delta u_d)\\ -\frac{u_d^2}{2}-\sum _{j=1}^{n_d}{m}_{dj}\hspace{0.17em}\text{log}\hspace{0.17em}\left\{1+\hspace{0.17em}\text{exp}\hspace{0.17em}\left({\mathit{x}}_{dj}^t\mathit{\beta }+\delta u_d\right)\right\}]\mathrm{d}{u}_d.\end{array}$$(10)

We can proceed with the estimation of the BP ${\tilde{p}}_{dj}(\mathit{\theta })$ and ${\tilde{\mu }}_d^U={\sum }_{j=1}^{N_d}{\tilde{p}}_{dj}$ only if we have access to the information on each population unit. In practice, however, the auxiliary information is available only for the sample units. Then, following the suggestion of Hobza and Morales (2016), we can still estimate the population quantity of interest by using only categorical covariates. Suppose that they take a finite number of values ${\mathit{x}}_{dj}\in \{{\mathit{z}}_1,\dots ,{\mathit{z}}_L\}$ for $d\in [D]$ and $j\in [n_d]$ with ${\mathit{z}}_l$ denoting the resulting covariate class. We then define(11) $$\begin{array}{c}{\overline{\mu }}_d^U=\frac{{\mu }_d^U}{N_d},\hspace{1em}{\mu }_d^U=\sum _{j=1}^{N_d}{p}_{dj}=\sum _{l=1}^L{N}_{dl}{r}_{dl},\hspace{1em}\text{with}\\ r_{dl}=\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{z}}_l\mathit{\beta }+\delta u_d)}{1+\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{z}}_l\mathit{\beta }+\delta u_d)},\end{array}$$(11) where $N_{dl}=\#\{l\in {\mathcal{P}}_d:{\mathit{x}}_{dj}={\mathit{z}}_l\}$ is the known size of class ${\mathit{z}}_l$ in area d. Hobza and Morales (2016) derived BP ${\tilde{\mu }}_d^U(\mathit{\theta })$ and EBP ${\widehat{\mu }}_d^U(\widehat{\mathit{\theta }})$ for ${\mu }_d^U$ as well as for other quantities in Equation (11)(11) $$\begin{array}{c}{\overline{\mu }}_d^U=\frac{{\mu }_d^U}{N_d},\hspace{1em}{\mu }_d^U=\sum _{j=1}^{N_d}{p}_{dj}=\sum _{l=1}^L{N}_{dl}{r}_{dl},\hspace{1em}\text{with}\\ r_{dl}=\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{z}}_l\mathit{\beta }+\delta u_d)}{1+\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{z}}_l\mathit{\beta }+\delta u_d)},\end{array}$$(11) . Due to the computational burden of the analytical estimator, in Section 4.2 we use bootstrap for obtaining an estimate of MSE.

3 Simultaneous Intervals and Multiple Testing

To construct CI for ${\zeta }_d$ that account for the effect of estimates from other areas, we need to find a region ${\mathcal{I}}_{1-\alpha }$ such that $P({\zeta }_d\in {\mathcal{I}}_{1-\alpha }\forall d\in [D])=1-\alpha$. Define(12) $$S_0=\underset{d=1,\dots ,D}{\max }\left|S_{0d}\right|, \text{with} S_{0d}=\frac{{\widehat{\zeta }}_d-{\zeta }_d}{\widehat{\sigma }({\widehat{\zeta }}_d)},\hspace{1em}\forall d\in \left[D\right],\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}$$(12) (13) $$q_{S_0}^{(1-\alpha )}=\inf \{t\in \mathbb{R}:P(S_0 \le t) \ge 1-\alpha \},$$(13) with $\widehat{\sigma }({\widehat{\zeta }}_d)$ being an estimate of the variability of EBP ${\widehat{\zeta }}_d$. We then consider(14) $$\begin{array}{c}\alpha =P\left(\left|{\widehat{\zeta }}_d-{\zeta }_d\right|>q_{S_0}^{(1-\alpha )}\widehat{\sigma }({\widehat{\zeta }}_d) \text{for} \text{some} d\in \left[D\right]\right)\\ =P\left(\underset{d=1,\dots ,D}{\max }\left|\frac{{\widehat{\zeta }}_d-{\zeta }_d}{\widehat{\sigma }({\widehat{\zeta }}_d)}\right|>q_{S_0}^{(1-\alpha )}\right).\end{array}$$(14)

Constructing SCI boils down to the estimation of $q_{S_0}^{(1-\alpha )}$, as one can define then(15) $${\mathcal{I}}_{1-\alpha }^S=\underset{d=1}{\overset{D}{\times }}{\mathcal{I}}_{d,1-\alpha }^S,\hspace{1em}\text{with}\hspace{1em}{\mathcal{I}}_{d,1-\alpha }^S=\left\{{\widehat{\zeta }}_d\pm q_{S_0}^{(1-\alpha )}\times \widehat{\sigma }({\widehat{\zeta }}_d)\right\}\mathrm{},$$(15) where × denotes a generalized Cartesian product. ${\mathcal{I}}_{1-\alpha }^S$ covers all ζ_d with probability $1-\alpha$, that is, its joint confidence level is $1-\alpha$. In contrast, for each $q_{S_{0d}}^{(1-\alpha )}$ defined analogously to $q_{S_0}^{(1-\alpha )}$, with S₀ replaced by $\left|S_{0d}\right|$, individual area CI (iCI) are given by(16) $${\mathcal{I}}_{d,1-\alpha }^{\mathit{iCI}}=\left\{{\widehat{\zeta }}_d\pm q_{S_{0d}}^{(1-\alpha )}\times \widehat{\sigma }({\widehat{\zeta }}_d)\right\}\hspace{1em}\forall d\in \left[D\right].$$(16)

By construction, iCI does not contain ζ_d for at least $100\alpha \%$ of all areas.

Remark 1.

${\mathcal{I}}_{d,1-\alpha }^{\mathit{iCI}}$ is designed to cover ζ_d at an individual confidence level. Consequently, the joint coverage probability of iCIs decreases in a cumulative way for increasing D. This highlights the need to construct SCI. Nevertheless, maintaining $1-\alpha$ simultaneous confidence level of SCI ${\mathcal{I}}_{1-\alpha }^S$ makes its constituents ${\mathcal{I}}_{d,1-\alpha }^S$ wider than corresponding iCIs ${\mathcal{I}}_{d,1-\alpha }^{\mathit{iCI}}$. This is not surprising because ${\mathcal{I}}_{d,1-\alpha }^{\mathit{iCI}}$ and ${\mathcal{I}}_{d,1-\alpha }^S$ were constructed to cover different sets which serve distinct inferential purposes. It is worth mentioning that the length of ${\mathcal{I}}_{d,1-\alpha }^S$ stabilizes as for growing D we observe two opposite trends: the increase of area parameters to cover and the decrease of MSE (see Tables 1 and 3).

Table 1 ECP, AIW, and AIWV of SCI under area-level models.

	Poisson-gamma				Poisson-lognormal
	B	BC	P	G	B	BC
	ECP (in %)				ECP (in %)
D = 26	95.7	95.9	95.8	95.3	95.0	94.6
D = 52	94.7	93.7	94.9	94.6	94.9	94.8
D = 78	94.7	94.8	94.9	94.4	94.9	94.6
	AIW $\times {10}^3$ (AIWV $\times {10}^3$)				AIW $\times {10}^3$ (AIWV $\times {10}^3$)
D = 26	24.4 (0.025)	24.5 (0.028)	24.5 (0.024)	23.9 (0.023)	18.0 (0.003)	18.0 (0.004)
D = 52	30.3 (0.030)	30.3 (0.034)	30.4 (0.029)	29.8 (0.028)	20.7 (0.003)	20.8 (0.004)
D = 78	33.4 (0.027)	33.4 (0.032)	33.5 (0.025)	33.0 (0.024)	21.9 (0.002)	22.0 (0.004)

NOTE: Nominal coverage: 95%.

Table 3 ECP, AIW and AIWV of 95% SCI under the unit-level model.

	ECP (in %)		AIW$\times {10}^3$ (AIWV$\times {10}^3$)
D	B	BC	B	BC
26	94.0	93.0	134.0 (0.193)	135.0 (0.268)
52	93.5	93.0	150.3 (0.139)	150.9 (0.189)
78	92.0	91.5	153.9 (0.125)	155.1 (0.234)

NOTE: Nominal coverage: 95%.

The SCI defined in Equation (15)(15) $${\mathcal{I}}_{1-\alpha }^S=\underset{d=1}{\overset{D}{\times }}{\mathcal{I}}_{d,1-\alpha }^S,\hspace{1em}\text{with}\hspace{1em}{\mathcal{I}}_{d,1-\alpha }^S=\left\{{\widehat{\zeta }}_d\pm q_{S_0}^{(1-\alpha )}\times \widehat{\sigma }({\widehat{\zeta }}_d)\right\}\mathrm{},$$(15) is not operational as the distribution of S₀ is unknown. The problem can be circumvented by bootstrap approximation: for $b_1=1,\dots ,B_1$ set(17) $$S_B^{(b_1)}=\underset{d=1,\dots ,D}{\max }\left|S_{Bd}^{(b_1)}\right|,\hspace{1em}{S}_{Bd}^{(b_1)}=\frac{{\widehat{\zeta }}_d^{*(b_1)}-{\zeta }_d^{*(b_1)}}{{\widehat{\sigma }}^{*(b_1)}({\widehat{\zeta }}_d^{*})},$$(17) and approximate the critical value $q_{S_B}^{(1-\alpha )}=\inf \{t\in \mathbb{R}:P(S_B \le t|(\mathit{y},\mathit{X})) \ge 1-\alpha \},$ by a $[(1-\alpha )B_1+1]$th-order statistic of the $S_B^{(b_1)}$. Then the bootstrap equivalent of Equation (15)(15) $${\mathcal{I}}_{1-\alpha }^S=\underset{d=1}{\overset{D}{\times }}{\mathcal{I}}_{d,1-\alpha }^S,\hspace{1em}\text{with}\hspace{1em}{\mathcal{I}}_{d,1-\alpha }^S=\left\{{\widehat{\zeta }}_d\pm q_{S_0}^{(1-\alpha )}\times \widehat{\sigma }({\widehat{\zeta }}_d)\right\}\mathrm{},$$(15) is(18) $$\begin{array}{c}{\mathcal{I}}_{1-\alpha }^B=\underset{d=1}{\overset{D}{\times }}{\mathcal{I}}_{d,1-\alpha }^B,\hspace{1em}\text{where}\\ {\mathcal{I}}_{d,1-\alpha }^B=\left\{{\widehat{\zeta }}_d\pm q_{S_B}^{(1-\alpha )}\times \widehat{\sigma }({\widehat{\zeta }}_d)\right\}.\end{array}$$(18)

An alternative approach to Equation (12)(12) $$S_0=\underset{d=1,\dots ,D}{\max }\left|S_{0d}\right|, \text{with} S_{0d}=\frac{{\widehat{\zeta }}_d-{\zeta }_d}{\widehat{\sigma }({\widehat{\zeta }}_d)},\hspace{1em}\forall d\in \left[D\right],\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}$$(12) could be to take computationally simpler nonstudentized statistics. Yet, already DiCiccio and Efron (1996) pointed out that the lack of studentization results in slower convergence rates. Since the application of nonstudentized SCI did not yield satisfactory results, we decided not to include them.

Our methodology is also applicable for hypothesis testing. Consider the test problem(19) $$H_0:\mathit{B\zeta }=\mathit{b}\hspace{1em}\text{vs}.\hspace{1em}{H}_1:\mathit{B\zeta }\ne \mathit{b},$$(19)

where $\mathit{B}\in {\mathbb{R}}^{D\prime \times D},D\prime \le D,\mathit{b}\in {\mathbb{R}}^{D\prime }$. We are interested in max-type statistic t_H such that(20) $$\begin{array}{c}{t}_H=\underset{d=1,\dots ,D\prime }{\max }\left|t_{H_d}\right|,t_{H_d}=\frac{{\widehat{\zeta }}_d^H-b_d}{\widehat{\sigma }({\widehat{\zeta }}_d^H)},\\ S_{H_0}=\underset{d=1,\dots ,D\prime }{\max }\left|S_{H_{0}d}\right|,S_{H_{0}d}=\frac{{\widehat{\zeta }}_d^H-{\zeta }_d^H}{\widehat{\sigma }({\widehat{\zeta }}_d^H)},\end{array}$$(20) where ${\mathit{\zeta }}^H={({\zeta }_1^H,\dots ,{\zeta }_{D\prime }^H)}^t=\mathit{B\zeta }\in {\mathbb{R}}^{D\prime }$ with ${\widehat{\mathit{\zeta }}}^H$ being its estimator. One rejects H₀ at the α-level if $t_H \ge q_{H_0}^{(1-\alpha )}$ with $q_{H_0}^{(1-\alpha )}=\inf \{t\in \mathbb{R}:P(S_{H_0} \le t) \ge 1-\alpha \}$.

In practice, we might use such a test to examine differences between area characteristics. Similarly as for SCI, we approximate $q_{H_0}^{(1-\alpha )}$ applying bootstrap to a modified version of statistic S_B, namely(21) $$q_{{\text{BH}}_0}^{(1-\alpha )}=\inf \{t\in \mathbb{R}:P(S_{{\text{BH}}_0} \le t|(\mathit{y},\mathit{X})) \ge 1-\alpha \},$$(21) where $S_{{\text{BH}}_0}$ in the $b_1^{th}$ bootstrap sample is(22) $$S_{{\text{BH}}_0}^{(b_1)}=\underset{d=1,\dots ,D\prime }{\max }\left|S_{{\text{BH}}_{0}d}^{(b_1)}\right|,\hspace{1em}{S}_{{\text{BH}}_{0}d}^{(b_1)}=\frac{{\widehat{\zeta }}_d^{*H(b_1)}-{\zeta }_d^{*H(b_1)}}{{\widehat{\sigma }}^{*}({\widehat{\zeta }}_d^{*H(b_1)})},$$(22) with ${\mathit{\zeta }}^{*H(b_1)}=({\zeta }_1^{*H(b_1)},\dots ,{\zeta }_{D\prime }^{*H(b_1)})=\mathit{B}{\mathit{\zeta }}^{*(b_1)}\in {\mathbb{R}}^{D\prime }$ and ${\widehat{\mathit{\zeta }}}^{*H(b_1)}=({\widehat{\zeta }}_1^{*H(b_1)},\dots ,{\widehat{\zeta }}_{D\prime }^{*H(b_1)})$ its corresponding estimated version.

We provide the consistency of our bootstrap-based CI and tests, as well as asymptotic convergence and coverage probability. Proofs are deferred to Appendix A.2 and A.3. Suppose that $\widehat{\mathit{\theta }}$ is consistent such that $\left|\right|\widehat{\mathit{\theta }}-\mathit{\theta }\left|\right|=O_P(n^{-c})$, c > 0. Since for the GLMM with clustered random effects the log-likelihood can be expressed as the sum of independent random components, the consistency of $\widehat{\mathit{\theta }}$ estimated by ML follows assuming a classical theory. The consistency under a general GLMM had been an open problem for many years until it was solved by Jiang (2013). Bianconcini (2014) and Huber, Ronchetti, and Victoria-Feser (2004) investigated the consistency of $\widehat{\mathit{\theta }}$ once we compute it using AGQ and LA respectively. For our purpose, we need to prove the bootstrap consistency

Proposition 2.

Under Assumptions 1–5 from Appendix A.1 it holds that$$\begin{array}{c}{\mathbb{E}}^{*}(y_{dj}^{*})-\mathbb{E}(y_{dj})=o_{P^{*}}(1),\\ \mathbb{V}{\text{ar}}^{*}({\mathit{y}}_d^{*})-\mathbb{V}\text{ar}({\mathit{y}}_d)={[o_{P^{*}}(1)]}_{n_d\times n_d},\\ \left|\right|{\widehat{\mathit{\theta }}}^{*}-\widehat{\mathit{\theta }}\left|\right|=O_{P^{*}}(n^{-c}).\end{array}$$

Given Proposition 2, we can derive the consistency of ${\mathcal{I}}_{1-\alpha }^B$ based on results from extreme value theory and asymptotic expansions of the standardized statistics using ideas from Chatterjee, Lahiri, and Li (2008). Let us assume $\widehat{\sigma }({\widehat{\zeta }}_d)=\sqrt{{\widehat{g}}_{1d}({\widehat{\zeta }}_d)}$, though similar results are immediate for $\widehat{\sigma }({\widehat{\zeta }}_d)=\sqrt{{\text{mse}}_{(·)}({\widehat{\mu }}_d^{(·)})}$ where $(·)$ stands for different types of estimators. We use $q:=q_{S_0}^{(1-\alpha )}$ where unambiguous, and denote the cumulative distribution function (cdf) of $S_{0d}$ and S_Bd by $G_d(w)=P(S_{0d} \le w)$ and $G_{Bd}(w)=P(S_{Bd} \le w)$. In Appendix A.3 we provide asymptotic expansions for both. Define $(S_{0(d+1)}\dots ,S_{0(2D)})=(-S_{01},\dots ,-S_{0D})$, and observe that $\underset{d=1,\dots ,D}{\max }\left|S_{0d}\right|=\underset{d=1,\dots ,2D}{\max }(S_{01},\dots ,S_{0D},-S_{01},\dots ,-S_{0D})$. From Equation (14)(14) $$\begin{array}{c}\alpha =P\left(\left|{\widehat{\zeta }}_d-{\zeta }_d\right|>q_{S_0}^{(1-\alpha )}\widehat{\sigma }({\widehat{\zeta }}_d) \text{for} \text{some} d\in \left[D\right]\right)\\ =P\left(\underset{d=1,\dots ,D}{\max }\left|\frac{{\widehat{\zeta }}_d-{\zeta }_d}{\widehat{\sigma }({\widehat{\zeta }}_d)}\right|>q_{S_0}^{(1-\alpha )}\right).\end{array}$$(14) , we have(23) $$\begin{array}{c}{\mathcal{T}}_D(q)=P\left(S_0 \le q\right)\\ =P\left(S_{01} \le q,\dots ,S_{0D} \le q,-S_{01} \le q,\dots ,-S_{0D} \le q\right)\\ =\prod _{d=1}^{2D}{G}_d(q).\end{array}$$(23)

As $D\to \infty$, unless standardized, the distribution in Equation (23)(23) $$\begin{array}{c}{\mathcal{T}}_D(q)=P\left(S_0 \le q\right)\\ =P\left(S_{01} \le q,\dots ,S_{0D} \le q,-S_{01} \le q,\dots ,-S_{0D} \le q\right)\\ =\prod _{d=1}^{2D}{G}_d(q).\end{array}$$(23) converges to 0 or 1. In Appendix A.3, we show that $G_d(w)$ is asymptotically normal, such that $P(S_0 \le q)\approx {\Phi }^{2D}(q)$. Since the cdf of the maxima of the standard normal random variables is in the domain of attraction of the Gumbel law, it follows that $\underset{D\to \infty }{\lim }{\Phi }^{2D}(q/b_D+b_D)=\hspace{0.17em}\text{exp}\hspace{0.17em}(\hspace{0.17em}\text{exp}\hspace{0.17em}(-q))={\mathcal{T}}_0(q)$, for all $q\in \mathbb{R}$ where b_D is a sequence of constants (see Leadbetter, Lindgren, and Rootzén 2012, theor.1.5.3). Unfortunately, this approximation has a poor convergence rate, but bootstrap is again a remedy. Notice that a similar representation holds for S_B, substituting P with $P^{*}$ and replacing the true parameters by their estimates. Application of Poyla’s theorem that combines the convergence in distribution with a convergence in $\sup$ norm results in our next proposition.

Proposition 3.

Define ${\mathcal{T}}_D^{*}(w)=P^{*}(S_B \le q)$ which is a bootstrap analogue of ${\mathcal{T}}_D(w)$ in Equation (23)(23) $$\begin{array}{c}{\mathcal{T}}_D(q)=P\left(S_0 \le q\right)\\ =P\left(S_{01} \le q,\dots ,S_{0D} \le q,-S_{01} \le q,\dots ,-S_{0D} \le q\right)\\ =\prod _{d=1}^{2D}{G}_d(q).\end{array}$$(23) . Under Assumptions 1–5 from Appendix A.1 it holds that$$\underset{w\in \mathbb{R}}{\sup }|{\mathcal{T}}_D(w)-{\mathcal{T}}_D^{*}(w)|=o_P(1).$$

Corollary 1.

Proposition 3 implies that under the same assumptions,$$P({\zeta }_d\in {\mathcal{I}}_{1-\alpha }^B \forall d\in [D])\to 1-\alpha .$$

Since we use almost identical max-type statistics in Equations (12)(12) $$S_0=\underset{d=1,\dots ,D}{\max }\left|S_{0d}\right|, \text{with} S_{0d}=\frac{{\widehat{\zeta }}_d-{\zeta }_d}{\widehat{\sigma }({\widehat{\zeta }}_d)},\hspace{1em}\forall d\in \left[D\right],\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}$$(12) and (20)(20) $$\begin{array}{c}{t}_H=\underset{d=1,\dots ,D\prime }{\max }\left|t_{H_d}\right|,t_{H_d}=\frac{{\widehat{\zeta }}_d^H-b_d}{\widehat{\sigma }({\widehat{\zeta }}_d^H)},\\ S_{H_0}=\underset{d=1,\dots ,D\prime }{\max }\left|S_{H_{0}d}\right|,S_{H_{0}d}=\frac{{\widehat{\zeta }}_d^H-{\zeta }_d^H}{\widehat{\sigma }({\widehat{\zeta }}_d^H)},\end{array}$$(20) , the construction of MTP follows almost immediately from the correspondence between tests and CI. In fact, the acceptance region of our test is ${\mathcal{I}}_{1-\alpha }^{H_0}=\underset{d=1}{\overset{D}{\times }}{\mathcal{I}}_{d,1-\alpha }^{H_0}$, where$${\mathcal{I}}_{d,1-\alpha }^{H_0}\mathrm{}=\mathrm{}\left\{{\widehat{\zeta }}_d-q_{S_0}^{(1-\alpha )}\times \widehat{\sigma }({\widehat{\zeta }}_d)\le b_d\le {\widehat{\zeta }}_d+q_{S_0}^{(1-\alpha )}\times \widehat{\sigma }({\widehat{\zeta }}_d)\right\},$$that is, we reject H₀ if $\mathit{b}\notin {\mathcal{I}}_{1-\alpha }^{H_0}$. We can write $P(h_d\in {\mathcal{I}}_{1-\alpha }^{H_0}\forall d\in [D])=1-\alpha$. Since this probability statement is true for any $h_d={\zeta }_d$, we obtain the CI defined in Equation (15)(15) $${\mathcal{I}}_{1-\alpha }^S=\underset{d=1}{\overset{D}{\times }}{\mathcal{I}}_{d,1-\alpha }^S,\hspace{1em}\text{with}\hspace{1em}{\mathcal{I}}_{d,1-\alpha }^S=\left\{{\widehat{\zeta }}_d\pm q_{S_0}^{(1-\alpha )}\times \widehat{\sigma }({\widehat{\zeta }}_d)\right\}\mathrm{},$$(15) by inverting the test.

Corollary 2.

Let H₀ be the null hypothesis defined in Equation (19)(19) $$H_0:\mathit{B\zeta }=\mathit{b}\hspace{1em}\text{vs}.\hspace{1em}{H}_1:\mathit{B\zeta }\ne \mathit{b},$$(19) and $\alpha \in (0,1)$. Under Proposition 3, we have$$P(t_H>q_{{\text{BH}}_0}) \le \alpha +o(1).$$

Remark 2.

Our single-step testing procedure in Equation (19)(19) $$H_0:\mathit{B\zeta }=\mathit{b}\hspace{1em}\text{vs}.\hspace{1em}{H}_1:\mathit{B\zeta }\ne \mathit{b},$$(19) with a bootstrap critical value in Equation (21)(21) $$q_{{\text{BH}}_0}^{(1-\alpha )}=\inf \{t\in \mathbb{R}:P(S_{{\text{BH}}_0} \le t|(\mathit{y},\mathit{X})) \ge 1-\alpha \},$$(21) controls weakly for the family-wise error rate (FWER), and might be limited in detecting false null hypotheses once we deal with a large $D\prime$. Yet, we can readily extend our test to a bootstrap-based step-down procedure of Romano, Shaikh, and Wolf (2008) which controls the false discovery rate with a better power to detect false $H_{0d}$ than FWER.

4 Empirical Reliability Study

We performed intensive simulation studies to assess the reliability of our methods. SCI and MTP for EBP were constructed with different estimators of variability under the models presented in Sections 2.2.1–2.2.3. First, we examined the relative bias and relative root-MSE of fixed effects $\widehat{\mathit{\beta }}$ and variability parameter $\widehat{\delta }$. Then, the performance of EBP was evaluated comparing bias, average absolute bias and MSE for $D=26,52,\text{and}78$. Since they did not show any atypical pattern, the results under Poisson area-level models and logistic unit-level model were deferred to the SM. Regarding SCIs, we calculated empirical coverage probability (ECP), average interval width (AIW), and the AIW variation (AIWV):$$\begin{array}{c}\text{ECP}=\frac{1}{K}\sum _{k=1}^{K}1\{{\zeta }_d^{(k)}\in {\mathcal{I}}_{1-\alpha }^S \forall d\in [D\left]\right\},\\ \text{AIW}=\frac{1}{DK}\sum _{d=1}^D\sum _{k=1}^K{\omega }_d^{(k)},\hspace{1em}{\omega }_d^{(k)}=2q_{(·)}^{(1-\alpha )}{}^{(k)}{\widehat{\sigma }}^{(k)}({\widehat{\zeta }}_d),\\ \text{AIWV}=\frac{1}{D(K-1)}\sum _{d=1}^D\sum _{k=1}^K{\left({\omega }_d^{(k)}-{\overline{\omega }}_d\right)}^2,\\ {\overline{\omega }}_d=\frac{1}{K}\sum _{k=1}^K{\omega }_d^{(k)},\hspace{1em}d=1\dots ,D.\end{array}$$

For each simulation run k we record the widths of the SCI and check whether they cover all EBPs. ECP is then computed by averaging over K simulation runs and is aimed to be close to $1-\alpha$. AIW is obtained by averaging over the simulation runs and areas. Narrower intervals are preferable if its ECP is close to the nominal level. These are standard measures to assess the quality of interval estimators (Chatterjee, Lahiri, and Li 2008; Ganesh 2009). Lower AIWV values indicate that the length is stable and does not depend on the simulation run.

4.1 Finite Sample Performance Under Area-Level Models

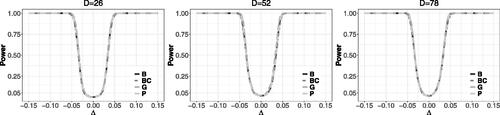
Under the Poisson-gamma model we set $y_d\sim \text{Poiss}({\mu }_d^{\text{PL}}),{\mu }_d^{\text{PL}}={\lambda }_d{w}_d$. Covariates, parameters and sample sizes are taken from our case study in Section 5, that is, we set $\mathit{\theta }=({\mathit{\beta }}^t,\delta )={(10.038,7.747,-3.136,11.317,-2.466,2.480)}^t$, and $D=\{26,52,78\}$, n_d = 1, $\forall d\in [D]$, n = D. For D = 52 we take covariates from the original sample, for D = 26 we randomly select the areas using simple random sampling without replacement, and for D = 78, we take the original sample plus 26 randomly selected areas, that is, these areas enter at most twice. Parameter of interest is the area proportion of individuals below the poverty line, ${\overline{\mu }}_d^{\text{PL}}={\mu }_d^{\text{PL}}/N_d$. The EBP for ${\mu }_d^{\text{PL}}$ is given in Equation (7)(7) $$\begin{array}{c}\mathbb{E}({\mu }_d^{\text{PG}}|y_d)=\frac{{\int }_0^{\infty }{\lambda }_d{w}_{d}g(y_d|w_d)h(w_d)d{w}_d}{{\int }_0^{\infty }g(y_d|w_d)h(w_d)d{w}_d}\\ =\frac{A_d^{\text{PG}}(y_d,\mathit{\theta })}{C_d^{\text{PG}}(y_d,\mathit{\theta })}=\frac{{\lambda }_d(y_d+\delta )}{({\lambda }_d+\delta )}\\ =:{\psi }_d^{\text{PG}}(y_d,\mathit{\theta }).\end{array}$$(7) . Since N_d is usually unknown, in practice it is replaced by its estimate, see Equation (25)(25) $$\begin{array}{c}{\widehat{Y}}_d^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{y}_j,\hspace{1em}{\widehat{N}}_d^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j,\hfill \\ {\widehat{N}}_{dl}^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{\mathit{x}}_j{1}_{\{{\mathit{x}}_j={\mathit{z}}_l\}},\hfill \\ {\widehat{X}}_{di}^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{x}_{ji},\hspace{1em}\text{and}\hspace{1em}{\widehat{\overline{X}}}_{di}^{\text{dir}}={\widehat{X}}_{di}^{\text{dir}}/{\widehat{N}}_d^{\text{dir}},\hfill \end{array}$$(25) in Section 5. We apply double bootstrap with $B_1=1000$ first-stage and $B_2=1$ second-stage bootstrap replicates (the choice of the latter is motivated by Erciulescu and Fuller 2014). We generate K = 1000 samples with the same areas and fixed covariates, but randomly drawn w_d and y_d. SCIs and iCIs are constructed as follows:

1. Fit the model to the data and obtain estimates $\widehat{\mathit{\theta }}=(\widehat{\mathit{\beta }},\widehat{\delta })$.

2. For $b_1=1,\dots ,B_1$ bootstrap samples, generate $w_d^{*(b_1)}\sim \text{Gamma}(\widehat{\delta },\widehat{\delta })$ iid and set$${\mu }_d^{\text{PG}*(b_1)}={\widehat{\lambda }}_d{w}_d^{*(b_1)}\hspace{1em}\text{and}\hspace{1em}{y}_d^{*(b_1)}\sim \text{Poisson}({\mu }_d^{\text{PG}*(b_1)}).$$

3. For each bootstrap sample calculate ${\widehat{\mathit{\theta }}}^{*(b_1)},{\widehat{\mu }}_d^{\text{PG}*(b_1)}({\widehat{\mathit{\theta }}}^{*(b_1)})$, $A{D}_{\text{PG},d}^{(b_1)}=\left|{\widehat{\mu }}_d^{\text{PG}*(b_1)}-{\mu }_d^{\text{PG}*(b_1)}\right|$.

4. For $b_2=1,\dots ,B_2$ generate samples $w_d^{**(b_1,b_2)}\sim \text{Gamma}({\widehat{\delta }}^{*(b_1)},{\widehat{\delta }}^{*(b_1)})$ iid and$$\begin{array}{c}{\mu }_d^{\text{PG}**(b_1,b_2)}={\widehat{\lambda }}_d^{*(b_1)}{w}_d^{**(b_1,b_2)},\\ y_d^{**(b_1,b_2)}\sim \text{Poisson}({\mu }_d^{\text{PG}**(b_1,b_2)}).\end{array}$$

5. For each bootstrap sample calculate ${\widehat{\mathit{\theta }}}^{**(b_1,b_2)}$ and ${\widehat{\mu }}_d^{\text{PG}**(b_1,b_2)}({\widehat{\mathit{\theta }}}^{**(b_1,b_2)})$.

6. Set ${\text{mse}}_d^{(b_1)}=\frac{1}{B_2}{\sum }_{b_2=1}^{B_2}{({\widehat{\mu }}_d^{\text{PG}**(b_1,b_2)}-{\mu }_d^{\text{PG}**(b_1,b_2)})}^2$.

7. Calculate bootstrap estimates ${\widehat{g}}_{\text{PG}1d}({\widehat{\mathit{\theta }}}^{*(b_1)})$ as in Equation (9)(9) $$\begin{array}{c}{g}_{\text{PG}1d}={\kappa }_{1d}(\mathit{\theta })-{\kappa }_{2d}(\mathit{\theta }),\\ {\widehat{g}}_{\text{PG}1d}={\kappa }_{1d}(\widehat{\mathit{\theta }})-{\widehat{\kappa }}_{2d}(\widehat{\mathit{\theta }}),\hspace{1em}d\in \left[D\right],\\ \mathrm{ }\text{with}\mathrm{ }{\kappa }_{1d}(\mathit{\theta })=\frac{{\lambda }_d^2(\delta +1)}{\delta }\hspace{1em}\mathrm{ }\text{and}\mathrm{ }\\ {\kappa }_{2d}(\mathit{\theta })=\sum _{j=0}^{\infty }\frac{{\lambda }_d^2{(j+\delta )}^2}{{({\lambda }_d+\delta )}^2}P(y_d=j),\\ \mathrm{ }\text{as}\mathrm{ }\text{well}\mathrm{ }\text{as}\mathrm{ }{c}_d(\mathit{\theta })=\sum _{j=0}^{\infty }{\left\{\frac{\partial }{\partial \mathit{\theta }}{\psi }_d^{\text{PG}}(y_d,\mathit{\theta })\right\}}^t\\ \times \mathbb{V}{\text{ar}}_d(\mathit{\theta })\left\{\frac{\partial }{\partial \mathit{\theta }}{\psi }_d^{\text{PG}}(y_d,\mathit{\theta })\right\}P(y_d=j).\end{array}$$(9) as well as$$\begin{array}{c}{\text{mse}}_B({\widehat{\mu }}_d^{\text{PG}})=\frac{1}{B_1}\sum _{b_1=1}^{B_1}{\left({\widehat{\mu }}_d^{\text{PG}*(b_1)}-{\mu }_d^{\text{PG}*(b_1)}\right)}^2,\\ {\text{mse}}_{\text{BC}}({\widehat{\mu }}_d^{\text{PG}})=2{\text{mse}}_B({\widehat{\mu }}_d^{\text{PG}})-\frac{1}{B_1}\sum _{b_1=1}^{B_1}{\text{mse}}_d^{(b_1)}.\end{array}$$

8. Calculate statistic $S_{\text{PG},B}$ with the critical value $q_{\text{PG},S_B}^{(1-\alpha )}$ obtained from the bootstrap sample ${\mathit{S}}_{\text{PG},B}={(S_{\text{PG},B}^{(1)},\dots S_{\text{PG},B}^{(B_1)})}^t$, where$$\begin{array}{c}{S}_{\text{PG},B}^{(b_1)}=\underset{d=1,\dots ,D}{\max }A{D}_{\text{PG},d}^{*(b_1)}/{\widehat{\sigma }}^{*(b1)}\left({\widehat{\mu }}_d^{\text{PG}*(b1)}\right)\hspace{1em}\text{and}\\ q_{\text{PG},S_B}^{(1-\alpha )}=Q_{1-\alpha }({\mathbf{S}}_{\text{PG},B})\end{array}$$

as well as a variance estimate for $\widehat{\mathit{\theta }}$:(24) $$\begin{array}{c}\widehat{\text{var}}(\widehat{\mathit{\theta }})=\frac{1}{B_1}\sum _{b_1=1}^{B_1}({\widehat{\mathit{\theta }}}^{*(b_1)}-\overline{\mathit{\theta }}){({\widehat{\mathit{\theta }}}^{*(b_1)}-\overline{\mathit{\theta }})}^t \text{with}\\ \overline{\mathit{\theta }}=\frac{1}{B_1}\sum _{b_1=1}^{B1}{\widehat{\mathit{\theta }}}^{*(b_1)}.\end{array}$$(24)

We compare the performance of SCI and MTP for different variability estimates $\widehat{\sigma }({\widehat{\mu }}_d^{\text{PG}})$ and their bootstrap equivalents ${\widehat{\sigma }}^{*}({\widehat{\mu }}_d^{*\text{PG}})$, namely for $\widehat{\sigma }({\widehat{\mu }}_d^{\text{PG}})=\sqrt{{\widehat{g}}_{\text{PG}1d}}$ and $\widehat{\sigma }({\widehat{\mu }}_d^{\text{PG}})=\sqrt{{\text{mse}}_{(·)}({\widehat{\mu }}_d^{\text{PG}})}$. Here, ${\text{mse}}_{(·)}$ refers to either the plug-in ${\text{mse}}_P$, the ${\text{mse}}_B$ or the ${\text{mse}}_{\text{BC}}$, defined in Equations (8)(8) $$\begin{array}{c}{\text{MSE}}_{\text{PG}}({\tilde{\mu }}_d^{\text{PG}})=g_{\text{PG}1d}+\frac{1}{D}{c}_d(\mathit{\theta })+o(1/D)\hspace{1em}\text{and}\\ {\text{mse}}_{\text{PG}}({\widehat{\mu }}_d^{\text{PG}})={\widehat{g}}_{\text{PG}1d}+\frac{1}{D}{\widehat{c}}_d(\widehat{\mathit{\theta }}),\end{array}$$(8) , (4)(4) $$\begin{array}{c}{\text{MSE}}_B^{*}({\widehat{\zeta }}_d)={\mathbb{E}}^{*}\left\{{({\widehat{\zeta }}_d^{*}-{\zeta }_d^{*})}^2\right\}\\ \approx B_1^{-1}\sum _{b_1=1}^{B_1}{\left({\widehat{\zeta }}_d^{*(b_1)}-{\zeta }_d^{*(b_1)}\right)}^2=:{\text{mse}}_B({\widehat{\zeta }}_d),\end{array}$$(4) , and (5)(5) $$\begin{array}{c}{\text{MSE}}_{\text{BC}}^{*}({\widehat{\zeta }}_d)=2{\text{MSE}}_B^{*}({\widehat{\zeta }}_d)-{\text{MSE}}_{B2}^{*}({\widehat{\zeta }}_d)\\ \approx 2{\text{mse}}_B({\widehat{\zeta }}_d)-{\text{mse}}_{B2}({\widehat{\zeta }}_d),\end{array}$$(5) . Steps 3(a)–(c) of the algorithm refer to the second-stage bootstrap which is only necessary to obtain bias-corrected ${\text{mse}}_{\text{BC}}$. Under the Poisson-gamma model, we are interested in the estimation of poverty rates. We thus consider ${\widehat{\overline{\mu }}}_d^{\text{PG}}={\widehat{\mu }}_d^{\text{PG}}/N_d$, ${\widehat{\overline{g}}}_{\text{PG}1d}={\widehat{g}}_{\text{PG}1d}/N_d^2$ and ${\text{mse}}_{(·)}({\widehat{\overline{\mu }}}_d^{\text{PG}})={\text{mse}}_{(·)}({\widehat{\overline{\mu }}}_d^{\text{PG}})/N_d^2$.

For the Poisson-lognormal model with $y_d\sim \text{Poisson}({\mu }_d^{\text{PL}}),{\mu }_d^{\text{PL}}={\nu }_d{\rho }_d$, the parameter of interest is ρ_d with $N_d={\nu }_d$ estimated by EBP derived by Boubeta, Lombardía, and Morales (2016). We take the fixed parameters from Section 5, that is, $({\mathit{\beta }}^t,\delta )={(-2.264,3.480,-0.870,4.842,0.125,0.322)}^t$. Covariates, sample sizes, number of simulation runs and bootstrap replicates are the same as in case of the Poisson-gamma model. The variability of ${\widehat{\rho }}_d$ was estimated using bootstrap MSEs, that is ${\text{mse}}_B$ and ${\text{mse}}_{\text{BC}}$. To obtain estimates of SCI and iCI one can use almost the same algorithm as above by changing the way we generate $y_d^{*(b_1)}$.

Table 1 summarizes the performance of 95% SCI for ${\widehat{\overline{\mu }}}_d^{\text{PG}}$ constructed with ${\text{mse}}_B$ (B), ${\text{mse}}_{\text{BC}}$ (BC), plug-in ${\text{mse}}_P$ (P) and ${\widehat{g}}_{\text{PG}1d}$ (G). For ${\widehat{\rho }}_d$, they were constructed using ${\text{mse}}_B$ (B) and ${\text{mse}}_{\text{BC}}$ (BC). All methods perform very well regarding the coverage ECP, even for D = 26. In contrast, SCIs constructed using a Bonferroni procedure yield unacceptably low ECP. For instance, for D = 52 and ${\text{mse}}_B$ it equals 78% for the Poisson-gamma, and 88% for the Poisson-lognormal model. Therefore, we do not further report them.

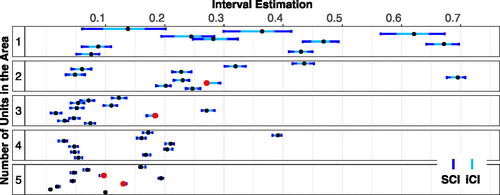
Figure 1 presents 95% SCI and iCI estimates for a randomly selected simulation under the Poisson-gamma model. The plot is divided into five panels according to the number of units ${\widehat{N}}_d^{\mathit{dir}}$ defined in Equation (25)(25) $$\begin{array}{c}{\widehat{Y}}_d^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{y}_j,\hspace{1em}{\widehat{N}}_d^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j,\hfill \\ {\widehat{N}}_{dl}^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{\mathit{x}}_j{1}_{\{{\mathit{x}}_j={\mathit{z}}_l\}},\hfill \\ {\widehat{X}}_{di}^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{x}_{ji},\hspace{1em}\text{and}\hspace{1em}{\widehat{\overline{X}}}_{di}^{\text{dir}}={\widehat{X}}_{di}^{\text{dir}}/{\widehat{N}}_d^{\text{dir}},\hfill \end{array}$$(25) with the first presenting the results for the areas with the fewest observations. The black and red dots represent the true proportions known in a simulation. The color red indicates true parameters not covered by theirs iCIs. In Figure 1, that holds for four of the true values ($\approx 7.7\%$). This illustrates well the difference between individual and simultaneous inference as well as a particular relevance of the latter. We obtain similar figures for other simulations (see our SM).

Fig. 1 95% iCI and SCI for proportions with D = 52. Red dots indicate true parameters outside iCI, whereas black dots indicate true parameters inside their iCI.

Finally, we studied the performance of our test (19) under Poisson-gamma and Poisson-lognormal models. Results for the latter are in our SM as they reveal the same features. Consider $H_0:{\overline{\mathit{\mu }}}^{\text{PG}}=\mathit{b}$ vs. $H_1:{\overline{\mathit{\mu }}}^{\text{PG}}=\mathit{b}+{\mathbf{1}}_D\Delta$, where $\mathit{b}:=\overline{\mathit{\mu }}$ for the same data-generating processes as before. Critical values are obtained from the bootstrap analogues of $S_{H_0}$ calculated similarly as in Step 5 of the algorithm above. Figure 2 shows the power functions of our test based on different variability estimates. They are visibly indistinguishable, which is not surprising given the similar ECPs and AIWs in Table 1. For D = 52, that is, the sample size of the real data, the nominal level of 5% is attained almost exactly under H₀.

Fig. 2 Simulated powers for multiple test $H_0:{\overline{\mathit{\mu }}}^{\text{PG}}=\mathit{b}$ versus $H_1:{\overline{\mathit{\mu }}}^{\text{PG}}=\mathit{b}+{\mathbf{1}}_D\Delta$ under the area-level Poisson-gamma model; (left) D = 26, (middle) D = 52, (right) D = 78.

4.2 Finite Sample Performance Under the Unit-Level Model

Under the unit-level model we assume $y_{dj}\sim \text{Bin}(m_{dj},p_{dj})$ with $p_{dj}=\{\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{x}}_{dj}^t\mathit{\beta }+\delta u_d)\}/\{1+\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{x}}_{dj}^t\mathit{\beta }+\delta u_d)\}$, m_dj = 1, $u_d\sim N(0,1)$. In our context, y_dj is binary and value 1 indicates an individual below the poverty threshold defined in Section 5. The regression parameters are taken from our case study: $\mathit{\theta }=({\mathit{\beta }}^t,\delta )={(-2.048,0.989,0.172,0.760,0.100,0.348)}^t$. Four categorical covariates result in 16 covariate classes ${\mathit{x}}_{dj}\in \{{\mathit{z}}_1,\dots ,{\mathit{z}}_{16}\}$ for which we need to estimate N_dl using Equation (25)(25) $$\begin{array}{c}{\widehat{Y}}_d^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{y}_j,\hspace{1em}{\widehat{N}}_d^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j,\hfill \\ {\widehat{N}}_{dl}^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{\mathit{x}}_j{1}_{\{{\mathit{x}}_j={\mathit{z}}_l\}},\hfill \\ {\widehat{X}}_{di}^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{x}_{ji},\hspace{1em}\text{and}\hspace{1em}{\widehat{\overline{X}}}_{di}^{\text{dir}}={\widehat{X}}_{di}^{\text{dir}}/{\widehat{N}}_d^{\text{dir}},\hfill \end{array}$$(25) , $l=1,\dots ,16$. We considered $D=\{26,52,78\}$ containing unit-level information with $n=\{11423,23628,35818\}$, respectively. Summary statistics for all samples are presented in Table 2. Furthermore, for D = 52, n_d, N_d, ${\mathit{x}}_{dj}$, ${\mathit{z}}_l$ are the same as in our case study. The areas for $D=\{26,78\}$ were selected in the same way as in Section 4.1. In addition, for D = 78, within each of the additional area we sampled with replacement n_d units (i.e., 26 newly sampled areas contained different units in comparison to the original sample). The parameter of interest is the area poverty proportion ${\overline{\mu }}_d^U$ defined in Equation (11)(11) $$\begin{array}{c}{\overline{\mu }}_d^U=\frac{{\mu }_d^U}{N_d},\hspace{1em}{\mu }_d^U=\sum _{j=1}^{N_d}{p}_{dj}=\sum _{l=1}^L{N}_{dl}{r}_{dl},\hspace{1em}\text{with}\\ r_{dl}=\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{z}}_l\mathit{\beta }+\delta u_d)}{1+\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{z}}_l\mathit{\beta }+\delta u_d)},\end{array}$$(11) . Given that the original sample size was n = 23, 628, under the unit-level model we restrict our simulations to K = 200, $B_1=500$, and $B_2=1$. As far as the algorithm for constructing SCI and iCI is concerned, it follows almost the same steps as in Section 4.1. The exact algorithm can be found in the SM.

Table 2 Summary statistics of n_d under different scenarios in the simulation study under the unit-level model.

D = 26						D = 52						D = 78
Min.	Q 1	Q2	Mean	Q3	Max.	Min.	Q1	Q2	Mean	Q3	Max.	Min.	Q1	Q2	Mean	Q3	Max.
47	139	260	439	454	1714	34	108	260	454	479	2631	34	114	289	459	482	2631

Table 3 presents the performance of SCI constructed using ${\text{mse}}_B$ (B) and ${\text{mse}}_{\text{BC}}$ (BC). The coverage probability is somewhat lower than the nominal level. In addition, it slightly decreases with increasing D, whereas the AIW increase stabilizes as expected (see Remark 1). The undercoverage might be related to the simulation design. Even though the latter is popular in SAE, it is suboptimal for random effects from the asymptotic point of view ($n_d\nrightarrow \infty ,d\in [D]$, recall Section 2.1). The results in Table 3 do not demonstrate any inconsistencies with respect to the theoretical developments, nor they exhibit unexpected findings. Due to their limited impact, the equivalents of Figures 1 and 2 for this simulation are deferred to our SM. In comparison to the area-level models, the coverage probability is worse and the average width of SCIs is much larger (it is also the case for the iCI, see our SM). Moreover, fitting unit-level models is computationally more expensive. In our case the estimation of MSE and construction of intervals took about 900–1000 times longer. Since the data-generation processes are different, the numerical results in our simulations are not directly comparable. However, our empirical studies suggest to give some preference to the area-level modeling in the considered GLMM settings.

Our simulations lead us to following conclusions. First, for a given sample size and data, our SCI attains the nominal coverage probability, almost independently from the choice of the estimator of variability. In particular, the area-level models yield very accurate results even for small samples. Second, the distinction between SCI and iCI is crucial, and the latter should not be employed in comparative studies. Third, the numerical performance of our test for comparative studies is satisfying. Given the simplicity of SCI and tests based on $\sqrt{{\widehat{g}}_{1d}}$, we restrict further presentations to them.

Remark 3.

In our simulation study, we do not analyze the performance of direct estimators for proportions, because our goal is to study the numerical performance of our MTP and SCIs, and to compare them to existing iCIs. Since MTP and SCI are the first tools for simultaneous inference with GLMM-based mixed parameter, we concentrate on their implementation and application to the well-known model-based estimators. These have been thoroughly examined in comparative analyses which included direct estimators (see for instance Boubeta, Lombardía, and Morales 2016; Hobza and Morales 2016). In our case study in Section 5, we include direct estimators in order to have an almost model-free benchmark.

5 Predicting Poverty Rates in Galicia

Poverty prediction is of great interest for statistical offices. It provides a basis on which local or central authorities can decide about resource allocation and related polices. The interest is not in individual, randomly chosen small areas but in the total picture. Resource distribution requires comparative statistics, and one would thus provide SCI instead of iCI. We illustrate our methodology calculating point estimates, iCIs and SCIs for the poverty rates in each county of Galicia, that is, the proportions of inhabitants who live under a poverty line. We make use of a general part of the Structural Survey for Homes (SSH) in Galicia in 2015 with 23,628 individuals within 9203 households located in 52 counties (small areas). The survey does not produce official estimates at the area level, but we managed to recover the direct estimates of the totals of people below the poverty line $(Y_d)$, as well as the number of inhabitants $(N_d)$ for each county. For the area-level models, we need to calculate the number of units which fall into a particular category $(X_{di})$, for example, number of employees or of graduates in each county of Galicia, $i=1,\dots ,p$. The latter are used to obtain the proportions of individuals in each category ${\overline{X}}_{di}=X_{di}/N_d$. For the unit-level model, we need to obtain the number of units N_dl falling into artificially created categories ${\mathit{z}}_{dl},d=1,\dots ,D,l=1,\dots ,L$, see Section 2.2.3. The explicit formulas are(25) $$\begin{array}{c}{\widehat{Y}}_d^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{y}_j,\hspace{1em}{\widehat{N}}_d^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j,\hfill \\ {\widehat{N}}_{dl}^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{\mathit{x}}_j{1}_{\{{\mathit{x}}_j={\mathit{z}}_l\}},\hfill \\ {\widehat{X}}_{di}^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{x}_{ji},\hspace{1em}\text{and}\hspace{1em}{\widehat{\overline{X}}}_{di}^{\text{dir}}={\widehat{X}}_{di}^{\text{dir}}/{\widehat{N}}_d^{\text{dir}},\hfill \end{array}$$(25) where ${\mathcal{R}}_d\in {\mathcal{P}}_d$ are the sample elements belonging to area d, $d\in [D]$, w_dj sampling weights, and y_dj binary variables with 1 indicating that an individual is below the poverty line. The poverty threshold is calculated from the survey. It is set to 0.6 of the median household income per capita in Galicia, that is, we do not use county specific poverty lines. This income is calculated in each household according to scale developed by the Organisation for Economic Co-operation and Development (the same technique is used by Eurostat). The model-based approach of this paper assumes that the estimates in Equation (25)(25) $$\begin{array}{c}{\widehat{Y}}_d^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{y}_j,\hspace{1em}{\widehat{N}}_d^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j,\hfill \\ {\widehat{N}}_{dl}^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{\mathit{x}}_j{1}_{\{{\mathit{x}}_j={\mathit{z}}_l\}},\hfill \\ {\widehat{X}}_{di}^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{x}_{ji},\hspace{1em}\text{and}\hspace{1em}{\widehat{\overline{X}}}_{di}^{\text{dir}}={\widehat{X}}_{di}^{\text{dir}}/{\widehat{N}}_d^{\text{dir}},\hfill \end{array}$$(25) are considered to be known, nonrandom quantities, following López-Vizcaíno, Lombardía, and Morales (2015). SSH provides many categorical, auxiliary variables. Under the unit-level model these are binary variables with 1 indicating that a person belongs to a particular category, whereas under area-level models we use the county proportions. We considered four variables for labor status: children (ls0), employed (ls1), unemployed (ls2), inactive (ls3), and four covariates for education: less than primary (ed0), primary (ed1), first- and second-level secondary (ed2), higher education (ed3). Furthermore, we analyzed three variables for the size of municipality: less than 10,000 (sm1), 10,000–50,000 (sm2), more than 50,000 (sm3). We have also investigated the effect of two variables indicating the nationality, that is, Spanish (n1), not Spanish (n2). Finally, we examined five age variables: < 15 (age1), $15-24$ (age2), $25-49$ (age3), $50-64$ (age4), $>=65$ (age5). We are interested in ${\overline{\mu }}_d^{(·)}:={\mu }_d^{(·)}/N_d$ with $(·)$ standing for PG or U in case of Poisson-gamma and binomial model, respectively, and in ρ_d in case of the Poisson-lognormal model. We first compute estimates of proportions and their variances using the same formulas as Boubeta, Lombardía, and Morales (2016)(26) $$\begin{array}{c}{\widehat{p}}_d^{\text{dir}}={\widehat{\overline{Y}}}_d^{\text{dir}}=\frac{{\overline{Y}}_d^{\text{dir}}}{{\widehat{N}}_d^{\text{dir}}},\\ \widehat{\text{var}}({\widehat{p}}_d^{\text{dir}})=\frac{1}{{({\widehat{N}}_d^{\text{dir}})}^2}\sum _{j\in {\mathcal{R}}_d}{w}_j(1-w_j){\left(y_j-{\widehat{p}}_d^{\text{dir}}\right)}^2.\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\end{array}$$(26)

We used estimates in Equation (26)(26) $$\begin{array}{c}{\widehat{p}}_d^{\text{dir}}={\widehat{\overline{Y}}}_d^{\text{dir}}=\frac{{\overline{Y}}_d^{\text{dir}}}{{\widehat{N}}_d^{\text{dir}}},\\ \widehat{\text{var}}({\widehat{p}}_d^{\text{dir}})=\frac{1}{{({\widehat{N}}_d^{\text{dir}})}^2}\sum _{j\in {\mathcal{R}}_d}{w}_j(1-w_j){\left(y_j-{\widehat{p}}_d^{\text{dir}}\right)}^2.\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\end{array}$$(26) to construct design-based iCI intervals (Dir) displayed in Figure 3. Following López-Vizcaíno, Lombardía, and Morales (2015), we then proceed with a variable selection inspired by the simulation results. More specifically, under the Poisson-gamma model we check if any of the levels of categorical variables for labor status, education and age are significant at the $\alpha =0.05$ level. We examined these covariates in the first place, because they turned out to be important in earlier studies on poverty rates (see, for instance, Boubeta, Lombardía, and Morales 2016). In this way, we selected ls2, ed2, and age2. Afterwards, we tested the levels of variables nationality and the size of the municipality and we additionally retained sm1 which was significant after the selection of ls2, ed2, and age2. The same categories were then used to other models, see Table 4. As we do not carry out a causality analysis, we refrain ourselves from a discussion of the magnitude or signs of estimates. We only notice that under the Poisson-gamma model, the signs are consistent with our expectations; unemployment and young age are associated with higher poverty rates, whereas higher level of studies or living in a small municipality is associated with lower poverty rates.

Fig. 3 Design and model-based 95% iCIs.

Table 4 Estimates of regression parameters under the area- and the unit-level models with ${\widehat{\delta }}^{\text{PG}}=2.48,{\widehat{\delta }}^{\text{PL}}=0.32$ and ${\widehat{\delta }}^U=0.35$, respectively.

	Poisson-gamma				Poisson-lognormal				Unit-level model
	$\widehat{\beta }$	SE	z-value	$P(>|z|)$	$\widehat{\beta }$	SE	z value	Pr($>\left|z\right|$)	$\widehat{\beta }$	SE	z-value	$P(>|z|)$
Int	10.038	0.669	15.005	0.000	−2.264	0.341	−6.633	0.000	−2.048	0.067	−30.415	0.000
ls2	7.747	3.091	2.506	0.012	3.480	1.577	2.207	0.027	0.989	0.052	19.160	0.000
ed2	−3.136	1.201	−2.611	0.009	−0.870	0.612	−1.422	0.155	0.172	0.039	4.442	0.000
age2	11.317	4.023	2.813	0.005	4.842	2.057	2.354	0.019	0.760	0.058	13.033	0.000
sm1	−2.466	0.267	−9.224	0.000	0.125	0.136	0.918	0.358	0.100	0.050	1.993	0.046

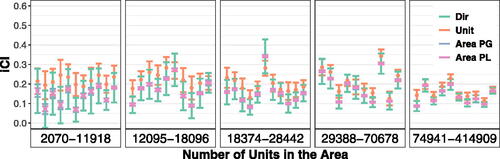
Figure 3 shows point and iCI estimates of proportions under Poisson-gamma (PG), Poisson-lognormal (PL), and binomial (Unit) models together with direct estimates (Dir). In this plot, we compare point estimates within four modeling frameworks; we do not compare them across different areas within the same model. First, the variability reflected by the width of iCIs decreases with the number of units in each area ${\widehat{N}}_d^{\text{dir}}$ defined in Equation (25)(25) $$\begin{array}{c}{\widehat{Y}}_d^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{y}_j,\hspace{1em}{\widehat{N}}_d^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j,\hfill \\ {\widehat{N}}_{dl}^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{\mathit{x}}_j{1}_{\{{\mathit{x}}_j={\mathit{z}}_l\}},\hfill \\ {\widehat{X}}_{di}^{\text{dir}}=\sum _{j\in {\mathcal{R}}_d}{w}_j{x}_{ji},\hspace{1em}\text{and}\hspace{1em}{\widehat{\overline{X}}}_{di}^{\text{dir}}={\widehat{X}}_{di}^{\text{dir}}/{\widehat{N}}_d^{\text{dir}},\hfill \end{array}$$(25) . Second, even though the area sample sizes n_d, $d\in [D]$ are not that small, the iCI of direct estimates are wider than model-based estimates, which is in accordance with the literature. The width difference is especially pronounced when comparing area-level-based with design-based direct estimates—the latter entirely cover the former. Unit-level model-based point and interval estimates are different with much wider iCIs than under area-level models, but still overlapping with the direct estimates. Only in one case (sixth area in the third panel), the iCIs under area-level models do not overlap with the iCI under the unit-level model which indicates a possible bias in one of the approaches. In contrast, both area-level models produce almost identical estimates.

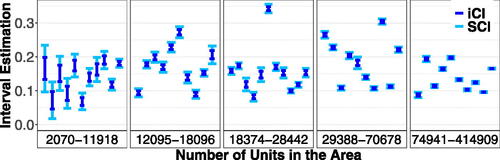
Figure 4 presents bootstrap iCI and SCI for ${\widehat{\overline{\mu }}}_d^{\text{PG}},d=1,\dots ,D$ constructed with $\widehat{\sigma }({\widehat{\zeta }}_d)=\sqrt{{\widehat{g}}_{\text{PG}1d}}$ as defined in Equation (9)(9) $$\begin{array}{c}{g}_{\text{PG}1d}={\kappa }_{1d}(\mathit{\theta })-{\kappa }_{2d}(\mathit{\theta }),\\ {\widehat{g}}_{\text{PG}1d}={\kappa }_{1d}(\widehat{\mathit{\theta }})-{\widehat{\kappa }}_{2d}(\widehat{\mathit{\theta }}),\hspace{1em}d\in \left[D\right],\\ \mathrm{ }\text{with}\mathrm{ }{\kappa }_{1d}(\mathit{\theta })=\frac{{\lambda }_d^2(\delta +1)}{\delta }\hspace{1em}\mathrm{ }\text{and}\mathrm{ }\\ {\kappa }_{2d}(\mathit{\theta })=\sum _{j=0}^{\infty }\frac{{\lambda }_d^2{(j+\delta )}^2}{{({\lambda }_d+\delta )}^2}P(y_d=j),\\ \mathrm{ }\text{as}\mathrm{ }\text{well}\mathrm{ }\text{as}\mathrm{ }{c}_d(\mathit{\theta })=\sum _{j=0}^{\infty }{\left\{\frac{\partial }{\partial \mathit{\theta }}{\psi }_d^{\text{PG}}(y_d,\mathit{\theta })\right\}}^t\\ \times \mathbb{V}{\text{ar}}_d(\mathit{\theta })\left\{\frac{\partial }{\partial \mathit{\theta }}{\psi }_d^{\text{PG}}(y_d,\mathit{\theta })\right\}P(y_d=j).\end{array}$$(9) . The plot is divided into five panels according to the numbers of units in each area obtained by direct estimates of county inhabitants ${\widehat{N}}_d^{\text{dir}}$ in (25). Figure 4 serves as an illustration of the differences between individual and simultaneous inference. When comparing iCI and SCI, in many cases (e.g., first and second county of the first panel in Figure 4) iCI would insinuate statistically different poverty rates, whereas SCI does not confirm this claim. Such multiple comparisons are valid only if we use SCI. In addition, at least 5% of the true poverty rates are not contained in their iCIs. Analogous figures under the Poisson-lognormal and binomial models lead to the same conclusions. They are thus deferred to the SM. Further model selection and specification testing might be interesting but they are beyond the scope of this article.

Fig. 4 95% bootstrap iCI and SCI estimates for poverty rates in counties of Galicia.

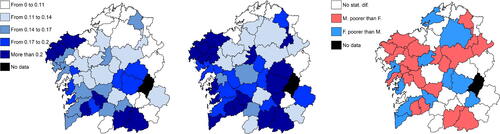
Since we do not know which model is closer to the real data-generating process, we proceed with the Poisson-gamma area-level model, as it is reliable and the least computer intensive. Left and middle panel of Figure 5 depict the resulting maps of the counties with the corresponding lower and upper bounds of our SCI. We observe a higher rate of poverty in the interior and a south-western part of the region whereas a lower level is typical for the northern part. These conclusions are similar to those drawn by Boubeta, Lombardía, and Morales (2017).

Fig. 5 SCI of EBP poverty proportions: (left) lower boundary, (middle) upper boundary; (right) significant differences in poverty rates between women (F) and men (M).

Finally, we investigate whether men and women are equally affected by poverty. We wish to test for equality on the county level across Galicia. Testing for each county individually at $\alpha =5\%$ error level results in rejection of at least 5% of the hypotheses of no significant difference. We thus use our MTP and consider clusters created from the cross section of sex and county such that $\mathit{\zeta }\in {\mathbb{R}}^{104}$. We test $H_0:\mathit{B\zeta }={\mathbf{0}}_{52}$ vs. $H_1:\mathit{B\zeta }\ne {\mathbf{0}}_{52}$ where $\mathit{B}\in {\mathbb{R}}^{52\times 104}$ with rows being vectors with 1 on the $2d-1$ place, –1 on 2d place, and 0 elsewhere. The max-type test statistic yields $t_H={\max }_{d=1,\dots ,104}\left|\mathit{B}\widehat{\mathit{\zeta }}\right|/\widehat{\sigma }(\widehat{\mathit{\zeta }})\approx 20.489$ while the bootstrap critical value under H₀ is $q_{{\text{BH}}_0}^{(1-\alpha )}\approx 2.999$. Thus, we strongly reject H₀. However, our test does not support the hypothesis that women are more affected than men, or vice versa, see the right panel of Figure 5. Additional results are deferred to our SM.

Remark 4.

Imagine that Galician counties were considered as a part of a macro region, for example, Spain with D_S counties, and consider two inferential problems: (a) the calculation of SCI for the poverty rates in all D_S Spanish counties, (b) the calculation of SCI only for D Galician counties, but using all data. Following Remark 1, we expect that the widths of our SCI in Figure 4 would increase in case (a) to maintain the joint coverage probability of 95% for all $D_S>D$ counties. In contrast, they would most likely slightly decrease in case (b). In fact, the simultaneous coverage probability of 95% would be requested for the set of D counties, but SCI would be constructed using a more precise estimate of MSE computed using a larger dataset with D_S counties.

6 Conclusions

We developed a methodology that allows for statistically valid simultaneous inference for EBP under GLMM. We constructed SCI and MTP applying a combination of max-type statistics and consistent bootstrap estimation of its distribution. These tools enable practitioners to make comparisons between areas. In contrast, the iCIs are not suitable for such comparative analyses because they are constructed at individual confidence level and disregard an additional variation which arises in joint studies. We do not claim that SCI and MTP are better than iCIs or t-tests. The former simply complete the toolbox for statistical inference for mixed parameter ζ_d. Similarly, the simultaneous inference completes the individual inference for fixed parameters. We introduced various versions of statistics to construct SCI and MTP. Within our framework, all of them exhibited similar performances without indicating a clear winner.

Our methodology can be extended to more complicated data structures such as GLMM with spatial or temporal correlation (see, e.g., Hobza, Morales, and Santamaría 2018; Chandra, Chambers, and Salvati 2019). One could also consider spatio-temporal or nonparametric models to build SCI by adjusting the statistic S₀ and choosing a bootstrap procedure accordingly. Apart from a mathematical challenge to develop a valid asymptotic theory, these extensions would require a construction of an appropriate bootstrap scheme and its computationally efficient implementation.

Supplementary Materials

The supplementary materials consist of: (a) a document with further developments, in particular additional MSE decomposition, a proof of Proposition 1, the derivations of estimators under area-level Poisson and unit-level binomial models, additional numerical results and a data analysis which completes the case study in Section 5, (b) codes for replicating the results in the main document, and (c) a document which contains additional information on the data set and the description of the codes.

Ministerio de Econom?a y Competitividad (Spain);

Additional information

Funding

The authors gratefully acknowledge the support from the Swiss National Science Foundation for the project 200021-192345. In addition, they acknowledge the support from the MINECO grants MTM2017-82724-R and MTM2014-52876-R, the Xunta de Galicia (Grupos de Referencia Competitiva ED431C-2016-015 and Centro Singular de Investigación de Galicia ED431G/01), all of them through the ERDF. The computations were performed at the University of Geneva on the Baobab cluster.

Appendix A:

Technical details

A.1 Regularity conditions

In this section, we state the regularity conditions used in our derivations.

1. ${\widehat{u}}_d=\text{arg} {\text{max}}_{u_d\in \mathbb{R}}\{\hspace{0.17em}\text{log}\hspace{0.17em}{g}_d({\mathit{y}}_{\mathit{d}}|u_d,\mathit{\theta })+\hspace{0.17em}\text{log}\hspace{0.17em}h(u_d)\}$.

2. $l(\mathit{\theta })$ exists and is well-defined if: (a) $l(\mathit{\theta })$ is continuous, uniquely maximized and ${\mathit{\theta }}_0\in \Theta$, where ${\mathit{\theta }}_0$ is a true parameter value; (b) $l(\mathit{\theta })$ and $\widehat{l}(\mathit{\theta })$ are concave; (c) ${\mathit{\theta }}_0$ is an interior point of the parameter space and the estimator $\widehat{\mathit{\theta }}$ is an interior point of the neighborhood of ${\mathit{\theta }}_0$; (d) $\widehat{l}(\mathit{\theta })$ converges uniformly in probability to $l(\mathit{\theta })$.

3. ${\mathit{x}}_{dj}$ are bounded and $\mathbb{E}(y_{dj}^m)<\infty$ for all $d\in [D],j\in [n_d]$, where m is suitable large.

4. For each fixed y, a score equation is continuously differentiable and $\mathbb{E}\{R({\mathit{\theta }}_0)\}=0$.

5. $\underset{n}{\lim \inf }\lambda [n^{-1}\mathbb{V}\text{ar}\{R(\mathit{\theta })\}]>0$ and $\underset{n}{\lim \inf }\lambda [-n^{-1}\mathbb{E}\{\nabla R(\mathit{\theta })\}]>0$ where $\nabla R(\mathit{\theta })=\frac{\partial R(\mathit{\theta })}{\partial \mathit{\theta }}$ and $\lambda [A]$ indicates the smallest eigenvalue of matrix A.

The first two conditions refer to the log-likelihood function (see, e.g., Bianconcini 2014), whereas conditions 3–5 are needed for the derivation of the $\text{MSE}$ estimators.

A.2 Proof of Proposition 2

Let $y_{dj}^{*}\sim \hspace{0.17em}\text{Exp}\hspace{0.17em}.\text{Family}(\mathit{\theta })$. If $u_d^{*}$ is sampled from a suitable distribution, then we have ${\gamma }_{dj}^{*}=M\{\mathbb{E}(y_{dj}^{*}|u_d)\}={\mathit{x}}_{dj}^t\widehat{\mathit{\beta }}+u_d^{*}$. Furthermore, $\mathbb{V}{\text{ar}}^{*}({\mathit{y}}_d^{*})=\mathbb{V}{\text{ar}}^{*}({\mathbb{E}}^{*}({\mathit{y}}_d^{*}|u_d^{*}))+{\mathbb{E}}^{*}(\mathbb{V}{\text{ar}}^{*}({\mathit{y}}_d^{*}|u_d^{*}))$. The first part of the Proposition follows from the way we generate the random effects as well as the results on the consistency of $\widehat{\mathit{\theta }}$. To show the second part we consider a general score equation. Replace y by ${\mathit{y}}^{*}$ and set $\mathit{\theta }=\widehat{\mathit{\theta }}$, that is, $R^{*}(\mathit{\theta })=\frac{\partial l^{*}(\widehat{\mathit{\theta }})}{\partial \widehat{\mathit{\theta }}}={\sum }_{d=1}^D\frac{\partial \hspace{0.17em}\text{log}\hspace{0.17em}{f}_d({\mathit{y}}_d^{*}|\widehat{\mathit{\theta }})}{\partial \widehat{\mathit{\theta }}}=0$. Then ${\mathbb{E}}^{*}\{R^{*}(\mathit{\theta })\}=0$ at $\mathit{\theta }=\widehat{\mathit{\theta }}$ which yields consistency of ${\widehat{\mathit{\theta }}}^{*}$. $\square$

A.3 Proof of Proposition 3

Let ζ_d be a general EBP, $g_d:=g_d(\mathit{\theta })$ and ${\widehat{g}}_d:={\widehat{g}}_d(\widehat{\mathit{\theta }})$. Assume that $\left|\right|{\widehat{g}}_d-g_d\left|\right|=O_P(n^{-c}),c>0$. The proof uses ideas of Chatterjee, Lahiri, and Li (2008). We investigate the properties of $G_d(a)$.$$\begin{array}{c}{G}_d(a)=P\left(\frac{{\widehat{\zeta }}_d-{\zeta }_d}{{\sqrt{\widehat{g}}}_d} \le a\right)\\ =\mathbb{E}\left(P\left[\frac{{\tilde{\zeta }}_d-{\zeta }_d}{{\sqrt{g}}_d} \le a+\left\{\frac{a({\sqrt{\widehat{g}}}_d-{\sqrt{g}}_d)+{\tilde{\zeta }}_d-\widehat{{\zeta }_d}}{{\sqrt{g}}_d}\right\}\right]|{\mathit{y}}_d\right)\\ =\mathbb{E}\left[\Phi \{a+Q(a,{\mathit{y}}_d)\}\right]\\ =\Phi (a)+\varphi (a)\mathbb{E}\left\{Q(a,{\mathit{y}}_d)\right\}-2^{-1}a\varphi (a)\mathbb{E}\left\{Q^2(a,{\mathit{y}}_d)\right\}\\ +2^{-1}\mathbb{E}\left[{\int }_a^{a+Q(a,{\mathit{y}}_d)}\{a+Q(a,{\mathit{y}}_d)-x{\}}^2(x^2-1)\varphi (x)\mathrm{d}x\right].\end{array}$$

Applying some classical results and a triangle inequality, it follows that the last term is bounded by $\mathbb{E}|Q{|}^3$, and is of smaller order than the first three terms. Therefore, the first step toward the consistency of SCI is to quantify the asymptotic expansions of $\mathbb{E}\{Q(a,{\mathit{y}}_d)\}$ and $\mathbb{E}\{Q^2(a,{\mathit{y}}_d)\}$. We decompose $Q(a,{\mathit{y}}_d)$ into$$Q(a,{\mathit{y}}_d)=g_d^{-1/2}({\tilde{\zeta }}_d-\widehat{{\zeta }_d})+a{g}_d^{-1/2}({\widehat{g}}_d^{1/2}-g_d^{1/2})=Q_1+Q_2.$$

Let ψ be a twice differentiable function with respect to $\mathit{\theta },y_{d.}=y_{d1}+\dots +y_{d{n}_d},\forall d\in [D]$. Observe that $y_{d.}=y_d$ under an area-level model. The specific form of ψ depends on the choice of the GLMM (for instance, under the Poisson-gamma model we spelled it out in Equation (7)(7) $$\begin{array}{c}\mathbb{E}({\mu }_d^{\text{PG}}|y_d)=\frac{{\int }_0^{\infty }{\lambda }_d{w}_{d}g(y_d|w_d)h(w_d)d{w}_d}{{\int }_0^{\infty }g(y_d|w_d)h(w_d)d{w}_d}\\ =\frac{A_d^{\text{PG}}(y_d,\mathit{\theta })}{C_d^{\text{PG}}(y_d,\mathit{\theta })}=\frac{{\lambda }_d(y_d+\delta )}{({\lambda }_d+\delta )}\\ =:{\psi }_d^{\text{PG}}(y_d,\mathit{\theta }).\end{array}$$(7) ). Function ψ satisfies the decomposition(A.1) $$\begin{array}{c}{\widehat{\zeta }}_d-{\tilde{\zeta }}_d={\psi }_d(y_{d.},\widehat{\mathit{\theta }})-{\psi }_d(y_{d.},\mathit{\theta })={\left\{\frac{\partial }{\partial \mathit{\theta }}{\psi }_d(y_{d.},\mathit{\theta })\right\}}^t\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)\hfill \\ +\frac{1}{2}{\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)}^t\left\{\frac{{\partial }^2}{{\partial }^2\mathit{\theta }}{\psi }_d(y_{d.},\mathit{\theta })\right\}\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)+o_P(||\widehat{\mathit{\theta }}-\mathit{\theta }|{|}^2).\hfill \end{array}$$(A.1)

Let $C=2c$ where c > 0. Since we assume $\left|\right|\widehat{\mathit{\theta }}-\mathit{\theta }\left|\right|=O_P(n^{-c})$, we have(A.2) $$\mathbb{E}\left[{\{{\widehat{\zeta }}_d(\widehat{\mathit{\theta }})-{\tilde{\zeta }}_d(\mathit{\theta })\}}^2\right]=\frac{1}{n^C}\mathbb{E}\left({\left[{\left\{\frac{\partial }{\partial \mathit{\theta }}{\psi }_d(y_{d.},\mathit{\theta })\right\}}^t{n}^c\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)\right]}^2\right)+o(n^{-C}).$$(A.2)

As for Q₁, it has been found in Equation (A.1)(A.1) $$\begin{array}{c}{\widehat{\zeta }}_d-{\tilde{\zeta }}_d={\psi }_d(y_{d.},\widehat{\mathit{\theta }})-{\psi }_d(y_{d.},\mathit{\theta })={\left\{\frac{\partial }{\partial \mathit{\theta }}{\psi }_d(y_{d.},\mathit{\theta })\right\}}^t\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)\hfill \\ +\frac{1}{2}{\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)}^t\left\{\frac{{\partial }^2}{{\partial }^2\mathit{\theta }}{\psi }_d(y_{d.},\mathit{\theta })\right\}\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)+o_P(||\widehat{\mathit{\theta }}-\mathit{\theta }|{|}^2).\hfill \end{array}$$(A.1) that$$\mathbb{E}({\widehat{\zeta }}_d-{\tilde{\zeta }}_d)=\frac{1}{n^c}\mathbb{E}\left[{\left\{\frac{\partial }{\partial \mathit{\theta }}{\psi }_d(y_{d.},\mathit{\theta })\right\}}^t{n}^c\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)\right]+o\left(n^{-c}\right),$$and $\mathbb{E}\left\{{({\widehat{\zeta }}_d-{\tilde{\zeta }}_d)}^2\right\}=O(n^{-C})$, thanks to the result in Equation (A.2)(A.2) $$\mathbb{E}\left[{\{{\widehat{\zeta }}_d(\widehat{\mathit{\theta }})-{\tilde{\zeta }}_d(\mathit{\theta })\}}^2\right]=\frac{1}{n^C}\mathbb{E}\left({\left[{\left\{\frac{\partial }{\partial \mathit{\theta }}{\psi }_d(y_{d.},\mathit{\theta })\right\}}^t{n}^c\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)\right]}^2\right)+o(n^{-C}).$$(A.2) . Furthermore, observe that g_d is of order O(1) which leads to $\mathbb{E}(Q_1)=O(D^{-c})$ as well as $\mathbb{E}(Q_1^2)=O(D^{-C})$. When we turn to Q₂, we have an immediate simplification $Q_2=a{g}_d^{-1/2}({\widehat{g}}_d^{1/2}-g_d^{1/2})=a\left\{{({\widehat{g}}_d/g_d)}^{1/2}-1\right\}$. Let g_d be twice differentiable with respect to $\mathit{\theta }$. Similarly to the computations above, we have the expansion$$\begin{array}{c}{\widehat{g}}_d(\widehat{\mathit{\theta }})=g_d(\mathit{\theta })+{\left(\frac{\partial }{\partial \mathit{\theta }}{g}_d(\mathit{\theta })\right)}^t\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)+\frac{1}{2}{\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)}^t\\ \times \left(\frac{{\partial }^2}{{\partial }^2\mathit{\theta }}{g}_d(\mathit{\theta })\right)\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)+o_P(||\widehat{\mathit{\theta }}-\mathit{\theta }|{|}^2).\end{array}$$

Therefore, we obtain$$\mathbb{E}\{{\widehat{g}}_d(\widehat{\mathit{\theta }})\}=g_d(\mathit{\theta })+\frac{1}{n^C}\mathbb{E}\left[{\left\{\frac{\partial }{\partial \mathit{\theta }}{g}_d(\mathit{\theta })\right\}}^t{n}^C\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)\right]+O(n^{-C}).$$

It follows that $\mathbb{E}\left\{{(\widehat{g}/g)}^{1/2}\right\}=O(n^{-c}),\mathbb{E}(Q_2)=O(n^{-C})$ and $\mathbb{E}(Q_2^2)=O(n^{-C})$. We can deduce that $G_d(a)$ attains the asymptotic expansion $G_d(a)=\Phi (a)+n^{-c}\gamma (a,\mathit{\theta })+O(n^{-C})$. A similar expansion can be established for $G_d^{*}(a)$ if we replace $\mathit{\theta }$ with $\widehat{\mathit{\theta }}$ and P with $P^{*}$.