Confidently Comparing Estimates with the c-value

Abstract

Modern statistics provides an ever-expanding toolkit for estimating unknown parameters. Consequently, applied statisticians frequently face a difficult decision: retain a parameter estimate from a familiar method or replace it with an estimate from a newer or more complex one. While it is traditional to compare estimates using risk, such comparisons are rarely conclusive in realistic settings. In response, we propose the “c-value” as a measure of confidence that a new estimate achieves smaller loss than an old estimate on a given dataset. We show that it is unlikely that a large c-value coincides with a larger loss for the new estimate. Therefore, just as a small p-value supports rejecting a null hypothesis, a large c-value supports using a new estimate in place of the old. For a wide class of problems and estimates, we show how to compute a c-value by first constructing a data-dependent high-probability lower bound on the difference in loss. The c-value is frequentist in nature, but we show that it can provide validation of shrinkage estimates derived from Bayesian models in real data applications involving hierarchical models and Gaussian processes. Supplementary materials for this article are available online.

Keywords:

• Decision theory
• Empirical Bayes
• Model selection
• Normal means
• Shrinkage

1 Introduction

Modern statistics provides an expansive toolkit of sophisticated methodology for estimating unknown parameters. However, the abundance of different estimators often presents practitioners with a difficult challenge: choosing between the output of a familiar method (e.g., a maximum likelihood estimate (MLE)) and that of a more complicated method (e.g., the posterior mean of a hierarchical Bayesian model). From a practical perspective, abandoning a familiar approach in favor of a newer alternative is unreasonable without some assurance that the latter provides a more accurate estimate. Our goal is to determine whether it is safe to abandon a default estimate in favor of an alternative, and to provide an assessment of the degree of confidence we should have in this decision.

Traditionally decisions between estimators are based on risk, the loss averaged over all possible realizations of the data with respect to a pre-specified likelihood model (Lehmann and Casella, 2006, chap. 4–5). We note two limitations of using risk. First, it is rare that one estimator within a given pair will have smaller risk across all possible parameter values. Instead, it is more often the case that one estimator will have smaller risk for some unknown parameter values but larger risk for other parameter values. Second, one estimator may have lower risk than another but incur higher loss on a majority of datasets; see Appendix S2 for an example in which an estimator with smaller risk has larger loss on nearly 70% of simulated datasets.

In this work we propose a framework for choosing between estimators based on their performance on the observed dataset rather than their risk. Specifically, we introduce the “c-value” (“c” for confidence in the new estimate), which we construct using a data-dependent high-probability lower bound on the difference in loss. We show that it is unlikely that simultaneously the c-value is large and the alternative estimate has larger loss than the default. For the c-value to be useful, it must meet two desiderata:

1. The c-value must not frequently guide practitioners to incorrectly report the alternative estimate when the default estimate has smaller loss.

2. The c-value must, in some cases, allow one to correctly identify that the alternative estimate has smaller loss.

We demonstrate that the c-value meets the first desideratum with theory showing how to use the c-value to select between two estimates in a principled, data-driven way. Critically, the c-value requires no assumptions on the unknown parameter; our guarantees hold uniformly across the parameter space. We demonstrate that the c-value can meet the second desideratum with case studies; we provide an overview of these next as motivating examples, and then proceed to present our general methodology.

Shrinkage estimates on educational testing data

We revisit Hoff’s (2021) estimates of average student reading ability at several schools in the 2002 Educational Longitudinal Study. These estimates are obtained from a hierarchical Bayesian model that “shares strength” by partially pooling data across similar schools. Hoff’s (2021) analysis relied on a simplifying and subjectively chosen prior. A practitioner might wonder whether the resulting estimates are more accurate than the MLE in terms of squared error loss. As we will see, a large c-value provides confidence that Hoff’s estimate is indeed more accurate. We additionally consider a clearly inappropriate prior and verify that our methodology does not always favor more complex alternative estimators. Although these estimates have a Bayesian provenance, the use of the c-value to justify these estimates does not require subjective belief in the prior.

Estimating violent crime density at the neighborhood level

Considerable empirical evidence links a community’s exposure to violent crime and adverse behavioral, mental, and physical health outcomes among its residents (Buka et al., 2001; Kondo et al., 2018). Although overall violent crimes rates in the United States have decreased over the last two decades, there is considerable variation in time trends at the neighborhood level (Balocchi and Jensen, 2019; Balocchi et al., 2022). A critical first step in understanding what drives neighborhood-level variation is accurate estimation of the actual amount of violent crime that occurs in each neighborhood.

Typically, researchers rely on the reported counts of violent crime aggregated at small spatial resolutions (e.g., at the census tract level). However, in light of sampling variability due to the relative infrequency of certain crime types in small areas, it is natural to wonder if auxiliary data could be used to improve estimates of violent crime incidence.

As a second application of our framework, we analyze the number of violent crimes reported per square mile in several neighborhoods in the city of Philadelphia. Our analysis suggests that one can obtain improved estimates of the violent crime density by using a shrinkage estimate that incorporates information about nonviolent crime incidence. Further c-value analysis reveals that leveraging spatial information on top of nonviolent incidence does not provide additional improvement.

Gaussian process kernel choice: Modeling ocean currents

Accurate estimation of ocean current dynamics is critical for forecasting the dispersion of oceanic contaminations (Poje et al., 2014). While it is commonplace to model ocean flow dynamics at or above the mesoscale (roughly 10 km), Lodise et al. (2020) have recently advocated modeling dynamics at both the mesoscale and the submesoscale (roughly 0.1–10 km). They specifically proposed a Gaussian process model that accounts for variation across multiple resolutions to estimate ocean currents from positional data taken from hundreds of free-floating buoys.

In a third application of our framework, we find that the multi-resolution procedure produces a large c-value, indicating that accounting for variation across multiple scales enables more accurate estimates than are obtained when accounting only for mesoscale variation.

1.1 Organization of the Article and Contributions

We formally present our general framework and define the c-value in Section 2. In Section 2.1 we highlight similarities and differences between our framework and existing work on preliminary testing and post-selection inference. Our approach to computing c-values depends on the availability of high-confidence lower bounds on the difference in the losses of the two estimates that holds uniformly across the parameter space. Sections 3–5 provide these bounds for several models and classes of estimators for squared error loss. In Section 3, we illustrate our general strategy in the canonical normal means problem. Then, in Section 4, we generalize this strategy to compare affine estimates of normal means with correlated observations. Section 5 shows how to extend the framework to cover two nonlinear cases: a nonlinear shrinkage estimator and regularized logistic regression. We provide simulations validating our approach in these settings. We apply our framework to the aforementioned motivating examples in Section 6. In our discussion in Section 7, we outline ways to extend our framework beyond the estimates considered here. Software that implements the c-value computation, and code that reproduces our analyses is available at: https://github.com/blt2114/c_values.

2 Introducing the c-value

We now describe our approach for quantifying confidence in the statement that one estimate of an unknown parameter is superior to another. We begin by introducing some notation and building up to a definition of the c-value, before stating our main results. This development is very general, and we defer practical considerations to the subsequent sections. We include proofs of the results of this section in Appendix.

Suppose that we observe data y drawn from some distribution that depends on an unknown parameter $\theta .$ We consider deciding between two estimates, $\widehat{\theta }(y)$ and ${\theta }^{*}(y),$ of θ on the basis of a loss function $L(\theta ,·).$ Our focus is on asymmetric situations in which $\widehat{\theta }(·)$ is a standard or more familiar estimator while ${\theta }^{*}(·)$ is a less familiar estimator. For simplicity, we will refer to $\widehat{\theta }(·)$ as the default estimator and ${\theta }^{*}(·)$ as the alternative estimator.

We next define the “win” obtained by using ${\theta }^{*}(y)$ rather than $\widehat{\theta }(y)$ as the difference in loss, $W(\theta ,y):=L(\theta ,\widehat{\theta }(y))-L(\theta ,{\theta }^{*}(y)).$ While a typical comparison based on risk would proceed by taking the expectation of $W(\theta ,y)$ over all possible datasets drawn for fixed $\theta ,$ we maintain focus on the single observed dataset. Notably, the win is positive whenever the alternative estimate achieves a smaller loss than the default estimate. As such, if we knew that $W(\theta ,y)>0$ for the given dataset y and unknown parameter $\theta ,$ then we would prefer to use the alternative ${\theta }^{*}(y)$ instead of the default $\widehat{\theta }(y).$

Since θ is unknown, determining whether $W(\theta ,y)>0$ is impossible. Nevertheless, for a broad class of estimators, we can determine whether the win is positive with high probability. To start, we construct a lower bound, $b(y,\alpha ),$ depending only on the data and a pre-specified level $\alpha \in [0,1],$ that satisfies for all θ (1) $${\mathbb{P}}_{\theta }\left[W(\theta ,y)\ge b(y,\alpha )\right]\ge \alpha .$$(1)

For values of α close to $1, b(y,\alpha )$ is a high-probability lower bound on the win that holds uniformly across all possible values of the unknown parameter $\theta .$ Loosely speaking, if $b(y,\alpha )>0$ for some α close to 1, then we can be confident that the alternative estimate has smaller loss than the default estimate.

To make this intuition more precise, we define a measure of confidence that ${\theta }^{*}(y)$ is superior to $\widehat{\theta }(y).$ We call our measure the c-value c(y): (2) $$c(y):=\underset{\alpha \in [0,1]}{\inf }\left\{\alpha |b(y,\alpha )\le 0\right\}.$$(2)

The c-value marks a meaningful boundary in the space of confidence levels; it is the largest value such that for every $\alpha <c(y),$ we have confidence α that the win is positive.

Remark 2.1.

An alternative definition for the c-value is $c^{+}(y)=\underset{\alpha \in [0,1]}{\sup }\left\{\alpha \right|b(y,\alpha )\ge 0\}.$ Although $c^{+}(y)=c(y)$ when $b(y,·)$ is continuous and strictly decreasing in $\alpha ,$ $c^{+}(·)$ may be overconfident otherwise. We detail a particularly pathological example in Appendix S3.

Our first main result formalizes the interpretation of c(y) as a measure of confidence.

Theorem 2.2.

Let $b(·,·)$ be any function satisfying the condition in Equation (1)(1) $${\mathbb{P}}_{\theta }\left[W(\theta ,y)\ge b(y,\alpha )\right]\ge \alpha .$$(1) . Then for any θ and $\alpha \in [0,1]$ and c(y) as defined in Equation (2)(2) $$c(y):=\underset{\alpha \in [0,1]}{\inf }\left\{\alpha |b(y,\alpha )\le 0\right\}.$$(2) , (3) $${\mathbb{P}}_{\theta }\left[W(\theta ,y)\le 0\text{and}c(y)>\alpha \right]\le 1-\alpha .$$(3)

The result follows directly from the definition of $c(·)$ and the condition on $b(·,·).$ Informally, Theorem 2.2 assures us that it is unlikely that simultaneously (A) the c-value is large and (B) ${\theta }^{*}(y)$ does not provide smaller loss than $\widehat{\theta }(y).$ Just as a small p-value supports rejecting a null hypothesis, a large c-value supports abandoning the default estimate in favor of the alternative.

The strategy described above necessarily uses the data twice, once to compute the two estimates and once more to compute the c-value to choose between them. Accordingly, one might justly ask how such double use of the data affects the quality of the resulting procedure. To address this question, we formalize this two-step procedure with a single estimator, (4) $${\theta }^{†}(y,\alpha ):=1[c(y)\le \alpha ]\widehat{\theta }(y)+1[c(y)>\alpha ]{\theta }^{*}(y).$$(4)

${\theta }^{†}(y,\alpha )$ picks between the two estimates $\widehat{\theta }(y)$ and ${\theta }^{*}(y)$ based on the value c(y) and a pre-specified level $\alpha \in [0,1].$ We can characterize the possible outcomes when using ${\theta }^{†}(·,\alpha )$ with a contingency table (Table 1), where rows correspond to the estimate with smaller loss, and the columns correspond to the reported estimate.

Table 1 Contingency table with possible outcomes when using the two-stage estimator ${\theta }^{†}(·,\alpha )$. ${\theta }^{†}(·,\alpha )$ controls the probability of the boldface event (Theorem 2.3).

	Default reported	Alternative reported
Default has lower loss	Correct	Incorrect
Alternative has lower loss	Incorrect	Correct

Recall that we are interested in an asymmetric situation where the alternative estimator is less familiar than the default estimator. This asymmetry makes desirable the reassurance that ${\theta }^{†}(·,\alpha )$ does not incur greater loss than $\widehat{\theta }(·).$ As such, we focus on the upper right hand entry of the table. Our second main result formalizes that when we use ${\theta }^{†}(·,\alpha )$ with α close to 1, the probability of the event represented by this table entry is small.

Theorem 2.3.

Let $b(·,·)$ be any function that satisfies the condition in Equation (1)(1) $${\mathbb{P}}_{\theta }\left[W(\theta ,y)\ge b(y,\alpha )\right]\ge \alpha .$$(1) . Then for any θ and $\alpha \in [0,1]$, (5) $${\mathbb{P}}_{\theta }\left[L\left(\theta ,{\theta }^{†}(y,\alpha )\right)>L\left(\theta ,\widehat{\theta }(y)\right)\right]\le 1-\alpha .$$(5)

Overview of the remainder of the article

The c-value is useful insofar as the lower bound $b(y,\alpha )$ is sufficiently tight and readily computable. It remains to show that such practical bounds exist. A primary contribution of this work is the explicit construction of these bounds in settings of practical interest. In what follows, we (A) illustrate one approach for constructing and computing $b(y,\alpha )$, (B) explore our proposed bounds’ empirical properties on simulated data, and (C) demonstrate their practical utility on real-world data.

2.1 Related Work

Hypothesis testing, p-values, and pretest estimation

Our proposed c-value bears a resemblance to the p-value in hypothesis testing, but with a few key differences. Indeed, just as a small p-value can support rejecting a simple null hypothesis in favor of a possibly more complex alternative, a large c-value can support rejecting a familiar default estimate in favor of a less familiar alternative. Furthermore both tools provide a frequentist notion of confidence based on the idea of repeated sampling. From this perspective, the two-step estimator ${\theta }^{†}(·,\alpha )$ resembles a preliminary testing estimator. Preliminary testing links the choice between estimators to the outcome of a hypothesis test for the null hypothesis that θ lies in some pre-specified subspace (Wallace 1977).

The similarities to hypothesis testing go only so far. Notably, we consider decisions made about a random quantity, $W(\theta ,y)$. Hypothesis tests, in contrast, concern only fixed statements about parameters, with nulls and alternatives corresponding to disjoint subsets of an underlying parameter space (Casella and Berger 2002, Definition 8.1.3). Our approach does not admit an interpretation as testing a fixed hypothesis.

Nevertheless, the connection to p-values can help us understand some limitations of the c-value. First, just as hypothesis tests may incur Type II errors (i.e., failures to reject a false null), for certain models and estimators there may be no bound $b(·,·)$ that consistently detects improvements by the alternative estimate. Accordingly, the two stage estimator ${\theta }^{†}(·,\alpha )$ does not control the probability that we report the default estimate when the alternative in fact has smaller loss. In such situations, our approach may consistently report the default estimate even though it has larger loss. Second, even if good choices of $b(·,·)$ exist, it could be challenging to derive them analytically. This analytical challenge is reminiscent of difficulties for hypothesis testing in many models, wherein conservative p-values that are stochastically larger than uniform under the null are used when analytic quantile functions are unavailable. Third, we note that it may be tempting to interpret a c-value as the conditional probability that an alternative estimate is superior to a default; however, just as it is incorrect to interpret a p-value as a probability that the null hypothesis is true, such an interpretation for a c-value is also incorrect.

Post-selection inference

In recent years, there has been considerable progress on understanding the behavior of inferential procedures that, like ${\theta }^{†}(·,\alpha )$, use the data twice, first to select amongst different models and then again to fit the selected model. Important recent work has focused on computing p-values and confidence intervals for linear regression parameters that are valid after selection with the lasso (Lockhart et al. 2014; Lee et al. 2016; Taylor and Tibshirani 2018) and arbitrary selection procedures (Berk et al. 2013). Somewhat more closely related to our focus on estimation are Tibshirani and Rosset (2019) and Tian (2020), which both bound prediction error after model selection. Unlike these papers, which study the effects of selection on downstream inference, we effectively perform inference on the selection itself.

3 Special Case: c-values for Estimating Normal Means

In this section, we derive a bound $b(y,\alpha )$ and compute the c-value in a simple case: we compare a certain class of shrinkage estimators to maximum likelihood estimates (MLE) of the mean of a multivariate normal from a single vector observation (i.e., the normal means problem). Our goal is to illustrate a simple strategy for lower bounding the win that we will later generalize to more complex estimators and models. In Section 3.1, we define the model and the estimators that we consider. In Section 3.2, we introduce our lower bound $b(·,·)$ and present a theorem that guarantees this bound satisfies Equation (1)(1) $${\mathbb{P}}_{\theta }\left[W(\theta ,y)\ge b(y,\alpha )\right]\ge \alpha .$$(1) . Then, in Section 3.3, we examine the resulting c-value empirically and study the performance of the estimator ${\theta }^{†}(·,\alpha )$ that chooses between the default and alternative estimators based on the c-value (Equation (4)(4) $${\theta }^{†}(y,\alpha ):=1[c(y)\le \alpha ]\widehat{\theta }(y)+1[c(y)>\alpha ]{\theta }^{*}(y).$$(4) ). Several details, including the proof of Theorem 3.1, are left to Appendix S4.

3.1 Normal Means: Notation and Estimates

Let $\theta \in {\mathbb{R}}^N$ be an unknown vector and consider estimating θ from a noisy vector observation $y=\theta +ϵ$ where $ϵ\sim \mathcal{N}(0,I_N)$ under squared error loss $L(\theta ,\widehat{\theta }):=\left|\right|\widehat{\theta }-\theta |{|}^2.$ For simplicity, we focus on the case of isotropic noise with variance one; we remove this restriction in Section 4. For our demonstration, we take the MLE $\widehat{\theta }(y)=y$ to be the default estimate. As the alternative estimator, we consider a shrinkage estimator that was first studied extensively by Lindley and Smith (1972), $${\theta }^{*}(y)=\frac{y+{\tau }^{-2}\overline{y}{\mathbf{1}}_N}{1+{\tau }^{-2}},$$where ${\mathbf{1}}_N$ is the vector of all ones, $\tau >0$ is a fixed positive constant, and $\overline{y}:=N^{-1}{\mathbf{1}}_N^{\top }y$ is the mean of the observed y_n’s. Operationally, ${\theta }^{*}(y)$ shrinks each coordinate of the MLE toward the grand mean $\overline{y}.$

3.2 Construction of the Lower Bound

To lower bound the win, we first rewrite ${\theta }^{*}(y)=\widehat{\theta }(y)-Gy$ where $G:={(1+{\tau }^2)}^{-1}{P}_1^{\perp }$ and $P_1^{\perp }:=I_N-N^{-1}{\mathbf{1}}_N{\mathbf{1}}_N^{\top }$ is the projection onto the subspace orthogonal to ${\mathbf{1}}_N$. The win in squared error loss may then be written as (6) $$W(\theta ,y):=\left|\right|\widehat{\theta }(y)-\theta |{|}^2-||{\theta }^{*}(y)-\theta |{|}^2=2{ϵ}^{\top }Gy-\Vert Gy{\Vert }^2.$$(6)

Observe that we can compute $\Vert Gy\Vert$ directly from our data. As a result, in order to lower bound the win $W(\theta ,y),$ it suffices to lower bound $2{ϵ}^{\top }Gy.$ As we detail in Appendix S4.1, $2{ϵ}^{\top }Gy$ follows a scaled and shifted noncentral Chi-squared distribution, $$2{ϵ}^{\top }Gy\sim \frac{2}{1+{\tau }^2}\left[{\chi }_{N-1}^2(\frac{1}{4}\Vert P_1^{\perp }\theta {\Vert }^2)-\frac{1}{4}\Vert P_1^{\perp }\theta {\Vert }^2\right],$$where ${\chi }_{N-1}^2(\lambda )$ denotes the noncentral Chi-squared distribution with N – 1 degrees of freedom and non-centrality parameter λ. Thus, for any $\alpha \in (0,1)$ and any fixed value of $\Vert P_1^{\perp }\theta {\Vert }^2$, (7) $$W(\theta ,y)\ge \frac{2}{1+{\tau }^2}{F}_{N-1}^{-1}(1-\alpha ;\frac{1}{4}\Vert P_1^{\perp }\theta {\Vert }^2)-\frac{\Vert P_1^{\perp }\theta {\Vert }^2}{2(1+{\tau }^2)}-\Vert Gy{\Vert }^2$$(7) with probability α, where $F_{N-1}^{-1}(1-\alpha ;\lambda )$ denotes the inverse cumulative distribution function of ${\chi }_{N-1}^2(\lambda )$ evaluated at $1-\alpha .$ Were $\Vert P_1^{\perp }\theta {\Vert }^2$ known, the right hand side of Equation (7)(7) $$W(\theta ,y)\ge \frac{2}{1+{\tau }^2}{F}_{N-1}^{-1}(1-\alpha ;\frac{1}{4}\Vert P_1^{\perp }\theta {\Vert }^2)-\frac{\Vert P_1^{\perp }\theta {\Vert }^2}{2(1+{\tau }^2)}-\Vert Gy{\Vert }^2$$(7) would immediately provide a valid bound. However, since $\Vert P_1^{\perp }\theta {\Vert }^2$ is not typically known, we use the data to address our uncertainty in this quantity. We obtain our bound by forming a one-sided confidence interval for $\Vert P_1^{\perp }\theta {\Vert }^2$ that holds simultaneously with Equation (7)(7) $$W(\theta ,y)\ge \frac{2}{1+{\tau }^2}{F}_{N-1}^{-1}(1-\alpha ;\frac{1}{4}\Vert P_1^{\perp }\theta {\Vert }^2)-\frac{\Vert P_1^{\perp }\theta {\Vert }^2}{2(1+{\tau }^2)}-\Vert Gy{\Vert }^2$$(7) .

Bound 3.1 (Normal means: Lindley and Smith estimate vs. MLE). Observe $y=\theta +ϵ$ with $ϵ\sim \mathcal{N}(0,I_N)$ and consider $\widehat{\theta }(y)=y$ versus ${\theta }^{*}(y)=(y+{\tau }^{-2}\overline{y}{\mathbf{1}}_N)/(1+{\tau }^{-2}).$ We propose (8) $$\begin{array}{c}b(y,\alpha ):=\underset{\lambda \in [0,U(y,\frac{1-\alpha }{2}\left)\right]}{\inf }\{\frac{2}{1+{\tau }^2}{F}_{N-1}^{-1}\left(\frac{1-\alpha }{2};\frac{\lambda }{4}\right)\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}-\frac{\lambda }{2(1+{\tau }^2)}-\frac{\Vert P_1^{\perp }y{\Vert }^2}{{(1+{\tau }^2)}^2}\}\end{array}$$(8) as an α-confidence lower bound on the win, where (9) $$U\left(y,\frac{1-\alpha }{2}\right):=\underset{\delta >0}{\inf }\left\{\delta |\Vert P_1^{\perp }y{\Vert }^2\le F_{N-1}^{-1}\left(\frac{1-\alpha }{2};\delta \right)\right\}$$(9) is a high-confidence upper bound on $\Vert P_1^{\perp }\theta {\Vert }^2$.

Bound 3.1 relies on a high-confidence upper bound on $\Vert P_1^{\perp }\theta {\Vert }^2,$ but a two-sided interval could in principle provide a valid bound as well. In Appendix S4.3 we provide an intuitive justification for the choice of an upper bound. Theorem 3.1 justifies the use of Bound 3.1 for computing c-values.

Theorem 3.1.

Define $c(y):=\underset{\alpha \in [0,1]}{\inf }\left\{\alpha \right|b(y,\alpha )\le 0\}$ for $b(·,·)$ in Bound 3.1. Then c(y) is a valid c-value, satisfying the guarantees of Theorems 2.2 and 2.3.

Remark 3.2

(Computability of the bound). Equation (8)(8) $$\begin{array}{c}b(y,\alpha ):=\underset{\lambda \in [0,U(y,\frac{1-\alpha }{2}\left)\right]}{\inf }\{\frac{2}{1+{\tau }^2}{F}_{N-1}^{-1}\left(\frac{1-\alpha }{2};\frac{\lambda }{4}\right)\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}-\frac{\lambda }{2(1+{\tau }^2)}-\frac{\Vert P_1^{\perp }y{\Vert }^2}{{(1+{\tau }^2)}^2}\}\end{array}$$(8) in Bound 3.1 can be readily computed. Notably, many standard statistical software packages provide numerical approximation to noncentral ${\chi }^2$ quantiles. Further, the one-dimensional optimization problems in Equations (8)(8) $$\begin{array}{c}b(y,\alpha ):=\underset{\lambda \in [0,U(y,\frac{1-\alpha }{2}\left)\right]}{\inf }\{\frac{2}{1+{\tau }^2}{F}_{N-1}^{-1}\left(\frac{1-\alpha }{2};\frac{\lambda }{4}\right)\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}-\frac{\lambda }{2(1+{\tau }^2)}-\frac{\Vert P_1^{\perp }y{\Vert }^2}{{(1+{\tau }^2)}^2}\}\end{array}$$(8) and (9)(9) $$U\left(y,\frac{1-\alpha }{2}\right):=\underset{\delta >0}{\inf }\left\{\delta |\Vert P_1^{\perp }y{\Vert }^2\le F_{N-1}^{-1}\left(\frac{1-\alpha }{2};\delta \right)\right\}$$(9) can be solved numerically.

Remark 3.3

(Unknown variance). For cases when the noise variance ${\sigma }^2$ is unknown but a confidence interval is available, one can adapt the procedure above by replacing $b(y,\alpha )$ with its infimum with respect to ${\sigma }^2$ over the confidence interval and reducing the confidence level α accordingly.

Remark 3.4.

The alternative estimator ${\theta }^{*}(y)$ considered in this section is the posterior mean of θ corresponding to the hierarchical prior $\theta |\mu \sim \mathcal{N}(\mu {\mathbf{1}}_N,{\tau }^2{I}_N)$ with further improper hyper-prior on $\mu .$ This prior encodes a belief that θ lies close to the one-dimensional subspace spanned by ${\mathbf{1}}_N.$ Using a similar approach to the one above, we can derive lower bounds on the win for a more general class of estimators that shrink the MLE toward a pre-specified D-dimensional subspace. See Appendix S4.4 for details and an application to a real dataset on which a large computed c-value indicates an improved estimate.

3.3 Empirical Verification

To explore the empirical properties of Bound 3.1, we simulated 500 datasets with N = 50 as $y\sim \mathcal{N}(\theta ,I_N)$ for each of several values of $\theta .$ For each simulated dataset y, we computed the win $W(\theta ,y),$ the proposed lower bound $b(y,\alpha ),$ and the c-value $c(y).$ Conveniently, for this likelihood, the distributions of $W(\theta ,y)$ and $b(y,\alpha )$ depend on θ only through $N^{-\frac{1}{2}}\Vert P_1^{\perp }\theta \Vert .$ Consequently, we can exhaustively assess how our procedure behaves for different θ by varying this norm. Throughout our simulation study, we fixed $\tau =1.$ With larger $\tau ,$ the alternative ${\theta }^{*}$ behaves more similarly to the default $\widehat{\theta }$, but the qualitative properties of the c-value and estimators remain similar.

We first checked that the empirical probability that the win $W(\theta ,y)$ exceeded the bound $b(y,\alpha )$ in Bound 3.1 was at least as large as the nominal probability α (Figure 1(a)). Across various choices of $N^{-\frac{1}{2}}\Vert P_1^{\perp }\theta \Vert ,$ we see that $b(·,\alpha )$ is conservative, typically providing higher than nominal coverage. Surprisingly, the gap between the actual and nominal coverages does not seem to depend heavily on θ, suggesting we could potentially obtain a tighter bound by calibrating $b(y,\alpha )$ to its actual coverage.

Fig. 1 Bound calibration and the two-stage estimator for a hierarchical normal model in simulation. (a) Empirical coverage of the lower bound $b(·,\alpha )$ across different levels $\alpha .$ Coverage is nearly identical across the parameter space. (b) Probability that the default has smaller loss but the alternative estimate is selected across the parameter space, with dashed lines reflecting nominal coverage. (c) Probability of selecting the alternative estimate. Selection probability is higher for lower thresholds $\alpha .$ (d) Risk profiles of the two-stage estimators for different choices of $\alpha ,$ as well as the MLE $\widehat{\theta }(·)$ and the shrinkage estimator ${\theta }^{*}(·).$ Each data point is computed from 500 replicates with N = 50.

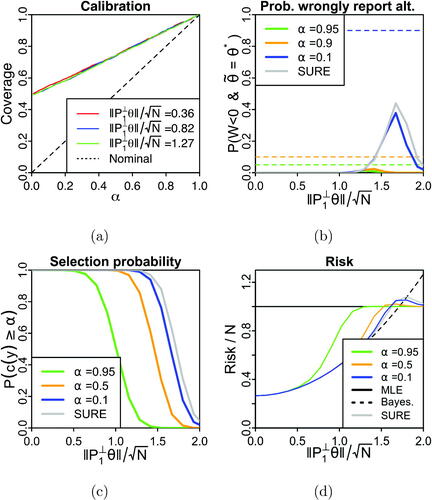
We next examined the probability that the alternative estimate is selected on the basis of a large c-value but obtains higher loss than the default estimate. Theorem 2.3 upper bounds this probability, and in Figure 1(b) we confirm this bound holds in practice across different thresholds α. Figure 1(b) additionally compares our proposed approach to using Stein’s unbiased estimate of the risk (Stein 1981) of ${\theta }^{*}(·)$ to select between the estimates. This approach, which we label “SURE”, returns $\widehat{\theta }(·)$ if the risk estimate exceeds N and returns ${\theta }^{*}(·)$ otherwise, and is akin to the focused information criterion (Claeskens and Hjort 2003). However, in contrast to the two-stage estimator ${\theta }^{†}(·,\alpha ),$ SURE does not provide tunable control over the probability that the alternative estimator ${\theta }^{*}(·)$ is mistakenly returned.

In the case that $\Vert P_1^{\perp }\theta \Vert /\sqrt{N}=1.7,$ choosing based on SURE gives the wrong estimate 80% of the time. Moreover, in the majority of these cases it is the alternative that is incorrectly returned (Table 2, Figure 1(b)). By contrast, the estimator that chooses based on the c-value (with a threshold $\alpha =0.95$) conservatively returns the default estimate in every replicate for this $\Vert P_1^{\perp }\theta \Vert /\sqrt{N}$ (Figure 1(c)). While this approach provides the estimate with greater loss in 54% of cases, it incorrectly reports the alternative in 0% of cases (Table 2). This behavior is expected as Theorem 2.3 provides an upper bound of $100*(1-\alpha )\%=5\%$. An estimator using the unbiased risk estimate satisfies no such guarantee.

Table 2 Contingency tables of simulation outcomes with $\Vert P_1^{\perp }\theta \Vert /\sqrt{N}=1.7$ when using Stein’s unbiased risk estimate (SURE), ${\theta }^{†}(·,\alpha =0.95)$, or ${\theta }^{†}(·,\alpha =0.5)$ to choose between the default and alternative estimates.

	SURE		${\theta }^{†}(·,\alpha =0.95)$		${\theta }^{†}(·,\alpha =0.5)$
	DR	AR	DR	AR	DR	AR
DLL	2%	44%	46%	0%	37%	9%
ALL	36%	18%	54%	0%	54%	0.1%

NOTE: DLL: default has lower loss, ALL: alternative has lower loss, DR: default reported, AR: alternative reported.

We next checked that our computed c-values successfully detected improvements by the alternative estimate. Recall that the alternative estimate ${\theta }^{*}(y)$ shrinks all components of y toward the global mean $\overline{y}.$ Further, recall that by construction ${\theta }^{†}(y,\alpha )={\theta }^{*}(y)$ if and only if $c(y)>\alpha .$ Intuitively, then, we would expect the alternative estimator to improve over the MLE and for the two-stage ${\theta }^{†}(·,\alpha )$ to select ${\theta }^{*}(·)$ when θ is close to the subspace spanned by ${\mathbf{1}}_N$ and $N^{-\frac{1}{2}}\Vert P_1^{\perp }\theta \Vert$ is small. Figure 1c, which plots the probability that ${\theta }^{†}(·,\alpha )$ selects ${\theta }^{*}(·)$ across different values of θ and $\alpha ,$ confirms this intuition; when $N^{-\frac{1}{2}}\Vert P_1^{\perp }\theta \Vert$ is small, we very often obtain large c-values and select the alternative estimator.

For completeness, we also considered the risk profile of the two-stage estimator ${\theta }^{†}(·,\alpha )$ (Figure 1(d)). Specifically, for different choices of θ we computed a Monte Carlo estimate of the expected squared error loss. For the most part, the risk of ${\theta }^{†}(·,\alpha )$ lies between the risks of $\widehat{\theta }(·)$ and ${\theta }^{*}(·).$ However, the risk of the two-stage estimator appears to exceed the risks of the default and alternative estimators for a narrow range of values of $\Vert P_1^{\perp }\theta \Vert .$ While it is tempting to characterize this excess risk as the price we must pay for “double-dipping” into our data, we note that the bump in risk appears to be nontrivial only for very small values of $\alpha .$ Recall again that we recommend choosing ${\theta }^{*}(y)$ in place of $\widehat{\theta }(y)$ only when c(y) is close to 1. As such, we do not expect this type of risk increase to be much of a concern in practice.

Interpreted together, Figure 1(c) and (d), illustrate the conservatism of the two stage approach with $\alpha =0.95$. For $\Vert P_1^{\perp }\theta \Vert$ between 1 and 1.5, ${\theta }^{†}(·,\alpha )$ only rarely evaluates to ${\theta }^{*}(·)$ even though this estimator has lower risk and typically has smaller loss.

Unlike conventional p-values under a null hypothesis, we should not expect the distribution of informative c-values to be uniform; indeed for parameters such that the win is consistently positive or negative, c-values can concentrate near 1 or 0, respectively.

4 Comparing Affine Estimates with Correlated Noise

We now generalize the situation described in the previous section in two ways. First, we consider correlated Gaussian noise with covariance Σ, where Σ is any N × N positive definite covariance matrix rather than restricting to $\Sigma =I_N$. Second, we let our default and alternative estimates, $\widehat{\theta }(y)$ and ${\theta }^{*}(y)$, be arbitrary affine transformations of the data y. Though these two estimates take similar functional forms in this section, we remain concerned with asymmetric comparisons wherein ${\theta }^{*}(y)$ is less familiar than $\widehat{\theta }(y).$

Although such generalization introduces considerable analytical challenges beyond those encountered in Section 3, we nevertheless can construct an approximate lower bound on the win that works well in practice. Specifically, for Bound 3.1, we used the tractable quantile function of the noncentral ${\chi }^2$ to guarantee exact coverage in Theorem 3.1. Now we encounter sums of differently scaled noncentral ${\chi }^2$ random variables, which do not admit analytically tractable quantiles. However, by approximating these sums with Gaussians with matched means and variances, we can proceed in essentially the same manner as in Section 3 to derive an approximate lower bound on the win. After introducing the bound, we comment on the key steps in its derivation to highlight the approximations involved, but leave details of intermediate steps to Appendix S5. We conclude with a non-asymptotic bound on the error introduced by these approximations on the coverage of the proposed bound on the win.

Approximate Bound 4.1 (Correlated Gaussian likelihood: arbitrary affine estimates). Observe $y=\theta +ϵ$ with $ϵ\sim \mathcal{N}(0,\Sigma )$ and consider $\widehat{\theta }(y)=Ay+k$ versus ${\theta }^{*}(y)=Cy+\mathcal{l},$ where $A,C\in {\mathbb{R}}^{N\times N}$ are matrices and $k,\mathcal{l}\in {\mathbb{R}}^N$ are N-vectors. We propose (10) $$\begin{array}{ccc}b(y,\alpha )& =& \Vert \widehat{\theta }-y{\Vert }^2-\Vert {\theta }^{*}-y{\Vert }^2+2\text{tr}[(A-C)\Sigma ]\\ & & +2z_{\frac{1-\alpha }{2}}\sqrt{\begin{array}{c}U(\Vert G(y){\Vert }_{\Sigma }^2,\frac{1-\alpha }{2})\hfill \\ \hspace{1em}+\frac{1}{2}\Vert {\Sigma }^{\frac{1}{2}}(A+A^{\top }-C-C^{\top }){\Sigma }^{\frac{1}{2}}{\Vert }_F^2\hfill \end{array}}\end{array}$$(10) as an approximate high-probability lower bound for the win. In this expression, $\text{tr}[·]$ denotes the trace of a matrix, $G(y):=(A-C)y+(k-\mathcal{l}),\Vert ·{\Vert }_{\Sigma }$ denotes the Σ quadratic norm of a vector ($\Vert v{\Vert }_{\Sigma }:=\sqrt{v^{\top }\Sigma v}$), $\Vert ·{\Vert }_F$ denotes the Frobenius norm of a matrix, and $z_{\alpha }$ denotes the α-quantile of the standard normal. (11) $$\begin{array}{c}U(\Vert G(y){\Vert }_{\Sigma }^2,1-\alpha )\hfill \\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}:=\underset{\delta >0}{\inf }\{\delta | \Vert G(y){\Vert }_{\Sigma }^2\le (\delta +\Vert {\Sigma }^{\frac{1}{2}}(A-C){\Sigma }^{\frac{1}{2}}{\Vert }_F^2)\hfill \\ \hspace{1em}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}+z_{1-\alpha }\sqrt{\begin{array}{c}2\Vert {\Sigma }^{\frac{1}{2}}(A-C)\Sigma {(A-C)}^{\top }{\Sigma }^{\frac{1}{2}}{\Vert }_F^2\hfill \\ \hspace{1em}+4\Vert {\Sigma }^{\frac{1}{2}}(A-C){\Sigma }^{\frac{1}{2}}{\Vert }_{\text{OP}}^2\delta \hfill \end{array}}\}\hfill \end{array}$$(11) is an approximate high-confidence upper bound on $\Vert G(\theta ){\Vert }_{\Sigma }^2$ where $\Vert ·{\Vert }_{\text{OP}}$ denotes the L2 operator norm of a matrix.

To derive Approximate Bound 4.1 we again start by rewriting the alternative estimate as ${\theta }^{*}(y)=\widehat{\theta }(y)-G(y)$, where now $G(·)$ is an affine transformation of y, $G(y):=(A-C)y+(k-\mathcal{l}).$ We next write the squared error win of using ${\theta }^{*}(y)$ in place of $\widehat{\theta }(y)$ as (12) $$\begin{array}{cc}W(\theta ,y)\hfill & =2{ϵ}^{\top }G(y)+\left(\Vert \widehat{\theta }(y)-y{\Vert }^2-\Vert {\theta }^{*}(y)-y{\Vert }^2\right)\hfill \end{array}$$(12) and observe that it suffices to obtain a high-probability lower bound for this first term. For tractability, we approximate the distribution of ${ϵ}^{\top }G(y)$ by a normal with matched mean and variance. As we will soon see, this approximation is accurate when N is large and A – C is well conditioned; in this case ${ϵ}^{\top }G(y)$ may be written as the sum of many of uncorrelated terms of similar size. The mean and variance may be expressed as (13) $$\begin{array}{c}\mathbb{E}[{ϵ}^{\top }G(y)]=\text{tr}[(A-C)\Sigma ],\\ \text{var}[{ϵ}^{\top }G(y)]=\Vert G(\theta ){\Vert }_{\Sigma }^2+\frac{\Vert {\Sigma }^{\frac{1}{2}}(A+A^{\top }-C-C^{\top }){\Sigma }^{\frac{1}{2}}{\Vert }_F^2}{2}.\end{array}$$(13)

With these moments in hand, we form a probability α lower bound approximately as (14) $$\begin{array}{c}W(\theta ,y)\ge \Vert \widehat{\theta }(y)-y{\Vert }^2-\Vert {\theta }^{*}(y)-y{\Vert }^2+2\text{tr}[(A-C)\Sigma ]\\ +2z_{1-\alpha }\sqrt{\Vert G(\theta ){\Vert }_{\Sigma }^2+\frac{1}{2}\Vert {\Sigma }^{\frac{1}{2}}(A+A^{\top }-C-C^{\top }){\Sigma }^{\frac{1}{2}}{\Vert }_F^2}.\end{array}$$(14)

However, as before, in order to use this approximate bound we require a simultaneous upper bound on a norm of a transformation of the unknown parameter, in this case $\Vert G(\theta ){\Vert }_{\Sigma }^2.$ We compute one by considering the test statistic $\Vert G(y){\Vert }_{\Sigma }^2$ and again appealing to approximate normality. In particular we characterize the dependence of the distribution of this statistic on $\Vert G(\theta ){\Vert }_{\Sigma }^2$ through its mean and variance. We find its mean as (15) $$\begin{array}{c}\mathbb{E}[\Vert G(y){\Vert }_{\Sigma }^2]=\Vert G(\theta ){\Vert }_{\Sigma }^2+\Vert {\Sigma }^{\frac{1}{2}}(A-C){\Sigma }^{\frac{1}{2}}{\Vert }_F^2\hfill \end{array}$$(15) and upper bound its variance by (16) $$\begin{array}{c}\text{var}[\Vert G(y){\Vert }_{\Sigma }^2]\le 2\Vert {\Sigma }^{\frac{1}{2}}(A-C)\Sigma {(A-C)}^{\top }{\Sigma }^{\frac{1}{2}}{\Vert }_F^2\\ \hspace{1em}+4\Vert {\Sigma }^{\frac{1}{2}}(A-C){\Sigma }^{\frac{1}{2}}{\Vert }_{\text{OP}}^2\Vert G(\theta ){\Vert }_{\Sigma }^2.\end{array}$$(16)

Using the two quantities above and an appeal to approximate normality, we propose the approximate high-confidence upper bound, $U(\Vert G(y){\Vert }_{\Sigma }^2,1-\alpha ),$ in Equation (11)(11) $$\begin{array}{c}U(\Vert G(y){\Vert }_{\Sigma }^2,1-\alpha )\hfill \\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}:=\underset{\delta >0}{\inf }\{\delta | \Vert G(y){\Vert }_{\Sigma }^2\le (\delta +\Vert {\Sigma }^{\frac{1}{2}}(A-C){\Sigma }^{\frac{1}{2}}{\Vert }_F^2)\hfill \\ \hspace{1em}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}+z_{1-\alpha }\sqrt{\begin{array}{c}2\Vert {\Sigma }^{\frac{1}{2}}(A-C)\Sigma {(A-C)}^{\top }{\Sigma }^{\frac{1}{2}}{\Vert }_F^2\hfill \\ \hspace{1em}+4\Vert {\Sigma }^{\frac{1}{2}}(A-C){\Sigma }^{\frac{1}{2}}{\Vert }_{\text{OP}}^2\delta \hfill \end{array}}\}\hfill \end{array}$$(11) . As before, by splitting our α across these two bounds we obtain the desired expression, Equation (10)(10) $$\begin{array}{ccc}b(y,\alpha )& =& \Vert \widehat{\theta }-y{\Vert }^2-\Vert {\theta }^{*}-y{\Vert }^2+2\text{tr}[(A-C)\Sigma ]\\ & & +2z_{\frac{1-\alpha }{2}}\sqrt{\begin{array}{c}U(\Vert G(y){\Vert }_{\Sigma }^2,\frac{1-\alpha }{2})\hfill \\ \hspace{1em}+\frac{1}{2}\Vert {\Sigma }^{\frac{1}{2}}(A+A^{\top }-C-C^{\top }){\Sigma }^{\frac{1}{2}}{\Vert }_F^2\hfill \end{array}}\end{array}$$(10) in Approximate Bound 4.1.

Approximation Quality

Due to the two Gaussian approximations, Approximate Bound 4.1 does not provide nominal coverage by construction. Our next result shows that little error is introduced when N is large enough and the problem is well conditioned.

Theorem 4.1

(Berry–Esseen bound). Let $\alpha \in (0,1)$ and consider $b(·,\alpha )$ in Approximate Bound 4.1. If both A and C are symmetric, then (17) $${\mathbb{P}}_{\theta }\left[W(\theta ,y)\ge b(y,\alpha )\right]\ge \alpha -\frac{10\sqrt{2}}{\sqrt{N}}{C}_1·\kappa {({\Sigma }^{\frac{1}{2}}(A-C){\Sigma }^{\frac{1}{2}})}^2$$(17) where $\kappa (·)$ denotes the condition number of its matrix argument (i.e., the ratio of its largest to smallest singular values) and $C_1\le 1.88$ is a universal constant (Berry, 1941, Theorem 1).

Remark 4.2.

Theorem 4.1 is a special case of a more general result that we provide in Appendix S5.4, which does not require A and C to be symmetric. We highlight this special case here because the bound takes a simpler form from which the dependence on the conditioning of A–C is clearer, and because this condition is satisfied for many important estimates. Notably A and C are symmetric in all applications discussed in this article.

Though Theorem 4.1 provides an expected $O\left(N^{-\frac{1}{2}}\right)$ drop in approximation error, the bound itself may be too loose to be useful in practice. In Section 6.1 we show in simulation that Approximate Bound 4.1 provides sufficient coverage even without this correction. This conservatism likely owes to slack from (A) the operator norm bound in Equation (16)(16) $$\begin{array}{c}\text{var}[\Vert G(y){\Vert }_{\Sigma }^2]\le 2\Vert {\Sigma }^{\frac{1}{2}}(A-C)\Sigma {(A-C)}^{\top }{\Sigma }^{\frac{1}{2}}{\Vert }_F^2\\ \hspace{1em}+4\Vert {\Sigma }^{\frac{1}{2}}(A-C){\Sigma }^{\frac{1}{2}}{\Vert }_{\text{OP}}^2\Vert G(\theta ){\Vert }_{\Sigma }^2.\end{array}$$(16) and (B) the union bound ensuring that the confidence interval for $\Vert G(\theta ){\Vert }_{\Sigma }^2$ and the quantile in Equation (14)(14) $$\begin{array}{c}W(\theta ,y)\ge \Vert \widehat{\theta }(y)-y{\Vert }^2-\Vert {\theta }^{*}(y)-y{\Vert }^2+2\text{tr}[(A-C)\Sigma ]\\ +2z_{1-\alpha }\sqrt{\Vert G(\theta ){\Vert }_{\Sigma }^2+\frac{1}{2}\Vert {\Sigma }^{\frac{1}{2}}(A+A^{\top }-C-C^{\top }){\Sigma }^{\frac{1}{2}}{\Vert }_F^2}.\end{array}$$(14) hold simultaneously.

Remark 4.3

(Fast computation of $b(y,\alpha )$ A naive approach to computing $b(y,\alpha )$ in Equation (10)(10) $$\begin{array}{ccc}b(y,\alpha )& =& \Vert \widehat{\theta }-y{\Vert }^2-\Vert {\theta }^{*}-y{\Vert }^2+2\text{tr}[(A-C)\Sigma ]\\ & & +2z_{\frac{1-\alpha }{2}}\sqrt{\begin{array}{c}U(\Vert G(y){\Vert }_{\Sigma }^2,\frac{1-\alpha }{2})\hfill \\ \hspace{1em}+\frac{1}{2}\Vert {\Sigma }^{\frac{1}{2}}(A+A^{\top }-C-C^{\top }){\Sigma }^{\frac{1}{2}}{\Vert }_F^2\hfill \end{array}}\end{array}$$(10) involves finding $U(\Vert G(y){\Vert }_{\Sigma }^2,\frac{1-\alpha }{2})$ with a binary search. For more rapid computation, we can recognize $U(\Vert G(y){\Vert }_{\Sigma }^2,\frac{1-\alpha }{2})$ as the root of a quadratic. Specifically, define $\gamma :=\Vert G(y){\Vert }_{\Sigma }^2-\Vert {\Sigma }^{\frac{1}{2}}(A-C){\Sigma }^{\frac{1}{2}}{\Vert }_F^2,\eta :=z_{\frac{\alpha }{2}}$, $\rho :=2\Vert {\Sigma }^{\frac{1}{2}}(A-C)\Sigma {(A-C)}^{\top }{\Sigma }^{\frac{1}{2}}{\Vert }_F^2$, and $\nu :=4\Vert {\Sigma }^{\frac{1}{2}}(A-C){\Sigma }^{\frac{1}{2}}{\Vert }_{\text{OP}}^2$; then from Equation (11)(11) $$\begin{array}{c}U(\Vert G(y){\Vert }_{\Sigma }^2,1-\alpha )\hfill \\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}:=\underset{\delta >0}{\inf }\{\delta | \Vert G(y){\Vert }_{\Sigma }^2\le (\delta +\Vert {\Sigma }^{\frac{1}{2}}(A-C){\Sigma }^{\frac{1}{2}}{\Vert }_F^2)\hfill \\ \hspace{1em}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}+z_{1-\alpha }\sqrt{\begin{array}{c}2\Vert {\Sigma }^{\frac{1}{2}}(A-C)\Sigma {(A-C)}^{\top }{\Sigma }^{\frac{1}{2}}{\Vert }_F^2\hfill \\ \hspace{1em}+4\Vert {\Sigma }^{\frac{1}{2}}(A-C){\Sigma }^{\frac{1}{2}}{\Vert }_{\text{OP}}^2\delta \hfill \end{array}}\}\hfill \end{array}$$(11) we have that the δ that achieves the supremum satisfies $\gamma =\delta +\eta \sqrt{\rho +\nu \delta }.$ Rearranging, we find that $U(\Vert G(y){\Vert }_{\Sigma }^2,\frac{1-\alpha }{2})$ is the larger root of $x^2-(2\gamma +{\eta }^2\nu )x+({\gamma }^2-{\eta }^2\rho )=0.$

5 Extending the Reach of the c-value

Up to this point, we focused on estimating normal means with fixed affine estimators. Now we extend our c-value framework in two important directions, which we support with both theoretical and empirical results. In Section 5.1, we derive c-values for a nonlinear shrinkage estimator of normal means. We then move beyond Gaussian likelihoods in Section 5.2 and derive c-values for regularized logistic regression. In contrast to the earlier cases, these settings introduce nonlinear estimates and non-Gaussian models. To gain analytical tractability, we approximate the estimates by linear transformations of a statistic that is asymptotically Gaussian. This approximation allows us to derive bounds $b(y,\alpha )$ that we show have the correct coverage in an asymptotic regime. Our approach provides a template that can be followed for other nonlinear estimates and models for which the MLE is asymptotically Gaussian. We defer all proofs and details of synthetic data experiments to Appendices S6 and S7.

5.1 Empirical Bayes Shrinkage Estimates

Many Bayesian estimates are affine in the data for fixed settings of prior parameters. But when prior parameters are chosen using the data, the resulting empirical Bayesian estimates are not affine in general. We next explore computation of approximate high-confidence lower bounds on the win of empirical Bayesian estimators. In particular, we consider an approach that essentially amounts to ignoring the randomness in estimated prior parameters and computing the bound as if the prior were fixed. For simplicity, we focus on a particularly simple empirical Bayesian estimator for the normal means problem that coincides with the James–Stein estimator (Efron and Morris 1973). We find that, in the high-dimensional limit, bounds obtained with this naive approach achieve at least the desired nominal coverage. Finally, we show in simulation that the approximate bound has favorable finite sample coverage properties.

Empirical Bayes for estimation of normal means

Consider a sequence of real-valued parameters ${\theta }_1,{\theta }_2,\dots ,$ and corresponding observations $y_n\stackrel{\text{indep}}{\sim }\mathcal{N}({\theta }_n,1)$. For each $N\in \mathbb{N}$, let ${\Theta }_N:={[{\theta }_1,{\theta }_2,\dots ,{\theta }_N]}^{\top }$ and $Y_N:={[y_1,y_2,\dots ,y_N]}^{\top }$ denote the first N parameters and observations, respectively.

We consider the MLE for Θ_N (i.e., Y_N) as our default, which we denote by ${\widehat{\Theta }}_N(Y_N)=Y_N,$ and we take the James–Stein estimate as our alternative; we compare on the basis of squared error loss. We write the James–Stein estimate on the first N data points as ${\Theta }_N^{*}(Y_N):=(1-{(1+{\widehat{\tau }}_N^2(Y_N))}^{-1})Y_N,$ where ${\widehat{\tau }}_N^2(Y_N):=\Vert Y_N{\Vert }^2/(N-2)-1$. ${\Theta }_N^{*}(Y_N)$ corresponds to the Bayes estimate under the prior ${\theta }_n\stackrel{\text{iid}}{\sim }\mathcal{N}(0,{\widehat{\tau }}_N^2)$ (Efron and Morris 1973). For this comparison, the win is $W_N(Y_N,{\Theta }_N):=\Vert {\widehat{\Theta }}_N(Y_N)-{\Theta }_N{\Vert }^2-\Vert {\Theta }_N^{*}(Y_N)-{\Theta }_N{\Vert }^2$, and Appendix S6 details the associated bound $b_N(Y_N,\alpha )$ obtained with Bound S4.1. In the following theorem, we lower bound the win by applying our earlier machinery for Bayes rules with fixed priors. We find that the desired coverage is obtained in the high-dimensional limit.

Theorem 5.1.

For each $N\in \mathbb{N}$, let ${\tau }_N^2:=N^{-1}{\sum }_{n=1}^N{\theta }_n^2$. If the sequence ${\tau }_1,{\tau }_2,\dots$ is bounded, then for any $\alpha \in [0,1],\underset{N\to \infty }{\lim }\mathbb{P}\left[W_N(Y_N,{\Theta }_N)\ge b_N(Y_N,\alpha )\right]\ge \alpha .$

The key step in the proof of Theorem 5.1 is establishing an $O_p\left(N^{-\frac{1}{2}}\right)$ rate of convergence of ${\widehat{\tau }}_N^2-{\tau }_N^2$ to zero; under this condition the empirical Bayes estimate and bound converge to the analogous estimates and bounds computed with the prior variance fixed to ${\tau }_N^2.$ Accordingly, we expect similar results to hold for other models and empirical Bayes estimates when the standard deviations of the empirical Bayes estimates of the prior parameters drop as $O_p\left(N^{-\frac{1}{2}}\right)$.

Remark 5.2.

Theorem 5.1 easily extends to cover the case in which we consider a sequence of random (rather than fixed) parameters drawn iid from a Bayesian prior, which is a more classical setup for guarantees of empirical Bayesian methods; see, for example, Robbins (1964). Specifically, our proof goes through in this Bayesian setting so long as the sequence ${\tau }_1^2,{\tau }_2^2,\dots$ is bounded in probability. This condition is satisfied, for example, when the θ_n are iid from any prior with a finite second moment.

To check finite sample coverage, we performed a simulation and evaluated calibration of the associated c-values (Figure S4 in Appendix S6). Despite the empirical Bayes step, the c-values appear to be similarly conservative to those computed with the exact bound in Figure 1(a). Furthermore, this calibration profile does not appear to be sensitive to the magnitude of the unknown parameter.

5.2 Logistic Regression

In this section we illustrate how to compute an approximate high-confidence lower bound on the win in squared error loss with a logistic regression likelihood. Our key insight is that by appealing to limiting behavior, we can tackle the non-Gaussianity using the machinery developed in Section 4.

Notation and estimates

Consider a collection of M data points with random covariates $X_M:={[x_1,x_2,\dots ,x_M]}^{\top }\in {\mathbb{R}}^{M\times N}$ and responses $Y_M:={[y_1,y_2,\dots ,y_M]}^{\top }\in {\{1,-1\}}^M$. For the mth data point, assume (18) $$\begin{array}{c}{y}_m\stackrel{\text{indep}}{\sim }p(·|x_m;\theta ):={(1+\hspace{0.17em}\exp \hspace{0.17em}\{-x_m^{\top }\theta \})}^{-1}{\delta }_1\\ \hspace{1em}+{(1+\hspace{0.17em}\exp \hspace{0.17em}\{x_m^{\top }\theta \})}^{-1}{\delta }_{-1},\end{array}$$(18) where $\theta \in {\mathbb{R}}^N$ is an unknown parameter of covariate effects and δ₁ and ${\delta }_{-1}$ denote Dirac masses on 1 and –1, respectively.

In this section, we choose the MLE as our default, $\widehat{\theta }(X_M,Y_M):=\text{arg} {\max }_{\theta }\hspace{0.17em}\log \hspace{0.17em}p(Y_M|X_M;\theta )$. And we choose our alternative to be a Bayesian maximum a posteriori (MAP) estimate under a standard normal prior ($\theta \sim \mathcal{N}(0,I_N)$): $${\theta }^{*}(X_M,Y_M):=\text{arg} {\max }_{\theta }\left\{\hspace{0.17em}\log \hspace{0.17em}p(Y_M|X_M;\theta )-\frac{1}{2}\Vert \theta {\Vert }^2\right\}.$$

While a first choice for a Bayesian estimate might be the posterior mean, the MAP is an effective and widely used alternative to the MLE in practice. Furthermore, ${\theta }^{*}(X_M,Y_M)$ is also of interest as an L2 regularized logistic regression estimate.

Approximating ${\theta }^{*}$ by an affine transformation

In moving away from a Gaussian likelihood we forfeit prior-to-likelihood conjugacy. In previous sections, conjugacy provided analytically convenient expressions for Bayes estimates. In order to regain analytical tractability, we appeal to a Gaussian approximation of the likelihood, defined with a second order Taylor approximation of the log-likelihood around the MLE. Under this approximation, $\widehat{\theta }(X_M,Y_M)\sim \mathcal{N}(\theta ,{\tilde{\Sigma }}_M),$ where ${\tilde{\Sigma }}_M:=-{\nabla }_{\theta }^2\hspace{0.17em}\log \hspace{0.17em}p(Y_M|X_M;\theta ){|}_{\theta =\widehat{\theta }(X_M,Y_M)}.$ As such, we regain conjugacy, and we obtain an approximate Bayes estimate as an affine transformation of the MLE, (19) $${\tilde{\theta }}^{*}(X_M,Y_M)={\left[I_N+{\tilde{\Sigma }}_M\right]}^{-1}\widehat{\theta }(X_M,Y_M).$$(19)

As we show in Appendix S7, ${\tilde{\theta }}^{*}(X_M,Y_M)$ is a very close approximation of ${\theta }^{*}(X_M,Y_M),$ with distance decreasing at an $O_p(M^{-2})$ rate.

An approximate bound and an asymptotic guarantee

We leverage the form in Equation (19)(19) $${\tilde{\theta }}^{*}(X_M,Y_M)={\left[I_N+{\tilde{\Sigma }}_M\right]}^{-1}\widehat{\theta }(X_M,Y_M).$$(19) to compute Approximate Bound 4.1 as a lower bound on the win in squared error of using the MAP estimate in place of the MLE. In particular, we take $y:=\widehat{\theta }(X_M,Y_M)$ as the data in Approximate Bound 4.1 (this corresponds to A = I_N and k = 0) and approximate the distribution of $ϵ:=\widehat{\theta }(X_M,Y_M)-\theta$ as $\mathcal{N}(0,{\tilde{\Sigma }}_M).$ Further, to compute the bound, we approximate ${\theta }^{*}(X_M,Y_M)$ by ${\tilde{\theta }}^{*}(X_M,Y_M)$ as in Equation (19)(19) $${\tilde{\theta }}^{*}(X_M,Y_M)={\left[I_N+{\tilde{\Sigma }}_M\right]}^{-1}\widehat{\theta }(X_M,Y_M).$$(19) , corresponding to $C={\left[I_N+{\tilde{\Sigma }}_M\right]}^{-1}$ and $\mathcal{l}=0$.

While the precise coverage of this bound is difficult to analyze, our next result reveals favorable properties in the large sample limit.

Theorem 5.3.

Consider a sequence of random covariates $x_1,x_2,\dots$ and responses $y_1,y_2,\dots$ distributed as in Equation (18)(18) $$\begin{array}{c}{y}_m\stackrel{\text{indep}}{\sim }p(·|x_m;\theta ):={(1+\hspace{0.17em}\exp \hspace{0.17em}\{-x_m^{\top }\theta \})}^{-1}{\delta }_1\\ \hspace{1em}+{(1+\hspace{0.17em}\exp \hspace{0.17em}\{x_m^{\top }\theta \})}^{-1}{\delta }_{-1},\end{array}$$(18) . For each $M\in \mathbb{N},$ let $W_M:=\Vert \widehat{\theta }(X_M,Y_M)-\theta {\Vert }^2-\Vert {\theta }^{*}(X_M,Y_M)-\theta {\Vert }^2$ be the win of using the MAP estimate in place of the MLE. Finally, let $b_M(\alpha )$ be the level-α approximate bound on W_M described above. If $x_1,x_2,\dots$ are iid with finite third moment and with positive definite covariance, then for any $\alpha \in (0,1),\underset{M\to \infty }{\lim }{\mathbb{P}}_{\theta }\left[W_M\ge b_M(\alpha )\right]\ge \alpha .$

Theorem 5.3 guarantees that in the large sample limit, $b_M(·)$ has at least nominal coverage. We provide a proof of the theorem and demonstrate its favorable empirical properties in simulation in Appendix S7.

6 Applications

We now demonstrate our approach on the three applications introduced in Section 1. Our goal in this section is to demonstrate how one can compute and interpret c-values in realistic workflows. In analogy to hypothesis testing, where a p-value cutoff of 0.05 is standard for rejecting a null, we require a c-value of at least 0.95 to accept the alternative estimate; with this threshold, we expect to incorrectly reject the default estimate in at most 5% of our decisions. This choice, instead of 0.5 for example, reflects the presumed asymmetry of the comparisons; we demand strong support to adopt the alternative over the default. For all applications, we provide substantial additional details in Appendix S8.

6.1 Estimation from Educational Testing Data and Empirical Bayes

In this section we apply our methodology to a model and dataset considered by (Hoff 2021, sec. 3.2), in which the goal is to estimate the average student reading ability at different schools in the 2002 Educational Longitudinal Study. At each of N = 676 schools, between 5 and 50 tenth grade students were given a standardized test of reading ability. We let $y={[y_1,y_2,\dots ,y_N]}^{\top }$ denote the average scores, and for each school, indexed by n, model $y_n\stackrel{\text{indep}}{\sim }\mathcal{N}({\theta }_n,{\sigma }_n^2),$ where $\theta ={[{\theta }_1,{\theta }_2,\dots ,{\theta }_N]}^{\top }$ denotes the school-level means and each σ_n is the school-level standard error; specifically ${\sigma }_n:=\sigma /\sqrt{N_n}$ where σ denotes a student-level standard deviation and N_n is the number of students tested at school N_n. For convenience, we let $\Sigma :=\text{diag}([{\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_N^2])$ so that we may write $y\sim \mathcal{N}(\theta ,\Sigma ).$ The goal is to estimate the school-level performances $\theta .$

Following Hoff (2021), we perform small area inference with the Fay-Herriot model (Fay and Herriot 1979) to estimate θ under the assumption that similar schools may have similar student performances. Specifically, we consider a vector of D = 8 attributes of each school $X={[x_1,x_2,\dots ,x_N]}^{\top }$; these include participation levels in a free lunch program, enrollment, and other characteristics such as region and school type. We model the school-level mean as a priori distributed as $\theta \sim \mathcal{N}(X\beta ,{\tau }^2{I}_N)$ where β is an unknown D-vector of fixed effects and ${\tau }^2$ is an unknown scalar that describes variation in θ not captured by the covariates. Following Hoff (2021), we take an empirical Bayesian approach and estimate $\beta ,\tau$, and σ with lme4 (Bates et al. 2015). We then compare the posterior mean—which is affine in y for fixed $\beta ,\tau$, and σ—as an alternative to the MLE as a default; we use Approximate Bound 4.1. Specifically, we take ${\theta }^{*}(y):=\mathbb{E}[\theta |y;\beta ,\tau ,\sigma ]={[I_N+{\tau }^{-2}\Sigma ]}^{-1}y+{[I_N+{\tau }^2{\Sigma }^{-1}]}^{-1}X\beta$ and $\widehat{\theta }(y)=y.$ We compute a large c-value (c = 0.9926); its closeness to one strongly suggests that ${\theta }^{*}(y)$ is more accurate than $\widehat{\theta }(y).$

We should not always expect to obtain a large c-value for any alternative estimate, however. We next describe a case where we expect the alternative estimate to be less accurate than the default, and we check that we obtain a small c-value. In particular, we now let our alternative estimate be the posterior mean under the same model as above but with the covariates, X, randomly permuted across schools. In this situation, the responses y have no relation to the covariates, and we should not expect an improvement. Indeed, on this dataset we compute a c-value of exactly zero. However, we recall that just as a large p-value in hypothesis testing does not provide support that a null hypothesis is true, a small c-value does not provide direct support that the alternative estimate is less accurate than the default.

We provide additional details for all parts of this application in Appendix S8.1. There, we demonstrate in a simulation study that our bounds remain substantially conservative for these estimators and model even with an empirical Bayes step.

6.2 Estimating Violent Crime Density in Philadelphia

As a second application, we consider estimating the areal density of violent crimes (i.e., counts per square mile) reported in each of Philadelphia’s N = 384 census tracts. Following Balocchi et al. (2022), we work with the inverse hyperbolic sine transformed density. Letting y_n be the observed transformed density of reported violent crimes in census tract n, we model $y_n\stackrel{\text{indep}}{\sim }\mathcal{N}({\theta }_n,{\sigma }_y^2)$ where θ_n represents the underlying transformed density and ${\sigma }_y^2$ is the noise variance. While one might interpret θ_n as the true density of violent crime in census tract n, we note that the implicit assumption of zero-mean error in each tract may not be realistic. Namely, systematic biases may impact the rates at which police receive and respond to calls and file incident reports in different parts of the city. Unfortunately, we are unable to probe this possibility with the available data. Nevertheless, our goal is to estimate the vector of unknown rates, $\theta ={[{\theta }_1,{\theta }_2,\dots ,{\theta }_N]}^{\top }$ from $y={[y_1,y_2,\dots ,y_N]}^{\top }.$ The observations y are a simple proxy of transformed violent crime density, but they are noisy. So it is natural to wonder if we might obtain a more accurate estimate of $\theta .$

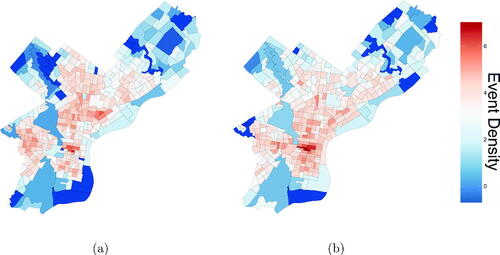
Figure 2 plots the transformed densities of both violent and nonviolent crimes reported in October 2018 in each census tract. Immediately, we see that, for any particular census tract, the observed densities of the two types of crime are similar. Further, we observe considerable spatial correlation in each plot. It is tempting to use a Bayesian hierarchical model that exploits this structure in order to produce more accurate estimates of $\theta .$ In this application, we consider iteratively refining an estimate of θ by (A) incorporating the observed nonviolent crime data and then by (B) carefully accounting for the observed spatial correlation. At each step of our refinement, we use a c-value to decide whether to continue. Before proceeding, we make a remark about our sequential approach.

Fig. 2 Transformed densities of reported (a) violent and (b) nonviolent crimes in each census tract in Philadelphia in October 2018.

Remark 6.1.

Consider using c-values and a chosen level α to choose one of three estimates (say $\widehat{\theta }(y),{\theta }^{*}(y)$, and ${\theta }^{°}(y)$) in two stages. Suppose we first choose ${\theta }^{*}(y)$ over $\widehat{\theta }(y)$ only if the associated c-value is greater than α. Second, only if we chose ${\theta }^{*}(y)$, we next choose ${\theta }^{°}(y)$ over ${\theta }^{*}(y)$ only if the new c-value associated with those estimates exceeds α. Then a union bound guarantees that ${\theta }^{°}(y)$ will be incorrectly chosen with probability at most $2(1-\alpha )$.

We begin by seeing if we can improve upon the MLE, $\widehat{\theta }(y)=y,$ by leveraging the auxiliary dataset of transformed nonviolent crimes in each tract, $z_1,z_2,\dots ,z_N.$ To this end, we model these auxiliary data analogously to y; in each tract n, we let η_n be the unknown transformed density and independently model $z_n\stackrel{\text{indep}}{\sim }\mathcal{N}({\eta }_n,{\sigma }_z^2).$ We next introduce a hierarchical prior that captures the apparent similarity between θ and η within each tract. Specifically, for each tract n we decompose ${\theta }_n={\mu }_n+{\delta }_n^y$ and ${\eta }_n={\mu }_n+{\delta }_n^z,$ where μ_n is a shared mean for the transformed densities of violent and nonviolent reports and ${\delta }_n^y$ and ${\delta }_n^z$ represent deviations from the shared mean specific to each crime type. Rather than encode explicit prior beliefs about ${\mu }_n,$ we express ignorance in these quantities with an improper uniform prior. Additionally, we model ${\delta }_n^y,{\delta }_n^z\stackrel{\text{iid}}{\sim }\mathcal{N}(0,{\sigma }_{\delta }^2)$. We fix the values of ${\sigma }_y,{\sigma }_z,$ and ${\sigma }_{\delta }$ using historical data. We then compute the posterior mean of θ as an alternative estimate, ${\theta }^{*}(y).$ Thanks to the Gaussian conjugacy of this model, ${\theta }^{*}(y)$ is affine in the data y, and a closed form expression is available. See Appendix S8.2 for additional details. The resulting c-value exceeded 0.999, suggesting that we should be highly confident that ${\theta }^{*}(y)$ is a more accurate estimate of θ than $\widehat{\theta }(y).$

We next consider additionally sharing strength amongst spatially adjacent census tracts. To this end, consider a second model with spatially correlated variance components: ${\theta }_n={\mu }_n+{\delta }_n^y+{\kappa }_n^y\mathrm{ }\text{and}\mathrm{ }{\eta }_n={\mu }_n+{\delta }_n^z+{\kappa }_n^z.$ The additional terms ${\kappa }^y={[{\kappa }_1^y,{\kappa }_2^y,\dots ,{\kappa }_N^y]}^{\top }$ and ${\kappa }^z={[{\kappa }_1^z,{\kappa }_2^z,\dots ,{\kappa }_N^z]}^{\top }$ capture a priori spatial correlations; we model ${\kappa }^y,{\kappa }^z\stackrel{\text{iid}}{\sim }\mathcal{N}(0,K),$ where K is an $N\times N$ covariance matrix determined by a squared exponential covariance function (Rasmussen and Williams 2006, chap. 4) that depends on the distance between the centroids of the census tracts. Once again, we exploit conjugacy in this second hierarchical model to derive the posterior mean ${\theta }^{°}(y)$ in closed form. As ${\theta }^{°}(y)$ is also an affine transformation of y, we can use Approximate Bound 4.1 to compute the c-value for comparing ${\theta }^{°}(y)$ to ${\theta }^{*}(y).$ The c-value for this comparison is only 0.843, providing much weaker support for using ${\theta }^{°}(y)$ over ${\theta }^{*}(y).$ Because this c-value is less than 0.95, we conclude our analysis content with ${\theta }^{*}(y)$ as our final estimate.

6.3 Gaussian Process Kernel Choice: Modeling Ocean Currents

Accurate understanding of ocean current dynamics is important for forecasting the dispersion of oceanic contaminations, such as after the Deepwater Horizon oil spill (Poje et al. 2014). Lodise et al. (2020) have recently advocated for a statistical approach to inferring ocean currents from observations of free-floating, GPS-trackable buoys. Their approach seeks to provide improved estimates by incorporating variation at the submesoscale (roughly 0.1–10 km) in addition to more commonly considered mesoscale variation (roughly 10 km and above). In this section we apply our methodology to assess if this approach provides improved estimates relative to a baseline including only mesoscale variation.

In our analysis, we consider a segment of the Carthe Grand Lagrangian Drifter (GLAD) deployment dataset (Özgökmen 2013). Specifically, we model a set of 50 buoys with velocities estimated at 3 hr intervals over one day (N = 400 observations total). Each observation n consists of latitudinal and longitudinal ocean current velocity measurements $y_n={[y_n^{(1)},y_n^{(2)}]}^{\top }\in {\mathbb{R}}^2$ and associated spatio-temporal coordinates $[{\text{lat}}_n,{\text{lon}}_n,t_n].$ Following Lodise et al. (2020), we model each measurement as a noisy observation of an underlying time varying vector-field distributed independently as $y_n\stackrel{\text{indep}}{\sim }\mathcal{N}(F({\text{lat}}_n,{\text{lon}}_n,t_n),{\sigma }_{ϵ}^2{I}_2),$ where $F:{\mathbb{R}}^3\to {\mathbb{R}}^2$ denotes the time evolving vector-field of ocean currents and ${\sigma }_{ϵ}^2$ is the error variance. Our goal is to estimate F at the observation points $\theta :={[{\theta }_1,{\theta }_2,\dots ,{\theta }_N]}^{\top },$ where for each $n,{\theta }_n={[{\theta }_n^{(1)},{\theta }_n^{(2)}]}^{\top }=F({\text{lat}}_n,{\text{lon}}_n,t_n).$

Following Lodise et al. (2020), we place a Gaussian process prior on F to encode expected spatio-temporal structure while allowing for variation at multiple scales. Specifically, we model $F\sim \mathcal{G}\mathcal{P}(0,k(·,·)),$ where (20) $$k({\theta }_n^{(i)},{\theta }_{n\prime }^{(i)})=k_1({\theta }_n^{(i)},{\theta }_{n\prime }^{(i)})+k_2({\theta }_n^{(i)},{\theta }_{n\prime }^{(i)}),\hspace{1em}i\in \{1,2\}.$$(20)

Here k₁ and k₂ are squared exponential kernels with spatial and temporal length-scales that reflect mesoscale and submesoscale variations, respectively; see Appendix S8.3 for details. For simplicity, we model the latitudinal and longitudinal components of F independently. We take the posterior mean of θ under this model as the alternative estimate, ${\theta }^{*}(y).$

As a baseline, we consider an analogous estimate with covariance function $k({\theta }_n^{(i)},{\theta }_{n\prime }^{(i)})=k_1({\theta }_n^{(i)},{\theta }_{n\prime }^{(i)})+k_2({\theta }_n^{(i)},{\theta }_{n\prime }^{(i)})1[n=n\prime ],$ which maintains the same marginal variance but excludes submesoscale covariances. We take the posterior mean under this model as the default estimate $\widehat{\theta }(y)$. Both ${\theta }^{*}(y)$ and $\widehat{\theta }(y)$ may be written as affine transformations of y.

Using Approximate Bound 4.1, we compute a c-value of 0.99981. This large c-value allows us to confidently conclude that modeling both mesoscale and submesocale variation can yield more accurate estimates of ocean currents than mesocale modeling alone.

7 Discussion

We have provided a simple method for quantifying confidence in improvements provided by a wide class of shrinkage estimates without relying on subjective assumptions about the parameter of interest. Our approach has compelling theoretical properties, and we have demonstrated its utility on several data analyses of recent interest. However, the scope of the current work has several limitations. The present article has explored the use of the c-value only for problems of moderate dimensionality (N between 20 and 700). Loosely speaking, we suspect c-values may be underpowered to robustly identify substantial improvements provided by estimates in lower dimensional problems. Further investigation into such dimension dependence is an important direction for future work. In addition, our approach depends crucially on a high-probability lower bound that is inherently specific to the underlying model of the data, a loss function, and the pair of estimators. In the present work, we have shown how to derive and compute this bound for models with general Gaussian likelihoods, when accuracy may be measured in terms of squared error loss, and when both estimates are affine transformations of the data. We have provided a first step to extending beyond simple Gaussian models with the application to logistic regression; while we have not yet explored the efficacy of this extension on real data, we view our work as an important starting point for generalizing to broader model classes and estimation problems. We believe that further extensions to the classes of models, estimates, and losses for which c-values can be computed provide fertile ground for future work.

One direction we believe is promising is to construct the bound $b(y,\alpha )$ in a model and loss agnostic manner using, for example, the parametric bootstrap. Constructing an informative c-value is possible because in some cases the distribution of the win depends on the unknown parameter only through some low-dimensional projection (or at least approximately so). We suspect that this phenomenon may extend to more complex models and estimates. In such cases, when this low-dimensional characteristic sufficiently captures the distribution of the win and is estimated well enough, a parametric bootstrap may present a powerful solution. In particular, one would begin by forming an initial estimate of the parameter, and simulate a collection of bootstrap datasets by sampling data from the likelihood parameterized by the initial estimate, compute the win for each simulated dataset, and return for each $b(y,\alpha )$ the $1-\alpha$ quantile of this distribution. We expect that this method may work in many important settings; indeed, much of modern statistics and nonlinear methods are predicated on the assumption that low-dimensional structure (e.g., sparsity) exists and may be inferred. We leave further development of this more flexible approach, including an investigation of the theoretical properties, to follow-up work.

Supplementary Materials

The readme in the github provides a list of the computational resources and experimental code. And the supplementary text includes a table of contents.

Acknowledgments

The authors thank Jonathan H. Huggins for the suggestions to consider Berry–Esseen bounds and the extension to logistic regression, Lorenzo Masoero and Hannah Diehl for insightful comments on the manuscript, and Matthew Stephens and Lucas Janson for useful early conversations.

Additional information

Funding

This work was supported in part by an ARPA-E project with program director David Tew, and an NSF CAREER Award. We are grateful to the Office of Naval Research for partial support under grant N00014-20-1-2023 (MURI ML-SCOPE) to the Massachusetts Institute of Technology. BLT is supported by NSF GRFP. SKD is supported by the Wisconsin Alumni Research Foundation.

Appendix

Proof of Theorem 2.2

Proof. The result follows directly from the definition of c(y) and the conditions on $b(·,·)$. More explicitly, $$\begin{array}{c}{\mathbb{P}}_{\theta }\left[W(\theta ,y)\le 0\mathrm{ }\text{and}\mathrm{ }c(y)>\alpha \right]\le {\mathbb{P}}_{\theta }\left[W(\theta ,y)\le 0\mathrm{ }\text{and}\mathrm{ }b(y,\alpha )>0\right]\\ \le {\mathbb{P}}_{\theta }\left[W(\theta ,y)<b(y,\alpha )\right]\\ \le 1-\alpha ,\end{array}$$where the first line follows from the definition of the c-value and the final line follows from Equation (1)(1) $${\mathbb{P}}_{\theta }\left[W(\theta ,y)\ge b(y,\alpha )\right]\ge \alpha .$$(1) . □

Proof of Theorem 2.3

Proof. The condition $L(\theta ,{\theta }^{†}(y,\alpha ))>L(\theta ,\widehat{\theta }(y))$ can occur only when both (A) $0>W(\theta ,y)$ and (B) ${\theta }^{†}(·,\alpha )$ evaluates to ${\theta }^{*}(·)$ rather than $\widehat{\theta }(·).$ Event (B) implies $c(y)>\alpha$ and therefore $b(y,\alpha )>0$. By transitivity, $b(y,\alpha )>0\mathrm{ }\text{and}\mathrm{ }0>W(\theta ,y)\Rightarrow b(y,\alpha )>W(\theta ,y)$. By assumption, the event $b(y,\alpha )>W(\theta ,y)$ occurs with probability at most $1-\alpha$. □