Estimation of Linear Functionals in High-Dimensional Linear Models: From Sparsity to Nonsparsity

ABSTRACT

High-dimensional linear models are commonly used in practice. In many applications, one is interested in linear transformations ${\mathit{\beta }}^{\top }x$ of regression coefficients $\mathit{\beta }\in {\mathbb{R}}^p$, where x is a specific point and is not required to be identically distributed as the training data. One common approach is the plug-in technique which first estimates $\mathit{\beta }$, then plugs the estimator in the linear transformation for prediction. Despite its popularity, estimation of $\mathit{\beta }$ can be difficult for high-dimensional problems. Commonly used assumptions in the literature include that the signal of coefficients $\mathit{\beta }$ is sparse and predictors are weakly correlated. These assumptions, however, may not be easily verified, and can be violated in practice. When $\mathit{\beta }$ is non-sparse or predictors are strongly correlated, estimation of $\mathit{\beta }$ can be very difficult. In this article, we propose a novel pointwise estimator for linear transformations of $\mathit{\beta }$. This new estimator greatly relaxes the common assumptions for high-dimensional problems, and is adaptive to the degree of sparsity of $\mathit{\beta }$ and strength of correlations among the predictors. In particular, $\mathit{\beta }$ can be sparse or nonsparse and predictors can be strongly or weakly correlated. The proposed method is simple for implementation. Numerical and theoretical results demonstrate the competitive advantages of the proposed method for a wide range of problems. Supplementary materials for this article are available online.

KEYWORDS:

• Correlated predictors
• Eigenvalue sparsity
• Linear transformation
• Prediction

1 Introduction

With the advance of technology, high-dimensional data are prevalent in many scientific disciplines such as biology, genetics, and finance. Linear regression models are commonly used for the analysis of high-dimensional data, typically with two important goals: prediction and interpretability. Variable selection can help to provide useful insights on the relationship between predictors and the response, and thus improve the interpretability of the resulting model. During the past several decades, many sparse penalized techniques have been proposed for simultaneous variable selection and prediction, including convex penalized methods (Tibshirani 1996; Zou and Hastie 2005), as well as nonconvex ones (Fan and Li 2001; Zhang 2010).

In this article, we are interested in estimating linear transformations ${\mathit{\beta }}^{\top }x$ of regression coefficients $\mathit{\beta }={({\beta }_1,\dots ,{\beta }_p)}^{\top }\in {\mathbb{R}}^p$ for high-dimensional linear models, where $x\in {\mathbb{R}}^p$ is a specific point and is not required to be from the same distribution as the training data. It relates to both coefficient estimation and prediction. For instance, sometimes we are interested in estimating β₁ and ${\beta }_1-{\beta }_2$, where both of them can be expressed as ${\mathit{\beta }}^{\top }x$ by taking x as ${(1,0,\dots ,0)}^{\top }$ and ${(1,-1,0,\dots ,0)}^{\top }$, respectively. On the other hand, for a typical prediction problem, x follows the same distribution as the training data.

To estimate ${\mathit{\beta }}^{\top }x$, a natural and commonly used solution is to estimate $\mathit{\beta }$ first by $\widehat{\mathit{\beta }}$ and construct the estimator ${\widehat{\mathit{\beta }}}^{\top }x$, which can be viewed as the plug-in one. The efficiency of the plug-in estimator depends on that of $\widehat{\mathit{\beta }}$. Despite its simplicity, obtaining a good estimate of $\mathit{\beta }$ may not be easy in high-dimensional problems. If $\mathit{\beta }$ is sparse (i.e., the support of $\mathit{\beta },\text{supp}(\mathit{\beta })$, is small), sparse regularized techniques such as the LASSO can be used to obtain a consistent estimator of $\mathit{\beta }$. Desirable theoretical and numerical results have been established for various sparse penalized methods in the literature (see, e.g., Bickel, Ritov, and Tsybakov 2009; Raskutti, Wainwright, and Yu 2011; Bühlmann and Van De Geer 2011; Negahban et al. 2012). These regularized methods assume that $\mathit{\beta }$ is a sparse vector, which is difficult to verify in practice and may fail when $\text{supp}(\mathit{\beta })$ has a magnitude compatible with the sample size n or larger than n. The problem becomes more difficult when the predictors are strongly correlated since most sparse regularized methods work well on weakly dependent predictors.

We use a small simulation to illustrate the adverse effects of the sparsity degree of $\mathit{\beta }$ on the plug-in estimator of ${\mathit{\beta }}^{\top }x$ in the linear regression model (2.1), where X_i follows the normal distribution $N(0,\Sigma )$, $\mathit{\beta }={\delta }_0{({\mathbf{1}}_{p_0}^{\top },{\mathbf{0}}_{p-p_0}^{\top })}^{\top }$ and $p_0=r_{0}p$, and $\Sigma =({\sigma }_{ij})$, ${\sigma }_{ij}={0.5}^{|i-j|/\eta }$ with η controlling the correlation strength among the predictors. A larger value of r₀ implies a denser $\mathit{\beta }$. The setup of δ₀ and other parameters are presented in Setting 1 of Section 5.1. The average testing errors of the plug-in estimators and our proposed PointWise Estimator (PWE) are shown in Figure 1. We can see that the errors of the plug-in estimators deteriorate quickly as r₀ increases. In contrast, our proposed estimator is much less sensitive to the change of the degree of non-sparsity.

Fig. 1 The effect of nonsparsity of $\mathit{\beta }$ on plug-in estimators in terms of prediction error, where p = 1000. “A-lasso” and “lasso” denote the results of plug-in estimators with $\widehat{\mathit{\beta }}$ being adaptive LASSO and LASSO, respectively, and PWE denotes the proposed method.

In typical prediction problems, a number of papers studied the convergence of prediction for various estimators, including LASSO, ridge, partial least squares, overparameterized estimators, and many others under different settings (Dalalyan, Hebiri, and Lederer 2017; Zhang, Wainwright, and Jordan 2017; Dobriban and Wager 2018; Bartlett et al. 2020, etc.). It has been observed that LASSO and related methods are less affected by the correlation strength among predictors in prediction than in estimation problems (Hebiri and Lederer 2013; Dalalyan, Hebiri, and Lederer 2017). However, for some sparse vectors for x such as $x={(1,0\dots ,0)}^{\top }$, the estimation of ${\mathit{\beta }}^{\top }x$ becomes that of the first coefficient and these methods are more affected by the correlation strength than prediction (Zou and Hastie 2005). All the above mentioned methods consider the plug-in estimator and the average prediction error.

Different from these existing methods, we focus on ${\mathit{\beta }}^{\top }x$ for a specific fixed x ($x\ne 0$) rather than on estimating $\mathit{\beta }$ and the average prediction error, where x is not required to have the same distribution as the training data. The line of works that are closely related to ours are those on the hypothesis testing and confidence intervals of ${\mathit{\beta }}^{\top }x$ in high-dimensional linear models (van de Geer et al. 2014; Zhang and Zhang 2014; Javanmard and Montanari 2014; Lu et al. 2017; Cai and Guo 2017; Zhu and Bradic 2018, etc.). Most of these papers considered the case of $\mathit{\beta }$ being ultra-sparse with $|\text{supp}(\mathit{\beta })|\ll \sqrt{n}/\hspace{0.17em}\log \hspace{0.17em}p$. Cai and Guo (2017) considered the broader range where $|\text{supp}(\mathit{\beta })|$ has an order no more than $n/\hspace{0.17em}\log \hspace{0.17em}p$. Zhu and Bradic (2018) considered the hypothesis testing and confidence intervals of ${\mathit{\beta }}^{\top }x$ where $\mathit{\beta }$ is allowed to be non-sparse by introducing a sparse auxiliary model, which can be restrictive. For example, if the predictor vector follows the normal distribution $N(0,\Sigma )$ and the sparse auxiliary model holds for any $x\in {\mathbb{R}}^p$ simultaneously, then Σ must be equal to I_p. Moreover, the estimator of ${\mathit{\beta }}^{\top }x$ obtained from the confidence interval of Zhu and Bradic (2018), despite allowing $\mathit{\beta }$ to be dense, works only when $p/n\to 0$ in prediction problems. Although these results have optimality in the minimax sense (Cai and Guo 2017; Zhu and Bradic 2018), they can be conservative and are actually determined by the most difficult case. In this article, we introduce the sparsity of eigenvalues (or approximately low rank) of some matrices, which is shown to be complementary to the sparsity of $\mathit{\beta }$. The most difficult case is actually the situation where both types of sparsity fail.

Our key observation is that we can directly target at ${\gamma }_x:={\mathit{\beta }}^{\top }x$, treating it as an unknown parameter for estimation. We refer to the resulting estimate as the pointwise estimator. To this end, we propose a unified framework to leverage multiple sources of information. In many cases, the eigenvalues of the covariance matrix decrease dramatically, due to correlations among the predictors, which will be referred as sparsity of eigenvalues in the following descriptions. This type of sparsity is generally viewed as an adverse factor, making the estimation of $\mathit{\beta }$ more difficult. Contrary to this popular view, we show that the sparsity of eigenvalues is beneficial in our framework and serves as a good complement to the sparsity of $\mathit{\beta }$. In practice, two different kinds of test points x are of particular interest: (a) x is a given sparse vector, and (b) x is a random vector having the same distribution as the training data (i.e., the prediction problem). We give detailed results on these two special cases and compare our estimator with several other methods. The main contribution of this article is that we propose a transformed model under a new basis, which provides a unified way to use different sources of information.

First, to use the sparsity of eigenvalues, we propose an estimator based on a basis consisting of eigenvectors of a specific matrix constructed from the training data. When the eigenvalues decrease at a certain rate, our estimator performs well for both kinds of test points x regardless of the sparsity of $\mathit{\beta }$. On the other hand, if eigenvalues decrease slowly (or covariance matrix close to I_p), this estimator is less efficient; and consequently is inferior to LASSO when $\mathit{\beta }$ is indeed sparse. In fact, the pointwise estimator using the sparsity of eigenvalues is complementary to LASSO.

Second, to leverage the information of $\mathit{\beta }$, such as $\mathit{\beta }$ being sparse, and the sparsity of eigenvalues jointly, we construct another basis based on an initial estimator $\widehat{\mathit{\beta }}$. It is shown that two types of information help each other: a faster decreasing rate of eigenvalues allows $\widehat{\mathit{\beta }}$ converging in a slower rate, and vice versa. When the test point x is a sparse vector, we show that the pointwise estimator performs well. The case of x being random as in prediction problems is more complicated in the sense that the sparsity degree of $\mathit{\beta }$ should be taken into account. Hence, we consider a subset S₁ of $\{1,\dots ,p\}$ satisfying $S_1\supseteq \text{supp}(\mathit{\beta })$, where S₁ can be estimated from data. Specifically, we consider two cases: (a) Let $S_1=\{1,\dots ,p\}$, which allows $\mathit{\beta }$ to be sparse or dense. When sparsity of eigenvalues holds, our pointwise estimator performs well. When the eigenvalues are less sparse (or covariance matrix is close to I_p), our pointwise estimator performs similarly to the existing results on dense $\mathit{\beta }$ in the literature. (b) When $\mathit{\beta }$ is sparse, a smaller $\left|S_1\right|$ leads to a better estimator. If a good initial estimator $\widehat{\mathit{\beta }}$ and a good S₁ are available, our estimator’s performance is similar to that of LASSO.

The rest of this article is organized as follows. In Section 2, we propose our pointwise estimator for the linear transformation ${\mathit{\beta }}^{\top }x$ in high-dimensional linear models. Theoretical properties are established in Sections 3 and 4. Some simulated examples and real data analysis are presented in Section 5, followed by some discussions in Section 6. Proofs of the theoretical results are provided in the Supplementary Materials.

Notation. We first introduce some notations to be used for the article. For any symmetric positive semidefinite matrix $A\in {\mathbb{R}}^{m\times m}$, denote the eigenvalues of A in a decreasing order as ${\lambda }_1(A)\ge \cdots \ge {\lambda }_m(A)$, and the smallest nonzero eigenvalues as ${\lambda }_{\min }^{+}(A)$. For any matrix $A\in {\mathbb{R}}^{m_1\times m_2},{\lambda }_{\max }(A),{\lambda }_{\min }(A)$ are the maximum and minimum singular values of A, respectively. For any vector $\mathit{v}={(v_1,\dots ,v_m)}^{\top }\in {\mathbb{R}}^m,⏧\mathit{v}⏧$ and $⏧\mathit{v}{⏧}_1$ denote the ${\mathcal{l}}_2$ and ${\mathcal{l}}_1$ norms of v, respectively, and $⏧\mathit{v}{⏧}_{\infty }=\underset{1\le j\le m}{\max }\left|v_j\right|$; the support set of v is denoted as supp $(\mathit{v})$. In addition, define $⏧\mathit{v}{⏧}_A=\sqrt{{\mathit{v}}^{\top }A\mathit{v}}$ for any positive semidefinite matrix $A\in {\mathbb{R}}^{m\times m}$. For two sequences $\left\{a_n\right\}$ and $\left\{b_n\right\}$, both $a_n\lesssim b_n$ and $a_n=O(b_n)$ imply $\underset{n}{\lim }{a}_n/b_n\le c$ for some constant $c<\infty$; both $a_n\gtrsim b_n$ and $a_n=\Omega (b_n)$ indicate that $\underset{n}{\lim }{a}_n/b_n\ge c$; $a_n\asymp b_n$ means that a_n has exactly the same order as b_n. For any integer i, let e_i denote the vector of zeros except the ith element being 1.

2 A Unified Framework for Pointwise Estimation

Suppose $(X_i,Y_i);1\le i\le n$, are iid from the following linear regression model (2.1) $$Y_i=X_i^{\top }\mathit{\beta }+{ϵ}_i;1\le i\le n,$$(2.1) where ${ϵ}_i\in \mathbb{R}$ satisfies $E({ϵ}_i)=0$ and $\text{var}({ϵ}_i)={\sigma }^2<\infty ,X_i\in {\mathbb{R}}^p$ is independent of ϵ_i satisfying $E(X_i)=0$, and $\text{cov}(X_i)=\Sigma =({\sigma }_{ij})$. Without loss of generality, we assume that ${\sigma }_{ii}=1;i=1,\dots ,p$, and that $\text{var}(Y_i)<\infty$. Denote $\mathbf{X}={(X_1,\dots ,X_n)}^{\top }\in {\mathbb{R}}^{n\times p},\mathbf{Y}={(Y_1,\dots ,Y_n)}^{\top }\in {\mathbb{R}}^n$, and $\epsilon ={({ϵ}_1,\dots ,{ϵ}_n)}^{\top }\in {\mathbb{R}}^n$. Then the model can be written as $\mathbf{Y}=\mathbf{X}\mathit{\beta }+\epsilon$. Here the dimension p can be much larger than the sample size n. Let $x\in {\mathbb{R}}^p$ be a given point at which we intend to estimate ${\mathit{\beta }}^{\top }x$. We assume that $X_i^{\top }x\ne 0$ for some $1\le i\le n$, which can be checked numerically. Let $S_0=\text{supp}(\mathit{\beta })$ of cardinality $s_0=\left|S_0\right|$. Since a nonsparse $\mathit{\beta }$ and the case where Σ might not be of full rank will be considered, we make the following identifiability condition and discuss some useful facts.

• When Σ is not of full rank, we assume that $\mathit{\beta }$ falls into the column space of Σ for identifiability, due to the following reasons. Denote $X_i={\Sigma }^{1/2}{\tilde{X}}_i;1\le i\le n$, where ${\tilde{X}}_i$ satisfies $E({\tilde{X}}_i)=0$ and $\text{cov}({\tilde{X}}_i)=I_p$. Let $P_{\Sigma }$ be the projection matrix on the column space of Σ and $Q_{\Sigma }=I_p-P_{\Sigma }$. Then $X_i^{\top }\mathit{\beta }={\tilde{X}}_i^{\top }{\Sigma }^{1/2}\mathit{\beta }={\tilde{X}}_i^{\top }{\Sigma }^{1/2}(P_{\Sigma }+Q_{\Sigma })\mathit{\beta }=X_i^{\top }{P}_{\Sigma }\mathit{\beta }$. Thus, the parameter can be set as $P_{\Sigma }\mathit{\beta }$, which falls into the column space of Σ.

• The magnitude of β_j; $j\in S_0$, depends on the sparsity degree s₀. Note that ${\lambda }_{\min }^{+}(\Sigma )⏧\mathit{\beta }{⏧}^2\le {\mathit{\beta }}^{\top }\Sigma \mathit{\beta }<\text{var}(Y_i)<\infty$, and consequently that $⏧\mathit{\beta }{⏧}^2\le \text{var}(Y_i)/{\lambda }_{\min }^{+}(\Sigma )$. Assume that β_j’s with $j\in S_0$ are of the same magnitude. Then it follows that $\left|{\beta }_j\right|\lesssim {[s_0{\lambda }_{\min }^{+}(\Sigma )/\text{var}(Y_i)]}^{-1/2},j\in S_0$. Particularly, if ${\lambda }_{\min }^{+}(\Sigma )\asymp 1,\left|{\beta }_j\right|$’s are of order $s_0^{-1/2}$, which can be small when s₀ is large.

Next we first introduce the transformed model based on a set of basis to leverage multiple sources of information in Section 2.1. The construction of basis is discussed in Section 2.2. A penalized estimator and a pointwise estimator are proposed in Section 2.3.

2.1 The Transformed Model

For any fixed $x\in {\mathbb{R}}^p$, let $P_x=x{x}^{\top }/⏧x{⏧}^2$ be the projection matrix on the space spanned by x and $Q_x=I_p-P_x$ be the projection matrix on the complementary space. Recall that ${\gamma }_x={\mathit{\beta }}^{\top }x$ and denote ${\mathit{\beta }}_{Q_x}=Q_x\mathit{\beta }$. Then one can write (2.2) $$\begin{array}{cc}\mathbf{X}\mathit{\beta }\hfill & =\mathbf{X}{P}_x\mathit{\beta }+\mathbf{X}{Q}_x\mathit{\beta }=\mathbf{X}x·x^{\top }\mathit{\beta }⏧x{⏧}^{-2}+\sqrt{n}{\zeta }_{\mathit{\beta }}\hfill \\ \hfill & :=\sqrt{n}{z}_x·{\alpha }_x+\sqrt{n}{\zeta }_{\mathit{\beta }},\hfill \end{array}$$(2.2) where ${\alpha }_x={\gamma }_x·⏧x{⏧}^{-2}\mathrm{⏧Xx⏧}{n}^{-1/2}\in \mathbb{R},z_x=\mathbf{X}x/\mathrm{⏧Xx⏧}\in {\mathbb{R}}^n$ and ${\zeta }_{\mathit{\beta }}=n^{-1/2}\mathbf{X}{\mathit{\beta }}_{Q_x}\in {\mathbb{R}}^n$. Here α_x is a scaled version of γ_x such that the ${\mathcal{l}}_2$ norm of the predictor $\sqrt{n}{z}_x$ equals $\sqrt{n}$. Estimating γ_x is equivalent to that of α_x, since given α_x, one can compute γ_x directly from data $(\mathbf{X},x)$. Then we get $\mathbf{Y}=\mathbf{X}\mathit{\beta }+\epsilon =\sqrt{n}{z}_x{\alpha }_x+\sqrt{n}{\zeta }_{\mathit{\beta }}+\epsilon ,$ where ${\zeta }_{\mathit{\beta }}$ is a nuisance parameter vector. Note that ${\zeta }_{\mathit{\beta }}$ is a nonsparse vector in general, particularly when X_i’s are iid variables; thus, we have n + 1 nonsparse parameters with the sample size n. To handle the difficulty, we introduce a set of basis $\Gamma \in {\mathbb{R}}^{n\times n}$ using different sources of information such that ${\zeta }_{\mathit{\beta }}$ can be expressed sparsely under the set of basis.

The construction of Γ depends on the information at hand and will be elaborated in Section 2.2. For an invertible matrix $\Gamma \in {\mathbb{R}}^{n\times n}$, of which the columns are of unit length (i.e., ${\Gamma }_{·j}^{\top }{\Gamma }_{·j}=1,1\le j\le n$), we denote $\sqrt{n}{\zeta }_{\mathit{\beta }}=\left(\sqrt{n}\Gamma \right)({\Gamma }^{-1}{\zeta }_{\mathit{\beta }})=\sqrt{n}\Gamma \mathit{\theta },$ where $\mathit{\theta }={\Gamma }^{-1}{\zeta }_{\mathit{\beta }}\in {\mathbb{R}}^n$. Although Γ here can be any invertible matrix, as shown later, the case we are interested in is Γ being (approximately) orthogonal. We hope that $\mathit{\theta }$ is (approximately) sparse when Γ is chosen properly. Combining these together, we have the transformed linear model (2.3) $$\mathbf{Y}=\sqrt{n}{z}_x·{\alpha }_x+\sqrt{n}\Gamma \mathit{\theta }+\epsilon =\mathbf{Z}\mathit{\alpha }+\epsilon ,$$(2.3) where $\mathbf{Z}=\sqrt{n}(z_x,\Gamma )\in {\mathbb{R}}^{n\times (n+1)},\mathit{\alpha }={({\alpha }_x,{\mathit{\theta }}^{\top })}^{\top }\in {\mathbb{R}}^{n+1}$. The parameter $\mathit{\theta }$ is treated as a n-dimensional nuisance parameter vector. As shown later in Section 2.2, Γ plays a critical role in this model, providing a flexible way to leverage different sources of information. A naive choice is $\Gamma =I_n$ without using additional information, which will be discussed further in Section F of supplementary materials. In contrast to p parameters of the original linear model, the transformed model (2.3) has only n + 1 unknown parameters that are (approximately) sparse. Without loss of generality, we assume that both $\left|{\alpha }_x\right|$ and consequently $⏧{\zeta }_{\mathit{\beta }}⏧$ are bounded, given x and X. This assumption is mild and holds in probability when x and X_i’s are iid from $N(0,\Sigma )$. Detailed discussions are presented in Section A of the supplementary materials.

Denote by ${\widehat{\alpha }}_x$a generic estimator of α_x. Then γ_x can be estimated by ${\widehat{\gamma }}_x={\widehat{\alpha }}_x·⏧x{⏧}^2\mathrm{⏧Xx}{⏧}^{-1}{n}^{1/2}$. Given x, noting that $n^{-1}\mathrm{⏧Xx}{⏧}^2{\to }_p⏧x{⏧}_{\Sigma }^2$, where $⏧x{⏧}_{\Sigma }=\sqrt{x^{\top }\Sigma x}$, we see that the quantity $⏧x{⏧}^2/⏧x{⏧}_{\Sigma }$ affects the convergence rate of the estimator ${\widehat{\gamma }}_x$. We investigate the magnitude of $⏧x{⏧}^2/⏧x{⏧}_{\Sigma }$, and consider two typical settings for clarity. Recall that x is a given vector, which may or may not have the same distribution as X_i.

Example 1.

Let x be a sparse vector with the support set $S_x=\text{supp}(x)$ and the cardinality $\left|S_x\right|:=s_x$. Examples of such x include x = e_i or $x=e_i-e_j$. Denote $X_{i{S}_x}=(X_{ij},j\in S_x)$. If the eigenvalues of ${\Sigma }_{S_x{S}_x}=\text{cov}(X_{i{S}_x})$ are both upper and lower bounded, and $⏧x{⏧}_{\infty }=O(1)$, then it follows that $⏧x{⏧}^2/⏧x{⏧}_{\Sigma }\mathit{\text{≍⏧x⏧≍}}{s}_x^{1/2}$.

Example 2.

Let x be a random vector as in prediction problems. For simplicity, we assume x and X_i’s are iid variables from $N(0,\Sigma )$. As shown in Section 4.2, it follows (2.4) $$⏧x{⏧}^2/⏧x{⏧}_{\Sigma }\asymp \sqrt{{[\text{tr}(\Sigma )]}^2/\text{tr}({\Sigma }^2)}:=M_{\Sigma },$$(2.4) in probability. Moreover, it holds that $1\le M_{\Sigma }\le p^{1/2}$ and $M_{\Sigma }^2$ can be viewed as the effective rank of Σ. Particularly, if some eigenvalues of Σ are much larger than the rest (e.g., the largest eigenvalue has the order p), then $M_{\Sigma }\asymp 1$; if Σ is close to I_p, then $M_{\Sigma }$ is close to $p^{1/2}$ and γ_x is close to $p^{1/2}{\alpha }_x$.

Clearly, the magnitude of $⏧x{⏧}^2/⏧x{⏧}_{\Sigma }$ with a sparse x in Example 1 can be smaller than that of the dense x in Example 2. If x is not sparse, the sparsity of $\mathit{\beta }$ can help as well. This observation motivates us to consider estimators using the information of the sparsity degree of $\mathit{\beta }$. For any subset $S_1\subseteq \{1,\dots ,p\}$ such that $S_0\subseteq S_1$, we observe that $${\gamma }_x={\mathit{\beta }}^{\top }x={\mathit{\beta }}_{S_0}^{\top }{x}_{S_0}={\mathit{\beta }}_{S_1}^{\top }{x}_{S_1}={\mathit{\beta }}^{\top }{\tilde{x}}_{S_1}={\gamma }_{{\tilde{x}}_{S_1}},$$where $x_{S_0}$ and ${\mathit{\beta }}_{S_0}$ are the subvectors of x and $\mathit{\beta }$, respectively, and ${\tilde{x}}_{S_1}$ is a p-dimensional vector obtained by setting $x_{S_1^c}=0$ in x. Thus, instead of estimating γ_x, one can equivalently consider prediction at the point ${\tilde{x}}_{S_1}$, which is a sparse vector when $\left|S_1\right|$ is small. Clearly, one can set $S_1=\{1,\dots ,p\}$, and then ${\gamma }_{{\tilde{x}}_{S_1}}$ becomes γ_x. Estimating ${\gamma }_{{\tilde{x}}_{S_1}}$ provides a way to take the sparsity degree of $\mathit{\beta }$ into account. In practice, one can choose different S₁’s and select the best one by CV, as shown later in Section 2.3. In Section 4 we will compare our method with several existing methods in details for Examples 1 and 2.

Remark 1.

In Example 2 above, a smaller set S₁ is preferred. However, the true support set S₀ is unknown. When s₀ is small, choosing a set S₁ that covers S₀ is feasible. For example, S₁ can be taken as the support set of the LASSO estimator, or constructed by some screening methods (Fan and Lv 2008).

2.2 Construct Basis Utilizing Multiple Sources of Information

Next we discuss the construction of Γ. For a positive semidefinite matrix $A\in {\mathbb{R}}^{p\times p}$, denote $\mathit{\lambda }(A)=({\lambda }_1(A),\dots ,{\lambda }_p(A))$ the vector of eigenvalues of A in a decreasing order. We say that $\mathit{\lambda }(A)$ is approximately sparse when only a few eigenvalues are much larger than the average $p^{-1}{\sum }_{i=1}^p{\lambda }_i(A)$, and the detailed requirements on the decreasing rate of eigenvalues will be elaborated later. In practice, different sources of information may be available. For clarity of the presentation, we focus on two different sources of information.

Source I. We use the information of $\mathit{\beta }$ through an initial estimator $\widehat{\mathit{\beta }}$. Note that a good estimator is available in some cases. In particular, if $\mathit{\beta }$ is sparse, then $\widehat{\mathit{\beta }}$ can be obtained from that of LASSO, or other sparse regression methods. However, an estimator $\widehat{\mathit{\beta }}$ may not be good enough in many cases especially when $\mathit{\beta }$ is less sparse and p is larger than n.

Source II. We use the dependence among predictors. Note that $\mathit{\lambda }(n^{-1}\mathbf{X}{Q}_x{\mathbf{X}}^{\top })=\mathit{\lambda }(n^{-1}\mathbf{X}{Q}_x{Q}_x{\mathbf{X}}^{\top })$ that equals the first n elements of $\mathit{\lambda }(n^{-1}{Q}_x{\mathbf{X}}^{\top }\mathbf{X}{Q}_x)$, of which the population version is $\mathit{\lambda }(Q_x\Sigma Q_x)$. When predictors are correlated such that $\mathit{\lambda }(n^{-1}\mathbf{X}{Q}_x{\mathbf{X}}^{\top })$ is (approximately) sparse, a key observation is that by choosing a suitable Γ, the parameter $\mathit{\theta }$ can be (approximately) sparse regardless $\mathit{\beta }$ being sparse or not (details are referred in Section 3.2). Thus, it is feasible to estimate the parameters well in the transformed model (2.3).

Denote ${\mathcal{C}}_1=\left\{\mathit{\beta }\text{ is sparse}\right\},{\mathcal{C}}_2=\{\mathit{\lambda }(n^{-1}\mathbf{X}{Q}_x{\mathbf{X}}^{\top })\text{ is sparse}\}$, and let $\tilde{\mathcal{C}}={\mathcal{C}}_1^c\cap {\mathcal{C}}_2^c$. The sparsity in ${\mathcal{C}}_2$ is complementary to that in ${\mathcal{C}}_1$. Both ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ are ideal cases with good estimators available (we will introduce estimators for Case ${\mathcal{C}}_2$ later), and the case $\tilde{\mathcal{C}}$ can be the least favorable case. There are intermediate cases between ${\mathcal{C}}_1$ and $\tilde{\mathcal{C}}$, when the degree of sparsity of $\mathit{\beta }$ increases gradually. A similar argument applies between ${\mathcal{C}}_2$ and $\tilde{\mathcal{C}}$. To handle these complicated cases, it is natural to use these two different sources of information jointly. In fact, our approach works well under the complementary condition in Section 3.3 where stronger requirements on one type of sparsity weaken those of the other. It is possible that both ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ hold simultaneously, where our estimators leverage both sources of information.

Denote the spectral decomposition of $n^{-1}\mathbf{X}{Q}_x{\mathbf{X}}^{\top }$ as ${\Gamma }_{\text{eg}}\Psi {\Gamma }_{\text{eg}}^{\top },$ where ${\Gamma }_{\text{eg}}=(u_{\text{eg},1},\dots ,$ $u_{\text{eg},n})\in {\mathbb{R}}^{n\times n}$ are eigenvectors and $\Psi =\text{diag}({\psi }_1,\dots ,{\psi }_n)$ is the diagonal matrix of the associated eigenvalues in a deceasing order. Denote ${\overline{\zeta }}_{\mathit{\beta }}={\zeta }_{\mathit{\beta }}/⏧{\zeta }_{\mathit{\beta }}⏧=\mathbf{X}{\mathit{\beta }}_{Q_x}/⏧\mathbf{X}{\mathit{\beta }}_{Q_x}⏧.$ When an initial estimator $\widehat{\mathit{\beta }}$ is available, ${\overline{\zeta }}_{\mathit{\beta }}$ can be estimated by ${\overline{\zeta }}_{\widehat{\mathit{\beta }}}$. To use two different sources of information jointly, or in other words to use both ${\overline{\zeta }}_{\widehat{\mathit{\beta }}}$ and the columns of ${\Gamma }_{\text{eg}}$, we construct Γ by replacing one of the columns (say for example the ith column) of ${\Gamma }_{\text{eg}}$ by ${\overline{\zeta }}_{\widehat{\mathit{\beta }}}$, that is, $\Gamma =\Gamma (\widehat{\mathit{\beta }})$, defined as (2.5) $$\Gamma (\widehat{\mathit{\beta }})=({\overline{\zeta }}_{\widehat{\mathit{\beta }}},u_{\text{eg},j},j\ne i),$$(2.5) which is the empirical version of $\Gamma (\mathit{\beta })=({\overline{\zeta }}_{\mathit{\beta }},u_{\text{eg},j},j\ne i)$. More discussion on this process is provided in Proposition 1 and Remark 2.

Recall that α_x, associated with predictor $\sqrt{n}{z}_x$, is the parameter of interest in the transformed model that has predictors $\sqrt{n}(z_x,\Gamma )$. It is desirable to avoid the collinearity between z_x and other predictors in the transformed model. Hence, we assume that $\widehat{\mathit{\beta }}$ satisfies that ${\overline{\zeta }}_{\widehat{\mathit{\beta }}}\ne z_x$, which can be checked from data, and require the matrix $(z_x,u_{\text{eg},j},j\ne i)$ being invertible. Note that it is also required that $\Gamma (\widehat{\mathit{\beta }})$, that is $({\overline{\zeta }}_{\widehat{\mathit{\beta }}},u_{\text{eg},j},j\ne i)$, is invertible.

Proposition 1.

Suppose that $\widehat{\mathit{\beta }}$ satisfies $\left|z_x^{\top }{\overline{\zeta }}_{\widehat{\mathit{\beta }}}\right|>0$ and ${\overline{\zeta }}_{\widehat{\mathit{\beta }}}\ne z_x$. Then for at least one $i\in \{1,\dots ,n\}$, it holds that both matrices $({\overline{\zeta }}_{\widehat{\mathit{\beta }}},u_{\text{eg},j},j\ne i)$ and $(z_x,u_{\text{eg},j},j\ne i)$ are invertible or equivalently that $\min \left\{\right|u_{\text{eg},i}^{\top }{\overline{\zeta }}_{\widehat{\mathit{\beta }}}|,|u_{\text{eg},i}^{\top }{z}_x\left|\right\}>0$.

In principle, we can replace any $u_{\text{eg},i}$ by ${\overline{\zeta }}_{\widehat{\mathit{\beta }}}$ as long as $\min \left\{\right|u_{\text{eg},i}^{\top }{\overline{\zeta }}_{\widehat{\mathit{\beta }}}|,|u_{\text{eg},i}^{\top }{z}_x\left|\right\}>0$. In our numerical studies, the strategy in Remark 2 below is used to further reduce collinearity.

Remark 2.

Reducing the collinearity between z_x and other predictors in the transformed model makes the estimator of α_x more stable. In our simulation studies, we replace $u_{\text{eg},i_0}$ by ${\overline{\zeta }}_{\widehat{\mathit{\beta }}}$ with $i_0=\text{arg}\underset{1\le i\le n}{\max }\left|u_{\text{eg},i}^{\top }{z}_x\right|$, and the resulting $\Gamma (\widehat{\mathit{\beta }})$ is observed nonsingular numerically.

Naturally, one can just use the information in Source II by setting $\Gamma ={\Gamma }_{\text{eg}}$. A good property for this choice is that it depends only on X without requiring an initial estimator $\widehat{\mathit{\beta }}$ and is free of any assumption on the sparsity of $\mathit{\beta }$. However, this choice may not be ideal if a reasonably good initial estimator $\widehat{\mathit{\beta }}$ can be obtained. We summarize the constructions of Γ used in this article in Table 1.

Table 1 Candidates of Γ for the pointwise estimator.

1.	$\Gamma ={\Gamma }_{\text{eg}}$, where ${\Gamma }_{\text{eg}}\in {\mathbb{R}}^{n\times n}$ contains the eigenvectors of $n^{-1}\mathbf{X}{Q}_x{\mathbf{X}}^{\top }$.
2.	$\Gamma =\Gamma (\widehat{\mathit{\beta }})=({\overline{\zeta }}_{\widehat{\mathit{\beta }}},u_{\text{eg},j},j\ne i_0)$, where i0 can be taken as any i satisfying the condition in Proposition 1 or selected by the procedure in Remark 2, when an initial estimator $\widehat{\mathit{\beta }}$ is available.

In Section 3, we show that when $\mathit{\lambda }(n^{-1}\mathbf{X}{Q}_x{\mathbf{X}}^{\top })$ is sparse enough, $\mathit{\theta }={\Gamma }_{\text{eg}}^{-1}{\zeta }_{\mathit{\beta }}$ is approximately sparse without any sparsity assumption on $\mathit{\beta }$. An extreme case is Σ being a low rank matrix, where $\mathit{\theta }$ is exactly sparse with at most $\text{rank}(\Sigma )+1$ nonzero elements. It is worth pointing out that which elements of $\mathit{\theta }$ are large are generally unknown since $\mathit{\beta }$ is involved. When $\mathit{\lambda }(n^{-1}\mathbf{X}{Q}_x{\mathbf{X}}^{\top })$ is less sparse, as discussed below, $\widehat{\mathit{\beta }}$ will provide additional information and $\mathit{\theta }$ can still be approximately sparse.

When $\Gamma =\Gamma (\widehat{\mathit{\beta }})$, the sparsity of $\mathit{\theta }$ also depends on the accuracy of $\widehat{\mathit{\beta }}$. For the ideal case that $\widehat{\mathit{\beta }}=\mathit{\beta }$, it can be shown that $\mathit{\theta }=\Gamma {(\mathit{\beta })}^{-1}{\zeta }_{\mathit{\beta }}\propto e_1={(1,0,\dots ,0)}^{\top }$, and consequently $\mathit{\theta }$ is a sparse vector. This argument still holds, if we replace $(u_{\text{eg},j},j\ne i_0)$ by any other vectors such that $\Gamma (\mathit{\beta })$ is invertible, implying that if we know $\mathit{\beta }$, there is no need for additional information. Consequently, if $\widehat{\mathit{\beta }}$ is good, $(u_{\text{eg},j},j\ne i_0)$ do not help much. When $\widehat{\mathit{\beta }}$ is not good enough (e.g., $\mathit{\beta }$ is less sparse in particular) but $\mathit{\lambda }(n^{-1}\mathbf{X}{Q}_x{\mathbf{X}}^{\top })$ is sufficiently sparse, using $u_{\text{eg},i}$’s will compensate the low accuracy of $\widehat{\mathit{\beta }}$. Thus, both types of information can help each other in our framework and the estimator becomes more robust to the underlying assumptions. Details are provided in Section 3.

2.3 Penalized Estimator and Pointwise Estimator

As discussed in Section 2.2, the parameters in the transformed model (2.3) can be approximately sparse if Γ is constructed properly. Thus, we consider the minimization of the following objective function (2.6) $$L_{\lambda ,\Gamma }(\mathit{\alpha })=n^{-1}⏧\mathbf{Y}-\mathbf{Z}\mathit{\alpha }{⏧}^2+P_{\text{en},\lambda }(\mathit{\alpha }),$$(2.6) where $P_{\text{en},\lambda }(\mathit{\alpha })=\lambda ⏧\mathit{\alpha }{⏧}_1$ is the ${\mathcal{l}}_1$ penalty function used by LASSO, and λ and Γ are the tuning parameters. The parameter λ plays the same role as that for the usual regularized estimator and can be selected by cross-validation (CV). The selection of Γ will be elaborated below. Since the ${\mathcal{l}}_1$ penalty usually induces biases for coefficients of large absolute values, to solve this problem, other nonconvex penalty functions, such as the SCAD (Fan and Li 2001) or MCP (Zhang 2010), can be used instead. Denote the minimizer as (2.7) $${\widehat{\mathit{\alpha }}}_{\lambda ,\Gamma }={({\widehat{\alpha }}_x,{\widehat{\mathit{\theta }}}^{\top })}^{\top }=\text{arg}\underset{\mathit{\alpha }\in {\mathbb{R}}^{n+1}}{\min }{L}_{\lambda ,\Gamma }(\mathit{\alpha }).$$(2.7)

Then we have ${\widehat{\gamma }}_x={\widehat{\alpha }}_x·⏧x{⏧}^2\mathrm{⏧Xx}{⏧}^{-1}{n}^{1/2}$.

Remark 3.

Our approach involves eigenvalue decomposition of the matrix $n^{-1}\mathbf{X}{Q}_x{\mathbf{X}}^{\top }\in {\mathbb{R}}^{n\times n}$ with the computational complexity of the order $O(n^3)$, which can be a burden when n is large. To reduce the complexity, the Divide-and-Conquer (DC) approach for handling big data can be used (Zhang, Duchi, and Wainwright 2015). Simulation results based on DC are presented in Section G.2 of the supplementary materials.

Next we briefly discuss the estimator in (2.7). First, the predictor Z in Model (2.3) involves the transformation matrix Γ, while in the classical model (2.1), the predictor is X, of which each row represents a realization of the predictors. Second, unlike the classical methods such as the LASSO, where the parameters are unknown constants, the parameter $\mathit{\alpha }$ here involves $(x,\mathbf{X},\Gamma )$, which makes the theoretical analysis challenging.

Remark 4.

In the above arguments, we consider a single point x that may or may not be from the same distribution as the predictor vector. However, if we are going to consider a large number of test points $\{x_i,i=1,\dots ,n_{te}\}$ that are iid observations of X_i, the bias should be taken into account. Because $E({\gamma }_{x_i})=E({\mathit{\beta }}^{\top }{x}_i)=0$ and $\text{var}({\gamma }_{x_i})={\mathit{\beta }}^{\top }\Sigma \mathit{\beta }<\text{var}(Y_1)$, there will be many ${\gamma }_{x_i}$’s that are close to 0 and the corresponding estimators are shrunken to 0 by the penalization, resulting in large biases in terms of the average estimation error. There are many bias correction methods for LASSO and related penalized estimators in the literature (Belloni and Chernozhukov 2013; Zhang and Zhang 2014, etc.). In our simulation results for the prediction problem, the method of Belloni and Chernozhukov (2013) is applied.

For clarity, we briefly summarize the estimation procedure for a given Γ as follows.

Algorithm 1

Estimator of γ_x (or ${\gamma }_{{\tilde{x}}_{S_1}}$) with given Γ

1. (Estimate α_x) Solve the optimization problem (2.6), where the optimal λ is chosen by CV; the corresponding parameter obtained is denoted as ${({\widehat{\alpha }}_x,{\widehat{\mathit{\theta }}}^{\top })}^{\top }$.

2. (Bias-correction) This is an optional step. Denote $\widehat{S}=\text{supp}(\widehat{\mathit{\theta }})$ and ${\Gamma }_{·\widehat{S}}$ the columns of Γ with index $\widehat{S}$. Apply the OLS with responses Y and predictors $\mathbf{Z}=\sqrt{n}(z_x,{\Gamma }_{·\widehat{S}})$ to get the updated coefficient ${\widehat{\alpha }}_x$ of $\sqrt{n}{z}_x$, which is a bias-corrected estimator of α_x.

3. (Estimate γ_x) γ_x is estimated by ${\widehat{\gamma }}_x={\widehat{\alpha }}_x·⏧x{⏧}^2\mathrm{⏧Xx}{⏧}^{-1}{n}^{1/2}.$

4. (Alternative Steps 1–3) Replacing x by ${\tilde{x}}_{S_1}$ in Steps 1–3, we get the estimator ${\widehat{\gamma }}_{{\tilde{x}}_{S_1}}$.

Step 2 is mainly applied for the setting in Remark 4 with a large number of testing points that are iid observations as of the training data X_i’s. For clarity, the pointwise estimator obtained by Algorithm 1 is named based on the specific Γ used. There are many estimators of $\mathit{\beta }$ available for different settings in the literature, and can be used as an initial estimator. Denote by ${\widehat{\mathit{\beta }}}_{\text{lasso}}$ and ${\widehat{\mathit{\beta }}}_{\text{ridge}}$ the estimators of LASSO and ridge regression, respectively, and by ${\widehat{\mathit{\beta }}}_{\text{rdl}}$ the overparameterized ridgeless OLS estimator using the Moore-Penrose generalized inverse (Bartlett et al. 2020; Azriel and Schwartzman 2020; Hastie et al. 2022). We consider the estimators ${\widehat{\gamma }}_x$ in Algorithm 1 with Γ being ${\Gamma }_{\text{eg}}$ and $\Gamma (\widehat{\mathit{\beta }})$ for $\widehat{\mathit{\beta }}\in \{{\widehat{\mathit{\beta }}}_{\text{lasso}},{\widehat{\mathit{\beta }}}_{\text{ridge}},{\widehat{\mathit{\beta }}}_{\text{rdl}}\}$, and the resulting estimators are denoted as $P_{\text{eg}},P_{\text{lasso}},P_{\text{ridge}},P_{\text{rdl}}$, respectively. Now we propose a procedure to select Γ adaptively. Denote by $\mathcal{M}$a set of estimators, for example, $\mathcal{M}=\{P_{\text{lasso}},P_{\text{ridge}},P_{\text{eg}},P_{\text{rdl}}\}$ in Setting 1 of our numerical study. The best estimator selected from $\mathcal{M}$ by the following CV procedure will be denoted as PWE.

Algorithm 2

Select Γ by CV

1. Compute the CV error for estimators in $\mathcal{M}$. Split randomly the whole data $\mathcal{D}$ of size n into K parts, denoted as $D_1,\dots ,D_K$. For each method $A\in \mathcal{M}$, compute the CV error, $n^{-1}{\sum }_{k=1}^K\sum _{(x_i,y_i)\in D_k}{({\widehat{\gamma }}_{x_i}^A-y_i)}^2$, where ${\widehat{\gamma }}_{x_i}^A$ is estimated by A with data $\mathcal{D}\setminus D_k$.

2. The method A₀ in $\mathcal{M}$ with the minimum CV error is chosen to be the best one.

3. The final estimator of γ_x is ${\widehat{\gamma }}_x^{A_0}$.

For Example 1 in Section 2.1 where x is a sparse vector, we apply Algorithm 2 to get the pointwise estimator. For the prediction problems in Example 2, since the sparsity degree of $\mathit{\beta }$ is unknown, we have two choices on the subset S₁: (a) simply taking $S_1=\{1,\dots ,p\}$ (i.e., estimate γ_x directly); (b) estimating S₁ from data using LASSO or screening methods. Given Γ, among the candidates of S₁, we can select the best one by CV, similar to Steps 1 and 2 of Algorithm 2. Note that x_i should be replaced by ${\tilde{x}}_{i{S}_1}$, which is defined in the way similar to ${\tilde{x}}_{S_1}$, when one computes the CV error in Step 1 of Algorithm 2. Moreover, one can select both Γ and S₁ simultaneously by CV.

3 Properties of the Penalized Estimator ${\widehat{\alpha }}_x$

Throughout our theoretical analysis, it is assumed that ϵ_i’s are iid from $N(0,{\sigma }^2)$, and $(x,\mathbf{X})$ can be fixed or random and will be specified later. In this section, we present theoretical properties of the regularized estimator ${\widehat{\alpha }}_x$ in (2.7), which lays a foundation for properties of the estimator ${\widehat{\gamma }}_x$ in Section 4. To this end, we first establish results for a generic invertible matrix Γ with fixed $(x,\mathbf{X})$ in Section 3.1, and then apply it to ${\Gamma }_{\text{eg}}$ and $\Gamma (\widehat{\mathit{\beta }})$ in Sections 3.2 and 3.3, respectively.

3.1 A General Result on ${\widehat{\alpha }}_x$ with a Generic Γ and Fixed $(x,\mathbf{X})$

Recall that $\mathbf{Z}=\sqrt{n}(z_x,\Gamma )$ in Model (2.3). Let $v_x={(1,-b_x^{\top })}^{\top }/{(1+b_x^{\top }{b}_x)}^{1/2}$ with $b_x={\Gamma }^{-1}{z}_x.$ It can be shown that v_x is the eigenvector associated with the zero eigenvalue of $n^{-1}{\mathbf{Z}}^{\top }\mathbf{Z}$ (see proof of Theorem E.1 in supplementary materials). For any $\mathit{v}={(v_1,\dots ,v_{n+1})}^{\top }\in {\mathbb{R}}^{n+1}$, denote $⏧\mathit{v}{⏧}_{(q)}={\sum }_{i=1}^{n+1}|v_i{|}^q;q\in [0,1].$ It is worth noting that $⏧\mathit{v}{⏧}_{(q)}$ here is not the ${\mathcal{l}}_q$ norm of v that is defined as $⏧\mathit{v}{⏧}_q=⏧\mathit{v}{⏧}_{(q)}^{1/q}$; and for q = 1, they are the same. This notation $⏧\mathit{v}{⏧}_{(q)}$ is convenient for our purpose, particularly for the discussions of the case with q = 0 or $q\to 0$.

For $\mathit{\alpha }={({\alpha }_x,{\mathit{\theta }}^{\top })}^{\top }$ and $q\in [0,1]$, denote $R_q=⏧\mathit{\alpha }{⏧}_{(q)}=|{\alpha }_x{|}^q+⏧\mathit{\theta }{⏧}_{(q)},$ which measures the sparsity of the parameter $\mathit{\alpha }$. Particularly, when q = 0, R_q is the number of nonzero elements in $\mathit{\alpha }$. Let the tuning parameter $\lambda ={\lambda }_n:=a_0\sigma \sqrt{(\hspace{0.17em}\log \hspace{0.17em}n)/n}$ with $a_0\ge 2$. We have the following result on a generic invertible matrix Γ.

Theorem 1.

Assume that $(x,\mathbf{X})$ are fixed. Let Γ be a generic invertible matrix that may depend on $(x,\mathbf{X})$. Assume the following $\mathit{\alpha }$-sparsity condition: $R_q\le C{\lambda }_n^q⏧v_x{⏧}_1^2$ for some $q\in [0,1]$ and some constant C > 0. Then with probability $1-C_1{n}^{-3}$, we have $$|{\widehat{\alpha }}_x-{\alpha }_x| \le \frac{5}{4}{\lambda }_n+C_{\kappa }{\lambda }_n^{1-q}{R}_q·\min \{{\lambda }_n^{q/2}{R}_q^{-1/2}⏧{\Gamma }^{\top }{z}_x⏧,⏧{\Gamma }^{\top }{z}_x{⏧}_{\infty }\},$$where C₁, $C_{\kappa }$ are positive constants. Furthermore, when Γ is a generic orthogonal matrix, the $\mathit{\alpha }$-sparsity condition can be simplified as $R_q\le C\prime {\lambda }_n^q⏧{\Gamma }^{\top }{z}_x{⏧}_1^2$ for some constant $C\prime >0$.

We make a brief discussion on the above result. First, note that $⏧{\Gamma }^{\top }{z}_x{⏧}_{\infty }\le ⏧{\Gamma }^{\top }{z}_x⏧$, where the latter equals 1 when Γ is an orthogonal matrix. Further discussions are referred to Section A of the supplementary materials. Second, since λ_n has the order $\sqrt{\hspace{0.17em}\log \hspace{0.17em}n/n}$, the bound of Theorem 1 does not explicitly depend on p, which is reasonable, since we have only n + 1 parameters in the transformed model (2.3). Third, the bound given above involves the sparsity of the parameter vector $\mathit{\alpha }$ in the transformed model instead of that of $\mathit{\beta }$, allowing $\mathit{\beta }$ being sparse or non-sparse. As an application of Theorem 1, we present the results for Γ being ${\Gamma }_{\text{eg}}$ and $\Gamma (\widehat{\mathit{\beta }})$, respectively below.

Proposition 2.

Suppose that $(x,\mathbf{X})$ are fixed. Let $\Gamma ={\Gamma }_{\text{eg}}$. Assume that the $\mathit{\alpha }$-sparsity condition $R_q\le C{\lambda }_n^q⏧{\Gamma }^{\top }{z}_x{⏧}_1^2$ holds for some constant C > 0. Then it holds that $|{\widehat{\alpha }}_x-{\alpha }_x|\le C\prime {\lambda }_n^{1-q/2}{R}_q^{1/2}$ with probability $1-C_1{n}^{-3}$, where $C_1,C\prime$ are positive constants.

Similar to Theorem 1, Proposition 2 allows $\mathit{\beta }$ to be sparse or non-sparse. Due to α_x being bounded, we have $R_q\asymp ⏧\mathit{\theta }{⏧}_{(q)}$, which can be bounded as shown in Section 3.2. When X_i’s are random, a lower bound on $⏧{\Gamma }_{\text{eg}}^{\top }{z}_x{⏧}_1$ is given in Section E of the supplementary materials.

3.2 Sparsity of $\mathit{\theta }$ and Properties of ${\widehat{\alpha }}_x$ when $\Gamma ={\Gamma }_{\text{eg}}$

We first show that for $\Gamma ={\Gamma }_{\text{eg}}$, if the eigenvalues of $n^{-1}\mathbf{X}{Q}_x{\mathbf{X}}^{\top }$ decrease at a certain rate, $\mathit{\theta }$ will be approximately sparse; specifically $⏧\mathit{\theta }{⏧}_{(q)}$ is bounded for some $q\in [0,1]$. Then we give the asymptotic results on ${\widehat{\alpha }}_x$. Recall ${\psi }_1\ge {\psi }_2\cdots \ge {\psi }_n\ge 0$ are the eigenvalues of $n^{-1}\mathbf{X}{Q}_x\mathbf{X}$; they are also the first n eigenvalues of $n^{-1}{Q}_x{\mathbf{X}}^{\top }\mathbf{X}{Q}_x$. For $q\in [0,1]$ and $k=0,1,\dots ,n-1$, let ${\overline{\psi }}_{q,k}={(n-k)}^{-1}{\sum }_{i=k+1}^n{\psi }_i^{q/(2-q)}$ and ${\varphi }_k^{1/2}(\mathit{\beta })$ be the norm of the projected vector of $\mathit{\beta }$ onto the subspace spanned by the eigenvectors of $n^{-1}{Q}_x{\mathbf{X}}^{\top }\mathbf{X}{Q}_x$ associated with eigenvalues ${\psi }_{k+1},\dots ,{\psi }_n$, ${\varphi }_n(\mathit{\beta })={\overline{\psi }}_{q,n}=0$, and ${\overline{\psi }}_{q,k}$ is the average magnitude of the smallest n – k eigenvalues. For any $x_1,x_2\ge 0$, denote $H_{q,k}(x_1,x_2)=k^{1-q/2}+{\left[(n-k)x_1\right]}^{1-q/2}{x}_2^{q/2}.$ The following Lemma 1 is a deterministic result on $⏧\mathit{\theta }{⏧}_{(q)}$.

Lemma 1.

For $q\in [0,1]$, it holds that $⏧\mathit{\theta }{⏧}_{(q)}\le \underset{0\le k\le n}{\min }\left\{⏧{\zeta }_{\mathit{\beta }}{⏧}^q{k}^{1-q/2}+{\left[(n-k){\overline{\psi }}_{q,k}\right]}^{1-q/2}{\varphi }_k^{q/2}(\mathit{\beta })\right\}.$ Moreover, since $⏧{\zeta }_{\mathit{\beta }}⏧=O(1)$ in Model (2.3), it holds that $⏧\mathit{\theta }{⏧}_{(q)}=O(\underset{0\le k\le n}{\min }{H}_{q,k}({\overline{\psi }}_{q,k},{\varphi }_k(\mathit{\beta })))$.

Generally, it is difficult to obtain the sharp upper bound in Lemma 1 without any information of eigenvalues and $\mathit{\beta }$. Simply setting k = n, we have the trivial bound (3.1) $$⏧\mathit{\theta }{⏧}_{(q)}\lesssim H_{q,n}({\overline{\psi }}_{q,n},{\varphi }_k(\mathit{\beta }))=n^{1-q/2},$$(3.1) which however is unbounded and undesirable. To get better bounds on $⏧\mathit{\theta }{⏧}_{(q)}$, we take into account of the properties of eigenvalues and $\mathit{\beta }$, and consider the following three cases:

• Case (a): $n^{-1}\mathbf{X}{\mathbf{X}}^{\top }$ has low rank, say $\text{rank}(n^{-1}\mathbf{X}{\mathbf{X}}^{\top })=r_{\mathbf{X}}=O(1)$;

• Case (b): $\mathit{\beta }$ is sparse with $⏧\mathit{\beta }{⏧}_0=s_0$ and that $⏧\mathit{\beta }{⏧}_{\infty }<C<\infty$;

• Case (c): $\mathit{\beta }$ is dense, following a normal distribution $N(0,{\Sigma }_{\mathit{\beta }})$.

Results are presented in Corollary 1 and Proposition 3, respectively.

Corollary 1.

The following conclusions are deterministic.

1. For Case (a), it holds that ${\overline{\psi }}_{q,k}=0$ for $k\ge r_{\mathbf{X}}+1$, and $⏧\mathit{\theta }{⏧}_{(q)}=O(r_{\mathbf{X}}^{1-q/2})=O(1)$.

2. For Case (b), assume that n < p, then $⏧\mathit{\theta }{⏧}_{(q)}\lesssim \underset{0\le k\le n}{\min }{H}_{q,k}({\overline{\psi }}_{q,k},s_0).$ Thus, if ${\overline{\psi }}_{q,k_0}=O(s_0^{-q/(2-q)}{n}^{-1})$ for some fixed k₀, then $⏧\mathit{\theta }{⏧}_{(q)}=O(k_0^{1-q/2})=O(1)$.

In Corollary 1, conclusion (1) holds regardless of the sparsity of $\mathit{\beta }$, while conclusion (2) relaxes the conditions on eigenvalues by taking advantages of the sparsity of $\mathit{\beta }$. For Case (c), we assume that the column space of ${\Sigma }_{\mathit{\beta }}$ is the same as that of Σ, accommodating the identifiability condition that $\mathit{\beta }\in \text{span}(\Sigma )$. We have the following results.

Proposition 3.

Suppose that $(\mathbf{X},x)$ is fixed. For Case (c) with span(${\Sigma }_{\mathit{\beta }}$)=span(Σ), assume the following conditions: (i) $⏧{\zeta }_{\mathit{\beta }}⏧=O_p(1)$; (ii) ${(np)}^{-1}{\sum }_{i=1}^n{X}_i^{\top }{Q}_x{X}_i\asymp 1$; (iii) n < p. Then it holds that ${\varphi }_k(\mathit{\beta })=O_p(d_{\mathit{\beta }}n/p)$ for all k and that $⏧\mathit{\theta }{⏧}_{(q)}=O_p(\underset{0\le k\le n}{\min }{H}_{q,k}({\overline{\psi }}_{q,k},d_{\mathit{\beta }}n/p)),$ where $d_{\mathit{\beta }}={\lambda }_{\max }({\Sigma }_{\mathit{\beta }})/{\lambda }_{\min }^{+}({\Sigma }_{\mathit{\beta }})$ can be viewed as the condition number of ${\Sigma }_{\mathit{\beta }}$. For clarity, we assume that $d_{\mathit{\beta }}=O(1)$ and consider the following two specific examples of eigenvalues:

1. Suppose that ${\psi }_1\ge \cdots \ge {\psi }_{k_0}=\Omega (p)$ and $\underset{j\ge k_0+1}{\max }{\psi }_j=O(p{n}^{-2/q})$ for some fixed k₀. Then it holds that $⏧\mathit{\theta }{⏧}_{(q)}=O_p(k_0^{1-q/2})=O_p(1)$.

2. Denote $f_{\psi }(i)={\psi }_i/{\sum }_{i=1}^n{\psi }_i$, the scaled version of ψ_i, $i=1,\dots ,n$. Assume that $f_{\psi }(i)$ decreases exponentially, that is, $f_{\psi }(w)=a\hspace{0.17em}\exp \hspace{0.17em}(-a(w-1))$ for $w\ge 1$, where $a=a_n>0$ may depend on n. Then $⏧\mathit{\theta }{⏧}_{(q)}=O_p(1)$ if $a_n=$ $\Omega (q^{-1}\hspace{0.17em}\log \hspace{0.17em}n)$.

Condition (i) is a natural extension of the condition $⏧{\zeta }_{\mathit{\beta }}⏧=O(1)$ for fixed $\mathit{\beta }$ in Section 2. Condition (ii) is mild, ruling out the extreme case that Σ has eigenvalues $(p,0,\dots ,0)$. Details are referred to the proof in supplementary materials. The two examples in Proposition 3 imply that $\mathit{\theta }$ can be approximately sparse, when eigenvalues decrease fast enough. Based on the results of $⏧\mathit{\theta }{⏧}_{(q)}$ in Corollary 1 and Propositions 3, by applying the conclusion of Proposition 2, we are ready to give the asymptotic results of ${\widehat{\alpha }}_x$.

Theorem 2.

Suppose that $(x,\mathbf{X})$ are fixed. Taking $\Gamma ={\Gamma }_{\text{eg}}$, we have the following conclusions for Cases (a)–(c):

1. For Case (a), $|{\widehat{\alpha }}_x-{\alpha }_x|=O_p({\lambda }_n{r}_{\mathbf{X}}^{1/2})$. For Case (b), suppose that ${\lambda }_n^q⏧{\Gamma }^{\top }{z}_x{⏧}_1^2=\Omega (1)$ and that n < p; if ${\overline{\psi }}_{q,k_0}=O(s_0^{-q/(2-q)}{n}^{-1})$ for some fixed k₀, then $|{\widehat{\alpha }}_x-{\alpha }_x|=O_p({\lambda }_n^{1-q/2}{k}_0^{1/2-q/4}).$

2. For Case (c) of a dense $\mathit{\beta }$, assume that the conditions of Proposition 3 hold and that ${\lambda }_n^q⏧{\Gamma }^{\top }{z}_x{⏧}_1^2=\Omega (1)$. If ψ_i’s are from Proposition 3 (1), then $|{\widehat{\alpha }}_x-{\alpha }_x|=O_p({\lambda }_n^{1-q/2}{k}_0^{1/2-q/4})$; if ψ_i’s are from Proposition 3 (2), then $|{\widehat{\alpha }}_x-{\alpha }_x|=O_p({\lambda }_n^{1-q/2})$.

The condition ${\lambda }_n^q⏧{\Gamma }^{\top }{z}_x{⏧}_1^2=\Omega (1)$ above can be checked from data. Here k₀ and $r_{\mathbf{X}}$ reflect the sparsity of the parameters in the transformed model. Faster decay rates of eigenvalues result in smaller values of k₀ and $r_{\mathbf{X}}$, and consequently better convergence rates of $|{\widehat{\alpha }}_x-{\alpha }_x|$. Moreover, a smaller value of q results in a smaller value of ${\lambda }_n^{1-q/2}$, but requires a faster decreasing rate of eigenvalues. Note that the above bounds only depend on n and the degree of sparsity in eigenvalues, and do not explicitly depend on p. Moreover, for Cases (a) and (c) where $\mathit{\beta }$ is allowed to be dense, the sparsity of eigenvalues is complementary to the sparsity of $\mathit{\beta }$.

3.3 Properties of the Regularized Estimator ${\widehat{\alpha }}_x$ with an Initial $\widehat{\mathit{\beta }}$

We study properties of our estimator with $\Gamma (\widehat{\mathit{\beta }})$, giving the convergence rate of ${\widehat{\alpha }}_x$, for fixed x and X_i’s being iid from $N(0,\Sigma )$. The normality assumption of X_i’s simplifies the proofs and can be relaxed to general distributions such as sub-Gaussian distributions. We first give a result on $⏧{\overline{\zeta }}_{\widehat{\mathit{\beta }}}-{\overline{\zeta }}_{\mathit{\beta }}⏧$. Recall that ${\zeta }_{\widehat{\mathit{\beta }}}=n^{-1/2}\mathbf{X}{\widehat{\mathit{\beta }}}_{Q_x}$.

Proposition 4.

Assume that x is fixed, X_i’s are iid from $N(0,\Sigma )$, and $\text{cov}(X_i^{\top }{\mathit{\beta }}_{Q_x})\asymp 1$. For any estimator $\widehat{\mathit{\beta }}$ in Model (2.1), it holds that $⏧{\overline{\zeta }}_{\widehat{\mathit{\beta }}}-{\overline{\zeta }}_{\mathit{\beta }}⏧=O_p(\min \{2,⏧{\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}⏧\})$. Assuming further that $⏧x{⏧}_{\infty }⏧x{⏧}_{\Sigma }/⏧x{⏧}^2=O(1)$, then $⏧{\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}⏧=O_p(⏧\widehat{\mathit{\beta }}-\mathit{\beta }{⏧}_1{(\hspace{0.17em}\log \hspace{0.17em}p)}^{1/2})$.

When $\widehat{\mathit{\beta }}$ is the LASSO estimator, we have $⏧\widehat{\mathit{\beta }}-\mathit{\beta }{⏧}_1=O_p\left(\sigma s_0\sqrt{\hspace{0.17em}\log \hspace{0.17em}p/n}\right)$ with $s_0=\text{supp}(\mathit{\beta })$ (Bickel, Ritov, and Tsybakov 2009), and consequently $⏧{\overline{\zeta }}_{\widehat{\mathit{\beta }}}-{\overline{\zeta }}_{\mathit{\beta }}⏧=O_p\left(\min \right\{2,\sigma s_0\sqrt{{(\hspace{0.17em}\log \hspace{0.17em}p)}^2/n}\left\}\right)$. Let $H_{1,k}({\overline{\psi }}_{1,k},x)$ be the function obtained by setting q = 1 in $H_{q,k}({\overline{\psi }}_{q,k},x)$ defined in Section 3.2.

Theorem 3.

Let $\Gamma =\Gamma (\widehat{\mathit{\beta }})$. Assume that following conditions: (i) X_i’s are iid from $N(0,\Sigma )$, x is fixed, and n < p; (ii) $\mathit{\beta }$ satisfies $\text{cov}(X_i^{\top }{\mathit{\beta }}_{Q_x})\asymp 1$ and $\widehat{\mathit{\beta }}$ is obtained from additional data independent of $(\mathbf{X},\mathbf{Y})$, satisfying $\text{cov}(X_i^{\top }{\widehat{\mathit{\beta }}}_{Q_x}|\widehat{\mathit{\beta }})\asymp 1$. Then it holds that $|{\widehat{\alpha }}_x-{\alpha }_x|=O_p({\lambda }_n[1+H_{\min }⏧{\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}⏧])$, where $H_{\min }=\underset{0\le k\le n}{\min }{H}_{1,k}({\overline{\psi }}_{1,k},n/[p{\lambda }_{{\min }^{+}}(\Sigma )])$. Assuming further the Complementary condition: $H_{\min }⏧{\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}⏧=O_p(1)$, it follows that $|{\widehat{\alpha }}_x-{\alpha }_x|=O_p({\lambda }_n)$.

Based on the proof, one can see that ${\zeta }_{\widehat{\mathit{\beta }}}$ and ${\zeta }_{\mathit{\beta }}$ in Theorem 3 can be replaced by ${\overline{\zeta }}_{\widehat{\mathit{\beta }}}$ and ${\overline{\zeta }}_{\mathit{\beta }}$ respectively. The assumption on $\mathit{\beta }$ in (ii) is mild as $\text{cov}(X_i^{\top }{\mathit{\beta }}_{Q_x})=E(⏧{\zeta }_{\mathit{\beta }}{⏧}^2)$ and $⏧{\zeta }_{\mathit{\beta }}⏧$ is bounded in probability. We give some examples on the magnitude of $H_{\min }$.

Corollary 2.

(a) If Σ is of low rank, say $\text{rank}(\Sigma )=r_{\Sigma }=O(1)$, then $H_{\min }=O(r_{\Sigma }^{1/2})$. (b) Suppose that $\underset{j\ge k_0+1}{\max }{\psi }_j=O_p(p{n}^{-2})$ for some fixed k₀ and that ${\lambda }_{{\min }^{+}}(\Sigma )\gtrsim 1$. Then $H_{\min }=O_p(k_0^{1/2})$. (c) Suppose that ${\lambda }_{{\min }^{+}}(\Sigma )\gtrsim 1$ and denote $f_{\psi }(i)={\psi }_i/{\sum }_{i=1}^n{\psi }_i,i=1,\dots ,n$. Assuming that $f_{\psi }(i)$ decreases exponentially in probability, that is, $f_{\psi }(w)=a\hspace{0.17em}\exp \hspace{0.17em}(-a(w-1))$ for $w\ge 1$, where $a=a_n\gtrsim \hspace{0.17em}\log \hspace{0.17em}n$, then $H_{\min }=O_p(1)$.

Proof of Corollary 2

is similar to those of Corollary 1 and Proposition 3 and is omitted. We point out two basic facts: $1\lesssim H_{\min }\lesssim \sqrt{n}$ from (3.1), and $⏧{\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}⏧=O_p(1)$ by Condition (ii) and the law of large numbers. Moreover, the error rate of an estimator is generally believed having an order no less than $n^{-1/2}$; thus, without loss of generality we have $⏧{\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}⏧={\Omega }_p(n^{-1/2})$ throughout this article. Hence, Theorem 3 leads to the error rate of order ${\lambda }_n{H}_{\min }⏧{\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}⏧\lesssim \min \{{\lambda }_n\sqrt{n}⏧{\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}⏧,{\lambda }_n{H}_{\min }\}$ in probability without any restriction on the decay rate of eigenvalues.

The complementary condition involves two terms, $H_{\min }$ and $⏧{\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}⏧$, where the former is controlled by the decay rate of the eigenvalues, and the latter depends on the accuracy of $\widehat{\mathit{\beta }}$. As argued before, as long as the eigenvalues decrease fast, $H_{\min }$ will be bounded, even if ${\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}\nrightarrow 0$. Therefore, if $\widehat{\mathit{\beta }}$ is not accurate but eigenvalues decay fast, we can still get good results. The same argument applies when $\widehat{\mathit{\beta }}$ is accurate but the eigenvalues decay slowly. Particularly, if $\widehat{\mathit{\beta }}$ is good enough such that $⏧{\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}⏧=O_p(n^{-1/2})$, then the requirement on the decaying rate of eigenvalues can be removed completely. Thus, the information of $\widehat{\mathit{\beta }}$ and eigenvalues are complementary to each other, requiring only the product of $H_{\min }$ and $⏧{\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}⏧$ being bounded. Theorem 3 assumes $\widehat{\mathit{\beta }}$ being independent of the data $(\mathbf{X},\mathbf{Y})$. When $\widehat{\mathit{\beta }}$ depends on $(\mathbf{X},\mathbf{Y})$, we get a similar result on ${\widehat{\alpha }}_x$ with some modifications on the Condition (i), which is presented in Section F of the supplementary materials.

4 Results of ${\widehat{\gamma }}_x$ for Two Types of Test Points

In Section 3, we establish theoretical properties of ${\widehat{\alpha }}_x$. With ${\widehat{\gamma }}_x={\widehat{\alpha }}_x·⏧x{⏧}^2\mathrm{⏧Xx}{⏧}^{-1}{n}^{1/2}$, it is natural to get the corresponding results on ${\widehat{\gamma }}_x$ for a generic x. As mentioned in Examples 1 and 2 in Section 2.1, we are interested in two typical settings in particular: (a) x is a sparse vector with $S_x=\text{supp}(x)$ and $s_x=\left|S_x\right|$, and (b) x is a random vector as an iid copy of X_i (i.e., the prediction problem). Next we give the theoretical results on ${\widehat{\gamma }}_x$ for these two examples, based on the simple fact that $|{\widehat{\gamma }}_x-{\gamma }_x|\le |{\widehat{\alpha }}_x-{\alpha }_x|·⏧x{⏧}^2\mathrm{⏧Xx}{⏧}^{-1}{n}^{1/2}$.

4.1 Properties of ${\widehat{\gamma }}_x$ for a Sparse x

Proposition 5.

Assume the following conditions: (i) x is a fixed sparse vector satisfying $⏧x{⏧}_{\infty }=O(1)$; (ii) ${\lambda }_{\min }(n^{-1}{\mathbf{X}}_{S_x}^{\top }{\mathbf{X}}_{S_x})>c>0$, where ${\mathbf{X}}_{S_x}$ is formed by the columns of X with index S_x. Then we have $⏧x{⏧}^2\mathrm{⏧Xx}{⏧}^{-1}{n}^{1/2}=O(⏧x⏧)=O(s_x^{1/2})$. Moreover, the following results hold.

1. Take $\Gamma ={\Gamma }_{\text{eg}}$ and assume that the conditions of Theorem 2 hold. For Case (a) in Section 3.2, it holds that $|{\widehat{\gamma }}_x-{\gamma }_x|=O_p({\lambda }_n⏧x⏧r_{\mathbf{X}}^{1/2})=O_p({\lambda }_n{(s_x{r}_{\mathbf{X}})}^{1/2})$; for Cases (b) and (c) in Section 3.2, $|{\widehat{\gamma }}_x-{\gamma }_x|=O_p({\lambda }_n^{1-q/2}⏧x⏧)=O_p(s_x^{1/2}{\lambda }_n^{1-q/2})$, where k₀ appeared in Theorem 2 is omitted due to $k_0=O(1)$.

2. Let $\Gamma =\Gamma (\widehat{\mathit{\beta }})$. Assume further that the conditions of Theorem 3 hold. Then it follows that $|{\widehat{\gamma }}_x-{\gamma }_x|=O_p(s_x^{1/2}{\lambda }_n{H}_{\min }⏧{\zeta }_{\widehat{\mathit{\beta }}}-{\zeta }_{\mathit{\beta }}⏧)$; assume further that the Complementary condition holds, then $|{\widehat{\gamma }}_x-{\gamma }_x|=O_p\left(⏧x⏧\sqrt{n^{-1}\hspace{0.17em}\log \hspace{0.17em}n}\right)=O_p\left(\sqrt{n^{-1}{s}_x\hspace{0.17em}\log \hspace{0.17em}n}\right)$.

The condition ${\lambda }_{\min }(n^{-1}{\mathbf{X}}_{S_x}^{\top }{\mathbf{X}}_{S_x})>c>0$ is a type of the restricted eigenvalue condition (Bickel, Ritov, and Tsybakov 2009). If X_i’s are iid variables, $n^{-1}{\mathbf{X}}_{S_x}^{\top }{\mathbf{X}}_{S_x}{\to }_p\text{cov}(X_{S_x})={\Sigma }_{S_x{S}_x}$. Recall that $(n^{-1}{\mathbf{X}}^{\top }\mathbf{X})=r_{\mathbf{X}}$ in Case (a) of Theorem 2; then the condition ${\lambda }_{\min }(n^{-1}{\mathbf{X}}_{S_x}^{\top }{\mathbf{X}}_{S_x})>c>0$ implies that $s_x\le r_{\mathbf{X}}$ there.

Remark 5.

We briefly discuss the case of $\Sigma =I_p$ or close to I_p for a sparse vector x. For $\Gamma ={\Gamma }_{\text{eg}}$, using the trivial bound in (3.1) on R_q and taking q = 1 in Proposition 2, we can see that the error of $|{\widehat{\alpha }}_x-{\alpha }_x|$ has the order $O_p({(\hspace{0.17em}\log \hspace{0.17em}n)}^{1/4})$, and consequently $|{\widehat{\gamma }}_x-{\gamma }_x|=O_p(⏧x⏧{(\hspace{0.17em}\log \hspace{0.17em}n)}^{1/4})$.

We briefly compare our method with the plug-in estimator using the LASSO estimator $\widehat{\mathit{\beta }}$ (named briefly as LASSO). For LASSO, the error varies depending on the direction of x, while results of our estimator depend only on the sparsity degree s_x of x. For simplicity of comparison, we consider a bound of LASSO depending only on s_x. Specifically, as $⏧x{⏧}_{\infty }=O(1)$, we have $|x^{\top }{\widehat{\mathit{\beta }}}_{\text{lasso}}-x^{\top }\mathit{\beta }|=O(\mathit{\text{⏧x⏧⏧}}{\widehat{\mathit{\beta }}}_{\text{lasso}}-\mathit{\beta }⏧)=O_p\left(\sqrt{s_x{s}_0\hspace{0.17em}\log \hspace{0.17em}p/n}\right)$ (Bickel, Ritov, and Tsybakov 2009); the latter will be used as the error rate of LASSO. Recall that $P_{\text{eg}}$ denote our estimator with $\Gamma ={\Gamma }_{\text{eg}}$. For Case (a), it follows from Proposition 5 that $P_{\text{eg}}$ is better than LASSO if and only if $r_{\mathbf{X}}(\hspace{0.17em}\log \hspace{0.17em}n){(\hspace{0.17em}\log \hspace{0.17em}p)}^{-1}=o(s_0)$. Cases (b) and (c) can be analyzed similarly. Recall that $P_{\text{lasso}}$ is our estimator with $\Gamma =\Gamma ({\widehat{\mathit{\beta }}}_{\text{lasso}})$.

Corollary 3.

Denote by $T_{n,\mathrm{f}ix}$ the ratio of error rate of $P_{\text{lasso}}$ over that of LASSO for a fixed sparse x. Suppose that the conditions (i) and (ii) in Proposition 5 and the conditions of Theorem 3 hold. Then $P_{\text{lasso}}$ has the error rate of order ${\lambda }_n{H}_{\min }\sqrt{s_x{(s_0\hspace{0.17em}\log \hspace{0.17em}p)}^2/n}$ and consequently $T_{n,\mathrm{f}ix}=O_p\left({\lambda }_n{H}_{\min }\sqrt{s_0\hspace{0.17em}\log \hspace{0.17em}p}\right)$. If $H_{\min }=o_p(n^{1/2}{[s_0(\hspace{0.17em}\log \hspace{0.17em}n)(\hspace{0.17em}\log \hspace{0.17em}p)]}^{-1/2})$, then $T_{n,\mathrm{f}ix}=o_p(1)$, impliying $P_{\text{lasso}}$ is superior to LASSO; otherwise $P_{\text{lasso}}$ is inferior or similar to LASSO.

The proof of Corollary 3 is a simple combination of Proposition 4 and (2) of Proposition 5 and is omitted here. Since we always have $H_{\min }\lesssim \sqrt{n}$, the requirement $H_{\min }=o_p(n^{1/2}{[s_0(\hspace{0.17em}\log \hspace{0.17em}n)(\hspace{0.17em}\log \hspace{0.17em}p)]}^{-1/2})$ is mild.

4.2 Properties of ${\widehat{\gamma }}_x$ for Prediction Problems

In a prediction problem, x and X_i’s are iid variables. Recall that $M_{\Sigma }=\sqrt{t{r}^2(\Sigma )/tr({\Sigma }^2)}$.

Proposition 6.

Suppose that x and X_i’s are iid from $N(0,\Sigma )$. Then $⏧x{⏧}^2\mathrm{⏧Xx}{⏧}^{-1}{n}^{1/2}=O_p(⏧x{⏧}^2/⏧x{⏧}_{\Sigma })=O_p(M_{\Sigma }).$ In addition, it holds that $1\le M_{\Sigma }\le p^{1/2}$. Particularly, $M_{\Sigma }\asymp 1$ when Σ is of low rank, and $M_{\Sigma }=p^{1/2}$ when $\Sigma =I_p$.

Next we first derive properties of ${\widehat{\gamma }}_x$ with $\Gamma ={\Gamma }_{\text{eg}}$. Then we consider the estimator ${\widehat{\gamma }}_{{\tilde{x}}_{S_1}}$ with $\Gamma =\Gamma (\widehat{\mathit{\beta }})$, given both an initial estimator $\widehat{\mathit{\beta }}$ and a subset S₁.

4.2.1 Properties of ${\widehat{\gamma }}_x$ for x in Prediction with $\Gamma ={\Gamma }_{\text{eg}}$

Recall that $|{\widehat{\gamma }}_x-{\gamma }_x|\le |{\widehat{\alpha }}_x-{\alpha }_x|·⏧x{⏧}^2\mathrm{⏧Xx}{⏧}^{-1}{n}^{1/2}$. Combining Proposition 6 and the result on $|{\widehat{\alpha }}_x-{\alpha }_x|$ with fixed $(x,\mathbf{X})$ given in Proposition 2 for $\Gamma ={\Gamma }_{\text{eg}}$, it can be inferred that $|{\widehat{\gamma }}_x-{\gamma }_x|=O_p({\lambda }_n^{1-q/2}{R}_q^{1/2}{M}_{\Sigma })$. Clearly, a faster decay rate of the eigenvalues $\mathit{\lambda }(\Sigma )$ leads to a smaller value of $M_{\Sigma }$, and a faster decay rate of ψ_i’s or equivalently a smaller value of R_q, consequently a better rate. Different from the fixed $(x,\mathbf{X})$ considered in Theorem 2, $(x,\mathbf{X})$ are random variables in this section. Thus, R_q lacks an explicit rate, due to randomness of the empirical eigenvalues ψ_i’s. The magnitudes of ψ_i’s, though can be checked from data, are hard to extract in theory generally, according to random matrix theory. To the best of our knowledge, there is no solution for a general case. To obtain an explicit result, we consider two extreme cases: (a) Σ is (approximately) low rank; (b) $\Sigma =I_p$, the least favorable case.

Proposition 7.

Suppose that x and X_i’s are independent from $N(0,\Sigma )$. Assume that n < p. Taking $\Gamma ={\Gamma }_{\text{eg}}$, we have the following conclusions:

1. If Σ is of low rank with $\text{rank}(\Sigma )=r_{\Sigma }$, we have $|{\widehat{\gamma }}_x-{\gamma }_x|=O_p\left(r_{\Sigma }\sqrt{n^{-1}\hspace{0.17em}\log \hspace{0.17em}n}\right)$. An extension to Σ being approximately low rank is presented in Proposition D.1 of supplementary material.

2. For the least favorable case of $\Sigma =I_p$, it holds that $|{\widehat{\gamma }}_x-{\gamma }_x|=O_p(p^{1/2}{(\hspace{0.17em}\log \hspace{0.17em}n)}^{1/4})$.

For the case of Σ having a low rank, $|{\widehat{\gamma }}_x-{\gamma }_x|$ has the order similar to that of $|{\widehat{\alpha }}_x-{\alpha }_x|$. But when $\Sigma =I_p$, the error diverges, which is not surprising since $\mathit{\theta }$ is nonsparse in the transformed model in this setting and the rate is determined by the most difficult case. Particularly, the rate for $\Sigma =I_p$ is the combination of the facts that $|{\widehat{\alpha }}_x-{\alpha }_x|=O_p({(\hspace{0.17em}\log \hspace{0.17em}n)}^{1/4})$ and $M_{\Sigma }=p^{1/2}$. Next we briefly compare LASSO with the proposed method with $\Gamma ={\Gamma }_{\text{eg}}$. LASSO performs well in prediction when $\mathit{\beta }$ is (approximately) sparse, and is less sensitive to the sparsity of eigenvalues. In contrast, the proposed method with $\Gamma ={\Gamma }_{\text{eg}}$ has good performance when the eigenvalues of Σ decrease fast, and $\mathit{\beta }$ can be sparse or less sparse. Thus, our method with $\Gamma ={\Gamma }_{\text{eg}}$ and LASSO are complementary to each other.

4.2.2 Error of ${\widehat{\gamma }}_{{\tilde{x}}_{S_1}}$ in Prediction with $\Gamma =\Gamma (\widehat{\mathit{\beta }})$

Recall that in Example 2 in Section 2.1, ${\gamma }_x={\gamma }_{{\tilde{x}}_{S_1}}$ for any $S_1\supseteq S_0$ with $S_0=\text{supp}(\mathit{\beta })$, implying that one can make prediction at the point ${\tilde{x}}_{S_1}$. Trivially, one can take $S_1=\{1,\dots ,p\}$ such that ${\tilde{x}}_{S_1}=x$. The subset S₁ takes the sparsity degree of $\mathit{\beta }$ into account. Given an initial estimator $\widehat{\mathit{\beta }}$ and a subset S₁ such that $S_1\supseteq S_0$, by applying our approach with $\Gamma =\Gamma (\widehat{\mathit{\beta }})$ that is constructed with x replaced by ${\tilde{x}}_{S_1}$, we obtain the estimator of ${\gamma }_{{\tilde{x}}_{S_1}}$ denoted as ${\widehat{\gamma }}_{{\tilde{x}}_{S_1}}$.

Denote $d(\widehat{\mathit{\beta }},\mathit{\beta })={[\max \{\text{var}(X_i^{\top }(\widehat{\mathit{\beta }}-\mathit{\beta })),\text{var}(X_{i{S}_1}^{\top }({\widehat{\mathit{\beta }}}_{S_1}-{\mathit{\beta }}_{S_1}))\}]}^{1/2}$, which stands for the prediction error of an initial estimator $\widehat{\mathit{\beta }}$. Without loss of generality, we assume $d(\widehat{\mathit{\beta }},\mathit{\beta })$ has magnitude of order no less than $n^{-1/2}$. Let ${\Sigma }_{S_1{S}_1}=\text{cov}(X_{i{S}_1})$ and $M_{S_1}={[t{r}^2({\Sigma }_{S_1{S}_1})/tr({\Sigma }_{S_1{S}_1}^2)]}^{1/2}$ with $M_{S_1}^2$ standing for the effective rank of matrix ${\Sigma }_{S_1{S}_1}$. Let ${\tilde{H}}_{\min }$ be the quantity defined similar to $H_{\min }$ but with the eigenvalues of $n^{-1}\mathbf{X}{\mathbf{X}}^{\top }$, satisfying $1\lesssim {\tilde{H}}_{\min }\lesssim \sqrt{n}$ (the detailed expression is given in the supplementary materials). We have the following conclusions from Theorem 3.

Theorem 4.

Let $\Gamma =\Gamma (\widehat{\mathit{\beta }})$. Assume that (i) x and X_i’s are iid variables from $N(0,\Sigma )$ and n < p; (ii) Both S₁ and $\widehat{\mathit{\beta }}$ are independent of $(\mathbf{X},\mathbf{Y})$ satisfying $\text{cov}(X_i^{\top }\widehat{\mathit{\beta }})\asymp 1$. Then it holds that $|{\widehat{\gamma }}_{{\tilde{x}}_{S_1}}-{\gamma }_x|=O_p({\lambda }_n{M}_{S_1}{\tilde{H}}_{\min }d(\widehat{\mathit{\beta }},\mathit{\beta }))$. If we further assume the complementary condition: $d(\widehat{\mathit{\beta }},\mathit{\beta })){\tilde{H}}_{\min }=O_p(1)$, it holds that $|{\widehat{\gamma }}_{{\tilde{x}}_{S_1}}-{\gamma }_x|=O_p({\lambda }_n{M}_{S_1})$. These conclusions are still valid for $S_1=\{1,\dots ,p\}$.

Theorem 4 shows that the rate depends on $M_{S_1},{\tilde{H}}_{\min }$, and $d(\widehat{\mathit{\beta }},\mathit{\beta })$. The first two depend on the decay rate of eigenvalues. Moreover, it holds that $d(\widehat{\mathit{\beta }},\mathit{\beta })=O_p(1)$ by the assumptions that both $\text{cov}(X_i^{\top }\mathit{\beta })$ and $\text{cov}(X_i^{\top }\widehat{\mathit{\beta }})$ are bounded, which imposes restrictions on $\widehat{\mathit{\beta }}$. Hence, by Theorem 4, without the complementary condition, we have the error rate $\min \{{\lambda }_n{M}_{S_1}\sqrt{n}d(\widehat{\mathit{\beta }},\mathit{\beta }),{\lambda }_n{M}_{S_1}{\tilde{H}}_{\min }\}$.

We compare $P_{\text{lasso}}$ with the plug-in method using LASSO estimator $\widehat{\mathit{\beta }}$ (briefly named LASSO). By the typical rate of LASSO, we have $d({\widehat{\mathit{\beta }}}_{\text{lasso}},\mathit{\beta })=O_p\left(\min \right\{1,\sqrt{s_0\hspace{0.17em}\log \hspace{0.17em}p/n}\left\}\right)$. To simplify the comparison, we assume that the LASSO estimator is consistent, that is, $\sqrt{s_0\hspace{0.17em}\log \hspace{0.17em}p/n}=o(1)$. Then one can see that the condition $d({\widehat{\mathit{\beta }}}_{\text{lasso}},\mathit{\beta }){\tilde{H}}_{\min }=O_p(1)$ becomes ${\tilde{H}}_{\min }=O_p(n^{1/2}{(s_0\hspace{0.17em}\log \hspace{0.17em}p)}^{-1/2})$, which is mild, since it always holds that ${\tilde{H}}_{\min }\lesssim n^{1/2}$.

Denote by $T_{n,\mathrm{r}ad}$ the ratio of the error rate of $P_{\text{lasso}}$ over $d({\widehat{\mathit{\beta }}}_{\text{lasso}},\mathit{\beta })$ for random test points. Then $T_{n,\mathrm{r}ad}=o_p(1)$ would imply that our method is better than LASSO. By Theorem 4, we see that $T_{n,\mathrm{r}ad}\asymp {\lambda }_n{M}_{S_1}{\tilde{H}}_{\min }$ in probably. To investigate the magnitude of the latter, we consider the following two cases:

• Suppose that $\mathit{\beta }$ is sparse with support set S₀ of cardinality $s_0=\left|S_0\right|$. Moreover, if a good S₁ is available such that $S_1\supseteq S_0$ and $\left|S_1\right|\asymp s_0$, that is, we know sufficiently well on the support set. Then we have $M_{S_1}\asymp s_0^{1/2}$. If ${\tilde{H}}_{\min }=o_p(n^{1/2}{(s_0\hspace{0.17em}\log \hspace{0.17em}n)}^{-1/2})$ (i.e., ${\lambda }_n{s}_0^{1/2}{\tilde{H}}_{\min }=o_p(1)$) which is mild as argued above, we have $T_{n,\mathrm{r}ad}=o_p(1)$; otherwise $T_{n,\mathrm{r}ad}={\Omega }_p(1)$. Moreover, $P_{\text{lasso}}$ has error $|{\widehat{\gamma }}_{{\tilde{x}}_{S_1}}-{\gamma }_x|=O_p(\sqrt{s_0(\hspace{0.17em}\log \hspace{0.17em}n)/n})$ under the mild condition ${\tilde{H}}_{\min }d({\widehat{\mathit{\beta }}}_{\text{lasso}},\mathit{\beta })=O_p(1)$. If one knows the support set S₀ in advance, the OLS estimator using the oracle predictor $X_{i{S}_0}$’s has the rate $\sqrt{s_0/n}$, which is similar to the rate of our estimator up to a term $\hspace{0.17em}\log \hspace{0.17em}n$. However, the performance of our estimator depends on that of S₁ and the decay of eigenvalues.

• If we simply set $S_1=\{1,\dots ,p\}$, ignoring the sparsity information of $\mathit{\beta }$, then $T_{n,\mathrm{r}ad}=o_p(1)$ if and only if $M_{S_1}{\tilde{H}}_{\min }=o_p({\lambda }_n^{-1})$; otherwise $T_{n,\mathrm{r}ad}={\Omega }_p(1)$. This condition $M_{S_1}{\tilde{H}}_{\min }=o_p({\lambda }_n^{-1})$ holds when eigenvalues decay fast. Moreover, under the settings similar to Corollary 2, we have ${\tilde{H}}_{\min }=O_p(1)$. For instance, if $\text{rank}(\Sigma )=o({\lambda }_n^{-1})$, then $M_{S_1}{\tilde{H}}_{\min }\lesssim \text{rank}(\Sigma )=o_p({\lambda }_n^{-1})$. However, $P_{\text{lasso}}$ is worse than LASSO when Σ is close to I_p and $\mathit{\beta }$ is indeed sparse; specifically, under the complementary condition, $P_{\text{lasso}}$ has error rate ${\lambda }_n{M}_{S_1}=O_p({(n^{-1}p\hspace{0.17em}\log \hspace{0.17em}n)}^{1/2})$, which is worse than that of LASSO. However, taking $S_1=\{1,\dots ,p\}$ accommodates both sparse and non-sparse $\mathit{\beta }$. The classical OLS estimator for a non-sparse $\mathit{\beta }$ has the order $\sqrt{p/n}$, close to that of $P_{\text{lasso}}$. In practice, we do not know the sparsity degree of $\mathit{\beta }$. The CV approach in Section 2.3 can be used to select between ${\widehat{\gamma }}_{x_{S_1}}$ and ${\widehat{\gamma }}_x$ in an automatic data adaptive manner.

5 Numerical Studies

We use simulation studies in Section 5.1 and real data analysis in Section 5.2 to further illustrate the numerical performance of our method.

5.1 Simulations

We consider the simulation studies with samples generated iid from the linear model (2.1) with p = 1000 dimensional vector $X_i\sim N(0,\Sigma )$ and ${ϵ}_i\sim N(0,1)$. Set $\Sigma =({\sigma }_{ij})$ with ${\sigma }_{ij}={0.5}^{|i-j|/\eta }$, where η controls the level of dependence strength among the predictors, with larger values of η implying stronger correlations among predictors. For the convenience of discussion, the plug-in estimator is named by the method used in estimating $\mathit{\beta }$. For example, “LASSO,” “ridge,” and “ridgeless” denote the plug-in estimators ${\widehat{\mathit{\beta }}}^{\top }x$ with $\widehat{\mathit{\beta }}$ being LASSO, ridge and ridgeless estimators, respectively.

Setting 1 (Prediction). We set $\mathit{\beta }={\delta }_0{({\mathbf{1}}_{p_0}^{\top },0,\dots ,0)}^{\top }\in {\mathbb{R}}^p$, where $p_0=r_{0}p,{\mathbf{1}}_{p_0}$ is the p₀-dimensional vector of 1, and ${\delta }_0=10/\sqrt{p_0}$ such that $⏧\mathit{\beta }⏧=10$. Clearly, $\mathit{\beta }$ is denser for larger values of r₀, and we set $r_0\in \{0.1,0.2,\dots ,0.9\}$. For prediction, we set $\mathcal{M}=\{P_{\text{lasso}},P_{\text{ridge}},P_{\text{eg}},P_{\text{rdl}}\}$ for Algorithm 2 in Section 2.3.

We compare the prediction performance of different methods. Split the data into two parts with the training sample of size n_tr = 200 and the testing sample of size n_te = 500 to compute the test error. PWE estimators are obtained by Algorithm 2 with the $\mathcal{M}$ given above and $S_1=\{1,\dots ,p\}$. For the implementation of Algorithm 1, the bias correction step is adopted. We repeat the procedure 100 times and calculate the average test error for each method. 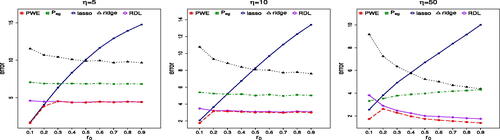We compare LASSO, ridge, ridgeless, $P_{\text{eg}}$ and the PWE estimators. For clarity, simulation results for Setting 1 are summarized as follows:

1. Comparison of LASSO, ridge, ridgeless with PWE and $P_{\text{eg}}$ on prediction. The simulation results are presented in Figure 2. When $\mathit{\beta }$ is sparse such as r = 0.1, PWE performs similar to (with small η) and better than (with large η) LASSO, and much better than other methods including ridgeless. When r₀ is large, PWE is similar to or slightly better than the ridgeless estimator, and is much better than other methods. By taking the advantages of different initial estimators, PWE performs well for both sparse and dense $\mathit{\beta }$. Moreover, $P_{\text{eg}}$ is insensitive to r₀, which supports our theoretical findings, and is better than LASSO when r₀ is large. Its advantage over LASSO is more clear when η is large.

2. Comparison of plug-in estimators with our proposed pointwise counterparts. Due to the limited space, the results are presented in Figure S.2 in Section G.1 of the supplementary material. It is seen that the performance of $P_{\text{lasso}}$ is similar to LASSO for small η and is better than LASSO for large η; in all cases, $P_{\text{ridge}}$ is better than $\text{ridge}$. The numerical results match with our theoretical findings in the sense that the sparsity in eigenvalues can be helpful. In addition, $P_{\text{rdl}}$ is close to ridgeless, especially when η is small. More comparisons are presented in Setting 4 and Section G.1 in Supplementary Materials.

Fig. 2 Simulation prediction results of PWE, LASSO, ridge, $P_{\text{eg}}$, and ridgeless (RDL).

Setting 2 (Sparse linear transformation). We consider x being sparse vectors in ${\gamma }_x={\mathit{\beta }}^{\top }x$. Set $\mathit{\beta }={(3,-3,3,1,{\delta }_1{\mathbf{1}}_{p_0-4}^{\top },{\mathbf{0}}_{p-p_0}^{\top })}^{\top }$, where ${\delta }_1=5/\sqrt{p_0}$. Consider γ_x being one of the four quantities β₁, ${\beta }_{p_0}$, β_p and ${\beta }_1-{\beta }_3$, corresponding to taking x being $e_1,e_{p_0},e_p$ and $e_1-e_3$, respectively in γ_x. Note that ${\beta }_1-{\beta }_3=0$, indicating that there is no difference between effects of the first and third predictors; ${\beta }_1=3$ and ${\beta }_{p_0}={\delta }_1$ stand for strong and weak signals, respectively. Moreover, ${\beta }_p=0$ indicates that the pth predictor is insignificant. Let $p_0=300$ and $\Sigma =({\sigma }_{ij})$ with ${\sigma }_{ij}={0.5}^{|i-j|/150}$, so that the predictors are highly correlated. We set the training data size n_tr = 150, and compute the average errors of $|{\widehat{\gamma }}_x-{\gamma }_x|$ over 100 replications. We compare the regularized estimators, $P_{\text{eg}},P_{\text{lasso}}$, and $P_{\text{ridge}}$, with the plug-in ones. Estimation comparison results are presented in Table 2.

Table 2 The average values of $|{\widehat{\gamma }}_x-{\gamma }_x|$.

γx	LASSO	A-LASSO	ridge	$P_{\text{lasso}}$	$P_{\text{ridge}}$	$P_{\text{eg}}$	PWE
β1	0.671	0.681	0.672	0.701	0.405	0.277	0.405
${\beta }_{p_0}$	0.072	0.072	0.036	0.072	0.072	0.128	0.072
βp	0	0	0.010	0	0	0	0
${\beta }_1-{\beta }_3$	0.251	1.062	0.005	0	0	0.022	0

NOTE: The PWE corresponds to the estimator automatically selected from $\{P_{\text{eg}},P_{\text{lasso}},P_{\text{ridge}}\}$; A-LASSO stands for the adaptive LASSO.

For a strong signal β₁, it can be inferred from Table 2 that the regularized pointwise estimators $P_{\text{ridge}}$ and $P_{\text{eg}}$ are better than LASSO, adaptive LASSO and ridge regression. For weak signal ${\beta }_{p_0}$, ridge estimator is better than others. The main reason is that other methods sometimes shrink the estimators to zero, resulting in large biases. For ${\beta }_p=0$, except ridge regression, other methods give zero estimates. Finally, for ${\beta }_1-{\beta }_3=0$, all the regularized pointwise estimators result in exactly zero estimates, while the plug-in estimators LASSO and adaptive LASSO lead to large biases.

Setting 3 (Comparison on different subset S₁). As pointed out in Sections 2.1 and 2.3, one can consider prediction at the point ${\tilde{x}}_{S_1}$ instead of x in prediction problems. Under the setup of Setting 1, we take $\Gamma =\Gamma ({\widehat{\mathit{\beta }}}_{\text{lasso}})$ and compare the following four candidates of S₁: (1) S₁ being $S_0=\text{supp}(\mathit{\beta })$, which is the ideal case; (2) S₁ being $S_{\text{full}}=\{1,\dots ,p\}$, that is, ${\gamma }_{{\tilde{x}}_{S_1}}={\gamma }_x$; (3) S₁ is obtained by SIS of Fan and Lv (2008), denoted as $S_{\text{SIS}}$; (4) S₁ being the $S_{\text{lasso}}=\text{supp}({\widehat{\mathit{\beta }}}_{\text{lasso}})$. For each candidate of S₁, we repeat 100 times and report the average values of the prediction error, true positive rate (TP) and the average length (LEN) that are defined as TP=$|S_1\cap S_0|/\left|S_0\right|$ and LEN=$\left|S_1\right|/p$, respectively.

Due to the limited space, we present the simulation results in Section G.2 in supplementary materials. It is seen that S₀ always leads to the best prediction errors in all cases. When $r_0=0.01$ where $\mathit{\beta }$ is very sparse, both $S_{\text{SIS}}$ and $S_{\text{lasso}}$ have higher values of TP and smaller values of LEN, leading to smaller prediction errors than those of $S_{\text{full}}$. As r₀ increases, the signal of β_j’s becomes weak due to the constraint $⏧\mathit{\beta }⏧=10$, and the values of TP for $S_{\text{SIS}}$ are very small and are the smallest ones among all subsets, which lead to the worst prediction errors. On the other hand, TP and consequently errors of $S_{\text{lasso}}$ are much better than those of $S_{\text{SIS}}$, because LASSO takes into account correlations among the predictors when selecting the significant variables, while SIS uses only the marginal correlations. In addition, it is observed that $S_{\text{lasso}}$ performs similar to that of $S_{\text{full}}$, which is partially due to the following reason. During the construction of $\Gamma ({\widehat{\mathit{\beta }}}_{\text{lasso}})$ with a given S₁, we need to compute ${\tilde{x}}_{S_1}^{\top }{\widehat{\mathit{\beta }}}_{\text{lasso}}$, which equals $x^{\top }{\widehat{\mathit{\beta }}}_{\text{lasso}}$ for S₁ being both $S_{\text{lasso}}$ and $S_{\text{full}}$.

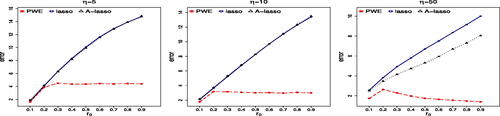
Setting 4 (Further comparison for heterogeneous test points). In Setting 1 where test points are iid copies from the training distribution, $P_{\text{lasso}}$ is nearly the same as LASSO when η is small such as η = 5 (results shown in Figure S.2 in supplementary material). We compare them further for the case of x_i’s following a distribution different from X_i’s, which is known as covariate shift in the literature of transfer learning (Weiss, Khoshgoftaar, and Wang 2016). We generate training data of size 100 as in Setting 1 with η = 5 and $\mathit{\beta }\propto {({\mathbf{1}}_{p_0}^{\top },0,\dots ,0)}^{\top }\in {\mathbb{R}}^p$ with $⏧\mathit{\beta }⏧=5$. The test points x_i’s are iid from $N(0,{\Sigma }_{\text{te}})$. The eigenvectors matrix $U_{\text{te}}$ of ${\Sigma }_{\text{te}}$ is uniformly distributed on the set of all orthogonal matrices in ${\mathbb{R}}^{p\times p}$. The eigenvalues of ${\Sigma }_{\text{te}}$, denoted as ${\varrho }_{\text{te},1},\dots ,{\varrho }_{\text{te},p}$, satisfy that ${\varrho }_{\text{te},i}=2(p-i+1)/(p+1)$ such that $tr({\Sigma }_{\text{te}})=p$. We first generate a ${\Sigma }_{\text{te}}$ and then 200 test points with given ${\Sigma }_{\text{te}}$, and repeat this procedure 100 times to compute average prediction errors. Results in Table 3 show that $P_{\text{lasso}}$ is much better than LASSO for the case of covariate shift even for small η, possibly due to the flexible pointwise prediction of our proposed method. Besides these examples, additional results demonstrate that $P_{\text{rdl}}$ can also substantially improve the ridgeless estimator when covariate shift exists for testing data (Section G.1 of supplementary materials).

Table 3 Test errors of LASSO and $P_{\text{lasso}}$ with η = 5 for testing points from $N(0,{\Sigma }_{\text{te}})$.

r0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
LASSO	3.976	5.878	6.749	7.172	7.461	7.569	7.792	8.108	8.164
$P_{\text{lasso}}$	3.278	3.796	4.077	4.197	4.391	4.421	4.469	4.614	4.737

5.2 Real Data Analysis

We apply our method to a dataset from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (https://adni.loni.usc.edu/). Alzheimer’s Disease (AD) is a form of dementia characterized by progressive cognitive and memory deficits. The Mini Mental State Examination (MMSE) is a very useful score in practice for the diagnosis of AD. Generally, any score greater than or equal to 27 points (out of 30) indicates a normal cognition. Below this, MMSE score can indicate severe ($\le 9$ points), moderate (10–18 points) or mild (19–24 points) cognitive impairment (Mungas 1991). Currently, structural magnetic resonance imaging (MRI) is one of the most popular and powerful techniques for the diagnosis of AD. One can use MRI data to predict the MMSE score and identify the important diagnostic and prognostic biomarkers. The dataset we used contains the MRI data and MMSE scores of 51 AD patients and 52 normal controls. After the image preprocessing steps for the MRI data, we obtain the subject-labeled image based on a template with 93 manually labeled regions of interest (ROI) (Zhang and Shen 2012). For each of the 93 ROI in the labeled MRI, the volume of gray matter tissue is used as a feature. Therefore, the final dataset has 103 subjects. For each subject, there are one MMSE score and 93 MRI features. We treat the MMSE score as the response variable and MRI features as predictors.

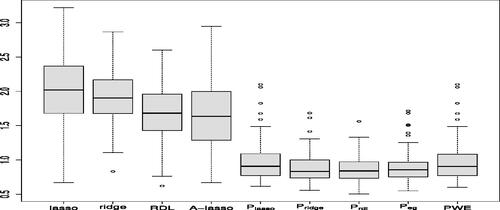
We split the data at random with 80% as the training set, denoted as ${\mathcal{S}}_{tr}$, and 20% as the testing set, denoted as ${\mathcal{S}}_{te}$, then compute the average test error $\sum _{Y_i\in {\mathcal{S}}_{te}}|{\widehat{Y}}_i-Y_i|/\left|{\mathcal{S}}_{te}\right|$. We repeat the procedure for 100 times and report the average test errors. The boxplots of different methods are presented in Figure 3. It shows that pointwise estimators are much better than plug-in estimators of LASSO, adaptive LASSO and ridge, respectively.

Fig. 3 Comparison of the test errors of different methods for the AD data analysis. Here $P_{\text{lasso}},P_{\text{ridge}},P_{\text{rdl}}$, and $P_{\text{eg}}$ represent our regularized estimators without bias-correction in Algorithm 1. The PWE is automatically selected from $P_{\text{lasso}},P_{\text{ridge}},P_{\text{rdl}}$, and $P_{\text{eg}}$.

6 Discussion

In this article, we estimate the linear transformation ${\mathit{\beta }}^{\top }x$ of parameters $\mathit{\beta }$ in high-dimensional linear models. We propose a pointwise estimator, which works well when $\mathit{\beta }$ is sparse or non-sparse, and predictors are highly or weakly correlated. The theoretical analysis reveals the significant difference between estimating a linear transformation of ${\mathit{\beta }}^{\top }x$ and that of $\mathit{\beta }$. When $\mathit{\beta }$ is non-sparse or predictors are highly correlated, estimating $\mathit{\beta }$ is difficult, but we can still get good estimate of ${\mathit{\beta }}^{\top }x$ using our proposed pointwise estimators.

Supplementary Materials

The supplementary materials contain two parts. The first part provides the proofs of the theoretical results in the main paper. The second part includes some simulation results for the settings 2 and 3 of the main paper, together with additional simulation results.

Acknowledgments

The authors would like to thank the Editor, the Associate Editor, and reviewers, whose helpful comments and suggestions led to a much improved presentation.

Additional information

Funding

Junlong Zhao’s research was supported in part by National Natural Science Foundation of China grants No. 11871104 and 12131006. Yang Zhou’s research was supported in part by China Postdoctoral Science Foundation grants No. 2020M680226 and 2020TQ0014, and Youth Fund, No.310422112. Yufeng Liu’s research was supported in part by US NIH grant R01GM126550 and NSF grants DMS2100729 and SES2217440.