Unveiling the Unobservable: Causal Inference on Multiple Derived Outcomes

Abstract

In many applications, the interest is in treatment effects on random quantities of subjects, where those random quantities are not directly observable but can be estimated based on data from each subject. In this article, we propose a general framework for conducting causal inference in a hierarchical data generation setting. The identifiability of causal parameters of interest is shown under a condition on the biasedness of subject level estimates and an ignorability condition on the treatment assignment. Estimation of the treatment effects is constructed by inverse propensity score weighting on the estimated subject level parameters. A multiple testing procedure able to control the false discovery proportion is proposed to identify the nonzero treatment effects. Theoretical results are developed to investigate the proposed procedure, and numerical simulations are carried out to evaluate its empirical performance. A case study of medication effects on brain functional connectivity of patients with Autism spectrum disorder (ASD) using fMRI data is conducted to demonstrate the utility of the proposed method. Supplementary materials for this article are available online.

Keywords:

• Brain functional connectivity
• Causal inference
• Correlation
• fMRI data
• High dimensionality
• Multiple testing procedure

1 Introduction

Studying treatment effects using observational data is one of the key questions in scientific, economic and social research. There is extensive research on causal inference under the ignorability assumption (Rosenbaum and Rubin 1983). However, the existing frameworks of causal inference are mainly built on the treatment effects of observable random variables. With the advance of automatic and high-throughput data collection techniques, collecting large-scale repeated measurements from each subject becomes more and more common in many studies, and the treatment effects of interest are typically on a large set of subject level parameters that take into account the heterogeneity among subjects. Compared to the classical setting which assumes variables of interest are observable and data from different subjects are iid, those subject level parameters are not directly observable, and the subject heterogeneity needs to be learned based on repeated measurements from each subject. The existing causal inference methods may not be directly applicable to the treatment effects on unobservable subject level parameters.

Our motivation example is to study treatment effects on brain connectivity using functional magnetic resonance imaging (fMRI) data. Here, brain functional connectivities are the subject level parameters of interest, which need to be estimated based on time course fMRI data from each subject (Qiu and Zhou 2022). To measure brain functional connectivity, Pearson’s correlation between distinct units within a brain nervous system (Andrews-Hanna et al. 2007; Palaniyappan et al. 2013) is widely used due to its simplicity and interpretability, which shows linear similarity/dissimilarity between brain signals arising from two regions. Other dependence measures have also been applied to study brain connectivity—such as precision coefficient or partial correlation (Marrelec et al. 2006), Spearman’s ρ and Kendall’s τ (Berto et al. 2022). Our interest is the average difference of brain connectivity under treatment and control. This is an important question in medical research as neurodevelopmental and neurodegenerative diseases, like Autism spectrum disorder and Alzheimer’s disease, may alter the connectivities among brain regions (Andrews-Hanna et al. 2007; Kana et al. 2014; Berto et al. 2022). Various treatments have been developed to maintain the brain functionality of patients, and their effects need to be evaluated using clinical trial data. Other examples include genotype effects on change rates of gene expression levels over plant growth and drug effects on variability of heart rate measured from wearable devices. To conduct statistical inference for treatment effects in this type of problems, it requires a new framework of causal inference on derived random variables under hierarchical models, and a multiple testing procedure to recover the nonzero treatment effects on the subject level parameters of interest.

Inverse probability weighting (IPW) estimators are commonly used to estimate average treatment effects (ATE) under the ignorability condition (Rosenbaum and Rubin 1983). This condition assumes the treatment selection is independent of the potential outcomes given the covariates, which means that there are no unobserved confounding variables that affect both the potential outcomes and the treatment selection. The effectiveness of IPW estimators was studied in Hirano, Imbens, and Ridder (2003). See the literature review and the practice of IPW estimation methods in Austin and Stuart (2015) and Imbens and Rubin (2015).

If an outcome regression model is also assumed, the augmented inverse probability weighted estimator (Bang and Robins 2005; Funk et al. 2011) can be used to estimate ATEs, which is doubly robust and is the efficient estimator for ATE if both the outcome and propensity score models are correctly specified (Cao, Tsiatis, and Davidian 2009). However, imposing valid outcome models could be challenging in our problem, due to the high dimensionality of subject level parameters and possible restricted parameter spaces. The restriction on the models of subject level parameters could further put constraints on the models of observed responses for each subject. Taking modeling correlations for fMRI data as an example, although an inverse Wishart distribution can be made on individual covariance matrices if the covariances are independent of covariates (Marrelec et al. 2006), it is unclear how to model the relationship between covariates and correlations that satisfies the positive definiteness constraint of the correlation matrix under any value of the covariates. Bayesian is another approach for causal inference under a joint potential outcome model and a propensity score model (Rubin 1978). Indeed, Marrelec et al. (2006) used Bayesian inference to model partial correlations among brain regions. Hierarchical models may also be employed for the estimation of treatment effect (Feller and Gelman 2015) and high-dimensional covariates can be added as well (Brown, Vannucci, and Fearn 1998). However, due to the nontrivial outcome models under restricted parameter spaces and the possible computational burden of Bayesian approaches, we choose the IPW estimation to study treatment effects on brain connectivity in this work.

Compared to the existing causal inference problems under the ignorability condition, our problem faces three new challenges. First, the subject level parameters of interest are not observable. The traditional identifiability conditions can not be directly applied to treatment effects on subject level parameters. New conditions for identifiability under a hierarchical data generation setting need to be developed. Second, the number of subject level parameters is usually large. A multiple testing procedure needs to be constructed to identify the nonzero treatment effects from a large set of candidates. Third, various types of dependence may exist in the data, which include the dependence among subject level parameters from a population distribution in a hierarchical model, the variable dependence among high-dimensional responses, and the temporal dependence of repeated measurements within each subject. Moreover, all the estimated treatment effects are dependent as they share common propensity score estimates. A valid testing procedure needs to control the dependence among the estimates of treatment effects.

Although multiple hypotheses testing has been well studied in the literature, how to control the false discovery proportion (FDP) under arbitrary dependence among test statistics is still an open question. Genovese and Wasserman (2004) studied the stochastic properties of FDP. van der Laan, Dudoit, and Pollard (2004a) constructed a step-down process on maximum statistics to control the family-wise error rate (FWER). van der Laan, Dudoit, and Pollard (2004b) and Genovese and Wasserman (2006) proposed an augmentation step to control the FDP exceedance rate. It is also worthwhile to mention the multiple testing procedures for sparse correlation and partial correlation matrices of one subject based on iid data (Cai and Liu 2016; Qiu and Zhou 2020). However, those works typically assume independence or sparse dependence among the test statistics for different hypotheses. Some works also assume exact Uniform(0, 1) distribution for the p-values under the null hypotheses. Our problem does not satisfy those assumptions due to the massive dependence among the data as mentioned above. Although van der Laan, Dudoit, and Pollard (2004a) considered controlling the FWER for dependent statistics by bootstrapping or by estimating the covariances of their statistics, this procedure is unlikely to succeed for high-dimensional parameters since the sample covariance matrix is no longer consistent in a high-dimensional setting, and no theoretical justification is provided for their bootstrap procedure.

In this article, we propose a general framework for studying treatment effects on derived random variables from each subject. Our framework is built on a hierarchical setting that assumes the observed data from each subject follow a subject-specific distribution, and the parameters of the subject level distributions are drawn from a population distribution. This setting allows heterogeneity among subjects so that the subject level distributions could be different. The interest is in the causal effect of treatment on the subject level parameters. As those subject level parameters are not observable, the ignorability condition of treatment assignment is not directly made on those parameters. Instead, the identifiability of the causal effect is derived under an ignorability condition on the potential responses of each subject and a condition regulating the bias of the estimates for the subject level parameters of interest. The estimation of the treatment effect is constructed by inverse propensity score weighting on each of the estimated subject level parameters. Simultaneous confidence intervals for all treatment effects are constructed based on Gaussian approximation (GA) for the maximum of the estimated effects. Our GA result is valid under general dependence among the IPW estimates, which extends the original GA for sample means (Chernozhukov, Chetverikov, and Kato 2013) to IPW estimates with derived outcomes. A multiple testing procedure built on multiplier bootstrap is proposed to identify the nonzero treatment effects among a large set of parameters. Theoretical results are established which show that the proposed test is able to control the exceedance rate of the FDP. Examples of treatment effects on subject level correlations and coefficients from nodewise regressions are provided. Numerical simulations are carried out to evaluate the empirical performance of the proposed multiple testing procedure. A case study of medication effects on brain functional connectivity of patients with Autism spectrum disorder (ASD) using fMRI data is conducted to demonstrate the utility of the proposed method.

This article is organized as follows. Section 2 introduces the hierarchical setting of data generation and the causal parameters of interest in our problem. Section 3 presents the conditions and shows the identifiability of the causal parameters on derived random variables. Section 4 proposes the IPW estimator for the treatment effects and constructs the simultaneous confidence intervals. Section 5 proposes the multiple testing procedure and derives its theoretical results. Section 6 and 7 present the simulation results and a case study of medication effects on brain connectivity for ASD patients. Section 8 concludes the article. The technical proofs are provided in the supplementary material (SM).

2 Preliminary and Parameter of Interest

Suppose that we have a random sample of size n from a target population. For the ith subject, let $D_i\in \{0,1\}$ be the treatment indicator, where D_i = 1 if this subject receives the treatment and 0 if not. Let ${\mathbf{W}}_i={(W_{i,1},\dots ,W_{i,q})}^{\mathrm{T}}$ be the q-dimensional time-independent covariates associated with the ith subject. Let $$ denote the potential response of the jth variable at time t from the ith subject for d = 1 and 0, where $i=1,\dots ,n,j=1,\dots ,p$ and $t=1,\dots ,m$. Let ${\mathbf{X}}_{i,t}(d)={(X_{i,t,1}(d),\dots ,X_{i,t,p}(d))}^{\mathrm{T}}$ be the p-dimensional time series of potential responses, ${\mathcal{X}}_i^m(d)={\{{\mathbf{X}}_{i,t}(d)\}}_{t=1}^m$ be the collection of ${\mathbf{X}}_{i,t}(d)$ over time, and ${\mathbf{X}}_{i,t}=D_i{\mathbf{X}}_{i,t}(1)+(1-D_i){\mathbf{X}}_{i,t}(0)$ be the observed response vector. Given the covariates W_i, let $F_{d,i}(·)=F_{d,i}(·,{\mathbf{T}}_i(d)|{\mathbf{W}}_i)$ be the subject level distribution function of ${\mathbf{X}}_{i,t}(d)$, where ${\mathbf{T}}_i(d)$ denotes the set of all subject level parameters that determine the distribution $F_{d,i}(·)$ for the ith subject and d = 0, 1. We assume $${\mathit{X}}_{i,t}(d)|{\mathit{T}}_i(d),{\mathit{W}}_i\sim F_{d,i}(·)\text{forall}\mathrm{t},\text{and}{\mathit{T}}_{\mathrm{i}}(\mathrm{d})\text{|}{\mathit{W}}_{\mathrm{i}}\sim {\mathcal{T}}_{\mathrm{d}}({\mathit{W}}_{\mathrm{i}}),$$ where ${\mathcal{T}}_d({\mathbf{W}}_i)$ is the super population of ${\mathbf{T}}_i(d)$. Under this model, ${\{{\mathbf{X}}_{i,t}(d)\}}_{t=1}^m$ are stationary with the same subject level distribution $F_{d,i}(·)$. We do not assume specified parametric forms for $F_{d,i}(·)$ or ${\mathcal{T}}_d({\mathbf{W}}_i)$.

Let ${\mathbf{Y}}_i(d)={(Y_{i,1}(d),\dots ,Y_{i,p_0}(d))}^{\mathrm{T}}$ be the potential outcomes of p₀-dimensional subject level parameters of interest, where ${\mathbf{Y}}_i(1)$ and ${\mathbf{Y}}_i(0)$ denote the target parameters under treatment and control, respectively. Note that ${\mathbf{Y}}_i(d)$ is a function or a part of ${\mathbf{T}}_i(d)$ for d = 0, 1, and ${\mathbf{T}}_i(d)$ also includes all other nuisance parameters for each subject. As only one level of D_i can be observed for each subject, in our context, we use potential responses and potential outcomes to denote the subject level data ${\mathbf{X}}_{i,t}(d)$ and parameters of interest ${\mathbf{Y}}_i(d)$ under D_i = d, respectively. Let ${\mathbf{Y}}_i=D_i{\mathbf{Y}}_i(1)+(1-D_i){\mathbf{Y}}_i(0)$. Different from the classical causal inference literature (Rubin 1974), ${\mathbf{Y}}_i$ is not observable, but can be estimated based on the observed measurements ${\left\{{\mathbf{X}}_{i,t}\right\}}_{t=1}^m$ of each subject. We are interested in the population average treatment effect (ATE) on the subject level parameters, (2.1) $$\mathit{\tau }=\mathrm{E}\{{\mathit{Y}}_i(1)-{\mathit{Y}}_i(0)\},$$(2.1) where $\mathit{\tau }={({\tau }_1,\dots ,{\tau }_{p_0})}^{\mathrm{T}}$. Here, the numbers of responses p and parameters of interest p₀ could be much larger than n and m, but the number of covariates q is a fixed constant.

For example, in a resting-state fMRI study, D_i could indicate the treatment group of the ith subject. The covariates ${\mathbf{W}}_i$ may include age, gender, medical records, preexisting conditions and genetic information, and the observed responses $\left\{{\mathbf{X}}_{i,t}\right\}$ are the measurements extracted from the time course fMRI data, representing the blood flow intensities in p brain regions of interest at time t. The potential outcomes ${\mathbf{Y}}_i(d)$ could be the subject level correlations or partial correlations among the brain regions. For resting-state fMRI data, it is reasonable to assume ${\mathbf{X}}_{i,t}$ being stationary so that ${\mathbf{Y}}_i(d)$ is fixed over time. We are interested in studying the treatment effects on brain connectivity, reflected by the average differences of the potential outcomes between treatment and control.

Note that the subject level parameters of interest ${\mathbf{Y}}_i(d)$ and the distributions of the potential responses ${\{{\mathbf{X}}_{i,t}(d)\}}_{t=1}^m$ depend on the covariates W_i and vary across subjects. Our setting allows subject heterogeneity, where the data are generated from a hierarchical system. In the first hierarchy, each subject has a specific distribution $F_{d,i}(·)$ depending on the covariates and treatment; in the second hierarchy, repeated measurements from the subject-specific distribution are taken over time. This causal inference framework under the hierarchical model can be applied to general applications with multi-layer structured data, for example, assessing drug effects using data from wearable devices in healthcare, testing genotype effects of crops on gene expression patterns changing over time, and studying treatment effects using repeated measurements or longitudinal data of subjects. In the following, we provide two brain imaging applications under our framework in detail. In both examples, we consider resting-state fMRI data.

Example 1

(Treatment Effects on Correlations). We are interested in the effects of certain treatments on brain connectivity measured by Pearson’s correlations among brain regions. In this case, the causal parameters of interest are the subject level correlations, where ${\mathbf{Y}}_i(d)=\{Y_{i,j_1{j}_2}(d):1\le j_1<j_2\le p\}$ and (2.2) $$Y_{i,j_1{j}_2}(d)=\text{Corr}\{X_{i,t,j_1}(d),X_{i,t,j_2}(d)|{\mathit{W}}_i,{\mathit{T}}_i(d)\}$$(2.2) for d = 0, 1. Here, the correlation is taken with respect to the subject level distribution $F_{d,i}(·)$. The ATEs on correlations are (2.3) $$\mathit{\tau }={({\tau }_{12},{\tau }_{13},\dots ,{\tau }_{p-1p})}^{\mathrm{T}}\text{where}{\tau }_{j_1{j}_2}=\mathrm{E}\{Y_{i,j_1{j}_2}(1)-Y_{i,j_1{j}_2}(0)\}$$(2.3) for $1\le j_1<j_2\le p$. The parameter ${\tau }_{j_1{j}_2}$ represents the average difference of the correlation between the j₁th and j₂th brain regions for taking the treatment. If ${\tau }_{j_1{j}_2}\ne 0$, the treatment has a nonzero average effect on the marginal correlation between the two brain regions over the whole population. Despite the sample correlations for each pair of brain regions can be readily obtained for each subject, the simultaneous inference procedure for the estimated treatment effects on subject level correlations is nontrivial due to the dependence among the large set of estimates.

Example 2

(Treatment Effects on Regression Coefficients). While Pearson’s correlation measures marginal dependence among variables, in many applications, we are also interested in the conditional association between two variables given all other variables. This motivates us to consider the nodewise regression (Meinshausen and Bühlmann 2006) (2.4) $$X_{i,t,j_1}(d)=Y_{i,j_1}^{\ast }(d)+\sum _{j_2\ne j_1}{X}_{i,t,j_2}(d)Y_{i,j_1{j}_2}^{\ast }(d)+{ϵ}_{i,t,j_1}(d),$$(2.4) where ${ϵ}_{i,t,j_1}(d)$ and $X_{i,t,j_2}(d)$ are uncorrelated for all $j_2\ne j_1$. Let ${\Sigma }_i(d)=({\sigma }_{i,j_1{j}_2}(d))=\text{cov}\{X_{i,t,j_1}(d),X_{i,t,j_2}(d)|{\mathbf{W}}_i,{\mathbf{T}}_i(d)\}$ and ${\Omega }_i(d)=({\omega }_{i,j_1{j}_2}(d))={\Sigma }_i^{-1}(d)$ be the subject level covariance and precision matrices of ${\mathbf{X}}_{i,t}(d)$ with respect to the distribution $F_{d,i}(·)$. Lemma 1 in Peng et al. (2009) shows that both the regression coefficients and error covariances of the nodewise regression are related to the precision matrix ${\Omega }_i(d)$ where $$\begin{array}{c}{Y}_{i,j_1{j}_2}^{\ast }(d)=-\frac{{\omega }_{i,j_1{j}_2}(d)}{{\omega }_{i,j_1{j}_1}(d)}\text{and}\text{cov}\{{ϵ}_{i,t,j_1}(d),{ϵ}_{i,t,j_2}(d)|{\mathit{W}}_i,{\mathit{T}}_i(d)\}\\ =\frac{{\omega }_{i,j_1{j}_2}(d)}{{\omega }_{i,j_1{j}_1}(d){\omega }_{i,j_2{j}_2}(d)}.\end{array}$$

Moreover, the partial correlation between $X_{i,t,j_1}(d)$ and $X_{i,t,j_2}(d)$ is equal to scaled coefficient $Y_{i,j_1{j}_2}^{\ast }(d){\{{\omega }_{i,j_1{j}_1}(d)/{\omega }_{i,j_2{j}_2}(d)\}}^{1/2}$. Based on this relationship, precision coefficient and partial correlation can be estimated from the nodewise regression (Qiu and Zhou 2020).

In brain connectivity analysis, $Y_{i,j_1{j}_2}^{\ast }(d)$ represents the conditional effect of the j₂th brain region on the j₁th region under the group d, after controlling the effects of other brain regions. We are interested in the ATE ${\tau }_{j_1{j}_2}=\mathrm{E}\{Y_{i,j_1{j}_2}^{\ast }(1)-Y_{i,j_1{j}_2}^{\ast }(0)\}$ on the regression coefficients $Y_{i,j_1{j}_2}^{\ast }(d)$ for $j_2\ne j_1$, which shows whether certain treatment could improve the conditional association between the j₁th and j₂th brain regions.

To identify nonzero ATEs in Examples 1 and 2, we consider the multiple hypotheses (2.5) $$H_{0,j_1{j}_2}:{\tau }_{j_1{j}_2}=0\text{versus}{\mathrm{H}}_{\mathrm{a},{\mathrm{j}}_1{\mathrm{j}}_2}:{\tau }_{{\mathrm{j}}_1{\mathrm{j}}_2}\ne 0$$(2.5) for $1\le j_1<j_2\le p$. In the following sections, we only use the subscript j in τ_j and $Y_{i,j}$ to denote the jth parameter of interest for $j=1,\dots ,p_0$ when there is no confusion, despite the double subscript $j_1{j}_2$ is used for correlation and regression coefficient between the j₁th and j₂th variables in Examples 1 and 2, where $p_0=p(p-1)/2$.

3 Conditions and Identifiability

As the outcomes of interest $\left\{{\mathbf{Y}}_i\right\}$ are not directly observable, we make the following conditions for the identifiability of the treatment effect $\mathit{\tau }$.

Condition 1. (i) The collection of covariates, treatment assignment and subject level parameters $\{{\mathbf{W}}_i,D_i,{\mathbf{T}}_i(0),{\mathbf{T}}_i(1)\}$ are independent among subjects and identically distributed (iid) from a super population for all $i=1,\dots ,n$.

(ii) The variable D_i takes a value of either 1 (treatment) or 0 (control) for all i with potential responses denoted by ${\mathcal{X}}_i^m(1)$ and ${\mathcal{X}}_i^m(0)$, and for each subject, there are no different forms or versions of each treatment level, which lead to different potential responses.

(iii) The potential responses $\{{\mathcal{X}}_{i_1}^m(0)$, ${\mathcal{X}}_{i_1}^m(1)\}$ and $\{{\mathcal{X}}_{i_2}^m(0)$, ${\mathcal{X}}_{i_2}^m(1)\}$ from different subjects are independent for $i_1\ne i_2$ and all $m\ge 1$.

The first two parts of Condition 1 are the stable unit treatment value assumption, or SUTVA (Imbens and Rubin 2015) for the problem. As the subject level parameters of interest ${\mathbf{Y}}_i(d)$ is a function of ${\mathbf{T}}_i(d)$, the independence assumption in Part (i) implies no interference, which means that the potential outcomes for any subject do not vary with the treatments assigned to other subjects. Part (ii) assumes no hidden variations of treatments. Part (iii) assumes the potential response variables ${\{{\mathbf{X}}_{i,t}(d)\}}_{t=1}^m$ are independent between subjects, but allows temporal dependence among $\{{\mathbf{X}}_{i,t}(d)\}$ over t within a subject.

To identify the causal parameter τ of interest, we make the strict overlap assumption on the propensity score $\mathbb{P}(D_i=1|{\mathbf{W}}_i)$ and the unconfoundedness assumption (Rosenbaum and Rubin 1983; Hirano, Imbens, and Ridder 2003) on the independence of the treatment indicator D_i and the potential responses ${\mathcal{X}}_i^m(d)$ given the covariates ${\mathbf{W}}_i$.

Condition 2. (Strict Overlap): There exists a small positive constant $c_{ϵ}\in (0,1/2)$ such that $c_{ϵ}\le \mathbb{P}(D_i=1|{\mathbf{W}}_i)\le 1-c_{ϵ}$ for all $i=1,\dots ,n$.

Condition 3. (Unconfounded Treatment Assignment): Given the covariates ${\mathbf{W}}_i$, (3.1) $$D_i \perp \{{\mathcal{X}}_i^m(0),{\mathcal{X}}_i^m(1)\}|{\mathit{W}}_i$$(3.1) for all $i=1,\dots ,n$ and all $m\ge 1$.

Condition 2 is the positivity assumption that every subject has some positive probability to be assigned to every level of D_i , which ensures the possibility to find both treated and control units for any given value of the covariates. Condition 3 implies that conditioning on the covariates, the probability of receiving the treatment is independent of the potential responses ${\mathbf{X}}_{i,t}(d)$ over the repeated measurements for each subject. This means that except for a random error independent of the potential responses, the covariates ${\mathbf{W}}_i$ include all the variables that determine D_i . Compared with the classical unconfoundedness assumption, we require conditional independence between the treatment assignment and the entire time course data of responses. This is because the subject level parameters ${\mathbf{Y}}_i$ are unobservable, and need to be estimated using the responses $\left\{{\mathbf{X}}_{i,t}\right\}$ from each subject.

For any estimate ${\widehat{\mathbf{Y}}}_i(d)={({\widehat{Y}}_{i,1}(d),\dots ,{\widehat{Y}}_{i,p_0}(d))}^{\mathrm{T}}$ of ${\mathbf{Y}}_i(d)$ based on ${\mathcal{X}}_i^m(d)$, let ${\widehat{\mathbf{Y}}}_i=D_i{\widehat{\mathbf{Y}}}_i(1)-(1-D_i){\widehat{\mathbf{Y}}}_i(0)$. As ${\widehat{\mathbf{Y}}}_i(d)$ is a function of ${\mathcal{X}}_i^m(d)$, Condition 3 leads to the conditional independence between D_i and $\{{\widehat{\mathbf{Y}}}_i(0),{\widehat{\mathbf{Y}}}_i(1)\}$ given the covariates, which implies $\mathrm{E}({\widehat{\mathbf{Y}}}_i|D_i=1,{\mathbf{W}}_i)\text{-}\mathrm{E}({\widehat{\mathbf{Y}}}_i|D_i=0,{\mathbf{W}}_i)=\mathrm{E}\{{\widehat{\mathbf{Y}}}_i(1)|{\mathbf{W}}_i\left\}\text{-}\mathrm{E}\right\{{\widehat{\mathbf{Y}}}_i(0)\left|{\mathbf{W}}_i\right\}$. Let ${\Delta }_{i,m}(d)=\mathrm{E}\{{\widehat{\mathbf{Y}}}_i(d)|{\mathbf{T}}_i(d),{\mathbf{W}}_i\}-{\mathbf{Y}}_i(d)$ be the bias of the estimator ${\widehat{\mathbf{Y}}}_i(d)$ for the ith subject, where ${\Delta }_{i,m}(d)={({\Delta }_{i,1,m}(d),\dots ,{\Delta }_{i,p_0,m}(d))}^{\mathrm{T}}$, and the expectation $\mathrm{E}\{{\widehat{\mathbf{Y}}}_i(d)|{\mathbf{T}}_i(d),{\mathbf{W}}_i\}$ is with respect to the subject level distribution $F_{d,i}(·)$ given all the subject level parameters and covariates. If there exists an estimate that satisfies (3.2) $${\max }_{1\le j\le p_0}\mathrm{E}\{{\Delta }_{i,j,m}(d)\}=o(1)\text{for}\text{d = 0},1$$(3.2) as $m\to \infty$, the difference between $\mathrm{E}\{{\widehat{\mathbf{Y}}}_i(d)\}$ and $\mathrm{E}\{{\mathbf{Y}}_i(d)\}$ converges to zero, and hence the population ATE $\mathit{\tau }$ in (2.1) can be identified based on $\{D_i,{\mathbf{W}}_i,{\widehat{\mathbf{Y}}}_i\}$. This identification result is summarized in the following lemma.

Lemma 1.

Assume that there exists an estimate ${\widehat{\mathbf{Y}}}_i(d)$ of ${\mathbf{Y}}_i(d)$ satisfying (3.2). Under Conditions 1–3, the population ATE $\mathit{\tau }$ can be identified by $\mathrm{E}\{\mathrm{E}({\widehat{\mathbf{Y}}}_i|D_i=1,{\mathbf{W}}_i)\text{-}\mathrm{E}({\widehat{\mathbf{Y}}}_i|D_i=0,{\mathbf{W}}_i)\}$, where the outer expectation is with respect to ${\mathbf{W}}_i$.

In our context, since the outcomes of interest ${\mathbf{Y}}_i$ are not observable, the identifiability of $\mathit{\tau }$ needs to be implied by an proper estimator ${\widehat{\mathbf{Y}}}_i(d)$ of ${\mathbf{Y}}_i(d)$ that satisfies (3.2). This is an additional condition compared with the classical argument for the identifiability of causal parameters with observable outcomes under the unconfoundedness assumption. Note that the identification of $\mathit{\tau }$ is independent of the sample size n, and if there exists an exactly unbiased estimator ${\widehat{\mathbf{Y}}}_i(d)$ of ${\mathbf{Y}}_i(d)$ such that ${\Delta }_{i,m}(d)=0$ for all $i=1,\dots ,n$, it does not require $m\to \infty$ either. Here, the condition in (3.2) could be understood as a model assumption for the identification of $\mathit{\tau }$. To identify the treatment effect on an unobservable random variable $Y_{i,j}$, we need to assume the existence of an approximately unbiased estimator of $Y_{i,j}$ in the model. Note that the existence of an estimator satisfying the condition (3.2) may not be trivially true for any parameter or subject distribution as the potential responses ${\mathcal{X}}_i^m(d)$ could be time-dependent and the dimension of the parameters could be very large.

Also notice that Lemma 1 holds under a weaker SUTVA condition on the derived potential outcomes ${\widehat{\mathbf{Y}}}_i(d)$ and a weaker unconfoundedness condition $D_i\perp {\widehat{\mathbf{Y}}}_i(d)|{\mathbf{W}}_i$ for d = 0, 1 than Conditions 1 and 3. Since SUTVA and unconfoundedness are properties of the designs of the experiments or observational studies that generate the data, we make those two conditions on the potential responses in Conditions 1 and 3, instead of on an estimator ${\widehat{\mathbf{Y}}}_i(d)$ chosen by the investigator.

To conduct statistical inference for $\mathit{\tau }$, we need a stronger condition than (3.2), which specifies the uniform ${\mathcal{l}}_1$-norm convergence rate of the estimate ${\widehat{\mathbf{Y}}}_i(d)$ to ${\mathbf{Y}}_i(d)$.

Condition 4. For the estimate ${\widehat{\mathbf{Y}}}_i(d)$ of ${\mathbf{Y}}_i(d)$, we have ${\max }_{1\le j\le p_0}\mathrm{E}|{\Delta }_{i,j,m}(d)|={\delta }_m$ for d = 0, 1, and $n^{1/2}{\delta }_m\to 0$ as $n,m\to \infty$.

The theoretical results in Sections 4 and 5 show that the proposed inference procedure for τ is valid if the bias term is small enough such that ${\delta }_m=o(n^{-1/2})$. Compared with (3.2), this additional requirement on the bias term is needed to achieve $n^{-1/2}$ convergence rate for the estimated $\mathit{\tau }$. Condition 4 can be satisfied for various types of estimators if the repeated measurements ${\mathcal{X}}_i^m(d)$ are weakly dependent in time and the sample size m for each subject is relatively large. Also notice that for unbiased estimators with ${\delta }_m=0$, Condition 4 holds for any m > 0, and m is not required to diverge to infinity.

Take Example 1 in Section 2 as an illustration. Let $v_{i,j_1{j}_2}(d)={\sum }_{t=1}^m\{X_{i,t,j_1}(d)-{\overline{X}}_{i,j_1}(d)\}\{X_{i,t,j_2}(d)-{\overline{X}}_{i,j_2}(d)\}/m$ be the sample variance of the ith subject, where ${\overline{X}}_{i,j}(d)={\sum }_{t=1}^m{X}_{i,t,j}(d)/m$. It can be shown that the subject level correlation $Y_{i,j_1{j}_2}(d)$ can be well approximated by the sample correlation ${\widehat{Y}}_{i,j_1{j}_2}(d)=v_{i,j_1{j}_2}(d){\{v_{i,j_1{j}_1}(d)v_{i,j_2{j}_2}(d)\}}^{-1/2}$ such that $\mathrm{E}\{{\widehat{Y}}_{i,j_1{j}_2}(d)|{\mathbf{T}}_i(d),{\mathbf{W}}_i\}=Y_{i,j_1{j}_2}(d)+O_p\{{(\hspace{0.17em}\log \hspace{0.17em}p+\hspace{0.17em}\log \hspace{0.17em}n)}^{1/2}/m\}$ if the sequence of potential responses ${\{{\mathbf{X}}_{i,t}(d)\}}_{t=1}^m$ satisfy certain mixing property and moment condition for each subject. For Example 2, under low-dimensional cases, since the least square estimator of the regression coefficient $Y_{i,j_1{j}_2}^{\ast }(d)$ is unbiased, Condition 4 is valid for this estimator under any m > p. Under high-dimensional cases, regulated regression estimators like lasso (Tibshirani 1996) are biased and are not suitable for our purpose. Instead, the de-sparsified lasso estimator (Van de Geer et al. 2014) can be applied to estimate $Y_{i,j_1{j}_2}^{\ast }(d)$, which also satisfies Condition 4 under certain sparsity conditions on the coefficients. The justification of Condition 4 for the sample correlation and the de-sparsified lasso estimator for Examples 1 and 2 is provided in the SM.

In the next section, we propose an estimator of the ATE $\mathit{\tau }$ via inverse propensity score weighting and a multiple testing procedure for the hypotheses (2.5) with FDP control.

4 Simultaneous Confidence Interval

To solve the challenges of many target parameters in $\mathit{\tau }$, high-dimensional ${\mathbf{X}}_{i,t}$ and multi-source dependence in the data, in this section, we develop the Gaussian approximation result on the maximum of the estimates of $\mathit{\tau }$. We assume the logistic regression for the propensity score model, where D_i follows a Bernoulli distribution with the probability (4.1) $$\mathbb{P}(D_i=1|{\mathit{W}}_i)=\Lambda ({\mathit{W}}_i^{\mathrm{T}}\mathit{\beta })$$(4.1) for $\Lambda (a)=\hspace{0.17em}\exp \hspace{0.17em}(a)/\{1+\hspace{0.17em}\exp \hspace{0.17em}(a)\}$ and unknown parameters $\mathit{\beta }={({\beta }_1,\dots ,{\beta }_q)}^{\mathrm{T}}\in {\mathbb{R}}^q$. Let ${\mathit{\beta }}_0={({\beta }_{0,1},\dots ,{\beta }_{0,q})}^{\mathrm{T}}$ denote the true value of $\mathit{\beta }$. The maximum likelihood estimator (MLE) $\widehat{\mathit{\beta }}$ of the logistic regression (4.1) solves (4.2) $$\begin{array}{cc}\widehat{\mathit{\beta }}\hfill & =\underset{\mathit{\beta }\in {\mathbb{R}}^q}{\arg \max }\sum _{i=1}^n{\rho }_{\beta }({\mathit{W}}_i,D_i)\text{for}\hfill \\ {\rho }_{\beta }({\mathit{W}}_i,D_i)\hfill & =D_i\hspace{0.17em}\log \hspace{0.17em}\Lambda ({\mathit{W}}_i^{\mathrm{T}}\mathit{\beta })+(1-D_i)\hspace{0.17em}\log \hspace{0.17em}\{1-\Lambda ({\mathit{W}}_i^{\mathrm{T}}\mathit{\beta })\}.\hfill \end{array}$$(4.2)

Let $\Lambda ({\mathbf{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})$ be the estimated propensity score for the ith subject. Recall that ${\widehat{\mathbf{Y}}}_i$ is an estimate of ${\mathbf{Y}}_i$ based on the responses $\left\{{\mathbf{X}}_{i,t}\right\}$. The ATE τ_j in (2.1) can be estimated by the inverse probability weighted estimator for derived random variables ${\left\{{\widehat{Y}}_{i,j}\right\}}_{i=1}^n$ as (4.3) $${\widehat{\tau }}_j=\frac{1}{n}\sum _{i=1}^n\{\frac{{\widehat{Y}}_{i,j}{D}_i}{\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})}-\frac{{\widehat{Y}}_{i,j}(1-D_i)}{1-\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})}\}.$$(4.3)

If we have the outcome models for $\mathrm{E}\{Y_{i,j}(d)|{\mathbf{W}}_i\}=g_d({\mathbf{W}}_i)$, the augmented inverse probability weighted estimator (AIPWE) $$\begin{array}{c}{\widehat{\tau }}_j^{\text{AIPW}}=\frac{1}{n}\sum _{i=1}^n\{{\widehat{g}}_1({\mathit{W}}_i)-{\widehat{g}}_0({\mathit{W}}_i)\}\\ +\frac{1}{n}\sum _{i=1}^n\{\frac{({\widehat{Y}}_{i,j}-{\widehat{g}}_1({\mathit{W}}_i))D_i}{\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})}-\frac{({\widehat{Y}}_{i,j}-{\widehat{g}}_0({\mathit{W}}_i))(1-D_i)}{1-\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})}\}\end{array}$$ can be applied to estimate τ_j , where ${\widehat{g}}_d({\mathbf{W}}_i)$ is the estimated outcome model by regressing ${\widehat{Y}}_{i,j}$ on D_i = d and ${\mathbf{W}}_i$. The AIPWE is doubly robust and is the efficient estimator for τ_j if both the outcome models and the propensity score model in (4.1) are correctly specified (Cao, Tsiatis, and Davidian 2009). However, in our problem, specifying the outcome model may not be easy as the number of parameters is large and the parameter space could be restricted. In Example 1, correlations are bounded in $(-1,1)$ and the subject level correlation matrices are positive definite for all subjects. In Example 2, coefficients of the nodewise regression are proportional to partial correlations, which also have the positive definiteness constraint.

In the following, we derive the asymptotic expansion of ${\widehat{\tau }}_j$, which implies the consistency of ${\widehat{\tau }}_j$ to τ_j and its limiting distribution. Let $\dot{\Lambda }=\Lambda (1-\Lambda )$ and $\ddot{\Lambda }=\dot{\Lambda }(1-2\Lambda )$ be the first and second derivatives of the logistic function $\Lambda (·)$, respectively, where $\dot{\Lambda }({\mathbf{W}}_i^{\mathrm{T}}\mathit{\beta })$ is the conditional variance of D_i given ${\mathbf{W}}_i$. Let ${\dot{\rho }}_{\beta }({\mathbf{W}}_i,D_i)=\{D_i-\Lambda ({\mathbf{W}}_i^{\mathrm{T}}\beta )\}{\mathbf{W}}_i$ be the first derivative of ${\rho }_{\beta }({\mathbf{W}}_i,D_i)$ with respect to $\mathit{\beta }$. Then, ${\mathcal{I}}_{\beta }=\mathrm{E}[{\dot{\rho }}_{\beta }({\mathbf{W}}_i,D_i){\dot{\rho }}_{\beta }^{\mathrm{T}}({\mathbf{W}}_i,D_i)]=\mathrm{E}[\dot{\Lambda }({\mathbf{W}}_i^{\mathrm{T}}\beta ){\mathbf{W}}_i{\mathbf{W}}_i^{\mathrm{T}}]$ is the Fisher information (FI) matrix of $\mathit{\beta }$ in the model (4.1). Let ${\mathbf{\Xi }}_{\beta }={\mathcal{I}}_{\beta }^{-1}$ be the inverse of the FI matrix, and (4.4) $$\mathcal{H}=\mathrm{E}([\{1-\Lambda ({\mathit{W}}_i^{\mathrm{T}}{\mathit{\beta }}_0)\}{\mathit{Y}}_i(1)+\Lambda ({\mathit{W}}_i^{\mathrm{T}}{\mathit{\beta }}_0){\mathit{Y}}_i(0)]{\mathit{W}}_i^{\mathrm{T}})$$(4.4) be the $p_0\times q$ dimensional influence matrix of $\widehat{\mathit{\beta }}$ on $\widehat{\mathit{\tau }}$. The following proposition provides the asymptotic expansion of ${\widehat{\tau }}_j$ in (4.3).

Proposition 1.

Assume the subject level parameters of interest $Y_{i,j}$, their estimates ${\widehat{Y}}_{i,j}$, the covariates $W_{i,k}$ and the true propensity score parameter ${\mathit{\beta }}_0$ are bounded such that ${\max }_{1\le k\le q}\left|W_{i,k}\right|\le C,{\max }_{1\le j\le p_0}\left\{\right|Y_{i,j}|,|{\widehat{Y}}_{i,j}\left|\right\}<C$ and ${\max }_{1\le k\le q}\left|{\beta }_{0,k}\right|\le C$ for all $i=1,\dots ,n$ and a positive constant C. Under Conditions 1–4 and (4.1), we have that (4.5) $$\widehat{\mathit{\tau }}-\mathit{\tau }=\frac{1}{n}\sum _{i=1}^n{\tilde{\mathit{\eta }}}_i+O_p\{{(\hspace{0.17em}\log \hspace{0.17em}{p}_0)}^{1/2}{n}^{-1}+{\delta }_m{n}^{-1/2}\},$$(4.5) where ${\tilde{\mathit{\eta }}}_i={({\tilde{\eta }}_{i1},\dots ,{\tilde{\eta }}_{i{p}_0})}^{\mathrm{T}}$, (4.6) $$\begin{array}{c}{\tilde{\eta }}_{ij}=\frac{{\widehat{Y}}_{i,j}{D}_i}{\Lambda ({\mathit{W}}_i^{\mathrm{T}}{\mathit{\beta }}_0)}-\frac{{\widehat{Y}}_{i,j}(1-D_i)}{1-\Lambda ({\mathit{W}}_i^{\mathrm{T}}{\mathit{\beta }}_0)}\\ -{\mathcal{H}}_j{\mathbf{\Xi }}_{{\beta }_0}\{D_i-\Lambda ({\mathit{W}}_i^{\mathrm{T}}{\mathit{\beta }}_0)\}{\mathit{W}}_i-{\tau }_j\end{array}$$(4.6) with $\mathrm{E}({\tilde{\eta }}_{ij})=O({\delta }_m)$ for all $j=1,\dots ,p_0$, and ${\mathcal{H}}_j$ is the jth row of $\mathcal{H}$.

Proposition 1 implies asymptotic normality of ${\widehat{\tau }}_j$ with the influence functions $\left\{{\tilde{\eta }}_{ij}\right\}$. Let (4.7) $$\begin{array}{c}{\theta }_j=\frac{1}{n}\sum _{i=1}^n\mathrm{E}\left[\right\{\frac{{\widehat{Y}}_{i,j}{D}_i}{\Lambda ({\mathit{W}}_i^{\mathrm{T}}{\mathit{\beta }}_0)}-\frac{{\widehat{Y}}_{i,j}(1-D_i)}{1-\Lambda ({\mathit{W}}_i^{\mathrm{T}}{\mathit{\beta }}_0)}-{\tau }_j\}\\ \hspace{1em}-{\mathcal{H}}_j{\mathbf{\Xi }}_{{\beta }_0}\{D_i-\Lambda ({\mathit{W}}_i^{\mathrm{T}}{\mathit{\beta }}_0)\}{\mathit{W}}_i{]}^2\end{array}$$(4.7) be the main order term of $\text{var}(n^{-1/2}{\sum }_{i=1}^n{\tilde{\eta }}_{ij})$. Under the conditions $(\hspace{0.17em}\log \hspace{0.17em}{p}_0)/n=o(1)$ and $n^{1/2}{\delta }_m=o(1)$, we have $n^{1/2}({\widehat{\tau }}_j-{\tau }_j)\to N(0,{\theta }_j)$ in distribution for all $j=1,\dots ,p_0$, as $n,m,p\to \infty$. Notice that the variance θ_j includes the variation of subject level parameters $Y_{i,j}$, the estimation variation of ${\widehat{Y}}_{i,j}$ for each subject, and the variation of the estimated propensity score. The decomposition of θ_j into each of those sources is provided in (S.7) in the SM. Let ${\widehat{\theta }}_j={\sum }_{i=1}^n{\widehat{\eta }}_{ij}^2/n$ be the estimator of θ_j , where (4.8) $$\begin{array}{c}{\widehat{\eta }}_{ij}=\frac{{\widehat{Y}}_{i,j}{D}_i}{\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})}-\frac{{\widehat{Y}}_{i,j}(1-D_i)}{1-\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})}\\ -{\widehat{\tau }}_j-{\widehat{\mathcal{H}}}_j{\widehat{\mathcal{I}}}^{-1}\{D_i-\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})\}{\mathit{W}}_i,\end{array}$$(4.8) $$\begin{array}{c}\widehat{\mathcal{I}}=\frac{1}{n}\sum _{i=1}^n\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})\{1-\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})\}{\mathit{W}}_i{\mathit{W}}_i^{\mathrm{T}}\text{and}\\ {\widehat{\mathcal{H}}}_j=\frac{1}{n}\sum _{i=1}^n\mathrm{}\{\frac{1-\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})}{\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})}{D}_i + \frac{\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})}{1-\Lambda ({\mathit{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})}(1-D_i)\mathrm{}\}{\widehat{Y}}_{i,j}{\mathit{W}}_i^{\mathrm{T}}.\end{array}$$

The following proposition provides the uniform convergence rate of ${\widehat{\theta }}_j$ to θ_j .

Proposition 2.

Under the conditions of Proposition 1, it can be shown that ${\max }_{1\le j\le p_0}|{\widehat{\theta }}_j-{\theta }_j|=O_p\{{(\hspace{0.17em}\log \hspace{0.17em}{p}_0)}^{1/2}{n}^{-1/2}+{\delta }_m\}$.

Although the responses ${\left\{{\mathbf{X}}_{i,t}\right\}}_{t=1}^m$ could be time dependent within each subject, due to the independence among subjects, Proposition 2 shows that θ_j can be consistently estimated by the sample variance of ${\left\{{\widehat{\eta }}_{ij}\right\}}_{i=1}^n$ without estimating the within-subject temporal dependence. The results in Propositions 1 and 2 directly imply the asymptotic normality of the standardized treatment effect $n^{1/2}({\widehat{\tau }}_j-{\tau }_j){\widehat{\theta }}_j^{-1/2}$ and the confidence interval of τ_j , which is presented in the following theorem.

Theorem 1.

Under the conditions of Proposition 1, $\hspace{0.17em}\log \hspace{0.17em}{p}_0=o(n)$, and ${\theta }_j\ge b_1$ for a small positive constant b₁, we have $n^{1/2}({\widehat{\tau }}_j-{\tau }_j){\widehat{\theta }}_j^{-1/2}\to N(0,1)$ in distribution as $n,m,p\to \infty$.

From Theorem 1, the $1-\alpha$ confidence interval for τ_j can be constructed as $({\widehat{\tau }}_j-z_{\alpha /2}{({\widehat{\theta }}_j/n)}^{1/2},{\widehat{\tau }}_j+z_{\alpha /2}{({\widehat{\theta }}_j/n)}^{1/2})$, where $z_{\alpha /2}$ is the upper $\alpha /2$ quantile of the standard normal distribution. The condition ${\theta }_j\ge b_1$ stands for nondegenerate variance of $n^{1/2}{\widehat{\tau }}_j$. To construct simultaneous confidence intervals of $\mathit{\tau }$, we need to screen out the noninformative components with θ_j converging to zero. Note that, from the decomposition of θ_j in (S.7) in the SM, ${\theta }_j\to 0$ if $Y_{i,j}(d)=0$ for d = 0, 1 and all $i=1,\dots ,n$, and the estimation variation of ${\widehat{Y}}_{i,j}(d)$ diminishes to zero with the increase of m. Let $S_{\text{AZ}}=\{j:{\theta }_j\to 0\text{as}\mathrm{n}\to \infty \}$ be the non-informative components of the subject level parameters. In Example 1 of causal effects on correlations, this means a common sparsity structure on all subject level correlation matrices such that some of the correlations are zero uniformly across all subjects.

Let $R_0=\{j:1\le j\le p_0,{\widehat{\theta }}_j\le \tilde{c}\}$ for a small positive constant $\tilde{c}$, and $R_1=\{j:1\le j\le p_0,{\widehat{\theta }}_j>\tilde{c}\}$ be the complement set of R₀. Here, the lower bound $\tilde{c}$ is needed to derive the asymptotic results in Theorems 1 and 2, which can be chosen arbitrarily small to exclude the components with ${\theta }_j\to 0$. Note that θ_j also includes the estimation variation $\text{var}\{{\widehat{\mathbf{Y}}}_i(d)|{\mathbf{T}}_i(d),{\mathbf{W}}_i\}$ which does not diminish to zero for bounded m. This screening procedure will typically not exclude any component for small m in real applications. In practice, we choose $\tilde{c}=0.01$ so that ${\widehat{\theta }}_j^{-1/2}\le 10$ for $j\in R_1$. In the real data analysis in Section 7, we find all ${\widehat{\theta }}_j$ are larger than 0.03 and $R_0=\varnothing$.

Let $S_{\text{AZ}}^c$ be the complement set of $S_{\text{AZ}}$. To construct the simultaneous confidence intervals of τ_j over $S_{\text{AZ}}^c$, we consider the maximal standardized estimates of treatment effects (4.9) $$\mathcal{V}={\max }_{j\in R_1}\sqrt{n}|({\widehat{\tau }}_j-{\tau }_j){\widehat{\theta }}_j^{-1/2}|$$(4.9) over $j\in R_1$. From the expansion (4.5), different components in $\widehat{\mathit{\tau }}$ are dependent due to correlations among the subject level parameters $\{Y_{i,j}:1\le j\le p_0\}$ from the population distribution and the common estimate $\Lambda ({\mathbf{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})$ of the propensity scores used in all $\left\{{\widehat{\tau }}_j\right\}$. The complex dependence among $\left\{{\widehat{\tau }}_j\right\}$ makes the asymptotic analysis of $\mathcal{V}$ challenging.

To tackle this problem, we derive a Gaussian approximation result for 𝒱, and use the multiplier bootstrap to estimate its quantile and construct the simultaneous confidence intervals for $\{{\tau }_j:j\in R_1\}$. To establish this approximation result, we make the following assumption on the lower bound of θ_j and the upper bound of the correlations of $\left\{{\tilde{\eta }}_{ij}\right\}$ for $j\in S_{\text{AZ}}^c$. Conditions on bounds of variances and covariances are needed for Gaussian approximation results (Chernozhukov, Chetverikov, and Kato 2013).

Condition 5. There exist small positive constants b₁ and b₂ such that ${\theta }_j\ge b_1$ for all $j\in S_{\text{AZ}}^c$ and $|\text{cor}({\tilde{\eta }}_{i{j}_1},{\tilde{\eta }}_{i{j}_2})|\le 1-b_2$ for all $j_1,j_2\in S_{\text{AZ}}^c$ and $j_1\ne j_2$.

Notice that the variance θ_j of ${\tilde{\eta }}_{ij}$ is bounded from above under the conditions of Proposition 1. Condition 5 assumes θ_j being bounded from below for all the components except those noninformative ones in $S_{\text{AZ}}$, and the correlations of $\left\{{\tilde{\eta }}_{ij}\right\}$ among those components are bounded away from 1. This implies nondegenerate influence functions $\left\{{\tilde{\eta }}_{ij}\right\}$ of ${\widehat{\tau }}_j$ for all $j\in S_{\text{AZ}}^c$. From Proposition 1, $\mathcal{V}$ is asymptotically equivalent to ${\max }_{j\in R_1}{(n{\widehat{\theta }}_j)}^{-1/2}\left|{\sum }_{i=1}^n{\tilde{\eta }}_{ij}\right|$, where ${\tilde{\eta }}_{ij}$ can be well approximated by ${\widehat{\eta }}_{ij}$. Let ${\tilde{\mathit{\eta }}}_{i,1}$ and ${\widehat{\mathit{\eta }}}_{i,1}$ be the vectorization of $\{{\tilde{\eta }}_{ij}:j\in R_1\}$ and $\{{\widehat{\eta }}_{ij}:j\in R_1\}$, respectively. Note that ${\sum }_{i=1}^n{\widehat{\eta }}_{ij}=0$ for all $j=1,\dots ,p_0$. Let ${\mathbf{S}}_{n,1}={\sum }_{i=1}^n{\widehat{\mathit{\eta }}}_{i,1}{\widehat{\mathit{\eta }}}_{i,1}^{\mathrm{T}}/n$ be the sample covariance of $\left\{{\widehat{\mathit{\eta }}}_{i,1}\right\}$, and ${\mathbf{U}}_{n,1}$ be the diagonal matrix of $\{{\widehat{\theta }}_j^{1/2}:j\in R_1\}$. Let $\mathcal{Z}={\{{\mathbf{W}}_i,D_i,{\mathbf{X}}_{i,1},\dots ,{\mathbf{X}}_{i,m}\}}_{i=1}^n$ be the collection of all data. The following theorem shows the distribution function of $\mathcal{V}$ can be approximated by that of the maximum of a Gaussian random vector when the sample size n is large.

Theorem 2.

Under the conditions of Proposition 1, Condition 5 and $\hspace{0.17em}\log \hspace{0.17em}{p}_0=o(n)$, we have $$\underset{x>0}{\sup }|\mathbb{P}(\mathcal{V}>x)-\mathbb{P}(|{\mathit{z}}_1{|}_{\infty }>x|\mathcal{Z})|\stackrel{p}{\to }0 \text{as} n\to \infty ,$$ where ${\mathbf{z}}_1\sim N(\mathbf{0},{\mathbf{U}}_{n,1}^{-1}{\mathbf{S}}_{n,1}{\mathbf{U}}_{n,1}^{-1})$ is a multivariate normal random vector.

Theorem 2 extends the original Gaussian approximation result for sample means (Chernozhukov, Chetverikov, and Kato 2013) to inverse probability weighted estimates with derived outcomes. From this result, the quantiles of $\mathcal{V}$ can be approximated by those of $|{\mathbf{z}}_1{|}_{\infty }$. To simulate ${\mathbf{z}}_1\sim N(\mathbf{0},{\mathbf{U}}_{n,1}^{-1}{\mathbf{S}}_{n,1}{\mathbf{U}}_{n,1}^{-1})$, we propose a multiplier bootstrap procedure that generates $g_{1,u},\dots ,g_{n,u}\stackrel{\text{iid}}{\sim }N(0,1)$ and calculates $${\mathit{z}}_{1,u}={\mathit{U}}_{n,1}^{-1}\sum _{i=1}^n{g}_{i,u}{\widehat{\mathit{\eta }}}_{i,1}/\sqrt{n}$$

for $u=1,\dots ,B$. It can be easily shown that ${\mathbf{z}}_{1,1},\dots ,{\mathbf{z}}_{1,B}\stackrel{\text{iid}}{\sim }N(\mathbf{0},{\mathbf{U}}_{n,1}^{-1}{\mathbf{S}}_{n,1}{\mathbf{U}}_{n,1}^{-1})$. The upper α quantile of $\mathcal{V}$ can be estimated by (4.10) $${\widehat{q}}_1(\alpha )=\inf \{x:\frac{1}{B}\sum _{u=1}^B\mathbb{I}(|{\mathit{z}}_{1,u}{|}_{\infty }\le x)\ge 1-\alpha \}.$$(4.10)

The $1-\alpha$ simultaneous confidence intervals for $\left\{{\tau }_j\right\}$ can be constructed as (4.11) $$({\widehat{\tau }}_j-{\widehat{q}}_1(\alpha ){({\widehat{\theta }}_j/n)}^{1/2},{\widehat{\tau }}_j+{\widehat{q}}_1(\alpha ){({\widehat{\theta }}_j/n)}^{1/2})$$(4.11) for $j\in R_1$, where $\mathbb{P}(R_1=S_{\text{AZ}}^c)\to 1$ as $n\to \infty$.

As the data from different individuals are assumed to be independent, the empirical bootstrap that re-samples individuals might also be able to estimate the distribution function of $\mathcal{V}$. Let ${\widehat{\mathit{\beta }}}^{\text{EBT}},{\widehat{\tau }}_j^{\text{EBT}}$, and ${\widehat{\theta }}_j^{\text{EBT}}$ be the re-sample estimates of $\mathit{\beta }$, τ_j and θ_j , respectively. The empirical bootstrap uses ${\mathcal{V}}^{\text{EBT}}={\max }_{j\in R_1}\sqrt{n}|({\widehat{\tau }}_j^{\text{EBT}}-{\widehat{\tau }}_j){({\widehat{\theta }}_j^{\text{EBT}})}^{-1/2}|$ to approximate the distribution of $\mathcal{V}$. Chernozhukov, Chetverikov, and Kato (2013) (Appendix K) showed that the empirical bootstrap can consistently estimate the distribution function of the maximum of sample means. However, the consistency of the empirical bootstrap for the maximum of the standardized IPW estimates in our problem is unclear as $\mathcal{V}$ requires the estimation of the propensity scores compared with sample means. We will investigate this question in future work.

5 Multiple Testing Procedure

In this section, we consider the multiple hypotheses $H_{0,j}:{\tau }_j=0$ versus $H_{a,j}:{\tau }_j\ne 0$ for $j=1,\dots ,p_0$. Note that the simultaneous confidence interval constructed in (4.11) can be directly used to identify nonzero τ_j . This procedure controls the FWER, defined as the probability of rejecting any true null hypothesis, at α asymptotically. However, the FWER control procedures are too conservative which lose power in detecting nonzero treatment effects. We aim to propose a more powerful multiple testing method that controls the FDP.

FDP is the ratio of the number of false positives over the number of discoveries, and false discovery rate (FDR) is the expectation of FDP. Given a small constant $c\in (0,1)$, the FDP exceedance rate (FDPex) is defined as $\mathbb{P}(\mathrm{FDP}>c)$, which gives the probability of the FDP exceeding level c in a random sample. FDR control procedures target on the average FDP over repeated random samples, which fail to consider the variation of FDP in a single experiment. To introduce a more stringent measure of Type I errors for one random sample, Genovese and Wasserman (2006) suggested to control the FDP exceedance rate $\mathbb{P}(\mathrm{FDP}>c)\le \alpha$ for pre-specified small positive constants c and α.

Following the step-down testing process with augmentation proposed in van der Laan, Dudoit, and Pollard (2004b); Genovese and Wasserman (2006), we use a similar construction of the multiple testing procedure to control the FDPex. However, the existing methods fail to work in our problem as any pair of the estimated ATEs $\left\{{\widehat{\tau }}_j\right\}$ are dependent. To solve this problem, we build the testing procedure on the maximum of $\left\{\sqrt{n}\right|{\widehat{\tau }}_j\left|{\widehat{\theta }}_j^{-1/2}\right\}$, and couple the step-down process with multiplier bootstrap, which approximates the distribution of the maximum statistic of standardized ${\widehat{\tau }}_j$ based on the Gaussian approximation result.

Specifically, we test the overall hypotheses $$H_{0,(\mathcal{l})}:{\tau }_j=0\text{forall}\mathrm{j}\in {\mathrm{R}}_{\mathcal{l}}\text{vs}.{\mathrm{H}}_{\mathrm{a},(\mathcal{l})}:{\tau }_{\mathrm{j}}\ne 0\text{forsome}\mathrm{j}\in {\mathrm{R}}_{\mathcal{l}}$$ sequentially by the maximum statistics (5.1) $${\mathcal{M}}_{\mathcal{l}}={\max }_{j\in R_{\mathcal{l}}}\sqrt{n}\left|{\widehat{\tau }}_j{\widehat{\theta }}_j^{-1/2}\right|,$$(5.1) where $R_{\mathcal{l}}\subset \{1,\dots ,p_0\}$ is a subset of indices. Let ${\widehat{\mathit{\eta }}}_{i,\mathcal{l}}$ be the vectorization of $\{{\widehat{\eta }}_{ij}:j\in R_{\mathcal{l}}\}$, and ${\mathbf{U}}_{n,\mathcal{l}}$ be the diagonal matrix of $\{{\widehat{\theta }}_j^{1/2}:j\in R_{\mathcal{l}}\}$, where ${\widehat{\eta }}_{ij}$ and ${\widehat{\theta }}_j$ are given in (4.8). Let ${\mathbf{S}}_{n,\mathcal{l}}={\sum }_{i=1}^n{\widehat{\mathit{\eta }}}_{i,\mathcal{l}}{\widehat{\mathit{\eta }}}_{i,\mathcal{l}}^{\mathrm{T}}/n$ be the sample covariance of $\left\{{\widehat{\mathit{\eta }}}_{i,\mathcal{l}}\right\}$. Similar to Theorem 2, it can be shown that the quantile of ${\mathcal{M}}_{\mathcal{l}}$ under $H_{0,(\mathcal{l})}$ can be consistently estimated by the quantile of $|{\mathbf{z}}_{\mathcal{l}}{|}_{\infty }$ where ${\mathbf{z}}_{\mathcal{l}}\sim N(\mathbf{0},{\mathbf{U}}_{n,\mathcal{l}}^{-1}{\mathbf{S}}_{n,\mathcal{l}}{\mathbf{U}}_{n,\mathcal{l}}^{-1})$. Therefore, multiplier bootstrap is applied to determine the rejection region of ${\mathcal{M}}_{\mathcal{l}}$ for testing hypotheses $H_{0,(\mathcal{l})}$. If $H_{0,(\mathcal{l})}$ is rejected, we remove the most significant index with the largest $\sqrt{n}\left|{\widehat{\tau }}_j\right|{\widehat{\theta }}_j^{-1/2}$ from $R_{\mathcal{l}}$ and continue this testing process until the null hypothesis is not rejected. It can be shown this step-down process can control the FWER. By augmenting the rejected set with the next few most significant components, the final discovered set of nonzero τ_j is able to control the FDPex.

Let $\left|U\right|$ be the cardinality of a set U, and $V_1=\varnothing$. Starting from the set $R_1=\{j:1\le j\le p_0,{\widehat{\theta }}_j>\tilde{c}\}$ and the maximum statistic ${\mathcal{M}}_1$, the proposed procedure is as follows.

• Generate $g_1,\dots ,g_n\stackrel{\text{iid}}{\sim }N(0,1)$. Let ${\mathbf{z}}_{\mathcal{l}}={\mathbf{U}}_{n,\mathcal{l}}^{-1}{\sum }_{i=1}^n{g}_i{\widehat{\mathit{\eta }}}_{i,\mathcal{l}}/\sqrt{n}$.

• Repeat the above step B times to generate iid Monte Carlo samples ${\mathbf{z}}_{\mathcal{l},1},\dots ,{\mathbf{z}}_{\mathcal{l},B}$ from $N(\mathbf{0},{\mathbf{U}}_{n,\mathcal{l}}^{-1}{\mathbf{S}}_{n,\mathcal{l}}{\mathbf{U}}_{n,\mathcal{l}}^{-1})$, and estimate the upper α quantile of ${\mathcal{M}}_{\mathcal{l}}$ under $H_{0,(\mathcal{l})}$ by

  ${\widehat{q}}_{\mathcal{l}}(\alpha )=\inf [x:\frac{1}{B}{\sum }_{u=1}^B\mathbb{I}\{|{\mathbf{z}}_{\mathcal{l},u}{|}_{\infty }\le x\}\ge 1-\alpha ].$ (5.2)

• Let $h_{\mathcal{l}}={\mathrm{argmax}}_{j\in R_{\mathcal{l}}}\left|{\widehat{\tau }}_j{\widehat{\theta }}_j^{-1/2}\right|$ and $R_{\mathcal{l}+1}=\{j\in R_{\mathcal{l}}:j\ne h_{\mathcal{l}}\}$. If ${\mathcal{M}}_{\mathcal{l}}>{\widehat{q}}_{\mathcal{l}}(\alpha )$, let $V_{\mathcal{l}+1}=V_{\mathcal{l}}\cup \left\{h_{\mathcal{l}}\right\}$; otherwise, declare the treatment effects τ_j in $R_{\mathcal{l}}$ are not significant.

• Repeat the first three steps until $R_{k_0}$ is not significant for some $k_0\ge 1$. Then, $V_{k_0}$ is the set of discovered nonzero treatment effects by the step-down process.

• Augment $V_{k_0}$ with the next $\lfloor c\left|V_{k_0}\right|/(1-c)\rfloor$ largest $\left|{\widehat{\tau }}_j{\widehat{\theta }}_j^{-1/2}\right|$ in $R_{k_0}$. Let V be the final discovery set from both the step-down process and the augmentation step.

Let $S_{\ast }=\{j:{\tau }_j\ne 0\}$ be the set of true nonzero causal effects. The following theorem states the asymptotic size and power of the proposed multiple testing procedure.

Theorem 3.

Under the conditions of Proposition 1, Condition 5 and $\hspace{0.17em}\log \hspace{0.17em}{p}_0=o(n)$, for testing the hypotheses $H_{0,j}:{\tau }_j=0$ vs. $H_{a,j}:{\tau }_j\ne 0$ for $j=1,\dots ,p_0$, we have that

1. $\underset{n,m,p\to \infty }{\lim }\mathbb{P}(\mathrm{FDP}>c)\le \alpha$, where $\mathrm{FDP}=|V\cap S_{\ast }^c|/\left|V\right|$;

2. $\mathbb{P}(S_{\ast }\subset V)\to 1$ if ${\min }_{j\in S_{\ast }}\left|{\tau }_j\right|\ge c{\{\hspace{0.17em}\log \hspace{0.17em}(p_0)/n\}}^{1/2}$ for a positive constant c.

Theorem 3 demonstrates that the proposed multiple testing procedure is able to control the FDP exceedance rate at α and has a power converging to 1 if all the nonzero τ_j is large than $c{\{\hspace{0.17em}\log \hspace{0.17em}(p_0)/n\}}^{1/2}$ for some positive constant c. Compared with the existing methods, we have theoretically shown the Type I error control of the proposed testing procedure under general dependence among $\left\{{\widehat{\tau }}_j\right\}$ based on the Gaussian approximation result. This theoretical result is justified by the empirical size and power of the proposed procedure reported in the simulation section.

6 Simulation

In this section, we conducted simulation studies to evaluate the false discovery proportion and power of the proposed multiple testing procedure for the hypotheses (2.5). We considered the treatment effects on subject level correlations and regression coefficients in Examples 1 and 2 in Section 2. As a comparison of the proposed procedure, we also implemented the Benjamini-Hochberg (BH) procedure (Benjamini and Hochberg 1995) on the standardized estimated treatment effect $n^{1/2}{\widehat{\tau }}_j{\widehat{\theta }}_j^{-1/2}$ based on Theorem 1.

For each subject $i\in \{1,\dots ,n\}$, the covariates ${\mathbf{W}}_i$ were iid generated from a q-dimensional multivariate normal distribution with zero mean and covariance matrix ${\Sigma }_w={({\sigma }_{w,j_1{j}_2})}_{q\times q}$, where ${\sigma }_{w,j_1{j}_2}={0.7}^{|j_1-j_2|}/2$. Let ${\mathbf{1}}_q$ be the q-dimensional vector of one. The treatment assignment D_i was generated from a logistic regression model with $\mathbb{P}(D_i=1|{\mathbf{W}}_i)=\Lambda ({\mathbf{W}}_i^{\mathrm{T}}\mathit{\beta })$, where $\mathit{\beta }=0.5{\mathbf{1}}_q$. To generate the potential responses ${\mathbf{X}}_{i,t}(d)$ of each subject, we first constructed the subject level correlation matrix ${\mathbf{Y}}_i(d)={(Y_{i,j_1{j}_2}(d))}_{p\times p}$. To model subject heterogeneity on correlations, let ${\delta }_i=\Lambda (|{\mathbf{W}}_i^{\mathrm{T}}\mathit{\gamma }|)-0.5+{\epsilon }_{\delta ,i}$, where $\mathit{\gamma }=0.4{\mathbf{1}}_q$ and ${\epsilon }_{\delta ,i}$ was generated from $N(0,{0.1}^2)$ independent with D_i . We set the potential covariance matrix under control (d = 0) to be fixed among all subjects where $Y_{i,j_1{j}_2}(0)={\rho }_0^{|j_1-j_2|}$. For the potential outcomes under treatment (d = 1), we considered block-diagonal and super-diagonal settings to construct signals on the individual covariance matrices as follows.

• Block-diagonal: $Y_{i,j_1{j}_2}(1)={\rho }_0^{|j_1-j_2|}+2{\rho }_0\left|{\delta }_i\right|$ for $(j_1,j_2)\in {\mathcal{S}}_{\text{bd}}$ and $Y_{i,j_1{j}_2}(1)={\rho }_0^{|j_1-j_2|}$ for $(j_1,j_2)\notin {\mathcal{S}}_{\text{bd}}$, where ${\mathcal{S}}_{\text{bd}}=\{(j_1,j_2):j_1\ne j_2,k{s}_0+1\le j_1,j_2\le (k+1)s_0\text{for}\text{k = 0},\dots ,\lfloor {\text{p/s}}_0\rfloor -1\}$, and $\lfloor ·\rfloor$ denotes the integer truncation function.

• Super-diagonal: $Y_{i,j_1{j}_2}(1)={\rho }_0^{|j_1-j_2|}+2{\rho }_0\left|{\delta }_i\right|$ for $(j_1,j_2)\in {\mathcal{S}}_{\text{sd}}$ and $Y_{i,j_1{j}_2}(1)={\rho }_0^{|j_1-j_2|}$ for $(j_1,j_2)\notin {\mathcal{S}}_{\text{sd}}$, where ${\mathcal{S}}_{\text{sd}}=\{(j_1,j_2):|j_1-j_2|=s_1\}$.

Under the block-diagonal setting, the nonzero treatment effects appear in the blocks of size s₀ along the main diagonal of the correlation matrices. There are no causal effects on subject level correlations outside those blocks. All the nonzero treatment effects have the same strength $2{\rho }_0\left|{\delta }_i\right|$ for the ith subject, and $2{\rho }_0\mathrm{E}\left\{\right|\Lambda (|{\mathbf{W}}_i^{\mathrm{T}}\mathit{\gamma }|)-0.5+{\epsilon }_{\delta ,i}\left|\right\}$ is the average treatment effect on correlations. Under the super-diagonal setting, the nonzero causal effects are only on the s₁th super diagonal of the correlation matrices. Comparing the two structures, the block-diagonal setting has more signals than the super-diagonal setting. In our settings, as D_i was independent of the subject level covariances $\{{\mathbf{Y}}_i(0),{\mathbf{Y}}_i(1)\}$ conditioning on the covariates ${\mathbf{W}}_i$, the unconfounded treatment assignment condition was satisfied. We chose $s_0=10$ and $s_1=6$ in the simulation.

Denote ${\mathbf{Y}}_i=D_i{\mathbf{Y}}_i(1)+(1-D_i){\mathbf{Y}}_i(0)$. For each individual, the time course data ${\mathbf{X}}_{i,t}$ over repeated measurements were generated via a vector autoregressive (VAR) model. Let ${\mathbf{X}}_{i,1}$ and ${\mathit{ϵ}}_{i,2},\dots ,{\mathit{ϵ}}_{i,m}$ be iid random vectors from the p-dimensional normal distribution $N(\mathbf{0},{\mathbf{Y}}_i)$ with mean zero and covariance matrix ${\mathbf{Y}}_i$, where m is the number of repeated measurements for each subject over time. As the number of fMRI scans from each subject is usually around 200 to 300, we set m = 300 in our study. Let ${\mathbf{X}}_{i,t}={\rho }_{\text{time}}{\mathbf{X}}_{i,t-1}+\sqrt{1-{\rho }_{\text{time}}^2}{\mathit{ϵ}}_{i,t}$ for $t=2,\dots ,m$, where the parameter ${\rho }_{\text{time}}$ specifies the strength of time dependence. Under this VAR model, the temporal correlation between $X_{i,t,j}$ and $X_{i,t-1,j}$ is equal to ${\rho }_{\text{time}}$ for all $j=1,\dots ,p$. We considered both ${\rho }_{\text{time}}=0$ and ${\rho }_{\text{time}}=0.3$ to evaluate the effect of time dependence on the proposed procedure. We set the number of covariates q = 4, n = 100, 200 and p = 50, 100. All the simulation settings were repeated 1000 times.

For the proposed multiple testing procedure, we aimed to control the FDPex rate over 0.1 at 0.05, namely, $\mathbb{P}(\text{FDP}>0.1)\le 0.05$. The number B of bootstrap samples in (5.2) was set to be 1000. The nominal level of FDR for the BH procedure was set as 0.05. Over the 1000 repetitions of each simulation setting, we calculated the average FDR, the proportion of FDP larger than 0.1, and the average true positive rate (TPR) as the power of the test, which is the number of true positives over the total number of nonzero signals. Note that the BH procedure targets to control the FDR, which may not be able to control the FDPex rate, and the dependence among the standardized estimates $n^{1/2}{\widehat{\tau }}_j{\widehat{\theta }}_j^{-1/2}$ due to sharing the common estimated propensity scores may also cause an inaccurate Type I error control for the BH procedure. The average FDPex rate, FDR and power of the two methods are reported in Figures 1 and 2.

Fig. 1 The average FDPex rate $\mathbb{P}(\text{FDP}>0.1)$, FDR and power of the proposed (red) and BH (blue) procedures for testing the hypotheses (2.5) to recover the nonzero treatment effects on the subject level correlations under the block-diagonal signal setting with $s_0=10$, m = 300, n = 100, 200, $p=50,100$ and ${\rho }_{\text{time}}=0$ and 0.3. The nominal level was 0.05.

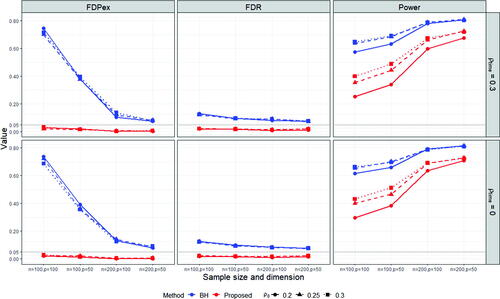
Fig. 2 The average FDPex rate $\mathbb{P}(\text{FDP}>0.1)$, FDR and power of the proposed (red) and BH (blue) procedures for testing the hypotheses (2.5) to recover the nonzero treatment effects on the subject level correlations under the super-diagonal signal setting with $s_1=6$, m = 300, n = 100, 200, $p=50,100$ and ${\rho }_{\text{time}}=0$ and 0.3. The nominal level was 0.05.

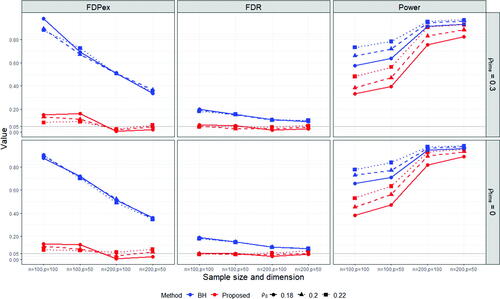
From Figures 1 and 2, we observe that the proposed method can control the FDPex rate for testing the hypotheses (2.5) smaller than 0.05 under most of the cases, except for the super-diagonal signal setting under n = 100, where the FDPex rate was around 0.1. But this error rate decreased to less than 0.05 when the number of subjects n was increased to 200. Meanwhile, the FDR of the proposed method was well controlled, around 5% under all the cases. In comparison, the empirical FDPex rate of the BH procedure was quite large, which reached over 0.7 and 0.9 under the block-diagonal and super-diagonal signal settings with n = 100, respectively. The FDPex rate of BH became much smaller under the block-diagonal setting when n was increased to 200, but it was still larger than 5%. This shows that the BH procedure can not control the FDP exceedance rate for testing many treatment effects derived from the same group of subjects. Also, notice that BH encountered a slight inflation on FDR. Its FDR was around 0.1 larger than the nominal level 5%. It reached around 0.2 under the super-diagonal setting and n = 100. This may be due to the dependence among the estimated treatment effects $\left\{{\widehat{\tau }}_j\right\}$ in (4.3) as they all use the common propensity scores.

The overall power of the proposed test was reasonable, and it was much increased with the increase of the sample size from 100 to 200. Compared with the BH procedure, the power of the proposed procedure was lower, especially under n = 100. This is because of the size inflation of the BH procedure and the more stringent Type I error control of our procedure. Notice that both procedures use the same estimates of the average treatment effects. The difference is solely from the ways of choosing the cutoff value for testing the multiple hypotheses (2.5). When n was increased to 200, the power of the proposed procedure became much closer to those of BH. Especially, under the super-diagonal setting and $n=200$, the power of both methods reached around 0.9. Also notice that the results under ${\rho }_{\text{time}}=0$ and ${\rho }_{\text{time}}=0.3$ were comparable for both methods. When ${\rho }_{\text{time}}=0$, the subject level data were temporally independent. The power under ${\rho }_{\text{time}}=0.3$ was slightly lower, which was due to the larger variation of the estimated subject level correlations under time-dependent data.

To evaluate the treatment effects on regression coefficients in Example 2, we compared the performance of the proposed method with the lasso estimate and the de-sparsified lasso estimate described in Section S1 in the SM. Note that the lasso estimate is biased, which does not satisfy Condition 4. The covariates ${\mathbf{W}}_i$, treatment assignment D_i and the subject level covariance matrix ${\mathbf{Y}}_i(0)$ under control were generated the same as the simulation settings for Example 1. Let ${\Omega }_i(d)=({\omega }_{i,j_1{j}_2}(d))={\mathbf{Y}}_i^{-1}(d)$ be the precision matrix. We added the signals on ${\Omega }_i(1)$ in the block-diagonal setting where ${\omega }_{i,j_1{j}_2}(1)={\omega }_{i,j_1{j}_2}(0)+{\rho }_0\left|{\delta }_i\right|$ for $(j_1,j_2)\in {\mathcal{S}}_{\text{bd}}$ and ${\omega }_{i,j_1{j}_2}(1)={\omega }_{i,j_1{j}_2}(0)$ for $(j_1,j_2)\notin {\mathcal{S}}_{\text{bd}}$. The subject level data ${\mathbf{X}}_{i,t}$ were generated by the VAR model with the error distribution $N(\mathbf{0},{\Omega }_i^{-1})$, where ${\Omega }_i=D_i{\Omega }_i(1)+(1-D_i){\Omega }_i(0)$. From Example 2, the support of the coefficients $\{Y_{i,j_1{j}_2}^{\ast }(d)\}$ of the nodewise regressions is the same as that of the precision matrix ${\Omega }_i(d)$. The lasso penalty parameters λ_j and ${\lambda }_{j_1{j}_2}$ were set as $\sqrt{2(\hspace{0.17em}\log \hspace{0.17em}p)/m}$ for all $j,j_1,j_2$.

The average FDPex rate, FDR and power are reported in Figure S1 in the SM. We observe that the proposed method with the de-sparsified lasso estimate was able to control the FDPex rate under the nominal level 5% with good power. Its FDR was also controlled at 5%. In contrast, the proposed method with the lasso estimate failed to work. Its power was lower than 0.1 for all the cases due to the underestimation of the true regression coefficients. These results show that the asymptotic unbiasedness condition (Condition 4) is essential for the validity of the proposed method. Simply using any consistent estimator for the subject level parameters may not lead to desirable estimates of the treatment effects.

7 Case Study

It is well recognized that neurodevelopmental and neurodegenerative disorders, like Autism spectrum disorder (ASD), are associated with altered patterns of over- and under-connectivity in brains (Kana et al. 2014). In this section, we studied medication effects on the brain functional connectivity of patients with ASD. We used the fMRI data of 79 ASD patients from New York University Langone Medical Center. The preprocessed data were downloaded from the Autism Brain Imaging Data Exchange I initiative (Craddock et al. 2013). Among the 79 patients, 16 of them had taken some kind of medications for alleviating the related symptoms of ASD, and the rest 60 had not. We estimated and identified the nonzero treatment effects on brain functional connectivity, measured by correlations among brain regions, between the groups taking and not taking medications within three months before taking fMRI scans.

For each subject, there were 175 scans of brain overtime in the fMRI data, and a set of 116 regions-of-interests (ROI) were extracted according to the automated anatomical labeling atlas. Following Liu and Huang (2020), those 116 ROIs can be divided into six common functional networks: the default mode network (DMN), the execution and attention network (EAN), the sensorimotor network (SMN), the visual network (Visual), the subcortical nuclei (SBN) regions and the cerebellum (Cerebel), which consist of 22, 17, 18, 14, 19, 26 regions, respectively. Data of three patients were deleted, one of which was due to missing covariates and the other two were due to missing values in the ROIs. The final data included 76 ASD patients.

Four covariates including age, sex, handedness, and FIQ were chosen in the analysis. Age and sex are binary variables, handedness is an integer score between –100 and 100 with a higher score implying more use of the right hand and vice versa, and FIQ is a positive integer score representing the standard estimate of intelligence. Note that the development of ASD symptoms is related to age, and ASD is a disorder of sexual differentiation (Alaerts, Swinnen, and Wenderoth 2016). IQ scores also affect the decision of taking medicine. An ASD patient may be treated if there is some abnormality in IQ. Meanwhile, those covariates are also related to the differences in brain connectivity among subjects. Therefore, age, sex, and IQ can be regarded as common causes for the treatment indicator and the potential responses. We make the unconfoundedness assumption that the treatment assignment and the potential fMRI readings are conditionally independent given the covariates.

We applied the proposed procedure for testing the multiple hypotheses (2.5) to identify the nonzero treatment effects on the subject level correlations among brain ROIs. Similar to the simulation study, we controlled the probability of FDP exceeding 0.1 at 0.05, namely, c = 0.1 and $\alpha =0.05$. We discovered four significant pairs of brain connections with nonzero ATE of medication on ASD patients, which are reported in Table 1 together with the corresponding functional network. The BH procedure that controls the FDR at 5% based on the standardized estimated treatment effects gives the same set of discovered connections as the proposed method for this dataset. The estimated treatment effects for the four discovered pairs, their 95% confidence intervals, the IPW averages for the treatment and control groups, $n^{-1}{\sum }_{i=1}^n{\widehat{Y}}_{i,j}{D}_i/\Lambda ({\mathbf{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})$ and $n^{-1}{\sum }_{i=1}^n{\widehat{Y}}_{i,j}(1-D_i)/\{1-\Lambda ({\mathbf{W}}_i^{\mathrm{T}}\widehat{\mathit{\beta }})\}$, are also reported in Table 1. The visualization of those connections is shown in Figure S2 in the SM. All six functional networks except the cerebellum network were involved in those significant connections. Notice that the correlation between SMA.L and HES.R were altered in the positive direction on average by medication, while the correlations of the other three pairs were negatively enhanced. Among the identified ROIs, HES.R was also reported to be strongly associated with the severity of ASD in Liu and Huang (2020). The discovered connections were mainly related to the execution and attention network (EAN). According to CDC, signs and symptoms of ASD are associated with execution and attention. Bernas et al. (2018) and Snyder and Troiani (2020) also found evidence that relates the abnormalities of neurodynamics and connectivity of ASD brains to brain regions associated with attention and execution. Our method reveals the medication effects on brain connectivities of some regions in EAN, which may alleviate the symptoms of ASD.

Table 1 The four pairs of ROIs (the functional networks they belong to in the parentheses) with the identified nonzero treatment effects on subject level correlations by the proposed multiple testing procedure, the estimated treatment effect, its 95% confidence interval, and the IPW averages for the treatment group (Ave-trt) and the control group (Ave-cl).

	ROI1 (Network)	ROI2 (Network)	Estimated effect	95% CI	Ave-trt	Ave-cl
1	SMA.L (EAN)	HES.R (SMN)	0.164	(0.098, 0.230)	0.136	–0.029
2	IPL.L (EAN)	CAU.R (SBN)	–0.138	(–0.198, –0.077)	–0.264	–0.126
3	IPL.R (EAN)	ITG.L (EAN)	–0.187	(–0.262, –0.111)	–0.231	–0.044
4	ORBsup.L (DMN)	MOG.L (Visual)	–0.163	(–0.233, –0.094)	–0.217	–0.053

We also applied the two-sample t-test directly on the subject level sample correlations $\left\{{\widehat{Y}}_{i,j_1{j}_2}\right\}$. This is equivalent to treating the propensity score in (4.3) being 16/76 for all subjects, as the ratio of the number of treated patients over the total sample size. Such a procedure is commonly used in many neuroscience studies. However, no significant difference in correlations between the treatment and control groups was found without the propensity score adjustment. This shows that simply conducting two-sample t-tests may not be able to identify treatment effects in observational studies for brain connectivity.

8 Discussion

In this article, we consider estimating the ATEs of unobservable random variables from each subject under the ignorability assumption. Those unobservable random variables need to be estimated using subject level data. Our theoretical analysis shows that an additional unbiasedness condition is needed for the identifiability and estimation of the ATEs, compared with the classical causal inference problems under the ignorability assumption. This implies that not all consistent estimators of the subject level parameters of interest can be used to estimate the population treatment effects. A de-biased estimator satisfying Condition 4 needs to be constructed.

We study the treatment effects on brain functional connectivity measured by Pearson’s correlation in the case study. The proposed method can be applied to other measures of brain connectivity, for example, Spearman’s ρ and Kendall’s τ for nonlinear association and partial correlation for conditional association. The proposed procedure can be extended to dynamic treatment effects over time as well, where the subject level potential outcomes ${\mathbf{Y}}_i(d,t)$ and the average treatment effects $\mathit{\tau }(t)=\mathrm{E}\{{\mathbf{Y}}_i(1,t)-{\mathbf{Y}}_i(0,t)\}$ are functions of time (Bojinov, Rambachan, and Shephard 2021). This setting is suitable for task-based fMRI data where the brain activity patterns are likely to change with respect to the given tasks. Developing more powerful multiple testing procedures able to control the FDP under a general dependence structure among the estimated ATEs is also worth investigating in future work.

Acknowledgments

The authors would like to thank the anonymous referees, the Associate Editor and the Editor for thoughtful comments and suggestions which have improved the presentation of the paper. Part of the work reported in the paper was conducted while Qiu was affiliated with Iowa State University. He thanks ISU’s statistics department for providing various support during the course of the project.

Supplementary Materials

The supplementary material provides justification of Condition 4 for the de-sparsified lasso estimator and sample correlation, proofs for all theoretical results and some additional numerical results.

Disclosure Statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

Zhou was partially supported by National Key Research and Development Program of China, grant No. 2021YFF0901400, National Natural Science Foundation of China, grant No. 12026606, and Novo Nordisk A/S.