An entropy approach for the optimization of cross-section spacing for river modelling

Abstract

An accurate definition of river geometry is essential to implement one-dimensional (1D) hydraulic models and, in particular, appropriate spacing between cross-sections is key for capturing a river’s hydraulic behaviour. This work explores the potential of an entropy-based approach, as a complementary method to existing guidelines, to determine the optimal number of cross-sections to support 1D hydraulic modelling. To this end, given a redundant collection of existing cross-sections, a location subset is selected minimizing total correlation (as a measure of redundancy) and maximizing joint entropy (as a measure of information content). The problem is posed as a multi-objective optimization problem and solved using a genetic algorithm: the Non-dominated Sorting Genetic Algorithm (NSGA)-II. The proposed method is applied to a river reach of the Po River (Italy) and compared to standard guidelines for 1D hydraulic modelling. Cross-sections selected through the proposed methodology were found to provide an accurate description of the flood water profile, while optimizing computational efficiency.

Editor D. Koutsoyiannis

Citation Ridolfi, E., Alfonso, L., Di Baldassarre, G., Dottori, F., Russo, F., and Napolitano, F., 2013. An entropy approach for the optimization of cross-section spacing for river modelling. Hydrological Sciences Journal, 59 (1), 126–137.

Résumé

Une définition précise de la géométrie de la riviére est essentielle pour mettre en œuvre des modéles hydrauliques unidimensionnels (1D). L’espacement approprié entre les sections en travers de la riviére est un élément clé pour reproduire son comportement hydraulique. Ce travail a pour objectif de fournir une méthode se basant sur l’entropie, complémentaire des guides existants et permettant de fournir des informations supplémentaires pour l’optimisation des modéles hydrauliques 1D et la gestion des jeux de données sur les sections en travers. Plus spécifiquement, sur la base d’une collecte redondante de sites de sections en travers existantes, un sous-ensemble de sites est sélectionné en minimisant la corrélation totale (comme mesure de redondance) et en maximisant l’entropie conjointe (comme mesure du contenu en information). Le probléme est posé sous la forme d’une optimisation multi-objectif, résolue en utilisant un algorithme génétique (NSGA-II). Nous appliquons la méthode proposée aux données de sections en travers sur le Po, en Italie, et nous la comparons aux méthodes existantes en utilisant un modéle hydraulique 1D. Les jeux de sections en travers sélectionnées par la méthodologie proposée fournissent une description précise du profil des eaux en crue, tout en optimisant l'efficacité de calcul.

Key words:

• cross-sections
• heuristic entropy
• hydraulic modelling
• one-dimensional flow
• network optimization
• genetic algorithm
• NGSA-II

Mots clefs:

• sections en travers
• entropie heuristique
• modélisation hydraulique
• flux unidimensionnel
• optimisation de réseau, algorithme génétique
• NGSA-II

1 INTRODUCTION

Hydraulic modelling of river flooding has become an important step in most flood risk studies (Cunge 2003, Abida et al. 2005, Di Baldassarre et al. 2009b, 2010). In this context, the optimal spacing of river cross-sections is fundamental to thoroughly describe the hydraulic behaviour of a river. The usual approach in hydraulic modelling is to use a large number of cross-sections, which implies not only significant computational modelling time, but also considerable fieldwork effort for data collection and updating. Therefore, it is very important to know the minimum number of cross-sections needed (and their locations) to yield an acceptable accuracy of modelling results, by identifying useful and non-redundant data. In particular, in developing countries and in inaccessible areas, model input optimization has a great impact on the development of models, because data may be of limited availability or poor quality.

Despite the relevance of estimating the optimal number of cross-sections in hydraulic modelling, only a few guidelines have been presented on this issue (e.g. Samuels 1990, Castellarin et al. 2009). In this work, we present an entropy approach to determine the optimal number of river cross-sections and their locations. The aim is to supply a complementary method to the existing guidelines, in order to provide additional information for optimization and management of cross-section data sets of one-dimensional (1D) models.

The so-called heuristic entropy was defined by Shannon (1948) as the measure of the uncertainty about the knowledge of the state of a given system. In recent years heuristic entropy has had a wide range of applications in hydrology and water resources; an extensive review of these applications is reported by Singh (1997a, 2000). In statistical analysis, the principle of maximum entropy (ME; Jaynes 1957) provided the least biased estimation of probability distributions on the basis of partial knowledge, opening the way to applications in several fields. Koutsoyiannis (2005a, 2005b, 2006) demonstrated that the principle of ME can be applied to derive the appropriate distribution of a studied variable and to evaluate the dependence properties of the rainfall occurrence process as clustering behaviour and persistence. Papalexiou and Koutsoyiannis (2012) used this principle to construct an appropriate probability distribution for rainfall processes.

In the context of flood mapping analysis, Horritt (2006) applied an entropy-based methodology for evaluating the uncertainty and assessing the accuracy of probabilistic flood maps. In the field of rainfall–runoff analysis, Pechlivanidis et al. (2010) proposed an entropy-based measure for the rainfall–runoff model diagnostic, and Pechlivanidis et al. (2012) extended the work evaluating the non-dynamical information contained in streamflow analysis; Montesarchio et al. (2011) and Ridolfi et al. (2013) defined rainfall threshold values minimizing a risk function based on the entropy concept.

Weijs et al. (2010) proposed a theoretical framework based on relative entropy involving the analysis of a divergence score measure to evaluate the quality of hydrological forecasts. Weijs and van de Giesen (2011) generalized the decomposition of the Kullback–Leibler divergence to the case where the observation is uncertain.

Informative entropy has been used effectively as a tool for optimizing, designing and managing networks. Husain (1989) used the entropy to choose the optimum raingauge stations from a dense network and to expand the network in an optimum way. Krstanowicz and Singh (1992) optimized rainfall networks describing the rainfall with continuous distribution functions, and Yoo et al. (2008) compared this to a mixed continuous-discrete method. By using the approach presented by Krstanowicz and Singh (1992), Ridolfi et al. (2011) found that the non-redundant information of a raingauge network has a scale-invariant behaviour. Using Information Theory quantities as objective functions, Alfonso et al. (2010a, 2010b) optimized the location of water-level monitors. In the field of the assessment and design of water-quality monitoring networks, Ozkul et al. (2000), Mogheir and Singh (2002) and Mogheir et al. (2003, 2004) used entropy as the main tool for leading optimal decisions.

In this work, the problem of finding the optimal number of cross-sections and their positions is posed as a multi-objective optimization problem (MOOP). Given a redundant set of cross-sections, their total correlation (C) and their joint entropy (JH) can be used as measures of redundancy and joint information content, respectively. The MOOP consists of minimizing the total correlation and maximizing the joint entropy of a given set of cross-sectional locations. Similarly to Alfonso et al. (2010b), the MOOP is solved by means of the Non-dominated Sorting Genetic Algorithm (NSGA)-II, which produces collections of solutions that evolve towards a Pareto-optimal front solution set (Deb et al. 2002).

First, an overview on the entropy method and existing guidelines in the literature is presented; second, the MOOP is posed and the two objective functions are formally introduced. Then, the Pareto front of the best set of solutions is presented. Finally, the methodology is applied to a river reach of the Po River (Italy) and the results are compared with guidelines presented by Samuels (1990) and with results proposed by Castellarin et al. (2009).

2 AN OVERVIEW OF ENTROPY AND TOTAL CORRELATION CONCEPTS

Heuristic entropy can be defined as the measure of uncertainty about the occurrence of a certain event (Papoulis 1991). Amorocho and Espildora (1973) provided one of the first applications of entropy concept to hydrology to evaluate the hydrologic information transfer among river points.

Formally, for any discrete random vector (RV) X, entropy is defined as:

(1)

where p(x_i) is the probability that X assumes the value x_i and n is the length of X (Shannon 1948). The units of entropy depend on the base of the logarithm used; if base 2 is adopted, entropy is measured in bits. For any probability distribution it is possible to define a quantity, called entropy, which measures the amount of information contained in a RV. This quantity can be used as an answer to questions in many fields such as communication, statistics and hydrology. A fully comprehensive introduction to entropy can be found in Cover and Thomas (1991).

If all the vector’s components are different, uncertainty about the outcome of randomly selecting a component will be maximum: this uncertainty is the RV’s entropy. However, if all the RV components are the same, there is no uncertainty about the outcome of randomly selecting a component, and RV’s entropy is equal to zero (Koutsoyiannis 2005a). For this reason, entropy can be considered as a measure of the information that is potentially contained in the RV.

Let us now take M discrete RVs. Their joint entropy is (Papoulis 1991):

(2)

where is the joint probability of the M variables.

In this paper, total correlation is used to evaluate the amount of redundant information among two or more RVs by providing an estimation of the non-linear, multi-order dependence among the variables. It is defined as the difference between the sum of the marginal entropies of the RVs and their joint entropy (Watanabe 1960):

(3)

where H(X_i) is the marginal entropy of the ith RV and H(X₁, X₂,..., X_M) is the joint entropy of the M RVs.

In order to estimate the marginal and joint entropy of M RVs, it is necessary to evaluate their marginal and joint probabilities, which is not trivial. In this paper, the joint entropy of the considered set of RVs is determined using the grouping property of mutual information (Kraskov et al. 2005). In particular, to evaluate marginal and joint probabilities, a non-parametric estimation is adopted through a data-binning procedure. This method is also used in the univariate analysis to build histograms. Therefore, considering two discrete RVs, X and Y, let us subdivide their values in bins. Several authors have explored the issue of bin size definition: Chapman (1986) studied the differences in using different class sizes; Singh (1997b) studied the effect of class interval width; Mogheir et al. (2003) defined the class intervals as a function of the RV length; Knuth (2006) proposed a Bayesian based method for determining the optimal bins size. Increasing the number of bin partitions of a RV, its entropy increases as well. For this reason the number of bins needs to be accurately defined.

In this paper, RV values are water depths; in order to avoid a subjective selection, each RV value is divided in bins that have a width of 0.20 m, corresponding to hydraulic model sensitivity (i.e. HEC-RAS, see Section 4). The marginal probability of each bin is determined by evaluating the number of components that fall in each bin and dividing it by the total length of the vector. In order to evaluate the joint probability of the two RVs, it is necessary to agglomerate their values, thereby obtaining a new RV. For instance, if two RVs are X = [a, c, b] and Y = [b, c, a], the resulting vector A obtained by agglomerating X and Y is A = [ab, cc, ba]. This procedure guarantees that the marginal entropy of the new variable A is equivalent to the joint entropy of the two RVs X and Y, i.e. H(A) = H(X,Y).

For evaluating the joint entropy of three RVs (X, Y and Z) it is necessary to agglomerate A with Z, obtaining a new variable (e.g. B), with marginal entropy H(B) = H(A,Z) = H(X,Y,Z). Thanks to the grouping property of mutual information (Kraskov et al. 2005), the joint entropy of M RVs can be easily evaluated by agglomerating them in pairs, without the need to estimate their joint probability p(x₁,...x_M).

3 OPTIMIZATION OF THE SPATIAL DISTANCE AMONG CROSS-SECTIONS

3.1 Hydraulic approaches

In the literature there are only a few guidelines on the selection of convenient spacing between river cross-sections in 1D hydraulic modelling; they were proposed by Samuels (1990) and Castellarin et al. (2009), hereinafter referred to as S90 and C09, respectively. These guidelines were derived by S90 by applying hydraulic theory and were verified by C09 by means of numerical experiments with real-world case studies. S90 presented some suggestions for the locations of cross-sections:

• – at the beginning and at the end of the considered reach;

• – at either side of structures (e.g. bridges);

• – at each point of interest;

• – at a location corresponding to each gauge located on the river profile.

In addition to these simple recommendations, S90 provided an equation for determining the distance between cross-sections:

(4)

where B (m) is the bankfull surface width of the main channel and k is a dimensionless constant, chosen in the range 10–20. In case of backwater at the end of the river reach:

(5)

where F is the dimensionless Froude number, D (m) is the bankfull depth of flow and s is the surface (or main channel) slope.

For unsteady conditions, the wave profile should be represented. S90 highlights that the wave is reasonably represented by a number of grid points N_gp from 30 to 50, and recommends:

(6)

where c (m s^-1) is the wave propagation speed and T (s) is the period of the flood wave (their product represents the wavelength). After some preliminary tests, in this case study the average value of 40 was found to provide an acceptable representation of the wave profile. Finally, a minimum distance:

(7)

takes into account the effect of rounding error. In equation (7), p is the number of numerical digits of precision, d is the digits lost due to cancellation of the leading digits of the stage values, s is the average surface slope, ε_s is the relative error on the surface that can be tolerated in the computation.

In Table 1 the spacing between cross-sections, found applying equations (5) and (6), are presented for the Po River case study (Section 4.1). The two equations are solved using parameters values reported in the table itself.

Table 1 Average and maximum values of the parameters of the Po River, Italy: D is the bankfull width, s is the slope, F is Froude’s number computed by the HEC-RAS model, c is the wave celerity and T is the period of the flood wave. Using equations (5) and (6), the spacing between cross-sections Δx₂ and Δx₃ are evaluated. Each optimum number of cross-sections n_i is evaluated dividing the length of the reach by the spacing Δx_i.

Parameter	D (m)	S	F	c (m s^-1)	T (s)	Δx2 (km)	n2	Δx3 (km)	n3
Average value	14.00	14 × 10^-5	0.12	2.46	7.74 × 10^5	20	4	47.62	2
Max value	21.82	14 × 10^-5	0.18	4.41	7.74 × 10^5	30	3	85.46	1

3.2 The proposed entropy-based approach

In order to explain the concept of locating optimal river cross-sections through the entropy concept, let us consider the Venn diagrams in Fig. 1. Assuming that high water level time series produced at a particular cross-section can be treated as a RV, the entropy of the series (or its information content) can be represented by a circle’s area. If a large number (M) of cross-sections is available and all of them are considered for modelling, they would provide redundant information, so that their corresponding circles will overlap, Fig. 1(a).

Fig. 1 (a) Venn diagram illustrating the multi-objective optimization problem of selecting three circles out of eight with the maximum covered area (JH) and the minimum multi-order overlapping area (C); (b) two possible solutions; (c) JH of each solution, representing the amount of information content of the set; and (d) C of each solution, representing the multi-order redundant information of the set. Adapted from Alfonso et al. (2013).

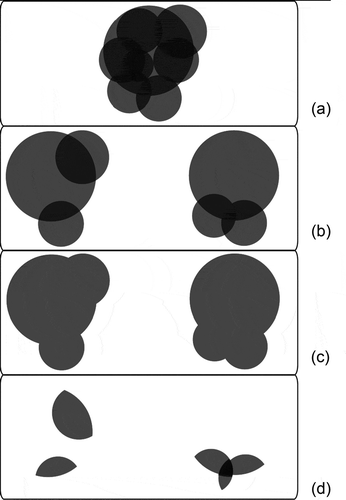
Let us now consider the task of selecting the three best cross-section sites out of the M sites. Referring back to the Venn diagrams, this translates into selecting a set of three circles from Fig. 1(a), such that the area contained by the three is maximized and, simultaneously, that their overlapped area is minimized. Two possible solutions are represented in Fig. 1. For each of these solutions, the marginal entropy (area of each circle), joint entropy (the total inscribed area) and total correlation (the total overlapping area) for the three RVs are shown in Fig. 1(b), (c) and (d), respectively. It should be noted that C sums up all multi-order dependencies, which implies that for a large number of variables (i.e. circles), the resulting C can be larger than JH. For example, the option on the left of Fig. 1(d) shows two second-order dependencies, while on the right there are three second-order dependencies and one three-order dependence. From the Venn diagram, the set of optimal locations for cross-sections must have minimum total correlation and maximum joint entropy, thus a multi-objective optimization approach is considered:

(8)

where C is the total correlation and JH is the joint entropy of M RVs.

In this way, the optimum set of cross-sections has the minimum redundant information and the maximum joint information. Both objectives are needed because simply minimizing the total correlation would result in a set of non-redundant RVs that would not necessarily provide enough information content. Likewise, only maximizing joint entropy would result in a set of very informative but highly redundant RVs. Here, each RV X_i is the series of maximum water stages at the ith cross-section, obtained using different combination of Manning’s coefficients in model calibration (see Section 4).

3.3 MOOP solution through NSGA-II genetic algorithm

In order to solve the MOOP, the NSGA-II, proposed by Deb et al. (2002), is used. The NSGA-II creates a mating pool by combining the parent and offspring population, selecting the best solution. The next generation is populated with the best non-dominated front until the population size is reached (Farmani et al. 2006). It searches for the best Pareto front solution among all the mutually non-dominated solutions determined, identifying the best trade-off between sets of competitive objectives (Olsson et al. 2009). In this case study, the two competitive objectives are represented by the minimization of total correlation and maximization of joint entropy of the M considered variables (equation (8)). The best solutions are found by the algorithm and then plotted on a Pareto front. Each point represents the best trade-off in fulfilling the two conditions. An enhanced performance in one of the two objectives is achieved to the detriment of the other objective.

4 CASE STUDY: PO RIVER, ITALY

The methods described in Section 3 were applied to the 98 km reach of the Po River between Cremona and Borgoforte (Italy), Fig. 2. The floodplain is confined by two continuous levee systems and the width of the channel is approximately constant (300 m) (Schumann et al. 2010, Brandimarte and Di Baldassarre 2012). The Po River Basin Authority has developed a high-quality 2-m digital terrain model (DTM) of the middle-lower part of the Po River, integrating airborne laser scanning with boat and ground surveys of channel bathimetry (Castellarin et al. 2009, 2011, Brandimarte and Di Baldassarre 2012).

Fig. 2 Po River, Italy, between Cremona and Borgoforte. LiDAR topography (grey scale) is shown.

4.1 Hydraulic model

The hydraulic behaviour of this site of study was analysed through the 1D code HEC-RAS (HEC 2001) in unsteady flow conditions. HEC-RAS has been largely applied for hydraulic modelling (e.g. Pappenberger et al. 2005, 2006, Cesur 2007, Schumann et al. 2007, Brandimarte et al. 2009, Di Baldassarre et al. 2009a, Brandimarte and Di Baldassarre 2012). Moreover, its reliability has been proven in a wide number of studies (e.g. Horritt and Bates 2002, Castellarin et al. 2009).

From the available DTM, it was possible to extract 88 cross-sections, which were used in the 1D model for describing the geometry of the river reach. The model built using the entire cross-section data set (henceforth referred to as Po-88) was calibrated considering the major flood that occurred in October 2000 (about 11 850 m³ s^-1). The inflow hydrograph at Cremona was taken as the upstream condition, whereas the friction slope at Borgoforte was used as the downstream boundary condition (Brandimarte and Di Baldassarre 2012).

The values of the Manning’s coefficient, n, were calibrated against the high water marks surveyed after the October 2000 flood event (Coratza 2005, Brandimarte and Di Baldassarre 2012). The set of n values considered for the floodplain varies between 0.050 m^-1/3 s and 0.140 m^-1/3 s with a step of 0.010 m^-1/3 s, while the channel n value varies between 0.020 m^-1/3 s and 0.060 m^-1/3 s with a step of 0.005 m^-1/3 s. Manning’s values are chosen according to values reported in commonly used tables in the literature (Chow 1959).

For each simulation with different values of roughness, the mean absolute error (MAE) evaluation metric is computed through:

(9)

where X_obs and X_sim are the vectors of observed and simulated maximum water stage for each Manning’s value combination, respectively. This metric evaluates the level of overall agreement between observations and simulations, determining the deviation of simulated from observed values (Dawson et al. 2007).

For the Po-88 configuration, the combination of n values that provided the lowest MAE was 0.045 m^-1/3 s for the channel and 0.050 m^-1/3 s for the floodplain.

5 NUMERICAL ANALYSIS AND RESULTS

The optimal spacing of river cross-sections was evaluated using both the proposed entropy approach and the guidelines provided by S90 and C09. The results were then compared with those given using the geometry of the Po-88 model. It is important to note that the application of the two approaches (i.e. guidelines and entropy) differs significantly. Guidelines provided in Samuels (1990) can be applied even when no cross-sections are available, being based on minimal topographic information of the river reach. In contrast, the entropy-based approach requires an existing cross-section data set to be applied.

5.1 Spacing optimization by the entropy method

The entropy method was applied to find the set of cross-sections that fulfilled the conditions presented in equation (8). As it is necessary to establish a priori the number of cross-sections for this equation, a preliminary analysis was performed to explore the value of adding cross-sections by looking at the increment of joint entropy in relation to the decrease in total correlation.

To compare the behaviour of different values of M (the number of cross-sections), the MOOP was solved considering M = 2, 3, 4, 5, 6, 10, 15 and 20 (excluding the upstream and downstream cross-sections). From HEC-RAS simulations, for each cross-section a vector (i.e. X_i) is created, the values of which are the maximum water stages associated with a particular combination of Manning’s coefficients. Once JH and C were calculated for a given set M, the Pareto front was obtained after solving the MOOP for each M (Fig. 3).

Fig. 3 Pareto-optimal set of solutions for joint entropy and total correlation, discriminated by the MOOP, considering an increasing number of cross-sections, M (see Sections 3.2 and 3.3 for details).

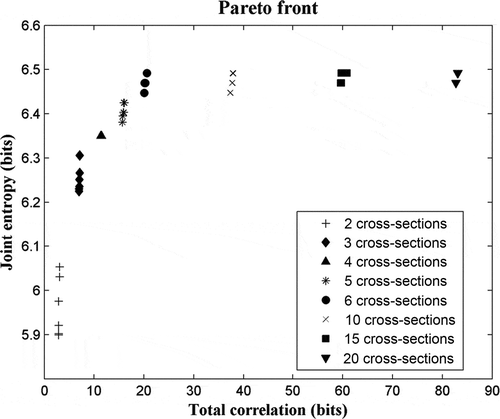
The total correlation and joint entropy (Fig. 3) indicate that the most informative sets of cross-sections are found when the value of M is between 3 and 5. When less than three sections are used, the value of joint entropy is low; using more than five sections results in a high total correlation. In addition, Fig. 3 shows that joint entropy does not increase when 6 or more sections are used, as JH tends to its maximum value log₂n, where n is the length of RV. Thus, using fewer cross-sections does not affect the description of the river profile in terms of information content.

Results in Fig. 3 for four and five cross-sections show that the difference between the two solutions in terms of total correlation is 4.55 bits, while the gain in joint entropy is only 0.07 bits. This means that the gain in information content is not as high as the redundancy increment.

The value of joint information corresponding to four cross-sections is 0.04 bits higher than the joint information related to three sections, and the loss in redundancy is 4.36 bits, as shown in Fig. 3. Figure 3 also shows that four sections provide as much information as five, but more than three. Because of this large difference in redundancy, the model was calibrated using three and four cross-sections and the results were compared in order to determine which was the optimal number.

The solution of the MOOP provided several sets of three and four cross-sections models. The model was calibrated considering these different sets and the MAE value was used as a discriminating factor for choosing the best combination of Manning’s coefficients. The Manning’s coefficients and MAE for each set of calibrated cross-sections are presented in Tables 2 and 3. All sets are characterized by a MAE value lower than 0.5 m, which is comparable with the expected accuracy of high water marks (Neal et al. 2009, Horritt et al. 2010, Brandimarte and Di Baldassarre 2012).

Table 2 River reach models built with all cross-sections (Po-88), three cross-sections given by S90 (Po-3) and by the MOOP solutions (Po3-Entropy1, ~2) and their corresponding MAE values, Manning’s coefficients for the channel (n_ch) and of the floodplain (n_f). The values for Po-88 are included for the sake of comparison.

Model	nch	nf	MAE
Po-88	0.045	0.050	0.202
Po-3	0.050	0.050	0.315
Po3-Entropy1	0.045	0.050	0.177
Po3-Entropy2	0.045	0.050	0.222

5.2 Cross-section spacing following S90 and C09

The optimum spacing among river cross-sections was evaluated using equations (5) and (6) from the S90 guidelines. The two equations were solved using parameter values reported in Table 1. As far as the bankfull depth of flow (D) is concerned, its variation range is 11.56–21.82 m with an average value of 14.00 m; the range of the Froude number (F) is 0.04–0.18 with an average value of 0.12; finally, the range of the flood wave celerity (c) is 0.65–4.41 m s^-1 with an average of 2.46 m s^-1. The resulting number of cross-sections n₂ and n₃ are computed by dividing the total length of the reach by the spacing Δx₂ and Δx₃ found applying equations (5) and (6), respectively. Table 1 shows that when one uses equation (6) (i.e. the relation to be used in the case of unsteady flow analysis) the mutual spacing among cross-sections (i.e. Δx₃) assumes high values. The consequent number of cross-sections is very low: 2 and 1 considering average and maximum parameters values, respectively. These results are not reliable for this test site. Therefore, the optimal spacing has been evaluated through equation (5), valid for steady flow conditions. This is consistent with the findings of the works by Brandimarte and Di Baldassarre (2012) and Di Baldassarre et al. (2009c), in which the performances of the steady and unsteady models were comparable in the same reach of the Po River. Considering the values of the parameters in Table 1, the application of equation (5) determines a maximum spacing (i.e. Δx₂) of 30 km and an average of 20 km. Dividing the spacing for the total length of the river reach, the number of optimal cross-sections is 3 and 4, respectively. Therefore, two different models, named Po-3 and Po-4, were built, adding the first and the last cross-sections, according to S90. These models were calibrated by varying Manning’s coefficients and the MAE was evaluated. In Tables 2 and 3 simulations with the lowest MAE and the corresponding combination of Manning’s coefficients are presented, reporting the cases of the model built with three and four cross-sections, respectively.

Considering three cross-sections, the simulation with the lowest MAE value corresponds to Manning’s n equal to 0.045 m^-1/3 s for the channel and 0.050 m^-1/3 s for the floodplain.

Considering four cross-sections, two simulations had the same minimum MAE: for both of these, n_ch was 0.040 m^-1/3 s while n_f is 0.09 m^-1/3 s for Po-4a and 0.10 m^-1/3 s for Po-4b, where n_f and n_ch represent the floodplain and the channel roughness, respectively.

It is interesting to note that using equation (7) with d = 2 (stage in cm), p = 6, s ≈ 10^-3 and ε_s ≈ 10^-3, as reported in Castellarin et al. (2009), Δx₄ > 100 m. This represents a lower limit to the choice of the optimal spacing, which is in agreement with results of equations (5) and (6).

6 DISCUSSION

Besides the evaluation of MAE for model configurations based on reduced cross-section data sets, further information can be obtained by the analysis of the roughness coefficients that provide the best results for each configuration.

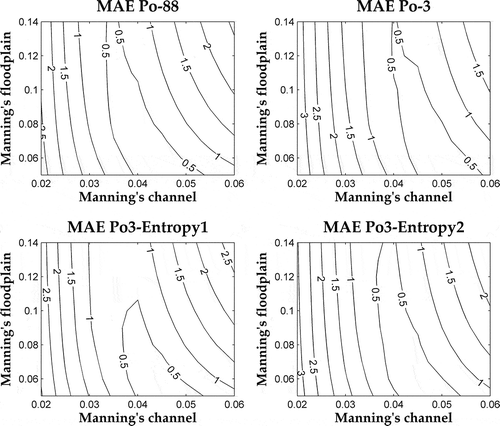
In Figs 4 and 5 the MAE contours are plotted for the Po-88 model configuration and for each chosen model with three and four cross-sections, respectively. The MAE contours of models built with three cross-sections are slightly shifted with respect to the contours of Po-88, as shown in Fig. 4. This shift is reflected in the Manning’s coefficients with the lowest MAE: the best Manning’s n_ch lies in the interval between 0.045 and 0.060 m^-1/3 s for Po-3, whereas it lies between 0.040 and 0.055 m^-1/3 s for Po-88, Po3-Entropy1 and ~2. However, this shift falls within the standard range of roughness values used for 1D modelling. Interestingly, the Po3-Entropy1 and ~2 models show the same contours as the Po-88 model: the minimum MAE value corresponds to the same combination of Manning’s coefficient values.

Fig. 4 MAE contours of the three models of the Po River built with three cross-sections and the values for the reference model with 88 cross-sections.

Similar considerations can be drawn comparing MAE contours of Po-88 and models built with four cross-sections (Fig. 5). The Po-4 results are shifted a bit, while for Po4-Entropy1 and ~2 the MAE value of 0.5 is limited to n_f equals 0.10 m^-1/3 s. The latter two contour plots confirm the similar performance of the two models, as shown in Table 3.

Fig. 5 MAE contours of the three models of the Po River built with four cross-sections and the values for the reference model with 88 cross-sections.

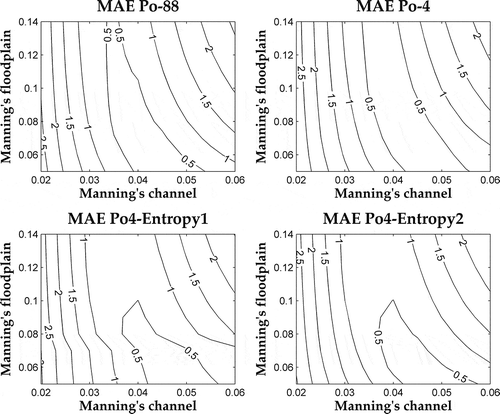
The model configurations obtained using the entropy approach show a better performance in terms of similarity with the Manning’s values of the original model, compared with Po-4a and ~4b, which are based on the S90 guidelines (Table 3). The Manning’s coefficient combinations yielded by Po-4a and ~4b (Table 3) are different to those of Po-88, although the MAE values of the former are low. As explained by Hunter et al. (2006), this is a typical example of parameters compensation: as the Manning’s value of the floodplain increases, the channel value decreases. This behaviour was also noticed by Brandimarte and Di Baldassarre (2012) for the same case study. A lower MAE value is presented only if the n_ch is lowered and balanced by an increased n_f. In spite of the fact that these two models show a lower MAE, their Manning’s values do not correspond to those of the redundant model.

Table 3 River reach models built with all cross-sections (Po-88), with four cross-sections given by S90 (Po-4a and ~b) and by the MOOP solutions (Po4-Entropy1, ~2) and their corresponding MAE values, Manning’s coefficients of the channel (n_ch) and of the floodplain (n_f). The values for Po-88 are included for the sake of comparison.

Model	nch	nf	MAE
Po-88	0.045	0.050	0.202
Po-4a	0.040	0.090	0.159
Po-4b	0.040	0.100	0.159
Po4-Entropy1	0.050	0.050	0.286
Po4-Entropy2	0.050	0.050	0.254

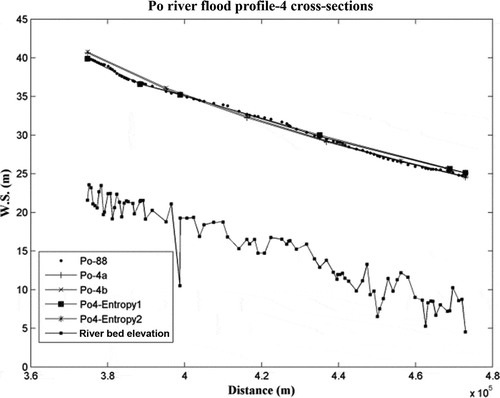
Despite the different number of cross-sections, flood profiles provided by sets of three and four cross-sections show a good fit to the profile of the original model (i.e. Po-88) (Figs 6 and 7). Concerning the accuracy of the flood profile at boundary conditions, the difference between the water stage values of Po3-Entropy1, ~2 and Po-88 is less than 0.20 m (Fig. 6). A difference lower than this threshold value is still acceptable: it represents the sensitivity of HEC-RAS, as explained at the end of Section 2.

Fig. 6 Po River flood profiles from different models, calibrated by minimizing the MAE: the models were built using S90 or the entropy approach (three cross-section sets), and are compared with the model using the entire data set of sections (Po-88).

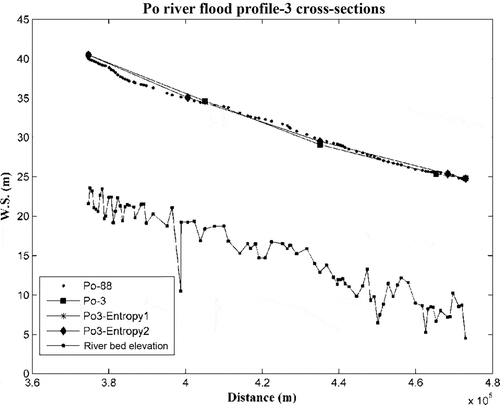
The accuracy of Po-3 at the upstream reach is lower: the difference is greater than 0.20 m, because of the difference in the Manning’s coefficient combination between this model and Po-88, as shown in Table 2.

As far as the models built with four cross-sections are concerned, the inaccuracy is located at the upstream reach for Po-4a and ~4b, while the error is less than 0.20 m and at the downstream reach for Po4-Entropy1 and ~2 (Fig. 7). For Po-4a and ~4b the difference is greater, because of the large difference between their best Manning’s coefficient combination and the Po-88 one (Table 3). The accuracy of the flood profile is due to the accuracy of HEC-RAS, to the different choice of roughness coefficient, but also to the fact that the downstream boundary generates an error that propagates upstream. For this reason, to increase model performance, the boundary condition should be placed far enough downstream. Thus, particular attention needs to be paid to the reach length and to the definition of the boundary conditions.

Fig. 7 Po River flood profiles from different models, calibrated by minimizing the MAE: the models were built using S90 or the entropy approach (four cross-section sets), and are compared with the model using the entire data set of sections (Po-88).

7 CONCLUSIONS

The entropy-based approach proposed in this work is founded on the evaluation of the information content of data sets of cross-sections applied within a 1D hydraulic model. The methodology aims at determining the optimum number and location of cross-sections needed to preserve an accurate description of the flow profile. The problem is posed as a MOOP, where the total correlation index and the joint entropy have been used as descriptors of redundancy and information content. Solving this problem, several optimal sets of cross-section locations are provided.

The proposed method has been applied to an existing data set of cross-sections for the Po River in Italy and compared to existing approaches based on hydraulic analyses (Samuels 1990, Castellarin et al. 2009). Results show that the four cross-section data sets selected through the proposed methodology can provide a description of the flow profile comparable to the one given by the original data set composed of 88 sections. These results were also consistent with those coming from literature approaches based on hydraulic analyses.

Therefore, the proposed methodology can be seen as complementing the guidelines proposed by Samuels (1990) and Castellarin et al. (2009). These can be used to design the first topographic survey of riverbed geometry, based on minimal topographic information of the river reach. Once a cross-section data set is available, the proposed methodology can be used to provide indications of the optimal spacing and location of cross-sections for each modelling application, by optimizing computational efficiency. As highlighted by Castellarin et al. (2009), it is important to point out that the results of the proposed method may be inappropriate for some specific applications, e.g. design of a new levee system or prediction of inundation extent. Nevertheless, for hydraulic issues, such as real-time flood forecasting, the proposed method can be extremely useful to determine the minimally redundant geometric description of the river and thus, improve computational efficiency.

A second important application of the entropy-based approach is the updating of existing data sets, by identifying the most valuable sections that should be updated more frequently to survey river bed changes. Optimizing the number of cross-sections is useful when it is necessary to update or extend river geometry surveys. Surveying only non-redundant cross-sections is more economically affordable than checking the whole data set; moreover, it would be possible to conduct field work more often, monitoring river changes over the time.

However, should significant river bed changes occur, the methodology would need the updated cross-sections to work correctly. In addition, the proposed approach can be applied, taking into account several constraints that determine the choice of cross-sections: the area, the river geometry, the presence of infrastructure and gauging stations, and the location of each cross-section itself.

If one or more sections cannot be deleted from the model, it is possible to insert a constraint into the code. A penalty will affect solutions that do not include these key sections into the optimal sets. This is the case of gauged sections providing data for model calibration, or bridge sections. On the other hand, it could be necessary to avoid that the chosen set of solutions comprehends some sections, for instance cross-sections difficult to be reached. As their monitoring is difficult and expensive, a penalty situation leads the genetic algorithm to prefer solutions that do not take into account these particular cross-sections.

Finally, the entropy methodology reported in this paper can also be applied in a 2D framework, for instance, for the optimization of a sensor network deployed in a river-floodplain system (Ridolfi et al., 2012). In particular, the method can assess the optimum amount of data necessary to build reliable flood maps while saving computational time and money in collecting data over the floodplain and the river channel.

Acknowledgements

The authors are grateful to the Interregional Agency for the Po River (Agenzia Interregionale per il Fiume Po, AIPO, Italy) and Po River Basin Authority (Autorità di Bacino del Fiume Po, Italy) for allowing access to their high-resolution DTM of the River Po and to data concerning the river. The authors would like to acknowledge Micah Mukolwe for his technical support. Ilias G. Pechlivanidis and Attilio Castellarin are also acknowledged for their valuable comments and suggestions in reviewing an earlier version of this paper.