How to discover modules in mind and brain: The curse of nonlinearity, and blessing of neuroimaging. A comment on Sternberg (2011)

Abstract

Sternberg (2011) elegantly formalizes how certain sets of hypotheses, specifically modularity and pure or composite measures, imply certain patterns of behavioural and neuroimaging data. Experimentalists are often interested in the converse, however: whether certain patterns of data distinguish certain hypotheses, specifically whether more than one module is involved. In this case, there is a striking reversal of the relative value of the data patterns that Sternberg considers. Foremost, the example of additive effects of two factors on one composite measure becomes noninformative for this converse question. Indeed, as soon as one allows for nonlinear measurement functions and nonlinear module processes, even a cross-over interaction between two factors is noninformative in this respect. Rather, one requires more than one measure, from which certain data patterns do provide strong evidence for multiple modules, assuming only that the measurement functions are monotonic. If two measures are not monotonically related to each other across the levels of one or more experimental factors, then one has evidence for more than one module (i.e., more than one nonmonotonic transform). Two special cases of this are illustrated here: a “reversed association” between two measures across three levels of a single factor, and Sternberg's example of selective effects of two factors on two measures. Fortunately, functional neuroimaging methods normally do provide multiple measures over space (e.g., functional magnetic resonance imaging, fMRI) and/or time (e.g., electroencephalography, EEG). Thus to the extent that brain modules imply mind modules (i.e., separate processors imply separate processes), the performance data offered by functional neuroimaging are likely to be more powerful in revealing modules than are the single behavioural measures (such as accuracy or reaction time, RT) traditionally considered in psychology.

Keywords:

• Cognitive neuroscience
• Cognitive psychology
• functional magnetic resonance imaging
• Electroencephalography
• Dissociations

1. INTRODUCTION: INFERENTIAL LOGIC

Sternberg's target article in this issue (Sternberg, 2011) illustrates the importance of formal analyses of the methodological approaches adopted in experimental psychology: formalization of ideas often held implicitly by most researchers, but rarely examined explicitly for their assumptions and limitations. Sternberg has continued this worthy enterprise ever since his pioneering work in the late 1960s (e.g., Sternberg, 1969, 2001), and his analyses are just as relevant, if not more relevant (as I argue below), to the more recent field of cognitive neuroscience, which tackles the mind–brain relationship “head-on”. For this pioneering work, Sternberg is to be congratulated, and the wider research community would do well to consider his arguments carefully. In this reply, I suggest a related, but alternative, perspective, at least for the specific question of inferring the number of modules from behavioural and neuroimaging data.

More specifically, while Sternberg's recent analysis (Sternberg, 2011) has focused on the implications of modularity for patterns of behavioural or neuroimaging data, I consider the converse case of what patterns of behavioural or neuroimaging data support modularity. Interestingly, this “inverse” perspective actually diminishes the value of some of Sternberg's principles, such as “additive factors”, and emphasizes the value of other principles, such as “selective effects” of factors, when applied to multiple measurements. This argument is formalized below, before three examples are given to illustrate what one might conclude about modules from certain patterns of behavioural and/or neuroimaging data, which are then discussed more generally in terms of modules in mind and brain.

1.1. Form of present argument

The inferential logic in Section 2.2 of Sternberg's paper is of the form (where → should be read as “implies”):

where H _i are hypotheses (related to the number of modules and the nature of their measurement, M) and p _i are properties of the data (e.g., significant experimental effects). It follows logically that (where ∼ should be read as “not”):

This is the classical “modus tollens”, or “denying the consequent”, argument: that failing to find that both p ₁ and p ₂ are true (ignoring for the moment the issues of null results in classical statistics; see Sternberg's Footnote 8) implies that at least one of the original hypotheses H _i is incorrect. However, a possible danger here is inappropriate “affirmation of the consequent”—that is, it does not follow logically that:

I am not suggesting that Sternberg ever made this logical error (he refers to this situation of confirming p ₁ and p ₂ as providing “support for joint hypotheses H _i ”). Nonetheless there is the danger that finding additive effects in the data of the type described by Sternberg is erroneously taken by others to imply modules. Thus in a nutshell, the gist of the present argument is that, while modules might imply additive factors, additive factors do not imply modules. I demonstrate this in the first example (Section 3.1) below.

Instead, I focus on the idea that, if there is only one module (H ₁), and measurements are monotonic functions of a module's output (H ₂), then certain properties of the data cannot be found—that is:

and therefore if those patterns are found (and assuming H ₂ is always true), then more than one module can be inferred—that is:

Before proceeding, it should be noted that the deductive “implications” in the above statements of propositional logic (Statements 1–3) are predicated on the terms (H _i , p _i ) being either true or false. The truth value of a property of data, p _i , however, is difficult if not impossible to ascertain, given that there are sources of measurement noise and fundamental measurement limits that generally make statements about data properties probabilistic rather than absolute (even if those probabilities satisfy conventional scientific levels of “significance”). With this in mind, for typical behavioural or neuroimaging data, Statement 3 should be read as “assuming monotonic measurement functions, certain patterns of data provide evidence against a single module account” (for further elaboration of deductive vs. abductive inference in science, see Coltheart, 2011).

2. TERMINOLOGY

I will adopt the same terminology as that of Sternberg (2011). In brief, let A and B be modules, F and G be experimental factors, and M _i (F,G) be a measurement function that maps the response of Modules A and B to F and G to the ith behavioural or neural dependent variable. One important aspect of the present argument is that M _i may not be linear in the levels of experimental factors (e.g., F, G); indeed, in the general case, it would seem unwise to assume that our measures are linearly related to underlying psychological processes. For example, many perceptual judgements (e.g., of “pitch”) are logarithmic functions of physical manipulations of a stimulus (e.g., frequency). Rather, the only assumption necessary in what follows is that M _i is monotonic.

Another important addition in the present argument is that Modules A and B perform nonlinear operations on their inputs, expressed by the functions a(F,G) and b(F,G) respectively—that is, M _i (F,G) = M _i (a(F,G),b(F,G)). The reason for this assumption becomes more apparent when considering interconnected neural processors later: However, in brief, there is little value in each processor within a system performing a linear operation, otherwise the same ultimate linear relationship between the system's inputs and outputs could be implemented in a single processor (since any linear combination of linear functions can be expressed as a single linear function; an argument also used to justify nonlinear activation functions within layers of an artificial neural network; e.g., Grossberg, 1988). If the mapping between the inputs to a module and its output (e.g., a), and between its output and the experimental measurement (M _i ), are both nonlinear and unknown, it may seem difficult to draw conclusions about modules from M _i alone; fortunately, the assumption that M _i is monotonic provides some leverage, as illustrated in the examples below.

3. THREE EXAMPLES

To illustrate the different perspective arising from making statements about modules from data, rather than testing predictions of modules with data, I consider three examples below. The first example (Section 3.1) is based on applying “additive factors” logic to two factors and a single behavioural measure, as formalized in Section 2.2 of Sternberg's (2011) article (when assuming a “summation” rule for the composite measure M _AB ). The purpose of this first example is to demonstrate the invalidity of Statement 2 above (i.e., to show how finding additive effects does not constitute strong evidence for multiple modules). This example also goes on to illustrate that the same problem applies to interactions, even cross-over interactions, between two factors on a single measurement.

The purpose of the second example (Section 3.2) is to illustrate the utility of Statement 3 above—namely, to argue that certain other, nonadditive patterns of data (with only a single factor but at least two different measurements) do provide strong evidence for multiple modules. This example also extends the argument to functional neuroimaging, which normally automatically provides multiple measurements (across different brain regions and/or different time points).

The third and final example (Section 3.3) reconsiders the case of two factors, but which now show selective effects on two independent measurements, a pattern that (providing one accepts the null hypothesis of no interaction) again provides strong evidence for multiple modules. This example also raises the difficult problem of applying the present argument to a network of modules, where the output of one module becomes the input of another (and where neural measurements may only be available on a subset of modules).

3.1. Two factors, one measurement: Insufficiency of additive factors

If we start with Sternberg's example of a single, composite measure, then my slightly modified version of his argument is as follows:

•	H 1: There are two modules, A and B, selectively affected by factors F and G respectively—that is, with processes a(F) and b(G).
•	H 2: The measurement M AB is a linear function of a and b—that is, M AB (F,G) = u · a(F) + v · b(G), where u and v are constants (and ignoring an overall intercept term).

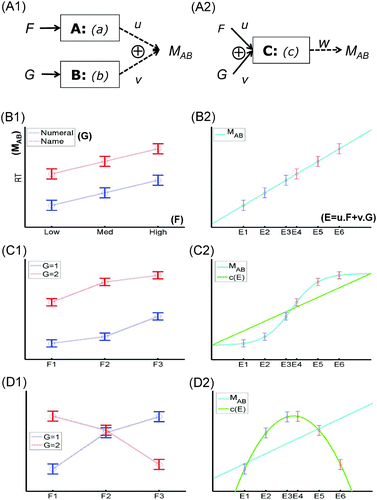
These hypotheses are illustrated schematically in Figure 1-A1. Now consider the case of a 3 × 2 design, where Factor F has three levels, and Factor G has two levels. An elegant example of such as design is the study of Pinel, Dehaene, Riviere, and LeBihan (2001) that Sternberg considers in his Section 6.3. In this first example, we consider just the behavioural data from that study—namely, the mean response times (M _AB ) to classify a probe number as greater or smaller than a target number, as a function of whether (a) the probe number is presented as a numeral or by its name (G), and (b) the absolute numerical difference between the probe and target, which was low, medium, or high (F). The results are shown schematically in Figure 1-B1, where F and G had additive effects on M _AB .

Figure 1. Two factors, one measurement: insufficiency of additive factors. Possible manner in which two experimental factors, F and G, could affect single measurement (M _AB ) of two modules, A and B (Panel A1), or of a single module, C (Panel A2). The functions a, b, and c describe processes performed by modules; u, v, and w are measurement functions (or constants that control linear measurement functions in the discussion of Sternberg's, 2011, additive factors in the text). Example data when F (with three levels) and G (with two levels) have additive effects (Panel B1), and how these data are explained by linear measurement of the single module C, whose output, c(E), is a linear function of E, itself a linear combination of F and G (Panel B2; see text). Example data when F and G interact (Panel C1), and how these data are explained by nonlinear (but monotonic) measurement of a single module whose output is a linear function of F and G (Panel C2). Example data when F and G show a cross-over interaction (Panel D1), and how these data are explained by linear measurement of a single module, whose output is a nonlinear function of F and G (Panel D2). None of these data patterns therefore constitute evidence against a single module account (according to present framework).

Using Sternberg's notation, the properties of the data associated with “additive factors” in this example are (where F ₁ and F ₂ refer to first and second level of F, etc.):

In a factorial analysis, this pattern entails (at a minimum) significant main effects of F and G, with no evidence for an interaction. In other words, the pattern reflects no differences among the simple main effects of the first factor over the different levels of the second.

Now simple algebra (in terms of u and v) shows that, provided the operations of the modules, a(F) and b(G), are linear, the assumption of linear measurement (H ₂) means that:

In other words, finding additive effects would be consistent with Sternberg's “separately modifiable” modules, A and B. However, finding additive effects can also be consistent with a single module. To appreciate this, consider a single module, C, whose operation depends on both F and G, as in Figure 1-A2. In the general case, the module's output, c(F,G), can be nonlinear, and the measurement of that output, M _AB  = w(c(F,G)), is assumed only to be monotonic. But to make the present point, we can assume that both of these functions are linear—that is, that c(F,G) = u · F + v · G, and M _AB  = w · c(F,G) (ignoring intercepts, and where u,v,w are now constants)—and still reproduce the pattern of additive factors. To see this, define a new, unidimensional (latent) variable, E = u · F + v · G, onto which the factors F and G map, and on which the functionality of C solely depends, and assume that the output c(E) is measured proportionally by M _AB . This is shown in Figure 1-B2, which is simply a replotting of the data in Figure 1-B1.1 In other words, the fact that we do not know how experimental factors F and G map onto the psychological dimension over which C operates means that additive factors on a single dependent variable do not constitute evidence for more than one module.

3.1.1. Insufficiency of other interaction patterns

Though the insufficiency of finding additive effects on a single composite measure is the main message of this example, it is instructive to consider other patterns of data. For example, what if there is an interaction between F and G, of the form shown in Figure 1-C1: Does this provide strong support for two modules? The answer is no, because even if the operation of module C, c(E), in Figure 1–A2 is linear (green line in Figure 1–C2), a nonlinear but monotonic (e.g., sigmoidal) measurement function, w(c(E)), for M _AB (cyan line in Figure 1–C2) can still explain the data (as could the converse case of a sigmoidal module process, c, and a linear measurement function, w).

Or what if there is a cross-over interaction between F and G, of the form shown in Figure 1-D1: Does this provide strong support for two modules? The answer is again no. Unlike Figure 1-C, these data cannot be explained by a linear module and a nonlinear but monotonic measurement function. However, assuming that modules should perform nonlinear operations on their input (as argued in Section 2 above), a cross-over interaction can be explained by a nonlinear function c(E) (green line in Figure 1-D2), even if the measurement function, w, is linear (cyan line in Figure 1-D2). Thus, while I have argued that nonlinearity is an important property of modules, the reason that I refer to it as a “curse” in the title of this article is that it makes the task of inferring modules even more challenging.

Fortunately, there are more compelling ways to question a single module account within the present framework, provided one takes more than one measurement of each experimental condition. The reason for this is expanded below, but in short, because the form of c is invariant over any measurement, then assuming that each measurement is monotonic in the output of c, certain patterns of data across multiple measurements cannot be explained even if c is nonlinear and unknown.

3.2. One factor, two measurements: Reversed associations

Now consider the case of one experimental factor, F, with three levels, and two measurements, M _A and M _B (note that the labels M _A and M _B are not meant to imply pure measures of A and B, as will be seen below, but are used for consistency with Sternberg's article). The question then concerns what pattern of data would constitute evidence for two modules (Figure 2-A1) rather than one single module (Figure 2-A2).

Figure 2. One factor, two measurements: reversed associations. Possible manner in which one experimental factor, F, could affect two independent measurements (M _A and M _B ) of two modules A and B (Panel A1), or a single module C (Panel A2). Example data when F (with three levels) has opposite effects of M _A and M _B (Panel B1), which can be explained by two modules (even with linear measurement functions u and v), but can also be explained by different, (non)linear but monotonic measurement functions, w and x, of the single module C (Panel B2). Example data that comprise a reversed association (Panel C1), which monotonic functions M _A and M _B cannot explain, given only a single module, even if that module implements a nonlinear function of F, c(F) (Panel C2; the cross by the label for M _B indicates that this measurement function has to be nonmonotonic in order to fit the data, violating the present assumptions). This data pattern therefore does constitute evidence against a single module account (see text).

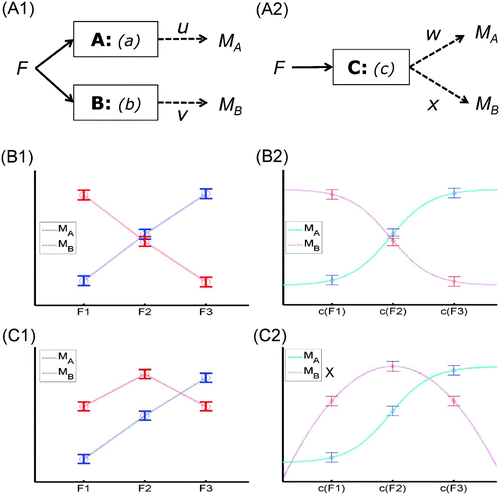
Let us start by considering the cross-over interaction in Section 3.1.1 above (Figure 1-D1), but where the two lines in Figure 2-B1 now refer to two measurements, rather than two levels of an orthogonal experimental factor. This pattern is not evidence against a single module explanation, because M _A and M _B could both be monotonic functions: one monotonic increasing (w, for M _A ) and one monotonic decreasing (x, for M _B ), as shown in Figure 2-B2.

Consider, however, the pattern shown in Figure 2–C1. This pattern is called a “reversed association” (Dunn & Kirsner, 1988), because it involves an association (positive correlation between effects of F ₂ versus F ₁ on both M _A and M _B ) that is reversed at other levels of F (a cross-over interaction between F ₃ versus F ₂ on M _A and M _B ). More precisely, it consists of:

As Dunn and Kirsner originally observed, this pattern questions a single underlying psychological process (module). Given that the mapping from F to the outputs c(F) of a single module C must be invariant across all measurements, there is no single way to remap the relative values of c(F ₁), c(F ₂), and c(F ₃) (even if c is nonlinear) and simultaneously fit the reversed association when assuming monotonic measurement functions (e.g., function x for M _B in Figure 2-C2 would need to be nonmonotonic in this case, violating our hypothesis H ₂, as indicated by the cross by its legend). In other words, a reversed association suggests that the modules respond in a qualitatively different manner to the levels of a factor, in that the relative order of effect sizes across levels produced by one module, a(F), does not match the relative order across levels produced by another module, b(F).

3.2.1. Processors and neuroimaging data

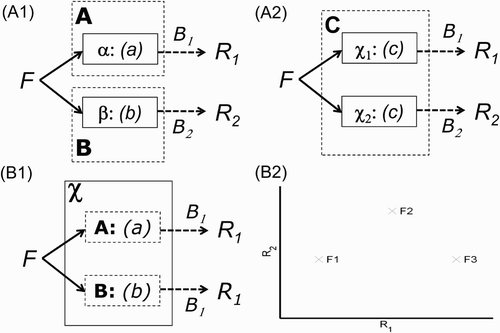
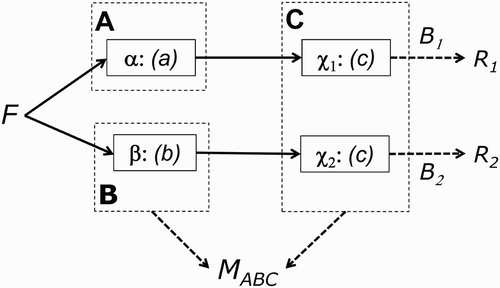
This is a suitable juncture to extend the present argument to brain modules and functional neuroimaging data. As Sternberg (2011) observes, it is important to distinguish psychological processes from the neural implementation of those processes (the “processors”). This is illustrated in Figure 3: Two modules A and B might be implemented by two separate processors, α and β (Figure 3-A1), or two modules A and B might be implemented within the same processor χ (Figure 3-B1), or the same module C might be implemented by two separate processors, χ₁ and χ₂ (Figure 3-A2). Furthermore, as Sternberg also notes: “The existence of functionally specialized processors (either localized or distributed) is a sufficient condition but not necessary one for functionally distinct processes … ” (Sternberg, 2011, Section 1). In other words, there is an asymmetry in the relationship between processors and processes: Modular processes need not imply modular processors, but there would seem little point in evolving modular processors unless they implemented modular processes (see also Shallice, 1988, for a similar argument about the relationship between double dissociations and isolable subsystems, and present Discussion for further consideration of modules in mind and brain).

Figure 3. Possible neural implementations of Modules A, B, and C. Greek letters α, β, χ₁, and χ₂ refer to distinct neural components (processors). Two modules implemented by two separate processors (Panel A1); the same module implemented by two separate processors (Panel A2); two modules implemented within the same processor (Panel B1). In the example of functional magnetic resonance imaging (fMRI) data in the text, B ₁ and B ₂ refer to the neural-to-BOLD (BOLD = blood-oxygen-level-dependent) mappings (monotonic measurement functions) for spatially resolvable brain regions R ₁ and R ₂. Panel B2 is a replotting of the reversed association data in Figure 2-C1, but now as BOLD signal in one region against that in another; the fact that these data points do not fall on a monotonic function again suggests that a single module (Panel A2)—that is, the same process that happens to be implemented across multiple processors—is unlikely.

For existing, noninvasive human neuroimaging techniques, the measurements (M) are now some signal integrated over many neurons within a brain region. This neural activity is also either integrated over time, as in haemodynamic techniques like functional magnetic resonance imaging (fMRI), or integrated over multiple brain regions, as in extracranial electrophysiological techniques like electro- and magnetoencephalography (E/MEG). For the present argument, we stick with fMRI, where the measurements are now labelled R ₁ and R ₂ to represent the fMRI signal from two brain regions (corresponding to processors α and β, or χ₁ and χ₂). However, the same basic argument can be extended to E/MEG measurements at different time points (or even electrophysiological signals occurring at the same time but believed to derive from different brain regions following source reconstruction of E/MEG data; Baillet, Mosher, & Leahy, 2001). Given the complex biophysical processes that govern, for example, the blood-oxygenation-level-dependent (BOLD) signal that is normally measured by fMRI, it would seem even more judicious to make minimal assumptions about how neuroimaging measurements relate to hypothetical psychological processes—that is, assume only that the measurement functions B ₁ and B ₂ in Figure 3 are monotonic.2 Nonetheless, the reason that I refer to neuroimaging as a “blessing” in the title of this article is that it normally automatically provides multiple, simultaneous measurements of brain activity.

Thus, according to the argument in Section 3.1 above, the finding of additive effects of two factors on the BOLD signal within a single region (such as the “parahippocampal place area” of the Epstein, Parker, & Feiler, 2008, study considered in Section 6.5 of Sternberg's, 2011, article) would not constitute evidence for multiple modules. Rather, one must find certain patterns, such as the reversed association described in Section 3.2, in the BOLD signal across two or more regions. This application of “reversed association logic” to neuroimaging data was originally outlined in Henson (2005), together with further examples of how one might use neuroimaging data from two or more brain regions to distinguish between competing psychological theories (and for a concrete example in the context of testing single- versus dual-process theories of recognition memory, see Henson, 2006a).

Note that another way of depicting the reversed association in Figure 2-C1 is to plot the two measurements directly against each other: If the data points fall on a monotonic function, then they can be explained by a single psychological process (dimension). This is the basis of “state-trace” analysis, of which the reversed association is a special case (Newell & Dunn, 2008). The analogous proposal here is that if neural measurements for two brain regions, R ₁ and R ₂, do not fall on a monotonic function (as in Figure 3-B2), then those two regions are unlikely to be implementing the same module. In other words, the pattern of neuroimaging data in Figure 3-B2 questions the scenario depicted in Figure 3-A2 and supports the scenario depicted in Figure 3-A1.3

3.3. Two factors, two measures: Selective effects on neuroimaging data

Despite their potential inferential power, few neuroimaging studies have produced a clear reversed association across three or more conditions and two or more brain regions, at least when those brain regions are defined independently (Henson, 2006a; though see Weber & Huettel, 2008, for one example). This is a shame, because reversed associations can be defined simply by four significant pairwise effects in the data (corresponding to data patterns p ₁ and p ₂ in Section 3.2 above), unlike the general case of “state-trace” analysis, for which statistical methods for quantifying deviations from monotonicity are yet to be fully established (Newell & Dunn, 2008). On the other hand, if one is prepared to accept the null hypothesis of no effect in the data, there are other patterns of data that also question a single module account.4 Here the combination of two or more factors that show selective effects on two or more independent measurements (related to Sternberg's Section 6.4) become informative, as illustrated below.

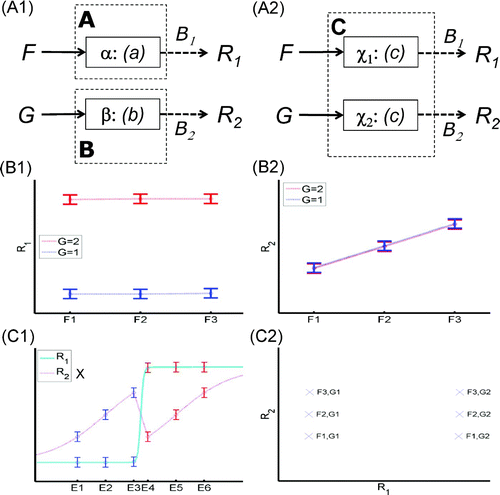
Consider an fMRI study with two experimental factors, F with three levels and G with two levels, and data from two regions of interest, R ₁ and R ₂. The desire is to distinguish the multiple modules (and multiple processors) from the single module (implemented by multiple processors) depicted in Figures 4-A1 and 4-A2, respectively. Now if one finds a main effect of Factor G but no effect of Factor F in region R ₁ (Figure 4-B1), plus a main effect of Factor F but no effect of Factor G in region R ₂ (Figure 4-B2), then one can question the single module in Figure 4-A2. (This was actually the general pattern and claim made from the fMRI data of the Pinel et al., 2001, study described in Section 3.1 above.) This is because again, there is no way that a single nonlinear function within Module C can simultaneous fit the data from two monotonic measurement functions, even if that same function c(F,G) happens to be implemented in two different brain regions, χ₁ and χ₂, on which the two independent measurement functions operate (to produce R ₁ and R ₂). This is illustrated in Figures 4-C1 and 4-C2. In Figure 4-C1, a linear mapping of F and G to E ₁–E ₆, over which c(E) operates, in conjunction with a sharp, sigmoidal measurement function R ₁ (cyan line), can fit the main effect of Factor G on R ₁, but cannot simultaneously fit the main effect of Factor F on R ₂, whatever the measurement function (i.e., the magenta dotted line requires a different relative ordering of E ₁–E ₆ in order to fit the data and remain monotonic, as indicated by the cross by its legend). In Figure 4-C2, this is demonstrated by the fact that the six data points from plotting R ₁ against R ₂ do not fall on a monotonically increasing or decreasing function (Newell & Dunn, 2008). Thus, while I agree with Sternberg that the combination of factorial experimental designs and neuroimaging techniques offers a powerful way to find evidence of “separately modifiable” processors, which in turn provides evidence for multiple modules, I would emphasize different aspects of the data, particularly the value of having multiple measurements across brain regions.

Figure 4. Two factors, two measurements: selective effects on two brain regions. Two modules implemented by two separate processors (Panel A1); the same module implemented by two separate processors (Panel A2). Example neuroimaging data where measurement R ₁ of one region shows a main effect of Factor G but not Factor F (Panel B1), and measurement R ₂ of a different region shows a main effect of F but not G (Panel B2). These data (accepting null hypotheses of no effects) are evidence against a single module C—that is, a single nonlinear function c(F,G) = c(E), where E is a linear function of F and G—even with different neural-to-BOLD (BOLD = blood-oxygen-level-dependent) mappings (measurements) in the two regions (Panel C1; the cross by the label for R ₂ indicates that this measurement function has to be nonmonotonic in order to fit the data, violating the present assumptions). This is again illustrated by fact that a plot of BOLD signal in two regions against one another (Panel C2) cannot be fitted by a monotonic function (see text).

3.3.1. Networks of processors

Once one begins to consider seriously the operation of a complex system like the brain, in which a number of modules are assumed to interact with one another, the inferences one can make from neuroimaging (or behavioural) data become less specific, however. To see this, consider the toy network shown in Figure 5. Here there are three modules, implemented across four processors, where Module C is implemented in two separate processors, χ₁ and χ₂, and where the inputs to C are the outputs of A and B. According to the argument in Section 3.2 above, a reversed association across three levels of a factor F and the two measurements R ₁ and R ₂ of χ₁ and χ₂ would question the existence of a single module C. However, the perturbations to the system induced by manipulating the levels of F may not impinge directly on module C (as was assumed in the examples above), but only indirectly via two earlier modules, A and B. For example, the levels of F could correspond to different levels of visual contrast, and the processors α and β could correspond to brain regions early in the visual processing pathway, while processors χ₁ and χ₂ could correspond to “higher order” brain regions further along that pathway, related, for example, to perceptual decisions (e.g., in prefrontal cortex).

Figure 5. Example network of modules, where different inputs to Module C, by virtue of different “upstream” modules A and B, mean that a reversed association between Factor F and measurements of two regions R ₁ and R ₂ (or any other discriminative data pattern considered in Figures 3–4) does not constitute evidence that regions χ₁ and χ₂ implement distinct modules, only that at least two different modules exist somewhere within the network including, or upstream of, χ₁ and χ₂ (see text). Note that the arrows between α and χ₁, and between β and χ₂, refer to the direction of causal influence (but not to a specific form of temporal interaction, e.g., staged or cascaded)—that is, a feedforward architecture here. In the alternative case of bidirectional arrows—that is, a fully interactive architecture where the outputs of Process c could also affect the outputs of Processes a and b—the same reversed association across measurements R ₁ and R ₂ would only constitute evidence of more than one module somewhere in the network (i.e., could arise from any two processors whose influence could be traced directly or indirectly to χ₁ and χ₂; see text).

In this case, because A and B are able to implement different, nonlinear operations on their input (the levels of F), and because their resulting outputs form separate inputs to χ₁ and χ₂, respectively, a reversed association on measurements R ₁ and R ₂ of χ₁ and χ₂ is no longer evidence against a single module C—that is, χ₁ and χ₂ may implement the same function, c, but the relative values of the input to χ₁ and χ₂ may differ by virtue of different prior nonlinear operations a(F) and b(F), respectively, causing a reversed association. For example, a(F) may be a linear function that maintains the relative order of F ₁ <F ₂ < F ₃, while b(F) may be a nonlinear function, like that in Figure 1-D2, which reorders the relative levels of F to F ₁ < F ₂ > F ₃, thereby jointly allowing C to produce a reversed association of the type shown in Figure 3-B2. This ambiguity can be resolved by simultaneous consideration of neuroimaging data from processors α and β (e.g., R ₃ and R ₄, not shown in Figure 5), but it is possible that such data might simply not be available for these processors for some reason (e.g., because of types of neural activity that are undetectable by fMRI). In this case, the specificity of the inference drawn from the reversed association on measurements R ₁ and R ₂, given the network depicted in Figure 5, is reduced to the claim that there are at least two different modules either within χ₁ and χ₂, or upstream of those processors. The same limitations would seem to apply to neuroimaging dissociations over time, as in the EEG examples considered in Sternberg's Section 3.1: Selective effects of factors on different poststimulus time windows would allow one to claim only that “separately modifiable” processes occur at some time prior to, or including, the measured time windows. Relating such neuroimaging data to simultaneous behavioural data also becomes a challenge, given that a behavioural measurement, M _ABC (e.g., accuracy), will be influenced by more than one module (e.g., a motor region driving that behavioural response, not shown in Figure 5, might “read out” the activity of both β and χ₂, i.e., depend directly on both B and C, and indirectly on A).

However, even the above restriction of inferring modules to “within or upstream of χ₁ and χ₂” is predicated on unidirectional communication from α to χ₁, and from β to χ₂—that is, a “feedforward” architecture. In the alternative case of a fully interactive architecture (i.e., bidirectional arrows between modules in Figure 5), where the outputs of Process c could also affect the outputs of Processes a and b, the same reversed association between the levels of F and measurements R ₁ and R ₂ would only constitute evidence of more than one module somewhere in the network as a whole (i.e., the reversed association could arise from any two processors whose influence could be traced directly or indirectly to χ₁ and χ₂). Indeed, in this highly interactive case, even knowing the BOLD signal in all the relevant processors will not help localize the multiple modules. While one might think that evidence for more than one module (nonlinear process) somewhere in the brain is not particularly informative, it should be remembered that one still has evidence for more than one module that is sensitive specifically to the experimental manipulation (F), which can still be theoretically important. More generally, this challenge of localizing modules within highly interactive systems probably requires testing multiple explicit, network models (e.g., structural equation modelling; see below).

4. DISCUSSION: MODULES IN BRAIN AND MIND

The present methodological argument continues a line of thinking introduced by Henson (2005), where it was called “function-to-structure deduction”, as one of two types of inference about psychological processes that one might make from neuroimaging data. The critical pattern of a reversed association across three experimental conditions and two brain regions was later spelled out in more detail by Henson (2006a), where it was called an example of “forward inference” (in contrast to the “reverse inference” coined by Poldrack, 2006). Here, the same basic argument is formalized more explicitly, using the terminology introduced by Sternberg (2011), and extended to data patterns beyond a reversed association (e.g., the selective effects of two factors described in Section 3.3 above). It has been explained how this perspective questions what Sternberg would conclude from additive effects on a single behavioural measure (e.g., the RT data of Pinel et al., 2001, considered in Sternberg's Section 6.3), or from additive effects on a single neural measure (e.g., the fMRI data from the parahippocampal place area of Epstein et al., 2008, considered in Sternberg's Section 6.5), but concurs with what Sternberg would conclude from selective effects on multiple neural measures (e.g., the fMRI data of Pinel et al., 2001, considered in Sternberg's Section 6.3).

More theoretical issues—for example, of what defines a module—have deliberately been avoided (though see Henson, 2006b, for some thoughts along these more philosophical lines, e.g., in terms of “locality” and “directionality”). Indeed, in many of these issues, I am in agreement with Sternberg. Thus I also accept the computational/evolutionary argument for the existence of modules (exemplified by the elegant quote of Marr's given in Footnote 2 of Sternberg's article in this issue) and do not use the word “module” in the strict Fodorian sense (Fodor, 1983).5 Rather, I use it in the same, simpler sense of Sternberg—that is, of being “separately modifiable”, analogous to Shallice's definition of “isolable subsystems” (Shallice, 1988). In this sense, modularity really describes a methodological approach, rather than purely theoretical enterprise—that is, the proposal that a complex system may be “decomposed” into its constituent parts (before those parts can be reassembled in a model of the system), an approach that has dominated biology (Bechtel, 2003).

Do dissociable processors imply separate processes (modules)? Page (2006) gives an example that questions the inference of multiple psychological processes from a reversed association in neuroimaging data: Imagine that one measured neural activity at distinct locations along a topologically organized part of cortex, where neurons show nonlinear (e.g., Gaussian) tuning curves as a function of a factor F (e.g., tone frequency). Comparison of three levels of F (e.g., three frequencies) might then produce a reversed association across two locations within that topographic map (see Henson, 2005, and Page, 2006, for further explanation). Does this imply two modules operating at those two locations? Well the answer depends on the level of theoretical description. At the level of those two processors (implementing nonlinear functions of their input), one would have to argue that they implement different processes—that is, are tuned to detect different frequencies. At the level of part of cortex as a whole, one could describe it as one module, whose function is to code the frequency of auditory input. This issue of multiple levels of description is discussed at greater length by Henson (2005).

Inferring the existence of more than one module is of course not the end goal of cognitive (neuro)scientists. The present criteria for inferring multiple modules do not proscribe the precise processes performed by each. The same scientists normally want to go further and describe the precise operation of those modules (e.g., the nature of processes a,b,c in examples above). This is generally achieved by hypothesizing further factors that affect those modules and testing these hypotheses in new experiments (see Henson, 2006a, for an example in the context of theories of recognition memory). Indeed, these hypothesize–test–hypothesize iterations appear a good description of most empirical sciences. This is the counterargument to the claim that one can always find dissociable data patterns (whatever the precise definition of “dissociable”), in the sense that if a participant can tell you the difference between two stimuli/tasks/contexts, then there must be a difference somewhere in their brain: It is the nature of that difference that is vital. So, for example, I was once asked whether, if one found different patterns of fMRI activity for pictures of Chinese versus Japanese food, would one infer separate modules for these two types of cuisine? Well, one might infer that (assuming that the fMRI data met the criteria for multiple modules in Section 3), but one would not stop there, but rather propose further experiments (experimental manipulations) that attempt to distinguish the “national cuisine” hypothesis from alternative hypotheses related to, for example, differences in the form or colour of the pictures of the foodstuffs (e.g., by using verbal labels instead), or gustatory differences normally experienced in the sugar/salt content of those foodstuffs, and so on.

A practical point that emerges from the above considerations is the importance of multifactorial, parametric designs for neuroimaging experiments: multiple factors in order to find selective effects of the type described in Section 3.3 above, and parametric in order to provide at least some insight into the nature of the psychological–neural (or “neurometric”) mapping (e.g., possibility of a linear mapping). This is, of course, advice that Sternberg has long given for behavioural experiments, though he states that “factorial experiments are relatively rare in studies of brain activation” (Sternberg, 2011, Section 2.3). While it is true that in practice most early neuroimaging studies focused on categorical, subtraction designs—where a handful of conditions are compared that are assumed to differ qualitatively in their component processes (often entailing different tasks), rather than conforming to parametrically related factors—the theoretical importance of factorial, parametric designs for neuroimaging has, in fact, been appreciated for many years (e.g., Friston et al., 1996; see also Friston & Price, 2011).

I should also note that much of Sternberg's article in this issue (Sternberg, 2011) concerns the use of additive factors on time-resolved measurements like reaction times (RTs) and event-related potentials (ERPs), in order to infer serial or parallel processing “stages” (e.g., Sternberg's Sections 3 and 4). This has perhaps been the most influential application of Sternberg's work since his seminal 1969 paper (Sternberg, 1969). I have not considered such temporal issues here. Rather, my focus has been on the basic process decomposition approach (outlined in Sternberg's Section 2) and its application to “stationary” data like behavioural accuracy or fMRI data (as in Sternberg's Section 6). Nonetheless, I do believe that an important future goal for neuroscientific methodological consideration will be to establish the types of inference one can make, if any, about staged versus cascaded, and/or independent versus interactive, processing of modules (Coltheart, 2011). Given what we know about the highly connected and complex dynamics of the brain's physiology, I suspect such direct inferences will be limited, and instead we will need to rely on indirect inferences based on formal model comparison of a range of explicit, dynamic, network models, which differ in the sets of connections, “forward” and/or “backward”, that are affected by an experimental manipulation (e.g., Stephan et al., 2007).

Finally, while I have argued for certain patterns of data being necessary to provide evidence for modules, I accept that scientists in practice normally consider a continuum of evidence, with some data patterns simply being more compelling than others (Henson, 2005). Nonetheless, the formalization of the assumptions and limitations associated with each type of evidence, as exemplified by Sternberg's continued endeavours, are vital for determining the relative value of that evidence for the precise inference intended.

Acknowledgments

This work is funded by the UK Medical Research Council (MC_US_A060_0046). The author thanks John Dunn, Niko Kriegeskorte, and the three reviewers for their helpful comments.

Notes

¹Note that this still holds, even if the data points for different levels of F and G (i.e., red and blue points in Figure 1-B1) overlap; in other words, the fact that M _AB (F ₁ ,G ₃) < M _AB (F ₂ ,G ₁) in these examples is just to aid visualization.

²The measurement function B in Figure 3 subsumes both of Sternberg's (2011) mappings from an experimental factor F to the neural activity within a processor (akin to N in Section 7.2 of Sternberg's article) and from neural activity within a processor to the BOLD signal measured by fMRI (Sternberg's B). The distinction between these mappings is not important for the present argument, but would become important if relating fMRI data to more direct neurophysiological measures. In other words, a 10% change in a parametric factor F—that is, (F ₂ – F ₁)/F ₁ = 0.1 (e.g., visual contrast) may or may not result in a 10% increase in neuronal firing rate (or local field potentials), which in turn may or may not result in a 10% increase in BOLD. Though Sternberg notes that the latter linearity has been observed under some conditions (e.g., Rees, Friston, & Koch, 2000), other (monotonic) nonlinearities, particularly in the mapping from blood flow to BOLD, have also been demonstrated (Friston, Mechelli, Turner, & Price, 2000). More generally, however (e.g., in the example of networks of processors in Figure 5), it might be prudent to introduce additional mappings from experimental factors (or psychological variables) to neural activity (e.g., that form the input to the “sensory” processors in a network) and possibly from the neural activity output from one processor to the input to another (reflecting effective connectivity between processors).

³The scenario depicted in Figure 3-B1 is not relevant because it only entails one brain measurement (R ₁), but serves to remind us that this measurement may itself be the product of multiple modules. This may be either because the spatial resolution of the neuroimaging technique is not sufficient to distinguish activity of different processors, or even because the same processor might implement different processes, dependent, for example, on control signals from other processors (i.e., networks of connected brain regions; see Section 3.3.1).

⁴The issue of null effects in classical statistics is discussed by Sternberg in his Footnote 8. While not in total agreement, I am happy to confer them with the same evidential value for the purpose of the present argument. More generally, Bayesian approaches would seem more suitable, in which one can assign a probability to an effect being within a certain range of zero (particularly “empirical Bayesian” approaches, in which the prior can be defined by the data themselves, provided there is an implicit hierarchical model; see Friston et al., 2002, for an example application in fMRI analysis).

⁵Nonetheless, a potentially important additional criterion I have proposed here for a module is that it implement a nonlinear function of its input (for the reasons given in Section 2). Whether this criterion is strictly necessary might be a topic for future discussion.