Sequential activation of multiple grounding pads reduces skin heating during radiofrequency tumor ablation

Abstract

Purpose: Radiofrequency (RF) tumor ablation has become an accepted treatment modality for tumors not amenable to surgery. Skin burns due to ground pad heating may become a limiting factor for further increase in ablation zone dimensions and generator power. We investigated a method were groups of ground pads are sequentially activated to reduce skin heating.

Methods: We compared conventional operation (i.e. simultaneous connection of all pads) to sequentially switched activation of the pads where different pad combinations are active for periods of ∼0.3 - 8 s. The timing during sequential activation was adjusted to keep the leading edge temperature equal between the pads. We created Finite Element Method computer models of three pads (5 × 5 cm, 1 cm apart) placed in line with the RF electrode on a human thigh to determine differences in tissue heating during simultaneous and sequential ground pad activation. We performed experiments with three ground pads (5 × 10 cm, 4 cm apart) placed on a tissue phantom (1.5 A, 12 min) and measured pad surface and leading edge temperatures.

Results: Temperature rise below the leading edge for proximal, middle and distal ground pad in relation to active electrode location was 5.9°C ± 0.1°C, 0.8°C ± 0.1°C and 0.3°C ± 0.1°C for conventional operation, and 3.3°C ± 0.1°C, 3.4°C ± 0.2°C and 3.4°C ± 0.2°C for sequentially activated operation in the experiments (p < 0.001).

Conclusion: Sequential activation of multiple ground pads resulted in reduced maximum tissue temperature. This may reduce the incidence of ground pad burns and may allow higher power RF generators.

• Thermal ablation
• radiofrequency/microwave
• modeling
• heat transfer
• EM

Introduction

Radio-frequency (RF) ablation is increasingly utilized as a minimally invasive treatment for primary and metastatic liver tumors, as well as tumors in kidney, lung, bone and adrenal gland in cases where surgery is not possible [1–6]. In RF ablation, RF current is delivered to the tissue via electrodes inserted percutaneously (i.e. through a small incision in the skin), laparoscopically or during open surgery. Tumor cell death results from the conversion of electromagnetic energy to heat by ionic agitation. Temperatures above ∼50°C for ∼2–5 min cause denaturation of intracellular proteins and destruction of membranes of tumor cells, eventually resulting in cell necrosis.

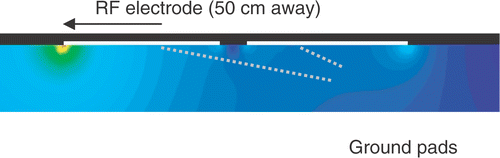
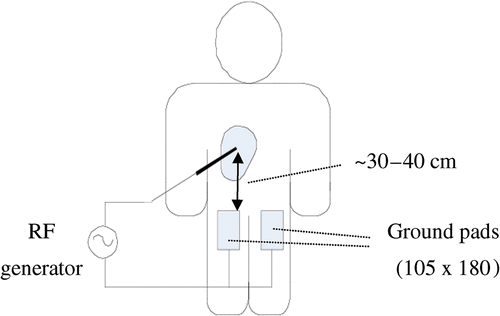
During RF ablation, ground pads (dispersive electrodes) serve as the return path for the applied RF current (Figure 1). Present ground pad systems in clinical use are composed of typically four pads connected in parallel to the RF power source. Each pad consists of a flexible, thin-layered electrical conductor coated by an adhesive polymer gel that attaches to the patient's skin. This adhesive increases the contact surface area of the pad to the skin, and ensures that contact is maintained over irregular surface contours. The ground pads for RF ablation are different from those in use with electrosurgery systems that are usually a simple metal plate. Electrosurgery systems are designed to create rapid superficial heating using short bursts of RF energy. RF ablation is characterized by much greater energy deposition than electrosurgery for a much longer amount of time (up to ∼35 minutes). This is due to the desire to create maximum tissue heating and large coagulation zones with RF ablation versus targeted, low volume surface coagulation in surgical electrocautery.

Figure 1. Ground pads are placed on patient's thighs, equidistant from the active electrode. If four pads are used they are placed on top and bottom of each thigh. RF electrode is inserted into the liver tumor, and power is applied between electrode and ground pads.

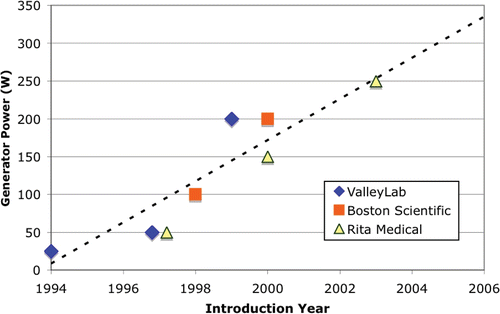
Since the introduction of RF ablation for tumor treatment, the size of the coagulation zone has been a major limitation in treatment of large tumors. While initial systems created coagulation zones of ∼1.5 cm diameter, current systems can create 4–6 cm diameter coagulation zones. This increase in treatment volume is a result of more sophisticated electrode design, as well as an increase in RF generator power. Initial systems used 25 W of power, while current systems use 200–250 W. Figure 2 demonstrates the increase of RF generator power with each new generation of devices for the three commercially available systems in the USA. This trend will likely continue as the interest in increasing size of the coagulation zone as well as speed of treatment continues, and is apparent in current research literature. Two recent in vivo studies showed potential benefits of obtaining larger coagulation zones with current commercial electrodes and high-power RF generators (up to 1000 W, and 4 A) [7], [8].

Figure 2. Generator power has been increasing since introduction of RF ablation.

As the maximum power provided by RF generators has increased, more energy is dissipated below ground pads and to avoid skin burns more and/or larger ground pads have been employed compared to initial devices. The current incidence of ground pad burns in the literature ranges from 0.1–3.2% for severe skin burns (second or third degree), with mild skin burns (first degree) ranging between 5–33% [9–15], though some recent studies suggest the incidence of skin burns after RF ablation may be under-reported [15], [16]. In addition to RF ablation devices, other electrosurgical devices may cause excessive skin heating near ground pads in pediatric patients where available skin area is limited [17].

The ‘leading edge’ effect

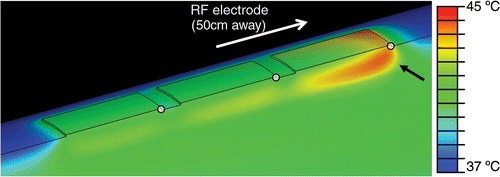
It is well known that the current density is highest at the edges of ground pads for electrosurgery devices, defibrillation electrodes, and RF ground pads, leading to maximum temperatures at the edges [17], [18], [19]. In particular, due to the specific geometric relationship between the electrodes and pads, maximum current density and heating occurs at the so-called ‘leading edge’ of the ground pad, meaning the edge closest to the electrode (Figure 3) [18]. Therefore the leading edge is the location where ground pad burns are most likely to be seen after RF ablation [20], [21], [22].

Figure 3. Central slice through ground pads and tissue shows RF current density. Current flows preferentially to the leading edge of the proximal pad, resulting in little heating at the distal pad.

Efforts to reduce ground pad burns

Because the early generation of RF devices were associated with low power output, to date there have only been rudimentary efforts to limit or avoid ground pad burns. Initially, the number of pads was increased, with current systems using typically four pads (two on each thigh); this method has reached its limit since it is not feasible to place more than four pads equidistant from the RF electrode. Equidistant placement of the pads is required because RF current preferentially flows to the closest pad (especially the leading edge), and placing additional pads further away from the active electrode provides little to no reduction in the maximum skin temperature reached during the procedure (Figure 3).

Some studies have suggested changing the shape of the ground pads to reduce heating at the edges of the pad [17], [19], or dividing circular pads into annular segments and employing resistors to equilibrate current between segments [23]. Others have suggested monitoring temperature at the leading edges of the pads [21], and using ice packs to reduce the risk of ground pad burns [16]. Due to the increasing generator power, two manufacturers recently introduced monitoring features in their latest RF devices to avoid skin burns. One system (Boston Scientific, Natick, MA) monitors current through each of the four pads and alerts the user of uneven current distribution among pads, which ensures proper pad placement (i.e. equidistant from the active electrode). Another commercial system (Rita Medical Systems, Fremont, CA) uses integrated temperature sensors located at the leading edge of the ground pads to alert the operator if the skin temperature exceeds a safety threshold.

In this study we examine whether sequentially switched activation of multiple ground pads can reduce ground pad related skin heating.

Materials and methods

Switched and simultaneous algorithms

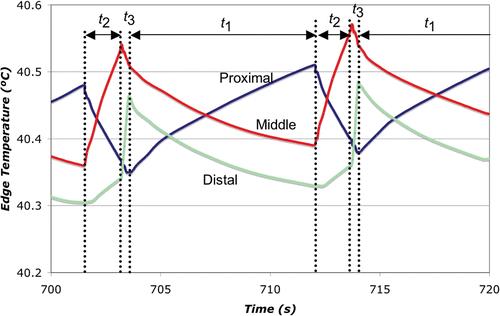
We compared simultaneous and sequentially switched activation of three ground pads placed at different distances from the active electrode. In the simultaneous algorithm, all of the pads are connected in parallel to the RF power ground (similar to the current clinical practice), and RF current preferentially flows to the pad that is proximal to the active electrode (see Figure 3). In our novel switched activation algorithm, different pad subsets were activated (i.e. connecting to the RF power ground) in a repeating cycle. The goal of this algorithm was to equilibrate the power dispersed (and therefore the temperature reached) below each pad. While this equilibration leads to higher temperatures at the more distal pads than in the simultaneous case, the more uniform distribution of power dispersion amongst all pads leads to a lower overall maximum tissue temperature. Our initial algorithm sequentially switched between each of the individual pads - first the proximal pad was activated, followed by the middle pad, and then the distal pad (Figure 4A).

Figure 4. A. Original activation pattern for three ground pads. Only one ground pad was active at a given time during the cycle. B. Revised activation pattern. During each part of the activation cycle, the closest active pad experiences the greatest temperature rise.

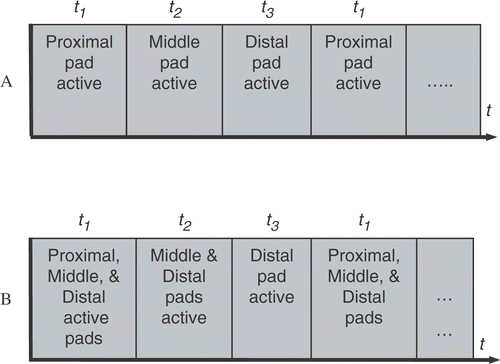
In preliminary experiments, although we were able to successfully equilibrate the temperature below each pad using this method (by adjustment of the activation times t₁, t₂, and t₃), subsequent analysis showed that the decrease in overall pad surface area caused by using only one pad at a time led to higher maximum tissue temperatures with switched activation than with the simultaneous case. Therefore, we modified the switched activation method as shown in Figure 4B. With this method, during each part of the activation cycle (t₁, t₂, and t₃), the closest activated pad dissipates the most power resulting in highest temperature below this pad (Figure 3). Therefore, the proximal pad has the greatest temperature rise during t₁, the middle pad during t₂, and the distal pad during t₃. However, the increase in overall surface area utilized by this method compared to the one in Figure 4A leads to lower power dispersion at each pad and consequently yields a lower overall maximum tissue temperature.

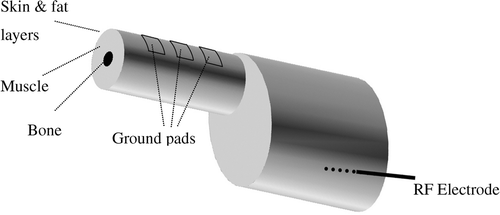
In this study we used computer models and experiments to determine whether switched activation of ground pads as described above results in reduced skin heating. We used an arrangement of three pads placed in line with the RF electrode (see Figure 5). The linear placement used in this study presents a worst-case scenario (compare Figure 3). However, the switched activation algorithm (Figure 4B) can be extended to arbitrarily placed ground pads (i.e. anywhere on the body) as outlined below:

• Apply RF energy simultaneously to all pads for a short period while measuring leading edge temperatures (requires pads with integrated temperatures sensors)

• Group pads according to temperature rise (e.g. for three arbitrarily placed pads: The proximal pad in Figure 4B corresponds to the pad with the highest temperature rise, the middle pad corresponds to the pad with medium temperature rise, and the distal pad corresponds to the pad with the lowest temperature rise)

• Use algorithm shown in Figure 4B with pads grouped as described above

Figure 5. 3-D model of simplified human thigh, attached to torso. Three ground pads (5 × 5 cm, 1 cm apart) are placed on the thigh (20 cm diameter, with 5 cm diameter bone, 2 mm skin layer, and 13 mm fat layer). The ground pads are simulated as a 1 mm thick gel layer (not shown here).

Alternatively, the impedance measured between each pad and the RF electrode may serve as the parameter to determine grouping of the pads instead of leading edge temperature, since typically the pads with lowest impedance will undergo the most heating.

Finite Element Method computer models

We created Finite Element Method (FEM) computer models to determine RF current density profile, as well as temperature profile within the tissue below ground pads while the pads are activated using either the simultaneous, or switched method. This model included muscle, bone, skin, fat, as well as temperature-dependent tissue properties and perfusion.

Pennes bioheat equation

During RF ablation, current flows from the RF electrode through the tissue to the ground pads. Tissue below ground pads is heated due to resistive heating from high RF current density near the pads. The heating of tissue during RF ablation is governed by the bioheat equation where blood perfusion is simulated according to Pennes’ model [24]:where ρ is the mass density (kg/m³), c is the specific heat (J/(kg K)), and k is the thermal conductivity (W/(m K)).  σ is the electric conductivity (S/m) and E is the electric field intensity (V/m). T_bl is the temperature of blood, ρ_bl is the blood density (kg/m³), c_bl is the specific heat of the blood (J/(kg·K)), and w_bl is the blood perfusion (1/s).

Tissue perfusion for each tissue type was modeled using different magnitude and temperature dependence as described below.

Model geometry

We created a FEM computer model with a geometry approximating a human torso and thigh (Figure 5). Three ground pads (5 × 5 cm, simulated as 1 mm thick gel layers) were lined up on the thigh surface, with an RF electrode located ∼40 cm distant from the proximal ground pad.

We used PATRAN Version 2003 (The MacNeal-Schwendler Co., Los Angeles, CA) to generate the geometric models, assign material properties, assign boundary conditions and perform meshing. We used ABAQUS/CAE 6.5 (Hibbitt, Karlsson  & Sorensen Inc., Pawtucket, RI) to solve the coupled thermo-electrical analysis. All analysis was performed on a PC equipped with a Pentium 4 CPU, and 3 GB of RAM.

We set the initial temperature of the liver tissue and temperature at the boundary of the model to 37°C, and allowed tissue temperature to reach steady state after assigning surface convection and radiation (resulting in ∼32°C skin temperature) before applying RF energy. We simulated ablation while applying constant RF current of 0.3 A for 12 min; the current was chosen such that maximum tissue temperature was ∼45°C in the simultaneous case. We controlled the applied potential difference between the RF electrode and ground pads such that RF current was kept constant. The model consisted of ∼170,000 tetrahedral elements and ∼34,000 nodes. We used a non-uniform mesh; mesh size was 0.1 mm close to the RF electrode and ground pads where we see large temperature and current gradients, and 5 mm at the model boundaries. We performed convergence tests to ensure adequate spatial resolution. The time steps during the solution of the FEM started at 0.05 s, and were subsequently automatically controlled by the solver software so that the maximum temperature change during the step was below 3°C.

We simulated simultaneous, and switched activation of ground pads. During simultaneous activation, a potential of 0 V was applied to all ground pads. During switched application, 0 V potential was applied to 1–3 ground pads according to the algorithm shown in Figure 4B. The activation times (t₁, t₂ and t₃) were determined in preliminary simulations by trial and error to obtain the same maximum temperature at the center of each ground pad's leading edge. The final activation times were 8 s, 1.71 s, and 0.32 s for t₁, t₂ and t₃, respectively. The activation times were chosen higher than in the experimental study to reduce computational demands of the simulation.

Material properties

We used electrical and thermal material properties from the literature [25], [26], [27]. Table I shows the properties used in this model.

Table I.  Thermal and electrical properties of the materials in the model (given at 37°C).

Material	ρ (kg/m^3)	c (J/(kg. k))	k (W/(m·k))	σ (S/m)
RF Electrode (stainless steel)	7930	132	71	1.4 × 10^6
Ground pad (gel)	1000	4185	0.6	1.11
Skin	1010	3663	0.29	0.015
Fat	900	4182	0.16	0.04
Muscle	1060	3600	0.512	0.4
Bone	1300	1500	0.36	0.03

We assumed a temperature coefficient of 2%/°C for all tissues [25], and temperature coefficient of thermal conductivity and specific heat according to previous studies [28].

Perfusion

Similar to a previous study [29], we included temperature-dependent perfusion of muscle and fat tissue in our model, in which perfusion changes according to a sigmoid profile with a plateau above 45°C (Equations 2 and 3:

For skin tissue, we also included temperature-dependent perfusion in the computer model. We assumed that the relative change in perfusion with temperature in humans is the same as that previously reported in a rat model [30], and applied a previously reported basal value for skin perfusion in humans [31] (Equation 4):

Since in our computer models we don’t observe tissue temperatures above 45°C, we did not include any reduction in blood flow due to higher temperatures where coagulation occurs.

Convection and radiation

We included convective and radiation heat loss in our model by assigning the heat fluxes as boundary conditions to skin and ground pad surfaces (Equation 5 and 6):where q_conv equals convective heat flux (W/m²), q_rad equals radiation heat flux (W/m²) h_f equals the convective heat transfer coefficient of skin (h_f = 2.68 W/(m²°C) (32), σ equals the Stefan-Boltzmann constant σ = 5.67 × 10⁻⁸ W/(m² K⁴), ε equals the emissivity of skin (ε = 0.98) (33), and T_air equals the temperature of the air in contact with the skin and ground pad (T_air = 22°C). Note that in Equation 6 the temperatures are set in kelvin.

Experimental setup

We filled a large plastic bath to a depth of 8 cm with 0.25% saline, which has the same electrical conductivity as muscle tissue at RF frequencies (σ = 0.44 S/m) (34, 27). At one end of the bath we fixed a stainless steel electrode for RF energy delivery. We then placed a gel block (35 cm long by 20 cm wide by 2 cm thick) made of Agar-water (5% Agar, 0.25% NaCl) on additional small Agar-water gel blocks in the bath such that the smooth top surface of the large block was approximately 5 mm above the surface of the saline. The initial temperature of the entire set-up before each trial was 22°C. Three thin copper sheets (hereafter ‘pads’) with dimensions 10 cm wide by 5 cm long were placed on the surface of the block so that the leading edge of the first pad was ∼40 cm from the stainless steel electrode. The two other pads were placed farther from the electrode such that there was a 4 cm distance between the pads (see Figure 6). A small amount of saline was spread on the large agar block before placement to ensure uniform contact between each pad and the agar. Each pad was connected to the switching circuit by a wire soldered to the top of the pad.

Figure 6. Experimental set-up (not to scale). Thermocouples were placed at the center of the leading edge of each pad.

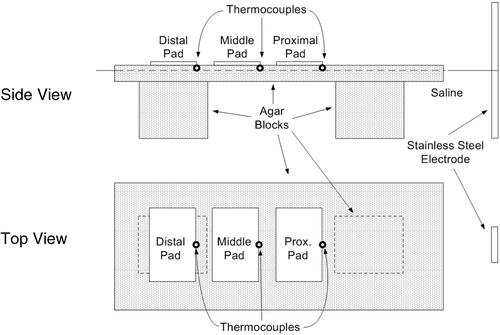
With rectangular pads, maximum temperatures are obtained at the corners of the leading edge (see Figures 13 and 14). However, to measure temperature during the trials we placed thermocouples at the center of the leading edge of each pad (see Figure 6), as it decreased the sensitivity of the measurements to initial placement errors. A data acquisition device (DAQPad-6020E, National Instruments, Austin, TX) recorded the temperatures at 10 Hz for later analysis. Although the recorded temperature values did not reflect the maximum temperatures reached in the tissue phantom, they did allow accurate comparison of temperatures reached below each pad from trial to trial and accurate control of temperature equilibration below each pad using the switched algorithm. The thermocouples were pressed into the agar to a depth of approximately 1 mm so that they did not interfere with the contact between the pad and the agar. In addition, we placed temperature-sensitive liquid crystal sheets that change color in the range of 25°C and 30°C (R25C5W, Hallcrest Inc., Glenview, IL) on top of each pad, and took photographs during each trial at 1, 3, 6, and 12 minutes. The location and orientation of the pads, thermocouples, and temperature-sensitive sheets were not altered between trials.

In initial measurements we determined current through each pad when all pads are active (t₁), when just the middle and distal pads are active (t₂), and when only the distal pad is active (t₃). Assuming similar current profile below the pads due to large distance from the RF electrodes, we calculated the activation times such that average power deposited below each pad during one activation cycle is the same.

We used a RF generator (PDX-500, Advanced Energy, Fort Collins, CO) at a frequency of 350 kHz to supply RF energy for all trials. We developed software (Microsoft Visual Basic) that both activates the ground pads according to the pattern described above (see Figure 4B) for an adjustable period of time, and separately controls the power delivered by the RF generator to each subset of pads. The software allows the user to apply either constant set power or constant set current to the pads. The impedance between the RF electrode and ground pad(s) decreases with increasing number of pads (e.g. from 64 to 55 to 49 ohms in our three-pad set-up). If we applied constant power as in the standard clinical practice, the power deposited around the RF electrode (i.e. in tissue) would change depending on which subset of pads was currently active. In other words, when fewer pads are active, the higher impedance between the RF electrode and the ground pad means that the current density (and therefore heating) around the RF electrode is reduced. Therefore, in a clinical application the ablation zone size would likely be different between switched and simultaneous activation even though the same total power is applied. Thus, to compare switched to simultaneous activation in a clinically relevant matter we adjusted the power applied during the switched activation for each subset of pads to keep the applied current constant, ensuring that the same power is delivered to the region around the RF electrode independently of the number of connected ground pads.

To calculate the current through each subset of pads (I_i), the software uses the commanded power (P_i) and the voltage (V_i) measured by a digital multimeter (34401A, Agilent, Santa Clara, CA) according to Equation 7:

The commanded RF power (P_i(n)) is then adjusted during each activation cycle n (using Equation 8) based on the calculated current (I_i) and the previously applied power (P_i(n − 1)) so that the desired set current (I_set) is delivered to each subset of pads.

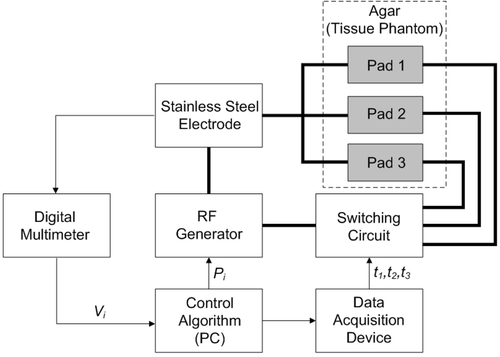
We designed and built a relay switching circuit that interfaced with the program via a data acquisition device (34970A, Agilent, Santa Clara, CA). Figure 7 shows a block diagram of the electrical set-up. The calculated activation times (from above) were adjusted slightly using temperature data acquired during preliminary experiments to equilibrate temperatures between pads. The final activation times t₁, t₂, and t₃, were 800, 600, and 300 ms, respectively.

Figure 7. Block diagram of the set-up. Software controlled the switching circuit to allow activation of different pad combinations. The activation times were selected to achieve uniform heating at the leading edge of each pad. Note: thick lines denote the RF power circuit, while thin lines denote control signal connections.

We performed a total of 20 trials in this study. In each, we applied a constant current of 1.5 A for 12 minutes. This current was chosen in preliminary experiments such that the pad surface temperature was in the range in which the temperature-sensitive liquid crystal sheets operate (25–30°C). In 10 of the trials, all of the pads were simultaneously connected to the RF power ground for the entire trial. In these simultaneous trials, the power was adjusted manually during the trial to keep the current constant, as electrical conductivity of the phantom increases during heating (∼2%/C). In the other 10 trials, we used the program and circuit described above to sequentially activate (hereafter switch) different combinations of pads (see Figure 4B) over the course of each trial. The final temperature reached at each particular thermocouple for the simultaneous and switched cases was compared using the Mann-Whitney U-test. Similarly, the final temperature reached at the three thermocouples for each particular case (switched or simultaneous) was analysed using the Kruskal-Wallis one-way analysis of variance.

Results

Computer models

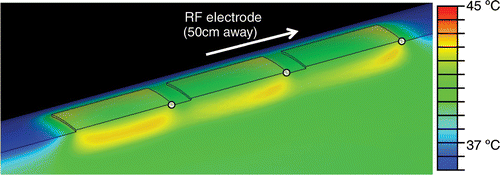
The tissue temperature profile below the three ground pads at the end of the 12 min ablation for simultaneous activation of pads (Figure 8), and for switched activation (Figure 9) are shown. Maximum tissue temperatures were 44.8°C for simultaneous activation, and 42.7°C for switched activation. Relative temperature rises cannot be determined due to the varying initial tissue temperature with 32°C at the skin surface up to 37°C in the muscle tissue (see Figures 8, 9). Figure 10 shows the time course of the leading edge temperatures during switched activation during the final activation cycle.

Figure 8. Simultaneous ground pad activation: temperature at skin and pad surfaces and in tissue (ground pads = black outline) after 12 min of RF ablation at 0.3 A current. Tissue is cut through center of thigh, and pads. Black arrow shows hottest area (leading edge). White dots mark locations where temperatures are shown in Figure 10.

Experimental results

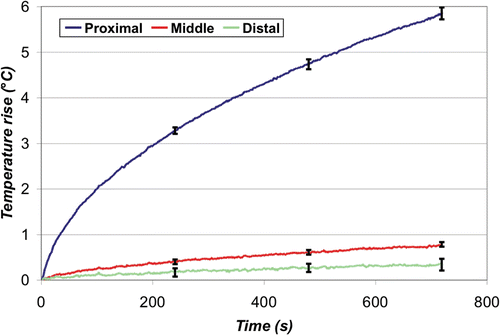
The average temperature rise over time at the leading edge of each ground pad is shown below for the simultaneous (Figure 11) and switched case (Figure 12). The final temperature rise (12 min) between the three pads was significantly different for the simultaneous case (p < 0.0001), but not for the switched case (p = 0.18). Overall, the maximum temperature rise recorded in the simultaneous case was 5.9 ± 0.1°C (at the proximal pad), which was significantly higher (p < 0.0001) than that recorded in the switched case, 3.4°C ± 0.2°C. At the middle and distal pads, the temperature was higher in the switched compared to the simultaneous case (p < 0.0001).

Figures 13 and 14 show the temperature profile after 12 minutes for a typical simultaneous and switched trial, respectively, using the temperature-sensitive liquid crystal sheets. In the simultaneous case, the dark blue coloring at the leading edge of the proximal pad denotes an area of high temperature (>30°C), while the middle and distal pads show little temperature rise. In contrast, uniform average current distribution among pads in the switched activation case leads to a relatively uniform temperature rise among the three pads, as well as a lower overall maximum temperature.

Figure 9. Switched ground pad activation: temperature at the skin and pad surfaces and in tissue (ground pads = black outline) after 12 min of RF ablation at 0.3 A current. Tissue is cut through the center of the thigh, and pads. White dots mark locations where temperatures are shown in Figure 10.

Figure 10. Switched ground pad activation: skin temperature below the leading edge (white dots in Figure 9) for each pad during the last 20 s of 12 min ablation. Arrows at the top denote different activation periods t₁, t₂, t₃ (see Figure 4B).

Discussion

Skin burns due to ground pad heating are a common complication during RF tumor ablation [9–15], and are a limiting factor preventing further increase in RF power, and ablation zone size [8]. Currently, up to four ground pads are placed on the patient (typically on the thighs), and it is it is extremely important that the pads are placed equidistant from the RF electrode. This arrangement results in nearly equal dispersion of the total current amongst the pads while increasing the total skin surface area over which the current is dispersed. Therefore, the current density below each pad is decreased, lessening the probability of skin burns. If one or more of the pads are placed closer to the electrode than others, a disproportionate amount of current may flow to this pad (assuming that closer distances result in lower impedance between electrode and pad) resulting in a skin burn. Likewise, the placement of a pad over a metallic device such as a hip prosthesis may create a low resistance path (short circuit) to the nearest part of the ground pad, resulting in a severe skin burn.

Figure 11. Simultaneous ground pad activation - leading edge temperature rise. Increased current density at the leading edge of the proximal pad resulted in an average maximum temperature rise of 5.9°C ±0.1°C after 12 min, while the middle and distal pads showed little heating.

Manufacturers of tumor ablation equipment have recognized the increased risk of ground pad burns and two manufacturers recently introduced monitoring features in their latest RF devices to limit current or temperature below ground pads. Research studies investigated several methods to reduce skin heating below ground pads; effects of different ground pad shapes were investigated [17], [19], others have suggested use of ice packs to reduce the risk of skin burns [16].

Figure 12. Switched ground pad activation - Leading edge temperature rise. The switching algorithm successfully produced uniform heating at the leading edge of all three pads. The average maximum temperature rise was 3.4°C ± 0.2°C, which was significantly lower than the simultaneous case (p < 0.0001).

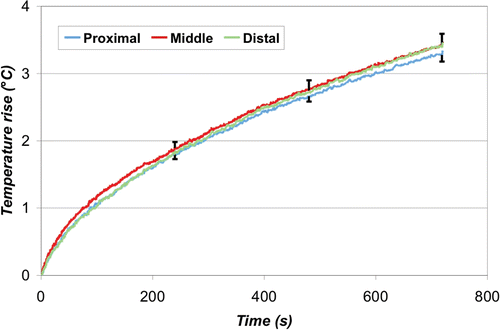
Figure 13. Simultaneous ground pad activation: representative image of ground pad heating. The proximal pad (right) heats up most with little heating of the other pads. Temperature-sensitive liquid crystal sheets show pad surface temperature profile (red = 25°C, blue = 30°C).

Figure 14. Switched ground pad activation: representative image of ground pad heating. All pads reach similar temperatures, with reduced maximum temperature. Temperature-sensitive liquid crystal sheets show pad surface temperature profile (red = 25°C, blue = 30°C).

In this study we investigated sequential activation (switched) of multiple ground pads and compared this to the current methodology of simultaneous activation. During sequential activation, groups of ground pads are activated for different time periods (Figure 4B). Temperature readings below the leading edges of the pads were used as feedback to control time periods and keep leading edge temperature of all pads equal. With this method we were able to achieve equal heating between different pads both in computer simulations and experiments (Figures 9 and 14). Simultaneous activation on the other hand results in preferential heating of the closest pad (Figures 8 and 13). In addition, the switched activation algorithm reduced the maximum temperature rise below the pads in experiments almost two-fold, from 5.9°C to 3.4°C (see Figures 11, 12). This maximum temperature reduction allows us to estimate possible increase in RF generator power when switched pad activation is used. In a worst case analysis we ignore the effects of thermal conduction and perfusion, both of which are non-linear effects that became more effective with increasing temperatures; then the temperature rise under each pad is directly proportional to the amount of power dispersed there. Therefore, applied RF power could be increased at least 1.75-fold during the switched activation of pads when compared with the simultaneous case, while giving the same maximum temperature rise with our ground pad configuration. It should be noted that tissue heating below the pads depends both on instantaneous power applied (for all systems), as well as on duty cycle for RF generators that employ pulsed heating (commercial systems by Valleylab and Berchtold).

In the computer models, maximum tissue temperature was reduced to 42.7°C from 44.8°C. The main reason temperatures are considerably higher in computer models compared to experiments is due to the low electrical conductivity of skin and fatty tissue compared to the gel phantom material (see Table I); i.e. lower conductive material (skin and fat) heats up more than higher conductive material (gel phantom) when RF current of same magnitude is applied. Also notice that the switching intervals should be sufficiently small to limit the ripple in tissue temperature (Figure 10), as longer switching intervals result in higher maximum tissue temperatures. Since the performance of switched activation is dependent on the number of pads, pad size, and spacing, further studies with different pad parameters may reveal configurations that produce an even greater improvement with switched activation.

Since the activation times are selected to account for differences in the distance (and therefore impedance) from each pad to the ablation electrode, the equidistant placement of the pads is no longer a requirement when using the switched algorithm, which is important for several reasons. First, ground pads could be placed virtually anywhere on the patient's body, allowing the use of more than the current number of pads; a similar algorithm to the one described here can be used to activate arbitrarily placed ground pads. This increase in effectively utilized ground pad surface area would lead to a reduction in the maximum skin temperature and correspondingly reduce the likelihood of skin burns, as well as allow higher generator power as discussed above. Secondly, removing the equidistant requirement for ground pad placement reduces the possibility of operator error. Another approach would be to design ground pads that consist of multiple small conductive areas that are sequentially activated as described above, which would allow for more effective use of the pad area and reduction of the ‘leading edge’ effect.

In addition to RF tumor ablation, this method may be useful for other electrosurgical devices, especially in pediatric patients where skin surface area is limited.

Conclusion

Switched activation of multiple ground pads allows equilibration of heating and reduces maximum temperature below pads. This may allow for increase in RF generator power and reduction of skin burn incidence.

Acknowledgements

This work was conducted in a facility constructed with support from the National Institutes of Health, Grant Number C06 RR018823 from the Extramural Research Facilities Program of the National Center for Research Resources, USA. In addition this project was supported by NIH Grant Number R01 CA118990.