Metamaterial lens applicator for microwave hyperthermia of breast cancer

Abstract

Artificial left-handed metamaterial (LHM) provides a new perspective for microwave hyperthermia. Four flat LHM slab lenses can be used to form a focus-flexible applicator for breast tumour hyperthermia. By adjusting microwave sources behind the four flat LHM lenses, microwaves emitted from the sources can be focused tightly at different points in the breast tissue so that necessary heating depth in breast tissue can be achieved. Numerical simulations with a two-dimensional finite-difference time-domain method indicate that hyperthermia with the proposed four-lens applicator of moderate LHM losses could be effective in achieving desired power deposition in a heterogeneous breast model. Temperature distribution obtained by solving the bio-heat transfer equation demonstrates that temperature above 43°C can be maintained in the tumour volume for specific periods of time. Flat slab LHM lenses offer a feasible alternative to traditional mechanically scanned lens applicator and electronically scanned phased-array applicators.

• Breast tumour
• hyperthermia
• microwave
• left-handed metamaterial (LHM)
• lens applicator

Introduction

In microwave hyperthermia treatment of localised cancerous tumour, it is highly desired that most of the microwave power is concentrated in the cancerous tissue so that the tumour can be heated without damaging the normal tissue surrounding it. To be an effective hyperthermia, the temperature in the tumour volume is generally raised above 42°C and kept for a certain period of time to ensure enough tumour damage, while normal physiological temperature is kept in the surrounding tissue to avoid tissue damage [1–4]. To meet this demand, specific microwave applicators must be designed.

Different applicators have been reported and tested for microwave hyperthermia. Lens applicator is a typical one due to its simple system implementation. Metal plate lenses and partially dielectric-filled waveguide lenses have been reported [5–10]. In the lens applicator system the focal length of the lens is generally fixed. To heat tumours at different locations the lens applicator must be mechanically adjusted. In some scenarios different lens structures must be used to adjust the heating depth. To increase the flexibility in controlling the localised power deposition in biological tissue, array applicators have been considered for hyperthermia [11–18]. Localised heating is obtained by transmitting microwave signals of specifically designated amplitude and phase so that microwaves emitted from the elements of the array can be constructively reinforced in the tumour volume. In the array, independent amplitude and phase control must be implemented for each element. Therefore, the array applicator is generally a complicated system when compared to the lens applicator.

The realisation of artificial left-handed metamaterial (LHM) provides a new perspective for microwave hyperthermia. Different from the conventional dielectric slab, a flat LHM slab can be used as a lens to concentrate microwaves emitted from a point source [19], and sub-wavelength focusing resolution beating the diffraction limit can be achieved by such a flat lens [20–25]. Although LHM losses will degrade the focusing resolution of a flat LHM lens to some extent, relative high focusing resolution can be achieved as well. The high focusing resolution of a flat LHM lens allows highly localised microwave power deposition in the tumour volume. In addition, the focal point of a flat LHM lens can be adjusted in both the lateral and depth directions by simply moving the point source behind the slab lens, so that hyperthermia of the tumour from different positions can be easily implemented by using a flat LHM lens.

At its early stage, a tumour is usually small. For hyperthermia treatment it is generally desirable that microwaves in tissue should be tightly concentrated so that the size of focusing spot is comparable to that of the early stage tumour. Surrounding tissue damage caused by the hyperthermia should be avoided as much as possible. From flat LHM lens physics it is well known that a small focusing spot can be generated by using a thin flat LHM lens and high frequency microwaves [26]. To guarantee enough heating depth in breast tissue, a thick LHM lens must be considered. A thick LHM lens will generate a large focusing spot. Moreover, the losses and heterogeneity of breast tissue will further enlarge the size of focusing spot of the flat LHM lens [27]. Therefore, microwaves of higher frequency (such as 6 GHz) may be considered if we want to generate a smaller heating spot for early breast tumour hyperthermia, although microwaves of higher frequency will suffer more from the dissipation caused by tissue loss when penetrating the breast tissue. At the late stage, breast tumours are usually large. The hyperthermia treatment may allow a relatively large heating spot without damaging the normal tissue surrounding the tumour. For this scenario, relatively low frequency of microwave (such as 2.45 GHz or lower) can be considered.

In this paper, a microwave hyperthermia applicator based on flat LHM lenses is proposed. The feasibility of the LHM lens applicator for microwave hyperthermia treatment of breast tumour is investigated by two-dimensional (2-D) finite-difference time-domain (FDTD) simulations. In the Methods and performance section, a four-lens LHM applicator is proposed, and performance of breast tumour hyperthermia with LHM lens applicator is demonstrated at 6 GHz by showing the power deposition and temperature distribution in a heterogeneous breast model. In the Effects of LHM losses section, influence of LHM losses on the hyperthermia with LHM lens applicators is studied. In the Further discussion section, hyperthermia of a tumour in a circular breast model and hyperthermia with microwaves of 2.45 GHz are further studied. The feasibility of the LHM lens applicator is thus demonstrated by this preliminary 2-D FDTD simulation.

Methods and performance

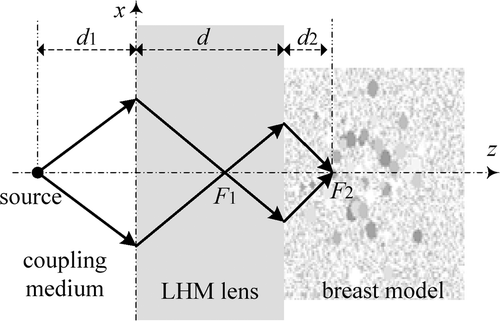
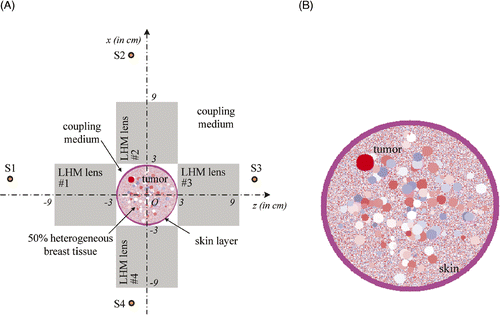
The focusing of the flat LHM lens is shown in Figure 1. Different from conventional convex dielectric lens, microwaves emitted from a point source on one side of the flat LHM slab can be focused first at a focal point F₁ inside the LHM lens and then at another focal point F₂ outside the LHM lens. The focal point F₂ in breast tissue can be adjusted in depth direction simply by moving the source towards and away from the LHM lens. It should be remarked that the source distance d₁, the lens thickness d, and the focal length d₂ in breast theoretically obey the following relationfor lossless LHM lens. In practice, the real focal length d₂ will be further modified by the loss and heterogeneity of the breast tissue [27]. In general, the lens thickness d should be selected larger than the maximum heating depth in breast.

Figure 1. Focusing of flat LHM lens in the breast model.

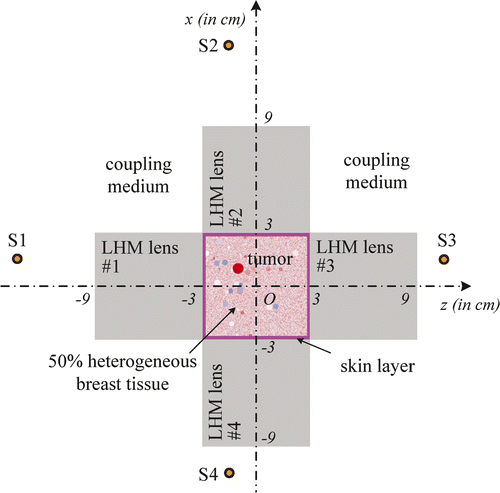
It is well known that the focusing resolution in the z-direction of the flat LHM lens is much worse than that in x-direction. To acquire better focusing as required in hyperthermia of breast tumours, four LHM lens applicators can be deployed orthogonally surrounding the breast as shown in Figure 2. The four sources, S1, S2, S3, and S4, are set behind the four lenses. In our hyperthermia simulation, the source excitation is set to be turned on slowly by using an exponential ramp function of with to avoid exciting other frequency components as pointed out in [28]. In clinic, the patent may lie prone so that the breast will be pendant in the region surrounded by the four flat lenses, and the breast may be slightly pressed by the LHM lens so that a local flat surface as shown in Figure 2 can be achieved.

Figure 2. Hyperthermia system with four LHM lenses.

In Figure 2, deployment of the four sources to heat a tumour at the origin is shown. The proposed system can heat tumours at different positions in breast by properly setting the positions of the four lenses. For example, when a tumour is centred at (x₀, z₀), by setting the four line sources at (x₀ - 2d, z₀), (x₀ + 2d, z₀), (x₀, z₀ - 2d) and (x₀, z₀ + 2d), respectively, microwaves emitted from S1, S2, S3, and S4 will be focused in the tumour volume and hyperthermia can be implemented.

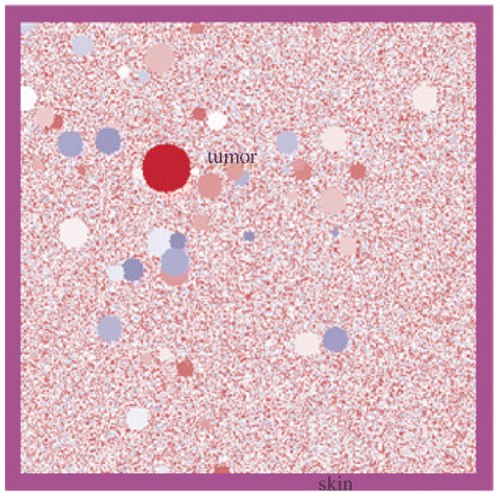
The hyperthermia system can be demonstrated by two-dimensional FDTD simulations. In the simulations, both the length and thickness of the LHM lens applicator are set to be 6 cm. Therefore, the dimensions of breast with tumour in are restricted to 6 cm × 6 cm. In the FDTD codes, a heterogeneous breast model must be defined, which includes the heterogeneous adipose tissue and the distribution of ductal and glandular tissues. The tissue can be defined as having complex relative permittivity of the following Debye modelwhere , . Different values of , , and σ define different tissues. For example, , , and characterise typical normal breast tissue [29].

To ensure enough heating depth and acquire a tight focusing spot in tissue as desired for early breast tumour hyperthermia, microwave frequency of 6 GHz is considered for demonstration. Lower frequencies as in prevailing microwave hyperthermia can also be used. At lower frequencies an enlarged focusing spot and deeper heating depth can be obtained. At 6 GHz, the Debye model (2) yields the median relative permittivity and conductivity for the adipose tissue, and for ductal and glandular tissue [29]. To define the random heterogeneity of breast, heterogeneity of ±30% random variability range about the median of , and , is considered for illustration, and 100 circular glandular tissue blocks of diameters ranging from 1 mm to 5 mm are spread randomly in adipose tissue. Surrounding the tissue, a skin layer with a thickness of 2 mm and , is considered [29]. The heterogeneous breast model used in our simulation is shown in Figure 3.

Figure 3. Heterogeneous breast model used in our simulation.

The artificial LHM is supposed to be isotropic and characterised by relative permittivity and permeability of the forms

By choosing different values of frequencies , and loss factor (which is related to the collision frequency), different permittivity and permeability of the LHM lens can be defined. At 6 GHz, we may set , , and in Equations 3 and 4 so that , , and are defined for the LHM lens. In the FDTD codes, extended uniaxial anisotropic perfectly matched layer and transition layer between the LHM and its surrounding medium [30] are considered.

We remark that the imaginary part of the refraction index indicates loss of LHM. The LHM loss characterised by the imaginary part of is to the order of practical LHM under present technical conditions [25]. For such a loss level, LHM lens of a thickness of 6 cm works well because a focusing gain of approximately 22 dB can be maintained. To reduce reflection caused by mismatch at the entrance surface of the flat LHM lens, coupling medium of is applied to surround the breast and LHM lens.

Figure 4 shows the focusing of the proposed four-lens system when the focal point is at the centre of the breast. Figure 4A gives the image of the focusing. In our simulation the value of the field strengths of the excitation sources S1-S4 are set to be unit amplitude, and the maximum field intensity recorded in skin is approximately 0.135. Figure 4B shows the field profiles of the focused spot in x- and z-directions, which turn out to be identical. From Figure 4B, the focusing resolution can be measured as 6 mm, which implies that a small heating spot can be provided for tumour hyperthermia. Figure 4C shows the typical waveform recorded at the source point.

Figure 4. Focusing of the LHM lens system: (A) Image of the focusing, (B) Profile of field distribution, and (C) Source waveform.

For demonstration, we may set a tumour of diameter of 6 mm at the origin. Typical permittivity and conductivity of the tumour are defined by Equation 2 as and . For the hyperthermia scenario proposed in Figure 2, Figure 5A shows the power deposition in the homogeneous tissue, where the tumour is marked by the black dashed circle. The amplitude of each source used in the simulation is 23.1 V/cm, the peak SAR in the tumour is calculated to be 943.407 W/kg, and in the skin is 174.589 W/kg. In Figure 5A, a highly localised power deposition in the tumour volume can be observed without any auxiliary foci in normal tissue. As noted elsewhere [31], further enhanced power deposition will be observed in the tumour volume because strong surface waves can be excited on the surface of LHM lens, which may be regarded as an array of sources with different phases for enhancement. By extracting the −3 dB contour line of power deposition, a quasi-circle contour line of diameter of approximately 2.5 mm is obtained, which is about 42% of the tumour diameter. Therefore, the power deposition in the tumour is further concentrated.

Figure 5. Power deposition and temperature distribution of hyperthermia of a 6 mm tumour centred at (0, 0): (A) Power deposition, and (B) Temperature distribution.

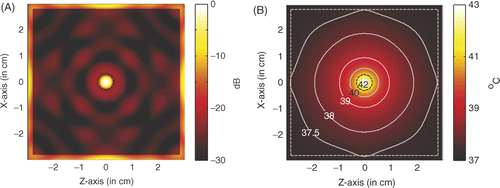
Figure 5B shows the corresponding temperature distribution after 60 min heating. The temperature is calculated by solving the bio-heat transfer equation (BHTE) with finite difference method [32], which is given as

In the temperature calculation, the perfusion and thermal properties used in the BHTE are listed in Table I following that in Converse et al. [18], where A₀ denotes the metabolic heat production, B denotes the heat exchange mechanism due to capillary blood perfusion, C_p denotes the specific heat capacity, ρ denotes the density, and K denotes the thermal conductivity. The initial temperature in the breast is set to be 37°C. Outside the breast model the temperature is fixed to be constant 37°C, which implies water-cooling as will be desired in the clinic. It is observed that the temperature in the tumour volume may increase about 6°C to approximately 43°C, while the temperature in surrounding normal tissue keeps below 42°C as required in hyperthermia treatment. The highest temperature recorded in the skin is 37.52°C. Therefore, microwave hyperthermia of breast tumour with a metamaterial lens applicator is feasible.

Table I.  Thermal constants suggested for the BHTE [18].

	K (W/m°C)	Cp (J/(kg°C))	A0 (W/m^3)	B (W/(m^3°C))	ρ (kg/m^3)
Tissue	0.499	3550	480	2700	1020
Tumour	0.5641	3510	480	2700	1020
Skin	0.376	3500	1620	9100	1100

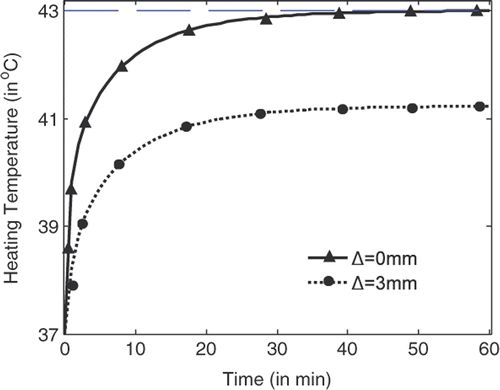
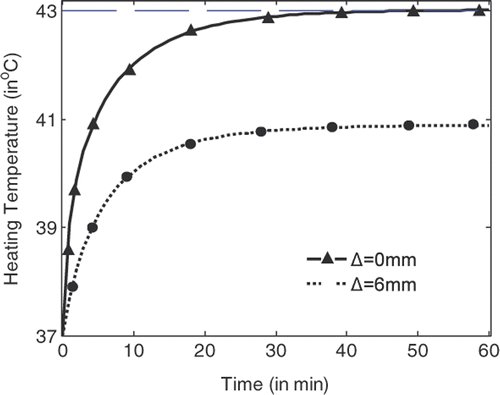
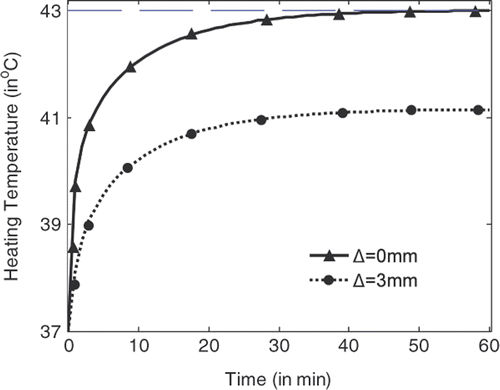
Figure 6 shows the temperature rise with heating time at the centre of the tumour (indicated by Δ = 0 mm) and at the position where the highest temperature can be recorded in normal tissue right outside the tumour (indicated by Δ = 3 mm). It is shown that the temperature at the tumour centre rises faster and higher than the temperature in the tissue. With source amplitude of 23.1 V/cm for each line source, a temperature of 43°C can be achieved and maintained after 54 min heating, while the highest temperature in tissue right outside the tumour is about 41.15°C. By using the temperature lines provided in Figure 6, damage integrals can be calculated for tumour and tissue. Thus tissue damage and tumour damage can be provided for better characterisation of the hyperthermia [33].

Figure 6. Temperature rise with heating time at the centre of the tumour and right outside the tumour.

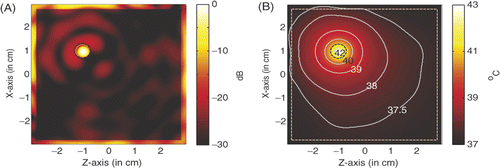
In practice, not all the tumours occur at the centre of the breast model. For a LHM lens hyperthermia of tumour centred at (1, −1), Figure 7A shows the power deposition in the homogeneous tissue, where the tumour is marked by the black dashed circle. Different from the scenario of the tumour at the centre, the source amplitude used here in the simulation is 29.2 V/m, the peak SAR in the tumour is 936.196 W/kg. Figure 7B shows the corresponding temperature distribution after 60 min heating. It is observed that the temperature in the tumour volume may increase about 6°C to approximately 43°C, while the highest temperature recorded in skin is 37.35°C. The proposed LHM lens applicator works well for this scenario, but not as effective as the scenario in Figure 5.

Figure 7. Power deposition and temperature distribution of hyperthermia of a 6 mm tumour centred at (1, −1): (A) Power deposition, and (B) Temperature distribution.

Figure 8 shows the temperature rise with heating time at the centre of the tumour (indicated by Δ = 0 mm) and at the position where the highest temperature can be recorded in normal tissue right outside the tumour (indicated by Δ = 3 mm). Also we have the observation that the temperature at the tumour centre rises faster and higher than the temperature in normal tissue right outside the tumour. With source amplitude of 29.2 V/cm for each line source, a temperature of 43°C can be achieved and maintained after 55 min heating, while the highest temperature in tissue right outside the tumour is about 41.23°C. From the temperature lines in Figure 8, almost the same tissue damage and tumour damage can be calculated as from Figure 6.

Figure 8. Temperature rise with heating time at the centre of tumour and right outside the tumour.

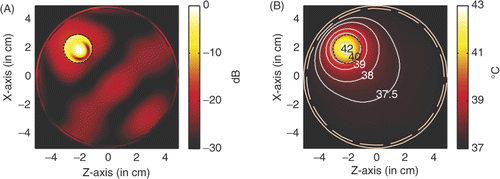
For the hyperthermia of a large tumour of diameter of 12 mm centred at (1, −1), Figure 9 shows the power deposition in the breast and the temperature distribution after 60 min heating. The amplitude of each source used in the simulation is 28.2 V/cm. Figure 9A shows the power deposition in the breast, where we find a different power deposition in the tumour. By extracting the −3 dB contour line of power deposition, a quasi-circle contour line of diameter of approximately 2.6 mm is obtained in the tumour, which indicates that the focusing properties of the proposed LHM lens applicator are almost the same as that with the small tumour. Figure 9B shows the temperature distribution in the breast. It is observed that the temperature in the tumour volume may increase about 6°C to approximately 43.02°C, while the highest temperature recorded in skin is 37.59°C. We note that small amplitude is needed here to achieve the temperature above 43°C in tumour as compared to the situation to heat a 6 mm tumour at (1, −1). This is due to the use of high frequency (6 GHz) in the simulation. Figure 9C shows the temperature distribution inside the tumour for details.

Figure 9. Power deposition and temperature distribution of hyperthermia of a 12 mm tumour centred at (1, −1): (A) Power deposition, (B) Temperature distribution, and (C) Temperature in tumour.

From Figure 9C it is observed that the above 43°C temperature is restricted at the centre region in the tumour. It seems that the tight focusing of the proposed LHM applicator is not as efficient if the tumour to be heated is large. But efficient hyperthermia can be had by using flat LHM lenses if lower frequency is used, because the flat LHM lens operating at lower frequency will provide a larger focusing spot.

Figure 10 shows the temperature rise with heating time at the centre of the tumour (indicated by Δ = 0 mm) and at a position where the highest temperature can be recorded in normal tissue right outside the tumour (indicated by Δ = 6 mm). From Figure 10, we have the observation that a temperature of 43°C can be achieved and maintained after 45 min heating with a source amplitude of 28.2 V/cm for each line source, while the highest temperature in tissue right outside the tumour is about 40.89°C, which is lower than that recorded in Figure 8. By calculating the tissue damage and tumour damage from Figure 10, a higher tumour damage/tissue damage rate will be obtained.

Figure 10. Temperature rise with heating time at the centre of tumour and right outside the tumour.

It should be remarked that the above results are obtained based on 2-D FDTD simulation. The power level needed for hyperthermia in 2-D FDTD simulation is generally far lower than the power level needed in 3-D FDTD simulation [34]. As reported in [34], the power level needed for hyperthermia in 3-D FDTD simulation will be comparable to that used in practical hyperthermia systems.

In our FDTD simulation, the breast model defined in Figure 3 is far from the real breast model. Realistic MRI-derived FDTD models of the breast will be more accurate for the FDTD simulation, but for temperature calculation, perfusion is of vital importance. The perfusion is not known exactly because it is generally dynamic and will change as tissue temperature increases during the heating treatment. Therefore, some temperature feedback techniques such as invasive or non-invasive thermometry are necessary in clinical practice for more accurate temperature feedback.

Effects of LHM losses

Several factors of the LHM lens applicator may affect hyperthermia performance. For an applicator of a specific LHM lens, the LHM losses play an important role.

In LHM, the losses may be characterised by the imaginary part of the refraction index. A small imaginary part of refraction index indicates a small LHM loss. The imaginary part in the above defined refraction index characterises losses to the order of practical LHM under present technical conditions. With the development of LHM technique, LHM with small losses can be developed, and thus the performance of the LHM applicator can be further improved.

In addition to the power deposition in the breast and the highest temperature in the tumour volume as demonstrated above, efficiency or heating time may be another indicator of applicator performance. The following results reveal the input power and heating time for LHM applicators of different losses.

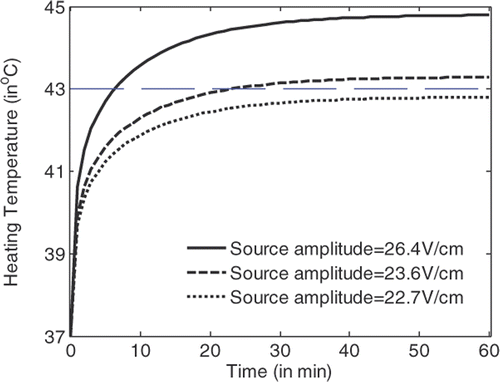
Figure 11 shows the temperature rise in a tumour volume with a diameter of 6 mm at the centre with the heating time for hyperthermia with flat LHM lenses of . It is observed that by using source amplitude of 22.7 V/cm, a temperature of 43°C in the tumour cannot be achieved; by using source amplitude of above 23.6 V/cm, 43°C temperature in the tumour can be definitely achieved. Detailed simulations indicate that the critical source amplitude to achieve 43°C is 23.1 V/cm. At this source level, 43°C in the tumour can be recorded after 54 min heating. When the source amplitude of 26.4 V/cm is applied, 43°C in the tumour can be achieved in approximately 7.2 min.

Figure 11. Temperature rise with the heating time for hyperthermia with a LHM lens applicator of .

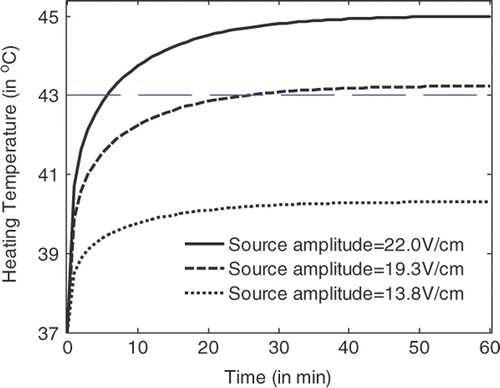
Figure 12 shows the temperature rise at the centre of a tumour volume of 6 mm diameter with the heating time for a hyperthermia system with flat LHM lenses of . It is observed that by using a source amplitude of 22.7 V/cm, temperature above 43°C in tumour volume can definitely be achieved. Detailed simulations indicate that the critical source amplitude is 19 V/cm. When the critical source amplitude is applied, 43°C temperature in the tumour can be recorded after 59 min heating.

Figure 12. Temperature rise with the heating time for hyperthermia with a LHM lens applicator of .

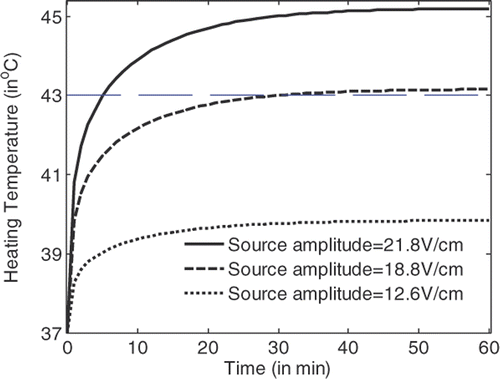
Figure 13 shows the temperature rise with the heating time for a hyperthermia system with flat LHM lenses of n ≈ −3 + 0.00025i. It is observed that by using a source amplitude of 18.8 V/cm 43°C temperature in the tumour volume can definitely be achieved. Detailed simulations indicate that the critical source amplitude is 18.5 V/cm. When the critical power is applied, 43°C can be recorded in the tumour after 54 min heating.

Figure 13. Temperature rise with the heating time for hyperthermia with a LHM lens applicator of .

From Figures 11, 12 and 13, it can be observed that the temperature in the tumour volume rises very fast in the first two min of heating, and rises slowly after about 30 min heating. Hyperthermia with applicators of smaller losses will have lower critical source amplitude to achieve the 43°C temperature in tumour volume. For LHM applicators of losses smaller than characterised by , there is no significant difference between the heating efficiencies. By recording the temperature rise with time in tumour and in tissue, the tumour damage and tissue damage can be calculated.

Further discussion

Hyperthermia of tumour in a circular breast model

In clinic, it is desirable to heat the tumour in a circular breast model. The hyperthermia scheme and the circular breast model used for demonstration are shown in Figure 14. The heterogeneous breast model used in our simulation is shown in Figure 14B. For comparison with the previous observations, the diameter of the circular breast model is kept as 6 cm, and the heterogeneity of the tissue is ±30%. As we discussed above, the breast model and the four LHM lenses are set in coupling medium of to reduce reflection caused by mismatch at the entrance surface of flat LHM lenses.

Figure 14. Hyperthermia of tumour in a circular breast model with four LHM lenses: (A) The system, and (B) Circular breast model.

Figure 15 shows the power deposition and temperature distribution in the circular breast model when a tumour of diameter of 6 mm and centred at (2, −2) is heated by four line sources of microwave of 6 GHz behind the four LHM lenses. From Figure 15, it is observed that, with a source amplitude of 41.5 V/cm for each line source, the peak SAR in the tumour is calculated to be 956.2 W/kg, and in the skin is 619.62 W/kg. In Figure 15A, a highly localised power deposition in the tumour volume can also be observed without any auxiliary foci in normal tissue. As pointed out in [31], further enhanced power deposition will be observed in the tumour volume. By extracting the −3 dB contour line of power deposition, a quasi-circle contour line of diameter of approximately 2.6 mm is obtained, which is about 43% of the tumour diameter. From Figure 15B it is observed that the highest temperature in the tumour volume may increase by about 6°C to approximately 43°C after 60 min heating, while the highest temperature recorded in skin is 38.57°C.

Figure 15. Power and temperature distribution of hyperthermia of a 6 mm tumour centred at (1.5, −1.5): (A) Power deposition, and (B) Temperature distribution.

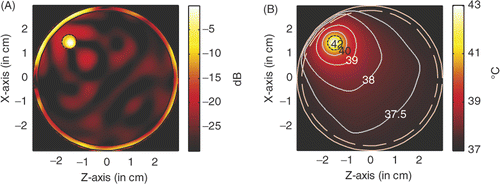
Therefore, for tumour in a circular breast model, microwave hyperthermia can also be implemented. But a large source amplitude is needed, and peak SAR in the skin layer is increased significantly and the highest temperature in skin layer is also raised. If it is acceptable, slightly pressing the breast to reshape it will benefit the hyperthermia to some extent.

Hyperthermia with microwave of different frequencies

In practice, microwaves of different frequencies can be used for hyperthermia. For breast tumour hyperthermia with the proposed four-lens applicator, the thickness of flat LHM lenses is generally defined by the size of breast model according to Equation 1. For specific lens thickness, a flat LHM lens will show a different electric thickness and thus provide focusing spots of different sizes [26] when microwaves of different frequencies are applied for hyperthermia. On the other hand, microwaves of different frequencies will suffer different attenuations when concentrated in the lossy breast tissue.

To show the influences of microwave frequency on the performance of breast tumour hyperthermia, two microwave frequencies, i.e. 6 GHz and 2.45 GHz, will be considered. In the following simulation the diameter of the circular breast model is increased to 10 cm, and thus flat LHM lenses of 10 cm thickness are used in the applicator. The heterogeneity of the tissue is raised to ±50%. All the breast model and the four LHM lenses are set in coupling medium of to reduce reflection caused by mismatch at the entrance surface of the flat LHM lens.

For comparison, we may centre the tumour at (2, −2). Figures 16 and 17 show the power deposition and temperature distribution in the circular breast model when a tumour of a diameter of 6 mm is heated by the four line sources operating at microwave frequence of 6 GHz and 2.45 GHz, respectively. The temperature distribution is obtained after 60 min heating with source amplitude of 41.6 V/cm for 6 GHz and 53.5 V/cm for 2.45 GHz.

Figure 16. Power and temperature distribution of hyperthermia of a 6 mm tumour with 6 GHz microwave: (A) Power deposition, and (B) Temperature distribution.

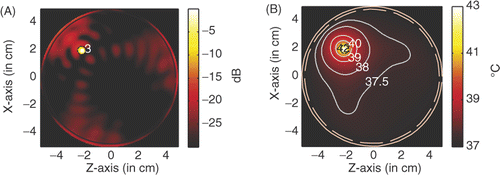
Figure 17. Power and temperature distribution of hyperthermia of a 6 mm tumour with 2.45 GHz microwave: (A) Power deposition, and (B) Temperature distribution.

A comparison between the hyperthermia of a 6 mm tumour with the 6 GHz microwave and 2.45 GHz microwave is shown in Table II. From Table II we have the observation that by using microwaves of 6 GHz, a small heating spot is acquired and a small source amplitude is needed to raise the temperature in the tumour volume to 43°C.

Table II.  Hyperthermia performance of a 6 mm tumour.

		In skin layer			In tumour volume
Microwave frequency	Source amplitude	Peak power level	Highest temperature	Peak SAR	−3 dB power region	Highest temperature	Peak SAR
6 GHz	41.6 V/cm	−14.08 dB	37°C	33.31 W/kg	2.6 mm	43°C	865.12 W/kg
2.45 GHz	53.5 V/cm	−12.81 dB	37°C	18.97 W/kg	5.2 mm	43°C	342.89 W/kg

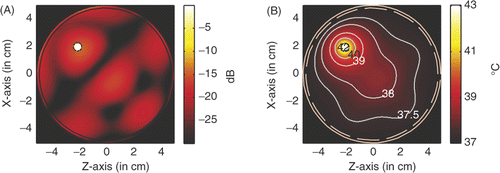
Figures 18 and 19 show the power deposition and temperature distribution in the circular breast model when a tumour of 20 mm diameter is heated by the four line sources of microwaves, of 6 GHz and 2.45 GHz, respectively. The temperature distribution is obtained after 60 min heating. Some major parameters characterising the hyperthermia are listed in Table III.

Figure 18. Power and temperature distribution of hyperthermia of a 20 mm tumour with 6 GHz microwave: (A) Power deposition, and (B) Temperature distribution.

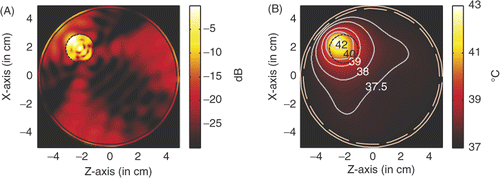
Figure 19. Power and temperature distribution of hyperthermia of a 20 mm tumour with 2.45 GHz microwave: (A) Power deposition, and (B) Temperature distribution.

It should be remarked that in Table III the heating spot for hyperthermia cannot be specified by measuring the −3 dB power region because in the tumour volume more than one peak can be observed in the power deposition shown in Figure 18A. This is due to the use of high frequency (6 GHz) in hyperthermia.

Table III.  Hyperthermia performance of a 20 mm tumour.

		In skin layer			In tumour volume
Microwave frequency	Source amplitude	Peak power level	Highest temperature	Peak SAR	−3 dB power region	Highest temperature	Peak SAR
6 GHz	40.7 V/cm	−8.13 dB	37°C	35.31 W/kg	–	43°C	228.43 W/kg
2.45 GHz	34.9 V/cm	−13.62 dB	37°C	0.52 W/kg	6.2 mm	43°C	11.85 W/kg

From the parameters listed in Tables II and III, we may draw the conclusion that significantly lower input power can be used and a larger heating spot can be acquired in clinic hyperthermia with microwaves of relatively low frequency. For clinical hyperthermia treatment, the lower frequency will be superior to the higher frequency because it will be much easier to guarantee reliable feedback with a large focus than it will be with a small focus.

Conclusions

Preliminary 2-D FDTD simulations demonstrate that flat LHM slabs can be used as hyperthermia applicators. The proposed LHM lens applicator has both the adjustable focal point as array applicators and the simple structure as convex RHM lens applicators. The focal point in the breast can be adjusted simply by changing the source position, without moving the LHM lens if the lens thickness is properly selected. Such convenience is highly desirable in the clinic.

Although the flexibility of the focal point of flat LHM lenses allows the use of a set of thick flat LHM lenses to accommodate varying breast size, the lens thickness or even the lens size should be further optimised for more efficient hyperthermia [35]. In practice, LHM lens applicators of other shapes can also be considered. For example, a Γ-shaped LHM lens applicator or a cylindrical LHM lens applicator would be helpful. The Γ-shaped LHM lens applicator allows the use of thinner and longer flat LHM slabs so that it may be used for efficient hyperthermia of tumours. Different from the four-lens applicator, the Γ-shaped LHM lens applicator is more flexible to accommodate varying breast size without squeezing.

Hyperthermia of a large tumour requires a relatively large focusing spot of flat LHM lens. This can be realised by operating with microwaves of lower frequency. The efficiency of the flat LHM lens hyperthermia system can be further improved by using a directive antenna instead of the point source so that more input power can be captured by the lens aperture and concentrated in the tumour.

Acknowledgements

This work is supported in part by the National Natural Science Foundation of China under Grant 60771041, and by the Department of Personnel of Jiangsu Province of China under Grant 06-E-40.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.