Thermal analysis of magnetic nanoparticle in alternating magnetic field on human HCT-116 colon cancer cell line

Abstract

Purpose: The purpose of this study was to closely investigate the effects of heat dissipation of superparamagnetic nanoparticles on HCT-116 human cancer cell lines cultured under laboratory conditions and also to examine important parameters including size and concentration of nanoparticles, magnetic field frequency, magnetic field intensity, and exposure time.

Materials and methods: Conducting experimental tests required special hardware capable of producing an AC magnetic field with various frequencies. The design and construction process for such an experimental set-up is presented here. First, three different Fe₃O₄ nanoparticle sizes (8, 15 and 20 nm) with different concentrations (d = 10, 20, 40, 80, 160 and 200 µg/ml) were added to cell culture medium and the resulting mixture was exposed to an AC magnetic field with maximum amplitude of 10 kOe for 30 min under three operating frequencies (f = 80, 120 and 180 kHz). The level of intracellular iron was estimated by the ferrozine-based colorimetric assay. Three concentrations including 20, 40 and 80 µg/ml from each of the three nanoparticles sizes were chosen for the study.

Results: It was shown that the power dissipation is a function of frequency, time, nanoparticles size and dose. It was also found that the alternating magnetic field with three different frequencies (f = 80, 120 and 180 kHz) and the maximum amplitude of 10 kOe did not have any adverse effect on cell survival.

Conclusions: Our results demonstrate that where thermal dose is equal to 4.5 ± 0.5 °C/30 min from a starting temperature of 37 °C, HCT-116 cell death is initiated when a magnetic nanoparticle electromagnetic field induced.

Keywords:

• Cancer cell line
• electromagnetic field
• hyperthermia
• magnetic nanoparticles
• thermal dose

Introduction

During recent decades, treating or eliminating cancer tissues through temperature gradients produced by presence of superparamagnetic nanoparticles inside an AC magnetic field has attracted much attention with numerous studies being conducted in this field. In fact, the reason for the destruction of cancer cells by exposure to a high temperature gradient is due to higher sensitivity of the cancer cells to high temperatures compared to healthy cells. Producing a thermal dose about 5–8 °C/30 min from a starting temperature of 37 °C in the cancer cells with respect to the surrounding healthy tissues would decrease oxygen level and normal level of acid concentration in the cells and would cause insufficient nutrients to reach the cancer tissue [1–3]. Thermal dose higher than 10–15 °C/30 min is destructive, causing inflammation and necrosis in the tissue. Therefore, it seems that the temperature difference produced for cells must be within a specific range which depends on design parameters such as nanoparticle size and dose, magnetic field frequency and intensity, exposure time, and type of nanoparticles. More importantly, it is necessary to keep healthy tissue undamaged and intact during the treatment which makes the research in this field more challenging. Nanoparticles generate heat via two mechanisms: Néel and Brownian losses. It has been well-established that these heat losses are functions of time, field intensity and frequency, and physical properties of nanoparticles [4–6]. Due to the similarity of agar gel with living tissue, the experimental tests for determining thermal effect of superparamagnetic nanoparticles on cancer tissue have been carried out on agar gel. However, since there is no blood microperfusion available in agar gel and also there is no criterion for determining the resistive property of tissue against temperature rise, therefore the results on agar gel would most likely be different from the test results on actual living tissues [7–12]. In order to examine thermal effect of superparamagnetic nanoparticles, several studies have been performed on dead tissues. Attar et al. [4] investigated temperature distribution within a cylindrical tissue. In their study, effects of variation of different parameters including blood flow rate and location of injecting the nanoparticles into the tissue were studied [4]. Lv and Liu [13] conducted a series of experimental tests to verify the Pennes bioheat transfer equation. They used symmetric form of the equation in the spherical coordinate and carried out experimental tests on dead tissues in order to compare the experimental results with results of the solution of the Pennes bioheat equation [13]. Numerous studies aimed to calculate temperature distribution by theoretical approaches. Bagaria and Johnson [14] analysed temperature distribution throughout the tissue by solving Pennes bioheat equation in a homogenous and symmetrical spherical coordinate. In their study power dissipation resulted from exposing the nanoparticles to an AC magnetic field, and was assumed to be a second-order function of sphere radius. Then, the optimum temperature distribution was determined with respect to the radius.

Hea et al. [15] studied the effects of micro-perfusion on temperature distribution within the tissue. In order to simulate micro-perfusion, oxygen exchange, and other physical factors they included an empirical relation into the Pennes equation as the term representing the micro-perfusion. They applied the finite element approach to solve Pennes bioheat equation. In another study, by assuming a targeted distribution of nanoparticles throughout the tissue, Liangruksa et al. investigated temperature distribution inside the tissue by solving Pennes bioheat transfer equation in the spherical coordinate. Both homogenous and Gaussian distributions of nanoparticles were examined in their study [16]. There are also a few studies on mouse tissue. The majority of these studies were performed on a particular type of cancer cell and explored the treatment process for a specific time interval (usually a couple of days) [17,18]. Lehui et al. [17] investigated the treatment process after injecting nanoparticles into cancer tissue of mice. Hyperthermic treatment duration was set at 30 min and results of the treatment were measured and reported after 5 days. Similarly, Zhang et al. studied the treatment process on rats with transplanted Guerin carcinoma in which the operating frequency was selected as 300 kHz [18]. Many articles have focused on the effects of electromagnetic fields with frequency of 50 Hz on cells growth and survival. One of the most important concerns in this research area is the effect of electromagnetic fields with frequency range of 80–180 kHz which was not well established. Thus, several studies have aimed at investigating this important area [19–22]. Rivet and et al. [23] investigated superparamagnetic iron oxide nanoparticles (SPIOs) to be used as adjunctive therapy for glioblastoma multiforme radiotherapy; they also used fluorescence imaging to evaluate the extent of neuritis retraction. In this paper retention of chick embryonic cortical neuron viability was analysed under the thermal conditions produced by radiofrequency stimulation of iron oxide nanoparticles.

Oliveira et al. [24] described a preclinical investigation of the feasibility of thermotherapy treatment of bladder cancer with magnetic nanoparticles, performed by analysing the thermal concentration of magnetic nanoparticle heating in rat tissue. Results in Tiago et al. [24] represented the ability of magnetic nanoparticles to increase and to control the thermal dose of rat bladder lumen ≥1 °C/min to a steady state of (41.5 ± 0.5)°C/30 min from a starting temperature of 37 °C with minimal heating of the surrounding healthy cells.

Petryk et al. [25] compared the efficacy of iron oxide nanoparticles and microwave hyperthermia under the same conditions in a mouse mammary adenocarcinoma model. Petryk et al. showed similar tumour treatment efficacy when the heating is delivered by locally delivered magnetic nanoparticles and 915 MHz microwaves at the similar measured thermal concentration. Ivkov [26], and Hilger [27], studied the most important factors in the treatment process with paramagnetic nanoparticles. In this paper, interactions of particle-particle and particle-tissue with respect to achievable heating mechanism of magnetic nanoparticle inside the tumour were examined. Dutz and Hergt [28], represented basic principles of magnetically induced heat generation of magnetic nanoparticles for application in magnetic nanoparticle hyperthermia. In Dutz and Hergt [28], the heating behaviour was derived as a function of tumour size. In previous works, the heating effect of supermagnetic nanoparticles on agar gel in an electromagnetic field with amplitude of 7.3 kOe at f = 50 kHz was investigated [29]. Attar et al. investigated the thermoviscoelastic behaviour of tumorous and healthy bovine liver tissue. In this paper the tumour is simulated as a solid sphere having radius denoted as r along with the surrounding healthy tissue [30]. Bulte et al. [31] studied the hysteresis cycles in magnetic fluid with relevance to hyperthermic applications in cancer therapy. Ruta et al. [32] presented the effects of inter-particle interactions within a self-consistent kinetic Monte-Carlo simulation framework. Tan et al. [33] studied the frequency and the strength of magnetic field dependence of the heat dissipated during hysteresis cycles in magnetic nanoparticles. In another study, Tan et al. [33], by using Monte Carlo methods, investigated the hysteresis cycle of NPs for fine optimisation of heating power.

The present article outlines the design and construction principles to produce a magnetic field appropriate for tests on cells. Then effects of different parameters such as nanoparticle size and dose, frequency and intensity of magnetic field and exposure time on HCT-116 human colon carcinoma cell lines cultured under laboratory conditions are examined. In the current study, for the first time, the effect of magnetic fields with range of 80–180 kHz is investigated in HCT-116 human colon carcinoma cell lines filled with super-paramagnetic nanoparticles. One of the most significant innovations of this article was the application of magnetic fields with frequencies more than 50 Hz which has been investigated for the first time in the present article.

Material and methods

Design and construction of the hardware required for the experimental tests

In order to determine the required size and dose for the superparamagnetic nanoparticles and the exposure time, the first step was to provide a magnetic field with constant and uniform properties. In other words, providing a uniform magnetic field is an important factor in hyperthermic tissue heating. It is also equally important to take into account other technical and medical factors relating to the magnetic field, such as accuracy and precision of the field intensity and frequency, safety, and the achievable field volume. The required field intensity for hyperthermic purpose is much higher than that used in other conventional techniques such as thermal-seeds heating or magnetic resonance images (MRI). The required amplitude for the magnetic fields used in hyperthermia cancer treatment with superparamagnetic nanoparticles is equal to 10 kOe, which is five times greater than that needed for the thermal-seeds heating process. This field requirement imposes some technical challenges and modifications to the coil design and construction; for example, the magnetic core should only be made of ferrite, as other magnetic materials would melt in only a fraction of this field intensity when used as the magnetic core. In order to produce such a magnetic field, a coil with a low number of winding turns and high electric current is needed. It is worth noting that the ohmic loss within coils exponentially increases with the increase in the electric current, and on the other hand temperature rise in the coils increases the coil electric resistance which consequently increases the coil temperature. Thus, a cooling fluid must be applied to decrease the coil temperature. Producing a strong magnetic field inside a coil requires either a high electric current or a large number of winding turns. In simple words, the electric field inside a simple solenoid is expressed by the following relation:

In the above relation, L is the coil’s inductance. Generating a strong alternating magnetic field with high field frequency requires several considerations mainly due to either increased equivalent impedance or increased frequency required for the hyperthermic purpose. The equivalent impedance is described as

At low frequencies, the equivalent impedance is equal to the coil’s ohmic resistance; while at very high frequencies, it is equal to Lω. At a specific frequency, called resonance frequency, the coil’s impedance reaches its maximum value. The resonance frequency is equal to

At frequencies lower than resonance frequencies the coil shows inductive characteristics; while at frequencies higher than resonance frequencies it acts like a capacitor. This is because impedance relating to LR part increases too much so that it only allows negligible electricity current to pass through it. The primary characteristic of a coil to be used in the magnetic fluid hyperthermia is that its operating frequency must be lower than the resonance frequency. Also, at higher frequencies the impedance would also be higher. For this reason, it is more desirable to keep the coil’s impedance as low as possible.

Two additional important points relating to the coil must also be discussed in this section. Conductive materials experience eddy currents at high frequencies. When an alternating flow is passing through a wire, an AC magnetic field is generated around the wire. Therefore, based on Faraday’s law of induction, some currents are formed to oppose the change of flux: eddy currents. The directions of these currents counteract the inner lines and support the outer lines. Although total current passing through the wire is constant, current would move to the surface of the conductor and occupy the lower portion of the wire’s cross section. In other words, at high frequencies, a considerable portion of the wire’s cross section is left without any current, which is equal to using a wire with lower diameter. At higher frequency, this phenomenon (also called skin effect) would be more significant. Skin effect increases the coil’s ohmic resistance due to the decreased cross section. High frequency increases the impedance from two perspectives: inductive resistance and ohmic resistance. According to the above mentioned discussion, characteristics of an appropriate coil for hyperthermic application can now be determined. To reduce the effect of inductive resistance, a coil with a lower number of winding turns must be used, because ohmic resistance and inductance of the coil would also be lower in this case. In this condition, producing the desired electric current for the coil requires lower power. When decreasing the number of winding turns, amplitude of the current must also be increased. The magnetic field inside the coil is directly proportional to both the number of winding turns and the electric current in such a way that decreasing one must be compensated by increasing the other. Decreasing the number of coil windings reduces the proximity effect. When increasing the current’s amplitude, a coil with higher diameter must be selected. And to reduce the skin effect, the ratio of the wire’s lateral surface to cross section must be large enough; i.e. the hollow copper tubes are more desirable for this purpose. Figure 1 demonstrates the coil used in this study.

Figure 1. Examples of the helical coil used in the research.

In order to produce an alternating current with high frequency, the following methods can be used: (1) full bridge, (2) resonance driver, (3) half bridge, and (4) forward and flyback. After closely examining these methods, the half-bridge method was applied for this study due to its higher efficiency and safety factor. Generally, this system has three main components: (1) rectifier and filter circuit, (2) oscillator circuit and gate actuator, and (3) power circuit (which contains a Schottky diode, MOSFET, optical driver, capacitor and coil).

Rectifier circuit

All electronic circuits need a power supply with positive polarity. In other words, a DC electric potential must be applied to the circuits. In this study, first the power supply was rectified and filtered and then it was converted to a DC current. In order to prevent risk of possible electric shocks and to provide a soft start-up for the power capacitor and also to control the current based on the negative feedback method, a series element which is capable of tolerating high power conditions was needed; therefore, a 1000 W lamp was used in the rectifier circuit.

Oscillator circuit

In order to produce an alternating wave, such as a sinusoidal or square wave, an oscillator circuit was required which is capable of producing an AC current with frequency up to 500 kHz supplied from a DC potential input. The oscillator was composed of a switching chipset along with other secondary equipment to control frequency and other parameters, and the frequency produced by the optic gate driver with high starting current was applied to the power element. The reason for the use of the optic gate driver was that the oscillator circuit was supplied with 20-V DC voltage, while the voltage of power element to be applied to the coils was around 350 V. Therefore, the purpose of the optic gate driver was to compensate this voltage difference. The circuit was safe against fluctuations within the amplitude range of the power supply which blocks the circuit input in case of emergency conditions. The frequency of the output wave could be set within 80–180 kHz by rotating a volume control switch.

Power circuit

In order to operate the coil the power components were required to convert DC current into an alternating wave. To produce a magnetic field with the desired intensity a current of 100 A was required which was produced by 10 20-V MOSFETs (by considering a safety factor equal to 2). These MOSFETs required some snubber and damper circuits to counteract the effects of the counter-electromotive force within the coil. Furthermore, to counteract the high frequency harmonics which cause damage to the power capacitors, 36 temperature-resistant capacitors with MKP polypropylene technology were used. The circuit used for testing is shown in Figure 2.

Figure 2. The circuit used for testing the medical device.

Synthesis of nanoparticles

When exposed to an AC magnetic field, superparamagnetic nanoparticles produce heat according to two mechanisms: Néel and Brownian relaxation losses. Power dissipation due to these two losses [4–6,29–30] can be obtained as

On the one hand, the power dissipation is a function of magnetic field frequency and intensity, and on the other hand, it is a function of time, dose and size of nanoparticles and most importantly nanoparticles distribution in the target cells. Achieving a desirable distribution for nanoparticles inside the cells via targeted delivery is an important factor and numerous articles have been published on this topic [4]. Nanoparticles used in this study were Fe₃O₄ with three different diameter sizes (D = 8, 15 and 20 nm). In order to prepare the nanoparticles for the experimental tests, first 200 mg of Fe₃O₄ and 3% oleic acid were uniformly mixed in 500 ml of toluene and then the mixture was poured into four different containers. Then, 4 ml of APTMS and 6 ml of 1 mol TMAH were added to each container. Next, all the containers were placed inside an incubator at 60 °C and 5% CO₂ for 1 h. Precipitated materials, having the same amount of toluene and methanol, were washed and stored in a sterile environment. In order to homogenise the resulting solution it was placed in a centrifugal device at 1000 rpm for 30 min. After this process the resulting solution was completely homogeneous and ready for the experimental tests. The size of the nanoparticles was determined by transmission electron microscopy (TEM) (JEOL, JEM-2010, Tokyo, Japan), see Figure 3.

Figure 3. TEM images of iron oxide magnetic nanoparticles with diameters 8, 15 and 20 nm.

Preparation of cancer cell lines

In order to carry out the tests, HCT human colon carcinoma cell lines were purchased from the Pasteur Institute of Iran and cultured in a Dulbecco’s modified Eagle medium laboratory environment containing 10% fetal bovine serum (FBS) and 2% penicillin–streptomycin antibiotics. The number of cells was counted by trypan blue solution; then, several Petri dishes with diameter of 30 mm were prepared, each having 1 × 10⁴ cultured cells. Next, to provide an appropriate environment for cell growth, the dishes were stored in an incubator at 37 °C, 5% CO₂ and 95% humidity.

Experimental test methods

Investigating the thermal effects of nanoparticles without including the effect of electromagnetic fields is practically impossible. Therefore, in this study three operating frequencies (80, 120 and 180 kHz) were selected and three samples of HCT-116 cell lines were exposed to the magnetic fields without adding any nanoparticle with the three above-mentioned frequencies for 30 min. Previous studies have investigated the influence of electromagnetic fields with frequency of 50 Hz on HCT-116 cell’s growth and survival but few studies have focused on the influence of electromagnetic fields within the frequency range of 80–180 kHz.

In order to study the effects of electromagnetic fields on HCT-116 cell growth, three control dishes were placed at centre of the coil under a constant temperature of 37 °C for 30 min under magnetic fields with frequencies of 80, 120 and 180 kHz and with intensity of 10 kOe. Then trypan blue assay was applied to determine the percentage of HCT-116 cells killed. When studying HCT-116 cell survival by trypan blue assay, the cell culture medium was replaced at 30 min by new cell culture medium containing 0.4% trypan blue solution.

Next, HCT-116 cells were stored in the incubator for about 3 to 4 h under complete darkness to allow the insoluble formazan crystals to form. After replacing the trypan blue solutions with dimethyl sulphoxide (DMSO) solution, the crystals were dissolved producing a crimson-coloured solution; principally, a stronger crimson colour suggested that more HCT-116 cells had survived. Optical absorbance of the samples was measured at wavelength of 550 nm. In the second step the toxic effect of the three types of nanoparticles should be examined. Therefore, different concentrations of each three nanoparticles, from 10 to 2000 µg/ml were added to the Petri dishes in an incubator at 37 °C for 24 h. Although for examination of toxic effect of nanoparticles, 30 min was probably enough, to be sure, 24 h was selected. After 24 h of adding nanoparticles and counting HCT-116 cells to a maximum concentration of 2000 µg/ml, no adverse effects were observed. So the conditions for testing for concentration equal or less than 2000 µg/ml were provided. Many studies have investigated the effectiveness of intracellular thermal therapy compared to extracellular thermal therapy. Percentage of nanoparticle absorption by cancer cells is very important during the treatment process. It is particularly important to find an accurate, simple and inexpensive method to calculate SPIOs during clinical tests. Various methods have been introduced to determine the appropriate level of nanoparticles inside the cells. In this study, in order to determine intracellular iron, a ferrozine-based colorimetric method was utilized [31]. The ferrozine-based assay is one of the most reliable methods to measure iron levels in cells and many studies have been conducted about it. Many researchers have used this method. The method used in this study was similar to as follows.

After adding the doses of nanoparticles to Petri dishes, the Petri dishes are placed in an incubator overnight at 37 °C. To determine the intracellular iron levels of the cells, the cells were washed three times with cell culture medium. Then a mixture of 100 µL of HCL, 100 µL of FeCl₃, 100 µL of iron-releasing reagent containing 4.5% of KMnO₄ was prepared. The mixture was incubated for 120 min at 42 °C. Then the mixture was cooled down and 30 µL of iron-detection reagent that contains 6 mol ferrozine, 6 mol neocuproine, 2.2 mol ammonium acetate, and 1.1 mol ascorbic acid) added to 150 µL of the mixture after 30 min and absorbance at 550 nm is measured. In fact, the iron level of cells is calculated by the amount of absorption of the mixture before and after adding the nanoparticles. In the following, a mixture composed of 3 cm³ of FBS with cell culture medium and different nanoparticle concentrations (d = 10, 20, 40, 80, 160 and 200 µg/ml) was prepared for each nanoparticle size and then stored in several 3-cm Petri dishes. Three operating frequencies (80, 120 and 180 kHz) were selected for the tests. Two samples/repetitions were prepared for each concentration value, each frequency and each nanoparticles size. Each Petri dish was then assigned a unique number. Next, the numbered Petri dishes were placed separately inside the machine in succession for about 30 min. Every 5 min, the temperature of the solution was measured and recorded by thermometer. Tests were performed in an environment with approximate temperature of 37 °C to eliminate or limit environmental factors. In order to eliminate environmental factors, two methods were proposed: in the first method, cell culture containers were completely insulated and then placed inside the coil. In the second method a completely insulated container that contained water at 37 °C was installed inside the coil; the container was also equipped with a heating element and a thermostat to maintain the water temperature at a constant value of 37 °C. In this approach the cell culture containers were carefully insulated so that no water could penetrate them. Through experimentation it was observed that presence or absence of cells in 3 cm³ of cell culture medium did not make any change to the values of temperature increase, so doses of 10, 20, 40, 80, 160 and 200 µg/ml were selected to draw curves of hyperthermic temperature difference/time. The experiment was repeated several times until the results were accurate. In order to measure the temperature, a highly accurate digital thermometer (calibrates by using plasma enhanced vapor deposition (PECVD) systems by Plasma Fanavar Jam in Iran) with accuracy of 0.01°C was used. In this experiment, temperature was measured every 5 min.

Figure 4. Percentage viability of HCT-116 human cancer cell lines under magnetic field with maximum intensity equal to 10 kOe and f = 80 kHz. D: diameter.

Results

Tests on the cells showed that regardless of type and size of the nanoparticles, all the cells were killed at thermal doses equal to 4.5 ± 0.5 °C/30 min from a starting temperature of 37 °C for non-toxic concentrations of nanoparticles with diameter 8, 15 and 20 nm under an alternating magnetic field with maximum intensity equal to 10 kOe. Therefore, in order to provide a better understanding and comparison of the results, hyperthermic thermal dose of 4.5 ± 0.5 °C/30 min for non-toxic concentrations of nanoparticles with diameter 8, 15 and 20 nm under an alternating magnetic field with maximum intensity equal to 10 kOe was considered the minimum required value to kill all the HCT-166 cells; obviously with increasing hyperthermic temperature difference the process of cell killing will accelerate. Tables 1, 2 and 3 represent values of the dimensionless temperature difference, Θ = (T − 37)/4.5 for 30 min. For Θ with initial temperature of 37 °C larger than 1 ± 0.1 for 30 min under an alternating magnetic field with maximum intensity equal to 10 kOe, all of the cancer cells will begin to die. By going further away from the resonance frequency, the coil operates like a capacitor, causing the magnetic field’s intensity to decrease. As a result, the resulting temperature gradient also decreases. It was observed that under the same frequency, by increasing nanoparticle sizes, the resulting temperature gradient decreased. Among three different nanoparticle sizes in this study, due to appropriate nanoparticle–AMF matching, 8-nm nanoparticles generated higher temperature difference under the same nanoparticle dose.

Table 1. Increase in the dimensionless temperature difference Θ for different concentrations of nanoparticles with diameter equal to 8 nm.

	d (µg/ml)
t (min)	10	20	40	80	160	200
f = 80 kHz
0	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01
5	0.08 ± 0.01	0.14 ± 0.01	0.22 ± 0.01	0.39 ± 0.01	0.65 ± 0.02	0.78 ± 0.01
10	0.14 ± 0.01	0.24 ± 0.01	0.38 ± 0.02	0.69 ± 0.01	1.14 ± 0.01	1.37 ± 0.02
15	0.20 ± 0.02	0.34 ± 0.02	0.60 ± 0.02	1.13 ± 0.01	1.89 ± 0.02	2.27 ± 0.02
20	0.28 ± 0.02	0.48 ± 0.02	0.85 ± 0.02	1.57 ± 0.01	2.62 ± 0.02	3.14 ± 0.03
25	0.36 ± 0.03	0.61 ± 0.02	1.10 ± 0.02	1.98 ± 0.02	3.20 ± 0.03	3.84 ± 0.03
30	0.42 ± 0.03	0.76 ± 0.02	1.21 ± 0.02	2.10 ± 0.02	3.40 ± 0.03	4.20 ± 0.03
f = 120 kHz
0	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01
5	0.06 ± 0.01	0.11 ± 0.01	0.17 ± 0.01	0.31 ± 0.01	0.52 ± 0.02	0.63 ± 0.01
10	0.11 ± 0.01	0.19 ± 0.01	0.34 ± 0.01	0.54 ± 0.01	0.90 ± 0.02	1.10 ± 0.01
15	0.16 ± 0.01	0.27 ± 0.02	0.48 ± 0.02	1.00 ± 0.01	1.49 ± 0.02	1.88 ± 0.01
20	0.22 ± 0.01	0.40 ± 0.02	0.68 ± 0.02	1.25 ± 0.02	2.07 ± 0.02	2.40 ± 0.02
25	0.30 ± 0.02	0.49 ± 0.02	0.88 ± 0.02	1.60 ± 0.02	2.32 ± 0.03	2.80 ± 0.03
30	0.34 ± 0.02	0.57 ± 0.03	0.97 ± 0.03	1.68 ± 0.02	2.69 ± 0.03	3.40 ± 0.03
f = 180 kHz
0	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01
5	0.06 ± 0.01	0.11 ± 0.01	0.17 ± 0.02	0.31 ± 0.01	0.49 ± 0.01	0.62 ± 0.01
10	0.11 ± 0.01	0.18 ± 0.01	0.29 ± 0.02	0.54 ± 0.02	0.90 ± 0.01	1.09 ± 0.02
15	0.16 ± 0.02	0.27 ± 0.02	0.48 ± 0.02	0.89 ± 0.02	1.42 ± 0.02	1.79 ± 0.03
20	0.22 ± 0.01	0.38 ± 0.02	0.68 ± 0.03	1.25 ± 0.03	2.09 ± 0.02	2.51 ± 0.02
25	0.29 ± 0.02	0.49 ± 0.02	0.88 ± 0.02	1.59 ± 0.03	2.56 ± 0.02	3.07 ± 0.02
30	0.33 ± 0.02	0.60 ± 0.02	0.97 ± 0.02	1.66 ± 0.03	2.55 ± 0.02	3.32 ± 0.03

Bold type indicated thermal dose can be dead all of HCT-116 cells at hyperthermia treatment under magnetic field with strength of 10 kOe.

Table 2. Increase in the dimensionless thermal dose Θ for different nanoparticle concentrations with diameter of 15 nm.

	d (µg/ml)
t (min)	10	20	40	80	160	200
f = 80 kHz
0	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01
5	0.07 ± 0.01	0.12 ± 0.01	0.18 ± 0.01	0.33 ± 0.01	0.57 ± 0.01	0.67 ± 0.01
10	0.11 ± 0.01	0.19 ± 0.01	0.30 ± 0.01	0.55 ± 0.01	0.92 ± 0.01	1.10 ± 0.01
15	0.17 ± 0.02	0.29 ± 0.02	0.51 ± 0.02	0.96 ± 0.02	1.60 ± 0.02	1.93 ± 0.02
20	0.24 ± 0.02	0.40 ± 0.01	0.72 ± 0.02	1.33 ± 0.02	2.23 ± 0.02	2.67 ± 0.02
25	0.32 ± 0.02	0.55 ± 0.02	0.99 ± 0.02	1.78 ± 0.02	2.88 ± 0.02	3.46 ± 0.02
30	0.36 ± 0.02	0.64 ± 0.01	1.09 ± 0.02	1.89 ± 0.03	2.89 ± 0.02	3.70 ± 0.03
f = 120 kHz
0	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01
5	0.05 ± 0.01	0.09 ± 0.02	0.14 ± 0.02	0.26 ± 0.01	0.44 ± 0.01	0.52 ± 0.01
10	0.09 ± 0.02	0.15 ± 0.01	0.24 ± 0.01	0.41 ± 0.01	0.71 ± 0.01	0.86 ± 0.01
15	0.13 ± 0.01	0.22 ± 0.02	0.38 ± 0.01	0.72 ± 0.01	1.20 ± 0.01	1.44 ± 0.02
20	0.19 ± 0.01	0.32 ± 0.01	0.56 ± 0.01	1.00 ± 0.02	1.74 ± 0.02	1.88 ± 0.02
25	0.26 ± 0.02	0.44 ± 0.03	0.78 ± 0.02	1.34 ± 0.02	2.28 ± 0.02	2.73 ± 0.02
30	0.28 ± 0.03	0.50 ± 0.02	0.85 ± 0.02	1.42 ± 0.02	2.40 ± 0.02	3.00 ± 0.02
f = 180 kHz
0	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01
5	0.04 ± 0.01	0.07 ± 0.02	0.12 ± 0.01	0.21 ± 0.01	0.37 ± 0.02	0.43 ± 0.01
10	0.07 ± 0.02	0.12 ± 0.01	0.19 ± 0.01	0.34 ± 0.01	0.60 ± 0.01	0.70 ± 0.02
15	0.10 ± 0.02	0.18 ± 0.01	0.30 ± 0.02	0.59 ± 0.02	1.01 ± 0.01	1.18 ± 0.03
20	0.15 ± 0.01	0.26 ± 0.02	0.45 ± 0.02	0.82 ± 0.02	1.40 ± 0.01	1.88 ± 0.02
25	0.20 ± 0.03	0.35 ± 0.02	0.63 ± 0.02	1.08 ± 0.02	1.84 ± 0.02	2.18 ± 0.02
30	0.23 ± 0.02	0.41 ± 0.01	0.68 ± 0.02	1.16 ± 0.02	1.94 ± 0.02	2.46 ± 0.02

Bold type indicated thermal dose can be dead all of HCT-116 cells at hyperthermia treatment under magnetic field with strength of 10 kOe.

Table 3. Increase in the dimensionless thermal dose Θ for different nanoparticles concentrations with diameter of 20 nm.

	d (µg/ml)
t (min)	10	20	40	80	160	200
f = 80 kHz
0	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01
5	0.06 ± 0.01	0.10 ± 0.01	0.17 ± 0.01	0.30 ± 0.01	0.51 ± 0.01	0.59 ± 0.01
10	0.10 ± 0.01	0.17 ± 0.01	0.27 ± 0.02	0.49 ± 0.02	0.82 ± 0.01	0.98 ± 0.01
15	0.15 ± 0.02	0.25 ± 0.02	0.44 ± 0.02	0.84 ± 0.02	1.44 ± 0.02	1.71 ± 0.02
20	0.21 ± 0.03	0.36 ± 0.02	0.65 ± 0.02	1.20 ± 0.02	2.00 ± 0.03	2.38 ± 0.02
25	0.29 ± 0.03	0.50 ± 0.02	0.90 ± 0.02	1.62 ± 0.02	2.62 ± 0.02	3.08 ± 0.02
30	0.32 ± 0.02	0.58 ± 0.03	0.98 ± 0.02	1.70 ± 0.03	2.66 ± 0.02	3.29 ± 0.02
f = 120 kHz
0	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01
5	0.04 ± 0.01	0.07 ± 0.01	0.11 ± 0.01	0.20 ± 0.01	0.34 ± 0.01	0.39 ± 0.01
10	0.07 ± 0.02	0.11 ± 0.01	0.17 ± 0.01	0.31 ± 0.02	0.54 ± 0.01	0.65 ± 0.02
15	0.10 ± 0.02	0.16 ± 0.02	0.28 ± 0.02	0.56 ± 0.02	0.93 ± 0.01	1.09 ± 0.03
20	0.14 ± 0.02	0.23 ± 0.02	0.41 ± 0.02	0.60 ± 0.01	1.29 ± 0.02	1.66 ± 0.02
25	0.18 ± 0.02	0.31 ± 0.02	0.56 ± 0.02	0.96 ± 0.03	1.70 ± 0.02	2.04 ± 0.02
30	0.21 ± 0.03	0.38 ± 0.03	0.62 ± 0.02	1.07 ± 0.01	1.78 ± 0.03	2.26 ± 0.03
f = 180 kHz
0	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01	0.00 ± 0.01
5	0.04 ± 0.01	0.07 ± 0.01	0.11 ± 0.01	0.20 ± 0.01	0.34 ± 0.01	0.40 ± 0.01
10	0.07 ± 0.01	0.11 ± 0.01	0.18 ± 0.02	0.32 ± 0.01	0.54 ± 0.02	0.66 ± 0.01
15	0.10 ± 0.02	0.17 ± 0.01	0.29 ± 0.02	0.56 ± 0.02	0.91 ± 0.02	1.05 ± 0.01
20	0.14 ± 0.02	0.23 ± 0.02	0.40 ± 0.03	0.73 ± 0.02	1.26 ± 0.01	1.67 ± 0.02
25	0.19 ± 0.02	0.33 ± 0.01	0.59 ± 0.02	1.02 ± 0.02	1.66 ± 0.01	2.05 ± 0.03
30	0.21 ± 0.03	0.39 ± 0.02	0.64 ± 0.01	1.10 ± 0.02	1.75 ± 0.02	2.31 ± 0.03

Bold type indicated thermal dose can be dead all of HCT-116 cells at hyperthermia treatment under magnetic field with strength of 10 kOe.

However, on the other hand, very high temperature difference may also be destructive for the surrounding healthy cells; therefore, further studies are required to determine the necessary temperature gradient inside the cells during magnetic fluid hyperthermia. In order to closely examine the thermal effect of nanoparticles on cells, all the nanoparticles concentrations must be studied; however, due to the following reason, only a limited number of concentrations were considered in this paper. First, concentrations higher than 80 µg/ml ∼ 30 min, (thermal dose >43 °C/30 min) ensures that all the cells would be destroyed under the thermal effect of the nanoparticles so any cell resistance against the temperature could not be fully examined. On the other hand, due to the high costs associated with the tests, it was not possible to perform the tests on all the samples and it seemed that three nanoparticles concentrations, 20, 40 and 80 µg/ml, from each of the nanoparticle types, were sufficient for 30-min testing. As explained before, a ferrozine-based colorimetric method was used according to Bulte et al. [31] to determine the iron content in the cells at the three concentrations considered in this study. The related results are shown in Table 4.

Table 4. The amount of intracellular iron for three concentration (d = 20, 40 and 80 µg/ml) as computed by the ferrozine-based colorimetric.

SPIOs: D = 8 nm
d (µg/ml)	20	40	80
Uptake, n = 3(pg Fe/cell)	8.1 ± 1.2	14.2 ± 1.8	20.1 ± 1.2
SPIOs: D = 15 nm
d (µg/ml)	20	40	80
Uptake, n = 3 (pg Fe/cell)	7.1 ± 1.7	13.8 ± 1.6	18.1 ± 2.0
SPIOs: D = 20 nm
d (µg/ml)	20	40	80
Uptake, n = 3 (pg Fe/cell)	6.2 ± 1.4	11.1 ± 1.7	16.1 ± 2.0

D: diameter; SPIOs: superparamagnetic iron oxide nanoparticles.

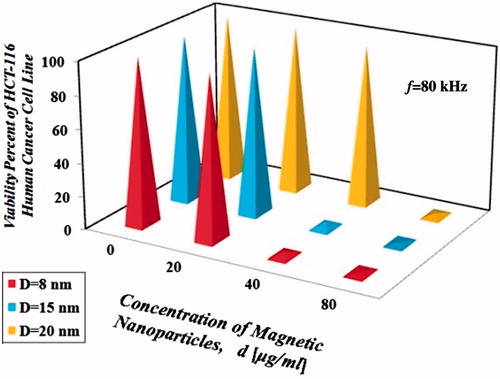
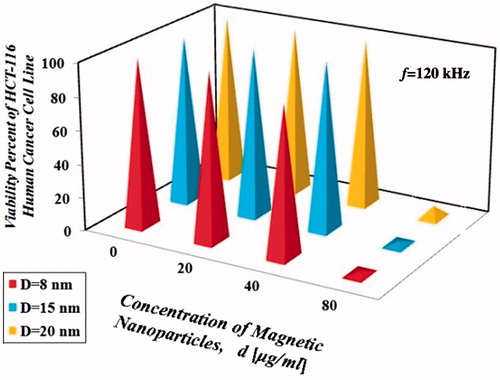
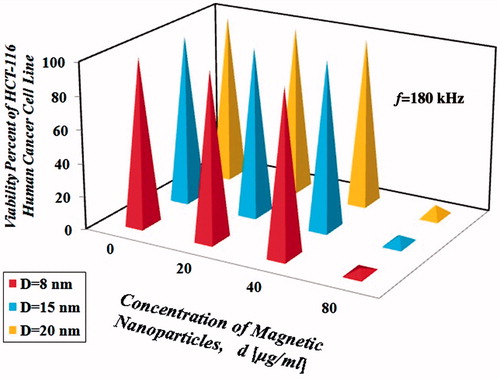
The amount of intracellular iron in HCT-116 human cancer cell line without nanoparticles was equal to 0.01 pg Fe/cell. Percentage of HCT-116 cells survival rate is shown in Figures 4–6 for the three operating frequencies.

Figure 5. Percentage viability of HCT-116 human cancer cell lines under magnetic field with maximum intensity equal to 10 kOe and f = 120 kHz. D: diameter.

Figure 6. Percentage viability of HCT-116 human cancer cell lines under magnetic field with maximum intensity equal to 10 kOe and f = 180 kHz. D: diameter.

Discussion

First, the effects of an electromagnetic field with maximum amplitude of 10 kOe and frequencies of f = 80, 120 and 180 kHz on HCT-116 cells were investigated. Results show that the 30-min exposure to the electromagnetic field did not have an adverse effect on the HCT-116 cells.

One of the primary objectives of this study was to investigate direct effects of thermal dose on hyperthermic treatment performance of HCT-116 human cancer cell lines. As indicated by the results, the increasing size of the nanoparticles decreased the dimensionless hyperthermic temperature difference; however, we cannot generalise this statement, i.e. according to Rosensweig [5], there exists an optimum size for nanoparticles that can generate the maximum temperature difference. Results related to iron content inside the cells are presented in Table 4. As mentioned earlier, these results were obtained using ferrozine-based colorimetric method. According to the results, nanoparticles with diameter equal to 8 nm were absorbed at greater rates than other diameters, under the same concentration. These results are in good agreement with results in Bulte et al. [31]. In a similar concentration (d = 40 µg/ml) of the three types of nanoparticles, nanoparticles with a size of 8 nm, for the same time (30 min), killed ahigher percentage of HCT-116 cells. Nanoparticles with a size of 8 nm at the same magnetic intensity, frequency, time, and concentration provided more effective heating/cytotoxicity than the 15 or 20 nm nanoparticles because of the following.

1. At the same concentration in comparison with other nanoparticles (15 and 20 nm), they had the same amount of intracellular iron level (see Table 4).

2. In comparison with other nanoparticles (D = 15 and 20 nm) in the same concentrations, they contained more concentration of Fe which is more important than the size of the nanoparticles.

As shown in Tables 1–3, it can be concluded that the resulting dimensionless hyperthermic temperature difference depends on various factors such as size, concentration and type of the nanoparticles and frequency of the magnetic field. According to the results, choosing an operating frequency closer to the resonance frequency obviously increased the power dissipation which yielded the same results, but in a shorter time period and with lower nanoparticle concentration. According to the results presented in the Tables 1–3, it was observed that the increasing trend in the temperature difference was not always linear and sometimes followed a relation in the order of two or more. By examining the results presented in Tables 1–3, it seems that when nanoparticle concentration was doubled, although temperature also increased, it was not doubled, which might be due to losses. Based on the results in Figures 4–6, hyperthermia treatment with frequency equal to 80 kHz, with the same type and concentration of nanoparticles (d = 40 µg/ml for 30 min with initial temperature of 37 °C) was more effective at heating than the other frequencies (f = 120 and 180 kHz), this situation is due to the fact that the resonance frequency of the coil used in this study (), is 80 kHz. Results show that concentration of all three sizes of nanoparticles (8, 15 and 20 nm), under magnetic field with intensity of 10 kOe and frequencies of 80, 120 and 180 kHz for 30 min with initial temperature of 37 °C, greater than or equal to 80 µg/ml, can easily kill all the HCT-116 cells.

Concentration of 200 µg/ml of three sizes of nanoparticles 8, 15 and 20 nm within 30 min under magnetic field with intensity 10 kOe and frequency 80 kHz can raise temperature to about 55.9, 53.6 and 51.8 °C (Θ = 4.20, 3.70 and 3.29 °C), from an initial temperature of 37 °C, respectively. Concentration of 200 µg/ml is not toxic, but this concentration unusually raises the temperature of HCT-116 much more than the amount needed to treat. So using smaller non-toxic concentrations of Θ > 1 + 0.1 is suggested.

Conclusion

In this study the effects of different parameters of magnetic fluid hyperthermia on HCT-116 human cancer cell survival were investigated by performing experimental tests. Comprehensive technical information about constructing a device capable of producing the required alternating magnetic field with maximum intensity H = 10 kOe and different frequencies f = 80, 120 and 180 kHz for hyperthermic purpose was presented in this article. According to the results, subjecting HCT-116 cells to a thermal dose equal to 41.5 °C/30 min would kill. The results obtained in this study suggest that an alternating field with maximum intensity H = 10 kOe and frequencies f = 80,120 and 180 kHz for about 30 min did not have an adverse effect on cell survival. According to the results, it seems that when the operating frequency gets closer to the resonance frequency (f = 80 kHz), the hyperthermic temperature difference of nanoparticles increases under the same conditions. Nanoparticles with a diameter of 8 nm exposed to a magnetic field of 10 kOe with three operating frequencies of 80, 120 and 180 kHz generated more heat compared to nanoparticles with diameters 15 and 20 nm.

Disclosure statement

The authors gratefully acknowledge funding of this research by the Islamic Azad University, Hamedan Branch, and Cancer Models Research Centre, Tehran University of Medical Sciences, Tehran, Iran. The authors alone are responsible for the content and writing of the paper.