Commentary on the clinical and preclinical dosage limits of interstitially administered magnetic fluids for therapeutic hyperthermia based on current practice and efficacy models

Abstract

We offer a critique of what constitutes a suitable dosage limit, in both clinical and preclinical studies, for interstitially administered magnetic nanoparticles in order to enable therapeutic hyperthermia under the action of an externally applied alternating magnetic field. We approach this first from the perspective of the currently approved clinical dosages of magnetic nanoparticles in the fields of MRI contrast enhancement, sentinel node detection, iron replacement therapy and magnetic thermoablation. We compare this to a simple analytical model of the achievable hyperthermia temperature rise in both humans and animals based on the interstitially administered dose, the heating and dispersion characteristics of the injected fluid, and the strength and frequency of the applied magnetic field. We show that under appropriately chosen conditions a therapeutic temperature rise is achievable in clinically relevant situations. We also show that in such cases it may paradoxically be harder to achieve the same therapeutic temperature rise in a preclinical model. We comment on the implications for the evidence-based translation of hyperthermia based interventions from the laboratory to the clinic.

Keywords:

• Magnetic hyperthermia
• magnetic nanoparticles
• SPIONs

Introduction

Although it is now sixty years since the concept of magnetic hyperthermia as a therapeutic modality was first proposed [1], and a decade or more since the first clinical results were reported [2,3], it is clear that it is of significant current interest. In the year 2015 alone, more than 750 scientific and clinical papers were published on magnetic hyperthermia [4], which surely reflects the substantial world-wide R&D effort that has been devoted to the field in recent years. This effort has been accompanied by significant funding at both national and international levels – the latter exemplified by the ca. EUR 40 million that the European Commission has allocated in the area in the last five years [5].

One likely reason for the large scale of this funding is that the research is increasingly moving beyond laboratory-scale experiments, towards preclinical studies with a variety of animal models, and in some cases even further, towards full-scale clinical studies, with all of the complexity and cost that this entails [6]. As such it is more important than ever for researchers to address the translational research imperatives of constructing appropriately scalable animal model experiments that generate data of a quality and relevance suitable for an ethics committee or a clinical R&D approvals committee. It is only when clear and cogent arguments can be made to link promising preclinical results to an expected advantageous outcome in man that clinical studies may be suitably designed, approvals sought and granted, and the study itself successfully undertaken and completed.

In this context, it is perhaps surprising that – to our knowledge at least – there is very little available in the literature regarding the practicalities of designing for the transition from preclinical to clinical studies of magnetic hyperthermia. There are a great many published works that report on preclinical models in isolation, but very few that take the next step to explain how to get from the animal model to man. Even in cases where the step has perforce been taken – such as in the work of Andreas Jordan and colleagues at MagForce AG in Berlin [2,3] – the process has not been spelled out in a way that makes it accessible or comprehensible to others. It may be that the reason for this is that it is impossible to provide a simplistic “one size fits all” solution for an extremely varied field in which there are numerous different clinical indications requiring very different materials, administration routes, formulations and medical device architectures – and that it is not useful to try to draw any generally applicable conclusions on the matter. However, in our opinion this is a subject that should be considered and discussed, even if at the same time we acknowledge that every study will be unique unto itself, and every study protocol – both preclinical and clinical – will still need to be evaluated on its own merit.

With this in mind, we present here a commentary on the question of what is an acceptable dosage for the interstitial injection of a magnetic fluid in both a preclinical model and in a clinical study of magnetic hyperthermia. We focus on interstitial administration rather than systemic intravenous injection on the basis that the former is both a much less complex route to clinical translation, and a more effective one. Where it is helpful to do so, we include descriptions of current practice for intravenous administration, to compare and contrast with the case for interstitial administration. We provide evidence to support our position based on both current regulatory and clinical practice, and on theoretical biophysical modelling of the heat flows associated with therapeutic magnetic hyperthermia and/or thermoablation.

Interstitial versus intravenous administration

We begin by commenting further on our rationale for focussing on interstitial rather than intravenous administration, which brings up several central issues of significance, namely in relation to formulation challenges, therapeutic efficacy, intended primary mode of action, adverse effect levels and preclinical-to-clinical scaling, and species-dependent local guidelines on maximum injection volumes.

Interstitial administration may allow less complex formulation

Iron oxide particles presenting in the bloodstream inherently come into direct contact with the body’s reticuloendothelial system (especially those elements in the blood, spleen and liver), so that blood clearance times can be very short [7]. For this reason, with intravenous administration, an additional step of surface functionalisation of the nanoparticles is usually pursued, in an effort to produce “stealth” particles. This may well be effective [8], but it undoubtedly adds to the complexity of the material. There are also issues related to the presence of any inorganic nanomaterial in the blood, such as the inducement of a protein corona effect, or of complement activation (a protein-mediated proxy stimulation of an immune response), that should preferably be avoided or at least controlled [9]. These all add to the challenges of gathering sufficient safety-related evidence to secure the ethical and regulatory approvals required before clinical studies may be conducted.

The corresponding situation for interstitial injection is not entirely different – after all, magnetic fluids injected into tissue, such as a tumour stroma, or the adjacent connective tissue, will still encounter active agents of the reticulo-endothelial system, especially those macrophages that pass through the extracellular matrix. However, the direct injection route allows for greater flexibility in the choice of the surface chemistry of the particles, including non-functionalised particles – such as the aminosilane-coated iron oxide nanoparticles used by MagForce [10] – that would be quickly taken up in the liver or spleen if they were delivered intravenously. Also, it should not be overlooked that it may well be a desirable aspect of the use of magnetic nanoparticles that the body does, over time (weeks or months), metabolise and clear the material away from the injection site.

Interstitial administration may be more effective

It has long been recognised that individual magnetic nanoparticles cannot deliver sufficient heat to be effective [11]. The problem is a fundamental one: to be good magnetic heaters, the particles need to be small – typically 10–30 nm in diameter – so that they contain only a single magnetic domain at body temperature [12]. (Multi-domain particles contain magnetic domain walls that can be relatively easily moved in a time-varying magnetic field, limiting the energy dissipation that is needed to generate heat.) However, this small size means that their surface area to volume ratio is large, so that heat dissipation is rapid and thermal equilibration with the environment almost instantaneous [13]. The only way to overcome this is to have an ensemble of nanoparticles at the target site, acting in unison, so that the summed action of the distributed heat sources may together raise the temperature of the local environment.

Even in such cases, substantial local concentrations of nanoparticles are needed. Hergt and Dutz estimated that with the then state-of-the-art materials and appliances, viz. those with a heat transfer rate of 100 W/g_FeOx (where the subscript “FeOx” denotes the heat-generating magnetite and/or maghemite iron oxide nanoparticles), a local concentration of ca. 10 mg_FeOx/ml would be needed to heat an 11 mm diameter tumour by ΔT = 15 K, while ca. 40 mg_FeOx/ml would be needed to heat a 3 mm diameter tumouroid (at the diagnostic size limit for metastatic cancer) by ΔT = 5 K [11]. Such high concentrations are conceivable following interstitial injection, but – to date at least – they are very challenging after intravenous injection, where an extremely effective (and not yet realised) local trapping and retention mechanism would need to be employed. This applies both to the lower threshold of achieving the ΔT ≈ 6 K required for clinical hyperthermia (an operating temperature in vivo of 43 °C), as typically employed as an adjuvant to chemotherapy or radiotherapy [14,15], and even more so for the higher threshold of ΔT ≥ 23 K required for the more demanding therapeutic treatment of thermoablation, which requires an operating temperature in vivo of 60 °C or more [16].

Factors affecting the dispersion of magnetic nanoparticles in tissue

A corollary of the requirement for there to be a substantial local concentration of magnetic nanoparticles at the treatment site is that the dispersion of the particles into the tissue, in and around the injection site, is a determining feature of the procedure. This is a complex field of research, where the physical factors of the procedure (such as the tissue density and porosity, the catheter size, design and placement, and the infusion rate and volume), and the physicochemical properties of the magnetic fluid (such as the particle size, charge and surface coating, and the osmolality, viscosity and concentration of the fluid as a whole), all contribute and are all inter-related. Operational issues such as the volume of the injectate or infusate relative to the tolerable tissue-loading limit (which varies between tissue types and from site to site in the body), the potential for tissue damage if the infusion rate is too high, and backflow (a.k.a. reflux) along the needle path leading to leakage of the infusate away from the intended site, are also factors to be considered and controlled.

The question of the homogeneity of the dispersion is a challenging one, as ideally the distribution should be as uniform as possible, to simplify the process of modelling and predicting the dose–response characteristics of the hyperthermia treatment. However, this is not easy to achieve, as typically the target tissue (e.g. a tumour) is itself heterogeneous, and in any case, the interstitial administration of any fluid will naturally result in a higher concentration of material near the tip of the needle than at a distance further removed from the tip. That said, there are strategies (discussed in more detail in Section “In vitro, preclinical and clinical measurements of V_d/V_i”) that can be adopted to abrogate these effects, including the use of slow infusion rates [17–21] and reflux-resistant catheters [20,22], and performing multiple-site small-volume injections rather than a single large-volume injection [2,3,10,23]. Theoretical models of the diffusion mehanistics can also be called upon to help understand the process and design best-practice administration protocols [23,24].

Defining and measuring the interstitial dispersion factor, V_d/V_i

A positive aspect of the situation is that in practical terms the post-administration outcome is an experimentally measurable quantity: viz. the dispersion factor V_d/V_i, where V_d is the tissue volume throughout which the injected material is dispersed, and V_i is the volume of fluid injected. As such, it is at least in principle possible to determine the optimum delivery conditions via post-hoc assessment and serial refinement. Indeed, V_d/V_i is measurable, depending on the nature of the fluid, in a number of ways, including in vivo methods such as magnetic resonance imaging (MRI), magnetic particle imaging (MPI), or X-ray computed tomography (CT) imaging, or ex vivo methods such as histochemistry or histopathology.

For clinical translation, the MRI and CT methods are attractive in that they are already routinely available world-wide, whereas while MPI is a promising emerging modality [25], it has a long way to go before it might become established in clinical settings. Regarding MRI versus CT, at first sight it might seem that MRI would be the natural modality to use, given that it is very sensitive to iron oxide nanoparticles, some of which are or have been used as intravenous T₁ and T₂* contrast agents [26]. However, this sensitivity leads to extensive artefacts in the MRI images obtained of locally concentrated magnetic particles [27], which make quantification difficult. For this reason, CT imaging is the preferred modality. This applies both to clinical CT studies, such as those undertaken by the MagForce team as part of their patient-specific treatment planning [10,28–30], and also to preclinical micro-focussed CT studies [18,31–33].

The key advantage for both CT and micro-CT is that the V_d/V_i dispersion factor is quantifiable in terms of the observed iron concentration in the tissue (measured in mg_Fe/ml_tissue), since the presence of the iron significantly affects the local value of the X-ray attenuation coefficient μ. This in turn is related to the greyscale contrast in any given X-ray scanner via the industry-standard Hounsfield Unit (HU) scale, which is a linear transformation in which the radiodensity of distilled water is defined as zero HU, and the radiodensity of air is defined as −1000 HU. In a voxel with average linear attenuation coefficient μ: (1) where μ_water and μ_air are respectively the linear attenuation coefficients of water and air. Gneveckow et al. have reported that for iron concentrations above ca. 10 mg_Fe/ml_tissue the radiodensity exceeds ca. 60 HU [30], which is a level that is distinguishable from, for example, breast cancer tumour tissue, which has a radiodensity of ca. 35 ± 20 HU [34]. The same authors subsequently reported on clinical studies of 10 prostate cancer patients, where radiodensities in the range ca. 150–200 HU were recorded for cases where the anticipated in situ iron concentration was ca. 55 mg_Fe/ml_tissue [2].

In vitro, preclinical and clinical measurements of V_d/V_i

Consequently, despite the complexity of the inter-related physical, chemical and material factors that contribute to V_d/V_i for a given system, progress has been made towards understanding and, just as importantly, controlling the interstitial administration process. For example, Zhu et al. have conducted some illuminating studies on infusion strategies for magnetic fluids, using both in vitro gel phantoms [17], and in vivo murine models [18]. They reported that quasi-homogeneous in vivo dispersions (as measured by micro-CT) could be repeatably obtained using a syringe pump to provide very slow (3 μl/min for 30 min) intratumoural delivery of the agent through a very fine gauge (26 gauge, 0.26 mm inner diameter) needle [18]. Furthermore, they were able to systematically vary the V_d/V_i dispersion factor in xenograft tumours from 0.77 ± 0.06 at the 3 μl/min rate, up to 1.26 ± 0.24 at a faster 5 μl/min rate [18].

A similarly slow and controlled infusion strategy is being clinically pioneered for the intracranial delivery of drugs to treat brain cancer [19–21]. Convection enhanced delivery (CED) involves the surgical placement of a catheter into the tumour, followed by infusion of the therapeutic agent into the target over a prolonged period, typically several hours. Reported data here include two clinical cases where Gd-DPTA was infused into human brain stem lesions, with measured V_d/V_i values of 2.4 and 3.7 [35], and preclinical experiments where ¹⁴C-labelled albumin was infused into the striatum of rats, yielding V_d/V_i values of order 5 [36]. Another aspect of CED that may be of particular note in the context of magnetic hyperthermia is that significant effort is being directed towards designing novel catheters that minimise or eliminate reflux of the infusate back up the catheter/tissue interface track [20,22].

The MagForce team’s approach has been to make multiple-site low-volume injections into a variety of tumour types in an effort to achieve quasi-homogeneous distribution of their magnetic fluid agent over entire tumours. For example, in one paper they report on the case of a prostate cancer patient for whom a total dose of 12.5 ml of agent was administered into a 35 ml target volume in the form of 24 depots of ca. 0.5 ml each [2]. In that particular case, it is not clear that the approach was successful, given that the post-administration CT image shows distinct separation between the neighbouring depots [2]. Other cases are more convincing, as seen in the CT scans they show for glioblastoma multiformae patients, for which the CT contrast does not discernibly vary over the entire tumour volume as treated [3,37]. The authors note that the total injected dosages that were applied in these cases corresponded to ca. 0.3–0.4 ml of magnetic fluid per ml of tumour tissue for one set of 22 prostate and cervical cancer and soft tissue sarcoma patients [3], and a median dosage of 0.28 ml of magnetic fluid per ml of tumour tissue for a set of 66 glioblastoma multiformae patients [37]. If we take these figures to be representative of V_i and V_d volumes respectively, this corresponds to clinical estimates of mean V_d/V_i values for the magnetic fluid of ca. 2.5–3.3 in the first instance, and ca. 3.6 in the second instance.

More individual-patient-specific data are presented in another report from the MagForce team, regarding a cohort of patients with non-resectable and pre-treated rectal, cervical and ovarian tumours [10]. Under CT-guidance, the administered magnetic fluid volumes in this study ranged up to ca. 83% of the tumour volume, with a mean of ca. 41%. The authors noted that at these levels: “instillation of the nanoparticles could be performed well and all patients tolerated the procedure without side effects” [10]. If we convert these percentages into corresponding V_d/V_i values (assuming homogeneous distribution, as was the team’s objective), we obtain a minimum of ca. 1.2 and a mean of ca. 2.4.

To place these values in context, it is perhaps instructive to note that V_d/V_i values in the vicinity of 3 are comparable to the figure that one might predict if one assumed that the injected fluid infiltrated only the extracellular part of the tissue. We can show this by taking, as a rough estimate, the commonly quoted figures for a 70 kg male, viz. that ca. 28 litres of the body’s fluid resides within cells, compared to 10.5 litres in the interstitial extracellular spaces [38]. In this case, if the injected fluid displaced all the interstitial fluid in a given volume of tissue, the corresponding V_d/V_i would be of order 38.5/10.5 ≈ 3.7. Of course this is not a very precise result, but it is perhaps a useful figure for comparative purposes. For example, the Zhu group’s reported dispersion factors of V_d/V_i ≈ 0.8–1.3, achieved using very slow infusion-pump-controlled delivery, and MagForce’s V_d/V_i ≈ 1.2 in one particular pelvic cancer patient, might both be considered to be examples of “beating” the intrinsic fluid displacement mechanism, while MagForce’s mean values of V_d/V_i ≈ 3.6 in brain cancer tumours might considered to be closer to the “natural” level.

Regulatory pathways may depend on the administration route

Another important reason to focus on interstitial administration is that the regulatory pathway to clinical translation may be substantially less complex than would be the case for intravenous injection, particularly in cases where the injectable fluid might be considered to be a medical device. National and international regulatory authorities, such as the US Food and Drug Administration (FDA) or the European Medicines Agency, set out many detailed criteria against which a given substance must be tested to gauge whether it should be treated as a medical device or as a medicinal product, the description of which is beyond the scope of this paper. Nevertheless, as a guiding principle, a product may be regulated as a medical device if its manufacturer can establish that its primary mode of action (PMOA) is physical in nature, and not pharmacological, immunological or metabolic.

With magnetic hyperthermia agents, it might reasonably be argued that the PMOA is a physical mechanism, namely the local generation of heat through the transduction of an externally applied time-varying magnetic field into heat-inducing magnetisation reversals in magnetic nanoparticles. Furthermore, in the case of interstitial administration of such an agent, parallels may be drawn with the PMOAs of implantable medical devices, such as the recently approved Magseed^® from Endomag Ltd (Cambridge, UK), which is a grain-of-rice sized magnetisable steel implant used for lesion localisation. In contrast, it is not so obvious how one could make a similar argument in the case of the administration route being intravenous.

In this paper, we will proceed under the assumption that the PMOA of the interstitially introduced hyperthermia agent is physical, and that as such the intervention associated with its use may be considered to be that of a medical device. It should be noted, however, that other PMOAs might be envisaged for hyperthermia agents, including their designation as drug-device combination products, in which case more pharmaceutical-oriented regulatory pathways might need to be adopted.

We note in passing that irrespective of whether the agent is regulated as a device or a drug or a combination product, there are also safety considerations regarding the time-varying magnetic field source itself, and regarding the effect of those time-varying fields on the human body. Detailed consideration of this is beyond the scope of the current work, but the subject has been addressed elsewhere [13,39–41]. Similarly, the clinical treatment plan for a given patient (which includes the duration and schedule of the hyperthermia treatment session or sessions) will have a direct impact on both the safety and efficacy of the intervention. Again, detailed discussion of this is beyond the scope of this work, and the subject has been reviewed elsewhere [42–45].

Lastly, it should be noted that with regard to regulatory pathways, the magnetic hyperthermia “system” as a whole may in some cases – depending on jurisdiction – be taken to include both the introduced hyperthermia agent and the attendant time-varying magnetic field source acting together, or as one acting as an accessory to the other. Such demarcations have significant implications with regard to the nature of the clinical studies that need to be performed to establish their safety for the respective national and international regulatory authorities.

Adverse effect levels and preclinical-to-clinical scaling depends on the administration route

Regulatory authorities have a responsibility to scrutinise all aspects of the safety of the proposed medical intervention, including setting the conditions under which clinical studies may be undertaken. In this context, we note that the FDA has published a “guidance for industry” document in which they describe how one should estimate the maximum safe starting dose for therapeutics (or other agents) in initial clinical trials in healthy adult volunteers – and that these conditions are quite different for interstitial versus intravenous administration [46]. In both cases, the safe starting dose in humans is estimated from preclinical studies, but the methodology is quite different.

Preclinical-to-clinical scaling for intravenous administration

For intravenously administered pharmaceuticals, the FDA stipulates that escalating-dose preclinical studies should be performed to establish the “no observed adverse effect level” (NOAEL) for a given agent in terms of the mg of administered agent per kg total mass of the animal. The FDA notes what it considers to be the sort of findings that can be used to determine the animal NOAEL, as follows: overt toxicity (e.g. clinical signs, macro- and microscopic lesions); surrogate markers (e.g. serum liver enzyme levels); and exaggerated pharmacodynamic effects [46]. However, it is up to the manufacturer to decide precisely which tests to undertake for a given agent.

Once an animal NOAEL has been determined, this is converted to a “human equivalent dose” (HED), which is then used to calculate a “maximum recommended starting dose” (MRSD) for the initial clinical studies after applying a downscaling factor, usually taken to be 10: (2) where the subscript i.v. denotes intravenous administration.

The HED_i.v. term is determined from the measured animal NOAEL_i.v. by normalising to body surface area, which is taken to correlate with the species-specific metabolic rate [46,47]. For a given species, the normalising factor K_m is estimated by dividing the average body weight of the species by its corresponding average body surface area. For example, for a mouse of body weight 0.021 kg and surface area 0.007 m², K_m^mouse = 3 kg/m²; while for humans the reference weight is taken to be 60 kg and body surface area 1.62 m², yielding K_m^human = 37 kg/m² [46,47]. The HED_i.v. is then calculated as: (3)

For example: for a murine preclinical model, the HED_i.v. in mg/kg equals the NOAEL_i.v. in mg/kg measured in the mouse, multiplied by a factor K_m^mouse/K_m^human = 0.081.

Preclinical-to-clinical scaling for interstitial administration

For interstitial administration of agents, the FDA guidance is that the NOAEL to HED_interstitial conversion may be achieved either by normalising to concentration, or to the amount, of the agent at the injection site. For magnetic hyperthermia agents where, as discussed above, we know that the local distribution and parameters such as V_d/V_i determine the efficacy of the agent, it is clear that from a regulatory perspective we should normalise to the local concentration at the injection site: (4) where the concentration is calculated as the mass of the injected agent (the magnetic nanoparticles) divided by the volume V_d (measured in ml_tissue) into which the agent is dispersed. The MRSD should be downscaled as before: (5)

The FDA does not provide any particular guidance on how to determine the animal NOAEL in the case of interstitial administration, but it is clear that one should consider potential local toxicity, as well as systemic toxicity. For the former, it is logical to look for indicators such as inflammation and granulation at the injection site, alongside the usual systemic toxicology biomarkers such as haematology, clinical observation and histopathology [48,49].

Maximum injection volume depends on the administration route

Regarding the scaling of preclinical NOAEL results to clinical HED and MRSD values, one final point to note is that in addition to the administration route, the selection of injection site has a bearing on the injection volume V_i that may be used [50]. This is illustrated in Table 1, which shows the Duke University Medical Center’s local guidelines for the site-dependent maximum injection volumes permitted in healthy mice, rats, rabbits and humans [47]. On inspection one can see clearly that the maximum allowable V_i does not scale either with body weight or body surface area. This species-dependent variation can be important when one considers which is the most suitable animal model to use for a given clinical indication.

Table 1. Exemplar guidelines for the maximum injection volumes of experimental compounds in mice, rats, rabbits and humans (of the given FDA reference body weights) on the basis of the administration route, as used by the Duke University Medical Center in Durham, NC, USA [47].

Route	Mouse (20 g)	Rat (150 g)	Rabbit (1.8 kg)	Human (60 kg)
Subcutaneous	2 ml/site	10 ml/site	50 ml/site	2 ml/site
Intramuscular	0.1 ml/site	0.3 ml/site	0.5 ml/site	5 ml/site
Intraperitoneal	3 ml	10 ml	100 ml	5 ml
Intravenous	0.2 ml	0.5 ml	5 ml	250 ml
Intradermal	0.05 ml/site	0.05 ml/site	0.1 ml/site	0.1 ml/site

Furthermore, the maximum guideline doses for one site (e.g. subcutaneous injections) may be tens or even hundreds of times greater than those for another site (e.g. intramuscular or intradermal ones). This rightly reflects the differing physiology and anatomy of those sites, and the different species’ respective tolerances to paternal administration at those sites; but again it may impact the choice of animal model, and as such should be duly considered.

It is also significant that guidelines such as those in Table 1 are local guidelines, falling within the purview of the local ethics and R&D approvals committees, so that they may well vary from one institution to the next. For example, the guidelines for the US National Cancer Institute in Frederick, MD, although being very similar to those at Duke University, nevertheless cite a 4× larger figure for mouse/subcutaneous injections, and 3× smaller figure for rat/intramuscular injections [51].

Lastly, the guidelines in Table 1 refer to injections into healthy tissue. The corresponding guidance for intratumoural injections is somewhat less explicit, as the acceptable dose scales with the tumour volume. Giustini et al. report on injecting a magnetic hyperthermia fluid into 50–200 mm³ murine adenocarcinoma tumours at a ratio of 0.34 μl per mm³ of tumour [52]. Assuming that in this case the magnetic fluid dispersed over the entire tumour volume, this corresponds to a V_d/V_i of order 3, which is in line with the values discussed above. In humans, intratumoural injection volumes can be of similar magnitudes, or larger. Hassenbusch et al., for example, reported a pharmaceutical dose escalation study on 40 patients with recurrent malignant glioma [53]. In the V_i-escalation part of this study, injection volumes of 25%, 50% and 75% of the tumour volumes were trialled, with no adverse events observed at either the 25% or the 50% level. The maximally tolerated dose was determined to be 5 ml.

Acceptable dosage limits according to current clinical practice

Having explored some of the issues associated with the administration route, we turn now to the question of what is an acceptable dosage for the interstitial injection of a magnetic fluid? Our starting point is to review the dosages that the manufacturers of currently available commercial products recommend to clinical users, as those manufacturers will certainly have already passed through the animal NOAEL to HED to MRSD pathway on their way to commercialisation.

There are four such products currently available: two of them, Resovist^® and Feraheme^®, are intravenously administered, and are regulated as drugs; the other two, Sienna+^® and Nanotherm^®, are interstitially administered, and are regulated as medical devices. (N.B. As described above, the drug/device designation is determined by the mode of action of the material, rather than the mode of administration.) All four manufacturers will have had to meet stringent regulatory standards as part of their respective accreditation processes, and as such the figures quoted in their published instructions for use (IFU) pamphlets¹ may be considered to be reliable indications of the acceptable limits for their product’s use, in terms of both tolerance and efficacy.

Review of recommended dosages for clinically approved materials

In the 1990 s and 2000 s, Resovist^® was manufactured in Europe by Schering AG (Berlin, Germany) and in Asia by Fujifilm RI Pharma (Tokyo, Japan), but since 2010 it has been made and used exclusively in Japan. Resovist^® – also known as “ferucarbotran” – is a medicinal product intended for intravenous use as an MRI contrast agent for liver lesions. It is supplied in 0.9 ml or 1.4 ml syringes and comprises dextran-coated multi-core iron oxide nanoparticles. According to its Schering-era IFU [54]:

The amount of iron in the recommended dose of Resovist^® (0.9 ml in patients <60 kg body weight, 1.4 ml in patients ≥60 kg body weight, corresponding to 5.8–12.9 μmol Fe/kg by weight) is equivalent to about 1% of normal whole-body iron content. This is equivalent to the normal dietary intake of iron in 2–3 days. Administration of this amount of iron will result in transient changes in serum iron, ferritin and iron-binding capacity, but there is no danger of iron overload.

Resovist^® contains 28 mg_Fe/ml, so the maximum recommended dose of 1.4 ml in a 60 kg human corresponds to 0.65 mg_Fe/kg, although, somewhat curiously, the 12.9 μmol_Fe/kg limit quoted in the IFU corresponds to the slightly higher figure of 0.72 mg_Fe/kg. Interestingly, another version of the IFU, published in 2002 by distributors Agis Commercial Agencies Ltd [55], contained the following note:

The maximum dose tested in humans, 0.08 ml Resovist^® (equivalent to 2.24 mg Fe) per kg body weight, was well tolerated.

which indicates that intravenous doses up to 2.24 mg_Fe/kg (or 40 μmol_Fe/kg) have been tested in humans with no adverse effects.

Feraheme^® – also known as “ferumoxytol” – is made by AMAG Pharmaceuticals (Waltham, MA, USA), and is a medicinal product intended for intravenous use as treatment of iron deficiency anaemia in adult patients with chronic kidney disease. It comprises carbohydrate-coated iron oxide nanoparticles, and is supplied in 17 ml vials at a concentration of 30 mg_Fe/ml. According to its IFU [56]:

The recommended dose of Feraheme^® is an initial 510 mg dose followed by a second 510 mg dose 3 to 8 days later. Administer Feraheme® as an intravenous infusion in 50–200 ml 0.9% Sodium Chloride Injection, USP or 5% Dextrose Injection, USP over at least 15 min.²

Assuming 60 kg as an adult human’s minimum weight, the 510 mg dose corresponds to 8.5 mg_Fe/kg, which is quite a lot higher than the Resovist^® dose. That said, elsewhere in the IFU, the manufacturers describe some preclinical models as follows:

Administration of ferumoxytol during organogenesis, at doses of 31.6 mg Fe/kg/day in rats and 16.5 mg Fe/kg/day in rabbits, did not result in maternal or foetal effects. These doses are approximately 2 times the estimated human daily dose based on body surface area.

Assuming that they followed the FDA’s guidelines for calculating HEDs from animal models [46], we can estimate what AMAG mean by “the estimated human daily dose”. For a rat the conversion factor is 6.2, while for a rabbit it is 3.1, so that it is apparent that AMAG is referring here to a safe-level human daily dose of ca. 2.6 mg_Fe/kg. This figure is close to the Day 0 dose divided by 3, which is understandable as AMAG advise that the second dose should be on Day 3 to Day 8. Thus, it is clear that AMAG advise that a bolus injection of up to 8.5 mg_Fe/kg is safe, so long as any repeat of that bolus injection comes at least 3 days later.

Sienna+^® is made by Endomag Ltd (Cambridge, UK) and is a medical device intended for interstitial use as a magnetic tracer as part of a system to mark and locate lymph nodes prior to surgical removal. It is supplied in 2.2 ml vials and comprises dextran-coated iron oxide nanoparticles. Each ml of Sienna+^® contains 28 mg Fe. According to its IFU [57]:

Recommended dose is 2 ml with the equivalent iron content of 55 mg ± 4 mg per dose. […] For Breast: Draw 2 ml of Sienna+^® [and] 3 ml of 0.9% sterile saline into the syringe [into a syringe and administer] by subcutaneous injection into either subareolar or peritumoural interstitial tissue, and follow with 5 min vigorous massage at the injection site. […] For other indications: Draw 2 ml of Sienna+^® [into a syringe and administer] by subcutaneous injection into peritumoural interstitial tissue and, where appropriate, follow with 5 min massage at the injection site.

From this, it is clear that the maximum recommended dose is 2 ml or 56 mg_Fe, delivered directly into the tissue. If this was given to a 60 kg adult the effective dose would be 0.93 mg_Fe/kg, although the more relevant parameter given the interstitial administration route is the local Fe concentration at the injection site, in mg_Fe/ml_tissue. Assuming, as per the MagForce data that was discussed in Section “In vitro, preclinical and clinical measurements of V_d/V_i”, a V_d/V_i dispersion factor of 2.4 – which we choose as being representative of that which has been clinically achieved following intratumoural injection [10] – we can speculate that the maximum injected in-tissue concentration may be 56 mg_Fe in 4.8 ml_tissue, or ca. 12 mg_Fe/ml_tissue. Note that this is for the non-breast indications; and that in the case of breast cancer, the administered concentration is lower due to the additional 3 ml of saline, taking the maximum in-tissue concentration down to ca. 5 mg_Fe/ml_tissue. Note also that it is likely that the V_d/V_i dispersion factor in peritumoural tissue will be different from the 2.4 figure used here, which was measured for tumour tissue.

Nanotherm^® is made by MagForce AG (Berlin, Germany), and is an aminosilane-coated iron oxide nanoparticle ferrofluid. At the time of writing, no official company-issued IFUs were found online, but several scientific publications are available, including a 2011 paper on the clinical treatment of recurrent glioblastoma multiformae, a type of brain cancer, that contained the following passage [37]:

The magnetic fluid MFL AS1 (NanoTherm AS1; MagForce Nanotechnologies), an aqueous dispersion of superparamagnetic nanoparticles with an iron concentration of 112 mg/ml, served as the energy transducer. […] The median amount of magnetic fluid injected was 4.5 ml (range 0.5–11.6 ml), corresponding to a median dosage of 0.28 ml of magnetic fluid per cm³ of tumour volume.

From this, we deduce that the maximum administered dose in the study was 11.6 ml or 1300 mg_Fe, delivered directly into the brain tissue – which is a substantial amount. If we again consider a representative V_d/V_i dispersion factor of 2.4, then, given that the injected fluid contained 112 mg_Fe/ml, the maximum in-tissue concentration in all cases was ca. 47 mg_Fe/ml_tissue. This figure appears to be internally consistent, given that the value quoted by MagForce as the median dosage of the treatment, viz. 0.28 ml of Nanotherm^® per ml of tumour tissue, equates to ca. 31 mg_Fe/ml_tissue.

Summary and implications of current clinical practice

The two intravenously introduced iron-oxide-based magnetic fluids, Resovist^® and Feraheme^®, have maximum indicated or reported doses of ca. 2.2 mg_Fe/kg and 8.5 mg_Fe/kg, respectively, with the proviso that Feraheme^® should not be administered more frequently than once every three days. If administered daily, it is separately reported by AMAG that up to ca. 2.6 mg_Fe/kg of Feraheme^® is safe and well tolerated.

For the two interstitially introduced fluids, Sienna+^® and Nanotherm^®, the most appropriate metric is the magnetic particle concentration at the injection site. Although neither manufacturer states the mg_Fe/ml_tissue values explicitly, we can make educated guesses as to their values, subject to assumptions regarding the dispersion characteristics of the injected fluid. Within these constraints, for Sienna+^® we estimate that the recommended dose equates to at most ca. 12 mg_Fe/ml_tissue, while the median and maximum reported Nanotherm^® doses are ca. 31 mg_Fe/ml_tissue and 47 mg_Fe/ml_tissue, respectively. Regarding the latter figure, given the wide spread reported in the MagForce studies, it seems prudent to regard this as an outlier; in which case a more representative value for the maximum level should be closer to the median – we suggest a value of ca. 40 mg_Fe/ml_tissue.

From this, we can draw some indicative conclusions regarding the dose limits that might be kept in mind when developing Fe-based magnetic fluids for therapeutic benefit in humans, as follows:

1. that for intravenous administration there are clinical products in use today for which total Fe dosage administered at any one time may be as high as 8.5 mg_Fe per kg of body weight; and for which the total daily Fe dosage may be as high as 2.5 mg_Fe per kg of body weight; and

2. that for interstitial administration, assuming a dispersion factor of V_d/V_i = 2.4, there are clinical products in use today for which the local Fe dose is up to 12 mg_Fe/ml_tissue per site for subcutaneous injections and up to 40 mg_Fe/ml_tissue per site for intratumoural injections.

The limits in (1) are derived from the published data on Feraheme^® for the one-off dose, and on both Feraheme^® and Resovist^® for the daily dose; and those in (2) are derived from the published data on Sienna+^® (subcutaneous) and Nanotherm^® (intratumoural), respectively.

It should be emphasised that these values are specific to the materials in question, and their intended uses. For example, Feraheme^® has been formulated to be well tolerated in the blood stream, and rapidly taken up in the liver and spleen, and therefore its intravenous dosage limit may be higher than that of other formulations of similar products. On the other hand, the intended use for Sienna+^® is that it should be transported away from the injection site through the lymphatic system, which is arguably not relevant to the situation one might foresee for a magnetic hyperthermia agent. In this context, the dose limit associated with Nanotherm^® is the most relevant for researchers in the field, although again it is likely to be formulation dependent – particularly with respect to the V_d/V_i dispersion factor. That said, the “up to 40 mg_Fe/ml_tissue per site for intratumoural injections” limit has clearly been clinically tested, and as such is a useful touchstone for the development of alternative hyperthermia agents and the designing of preclinical and first-in-man clinical safety and dose-escalation studies.

Design of preclinical studies of intratumoural magnetic hyperthermia

We return now to the issue of how to design for the transition from preclinical to clinical studies of hyperthermia. We illustrate the process here with respect to a prospective intratumoural administration route, but similar steps will need to be taken for whichever injection site is relevant for a given therapeutic indication.

Establish dose limits based on the intended clinical use

Let us imagine, for illustrative purposes, that we have formulated a magnetic hyperthermia agent with an intratumoural V_d/V_i dispersion factor of 2.4, and that the iron concentration of the agent can be varied continuously up to, say, 120 mg_Fe/ml. (N.B. We are ignoring here the problems associated with the high viscosity of highly concentrated fluids.) Using the clinical experience of the Nanotherm^® intratumoural injections, we can anticipate an in situ dosage limit of C_o = 40 mg_Fe/ml_tissue per site of injection, which – given that V_d/V_i = 2.4 – means that the concentration of the fluid should not exceed (V_d/V_i) × C_o = 96 mg_Fe/ml.

Next we must consider the degree of retention of the injected agent at the tumour site. There are many factors that contribute to this, including the formulation of the agent, the injection method employed (e.g. multiple or single doses; infusion or bolus; speed of withdrawal of the needle), the character of the tumour and its surrounding tissue, and the kinetics of both the initial dispersion of the agent and its subsequent clearance, over time, by the reticuloendothelial system. Bazan-Peregrino et al. have reported on a number of the non-formulation factors that affect retention, showing for one particular tumour type in a murine model that the injection method could change the retention from ca. 80% down to ca. 40% of the administered dose, and that changing to another tumour type brought the retention up to ca. 95% [58]. Their injectate was an adenovirus, and their measurements were recorded 30 min after injection, which they inherently considered to be sufficient to achieve homeostasis. We might reasonably expect that a magnetic fluid injectate might be formulated to have a similar degree of retention at a similar timepoint. Regarding the rate of macrophage-mediated clearance, MagForce have reported clinical CT imaging data for a prostate cancer patient that clearly shows substantial retention of intratumourally administered magnetic nanoparticles a full six weeks after the injection date [2]. In this respect, we can therefore reasonably expect that formulations can be found that allow for prolonged material retention at the injection site.

Regarding the character of the tumour and its surrounding tissue, the Bazan-Peregrino et al. data show that different tumours types have different retention characteristics. It should also be noted that the intratumoural injection site itself may have an effect: e.g. whether the injectate is encountering the stroma or the parenchyma of the tumour, or the proliferative versus quiescent versus necrotic regions of the tumour. Furthermore, tumours often have different microenvironments (including elevated interstitial pressures, hypoxia and acidosis) than do the surrounding tissues, and different tissues themselves have different perfusion and clearance characteristics. All of these biological factors represent challenges to successful delivery and retention [59,60]. While this is clearly difficult and unpredictable, nevertheless it is also clearly surmountable, as the MagForce experience shows, given the right formulation and the right mode of (interstitial) administration.

Let us therefore proceed, and assume, for our hypothetical clinical indication, that we expect the retention of the magnetic agent to be “good”, at  = 85%, so that only (1 – ) = 15% of the dose is lost via perfusion into the bloodstream. Let us further assume that the formulation of our agent, albeit not explicitly intended for intravenous use, is also “good”, and that the maximum allowable systemic dose is a factor  = 85% of the daily intravenous administration limit ( = 2.5 mg_Fe/kg) established for Feraheme^® and Resovist^®.³ We can then estimate the maximum allowable intratumoural injected dose limit, as per the formula: (6) to be  = 14.2 mg_Fe/kg for this “good” retention and formulation scenario. It should be noted that will vary between one agent and another. For example, an agent with a relatively “poor” performance scenario of low retention ( = 0.5) and low systemic tolerance ( = 0.5) would be limited to a  = 2.5 mg_Fe/kg. In an “excellent” scenario, with say  = 0.95 and  = 1.00, the maximum would be much higher, with  = 50 mg_Fe/kg. We note in passing that MagForce have reported on clinical studies that have involved the injection of magnetic fluids into the human prostate of doses in the range 1.1 to 1.5 g of iron [61], which, assuming that their subjects had total body masses up to say 90 kg, would fall within the expected limits of a “very good” product with both and values of order 87%.

Equation (6)(6) embodies the notion that despite the agent being formulated with interstitial administration in mind, we still need to consider its safety with regard to systemic delivery. This also impacts on preclinical studies, in that it indicates that dose-escalation studies should be undertaken to establish or verify intravenous NOAELs and HEDs – just as for systemic agents – using the FDA’s body surface area factors to scale between the preclinical and clinical cases. For example in a murine preclinical model the Feraheme^® and Resovist^® daily intravenous dose level of  = 2.5 mg_Fe/kg_human would correspond, using Equation (3)(3) and the scaling factor K_m^human/K_m^mouse = 12.3, to an intravenous NOAEL dose limit of ^mouse = 30.8 mg_Fe/kg_mouse. Applying this to the “poor”, “good” and “excellent” retention and tolerance scenarios discussed for man, and assuming a mouse of body mass 20 g, the corresponding ^mouse estimates are ca. 0.6, 3.5 and 12.3 mg_Fe, respectively.

With these figures in mind, we note from the literature that research groups around the world are adopting a wide range of different dosing protocols in their mouse models. Some apply less than 1 mg_Fe per mouse [62,63], while others use ca. 4 mg_Fe per mouse [64]. The largest doses we found were ca. 25 mg_Fe per mouse, as used by the Zhu group [18,31]. At a glance these seem high doses, although it should be noted that they were achieved using that group’s controlled infusion strategy, so that near 100% interstitial retention might be assumed. Indeed, putting  = 0.98 and  = 1.00 into Equation (6)(6) one obtains ^mouse = 25 mg_Fe.

Consider formulation with reference to projected clinical efficacy

The next step is to model the efficacy of the projected treatment, in order to establish the functional bounds within which the magnetic heating agent will need to operate. The efficacy depends on both the physical properties of the agent (in particular the magnetic heating characteristics of the magnetic nanoparticles) and the physical properties of the time-varying activation field (in particular its amplitude H and frequency f).

Given these parameters, various theoretical models exist that describe the expected biophysical heat flows in different conditions, which we can use to predict in silico the temperature increase ΔT at and around the injection site. Surveying a selection of recent publications on such models in the field of magnetic hyperthermia [65–72], two things are apparent: (i) that the methods that different authors adopt to address the problem are many and varied, and can be mathematically very complex; and (ii) they all take as their starting point the “Pennes equation”: (7) where , and are the density, specific heat capacity and temperature of the tissue; , and are the corresponding parameters for blood; is the thermal conductivity of the tissue; is the blood flow rate per unit tissue volume; and and are heat generation rates due to tissue metabolism and external sources, respectively. The Pennes equation is named after an American neurologist who in 1948 was the first to introduce the terms representing the heat transfer due to perfusion and metabolism to the classical heat equation [73]. The external power dissipation term is an additional term which in the current context equates to the heating through magnetic hyperthermia, but which more generally can refer to any non-metabolic heat source.

In this paper, it is not our intention to critique the various available bioheat models for magnetic heating, nor do we wish to introduce a comprehensive but complex model that covers multiple scenarios such as time-dependent effects, thermally-varying perfusion or variations in metabolic rate between tumour tissue and healthy tissue. Such considerations have been covered in other works, including those already cited [65–72]. Instead, we present here a simple analytical model that enables a “first approximation” predictive step to be taken in the translation of magnetic hyperthermia, directed towards treatment planning. This is the magnetic thermotherapy equivalent of the “dose–response” therapeutic paradigm: i.e. that it is incumbent on the practitioner to understand and be able to predict the expected response to a given treatment dose.

We therefore consider here a simple analytical model, in which the effects of both perfusion and metabolism are neglected, and in which it is assumed that an equilibrium state has been achieved, so that . The model is based on that of Andrä et al. [74], who considered the temperature distribution within and surrounding a spherical volume of radius R containing a uniform distribution of magnetic nanoparticle heat sources that in effect acts as a composite heat source. Although Andrä et al. describe in some detail the time evolution of the heat distribution around the source, they also showed that in the equilibrium state – achieved after prolonged exposure – the temperature distribution as a function of distance r from the centre of the sphere could be expressed analytically as: (8a) (8b) where is the power density (in W/m³_composite) being delivered to the sphere, and and are the thermal conductivities (in W/Km) of the composite core and the surrounding medium. This distribution is plotted in Figure 1 for various realistically achievable values of , from which it can be seen that the temperature distribution is largely unaffected by such changes, and that the more important determinant of the observed ΔT is the power density P.

Figure 1. Equilibrium temperature profile ΔT(r) within and surrounding a sphere of radius R of a medium of thermal conductivity within a medium of thermal conductivity , after prolonged exposure to an energy source depositing power P into the sphere [74]. The solid lines represent solutions to Equation (8)(8a) for values of the ratio / ranging from 1.0 to 2.0, plotted in the reduced coordinate system where r′ = r/R, and ΔT′(r′) = 3 ΔT(r)/PR².

Although this simplified model is clearly unrealistic in that it ignores the question of how the body’s thermoregulatory system will respond to the local deposition of thermal energy, it can be inferred from the literature that it is in fact a reasonably good approximation. Cheng and Liu describe in detail a numerical model of thermal dissipation in spherical breast cancer tumours and surrounding healthy tissue, using the full Pennes equation, and including independent perfusion and metabolic heat generation terms for the tumour and healthy tissues respectively [65]. They compare their results directly with the Andrä et al. model, and show that the results overlap when they set the perfusion and metabolism terms in their model to zero. They then also compare the time dependence of the predicted values at the origin (r = 0) and at the boundary of the magnetic-particle infused spherical region (r = R) for both the zero perfusion and metabolism model, and their fully-implemented breast cancer model. The difference between the two models is significant, viz. a ca. 15% decrease in the values at both the origin and at the boundary after prolonged (t 250 s) exposure to the magnetic heat source [65]. (For further details, see the Supplementary Information, section S2.) Nevertheless, we consider that the model expressed in Equation (8) is a reasonable first approximation to the temperature distribution that may be achievable in vivo, albeit that depending on the physiological characteristics of the target site in the body, it will almost certainly be an over-estimate of the actual sustainable values. We will return to this point later (see below).

In passing, it may be interesting to note that Figure 1 illustrates an often-neglected aspect of magnetic hyperthermia, namely the degree to which the tissue surrounding the focal point of the thermal treatment is subject to elevated temperatures. For example, if one is intending to heat a 1 cm³ tumour by ΔT ≥ 6 K for therapeutic hyperthermia, Figure 1 shows that a sphere of volume 8 cm³ will be heated by ΔT ≥ 3 K. This is not particularly surprising or unusual – it is after all a natural consequence of the relatively gradual 1/r drop-off in Equation 8(b)(8a) , which persists even in perfused tissue [65] – but it is something to keep in mind for interventions such as hyperthermia where prolonged exposure is anticipated. (The situation is likely to be different in the case of therapeutic thermoablation, where the intended ΔT ≥ 23 K treatment is more transient, so that the equilibrium state is not reached.)

The power density P delivered into the composite is related to the heating characteristics of the magnetic particles, through either the specific loss power (SLP, typically reported in W/g_Fe) or the intrinsic loss power (ILP = SLP/H²f, measured in nHm²/kg_Fe) parameters. Thus: (9) where m_Fe is the mass of iron contained within the magnetic nanoparticles, and we use V_d =  π R³ to denote the volume of the composite sphere in the model, and to draw a parallel with the V_d/V_i dispersion factor we have discussed previously.

We should note here that the ILP parameter is strictly only valid in the low-field linear-magnetic-susceptibility activation regime, where the SLP parameter varies linearly as a function of frequency f and quadratically as a function of field amplitude H [13,75]. “Low-field” in this context corresponds to the experimentally determined value, for iron-oxide nanoparticles, of H 5 kA/m [75–77]. This is also a field amplitude that has been clinically shown to be tolerable (i.e. not producing any noticeable adverse effects such as nerve stimulation or non-specific heating of tissue) for at least an hour of continuous application [61], and which has separately been theoretically predicted to be a limit below which electrophysiological stimulation is not possible, irrespective of rise time, frequency or slew rate [78].

It is convenient to rearrange Equations (8) and (9)(9) into a form that highlights the role of the most easily adjusted parameters of the agent, namely the iron concentration c and the injection volume V_i, in determining the achievable ΔT(r) distributions. If we focus on the temperature rise at the interface between the magnetic particle impregnated core and the surrounding medium, ΔT(r = R) = ΔT_R, and make the substitutions c = m_Fe/V_i and v = V_d/V_i, it is straightforward to show that: (10) which can be rearranged to give: (11)

The factors in brackets are constant for a given agent formulation and a given activation field system, so that Equation (10)(10) can be used to plot a series of ΔT_R isotherms in the V_i-c plane. This is illustrated in Figure 2 for a model scenario wherein the magnetic hyperthermia agent has an ILP = 3.0 nHm²/kg_Fe, a level that has been reported previously in several commercially available magnetic fluids [79]; a dispersion factor v = 2.4, in line with the values reported for the MagForce clinical studies on a variety of different tumours [10]; and an activation field of amplitude H = 5 kA/m and frequency f = 300 kHz, which are values that are considered to be acceptable and achievable in a clinical system [13].

Figure 2. Illustrative bioheat model calculations in the steady-state, zero perfusion, zero metabolic heat generation limit, for a 60 kg human, as per Equation (10)(9) , showing ΔT_R isotherms in the V_i-c plane, where ΔT_R is the equilibrium temperature at the surface of a sphere of radius R containing a uniform distribution of heat-evolving magnetic nanoparticles. Assumed parameters are: intrinsic loss power ILP = 3.0 nHm²/kg_Fe; dispersion factor v = V_d/V_i = 2.4; thermal conductivity of the surrounding medium λ₂ = 0.52 W/Km; and activation field amplitude H = 5 kA/m and frequency f = 300 kHz. The shaded region demarcates the clinically acceptable dose region, as determined from both the material loading capacities of the local tissue, viz. 40 mg_Fe/ml_tissue, and of the body as a whole, viz. 850 mg_Fe. The latter value is derived, as per Equation (6)(6) , assuming a “good” agent formulation scenario of relatively high retention ( = 0.85) and systemic tolerance ( = 0.85). The points A and B denote two possible treatment scenarios, as discussed in the text.

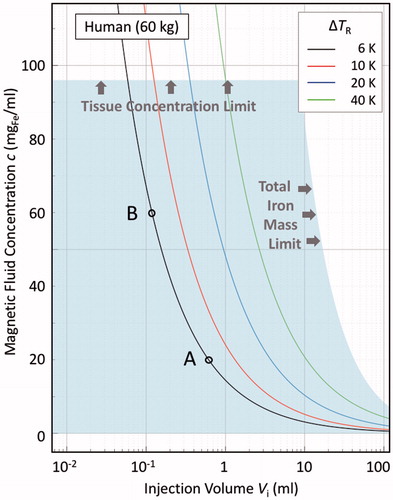
The only other parameter needed to generate Figure 2 is the thermal conductivity of the tissue surrounding the injection site. This can vary significantly depending on where in the body that site is. For example, according to the IT’IS Foundation’s database of tissue properties [80], the human brain, liver, pancreas and prostate gland all have conductivities at 37 °C of order 0.52 W/Km, and the figure for blood is similar; but the conductivity of human fat is less, at ca. 0.21 W/Km. Other tissues lie between these values, for example connective tissue, at ca. 0.39 W/Km, and skin, at ca. 0.37 W/Km; and the breast gland and cortical bone, both of which lie at ca. 0.32 W/Km. In Figure 2, we have assumed a value of  = 0.52 W/Km.

Nevertheless, Figure 2 is informative in that it allows us to quickly establish – at least in broad terms – the formulation and addressable tumour parameters that will determine whether a given target is treatable. For example, to achieve a hyperthermia-threshold temperature rise of ΔT_R = 6 K, then if c = 20 mg_Fe/ml_fluid, V_i must equal or exceed 0.61 ml_fluid (the point marked A on the figure), which, given that v = 2.4, means that the minimum treatable tumour size is 1.5 ml_tissue. If, in contrast, c = 60 mg_Fe/ml_fluid, V_i must equal or exceed 0.12 ml_fluid (point B), and the minimum treatable tumour size is now much smaller, at 0.29 ml_tissue. It is also immediately apparent that both points A and B fall within the shaded region in Figure 2. That region is important as it encompasses the acceptable dose limits for the treatment: the upper limit at c = 96 mg_Fe/ml_fluid determined from the 40 mg_Fe/ml_tissue limit and the dispersion factor v = 2.4; and the other limit being those points for which the product V_i.c = 850 mg_Fe. As such, both of the treatment scenarios, represented by the points A and B, are allowable in terms of the material loading of the local tissue and of the body as a whole.

Lastly, it is perhaps useful to note the parametric correlations that are apparent in Equations (10)(10) and (11)(11) . For example, c is inversely proportional to the ILP, which means that if one develops an agent #2 which has twice the heating capacity as an agent #1 (ILP₂ = 2ILP₁), then one could achieve the same heating effect with a formulation at half the concentration (c₂ = c₁/2), if all else was unchanged. Alternatively, if one wanted to achieve twice as much heat generation ( = ), this could be achieved by doubling the concentration (c₂ = 2c₁), if all else was unchanged.

Translate to the appropriate preclinical model

The final step is to translate the projected clinical treatment – with the formulation and dose levels determined for a given heating agent and target using a theoretical scenario such as the one discussed above – into an appropriate corresponding preclinical model. This is, however, not always entirely straightforward.

One aspect is that there are numerous instrumental and experimental differences between preclinical and clinical studies, which need to be understood and managed. These include eddy current effects, which are often more evident in larger animals and in man, where large-diameter coil geometries may be used, for which the induced surface currents (which scale with the square of the coil radius) are larger [81]; and non-specific peripheral heating effects due to resistive heating of the field-generating coils, which generally affect small animals more [82]. Similarly, the need to maintain thermoregulation and maintain core temperatures in preclinical models even when the animals are under anaesthetic, is a major challenge [83,84]. This is especially important in small animals where the loss of heat through the skin is much faster than it is in larger animals or man.

However, even in the case that all such experimental differences have been identified and overcome, there are still fundamental challenges that may come into play. We illustrate this by assuming that our goal is to translate the human treatment scenario represented by points A and B in Figure 2 onto a mouse model, as shown in Figure 3. Since we have not changed the properties of the agent, the ILP parameter is the same. If we have an excellent tissue model – for example, if we are using xenografted human tumours in immunosuppressed mice – we might broadly assume that the dispersion factor v and the thermal conductivity will also be the same as in the clinical case. Then, for a given activation field H and frequency f, the V_i-c plane plots of ΔT_R isotherms, as calculated using Equation (7)(7) , will be identical to the clinical case – see Figure 3. What is very different, though, is the acceptable dose region – the shaded region in Figure 3 – with respect to the allowable whole body dose, which for the 20 g mouse is V_i.c = 3.5 mg_Fe, rather than the 850 mg_Fe in a 60 kg human.⁴ This has the major consequence that now the treatment scenarios A and B fall well outside maximum allowable dose region for the mouse, making the experiment ethically impossible to perform.

Figure 3. Illustrative bioheat model calculations in the steady-state, zero perfusion, zero metabolic heat generation limit, for a 20 g mouse, as per Equation (10)(9) , under the same material conditions as in Figure 2, viz. ILP = 3.0 nHm²/kg_Fe, v = V_d/V_i = 2.4, and λ₂ = 0.52 W/Km. The solid lines are ΔT_R = 6 K isotherms, indicating the thresholds for therapeutic hyperthermia. The shaded region demarcates the murine “acceptable dose region”, as determined from both the material loading capacities of the local tissue, viz. 40 mg_Fe/ml_tissue, and of the mouse as a whole, viz. 3.5 mg_Fe. The latter value is derived, as per Equation (6)(6) , assuming a “good” agent formulation scenario of relatively high retention ( = 0.85) and systemic tolerance ( = 0.85). The red line, corresponding to H = 5 kA/m and f = 300 kHz (the same conditions as in Figure 2), lies outside the acceptable dose region, and as such is inaccessible. The black line, corresponding to H = 10 kA/m and f = 1 MHz, lies within the acceptable dose region, as therefore is accessible. The points A, A′, B and B′ are discussed in the text.

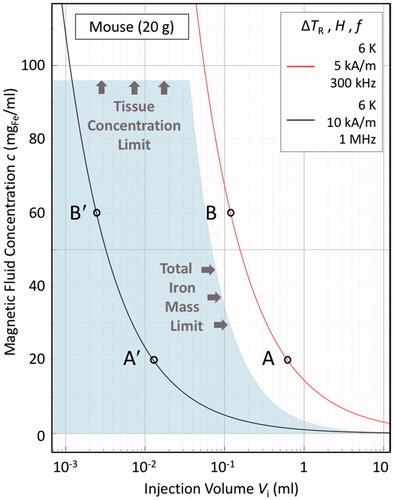
However, there is an alternative. That is: to alter the activation field parameters to bring the treatment points within the allowable region. This is illustrated in Figure 3 for points A′ and B′, which lie on the ΔT_R = 6 K isotherm for the case that H′ = 10 kA/m and f ′ = 1 MHz. Although these are field parameters that are well beyond those acceptable in a human, they are certainly achievable and acceptable in a mouse model. Furthermore, by carefully choosing the H′ and f′ parameters, the injection volumes V_i required for the experimental treatments may be tailored to the animal model tumour volumes, in accordance with the dispersion factor v.

To our knowledge this is not an animal model design strategy that has yet been explored for hyperthermia studies, but in principle it looks to be a well-defined approach that has the benefit of focussing on equating the thermal load per tumour from one animal to the next.

Discussion

In this paper, we have set out to comment on the practicalities of designing for the transition from preclinical to clinical studies of magnetic hyperthermia. Perhaps unsurprisingly, we have found that the best way to do this has been to first think carefully about the intended clinical intervention that constitutes the ultimate goal of the research, and to work backwards from that point to consider which is the best preclinical model to adopt en route to that goal.

We first addressed the question of administration route. In our opinion, the interstitial route is best suited to early clinical translation in magnetic hyperthermia, primarily because of the relative simplicity of the required formulation of the agent (which does not need to be explicitly designed to evade the body’s reticuloendothelial system, as is the case for intravenous agents), and the ease with which substantial local concentrations of magnetic nanoparticles can be deposited at a target site. That said, an important determinant for efficacy is the in situ dispersion factor, v = V_d/V_i, where V_d is the tissue volume throughout which the injected material is dispersed, and V_i is the volume of fluid injected. Values in the range v = 1 to 5 have been reported. Depending on the injection site it may also be important to consider peripheral or accidental injection into the bloodstream, so that even though the intended route is interstitial, there may be some fraction of the agent that is delivered intravenously.

We have reviewed the ethical, safety and regulatory aspects of the interstitial versus the intravenous route, and in particular the way in which preclinical-to-clinical dose scaling depends on the administration route. It is clear (as per the US Food and Drug Administration’s 2005 guidance for industry) that whereas for intravenous injection it is expected that dose scaling should be done by normalising to body surface area (on the basis that this correlates with species-specific metabolic rates), for interstitial injection the normalisation is made with respect to the local concentration of the agent at the injection site. It is also notable that the maximum allowable injection volume is both species-dependent and site-dependent, and governed by institutional-level rather than national or international standards; and that for intratumoural injections a volume percentage approach (typically V_i ≈ 33% V_tumour) is commonly adopted.

We have benchmarked the intravenous and interstitial clinical dosage limits of four commercially available magnetic fluids, viz. the MRI contrast agent Resovist^®, the iron replacement agent Feraheme^®, the sentinel node detection agent Sienna+^® and the magnetic thermoablation agent Nanotherm^®. This has led us to propose the following potentially useful rules-of-thumb:

• that for intravenous administration, there are clinical products in use today for which total Fe dosage administered at any one time may be as high as 8.5 mg_Fe per kg of body weight; and for which the total daily Fe dosage may be as high as 2.5 mg_Fe per kg of body weight; and

• that for interstitial administration, there are clinical products in use today for which the local Fe dose is up to 12 mg_Fe/ml_tissue per site for subcutaneous injections and up to 40 mg_Fe/ml_tissue per site for intratumoural injections.

We should treat these figures with caution: they are indicative only, and they may even be mutually exclusive. The intravenous limits are derived from published data on Feraheme^® for one-off doses, and on both Feraheme^® and Resovist^® for the daily doses; and the interstitial limits are derived from data on Sienna+^® for subcutaneous injection and Nanotherm^® for intratumoural injection. These are four quite different materials, with most likely quite different biodistribution and biocompatibility characteristics. Even so, we think that it is useful to have such figures at hand, if only to give some sense of the range of possibilities that might be available for any new formulations that might be explored.

We have illustrated the process of designing for the transition from preclinical to clinical studies for the hypothetical case of an intratumoural hyperthermia agent with a given set of assumed material properties for the agent (viz. its heating capacity) and the injection site (viz. the tissue dispersion factor and thermal conductivity). As part of this we have shown – as embodied in Equation (6)(6) – that two key parameters to note are the assumed degree of retention of the agent at the injection site, and its systemic tolerance factor (relative to the safe intravenous dosing limit established from other agents), as these both have a direct bearing on the study design. In Figures 2 and 3, we illustrated the case for an agent with good (85%) retention and tolerance factors, and took  = 2.5 mg_Fe/kg (i.e. the daily intravenous dose limit of Feraheme^® and Resovist^®), which led to the estimation that the maximum total dosages should not exceed either 850 mg_Fe in a 60 kg human or 3.5 mg_Fe in a 20 g mouse. However, these limits could be set higher if the formulation of the agent warrants it, and the and factors are closer to one. Also, depending on the intended use of the agent, an argument could be made that the should be closer to the 8.5 mg_Fe/kg limit established for one-off doses of Feraheme^®.

Lastly, we have shown how these dosage limits can be used (alongside a simple theoretical model of thermal transfer from a sphere containing a homogeneous distribution of magnetic nanoparticles in the presence of an activating field of amplitude H and frequency f) to explore the clinical efficacy of any given proposed therapy as a function of the hypothetical formulation of the agent. We have found a simple analytical model – as formulated in Equations (8) and (10)(10) , and as displayed in Figures (2) and (3) – to be a useful tool to help visualise the design parameter space, and to help to make the transition between clinical and preclinical study requirements.

There is, however, one final matter that we have not fully addressed, which is the question of how good or how bad the zero perfusion, zero metabolism model of Equations (8) and (10)(10) really is, when it comes to predicting actual heating scenarios in vivo. It is not particularly easy to make a definitive assessment of this, as there are very few clinical or preclinical studies for which the requisite data are available in sufficient detail to enable point-by-point comparisons to be made. Fortunately, however, one of the MagForce team’s publications – the Johannsen et al. report on a clinical study of magnetic hyperthermia in 10 prostate cancer patients [61] – does provide suitably specific data: viz. thermal probe measurements of the maximum temperature ΔT_max attained at the magnetic fluid injection site for both the first and last heating sessions for each patient; and CT scan data for each patient and session. The latter is important as it allows estimates to be made of both the retention factor (which ranged from ca. 0.8 to 1.0 between individuals, and in some cases fell between treatments) and the dispersion factor v (which ranged from ca. 1.0 to 2.2 between individuals, and generally increased between treatments).

With this information at hand, we can then compare the measured ΔT_max to the maximum temperature predicted from Equation (8), namely the temperature achieved at the central point, r = 0: (12) where we take into account the possibility of non-ideal retention by including as a scaling factor to the injectate volume , and where the pre-factor 1.5 represents the factor in the case that . Strictly speaking the latter is only valid for materials such as magnetite, Fe₃O₄, where the thermal conductivity contribution of the particles is negligible compared to that of the tissue itself. (Concentration dependent data show that even at 100 mg_Fe/ml the contribution would be ca. 5 mW/Km [85], which is less than 1% of the  ≈ 0.52 W/Km of the prostate [80].) The last parameter needed to compute Equation (12)(12) is the intrinsic loss power of the magnetic particles. For this we use an ILP of ca. 0.4 nHm²/kg inferred from the rat model heating curves reported in an earlier MagForce paper [86]. (Further details on this, and other aspects of the data handling, are given in the Supplementary Information, section S3.)

The resultant comparison between predicted and clinically observed ΔT_max values is shown in Figure 4. The expected over-estimation of ΔT_max due to having neglected the thermally moderating effects of blood perfusion and tissue metabolism is clearly evident, but it is also apparent that the approximation becomes better as ΔT_max increases. This is logical, given that as more and more heat is deposited into the tissue, the body’s capacity to physiologically regulate and overcome that thermal load becomes less and less effective. Furthermore, it is possible that at high ΔT_max values there could be physical (ablative) damage to the vascular bed that would disrupt blood flow, and lead to reduced or even zero perfusion. That said, the somewhat surprising aspect of the data in Figure 4 is that the conditions under which the perfusion and metabolism effects seem to be overwhelmed come at ΔT_max ≈ 12 K, which corresponds to ΔT_R ≈ 8 K, which is a target value that one might realistically seek to achieve in a therapeutic hyperthermia intervention. Another positive aspect of Figure 4 is that it opens the prospect of applying a post-hoc, clinical (or preclinical) observation-based correction to the analytical model, which in some situations might be useful. (We illustrate this in the Supplementary Information, section S3, for the case of the Johannsen et al. prostate cancer patients [61].) We conclude therefore that the zero-perfusion, zero-metabolism analytical model is actually a reasonable first-approximation model of therapeutic effect, and that so long as it is used advisedly and cautiously, it represents a useful tool for practical purposes.

Figure 4. Comparison between maximum temperature rises ΔT_max due to magnetic heating as calculated using the first-order approximation method of Equation (8)(8a) and (10)(9) , and the reported ΔT_max for a clinical study of prostate cancer patients undertaken by the MagForce team [61]. The limitations of the zero-perfusion, zero-metabolism model are evident at the lower ΔT_max values, but the model is more valid as ΔT_max increases. The arrow denotes the ΔT_max value for which the temperature of the entire magnetic-nanoparticle-infused tissue volume reaches the therapeutically significant value of ΔT = 6 K or above. The dashed line is a guide to the eye only.

Conclusions

Magnetic hyperthermia is a highly promising therapeutic modality that has commanded substantial international R&D effort and funding for a decade or more. However, the vast majority of reported work to date is laboratory based, or at most preclinical. There have been very few reports on the development of clinical studies of magnetic hyperthermia, and therefore very little in the way of accumulated knowledge as to how such translation can be achieved.

In this work, we have attempted to address this lack of experience-based information from a more pedagogical perspective. Specifically, we have considered how to manage the transition from preclinical to clinical studies from first principles, and have focussed on some of the unique aspects of the intervention – such as the strong dependence of efficacy on the local concentration of the delivered magnetic heating agent – that make it so different from more conventional treatments. In particular, we have reviewed the ethical and regulatory guidelines for both interstitial and intravenous injections of magnetic agents, and established that while the former scales between species as a function of body surface area, the latter translates as a species-independent local concentration.

In addition, we have reviewed current benchmarks in the form of commercially available iron oxide-based magnetic fluids that have clinical applications, and thereby derived quantitative rules-of-thumb regarding the clinically acceptable dosage limits for both their intravenous and interstitial administration. From this, we have shown that by applying suitable theoretical models of clinical efficacy (based on biophysical models of heat flows in tissue) it is possible to establish design parameters that inform the formulation criteria required for any given target intervention. Furthermore, we have shown that these same biophysical models can then inform the design of the corresponding preclinical models that are needed to establish the positive therapeutic benefits of the hyperthermia treatment, as a necessary step towards obtaining permission to proceed to first-in-man studies.

It is our hope that setting out the framework for systematically establishing the link between preclinical and clinical study designs in this way may prove to be useful for others, and that in the near future we might see many more clinical studies of therapeutic magnetic hyperthermia being undertaken, for the benefit of us all.

Acknowledgements

We thank Simon Hattersley of Resonant Circuits Limited (London) for his helpful comments on this manuscript.

Disclosure statement

The authors respectively fulfil part-time paid executive (PS) and advisory (QAP) roles to a company (Resonant Circuits Limited) that has a commercial interest in magnetic hyperthermia. QAP also fulfils a part-time paid advisory role to a company (Endomagnetics Limited) that has a commercial interest in magnetic nanoparticles.

Additional information

Funding

European Commission Seventh Framework Programme10.13039/100011102

Horizon

Framework Programme

European Commission Horizon 2020 ProgrammeGrant 685795This work was supported in part by the European Commission Seventh Framework Programme through the Dartrix and NanoMag projects, under Grants 278580 and 604448, and by the European Commission Horizon 2020 Framework Programme through the NoCanTher project, Grant 685795.

Notes

1 For convenience, copies of all the IFUs referenced in this paper are included in the Supplementary Information, section S1.

2 “USP” here refers to substances defined in the United States Pharmacopeia.

3 Note that it could be argued that the one-off intravenous administration limit of  = 8.5 mg_Fe/kg that has been established for Feraheme^® might be equally suitable here, but that for the purpose of illustration we have chosen to use the lower, daily administration value.

4 Note that this is for the assumed “good” agent formulation scenario of retention ( = 0.85) and systemic tolerance ( = 0.85), and that in general the allowable whole body doses will vary between different formulations of agent.