Summary of numerical analyses for therapeutic uses of laser-activated gold nanoparticles

Abstract

The optimal light dose, heat generation, consequent heat spread and an accurate thermal damage model, are key components of effective laser therapies. Recent advances in nanotechnology offer numerous possibilities on how to increase the efficacy of hyperthermia for tumour treatments. Gold nanoparticles are a promising candidate towards the achievement of this goal owing to their properties for efficiently converting light to heat. In this review, we summarise the numerical tools that are available for theoretical studies of gold-nanoparticle-mediated photo-thermal therapy. The processes that occur in the treatments based on light propagation inside biological tissues and the subsequent temperature distributions are considered first, followed by evaluation of the thermal damage. The fundamental ideas underlying the presented methods are described in addition to their applications in photo-thermal therapy and its effects. The descriptions of extensively used tools for the characterisation of nanoparticles across multiple research fields are also presented for estimating the electromagnetic properties of gold nanoparticles (e.g. discrete dipole approximations, finite-difference time-domain simulations), the Monte Carlo model of light propagation in biological tissues, and the Pennes’ bio-heat equation. In addition, the Arrhenius damage evaluation and the cumulative effective minutes normalisation methods are described. Finally, recent in vivo and in vitro results from the rapidly growing field of nanomedicine are presented.

Keywords:

• Monte Carlo
• gold nanoparticles
• photo-thermal therapy
• bio-heat transfer model
• localised surface plasmon resonance

Introduction

Hyperthermia has become one of the most popular modern methods to treat solid tumours. Temperatures above certain levels are either lethal to cancer cells, or make them more susceptible to other therapies. Promising clinical experiments of hyperthermia as adjuvant therapy to traditional radiotherapy or chemotherapy have been conducted on bladder, cervix or neck tumours [1–3]. To achieve the expected results, an appropriate source of energy has to be carefully selected to generate the required amount of heat, according to tumour location, size, etc. Such a source can deliver energy in the form of radiofrequency, microwave and ultrasound waves, or by using intensive laser light [4–6].

Rapid development in nanotechnology offers researchers in the area of hyperthermia new possibilities for developing effective methods for tumour treatments. Nanoparticles are introduced into the body, amplify the generated heat in the desired location and leave the surrounding tissue temperature unchanged. There are several groups of nanoparticles that respond to different energy sources. One of the promising groups uses laser-irradiated gold nanoparticles that effectively convert light to heat. The conversion is achieved via localised surface Plasmon resonance (LSPR), which is a coherent oscillation of electrons in a nanoparticle [7]. The treatment via LSPR is usually referred to as photo-thermal therapy (PTT), or nano-photo-thermal therapy (NPTT), a term used to emphasise the use of nanoparticles, or even plasmonic-photothermal therapy (PPTT), a term introduced to emphasise basic physical phenomena responsible for heat production. The gold nanoparticles can be easily modified to accomplish the desired purpose, and are covered with different coatings, or irradiated at different wavelengths [7]. Various numerical analysis tools can be applied to analyse generated results, and/or modify the design of the treatment in accordance to theoretical predictions.

Thus far, only a few mathematical models have enabled the description of the various underlying phenomena. First, radiative transfer in biological tissues can be applied to evaluate light propagation and penetration inside the spatial domain of the simulation [8]. As a result, one obtains the distribution of light energy and estimates the amount that is important to initiate the occurrence of desired effects. Second, different shapes of nanoparticles respond differently to different wavelengths of visible and near infra-red radiations. Therefore, their properties and influence must be considered. Finally, the absorbed energy is converted into heat that causes several effects, such as apoptosis, necrosis or disruption, via the use of nanobubbles [9]. To evaluate these effects, the temperature distribution in the considered region must be known, and a suitable thermal damage model should be applied.

This review summarises the recent advances and approaches pertaining to the use of gold-nanoparticle-mediated PTT with emphasis on numerical analyses. The content is structured according to the steps described above. The problem of light propagation inside biological tissues is addressed using a Monte Carlo (MC) algorithm, the most popular and accurate method currently used to simulate laser irradiation. For the estimation of gold nanoparticle responses to irradiation, discrete-dipole approximation or time-domain finite-differences methods are presented in the subsequent session. The utilisation of results of these methods and the temperature distribution are calculated based on the Pennes’ bio-heat equation and its modifications, or are based on two- or three-temperature models in the case of ultrashort pulses. Finally, a brief discussion on a thermal damage model is outlined.

This review is intended to provide a perspective to researchers with an interest in the area of photothermal therapy who would like to enrich their work. The use of the presented numerical analysis tools could make their research more rational, less time consuming, and more cost-effective, than embarking on extensively used trial-and-error attempts using a multitude of experimental setup parameters.

Light propagation in biological tissue

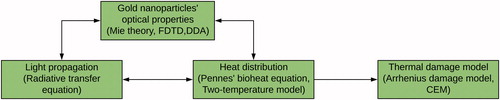
The algorithm used to conduct the thermal damage evaluation of the PTT from simulations is depicted in Figure 1. As it can be seen, the workflow consists of four parts, whereby every node provides the necessary data to others. Modelling of gold nanoparticles generates data that indicate how light absorption is enhanced, whereas the light propagation determines the source of the heat used in the Pennes’ bio-heat equation. On the other hand, the temperature distribution in biological tissue influences the optical parameters used for light simulations, and may also influence the behaviour of gold nanoparticles. Therefore, to ensure accurate modelling, all parts of the algorithm have to operate synergistically.

Figure 1. The workflow of the whole photothermal therapy simulation concept.

Since lasers mostly emit in the visible and infra-red electromagnetic spectral ranges, only this part of the spectral region is considered in the remaining text. In biological tissues, visible and infra-red radiations are gradually attenuated, mostly owing to the presence of proteins, DNA, melanin or haemoglobin [10]. At the boundary of the visible and near-infra-red spectral region (700–1100 nm) the probability that light is absorbed is minimised, and maximum penetration is thus allowed. Therefore, this spectral window is extensively used in various optical imaging [11–14] and treatment techniques [15–19]. In addition to the absorption capacity, the optical response of biological tissue is known for its high-scattering properties. These facts limit the use of visible and infra-red imaging techniques in medicine [20].

For theoretical calculations, the absorption μ_a and the scattering μ_s coefficients are introduced. In most tissues, the scattering coefficient is much larger (∼10 times) than the absorption coefficient. Thus, while the light penetrates a few centimetres until it is absorbed, its direction changes dramatically within a penetration distance of the order of hundreds of microns owing to scattering [20]. However, the absorption of light increases the temperature in the region it propagates and changes both the absorption and scattering coefficients. Correspondingly, this effect should be considered and accounted for in the case of high-power lasers [21].

In addition to these two coefficients, the tissue is characterised by the anisotropy parameter g that expresses the mean value of the scattering angle, and ranges from 0 to 1. Zero value indicates the propagation with no direction preferences (light scatters in all directions with the same probability). As the value of g increases, forward scattering increases (light likely continues in the same direction before scattering) [20]. Tissues typically have g ≈ 0.9, and the deepest propagation is on the axis of the incoming laser beam considering the same absorption and scattering within the spatial domain of the simulation.

Light behaviour is completely described using Maxwell’s equations. However, the complexity and variability of an environment where light propagates, makes the use of Maxwell’s equations almost impossible. Therefore, the biological optics community used the radiative transfer equation (RTE) for solving problems in this area. The solution of a particular problem can be achieved using numerous existing methods, such as diffusion approximation [22] or the simplified spherical harmonics approximation [23]. Each method takes advantage of several assumptions that simplify calculations, but the Monte Carlo (MC) method solves the RTE directly. This makes MC a universal solver that is also applicable in photo-thermal therapy. Thus, detailed descriptions of the MC algorithm follow.

MC algorithm description

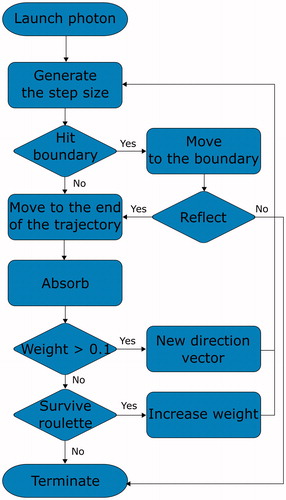
The MC method is a very popular and an accurate way to simulate light propagation in biological tissues [24–27]. The algorithm is easy to implement but requires extensive computational resources to be accurate. The requirements arise because of the method itself, which splits the incoming radiation into single units, known as photons and traces their trajectories. In a single simulation, usually 10⁸ photons are traced and gradually absorbed within media. Each photon follows the basic rules that describe their motion, as displayed in Figure 2. First, the step length is calculated based on the generated random number and the attenuation coefficient μ_t (which equals to the sum of the absorption coefficient μ_a and the scattering coefficient μ_s). The absorbed energy is stored at the end of the step in older implementation versions [24]. In newer implementations, the photon energy (referred to as weight) is being gradually lost according to Beer's law [28], and is stored along the trajectory. The differences of both absorption methods were examined by proving the equivalence of these methods [29]. When the photon arrives at the end of the step, a new direction of propagation is determined. The direction is usually derived using the Henyey–Greenstein or Mie functions [30]. After the calculation of the new propagation direction, another step length is generated. The routine is repeated until the photon weight drops below a certain value. Since scattering dominates over absorption in the therapeutic window of 700–1100 nm, the photon undergoes many scattering events, and the penetration depth is determined mostly by this phenomenon.

Figure 2. An example of MC algorithm.

One of the first and most successful codes used is called MCML, which denotes a Monte Carlo model of steady-state light transport in multi-layered tissues [24]. The model is calculated with semi-infinite tissue layers, and an infinitely narrow beam incident at right angles with respect to the tissue. The same authors also presented programme CONV that calculated the propagation of a beam with finite dimensions based on results that were obtained using MCML [31]. Since MCML was created more than 20 years ago, computers at that time had low memory and computing performance. Thus, the model was capable of conducting simulations of tissues with spatial cylindrical symmetry only, and lacked temporal dependence. As computer performance improved, time-resolved simulations of arbitrary-shaped media were introduced with the code known as tMCing [25]. Heterogeneous structures were modelled using scalable cubes, referred to as voxels. Recently, tetrahedral mesh-based MC models were simultaneously published by two independent groups [28,32]. The tetrahedral mesh is more suitable for modelling curvatures and complex shapes owing to the smaller spatial discretisation error compared to that for the cubic mesh. Additionally, this mesh consumes less memory in comparison to voxel-based modelling [28].

Acceleration methods

The Monte Carlo method received increased attention after the release of the computer unified device architecture (CUDA). CUDA has allowed easier development of the code computed on graphics processing units (GPU). The GPU contains numerous computational units each being capable of calculating the propagation of a single photon. Therefore, several photons can be simulated in parallel, thereby resulting in the reduction of the required simulation time. First, to demonstrate the benefits of parallel computing on MC light propagation was the original MCML code modified for CUDA. A maximum speedup factor of 1000 was reported by Alerstam [26]. The advantages of the CUDA platform benefitted the Monte Carlo eXtreme (MCX) project that allowed simulations of time-resolved propagation in arbitrarily shaped 3D media [27].

There are other parallel platforms in addition to the GPU platform. Utilising Hadoop, an open-source MapReduce framework was reported in [33] on Amazon’s elastic compute cloud. The MC code was also imported to Intel’s many-integrated core (MIC) architecture [34], or to field-programmable gate arrays (FPGA) [35]. Doronin et al. developed a fast peer-to-peer MC code that allowed multiple users to simultaneously access the online MC simulation [36].

Besides parallel computing, the scaling method is another possible way used to accelerate the simulation. The scaling method requires a single simulation run and records the history of photon trajectories. The generated results for different media with different optical properties can be then obtained from the scaling relations [37].

Gold nanoparticles

Gold nanoparticles (AuNP) constitute a promising tool in cancer diagnosis and treatment [38–43]. AuNPs benefit from enhanced permeability and retention (EPR) that causes accumulation in tumour tissue [44]. Moreover, various coatings have been studied to improve their delivery and binding ability. This targeting via surface modifications vastly increase treatment efficacy and decrease toxicity. One of the most popular ligands in PTT, polyethylene glycol (PEG), has been extensively conjugated to AuNPs, thereby eliciting promising low-toxicity responses [7,45]. Recently, rifampicin-conjugated AuNPs were demonstrated to yield increased internalisation into tumour cells. Compared to PEG-conjugated AuNPs, they showed much better effectiveness in reducing neck tumour volumes in a mouse model. The mouse models were then observed for 15 months with no signs of toxicity [46].

Once the nanoparticles are delivered and bound to tumour tissue, they can be irradiated with visible or infra-red radiation from a laser. When the light interacts with a nanoparticle, the energy is converted into coherent oscillations of electrons referred to as localised surface plasmon resonance (LSPR) [47]. The oscillations gradually relax via electron–phonon relaxation, releasing their energy to the lattice of the nanoparticle and the surrounding environment. The time needed for this transfer is called relaxation time. If the laser pulse is longer than the relaxation time, the nanoparticles are in quasi-stationary state with their environment, a state that is governed by the diffusion of heat. However, if the pulse is shorter (femtoseconds), the temperature of the electrons rapidly increases causing various effects, as described in the next section.

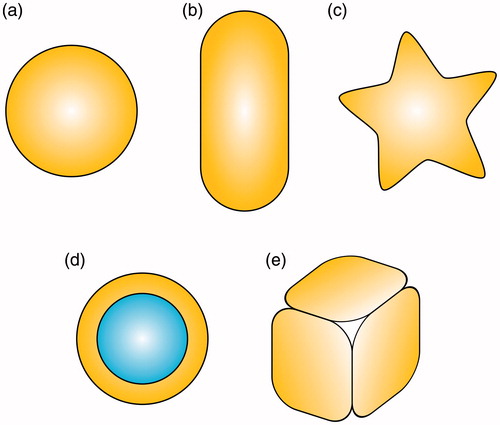
The resonant frequency of LSPR strongly depends on the shape of a nanoparticle and its composition. During the past few years, many variations of these nanoparticles have been synthesised, such as nanospheres, nanorods, nanoshells, nanostars or nanocages, as displayed in Figure 3. Among the existing AuNP types, nanorods have gained huge popularity because of their tunability. While the nanospheres exhibit peak absorption at approximately 520 nm, the absorption of nanorods can be tuned by changing the aspect ratio corresponding to the two modes of electron oscillations [48]. Since human tissues are almost transparent to radiation in the range of 700–1100 nm, gold nanorods are usually being tuned to these wavelengths [49]. Laser-irradiated gold nanorods were successfully employed in killing various types of cancer cells, such as prostate [50], breast [51] and gastric [52], or for treatments targeted to Staphylococcus aureus [53], and killing Pseudomonas aeruginosa bacteria in wounds [54]. Similarly, gold nanoshells gained popularity owing to their capacity to shift the resonant frequency based on the variation of the radii of silica core and gold shells [55]. Gold nanostars are another potential agent for photo-thermal therapy, but their major strength lies in the strong surface-enhanced Raman scattering (SERS) signal [56]. This attribute provided them with the potential for use in real time SERS during laser irradiation, where minor changes can be observed in the Raman spectra [57]. The changes were attributed to modifications of the protein structure, such as sulphur–sulphur, or carbon–sulphur bonds, since the signal that arose from the bond vibration changed. Gold nanocages, which are hollow nanoparticles, were also demonstrated to be efficient light-to-heat transducers. It was discovered that the concentration of the nanocages that was needed to destroy prostate tumour cells was 18 times lower than the concentration of the nanorods [58].

Figure 3. Various shapes of gold nanoparticles: (a) nanosphere, (b) nanorod, (c) nanostar, (d) nanoshell with silica core and (e) nanocage.

In addition to the particular shape of one nanoparticle, an entire complex can be designed for PTT and for additional modalities. Kang et al. recently prepared a novel nanocomplex made of gold nanorods, porphyrin and trastuzumab, and tested it as a potential treatment medication for HER2-positive breast cancer. Porphyrin possesses fluorescence properties that were employed during the investigation of the targeting ability of the nanoparticles [59]. The elimination of the nanoparticles from within the body was demonstrated with the use of biodegradable material with small gold nanoparticles (<5.5 nm in diameter) [60].

It is important to emphasise that the resonance magnitude and heat amount is not the only parameter on which PTT depends on. Espinosa et al. found out that the efficiency of PTT is mainly determined by the internalisation of AuNPs into cancer cells rather than the peak value of their plasmonic resonance [61]. Alfranca et al. showed that even higher photo-thermal efficiencies do not necessarily mean higher killing rates of cancer cells. Other nanoparticle characteristics, like their ability to be internalised by tumours, can be much more important, and consequently crucial for nanoparticle selection [62].

Therefore, the efficacy of the treatment is not only determined solely based on optical properties, but it is rather a combination of many factors.

Modelling optical response

To evaluate the response of the nanoparticles to incident light, several models have been developed to calculate the absorption and scattering cross-sections. The first theory, known as Mie theory, was introduced in the early twentieth century. However, this theory is limited to spherical or cylindrical particles, which makes it inapplicable or rarely applicable given the variety of particle shapes produced, and the coupling effects encountered nowadays [63]. In addition to this fact, there are two additional assumptions based on which this theory is based: (i) the dielectric function of a nanoparticle and the surrounding environment are the same as bulk dielectric function, and (ii) the size of a nanoparticle is much smaller than the wavelength of the incident light [64]. According to the theory, the absorption and scattering coefficients are expressed as an infinite series of Ricatti–Bessel functions [65].

Mie’s theory was employed to investigate the photothermal conversion efficiency, and after validation with green laser light, the response was extended to a broader range of wavelengths and sizes of nanoparticles [66].

Nowadays, the most common modelling approaches are the finite-difference time-domain (FDTD), boundary element method (BEM) or the discrete-dipole approximation (DDA).

Discrete-dipole approximation

The method divides a particle into a finite lattice of discrete dipoles interacting with each other. When an external electric field, e.g. light, is applied, the dipoles start to behave in accordance to Maxwell’s equations. The method provides an advantage in modelling particles of arbitrary shapes.

The first version of the extensively and publicly available code, called DDSCAT, was released in 1994 [67]. Since then, additional modifications were developed, including hardware accelerated calculations on GPUs [68]. DDSCAT was used in simulations for many studies, such as the size comparison of different gold nanorods [65,69], and the transfection by femtosecond lasers [70]. The applicability of DDA for plasmonic particles was investigated in [71], whereby DDA was shown to possess a convergence issue for particles with diameters that are much smaller than the resonant wavelength.

Finite-difference time-domain

FDTD is extensively accepted and an easy to implement method that solves partial differential equations. Thus, it is applicable in every field of electromagnetism. The simulation spatial domain is divided into sub-volumes with the same dimensions. The sub-volume is characterised by their electric parameters, and the Maxwell’s equations are then gradually solved for each of these. In a similar manner to DDA, the method can solve the equations for arbitrary shapes of nanoparticles.

As stated above, numerical methods are advantageous for modelling the coupling effects among particles. This was used to study the ordering of gold nanorods within cylindrically confined spaces [72]. Similarly, FDTD calculated the electric field enhancement of linear chain gold nanoparticles inside silica nanotube peapods [73]. The simulations are also useful for the estimation of nano-engineered hotspots in SERS. These hotspots were located at the tips of specific types of nanoparticles, such as concave nanocubes, or nanostars, as was calculated recently [74,75].

Bio-heat transfer

Heat production and distribution are the key components of effective hyperthermia treatment. In PTT, gold nanoparticles are used to enhance the absorption of laser radiation, as depicted in Figure 4. Depending on the produced amount of heat, cells basically undergo two processes: programmed-cell death necrosis, or directly induced necrosis. However, during necrosis, components that leak out of the cytoplasmic membrane possibly induce metastasis and cancer. Thus, programmed cell death, is more favourable [76]. For the macroscopic temperature estimation, Pennes’ bio-heat transfer equation (PBTE) is usually used in the theoretical analyses of heat transfer in human tissues. Influences of the blood flow and metabolic heat are considered. In simulations with light deposition, the equation can be written as [77], (1) $$c\rho \frac{\partial T(\mathit{r},t)}{\partial t}=\nabla \left(k\nabla T\left(\mathit{r},t\right)\right)+P_{\mathrm{a}\mathrm{b}\mathrm{s}}\left(\mathit{r},t\right)+\omega c_b{\rho }_b\left(T_{\mathrm{a}\mathrm{r}\mathrm{t}}-T\left(\mathit{r},t\right)\right)+Q_{\mathrm{m}\mathrm{e}\mathrm{t}}$$(1) where c, ρ and k, are the specific heat, density and thermal conductivity of tissue, respectively. It must be pointed out that these parameters are also temperature dependent, and this dependence might be significant for the calculation [78]. Additionally, ω is the blood perfusion rate, T_art is the arterial blood temperature, T is the temperature and r and t are space and time coordinates, respectively. Equivalently, Q_met is the metabolic heat source, and P_abs is the source term, and represents the absorbed energy that is obtained from solving the RTE, as described above. Additionally, the boundary conditions and initial temperature should be formulated.

Figure 4. Photothermal therapy: near infra-red radiation is absorbed by tumour with embedded gold nanoparticles.

Several attempts were made to solve the equation analytically using the Green's function method [79]. However, the equation is mostly solved numerically using the finite difference method [80], the finite element method [81], the finite volume method [82] or the boundary element method [83]. To overcome the issue of parameter uncertainties in the PBTE, Fahrenholtz et al. [84] described an approach that used inverse problems on patient MRTI data to train the PBTE parameter values. The trained laser treatment model’s performance was then evaluated using leave-one-out cross-validation.

An in-depth investigation of the treatment protocol of prostatic cancer was presented in Ref. [85]. The study involved Monte Carlo simulations of light propagation inside the prostate, and the absorbed energy was then used in Pennes’ bio-heat equation. Furthermore, the Arrhenius integral was employed to determine the effect of destruction of cancer cells.

Recently, an extension of the Geant4 Application for Emission Tomography (GATE) simulation platform was presented [85]. The extension included a hybrid Monte Carlo light propagation simulator (that calculates directly the source term P_abs) combined with the analytical solution of the Pennes’ bio-heat equation. The merging of these two methods allowed users to form a closed-loop among the calculation of the absorbed energy in time, temperature evolution in time, and the incorporation of temperature dependence in the optical coefficients. The functionality of the heat model was validated against other finite-difference methods, phantoms or in vivo mouse model data, and the implementation showed good agreement.

The PBTE was also employed by Sugiura et al. in the analysis of a tumour in lymph nodes. The results were used for the in-depth investigation of in vivo experimental results on a mouse model. Surface temperature was controlled by an additional cooling system and lymph nodes with and without gold nanorods were compared [86].

Modelling gold-nanoparticle-mediated photo-thermal ablation

The main question in a theoretical analysis is how to incorporate the effect of gold nanoparticles into a macroscopic equation like the PBTE. From the optical point of view, AuNPs act as a strong absorber inside tumour tissue, and their influence on light propagation can thus be considered. The absorbed light energy, given by term P_abs in Equation (1)(1) $$c\rho \frac{\partial T(\mathit{r},t)}{\partial t}=\nabla \left(k\nabla T\left(\mathit{r},t\right)\right)+P_{\mathrm{a}\mathrm{b}\mathrm{s}}\left(\mathit{r},t\right)+\omega c_b{\rho }_b\left(T_{\mathrm{a}\mathrm{r}\mathrm{t}}-T\left(\mathit{r},t\right)\right)+Q_{\mathrm{m}\mathrm{e}\mathrm{t}}$$(1) , is thus a sum of tissue absorption and gold nanoparticles, and no other term should be added to the PBTE. This approach was used by Dombrovsky et al. [87]. In their approach, the two-flux approximation was employed to solve the radiative transport equation, and optical properties of tissue-embedded-nanoparticles were calculated from the relations, (2) $${\mu }_{\alpha ,\lambda }={\mu }_{\alpha ,h,\lambda }+0.75f_v\frac{Q_a}{r}$$(2) (3) $${\mu }_{s,\lambda }^{tr}={\mu }_{s,h,\lambda }^{tr}+0.75f_v\frac{Q_s^{tr}}{r}$$(3) where μ_α,λ is the absorption coefficient at the specific wavelength denoted by index λ, ${\mu }_{s,\lambda }^{tr}=\left(1-g\right){\mu }_{s,\lambda }$ is the transport scattering coefficient, f_v is the volume fraction of nanoparticles, r is the nanoparticle radius, and Q_a and Q_s^tr are the efficiency factors of absorption and scattering for single particles. The first terms of the sums on the right side ${\mathrm{(\mu }}_{\alpha ,h,\lambda }\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }{\mu }_{s,h,\lambda }^{t\mathrm{r)}}$ of the equations correspond to the host, i.e. tissue properties, while the second term denotes the properties of nanoparticles. Furthermore, the role of the metabolic heat and blood perfusion was investigated showing only a minor significance for these terms [87].

Previously, this approach was employed in the highly cited paper of Maltzahn et al. [45]. However, the absorption coefficient was estimated from in vivo experimental results and the light propagation was modelled simply by an analytical function. The obtained results from the finite element method applied on the PBTE showed good agreement with those elicited from in vitro PTT applied on a mouse model.

The opposite approach is to neglect the absorption of gold nanoparticles during light propagation, and add an additional term to the heat equations. Cheong et al. presented the modelling of plasmonic heating from an individual gold nanoshell [88]. Gold nanoshells were introduced as an additional contributor to the total temperature increase. However, their contribution to the absorption was completely neglected in the model [88].

The optimisation of PTT via simulations was proposed in several studies [81,89]. In [81], an optimisation algorithm determining optimal gold nanoparticle concentration was proposed. Additionally, new strategies that increased the efficacy of PTT were numerically analysed, such as the multi-source model [90], or the indirect heating strategy [91]. With the Monte Carlo model, the light fluence threshold of the gold nanorods for PTT was determined [92]. The role of the optical coefficients in gold nanorod-assisted thermal therapy was studied in [93]. A combination of the Monte Carlo method and the Pennes’ bio-heat equation was used to simulate the temperature distribution during prostate tumour treatment utilising gold nanoshells, and based on the influences of the nonlinearity effects of the simulation parameters [94]. Recently, a study of intra-tumour and tumour surface temperature dependence on laser power and gold nanorod concentration was published [95]. The results of the developed theoretical model showed good agreement with in vivo experiments on xenograft mice.

Microscopic heat production

Microscopic simulations provide a better insight into the processes that occur around a single nanoparticle or a cluster comprising a few nanoparticles. In these types of simulations, usually encountered macroscopic effects, like blood perfusion in the PBTE, or light diffusion, are ignored.

The microscopic interaction of the electromagnetic field with gold nanoparticles and consequent heat spreading under different time regimes of the irradiation was investigated in Ref. [96]. A finite-element method was implemented for solving Maxwell’s equations, and a consequent thermal evolution was studied with the heat diffusion equation for continuous wave and nanosecond pulses, or with a two-temperature model for femtosecond pulses.

Yakunin et al. presented a model which studied the heat distribution around a nanoparticle calculated based on Mie‘s theory and the steady-state heat equation [97]. From the obtained results, they were capable in quantifying the nanoparticle effectiveness in the two-dimensional space, including the laser wavelength and nanoparticle radius.

Multi-pulse effects were studied by Letfullin et al. The results showed that with the use of nanoparticles it is impossible to achieve a cumulative effect in the aqueous medium because of rapid cooling kinetics. However, the cell organelles possess higher specific heat, and in that case, accumulation is possible [96].

Macroscopic and microscopic calculations and experimental validation of these calculations indicated that large nanoparticle concentrations, and low-laser intensities, elicit higher temperatures at the macroscale, and low temperatures at the nanoscale, whereas the small concentration and large laser intensity showed the opposite [97].

Considering the ultrashort interaction of nanoparticles with laser, the system is not in the equilibrium state, and the standard diffusion equation cannot be applied. The first particles that interact with laser light are the electrons. The energy is then transferred to the lattice via electron–phonon relaxation. Since the pulse duration is very short, and the delivered amount of energy is tremendous, the temperature of the electrons rises rapidly to several Kelvin. Meanwhile, the lattice temperature is maintained at the initial temperature.

In case the nanoparticles, water is usually considered as the surrounding medium where the heat spreads further. Thus, a third equation that represents the temperature of water is added into a standard two-temperature model [98], (4) $$C_e\left(T_e\right)\frac{d{T}_e}{dt}=-G\left(T_e\right)\left(T_e-T_l\right)+S\left(t\right)$$(4) (5) $$C_l\left(T_l\right)\frac{d{T}_l}{dt}=G\left(T_e\right)\left(T_e-T_l\right)-F$$(5) (6) $$C_m\left(T_m\right)\frac{d{T}_m}{dt}=F$$(6) where C_e, C_l and C_m, are the electron, lattice and medium heat capacities, respectively, T_e, T_l and T_v, are the temperatures of the electrons, lattice and media, respectively, G is the electron–phonon coupling constant, F is the energy loss due to heat exchange with media and the source term S(t) represents the temporally dependent energy absorption by the nanoparticles.

As the temperature rises to a certain threshold, a nanobubble is formed around a nanoparticle owing to the evaporation of surrounding media. The nanobubble size determines its behaviour in biological systems. Small-sized bubbles serve as imaging agents, while large bubbles cause mechanical injuries to cells, such as membrane disruption [99].

The thermodynamics of nanobubble formation were studied in [100]. The nonlinear behaviour of the nanoparticles was determined by time-resolved optical spectroscopy and X-ray scattering. For the explanation of the behaviour, the heat transfer equation had to be solved.

Recent experiments show that the thermal transport in nano-dimensions (<80 nm) is not governed by diffusive laws, but is ballistic, similar to light propagation in the first few micrometers in tissues. The ballistic nature is responsible for the production of large bubbles [101].

Thermal damage models

As mentioned previously, the main goal of PTT is to induce cell death owing to hyperthermia. The influence of heat on cells was studied in vitro and in vivo in numerous studies, showing that the rate of cell killing is exponentially dependent on time and temperature above a certain threshold [102].

To perform a comparison among different cells, the Arrhenius analysis can be employed. The results of such an analysis are displayed in a plot where the x-axis represents the reciprocal of temperature, and the y-axis represents the reciprocal of the time that is needed to reduce the cell survival rate by 63%. Every plot has a certain breakpoint. Below the breakpoint, the curve is steeper, and above the breakpoint, time halves each time temperature increases by a single degree to achieve the same survival rate.

A method known as the “thermal isoeffective dose” was developed to normalise time–temperature data to a single number [103,104]. This number is usually converted to minutes at 43 °C, and is referred to as the cumulative number of equivalent minutes, or equivalently as CEM 43 °C. More details on these thermal damage indices and their evaluation can be found in the comprehensive review written by Dewhirst et al. [102] or in the comparative analysis by Pearce et al. [105].

In the theoretical analysis of the PTT efficacy, the thermal damage Ω, defined as logarithm of undamaged and damaged cells concentration ratio, was obtained by solving the first-order thermal chemical rate equation and the Arrhenius integral [106] in accordance to, (7) $$\mathrm{\Omega }\left(\mathit{r},t\right)=A\underset{0}{\overset{t}{\int }}{e}^{-\frac{E_a}{R_{u}T(\mathit{r},\tau )}}\mathrm{ }d\tau ,$$(7) where t is the time, A is the frequency factor, E_a is the activation energy, R_u is the universal gas constant and T(r,τ) is the temperature at the point r in space at the time τ. This approach was based on the empirical law founded in the 1940s, and can be replaced by the more accurate two-state model derived by Feng et al. from statistical thermodynamics [107].

Conclusions

Plasmonic photo-thermal therapy is a promising approach in the treatment of hyperthermia. Gold nanoparticles possess unique properties that make them suitable therapeutic agents in tumour tissue destruction. Furthermore, their properties are easily tailored to fit the particular purposes by changing their shapes, or by imposing surface modifications. However, to become a clinical praxis standard, more investigations are still needed. First, toxicity was reported in some studies, especially in earlier research studies mainly owing to the use of cetrimonium bromide (CTAB) in the preparation. Second, the effective target binding on the tumour site has been shown to be of great importance. An intensive research and rapid development is still in progress investigating both tasks.

However, this review was concerned with gold nanoparticles and their application in thermal therapy mainly from the physical perspective viewpoint. The detailed descriptions contained herein dealt with the theoretical light activation of gold nanoparticles, consequent heat that is produced by irradiation, and the estimation of damage to cancer cells. As was described, these three processes can be modelled separately, depending on whether the researchers’ interests are only on one therapeutic parameter, or on a complex study that will yield an assessment of the entire therapeutic efficacy. First, researchers must strive with the irradiation of a tumour. A low, yet a sufficient light dose should be applied on the tumour to accomplish its complete removal without harming the surrounding healthy tissue. To achieve this task, several parameters have to be adjusted, such as the laser wavelength and power, and the dimensions and concentrations of nanoparticles. In this review, we focussed on extensively adopted modelling methods based on the radiative transfer equation. The equation was solved using the Monte Carlo method that constitutes a gold standard, and provides excellent accuracy in simulations. Owing to advances in parallel computing techniques (e.g. CUDA), the simulation duration time has been drastically reduced. State-of-the-art MC algorithms even offer great capabilities to handle curved boundaries and arbitrary-shaped media. Thus, this approach is perfectly suitable for absorbed energy estimation in PTT, but it still requires further development, e.g. to obtain Raman scattering spectra or fluorescence phenomena, which could be useful for gold nanoparticles used as contrast agents in imaging-guided therapy.

Additionally, the basic description of modelling optical responses of gold nanoparticles was described in this review. For this purpose, one can employ methods from electrodynamics, like DDA and FDTD. With the use of simulation software, the synthesis of the particles can be tailored exactly for the required behaviour, instead of attempting time-consuming trial-and-errors. Absorption and scattering spectra of nanoparticles in water can be obtained based on simulations. However, the real-life conditions are much more complex, and nanoparticles are surrounded by various compounds that could cause disparities in the elicited responses. Additionally, coupling effects of clustered nanoparticles close to each other have to be considered to achieve an increase in the accuracy of elicited outcomes. Finally, a reliable method for inclusion of the nanoparticles in modelling light propagation in biological tissues still constitutes a major challenge.

Heat transfer and thermal damage models help estimate the influence of laser radiation on biological tissue. While insufficient radiation energy decreases the treatment efficacy, high temperatures are harmful to surrounding healthy tissue. Moreover, the optical properties change with temperature, and thus, the use of Pennes' bio-heat equation can provide feedback for time-resolved light propagation effects. Modified versions of this equation were published many times, but they are not extensively used in PTT simulations and could provide an inspiration for further research.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by UHK FIM Excellence project and by the project and by the Czech Science Foundation project [GA16–13967S].