A planning strategy for combined motion-assisted/gated MR guided focused ultrasound treatment of the pancreas

Abstract

Objective: To develop and evaluate a combined motion-assisted/gated MRHIFU heating strategy designed to accelerate the treatment procedure by reducing the required number of sonications to ablate a target volume in the pancreas.

Methods: A planning method for combined motion-assisted/gated MRHIFU using 4D-MRI and motion characterization is introduced. Six healthy volunteers underwent 4D-MRI for target motion characterization on a 3.0-T clinical scanner. Using displacement patterns, simulations were performed for all volunteers for three sonication approaches: gated, combined motion-assisted/gated, and static. The number of sonications needed to ablate the pancreas head was compared. The influence of displacement amplitude and target volume size was investigated. Spherical target volumes (8, 15, 20 and 34 mL) and displacement amplitudes ranging from 5 to 25 mm were evaluated. For this case, the number of sonications required to ablate the whole target was determined.

Results: The number of required sonications was lowest for a static target, 62 on average (range 49–78). The gated approach required most sonications, 126 (range 97–159). The combined approach was almost as efficient as the hypothetical static case, with an average of 78 (range 53–123). Simulations showed that with a 5-mm displacement amplitude, the target could be treated by making use of motion-assisted MRHIFU sonications only. In that case, this approach allowed the lowest number of sonication, while for 10 mm and above, the number of required sonications increased.

Conclusion: The use of a combined motion-assisted/gated MRHIFU strategy may accelerate tumor ablation in the pancreas when respiratory-induced displacement amplitudes are between 5 and 10 mm.

Keywords:

• Thermal ablation
• high intensity focused ultrasound
• imaging (i.e.
• MRI)
• modeling (i.e.
• treatment planning)

Introduction

At present, surgical resection is the only option for curative treatment of pancreatic cancer. Unfortunately, 80–85% of the patients diagnosed with pancreatic adenocarcinoma present advanced unresectable disease [1]. Therefore new treatment alternatives are dearly needed. The use of High Intensity Focused Ultrasound (HIFU) for thermal ablation of tumors in the pancreas has been demonstrated to be feasible and preclinical studies have shown benefits in terms of pain palliation and prolonged survival [2–6]. Improved guidance of HIFU therapy can be achieved by combining HIFU with Magnetic Resonance Imaging (MRI), also called MRHIFU [7]. However, MRHIFU treatment of tumors located in the abdomen remains challenging. First, there are problems related to organ motion, mostly due to respiration [8]. Second, it has been demonstrated that the heat sink effect caused by a high tissue perfusion rate may negatively affect the HIFU treatment efficiency [9]. The pancreas is an organ with a relatively low blood perfusion (blood flow of 94.1 ± 24 mL/100 mL of tissue min) and it has also been shown that perfusion is decreased in pancreatic adenocarcinoma especially, (blood flow of 16.6 ± 13.1 mL/100 mL of tissue min) [10]. Pancreatic tissue displacement due to respiratory motion has also been characterized and is known to occur mainly in the cranio-caudal direction, with an average maximum amplitude of 7.5 ± 4.6mm in prone position [11].

Three main solutions have been proposed to achieve motion compensation for HIFU energy delivery: induced apneas, respiratory gating, and beam steering strategies [12–15]. Induced apneas under general anesthesia and mechanical ventilation, or pharmacological control of the respiratory cycle under deep sedation allow for temporary interruption of the respiratory cycle to deliver ultrasound energy [16,17]. One drawback of that approach is that it reduces the noninvasive nature of HIFU treatment approach. In addition, this approach may not be suitable for patients with advanced cancer [18]. Alternatively, respiratory-gating limits energy delivery to the period, in which the diaphragm remains stationary [19]. In this case, time-synchronized modulation of the HIFU energy delivery is performed as a function of the position of the target volume in the pancreas. Finally, beam steering strategies with real-time tracking have been proposed [20]. These strategies exploit the beam steering capabilities of phased array transducers to continuously reposition the HIFU focus to the current target location, which allows for continuous energy delivery. This approach is technically challenging because the delay between the target position determination and the actual sonication should be kept as short as possible (order of 100 ms) [14]. In this time, multiple intensive computational tasks need to be performed (image acquisition, image processing, switching of the HIFU generator and data transport).

Besides motion tracking and beam steering, it might be advantageous to use a static HIFU beam and let the respiration-induced motion assist the HIFU (MA-HIFU) energy delivery process. Typically, the target volume is covered by a number of sonications, either single cell or, in order to accelerate target coverage, volumetric cells with cool-down periods in between sonications.

Using MA-HIFU, the induced thermal dose for a given location will be distributed inside the target as a function of the displacement pattern during the respiratory cycle. Therefore, delivering the required thermal dose to the whole target volume in MA-HIFU might not always be feasible depending on the maximum displacement. For this reason the planning method should be supplemented by alternative options for energy delivery (i.e., by gated sonications). This study follows on a recently proposed HIFU approach leveraging respiratory organ motion [21]. This planning was simulated using a simplified model for a typical displacement pattern, and showed that treatment durations may indeed be shortened.

Because of the relatively low displacement amplitude and low perfusion values of the pancreas, we hypothesized that MA-HIFU may accelerate HIFU treatment in the pancreas by lowering the total number of treatment cells to cover the target lesion. Recent studies have demonstrated the use of MRI to acquire 4D imaging information to fully characterize the tumor displacement over the respiratory cycle [22].

Here, we demonstrate a practical implementation of planning a combined motion-assisted/gated MRHIFU in the pancreas: it makes use of 4D-MRI data to identify locations where motion-assisted sonications can be used and those that should be targeted with gating. This approach was tested using simulations based on 4D-MRI data obtained in volunteers. To evaluate its potential treatment acceleration, the number of sonications needed for ablation of the pancreatic head using the combined motion-assisted/gated MRHIFU approach was compared to the number needed with the gated approach and in a hypothetical case without motion. In addition, we investigated the influence of target size and displacement amplitude on the efficiency of the proposed method in a simulation study.

Materials and methods

Combined motion-assisted/gated MRHIFU strategy

The premise of the motion-assisted/gated treatment approach is that given the target motion within the respiratory cycle, a part of the target volume can potentially be identified for motion-assisted sonication. It is a fair assumption that this volume would consist of positions (in the stationary frame of the MRHIFU system) where part of the target is present, always, regardless the respiratory phase. Then by placing the HIFU transducer focus at such a location, a MA-HIFU sonication can be delivered.

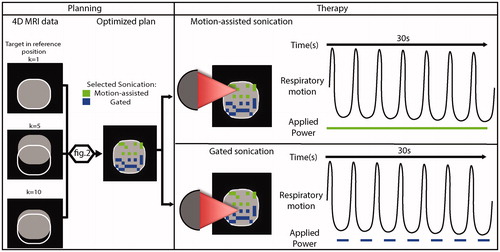
As illustrated in Figure 1, based on acquired 4D MRI data, the system takes into account tissue displacement throughout the respiratory cycle and generates an optimized plan for therapy, consisting of motion-assisted sonications (green), where energy is delivered throughout the respiratory cycle, and gated sonications (blue), where gating is limited to end expiration. In the following sections, the key steps and a possible implementation of an algorithm for motion-assisted/gated MRHIFU planning are introduced.

Figure 1. Illustration of combined motion-assisted/gated HIFU treatment. Motion-assisted/gated HIFU treatment follows the same steps as conventional MRHIFU with a planning and therapy delivery phase. As part of the planning, a 4D-MRI set to characterize the target motion is acquired and is then used to generate an optimized plan that takes into account this target motion. More details on this optimization are provided in Figure 2. In the treatment phase, the system delivers motion-assisted sonications by applying power throughout the respiratory cycle, or gated sonications by limiting energy delivery to end expiration.

The planning of the combined motion-assisted/gated MRHIFU method is divided into four steps, as described below and illustrated in Figure 2:

Figure 2. Illustration of the combined motion-assisted/gated sonication planning approach and its four main steps.

1. 4D Motion characterization

2. Target volume segmentation

3. Thermal dose simulation

4. Planning optimization

4D Motion characterization

First, a 4D MRI data is acquired from which the displacement fields are extracted describing the target motion throughout the respiratory cycle. A golden angle self-navigated stack of stars 4D-MRI sequence as described by Stemkens et al. [23] was used for image acquisition, The main sequence parameter settings were: TR = 3.0 ms, TE = 1.45 ms, Flip angle = 30°, FOV = 350 mm³ × 350 mm³ × 200 mm³, Matrix size = 233 × 233 × 51. After acquisition, all spokes were sorted into (K = 10) phases covering the respiratory cycle using phase binning.

For planning in this framework, a common coordinate system to the patient and MRHIFU hardware needs to be defined. In this study this domain will be called Ω, which is equal to the acquired 4D-MRI volume dimensions and discretized at the imaging resolution: $\mathrm{\Omega }\subset {\mathbb{R}}^3.$ In this domain (x,y,z) are indices of locations centered in the voxels of Ω. For motion characterization, an L²–L¹ optical flow 3 D image registration algorithm was used to extract the displacement fields describing the target motion [24]. Optical-flow image registration is a non-rigid registration method based on a spatially constrained model (i.e., voxel intensity conservation along the trajectory, using a transport equation) [25]. As implemented, the L²-L¹ algorithm allows to capture any type of elastic deformation under the assumption that motion amplitude between one pixel and its neighbors is encompassed within the 3 D acquired volume and locally constrained to smooth spatial variations [24]. The motion estimation in the pancreas with this acquisition and registration method has previously been evaluated, and a mean residual error of 0.51 mm was found [23].

For each respiratory phase the MRI image was registered to the first respiratory phase. In this volume, a target volume and its margins were manually segmented defining${\mathrm{ }M}_1\left(x,y,z\right),$ a binary mask which contains N locations in Ω. From the registration step, as an output, vector field displacement are saved and will be used in the next step.

Target volume segmentation

As opposed to treatment planning for a static organ, for motion-assisted/gated MRHIFU, a sonication strategy has to be assigned to all points within the target volume. This is achieved by segmenting the target into two subsets. For each target location, the sonication strategy is allocated based on the calculated presence probability throughout the respiratory cycle as explained below.

First all positions of $M_1\left(x,y,z\right)$ are spatially transformed to take into account the target displacement: (1) $$M_k\left(x,y,z\right)=T_k\left(M_1\left(x,y,z\right)\right)$$(1)

The $M_k$ set constitutes a set of binary masks that is obtained by applying the transformation $T_k,$ which describes the respiratory motion, to the binary mask $M_1,$ defining the target in the first volume of the 4D series. In applying the transformation $T_k,\mathrm{ }$we used a linear interpolation followed by a thresholding at 0.5 in order to obtain a transformed binary mask. Thus, the $M_k$ describe the position of target through the respiratory cycle.$\mathrm{ }$Then, projection over the respiratory phases, i.e. along the time axis, of the segmented target volume yields a 3 D likelihood map P(x,y,z), according to: (2) $$P\left(x,y,z\right)=\frac{1}{K}\sum _{k=1}^K{M}_k\left(x,y,z\right),\mathrm{ }\forall \mathrm{ }\left(x,y,z\right)\in \mathrm{\Omega }\subset {\mathbb{R}}^3$$(2)

P(x, y, z) indicates the presence of ${\mathrm{ }M}_1\mathrm{ }$at all given positions (x,y,z) through all respiratory phase k. At all positions, P has a value between 0 and 1 with a step of 1/K.

If P(x, y, z) = 1, then sonications at this location would at all times fall within the target volume, therefore making this location a candidate for MA-HIFU.

Based on this threshold value P = 1, we propose to create two subsamples of locations: (3) $$C_s=\left\{\mathrm{ }\left(x,y,z\right)\in {\mathrm{ }M}_1\mathrm{ }\left|\mathrm{ }P\right(x,y,z)=1\right\}$$(3) (4) $$G_s={\mathrm{ }M}_1\backslash C_s,$$(4)

Here C_s is the set of points where continuous sonications are possible and G_s is the set of points where gated sonications should be performed. The subset $C_s$ are the points within ${\mathrm{ }M}_1$ where the likelihood is 1 and $G_s$ are all the others points within ${\mathrm{ }M}_1.$ Therefore by the definition of $C_s$ and $G_s\mathrm{ }$from Equations (3)(3) $$C_s=\left\{\mathrm{ }\left(x,y,z\right)\in {\mathrm{ }M}_1\mathrm{ }\left|\mathrm{ }P\right(x,y,z)=1\right\}$$(3) and 4 the number of elements of their union should be equal to N.

Thermal dose simulation

It is assumed that an acoustic window exists that allows HIFU sonications at all N selected locations in our target. As a next step, temperature profiles were simulated and the associated thermal dose calculated.

The temperature profiles were simulated using Pennes Bio Heat Transfer Equations (BHTE) model [26]. The bio-heat transfer equation (BHTE) was employed as the model for 3 D temperature prediction, which includes the applied acoustic power$P,$ a priori knowledge of the absorption rate $\alpha ,$ the heat diffusion coefficient $D$ and the perfusion value$\omega .$ (5) $$\frac{\vartheta }{\vartheta t}T\left(\overrightarrow{r},t\right)=\alpha .P\left(\overrightarrow{r},t\right)+D{.\nabla }^{2}T\left(\overrightarrow{r},t\right)-\omega .T\left(\overrightarrow{r},t\right)$$(5) where ${\nabla }^2$ is the Laplacian operator, and $\overrightarrow{r}=(x,y,z)$ is the spatial location.

In the implemented model, the coefficients$\mathrm{ }P,$ $\alpha ,$ $D$ and $\omega ,$ were assumed to be spatially and temporally invariant. The spatial distribution of the acoustic pressure field was assumed to have a Gaussian pressure model aspect (σ = 2mm). Simulations [27] were performed with an applied acoustic power P of 450 W and 30 s duration.

The acoustic properties of the pancreas were taken from [28]: density = 1045 kg/m³, Thermal conductivity = 0.51 W/m/°C, Specific Heat = 3164 J/kg/°C, Perfusion rate= 4.5 kg/m³/s.

To evaluate the effect of motion on the sonication protocol at all locations included in C_s, the extracted displacement vectors from the 4D-MRI data were used in Equation (5)(5) $$\frac{\vartheta }{\vartheta t}T\left(\overrightarrow{r},t\right)=\alpha .P\left(\overrightarrow{r},t\right)+D{.\nabla }^{2}T\left(\overrightarrow{r},t\right)-\omega .T\left(\overrightarrow{r},t\right)$$(5) as a trajectory$\mathrm{ }\overrightarrow{r}\left(t\right).$ The extracted displacement vectors were interpolated in the time domain to match the temporal resolution of the thermal simulations, which was set to 40 ms to guarantee numerical stability. For interpolation in the time domain, a symmetrical low pass Finite-duration Impulse response Filter (FIR) was used with the purpose to minimize the interpolated errors [29]. The extracted displacement vector fields were applied as a trajectory on the reference volume to simulate the effect of MA-HIFU.

For the simulated sonications, the applied power duration was set as follows. For MA-HIFU and static sonications, power was applied during 30 s. For gated sonications, the maximum sonication duration was 30 s, but during this 30 s the energy delivery was only allowed during end expiration as shown in Figure 1, as it has been shown to be feasible in the liver in a preclinical study [19].

For all simulated sonication locations in both C_s and G_s, the delivered thermal dose was calculated from the temperature profile using the Sapareto–Dewey expression to convert temperature history to equivalent minutes (EM) [30]. In the EM representation, the thermal dose required to create a thermal lesion is equivalent to an exposure of 240-min at 43 °C [31]. In this study, the 240 EM threshold was used as ablation threshold.

At the end of this step a set of N thermal dose volumes D_i(x,y,z) associated to all locations, was created and saved.

Planning optimization

This step aims at minimizing the total number of sonications required to ablate the whole target. An optimization problem can be formulated with the purpose to minimize the number of locations sonicated in C_s and G_s combined to reach total ablation of the target volume. The optimization problem can be considered linear because the thermal dose is additive, and assuming that all sonications can be considered independent (i.e., that sufficient cooling time is allowed between the sonications). Therefore, the optimization problem to find the minimum number of sonications needed can be written as: (5) $$\left\{\begin{array}{c}m\mathit{in}\sum _{i=1}^N{x}_i\\ x_i\mathrm{ }\in \mathrm{ }\left\{0,1\right\}\mathrm{ }1\le i\mathrm{ }\le N\\ s\mathit{ubject}\mathrm{ }\mathit{to}\mathrm{ }\mathit{Cx}\mathrm{ }\ge \gamma \end{array}\mathrm{ }\right.$$(5)

• Here, $\mathrm{ }i,\mathrm{ }1\le i\mathrm{ }\le N$ is the index of a spatial location (x,y,z) in ${\mathrm{ }M}_1$

• $x_i,\mathrm{ }1\le i\mathrm{ }\le N$ is a binary variable associated with each spatial location i:

  • ○ $$x_{i\mathrm{ }}=\left\{\begin{array}{l}1 \mathit{if} \mathit{the} \mathit{point} i \mathit{has} \mathit{to} \mathit{be} \mathit{sonicated}\\ 0 \mathit{otherwise}\end{array}\right.$$

• ${\sum }_{i=1}^N{x}_i$ corresponds to the number of points to be sonicated

• γ is 1D representation of the 3D target volume:

  • ○${\mathrm{\gamma }}_i\in {\mathbb{R}}^N$

  • ○ $${\mathrm{\gamma }}_i=\left\{\begin{array}{l}240 \mathit{if} \mathit{the} \mathit{lethal} \mathit{dose} \mathit{has} \mathit{to} \mathit{be} \mathit{\hspace{1em}\hspace{1em}achieved} \mathit{at} \mathit{the} \mathit{location} i\\ 0 \mathit{otherwise}\end{array}\right.$$

• $C$ is a cover matrix $C\in {\mathbb{R}}^{N\mathrm{*}N}$, $C_{\mathit{ij}}$ is obtained from the simulated doses D_i(x,y,z) and represents the simulated dose at location j when the sonication is applied at location i.

To solve the optimization problem from Equation (5)(5) $$\frac{\vartheta }{\vartheta t}T\left(\overrightarrow{r},t\right)=\alpha .P\left(\overrightarrow{r},t\right)+D{.\nabla }^{2}T\left(\overrightarrow{r},t\right)-\omega .T\left(\overrightarrow{r},t\right)$$(5) the dual-simplex method for solving large scale problems from the optimization toolbox of matlab^TM (MathWorks, Natick, MA, USA) was used [32]. This final step leads to creation of set of points with$\mathrm{ }{x}_i=1,$ composed of both continuous and gated sonications optimized to reach ablation of 100% of the target (i.e., 240 EM within the tumor volume).

Planning studies on volunteers and method comparison

In order to investigate the feasibility of our approach, six volunteers were scanned on a 3.0-T clinical scanner (Ingenia, Philips, Best, The Netherlands) using the 28-channel body array receive coil. Institutional Review Board approval for this volunteer study aimed at MRI protocol development had been granted and written informed consent was obtained from all volunteers. In clinical practice, to create a proper acoustic window on the pancreas with the patient lying prone on the MRHIFU table top, compression of the tissues on the ventral side of the pancreas would be needed. Therefore, all volunteers were scanned prone on a flat table with a compression device positioned under their xiphoid process [30]. Data were acquired to cover the whole pancreas throughout the respiratory cycle. For the evaluation, the target volume was defined as the entire pancreas head for every volunteer. The target was manually segmented on the first phase of the 4D-MRI data set.

Three scenarios were evaluated, first, the proposed combined motion-assisted/gated approach. Second, the target was assumed to be static and in the third, only gated sonications were used. For scenarios 2 and 3, single point sonications were simulated at every location in the target with the same protocol as the one we used in the combined motion-assisted/gated approach. The linear optimization step described above was used for all three scenarios. This led to creation of three sets of optimized sonications for every volunteer. The number of sonications needed to reach 100% of ablation of the target was used to compare the efficiency of the strategies. For the combined method, the percentage of the target volume ablated using continuous sonications was also assessed.

Influence of target size and displacement amplitude

Between subjects, tumor size and induced respiratory displacement may vary considerably and these parameters are expected to significantly influence the applicability and performance of the sonication strategies. Therefore, a simulation study was carried out using in-vivo displacement patterns obtained in the volunteers. The effect of both displacement amplitude and target volume size on the planning and number of sonications needed to ablate the target was investigated. A spherical tumor model instead of the pancreas head was used as the target. Four spherical models of varying diameter (25, 30, 35 and 40 mm) with respective target volumes of (8, 15, 22 and 34 mL) were evaluated. For each target volume, the number of sonication to reach total ablation with our method was evaluated. This was done for different displacement amplitudes, ranging from 5 to 25 mm.

Results

Planning studies on volunteers and method comparison

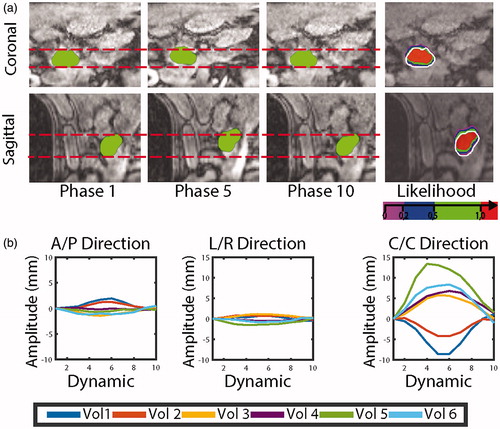
An example of the 4D-MRI data, with the segmented pancreas head and the resulting likelihood maps is shown in Figure 3(a). In this volunteer, the maximum displacement amplitudes were 8 mm in the cranio-caudal direction, and less than 1 mm in the antero-posterior and left-right directions. In this volunteer, the volume for which P = 1 covers 90% of the target volume. Overall, in our six volunteers the main direction of motion was cranio-caudal with displacement amplitudes varying between 4 to 13 mm with an average of 8 mm. In the antero-posterior direction the maximum displacement was found to be less than 3 mm, while in the left-right direction it was less than 2 mm (Figure 3b).

Figure 3. (a) Typical example of acquired 4D images and likelihood map. A red referenced line positioned at the boundary of the organ in the reference phase are there to help the reader to visualize the motion of the target. The color overlaid represents the likelihood map P(x,y,z) in Ω, while the contour of the target in the reference phase is represented with a white contour. (b) Average displacement per ROI measured in all volunteer in the three main direction (antero-posterior, left-right and caudo-cranial).

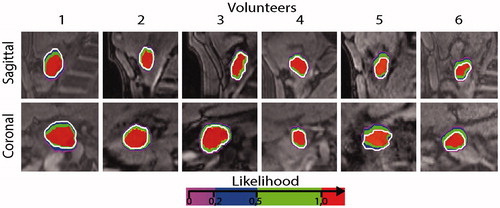
Figure 4 shows an overview of the likelihood maps for all volunteers. It can be noticed that in all volunteers, most of the target was covered by locations with P = 1 and the percentage of the target volume covered by continuous sonications varied from 76 to 94% with an average of 88%.

Figure 4. Likelihood P(x,y,z) overlay in Ω on the reference image in all our volunteer. A single slice through the coronal and sagittal orientations are represented for all volunteers, while the contour of the target in the reference phase is represented with a white contour.

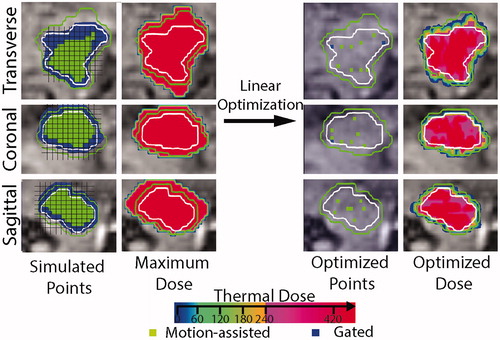
Figure 5 illustrates the effect of the optimization step where sonication locations are selected. If we were to sonicate all 1260 motion-assisted/gated locations the tumor would be severely overtreated, with the ablation threshold (240 EM) far exceeding the margins of the target, as delineated by the green line. The optimization step only selected 53 shots, viz. 49 (green voxels) in the motion-assisted volume C_s and 4 (blue voxel) in the gated sonication volume G_s. In addition, the 240 EM contour of the overall delivered dose is well within the margin volume, while still covering the full target delimited by the white contour.

Figure 5. Typical example showcasing the linear optimization step. Single slices in the three orientations are showing, from left to right: all simulated locations (i.e., C_s and G_s), the maximum thermal dose associated with all these locations, the optimized points selected by our algorithm and its associated thermal dose. The contour of the target in the reference phase is represented with a white contour and as an indication a margin contour at 3 mm of the target is indicated in green. Blue and green voxel are locations where gated and motion-assisted sonication can be achieved, respectively.

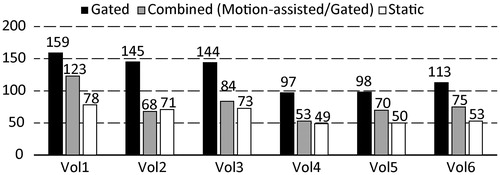
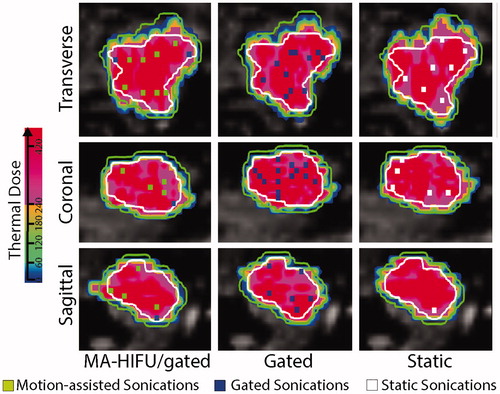
With all evaluated strategies (hybrid, gating and static), the desired thermal dose of 240 EM was delivered to the target volume, as shown in Figure 6. From the same number of simulated locations, in this volunteer 1260, a total of 97 locations were needed with gating, 53 with our hybrid strategy and 49 for the hypothetical static target.

Figure 6. Comparison of delivered thermal dose and planning sonications after optimization in three scenarios respectively, motion-assisted/gated, gated and static scenario. The contour of the target in the reference phase is represented with a white contour and as an indication a margin contour at 3 mm of the target is indicated in green.

In Figure 7, the number of sonications needed to ablate the complete target volume is shown for all volunteers and strategies. In the hypothetical case of a static organ the number of sonications was the lowest, ranging from 49 to 78, with an average of 62 sonications. The gated scenario needed the highest number of sonications within a range of 97 to 159 sonications with an average of 126. Our combined approach came close to the hypothetical static case with a range of 53 to 123 sonications with an average of 78. Overall, a stationary target would have allowed the lowest number of sonications, except in volunteer 2, where the combined motion-assisted/gated approach achieved the lowest number of sonications to ablate the complete target. In average in this study, gated sonication allowed energy delivery during 16 s ± 1 s per sonication.

Figure 7. Optimized number of sonications to ablate the overall target in all volunteers as a function of different energy delivery strategies: gated, combined (motion-assisted/gated) and static.

Influence of target size and displacement amplitude

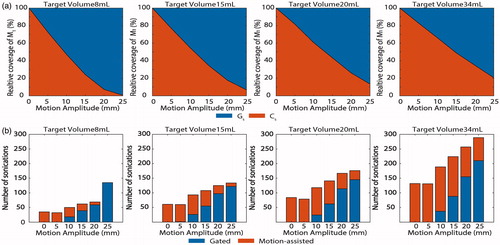
The variations of the two sonication volumes (C_s and G_s) are shown as a function of the displacement amplitude, for all target volumes in Figure 8(a). C_s volume linearly decreases for an increase in displacement amplitude while G_s increases for an increase in displacement amplitude. For all target volume sizes, the same tendency can be observed. Conversely, for the same displacement amplitude an increase in tumor volume leads to superior $C_s$ volume coverage. For an 8 mL target volume, at 25 mm displacement amplitude none of the target is suited for continuous sonication, while with a 34 mL target 25% of the target could be accessed. Overall, the number of sonications required to reach ablation of 100% of the target volume increased as a function of the maximum motion amplitude and the tumor volume (Figure 8b). For all target volumes, a 5-mm displacement amplitude, would allow coverage of the complete target with MA-HIFU sonications only, while for 10 mm and over the number of gated sonications required increased with increasing motion amplitude.

Figure 8. (a) Evolution of the continuous sonication (C_s) and gated sonication (G_s) volume as a function of the maximum motion displacement in four different tumor volumes (8, 15, 20, 34 mL). Coverage volume is expressed as a percentage coverage of the target M₁. (b) Number of sonications needed to achieve 100% ablation as a function of the maximum motion displacement for the same four different tumor volumes. The number of continuous and gated sonications within the overall number of sonications is also represented.

Discussion

In this study, an automated planning approach for a combined motion-assisted/gated MRHIFU approach was introduced for the treatment of the pancreas head and compared to a gating scenario and a hypothetical static case. Based on the acquired in-vivo motion data the combined approach would outperform a fully gated sonication strategy and reduce the number of required sonications for ablation of the full target. The hypothetical case of the static pancreas represented a reference scenario with respect to the achievable treatment time, given the chosen and simulated HIFU energy delivery protocol. We demonstrated that similar results could be achieved using combined MA-HIFU and gating. Furthermore, in one volunteer our proposed method achieved a lower number of sonication which can be due to the specific geometry of the target. Therefore, this approach holds potential for time efficient MRHIFU treatment in the pancreas head, making it of interest for further evaluation.

Clinically, promising results with Ultrasound guided and MR guided HIFU have already been shown for pancreatic tumors [6,33]. However, in both reports, respiratory motion has been outlined as a remaining technical challenge and this approach could contribute to a solution. In the pancreas, displacement amplitudes of 7.5 ± 4.6mm in prone position were observed [11]. The motion estimates in the volunteers in this study fall within the same range. From the literature, the average tumor size for pancreatic adenocarcinoma has been reported to be 33 ± 10 mm [34]. When looking at the results of our simulation study, it appears that the pancreas benefits from its relative low displacement amplitude versus organ size which leads to a large target volume available for the MA-HIFU approach.

The method proposed here represents one possible implementation for this planning approach. The golden-angle stack of stars 4D-MRI acquisition is not yet widely available on all systems, and investigating the use of other sequences could be of interest. The authors made the choice to design an optimization step based on thermal dose. This choice was motivated by the additive property of the thermal dose, making the formulation of the optimization problem simple. In this study, the dual simplex method allowed us to find a solution to the optimization problem in all cases. The development of algorithms to solve minimization of linear functions is an ongoing field of research in computer science, so the optimization approach used is by no means the only one possible. However, improving the solver for the optimization problem itself was beyond the scope of this paper. As implemented the optimization step creates a minimum thermal dose of 240 EM over the entire target, but no maximum was set. As such, the authors made sure that the obtained planning would lead to ablation of the entire target, possibly with areas receiving a thermal dose above 240EM.

In our matlab^TM implementation the image registration of each 4D-MRI dataset was performed under a minute. The linear optimization was done within a maximum time of 90 s. The BHTE simulation was the most time consuming task because the thermal dose was computed sequentially for all points, however, all sonications are independent and can therefore be computed in parallel under a GPU implementation.

In this combined strategy, the temporal projection step is crucial to determine which parts of the target should be treated with MA-HIFU and gating. From our volunteer study, it appears that the likelihood threshold value of 1 allows to cover most part of the pancreas with MA-HIFU sonications, which is one of the main reasons behind the improved sonication efficiency. These results were obtained for a spherical target, which is representative for many pancreas tumors. However, for tumors with a different shape, the extent of the tumor volume in the main direction of respiratory motion will play a key role in determining the fraction of the target covered by $C_s.$

Some limitations in this study need to be addressed. The acoustic access was assumed to be similar for all target points, which may not be the case during real treatment. This should be investigated in further studies. In this work, the respiratory motion was assumed to be regular and cyclic. During prolonged MA-HIFU treatment, bulk motion or variation in displacement amplitude may occur. Thus, the use of motion tracking and displacement anticipation solutions might be needed to enable safe treatment. Solutions have already been proposed for tracking three-dimensional respiratory motion with two–dimensional real-time MRI image series [35] and adaptive methods anticipating organ motion as well [36]. Evaluation of these approaches in the context of MA-HIFU sonication would be of interest. Real-time temperature and motion monitoring would play a major role in this treatment procedure. Some online tools have been already proposed to achieve these tasks but it would be needed to evaluate them in this context [15,37–41]. Future work should include pre-clinical and clinical experiments to demonstrate its in-vivo feasibility with actual HIFU heating. It should also include the development and evaluation of online adaptive planning tools and dose deposition update.

We introduced a planning strategy for combined motion-assisted/gated MRHIFU for tumor ablation in the pancreas. When compared to the gated sonication approach, a careful planning for combined motion-assisted/gated MRHIFU may accelerate the treatment procedure.

Disclosure statement

B. Stemkens is an employee of MR Code B.V.

Additional information

Funding

This work was supported by the European Union Seventh Framework Program [FP7/2007–2013] under grant agreement 603028 (iPact project).