Microscopic origin of ferroelectricity in chiral smectic C* liquid crystals and ordering of ‘ferroelectric fishes’ proposed by de Gennes

Abstract

The qualitative microscopic mechanism of ferroelectric ordering in smectic C* liquid crystals originally proposed by de Gennes and others is analysed in detail using the molecular-statistical approach. The general expression is obtained for the spontaneous polarisation of the smectic C* phase composed of chiral and polar molecules of the C ₂ symmetry. The polarisation is shown to be determined by molecular chirality, molecular transverse dipole and the non-polar biaxial order parameter which does not vanish in the non-chiral smectic C phase. A particular molecular model is considered in which molecular chirality and molecular biaxiality are determined by the pair of off-centre transverse molecular dipoles. In the context of this model the spontaneous polarisation is evaluated both analytically and numerically.

Keywords:

• ferroelectric liquid crystals
• chirality
• intermolecular interactions

1. Introduction

Ferroelectricity in smectic liquid crystals continues to attract significant attention because of the unusual structure and properties of various ferroelectric, antiferroelectric and ferrielectric phases, and because of their applications in electro-optical devices ( 1 ). Ferroelectric ordering in the chiral smectic C* (SmC*) phase was predicted theoretically about three decades ago by Meyer et al. ( 2 ), and the phenomenological theory of ferroelectric ordering in tilted smectics is well established ( 3, 4 ) Ferroelectric smectic liquid crystals are unique in the sense that the spontaneous polarisation is determined by molecular chirality. It is well known that in smectic phases the spontaneous polarisation is induced by the tilt and does not appear self-consistently as in proper solid ferroelectric materials. Thus the primary order parameter of the smectic A (SmA)–smectic C (SmC) transition is the tilt pseudovector which possesses a different symmetry compared with the polarisation which is a polar vector. The polarisation can then be induced by the tilt pseudovector only in a chiral medium. Thus, ferroelectricity observed in conventional tilted smectics is very different from that which has been found recently in a novel class of smectic liquid crystal phases formed by achiral bent-core molecules. In bent-core phases the spontaneous polarisation is not induced by the tilt and thus appears also in orthogonal smectic phases ( 5 ).

A particular microscopic mechanism of ferroelectric ordering in tilted smectics has been the issue of debate during the past two decades. In particular, the role of molecular chirality on the microscopic level has not been clarified completely. On the one hand, it is well known that spontaneous polarisation in tilted smectics cannot exist without molecular chirality, and thus at least a fraction of molecules must be chiral. On the other hand, it is not immediately clear whether some specific chiral intermolecular interactions are required to induce the macroscopic polarisation in tilted chiral phases. The spontaneous polarisation is not the primary order parameter of the corresponding tilting transition, and thus the polar ordering of chiral molecules may, in principle, be induced by some non-polar ordering of the same molecules which is not necessarily dependent on molecular chirality.

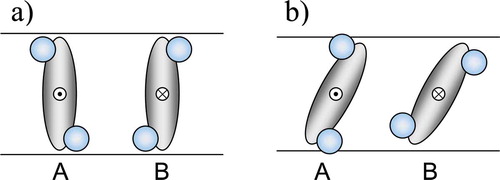
It is interesting to note that possibly the first qualitative microscopic mechanism of this kind was proposed by de Gennes (see his book ( 6 )). Dipolar ordering of chiral molecules in the SmC* phase is qualitatively illustrated by de Gennes using the two ‘ferroelectric fishes’ presented schematically in Figure 1. The ‘fishes’ possess electric dipoles which point from one of their eyes in the direction perpendicular to the plane of the ‘fish’. Thus, the ‘fishes’ possess a symmetry plane if the dipole is removed. At the same time, the presence of the transverse dipole determines the chirality of the ‘fish’. The reversal of the direction of the transverse dipole results in the reversal of the handedness of the chiral ‘fish’, i.e. the two enantiomers here possess the dipoles pointing out from the left eye and the right eye of the ‘fish’, respectively.

Figure 1. Schematic representation of the dipolar ordering of the two chiral and polar ‘fishes’ in the tilted SmC* phase as originally proposed by de Gennes. If the fins of both ‘fishes’ point in the direction of the neighbouring layer boundary, the transverse dipoles of the ‘fishes’ are parallel and point in the direction perpendicular to the tilt plane.

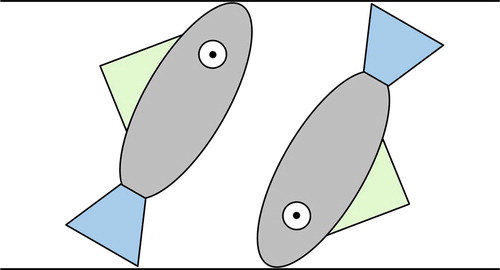
The shape of the ‘fishes’ of de Gennes is polar also along the ‘long axis’ of the fish. It is also important that the ‘fishes’ are biaxial even without the transverse dipoles. The direction of the first short ‘molecular axis’ is then naturally determined by the dorsal fin of the ‘fish’. The second short axis is then in the direction of the transverse electric dipole. The qualitative mechanism of dipolar ordering of such chiral ‘fishes’ in the tilted plane, illustrated in Figure 1, is related to the biaxial ordering of short ‘molecular’ axes (i.e. the ordering of the fins). If, for some reason, the fins have a tendency to point towards the nearest region between the smectic layers, the fins of the two tilted ‘fishes’ in Figure 1 point in the opposite directions while the transverse dipoles appear to be parallel, and thus the whole system is polar in the direction perpendicular to the tilt plane. The two orientations of the same fish are statistically equivalent, and the corresponding pair of ‘fishes’ possesses the C ₂ symmetry axis along the total dipole which corresponds to the only point symmetry element of the ferroelectric SmC* phase. At the same time the pair of ‘fishes’ does not possess any polar order in the tilt plane even if a single fish possesses additional electric dipoles along the long axes and the fin. This is consistent with the absence of the macroscopic polar order in the tilt plane determined by the C ₂ symmetry of the SmC* phase.

The qualitative mechanism of ferroelectric ordering proposed by de Gennes has been independently employed by several authors who have proposed more detailed molecular models ( 7 , 8 , 10–14). It has been recognised that it is possible to use models of individual molecules which possess higher symmetry than the ‘ferroelectric fish’ in Figure 1. The two main molecular models of this kind, used in the Boulder model ( 7 , 8 ) and in the Goossens theory ( 12 , 13 ), are presented in Figure 2. One can readily see that both molecules in Figure 2 possess a transverse dipole in the direction of the ‘molecular plane’. This dipole makes the molecules chiral, and without it both molecules are characterised by the C _2v symmetry, i.e. they possess one symmetry plane and the C ₂ symmetry axis perpendicular to the plane. In the case of the zigzag molecule (Figure 2(a)) this symmetry is determined by the molecular shape while in the molecule with permanent dipoles (Figure 2(b)) it is determined by the two antiparallel dipoles of same magnitude. These molecules have the same symmetry as the pair of ‘fishes’ in Figure 1.

Figure 2. Simple models for chiral biaxial molecules of the C _2h symmetry with transverse molecular dipoles.

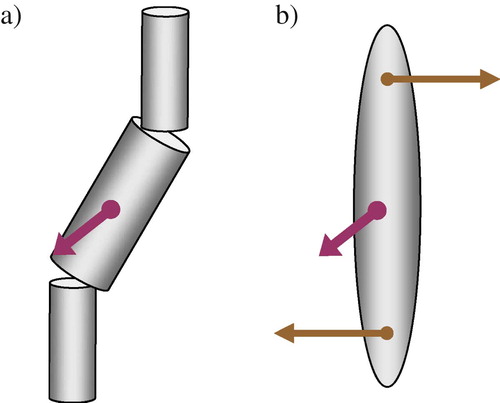
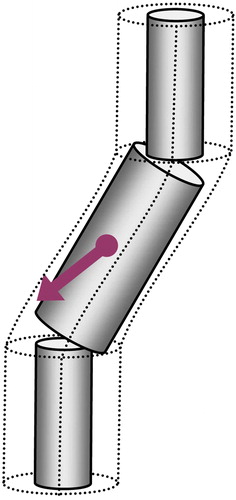
The general qualitative mechanism of the polar ordering of the molecules of the C _2v symmetry in the tilted smectic phase is illustrated in Figure 3. Here a chiral biaxial molecule is schematically represented as a rigid rod with two ‘lateral groups’ and a permanent dipole perpendicular to the molecular plane. In this model also the lateral groups make the molecule biaxial while the chirality is determined by the transverse dipole. Without this dipole, the molecule possesses a mirror plane. Now let us assume that the lateral groups have a tendency to point in the direction of the region between two adjacent smectic layers (similar to the fins of the ‘fishes’ in Figure 1). One can readily see that in the SmA phase (i.e. without any tilt) the two orientations of such a molecule, which correspond to opposite directions of the transverse dipole μ, are energetically equivalent. Thus, the macroscopic polarisation in the untilted smectic phase should vanish. In contrast, in the tilted phase the balance between two opposite directions of the transverse molecular dipole is violated because the molecular orientation A, say, is more favourable than the orientation B (see Figure 3(b)). As a result, the average molecular dipole does not vanish, and a macroscopic polarisation appears in the direction perpendicular to the tilt plane.

Figure 3. (a) In the SmA phase the molecular orientations A and B, which correspond to the opposite directions of the molecular transverse dipole, are equivalent and there is no macroscopic polarisation. (b) In the SmC* phase, molecular orientation A, say, is more energetically favourable than the orientation B, and there is a non-zero average dipole in the direction normal to the tilt plane.

The primary example of the detailed model based on this general mechanism is the classical Boulder model (see, for example, (7–9)). In the Boulder model the molecules of the zigzag shape (see Figure 4), which possess the C _2v symmetry, are ordering in the so-called binding sites which have the same point symmetry as that of the zigzag molecules, and which also represents the point symmetry of non-chiral SmC phase itself. In this model the transverse molecular dipoles are ordered in the particular direction perpendicular to the tilt plane simply because the zigzag molecule fits into the binding site of the same shape only for a particular direction of the transverse dipole. The Boulder model has been successfully used to describe and predict the value and sign of the spontaneous polarisation for a significant number of chiral smectic materials. One notes that the interaction between the molecule and the binding site, which is responsible for the polar order, is non-chiral in nature because the binding site itself is non-chiral. The earlier version of the Boulder model emphasises the steric mechanisms of the ordering, while in the recent paper ( 9 ) the ordering of a molecule in the binding site has been interpreted as an ordering in the effective mean-field potential.

Figure 4. Orientation of the biaxial molecule of the zigzag shape (C _2v molecular symmetry) in the binding site of the same symmetry as assumed in the Boulder model.

Terzis, Photinos and Samulski et al. have developed a similar model ( 10 , 11 ) which is based on a mean-field-like one-particle orientational potential for each molecular segment. Using this model Terzis et al. have obtained good quantitative results for a number of ferroelectric SmC* phases (see ( 11 )). Very recently the general molecular-statistical theory of ferroelectric ordering based on the general mechanism described above has been developed by the present authors ( 15 , 16 ).

One notes that the mechanism of ferroelectric ordering proposed by de Gennes and other authors implies some non-polar ordering of short molecular axes (i.e. ordering of fins in Figure 1, for example) in the tilt plane. This ordering in itself is not related to molecular chirality and should also exist in the non-chiral SmC phase. If the molecules are chiral, this in-plane non-polar biaxial ordering also causes the alignment of transverse molecular dipoles (which makes the molecules chiral within this model) in the direction perpendicular to the tilt plane. In this paper we consider in detail the relationship between the spontaneous polarisation and the non-chiral biaxial order parameters of the SmC* phase and present a consistent description of the microscopic mechanism of the ferroelectric ordering using the molecular-statistical approach.

2. Relationship between spontaneous polarisation and non-polar biaxial ordering in the SmC* phase

It is well known that from the phenomenological point of view the ferroelectric ordering in tilted smectics is determined by the linear coupling between the polarisation and the tilt in a chiral medium. The spontaneous polarisation can then be expressed in the following general form (see, for example, ( 3 )):

(1)

where w = (n · k)(k × n) is the so-called pseudovector tilt order parameter of the SmC phase, n is the director and k is the smectic layer normal as shown in Figure 5.

Figure 5. Spontaneous polarisation P_s and the pseudovector tilt order parameter w in the SmC* phase.

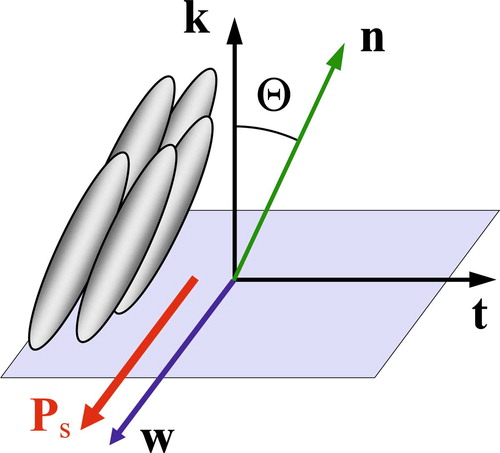
One notes that the polarisation is a polar vector while the tilt order parameter w is a pseudovector and thus the linear relationship between polarisation and the tilt is only possible if the coupling constant c_p is a pseudoscalar determined by molecular chirality. Accordingly, the polarisation vanishes if the molecules are non-chiral and changes sign when all chiral molecules reverse their handedness.

At the same time, the pseudovector order parameter w is also non-zero in the non-chiral SmC phase. Indeed, w is invariant under all symmetry transformations of the SmC phase including the reflection with respect to the tilt plane because both vectors n and k are in the tilt plane and thus are not affected by the reflection. In contrast, the spontaneous polarisation P _s , of course, changes sign under a reflection with respect to the tilt plane. One notes that this does not violate the linear relationship (2) because the pseudoscalar parameter c_p also changes sign under the reflection. In a non-chiral SmC phase the coupling constant c_p vanishes identically.

Let us now describe the appearance of the spontaneous polarisation from the molecular point of view. Orientation of any rigid biaxial molecule can be specified by the unit vectors a and b in the direction of short and long molecular axis, respectively. The biaxial molecules of high symmetry (similar to the biaxial ellipsoid or a brick) are invariant under simultaneous inversion of both axes a and b. In contrast, the molecules of the C ₂ symmetry presented in Figure 2 are not invariant under the sign inversion of the axes a or b individually. At the same time, these molecules are invariant under simultaneous inversion of both axis a and b. This symmetry enables one to introduce the transverse molecular pseudovector (a × b). One notes that the existence of this transverse pseudovector does not violate the mirror symmetry of the molecule because the pseudovector (a × b) is invariant under a reflection with respect to the molecular mirror plane which is parallel to a and b.

Now the transverse molecular dipole can be expressed explicitly in terms of this molecular pseudovector. Indeed, for molecules in Figure 2 the transverse molecular dipole is parallel to the short molecular axis c⊥b⊥a, i.e. μ = μ⊥c. Now the unit vector c can be expressed in terms of the unit vectors a and b in the following way

(2)

where Δ = ((a × b) · c) is the molecular unit pseudoscalar which specifies the handedness of the molecule. Note that c is the conventional polar vector which is expressed as a product of the pseudovector (a × b) and the pseudoscalar Δ. Finally, the transverse dipole can be expressed as

(3)

Then the macroscopic polarisation in the SmC* phase can be written in the form which contains the statistical average of the molecular pseudoscalar ⟨a × b⟩:

(4)

where ρ is the molecular number density.

Now it can readily be shown that the average ⟨a × b⟩ is non-zero only in a tilted smectic phase and is parallel to the C ₂ symmetry axis of the smectic C phase. Indeed let us express the unit vectors a and b using the orthogonal basis composed of the unit vector k in the direction of the smectic layer normal, the unit vector h in the direction of the C ₂ symmetry axis which is normal to the tilt plane and the unit vector t which is normal to k and is parallel to the tilt plane:

(5)

where γ, ϕ and ψ are the Euler angles.

Substituting these equations into the equation for the average molecular pseudoscalar one obtains

(6)

where

All macroscopic quantities in both chiral and non-chiral SmC phase must be invariant under a corresponding rotation about the C ₂ symmetry axis. In Equation (6)(6) the first term is parallel to the C ₂ axis and thus it is invariant. At the same time the second and the third terms in Equation (6)(6) are normal to the C ₂ axis and are not invariant under the corresponding rotation. Thus, one concludes that the averages A and B must vanish identically in the SmC phase. As a result the average molecular pseudoscalar ⟨a × b⟩ = Ω ⟨k × t⟩, and the spontaneous polarisation can finally be expressed as

(7)

Equation (7)(7) is the general exact expression for the spontaneous polarisation in the SmC* phase composed of molecules of the C _2v symmetry with a transverse dipole perpendicular to the ‘molecular plane’. According to Equation (7)(7) the magnitude of the spontaneous polarisation is essentially the product of the two important factors: the pseudoscalar parameter Δ_μ which represents molecular chirality and which vanishes if the molecules are non-chiral, and the non-polar biaxial order parameter Ω which can also be written in the concise form:

(8)

It is important to note that the biaxial order parameter Ω is not related to molecular chirality and does not vanish in the non-chiral SmC* phase. The order parameter Ω has been calculated numerically ( 17 ) using a molecular model of the non-chiral SmC phase composed of non-chiral molecules. This indicates that the order parameter Ω may predominantly be determined by non-chiral intermolecular interactions also in the chiral SmC* phase.

3. Molecular model of the ferroelectric SmC* phase based on dipole–dipole interactions

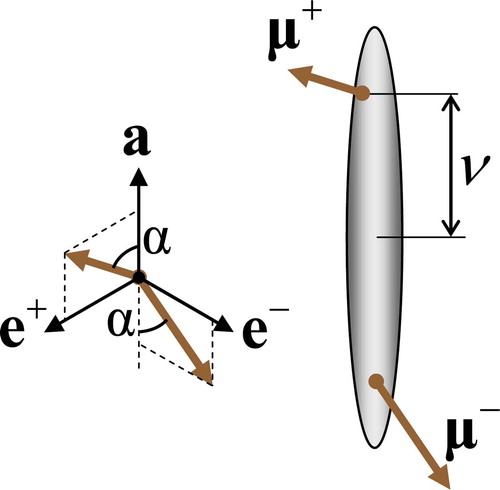
Let us consider the dipolar model of a chiral molecule shown in Figure 6. In this model, the molecule is represented by a rigid rod and a pair of off-centre transverse dipoles which do not belong to the same plane. One can readily see that the molecule presented in Figure 6 is chiral because it does not have any symmetry planes. Moreover, in this model molecular biaxiality, chirality and polarity is determined by the pair of non-parallel dipoles. Real molecules with similar structure (i.e. with a pair of almost orthogonal transverse dipoles) have recently been synthesised by Lemieux et al. (18–21) and used as chiral dopants to induce polarisation in an achiral SmC host.

Figure 6. A model of biaxial and chiral molecule with two non-parallel transverse dipoles.

Introducing the orthogonal transverse unit vectors e ^± one obtains

(9)

The total dipole moment of the molecule is transverse μ⊥ = (μ ⁺ + μ⁻) and is in the direction of the short molecular axis . The second short molecular axis is .

An interaction potential for a pair of molecules presented in Figure 6 can be written as a sum of the effective interaction potentials between rigid uniaxial cores and the electrostatic dipole–dipole interactions between all molecular dipoles:

(10)

where the uniaxial interaction potential U _uni depends on the molecular long axes a ₁, a ₂) and the intermolecular vector r, and U _dd(1,2) is the sum of all dipole–dipole interaction potentials:

(11)

Here D(R) is the dipole–dipole tensor

(12)

where R is the distance between the two interaction dipoles which depends both on the intermolecular vector r and the molecular long axes. In Equation (11)(11), , , and . We assume that the tilting of the director in the SmC phase is determined by the uniaxial interaction potential U _uni(1,2) while the biaxial ordering and the spontaneous polarisation are determined by the dipole–dipole interaction.

The spontaneous polarisation in the SmC* phase composed of such molecules is given by the general Equation (7)(7) where the biaxial order parameter Ω can be expressed in the following way using the mean-field approximation ( 16 , 17 ):

(13)

Here the orientational distribution function f ₁(a,b) can be written in the mean-field form:

(14)

where Z is the normalisation constant, and U _MF is the mean-field potential which has the following general form:

(15)

A model interaction potential between uniaxial molecules has been discussed in detail in ( 22 ), and here we can use the following simple expression for the uniaxial part of the total mean-field potential derived in ( 22 ):

(16)

where w ₁ − w ₄ are the coupling constants which can be calculated numerically for a given pair of interaction potentials ( 22 ), and the orientational order parameters S_k, P_k and V are expressed explicitly as statistical averages

(17)

(18)

(19)

The order parameters S_k and P_k characterise the uniaxial and biaxial orientational order of the long molecular axes with respect to the layer normal and V is the tilt order parameter, which vanishes in the SmA phase. At small director tilt angles Θ in the SmC phase the tilt order parameter V is approximately proportional to Θ and can generally be expressed as ( 22 )

(20)

The dipole–dipole interaction between the molecules presented in Figure 6 has been considered in detail in ( 16 ). It has been shown that the uniaxial part of the dipole–dipole interaction potential typically makes only a small contribution to the total uniaxial potential while the biaxial part of the dipole–dipole contribution to the mean-field potential can approximately be written in the following simple form:

(21)

where V _Γ = ⟨(a · k)(b · t) + (a · t)(b · k)⟩ is the biaxial tilt order parameter ( 17 ) which is also proportional to tan 2Θ similarly to V.

Many ferroelectric liquid crystal materials possess relatively low spontaneous polarisation, i.e. the average dipole per molecule is one or even two orders of magnitude smaller than the permanent transverse molecular dipole. This means that the biaxial ordering of the short molecular axis is sufficiently weak and the biaxial order parameter Ω is small. In this case the orientational distribution function may be expanded in powers of w ₅ keeping the first term:

(22)

Substituting Equations (19)(19) and (16) into Equation (13)(13) one obtains

(23)

and, hence,

(24)

where . Finally, the spontaneous polarisation can be expressed approximately as

(25)

According to Equation (23)(23) the spontaneous polarisation in the context of this model is expressed as a sum of two terms which are proportional to the uniaxial and biaxial tilt order parameters, respectively. The uniaxial tilt order parameter V is proportional to tan 2Θ where Θ is the director tilt angle. At the same time the biaxial tilt order parameter V _γ is related to the tilt of the biaxial ordering tensor which is generally different from that of the director ( 17 ) and only coincides with it close to the SmA–SmC transition point. Thus, for relatively large tilt, Equation (23)(23) does not suggest any simple relationship between the spontaneous polarisation and the tilt of the director, and thus they may have a completely different temperature dependence.

In the case of relatively strong biaxial ordering one cannot expand the orientational distribution function and the approximate Equation (23)(23) is no longer valid. In this case the polarisation and all order parameters can be calculated numerically by direct minimisation of the mean-field free energy which can be written in the form ( 16 ):

(26)

where

(27)

and where the total mean-field potential U _MF(a,b) is the sum of the uniaxial and biaxial contributions given by Equation (16)(16) and (19), respectively.

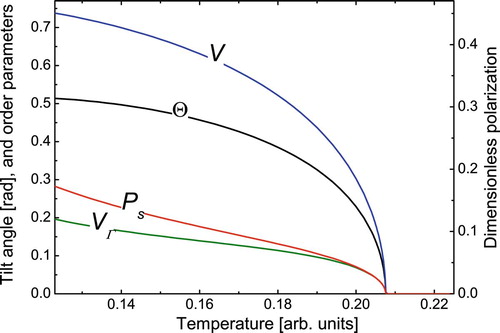
Typical temperature dependencies of the spontaneous polarisation P_s , primary director tilt angle Θ, the uniaxial tilt order parameter V and the biaxial tilt order parameter V _Γ are presented in Figure 7. α = π/3, w ₁ =   − 0.05, w ₂ =   − 1, w ₃ =   − 0.9, w ₄ =   − 0.8 and w ₅ =   − 0.1. One can readily see that the temperature variation of the uniaxial tilt order parameter V is similar to that of the tilt angle Θ. At the same time, the temperature variation of the polarisation qualitative follows that of the biaxial tilt order parameter V _Γ rather than Θ.

Figure 7. Temperature variation of the dimensionless spontaneous polarisation P_s /ρΔ_μ, tilt angle Θ, uniaxial tilt order parameter V and the biaxial tilt order parameter V _Γ in the SmC* phase calculated numerically by minimisation of the mean-field free energy.

4. Conclusions

In this paper we have used the molecular-statistical theory of SmC liquid crystals to analyse the qualitative microscopic mechanism of ferroelectric ordering proposed by de Gennes and others including the authors of the well-known Boulder model. It has been shown in this paper that this mechanism implies the non-polar biaxial ordering of short molecular axes in the tilt plane of the SmC phase, which is specific for molecules of the C ₂ symmetry or lower. This biaxial ordering exists already in the non-chiral SmC phase, and is determined predominantly by non-chiral intermolecular interactions.

If the molecules are chiral and polar, the non-polar biaxial ordering in the tilt plane also causes the alignment of transverse molecular dipoles, which are parallel to the C ₂ axes of the molecules, in the direction perpendicular to the tilt plane thus resulting in the macroscopic polarisation.

The formally exact general expression for the spontaneous polarisation in the SmC* phase composed of such molecules is obtained. The polarisation appears to be a product of the pseudoscalar quantity which accounts for molecular chirality, and the biaxial order parameter which is also defined in the non-chiral SmC phase.

In this paper we have also used a particular model of a biaxial chiral molecule composed of the uniaxial rigid core and two non-parallel off-centre dipoles. In this model the pair of dipoles is responsible for molecular chirality, biaxiality and polarity, and the spontaneous polarisation is determined by the electrostatic interactions between the chiral pairs of dipoles. In the case of weak biaxial ordering the approximate explicit expression for the spontaneous polarisation has been obtained which establishes a relationship with the uniaxial and biaxial tilt order parameters.

Close to the SmA–SmC phase transition the tilt is small, and both tilt order parameters are approximately proportional to the same tilt angle of the primary director. In contrast, far from the transition the tilt order parameters are proportional to generally different tilt angles, which correspond to uniaxial and biaxial ordering tensors. Thus, in a relatively broad temperature range the temperature variation of the spontaneous polarisation may differ significantly from that of the primary director tilt angle. This is supported by numerous experimental data (see, for example, ( 23 )).

Finally, the spontaneous polarisation, primary tilt angle and the tilt order parameters have been calculated numerically as functions of temperature using the same molecular model. The results demonstrate that, at least in the context of this model, the temperature variation of the polarisation follows that of the biaxial tilt order parameter rather than the primary director tilt angle.

Acknowledgements

The authors are grateful to H. Gleeson and R. P. Lemieux for valuable discussions.