Computing equilibrium states of cholesteric liquid crystals in elliptical channels with deflation algorithms

ABSTRACT

We study the problem of a cholesteric liquid crystal confined to an elliptical channel. The system is geometrically frustrated because the cholesteric prefers to adopt a uniform rate of twist deformation, but the elliptical domain precludes this. The frustration is resolved by deformation of the layers or introduction of defects, leading to a particularly rich family of equilibrium configurations. To identify the solution set, we adapt and apply a new family of algorithms, known as deflation methods that iteratively modify the free energy extremisation problem by removing previously known solutions. A second algorithm, deflated continuation, is used to track solution branches as a function of the aspect ratio of the ellipse and preferred pitch of the cholesteric.

GRAPHICAL ABSTRACT

KEYWORDS:

• Cholesterics
• confinement
• defects
• simulation techniques

1. Introduction

Cholesteric liquid crystals are complex fluids that exhibit long-range orientational order, elasticity, local alignment at surfaces, optical activity and response to external stimuli [1]. They are composed of chiral molecules that, in the absence of boundaries, adopt a helical structure with a preferred pitch, , set by the molecular structure and the ambient temperature. There has recently been a great deal of interest in cholesterics in confined geometries because of parallels with other condensed matter systems such as chiral ferromagnets, Bose–Einstein condensates and the Quantum Hall effect. All of these systems exhibit topological defects under confinement, including skyrmions and torons, where the boundary conditions preclude adoption of the energetically preferred uniformly twisted state. Hence, they are geometrically frustrated. It was recognised some time ago that nematic liquid crystals also may potentially form skyrmions, but these are only metastable due to the lack of preferred twist [2].

Liquid crystals are particularly attractive to study these defect structures, because they can be conveniently produced and imaged in three dimensions with techniques such as confocal microscopy [3]. Cholesterics may form skyrmion lattices in two dimensions [4]. In three dimensions, torons resemble particulate inclusions [5,6] and form chains or lattices [7]. Other more complicated defect structures called ‘twistions’ occur in films thinner than the cholesteric pitch [8]. They also provide an elegant experimental actualisation of the Hopf fibration, a map from the 3-sphere onto the 2-sphere such that each distinct point of the 2-sphere comes from a distinct circle of the 3-sphere [9], and are an ideal model system for experimental exploration of Hopf solitons [10]. Strongly confined geometries such as micropatterned surfaces [11], channels [12,13] and droplets [14] can all be used to control and order the location of skyrmions.

A key challenge in simulating these systems is that, due to the geometric frustration, they possess a particularly rich family of stationary solutions of the free energy. The ground state strongly depends on the shape of the domain and material parameters, including the cholesteric pitch. Typically, extremisation is performed from an initial guess using a relaxation algorithm, or by solving a set of non-linear Euler–Lagrange equations. In either case, having found a solution, the question remains: are there others? It is also highly desirable to track the solution set as a function of geometric and material parameters to assemble a bifurcation diagram.

A common approach to identify distinct solutions, referred to in the mathematics literature under the umbrella term of multistart methods [15], is to begin from a significant number of initial guesses. This requires extensive knowledge of the problem to devise a suitable set of initial guesses and can be inefficient as multiple guesses often converge to the same configuration. Other well-established techniques include numerical continuation [16,17], which is particularly effective in fully resolving connected bifurcation branches but can neglect solutions if they are not homotopic with respect to the continuation parameters [18], and approaches, such as Branin’s method, that rely on numerical integration of the Davidenko differential equation corresponding to the original non-linear problem [19,20]. Branin’s method is capable of systematic computation of multiple solutions but requires determinant calculations that become prohibitively expensive for large-scale problems without special structure.

In this paper, we adapt a new technique known as the deflation method [21,22] to a model problem in this class, the configuration of a cholesteric in an elliptical channel. The method is generalisable, robust and computationally efficient for large-scale applications. It has been successfully applied to a diverse set of non-linear problems including non-linear partial differential equations (PDEs), singularly perturbed problems, the analysis of Bose–Einstein condensates and the computation of disconnected bifurcation diagrams [18,21,23,24]. This paper is structured as follows: in Section 2, we briefly describe the problem; in Section 3, we introduce the deflation technique with an illustrative toy example. In Section 4, we present results for the cholesteric problem. Conclusions are drawn, with prospects for further enhancement of the algorithm, in Section 5.

2. Model

We consider a cholesteric liquid crystal in a channel with elliptical cross section. Equilibrium structures are found by identifying critical points of the Frank energy,

(1)

where , and are the splay, twist and bend elastic constants; n is a headless unit vector, the director, that corresponds to the local symmetry axis of the molecular orientational distribution and is the preferred pitch for the cholesteric. Rigid anchoring (Dirichlet) boundary conditions are imposed on the boundary , where the director is required to point perpendicular to the plane of the cross section. The energy is readily non-dimensionalised by introducing a typical length and dividing through by a characteristic magnitude of the elastic constants ; henceforth, we use dimensionless parameters.

As discussed in the introduction, this problem promotes the existence of multiple local equilibria by construction. To see why, first consider the cholesteric in the absence of boundaries. As is well known, the minimiser of (1) is a unique uniformly twisted state. Level sets of n form families of equally spaced planes often referred to as cholesteric ‘layers’. We note a valuable discussion of the limitations of this view is found in Ref. [25]. Variation away from this preferred structure, which is equivalent to compressing or bending the layers, implies an elastic cost. Considering a cholesteric in a disc, the minimisers of (1) are solutions where n rotates about the radial axis and lies everywhere perpendicular to it. The number of rotations is determined by the cholesteric pitch, , which promotes a constant rotation rate, and level sets of constant orientation therefore form equally spaced concentric circles.

For an elliptical domain, however, it is not possible to fill the ellipse with equally spaced layers, and so defects or a variable layer spacing must be introduced. The cholesteric order, which prefers a uniformly twisted state, and the shape of the domain are in competition, so the system is said to be geometrically frustrated. The frustration is resolved by adopting a compromise state, incorporating some combination of layer deformation or defects; in common with other frustrated systems, there is typically more than one way to do this, leading to the possibility of more than one minimiser.

Further, we explore solutions where , which might occur in exotic liquid crystal systems [26]. This choice of parameters leads to a material that is doubly frustrated because it is required to twist by the cholesteric term but, nonetheless, the twist is relatively expensive compared to other deformation modes. As a result, the cost of modulating the cholesteric layers is reduced. The interaction of geometric and internal frustration is expected to lead to a particularly rich solution set because they permit multiple ways of relieving the frustration: one solution might accommodate an incommensurate number of cholesteric periods by folding the layers; another might introduce a defect. These parameters therefore yield an extremisation problem that we anticipate a priori to be very challenging to explore by naive multistart methods.

3. Deflation

In solving problems that possess multiple equilibrium solutions, such as that posed in Section 2, a key challenge is to ensure that the true ground state has been found from the set of energetically low-lying solutions. The idea of the deflation algorithm is to successively modify the non-linear problem under consideration to eliminate known solutions, enabling the discovery of additional distinct solutions. Consider , a set of non-linear equations, that may admit multiple solutions. This system, for instance, could represent a set of continuous or discretised non-linear PDEs; here, we minimise the Frank energy in (1), subject to the unit-length constraint of the director, and consider the resulting system of non-linear first-order optimality conditions. Using a known solution, v, to the system , we define the deflation operator,

(2)

where is a shift scalar, is the deflation exponent and I is the identity operator. An appropriate norm must be chosen for the solution space to which the solutions belong. The deflated system is then formed by applying the deflation operator to the original non-linear system as

(3)

Iterative techniques, such as Newton’s method, may then be applied to solve the deflated system. While these iterations are guaranteed to not converge to the known solution v under mild regularity conditions, the remainder of the solution space for the original system is preserved by the deflation operator. Numerical experiments have found the effectiveness of the deflation operator to be relatively insensitive to the choice of deflation parameters. However, for certain problems, performance improvements may be obtained by varying p and [21,22]. Typical values, used throughout this paper, are and .

Having found two solutions , an expanded deflation operator can be constructed by composition of single-solution deflation operators,

(4)

and applied to the original non-linear system. As the set of known solutions is expanded, the deflation operator is grown as the product of the single deflation operators for each distinct solution in the set,

(5)

and its action remains multiplicative on the original system.

To provide a simple and tractable illustration of the deflation process, we apply it to the problem of locating critical values of a one dimensional objective function,

(6)

displayed in Figure 1 by solving the equation,

(7)

Figure 1. Toy 1D example of deflation. Critical values of the function (black), found by solving (grey). Having located a minimum at , a deflated function (grey; dashed) is constructed; this now contains a pole at but retains zeros in common with .

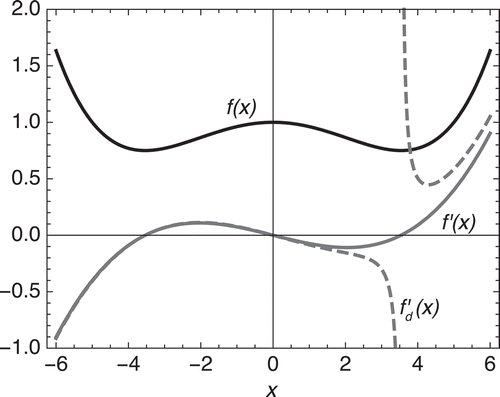
Starting from the initial guess , Newton’s method locates the first solution . The deflation operator is constructed following the definition in (2) as

(8)

where denotes the standard absolute value. Applying this to (7) yields the deflated optimality condition,

(9)

to be solved for x. The function is also plotted in Figure 1 for deflation parameters and . Notice that is not a solution to , while the remaining solutions to persist as solutions to . Use of the deflation operator precludes convergence of certain iterative techniques, such as Newton’s method, to while facilitating convergence to additional distinct solutions from the same initial guess. With the deflation parameters chosen previously and the same initial point, , Newton’s method converges to the critical point . Thus, two solutions are obtained from the same initial guess. The process may then be repeated by constructing a multi-deflation operator, incorporating both known roots, to enable the discovery of the third distinct solution at to (7) and hence identify all extremal values of .

While deflation is a useful device for finding distinct solutions, the number of solutions discovered may still depend on the analyst supplying a suitable set of initial guesses. A systematic way to generate the set of initial guesses to use is provided by continuation. Suppose that the problem incorporates some set of parameters k, which for the liquid crystal problem includes the elastic constants and preferred pitch . Given a set of solutions for some initial value of these parameters , we use each of these solutions as an initial guess for Newton’s method at a nearby parameter , deflating each solution as we find it. Subsequently, we use the full power of the deflation approach to search for new solution branches that, if discovered, can be extended to other values of using standard continuation techniques. The solutions at can in turn be used as initial guesses to find the solutions at , and so on. This combination of deflation and continuation is referred to as deflated continuation and is an even more powerful algorithm than standard deflation applied to a single non-linear problem [18]. It can be interpreted physically as computing a bifurcation diagram, a portrait of the solutions of an equation as a parameter varies. We shall use both the deflation and the deflated continuation approaches to resolve ground state solutions of the cholesteric problem in the next section.

4. Results

We apply the deflation algorithm described above to the cholesteric problem in an ellipse, varying the aspect ratio of the domain, , and preferred cholesteric pitch, . In each simulation, the director is held fixed on the boundary such that the director points out of the plane, i.e. . Elastic constants are chosen to be , and , corresponding to the exotic splay–bend cholesteric described above. The computational domain is centred on the origin with major axis parallel to the x-axis. The area of each bounding ellipse is held fixed at .

Our multilevel finite-element code used to compute stationary points of the free energy (1) is thoroughly described elsewhere [22,27–29]. Briefly, the code uses the Cartesian representation of the director and directly finds equilibrium points of the Frank energy (1) by applying Newton linearisation to the first-order optimality conditions in variational form, resulting from the constrained minimisation. The code is based on deal.II [30] and features mesh refinement and nested iteration [31] such that the problem is discretised and solved first on coarse meshes where computation is cheap, resolving major solution features, and then interpolated to more refined meshes to determine finer attributes of the computed approximation. Nested iteration has been shown to significantly improve computational efficiency in a wide variety of problems including liquid crystal simulations [29,32,33]. Here, we use a nested iteration mesh hierarchy of four mesh levels of refinement with 4884 degrees of freedom on the coarsest grid and ending with 297,988 degrees of freedom at the finest level. Finally, a damping factor, , is applied to each Newton step for both the undeflated and deflated systems. This damped Newton stepping is combined with an increased step size, , when the non-linear residual drops below 0.1. The accelerated Newton stepping is applied to increase the rate of convergence when the candidate solution begins to closely satisfy the optimality conditions.

As a first example, in Figure 2, we display the results of a typical run for aspect ratio and . The algorithm is initialised from three initial guesses (shown in the left column of Figure 2). As anticipated, deflation enables the discovery of several solutions for each value by successively removing them with the deflation operator. Several of these solutions possess energetically degenerate partners that are obtained by simple reflection about an axis of the ellipse. These are also found by deflation, even though knowledge of the symmetry of the problem is not explicitly built into the algorithm.

Figure 2. (Colour online) Example solution set found with deflation. Solution set for cholesteric pitch and aspect ratio . Rows A–C depict different initial guesses (left) and the solution set (right) recovered for each through successive applications of the deflation operator (5). The computed free energy of each solution is also given.

It is important to note that the solutions to which the code converges are stationary points of the Lagrangian (Frank energy plus unit-length constraint), not necessarily minimisers of the energy. It is therefore highly desirable to characterise the nature of each solution as it is found, i.e. determine if it is a local minimum, a local maximum or a saddle point. To do this, we must verify the second-order sufficiency conditions: a stationary point is a local minimum if the reduced Hessian of the energy (the Hessian projected onto the nullspace of the linearised constraints, i.e. restricted to feasible perturbations) is positive definite. One approach would be to assemble the linearised constraint Jacobian, compute a (dense) basis for its nullspace using the singular value decomposition, construct the (dense) reduced Hessian and compute its eigenvalues; but this would be unaffordably expensive. A better way is to exploit the fact that the eigenvalues of the reduced Hessian of the energy are related to the eigenvalues of the (sparse) Hessian of the Lagrangian: by counting the number of negative eigenvalues of the Hessian of the Lagrangian, and comparing it to the dimension of the constraint space, we can determine the inertia (the number of positive, zero and negative eigenvalues) of the associated reduced Hessian of the energy [34, Thm. 16.3]. This allows for the characterisation of the nature of each solution found using a single sparse decomposition, computed using the FEniCS, PETSc and MUMPS software packages [35–37].

In Figure 3, we show the computed ground state (lowest energy solution) as a function of and . For each solution, we display the value of the energy functional and also compute the Skyrmion number [2],

(10)

Figure 3. (Colour online) Cholesteric liquid crystal in an elliptical domain. Ground state solutions shown as a function of pitch and aspect ratio . For each solution, the value of the energy functional is displayed in the top right, with the Skyrmion number shown bottom right. Solutions indicated by *, marked top left, were found using the deflated continuation technique.

a topological index that represents the number of times n covers the unit sphere. Such indices help identify topologically distinct solutions: as the parameters and are slowly varied in Figure 3, the ground state mostly changes smoothly. However, between certain values, e.g. and 5 with , a transition to a new solution as the ground state occurs; this is accompanied by a change in the Skyrmion number. Some solutions that are quite different in appearance, e.g. , between and 5 or and 9 have identical Q because they are linked by a continuous deformation of the director field. While deflated continuation will enable us to find intermediate solutions between chosen values, and resolve any transitions that take place, the Skyrmion number provides a classification of the distinct branches that arise.

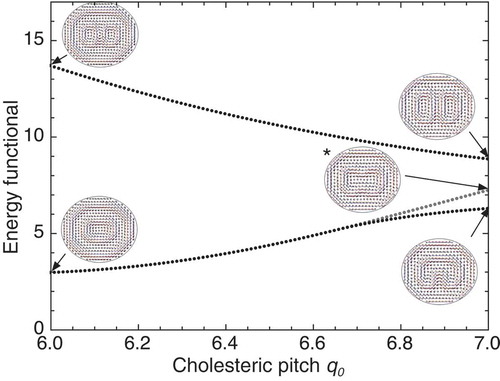
For certain values of and , the solution set discovered by deflation alone failed to include a minimal energy solution that was stable. These values are indicated in Figure 2 with an asterisk. For these values, we applied the deflated continuation technique described above to identify the stable ground state shown in Figure 3. For instance, consider the case and . The lowest energy solution found using deflation is displayed as an inset indicated by an asterisk in Figure 4 but possesses unstable directions according to the Hessian analysis described above. We therefore use the and solution set and continue in from 6 to 7. The energies of intermediate solutions obtained in the process are plotted in Figure 4 as a bifurcation diagram; the initial and final solution set recovered in this process are displayed in Figure 4 as insets. A new pair of solutions, not in the solution set, emerges through a fold bifurcation at approximately and represents the stable ground state at higher values of ; the prior ground state becomes higher in energy and is now unstable.

Figure 4. (Colour online) Bifurcation diagram as a function of generated by deflated continuation for aspect ratio . The solution set is visualised at and . Black points represent stable solutions and grey points indicate one unstable direction. The lowest energy, yet non-stable, solution identified by deflation without continuation for is indicated by an asterisk.

The same procedure was applied to all the problematic cases in Figure 3, where the solutions shown are the lowest energy solutions found and are all verified as stable. This example illustrates the power of deflated continuation to track distinct branches in the solution set and identify solutions very different from the initial guesses provided. While it remains possible that the true ground state remains elusive for some values in space, it is clear that deflation and deflated continuation are powerful tools to assist in the assembly of phase diagrams.

The solutions found in Figure 3 catalogue the interesting interplay of the elastic constants, cholesteric parameter and confining geometry. For , a circular domain, increasing initially leads only to the incorporation of additional rotations as expected. Around a critical value of , the contours of constant orientation are greatly deformed as the number of radial rotations in the channel increases from at to for . A similarly deformed structure is visible at , which is apparently close to a jump from rotations to .

For higher aspect ratios, the contours of constant orientation can be deformed by the geometry of the channel. For example, for aspect ratio and , the ground state consists of the director rotating by about the radial direction from the centre; above this value, an extra rotation is incorporated. Comparing the shape of contours of constant tilt, notice that the interior ‘layer’ is approximately circular for but becomes more elongated with increasing . For , the ground state is strikingly different: two highly deformed interior circular layers are accommodated within one contiguous outer layer. The ground state for reverts to the expected pattern, simply incorporating an additional twist. Furthermore, as increases, the transition points between states with different amounts of twist occur at higher values of and are typically proceeded by substantial layer deformation. Therefore, the confining geometry plays a role in deterring or encouraging the addition of layers.

We note that deflation uncovers a particularly large number of solutions for and that many of the solutions have relatively low energy compared to the ground state. For other values of , only a few of the solutions are close to the ground state in energy. We speculate that this phenomenon is due to commensurability, with some values of being more compatible with the shape of the domain than others. For a circular domain, commensurate solutions exist where happens to allow an integer multiple of rotations from the centre. Maximally strained solutions occur between these special values, potentially inducing deformation of the layers to relieve the frustration. This is clearly visible at and , or at and , where the inner layer in both cases is highly tortuous to fill the interior of the domain.

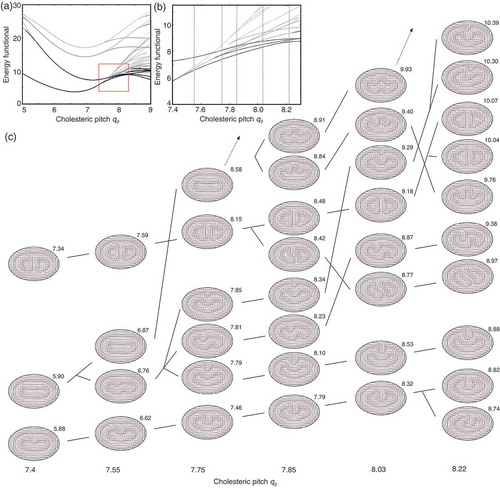
To resolve the sequence of transitions that occurs around one of the maximally strained solutions, we visualise a bifurcation diagram in Figure 5 for an elliptical domain with aspect ratio and with the preferred pitch ranging from to . We initialise the computation with the solutions found by our previous analysis. The diagram shown in Figure 5(a) displays a relatively small solution set for , but above , a dense thicket of additional solutions appears. As is visible in the expanded region depicted in Figure 5(b), this consists of a rapid succession of fold and pitchfork bifurcations. The corresponding solutions at several values of are displayed in Figure 5(c), illustrating the striking complexity of solution sets that can be uncovered using deflated continuation.

Figure 5. (Colour online) Deflated continuation. (a) Bifurcation diagram computed for fixed and continuing in . Points are coloured by the number of unstable directions, with black indicating a stable solution, and lighter grey indicating more unstable directions. A particularly dense portion of the diagram, outlined in red, is shown in greater detail in (b) where vertical dashed lines indicate values of for which the solution set is displayed in (c).

Because deflation suppresses solutions close to the initial guess, even very distant solutions can be recovered. A particularly important result is that while our initial guesses are smooth functions, the algorithm was able to spontaneously identify solutions with disclinations. Confined cholesterics in rectangular domains or channels have been experimentally and numerically shown to exhibit structures with disclinations [5,12,13], as discussed in the introduction. The existence, type and number of the disclinations were shown to be modulated by changes to the depth and width of the channel, as well as the cholesteric pitch. Figure 6 displays three examples for and varying with computed director fields and associated elastic energy densities from which disclinations are readily identified. For , the solution shown in Figure 6(a) has four defect points, arranged in a diamond pattern near the centre of the domain. The solutions in Figure 6(b,c) were found for and possess two and one disclinations, respectively. Comparing the solutions’ free energies, it is clear that the single defect structure is energetically preferred. We note that the energy of the solution in Figure 5(c) corresponds to the third lowest energy (and first unstable state) shown for in the bifurcation diagram in Figure 5(a). Thus, our results suggest that the propensity of the cholesteric to forming metastable structures with disclinations in elliptical channels, perhaps upon quenching from the isotropic phase, strongly depends on the aspect ratio of the channel boundary. Moreover, our numerical experiments indicate that multiple equilibrium configurations with distinct disclination patterns may exist for the same geometry and material parameters.

Figure 6. (Colour online) Channel induced disclinations: (above) plots of the director field and (below) the free energy density, displaying the formation of defects for different cholesteric pitch . Red circles indicate the location of each defect. Each ellipse has an aspect ratio of . Cholesteric configurations with (a) forming four symmetrically arranged defects with free energy of 67.684; (b) with two disclinations and free energy of 32.434; (c) , free energy 14.959, and a single central defect.

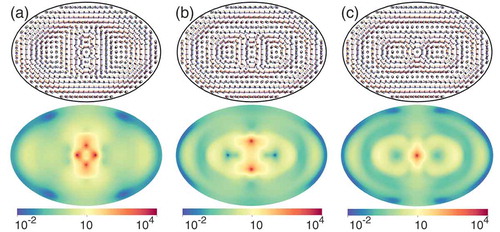
The deflation technique plays a central role in the discovery of these disclination arrangements. For instance, numerical simulations in Ref. [13] relied on a priori knowledge, gained from experimental observations, that disclination structures should be present in order to initialise the Newton iterations within a basin of attraction. We emphasise that here the simulations are initialised with smooth director fields. Multiple solutions and the emergence of disclinations occurred as spontaneous discoveries enabled by the deflation computations. In situations where experimental and analytical information is limited, such numerical capabilities facilitate a more robust and thorough exploration of the admissible solution space of a given problem.

5. Conclusion

In this paper, we present a new technique, deflation, for recovering equilibrium solutions of the free energy of a liquid crystal. The utility of the method is shown on a toy example and then used to determine the structure of a cholesteric in an elliptical domain. The ground state is identified for a range of aspect ratios and preferred pitches , showing gradual deformation of the solutions as a function of these parameters and transitions to different solutions at critical values. For selected values of and , we reconstruct the bifurcation diagram for the low energy solution set, finding remarkably dense solutions sets near the transition points. In future work, we will apply the method to characterise the solution set of more complex geometries involving cholesterics, such as the rich 3D structures observed in Ref. [3]. It will also be important to include weak anchoring, and other experimentally relevant anchoring conditions such as degenerate tangential anchoring rather than the vertical Dirichlet condition imposed here. The surface saddle-splay elastic term must also be included together with weak anchoring and will likely further modify the solution set.

The deflation methodology significantly enhances the utility of Newton iterations applied to non-linear systems by enabling Newton’s method to converge to multiple solutions from the same initial guess. Applying the deflation operator ensures that subsequent Newton iterations do not converge to previously discovered solutions and effectively modifies the basin of attraction to include unknown solutions. While convergence to multiple solutions is not guaranteed through use of the deflation operator, sufficient conditions for convergence of deflated iterations are constructed in Ref. [18] based on a generalisation of the Rall–Rheinboldt theorem. Our results not only illuminate the effect of deflation but also highlight the case that the use of multiple initial guesses to discover all solutions is not entirely eliminated with deflation. However, deflated continuation systematically provides a sequence of good initial guesses and increases overall efficiency and reliability of multiple solution discovery through more systematic exploration of the solution space.

More generally, deflation and deflated continuation therefore allows theorists to recover energetically low-lying solutions in which a liquid crystal may become kinetically trapped. It can also be used to track different solution branches when a system exhibits a bifurcation with respect to some external parameter, e.g. the applied field in a Freedericksz transition. The method is very general and can be readily adapted to different representations, e.g. the Q-tensor and parametrisations; it is likely to be most useful in systems where little analytical guidance or experimental imaging is available.

Acknowledgements

The authors contributed to the work as follows: SPM devised the toy example in Section 3; DBE, PEF and JHA performed the simulations in Section 4 and all authors contributed to their analysis; TJA wrote the paper, which was revised by all authors.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by NSERC discovery grant. TJA is supported by a Cottrell Award from the Research Corporation for Science Advancement, and a CAREER award from the National Science Foundation (award number DMR-CMMT-1654283). PEF is supported by an EPSRC Early Career Research Fellowship (award number EP/K030930/1).