Performance of a New Commercial Electrical Mobility Spectrometer

Abstract

A commercial electrical mobility spectrometer (Grimm 5.4-900 DMA and Grimm 5.403 CPC) was examined with respect to size, concentration and time-dependent responses of the CPC, the transfer function of the DMA, as well as the performance of the data inversion algorithm. For comparison with previously published results, the responses were also measured for two other commercial CPCs (TSI Model 3010 and TSI Model 3022).

All measurements were performed using sodium chloride aerosol produced by an atomizer, except for size-dependent counting efficiency measurements, where an evaporation and condensation method was used to produce particles down to a size of 2 nm. The concentration-dependent CPC counting efficiency was measured against a reference instrument working in the single particle count mode following dilution. The CPC time response was evaluated for monodisperse aerosol by measuring the step response using a solenoid valve technique. The transfer function of the Grimm DMA 5.4-900 was determined between 10 and 100 nm with two verified identical DMAs in series following the approach of Fissan et al. Measured tandem-DMA responses were compared to simulated responses based on the diffusion-broadened transfer function of Stolzenburg to define the factors influencing resolution. Finally the data inversion algorithm was tested by comparison with other devices.

INTRODUCTION

Electrical mobility spectrometers (EMS) such as the scanning mobility particle sizer (SMPS) or the differential mobility particle sizer (DMPS) are among the most commonly used instruments for measuring particle size distributions in the submicron particle size range. A typical EMS consists of a differential mobility analyzer (DMA) to classify particles due to their size and charge into electrical mobility fractions and a counter such as a condensation particle counter (CPC) or a Faraday cup electrometer (FCE). The performance of such a system depends on the performance of these two elements. The main criteria for a CPC are size-dependent counting efficiency, concentration-dependent counting accuracy, and its time response function to a sharp concentration change. The quality of a DMA is usually determined by measuring its transfer function, which gives information about the sharpness of the classification and the particle losses that occur in the instrument.

Much work was done in the past to test commercial CPCs and DMAs. Wiedensohler et al. (1997) determined the size-dependent counting efficiency of 26 CPCs by comparing them with two TSI 3025 CPCs calibrated previously against a FCE. A good review of measurement data published on the characteristics of the TSI CPCs is also given by Sem (2002). The measurement of the particle size-dependent counting efficiency generally requires monodisperse particles, usually generated by an evaporation/condensation method and subsequent DMA classification, and a sensitive FCE as concentration reference. This is the approach taken here.

Data on concentration-dependent counting efficiencies of CPCs were published by Quant et al. (1992) and by Ankilov et al. (2002a). Quant et al. used a previously calibrated TSI 3022 CPC as the reference instrument, whereas Ankilov et al. worked with the mean concentration of all participating test instruments. The present study uses a TSI 3010 CPC as reference but in the single-particle count mode, which is considered absolute because inlet losses in that particle size range are negligible (Wen and Kasper 1986; Niida et al. 1988).

Quant et al. (1992) published time response measurements using a solenoid valve to switch between polydisperse ambient air and filtered air; Wang et al. (2002) determined the time response from a concentration pulse of spark-source aerosol. In either case it is important to assure that the upper concentration level remains below the saturation range of the single particle count mode; otherwise the CPC response slows down. It is not entirely clear from either article whether that saturation limit was reached or not, because the latter data show a slower response than Quant et al., although the same optical detector was used (also see our data later on). The setup was therefore altered for the present purposes by switching between well-defined concentration levels generated with monodisperse aerosol.

The DMA transfer function can be obtained either by using highly monodisperse particles of variable and well-known size as input aerosols, which is quite difficult, aside from certain molecules (Fernandez de la Mora et al. 1998; Tanaka and Takeuchi 2003). The more practical option is to use tandem DMA techniques, which require a mathematical deconvolution of the data, e.g., by the method of Fissan et al. (1996). This latter approach is predicated upon the use of two identical DMAs, a condition that is rarely met with sufficient accuracy, even for nominally identical devices (Karlsson and Martinsson 2003), unless specifically proven. This route was taken in the present article.

ESSENTIAL DEVICE CHARACTERISTICS

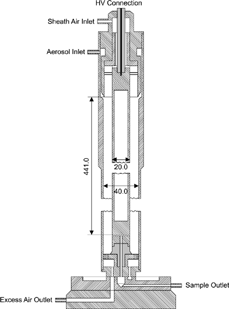
Figure 1 shows the geometry of the Grimm DMA Model 5.4-900. The outer electrode has an i.d. of 40 mm, the center electrode an o.d. of 20 mm; the distance between the aerosol inlet and outlet is 441 mm. The aerosol enters the classifier through a tangential inlet similar to the “Vienna DMA” (Winkelmayr 1991) and is then distributed uniformly via a narrow annular slit before merging with the particle-free sheath air flow. Sheath air distribution, excess air, and the monodisperse outlet design are comparable to the that of Knutson and Whitby (1975). Typical flow rates of the classifier are Q _a = Q _s = 0.3 l/min and Q _sh = Q _ex = 3 l/min, which are controlled by a closed-loop system using rotary vane pumps and a flow controller included in the housing of the CPC. The classifier housing also includes a single-stage impactor and a high voltage module, as well as the possibility to connect an additional ²⁴¹Am charger (Grimm Neutralizer 5.422) between the impactor and the aerosol inlet of the classifier. The Grimm neutralizer was not available for the examination of the system; therefore, an available ⁸⁵Kr charger was used for the present measurements.

FIG. 1 Schematic drawing of the Grimm 5.4-900 DMA. All dimensions are given in millimeters.

The Grimm CPC Model 5.403 is a continuous flow device like several others based on the concept of Bricard et al. (1976), using butanol as working fluid. Condenser and saturator temperatures are 10°C and 35°C, respectively, resulting in a temperature difference of 25°C. Instead of a butanol reservoir in the saturator, a sensor-controlled micropump is used to wet the felt, thereby preventing accidental flooding of the optics by the working fluid. A drainage system with a peristaltic pump is used to drain the condensate from the system to prevent contamination of the working fluid by condensing water from the condenser walls. The optical detection unit consists of a combination of laser and a fast photodiode, which detects scattered light at an angle of 90°. An integrated pulse height analyzer detects droplet sizes at two trigger levels, depending on particle concentration level. Concentrations below 500 cm⁻³ are detected at the higher trigger level, which is less sensitive to noise, and higher concentrations up to the upper level of the single particle mode of 6000 cm⁻³ are measured at the lower level. Concentrations above 14000 cm⁻³ are determined by a photometric signal from the optical detector. Between these two ranges a mix of both signals (photometric and single-particle counting) is used to obtain a smooth transition between both measurement principles. The coincidence correction in this range is included by using the two trigger signals from the pulse height analyzer. The transition region is also used to control the possibility of misadjustments between the photometric mode and the single-particle count mode resulting from a contaminated optics or a diluted working fluid.

The tested Grimm EMS system uses a data reduction algorithm based on a mixture of the scanning mode (Wang and Flagan 1990) and an advanced method of the classical stepping mode (Knutson 1976; Winklmayr 1987). The method was developed by the Vienna Group and is an improved version of the algorithm described by Reischl et al. (1991). By stepping the voltage and using each concentration detected by the CPC with a frequency of 1 Hz, this method derives a faster measurement than a classical stepping technique.

The detected number size distribution function of the classified sample aerosol F _C (d _P ) from the DMA at voltage V is given by the original number size distribution function F(d _P ), the ideal transfer function Tr(Z(d _P ,i)), the system detection efficiency E(d _P ), and the charge distribution of the particles α (d _P ) (Fuchs 1963):

[1]

This equation can only be solved analytically to give a unique value of the original number particle size distribution under the following restrictions (Winklmayr 1987):

•	knowledge on the DMA Transfer function Tr(Z(d P ,i)),
•	knowledge on the charge distribution α(d P ),
•	knowledge on the system detection efficiency E(d P ),
•	sharply limited upper particle size, and
•	fixed voltage steps/mobility channels.

The calculation includes a correction for the time response characteristic of the CPC in terms of flow and voltage stepping, the aerosol residence time in the DMA, and particle losses in the DMA. The measurement is done within a downscan, beginning with the largest particle size. The channel width is adjusted to the breadth of the ideal transfer function (Reischl 1991).

The normal operational mode uses 44 voltage channels, with an integration time of 2 s. The fast mode only uses 22 voltage channels; however, the information from the counts detected in the time between the voltage step and steady-state conditions being reached are utilized to calculate an additional series of 22 pseudovoltage channels. This results in a total number of 44 channels.

SIZE-DEPENDENT CPC RESPONSE

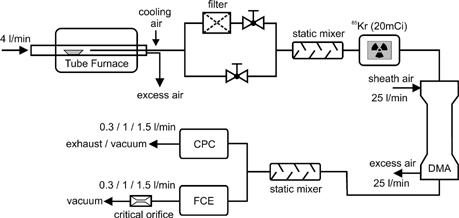
The experimental setup for the determination of the counting efficiency is shown in Figure 2. Sodium chloride aerosol in the size range from 2 to 20 nm was produced by evaporation/condensation in a tube furnace (Kasper and Berner 1978). Particles larger than 20 nm were generated by atomizing a salt solution to obtain droplets and dried in a diffusion dryer (not shown in Figure 2). Dry pressurized air was used for the generation of the particles as well as for DMA operation to avoid hygroscopic growth effects.

FIG. 2 Experimental setup used for the determination of the counting efficiency.

The aerosol was diluted in a bypass diluter to ensure that all measurements were made in the more accurate single-particle count mode (below 6 · 10³ cm⁻³). The neutralized aerosol (⁸⁵Kr; 20 mCi) was classified using a short Vienna-type DMA (R ₂ = 33 mm, R ₁ = 25 mm, L = 114 mm) operated under symmetric flow conditions Q _sh = Q _ex = 25 l/min.

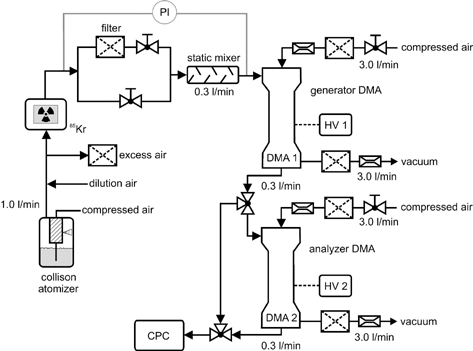
A FCE (University of Karlsruhe design; 0.2 fA detection limit) operated with the same flow rate as the CPC was used as a concentration reference for two CPCs, a Grimm Model 5.403 and a TSI Model 3010. The efficiency curve for the TSI 3010 counter is shown in Figure 3, together with other published data for the same type of instrument. A three-parameter sigmoidal fit (Mertes et al. 1995) was applied to the data to calculate the 50% counting efficiency diameter d ₅₀ for all measurements shown in Table 1.

FIG. 3 Measured counting efficiency of the TSI 3010 CPC (d ₅₀ = 10.9 nm) together with previously published data for the same instrument.

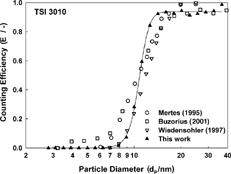
TABLE 1 Cutoff diameters for all instruments used

Model	d 50	Material	Source
TSI 3025	3.1 nm	NaCl	Kesten et al. (1991)
TSI 3010 ^a	5.7 nm	NaCl	Russell et al. (1996)
Grimm 5.403	7.5 nm	NaCl	This work
TSI 3022	8.3 nm	NaCl	Ankilov (2002b)
TSI 3010	10.9 nm	NaCl	This work
TSI 3010	10.5 nm	Ag	Mertes et al. (1995)
TSI 3010	10.3 nm	Ag	Buzorius (2001)
TSI 3010	11.9 nm	Ag	Wiedensohler et al. (1997)

Figure 4 shows a comparison between measured counting efficiency curves of the Grimm 5.403 device and other commercial CPCs. The data include measurements taken in two different years using the same Grimm 5.403 device, giving an indication of the reproducibility. The resulting cutoff diameter for both measurements is 7.5 nm. The TSI 3010 counter used by Russell et al. (1996) was modified to operate with a higher temperature difference (25 K) between saturator and condenser, comparable to the temperature difference used by the Grimm 5.403 counter. The lower cutoff diameter of 5.7 nm obtained by the latter authors could be a result of a different condenser design, consisting of eight tubular channels merging at the exit of the condenser (Keady 1988), and hence a better supersaturation profile.

FIG. 4 Counting efficiency for NaCl particles for different commercial CPCs. The two measurements for the Grimm 5.403 CPC were taken two years apart. The TSI 3010 CPC used by Russell et al. (1996) was operated with a higher temperature difference of 25 K between saturator and condenser.

CONCENTRATION-DEPENDENT CPC RESPONSE

Beside the particle size dependence, the single-particle count mode has a concentration-dependent efficiency caused by optical coincidence effects (Raasch and Umhauer 1984). The calibration of the photometric mode can also result in erroneous concentration values, e.g., if the final droplet size reached in the CPC is not identical to the droplet size used during factory calibration due to a dilution of the butanol by condensing water, or due to contaminated detection optics.

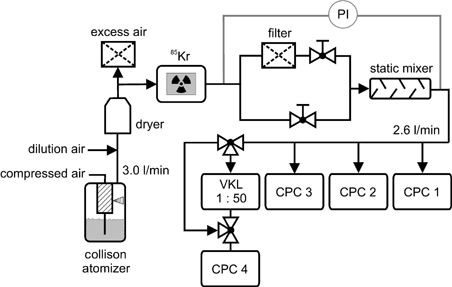
The experimental setup shown in Figure 5 was used to measure the concentration-dependent counting efficiency for the Grimm 5.403, the TSI 3022, and the TSI 3010 CPC with NaCl aerosol having a median diameter (d ₅₀) of 52 nm, a standard deviation (σ _g ) of 1.44, and total concentrations between 10 and 6 · 10⁵ cm⁻³. A static mixer was installed to assure a uniform concentration profile after the dilution unit. The aerosol was then divided into four separate streams, one for each CPC. An optional second diluter (Palas, Injection-Type VKL) could be installed between CPC 4 and the sampling port for the measurement of higher aerosol concentrations.

FIG. 5 Experimental setup used for the determination of the concentration-dependent CPC response.

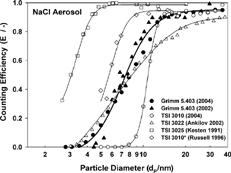
Initial measurements were performed without the second diluter, in order to compare all CPC models in the single-particle count mode. Figure 6 shows the ratio of measured to average particle number concentrations (c _meas/c _avg) versus average particle number concentration c _avg. In the examined concentration range, all CPC models are within 10% of the average value. Quant et al. (1992) also found a good agreement for the TSI 3022, TSI 3025, and the TSI 3010 for concentrations below 10⁴ cm⁻³, where all instruments operate in the single-particle count mode.

FIG. 6 Results of the concentration comparisons in the single-particle count mode. All concentrations below 10⁴ cm⁻³.

To obtain an appropriate reference concentration above 10⁴ cm⁻³, the injector diluter was used upstream of CPC 4 (identified as “TSI 3010 Ref.” in Figure 6). The dilution ratio was determined experimentally by comparing the diluted concentration to the average concentration of the first three CPCs in the range below 10⁴ cm⁻³. A least-squares fit was then used to calculate the dilution ratio. The obtained dilution ratio allowed a reference concentration with a relative accuracy of ±20% to be calculated for concentrations of up to 6 · 10⁵ cm⁻³. The measured concentrations for all three counters examined are shown in Figure 7 as a function of the calculated reference concentration. For the TSI 3010, a deviation from the reference concentration is observed commencing at approximately 2 · 10⁴ cm⁻³, and reaching a saturation value at 4 · 10⁵ cm⁻³. As this instrument is designed for single-particle counting only, this behavior is most likely caused by coincidence effects. This is consistent with the data observed by Quant et al. (1992); however, the saturation value determined here is approximately four times higher.

FIG. 7 Results of the concentration comparisons against a reference concentration calculated from the concentration measured by a TSI 3010 CPC in the single-particle count mode behind an injector diluter.

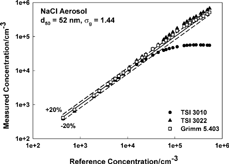
The Grimm 5.403 and the TSI 3022 CPC both use a factory-calibrated photometric mode for concentrations above 10⁴ cm⁻³. According to Figure 7, the measured concentration of the Grimm 5.403 CPC stays almost completely within the validity range (5% deviation), while the TSI model 3022 tends to slightly overestimate the validity range of the reference concentration (20% deviation) between 3 · 10⁴ cm⁻³ and 3 · 10⁵ cm⁻³. The last factory calibration of the TSI 3022 was one year ago, and because of this it is possible that the photometric mode was slightly misadjusted. Also, according to the TSI manual the calibration of the TSI 3022 is performed with monodisperse 50 nm NaCl particles, whereas the Grimm 5.403 is factory calibrated with a polydisperse NaCl aerosol with a mean diameter of about 50 nm. A polydisperse aerosol was also used for the present measurements.

CPC TIME RESPONSE

In order to measure transient aerosol concentrations or to perform fast particle size distribution scans (Collins et al. 2002), the time response of the particle counter must be known. This characteristic is usually measured in terms of the response of the CPC to a particle concentration step function.

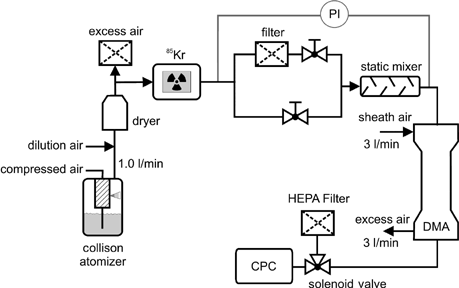
The experimental setup for this part of the study (Figure 8) is based on monodisperse NaCl particles with a mean diameter of 100 nm generated by narrow-band DMA classification. This size was chosen to avoid the influence of time-dependent diffusional losses (Okuyama et al. 1986), which can effect the time response. The necessary concentration step signal was generated by switching a solenoid three-way valve from the inlet of the CPC to the DMA or the high efficiency particle (HEPA) filter. The start time t ₀ for the measurement was defined by a trigger signal from the solenoid valve with an uncertainty of 50 ms, due to the switching time of the valve. The time-resolved response was measured by using the digital pulse output from the optics with a frequency of 60 Hz. (This required minor electrical modifications on the Grimm 5.403 CPC).

FIG. 8 Experimental setup used for the determination of the CPC time response.

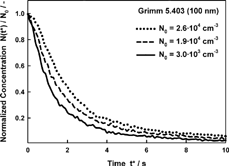
Due to coincidence effects, a CPC's time response may appear to depend on aerosol concentration (Heim 2003). This is also the case for the time response of the Grimm Model 5.403 shown in Figure 9 for three different starting concentrations N ₀ (the initial dead time is not shown). Time response measurements in this study were therefore made at concentrations below 5000 cm⁻³.

FIG. 9 Time responses of the Grimm 5.403 CPC (the initial dead time is not shown) for a concentration step for three different starting concentrations N₀, neglecting the coincidence effect.

According to Russell et al. (1995), the ideal step response of a CPC can be described by a series connection of residence time distributions (RTD) in a plug flow reactor (PFR) and a continuously stirred tank reactor (CSTR; see, for example, Levenspiel 1972).

Given its inner geometry and a Reynolds number Re ≈ 25 for the flow in the main volume (saturator), it is unlikely that the Grimm 5.403 CPC will behave as an ideally mixed volume (CSTR). A more physical description is based on a laminar flow reactor (LFR) in series with a PFR, the latter to describe inlet phenomena resulting in a deviation of an ideal laminar flow. The response function of a CPC is then described by the following expression:

[2]

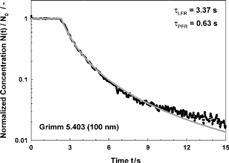
The response function of the Grimm 5.403 is shown in Figure 10, giving characteristic time constants of τ _LFR = 3.37 s for the LFR and τ _PFR = 0.63 s for the PFR. Agreement with the model is very good up to about 10 s. A small deviation for longer times may be due to nonideal effects such as the surface roughness of the saturator felt, which disturbs the boundary layer of the laminar flow and leads to a decay that is slower than predicted.

FIG. 10 Time response of the Grimm 5.403 CPC for a concentration step. The response can be approximated by a combination of the response for a PFR and an LFR, and it is described in Equation (2).

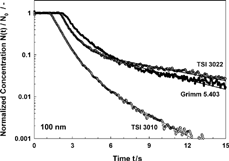
Step response measurements for two other CPCs (TSI Model 3022 and TSI Model 3010) are shown in Figure 11. The response of the Model 3010 is significantly faster due to its three-fold higher volume flow rate, and a different condenser and saturator geometry (Keady 1988). The responses of the TSI Model 3022 and the Grimm Model 5.403 are comparable, due to similar internal flow geometries and the same operating flow rate of 0.3 l/min. However, the LFR–PFR model according to Equation (2) does not fit well to the Model 3022 reponse. Therefore, a more pragmatic approach was taken that models the response function by a series connection of a PFR and a parallel connection of two CSTRs (Equation (3)). This approach gives a good numerical representation of the response functions of all three instruments:

[3]

FIG. 11 Comparison of the step response of the Grimm 5.403, the TSI 3022 and the TSI 3010 CPCs. The solid lines represent fits according to Equation (3) based on the parameters given in Table 2.

Herein a denotes a factor that can vary between 0 and 1, τ _PFR the systems' dead time, and τ _CSTR1 and τ _CSTR2 the characteristic times of both CSTRs. The corresponding values for all three counters are presented in Table 2.

TABLE 2 Parameters to describe the time response of three CPCs for a particle size of 100 nm according to Equation (3)

Model	a	τ PFR	τ CSTR1	τ CSTR2
Grimm 5.403	0.861	2.27 s	0.97 s	5.72 s
TSI 3022	0.859	2.03 s	0.71 s	7.32 s
TSI 3010	0.929	1.27 s	0.76 s	2.61 s

DMA TRANSFER FUNCTION

In order to obtain information concerning the transfer function of the Grimm DMA 5.4-900, tandem measurements were made using two identical instruments connected in series. The transfer function of the DMA was derived from the resulting tandem signal using a deconvolution technique similar to the one described by Stratmann et al. (1997). The instrument setup is shown in Figure 12.

FIG. 12 Instrumental setup for the tandem measurements.

The NaCl particle concentration was controlled so that all measurements could be performed in the more accurate single-particle count mode of the Grimm 5.403 CPC, where distortions of the transfer function due to space charge effects (Alonso et al. 2001) are also considered to be negligible. The air flow rates of both classifiers were controlled by means of critical orifices to assure a constant flow. The fixed voltage for the first classifier (Generator DMA) was produced either by an HP 6674A (0–60 Volt) or an HV supply based on the Brandenburg HV 590-124 module (60–10.000 V). For the second classifier (Analyzer DMA) operated in a stepping mode, we used the internal HV supply. The mobility distribution of the Generator DMA was measured in 22 steps, with an interval length of 50 s, resulting in a total measuring time of 18 min. Before and after each measurement, the particle number concentration downstream of the Generator DMA was measured to ensure that the concentration had not changed during measurement. To avoid any influence from the shape of the NaCl aerosol size distribution, the salt solution in the atomizer was adjusted so that the particle size selected by the Generator DMA was at the peak of the particle size distribution, where concentration changes within the range of the expected width of the transfer function could be neglected. Diffusional losses in the interconnecting tubes between the classifiers and the CPC were measured and also taken into account according to the method of Fissan et al. (1996).

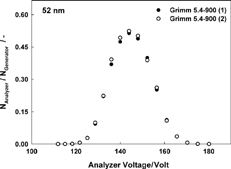
Karlsson et al. (2003) showed that manufacturing imperfections of DMAs with identical design can result in substantially different transfer functions. Therefore, the equality of both instruments was determined by using a third, short Vienna-type DMA (R ₂ = 33 mm, R ₁ = 25 mm, L = 114 mm) as the Generator DMA and the two Grimm 5.4-900s as Analyzer DMAs. Figure 13 shows that the tandem signals measured with the two Grimm DMAs are very close, so that the assumption of identical transfer functions is justified.

FIG. 13 Tandem signals for both Grimm 5.4-900 DMAs examined, downstream of a short Vienna DMA at a selected particle size of 52 nm.

For the deconvolution process we used a triangular transfer function (Martinsson et al. 2001) with broadening parameter (μ) and loss parameter (λ) according to Equation (4):

[4]

Here Q _a and Q _sh denote the aerosol and sheath air flow rates, Z the mobility, and Z ₀ the center mobility of the classifier. Transfer functions are usually described in terms of three parameters, height (h), area (A), and full width at half maximum (FWHM), which become dimensionless in the normalized mobility space. The parameters can be calculated from λ and μ (Equation (5)) and are included in Figures 14–16:

[5]

FIG. 14 Height of the transfer function of the Grimm 5.4–900 DMA as function of the particle diameter. The solid line represents a fit to the measurement data.

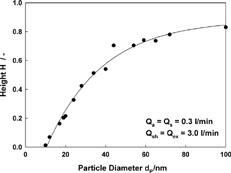
FIG. 15 Area of the transfer function of the Grimm 5.4–900 DMA as function of the particle diameter. The solid line represents a fit to the measurement data.

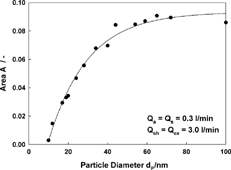
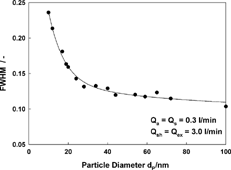
FIG. 16 Full width at half maximum of the Grimm 5.4–900 DMA as function of the particle diameter. The solid line represents a fit to the measurement data.

With decreasing particle size the height and the area of the transfer function decrease, most likely due to diffusional losses inside the classifier. The area does not reach the ideal value of 0.1 (Knutson and Whitby 1975) even for the largest particle sizes used in this study, where diffusional losses are expected to be negligible. The reason for this can be explained by particle losses due to electrophoretic migration in the exit region of the classifier (Zhang and Flagan 1996) induced by the local electric field near the insulator, where the aerosol passes from a region of high voltage at the outlet of the center electrode to the grounded bottom section of the classifier.

For the largest particle size examined, the FWHM reaches the ideal value of 0.1, which can be interpreted as a sign that only a very minor part of the broadening is caused by geometric imperfections or flow disturbances inside the classifiers.

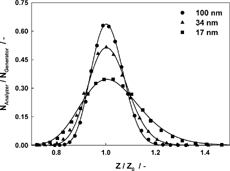
For smaller particle sizes, the FWHM increases due to diffusional broadening (Kousaka et al. 1986). In order to prove this, simulations of the tandem measurements were performed based on the diffusion-broadened transfer function described by Stolzenburg (1988). The simulations account for the diffusional broadening inside the classifying zone of the DMA, but not for losses in the aerosol inlet and outlet of the classifier. In order to compare the model and the experiment, a loss correction function was applied to the measured data. The function was derived from the area ratio of the experimental and ideal transfer functions as shown in Equation (6). The particle diameter term (d _P ) in Equation (6) was derived from the voltage of the first DMA. Figure 17 shows a comparison between the simulations and the tandem measurements for three different particle sizes. All three particle sizes show good agreement between the measurements and the simulations, indicating that the resolution of the classifier at the given flow rate was only limited by particle diffusion:

[6]

FIG. 17 Comparison between loss-corrected tandem measurements (loss correction: Equation (6)) for the Grimm 5.4–900 DMA and simulated tandem signals based on Stolzenburg's diffusion-broadened transfer function for three different particle sizes and a flow rate of 0.3 l/min to 3.0 l/min.

DATA INVERSION

The data inversion algorithm included in the software of the Grimm EMS System (Version 1.3b) was tested by comparison with a TSI SMPS model 3934, consisting of a 3071 classifier and a 3010 CPC using the same flow ratio of 0.3 l/min to 3.0 l/min for both systems. Therefore an additional particle-free air flow was added between the outlet of the TSI DMA and the TSI 3010 CPC. The scan time for the TSI instrument was 3 min (60 s downscan and 120 s upscan); for the Grimm EMS system, which was operated in the fast mode, it was 198 seconds.

The particle size distributions measured by the two instruments are shown in Figure 18. It has to be mentioned that the Grimm software displays the size distribution data referring to the natural logarithm instead of the decimal logarithm used by TSI. Therefore, the data points of the Grimm EMS System are corrected by a factor of 2.303 for the comparison.

FIG. 18 Size distribution of a NaCl Aerosol measured with the Grimm EMS system and the TSI SMPS model 3934.

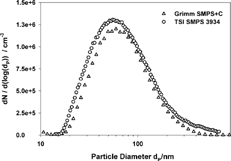
The two particle size distributions in Figure 18 look very similar, with median diameters of 67.5 nm (Grimm) and 68.7 nm (TSI); the total concentration shows a difference of 16%, a value of the order that is apparently typical for identical EMS Systems (Dahmann et al. 2002).

SUMMARY

The performance of a new CPC (Grimm Model 5.403) and a new DMA (Grimm Model 5.4-900) were thoroughly examined using NaCl aerosol and compared to other commercial instruments. The size-dependent 50% counting efficiency diameter of the Grimm and the TSI 3010 CPC were determined to 7.5 nm and 10.9 nm, respectively.

The counting accuracy for aerosol concentrations between 10 and 6 · 10⁵ cm⁻³ was measured for three different CPCs by comparing with a reference concentration derived from a diluted concentration measured by a TSI 3010 CPC in the single-particle count mode. In the photometric mode, both TSI Model 3022 and Grimm Model 5.403 determined the concentrations almost correctly with a maximum relative error of 20%. The TSI Model 3010, which uses only the single-particle count mode, saturates above about 4 · 10⁵ cm⁻³.

The responses to a step function input signal for the Grimm 5.403, the TSI 3022, and the TSI 3010 CPCs each exhibit a long-term behavior that can be very well represented numerically by a delay time followed by two superimposed exponential decay functions.

The transfer function of the Grimm 5.4-900 DMA was determined in the size range between 10 and 100 nm for a flow ratio of 0.3/3.0 (l/min) by using two virtually identical instruments in series. It was shown by comparison with simulations based on Stolzenburg's diffusion-broadened transfer function that particle diffusion was the only broadening factor.

For a polydisperse test aerosol, the Grimm EMS and TSI SMPS systems both measured the same median diameter within 1 nm, with a difference in total concentration of 16%.

Notes

^a (Δ T = 25 K).