Does Shape Anisotropy Control the Fractal Dimension in Diffusion-Limited Cluster-Cluster Aggregation?

Abstract

Motivated by recent experiments of soot formation in premixed flames where a minority population of the “stringy” aggregates is found to have a fractal dimension as low as 1.2 instead of the classic diffusion-limited cluster-cluster aggregation (DLCA) value of 1.8, we address this same question in our simulation study: is there a distribution of fractal dimensions in a given ensemble of aggregates and does shape anisotropy of clusters control the fractal dimension? Our results, however, clearly show classic DLCA yields aggregates of a broad range of shapes all with D_f≈1.8 independent of their shape, but with a shape dependent pre-factor k₀ , in the relation between radius of gyration R_g , mass N, monomer radius a, and fractal dimension . Thus the pre-factor k₀ gains in status as a descriptor of aggregate morphology so that aggregates should be described by the pair of parameters D_f and k ₀ , i.e., (D_f, k₀).

Aggregation of particles in aerosols and colloids is important in diverse fields (Family and Landau 1984; Friedlander 2000; Jullien and Botet 1987; Meakin 1999) such as materials science, biology, food science, and atmospheric science. In the absence of coalescence, clusters formed by irreversible aggregation are self-similar fractals characterized by a mass fractal dimension D_f that describes the scaling of the number of monomers in the cluster, N, (proportional to the mass) with the cluster's linear size quantified by its radius of gyration R_g as

In Equation (1) a is the monomer radius and k ₀ is a constant pre-factor (Sorensen and Roberts 1997) of order unity. Common fractal aggregates formed in aerosols and colloids are successfully modeled by computer simulation of diffusion-limited cluster-cluster aggregation (DLCA) models (Family and Landau 1984; Jullien and Botet 1987; Meakin 1999) which yield D_f ≈1.8 in three dimensions. The morphology of the aggregates is described by both D_f and the sometimes overlooked k ₀ and is a consequence of how the aggregates form and has significant effect on their physical properties. Thus the advent of the quantitative fractal description of cluster aggregates formed via random aggregation must be considered as one of the major advances in our descriptive ability of the world around us (Forrest and Witten 1979; Witten and Sander 1981; Mandelbrot 1977). In this letter we show that cluster shape affects the pre-factor k ₀ but not the fractal dimension D_f .

Indeed, much less is known about the shape anisotropy of the fractal aggregates (Lindsay et al. 1989; Fry et al. 2004) and its relation to the fractal dimension of the clusters. Shape anisotropy of aggregates can influence transport, optical, and mechanical properties of clusters. Recent experiments (Chakrabarty et al. 2009) of soot formation in premixed flames suggest that a minority population of the aggregates is “stringy” with a fractal dimension as low as 1.2 instead of the DLCA value of 1.8. Although electric field, sampling, and processing effects (Sander et al. 2010; Chakrabarty et al. 2010) might have played an important role in the formation of these soot aggregates, these recent experiments raise an important question: will a subset of pre-selected “stringy” DLCA aggregates have a different fractal dimension than the well accepted value of D_f ≈1.8? In other words, is there a distribution of fractal dimensions for the aggregates created via DLCA and does the shape anisotropy of clusters control the fractal dimension?

We have performed off-lattice Monte Carlo simulations to investigate how cluster anisotropy affects fractal dimension. Cluster shape anisotropy was measured using eigenvalues of the inertia tensor. The fractal dimension was measured using both the ensemble and structure factor methods. Both methods show that even as anisotropy of the clusters increases, fractal dimension remains the same with the DLCA value of 1.8 for all shapes. A general and somewhat surprising conclusion of this work is that shape should not be used as an indicator of fractal dimension.

FIG. 1 Number density n(A ₁₃) of clusters with anisotropyA ₁₃, for 3d DLCA model with monomer volume fraction off_v =0.001. The peak of the distribution is near 2.5 with a long, exponential tail extending to high values of A ₁₃. This exponential tail is described by n(A ₁₃)≈exp[−μA ₁₃] with μ=0.45.

FIG. 2 N versus R_g for clusters in differnent A ₁₃ bins in a log-log plot. R_g is rescaled by the monomer radius a. The legend gives each bin's A ₁₃ range. By the relation

fractal dimension, D_f is the linear fit to a bin's ensemble of points. Note that results for each bin runs parallel to the guide line with slope 1.75, typical D_f value for DLCA. k ₀ for each bin is also included in the legend.

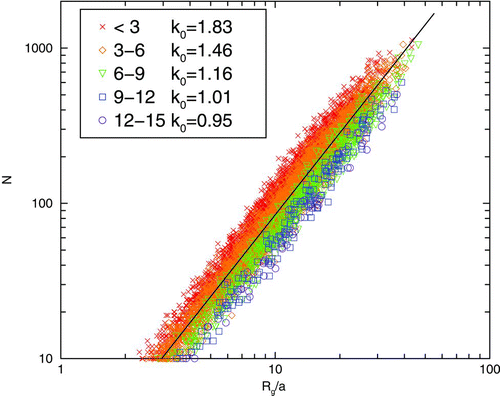
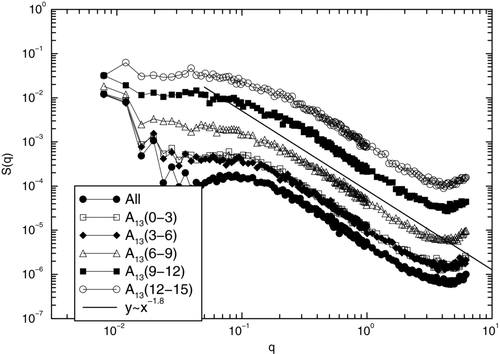
FIG. 3 Structure factor, S(q) for the whole sytem and individual A ₁₃ bins in a log-log plot. The legend gives each bin's A ₁₃ range. At large q values, one expects

. Curves for different bins are separated because the total number of monomers (N_m ) in each bin is different and decreases exponentially as A ₁₃ increases. For large values of q all plots become parallel to the guide line of slope −1.8 (before the curves flatten out at very large q because we are treating the monomers as point masses) typical D_f for a DLCA system.

We have used an off-lattice Monte-Carlo algorithm for DLCA simulations (Fry et al. 2004) using an efficient link-list method (Allen and Tildesly 1987). Our results should be applicable in the continuum limit where the frictional drag is given by the Stokes-Einstein expression. In addition, rotational motions of the aggregates were neglected in the simulation. These simulations started with 10⁶ particles at a monomer volume fraction of f_v =0.001 and ran until a final time when 7000 clusters were left in the system. The results were averaged over 5 independent runs. Cluster shape is described by the inertia tensor (Fry et al. 2004). For a three-dimensional (3d) body of N discrete masses the inertia tensor is

Diagonalizing T and dividing by the cluster mass N, one obtains the square of principle radii of gyration R ² _i for i=1, 2, 3 with R ₁⩾R ₂⩾R ₃. Anisotropy is used has a measure of cluster “stringiness” and is defined by ratio of the squares of principle radii of gyration (Fry et al. 2004):

where i, j=1, 2, 3. Here we focus on the ratio A ₁₃. The radius of gyration R_g is used as a measure of the overall cluster size which is related to the principle radii of gyration R ² _i in the following way:

The distribution of shape anisotropy is shown in a semi-log plot in Figure 1. The results show that the number density of clusters with anisotropy A ₁₃, n(A ₁₃), is asymmetric about a peak near 2.5 with a long, exponential tail extending to high values of A ₁₃ described by n(A ₁₃)≈exp[−μA ₁₃] with μ=0.45.

Clusters are divided into bins according to their A ₁₃ value, e.g., all cluster with A ₁₃<3 are in the first bin, cluster with 3⩽A ₁₃<6 are in the next bin and so on. Fractal dimension D_f is measured for all bins. In this work D_f is measured in two ways. First is the ensemble method, in which N versus R_g is plotted on a log-log plot for all clusters in each A ₁₃ bin. Using Equation (1) one finds D_f from the linear fit of the ensemble of points. Figure 2 shows such a graph for the first five A ₁₃ bins, with R_g being rescaled by the monomer radius a.

Each bin's ensemble runs parallel in the log-log plot of Figure 2; thus D_f for each bin is the same independent of shape. The guide line for Figure 2 runs parallel with each ensemble and has a slope 1.75, typical value of D_f for a DLCA system. Yet as A ₁₃ becomes larger the data points move lower, yielding smaller values for the pre-factor k ₀ as the clusters become more anisotropic.

The fractal dimension of the clusters in different bins is also measured using the structure factor S(q). We compute S(q) separately for each subsystem containing clusters in a specific A ₁₃ bin. In each case, for large q values, . Figure 3 shows the structure factor in a log-log plot for the whole system and the first five A ₁₃ bins. Curves for different bins are separated because the total number of monomers (N_m ) in each bin is different and decreases exponentially as A ₁₃ increases. For large values of q all plots become parallel to the guide line of slope −1.8 (before the curves flatten out at very large q because we are treating the monomers as point masses) typical D_f for a DLCA system. Figure 3 confirms our previous conclusion that D_f does not change with A ₁₃.

Our results show that fractal scaling of the mass with the linear dimension and the concomitant fractal dimension are independent of the cluster shape for clusters made via the DLCA process. Shape dispersion, which can be expressed by n(A ₁₃) affects the pre-factor k ₀, which now gains in status as a descriptor of aggregate morphology (Sorensen and Roberts 1997). Other physical properties of aggregates could have a dispersion based on shape dispersion but not dimensional dispersion. For example, it has been recognized for some time that light scattering from fractal aggregates depends directly on k₀ (Sorensen 2001), but this functionality appears to be more complex for extremely elongated aggregates; an issue we intend to address in the future. Thus it now appears important to describe an aggregate by the pair of parameters D_f and k ₀, i.e., (D_f , k ₀).

These results are also important because there is considerable literature which holds the intuitive notion that “stringier” clusters, i.e. those with a greater anisotropy, have a lower fractal dimension. As an example, Table 1 shows a group of clusters of size N = 50, 200, and 500 with different anisotropies. The clusters with greater anisotropy are stringier and thus may appear of lower dimension, but, in fact, all these clusters have a fractal dimension of ca. 1.8. There are also cluster forming algorithms that tailor make clusters with a preconceived fractal dimension. Such algorithms can create low fractal dimension clusters which are indeed stringy. However, given our results here, it is evident that such clusters should not be taken as low dimension, stringy DLCA clusters because such clusters do not exist. On the other hand, anisotropy does affect the pre-factor k ₀. This follows directly from Equation (1) since for a given mass N, R_g increases with increasing anisotropy thus k ₀ must decrease.

TABLE 1 Representative DLCA clusters of size N=50, 200, 500 for three different values of A ₁₃. As A ₁₃ increases and the clusters become more “stringy” R_g becomes larger yet D_f remains unchanged. This indicates that shape anisotropy does not affect the fractal dimension of DLCA clusters

To summarize, classic DLCA yields aggregates of a broad range of shapes all with D_f ≈1.8 independent of their shape, but with a shape dependent pre-factor k ₀. We propose that aggregates are best described by the pair of parameters (D_f , k ₀).

This work was supported by the Kansas State University Targeted Excellence program.