Symmetric Inclined Grid Mobility Analyzer for the Measurement of Charged Clusters and Fine Nanoparticles in Atmospheric Air

Abstract

The Symmetric Inclined Grid Mobility Analyzer (SIGMA) was developed for applications in atmospheric aerosol nucleation research with special attention to long-term routine measurements in natural atmospheric conditions. The new instrument was elaborated using the experience of the preceding scanning mobility analyzers Inclined Grid Mobility Analyzer (IGMA) and Balanced Scanning Mobility Analyzer (BSMA). The range of electric mobility is 0.032−3.2 cm²V⁻¹s⁻¹. The particle diameter distribution in the range of 0.4−7.5 nm is resolved considering the size-mobility correlation at air temperature and pressure measured with built-in sensors. The scanning technique ensures that possible peculiarities in the recorded size or mobility distribution are not caused by the technical troubles of individual mobility channels. High rate of air flow and isopotential principle suppress the disturbing effect of external electric fields and assure the representative sampling of air ions. The sheath air is coming from the atmosphere together with the sample air and is deionized by means of electrostatic filters. The residence time of the air in the instrument is 0.16 s and the temperature change does not exceed 0.5 K. Different of the previous instruments the positive and negative air ions are sampled from the same inlet air flow and measured exactly simultaneously. The sensitivity of the instrument is increased and allows measuring the mobility fraction concentrations of charged fine nanometer particles in atmospheric air at a standard 5-min time resolution with random errors of about 1 cm⁻³. The time resolution of 20 s is available at random errors of about 5 cm⁻³.

INTRODUCTION

The effect of atmospheric aerosols on climate change is comparable with the effect of greenhouse gases. The fine aerosol particles in the atmosphere grow from atmospheric trace gases through complicated physical–chemical processes. The role of aerosols among anthropogenic climate factors is ill known not because of the shortage of data about the emission of pollutants, but because of poor knowledge of the gas-to-particle conversion and the evolution of newly born aerosol particles in the atmosphere. Understanding the birth and evolution mechanisms of atmospheric aerosol particles starting in the subnanometer size range is a fundamental task of atmospheric physics and chemistry (Kulmala et al. 2004b, 2007).

Initial processes, which occur in the particle diameter range below 10 nm, are the subjects of extensive research (Kulmala et al. 2004a, 2007; Winkler et al. 2008). Theoretical models of aerosol nucleation contain many parameters whose values are commonly ill known. Thus the immediate measurement of clusters and fine nanometer particles is a source of essential information about the initial processes of aerosol formation in the atmosphere and the success of atmospheric aerosol nucleation studies depends on the advances in the measurement methods and development of instruments.

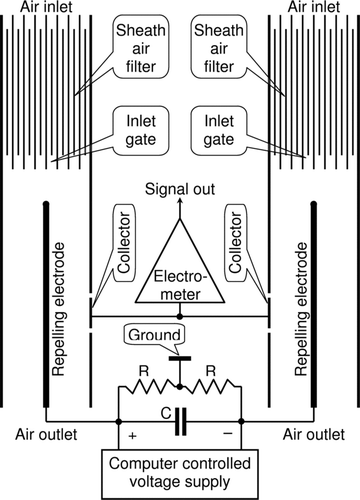
The present article introduces the Symmetric Inclined Grid Mobility Analyzer SIGMA, which was developed for applications in atmospheric aerosol nucleation research with special attention to the long-term routine measurements in natural atmospheric conditions. The SIGMA is a successor of the earlier scanning mobility analyzers IGMA (Inclined Grid Mobility Analyzer, Tammet 2003) and BSMA (Balanced Scanning Mobility Analyzer, Tammet 2006) and proposed for the measurement of initially charged airborne particles starting from the molecular size up to diameter of 7.5 nm. The measuring range on the scale of electric mobility is 0.032−3.2 cm²V⁻¹s⁻¹.

Charged molecular clusters and nanometer particles act as carriers of the electric current in the air. Therefore, they are called air ions in many publications including the present one. Hõrrak et al. (2000) carried out long-term measurements of natural air ion mobility distribution in the rural air. The dataset was analyzed using the method of principal components, which produces a classification of atmospheric ions according to their mobility and size in such a way that the variation of the values of the size distribution function is well correlated inside the classes and ill correlated between the classes. The principal component classification is in good accordance with the earlier intuitive classification of air ions (Israël 1970) and the classes are called the cluster ions (diameters 0.5−1.6 nm), intermediate ions (charged fine nanometer particles of diameter 1.6−7.4 nm) and large ions (charged aerosol particles of diameter above 7.4 nm). The physical background of the 1.6 nm threshold is the transition from elastic collisions with gas molecules characteristic for the electron structure of a molecular ion to the inelastic collisions characteristic for the condensed matter electron structure of aerosol particles (Tammet 1995). The physical background of the 7.4 nm correlation threshold has no definite explanation.

Traditional methods of measuring ions in atmospheric air were reviewed from the viewpoint of atmospheric electricity by Israël (1970) and Tammet (1970), and from the viewpoint of aerosol science by Flagan (1998).

SPECIAL REQUIREMENTS

The measurement range of an instrument for applications in atmospheric aerosol nucleation studies must include cluster ions and intermediate ions up to diameter of at least 7.4 nm. The nonlinear character of the size-mobility relation makes the relative range of ion mobility wider than the size range. As a minimum, it should cover two magnitudes of mobility.

Measurement of intermediate ions in the natural atmospheric air is a hard challenge for an instrument. The charging probability of a neutral-born nanometer particle is very low and the concentration of fine intermediate ions is often less than ten particles per cm³. If the particles are divided into narrow mobility or size fractions, then the concentration of charged particles in some fractions may appear less than 1 cm⁻³. The particles of the diameter of below 3 nm are usually measured by collecting the electric current carried by the charged particles. This current may come out very low. An example: if a size fraction contains 10 charged particles per cm³ and the sample air flow rate is 1 liter per minute, then the collected current of about 3 × 10⁻¹⁷ amperes is much less than the noise level of the best electrometric instruments when applied in atmospheric conditions. Hence, to collect more particles and make the measurement possible, the sample air flow rate should be much larger.

The clusters and the smallest nanoparticles are subjects to rapid transformations and their composition can be changed when the air is heated during passage through the instrument. If the subject of the measurement is the size distribution of particles in natural conditions then the residence time of the air in the instrument should be short and the temperature and humidity of the sheath air should be preserved as in the atmosphere. This is a high-priority requirement at many applications.

The necessity of sampling the finest particles from the open atmospheric air generates some extra difficulties. The high diffusivity causes a loss of ions in the inlet tract. The numerical correction of the diffusion loss may include considerable uncertainty and complicate the calibration of the instruments. The higher the loss the greater is the uncertainty. Minimizing of the inlet loss of the highly diffusive clusters and nanoparticles is an essential requirement for the instrument.

Some hardly controlled distortions can appear due to the effect of the external electric field on the sampling of ions. A typical fine weather atmospheric electric field over the flat ground is 100–200 V m⁻¹ and it can be largely increased during the presence of convective clouds in the neighborhood. The electric field-driven speed of a cluster ion near the instrument inlet may exceed tens of cm s⁻¹, which can modify the amount of sampled ions. The effect is asymmetric: the amount of ions forced by the electric field opposite the intake air flow is decreased but the sampled amount of ions attracted to the inlet remains unchanged (Tammet 1970).

The control voltage required for the classification of intermediate ions at a high flow rate is thousands of volts. Keeping the electrometric collector on high potential is technically inconvenient and can lead to troubles in exploitation. On the other hand, the inlet of the instrument must be grounded to avoid the effect of the electric field on the sampling of ions. The distortion caused by the electric field in the inlet channel is known as the edge effect in atmospheric electric instruments (Israël 1970; Tammet 1970). Labowsky and Fernández de la Mora (2006) introduced the term isopotential to mark the DMAs where both the inlet and outlet are on the same potential and can be connected to the ground. Instruments for the research of intermediate ions in natural atmospheric air must be isopotential. This requirement is satisfied in modern air ion analyzers designed for atmospheric research (Mirme et al. 2007).

CONFIGURATIONS OF DMA

Simplified schemes of three DMA configurations suitable for measuring ions in natural atmospheric air are illustrated in Figure 1.

FIG. 1 Three configurations of the DMA. (a) Air outlet DMA, (b) DMA with an open internal electrometric collector, and (c) DMA with a shielded internal electrometric collector.

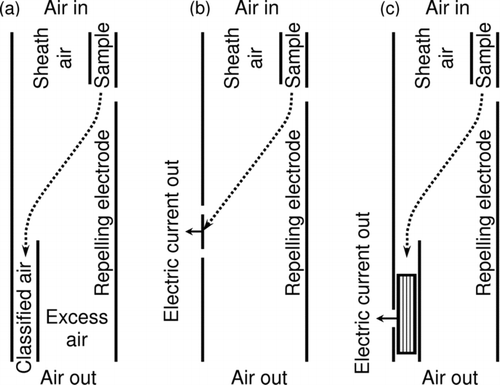
In aerosol research, the variant with an air outlet is dominating. This version of the DMA can be used as a preparative instrument sometimes called the aerosol separator. The air outlet DMA as a complete analytic instrument includes a mobility classifier and an external particle detector. The CPC and the electrometric detector are the two variants of external aerosol detectors; the latter is often called the Faraday cage filter. The CPCs ability to work with low flow rates and a low concentration of particles is its strong advantage. Unfortunately, the clusters and particles of the diameter of below 3 nm are out of the size range of the standard CPCs. The special CPCs for detecting subnanometer particles (Gamero-Castaño and Fernández de la Mora 2000; Sipilä et al. 2009) are not well adapted for routine measurements in natural atmospheric air, or still encounter restrictions in the cluster ion size range. However, recent results in the development of the CPCs (Iida et al. 2009) are promising for applications in atmospheric measurement in future. Today, the electrometric detectors are still preferred in the instruments that have to be able to measure cluster ions in long-term routine atmospheric measurements.

In atmospheric electricity studies, the mobility analyzers with an open internal electrometric collector (Figure 1b) have been dominating. The variants (b) and (c) shown in Figure 1 were implemented and tested during the development of instruments the IGMA, BSMA, and SIGMA.

A DMA where the flow rate of classified air is equal to the flow rate of sample air can be called the well-adjusted DMA. This is accepted as an optimum solution for typical applications. The definition of the well-adjusted DMA above cannot be immediately used in case of the DMA with an open internal electrometric collector shown in Figure 1b. In this case the ratio of air flows in the inlet should be adjusted equal to the ratio of fluxes of electric field to the divided attracting electrode (Tammet 1970). We will consider only the well-adjusted DMAs in the following discussion.

If the diffusion of ions is neglected, then the diagram of the transfer function of a well-adjusted DMA has a triangular shape with maximum at the central critical mobility. The value of the central critical mobility is independent of the laminar air flow profile in the classifier and is calculated as

where ϵ _abs ≈ ϵ_o is the absolute permittivity of the air, Q_sheath is the sheath air flow rate, Φ _E is the electric flux through the sheath air, C_eff = Φ _E /V is the effective capacitance, and V is the voltage between the electrodes of the classifier (Tammet 1970). If the air flow turbulence and diffusion of ions are negligible then all inlet ions of the central critical mobility are expected to be trapped by the collector in a well-adjusted DMA.

A DMA for atmospheric applications must cover a wide mobility range. Three arguments controlling the central critical mobility are Q_sheath , C_eff , and V. The effective capacitance is used as an argument in the recording of mobility distribution only in multichannel instruments (Tammet et al. 1973; Mirme et al. 2007). Multichannel instruments have many advantages. The measuring information is collected simultaneously with several electrometers and the full distribution is measured as fast as the signal from a single channel. A weak point is that it is difficult to identify the events where signals of one or a few channels include a moderate systematic error. However, the main factor limiting the usage of multichannel instruments is complicated construction and calibration, bringing about a high price and complex maintenance.

Air flow variation was used for scanning through a mobility range by Nolan and Kenny (1952). This method had many drawbacks and was not used later. The variation of air flow affects the sampling efficiency and may affect the thermal regime in the analyzer. The possible span of a flow-rate variation is narrow and does not allow covering the necessary range of mobility required in atmospheric aerosol nucleation research.

The critical mobility in most of DMAs is controlled by means of voltage. A traditional method is the stepwise variation of the voltage. An alternative method is continuous scanning. The continuous scanning in the air outlet DMAs has thoroughly been discussed by several authors (Wang and Flagan 1990; Dubey and Dhaniyala 2008; Mamakos et al. 2008).

The scanning DMAs with an open internal electrometric collector, like the BSMA, meet a difficult problem, originating in the electrostatically induced displacement current. The density of the displacement current is ϵ _absdE/dt while the density of the ion current is neZE. Here n is the number concentration of ions, e is the elementary charge, Z is the mobility and E is the electric field. The displacement current reaches the value of the ion current when the relative speed of the variation of the electric field and the control voltage are

If the concentration of a fraction of intermediate ions around the mobility of 0.1 cm²V⁻¹s⁻¹ is 10 cm⁻³ then the relative variation of the classifier control voltage 2 × 10⁻⁶ s⁻¹ produces about the same effect as the deposition of ions. Thus the classifier control voltage of a DMA with an open internal electrometric collector must be extremely stable, which is a hard requirement even for instruments with stationary voltage, e.g., for multichannel instruments. Thus the stepwise scanning is applied in most of the scanning DMAs. In this case, the electrometric collector is temporarily grounded for short periods when the voltage is changed. During these periods, the displacement current is led to the ground circumventing the electrometer.

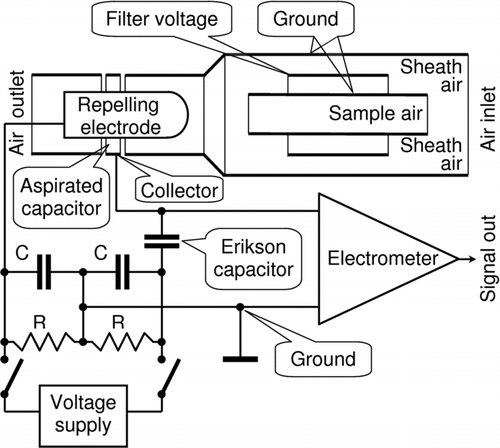
Continuous variation of voltage in a DMA with an open internal electrometric collector is possible only when the displacement current is well compensated. The classic method of compensation is the balanced capacitance bridge proposed by Erikson (1921) and illustrated in Figure 2 as used in the mobility analyzer UT-7509. A modified bridge method was proposed by Komarov (Komarov et al. 1961). The Komarov bridge consists of two equal aspiration capacitors both ventilated with the natural air. Thus the changes in the air temperature and humidity affect the capacitance in both arms of the bridge in the same way. The Komarov bridge is implemented in the BSMA illustrated in Figure 3. Sample air ions should pass one condenser of the Komarov bridge while all ions should be filtered out during the entrance into the other condenser. Exploitation of the BSMA showed a weak point of the Komarov bridge: the compensation condenser aspirated with deionized air still generates a random noise signal which is physically added to the noise generated in the working condenser. Thus the random noise is increased about 1.4 times when compared with the random noise in the Erikson bridge.

FIG. 2 Diagram of the cluster ion mobility analyzer UT-7509, which includes the Erikson bridge.

FIG. 3 Diagram of the mobility analyzer BSMA, which includes the Komarov bridge.

Ungethüm (1974) proposed an original method, where the signals from the measuring condenser and compensation condenser are connected to two inverted inputs of an operational amplifier. This method had serious technical drawbacks and was not used afterwards.

Full elimination of the effect of displacement current requires at least of a 6 magnitude reduction in the uncompensated or unshielded electric flux. This may be an unrealizable technical task. Thus the periodical check of the zero level and an additional numerical compensation of the residual displacement current are recommended in the instruments for measuring low concentration air ions.

Wang and Flagan (1990) used the exponential variation of the voltage, which makes the time intervals of passing the mobility distribution fractions equal on the logarithmic scale. The voltage was controlled by a computer via a digital-analog converter. However, there exists a very simple alternative way to generate the exponentially decreasing voltage: the discharging of a RC-circuit. This method, called below the RC-scanning, was implemented in several instruments designed at the University of Tartu and considered as immediate predecessors of the SIGMA.

The diagram of the first RC-scanning mobility analyzer of the University of Tartu UT-7509 (Tammet et al. 1977) is presented in Figure 2. The displacement current is here compensated by means of an Erikson bridge. The technologically limited sensitivity of this instrument is not sufficient for measuring ions of low concentration in natural atmospheric air. The ions are created immediately in the sample air inlet by means of corona discharge and aged during about 1 s-long passage to the classification section. This old instrument is still used for studying the effect of different trace gases on the mobility of cluster ions (Parts and Luts 2004).

An RC-scanning instrument for the measurement of natural atmospheric ions, the IGMA (Tammet 2003), is the first application of the method of inclined grids. This method carries out the idea by Loscertales (1998) to design a DMA with the electric field inclined relative to the air flow. Loscertales proposed the inclined field with the aim to improve the diffusion-limited mobility resolution. However, the IGMA is a low-resolution instrument, where the diffusion of ions is of secondary importance. The configuration with inclined grids was chosen in consideration of some engineering aims and for testing the new principle in the air ion mobility analysis. The IGMA was used in a few research projects studying the atmospheric aerosol nucleation (Iida et al. 2006).

An alternative instrument intended for the same applications is the BSMA (Tammet 2006). The simplified schematic of the BSMA is illustrated in Figure 3. Different of the IGMA, the aspiration condensers of the BSMA have a classic configuration (Figure 1b), which is familiar in atmospheric electric research. One instrument contains two identical aspiration condensers connected as the Komarov bridge. The BSMA was applied in studies of atmospheric aerosol nucleation (Kulmala and Tammet 2007).

Experience of exploitation of the instruments showed that the strength of the BSMA is its easier maintenance, but its drawback is a higher noise level when compared with the IGMA. There are two reasons: two collectors are connected to the same electrometer and the fluctuations of the bridge balance are generating an extra noise component, especially at high humidity that deteriorates the insulation of the analyzer electrodes.

ASPIRATION CONDENSER

A section of a SIGMA plain aspiration condenser is illustrated in Figure 4. The atmospheric air enters the instrument through the inlet grid. The disturbing effect of external electric fields near the inlet is inversely proportional to the total air-flow rate and the extra high air-flow of 32 dm³s⁻¹ well suppresses the distortions. The grid is made of a perforated metal sheet with the perforation diameter of 1 mm and the transparency of 46%. The inlet grid is necessary to prevent the entering of spiders, insects, fuzz, and hairs. Next, the air will pass the inlet gate and the sheath air filter. The flat filter plates are 1 mm thick and the distance between the plates is 4 mm. The mean air flow speed in the filter is about 1.8 m s⁻¹ and the Reynolds number between the plates of about 500 ensures the damping of the carried-on turbulence. The potential of the sheath air filter odd plates is –520 V (left side) or + 520 V (right side), while all the even plates are on the zero potential. The low mobility ions passing the middle sections will not reach the collectors even if they are not precipitated in the filter. The crucial regions of the filter are the outermost sections, whose critical mobility is tenfold less than the lowest mobility of ions to be measured using the SIGMA. However, the concentration of low mobility ions can largely exceed the concentration of intermediate ions and still cause systematic errors in the collector signal. For correcting this systematic error, the zero level of the signal is to be determined and subtracted from the general measurement signal.

FIG. 4 Simplified section of the SIGMA aspiration condenser. The plates are marked in the drawing with their ends indicating the polarity: rhombs mark positive, round spots negative, and plain ends zero potential. The real geometric edges of all plates are still plain.

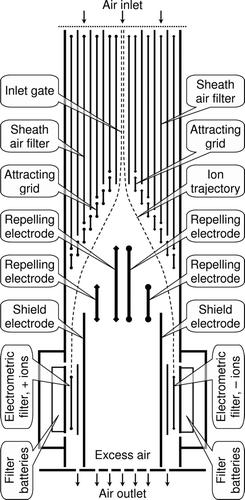
The inlet gate is composed of the two central plates of the filter and the space between these plates (Figure 4). The voltages of the inlet gate plates are computer-controlled. The distance between the gate plates is 10 mm and the mean air speed is about 2 m/s. The gate is open when the plates are on the zero potential and closed when the plates are switched to potentials –260 V and +260 V. The critical mobility of the closed gate of 0.031 cm²V⁻¹s⁻¹ is about the same as the mobility of the largest particles to be measured. A closed gate scan yields a zero level record, which includes the effect of large ions passed through the sheath air filter, as well as the effect of the residual displacement current. The air flow between the gate plates at Reynolds number of about 1400 does not suppress the incoming turbulence. However, the main part of an ion trajectory from the gate to the collector passes the sheath air, where turbulence is damped in the filter.

The ions, which have passed the inlet gate, are deflected in the electric field between the attracting and repelling electrodes depending on their polarity and mobility. In the IGMA both the attracting and repelling electrode were made of a perforated sheet, which caused distortions in the air flow in the mobility classification zone. In the SIGMA, the attracting grid is a slat grid of the same step as the sheath air filter and does no distort the air flow. The repelling grid is replaced by particular repelling electrodes, whose geometric positions were optimized using the numerical model of the analyzer. The numerical model solves the Laplace equation according to the Jacobi-Seidel method on the uniform rectangular grid with a step of 0.1 mm. The ion trajectories were calculated integrating the displacements of ions when passing in electric field and air flow from a grid cell into the next one. The diffusionless geometric transfer function was found out by repeating the calculation of trajectories at different control voltages. The calculations were carried out on the assumption of plug air flow. However, the diffusionless transfer function depends only on the fluxes of air flow and electric field and is not sensitive to the air flow profile while it remains laminar (Tammet 1970).

The model was the crucial tool that allowed discovering the possibility to separate the positive and negative ions from the common inlet flow with a minor internal edge effect. The internal edge effect, which means the loss of ions on the rear edges of the plates of the inlet gate, is considered in the numerical model when estimating the effective width of the gate.

The Reynolds number is high in the classification zone and turbulence is one of the main factors limiting the mobility resolution discussed in the next section. However, the high Reynolds number in a short zone cannot lead to large distortions because there is not enough time for developing the turbulence as shown by Tammet (1970) and comprehensively verified by Rosell-Llompart et al. (1996).

Nearly all ions of the central critical mobility will travel to the electrometric collector filters. The electrometric filters are shielded from the variable electric field issued from the classifier electrodes with long zero-potential shield plates. A minor part of the electric field still penetrates the channel to the collector. The penetration capacitance of 45 aF is estimated using the numerical model. The small signal of the residual displacement current is effectively removed by the procedure of subtracting the records of the closed-gate scans.

An electrometric filter consists of one attracting plate between the two zero-potential plates. The distance between the plates is 0.45 cm, the effective electrostatic length about 5 cm, the voltage 240 V, and the air flow velocity 180 cm s⁻¹. This ensures the critical mobility of about 0.03 cm²V⁻¹s⁻¹, which is just low enough to collect the ions in the instrument mobility range and high enough to minimize collecting the large ions penetrating the inlet sheath air filter.

The time of passage of the ions through the classification zone is about 0.07 s. The passage of the air of the total distance of about 27 cm from the inlet grid to the collector entrance requires about 0.16 s. The walls of the analyzer are thermally insulated by foam polystyrene. In an extreme situation of 20 K temperature difference, the heat flux causes the mean temperature change of the air flow by about 0.5 K.

A detailed technical description of the instrument is available on the Web (see http://ael.physic.ut.ee/tammet/sigma).

MOBILITY RESOLUTION

Research of nucleating nanoparticles in atmospheric air brings up specific requirements, which radically differ from the requirements for a laboratory mobility analyzer. The signal to noise ratio turns up to be critical due to the extremely low concentration of nanometer ions in atmospheric air (Figure 7). Theoretical models of atmospheric aerosol nucleation include continuous growth of nanometer particles and the mobility distribution is expected to be relatively smooth. Thus the factors of sensitivity will have priority before the factors of resolution. Request of high sensitivity requires increasing the collected ion current. The inlet slit and the collector of the analyzer cannot be narrow and the geometric resolving power is limited. The air is sucked into the instrument immediately from the turbulent atmosphere and the flow rate should be large. Some turbulence inside the analyzer is inevitable in these conditions. As a result, the mobility resolution of instruments for atmospheric measurements cannot be high.

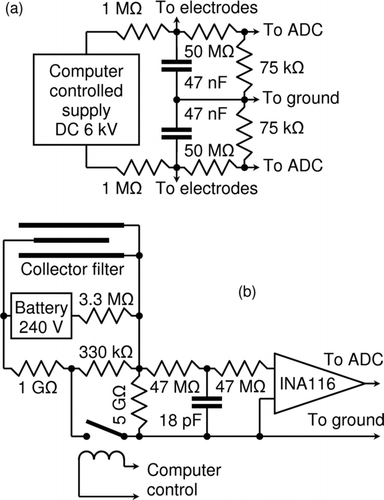
FIG. 5 Simplified electric diagrams of the SIGMA. (a) High voltage relaxation RC-circuit and (b) electrometric collector and amplifier.

Traditional parameters of the DMA resolution are the relative standard deviation of measured mobilities in case of actually monomobile ions of mobility Z, and the ratio of this mobility to the width of the transfer function at the half height ΔZ _1/2. These parameters are denoted below RSTD = σ/Z and RES = Z/ΔZ _1/2. In case of a Gaussian transfer function RES = 0.425/RSTD.

The resolution depends on several factors:

•	width of the inlet slit and width of the electrometric collector,
•	representing the distribution with averages over mobility fractions of definite width,
•	smoothing due to the response time of the electrometer,
•	thermal diffusion,
•	turbulent diffusion.

The resulting composite transfer function is approximated by a Gaussian curve and the relative standard deviation of this curve is considered as the measure of the resolution. The geometric transfer function is determined by the widths of the inlet slit and the electrometric collector. According to the numerical model the geometric transfer function of the SIGMA is very similar to the earlier discussed triangular transfer function of the BSMA (Tammet 2006). The RSTD of this component of the transfer function proved to be 0.115. Presenting the spectra by fraction averages is necessary for increasing the signal to noise ratio. This procedure generates a rectangular smoothing function with the relative width of 1.33 and the corresponding component RSTD = 0.081. The time constant of the electrometric amplifier is 0.32 s and the smoothed response creates component RSTD of about 0.027. The effect of thermal diffusion in the SIGMA is low and noteworthy only in case of the smallest ions. The estimate for the ions of mobility 1.7 cm²V⁻¹s⁻¹ is a component RSTD = 0.026.

Exact estimating of the mobility resolution of the SIGMA was embarrassed by lack of tools for correct measurement of the turbulence inside the analyzer and lack of the sources of monomobile ions with a large air flow rate. Thus the following estimates are rough. The turbulence in the analyzer was visualized using a thin soft thread vibrating in the air flow in the mobility classification zone. The position of the free tip of the thread was measured from 130 photos and the standard deviation proved to be 1.2 mm. The vibration of the thread is damped by inertia and the standard deviation of air parcels exceeds this value. Thus the value of 1.2 mm is considered only as a lower margin of the turbulent pulsations. The lower margin of the corresponding turbulent dispersion of the mobility was estimated by a component RSTD = 0.04 when considering the dimensions of the classification zone. The composite RSTD is a square root of the squares of the five components (0.115, 0.081, 0.027, 0.028, and 0.04), the result is the RSTD = 0.15. This value is considered as a lower margin of the estimate of the resolution of the SIGMA.

An estimate of the upper margin of the resolution can be found analyzing the measured spectra of small ions. A spectrum of small ions contains several components and it is always wider than the transfer function. The effect of side components of the ions near the main component is minimized when the spectrum is approximated by a Gaussian line using values of the measured distribution function only near the spectrum peak. The sharpest peak with a mobility of 1.7 cm²V⁻¹s⁻¹ was found in the spectrum of negative small ions in the artificially ionized laboratory air, where the concentration of ions was about 200,00 cm⁻³. The RSTD = 0.20 of this peak is considered as the upper margin of the resolution.

The two margins allow estimating the mobility resolution parameter RSTD to be between 0.15 and 0.2 that corresponds to the values of the RES between 2.1 and 2.8.

CONTROL OF MEASUREMENT

Performance of the SIGMA substantially depends on manipulating the instrument by the computer and internal processing of the recorded signals under the supervision of the control program. The computer is connected to the electronic circuits inside the instrument via the USB port. The data acquisition unit USB-1608FS, manufactured by the Measurement Computing Corporation, is built into the SIGMA. The control program, which was used during the test measurements, had been written for a PC-compatible computer running under Windows XP.

The circuit for the control of the voltage between the attracting and repelling electrodes of the mobility classifier is illustrated in Figure 5a. The high voltage up to 6 kV is generated by a well-insulated voltage converter U3-6PN manufactured by the Matsusada Precision Inc. The output internal capacitance of the converter is about 15 nF and the time constant of the RC-circuit is about 3.8 s. The positive output is connected to the attracting grid for the negative ions and to the repelling electrodes for the positive ions. The negative output is connected to the attracting grid for the positive ions and to the repelling electrodes for the negative ions. The control computer can switch the inlet power of the converter on and off. About one second of power on is enough to charge the capacitors. After charging, the power is switched off and the classifier voltage will exponentially decay, which follows in a logarithmically uniform increase in the critical mobility. The decaying voltages are monitored using two ADC inputs of the data acquisition unit. The full mobility range with some reserve is passed during 18 s. The period composed of charging and discharging of the RC circuit is called a scan. Typically, three scans are performed during one min. This provides the time resolution of 20 s.

The circuit for collecting and recording the ion current is illustrated in Figure 5b. An electrometric collector filter is powered by twenty 12 V miniature batteries type GP27A. The batteries have the capacity to serve for at least one year without changing. They are enclosed into a metal box connected to the electrometric collector and well insulated from the other details. The computer-controlled electrometric relay shown in Figure 5b is open during the measuring of the ion current. The ion current is converted to the voltage on a precision 5 ± 1% GΩ resistor and amplified with the electrometric instrumental amplifier INA116. The 1 GΩ load of the battery is required to make possible a regular check of the voltage using the computer-controlled electrometric relay. The checking procedure includes two measurements of the electrometer outlet voltage in the closed inlet gate regime. One measurement is made with the open relay and the second with the closed relay. The difference between these measurements corresponds to the voltage drop on the 330 kΩ resistor and allows estimating the actual voltage of the battery.

During the routine measurement the scans are performed alternately with the open inlet gate and the closed inlet gate. The schedule usually contains the groups of three scans where two scans are made with the open inlet gate and one scan with the closed inlet gate. The zero level is estimated according to the closed gate measurements. The zero level can drift due to the technical drift of the electrometric amplifier and the variation of the residual signal of large ions. The drift is slow, which allows integrating the zero signals over a three to five times longer time interval than the open gate signals. Additionally, the analysis of repeated closed gate measurements provides an estimate of the instrumental noise.

During a scan the classifier voltages and the electrometric signals are recorded every 0.01 s. After the required lower border of the voltage has been reached, the collected data are processed while the voltage range is split into one set of subintervals corresponding to the mobility fractions and, independently, into the second set of subintervals corresponding to the size fractions. The parameters of the air are measured using built-in sensors during every scan and the mobility borders of the size fractions are determined considering the air temperature and pressure according to the algorithm by Tammet (1995).

INLET LOSS OF IONS

Some amount of ions is lost in the inlet tract before entering the mobility classifying zone (von der Weiden et al. 2009). The effect of electrostatic image forces on the deposition of ions is negligible when compared with the diffusion (Tammet 1970), and the inertial deposition is not important because the size range of the SIGMA is limited to fine nanometer particles. The ion concentration is limited by technical constraints of the instrument in the range, where the space charge effects can be neglected. Simple geometry of the inlet enables estimating the diffusion losses directly using the well-proven semiempirical methods of the heat transfer theory. In case of the ion and nanometer aerosol particles the preconditions required for the full analogy of heat and mass transfer (Kays et al. 2005, Chapter 18) are satisfied and the equations of the heat transfer to the surface of constant temperature can be used when replacing the Nusselt number Nu with the Sherwood number Sh and the Prandtl number Pr with the Schmidt number Sc (Incropera and Dewitt 2002).

The diffusion deposition flux of ions onto a flat surface is q_dep = WLnu_dep , where W is the width, L is the length of the surface along the air flow, n is the undisturbed concentration of ions and u_dep is the mean deposition velocity along the length L. The mean deposition velocity is

where Sh_mL is the mean Sherwood number related to the length L, and D is the ion diffusion coefficient. The air enters as a plug flow and the boundary layer over the surface will develop along the channel. The displacement thickness of the boundary layer is estimated as

where ν is the kinematic viscosity of the air and u_flow is the free flow velocity (Incropera and Dewitt 2002). A numeric calculation shows that the displacement thickness in the SIGMA inlet grid and filter is much less than the distance between the surfaces. Thus a semiempirical equation obtained for the boundary layer over a flat plate (Incropera and Dewitt 2002) can be adopted in our problem:

The equation above takes into account the entrance profiles for both the ion concentration and for the air flow velocity. The Reynolds number related to the same length L and the velocity u_flow as the Sherwood number is

Equation (5) is valid when Sc > 0.6 (Incropera and Dewitt 2002). The Schmidt number Sc  =  ν/D has the lowest value of about 3 in the case of cluster ions. Thus the concentration boundary layer is always thinner than the velocity boundary layer and Equation (5) can be used for the evaluation of the ion deposition without restrictions so far as the boundary layer remains thin enough. The diffusion coefficient of single charged ions of the electric mobility Z is

where k is the Boltzmann constant, T is the absolute temperature, and e is the elementary charge. The composite equation is

The inlet grid is made of a perforated sheet and the air enters through cylindrical channels. The inlet flux of the air is πR ² u_flow and the loss flux is 2πRLu_griddep . Thus the relative loss is

The gate filter is a flat channel between two parallel plates separated with a distance h. The inlet flux of the air is Whu_flow and the flux of the loss onto both surfaces is 2WLu_gatedep . The relative loss is

In the control program of the BSMA, the values of the distribution function or the fraction concentration f were corrected assuming a very low adsorption (Tammet 2006):

In the control program of the SIGMA the next approximation is used, where 1−A is replaced by exp (−A). The result is

Let the index 0 mark the standard values of the parameters T ₀ = 273 K, p ₀ = 1013 mb, Z ₀  =  1 cm²V⁻¹s⁻¹, and ν₀ = 1.33 × 10⁻⁵ m²/s. The dependence of the deposition velocity on the air viscosity is weak and a rough approximation is sufficient:

If the deposition velocity at standard conditions is u_{dep 0}, then

The estimate of the total relative adsorption A = A_grid + A_gate is now calculated as:

where

and

The air flow rate in the SIGMA is 32,000 cm³/s. The parameters of the grid are L  =  0.7 mm, R  =  0.5 mm, and u = 3.2 m/s. The parameters of the gate are L = 123 mm, h  =  10 mm, and u = 2 m/s. The calculation yields estimates for the SIGMA:

The relative uncertainty of the fraction concentrations induced by the uncertainty of the 5% correction is about 20 times less than the uncertainty of the estimate of the relative adsorption A.

TEST MEASUREMENTS

The test measurements were carried out at a rural site 58°05’39” N & 26°43’09” E, located about 30 km south of Tartu, Estonia. About 10,000 5-min cycles were recorded during July–October 2009. The main goal was testing and improving the control program, which should include adequate reactions in different extraordinary situations. Additionally, the test measurements were necessary for estimating of the sensitivity of the instrument, which is limited by the noise level. The noise is characterized by the standard deviation of the random measurement errors. In a mobility analyzer the noise depends on the critical mobility and should be estimated for all mobility fractions. The control program of the SIGMA includes a special regime for checking the noise. In this regime all operations and internal processing of measurements are performed exactly as during an actual measurement, except the fact that the inlet gate is kept permanently closed during all scans.

The special noise measurements were performed September 26–28, 2009. The weather was windy during the measurements, which included the noise component induced by charged dust particles passing the instrument. The relative humidity was between 80 and 100% and about one quarter of the period had a drizzling rain. The 506 5-min noise records covered about 42 h. In the first stage of data processing the integral noise was estimated including all mobility fractions. Next the 506 noise records were sorted into two equal subsets corresponding to the integral noise less or more than the median. Standard deviations of the mobility fractions are shown in Figure 6.

FIG. 6 Standard deviation or random errors in the fraction concentrations of the mobility distribution. The upper curve corresponds to 253 high-noise measurements, whose integral noise exceeds the median, and the lower curve to 253 low-noise measurements where the integral noise remains below the median. The middle curve characterizes all 506 5-min records.

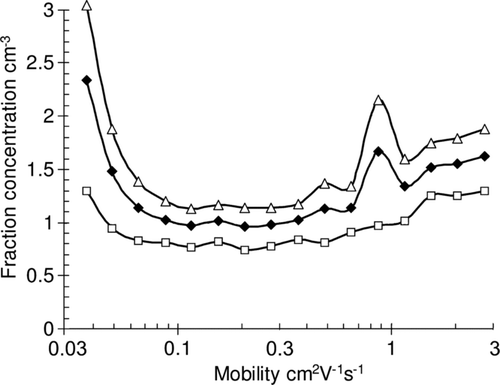
If several narrow fractions are aggregated into one wide fraction, then the absolute standard deviation of the fraction concentration increases and the relative standard deviation decreases. The standard deviations of integral concentrations of cluster ions (the sum of 6 fractions in the range of 0.562−3.16 cm²V⁻¹s⁻¹) for the low and high noise data were 1.4 and 2.9 cm⁻³. The same for intermediate ions (the sum of 10 fractions in the range of 0.032−0.562 cm²V⁻¹s⁻¹) provided the values of standard deviations 3.5 and 7.9 cm⁻³.

Noise of the three RC-scanning instruments is compared in Table 1.

TABLE 1 Estimates of standard deviations of the decade-to-eight mobility fraction concentrations for 5-min cycles, cm⁻³

Mobility range cm^2V^−1s^−1	IGMA	BSMA	SIGMA
0.03–0.06	1.7	20	1.7
0.08–0.5	1.7	7	1
0.5–3.2	6	5	1.5

The IGMA and BSMA were actually not used in the regime of five-minute cycles and the corresponding estimates in Table 1 were numerically reduced to the 5-min cycle. The reduction is based on the assumption that the correlation of noise signal in sequential measurements is weak and the standard deviation is inversely proportional to the square root of the cycle duration.

Unfortunately, the noise measurements with different instruments were performed in different environmental conditions and the comparison in Table 1 is not well representative.

The increase in noise level of the IGMA and SIGMA with an increasing mobility in the region of cluster ions is caused by pulses generated by ion tracks of alpha-particles inside the analyzer. The recoil energy of a ²¹⁸Po atom formed after the decay of ²²²Rn is about 100 keV. As a result of an impact with gas molecules, a ²¹⁸Po atom loses electrons and turns into a positive ion. The positive ions are accumulated on the negative electrodes in the analyzer. ²¹⁸Po and its daughter ²¹⁴Po emit alpha particles with the energies of 6.1 and 7.8 MeV. One alpha-particle can create up to 200,000 pairs of cluster ions in the limited space inside the analyzer. If 100,000 ions are deposited on the collector during a short time, then the voltage pulse reaches the level equivalent to the effect of a fraction concentration of about 100 cm⁻³. In the BSMA the alpha particle-generated ions are collected independent of the control voltage with about the same efficiency. In the IGMA the electric field canalizes the alpha-pulse ions of one polarity into the collector only in case of a high critical mobility. This selective effect is suppressed in the SIGMA, where the alpha particle-generated noise is only slightly increased in the cluster ion mobility range.

Both the IGMA and SIGMA are free of the noise component that is generated in the BSMA by fluctuations in the bridge balance when the insulators of the analyzer are polluted and leak in conditions of high humidity. This component of noise is high in the range of low mobility.

An important component of noise present in all three instruments is caused by the large charged airborne particles, which induce pulses of electric current on the collector even they are not deposited. In summertime this component of noise depends on wind that blows up charged dust from the ground. In wintertime a strong noise can be generated by tiny ice crystals passing the analyzer.

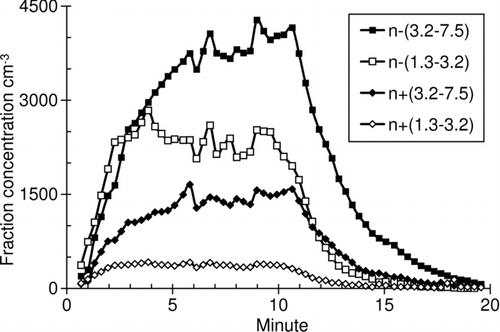
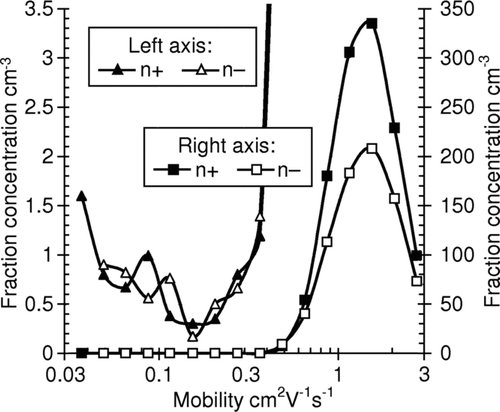
The low noise level in the SIGMA allows detecting the intermediate ions during the periods without atmospheric aerosol nucleation events. An example is presented in Figure 7. The fraction concentrations in the mobility range of 0.1–0.3 cm²V⁻¹s⁻¹ drop below 1 cm⁻³, which is far out of the sensitivity limits of the BSMA.

The waves in the curves on Figure 7 are obviously a result of the noise induced by charged dust particles. The pulses induced by charged particles are inverted in the records of positive and negative ions, which follow in negative correlation. The dust-induced noise can be partially suppressed during the processing of the data, but this was not done when preparing the data for Figure 7.

FIG. 7 Air ion mobility distribution recorded at the test site between UT 20:00 and 23:00 on September 30, 2009. The wide range of the fraction concentrations is made visible using a simultaneous presentation of the distributions on the left and right axes.

The maximum time resolution of the SIGMA is demonstrated in Figure 8, which shows some results of a repeated experiment of generating the balloelectric ions in a closed room of the volume of about 17 m³. The original experiment (Tammet et al. 2009) was carried out using the BSMA, whose noise-limited 10-min time resolution did not allow observing the dynamic of processes. The standard deviation of the instrumental noise of the SIGMA is less than the thickness of lines in Figure 8. The fluctuations during the first 10 min are caused by the turbulent character of the transfer of the ions from the splashing point to the instrument. The discussion of the physics of the dynamics remains out of the scope of the present article.

FIG. 8 Results of high time resolution measurements of balloelectric ions generated by water jet experiment. The numbers in the legend show diameter limits of the ion groups expressed in nanometers. The water jet was opened at 0 and closed at 10 minutes from beginning the experiment.

CONCLUSIONS

A new mobility analyzer of charged clusters and fine nanometer particles, the SIGMA, was developed for applications in research of atmospheric air nucleation. The principles and technical solutions were based on the experience of the exploitation of the preceding scanning mobility analyzers IGMA (Tammet 2003) and BSMA (Tammet 2006). The essential properties of the instrument are:

•	The positive and negative air ions are sampled from the same inlet air flow and measured exactly simultaneously.
•	A high rate of air flow of 32 dm3/s and the isopotential principle suppress the disturbing effect of the external electric field and assure representative sampling of air ions.
•	The sheath air is sucked into the instrument directly from the atmosphere together with the analyzed air and ions pass during the analysis only the unaffected atmospheric air.
•	The loss of ions in the inlet tract due to the adsorption is 5% at the mobility of 1 cm2V−1s−1.
•	A short residence time of 0.16 s and low heating of air less than 0.5 K suppress the risk of changing of the ions during the measurement.
•	High sensitivity allows measuring of 8 fractions of intermediate ions on a mobility decade in atmospheric air at standard 5-min time resolution with random errors of about 1 cm−3.
•	Time resolution of 20 s is available at random errors in the mobility fraction concentrations between 4 and 10 cm−3.
•	The ions are independently distributed into the mobility fractions and the size fractions while the mobility borders of the size fractions are determined considering the simultaneously measured air temperature and pressure.
•	The scanning technique assures that possible peculiarities in the recorded distributions are not generated by the technical troubles of individual mobility channels.

Acknowledgments

This research was in part supported by the Estonian Science Foundation through grant 8342 and the Estonian Research Council Project SF0180043s08.