Determination of the Transition Regime Collision Kernel from Mean First Passage Times

Abstract

Particle–vapor molecule (condensation) and particle–particle (coagulation) collision kernels are critically important parameters for the description of particle size distribution evolution in aerosols. We use mean first passage time calculations to find a dimensionless form of the collision kernel that applies in the limit where the ratio of the masses of colliding entities (aerosol particles or vapor molecules) to gas molecule mass, Z, approaches infinity, and the colliding entities are dilute in concentration. In these calculations, the motion of colliding entities is monitored with Langevin dynamics, and the collision kernel is inferred from the time required for collision. The presented analysis reveals that the dimensionless collisional kernel (H) is a function solely of the diffusive Knudsen number (Kn_D , the square root of the product of kT and the reduced mass divided by the product of the reduced friction factor and collision radius), and a number of commonly used expressions for the collision kernel also collapse to the functional form H(Kn_D ), irrespective of whether they were derived for Z → ∞ or Z → 0 conditions. The examined collision kernel expressions are further found to agree within 10% of our calculations as well as with each other across the entire Kn_D range. This result suggests that a single collision kernel can be used to describe all transition regime collision rates, i.e., both condensation and coagulation rates, with reasonable accuracy, and establishes that Langevin-equation-based mean first passage time calculations can serve as a simple approach to examine transition regime collision phenomena.

INTRODUCTION

The growth of particles in the gas phase by thermally driven collisions between particles (coagulation), particles and molecular clusters, and particles and vapor molecules (condensation/surface growth) plays a critical role in a number of aerosol processes, including new particle formation in the atmosphere (Kuang et al. 2009) and nanomaterials synthesis (Gurav et al. 1993; Swihart 2003). The behavior of these systems is largely governed by the collision rate, R (the number of collisions per unit time per unit volume of aerosol), the calculation of which is simplified by the fact that particles, clusters, and vapor molecules are typically found at low volume fractions in the gas phase. Under such dilute conditions, collisions can be modeled as two-body interactions wherein thermal motion drives collisions (Narsimhan and Ruckenstein 1985; Friedlander 2000), and the collision rate is given as:

where n_i is the number concentration of particles of type i (of a specific size), n_j is concentration of particles/clusters/vapor molecules of type j, and β is the collision kernel/collision rate coefficient for collisions between type i and type j entities.

Accurate calculation of collision rates thus requires accurate calculation of β. When the radius of at least one object is large relative to the mean persistence distance of the colliding entities (Rader 1985), the continuum approximation is satisfied and Smoluchowski's β applies (Chandrasekhar 1943; Given et al. 1997):

for collisions between entities of type i and type j, where f_i and f_j are the friction factors of type i and type j entities, respectively, with  f_i = kT/D_i , D_i is the diffusion coefficient defined appropriately for the entity i, a_i and a_j are the radii of type i and type j entities, respectively, k is Boltzmann's constant (1.38 × 10⁻²³ J K⁻¹), and T is the temperature of the colliding entities and background gas. Conversely, for moving hard-spheres with radii that are small relative to the mean persistence distance, the free molecular approximation applies, and from kinetic theory, the collision kernel is given as (Vincenti and Kruger 1975):

with μ_ij = m_im_j /(m_i + m_j ) (the reduced mass), where m_i and m_j are the masses of entities i and j, respectively. While both Equations (2) and (3) apply exactly in the continuum and free molecular limits, respectively, aerosol particles in atmospheric pressure environments typically have radii ranging from tens to hundreds of nanometers. In this “transition regime” (Brock 1966; Sitarski and Nowakowski 1979), the continuum and free molecular collision models break down. Motivated by this issue, a variety of approaches have been used to determine transition regime collision kernels, with work on this topic dating back over 65 years. Two types of transition regime collisions have generally been examined: those between aerosol particles and low-mass vapor molecules, and collisions between two aerosol particles. In the former, the vapor molecule to gas molecule mass ratio, Z, is often taken as zero (Li and Davis 1996), and the motion of the particle relative to the vapor molecule is neglected. Conversely, in the latter, the motion of both particles is considered, and Z is considered large (Z → ∞). In examining Z → 0 collisions, Fuchs (1934, 1959, 1963) first proposed the “limiting sphere model,” in which distant from the particle, a vapor molecule/cluster moves diffusively (as in a continuum) but when the distance between the vapor molecule/cluster and particle is less than a critical value Δ _F , it moves ballistically (as in a vacuum). Although this approach results in an analytical expression for β, Δ _F remains as a free parameter, which precludes β calculation without additional information. As an alternative, Fuchs and Sutugin (1970) later interpolated Sahni's (1966) solution to the Boltzmann equation for neutron absorption by a black body, giving an expression for β for all ratios of the colliding entities’ persistence distance to particle radius. Collision kernel expressions for particle collisions with small entities have also been proposed by Loyalka (1973, 1982), Seaver (1984), and Sitarski and Nowakowski (1979). Experimental measurements (Davis and Ray 1978; Ray et al. 1979; Li and Davis 1996; of evaporation, the reverse process) show reasonable agreement with these expressions in the transition regime, with particularly good agreement with the Fuchs–Sutugin expression; thus, it is the most widely used expression to describe particle–vapor molecule collisions (Kuang et al. 2009). Similarly, Fuchs (1964) has used physical arguments to develop an expression for β for collisions between particles in the Z → ∞ limit, with several other researchers likewise developing expressions for the particle–particle collision kernel (Sitarski and Seinfeld 1977; Dahneke 1983; Sahni 1983; Veshchunov 2010). Fuchs's particle–particle collision expression remains the most widely used for β calculation in this instance as well, based upon reasonable agreement with experimental measurements (Chatterjee et al. 1975; Wagner and Kerker 1977; Shon et al. 1980; Szymanski et al. 1989; Kim et al. 2003).

With few exceptions (Chernyak 1995; Gutsch et al. 1995; Heine and Pratsinis 2007; Azarov and Veshchunov 2010; Veshchunov 2010), there has been little recent focus on better understanding both Z → 0 and Z → ∞ thermally driven collision processes. Nonetheless, there are several reasons for further examination of the transition regime collision kernel. First, collision kernel expressions have been sparingly compared with results of Brownian dynamics simulations (Trzeciak et al. 2004; Madler et al. 2006; Heine and Pratsinis 2007), and when comparison has been performed (Nowakowski and Sitarski 1981; Narsimhan and Ruckenstein 1985), it has been limited to collisions between identical-sized particles or led to poor agreement with the unambiguous free molecular and continuum limiting expressions (Gutsch et al. 1995). With recent advances in computational capabilities, Brownian dynamics simulations can accurately predict thermally driven particle–particle collision rates (the Z → ∞ limit); hence, they should be able to provide a means for more detailed examination of collision kernel expressions than is possible with currently available experimental approaches. Second, various authors have used different definitions for the mean persistence distance of the colliding entities (Jeans 1954; Dahneke 1983; Adachi et al. 1985; Rader 1985; Sceats 1989; Gatti and Kortshagen 2008), and hence different definitions of the dimensionless parameter (i.e., the ratio of the persistence distance to the collision radius) used to determine whether a collision is continuum, free molecular, or transition regime process. We refer to this parameter as Kn_D , the diffusive Knudsen number (Loyalka 1976; Dahneke 1983; Rogak and Flagan 1992), which must approach zero in the continuum limit and approach ∞ in the free molecular limit. The lack of consensus on an appropriate definition of Kn_D has complicated comparisons between different collision rate expressions (Rader 1985), and therefore comparisons of available collision kernel expressions are sparsely performed. Finally, in examining collision processes, vapor molecule condensation has been examined in a distinctly different manner than has particle–particle coagulation. As noted above, the theoretical basis for this is clear; while aerosol particles are significantly more massive than gas molecules (Z ≫ 1), this need not be the case for vapor molecules. However, while the most commonly used collision kernel expression in condensation (the Fuchs–Sutugin kernel) derives from a Boltzmann equation solution in the limit of Z = 0, condensing vapor molecules or molecular clusters are often significantly more massive than the surrounding background gas (Li and Davis 1996), and for these species, the Z → ∞ collision kernel would be preferred. A single collision kernel should be able to describe both thermally driven condensation and coagulation in the dilute limit as Z → ∞, as the motion of all entities can be described in a similar manner. Furthermore, the extent to which Z influences the collision kernel can be better understood by comparing kernels inferred with the assumption Z = 0 to those inferred as Z → ∞.

Motivated by these issues, the purpose of this work is two-fold. First, we develop an expression for the collision kernel in the Z → ∞ limit, which converges to the correct continuum and free molecular expressions and, with an appropriate definition of Kn_D , can correctly predict collision kernels in the transition regime. For this purpose, we make use of mean first passage time calculations (Klein 1952; Narsimhan and Ruckenstein 1985), with the assumptions that the colliding entities are dilute in concentration and that the motion of colliding entities is accurately described by Langevin dynamics (Chandrasekhar 1943; Sitarski and Seinfeld 1977; Ermak and Buckholz 1980; Madler et al. 2006; Isella and Drossinos 2010). We further show that the transition regime collision kernel is best represented in a nondimensionalized form that can be predicted with Buckingham Π theorem (Buckingham 1914, 1915). The second goal of this study is to compare the mean first passage time derived collision kernel expression to previously developed Z → 0 and Z → ∞ expressions. In doing so, we show that all examined collision kernel expressions can also be written in this nondimensionalized form and that are all in good agreement with the results of first passage calculations, regardless of whether they were derived for low-mass vapor molecule condensation, coagulation, or using Fuchs’ limiting sphere approach.

MEAN FIRST PASSAGE TIME CALCULATIONS

Motion in the Transition Regime

To utilize mean first passage time calculations to determine the collision kernel, an appropriate model of the motion of colliding entities is necessary. This model is first described, followed by a description of the mean first passage time calculation procedure. We assume that for a dilute, hard-sphere, Z → ∞ entity surrounded by a homogenous bath gas under isothermal conditions, motion is well described by a Langevin equation (Chandrasekhar 1943), given as:

where is the velocity vector of the diffusing entity and is the “effective diffusion force,” which is a time varying, Gaussian distributed vector with the following properties:

Use of the Langevin equation restricts the presented analysis to situations where the time required for entities to collide is significantly longer than the characteristic time of motion, thus allowing separation of the drag force and the fluctuating diffusion force acting on moving entities in the force balance equation. Fortunately, most realistic aerosol systems are sufficiently dilute in concentration for this criterion to hold valid. Solutions to Equation (4) were developed by Ermak and Buckholtz (1980), with which the velocity vector, , and position vector, , at any time, t + Δt, can be predicted, provided that the velocity and position are known at the previous time, t, and that moving entity has a known mass and diffusion coefficient/friction factor. For hard-sphere entities, this solution can be expressed by the following equations:

where and are Gaussian distributed random vectors with zero means and variances defined by Equation (5c).

Figure 1 Outlines of the single- and two-entity mean first passage time calculations used to determine dimensionless collision kernels. (Color figure available online.)

Simulation Procedure

A number of previous studies have used the Langevin equation to examine transition regime collisions (Nowakowski and Sitarski 1981; Gutsch et al. 1995; Trzeciak et al. 2004; Heine and Pratsinis 2007; Isella and Drossinos 2010). For our calculations, we build upon the methods of Narsimhan and Ruckenstein (1985), who were the first to note that in examining dilute systems, only the motion of two colliding entities need to be considered, as opposed to a large multientity computational domain. Here, however, we must be specific about the definition of a dilute system, as the simplification to monitoring two entities places a second condition on the presented analysis. In aerosol systems at thermal equilibrium, a large number of aerosol particles and vapor molecules are dispersed within a background gas. Assuming that initially there are no concentration gradients of particles or vapor molecules within this medium, the collision and subsequent sticking of two entities reduces the local particle/vapor molecule concentration, such that the probability of a collision occurring within the same region of space is reduced as compared with regions where a collision has not occurred. In a sufficiently dilute system, prior to any further collisions, aerosol particles and vapor molecules will again redisperse themselves via thermal motion such that no concentration gradients exist within the medium, hence the probability of collision is spatially uniform at all times. The simplification to monitor the motion of only two bodies applies only in this instance. Combined with the prior restriction arising from the use of the Langevin equation, the calculations utilized here thus only apply when the characteristic time of particle/vapor molecule motion is faster than the characteristic time for particle mixing, which in turn must be faster than the time for collision. Again, with the exception of highly concentrated aerosol systems (Heine and Pratsinis 2007), this assumption is reasonable for most systems studied experimentally. We also note that the assumption of homogenously distributed particles and vapor molecules differs from the assumption traditionally made in analyzing continuum regime collisions, i.e., that concentration gradients of particles and vapor molecules exist at steady state, driving the flux of particles and vapor molecules to a collector particle surface (Chandrasekhar 1943; Friedlander 2000). However, as shown by Veshchunov (2010), in the continuum limit, analysis via the steady-state flux approach (the diffusion regime) and of dilute, homogenously distributed systems (the kinetic regime) lead to matching functional forms of the continuum regime collision kernel. For this reason, mean first passage time calculations and related Brownian Dynamics algorithms can and have been successfully employed to determine diffusion-limited reaction rates in the continuum regime (Klein 1952; Northrup et al. 1984, 1986; Douglas et al. 1994; Given et al. 1997) and are employed here for rate determination in the continuum, transition, and free molecular regimes.

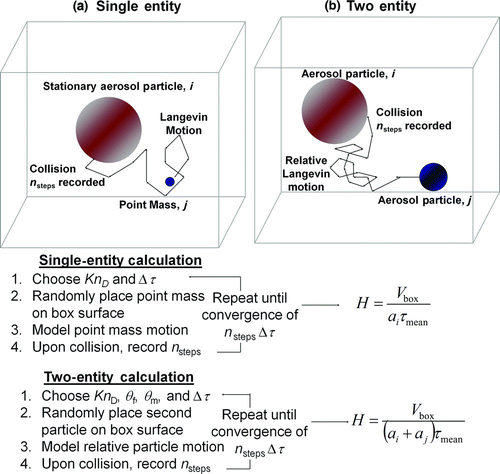
Two types of mean first passage time calculations are performed in this work. First, collisions in which one entity is considerably smaller and faster than the other are examined, which represent collisions between a heavy vapor molecule or molecular cluster and a particle. In this case, the radius, mass, and friction factor of the particle are >> than that of the vapor molecule/cluster; thus, particle motion is negligible, and moving vapor molecule/cluster may be treated as a point mass. Figure 1a shows a simple depiction of this mean first passage time calculation, which we henceforth refer to as the single-entity calculation. A spherical particle of radius, a_i , is placed in the center of a square box with a side length of 50a_i and periodic boundary conditions. A single moving point mass of zero radius but nonzero f_j and m_j is also placed at a random location on the surface of the box, and a given a random velocity sampled from a Maxwell–Boltzmann distribution (Vincenti and Kruger 1975; at the specified temperature). To move the point mass in the simulation domain, we first nondimensionalize Equations (5a)–(5c) by defining Δτ = (f_j /m_j )Δt, , and , where i denotes the immobile particle and j denotes the moving point mass, which gives:

where and are dimensionless vectors, which, like and , are Gaussian distributed random vectors with zero means and variances defined by Equation (6c). Through this nondimensionalization, we also find that Kn_D = (kTm_j )^1/2/(f_ja_i ), which we propose to be a simple and appropriate form for Kn_D in the limit where one entity moves significantly faster than its collision partner. It is apparent from Equations (6a)–(6c) that calculated trajectories are dependent on the parameters Kn_D and Δτ. We are only interested in results where Δτ → 0, i.e., a sufficiently small time step is needed to ensure correct simulation results. The criterion Δτ ≤ 0.005Kn_D ⁻² is found sufficient to mitigate any influence of time step in all simulations. With Δτ selected for a given Kn_D , Equations (6a)–(6c) are used to monitor the motion of the point mass until it collides with the particle. Upon collision, the number of time steps required for collision, n _steps, is recorded. A new point mass is subsequently placed randomly on the surface of the simulation box, at which time the collision simulation is repeated. After N collisions are simulated, the dimensionless mean first passage time τ _mean is calculated as:

from which the dimensionless collision rate, H, is calculated as:

where V _box/a_i ³ is the normalized size of the simulation box (50³). We note that for convergence of the mean first passage time to the correct value, a sufficiently large simulation domain must be used. Furthermore, with a sufficiently large simulation domain and periodic boundary conditions, equivalent results are found regardless of whether the point mass is initiated within the domain volume or on the domain surface (see calculation results in the supplementary information). For each selected Kn_D , successive collisions are monitored, and after each collision, τ _mean is calculated. Each simulation is stopped once the standard deviation on τ _mean is less than 1% of its average value over the past 200 collisions. This generally leads to each τ _mean calculation requiring simulation of 500–1200 collisions. For H determination, each calculation is, in turn, repeated 10 times. In total, 5000–12,000 collisions per calculated value are used, with a relative standard deviation of ∼3%–5% and 12–24 h of computation time required per value reported.

The second set of mean first passage time calculations mimics particle–particle collisions (Figure 1b), in which the motion of both colliding entities is monitored. As two equations of motion are needed, we refer to this calculation as the two-entity calculation. Equations are again solved in a dimensionless fashion, with Δτ = (f_ij /μ_ij)Δt, , and , where f_ij = f_i f_j /(f_i + f_j ) is the reduced friction factor. This normalization gives the following two solutions for the motions of particles type i and type j:

where is the diffusive Knudsen number for the two-entity calculation, θ_m = m_j /(m_i + m_j ) and θ_f = f_j /(f_i + f_j ). In two-entity calculations, Equations (8a)–(8f) are used to monitor the motion of both particles, with the motion of particle i superimposed onto particle j such that particle i remains stationary in the simulation domain (though all equations are used in simulations without simplification). To initialize each simulation, particle i is placed at the center of the simulation domain, while particle j is placed at a random location on the domain surface. A specific set of values of Kn_D , θ_m , and θ_f is used for each simulation. As with single-entity calculations, Δτ ≤ 0.005Kn_D ⁻², while the side length of the simulation box size is L ₁(a_i + a_j ), where L ₁ ranges from 10 to 40, with smaller values of L ₁ generally used at higher Kn_D . After N trials, the dimensionless collision rate is calculated as:

Identical convergence criteria are used for two-entity calculations as are for single-entity calculations, again with 500–1200 collisions necessary for each τ _mean calculation and 10 τ _mean calculations used for each reported value.

RESULTS AND DISCUSSION

Nondimensionalized Collision Kernels

Nondimensionalization of the Ermak and Buckholtz solution suggests that the dimensionless collision kernel, H, is dependent upon Kn_D for the single-entity system and upon Kn_D , θ_m , and θ_f for the two-entity system. With dimensional analysis, we can gain further insight into the correct functional form for the transition regime collision kernel. From Equations (2) and (3), it is apparent that the collision kernel when a single entity of negligible radius is moving depends upon the thermal energy, kT; the moving entity friction factor, f_j ; the stationary particle radius, a_i ; and the moving entity mass, m_j (note f_i → ∞, a_j → 0, and m_i → ∞ in the single-entity limit). These five variables form two dimensionless groups, which can be used to fully describe transition regime collisions: H and Kn_D (as defined for single-entity collisions), which are the nondimensionalizations of β and kT, respectively. The traditional normalization of β/β_c (Fuchs 1964; Loyalka 1976; Narsimhan and Ruckenstein 1985; Veshchunov 2010) can also follow from dimensional analysis, where β_c is the continuum collision kernel (Equation (2)) and the second dimensionless number is again Kn_D , but in this system it is the nondimensionalization of m_j . A final approach to scale the collision process is to normalize β by β_FM , the free molecular collision rate (Equation (3)), leading to Kn_D as a nondimensionalization of the friction factor. Here, we elect to use H for the dimensionless collision kernel as opposed to β/β_c or β/β_FM as nondimensionalization of the Langevin equations allows for H to be directly determined from mean first passage time calculations, and in both the continuum and free molecular regime, thermal energy drives collisions; hence, β and kT are the most appropriate nonrepeating variables in describing the collision process. H can be expressed in terms of the aforementioned variables as:

By comparing with Equations (2) and (3), the following, simple, limiting expressions for H are obtained:

For collision processes with two moving entities, from Equations (2) and (3), β is found to be a function of kT, f_i , f_j , m_i , m_j , a_i , and a_j . The description of a system of eight variables should require five dimensionless groups. However, in Equations (2) and (3), the following groupings are found: f_i and f_j as f_ij , m_i and m_j as μ_ij , and a_i and a_j as a_i + a_j . This again reduces the system to five variables, which can be described by H and Kn_D , where H is redefined as:

Kn_D is also redefined with μ_ij and f_ij substituted for m_j and f_j (as noted in the previous section). The reduction to two dimensionless groups would at first seem at odds with the nondimensionalization performed for two-entity mean first passage time calculations, which leads to H dependent upon Kn_D , θ_m , and θ_f . However, the definitions of type i and type j entities are arbitrary, i.e., H(Kn_D , θ_m , θ_f ) = H(Kn_D , 1 − θ_m ,1 − θ_f ) = H(Kn_D , θ_m , 1 − θ_f ) = H(Kn_D , 1 − θ_m , θ_f ) for 0 < θ_m < 1 and 0 < θ_f < 1, which suggests (but by no means proves) that H depends upon neither θ_m nor θ_f , although they are still inputs for mean first passage time calculations. As Kn_D → 0 and Kn_D → ∞, H for two moving entities is again described by the limiting Equations (11a) and (11b), respectively; thus, single moving entity and two moving entities are described by the same collision kernel in the continuum and free molecular limits.

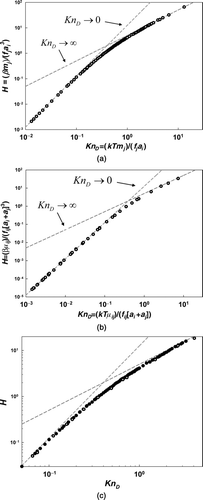
Figure 2 The nondimensionalized collision rate, H, for (a) single-entity and (b) two-entity mean first passage simulations as a function of Kn_D . Gray lines denote the expected limits as Kn_D → 0 and Kn_D → ∞. (c) A zoomed in plot of H(Kn_D ) in the region 0.05< Kn_D < 5. Closed symbols: single-entity mean first passage time calculations. Open symbols: two-entity mean first passage time calculations.

Mean First Passage Time Results

Mean first passage time simulations are performed at varying Kn_D for single entities and at varying Kn_D , θ_m , and θ_f for two moving entities. Calculated H values are shown at varying Kn_D for single- and two-entity systems in Figure 2a and b, respectively. Also shown in both figures are the low and high Knudsen number limiting expressions for H (Equations (11a) and (11b), dashed gray lines). Tables of results from mean first passage time calculations are given in the supplementary information. In performing two-entity calculations, we have used only θ_m and θ_f values that are realistic for collisions between entities of similar density in the continuum, transition, and free molecular regimes. This leads to a correlation between the examined θ_m and θ_f values, and although this places a restriction on the presented results, in realistic systems dominated by collision growth in which the motion of both colliding entities is important, the colliding entities typically have a similar density (i.e., collisions between a massive small particle and much less massive larger particle are rare). From both figures it is apparent that (1) H is a single valued function of Kn_D for both types of collisions (with further direct evidence provided in the supplementary information) and (2), at low and high Knudsen numbers, both shown data sets converge to the appropriate Kn_D → 0 and Kn_D → ∞ limits, respectively. This is in contrast with the earlier related study of Gutsch et al (1995), in which mean first passage time calculations grossly underpredicted both the continuum and free molecular collision kernels. How this underpediction arose is unclear, though it is perhaps due to an overly large time step used in order to minimize the time necessary for computation.

Figure 2c shows a zoomed in plot about the Knudsen number range from 0.05 to 5, with results from both single-entity (closed circles) and two-entity (open circles) calculations. Although several calculated two-entity results are slightly (∼3%) lower than single-entity results near Kn_D ≈ 1, the two sets of results collapse to a single curve remarkably well. Overall, these results support predictions made from dimensional analysis, namely, there is a single curve, H(Kn_D ), to describe collisions between dilute concentration, transition regime entities in the Z → ∞ limit.

Table 1 A summary of previous developed collision kernels for transition regime condensation and coagulation, expressed in the form H(Kn_D )

Expression	Z restriction	Nondimensionalized form
a. Fuchs–Sutugin (1970)	Z → 0
b. Loyalka (1973)	Z → 0
c. Fuchs (1964) ^a	Z → ∞
d. Dahneke (1983)	Z → ∞
e. Veshchunov (2010)	Z → ∞
f. Fuchs (1963) ^b	Flux matching
g. First passage regression (this study)	Z → ∞
^a
^b

Comparison to Existing Kernels

Earlier studies of transition regime collisions via Langevin simulations suffered from high statistical variability in the obtained results or made use of a limited number of calculated values (Nowakowski and Sitarski 1981; Narsimhan and Ruckenstein 1985; Gutsch et al. 1995). Due to the small time steps used in calculations as well as the strict convergence criteria employed, the results obtained in this study do not suffer from the same degree statistical variability as prior work (though some random variations in results from Brownian Dynamics are inevitable). Therefore, we may consider results from mean first passage time calculations to be “in silico” derived data for comparison with existing collision kernels. While there are a number of collision kernels derived elsewhere, we choose to examine the following, which are used numerously in investigations of collision-governed systems: (a) the Fuchs–Sutugin (1970) expression for the condensation collision kernel in the limit Z = 0, (b) Loyalka's condensation collision kernel in the limit Z = 0 (Loyalka 1973), (c) Fuchs's expression (1964) for the coagulation kernel for which Z → ∞, (d) Dahneke's (1983) expression for the coagulation collision kernel with Z → ∞, (e) the recently developed collision kernel from Veshchunov (2010) with Z → ∞, and (f) the hard-sphere limit of the collision kernel from Fuchs's diffusion charging theory (Fuchs 1963), which utilizes the limiting sphere concept. For appropriate comparison, each of these expressions must be recast in terms of H and Kn_D , which is shown in Table 1. We note that in rewriting these expressions, for any entity i, the diffusion coefficient in the original expression is replaced with kT/f_i . This leads to f_i as a function of Z in several expressions (as D_i depends on Z for vapor molecules), but isolates all Z dependencies within the friction factor, which is an input to dimensionless collision kernel expressions. If present in expressions developed for coagulation collision kernels, the quantity 6πηa_i /C_c (Kn_i ) is also replaced with f_i , where η is the dynamic viscosity of the surrounding gaseous medium. C_c (Kn_i ) is the empirical Cunningham (1910) correction factor, which is a function of Kn_i , the momentum Knudsen number (Friedlander 2000) for entity i, as opposed to the diffusive Knudsen number, which applies to mass transfer processes and is dependent upon f_i . Finally, in the nondimensionalization of Fuchs’ diffusion charging theory, the mean free path of the diffusing entity is taken to be (1.329/f_i )(kTm_i )^1/2 (Adachi et al. 1985) and the expression given by Natanson (1960) is used to determine the limiting sphere radius. With these definitions, all six examined collision kernel expressions appropriately collapse into the form H(Kn_D ), allowing for comparison to mean first passage time calculations. The Fuchs–Sutugin (“a” in Table 1), Loyalka's (“b” in Table 1), and Dahneke's expression (“d” in Table 1) all fit the general form of:

where C ₁ and C ₂ are “tuning” constants for the calculation of the collision rate in the transition regime. Fuchs’ coagulation theory and diffusion charging theory similarly contain these tuning constants, embedded into the polynomials g′(Kn_D ) and j′(Kn_D ), respectively. Figure 3a–e shows the quantity (H _express − H _sim)/H _sim × 100% as a function of Kn_D for the aforementioned collision kernels, where H _express is the dimensionless collision kernel determined from the expression in question and H _sim is the dimensionless collision kernel from mean first passage time calculations. Similarly, H values from each expression are plotted in Figure 4 as functions of Kn_D in range 0.3 < Kn_D < 2.5. Any disagreement between H _express and H _sim values at low (Kn_D < 0.01) and high (Kn_D > 5) is a result of statistical variation in calculations, as all expressions for H are set to converge to the appropriate continuum and free molecular limits. As seen in Figure 3a–f, there is excellent agreement between existing expressions and mean first passage time calculations in these limits, with most values falling within ±5% of each other. At intermediate Kn_D , good agreement is also found between simulation results (both for single- and two-entity systems) with almost all simulation results within 10% of those predicted by the examined collision kernels. The best agreement is found with the Veshchunov coagulation kernel and the Dahneke coagulation kernel, both of which apply in the Z → ∞ limit. Successively worse (but still within 10% excluding a single anomalous mean first passage time calculation value) agreement is found with Fuchs’ diffusion charging theory kernel, the Loyalka condensation kernel, the Fuchs–Sutugin condensation kernel, and the Fuchs coagulation kernel.

Figure 3 Percent deviation of previously developed expressions for the collision kernel as a function of Kn_D . (a) Fuchs–Sutugin's condensation kernel, (b) Loyalka's condensation kernel, (c) Fuchs's coagulation kernel, (d) Dahneke's coagulation kernel, (e) Veshchunov's coagulation kernel, (f) the hard-sphere limit of Fuchs collision kernel, and (g) the regression Equation (14). Closed symbols: single-entity mean first passage time calculations. Open symbols: two-entity mean first passage time calculations. Black guide lines are marked at /±5% deviation, and gray guidelines are marked at ±10% deviation.

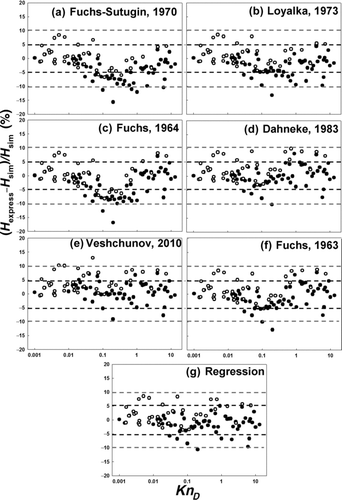
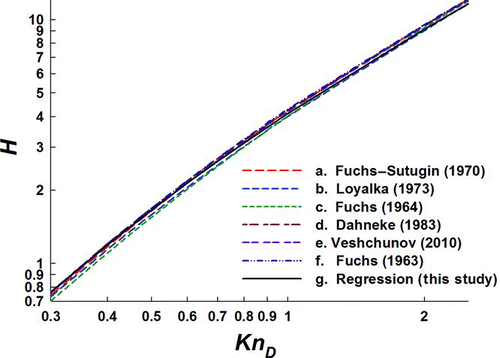
Figure 4 Comparison of six selected transition regime collision kernels (two derived for condensation, three for coagulation, and the limiting sphere model) to the collision kernel based on regression analysis of mean first passage time calculations. (Color figure available online.)

In addition to this comparison, we use mean first passage time calculations to construct a nondimensionalized collision kernel which may be used to predict particle–particle collision rates and, based on the good agreement with the Fuchs–Sutugin and Loyalka curves, also particle–vapor molecule collision rate with reasonable accuracy. Following Veshchunov (2010), we propose a four parameter fit of the form:

which must converge to Equations (11a) and (11b) at low and high Knudsen numbers, respectively, and where C ₁, C ₂, C ₃, and C ₄ are tuning constants that describe the transition regime. Nonlinear least squares regression of mean first passage time calculations in the region 0.05 < Kn_D < 2.0 (the transition regime) gives C ₁ = 25.836, C ₂ = 11.211, C ₃ = 3.502, and C ₄ = 7.211. Figure 3g shows the calculated (H _express − H _sim)/H _sim × 100% value for this regression equation for all mean first passage time calculations, and the resulting equation is plotted in Figure 4 with all other expressions. With the exception of several apparent outlier data points, regression calculated H values are within 5% of mean first passage time H values.

Overall, through comparison of mean first passage time calculations to existing collision kernel expressions, we find that all examined expressions, regardless of the limits imposed during their derivation, are within several percent of mean first passage derived values and of one another across the entire diffusive Knudsen number range. On the basis of the comparisons made by Veshchunov (2010), this excellent agreement is somewhat anticipated. Nonetheless, that mean first passage time calculations give rise to a similar collision kernel expression as do other approaches further suggests that a single collision kernel expression can be used to describe collision processes at all Z (both condensation and coagulation) across the entire Kn_D range, with an accuracy suitable for examination of almost all dilute aerosol systems.

As all examined collision kernel expressions are in excellent agreement with one another, we make no claim that the collision kernel expression inferred here is superior to others; rather, it is only introduced for appropriate comparison. We do note, however, that prior examinations of transition regime collisions have either required solution of the Boltzmann equation or unique mathematical insight into the collision process. For this reason, an understanding of particle collision processes outside of the continuum and free molecular limits is often difficult to gain for beginning practitioners in aerosol science. Unlike prior examinations, the approach employed here requires only prior knowledge of dimensional analysis (taught at the undergraduate level in most engineering curricula) as well as an understanding of force balances (such as the Langevin equation of motion). We therefore suggest that for pedagogical purposes, the mean first passage time approach to collision kernel development be widely utilized. Further, mean first passage time calculations can be applied to examine collisions with nonspherical particles much more readily than prior approaches, and via first passage analysis nonspherical particle collision examination is underway in our laboratory (Gopalakrishnan et al. 2011).

CONCLUSIONS

Mean first passage time calculations coupled with dimensional analysis are used to study transition regime collisions. On the basis of this work, we conclude the following:

1.	For hard-sphere, dilute entities whose motion can be described by the Langevin equation, the dimensionless collision kernel, H, can be determined solely as a function of the diffusive Knudsen number, KnD . Both H and KnD can be derived from nondimensionalization of the Langevin-based first passage time calculations, as well as by use of traditional dimensional analysis.
2.	A number of existing expressions for the collision kernel also collapse into the dimensionless functional form H(KnD ), and are compared with mean first passage time results. The good agreement between all examined kernels and our calculations strongly suggests that a single dimensionless collision kernel can be used to reliably infer both condensation and coagulation rates. Along these lines, a four parameter fit is developed from first passage time calculations for the collision kernel.
3.	The determined collision kernel applies rigorously only to hard-sphere, Z → ∞, entities in the dilute limit, whose friction factors (diffusion coefficients) do not vary spatially. Electrostatic and van der Waals forces often have an influence in gas-phase systems (Fuchs 1963; Sceats 1989; Huang et al. 1991; Filippov and Burtscher 1994) and may be included in analysis in future work. Such forces can be easily incorporated into the Langevin equation, and with forces included dimensional analysis will lead to the dimensionless collision kernel as a function not only of the diffusive Knudsen number, but also on additional dimensionless numbers that represent the magnitude of the potential interactions. It is also important to note that the determined function H(KnD ) is not influenced by the functional form of the friction factor [e.g., it may be inferred from the Stokes–Millikan equation (Larriba et al. 2011) or from Chapman–Enskog based diffusion coefficients], though friction factors must be known in order to determine β at a given H.
4.	While our findings indeed suggest that the influence of Z on the dimensionless collision kernel is small, the approach utilized here is vastly simpler than Boltzmann-equation-based approaches and results in an approximation to the true form of H(KnD ). More exact analysis, however, particularly of low-mass vapor molecule and particle collisions under nonisothermal conditions is still required to fully describe transition regime collisions.

Acknowledgments

The authors thank Professor Peter McMurry for numerous discussions on mass transfer processes in the transition regime. We also thank two anonymous referees for their thought-provoking comments on this work, as well as the Minnesota Supercomputing Institute (MSI) for providing the high performance computing hardware used in mean first passage time calculations. Partial support for this work was provided by National Science Foundation grants NSF-BES-0646507 and NSF-CHE-1011810.

[Supplementary materials are available for this article. Go to the publisher's online edition of Aerosol Science and Technology to view the free supplementary files.]