The Collision Rate of Nonspherical Particles and Aggregates for all Diffusive Knudsen Numbers

Abstract

We examine theoretically and numerically collisions of arbitrarily shaped particles in the mass transfer transition regime, where ambiguities remain regarding the collision rate coefficient (collision kernel). Specifically, we show that the dimensionless collision kernel for arbitrarily shaped particles, H, depends solely on a correctly defined diffusive Knudsen number (Kn_D , in contrast with the traditional Knudsen number), and to determine the diffusive Knudsen number, it is necessary to calculate two combined size parameters for the colliding particles: the Smoluchowski radius, which defines the collision rate in the continuum (Kn_D →0) regime, and the projected area, which defines the collision rate in the free molecular (Kn_D →∞) regime. Algorithms are provided to compute these parameters. Using mean first passage time calculations with computationally generated quasifractal (statistically fractal) aggregates, we find that with correct definitions of H and Kn_D , the H(Kn_D) relationship found valid for sphere–sphere collisions predicts the collision kernel for aggregates extremely well (to within ±5%). We also show that it is critical to calculate combined size parameters for colliding particles, that is, a collision size/radius cannot necessarily be defined for a nonspherical particle without foreknowledge of the geometry of its collision partner. Specifically for sequentially produced model aggregates, expressions are developed through regression to evaluate all parameters necessary to predict the transition regime collision kernel directly from fractal descriptors.

Copyright 2012 American Association for Aerosol Research

INTRODUCTION

The growth of nonspherical aerosol particles via particle– particle collisions is difficult to examine theoretically, as collision dynamics are governed by both gas molecule to particle momentum transfer, and particle to particle mass transfer. For particles in the submicrometer and nanometer size ranges in atmospheric pressure environments, or for micrometer sized particles in reduced pressure environments, both momentum and mass transfer processes occur in the transition regime, with the rates of transition regime momentum transfer and mass transfer functions of the Knudsen number (Kn, the ratio of the gas molecule mean free path to particle length scale) and diffusive Knudsen number (Kn_D , the ratio of the particle–particle mean persistence distance to the collision length scale) (Dahneke 1983), respectively. Knudsen number calculations require a priori knowledge of the appropriate length scales for gas molecule–particle collisions and particle–particle collisions. However, neither of these length scales have been identified clearly for nonspherical particles (Schmidt-Ott et al. 1990), nor are they necessarily identical for Kn and Kn_D (Zurita-Gotor and Rosner 2002).

Despite this complexity, collisional growth of nonspherical particles plays an important role in many aerosol systems, particularly those in which aggregates form and evolve (Maricq 2007; Chakrabarty et al. 2009; Sorensen and Chakrabarti 2011), and for this reason analysis of nonspherical particle collision dynamics is often necessary. Colliding entities are sufficiently dilute and well-mixed in most aerosol systems, such that the collision rate for two nonspherical particles of type i and j can be expressed as:

where R_ij is the number of collisions per unit volume of space per unit time, n_i and n_j are the number concentrations of type i and j particles, respectively, and β_ij is the collision kernel. The complications of nonspherical particle momentum and mass transfer are locked within the collision kernel function, and thus there have been several prior efforts to develop an expression for this function for nonspherical particles, with a specific focus on aggregates composed of a number of point contacting primary spheres. In examining such aggregates, Sorensen and coworkers have assumed that the collision kernel is a homogenous function, and attempted to determine the collision kernel homogeneity factor both experimentally (Wang and Sorensen 2001) and theoretically (Pierce et al. 2006). Their analyses, however, do not account for the noncontinuum nature of the collision process, that is, they neglect Kn_D dependencies. To account for noncontinuum mass transfer, Rogak and Flagan (1992) used Dahneke's transition regime collision kernel expression (Dahneke 1983) as a basis for an expression for aggregates. Required in their proposed expression are appropriate length scales for the Knudsen number and the diffusive Knudsen number. While some theoretical justification is provided for the length scales selected, further study is necessary to determine validity of the choices made. More recently, Cho et al. (2011) examined the collision kernel for aggregates in a manner similar to Rogak and Flagan (1992), only differing in their use of Fuchs's transition regime collision kernel (Fuchs 1964) and of simpler expressions for the length scales used in Knudsen number definition. Using Brownian Dynamics simulations, Gutsch et al. (1995) attempted to determine the collision kernel for monomer spheres with aggregates across the entire Kn_D range. Unfortunately, their inferred collision kernels for spherical particles are substantially below the β_ij (Kn_D ) found both theoretically and experimentally elsewhere (Wagner and Kerker 1977; Veshchunov 2010; Gopalakrishnan and Hogan 2011), drawing the conclusions of this work into question. To our knowledge, the most theoretically rigorous examination of nonspherical aerosol particle collisions is the work of Zurita-Gotor and Rosner (2002), who determined the appropriate collision area for the collision kernel in the mass transfer free molecular regime (Kn_D → ∞), accounting for the rotational energy of both particles. Outside the mass transfer free molecular regime, however, the equation they develop cannot be accurately applied.

In addition to the aforementioned limitations of prior work, nonspherical particle collisional growth in the transition regime and the important concept of the diffusive Knudsen number are both disregarded in several widely used introductory texts on aerosol science (Hinds 1999; Friedlander 2000). Thus, the present study is motivated by the need to further examine collisional growth in aerosol systems with nonspherical particles in both the mass and momentum transfer transition regimes. In subsequent sections, collisional growth in the mass transfer continuum regime (Kn_D → 0), free molecule regime (Kn_D → ∞), and transition regime (0 < Kn_D < ∞) is discussed theoretically, as is a combined dimensional analysis—mean first passage time simulation approach to infer the collision kernel in all regimes. This approach has been used successfully to analyze mass transfer transition regime sphere–sphere collisions (Gopalakrishnan and Hogan 2011), vapor molecule uptake by nonspherical particles (Gopalakrishnan et al. 2011), and charged particle-ion collisions (Gopalakrishnan and Hogan 2012). The influence of transition regime momentum transfer on the collision process is incorporated into this analysis through the relationship examined in a recent study (Zhang et al. 2012) of the orientationally averaged, scalar friction factor of an arbitrarily shaped particle moving at low Reynolds number and low Mach number. The result of the analysis performed here is a dimensionless expression for the collision kernel, which is applicable to nonspherical particles across the entire Kn and Kn_D ranges, and receives as inputs clearly defined and calculable length scales for the particles. While the developed expression is applicable for particles of any morphology, detailed analysis is given for collisions specifically between quasifractal (statistically fractal) aggregates.

THEORY AND NUMERICAL METHODS

Mass Transfer Continuum Regime

In the mass transfer continuum regime, the Smoluchowski equation is commonly used to express the collision kernel between two spherical entities i and j, given as (Friedlander 2000):

where k is Boltzmann's constant, T is the background gas temperature, f_i and f_j are the scalar friction factors, and a_i and a_j are the radii of particles i and j, respectively. f_ij is defined as the reduced friction factor (Gopalakrishnan and Hogan 2011), calculated from the equation l/f_ij = 1/f_i + 1/f_j . To adapt Equation (2) for collisions between two nonspherical entities, it is clear that the friction factors must be appropriately defined, as must an appropriate length for the collision in lieu of a_i + a_j (Ziff et al. 1985). Described in Zhang et al. (2012), the orientationally averaged scalar friction factor of an arbitrarily shaped particle i can be expressed by the equation:

where μ is the dynamic viscosity of the background gas, λ is the (hard sphere) gas mean free path, Kn is the Knudsen number for momentum transfer, R_S,i is the Smoluchowski radius for particle i, and PA_i is the orientationally averaged projected area of particle i. Both R_S,i and PA_i are purely geometric properties of an object (Gopalakrishnan et al. 2011), and there are algorithms available to calculate both R_S,i (referred to also as the Capacity) (Douglas et al. 1994; Zhou et al. 1994; Given et al. 1997; Isella and Drossinos 2011) and PA_i accurately for arbitrarily shaped entities. Use of Equations (3a) and (3b) to describe particle motion accounts entirely for noncontinuum effects on particle drag; thus, it is valid across the entire Kn range. However, any hydrodynamic interaction between entities as they collide (Alam 1987; Gopinath and Koch 1999; Chun and Koch 2006) is neglected in these equations.

FIG. 1 Schematic of the procedures used for (a) Smoluchowski radius and (b) projected area calculation for a colliding pair of particles. (Color figure available online.)

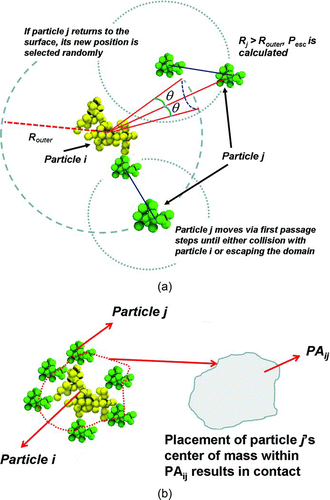
To then account for the influence of nonspherical particle geometry on the collision length scale, Equation (2) is rewritten as:

where R_S,ij is the combined Smoluchowski radius for the collision of particles i and j. Like the Smoluchowski radius for a single entity, the combined Smoluchowski radius for the collision of two particles can be calculated using Brownian Dynamics approaches that derive from procedures used to examine bimolecular reaction rates in solution (Northrup et al. 1984, 1986; Potter et al. 1996). A schematic describing the Brownian Dynamics procedure adopted here is shown in Figure 1a, in which particle rotation during collision is neglected. To use this algorithm, the boundaries of the two nonspherical particles under examination must be clearly described mathematically. One of the particles (henceforth referred as particle i) is oriented randomly with its center of mass at the center of a sphere of radius R _outer, which is large enough to completely enclose both particles (though it does not completely enclose both entities throughout the entire simulation). The second particle, particle j, is oriented randomly with its center of mass at a random location on the surface of the outer sphere. Particle j is then moved via diffusive first passage motion (Kim and Torquato 1991, 1992; Given et al. 1997; Thajudeen and Hogan 2012), which is accomplished in two steps. First, another sphere is formed, with its center at particle j's center of mass and its radius defined by the minimum distance particle j needs to move to reach point contact with particle i. Second, particle j is moved to a random location on the surface of this formed sphere. If, after the first passage step, the center of mass of particle j is a distance less than R _outer from the center of particle i but the distance between the edges of both particles is greater than a prescribed distance Λ (0.1% of the local radius of curvature, i.e., the primary particle radius in the case of aggregates), particle j is again moved via first passage motion and procedure continues until the edge to edge distance between the two particles is less than Λ. At this point, the two particles are considered to have collided, particles i and j are placed at the center and on the surface of the large sphere, respectively, again with randomly chosen orientations, and the process is repeated. However, if, at any time particle j reaches a point at which its center of mass is a distance R_j from the calculation domain center that is greater than R _outer, then the probability that particle j will escape the simulation domain entirely rather than return to the outer sphere surface, P _esc, is calculated as:

A random number is generated from a uniform distribution between 0 and 1; if this number is less than P _esc then particle j leaves the calculation domain without colliding with particle i, and the calculation procedure is reset and repeated. Finally, if the random number is greater than P _esc, then particle j is returned to the calculation domain with its center of mass placed on R _outer and with its specific location determined by sampling from the equation (Luty et al. 1992):

where θ is the angle noted in Figure 1a, and w is the probability distribution density for particle j returning to R _outer at θ. As all points with a specific θ define a circle on the surface at R _outer, to identify the precise point to which particle j returns, a second angle φ is sampled randomly from a uniform distribution (once a θ value is identified all points on the circle are equally probable). Particle j again moves via diffusive first passage motion (Kim and Torquato 1991; Gopalakrishnan et al. 2011) once returning to R _outer. Each portion of this calculation results either in particle j colliding with particle i, or particle j leaving the calculation domain. After a sufficient number of trials, if N _col is the number of collisions between i and j and N _miss is the number of instances where particle j leaves the simulation domain, then the combined Smoluchowski radius for i and j is evaluated as:

Free Molecular Regime

Following Zurita-Gotor and Rosner (2002), the collision kernel in the mass transfer free molecular regime considering hard sphere interactions between particles i and j can be expressed as:

where m_ij is the reduced mass for i and j, that is, 1/m_ij = 1/m_i + 1/m_j (m_i = mass of particle i, m_j = mass of particle j), and PA_ij is the collisional projected area. Like R_S,ij , PA_ij is a combined geometric parameter for i and j, which can be calculated for particles provided their geometries are appropriately described. Zurita-Gotor and Rosner (2002) describe a procedure to rigorously calculate PA_ij , accounting for the thermal rotation of two particles as they approach each other. As we neglect particle rotations in R_S,ij calculations, we also neglect particle rotation in the simplified PA_ij calculation procedure adopted here, with the consequences of neglecting particle rotation discussed in subsequent sections. An orthographic projection of particle i is placed with its (three-dimensional) center of mass in the center of a rectangle whose area, A _rect, is much larger than the sum of the orientationally averaged projected areas of particle i and particle j. Particle j is then projected onto the rectangle at a random orientation, with its center of mass at a randomly chosen coordinate in the domain. If, in this configuration, the projections of particles i and j are in contact, a collision is counted, while if the particles do not contact, a miss is counted. The procedure is continuously repeated for random orientations of particle i and random orientations and positions of particle j, and after a sufficient number of collisions, N _col, and misses, N _miss, have been monitored, PA_ij is determined as:

As shown in Figure 1b, PA_ij can be interpreted as the area of the projection bounded within the region where particle j's center of mass must lie in order for the two particles to contact. However, the depiction in the figure is only PA_ij for a specific orientation of the particles, while the PA_ij calculation algorithm determines the orientationally averaged value, that is, the parameter used in Equation (8).

Transition Regime

β_ij depends only on the parameters kT, f_ij , m_ij , R_S,ij , and PA_ij in the continuum and free molecular limits. In examining transition regime collisions between a point mass and an arbitrarily shaped particle, Gopalakrishnan et al. (2011) found that the interdependencies of a similar set of variables could be described using two dimensionless parameters, H, the nondimensionalization of β_ij , and Kn_D , the nondimensionalization of kT. Accounting for the aforementioned definitions of R_S,_ij and PA_ij and repeating the dimensional analysis employed in the prior study leads to H defined by the equation:

and Kn_D defined by the equation:

This definition of Kn_D is comparable to the definition of the momentum transfer Knudsen number for nonspherical particles used here and elsewhere (Dahneke 1973; Rogak and Flagan 1992; Zhang et al. 2012), with the ratio of the size scale describing continuum transport (R_S,ij ) and the size scale describing free molecular transport (PA_ij ) appearing in the numerator and denominator, respectively. Noting that dimensional Equations (2) and (8) must hold valid at Kn_D → 0 and Kn_D → ∞, respectively, reveals that:

Further, in investigating sphere–sphere, and nonspherical particle-point mass collisions, prior analysis shows that across the entire Kn_D range, H(Kn_D ) can be determined from the expression (Gopalakrishnan and Hogan 2011):

where C ₁ = 25.836, C ₂ = 11.211, C ₃ = 3.502, and C ₄ = 7.211. Alternative collision kernel expressions for particle-vapor molecule collisions (Fuchs 1964; Fuchs and Sutugin 1970; Loyalka 1973), agree well with Equation (13) (to within 5% for most Kn_D ), as do expressions for high-mass entity collisions proposed elsewhere (Dahneke 1983; Veshchunov 2010; Veshchunov and Azarov 2012), giving high confidence that it is a reasonably accurate expression for H(Kn_D ) for spheres.

The challenge then becomes evaluation of the validity of Equation (13) for nonspherical particle collisions with one another, for which we use mean first passage time simulations (Nowakowski and Sitarski 1981; Narsimhan and Ruckenstein 1985). In these simulations, we assume that particles are sufficiently dilute such that between collisions, there is ample time for particles to redistribute themselves homogenously within the surrounding background gas, that is, the characteristic time for collision is ≫ than the time required for particles to homogenously redistribute themselves in the background gas (Veshchunov 2010a,b). Particle motion is subject to inertia (mass x acceleration), drag, and diffusion (Ermak and Buckholz 1980). The equations of motion for two particles i and j, subject to these conditions, can be found in Gopalakrishnan and Hogan (2011). By subtracting the acceleration of particle i from that of particle j and nondimensionalizing the resulting equation, we can write the dimensionless difference in acceleration between i and j as:

where and are the dimensionless velocities for particles j and i, respectively, is the dimensionless time, , , and is a dimensionless vector that is Gaussian distributed in each direction, has zero mean, and variance given by:

It is apparent from Equations (14a) and (14b) that unlike the Kn_D →0 and Kn_D →∞ limits, in the transition regime the parameters θ_m and θ_f influence particle motion. However, it is also clear that under the condition θ_m = θ_f , θ_m and θ_f dependencies are mitigated. The approximation θ_m ≈ θ_f ≈ 0.5 applies for collisions between particles of nearly the same size (friction factor) and mass, and similarly the approximation θ_m ≈ θ_f ≈ 0.0 applies for collisions involving particles of highly disparate size and mass (provided that the more massive particle also has the higher friction factor). Because collisions under either of these conditions are quite commonplace, nearly all prior analyses of collisions neglect θ_f and θ_m effects (Dahneke 1983), and as a first approximation we also use the relationship θ_m ≈ θ_f here, with which Equation (14a) becomes similar to a Langevin equation of motion for a single particle. Defining the relative velocity vector and the relative position vector :

the changes in relative velocity and position between particles i and j as dimensionless time evolves from τ to τ +Δτ can then be monitored with the equations (Ermak and Buckholz 1980; Gopalakrishnan et al. 2011):

FIG. 2 Schematic of the mean first passage time calculation procedure. (Color figure available online.)

Using these equations of relative motion, the average dimensionless collision time (mean first passage time, τ _mean) between particles i and j is determined by placing particle i at the center of a cubic simulation domain (with dimensionless side length s, represented in Figure 2) with a fixed but random orientation, and particle j at a random location on the surface of the simulation domain, and also oriented randomly. While particle i remains fixed in the domain center, particle j's initial dimensionless velocity vector is determined from randomly sampling . With a prescribed Δτ and Kn_D , particle j then moves throughout the domain via Equations (15a)–(15c). Periodic boundary conditions are employed on the domain surface, and once the two particles contact one another, the dimensionless time required for collision is recorded, the positions and orientations of the two particles are reset, and the process is repeated. After M collisions have been monitored, τ _mean is calculated as:

where τ_l refers to the time necessary for collision in trial l. The dimensionless collision kernel H is subsequently determined from the equation:

As with purely continuum regime calculations, in mean first passage time calculations drag is accounted for via orientationally averaged scalar friction factor, entities are moved via translation only, and the hydrodynamic interaction as well as other potential interactions between colliding entities are neglected. It is therefore not a direct test of the validity of these assumptions, and is used simply to examine the functional form H(Kn_D ) when these assumptions are in place. Further, calculation results are independent of the functional form of the friction factor employed, as all momentum transfer effects are directly absorbed into the diffusive Knudsen number. To determine a dimensional β_ij from the dimensionless H(Kn_D ) relationship outside the free molecular regime, however, requires determination of the colliding particle friction factors, thus, it is noted in a prior section for completeness.

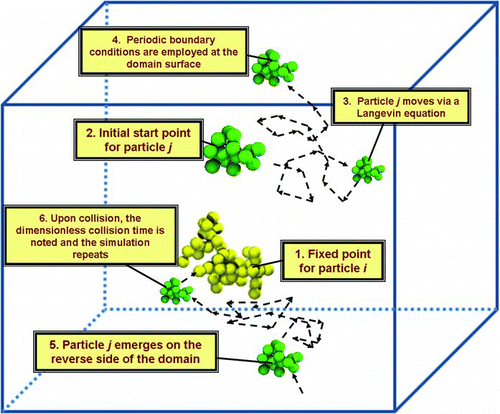
Ten combinations of test particle geometries are used in mean first passage time calculations, from which H is inferred for a specified Kn_D (12 different Kn_D values per aggregate pair). All test particles are quasifractal aggregates composed of 50 or less point contacting spherical subunits (of arbitrary unit radius), which satisfy the relationship:

where N_i is the number of primary spheres in aggregate i, k_f,i is the pre-exponential factor for aggregate i (set to 1.3 for all cases), a_i is the primary sphere radius, and D_f,i is aggregate i's fractal dimension. Each of the test particles is produced by a sequential algorithm (Filippov et al. 2000), which generates random aggregates with prescribed N_i , k_f,i , and D_f,i . Table 1 displays an image of each test aggregate, and notes the number of primary particles, and fractal dimension. The aforementioned algorithms to compute R_S,_ij and PA_ij are employed on each aggregate pair, as are the algorithms to compute R_S,i and PA_i noted in Gopalakrishnan et al. (2011) on each individual aggregate. All computed Smoluchowski radii and orientationally averaged projected areas are also listed in Table 1. Sufficiently large simulation domain side lengths (s) and sufficiently small time steps (Δτ) must be utilized to mitigate their influence on mean first passage time calculation results. For this purpose, domain side lengths of s = 400–800 (units of primary sphere radii) are used, with larger side lengths required for smaller Kn_D and larger aggregates. As in prior work (Gopalakrishnan and Hogan 2011, 2012; Gopalakrishnan et al. 2011), the restriction Δτ ≤ 0.005 Kn_D ² sufficiently mitigates timestep influences in these calculation results. Finally, to ensure convergence of τ _mean and H, dimensionless collision times are inferred for 5000—15,000 collisions and averaged for each reported H value.

TABLE 1 Summary of the properties of the ten test aggregate pairs used in mean first passage time simulations. Reported R_S,i , R_S,j , PA_i , PA_j , R_S,ij , and PA_ij are for aggregates with primary particle radii of 1 (arbitrary units)

RESULTS AND DISCUSSION

Mean First Passage Time Calculations

H(Kn_D ) values for nonspherical particle collisions, as inferred from mean first passage time calculations, are shown in Figure 3 (upper panel). For comparison, lines representing the continuum (Equation (12a)) and free molecular (Equation (12b)) limiting curves, as well as a curve corresponding to Equation (13), are also shown. It is apparent from this curve that as Kn_D → 0 and Kn_D → ∞, the calculated values are in excellent agreement with the correct continuum and free molecular expressions, respectively. Also apparent is the good agreement between Equation (13) and calculated values in the intermediate Kn_D range. This is further evident in the lower panel of Figure 3, where the relative difference, defined as (H _MFPT − H _eq13)/H _eq13 (where the subscripts MFPT and eq13 denote values determined from mean first passage time calculations and Equation (13)), respectively, is plotted as a function of Kn_D . All calculated values are within ±5% of Equation (13) predictions, and the small but apparent oscillation of the relative difference as Kn_D varies is attributable to the fact that Equation (13) is a regression equation with a finite number of terms (Gopalakrishnan and Hogan 2011). These results indicate, with little ambiguity, that the H(Kn_D ) relationship found for spherical particles can be extended to nonspherical aggregates, and subject to the assumptions of negligible particle rotation and zero particle–particle interaction, it is reasonably valid for collisions between particles of arbitrary shape.

FIG. 3 (a). Summary of the H(Kn_D ) results obtained with mean first passage time simulations for ten test aggregate pairs. For comparison, H(Kn_D ) curves corresponding to the continuum limit (12a), free molecular limit (12b), and regression equation from (Gopalakrishnan and Hogan [2011], Equation (13)) are shown. (b) The relative difference between H(Kn_D ) inferred from mean first passage time calculations and Equation (13) as a function of Kn_D . Relative difference is defined in the text. (Color figure available online.)

With this success in predicting collision rates in the mass transfer transition regime and with the good agreement between measurements, numerical calculations, and Equation (3a) for transition regime momentum transfer rates found in Zhang et al. (2012), we can construct a universal “operating schematic” for aerosol particle collisions in the absence of potential interactions. This schematic is shown in Figure 4. The dimensional collision rate between two particles i and j is dependent upon the Knudsen numbers for i and j (Equation (3b)), as well as the diffusive Knudsen number, calculated with the combined particle properties by Equation (11). Based upon these numbers, particles may migrate through background gas in the momentum transfer continuum, transition, or free molecular regimes, the boundaries between which are noted in Figure 4 by vertical lines at Kn = 0.04 (boundary between continuum and transition, below which the friction factor deviates less than 5% of the expected continuum regime value) and Kn = 7.1 (boundary between transition and free molecular, above which the friction factor deviates less than 5% from the expected free molecular regime value). Independent of Kn but based on Kn_D , the collision dynamics between two particles may occur in the mass transfer continuum, transition, or free molecular regime, with the bounds between continuum and transition regimes at Kn_D = 0.035 and between the transition and free molecular regimes at Kn_D = 3.7 (again based upon 5% or less deviation from limiting expressions). While the diffusive Knudsen number is dependent upon the individual Knudsen numbers of both particles through the friction factor and there is some degree of correlation between Kn_D and the Kn of the larger of the two colliding particles, the fact remains that aerosol particle collision dynamics are dependent upon three separate Knudsen numbers, and the dimensional collision kernel is expressed as:

FIG. 4 Depiction of the phase space noting when gas to particle momentum transfer and particle–particle mass transfer (collisions) lie within the continuum, transition, and free molecular regimes. (Color figure available online.)

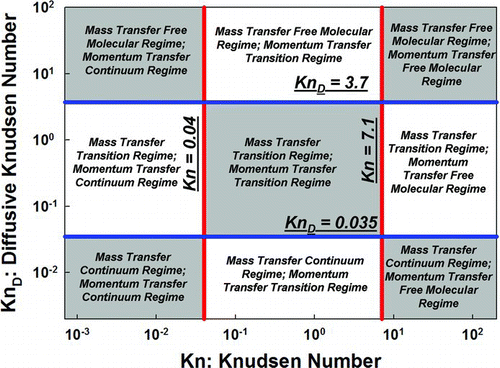
TABLE 2 Summary of the properties of the four test aggregate pairs used for comparison to previously developed aggregate collision kernel models. Reported length scales are for aggregates with primary particle radii of 1 (arbitrary units)

Influence of Particle Rotation

While the orientationally averaged friction factor is employed to model the motion of particles in this work, the act of rotation during a collision event is not explicitly considered. The influence of particle rotation on the length scale of particle–particle collisions is, however, considered by Zurita-Gotor and Rosner (2002) in the mass transfer free molecular regime. In doing so, they define the ratio ϕ as:

where PA_{ij ,rot} is a modified definition of the combined projected area accounting for particle rotation. Should rotations have minimal influence, then ϕ approaches 1.0, while with significant rotation influence ϕ ≪ 1. For aggregates obeying Equation (17) with a pre-exponential factor of 2.3 and a fractal dimension of 1.8, they find that ϕ is well-described by the equation:

where N _min is the smaller of N_i and N_j , N _max is the larger of these numbers, and σ is defined as N _min/N _max. Using Equation (19b), ϕ is plotted as a function of σ for varying N _min in the supplemental information (Figure S1). ϕ remains greater than 0.95 under all circumstances, and presumably, ϕ remains even closer to unity for higher fractal dimension aggregates than Zurita-Gotor and Rosner's test aggregates. Further, while their analysis is restricted to free molecular motion, the influence of rotational motion in the continuum regime, which would be quantified by a correction to R_S,ij , is also presumably similar in magnitude. In total, this prior work suggests that the influence of rotations on the length scale for particle–particle collision is minimal except in rare circumstances of collisions between extremely high aspect ratio entities of near equivalent size.

Comparison to Previously Proposed Expressions

We compare our H(Kn_D ) curve (Equation (13)) to the expression proposed by Cho et al. (2011), as well as to that proposed by Rogak and Flagan (1992). In many regards, these comparisons resemble prior comparison of the H(Kn_D ) curve developed through mean first passage time calculations to collision kernels of Fuchs (1964) and Dahneke (1983), which is performed elsewhere (Gopalakrishnan and Hogan 2011). For collisions betweens spheres, both the Fuchs (1964) and Dahneke (1983) collision kernel expressions differ from Equation (13) by only several percent across the entire Kn_D range. In making these comparisons, we further assume that all theories employ the same model for the friction factor of the particles (Zhang et al. 2012). Therefore, the comparison is solely limited to the choice of collision length scale employed in substitute of what is employed here, that is, (PA² _ij /π ² R_S,ij )^1/3 for H and PA_ij /πR_S,ij for Kn_D . We first compare to the equation of Cho et al. (2011), which derives from Fuchs (1964). In lieu of R_S,ij or PA_ij calculation, Cho et al. (2011) simply assume that the collision length scale can be calculated as the sum of size scales for the individual particles, that is, an appropriate “collision size” can be defined for a particle without consideration of the size and shape of the colliding partner. Specifically, they assume that the radius of gyration for a particle is its contribution to the collision length; hence, rather than make use of R_S,ij or (PA_ij /π)^1/2 they use R_g,i + R_g,j . With the assumption that the “limiting sphere” radius in Fuchs's collision kernel model is an amount (π/8)^1/2(kTm_ij )^1/2/f_ij larger than the collision length (an assumption that has little effect on the calculation collision kernel [Fuchs 1963; D’yachkov et al. 2007]), the dimensionless version of the collision kernel given by Cho et al. (2011), H _Cho, is written as:

For four sets of quasifractal aggregate pairs that have properties specified in Table 2 (with all pre-exponential factors equal to 1.3), the value (H _Cho − H _eq13)/H _eq13 is plotted in Figure 5a as a function of Kn_D . For all test aggregate pairs, deviations are evident with the collision kernel from Cho et al. (2011). Specifically, a slight overestimation in the collision kernel is apparent at a fractal dimension 1.6, and underestimation in the collision kernel is found for all other fractal dimensions, increasing in magnitude with increasing fractal dimension and approaching 40% at a fractal dimension of 2.4. The difference between the collision kernel predicted by Cho et al. (2011) from that predicted by Equation (13) further varies with Kn_D and as Kn_D is a function of R_S,ij and PA_ij. Without these parameters known a priori it is difficult to quantify the error introduced via the assumption R_S,ij = (PA_ij /π)^1/2 = R_g,i + R_g,j .

FIG. 5 Comparison of the relative difference between H predicted by (a) Cho et al. (2011) and (b) Rogak and Flagan (1992) and H predicted by Equation (13), as a function of Kn_D , for four test aggregate pairs with properties noted in Table 2. (Color figure available online.)

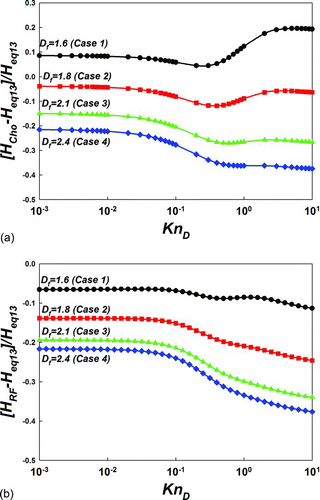
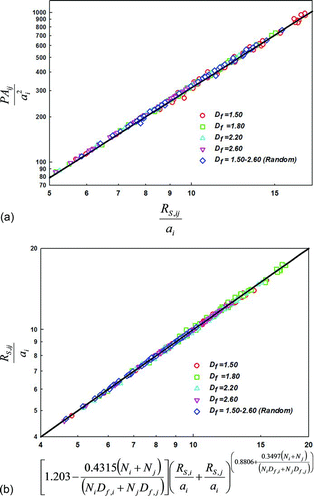
FIG. 6 (a) A comparison of PA_ij to R_S,ij for test aggregate pairs. The black line denotes the curve PA_ij = πR² _S,ij . (b) A comparison between calculated R_S,ij and a regression Equation (21) developed to predict R_S,ij from R_S,i , and R_S,j . (Color figure available online.)

Unlike Cho et al. (2011), Rogak and Flagan (1992) acknowledge that the collision length scale (termed the absorbing sphere radius in their work) cannot necessarily be defined as the sum of individual length scales calculated separately for the colliding particles. Nonetheless, the collision length employed in their work, L _RF, is distinct from the collision length scale in this study. L _RF calculation, shown in the supplemental information, requires use of “max” and “min” functions that contain several theoretical correlations that apply in the low (D_f = 1.0) and high (D_f = 3.0) fractal dimension limits. Furthermore, L _RF is not a pure geometric parameter in all circumstances, but takes a specific value in the continuum limit, L _RF,C, the free molecular limit, L _RF,FM, and in the transition regime it can depend upon Kn_D (aggregate masses, friction factors, and the temperature). For the test aggregates examined, however, L _RF = L _RF,C = L _RF,FM is found, and is reported in Table 2. The dimensionless version of the collision kernel used by Rogak and Flagan (1992), H _RF, is expressed as:

Figure 5b, shows the ratio (H _RF – H _eq13)/H _eq13 as a function of Kn_D . Equation (20b) consistently underestimates the collision kernel, with the degree of underestimation dependent on Kn_D and increasing with increasing fractal dimension, again approaching 40% underestimation at a fractal dimension of 2.4. Based on comparison to both expressions, we henceforth suggest that whenever possible, in the examination of nonspherical particle collisions/aggregation, the proper values of R_S,ij and PA_ij be employed, as in many instances, previously utilized collision length scales lead to underestimation of the collision kernel.

Case Study: Relationships for Quasifractal Aggregates

To apply the H(Kn_D ) curve to models of collisional growth, or to compare the experimental measurements, it is thus necessary to compute R_S,ij and PA_ij . Geometric models of the colliding particles are required to calculate these parameters. As such information is not necessarily available, or as often the purpose of the calculation or experiment is indeed to predict particle geometry/morphology, we develop relationships between PA_ij , R_S,ij , PA_i , PA_j , R_S,i , and R_S,j for quasifractal aggregates composed of 50 or fewer primary particles of equal sizes with the number of primary particles selected randomly for each aggregate. Similar efforts have been made previously to develop regression expressions relating aggregate geometric descriptors to physical length scales (Naumann 2003). To develop regression expressions for the necessary transport size scales, test aggregates are produced with the sequential algorithm. Although the equations developed are admittedly limited in application to this specific class of particles (i.e., fixed pre-exponential factor, limited number of primary particles, and limited fractal dimension range) and further limited because the sequential algorithm is known to produce “unrealistic” aggregates with 100 or more primary particles (Filippov et al. 2000), the approach we employ in this case study can be used similarly to develop relationships between the size descriptors for collisions involving any type of particle morphology. PA_ij , R_S,ij , PA_i , PA_j , R_S,i , and R_S,j are calculated for 50 aggregate pairs with D_f = 1.50, 1.80, 2.20, and 2.60, as well as with aggregates with randomly selected fractal dimensions in the 1.50–2.60 range (with different fractal dimensions for the two colliding aggregates). For all test aggregates, k_f = 1.30. Figure 6a shows a plot of PA_ij /a_i ² versus R_S,ij /a_i for all test pairs, as well as a line denoting PA_ij = πR ² _S,ij . It is known that for point mass (i.e., gas or vapor molecule) collisions with a nonspherical particle PA_ij = πR ² _S,ij does not necessarily hold valid, particularly for high aspect ratio particles (Gopalakrishnan et al. 2011). Conversely, it appears for collisions between particles that are more similar in size, there is a direct relation between the continuum and free molecular size descriptors for collisions; thus, only calculation of either R_S,ij or PA_ij is required. However, we reiterate that this is by no means a universal conclusion, and only applies approximately for the class of aggregates under examination.

FIG. 7 (a) The average Smoluchowski radii and (b) and orientationally averaged projected area of aggregates formed from the collision of test aggregate pairs, as functions of Kn_D . (Color figure available online.)

We next attempt to relate R_S,ij to R_S,i and R_S,j , the Smoluchowski radii for the individual aggregates. Figure 6b shows R_S,ij /a_i for all test aggregate pairs as a function of the right hand side of the equation:

As is observable in this figure, Equation (21), determined via regression with all aggregate test pairs, applies well to this class of aggregates, to within 1% error. What follows is then to relate PA_i and R_S,i, for aggregates to their fractal descriptors. Considering sequential algorithm generated aggregates composed of 10–100 primary particles, k_f,i = 1.30, and D_f,i = 1.30–2.60, we find that the following equations predict R_S,i to within ±3% for the examined range of fractal dimensions:

As confirmation of the approximate validity of this regression, in the supplemental information Figure S2a shows a plot of R_S,i as a function of the right side of Equation (21). The following equation is similarly found for PA_i :

that agrees to within 5% of directly calculated PA_i for D_f,i = 1.6–2.6. Comparable to Figure S2 a, a plot of PA_i for test aggregates as a function of the right side of Equation (23a) is shown in Figure S2b.

In total, to employ Equation (13) (or equivalently Equation (18)) for similarly sized quasifractal aggregates of known fractal properties, R_S,i and PA_i can be approximated by Equations (22) and (23), which subsequently allows for evaluation of R_S,ij (Equation (21)), PA_ij (via PA_ij = πR ² _S,ij ), f_i (Equation (3a)), f_ij , and for known gas conditions and aggregate material density, Kn_D . Then, H(Kn_D ) can be calculated and used to infer β_ij for type i and type j aggregates.

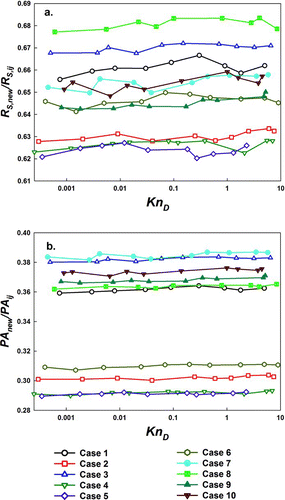
Finally, perhaps as important as proper calculation of the collision kernel is correct determination of the properties of the new particle formed from the irreversible contact-point binding of the two colliding aggregates (assuming little-to-no coalescence). Figures 7a and b show the ratios R_{S ,new}/R_S,ij and PA _new/PA_ij and as functions of Kn_D for the ten test cases shown in Table 1, where R_{S ,new} and PA _new denote the orientationally averaged projected area and Smoluchowski radius of the newly formed aggregate. Reported ratios are the averages from 50 collisions at the specified Kn_D and in most cases the standard deviation is ∼1% of the reported average value. Little-to-no variation with Kn_D is found for both R_{S ,new}/R_S,ij and PA _new/PA_ij . Further, all examined R_{S ,new}/R_S,ij fall within a narrow 0.62–0.68 range, while two similar populations of PA _new/PA_ij are evident, the first centered of 0.30, and the second on 0.37. Given the low degree of variation from collision to collision, amongst all examined aggregate pairs, and across the entire Kn_D range, these results demonstrate that from R_Sij and PA_ij (which, can be inferred from R_S,i and R_S,j for aggregates) it is possible to estimate the properties of the new aggregate formed during a collision.

CONCLUSIONS

The collisions of arbitrarily shaped particles are examined theoretically and numerically in the mass transfer transition regime. Based upon results of this examination specific regression equations for quasifractal aggregates composed of 50 or fewer primary particles are developed, which allow for determination of the transition regime collision rate for aggregates as functions of the fractal descriptors for each aggregate. From this work, we draw the following conclusions as well as note the following limitations to our analyses:

1.	The H(KnD ) relationship found valid previously for collisions between spheres can be generalized for arbitrarily shaped particles by appropriately redefining H and KnD .
2.	The universality of the H(KnD ) relationship in the absence of potential and viscous interaction permits generation of a phase space diagram, defining when collision processes lie within the mass transfer continuum, transition, or free molecular regimes. Significant about this is that the diffusive Knudsen number influence on mass transfer and collision processes in aerosols has been largely ignored in many studies of particle transport. Further, combining the results of this work with the conclusions of Zhang et al (2012), a complete phase space for gas molecule–particle momentum transfer (dependent on Kn) and for particle–particle mass transfer (dependent on KnD ) can be constructed.
3.	For quasifractal aggregates composed of monodisperse primary particles that are similar in size, regression relations can be developed that enable calculation of the collision kernel directly from the quasifractal descriptors. Population balance models (Heine and Pratsinis 2007) of aggregation should gain accuracy through use of the developed equations. For growth of particles of a different morphological class (e.g., fibers), the procedure used here to find relationships approximating RS,ij , PAij , RS,i , RS,j , PAi , and PAj as functions of more direct particle morphological descriptors can be repeated.
4.	While based on prior work, we anticipate that the rotation of nonspherical particles during collision minimally alters the collision rate, particle–particle interactions, both viscous and through potential energy (Sceats 1989; Arunachalam et al. 1999; Isella and Drossinos 2010), no doubt influence collision rates. Refined rate prediction for aggregates with need to address the influence of such forces, and examination along these lines is currently underway. That the H(KnD ) functional form has been generalized for collisions between particles weakly attracting or repelling one another Coulombically (Gopalakrishnan and Hogan 2012) suggests that such interactions can be accounted for in a realistic manner without major modification to the approach used here.

SUPPLEMENTAL INFORMATION

A plot of the parameter ϕ as a function of the parameter σ, the method to determine the collision length scale in Rogak and Flagan's (1992) collision kernel, and figures demonstrating the validity of Equations (22) and (23) are available online.

Acknowledgments

We thank the Minnesota Supercomputing Institute (MSI) for providing the high performance computing hardware used in some of the reported calculations. Partial support for this work was provided by the University of Minnesota Center for Filtration Research and the University of Minnesota Office of the Vice President for Research (OVPR).

[Supplementary materials are available for this article. Go to the publisher's online edition of Aerosol Science and Technology to view the free supplementary files.]