Closing the ultrafine particle number concentration budget at road-to-ambient scale: Implications for particle dynamics

ABSTRACT

Freshly emitted vehicle exhaust particles are diluted quickly as they mix into ambient air, but the contribution of evaporation, coagulation, and/or nucleation of new particles to the number concentration has been the subject of some debate. We analyzed one-second time resolution size distribution data from an early morning field campaign, data collected at a time at which dilution has a smaller (but still dominant; ∼70−80%) impact on particle concentrations. Because the plume is diluted over an hour, and a distance of 1500 m, we can constrain the processes with higher accuracy. We find that concentrations in the smaller size bins (5.6–23.7 nm) peak further downwind than the reference particles (42.1–562 nm), and decay significantly faster than larger particles particularly in the area 100−400 m downwind. Comparisons of the cumulative contributions of van der Waals enhanced coagulation, dry deposition, and dilution and the observed decay curves, imply that for up to the first 50–100 m there is nucleation and/or growth of particles smaller than 5.6 nm. In contrast, in the ∼100–400 m region, some of the smaller particles evaporate. In the further downwind areas (>400 m) the particles all appear to decay at rates consistent with the sum of dilution, coagulation, and deposition. We also find that a dry deposition parameterization at the low end of those available in the literature is most consistent with the observational data.

© 2016 American Association for Aerosol Research

EDITOR:

• Spyros Pandis

1. Introduction

In polluted urban areas traffic is the largest source of airborne particles, particularly for ultrafine particles (UPF) smaller than 100 nm in diameter (Morawska et al. 2008; Harrison et al. 2011), accounting for generally about 80% of the total particle number concentrations (PNC) (Heal et al. 2012) and up to >90% near major roadways (Harrison et al. 2011; Choi et al. 2014). High urban PNC from anthropogenic activities have been of growing concern in recent decades. Numerous epidemiological studies indicate that exposure to roadway emissions is associated with increases in various adverse health effects, including respiratory illness, DNA damage, cardiovascular disease, and adverse birth outcomes (Moller et al. 2008; Knol et al. 2009; Hoek et al. 2010). A subset of PNC, diesel engine exhaust, has been designated as carcinogenic to humans (Group 1) by the International Agency for Research on Cancer (IARC, part of the World Health Organization) due to risk for lung cancer (Benbrahim-Tallaa et al. 2012).

The manner in which the material in UFP is incorporated into larger particles can have a significant impact on the chemical composition of resulting particles, particularly on shorter time scales. Particles can be incorporated into the accumulation mode either directly via coagulation, or indirectly via evaporation and then condensational growth, generally after some gas phase oxidation (Robinson et al. 2007; Canagaratna et al. 2010; Kumar et al. 2011). Alternatively they can be lost altogether via dry deposition. Robinson et al. (2007) suggested that evaporation of diesel emissions and subsequent recondensation onto existing particles (after some oxidation) contributes substantially to secondary organic aerosols (SOA) formation. Bahreini et al. (2012) suggest, however, that in the Los Angeles area, gasoline emissions can contribute more than diesel emissions to the SOA, based on comparisons of enhanced OA to CO ratios (ΔOA/ΔCO) between weekdays (with higher diesel traffic) and weekends (with significantly decreased diesel traffic), although they did not differentiate OA origins between emissions of organic vapors and evaporation from POA. Further, several studies indicate that secondary formation of particulate organic matter can be much faster than estimates based on traditionally recognized lighter VOC precursors (de Gouw et al. 2005; Robinson et al. 2007; Ensberg et al. 2014).

Several studies have investigated the volatility of vehicular primary nanoparticles by comparing particle size distributions before and after a thermo-denuder/conditioner, and have concluded that most primary nanoparticles from gasoline vehicular emissions consist of semivolatile compounds (Wehner et al. 2004; Tiitta et al. 2010; Verma et al. 2011). This raises the possibility that evaporative repartitioning of gasoline-vehicular primary organic particles (POA) onto preexisting particles after experiencing photochemical processing might be significant. To accurately estimate the effects of evaporative repartitioning, it is necessary to understand the evaporative loss rates of exhaust POA and the effective spatial scales for those processes.

Particles emitted from tailpipes undergo complex processes as they are incorporated into ambient air, potentially including nucleation and condensational growth as the plume cools, evaporation from particles as the plume is diluted, coagulation with other particles and dry deposition to the surface. All previous studies have concluded that dilution plays a dominant role, but they have come to different conclusions on the relative contributions of each of the processes. Studies to date have used data collected during daytime, when dilution is particularly dominant, making determination of the contributions of the other processes more difficult to differentiate. Quantitative investigations of those effects on the SOA formation is further challenging due to dynamic characteristics of exhaust nanoparticles. For example, some studies have reported that coagulation plays a dominant role (after dilution) in particle dynamics (Wehner et al. 2002; Zhu et al. 2002a; Jacobson and Seinfeld 2004) in near-roadway and urban environments. Others argue coagulation is too slow to effectively alter a particle number budget, and have instead attributed a significant role in particle loss to evaporation (Zhang et al. 2004; Dall'Osto et al. 2011). It has been suggested that dry deposition can play a significant role in altering PNC when dilution is not a dominant loss mechanism (Kumar et al. 2011). Moreover, dry deposition of UFP is strongly dependent on particle size, surface environment, meteorological conditions, as well as vertical mixing height. Observations in various environments are limited, and parameterizations of those effects showed wide variations among studies (Zhang et al. 2001; Petroff and Zhang 2010).

One study (Kerminen et al. 2007) used data collected in stable air, in which dilution plays a smaller role, thus the contributions of other particle dynamics would be more important. Kerminen et al. (2007) concluded that condensation and coagulation are the most important processes in road-to-ambient evolution stage at night and in the morning, respectively, after dilution; they were not able to assess the contribution of evaporation from their data.

We collected size distribution data for early morning periods during a field campaign in 2011 (Choi et al. 2012), a time at which dilution has a smaller effect compared to daytime. Highly resolved size-segregated UFP concentration profiles (20 m resolution) observed with a mobile monitoring platform (MMP) allowed us to examine the continuous variations of particle dynamical processes as well as dilution rates, since freeway plumes traveled more than 1 km from the source. The particle dynamics considered in this study include coagulation (Brownian and enhanced due to von der Waals and viscous forces), dry deposition with varying mixing heights of a freeway plume, and evaporation/condensation, which is inferred from the particle number budget after correcting dilution loss rates.

2. Instrumentation, sampling, and post-data analyses

2.1. Sampling area, route, and instrumentation

The dataset used for this analysis was collected in 2011 in a residential neighborhood located about 4 km northwest of downtown Los Angeles, on a minor two-lane street with little traffic of its own (34.074N/118.272W, Choi et al. 2012). The measurement route (Coronado Ave.) is perpendicular to the 101 freeway, passing below it, and does not have direct freeway access. Coronado Ave. is 3.4 km long—2.2 km on the downwind (south) side, surrounded mostly with single family houses.

Measurements of ultrafine particle size distributions, together with several other pollutants and physical metrics, were collected using a mobile monitoring platform (MMP). The MMP is an instrumented electric Toyota RAV4, and has been described in detail elsewhere (Hu et al. 2009; Choi et al. 2012). Here we focus on particle size distribution data, collected using a Fast Mobility Particle Sizer (FMPS 3091, TSI), and also use total particle number collected with a condensation particle counter (CPC 3007, TSI). Each of these instruments has 1-s time resolution. The MMP was driven at consistent speeds below 30 km·h⁻¹ where possible (allowing for traffic lights and stop signs), and made three round trips on the transect during each measurement session. Measurements were collected for presunrise hours between 4:30 and 6:30 AM on four days; 2/24, 3/9, 3/14, and 3/17, for which atmosphere was slightly stable and calm.

2.2. Concentration profiles, site meteorology and traffic

As pollution data were collected every second, the data have spatial resolution of about 5–7 m. After synchronizing the instrument response time and removing the signals from high emitters on the sampling transect using the method of Choi et al. (2012) (a brief description concerning this method is also presented in online supplementary information (SI), Section S1), all data (a total of 20 concentration profiles with 5–7 m spatial resolution) were averaged to 20-m intervals. An individual profile is a combination of fresh emissions near the freeway and aged plumes in the far downwind area. In addition, the concentration the near freeway is influenced by transient variations in the traffic density on the freeway. This caused significant concentration variations near the freeway (see online SI, Figures S1 and S5). Thus, the averaged concentration profiles represent more general characteristics of freeway plume transport.

The average wind speed, collected with a 2D sonic anemometer when the vehicle was stopped for 5 min between each transect was 0.7 ± 0.3 m·s⁻¹, and had an angle of 73 ± 16° relative to the freeway (90° is normal to the freeway and parallel to the transect). We also measured dΘ/dz using a tethered balloon for the lowest 100 m of the atmosphere at a site located 560 m from the center of the transect. The mean dΘ/dz was 7.3 ± 3.8 × 10⁻³ K·m⁻¹, characteristic of a slightly stable and calm atmosphere. Traffic on the 101 freeway during sampling was dominated by gasoline-fueled vehicles accounting for 94% of the averaged total flow rate, 797 ± 215 veh·5 min⁻¹. The contribution from heavy duty diesel trucks was modest with a flow rate of 48 veh·5 min⁻¹ (Freeway Performance Measurement System, PeMS, operated by the Institute of Transportation at UC Berkeley) (PeMS 2011).

2.3. Modified gaussian-briggs (GB) model and general features of the dataset

Our treatment builds on the assumptions that the only significant sources of primary particles are traffic emissions from the freeway, while local emissions from the downwind surface streets are negligible, which has been shown in Choi et al. (2012) and Hu et al. (2009). We also assume that background UFP distributions obtained from upwind areas are consistent over the 1-km sampling transect. Additionally we average the small variations in meteorological conditions, and assume consistent and homogeneous behavior for the 1.5–2-h sampling periods. Thus, consistent and smooth concentration decay rates from all loss processes are expected.

The highly resolved concentration profiles include many types of variability, including that due to instrument noise, meteorological (eddy) fluctuations, and/or residual error from removing transient spikes from local high emitters. Because we are interested in the contribution of particle dynamics to the mean concentration profile, we averaged all of the collected data (20 runs, high emitter spikes removed). Additionally, we applied the modified Gaussian-Briggs (GB) model to reproduce observed concentration profiles. Choi et al (2014) showed that the GB model fits the background-subtracted UFP number decay curves very well (with R²> 0.9) and offers the computational convenience of a smooth function for the theoretical analyses that follow. Calculations for particle loss rates due to coagulation and dry deposition were, however, made without subtracting background concentrations. In addition, a large quantity of observational data assures the accuracy of the GB model results. The application of the GB model to the mean profile also averages out the concentration variability outlined above.

In the simplified analytical form of the Gaussian dispersion model for infinite line sources (Equation (1[1] )) combined with Briggs' formulation (Equation (2[2] )), the emission factor (Q_c) and dispersion coefficients α and β are treated as free variables in the fitting processes to obtain the best fit curves to the observations:[1] [2]

where x is distance from the source, z and H are receptor and source heights, respectively, Q_c is the wind corrected emission factor, and σ_z is a vertical dispersion parameter. σ_z represents the standard deviation of the time-averaged concentration distributions in the vertical direction at distance x from the source (Luhar and Patil 1989) and is parameterized with dispersion coefficients α and β (Briggs 1973). The particular form of the dependence of σ_z on α, β, and x depends on the stability conditions; this is the form for stable environments. The detailed justification for the application of the modified GB model to the analysis of presunrise freeway plumes is found in Choi et al. (2014). However, for the purpose of the analysis presented here, the salient point is that Equations (1[1] ) and (2[2] ) reproduce the data well and, thus, provide a straightforward and accurate mathematical description of the shape of the decay curves.

3. Theoretical basis

Particle dynamic processes affecting ultrafine particle number concentrations (PNC) include nucleation/emissions, coagulation, dry deposition, evaporation/condensation, and dilution (Seinfeld and Pandis 1998; Kerminen et al. 2004; Kumar et al. 2011):[3] where N_k denotes a number concentration of the kth size bin of ultrafine particles, t is time, J is a source term that includes growth from the undetectable particles or shrinkage from a larger size bin, or in the case of nucleation mode particles, nucleation. Subscripts dil, coag, evap/cond, and deposit represent loss processes due to dilution, coagulation, evaporation/condensation, and dry deposition for particles in the kth size bin, respectively. In the present study, concentration variations with respect to time, dN_k/dt were converted to air parcel travel distance dN_k/dx by assuming consistent winds (air travel distance, Δx = U×Δt, where U is the mean wind speed) to compare to the form of the observational data. In this study, we attempt to quantitatively explain the effects of individual particle process and close the UFP number budget (Equation (3[3] )) by using a combination of observations and theoretical estimates. Term III is determined from an observed profile of passive species (see Section 3.1), while terms IV and V are estimated from theory (Sections 3.2 and 3.3, respectively). The remaining terms II and VI are combined to represent a net production/loss rate, and these terms are constrained by the difference between term I and the sum of terms III, IV, and V.

3.1. Observationally constrained dilution rates

Dilution rates are calculated using Equation (4[4] ) from Zhang et al. (2004) and Kerminen and Wexler (1995):[4]

where C(x) denotes concentration of the reference species at downwind distance x, f is dilution ratio, and subscripts peak and bkgd represent the freeway plume peak and upwind background, respectively. In this way, the stepwise UFP loss rates due to dilution can be easily obtained from Equations (5[5] ) and (6[6] ):[5] [6]

The implied assumption here is that both the reference and target species dilute at the same rate, which is reasonable given that dilution in the atmosphere is governed by atmospheric eddies; eddy diffusivity is a function of the flow (Stull 1988), and turbulent transport is independent of species involved (Seinfeld and Pandis 1998). We also note that the sharply increasing traffic density during the morning commute can affect the plume shape (thus, Equation (5[5] )), as the downwind areas of the plume result from lower traffic from up to about an hour earlier, while the near roadway concentrations result from much more recent traffic. Thus, Equation (5[5] ) corrects both the dilution effects and other processes that simultaneously affect concentration profiles to the same extent, including traffic changes and air-mass travel time. This is still valid because the calculation is based on background-subtracted concentrations, so that reference and target of interest share a common (freeway) source and are transported in the same air flow. Additionally, traffic changes insignificantly affect Equation (6[6] ), because the results were obtained from pairs of data points adjacent each other (ca. Δx = 20 m), corresponding to about 29 seconds in air travel time-scale (with mean wind speed of 0.7 m·s⁻¹).

In their earlier study of UFP evolution, Zhang et al. (2004) used CO as the reference species to derive dilution. Although CO was measured concurrently with UFP in our dataset (Choi et al. 2012), the CO instrument response was much slower than the FMPS, and had longer memory (carry-over) effects. As a result, it produced broader spikes in the time-series. In addition, modern vehicular CO emissions have been significantly reduced, so that CO peaks are much less intense, exhibiting only a 45% increase from the background concentration for the transect (Choi et al., 2012).

For our dilution reference, we chose the largest particle size bin associated with primary combustion emissions (particles larger than 42.1 nm with a mean of 72.2 nm, here called “accumulation mode (ACC)” for convenience; see Section 4.1). This was the best reference species given that (1) the ACC mode was measured with the same instrument as that of smaller particles, eliminating potential for artifacts created by using different instruments; (2) the ACC mode was particle-dynamically stable for time scales of interest in the present study (1–2 h) as reported in Kerminen et al. (2007) and shown by the upwind background air size distributions; (3) coagulation and dry deposition of ACC was insignificant (estimated coagulation and dry-deposition loss rates for ACC are negligible with time scales >15 and >17 h, respectively; however, this was explicitly included in our analysis (see Sections 4.3 and 4.4); (4) coagulation of smaller particles onto ACC does not alter ACC number concentrations; (5) the mode diameter of the ACC did not change with distance during plume transport. Kerminen et al. (2007) reported that under calm surface inversion conditions, the number concentration of particles larger than 63 nm was controlled almost entirely by dilution.

3.2. Estimates of coagulation rates

Coagulational loss rates of UFP near roadways were calculated with an enhanced Brownian coagulation kernel that accounts for van der Waals and viscous forces, assuming spherical particles (Alam 1987; Seinfeld and Pandis 1998; Jacobson and Seinfeld 2004) (Equations (7)–(9)).[7] [8] [9] where K(d_k,d_j) is the coagulation coefficient between two interacting particles with diameters d_k and d_j, U is the mean wind speed, D is the particle diffusivity, ω is a mean distance used in the Fuchs interpolation formula, is the mean thermal speed of a particle, EnF is an enhancement factor due to van der Waals and viscous forces, and W_C and W_K are correction factors in the continuum and kinetic size ranges, respectively. The enhancement factor formula is described in more detail in the SI, section S3, and can be found elsewhere (Alam 1987; Jacobson and Seinfeld 2004). For spherical particles unaffected by van der Waals and viscous forces, EnF is simply unity. The enhancement factor is a function of particle's van der Waals property, referred to as the Hamaker constant, A. The Hamaker constant depends on the composition of a particle; however, Hamaker constants for UFP emitted from vehicular sources have yet to be determined.

Although Jacobson and Seinfeld (2004) (and other researchers listed there) argue that treating aggregates as fractal particles increases coagulation rates, fractal effects are not considered in this study due primarily to lack of information on the contributions of very nonspherical particles. However, several lines of evidence indicate that the contribution of diesel fractal agglomerates to the particle concentrations at our site were modest. First, the fleet for this study was dominated by gasoline passenger vehicles (ca. 94%), which tend to produce semivolatile spherical particles (Wehner et al. 2004; Verma et al. 2011). Second, the grade along this section of freeway was low (∼1.3%) and the early morning traffic was free flowing (minimal accelerations), leading to engine load conditions conducive to lower emissions of fractal agglomerate particles for the diesel fleet (Chung et al. 2008). Also, in early 2011, the fleet was already well along its way to dramatic reductions in emissions (Preble et al. 2015) mandated by state and local regulations put in place in 2008–2010 aimed at the drayage trucks which make up a large fraction of HDDT in the area. Our data from other sites (Choi et al. 2012) include several cases with lower HDDT volumes but higher UFP concentrations after normalizing to traffic flows, further supporting the notion that fractal agglomerates do not play a large role in the particle dynamics studied here. Finally, to the extent that condensation occurs, it increases the fractal dimension of agglomerates (increasing their sphericity), reduces agglomerate effects. Evidence for this type of reduction of agglomerate effects from condensation on soot has recently been reported in rapidly diluted aircraft exhaust plumes (Timko et al. 2013).

3.3. Estimates of deposition rates

The dry deposition velocity (V_d) for UFP is one of the most uncertain parameters in the UFP number budget. UFP V_d values can vary by up to two orders of magnitude depending on particle size and surface environment, as well as atmospheric turbulence (Seinfeld and Pandis 1998; Petroff and Zhang 2010). The large variations in UFP dry deposition velocities were also attributed partly to lack of observations, and consequently incomplete parameterizations for nanoparticles (Zhang et al. 2001; Petroff and Zhang 2010). In the present study, the resistance model approaches are applied (Equation (10[10] ) (Seinfeld and Pandis 1998; Zhang et al. 2001; Petroff and Zhang 2010):[10]

where V_d and V_s are dry deposition and gravitational settling velocities for of UFP, and R_a and R_s are parameters for aerodynamic resistance and quasi-laminar layer resistance, respectively. Aerodynamic resistance R_a is a function of turbulence transfer (Equation (11[11] )), and quasi-laminar layer resistance R_s is related to aerosol transport in close proximity to the surface (Equation (12[12] )). Thus R_a is a function of particle and surface characteristics (Seinfeld and Pandis 1998):[11] where is friction velocity, κ is the von Karman constant, z is height, z₀ is the surface roughness, and ζ is the unitless Monin–Obukhov length (z/L). We note that R_a can be expressed simply by the mean wind speed and using the Businger-Dyer relationships which parameterize vertical wind speed profiles in terms of , z₀, and ζ (Businger et al. 1971; Stull 1988). 

The quasi-laminar layer resistance R_s is the rate determining step for dry deposition rates of small particles. Here we use the parameterization presented by Petroff and Zhang (2010) for deposition on nonvegetated ground, appropriate for our sparsely vegetated street environments (Equation (12[12] )):[12] [13] [14]

where E_gB and E_gT represent deposition efficiencies due to Brownian diffusion and turbulent impaction, respectively (see online SI 4 for details). Sc ( = ν_air/D) and St ( = V_s· /g·ν_air) are particle Schmidt and Stokes numbers, respectively, and F is a function of the Schmidt number ( = Sc^1/3/2.9). The parameterization used in Zhang et al. (2001) was also examined here (online SI 4), but as Petroff and Zhang (2010) (P-Z, hereinafter) reported that they made updates the 2001 study (Zhang et al., 2001) based on more observations with nanoparticles which were not available in 2001, we have adopted the recent P-Z parameterization (see also Section 4.4).

Finally, the dry deposition loss rates for UFP were calculated with Equation (15[15] ):[15] where H(x) is the mechanical mixing height of the plume. This is a function of distance, because plumes spread vertically as they travel. In this near-roadway environment, H is the plume mixing height rather than the stable boundary layer height, due to very close proximity to the source. The plume mixing heights were determined from vertical UFP concentration profiles, which were obtained from the observationally constrained semiempirical Gaussian-Briggs model described by Choi et al. (2014) and Section 2.3. We define H(x) as the height below which 90% of UFP are confined (see online SI 5 for the details).

3.4. Undefined UFP variation rates: Evaporation/condensation effects

Due to extremely wide ranges in saturation concentrations of atmospheric organic compounds as well as a myriad number of organic species emitted from combustion sources (Schauer et al. 2002; Donahue et al. 2006), it is difficult to directly estimate the evaporative loss/condensational growth rates of UFP in roadway plumes. In addition, changes in primary organic aerosols with varying atmospheric conditions, including dilution ratio, preexisting particles, and temperature, add more complexity in estimating these effects (Shrivastava et al. 2006). Thus, we combine the remaining terms II and VI in Equation (3[3] ) to become undefined variation rates of UFP (dN/dx_undef) instead of estimating them directly. We assume that there are no additional primary emissions other than the freeway, which is valid for the presunrise measurement periods given that the traffic in the surface streets crossing the transect was negligible compared to the freeway (Hu et al. 2009; Choi et al. 2012). Additionally, we removed the possible interferences from the individual high emitting vehicles encountered by the MMP in data post processes (Choi et al. 2012). Thus, the production term II involves only the growth from the smaller size bin via condensation or for the smallest size range, production via nucleation, if any.

4. Results and discussion

4.1. Observed size distributions and selected size bins

The mean size distributions of UFP number obtained at the Downtown Los Angeles site (DTLA) at several distances from the freeway are shown in Figure 1. At the freeway plume peak location, four distinct modes were consistently observed: the dominant peak at 11 nm, a secondary peak around 34 nm, and two shoulder peaks at 17 and 52 nm. There is a striking contribution from nucleation mode particles (<30 nm) near the freeway, and these elevated concentrations of very small particles decrease rapidly with distance from the roadway (Figure 1). Similar patterns in size distributions with four-modes were also found near the I-405 freeway (Zhu et al. 2002b; Zhang et al. 2004) and in other freeway transects in the SoCAB (Choi et al. 2012). The size distributions for the upwind background air (collected on the transect upwind of the freeway) showed a clear dominant mode around 52 nm with the expected low levels of particles less than 20 nm, indicating aged urban background air (Figure 1).

Figure 1. Mean particle size distributions obtained at the Downtown Los Angeles site for stable presunrise hours at various downwind locations from the freeway plume peak: Black solid line is size distribution at the peak location; dashed (blue) line at 300 m downwind from the peak; grey solid (green) at 500 m downwind; dash-dotted (orange) at 1 km downwind; and grey dotted line for the upwind background. Black dashed (brown) rectangles represent selected size-bins for the present study (see text for the details of selected size-bins).

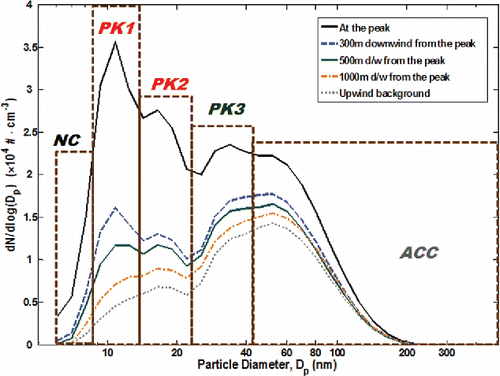
Here we group UFP sizes into five discrete size bins based on the observed size distributions: the smallest nucleation mode (NC: 5.6–8.7 nm); the dominant peak from fresh freeway emissions (PK1: 8.7–13.3 nm); a second dominant peak from emissions (PK2: 13.3–23.7 nm); large diameter mode from emissions (PK3: 23.7–42.1 nm); and the “accumulation mode” for urban background (ACC: > 42.1 nm), which was also elevated due to freeway emissions (peak concentration of ACC is 8.5 × 10³ particles cm⁻³, 54% higher than its upwind background 5.5 × 10³ particles cm⁻³; Figure 1), and the dilution rates were calculated with background-subtracted ACC particles. It should be noted that we are using the term ACC mode to refer to the right tail of the mode associated with roadway emissions; this is smaller than the conventional definition of the accumulation mode, which is centered at approximately 400 nm using a mass basis. The mean particle diameters in each size bin are 7.7, 10.9, 17.8, 32.8, and 72.2 nm for NC, PK1, PK2, PK3, and ACC modes, respectively.

4.2. Modified GB model fits and dilution corrections

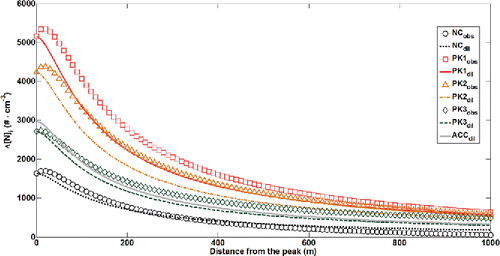
Observed size-segregated UFP concentration profiles and corresponding fitted profiles derived from the modified semiempirical GB model are shown in Figure 2. PNC shown here are background-subtracted values (ΔN = N_obs−N_bknd). Background values were defined as the lower quartile of the values observed in the upwind areas (200–800 m upwind of the freeway). PNC in all size bins shot up at the freeway plume peak location and sharply decreased with distance. However, the most striking elevation in particle number was found in the two smaller size bins (PK1 and PK2). The daily variations in spatial PNC profiles obtained from averaging 20 individual profiles are shown in online SI Figure S1.

Figure 2. Background subtracted particle number concentration (PNC, Δ[N]) profiles with distance from the center of freeway for each size bin. Symbols represent observation values and dotted lines show the fitting results using the modified GB model.

The modified GB model fits observations with R² values of 0.98, 0.96, 0.94, 0.96, and 0.85 for NC, PK1, PK2, PK3, and ACC particles, respectively (Figure 2). The slightly lower R² value obtained for the largest ACC particles results from more scatter in observations. Dilution corrections were made based on the decreasing ratio of ACC particles to the peak ACC concentration with distance (Section 3.1). The timescale of coagulational loss for ACC particles is much longer (∼15 h; see online SI 3) than the plume advection timescale (ca. 1–2 h). Coagulational loss of ACC particles was explicitly included in the dilution rate calculation (Equation (16[16] )). Dry deposition velocity for the ACC particles is believed to be one or two orders of magnitude smaller than the other size ranges (Petroff and Zhang 2010; Figure S4; Zhang et al. 2001). Nonetheless, dry deposition loss for ACC particles was also considered in the dilution rate calculation as expressed in Equation (16[16] ):[16]

The expected concentration profiles due only to dilution (and other environmental factors controlling concentration profiles) are shown in Figure 3, together with the observed concentration profiles for each size bin. It is clear that smaller particles, particularly NC, PK1, and PK2, drop off more rapidly than the larger size bins. This behavior is expected from processes whose rates have strong size dependence, which include coagulation, dry deposition, and evaporation/condensation. It is also interesting that the peak concentrations for smaller particle size bins appeared farther downwind than those of the two largest size bins. Considering Brownian diffusion is isotropic and much slower than advection in the along-wind direction, this late peak appearance possibly resulted from the secondary formation or growth of UFP near the sources. Detailed discussions concerning the roles of particle dynamics appear in the following sections.

Figure 3. Observed (symbols with subscript ‘obs’ in the legend) and expected concentration profiles due only to combined dilution and other processes that simultaneously affect the concentration profiles (solid and broken lines with subscript ‘dil’ in legend) for each size bin to the same extent such as traffic changes.

4.3. Estimated coagulational loss rates, and a simple form for estimating EnF

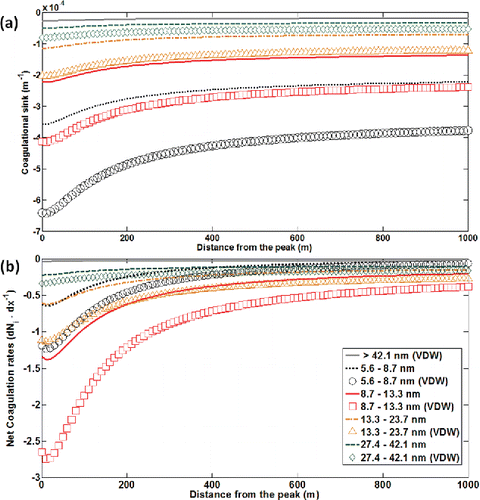
Coagulational loss rates were computed assuming spherical particles with density 1.2 g/cm³ for all particles. Figure 4 shows loss rate variations with distance for each size-bin, computed with both the basic Brownian diffusion coagulation module and with enhanced coagulation due to van der Waals and viscous forces.

Figure 4. (a) The coagulational sink (m⁻¹) and (b) coagulational loss rates (dN/dx, particles·cm⁻³·m⁻¹) with plume travel distance for each size bin (NC: circles and dotted line (black); PK1: squares and solid line (red); PK2: triangles and dash-dotted line (orange); PK3: diamonds and dashed line (green); ACC: solid grey). The mean diameters of NC (5.6–8.7 nm), PK1 (8.7–13.3 nm), PK2 (13.3–23.7 nm), PK3 (23.7–42.1 nm), ACC (>42.1 nm) particles are 7.7, 10.9, 17.8, 32.8, and 72.2 nm, respectively. Lines represent Brownian coagulation process and symbols represent enhanced coagulation due to van der Waals and viscous forces (VDW).

The enhancement factor (EnF) due to van der Waals and viscous forces is a function of the sizes of the two interacting particles and the Hamaker constant A, which depends on van der Waals properties of the particles (note that the usual functional form of the Hamaker constant is A·(k_B·T)⁻¹, which we refer to as the Hamaker coefficient, where k_B is the Boltzmann constant and T is temperature). Due to lack of knowledge about the composition of freshly emitted particles from vehicular sources, A·(k_B·T)⁻¹ is highly uncertain. Here, we assume a Hamaker coefficient of A·(k_B·T)⁻¹ = 150. This is likely an upper limit, given that A·(k_B·T)⁻¹ for many pure organic substances is less than 100 (online SI, Table S1).

It turns out that for given pairs of different sized interacting particles, the estimated EnF values can be fitted to a much simpler expression, itself a function only of A·(k_B·T)⁻¹ and three constants, with great accuracy (R² > 0.9995; Equation (17[17] ) and Figure 5):

Figure 5. Calculated coagulation enhancement factors (EnF) with varying Hamaker coefficients, A·(k_B·T)⁻¹ for a 10.9 nm particle coagulating with different particle sizes. Particles were assumed to have density of 1.2 g·cm⁻³ and calculations are for 1 atm and 300 K. Symbols denote calculated data points, and dotted lines represent the best-fit results in the form of Equation (17[17] ).

[17] where α, β, and n are constants determined by the best-fit obtained with an unconstrained nonlinear minimization of the sum of squared residuals method, and vary with particle size. Detailed α, β, and n values are shown in online SI Table S2. Figure 5 shows the estimated EnF as a function of A·(k_B·T)⁻¹ for NC particles (11 nm in diameter) interacting with particles with different sizes. The EnF sharply increases with A·(k_B·T)⁻¹ initially (when A·(k_B·T)⁻¹< 80), but more slowly as A·(k_B·T)⁻¹> 80 (Figure 5). This relationship can be used as a quick reference without calculating complicated van der Waals correction factors (W_C and W_K) in Equations (9[9] ) and online (S6) through (S9) for computational efficiency if needed.

The coagulational loss rates were enhanced by about a factor of two when van der Waals and viscous forces were considered. The enhancement is largest for the smallest particles, as expected (Figure 4). Because coagulation coefficients depend only on particle properties, particle concentrations, and meteorological conditions (which are fixed here), coagulational loss rates of UFP change with distance in response to the decaying UFP concentrations of each size bin. We note that using a lower value of A·(k_B·T)⁻¹ weakens the coagulation enhancement effects, thus in turn, magnifies the effects of unexplained loss/production rates described in Section 4.5, and discussed in detail in Section 4.6. A sort of upper limit for the unexplained loss/production rates can be inferred from the black dashed curve in Figure 8.

4.4. Dry deposition loss rates estimated with resistance models

To estimate aerodynamic resistance (Equation (11[11] )) and Stokes number (St) for quasi-laminar layer resistance (Equation (12[12] )), it would be ideal to know the surface friction velocity (); unfortunately these were not obtained during field measurements. Instead, we used a 30-min. averaged value (0.2 m·s⁻¹) for presunrise hours (4:00–6:00 a.m.) obtained from a 3-D sonic anemometer (CSAT3, Campbell Sci. Inc.) in a similar built-environment in the Los Angeles area, collected on September 18, 2013. This sonic anemometer was installed on the roof of a building, next to a minor street in a residential area 9 m from the ground and 3 m above the roof. Given that the mean wind speed for this period (0.75 ± 0.18 m·s⁻¹) was almost identical to that for the measurement periods (0.7 m·s⁻¹) and the surface conditions at both sites are also similar (mostly low buildings and scarce vegetation), it is reasonable to use the same value for this study. We further assume a homogeneous distribution along the 1 km-long transect.

The P-Z parameterization yielded negligible dry deposition rates compared to coagulational loss rates. Use of the varying vertical plume length scale, with distance from the freeway (H in Equation (15[15] ), in online SI, Figure S6), yielded about 30% higher dry deposition rates near the plume peak compared to a fixed H of 20 m. Likewise, depositional loss rates decreased more rapidly than they would if H were fixed (Figure 6). It should be noted that with Zhang et al. (2001)'s (earlier) parameterization, dry deposition rates exceed coagulational loss rates (online SI 2).

Figure 6. Dry depositional loss rates for each particle size bin with varying vertical plume length H (symbols) and with a fixed H of 20 m (lines with subscript ‘H = 20 m’ in legend). For variable mixing heights, H is defined as the height below which 90% of freeway UFP emissions were confined. Dry deposition velocities were calculated with a parameterization in Petroff and Zhang (2010) under the conditions of 0.7 m/s wind speed and 0.21 m/s friction velocity.

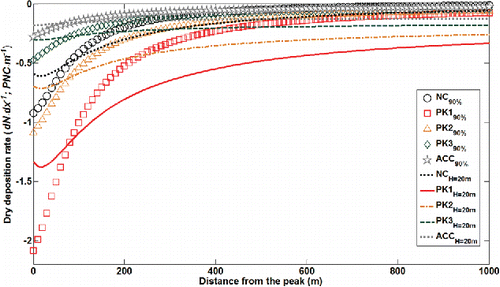
We also note that the three different deposition parameterizations predict very different contributions. For example, the loss rates from P-Z parameterization is only 10% of that from the parameterization in Seinfeld and Pandis (1998) and even less than that in Zhang et al. (2001). This strongly suggests UFP dry deposition velocities remain poorly constrained and more observations should be conducted to evaluate the current models in urban environments (see online SI Figure S4). Nonetheless, it appears that the P-Z parameterization is more realistic and consistent with our observational data. Agreement with parameterizations in Zhang et al. (2001) and Seinfeld and Pandis (1998) in the far downwind areas would require the presence of strong particle sources to balance the higher deposition rates; these parameterizations yielded large positive unexplained (dN/dx)_net (shown in dotted lines in Figure 7). This would imply an additional source only present in the far downwind areas in the far downwind areas, which appears unrealistic. Photochemistry producing secondary organic aerosol should be absent in the pre-sunrise period, the upwind size distributions do not show evidence of substantial numbers of very small particles, and we are not aware of an additional emission source covering the entire downwind areas.

Figure 7. Unexplained particle number variations with plume travel distance from the peak (dN/dx) for size-segregated UFP with an assumption of (A·(k_B·T)⁻¹ = 150). Subscripts P-Z (symbols) and S-P (lines) denote the dry deposition parameterization methods in Petroff and Zhang (2010) and Seinfeld and Pandis (1998), respectively. A dark-colored (blue) ellipse shows the regime in which additional losses (likely evaporation) are needed to close the number budget and a light-colored (yellow) rectangular area shows the range where net production of UPF (likely due to a combination of growth of sub-5.6 nm particles via coagulation/condensation growth, and potentially nucleation of new particles and subsequent growth) is needed to balance the observations.

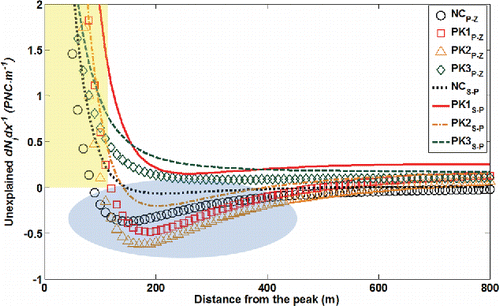
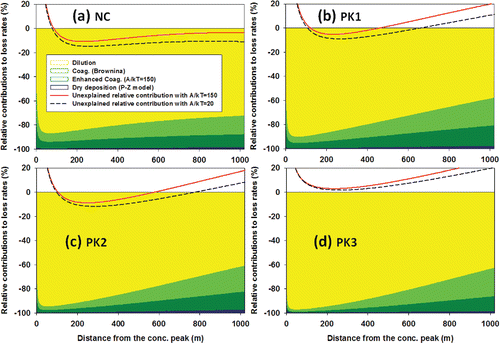
Figure 8. Relative contributions (%) of each dynamical process quantified to the cumulative loss rates of dilution, coagulation, and dry deposition with P-Z parameterization: (a) for NC particles; (b) for PK1, (c) PK2, and (d) PK3. Dilution is colored with light grey (yellow), Brownian coagulation with white (light green), enhanced coagulation with dark grey (dark green), and dry deposition with black (blue). Unexplained particle variation rates relative to the cumulative loss rates are shown with solid (red) (A·(k_B·T)⁻¹ = 150) and dashed (black) (A·(k_B·T)⁻¹ = 20) curves.

4.5. Unexplained loss rates and their implications

Of the UFP budget equation (Equation (3[3] )), observed concentration variations (term I) and UFP loss rates due to dilution (term III), coagulation (term IV), and dry deposition (term V) were quantified (above). The unexplained loss/production rates needed to balance the observed concentration profiles should result primarily from a combination of terms II and VI; (dN/dx)_net= J_k−(dN/dx)_evap (Figure 7). It should also be noted that the unexplained variation term may also include the errors associated with the estimates for the other terms. Although our calculations use accurate observational data (obtained with high spatial-temporal resolution and with the same instrument for all size bins) and state-of-the-science parameterizations from the literature, substantial uncertainties arise from several sources, particularly related to the coagulation rate. However, these errors overwhelmingly alter the magnitude of (dN/dx)_net and in any case do not account for the qualitative differences in the decay curves of the different size bins; the variation trends would remain the same as discussed below.

Significant positive (dN/dx)_net is needed to balance the observed concentrations within the first 60 m of the plume peak, as the peak for the small particles appeared further downwind than the ACC peak. A potential explanation of the discordance of peak locations is the growth of undetectable particles (smaller than 5.6 nm) due to condensational growth onto and/or self-coagulation of sub-5.6 nm particles into the smallest measureable size range. This hypothesis is based on the observation that the peak locations for particles in the smallest three size bin (5.6–23.7 nm) consistently appeared later than the peak of the two largest particle bins (PK3 and ACC), whose behavior is overwhelmingly controlled by dilution. Given that all particle number data were collected simultaneously with a single instrument, that peak concentrations were much higher than instrumental noise levels, and that diffusion should be isotropic for all particles, and eddy diffusion is a matter of flow not particle properties, the observation is robust. The hypothesis is also consistent with evidence from previous studies indicating nucleation and/or condensational growth is happening in the tailpipe-to-roadway stage (Arnold et al. 2006; Ronkko et al. 2007). The possible importance of condensation/self-coagulation for the nucleation mode particles under conditions with limited mixing has also been suggested by Kerminen et al. (2007) for areas close to the source (within 65 m downwind). More recently, Timko et al. (2013)'s findings further support our hypothesis, showing that nucleation or growth from undetected particles via gas-to-particle conversion is conspicuous during aircraft plume transport. Nonetheless, we acknowledge that further study to quantify this secondary growth or formation of nucleation mode particles is necessary in near roadway environments.

Beyond 60 to 80 m, the number concentrations of smaller particles dropped off more sharply than explained by the cumulative effects of dilution, coagulation, and dry deposition (Figure 7), most conspicuously for the smallest particles. The largest negative unexplained (dN/dx)_net appeared in the 100 to 400 m range; here the enhanced decayed relative to the predictions was most evident. This is consistent with evaporation taking over; potentially the concentrations of semivolatile compounds in the diluted plume decreased sufficiently to allow evaporation. While this may also take place in the areas closer than ∼100 m, in the very near roadway region nucleation and coagulation of very small particles dominates. As the plume is diluted further, the particles presumably approach a steady state, and the role of evaporation weakens. The road-to-ambient stage, characterized by vigorous dilution/dynamical processes, appears to give way to the urban/ambient scale beyond ∼400 m. The importance of evaporation for nucleation mode particles in the urban core was also suggested by Dall'Osto et al. (2011). This argument supports the recent hypothesis that evaporation from primary organic aerosols (exhaust UFP) may contribute to secondary organic aerosols once the evaporated semi-volatile materials have undergone some oxidation (Robinson et al. 2007).

We also note that for PK1 and PK2 particles, a positive (dN/dx)_net is needed to balance the observations farther downwind than 500 m. As dry deposition rates with P-Z parameterization are insignificant for PK1 and PK2 particles, coagulation rates appear to be overestimated, which implies that the A·(k_BT)⁻¹ for freshly emitted UFP should be smaller than 150, consistent with 150 being an upper limit.

Relative contributions to the cumulative loss rates of dilution, Brownian coagulation, enhanced coagulation due to van der Waals and viscous forces, and dry deposition are shown in Figure 8. As expected, dilution was dominant, accounting for 70–80% of the drop in the number concentrations even under the limited mixing in the slightly stable nocturnal boundary layer, consistent with the results in Kerminen et al. (2007). Coagulation becomes more important as the plume is diluted more, consistent with the notion that coagulation is the dominant particle number loss process at the urban scale (Kerminen et al. 2004).

4.6. Uncertainties from meteorology and model parameterizations and further studies

Although the atmospheric conditions were consistent and slightly stable with low wind speeds for all sampling days, we acknowledge that our analysis is affected by wind variations because time-based parameterizations for coagulation and dry deposition rates were converted to a space-based calculation using the mean wind speed. The estimated uncertainties linked with wind variations were ±42% for coagulation loss rates independent of particle sizes. Estimates of the uncertainties in dry deposition rates were ±13–±33% in ascending order with particle sizes. These are unavoidable uncertainties linked with natural meteorological variations.

More importantly, we also note that this study suffers from significant uncertainties caused by uncertainties in the state of the science understanding on parameterizations for coagulation and dry deposition (see also above and online SI S3–S5). For example, large uncertainties in calculated coagulation rates resulted from the unknown appropriate value for A·(kT)⁻¹. The coagulation enhancement factor increases by about a factor of 2 when A·(kT)⁻¹ increases from 20 to 200 (Figure S3), and this increase in A·(kT)⁻¹ yields a 45% increase in coagulation rates. Dry deposition is also an active area of research. The literature parameterizations (Zhang et al. 2001; Petroff and Zhang 2010) for dry deposition velocities vary by up to two orders of magnitude, although this study suggests Petroff and Zhang (2010)'s parameterization is reasonable. Vertical plume mixing adds a modest amount of additional uncertainty. Thus, these uncertainties pertaining to both coagulation rates and dry deposition estimates should be reduced by further investigations and more detailed 3D modeling studies would be necessary.

Due to the nonlinear dependence of coagulation rates on concentrations (Equation (3[3] )), coagulation rate calculation using the mean concentrations can be somewhat lower than the mean of coagulation rates obtained from individual concentrations particularly around the peak where concentrations showed the large variations, largely due to uneven distributions of traffic on the freeway. We estimate the coagulation rates from the mean concentrations were 15% less than the mean of coagulation rates from individual data points around the peak. However, this discrepancy sharply decreased, becoming negligible around 250 m from the peak and farther (less than 3%) where evaporational loss rates are required. This potential elevation in coagulation rates around the peak, however, enhances the effects of secondary formation or growth from undetectable particles because it requires larger positive unexplained dN/dx in this distance range. In addition, we have no vertical concentration gradient observations, thus this study does not include the potential effects of vertical concentration gradients on coagulation rates and their feedbacks to surface concentration variations. Nonetheless, our GB model (Sections 2.3 and 4.2) indicates the vertical gradient of UFP between the plume center-line (about 8 m above the ground) and observation height (1.5 m above the ground) were small compared to observed surface concentrations, and sharply decreases as the plume travels. For example, the 1.5–8 m concentration gradient for the particles with the largest mode mean concentration (PK1) was 11% of the surface concentration around the plume peak but sharply decreases to less than 1% at 70 m from the peak.

5. Conclusions

Despite the slight overestimation of particle loss rates in the far downwind areas of the plume source, additional loss processes are required to explain observations near the source when road-to-ambient dilution begins vigorously. In addition, a production term is needed close to the plume peak location. Our hypotheses for these phenomena are that in the very initial stage of road-to-ambient dilution, secondary formation and/or growth from undetectable size increases number concentrations of UFP smaller than 30 nm. Soon after (within 60–80 m of plume travel distances), fast evaporation due to rapidly diluted plume that decreases organic vapor pressure around particles combined with coagulation (due to elevated particle numbers and surface areas) and dry deposition due to limited mixing length scale of the initial plume leads to rapid decreases in PNC. The contribution of evaporation to the total loss rates tapers off with the plume travel distance since gas-phase semivolatile organic compounds in the plume approach ambient levels. The importance of evaporation even under stable and cool presunrise conditions supports the hypothesis recently suggested in Robinson et al. (2007) that evaporative repartition from POA into SOA contributes significantly to SOA formation unexplained with known VOCs emissions.

Acknowledgments

The authors gratefully acknowledge Dr. Meilu He and Mr. Vincent Barbesant for their contribution to the field measurements. The authors also thank Dr. Arthur M. Winer for helpful discussions and Dr. Akula Venkatram for the use of sonic anemometer data. The mobile monitoring platform measurements were made possible with the generous assistance of our colleagues Dr. Kathleen Kozawa and Mr. Steve Mara of CARB.