Error estimation of TEMOM for Brownian coagulation

ABSTRACT

In the present study, the error estimation of Taylor series expansion method of moment (TEMOM) for particle population balance equation due to Brownian coagulation is proposed. The app-roximation introduced by Taylor series polynomials has two parts: one is the approximation of nonlinear collision kernel, and the other is the approximation of higher and fractional particle moment. The results show that the two kinds of errors have the same order in the original TEMOM model, which is related to the third derivative of collision kernel and the first four integer order particle moments, i.e., M₀, M₁, M₂, and M₃. Based on the lognormal size distribution assumption, the system errors are obtained for different TEMOM models due to Brownian coagulation; and all the errors are small and acceptable. The results have confirmed the validity of TEMOM model.

Copyright © 2016 American Association for Aerosol Research

EDITOR:

• Nicole Riemer

1. Introduction

In terms of continuous variables, the population balance equation (PBE) due to Brownian coagulation is written as[1] in which n(v,t)dv is the number of particles per unit spatial volume with particle volume from v to v + dv at time t; and β is the collision frequency function of coagulation. In theory, there exists a unique solution for chosen kernel function. However, the solution of PBE can only be solved for simple kernel functions, known as the constant (β ∼ 1), additive (β ∼ v_i + v_j), and multiplicative (β ∼ v_iv_j) kernels, respectively. In most practical applications, the kernel takes on a significantly more complex form. For example, the free molecule kernel describes collision in a dilute gas-phase system as[2] in which B₁ = (3/4π)^1/6(6k_BT/ρ_p)^1/2, and k_B is the Boltzmann constant, T is the temperature; and ρ_p is the particle density. Generally, the coagulations that result from such physically realistic kernels are not solvable, and it is necessary to appeal to numerical method. The principal methods are the deterministic method of moment, sectional method, and the stochastic Monte Carlo method. Because of the relative simplicity of implementation and low computational costs, the moment method has become a powerful tool for investigating aerosol microphysical processes for many applications (Pratsinis 1988).

The kth-order moment M_k of particle size distribution is defined as follows:[3]

By multiplying both sides of PBE, Equation (1[1] ), with v^k and integrating over all particle sizes, a system of transport equations for M_k is obtained. In a spatially homogeneous system, the particle moments evolve in time due to the Brownian coagulation and can be expressed as follows:[4]

Recently, Yu et al. (2008) have proposed a moment-based approach, termed as the Taylor series expansion method of moment (TEMOM), to approximate PBE. This approach makes no prior assumption on the shape of particle size distribution; the derivation of TEMOM is completely based on Taylor series expansion; and the form of TEMOM is relatively simple. Therefore, TEMOM not only has advantages in the speed and accuracy of computation, it also provides a new way to analyze the characteristic of PBE theoretically. Based on the TEMOM model, Xie and Wang (2013) and Xie (2014, 2015) provide a series of asymptotic solutions of PBE for Brownian coagulation and agglomeration. Some analytical solutions of PBE are also proposed in the previous work, e.g. solution of PBE for Brownian coagulation in free molecule and continuum regime (Xie and He 2013; Yu et al. 2015a,b), solution of PBE for Brownian agglomeration in continuum regime (He et al. 2015; Yu et al. 2016).

It should be pointed out that TEMOM corresponds to a general perturbation theory approach, which is well known in the theoretical physics and requires very careful justification in each case. In the present study, as a basic problem of perturbation theory, the truncated error of TEMOM is estimated.

2. Error estimation

In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at an expansion point (in TEMOM, the expansion point u = M₁/M₀ is the mean particle volume). In the derivation of the TEMOM model, Taylor series approximations are introduced twice, one is the approximation of nonlinear collision kernel function, and the other is the approximation of higher and fractional order moment.

2.1. The truncation error for the approximation of collision kernel

Without loss of generality, the Taylor series approximation for the collision kernel with bivariate can be expressed as follows:[5] where TP is the Taylor series polynomial, then its truncation error in the original TEMOM model of degree 2 (Yu et al. 2008) is[6]

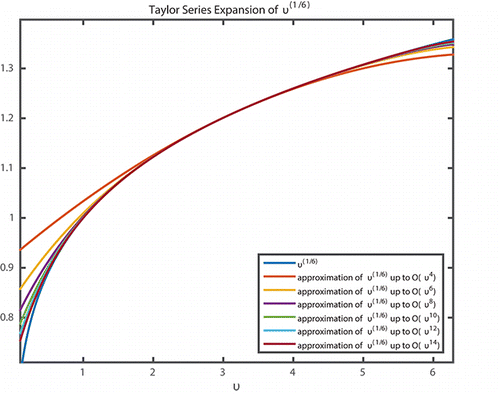
Taking the nonlinear collision kernel in the free molecule regime as example, difference between the collision kernel and its Taylor series approximation is shown in Figure 1. It can be found that the maximum error occurs at the margin of the particle volume domain (v_i > 0, v_j > 0). In the contour plot of the relative error (error 1/β), all the contour lines are straight and perpendicular to the line v_i = v_j in the Cartesian coordinate system. Therefore, it is reasonable to simplify the truncation error estimation of collision kernel with bivariate into the ones with mono-variant. For a free molecule kernel, it is simplified as β ∼ v^1/6. With the increasing number of Taylor series, the Taylor series polynomials are infinitely close to the original function in the region v > 0, which is shown in Figure 2. This result reveals that the convergence of Taylor series is obvious, and the truncation error can be reduced as[7]

Figure 1. Difference between nonlinear collision kernel and its Taylor series approximations of degree 2 at expansion point u (particle mean volume): (a) the absolute error of collision kernel; (b) the contour plot for relative error of collision kernel.

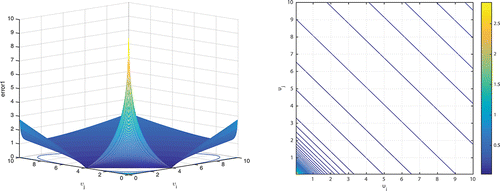
Figure 2. As the degree of Taylor polynomial rises, it approaches the correct functions; this image shows v^1/6 and its Taylor approximations at the expansion point u (particle mean volume), polynomials of degrees 3, 5, 7, 9, 11, and 13.

where L₁ is the maximum of the third derivative of collision kernel. Integrating it over all particle sizes, the global error for the approximation of nonlinear collision kernel can be represented as[8]

The truncation error is related to the third derivative of collision kernel and the first four integer order particle moments, i.e., M₀, M₁, M₂, and M₃.

2.2. The truncation error for the approximation of higher and fractional order moment

In the closure of higher and fractional order particle moment, v^k can be expanded as follows:[9] and its corresponding moment is[10]

Analogously, its truncation error in the original TEMOM model of degree 2 (Yu et al. 2008) is[11] where L₂ is the maximum of the third derivative of v^k in the range of particle volume v > 0. The truncation error of the approximation of higher and fraction order moment has the same order as that of the approximation of collision kernel.

To calculate the error of kth order particle moment, the particle size distribution (PSD) should be given in advance. Without loss of generality, assuming that PSD is a lognormal function,[12] in which the geometric average particle volume v_g and standard deviation σ can be expressed in terms of the first three moments of the lognormal size distribution:[13] where M_C = M₀M₂/M₁² is the dimensionless particle moment.

The comparison of M_k calculated by the first three integer order particle moment based on Equation (10[10] ) with that based on Equation (3[3] ) is shown in Figure 3. In the original TEMOM model (Yu et al. 2008), the maximum and minimum of k is 19/6 and –1/2, respectively. Generally, the values of M_k calculated by the two kinds of methods are in good agreement. Figure 4 shows the effect of parameters of lognormal size distribution on the relative error of M_k, which is defined as[14]

Figure 3. Comparison of M_k based on Equation (10[10] ) with that based on Equation (3[3] ) in terms of lognormal size distribution. The geometric average particle volume and standard deviation are v_g = 0.1 and σ = 1.3445 (or M_C = 2.2001), respectively.

Figure 4. Effect of parameters of lognormal size distribution on the error of M_k. (a) Effect of geometric average particle volume on the error of of M_k with σ = 1.3445 (or M_C = 2.2201); (b) effect of standard deviation on the error of M_k with v_g = 0.1.

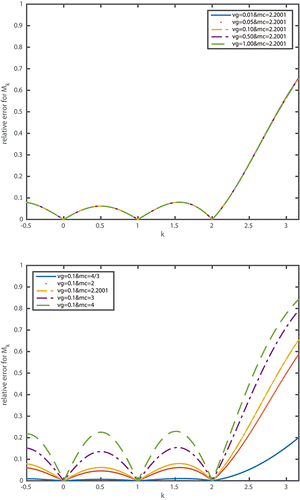
The relative error increases rapidly with the increase of k (k > 2). The results also show that the geometric average particle volume has a little influence on the error; but the effect of standard deviation on the error is significant, the greater the standard deviation, the greater the relative error. The reason can be found in the formula rearranged from Equation (10[10] ) as[15a] In addition, based on the assumption of lognormal size distribution, there is another approximation of M_k as (Pratsinis 1988)[15b]

However, this method is only valid for smaller geometric average particle volume and standard deviation; for larger ones, the error is as large as that of TEMOM. It should be pointed out that the first three integer order moments (i.e., M₀, M₁, and M₂) are calculated accurately.

2.3. System error of TEMOM model

Based on the above analysis, the system error of TEMOM model is[16] where L is a constant, which can be regarded as the maximum of the third derivative of (Chen et al. 2014; Yu et al. 2015c). Since M₀, M₁, M₂, and u are calculated accurately, the key point of error estimation is how to calculate the third order particle moment M₃ and the third derivative of collision kernel. In the original TEMOM model, the third order particle moment is approximated with Equation (15a[15a] ) as follows:[17]

Substituting it into Equation (10[10] ), the calculation of M_k can be obtained as[18]

which is a recursive iteration process. Therefore, the value of M₃ and its error estimation should be obtained in another way. The best way to calculate M₃ accurately is the definition of particle moment as Equation (3[3] ). In the next section, the error estimation will be discussed with concrete examples.

3. Results and discussions

3.1. The error for simple kernels

For the constant, additive, and multiplicative kernels, the maximum of the three-order derivative of collision kernel is zero (L₁ = 0); moreover, there is no need to close higher and fractional order moment with Taylor series polynomials. Therefore, the TEMOM is just the moment transformation of PBE, and their errors are all zero.

For a constant kernel (β ∼ 1), its TEMOM models are[19]

For additive kernel (β ∼ v_i + v_j), its TEMOM models are[20]

For multiplicative kernel (β ∼ v_iv_j), its TEMOM models are[21]

These results are consistent with the previous analysis (Wattis 2006).

3.2. The error for Brownian agglomeration in the continuum regime

For the collision kernel in continuum regime,[22] where the constant B₂ = 3k_BT/2μ, and μ is the gas viscosity. The moment equation based on Equation (4[4] ) without approximation is[23]

In this case, only the approximation of fractional order moment is needed to obtain the corresponding TEMOM (He et al. 2015) as[24]

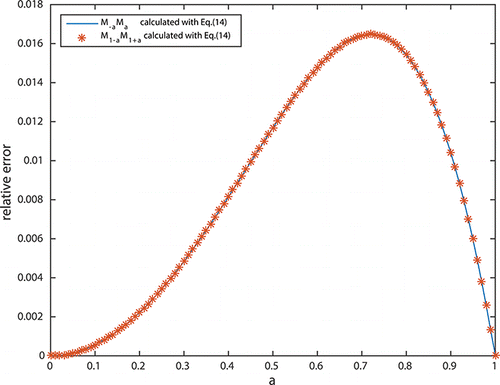
The relative error defined as in Equation (14[14] ) for M_–aM_a and M_1–aM_1+a in terms of lognormal size distribution with v_g = 0.1 and M_C = 2 is show in Figure 5; and their maximums are the same as 1.65%.

Figure 5. The relative error for M_–aM_a and M_1–aM_1+a in terms of lognormal size distribution with M_C = 2 and v_g = 0.1.

3.3. The error for Brownian coagulation in the free molecule regime

Similarly, the moment equation for Brownian coagulation in the free molecule regime without approximation is[25]

The growth rates of M₀ and M₂ (right-hand side of Equation (25[25] )) are double integrals over the domain. Its corresponding TEMOM model is[26]

In terms of lognormal size distribution with v_g = 0.1 and σ = 1.3445 (or M_C = 2.2001), the relative errors of growth rate for M₀ and M₂ are 2.65% and 0.98%, respectively. Due to the wide range of particle size (in this article, the particle volume ranges from 10⁻⁴ to 10² to obtain a more accurate error estimate), the double integrals for growth rates of M₀ and M₂ have high cost and low efficiency.

In previous studies (Xie and He 2014; Yu et al. 2015c), it has been revealed that different approximations of collision kernel using the same order of Taylor series and the same expansion point are almost equivalent. Therefore, the error of collision kernel expanded in part in the original TEMOM (Yu et al. 2008) is equivalent to that of the collision kernel expanded as a whole (Chen et al. 2014). Moreover, as mentioned in Section 2.1, the error estimation of collision kernel with bivariate can be simplified as the ones with mono-variant. Therefore, the system error of the TEMOM model can be approximated by the global error of collision kernel, and the influence of parameters of particle size distribution on the system error is reduced to influence of parameters on particle moment; this problem has been discussed in Section 2.2. In a free molecule regime, the relative errors of growth rates for M₀ and M₂ of the TEMOM model can be reduced to the ones of M_1/6 and M_7/6, which are 3.17% and 3.42%, respectively. From the point of view of errors, the original TEMOM (Yu et al. 2008) is more reasonable.

4. Conclusions

In the present study, the error estimation of TEMOM for population balance equation due to Brownian coagulation is proposed. The results show that the errors introduced by the approximation of nonlinear collision kernel and higher and fractional order particle moment have the same order as in the original TEMOM model, which is related to the first four integer order particle moments, i.e., M₀, M₁, M₂, and M₃. Based on the lognormal size distribution assumption, the system errors are obtained for different TEMOM models due to Brownian coagulation. For population balance equation with simple kernels, such as constant, additive, and multiplicative kernels, the system errors of TEMOM are zero; for the TEMOM model in the continuum regime, the relative errors of growth rates for M₀ and M₂ are the same; for the TEMOM model in the free molecule regime, the relative errors of growth rates for M₀ and M₂ are of little difference, but the errors are small and acceptable. The error estimations show that TEMOM is a promising tool to investigate particle population balance equation.

Funding

This work was supported by the National Natural Science Foundation of China with Grant Nos. 50806023 and 11572138.