Estimated risk for secondary cancer in the contra-lateral breast following radiation therapy of breast cancer

Abstract

Purpose. To facilitate a discussion about the impact of dose heterogeneity on the risk for secondary contralateral breast (CB) cancer predicted with linear and non linear models associated with primary breast irradiation. Methods and materials. Dose volume statistics of the CB calculated for eight patients using a collapsed cone algorithm were used to predict the excess relative risk (ERR) for cancer induction in CB. Both linear and non-linear models were employed. A sensitivity analysis demonstrating the impact of different parameter values on calculated ERR for the eight patients was also included in this study. Results. A proportionality assumption was established to make the calculations with a linear and non-linear model comparable. ERR of secondary cancer predicted by the linear model varied considerably between the patients, while the predicted ERR for the same patients using the non-linear model showed very small variation. The predicted ERRs by the two models were indistinguishable for small doses, i.e. below ∼3 Gy. The sensitivity analysis showed that the quadratic component of the radiation-induction pre-malignant cell term is negligible for lower dose level. The ERR is highly sensitive to the value of α₁ and α₂. Conclusions. Optimization of breast cancer radiation therapy, where also the risk for radiation induced secondary malignancies in the contralateral breast is taken into account, requires robust and valid risk assessment. The linear dose-risk model does not account for the complexity in the mechanisms underlying the development of secondary malignancies following exposure to radiation; this is particularly important when estimating risk associated with highly heterogeneous dose distributions as is the case in the contralateral breast of women receiving breast cancer irradiation.

Breast cancer is one of the most commonly diagnosed cancers and increases significantly in most countries. In Norway, around 2500 women are diagnosed with breast cancer each year, of which more than 50% are younger than 60 years of age [1]. The survival is strongly dependent on how early the disease is diagnosed; in stage I the 5-year cancer specific survival is 90.2% but only 17.0% in stage IV [1]. It is well established that postoperative radiation therapy reduces local-regional recurrence rates of primary breast cancers. There is also clinical evidence that radiation therapy may increase long-term survival rates of early breast cancer [2]. In patients treated for a breast cancer, the most common second primary cancer is contralateral breast cancer (CBC), accounting for approximately 50% of all second cancers [3]. Previous studies support the notion that breast cancer development is an acknowledged risk of radiation exposure [4–12]. It is therefore conceivable that a fraction of the secondary contralateral breast cancers are caused by the radiation exposure. Additionally the progressively earlier diagnoses of breast cancer and its relatively longer survival emphasize the concern for treatment induced malignancies in the contralateral breast following radiotherapy of the primary tumor.

Different models have been developed for the assessment of risk of cancer following radiotherapy, taking into account the influences of fractionation, heterogeneous dose distribution in the irradiated organ, cell repopulation and inducible repair [13–17]. The most simplistic model describes a linear dose-risk relationship, whilst more elaborate models are highly non-linear. The linear model predicts a continuously increasing risk with dose [13], whereas the non-linear models generally forecast an increased risk and then either a levelling off of risk or even a risk reduction [14–17]. Sachs and colleagues introduced a repopulation model that predicts no cancer risk reduction with increasing dose over the approximate dose range from 3 to 40 Gy [16]. Also, the inducible repair model, suggested by Dasu and co-workers, demonstrates a levelling-off of risk after the initial increase when using a competition model [17]. This plateau appearance of the dose-risk relationship may either be attributed to moderate to high inducible repair impact on cell survival, or the effect of dose heterogeneity, or both [17]. In another study by Dasu et al., a competition model was suggested; at higher doses the cell kill becomes more predominant than the yield of pre-malignant cells caused by radiation-induced mutations [15].

In the current study we discuss the impact of dose heterogeneity with respect to risk for secondary malignancies in the CB associated with breast cancer irradiation, using both linear and non linear models for risk prediction.

Methods and materials

Eight patients with stage II–III breast cancer undergoing post-operative radiotherapy of the breast and regional lymph nodes were included in this analysis. The prescribed doses were 46 Gy to the lymph nodes and 50 Gy to the breast, given in 2 Gy fractions, using 4 half-beams of 6 MV. Radiation therapy planning was based on CT scans covering a region from the 6th cervical vertebra to the middle part of abdomen. Treatment planning and dose calculation was performed using the Helax-TMS (Version 6.1b) system. CB was delineated in the planning CT images. Extensive analysis of the dose to the CB for these patients, using pencil-beam and collapsed cone algorithms as well as TLD for dosimetry, have been carried out and reported earlier [18].

Both linear and non-linear models were employed. The linear model used in this study is based on Preston et al.'s [13] model for excess relative risk (ERR), see Equation 1. ERR is defined as R(D) = R₀(1 + ERR_D×D) where R(D) is risk for treatment induced cancer for a given population and a given dose (D) and R₀ is the baseline risk (i.e. the natural occurrence of breast cancers):1 where ERR_D is ERR per dose (Gy) and with a suggested value of 0.86 Gy⁻¹ for breast cancer induction caused by acute irradiation [13]. This value is based on a pooled analysis of 8 cohorts of radiation induced breast cancer patients, by Preston et al. [13]. Radiation therapy is, however, fractionated and it has been suggested that the risk can be reduced by a factor of 2–10 when irradiated with multiple fractions as compared to acute irradiation [19–22]. In this study ERR_D was reduced by a factor of 2 and set to 0.43 Gy⁻¹.

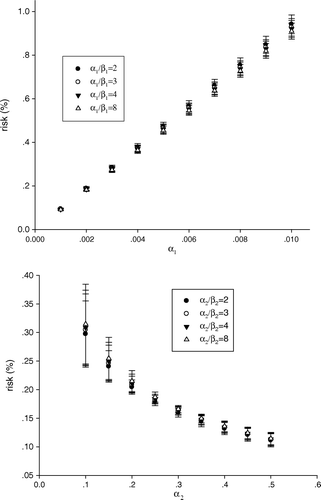
The non-linear competition model used in our estimation of risk for treatment induced cancer is based on a calculation of pre-malignant cells and has previously been suggested by Dasu et al. [15]. The model consists of two terms that effectively gives the yield of pre malignant cells. The first term describes the induction of DNA mutations, and thus pre-malignant cells. The second term describes the cell survival:2 where D is dose, n number of fractions, α₁ and β₁ are radiation induced mutation parameters, and α₂ and β₂ are cell survival parameters. Different parameters were investigated: α₁=0.001–0.1 Gy⁻¹, α₂=0.25 Gy⁻¹, and α₁/β₁ and α₂/β₂=2–8 Gy. Available data on the value of α1 is scarce, consequently a wide range of potential values have been employed in the analysis.

The above calculated effect varies non-linearly with dose. Mean dose to CB will thus not predict the risk for radiation induced malignancies. Instead of using mean dose in the risk assessment, the risk of treatment induced malignancy is calculated for each dose interval of the dose-volume histogram, in accordance with Equation 2, and weighted according to the relative volume fraction [15]:3 where υ_i is the volume of tissue receiving dose D_i.

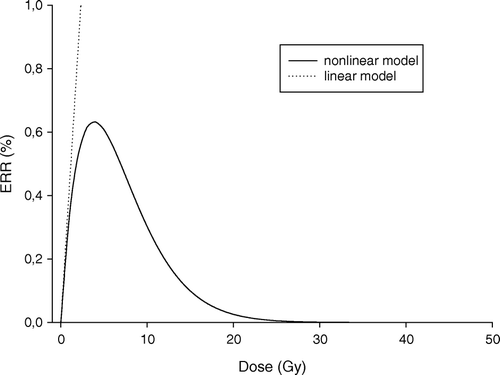
The non-linear model reflects the yield of radiation induced pre-malignant cells in CB [16] and thus only indirectly the excess relative risk for treatment induced malignancy. According to Sachs & Brenner proportionality between excess relative risk and yield of radiation-associated pre-malignant cells can be assumed [16]:4 where K is the proportionality factor linking the yield of pre-malignant cells and excess relative risk. K is independent of radiation parameters, but will generally depends on demographic and cohort factors such as nationality, sex, age at exposure, attained age, latency period, smoking patterns as explained in the study of Sachs & Brenner [16]. K is not a specified value for a population, but this factor makes it possible to discuss the consequence of uncertainty which is related to effect. In this study K was established by requiring identical initial slopes of the dose-risk relationship for the two models (Figure 1) and was found from the derivative of Equations 1 and 2, for dose approaching zero. K was found to be equal to 215 for α₁=0.002 Gy⁻¹.

Figure 1.  Dose effect curves for the two models. Calculated ERR for second primary cancer induction as function of dose using the linear and non-linear model (Equation 1 and 4). (α₁=0.002 Gy⁻¹, α₂=0.25 Gy⁻¹, α₁/β₁=α₂/β₂=4 Gy, ERR_D=0.43 Gy⁻¹).

Results

Typical dose-risk curves for the two models are shown in Figure 1. The two models cannot be compared directly as the linear model provide excess relative risk (ERR) whereas the yield of radiation-associated pre-malignant cells is calculated using the non-linear model. However, by assuming proportionality between excess relative risk and yield of radiation-associated pre-malignant cells (Equation 4) also the non-linear model can be used for calculations of excess relative risk. The predicted ERR by the two models are indistinguishable for small doses, i.e. below ∼3 Gy in this case (Figure 1). The dose level where the ERR prediction becomes significantly different between the two models is obviously parameter dependent.

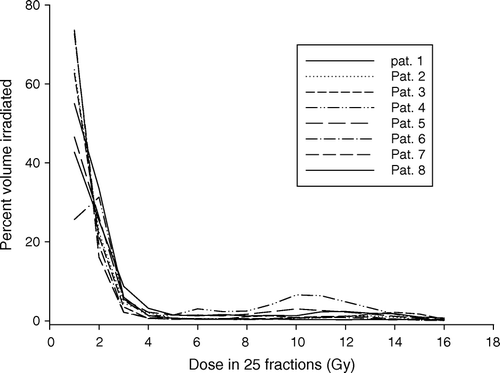
Dose volume histograms of CB in cumulative form following radiation treatment of the 8 breast cancer patients included in this analysis are shown in Figure 2. Relatively larger volumes of the CB are exposed to doses below 4 Gy, while very small volume fractions of the CB receive doses higher than 4 Gy. As expected, the dose distribution of the CB for each of the patients is highly inhomogeneous but varies moderately between the patients.

Figure 2.  Dose volume histogram of CB in cumulative form for each of the 8 patients. Each patient was treated using a 4-field technique with 6 MV beams to a dose of 50 Gy in 25 fractions to the breast and 46 Gy to the lymph nodes.

Mean dose to CB for the eight patients included in the analysis is shown in Table I. The average mean CB dose for each of the eight patients is below 5% of the prescribed dose, but varies from 1.3 to 4.3 Gy between the patients, i.e. by a factor of more than 3.

Table I.  Mean dose to CB and ERR calculated using the linear (Equation 1) and non-linear model (Equation 4) for the 8 patients. Calculations applying the non-linear model is based on the patients’ individual dose volume histogram and assuming α₁=0.002 Gy⁻¹, α₂=0.25 Gy⁻¹ and both α₁/β₁=α₂/β₂=4 Gy. The mean CB dose is used to predict the risk for radiation induced malignancies using the linear model.

Patient	Mean dose (Gy)	ERR-linear model	ERR-non-linear model
1	3.25	1.40	0.41
2	1.65	0.71	0.39
3	2.15	0.93	0.38
4	4.30	1.85	0.41
5	2.75	1.18	0.41
6	1.35	0.58	0.38
7	1.45	0.62	0.37
8	1.30	0.56	0.42

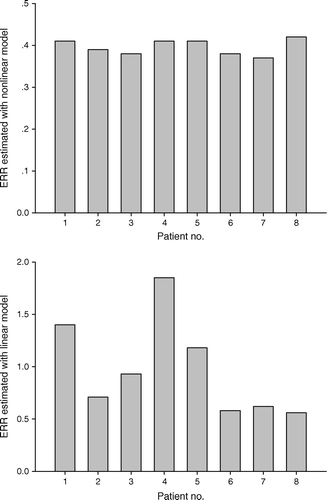
Excess relative risk (ERR) calculated using the linear and non-linear models, as described in the Equations 1 and 4, is shown in Table I and Figure 3 for the eight patients included in this analysis. The calculated average ERR for the eight patients is approximately 2.5 times higher when using the linear model as compared to predicted ERR using the non-linear model. ERR of secondary cancer predicted by the linear model varies considerably between the patients as the mean CB dose varies by a factor of 3. In contrast, the predicted ERR for the same patients using the non-linear model show very small variation. As expected for the patient that received the lowest mean CB dose, the ERR differed insignificantly between the two models. For the patients with higher mean CB dose the difference in ERR between the two models becomes more distinct.

Figure 3.  Predicted ERR for second primary cancer in the CB following breast radiation therapy for each of 8 patients, using the linear model (Equation 1) (lower panel) and non-linear model (Equation 4) (upper panel) with the parameter values; α₁/β₁ and α₂/β₂=4 Gy, α₁=0.002 Gy⁻¹, α₂=0.25 Gy⁻¹.

The non-linear model used for ERR calculations is, with its four parameters, significantly more complex than the linear model. Our knowledge about the different parameter values is thus scarce, which motivates a sensitivity analysis. Figure 4 demonstrates the impact of different parameter values on calculated risk for the eight patients included in our analysis. The predicted risk is highly sensitive to the value of α₁, but varies insignificantly with the α₁/β₁-ratio (Figure 4-upper panel). Thus, for the relatively low levels of dose to the CB for these eight patients, the quadratic component of the radiation-induction pre-malignant cell term is negligible (Equation 2). Moreover, Figure 4-lower panel- demonstrates that the estimated risk is relatively insensitive to the values of the α₂/β₂-ratio, but highly sensitive to the value of α₂. Again this is related to the fact that the impact of the linear component on cell survival is much more predominant than the quadratic component at relatively low dose level. For α₂ values of 0.25 Gy⁻¹ and above the variation in risk is negligible; however for lower values a marked variation in risk is seen. This increased variation is a consequence of reduced cell kill as α₂ becomes lower, and that at the same time the induction of pre-malignant cells is more susceptible to variations in dose than cell kill.

Figure 4.  The impact of different parameter values on calculated risk for the 8 patients. The impact of α₁ and α₂ values on the predicted risk, when α₁ and α₂ value respectively vary from 0.001–0.01 Gy⁻¹ and 0.1–0.5 Gy⁻¹ (upper and lower panel). Standard deviations are indicated by error bars.

Discussion

The most common secondary malignant disease amongst patients that previously have received radiation therapy for breast cancer is cancer of the contralateral breast. Based on our knowledge of the carcinogenic effect of ionizing radiation, it is likely that at least a fraction of these are caused by the exposure to radiation.

In order to optimize the radiation therapy for breast cancer patients, thus minimizing the risk of radiation induced secondary malignancies, robust and valid risk assessment is critical. Different models have been employed to predict the risk for secondary cancer. The most simplistic relationship between radiation exposure and risk, represented by a linear model, predicts a continuously increasing risk with dose. Preston and colleagues’ analysis of excess relative risks (ERRs) and excess absolute rates (EARs) for breast cancer in eight large cohorts exposed to radiation is based on the assumption of a linear dose-risk relationship [13]. Preston et al.'s study supports among others the linearity of the radiation dose response for breast cancer [13]. More complex, non-linear models deviate conceptually from the linear dose-risk assumption and project an increased risk with dose followed either by a plateau or even a risk reduction. Dasu and co-workers’ competition model projects a continuously increasing risk with dose up to approximately 4–5 Gy followed by a reduced risk [15]. This is explained by a shift in the balance between cell kill and the induction of DNA mutations and subsequent pre-malignant cells [15]. Dasu's conclusions are in accordance with a previous study by Lindsay and co-workers, also using a competition model [14]. Additionally, Lindsay et al. discuss the possibility and consequences of altered proliferation of the pre-malignant cells. It is well documented that normal cells may respond to radiation by enhanced cell proliferation. Whether pre-malignant mutant cells demonstrate similar behaviour is yet not known; if proliferation of pre-malignant mutant cells turns out to be affected by exposure to radiation one would expect this to influence the risk for developing radiation induced malignancies. Sachs & Brenner have investigated the possible impact of enhanced proliferation on risk for radiation-induced second malignancies [16]. In contrast to decreased risk for radiation-induced cancers at higher doses, their simulations forecast a plateau in risk or even a further risk increase.

In our study rather typical dose distributions to the CB have been subjected to analysis of risk for secondary malignancy of the contralateral breast following a standard 4 field irradiation technique for breast cancer. In half of the patients the mean dose to CB was below 2 Gy, ranging from 1.30 to 1.65 Gy, whereas for the other half the mean dose ranged from 2.15 to 4.30 Gy (Table I). For those patients with a mean dose to CB below 2 Gy, the calculated ERR was in the order of 0.5, irrespectively of the model employed. For the high dose group of patients the linear model predicted a substantially higher ERR of 1.2–1.8 using the linear model, but similar ERR as for the low dose group using the non-linear model (Figure 3). The difference in ERR predicted by the two models for the high dose group is clearly attributed to inherent assumption in our calculations that inactivation of pre-malignant stem cells becomes increasingly important at higher dose levels. Enhanced proliferation of pre-malignant stem cells due to exposure to radiation is, however, not accounted for in these simulations. Nevertheless, the simulations indicate that if radiation induced malignancies depend on the balance between the induction of DNA mutations and thus pre-malignant stem cells, inactivation and altered proliferation of pre-malignant stem cells, linear models are thus inadequate in assessing risk for radiation induced malignancies caused by highly inhomogeneous radiation doses. Mechanistic, non-linear models are in principle able to account for the different effects governing the development of radiation-induced malignancies. On the other hand they are also characterized by numerous parameters that are not always well established, and associated with large uncertainties. In the sensitivity analysis presented here it was evidently the two first order parameters, i.e. α₁ and α₂, that influenced the calculated ERR to the largest extent, whilst the two second order parameters, i.e. β₁ and β₂, were less influential. The four parameters of the non-linear model employed in our analysis will primarily influence the shape of the dose-risk curve and the relative ERR values; however, the absolute ERR values calculated employing this model depend on the proportionality factor, K, linking the yield of pre-malignant cells and excess relative risk. In our case K is established from the published values of ERR_D by Preston and co-workers and is the sole parameter of the linear model [13]. However, also the parameter of the linear ERR-model is hampered with uncertainties as it is derived from acute irradiation data and not protracted irradiation as fractionated radiation therapy represent. A fractionation factor of 2–10 has been suggested [19], but must be regarded as rather rough estimates.

A consequence of the two-component models discussed by Dasu and Lindsay [14], [15], [17] is that further reduction of risk for radiation induced malignancies best is achieved by reducing the dose to regions where the dose already is low [14]. This may, however, be incompatible with what's required to reduce the incidence of other late normal tissue effect. In contrast, Sachs & Brenner conclude that normal tissue adjacent to the target volume, that already receives the highest dose, also is at the highest risk with respect to developing radiation induced malignancies [16]. Consequently, further reduction of the risk for radiation induced malignancies is achieved best by reducing the dose to those regions receiving the highest dose. Until this discrepancy is resolved it would be nearly impossible to conclude how to further improve dose distributions with the overall aim of optimizing radiation therapy. If Sachs & Brenners’ conclusion is valid, reduced risk for radiation induced secondary malignancies can probably be achieved by introducing intensity modulated radiation therapy (IMRT), also in the case of breast cancer irradiation. On the other hand, if further reduction of dose to regions where the dose already is low is the most beneficial strategy, IMRT may not be the optimal solution as larger volumes of normal tissue usually is irradiated using this technique, increasing the potential radiation induced pre-malignant stem cells.

In conclusion, optimization of breast cancer radiation therapy, where also the risk for radiation induced secondary malignancies in the contralateral breast is taken into account, requires robust and valid risk assessment. The linear dose-risk model does not account for the complexity in the mechanisms underlying the development of secondary malignancies following exposure to radiation; this in particular important when estimating risk associated with highly heterogeneous dose distributions as is the case in the contralateral breast of women receiving breast cancer irradiation.