A beam-matching concept for medical linear accelerators

Abstract

The flexibility in radiotherapy can be improved if a patient can be moved between any one of the department's medical linear accelerators without the need to change anything in the patient's treatment plan. For this to be possible, the dosimetric characteristics of the various accelerators must be the same, or nearly the same i.e. the accelerators must be beam-matched.

During a period of nine months, eight Varian iX accelerators with 6 and 15 MV photon beams and 6–18 MeV electron beams (only four of the eight) were installed at our clinic. All accelerators fulfilled the vendor-defined “fine beam-match” criteria, and a more extensive set of measurements was carried out during commissioning. The measured absorbed dose data for each accelerator were compared with the first accelerator, chosen as reference, and the TPS calculations.

Two of the eight accelerators showed a larger discrepancy for the 15 MV beam not revealed by the vendor-defined acceptance criteria, whereas the other six accelerators were satisfactorily matched. The beam-matching acceptance criteria defined by the vendor are not strict enough to guarantee optimal beam-match. Deviations related to dose calculations and to beam-matched accelerators may add up. The safest and most practical way to ensure that all accelerators are within clinical acceptable accuracy is to include TPS calculations in the evaluation. Further, comparisons between measurements and calculations should be done in absolute dose terms.

The success of curative intended radiation therapy largely depends on the ability to deliver the prescribed dose to the patient within a narrow tolerance. A 5% difference in the delivered dose may result in changes in the order of 10–20% in tumor control probability and 20–30% in normal tissue complication probability [1]. Thus, there is a need for accurate treatment planning and delivery. This imposes narrow tolerance limits on all links in the treatment chain from planning to delivery, including imaging and structure delineation, absorbed dose measurements and calculations, treatment machine performance, and patient setup. Several publications present recommendations for such tolerance levels [e.g. [2–5]. Ahnesjö et al. [6] estimates that with the present techniques the uncertainty of the dose delivered to the patient is 3.9% (1 SD) excluding uncertainty related to dose calculation. Thus, if the uncertainty in dose calculation is between 1.0 and 5.0% (1 SD) the total uncertainty in the dose delivered to the patient will be between 4.0 and 6.3% (1 SD) [6]. Wambersie [7] and Mijnheer et al. [8] recommend a total uncertainty limit of 3.5% (1 SD) for the dose prescription point although 5% (1SD) is considered more appropriate for other points in the planning target volume [7]. Often cited is the ICRU 24 [2] ±5% accuracy requirement that can be interpreted as an action level [6] or as 1.5 SD [9], [10]. These recommendations on uncertainty limits and estimations of what can be achieved demonstrate that there is not much room for inaccurate dose calculations. Efforts must be made to reduce the uncertainty of every link in the treatment chain from planning to delivery.

Treatment flexibility and efficiency of a radiotherapy department are very important, and can be greatly improved if several linear accelerators (linacs) can be considered dosimetrically identical and patients can be treated using any linac without the need to adjust the treatment plans. In order to make this possible, the dosimetric characteristics of the various accelerators must be the same, or nearly the same i.e. the accelerators must be beam-matched. Beam-match results for Varian accelerators have previously been presented e.g. [11], [12]. In addition to beam-matched accelerators only one set of data representing all the accelerators needs to be implemented in the treatment planning system (TPS).

Due to the strict requirements on accuracy in radiotherapy, the following two questions arises: Is it possible to beam-match several medical accelerators to such a degree that they can be acceptably represented by only one set of data in the TPS? If so, how should this be undertaken? The aim of this study is to address these two questions using the commissioning data obtained from eight newly installed accelerators.

Material and methods

During a period of about nine months, eight Varian 2300 iX (Varian Medical Systems, Inc., Palo Alto, CA, USA) linacs were installed at our clinic. The linacs have two photon beams of nominal energies 6 and 15 MV and four of the eight linacs have electron beams with nominal energies 6, 9, 12, 15, and 18 MeV. The beam-matching procedure is described in detail in the vendor Customer Acceptance Procedure (CAP) manual [13] and the vendor accelerator specifications [14] and also by Hrbacek et al. [11]. The accelerators were purchased with the vendor-defined “fine beam-matching” option [11], [14]. The beam-matching criteria are based on depth ionization curves as well as inline and crossline profiles measured in the vendor-defined prescribed geometry. During the CAP of the accelerators, all the vendor-defined criteria were fulfilled. Even if the measurements were within the vendor-defined criteria adjustments were made to improve the match between each accelerator and the first accelerator, chosen as a reference during the CAP. Primarily adjustments were made to make both the photon and electron profiles as symmetrical as possible, but for some of the photon and electron beams it was necessary to tune the energy in order to improve the match of the depth dose curves. Following the CAP more extensive commissioning measurements were undertaken (Tables I and II) in view of the fact that; (i) the vendor-defined criteria does not consider full profiles or depth dose curves to evaluate the quality of beam-matching but instead only some points on the curves, (ii) all vendor-specified measurements for both electrons and photons are done with an ionization chamber and there is no or incorrect ionization chamber offset, (iii) the vendor-defined criteria are limited to only a few parameters for a limited set of beam geometries, (iv) the beam-matching criteria do not include output factors and therefore a risk of good agreement solely due to normalization may exist, (v) only open static fields are included in the CAP.

Table I.  Measurements carried out for photons.

		Geometry
Measurements	Equipment	FSD [cm]	Depth [cm]	Field size [cm^2]
Absolute dosimetry	Farmer chamber NE2571***, electrometer NE2570/1***, 41023 water fantom**	100	10	10
TPR2010	CC13 ionization chamber*, Blue phantom*, OmniPro Accept v.6.5A*	100	-	10
Output factors (OF) open fields in water	Waterproof farmer chamber 30006**, Unidos electrometer**, Blue phantom*	90	10	5, 8, 10, 15, 20, 30, 40
Depth dose open fields	CC13 ion chamber*, Blue phantom* OmniPro Accept v.6.5A*	90	-	5, 8, 10, 15, 20, 30, 40
Inline and crossline profiles open fields	Photon diode PFD-36*, Blue phantom*, and OmniPro Accept v.6.5A*	90	10	10, 40
2D distribution open fields	Seven29**, water-equivalent RW3 slab phantom**, Verisoft**	100	5, 10, 15	5, 10, 15, 20
2D distribution EDW30	Seven29**, water-equivalent RW3 slab phantom**, Verisoft**	100	5, 10, 15	5, 10, 15, 20
2D distribution EDW45	Seven29**, water-equivalent RW3 slab phantom**, Verisoft**	100	5, 10, 15	5, 10, 15, 20
2D distribution EDW60	Seven29**, water-equivalent RW3 slab phantom**, Verisoft**	100	5, 10, 15	5, 10, 15, 20
Head scatter factors (HSc)	Farmer chamber FC65-P* with brass buildup cap, Unidos electrometer**, in air measurements	98,55/98.17 for 6/15 MV ****	Brass****: 0.25/0.63 for 6/15 MV	2-10(step 1), 13, 15-40(step 5)

*IBA Dosimetry, AB, Uppsala, Sweden.

**PTW, Freiburg, Germany.

***Nuclear Enterprises, Beenham, Reading, England.

****Effective point of measurement at the isocenter, brass buildup cap different for 6 and 15 MV.

Table II.  Measurements carried out for electrons.

		Geometry
Measurements	Equipment	FSD [cm]	Depth [cm]	Applicator [cm^2]
Absolute dosimetry	Roos ionization chamber TW34001**, Unidos electrometer**, 41023 water fantom**	100	Zref	10
Output factors	Electron diode EFD-36*, Blue phantom*	100	Zref	6, 10, 15, 20, 25
Depth dose	Electron diode EFD-36*, Blue phantom*, OmniPro Accept v.6.5A*	100	-	6, 10, 15, 20, 25
Inline and crossline profiles	Electron diode EFD-36*, Blue phantom*, OmniPro Accept v.6.5A*	100	zref	6, 10, 15, 20, 25

*IBA Dosimetry, AB, Uppsala, Sweden.

**PTW, Freiburg, Germany.

To ensure that the beam-matching was clinically acceptable for photons the commissioning measurements were compared with the TPS, Eclipse 8.0 (Varian Medical Systems), pencil beam algorithm (PBC) calculations. Furthermore, all data were compared in absolute terms, i.e. depth dose curves and profiles for both open and wedged beams were not relatively normalized to the same value at a specific point but to the output factors for each individual accelerator. The 2D array measurements were normalized by defining a calibration factor for each depth for the open 10x10 cm² field size that gave the same value as the reference conditions i.e. measurements in water. In that way, any possible differences in attenuation between the solid water and the water were eliminated. Three of the linacs were prepared and used for IMRT treatments and as a further test of the beam-matching the same IMRT plans were delivered with these accelerators, measured with the 2D array and compared with TPS calculation.

The input data for the TPS were obtained from the first accelerator, and in the TPS only one set of data is used to represent all accelerators. The commissioning of the TPS will not be described in detail in this paper.

All electron beam treatment plans utilized at our clinic today are calculated manually using the output factors and depth dose curves and without sophisticated calculation algorithms such as TPS calculations. Hence, the commissioning measurements were not compared with TPS calculations but instead with the average of the measured values for all four accelerators. The reference depth (z_ref) used for absolute calibration and output factor measurements is defined in IAEA TRS 398 [15] and the same z_ref was used for all linacs. The reference depth for 6, 9, 12, 15, and 18 MeV are 13.9, 21.2, 29.8, 37.4 and 45.0 mm, respectively. On the basis of the output factors at z_ref and the depth dose curves the output at dose maximum (d_max) can be calculated. Other parameters such as the 85% depth (R₈₅) and the 50% depth (R₅₀) can also be extracted from the depth dose curves.

Isodose plots for IMRT were taken directly from Verisoft version 3.1 (PTW, Freiburg, Germany) as screen dumps. All other figures were created in Matlab R2006a. TPS calculations were exported as DICOM and imported in Matlab using functionalities in the Matlab Image Processing Toolbox and Emiliano Spezis DICOM–RT toolbox [16]. 2D array measurements were saved as bitmap files in Verisoft and depth dose and profile measurements were converted to and saved as ASCII files in OmniPro Accept (IBA Dosimetry, AB, Uppsala, Sweden) and imported into Matlab.

Results

Photons

All results are output factor normalized using the calibration geometry for each specific beam energy. Hence, the normalization retains all absolute dose properties and avoids any ambiguities related to normalization. The calibration geometry used is a 10x10 cm² field, FSD = 100 cm at depth 10 cm for both the 6 and 15 MV beam. The TPR_20,10 and the percentage depth dose at 10 cm depth (PDD₁₀) vary slightly between the accelerators for the calibration geometry. For both the 6 and 15 MV beam the mean values <PDD₁₀> and <TPR_20,10> of all eight accelerators are used for absolute dose calibration. The mean values were also used as reference for the output factor normalization. For the 6 MV beam the mean values and intervals ([min;max]) are: <PDD₁₀> = 66.3%, [66.2;66.4]% and <TPR₂₀₁₀>= 0.669, [0.666; 0.670]. For the 15 MV beam the corresponding numbers are <PDD₁₀> = 76.5%, [76.3;76.7]% and <TPR₂₀₁₀>= 0.762, [0.760;0.763].

For accelerators no. 1 to 6, the measured output factors (OF) are within 0.2% of the mean (<OF > _1-6). Accelerators 7 and 8 are the most recently installed and not yet taken into clinical use. Larger discrepancies for these two accelerators are found for the 15 MV beam ranging from -1.2% to +0.9% relative to <OF > _1-6 for field size 5×5 cm² and 30×30 cm², respectively (Figure 1). The discrepancies in OF between these two accelerators and the rest reflect a difference in head scatter (Figure 1). Further investigations into the cause and possible solution to the problem remains and will be undertaken in the near future. Based on a preliminary analysis of the data for accelerator 7 and 8, however, we expect the results presented bellow to apply also to these two accelerators except where explicit noted.

Figure 1.  Head scatter factors (HSc) and output factors in water (OF) versus field size for 15 MV photon beams.

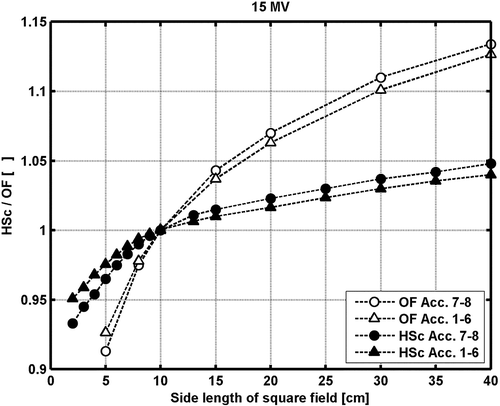
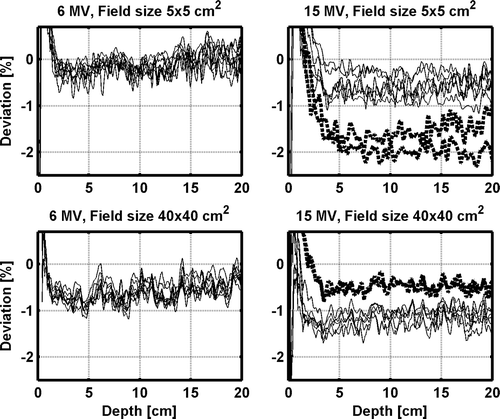
The relative depth dose data for the various accelerators are within 1%, when the measured output factors for the different accelerators are ignored. Larger systematic deviations are noticed in the comparison between the measured and calculated depth dose data, owing to the differences in calculated and measured OF (Figure 2). The largest deviation found is for 15 MV 5×5 cm² field size for accelerator 7 and 8, where the measured output factor are around 2% lower than the calculated (Figure 2). For field sizes larger than 10×10 cm², the measured output factors increase for accelerators 7 and 8 relative to the other accelerators, resulting in slightly better agreement with the TPS calculations for these accelerators. Except for 15 MV 5×5 cm² field size, all points in the output factor normalized depth dose data beyond the depth of d_max are within ±2% compared with the TPS calculations. The percentage deviations are larger at shallower depths. However, all data points for all field sizes and depths for all accelerators for both the 6 and 15 MV beams pass a 2%/2 mm gamma evaluation criteria, i.e. γ_2%,2mm≤1.

Figure 2.  The deviations between measured and TPS calculated depth dose data for each individual accelerator for the 5×5 and 40×40 cm² field size for the 6 MV and 15 MV open beams. The solid (thin) lines represent accelerator 1–6 and the dotted (thick) lines represent accelerator 7–8.

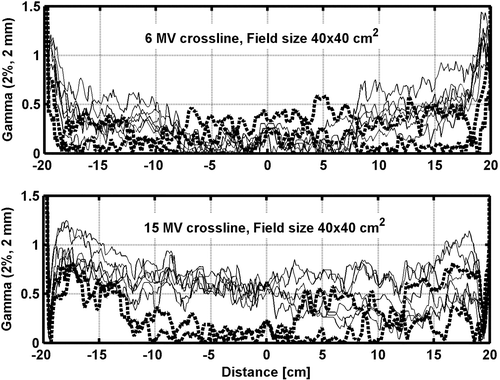
In most cases, the result of a gamma evaluation between measured and calculated profiles for open beams along the major axes (gun-target and A–B: perpendicular to and crossing the central axis) pass the γ_2%,2mm. However, close to the field edges for larger field sizes only some of the accelerators pass the criteria (Figure 3). The comparison of relative dose profile measurements from one accelerator with another, normalized to 100% at the central axis show that the profiles generally are within 1% except for larger field sizes close to the field edges were the largest deviation between two accelerators generally are around 1.5% for both the 6 and 15 MV beams. Comparing the measured and calculated 2D dose distribution for open beams the 6 MV does not fulfill the γ_2%,2mm for all accelerators for 15×15 cm² nor a γ_3%,2mm for the 20×20 cm² field size. Only data points that are off-axis fail. Along the major axes data agree well with the results of measurements in water. A comparison between the 2D measurements and calculated 2D dose distribution for the 15 MV open beams reveal a better result since all the accelerators pass γ_3%,2mm and only a few points for two accelerators for the 20x20 cm² field size fail γ_2%,2mm for all depths.

Figure 3.  Comparison between measured and calculated dose profiles at 10 cm depth for 6 and 15 MV open field. The lines correspond to the result of a γ_2%,2mm evaluation between the measured and calculated dose profiles for each accelerator. The solid (thin) lines represent accelerator 1–6 and the dotted (thick) lines represent accelerator 7–8.

The penumbra (20%–80%) for the eight accelerators were determined from the measured profiles for the 10x10 cm² field size. For the 6 MV beams the values are 4.4±0.4 mm for the upper jaws and 3.8±0.2 mm for the lower jaws. For 15 MV the corresponding values are 5.3±0.3 mm and 4.9±0.3 mm.

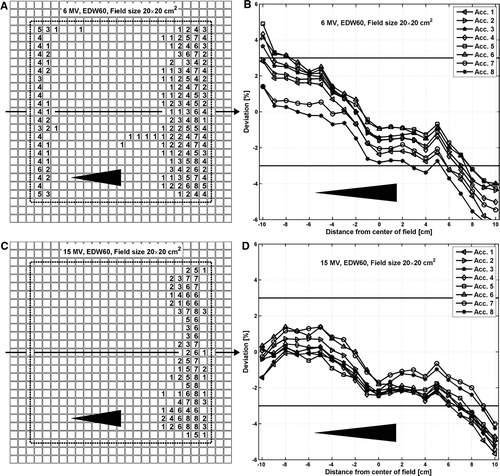
For wedged beams, the deviations among the accelerators are larger than for open beams. The measured data are generally within 2–3% for both the 6 MV and the 15 MV beams (Figure 4B, D). For the 60° enhanced dynamic wedge (EDW60), 6 MV beams, 15×15 and 20×20 cm² field sizes, most of the accelerators fail γ_3%,3mm in both the low and the high dose region (Figure 4A) when compared to the TPS calculations. Agreement is better for smaller wedge angles and smaller field sizes. For 15 MV, all the accelerators pass γ_3%,3mm for 15×15 cm² field size or smaller but fail in the low dose region for the 20×20 cm² field size (Figure 4C).

Figure 4.  Comparison between measured and calculated 2D absorbed dose distributions for the EDW60 beams at 10 cm depth for the 6 and 15 MV beams. Each square (?) in A and C corresponds to one of the 729 ionization chambers in the 2D array. The numbers within the squares correspond to the number of accelerators that fails the γ_%,3mm for that specific chamber. The dotted line indicates the field size. The percentage deviations between the measured and calculated dose distributions along the arrows in A and C, i.e. in the wedge direction at the center of the beam, are presented in B and D, respectively.

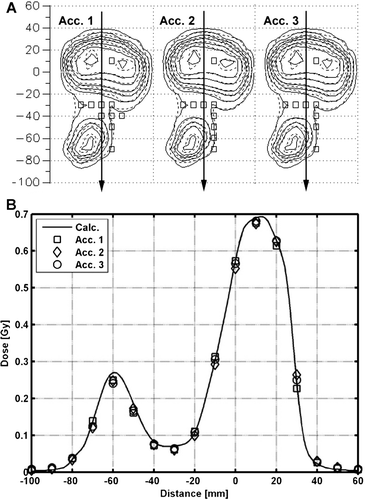
The comparison of a measured and a calculated dynamic IMRT field for three accelerators is presented in Figure 5. Both the profile (Figure 5B) and the 2D dose distribution (Figure 5A) demonstrate that measurements and the calculation agree well and that the accelerators are well matched. The γ_3%,3mm fail at exactly the same point in the high dose region for the three accelerators. Two additional points fail for accelerator 1 as compared to accelerator 2 and 3 in the lower dose area (Figure 5A). However, the dose in this area corresponds to about 5% of the maximum and the measurements are therefore very sensitive.

Figure 5.  Comparison between measured and calculated 2D dose distributions for an 15 MV IMRT field for three different accelerators measured at 5.5 cm depth and SSD = 94.5 cm. The squares (□) in A corresponds to ionization chambers in the 2D array that fails γ_3%,3mm. Solid and dashed lines in A corresponds to the measured and calculated data, respectively. The calculated and the measured dose profiles along arrows in A, perpendicular to the MLC, are presented in B.

Electrons

The largest deviation (M_R85, M_R50) is 0.7 mm for all electron energies and applicators when comparing the depth of the 85% (R₈₅) and the depth of the 50% dose (R₅₀) with the mean value (Table III). Also the output factors at d_max are in good agreement. The largest deviation of OF between any two accelerators is about 1% and compared to the mean OF the largest deviation (M_OF) is 0.6% (Table III). In addition, the profiles agree within a clinically acceptable level. Better agreement is generally found for smaller applicators (Figure 6). The largest deviation between profiles for any of two accelerators is less than 2%, and the agreement is generally within 1% for applicators smaller than 20x20 cm².

Figure 6.  12 MeV electron beam inline profiles from four linacs. Profiles are at z_ref for the 6×6, 10×10, 15×15, 20×20, and 25×25 cm² applicators. The profiles were first normalized to 100% at the central axis (CAX) then multiplied by the output factors. The curves are separated by shifting the 6×6, 10×10, 15×15, 20×20, and 25×25 cm² applicator and the difference at the CAX for one applicator corresponds to the difference in output factors between the different linacs.

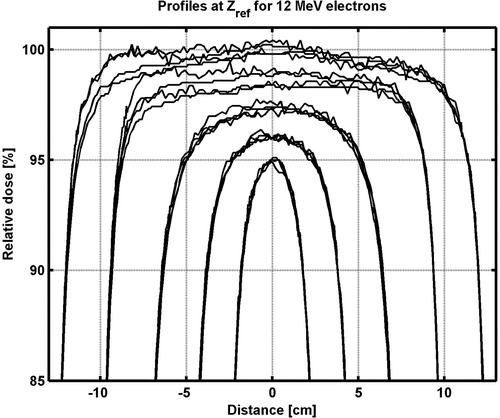
Table III.  The maximum deviation (M_R50, M_R85, and M_OF) between the individual values for R₅₀, R₈₅ and output factors (OF) for all accelerators compared to the mean value of the four accelerators (<R₅₀>, <R₈₅>, and <OF > ).

	Applicator size [cm x cm]
	6×6			10×10			15×15			20×20			25×25
	MR50 [mm]	MR85 [mm]	MOF [%]	MR50 [mm]	MR85 [mm]	MOF [%]	MR50 [mm]	MR85 [mm]	MOF [%]	MR50 [mm]	MR85 [mm]	MOF [%]	MR50 [mm]	MR85 [mm]	MOF [%]
E [MeV]	<R50> [mm]	<R85> [mm]	<OF>[ ]	<R50> [mm]	<R85> [mm]	<OF> [ ]	<R50> [mm]	<R85> [mm]	<OF> [ ]	<R50> [mm]	<R85> [mm]	<OF> [ ]	<R50> [mm]	<R85> [mm]	<OF> [ ]
6	+0.5	+0.4	±0.5	-0.3	±0.2	–	−0.3	−0.2	−0.2	−0.4	±0.3	−0.3	−0.7	−0.6	−0.5
	24.9	20.3	0.970	24.8	20.2	1.000	24.8	20.1	1.000	25.0	20.4	1.010	25.1	20.4	1.006
9	−0.3	−0.3	±0.1	±0.1	±0.1	–	±0.1	±0.1	±0.1	+0.2	±0.1	±0.1	±0.4	±0.4	±0.4
	36.8	30.3	0.984	37.0	30.4	1.000	37.1	30.5	0.997	37.0	30.4	0.984	37.2	30.6	0.965
12	−0.5	±0.3	±0.1	+0.3	+0.2	–	−0.2	−0.2	+0.2	±0.2	−0.1	+0.4	−0.6	−0.6	+0.4
	51.1	41.9	0.980	51.2	42.3	1.000	51.3	42.4	0.994	51.2	42.3	0.977	51.4	42.5	0.950
15	+0.6	±0.5	−0.6	±0.3	±0.3	–	−0.4	−0.3	+0.3	±0.1	±0.1	±0.3	±0.3	±0.3	+0.4
	63.1	50.7	0.985	63.8	52.2	1.000	63.9	52.4	0.989	63.6	52.0	0.973	64.0	52.5	0.942
18	±0.3	+0.4	−0.3	+0.1	+0.3	–	−0.2	+0.2	−0.3	−0.1	+0.1	±0.2	±0.3	+0.3	−0.3
	74.8	57.1	0.997	76.4	60.7	1.000	76.6	61.1	0.982	76.6	61.0	0.962	76.9	61.4	0.932

Discussion

We conclude that all photon and electron beams, except the 15 MV photon beam from accelerators no. 7 and 8, can be represented by one set of data. For 15 MV it might be necessary to implement an additional set of data in the TPS to represent the two deviant accelerators. To ensure a satisfactory beam-match the dose prediction (e.g. TPS calculations) must be adopted in the beam-matching procedure. Further, comparisons between measurements and calculations should be done in absolute dose terms.

The beam-matching performed during the CAP far from ensures that the linacs are matched to a clinically acceptable degree. The discrepancy in measured OF for accelerators no. 7 and 8 compared to the other accelerators is one example proving this. These two accelerators passed all tests in the CAP and showed results similar to all other accelerators. This illustrates that even if all relative comparisons, e.g. during the acceptance procedure, indicate a high-quality beam-match the result might turn out to be unacceptable when compared in absolute dose terms. Since the discrepancies in OF between accelerator no.7 and 8 and the other six are evident only for 15 MV our hypothesis is that this is due to a difference in the flattening filter.

A systematic deviation between TPS calculations and measurements is caused by a difference in the measured and calculated OF (Figure 2). However, this was expected. The OF was measured for FSD = 90 cm, at 10 cm depth. If isocentric OF is used as input to Eclipse the deviation between the calculated and measured dose for the calibration geometry (FSD = 100, 10 cm depth) will be around 0.5%. According to personal communication with the vendor, zero deviation for the calibration geometry can only be achieved if Eclipse OF are defined at d_max for FSD = 100 cm. Several possibilities exist to overcome the discrepancy. The OF can be found at d_max by direct measurements or calculations. The OF can be manually adjusted in the TPS until the match is improved. Alternatively, the calibration of the accelerators can be changed to minimize the difference. Since we will implement the Eclipse AAA calculation algorithm in the near future we expect to do neither.

Larger differences among the linacs for the measured profiles were observed for EDW60 beams than for open beams. The EDW delivery is more complicated than open beam delivery and the EDW beam profiles are more likely to be influenced by variations in beam spectrum and jaw calibration than open beams. Thus, slight difference in jaw calibration may cause some of the differences seen between the linacs for EDW delivery. However, any difference in jaw calibration between the accelerators used in this study reflects what one can expect in clinical practice since all jaws were well calibrated.

All electron beams utilized at our clinic today are calculated manually. In practice, the profiles are not used directly for selecting an applicator or insert although the necessary margins needed to achieve full coverage laterally are considered. The measurements for electrons reveals deviations smaller than 1% in OF and 1 mm in depth compared to the mean values of all accelerators. If more sophisticated treatment planning calculations are used to predict the dose, e.g. the Eclipse Electron Monte Carlo calculation algorithm, the matching of electron profiles with TPS calculations might be a matter of concern.

One approach to ensure a satisfactory beam-match could be to use one set of beam data from one linear accelerator as a reference. The other linac(s) should then be matched to this data set as closely as possible and within certain tolerance levels. However, it is equally important that the TPS calculated dose closely resembles the delivered dose from all accelerators. When one accelerator is used as a reference there is a risk that another accelerator will be considered well matched while it does not fulfill the requirements in terms of accuracy when compared with the TPS. For instance, if the TPS predicts a slightly higher dose than delivered by the reference linac and the other linac delivers a dose slightly lower than the reference linac, the two uncertainties add up. Therefore we advocate for the approach to include the TPS calculations in the beam-matching procedure as presented in this work.

In future QA procedures, we recommend using the TPS as reference. If the QA procedures reveal deviations that are too large to be ignored the procedure is to adjust the accelerator to fit the TPS instead of vice versa. Obviously, also comparisons between the different accelerators can be included in the QA procedures but either much narrower tolerance levels must be applied or a direct comparison with the TPS is needed in order to ensure that the deviations between calculated and delivered dose stay within acceptable limits.

Acknowledgements

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.