The first direct method of spot sparsity optimization for proton arc therapy

Introduction

Spot-scanning proton arc (SPArc) therapy was introduced in 2016 offering superior target conformity and simplifying the proton therapy treatment workflow [1,2]. It is considered an advanced intensity modulated proton therapy (IMPT) technique through arc trajectory optimization. This new approach allows the proton system to deliver the proton beam following a sequence of control points while the gantry continuously rotates around the patient.

One of the challenges in the clinical implementation of proton arc therapy is to minimize its beam delivery time (BDT), as the plan might contain numerous energy layers and spots. In the beginning stage of the pencil beam scanning (PBS) clinical implementation, energy layer switching time (ELST) is the bottleneck due to the technical limitation that prolongs the treatment delivery time. Thus, several studies focused on reducing energy layer switching time through energy sequence optimization [3–7]. However, a recent study [8] found that the BDT is approximately proportional to the spot number for IBA’s ProteusONE PBS proton therapy system in Beaumont where about half the treatment delivery time is spent on the spot switching [9]. It becomes a new bottleneck of SPArc therapy, which normally contains thousands of spots making it very challenging to deliver in a timely manner. Thus, it is critical to reducing the spot number while maintaining the optimal treatment plan quality.

Searching for the minimum spot number solution can be considered as a sparsity optimization problem [10,11], where the sparsity is the number of zero-valued elements divided by the total number of elements. The most natural measure of sparsity is the counting function $\left|\right|.|{|}_0,$ called usually the l₀-norm [12]. The l₀-norm counts the total number of nonzero elements of a vector (spots). Minimizing the number of nonzeroes of the solution (its l₀-norm) is a difficult nonconvex and non-deterministic polynomial-time hardness (NP hard) optimization problem [13,14]. One widely used replacement method is using l₁-norm [13,15] as convex approximation to the l₀-norm (See supplemental material for their comparison). Meanwhile, a novel primal dual active set (PDAS) algorithm was developed by Bergounioux et al. [16] and Ito et al. [11] to solve the nonsmooth optimization [17] (not necessarily differentiable optimization) problem. For l₀-regularized minimization problem, Jiao et al. [18] and Huang et al. [19] propose a PDASC algorithm, which couples the PDAS with a continuation strategy on the regularization parameter in outer iteration. Each inner iteration first identifies the active set from both primal and dual variables, then updates the primal variable by solving a (typically small) least-squares problem defined on the active set, from which the dual variable can be updated explicitly. It is observed that the PDASC algorithm yields optimal solutions that are comparable with other methods, e.g., OMP, CoSaMP, and AIHT [20], but usually with less computing time.

In this paper, we introduced the first optimization framework for SPArc by searching the optimal spot sparsity solution using PDASC or we called it SPArc-PDASC. The proposed study aims to solve the two main challenges (a) simultaneous optimization of treatment delivery efficiency and dosimetric plan quality; (b) optimization speed, the proposed approach can be hundreds of times more efficient. The successful integration of the PDASC algorithm into SPArc could serve as one option to provide more delivery-efficient plans.

Material and Methods

Problem formulation

Based on the previously studied beam delivery sequence model of the new generation of the single room system, Beaumont’s IBA ProteusONE, proton treatment delivery time is actually dominated by spot switching time (SSWT) [9]. SSWT is approximately linearly dependent on spot numbers [8]. Let $\mathit{w}={\left\{w_i\right\}}_{i=1}^n$ be the vector of spot intensity (MU), where n is the full (initial) spot number. Spot index set $\mathit{S}=\{1,2,\dots ,n\}.$ w_i = 0 means this spot has been removed. The true spots $w_i>0$ of nonzero MU form a primal dual active set denoted by $\mathrm{A}.$

Let $\mathbf{\Phi }\in {\mathbb{R}}^{m\times n}$ be kernel fluence matrix (also called the dose deposition matrix [21]) simulated using MatRad dose calculation engine [22], where m is the total number of voxels. Denote ${\mathit{p}}_0\in {\mathbb{R}}^m$ as prescribed dose vector. It is a common approach to minimize the least-squares fitting, i.e., $\frac{1}{2}\left|\right|\mathbf{\Phi }\mathit{w}-{\mathit{p}}_0|{|}_{l_2}^2$ [13,23]. Further, by utilizing the sparsity in $\mathit{w}\in {\mathbb{R}}^n,$ it is possible to introduce efficient solvers for the problem. In the work, to enforce a sparse solution to the objective function, we consider solving the following l₀-regularized optimization problem: (1a) $$\underset{\mathit{w}\in {\mathbb{R}}^n}{\text{minimize}} \frac{1}{2}\left|\right|\mathbf{\Phi }\mathit{w}-{\mathit{p}}_0|{|}_{l_2}^2+\lambda |\left|\mathit{w}\right|{|}_{l_0}$$(1a) (1b) $$\text{subject}\mathrm{ }\text{to} \mathit{w}\ge 0,$$(1b) where $\lambda >0$ is a regularization parameter, controlling the sparsity level of the regularized solution, and (1 b) follows from the fact that w is non-negative.

The necessary and sufficient condition for a coordinate-wise minimizer w to a problem (1a) is given by [18] (2) $$\{\begin{array}{c}|w_i+d_i|<\sqrt{2\lambda }\Rightarrow w_i=0\hfill \\ |w_i+d_i|=\sqrt{2\lambda }\Rightarrow w_i=0\mathit{\text{\hspace{1em}or\hspace{1em}}}{d}_i=0\hfill \\ |w_i+d_i|>\sqrt{2\lambda }\Rightarrow d_i=0\hfill \end{array}$$(2) where $\mathit{d}={\left\{d_i\right\}}_{i=1}^n={\mathbf{\Phi }}^T({\mathit{p}}_0-\mathbf{\Phi }\mathit{w})$ denotes the dual variable.

For (1 b), we can simply project the estimation of (1a) onto the space ${\mathbb{R}}_{+}^n.$

Algorithm procedure

Our algorithm includes an outer iteration and inner loop. The initial spot intensity is chosen as zero vector ${\mathit{w}}^0=\mathbf{0}.$ Regularization parameter is chosen among intervals ${\lambda }_{\min }\le \lambda \le {\lambda }_{\max }.$ In kth outer iteration ($k=1,2,\dots ,K_{\max }$), λ is given by (3) $${\lambda }^k=\frac{1}{2}\left|\right|{\mathbf{\Phi }}^T{\mathit{p}}_{\mathit{0}}|{|}_{l_{\infty }}\hspace{0.17em}\exp \hspace{0.17em}\left[\ln \hspace{0.17em}{\lambda }_{\max }-\frac{k-1}{K_{\max }-1}\ln \hspace{0.17em}\frac{{\lambda }_{\max }}{{\lambda }_{\min }}\right]$$(3)

At jth inner loop ($j=1,2,\dots ,J_{\max }$), it identifies the active set from primal variable ${\mathit{w}}^{j-1}$ and dual variable ${\mathit{d}}^{j-1}$ by condition (2): (4) $${\mathrm{A}}^j=\{i:|w_i^{j-1}+\eta d_i^{j-1}|>\sqrt{2{\lambda }_k}\},$$(4) where $\eta >0$ is a step size parameter to be adjusted when condition number of $\mathbf{\Phi }$ is large, ${\mathit{w}}^j$ and ${\mathbf{d}}^j$ are updated by solving a (typically small) least-squares problem defined on the dual active set:   $$\{\begin{array}{cc}{\mathit{w}}_{{\mathrm{A}}_j}^j=\mathbf{0}\hspace{1em}\hspace{1em}\text{(5a)}\hfill & \hfill \\ {\mathbf{\Phi }}_{{\mathrm{A}}^j}^T{\mathbf{\Phi }}_{{\mathrm{A}}^j}{\mathit{w}}_{{\mathrm{A}}^j}^j={\mathbf{\Phi }}_{{\mathrm{A}}^j}^T{\mathit{p}}_0\hfill & \text{(5b)}\hfill \\ {\mathit{d}}^j={\mathbf{\Phi }}^T({\mathit{p}}_{\mathit{0}}-\mathbf{\Phi }{\mathit{w}}^j)\hfill & \text{(5b)}\hfill \end{array}$$ 

 The complete procedure is summarized below:

Algorithm 1

SPArc-PDASC algorithm

• 1: Set parameter η,λ_min,λ_max, K_max and J_max.

• 2: for k = 1,2,…,K_max do

• 3:  Set λ^k by formula (3)

• 4:  for j = 1,2,…,J_max do

• 5:   Compute the ${\mathrm{A}}^j$ by (4)

• 6:   Check the inner stopping criterion ${\mathrm{A}}^{j-1}={\mathrm{A}}^j$

• 7:   Update the ${\mathit{w}}^j$ and ${\mathit{d}}^j$ by (5)

• 8:  end for

• 9:  Check sparsity for outer stopping criterion

• 10: end for

• 11: return $\mathit{w}=\max \{\mathit{w},\mathbf{0}\},$ the best solution found

We can adjust the outer stopping criterion in the loop to obtain the different sparsity level solutions.

Evaluation

Two clinical cases: One intracranial cancer case and one lung cancer case from a previous study [8] were used for the evaluation. For each patient, only the primary clinical target volume (CTV) was considered in the optimization. The prescription dose for the intracranial tumor is 54 Gy in 30 fractions (1.8 Gy per fraction) and for the lung tumor is 48 Gy in 4 fractions (12 Gy per fraction) using stereotactic body radiotherapy (SBRT) [24]. Their CT resolution is in 2.5 mm. Single arc was used in the planning. Other specific information is listed in supplemental material table 1.

The cumulative dose volume histogram (DVH) was plotted for evaluating the plan quality [25]. In addition, the optimization time is compared with the original SPArc algorithm (SPArc-original, [1]) which was implemented in a commercial treatment planning system (TPS) RayStation (RaySearch Laboratories AB, Stockholm, Sweden, ver. 6) through in-house scripts. The optimizer of RayStation RayOptimizer [26] utilizes the sequential quadratic programming (SQP) software package NPSOL [27] in which the SQP uses Broyden–Fletcher–Goldfarb–Shanno (BFGS) updates [21]. The sparsity optimization is implemented by gradually increasing the parameter of the minimal spot weight. It is one of the limitations when filtering out low-weight spots in RayStation which prohibits the user to reactive the filtered spots [28]. SPArc-original is an iterative approach, which will take much longer time to optimize. The objective function in RayStation is set as a uniform dose function, which penalizes the deviation from a certain dose level [29], to compare with l₂-norm objective term in PDASC.

Results

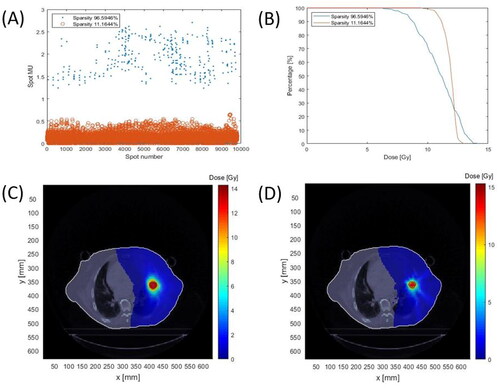
We obtained different sparsity-level solutions by manually adjusting the outer stopping criterion. Figure 1 showed the comparison between 96.6% high spot sparsity and 11.2% low sparsity for lung SBRT cases. Their optimized spot intensities were compared in Figure 1(A), which indicates that less spot number plan has greater intensity. The DVH is compared in Figure 1(B). High spot sparsity reduced the plan quality because of losing too much degree of freedom in terms of spot number. Their plan dose was demonstrated in Figure 1(C,D).

Figure 1. An example of comparison between high sparsity and low sparsity in a lung SBRT case. The prescription dose is 48 Gy and 12 Gy per fraction. (A) High sparsity resulted in a higher averaged spot MU. (B) Dose-volume histogram (DVH) per fraction shows low sparsity has better plan quality. (C) Dose distribution for 11.2% sparsity. (D) Dose distribution for 96.6% sparsity.

Supplemental material Figure s1 showed the comparison between 93.4% high spot sparsity plan and 11.7% low sparsity for the intracranial case. Figure s1A compared their spot MU. Since high sparsity plan has much fewer spot number, their spot MU (blue dot, around 0.2 MU) are greater than the low sparsity plan (red circle, around 0–0.05MU). Figure s1B compared their DVH. High spot sparsity (blue line) loses the plan quality due to the lack of optimization freedom from the limited spot number. Figures s1C and s1D show their plan dose. Spot MU in Figure (1(A)) (about 1.5–2.5MU for high sparsity plan and 0-0.5MU for low sparsity plan) is greater than in Figure s1A because SBRT has a lower number of fractions.

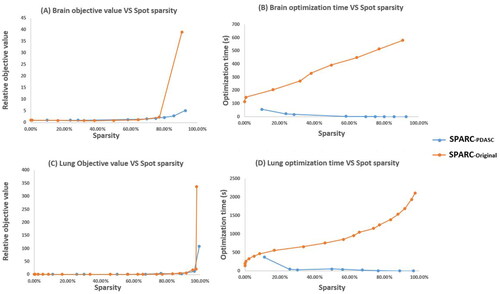
Figure 2 plotted the plan quality and optimization time with respect to different sparsity level for both intracranial and lung SBRT case, which are compared with SPArc-original implemented in RayStation. Figure 2(A,C) showed the plan quality degraded as the number of spots is reduced. The plan quality is measured by relative objective value, which is normalized by the lowest sparsity plan’s clinic objective value at each case for different methods separately. Compared to SPArc-original, SPArc-PDASC was able to find a better plan quality with the same spot sparsity, which could be critical to the SPArc therapy. In the optimization speed evaluation (Figure 2(B,D)), the study found that the PDASC could significantly reduce the optimization time: this new planning framework could effectively improve the optimization speed by a factor of about three hundred on average (8.8 times to 536.5 times from 20%-80% sparsity) compared to the SPArc-original implemented in RayStation. Opposite to RayStation’s sparsity optimization through filtering spot from low sparsity to high sparsity, SPArc-PDASC searches the global sparsity solution from its zero initial solution. The higher the sparsity, the less optimization time PDASC spends. This can be theoretically explained by Jiao et al. [18]: there is an important monotonicity relationship on the active set during the PDASC iteration. The greater the active set size is, the greater the computation complexity will be (See supplemental material for complexity analysis).

Figure 2. Compared with SPArc-original implemented in RayStation (Stockholm, Sweden). (A) Brain case objective value vs. sparsity curve using SPArc-PDASC. (B) Brain otimization time vs. sparsity curve. (C) Lung SBRT case objective value vs. sparsity curve using SPArc-PDASC. (D) Lung SBRT optimization time vs. sparsity curve.

Discussion

Shortening the beam delivery time (BDT) is important to radiation therapy which can be used to mitigate the intra-factional motion [30] and improve the treatment throughput. PDASC combines the fast local convergence of the active set technique and the globalizing property of the continuation technique for sparsity optimization, which demonstrates its value in proton arc optimization and plan generation. The study demonstrated that the BDT could be shortened through PDASC with a faster optimization speed compared to the SPArc-original. However, too many constraints on the BDT might affect the plan quality as the treatment plan starts losing degrees of freedom in terms of the number of spots. An optimal proton arc therapy plan is to find a tradeoff between the plan quality and BDT. In our institution’s proton delivery system, the BDT is reduced by decreasing the spot number through sparsity optimization. In reality, a tradeoff might consist of a series of solutions, which could be given by Pareto surface through multi-criterion optimization (MCO) [31]. PDASC could provide a proper optimizer for MCO search, i.e., the individual point on a Pareto surface.

In the clinic, only spot with MU being greater than a machine threshold can be delivered. PDASC has separation from zero property [18]: (6) $$\underset{{}_{i\in A}}{\min }{w}_i\ge \sqrt{2\lambda }$$(6)

But λ could be finally chosen as a very small value in PDASC iteration, which might not satisfy the machine threshold. How to choose the proper stopping criterion to meet the machine threshold might be a potential improvement to this algorithm.

One limitation of this work is that robustness optimization is not considered in this method. The difficulty is how the mathematically-defined robustness in this PDASC optimization formulation remains uncleared, which will be the focus of the next development (See supplemental material for more discussion). Another limitation of this paper is only investigating spot numbers without considering the spot scanning paths. Different scanning paths lead to different dose distributions and BDT due to the contribution of the unintended transit dose and spot swi time between spots [32]. A simulated annealing algorithm has been applied to scanning path optimization of particle therapy beams [33]. It is a heuristic algorithm to optimize the scanning path for quasi-discrete scanned beams. PDASC used in this paper might provide a methodology for a direct method for proton arc spot scanning path optimization.

Conclusion

The study developed the first fast-planning framework for proton arc therapy spot-sparsity optimization. Such advancement in spot-sparsity optimization is critical to the SPArc therapy for an efficient treatment delivery with a balanced plan quality. This work also paves the roadmap for clinical implementation in the TPS platform efficiently.

Disclosure statement

The corresponding author X.D report honorarium from the Ion Beam Applications (IBA) and ELEKTA speaker Bureau.

Data availability statement

The data that support the findings of this study are available from the corresponding author, X.D, upon reasonable request.

Additional information

Funding

G.L is supported by the National Natural Science Foundation of China (No.12005072). L.Z is supported by Beaumont Seed Grant Award. This work was supported by William Beaumont Hospital.