A splitting algorithm for simulation-based optimization problems with categorical variables

ABSTRACT

In the design of complex products, some product components can only be chosen from a finite set of options. Each option then corresponds to a multidimensional point representing the specifications of the chosen components. A splitting algorithm that explores the resulting discrete search space and is suitable for optimization problems with simulation-based objective functions is presented. The splitting rule is based on the representation of a convex relaxation of the search space in terms of a minimum spanning tree and adopts ideas from multilevel coordinate search. The objective function is underestimated on its domain by a convex quadratic function. The main motivation is the aim to find—for a vehicle and environment specification—a configuration of the tyres such that the energy losses caused by them are minimized. Numerical tests on a set of optimization problems are presented to compare the performance of the algorithm developed with that of other existing algorithms.

KEYWORDS:

• Design optimization
• simulation-based optimization
• splitting
• categorical variables
• tyres

1. Introduction

A new discrete search algorithm for solving design optimization problems with simulation-based objective functions is proposed. The research leading to this article is motivated by the optimization of truck tyres selection (see Lindroth 2012; Šabartová et al. 2014). The purpose is to enable—for each combination of truck configuration and operating environment—the identification of a tyres configuration that minimizes the energy losses caused by the tyres. The tyres for the individual truck axles are to be chosen from a tyre database. Each tyre is specified by the values of so-called tyre design variables and the truck tyres selection problem involves computationally expensive black-box simulations (Nedělková et al. 2016).

A splitting algorithm to explore the multidimensional discrete search space of design points for the tyres selection problem as well as other simulation-based optimization problems with categorical variables is developed and presented. The splitting strategy used in the algorithm developed is inspired by that presented by Fuchs and Neumaier (2010a); it uses only the objective function evaluations and is therefore applicable to simulation-based optimization problems. The strategy exploits the structure of a convex relaxation of the discrete search space, represented by a minimum spanning tree among the edges of a complete graph defined on the design points (see Graham and Hell 1985). The use of this knowledge may have significant advantages, since the objective function typically depends more on the selection of the design point rather than on the values of the integer choices stemming from numbering of the design points and not representing any physical entity. The splitting strategy is complemented by a global underestimation of the objective function in order to determine approximate lower bounds along the search tree. The bounds are then used within a multilevel coordinate search (see Huyer and Neumaier 1999) to decide on which node of the search tree to split. A pattern search algorithm (see Audet and Dennis Jr 2004) is used to obtain a feasible solution from a relaxed solution and also to improve the current smallest objective value.

Utilizing a variety of both artificial and real test problems, differing with respect to both mathematical properties and sizes, the performance of the algorithm developed is compared with that of other existing algorithms that can be used to solve simulation-based optimization problems with categorical variables. It is concluded that the algorithm developed outperforms the other algorithms tested.

1.1. Previous work

In design optimization (see, e.g., Alexandrov and Hussaini 1997; Neumaier et al. 2007; Fuchs et al. 2008) a design choice is typically modelled by a categorical variable, i.e. an integer variable arising from reformulations of discrete multidimensional sets of design points. Depending on the mathematical properties of the objective function and the constraints, the resulting problem falls into one of several classes of mixed integer optimization problems. For each such class identified, algorithms exist that employ splitting of the search space.

For studies of efficient search space splitting methods, see Floudas (1995, Chap. 5) and Nemhauser and Wolsey (1999, Chap. II.4) for mixed integer linear optimization, and Leyffer (1993) and Tawarmalani and Sahinidis (2004) for mixed integer nonlinear optimization. Splitting in simulation-based optimization with continuous variables only is studied in Jones, Perttunen, and Stuckman (1993) and Huyer and Neumaier (1999). For a survey on discrete optimization, including splitting methods, see Parker and Rardin (2014, Chaps 1 and 5).

1.2. Motivation

The present sales tool at Volvo Group Trucks Technology (Volvo GTT) generates a large set of feasible tyres for each truck; these tyres are suitable for their potential utilization and fit the truck dimensionally. The truck tyres selection process is then based on experience and customer input, which can be improved further by means of scientific methodologies. A goal for Volvo GTT is to find an optimal configuration of the tyres for each vehicle configuration and operating environment specification such that the energy losses caused by the tyres are minimized. Each tyre is determined by specific values of tyre design variables (tyre diameter, tyre width, tread depth, and inflation pressure) and an extensive tyre database is available; see Šabartová (2015) for details.

To support the truck tyres selection process, an optimization model has been developed by Nedělková, Lindroth, and Jacobson (2017) with the aim of determining an optimal set of tyres for each vehicle and operation specification. A complex, interacting set of vehicle, tyres and operating environment was modelled in order to evaluate the fuel consumption. Each evaluation of the objective function requires a significant computational effort. One can afford to evaluate the objective function and constraints only for a limited number of sample points (settings of tyre design variables). Moreover, the tyres to be selected are described by a set of discrete variables. Therefore, an efficient optimization algorithm to find the optimal tyres configuration—even for one customer having a specific vehicle configuration and operating environment—is needed.

The algorithm presented in this article can be used to solve any simulation-based optimization problem with categorical variables. Applications include the component selection problem (Carlson 1996), vehicle design (Alexandrov and Hussaini 1997, 3–21), optimal design of large engineering systems in general (Alexandrov and Hussaini 1997, 209–226), surface structure determination for nanomaterials (Zhao, Meza, and Van Hove 2006), space system design (Fuchs et al. 2008) and the optimization of thermal insulation systems (Abhishek, Leyffer, and Linderoth 2010).

1.3. Outline

This article is organized as follows. In Section 2, the design optimization problem with a simulation-based objective function considered is described, as well as basic principles and terminology of the splitting algorithm and a means to underestimate the objective function. The splitting strategy is introduced in Section 3. The local search algorithm used along the search tree is explained in Section 4. The resulting splitting algorithm is described in Section 5. Numerical tests of the suggested algorithm and other competing algorithms are presented in Section 6. Section 7 provides conclusions as well as topics for future research.

2. Design optimization

Design optimization problems typically involve categorical variables. The case when the discrete choice modelled by the categorical variable has a natural ordering that can be associated with integer values is considered, because then a reformulation into an integer optimization problem can be performed.

2.1. Problem formulation

Let $\mathbf{x}=(x_1,\dots ,x_m)$ be a vector of discrete choice variables, where $x_i\in X_i:=\{1,\dots ,N_i\}$, i.e. $X_i$ is the choice domain¹ of $x_i$, $i=1,\dots ,m$. Then, $X:=X_1\times \cdots \times X_m$ is the discrete domain of possible choices of $x$. Each choice variable $x_i$ determines the values of the $n_i$ components of a vector ${\mathbf{z}}^i\in {\mathbb{R}}^{n_i}$, where $\sum _{i=1}^m{n}_i=n$. The composite vector $\mathbf{z}=({\mathbf{z}}^1,\dots ,{\mathbf{z}}^m)\in {\mathbb{R}}^n$ denotes the argument of the simulation-based function $F:{\mathbb{R}}^n\mapsto \mathbb{R}$. For each $i=1,\dots ,m$, the so-called table mapping² $Z_i:\mathbb{R}\mapsto {\mathbb{R}}^{n_i}$ transforms the set $X_i$ of discrete choices into the multivariate discrete design domain $\left\{Z_i\right(j):j\in X_i\}$. The design optimization problem is now formulated as (1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) (1b) $\mathrm{subject}\mathrm{to}{\mathbf{z}}^i=Z_i\left(x_i\right),i=1,\dots ,m,$(1b) (1c) $x_i\in X_i,i=1,\dots ,m.$(1c)

Example

Consider a heavy vehicle with m=2 axles; then $X=X_1\times X_2$. Each axle is equipped with two identical tyres. For example, if ten tyres feasible for the front axle and five for the rear axle are available, then $x_1\in X_1:=\{1,\dots ,10\}$ and $x_2\in X_2:=\{1,\dots ,5\}$. The choice of $x_1$ ($x_2$) determines the values of tyre width, tyre diameter, and inflation pressure for the tyres mounted on the front (rear) axle. The resulting vector $\mathbf{z}$ with six components is the argument of the objective function F, which represents the fuel consumption for the selected tyre configuration.

2.2. A splitting algorithm for design optimization

A widely used method to solve global optimization problems is branch-and-bound (Horst and Tuy 1996, Chap. 4, and Locatelli and Schoen 2013, Chap. 5), where the idea is to split the feasible region into smaller subregions and solve what is called a subproblem, i.e. a relaxed (simplified) problem in each subregion. The splitting stops when the best solution found is located in a sufficiently small subregion, such that the prescribed solution accuracy is guaranteed. The splitting is accomplished by adding constraints to the relaxed problem. In order to manage the extra constraints, a search tree is created. This tree is defined by nodes representing subproblems and edges representing the constraints corresponding to the splitting added to define new subproblems. The very first node in the search tree is called the root node. See Nemhauser and Wolsey (1999, Chap. I.3) and Žilinskas (2008) for more details and examples.

In general branch-and-bound algorithms, a lower bound on the optimal value of the objective function over a subregion may be used to indicate the subregions which can be discarded early in the procedure, so that only part of the search tree has to be generated and processed. The bounding procedures are only applicable if enough information about the mathematical properties of the objective function is available, since generally tight and reliable underestimating functions have to be computed. For the simulation-based optimization problems studied in this article, with no known mathematical properties, the lower bounds on the approximation of the objective function can be used only to guide the splitting.

Considering the optimization problem (1(1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) ), a splitting algorithm is formulated in which a convex relaxation of problem (1(1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) ) is solved in each subregion. An iteration of the algorithm then processes a node in the search tree, representing a not yet explored subregion of the feasible region. Each iteration of the splitting algorithm corresponds to a node in the search tree and has six main steps, which are detailed in Algorithm 1.

The lower bounds on the objective function value in the subregions are used to choose the next tree node to process. A local search is used to find a feasible design nearest to the solution from step 3 of Algorithm 1 and also to improve it if possible. A feasible design is evaluated if the value of F at that solution is already known. All evaluated feasible designs are stored in an auxiliary list. To select the tree node to process, a multilevel coordinate search (Huyer and Neumaier 1999) is used. At the selected node the search tree is branched into two child nodes. Nodes with no child nodes will henceforth be called leaf nodes. The notation $X_i^s\subseteq X_i$ to denote the restricted choice domain is also introduced, i.e. the set of feasible choices, for node s.

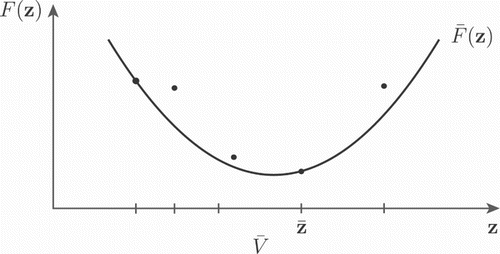
2.3. A convex underestimation of the objective function

As part of formulating a convex relaxation of problem (1(1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) ), its generally non-convex objective function F is approximated and underestimated by a convex quadratic underestimator³ $\overline{F}:{\mathbb{R}}^n\mapsto \mathbb{R}$, defined as $\overline{F}\left(\mathbf{z}\right):={\mathbf{z}}^{\mathrm{T}}\mathbf{A}\mathbf{z}+{\mathbf{b}}^{\mathrm{T}}\mathbf{z}+c$, over a subset of ${\mathbb{R}}^n$. Let $S_{+}^n:=\{\mathbf{A}\in {\mathbb{R}}^{n\times n}|\mathbf{A}={\mathbf{A}}^{\mathrm{T}},\mathbf{A}⪰0\}$ denote the set of symmetric positive semi-definite matrices of dimension $n\times n$. The coefficients $\mathbf{A}\in S_{+}^n$, $\mathbf{b}\in {\mathbb{R}}^n$, and $c\in \mathbb{R}$ are computed through the solution of the SemiDefinite optimization Problem (SDP, see Wolkowicz, Saigal, and Vandenberghe 2012) to (2a) $\underset{\mathbf{A}\in S_{+}^n,\mathbf{b}\in {\mathbb{R}}^n,c\in \mathbb{R}}{\mathrm{minimize}}\sum _{\mathbf{z}\in \overline{V}}\left[F\right(\mathbf{z})-{\mathbf{z}}^{\mathrm{T}}\mathbf{A}\mathbf{z}-{\mathbf{b}}^{\mathrm{T}}\mathbf{z}-c],$(2a) (2b) $\mathrm{subject}\mathrm{to}F\left(\mathbf{z}\right)\ge {\mathbf{z}}^{\mathrm{T}}\mathbf{A}\mathbf{z}+{\mathbf{b}}^{\mathrm{T}}\mathbf{z}+c,\mathbf{z}\in \overline{V},$(2b) (2c) $F\left(\overline{\mathbf{z}}\right)={\overline{\mathbf{z}}}^{\mathrm{T}}\mathbf{A}\overline{\mathbf{z}}+{\mathbf{b}}^{\mathrm{T}}\overline{\mathbf{z}}+c,$(2c) where $\overline{V}\subset {\mathbb{R}}^n$ is a set of sample points and $\overline{\mathbf{z}}\in \overline{V}$ is a reference point; see Figure 1. The function $\overline{F}$ is called the underestimator of F even though it is guaranteed to underestimate F (i.e. $\overline{F}$ has lower values than F) only on the sample set $\overline{V}$, on which the accuracy of fit and the degree of underestimation is strongly dependent. To guarantee the existence of a solution to optimization problem (2(2a) $\underset{\mathbf{A}\in S_{+}^n,\mathbf{b}\in {\mathbb{R}}^n,c\in \mathbb{R}}{\mathrm{minimize}}\sum _{\mathbf{z}\in \overline{V}}\left[F\right(\mathbf{z})-{\mathbf{z}}^{\mathrm{T}}\mathbf{A}\mathbf{z}-{\mathbf{b}}^{\mathrm{T}}\mathbf{z}-c],$(2a) ), the reference point is chosen as $\overline{\mathbf{z}}\in {\arg min}_{\mathbf{z}\in \overline{V}}F\left(\mathbf{z}\right)$.

Figure 1. Illustration of the quadratic underestimating function $\overline{F}$. The objective function F is evaluated at the set of sample points $\overline{V}$ (illustrated by the dots).

The function $\overline{F}$ is constructed using $|\overline{V}|=2\left(n\right(n+1)/2+n+1)$ sample points through the solution of optimization problem (2(2a) $\underset{\mathbf{A}\in S_{+}^n,\mathbf{b}\in {\mathbb{R}}^n,c\in \mathbb{R}}{\mathrm{minimize}}\sum _{\mathbf{z}\in \overline{V}}\left[F\right(\mathbf{z})-{\mathbf{z}}^{\mathrm{T}}\mathbf{A}\mathbf{z}-{\mathbf{b}}^{\mathrm{T}}\mathbf{z}-c],$(2a) ), having $n(n+1)/2+n+1$ variables. The sample points are selected from the evaluated feasible designs. If not enough many feasible designs are available, then they are extended with infeasible designs.

Optimization problem (2(2a) $\underset{\mathbf{A}\in S_{+}^n,\mathbf{b}\in {\mathbb{R}}^n,c\in \mathbb{R}}{\mathrm{minimize}}\sum _{\mathbf{z}\in \overline{V}}\left[F\right(\mathbf{z})-{\mathbf{z}}^{\mathrm{T}}\mathbf{A}\mathbf{z}-{\mathbf{b}}^{\mathrm{T}}\mathbf{z}-c],$(2a) ) is put into standard form by introducing the notation $\mathbf{\Lambda }\left(\mathbf{z}\right):=\mathbf{z}{\mathbf{z}}^{\mathrm{T}}$ and $\mathrm{tr}(\cdot )$ denoting the trace of a square matrix, and reaching the identity $\overline{F}\left(\mathbf{z}\right)=\mathrm{tr}\left(\mathbf{A}\mathbf{\Lambda }\right(\mathbf{z}\left)\right)+{\mathbf{b}}^{\mathrm{T}}\mathbf{z}+c$ (see Boyd and Vandenberghe 2004, Chap. 4.6.2]) and solved by a standard SDP solver. Furthermore, optimization problem (2(2a) $\underset{\mathbf{A}\in S_{+}^n,\mathbf{b}\in {\mathbb{R}}^n,c\in \mathbb{R}}{\mathrm{minimize}}\sum _{\mathbf{z}\in \overline{V}}\left[F\right(\mathbf{z})-{\mathbf{z}}^{\mathrm{T}}\mathbf{A}\mathbf{z}-{\mathbf{b}}^{\mathrm{T}}\mathbf{z}-c],$(2a) ) can be restricted by utilizing a sparsity pattern for the Hessian of $\overline{F}$ (Coleman, Garbow, and Moré 1985). For the case of a diagonal Hessian, the conditions on positive definiteness reduce to lower bounds on the coefficients A, which means that SDP (2(2a) $\underset{\mathbf{A}\in S_{+}^n,\mathbf{b}\in {\mathbb{R}}^n,c\in \mathbb{R}}{\mathrm{minimize}}\sum _{\mathbf{z}\in \overline{V}}\left[F\right(\mathbf{z})-{\mathbf{z}}^{\mathrm{T}}\mathbf{A}\mathbf{z}-{\mathbf{b}}^{\mathrm{T}}\mathbf{z}-c],$(2a) ) is reduced to a separable linear optimization problem. Note that, even when the underlying objective function F has no sparsity pattern, the use of the underestimator $\overline{F}$ with a sparse Hessian can still be efficient, as illustrated by the numerical results in Section 6.5.

If the objective function F is convex quadratic or linear, then the convex function $\overline{F}$ is an exact underestimator, thus providing lower bounds on the optimal objective value of problem (1(1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) ). These lower bounds can be used to eliminate portions of the feasible region, thus turning the suggested splitting algorithm into a branch-and-bound algorithm.

3. A convex relaxation based splitting strategy

The splitting strategy for each node s in the search tree, whose feasible region is denoted $X_s$, is derived from Fuchs and Neumaier (2010b) and consists of the following three parts.

1. A convex relaxation of optimization problem (1(1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) ) is constructed, with the objective function $\overline{F}$ (see Section 2.3) and the feasible region $\mathrm{conv}{X}^s$, where ‘$\mathrm{conv}$’ denotes convex hull and $X^s:=X_1^s\times \cdots \times X_m^s$.

2. One choice domain $X_i^s$ is selected for splitting.

3. In the design domain $\left\{Z_i\right(j):j\in X_i^s\}$, construct a complete graph⁴ on the designs feasible at node s and its minimum spanning tree. A split of the feasible region into two subregions is then defined by this tree along with an optimal solution to the convex relaxation of problem (1(1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) ).

Fuchs and Neumaier (2010b) approximate the objective function by a linear combination of the function values evaluated and apply a splitting strategy, denoted balanced split and presented in Section 3.1. They also add a penalty term (i.e. a regularization) to the objective function in order to receive a selection of boundary solutions. In contrast, the algorithm developed in this article uses a quadratic approximation of the black-box objective function without any penalty parameters, and a splitting method denoted nearest edge projection, described in Section 3.2.

The relaxation of problem (1(1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) ), restricted to a node s, is (3a) $\underset{\mathbf{v},\mathit{\lambda }}{\mathrm{minimize}}\overline{F}({\mathbf{v}}^1,\dots ,{\mathbf{v}}^m),$(3a) (3b) $\mathrm{subject}\mathrm{to}{\mathbf{v}}^i=\sum _{j\in X_i^s}{\lambda }_i^j{Z}_i\left(j\right),i=1,\dots ,m,$(3b) (3c) $\sum _{j\in X_i^s}{\lambda }_i^j=1,i=1,\dots ,m,$(3c) (3d) ${\lambda }_i^j\ge 0,j\in X_i^s,i=1,\dots ,m,$(3d) where $\overline{F}$ is the underestimator of F presented in Section 2.3. The solution to optimization problem (3(3a) $\underset{\mathbf{v},\mathit{\lambda }}{\mathrm{minimize}}\overline{F}({\mathbf{v}}^1,\dots ,{\mathbf{v}}^m),$(3a) ), in terms of ${\mathbf{v}}^i\in {\mathbb{R}}^{n_i}$, $i=1,\dots ,m$, is a convex combination of the designs $Z_i\left(j\right)$, $j\in X_i^s$. The values of the convex combination coefficients ${\lambda }_i^j$, $j\in X_i^s$, $i=1,\dots ,m$, are further used to determine the splitting of the choice domain $X_i^s$, where i is chosen to fulfil the inclusion (4) $i\in \underset{k\in \{1,\dots ,m\}}{\arg max}\left\{|X_k^s|\right\}.$(4)

3.1. Balanced splitting strategy

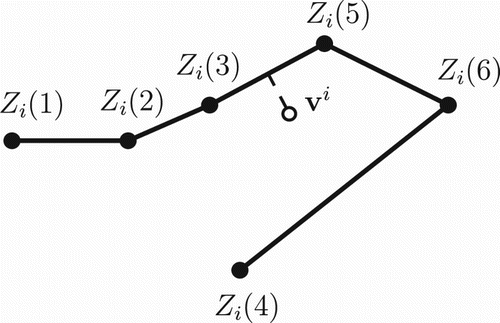
The balanced splitting strategy by Fuchs and Neumaier (2010b) is stated next, for completeness. For each $i\in \{1,\dots ,m\}$, consider the ith coordinate $x_i\in X_i^s$. The minimum spanning tree corresponding to the designs $Z_i\left(X_i^s\right):=\left\{Z_i\right(j)\mid j\in X_i^s\}\subset {\mathbb{R}}^{n_i}$ is constructed. For any fixed edge k in the graph of the tree corresponding to $Z_i\left(X_i^s\right)$, the set of all designs on the left (right) side of the edge k is denoted by $Z_i^{k1}$ ($Z_i^{k2}$). In Figure 2, let k be the edge (3–5), then $Z_i^{k1}=\left\{Z_i\right(1),Z_i(2),Z_i(3\left)\right\}$, and $Z_i^{k2}=\left\{Z_i\right(4),Z_i(5),Z_i(6\left)\right\}$.

Figure 2. Illustration in ${\mathbb{R}}^2$ of the nearest edge projection splitting strategy. The split is identified across the edge $Z_i\left(3\right)$–$Z_i\left(5\right)$ of the minimum spanning tree corresponding to the designs $Z_i\left(X_i^s\right)=\left\{Z_i\right(1),\dots ,Z_i(6\left)\right\}$ by projecting (illustrated by the dashed line) the solution to (3(3a) $\underset{\mathbf{v},\mathit{\lambda }}{\mathrm{minimize}}\overline{F}({\mathbf{v}}^1,\dots ,{\mathbf{v}}^m),$(3a) ), in terms of ${\mathbf{v}}^i$, onto the tree.

For every edge k in the minimum spanning tree corresponding to $Z_i\left(X_i^s\right)$, the sums $w_i^{k1}$ and $w_i^{k2}$ of the weights of all designs in $Z_i^{k1}$ and $Z_i^{k2}$, respectively, are computed as (5) $w_i^{k1}:=\sum _{\{j\in X_i^s|Z_i(j)\in Z_i^{k1}\}}{\lambda }_i^j\mathrm{and}{w}_i^{k2}:=\sum _{\{j\in X_i^s|Z_i(j)\in Z_i^{k2}\}}{\lambda }_i^j.$(5) In the balanced splitting strategy, the feasible region $X_i^s$ is split into two subregions $X_i^{s1}=\{j\in X_i^s\mid Z_i(j)\in Z_i^{k1}\}$ and $X_i^{s2}=\{j\in X_i^s\mid Z_i(j)\in Z_i^{k2}\}$ across the edge k, such that the weights $w_i^{k1}$ and $w_i^{k2}$ are as close as possible to 1/2.

3.2. Nearest edge projection splitting strategy

The optimal solution to optimization problem (3(3a) $\underset{\mathbf{v},\mathit{\lambda }}{\mathrm{minimize}}\overline{F}({\mathbf{v}}^1,\dots ,{\mathbf{v}}^m),$(3a) ) is non-unique if the number of evaluated and feasible designs is at least n+2, or if the evaluated designs span a space of dimension at most n. In such a case, no unique edge exists for the balanced splitting strategy. Since it is not clear from Fuchs and Neumaier (2010b) in what sense a balanced split provides an efficient splitting strategy, a more basic splitting strategy is proposed.

The nearest edge projection splitting strategy starts with the construction of the minimum spanning tree corresponding to the designs $Z_i\left(X_i^s\right):=\left\{Z_i\right(j)\mid j\in X_i^s\}\subset {\mathbb{R}}^{n_i}$. The edge defining the split is then identified by projecting the optimal solution to optimization problem (3(3a) $\underset{\mathbf{v},\mathit{\lambda }}{\mathrm{minimize}}\overline{F}({\mathbf{v}}^1,\dots ,{\mathbf{v}}^m),$(3a) ) onto the minimum spanning tree (in terms of Euclidean distance in the z-space); see Figure 2. In case of ties concerning which edge is closest to the relaxed solution, the first edge in a list of the minimum spanning tree edges is chosen.

The idea of splitting the feasible region $X_i^s$ in the vicinity of the optimal solution of optimization problem (3(3a) $\underset{\mathbf{v},\mathit{\lambda }}{\mathrm{minimize}}\overline{F}({\mathbf{v}}^1,\dots ,{\mathbf{v}}^m),$(3a) ) is motivated by the fact that the area of convex hull of the two resulting feasible subregions $X_i^{s1}$ and $X_i^{s2}$ of child nodes will be significantly reduced at the split, which increases the probability of the relaxed solution to optimization problem (3(3a) $\underset{\mathbf{v},\mathit{\lambda }}{\mathrm{minimize}}\overline{F}({\mathbf{v}}^1,\dots ,{\mathbf{v}}^m),$(3a) ) being closer to the optimal solution to problem (1(1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) ).

3.3. Selection of node to split

The choice of tree node to process in the search tree (i.e. step 1 of Algorithm 1) has an impact on the performance of Algorithm 1. Instead of general depth-first or breadth-first strategies (e.g. Nemhauser and Wolsey 1999, Chap. II.4]) the strategy presented below is based on the multilevel coordinate search algorithm (Huyer and Neumaier 1999).

The idea is to generate a so-called record list (denoted by R) of tree nodes scheduled for future selection of searching and splitting. Once a node is processed, it is removed from the list. When all nodes are processed and the list is empty, a new list is created based on the updated search tree. The record list is computed as follows.

Let N denote the set of all nodes in the tree that are created so far, and let $J\subseteq N$ denote the set of leaf nodes, i.e. the nodes that are not yet split. The level ${\ell }_j$ of node $j\in N$ denotes the number of times the node j has been split, where ${\ell }_j\in \{0,\dots ,{\ell }^{\max }\}$ and ${\ell }^{\max }+1$ is the maximum number of levels in the tree. The root node, i.e. node 1, belongs to level ${\ell }_1=0$ and the splitting of a node j results in two child nodes at level ${\ell }_j+1$. Let $L:=\bigcup _{j\in J}\left\{{\ell }_j\right\}\subseteq \{0,\dots ,{\ell }^{\max }\}$ denote the set of levels containing at least one leaf node and let $I_l:=\{j\in J|{\ell }_j=l\}$ denote the set of leaf nodes at level $l\in L$.⁵ Letting ${\overline{F}}_i$ denote the optimal value of optimization problem (3(3a) $\underset{\mathbf{v},\mathit{\lambda }}{\mathrm{minimize}}\overline{F}({\mathbf{v}}^1,\dots ,{\mathbf{v}}^m),$(3a) ) for leaf node $i\in J$, the record list is then defined as (6) $R:=\bigcup _{l\in L}\left\{\underset{i\in I_l}{\mathrm{argmin}}\left\{{\overline{F}}_i\right\}\right\}.$(6)

The fact that the leaf nodes at all levels in L are included in the record list ensures a mix of global and local search: the selection of the nodes with the lowest levels constitutes the global search, while the selection of the nodes with the lowest values of ${\overline{F}}_i$, $i\in J$, constitute the local search.

4. Local search

In Algorithm 1, a local search is performed when the feasible design that is nearest to the optimal solution of problem (3(3a) $\underset{\mathbf{v},\mathit{\lambda }}{\mathrm{minimize}}\overline{F}({\mathbf{v}}^1,\dots ,{\mathbf{v}}^m),$(3a) ) is to be found in each node being processed and also to improve the lowest objective function value in each subproblem. The direct search algorithm pattern search, originating from Box (1957) and described in detail by Audet and Dennis Jr (2004), was implemented because of its simplicity. Within a certain neighbourhood of the current design, it searches for a design with a lower objective value. The finite set of neighbouring design points is determined by a prefixed or random pattern. Pattern search does not require gradient information for the objective function, and the algorithm is robust and flexible (Audet and Dennis Jr 2006).

5. Splitting algorithm for simulation-based optimization problems with categorical variables: quadDS

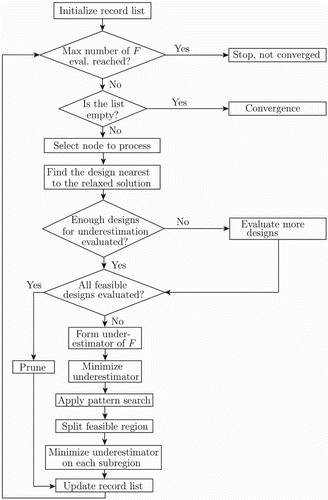
The splitting algorithm for simulation-based optimization problems with categorical variables developed in this article is called ‘quadDS’ (quadratically underestimating discrete search). A flowchart of the algorithm is provided in Figure 3. The terms used in the flowchart are interpreted below.

1. Initialize record list. For each node $i\in R$, store the optimal value of problem (3(3a) $\underset{\mathbf{v},\mathit{\lambda }}{\mathrm{minimize}}\overline{F}({\mathbf{v}}^1,\dots ,{\mathbf{v}}^m),$(3a) ), denoted ${\overline{F}}_i$, i.e. the approximate lower bound on the optimal value of problem (1(1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) ), and the corresponding set of feasible designs.

2. Select node to process. If the record list $R=\mathrm{\varnothing }$, then create a new list as described in Section 3.3. If $R\ne \mathrm{\varnothing }$, then select the first node in the list.

3. Find the design nearest to the relaxed solution. In each tree node an approximate lower bound on the optimal value of F in (1a(1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) ) is attained at the relaxed solution, the nearest feasible design of which is then found using one iteration of pattern search.

4. Enough designs for underestimation evaluated? A certain number of designs has to be sampled in order to form the underestimating function $\overline{F}$. If not enough designs have been evaluated, then pattern search and/or stochastic sampling are/is used to select additional designs to evaluate (see Section 2.3).

5. Apply pattern search. The pattern search starts from the evaluated design with a minimum value of F in (1a(1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) ), among the set of feasible designs in the current node. The M designs that are closest to the starting design are evaluated; the one with the minimal value of F is chosen; repeat if needed.

6. Evaluate more designs. Designs that are feasible in the processed node are evaluated through the (computationally expensive) simulations of the objective function F. Form underestimator of F. A quadratic convex approximate underestimating $\overline{F}$ is formed based on the evaluated designs.

7. Minimize underestimator. The function $\overline{F}$ is minimized over the convex hull of the feasible designs of the processed node.

8. Split feasible region. The feasible region is split according to the convex relaxation-based splitting strategy, with $X_i^s$ selected according to (4(4) $i\in \underset{k\in \{1,\dots ,m\}}{\arg max}\left\{|X_k^s|\right\}.$(4) ).

9. Minimize underestimator on each subregion. The function $\overline{F}$ is minimized over the convex hull of the feasible designs of each child node of the processed node resulting in relaxed optimal solutions to problems (3(3a) $\underset{\mathbf{v},\mathit{\lambda }}{\mathrm{minimize}}\overline{F}({\mathbf{v}}^1,\dots ,{\mathbf{v}}^m),$(3a) ) in the corresponding child nodes.

10. Convergence. The algorithm is terminated based on a maximum number of evaluations of F. Convergence is, however, guaranteed only when all feasible designs have been evaluated.

Figure 3. Flowchart of the algorithm quadDS.

In each iteration of quadDS, one linear optimization problem (LP) (or semidefinite optimization problem [SDP]) and three convex quadratic optimization problems (QPs) are solved. The algorithm quadDS is particularly suitable when the magnitude of the time needed for objective function simulations substantially exceeds the magnitude of the time required to solve these four optimization problems.

6. Computational experiments

This section describes the computational experiments conducted to assess the performance of quadDS, measured by the number of objective function evaluations. The implementation of quadDS is described in Section 6.1. The algorithms used for performance evaluation of quadDS are described in Section 6.2. The test problems used to assess the performance of the algorithms tested are described in Section 6.3. The assessment methodology chosen is introduced in Section 6.4, and the numerical results are presented in Section 6.5.

6.1. Implementation

All experiments were carried out on a laptop computer equipped with Intel${}^{\circledR }$ Core${}^{\mathcal{T}\mathcal{M}}$ i7-5600U 2.60 GHz CPU and 16 GB of RAM, running 64-bit Windows${}^{\circledR }$ 7 Enterprise. The algorithm quadDS, as described in this article, was implemented in MATLAB${}^{\text{ȍ}}$ R2015b (The MathWorks 2015). To find the convex underestimator $\overline{F}$ through solving optimization problem (2(2a) $\underset{\mathbf{A}\in S_{+}^n,\mathbf{b}\in {\mathbb{R}}^n,c\in \mathbb{R}}{\mathrm{minimize}}\sum _{\mathbf{z}\in \overline{V}}\left[F\right(\mathbf{z})-{\mathbf{z}}^{\mathrm{T}}\mathbf{A}\mathbf{z}-{\mathbf{b}}^{\mathrm{T}}\mathbf{z}-c],$(2a) ), either the solver for linear and quadratic semi-definite optimization problems SDPT3-4.0 (Toh, Todd, and Tutuncu 1999) was used, or the LP solver linprog (Coleman and Zhang 2015) from MATLAB's R2015b Optimization Toolbox for the case when the underestimator $\overline{F}$ has a diagonal Hessian was utilized; see Section 6.5. Quadratic optimization problem (3(3a) $\underset{\mathbf{v},\mathit{\lambda }}{\mathrm{minimize}}\overline{F}({\mathbf{v}}^1,\dots ,{\mathbf{v}}^m),$(3a) ) was solved using the QP solver quadprog (Coleman and Zhang 2015) from MATLAB's R2015b Optimization Toolbox. The implementation of quadDS is available upon request.

6.2. Tested algorithms

The considered class of design optimization problem with simulation-based objective functions is in engineering practice often solved using genetic algorithms (Dhingra and Rao 1992; Atiqullah and Rao 2000; Ryoo and Hajela 2004). An alternative is to use a nonlinear optimization algorithm, designed for non-convex optimization problems or simulation-based objective functions, and which can also handle discrete variables. The performance of three variants of quadDS is compared with one genetic algorithm (MATLAB GA)—which is often used and is readily available—and one algorithm developed for simulation-based optimization (NOMAD [nonlinear optimization with the mesh aaptive search algorithm])—which is easy to use.

quadDS

Three variants of quadDS are considered, denoted quadDSLP, quadDSSDP and quadDSFN, respectively. The variants quadDSLP and quadDSSDP both use the nearest edge projection splitting method, but differ in the approach to determining the quadratic underestimator $\overline{F}$ by solving optimization problem (2(2a) $\underset{\mathbf{A}\in S_{+}^n,\mathbf{b}\in {\mathbb{R}}^n,c\in \mathbb{R}}{\mathrm{minimize}}\sum _{\mathbf{z}\in \overline{V}}\left[F\right(\mathbf{z})-{\mathbf{z}}^{\mathrm{T}}\mathbf{A}\mathbf{z}-{\mathbf{b}}^{\mathrm{T}}\mathbf{z}-c],$(2a) ). In quadDSLP, the Hessian of $\overline{F}$ is diagonal, thus reducing the SDP (2(2a) $\underset{\mathbf{A}\in S_{+}^n,\mathbf{b}\in {\mathbb{R}}^n,c\in \mathbb{R}}{\mathrm{minimize}}\sum _{\mathbf{z}\in \overline{V}}\left[F\right(\mathbf{z})-{\mathbf{z}}^{\mathrm{T}}\mathbf{A}\mathbf{z}-{\mathbf{b}}^{\mathrm{T}}\mathbf{z}-c],$(2a) ) to a separable LP. In quadDSSDP, no assumption on the sparsity of the Hessian of $\overline{F}$ is made. A complete algorithm has been defined from the techniques described by Fuchs and Neumaier (2010b): quadDSFN, in which the objective function is approximated by a linear combination of the function values at the evaluated designs and the balanced split method is used.

Genetic algorithm solver

The genetic algorithm solver is part of the MATLAB Optimization Toolbox (Coleman and Zhang 2015; The MathWorks 2015) and solves optimization problems by mimicking the principles of biological evolution, repeatedly modifying a population of individual points using rules based on gene combinations in biological reproduction. The solver contains algorithms for a large variety of optimization problem with continuous, integer or mixed variables. The algorithms within the solver can to some extent be customized to simulation-based optimization problems with categorical variables.

NOMAD

The software application for simulation-based optimization, NOMAD, is based on the Mesh Adaptive Direct Search (MADS) algorithm (Audet and Dennis Jr 2006). MADS is an iterative method in which the simulation-based functions are evaluated at trial points lying on a mesh. It can explore a design space efficiently in the search for better solutions for a large spectrum of optimization problem types. Recent implementations of NOMAD can also handle categorical and mixed variables (Audet, Le Digabel, and Tribes 2009). To be able to incorporate categorical variables, a definition of neighbourhood has to be supplied. This definition then determines the behaviour of the algorithm. The approach suggested is to solve a reformulation of the problem in which the categorical variables are transformed into discrete variables. NOMAD was allowed to use built-in Latin-hypercube search and variable neighbourhood search in order to improve its performance.

6.3. Test problems

An artificial problem

A set of problem instances with cubic objective functions was randomized, according to (7a) $\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}\frac{1}{2}{\mathbf{z}}^{\mathrm{T}}\mathbf{Q}\mathbf{z}+{\mathbf{p}}^{\mathrm{T}}\mathbf{z}+\left(\mathrm{diag}\right(\mathbf{z})\mathbf{z}{)}^{\mathrm{T}}\mathbf{S}\mathbf{z},$(7a) (7b) $\mathrm{subject}\mathrm{to}{\mathbf{z}}^i=Z_i\left(x_i\right),i=1,\dots ,m,$(7b) (7c) $x_i\in X_i,i=1,\dots ,m,$(7c) where $\mathbf{S}$ is a diagonal matrix and the coefficients ${\mathbf{S}}_{ii}\in [-3,3]$ and $p_i\in [-1,1]$ are uniformly distributed. Two sets with 120 instances, each corresponding to two variants of problem (7(7a) $\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}\frac{1}{2}{\mathbf{z}}^{\mathrm{T}}\mathbf{Q}\mathbf{z}+{\mathbf{p}}^{\mathrm{T}}\mathbf{z}+\left(\mathrm{diag}\right(\mathbf{z})\mathbf{z}{)}^{\mathrm{T}}\mathbf{S}\mathbf{z},$(7a) ), were generated. In (i) the sparse artificial problem, $\mathbf{Q}$ is a diagonal matrix with the elements ${\mathbf{Q}}_{ii}\in [-3,3]$ uniformly randomly generated. In (ii) fully artificial problem, $\mathbf{Q}$ is a full matrix with the elements ${\mathbf{Q}}_{ij}\in [-3,3]$ uniformly randomly generated. The feasible designs are generated using Latin-hypercube sampling (Sóbester et al. 2014) with ${\mathbf{z}}^i\in [-1,1{]}^{n_i}$, where $n_i\in \{2,\dots ,8\}$. The number $N_i$ of feasible designs in each choice domain $X_i$, and the number m of choice domains, are randomized from the integer uniform distribution on the intervals $[10,50]$ and $[2,8]$, respectively.

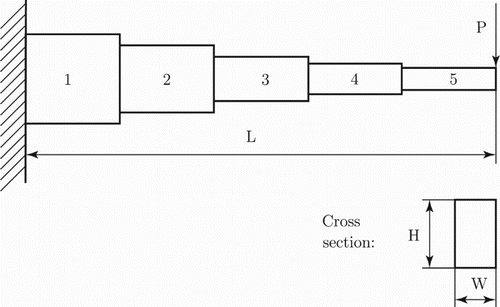
A beam design problem

The second test problem is a relaxation of the stepped beam example in Thanedar and Vanderplaats (1995). A cantilever beam, consisting of five segments with rectangular cross sections, is subjected to an end shear force; see Figure 4. The height and width of the cross sections constitute the design variables, and in the original setting the optimization problem is to minimize the volume of the beam with constraints on the maximum bending stress and tip displacement. In the relaxation considered, these constraints are dropped and the tip displacement is minimized while penalizing the volume. The beam is modelled using the finite element method utilizing Timoshenko beam theory (Timoshenko and Gere 1972, Chap. 5). The beam is subdivided into a set of connected elements with nodes at the ends of the beam. The displacement is assumed to be a piecewise linear function on $[0,L]$.

Figure 4. A stepped cantilever beam with m=5 segments.

Let k denote the number of elements and q=k+1 the number of nodes. The number of segments corresponds to the length of the vector m of discrete choice variables in Section 2.1. Each segment is composed of p elements, i.e. k=mp. The choices of $x_i\in X_i=\{1,\dots ,N_i\}$, $i=1,\dots ,m$, determine the composite vector $\mathbf{z}$ of widths and heights of the cross sections. Furthermore let $\mathbf{K}\left(\mathbf{z}\right)\in {\mathbb{R}}^{q\times q}$ and $\mathbf{f}\in {\mathbb{R}}^q$ denote the stiffness matrix and load vector, respectively, and let $\mathbf{d}\in {\mathbb{R}}^q$ denote the vertical displacements of the beam. With a force P applied to the end tip resulting in the end displacement $d_n$, it follows that $f_{k+1}=P$ and $f_i=0$ for $i\le k$, and the optimization problem is formulated as (8a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}{d}_n+\kappa V\left(\mathbf{z}\right),$(8a) (8b) $\mathrm{subject}\mathrm{to}\mathbf{K}\left(\mathbf{z}\right)\mathbf{d}=\mathbf{f},$(8b) (8c) ${\mathbf{z}}^i=Z_i\left(x_i\right),i=1,\dots ,m,$(8c) (8d) $x_i\in X_i,i=1,\dots ,m,$(8d) where $\kappa \in {\mathbb{R}}_{\mathbb{+}}$ denotes the penalty parameter and $V\left(\mathbf{z}\right)$ is the volume of the beam. The length, the material properties and the load are set according to Thanedar and Vanderplaats (1995).

The number of segments $m\in \{2,\dots ,10\}$ and the number of cross sections available for each segment $N_i\in \{10,\dots ,50\},i=1,2$, are randomly uniformly generated. For each segment, the cross sections are selected from a discrete set $Z_i\left(j\right):=H\times W$, $j\in X_i$, with heights $H\in \{h|h=0.45+0.15j/N_1,j=0,\dots ,N_1-1\}$ and widths $W\in \{w|w=0.02+0.03j/N_2,\text{j}=0,\dots ,N_2-1\}$. For the numerical tests, to receive a problem with a known optimal solution, $\kappa :=0$ is set, which implies that the optimal solution can be found by choosing the cross section with both the largest height and the largest width on each segment.

The tyres selection problem

Vehicles with two and three axles, respectively, are considered for the instances of the tyres selection problem introduced in Section 1.2. The operation of the vehicle is varied in order to obtain different optimal tyre configurations, i.e. the optimal tyres to be mounted on the individual axles.

For a vehicle with two axles, i.e. $X=X_1\times X_2$, 35 feasible tyres are available for each axle, resulting in ${35}^2=1225$ feasible tyre designs. The choice of the tyre $x_1$ ($x_2$) determines the values of the three design parameters tyre width, tyre diameter, and inflation pressure for the tyres mounted on the front (rear) axle. The resulting vector $\mathbf{z}$ thus has six components. For a vehicle with three axles, i.e. $X=X_1\times X_2\times X_3$, and 35 feasible tyres per axle, the vector $\mathbf{z}$ has nine components and there are ${35}^3=\mathrm{42,875}$ feasible tyre designs.

6.4. Assessment methodology

The measures performance profile and data profile introduced by Moré and Wild (2009) have been utilized to assess the performance of quadDS, the MATLAB GA and NOMAD on the three sets of test problems described in Section 6.3. While performance profiles are used to compare different algorithms, data profiles provide—for each specific algorithm—the average number of function simulations required to solve the test problems.

The following convergence test, commonly used to assess derivative-free solvers (Moré and Wild 2009), is employed: a feasible design z fulfils the convergence test if (9) $F\left({\mathbf{z}}^{\left(0\right)}\right)-F\left(\mathbf{z}\right)\ge (1-\tau )\left(F\right({\mathbf{z}}^{\left(0\right)})-F^L)$(9) holds, where $\tau \in [0,1]$ is a tolerance parameter that represents decrease from the starting value $F\left({\mathbf{z}}^{\left(0\right)}\right)$, ${\mathbf{z}}^{\left(0\right)}$ is the initial feasible design, and $F^L$ is the smallest value of F in (1a(1a) $2\underset{\mathbf{x},\mathbf{z}}{\mathrm{minimize}}F\left(\mathbf{z}\right),$(1a) ) obtained by any solver within a given number of function evaluations for a given problem, or the optimal value of F if available. The convergence test requires that the reduction $F\left({\mathbf{z}}^{\left(0\right)}\right)-F\left(\mathbf{z}\right)$ achieved by $\mathbf{z}$ be at least $(1-\tau )$ times the reduction $F\left({\mathbf{z}}^{\left(0\right)}\right)-F^L$.

Performance profile

The performance profile for an algorithm originally introduced by Dolan and Moré (2002) is defined in terms of a performance measure; here it is represented by the number of evaluations of the objective function F required to satisfy the convergence test in (9(9) $F\left({\mathbf{z}}^{\left(0\right)}\right)-F\left(\mathbf{z}\right)\ge (1-\tau )\left(F\right({\mathbf{z}}^{\left(0\right)})-F^L)$(9) ). Assuming a set $\mathcal{A}$ of algorithms applied to a set $\mathcal{P}$ of problems, $t_{pa}$ is for each $p\in \mathcal{P}$ and $a\in \mathcal{A}$ defined as the number of function evaluations required to satisfy the convergence test (9(9) $F\left({\mathbf{z}}^{\left(0\right)}\right)-F\left(\mathbf{z}\right)\ge (1-\tau )\left(F\right({\mathbf{z}}^{\left(0\right)})-F^L)$(9) ). The performance ratio, defined as $t_{pa}({\min }_{b\in \mathcal{A}}\{t_{pb}\}{)}^{-1},p\in \mathcal{P},a\in \mathcal{A},$ relates the performance of algorithm a as applied to the problem p to the best performance of any of the algorithms in the set $\mathcal{A}$. If algorithm a fails to satisfy the convergence test on problem p, then by convention $t_{pa}:=\mathrm{\infty }$. An overall assessment of the performance of algorithm a is obtained by defining the probability that the performance ratio is at most α, where $\alpha \in [0,1]$, that is, ${\rho }_a\left(\alpha \right):={|\mathcal{P}|}^{-1}\left|\left\{p\in \mathcal{P}:t_{pa}\le \alpha \cdot \underset{b\in \mathcal{A}}{min}\left\{t_{pb}\right\}\right\}\right|.$ The function ${\rho }_a:[1,\mathrm{\infty })\mapsto [0,1]$ is the cumulative distribution function of the performance ratio. A plot of the performance profile for the set of tested algorithms $\mathcal{A}$ reveals the major performance characteristics of the algorithms (the relative performance of each solver, the probability of successful solution, and the percentages of problems on which the algorithms perform the best).

Data profile

While performance profiles provide an accurate view of the relative performance of solvers within a given number of function evaluations, they do not provide sufficient information in the case of computationally expensive objective functions, when a more relevant measure is the performance of a solver as a function of the number of expensive function evaluations. The data profile of an algorithm $a\in \mathcal{A}$ is thus employed, introduced by Moré and Wild (2009) and defined by $d_a\left(\beta \right):={|\mathcal{P}|}^{-1}|\{p\in \mathcal{P}:t_{pa}\le \beta \}|,$ which is the proportion of problems that are solved within β function evaluations.

Performance profiles are used to compare different algorithms, while data profiles provide the number of function simulations required to solve any of the problems by each specific algorithm.

6.5. Results

The numerical results are evaluated using the performance measures introduced in Section 6.4. The algorithm set $\mathcal{A}$ consists of quadDSLP, quadDSSDP, quadDSFN, the MATLAB GA and NOMAD. As benchmark problems, 120 randomly generated instances of each of the four test problems (sparse artificial, fully artificial, beam design and tyres selection) described in Section 6.3 are considered. The tolerance $\tau =0.1$ is used in the inequality (9(9) $F\left({\mathbf{z}}^{\left(0\right)}\right)-F\left(\mathbf{z}\right)\ge (1-\tau )\left(F\right({\mathbf{z}}^{\left(0\right)})-F^L)$(9) ) used for the convergence test for the artificial and beam problems, and $\tau =0.01$ for the tyres selection problem.

Figures 5–8 show the data and performance profiles (Moré and Wild 2009) of quadDS (three variants), the MATLAB GA and NOMAD. The three variants of quadDS outperform the competing algorithms, the MATLAB GA and NOMAD, on all the benchmark problems. The variant quadDSLP performs the best on all sets of problems, except for the fully artificial problems. For these problems, quadDSSDP and quadDSFN perform nearly equally well, and significantly better than quadDSLP.

Figure 5. Data profiles $d_a\left(\beta \right)$ and performance profiles ${\rho }_a\left(\alpha \right)$ for three variants of quadDS, the MATLAB GA and NOMAD applied to 120 instances of the sparse artificial problem with $\tau =0.1$.

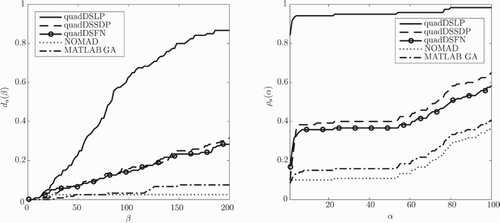
Figure 6. Data profiles $d_a\left(\beta \right)$ and performance profiles ${\rho }_a\left(\alpha \right)$ for three variants of quadDS, the MATLAB GA and NOMAD applied to 120 instances of the fully artificial problem with $\tau =0.1$.

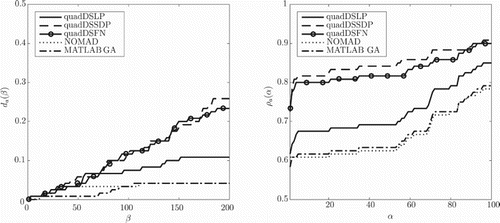
Figure 7. Data profiles $d_a\left(\beta \right)$ and performance profiles ${\rho }_a\left(\alpha \right)$ for three variants of quadDS, the MATLAB GA and NOMAD applied to 120 instances of the beam problem with $\tau =0.1$.

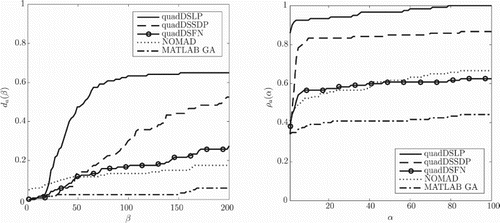
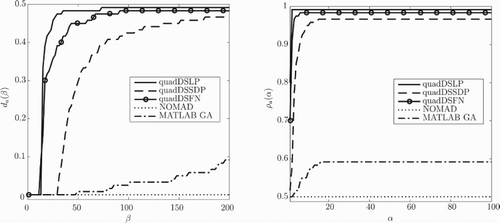
Figure 8. Data profiles $d_a\left(\beta \right)$ and performance profiles ${\rho }_a\left(\alpha \right)$ for three variants of quadDS, the MATLAB GA and NOMAD applied to 120 instances of the tyres selection problem with $\tau =0.001$. Note that $d_{\mathrm{NOMAD}}\left(\beta \right)=0$ for all values of β and ${\rho }_{\mathrm{NOMAD}}\left(\alpha \right)=0.5$ for all values of α, because NOMAD did not solve any of the instances of the tyres selection problem within the maximum allowed number of objective function evaluations.

For the instances of the sparse artificial problem, quadDSLP performs substantially better than the other algorithms tested, see Figure 5. The performance of the other algorithms tested improves when the maximum number of allowed objective function evaluations is increased.

When the fully artificial problem is considered, both quadDSSDP and quadDSFN outperform the other algorithms tested, as can be seen in Figure 6. The underestimator with a sparse Hessian as used within quadDSLP forms an inaccurate approximation of the objective function of the fully artificial problem, resulting in the worse performance of quadDSLP. The performance of NOMAD and the MATLAB GA are almost the same and improve when the maximal number of objective function evaluations is increased.

For the beam problem, quadDSLP outperforms the other algorithms when the maximum number of allowed objective function evaluations exceeds the number of evaluated designs required to form the underestimator, as Figure 7 shows. For fewer evaluated designs, NOMAD would be the best choice.

When the tyre problem is considered, all three variants of quadDS clearly outperform NOMAD and the MATLAB GA, see Figure 8. The performance of the MATLAB GA improves when the allowed number of function evaluations increases. NOMAD did not solve any of the instances of the tyres selection problem within the maximum allowed number of objective function evaluations.

The number of evaluated designs required to form the underestimator in each of the variants of quadDS influences the performance for low values of β; quadDSLP requires substantially fewer evaluated designs than quadDSSDP to start to iterate (see Enough designs for underestimation evaluated in Figure 3). In quadDSFN, no underestimator is created. It is observed that quadDSLP performs better than quadDSSDP on test problems having an objective function with a sparse or even diagonal Hessian. The reason is that the underestimator with a diagonal Hessian formed in quadDSLP approximates the objective function better and requires substantially fewer function evaluations to be formed than an underestimator with a full Hessian (quadDSSDP). Subsequently, more iterations of quadDSLP can also be performed. The objective function of the sparse artificial problem is constructed to have a diagonal Hessian. It is observed that the Hessian of the objective function of the beam problem is indeed sparse and nearly diagonal. The objective function of the tyres selection problem is almost separable with respect to choice domains, resulting in an almost block-diagonal Hessian. For a general optimization problem, for which no information about the sparsity of the objective function can be obtained, quadDSSDP is recommended if sufficiently many function evaluations can be performed, since this algorithm provides tighter lower bounds. If the number of function evaluations allowed is very low, then quadDSLP should be preferred since it requires substantially fewer function evaluations to form the underestimator of the objective function.

7. Conclusions and future research

A discrete search algorithm for design optimization, quadDS, has been developed and implemented. The algorithm is suitable for optimization problems with computationally expensive simulation-based objective functions and categorical variables.

The algorithm has been tested utilizing a variety of both artificial and real test problems, and compared with other existing algorithms that can be used to solve the described class of optimization problems. The performance of the algorithms has been assessed using so-called performance and data profiles. The algorithm quadDS outperforms the competing algorithms considered on the selected benchmark problems.

The proposed algorithm enables the efficient solution of the true tyres selection problem for a limited number of customers corresponding to a specific vehicle configuration and operating environment. A technique for finding approximately optimal tyre configurations for many other customers is being developed, based on the forthcoming work by Nedělková et al. (2018).

The algorithm quadDS can be extended to include simple constraints on the discrete choice variables except for those already included. Separable constraints can be handled through a preprocessing of the search domain. Linear constraints can be included in the convex relaxation of the original problem used by the algorithm. To handle more complicated constraints, such as nonlinear and/or simulation-based ones, will require further development. The variant of quadDS presented here is developed for purely categorical variables; continuous and discrete variables can, however, be handled by a simple adjustment of the splitting method.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Zuzana Nedělková http://orcid.org/0000-0003-1551-9713

Christoffer Cromvik http://orcid.org/0000-0001-5421-7967

Peter Lindroth http://orcid.org/0000-0001-5344-3858

Michael Patriksson http://orcid.org/0000-0001-7675-7454

Ann-Brith Strömberg http://orcid.org/0000-0003-1962-7279

Additional information

Funding

The work leading to this article was supported by the Swedish Energy Agency [project number P34882-1]; Chalmers University of Technology and University of Gothenburg; and Volvo Group Trucks Technology.

Notes

1. Note that the integer values $1,2,\dots ,N_i$ do not represent any physical entities.

2. The values $Z_i\left(j\right)$, $j=1,\dots ,N_i$, are usually provided in an $N_i\times n_i$ table, $i=1,\dots ,m$.

3. A more accurate underestimation would be computationally more expensive to construct and minimize (Nowak and Vigerske 2008).

4. The costs of edges are determined by their lengths in terms of Euclidean distance in the $\mathbf{z}$-space.

5. It holds that $\bigcup _{l\in L}{I}_l=J$.