Residual plots for linear regression models with censored outcome data: A refined method for visualizing residual uncertainty

ABSTRACT

Residual plots are a standard tool for assessing model fit. When some outcome data are censored, standard residual plots become less appropriate. Here, we develop a new procedure for producing residual plots for linear regression models where some or all of the outcome data are censored. We implement two approaches for incorporating parameter uncertainty. We illustrate our methodology by examining the model fit for an analysis of bacterial load data from a trial for chronic obstructive pulmonary disease. Simulated datasets show that the method can be used when the outcome data consist of a variety of types of censoring.

KEYWORDS:

• Bootstrapping
• Censoring
• Linear models
• Multiple imputation
• Residuals
• Regression diagnostics

MATHEMATICS SUBJECT CLASSIFICATION:

• 62-09

1. Introduction

Censored data occur when the value of a measurement or observation is only partially known. Such data are commonly, but not exclusively, associated with survival or time to event data. For example, if the event of interest does not occur by the end of a subject’s follow-up period, then this event is usually assumed to occur at some time afterward. This results in right censoring. Conversely, if the event time is only known to be before some given time, then the result is left censoring. If instead an event time is only known to lie within a finite interval, then the result is interval censoring. More complicated forms of censoring are possible, for example, doubly censored failure time data and panel count data (Sun, 2006). Our method could be extended to include more complicated censoring types, but here we focus on right, left, and interval censoring, as these are the types of censoring most commonly encountered in practice.

Assumptions are made when using any statistical model. If the data violate these assumptions, then the resulting statistical inference may be misleading. Therefore, the assumptions made by any given model should be carefully checked. For example, a very commonly used model is linear regression, where a key assumption is that the errors are independent and identically normally distributed. This assumption implies a range of other assumptions, including that of homoscedasticity, that is, that the data have the same variance, which is often overlooked. The adequacy of the modeling assumptions in linear regression are often informally checked by examining residual plots, where we typically plot the difference between observed and fitted outcome values (the residuals) against covariates or fitted values. A QQ plot of residuals will also help discern if the assumption of normality does not hold. Studentized residuals are generally preferred to raw residuals (Andrews and Pregibon, 1978; Cook and Weisberg, 1982), and we address this issue later. If the assumptions are adequate, then we expect to see random scatter in the residual plots. Here, our focus is on checking that the assumptions made in linear regression models are not violated, using residual plots, where some or all of the outcome data are right-, left-, or interval-censored. Random scatter in residual plots are a necessary but not sufficient condition for concluding that the model assumptions hold; residual plots thus may be regarded as a “first line of defense” with regard to checking model assumptions (Draper and Smith, 1998, chap. 2).

Censored outcome data create numerous difficulties in practice. Assuming that the censoring is noninformative (Andersen and Keiding, 2006), and in the context of using a fully parametric model, the contribution to the likelihood for a censored observation is given by the probability that the censored value lies in the corresponding interval. The numerical maximization required to fit parametric models using maximum likelihood makes fitting the type of model we consider here quite computationally intensive when some outcome data are censored. However, in the current computational climate, this is usually of little concern unless the sample size or the number of regression parameters is large.

The Buckley–James estimator (Armitage and Colton, 2005; Buckley and James, 1979) provides a less computationally intensive estimation method compared to maximum likelihood estimation when fitting linear regression models with censored outcome data. This method is a two-step interative process: Using some prespecified initial estimates of model coefficients, censored outcomes are replaced by estimates of their expected values, which are calculated using a method based on the Kaplan–Meier estimator (Kaplan and Meier, 1958). These estimates of expected values are then used to update the estimates of the coefficients, which can then in turn be used to calculate expected values for the censored observations. Iteration continues until convergence, or if convergence does not occur, the mean of oscillations is taken. The Buckley–James method makes no parametric assumptions regarding the errors and so also possesses the advantage of being semiparametric. The Buckley–James method was proceeded by Cox’s proportional hazards regression model (Cox, 1972), which has since become the most popular method for modeling censored data. The main difference between these two methods is that Buckley–James focuses on finding expected values of survival times; this is in contrast to the Cox model, which deals with relative risk of failure due to included covariates, and relies on the assumption of proportional hazards.

Once convergence of the Buckley–James estimator is reached, the expected values for censored observations can be used as if they were the observed values to calculate residuals and so produce “renovated” residual plots. See Cui (2005)) and Smith and Zhang (1995)) for further explanation of this procedure. However, the residuals that result directly from this form of estimation do not take into account the uncertainty in the censored values, and here we fit our models using maximum likelihood, where residuals for censored observations are not immediate. A variety of types of residuals are available when using likelihood-based methods (Armitage and Colton, 2005). Here, we take the residual to be the difference between the observed and fitted value. This is because this is the residual definition that most practitioners are familiar with, it is the standard definition of a residual for linear models such as ours in the case that no data are censored (Draper and Smith, 1998), and it corresponds to the type of residual in the renovated plots resulting from the Buckley–James method.

The difficulty in using this definition of a residual for censored outcome data is that these outcomes are not observed exactly, which raises the obvious question of what constitutes a reasonable definition of the difference between observed and fitted values. A simple solution, for right- and left-censored data, is to calculate residuals using the censoring value as if it were the observed value; this is how the parametric survival regression function survreg reports residuals for right- and left-censored outcome data in R (R Core Team, 2013; Therneau, 2015). The related function residuals.survreg provides nine different types of residuals for parametric survival regression models. Similarly, for interval-censored data, residuals could be calculated using the midpoint of the interval as if it were the observed value. However, using the censoring value (or the midpoint of the interval) ignores both the uncertainty in the location of the censored outcome data and the distributional assumptions made by the model. Further, for right- and left-censored data, this method generally results in a conservative estimate of the residual. Hence, one concern is that this type of procedure may suggest that the model fit is better than it actually is. Another possibility is to mark residuals from censored outcomes differently to residuals from observed outcomes, but still this makes interpretation difficult (Hillis, 1995).

A variety of more sophisticated methods for producing residual plots for linear regression models with censored data have previously been proposed. Some of these methods avoid assuming that the errors are normally distributed and so are in the spirit of the Buckley–James estimation method. For example, Hillis (1995)) presents such a method, using Buckley–James to generate error terms from a nonparametric distribution of the errors. This work is extended by Topp and Gomez (2004)), who present a method for obtaining residuals from the estimated mean of the (truncated) model error distribution, under the assumption of normally distributed error terms. The residual theory proposed by Topp and Gomez pertains to censoring of a covariate, but is extended to censoring in the outcome in sec. 4.2 of their article. Our proposed method extends these methods by producing residual plots that explicitly display the uncertainty in the location of the error terms, and we provide corresponding freely available software.

The remainder of this article is as follows: In Section 2, we introduce the motivating dataset and our model; in Section 3, we describe our method for creating residual plots using the function censplot and compare our approach to multiple imputation; in Section 4, we show the results of using the proposed method. We conclude with a discussion. Included as supplementary material are a number of illustrative studies, the full R code with an example, and a detailed explanation of how to use the function.

2. Dataset and model

Our data come from a Phase III randomized control trial (Clinical Trial NCT01398072) of 99 patients with chronic obstructive pulmonary disease (COPD). This was a multi-arm, single-center trial based at the Royal Free Hospital in London. The trial investigated the effectiveness of three different antibiotics against placebo, and so there were four trial arms: Moxifloxacin, Doxycycline, Azithromycin, and placebo. Participants were recruited between February 2012 and March 2013, and followed up for a maximum of 13 weeks. The primary aim of the study, as described in detail by Brill et al. (2015), was to compare bacterial load from patient sputum samples between each active treatment group and placebo at the end of the follow-up.

Due to the microbiological method used, bacterial load could not be detected below a threshold of 6 × 10⁶ colony forming units per ml (cfu/ml). Participants whose bacterial load was below this threshold therefore provided left-censored outcome data at this threshold level. Table 1 summarizes the proportion of censoring at follow-up. There were 76 complete cases with regard to the primary analysis covariates and outcome, and 6 left-censored outcomes. The remaining 17 patients had censored bacterial load at baseline (a covariate) and were not included in this analysis.

Table 1. Follow-up bacterial load ( cfu/ml) censoring frequency among otherwise complete cases; summary of baseline and follow-up bacterial load among complete cases.

Drug	Censored (%)	Baseline mean (SD)	Follow-up mean (SD)
Moxifloxacin	0/18 (0.0%)	7.9 (0.6)	8.5 (0.8)
Doxycycline	1/22 (4.5%)	8.1 (0.7)	8.0 (0.6)
Azithromycin	4/21 (19.0%)	8.3 (0.5)	8.1 (0.8)
Placebo	1/21 (4.8%)	8.1 (0.8)	7.9 (0.7)

The bacterial load outcome data appeared to be skew, so a transformation was applied before performing the analysis. Specifically, after taking the (base 10) logarithm of bacterial load, the outcome data appeared to be approximately normally distributed. The outcome data were then modeled using parametric survival regression. This was undertaken using the survreg function in R (Therneau, 2015), which uses, for the ith individual, (1) as a modeling framework. Upon specifying the desired distributional assumption for Z, survreg estimates the regression parameters and the scale parameter σ using maximum likelihood. The role of Z in model (1(1) ) is discussed by Tableman and Kim (2004). The function survreg allows the inclusion of right-, left-, and interval-censored outcome data in the model.

For our analysis, to make the normality assumption in model (2)(2) below more reasonable, we take the outcome data Y to be the log-transformed bacterial load ( cfu/ml) at follow-up. The bacterial loads were transformed in this way prior to analysis. Included in the model were the following covariates: An intercept term, three indicator variables representing the three treatment groups, and (bacterial load) at baseline. Thus, we estimate the three antibiotic treatment effects, relative to the placebo group, while adjusting for baseline bacterial load. We assume a normal distribution for the outcome data, that is, Z_i ∼ N(0, 1). The model therefore collapses to the more familiar linear regression model (2) where the errors ε_i are independent and identically distributed with distribution ε_i ∼ N(0, σ²).

In the event of there being no censored outcome data, model (2(2) ) can be fitted using ordinary least squares in the usual way, but to incorporate the six censored observations in the most appropriate way we use the survreg function with the normality assumption. The survreg function we use fits a fully parametric regression, in contrast to Buckley–James. Model (2(2) ) was fitted to the COPD trial data, and some results are shown in Table 2. In each case, the confidence interval includes zero, and so, at a 5% significance level, there is no evidence of lower bacterial load for patients on any active treatment compared to placebo. A plot of standardized residuals against fitted values is shown in Fig. 1, where “standardized” is taken to mean scaling by dividing by ; this choice is discussed further in Section 3.4. Figure 1 shows random scatter about zero, suggesting good fit and that homoscedasticity is a reasonable assumption. A standard QQ plot of the observed residuals (not shown) to check the normality assumption strengthens our confidence in the model; we leave the best way to more appropriately produce QQ plots with censored data as future work. However, by default, the residual for each censored observation in the residual plot is taken to be the difference between the fitted value and the censoring value. This means that the residuals plotted for censored observations are conservative; they are at least as extreme as those shown in the residual plot. It is possible to manually mark them differently, and this is indeed shown in Fig. 1, but their interpretation remains difficult.

Figure 1. Standard residual plot from COPD trial. Crosses correspond to censored observations, and are calculated using censoring values. The aim of this article is to improve upon standard residual plots such as these.

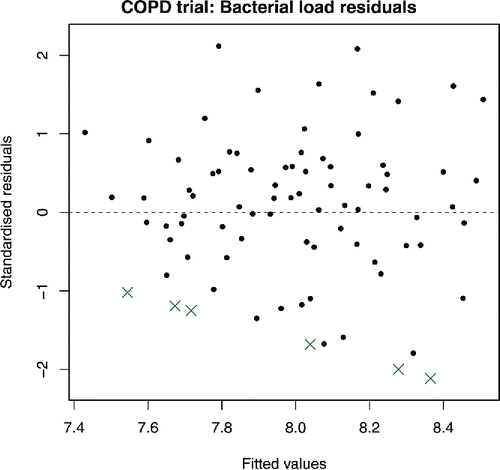
Table 2. Estimated regression parameters representing treatment effects, adjusted for baseline bacterial load ( cfu/ml), from fitting model (2(2) ) to COPD trial data summarized in Table 1.

Drug	Mean change from placebo (95% CI)	p-Value
Moxifloxacin	−0.32 (−0.81, 0.17)	0.20
Doxycycline	−0.05 (−0.50, 0.40)	0.82
Azithromycin	−0.17 (−0.62, 0.29)	0.73

We will more carefully and appropriately examine the independent and identically distributed assumption of the residuals, using more elaborate residual plots created using the methods described in the following sections.

3. Method

We now present our method for creating residual plots for linear regression models where some or all outcome data are right-, left-, or interval-censored. Our methodology takes into account both the uncertainty in the location of the censored data and in the parameter estimates in the linear model, which can be considerable in small samples such as those we examine, while making full use of this model’s assumptions.

3.1. Taking into account the parameter uncertainty

The method comprises two approaches for taking parameter uncertainty into account. In both approaches we initially fit our analysis model, a linear regression with censored outcome data, using maximum likelihood in standard software. This analysis model provides our primary inferences. In our first approach, we draw parameter values from the asymptotic normal approximation to the maximum likelihood estimates. In our second approach, bootstrap samples are produced to provide bootstrap replicates of the parameter estimates, so that both approaches produce simulated sets of parameter values, which consist of regression coefficients and standard deviations. Regardless of which approach to taking into account parameter uncertainty is used, a “pseudo outcome” is simulated from a truncated normal distribution for each censored observation and set of parameters, where the truncation points are equal to the censoring values. The sets of residuals for each censored observation are then given by the difference between the pseudo outcomes and the fitted values, where the fitted values are obtained from the fitted analysis model. We then include the distributions of these residuals for censored outcomes in otherwise standard residual plots. The first approach is the default for our software because it is faster than the alternative method, though we have found both to perform well for a variety of simulated datasets, details of which are contained within the supplementary materials.

3.1.1. Method one

The survreg function provides a full variance-covariance matrix of the regression parameters and the natural logarithm of the scale parameter σ. Using the mvtnorm package (Genz et al., 2016), N_S random realizations from a multivariate normal distribution can easily be produced, where this distribution is centered at the maximum likelihood estimates and with variance-covariance matrix equal to the variance-covariance matrix reported by survreg. Each resulting simulated log(σ) can then be transformed to σ. This gives rise to N_S sets of and σ, which can be used to simulate fitted values for each of the censored outcomes as explained below in Section 3.2. This method for taking into account the parameter uncertainty, which uses the asymptotic distribution of the maximum likelihood estimates, is akin to using a parametric bootstrap procedure. We denote the resulting sets of parameters .

3.1.2. Method two

An alternative method, which is instead akin to using nonparametric bootstrapping, produces N_S random samples, with replacement, from the original dataset (including both censored and uncensored participants). The linear regression model is fitted to each of the N_S simulated datasets and the resulting parameter sets are again denoted as . This method is more computationally expensive because of the resampling involved and, in particular, the repeated fitting of models with censored data, which requires more computing time. We anticipate that this method will be preferable in smaller samples where the asymptotic theory of maximum likelihood provides a less accurate approximation. As our method using survreg for fitting the model relies on this asymptotic theory however, it is likely that our methods will only be applied in situations where our default method is appropriate.

Although we propose this alternative method based on nonparametric bootstrapping, methods based on the Bayesian bootstrap (Rubin, 1981; Rubin and Schenker, 1986) may be considered preferable in very small samples. It may also be preferable to sample with replacement within structural strata such as the treatment groups here, when such strata are included in the model.

3.2. Simulating realizations of the censored observations

Once N_S sets of parameters have been produced, the procedure is the same for both methods: We simulate realizations from the distributions of the censored observations and so obtain their distributions numerically. We do this by simulating outcome data N_S times for each censored observation, where is used to simulate the jth outcome for all censored participants. By using different values of for each of the N_S simulated realizations of the censored outcome data, the uncertainty in the model parameters is taken into account.

Specifically, we simulate the pseudo outcomes y*_ij, j = 1, …, N_S, for each censored observation i, from truncated normal distributions, where we take the truncated distribution to have support over the interval where the censored observation is known to exist. We calculate the linear predictor used for simulating y*_ij as and σ*_j gives the standard deviation. Random realizations from truncated normal distributions can conveniently be obtained using the R package msm (Jackson, 2011).

When fitting models using the classical paradigm we treat the observed data as a random realization from a population with some distribution.

Using fixed values of the observed data when calculating the residuals is reminiscent of conditioning on the observed data, as this conditioning gives the statistical license to treat a random variable as fixed. This observed data for a censored observation is the censoring interval and conditioning on this interval gives rise to a truncated distribution. Hence, we propose a mantra for censored outcome data: “Use censored distributions for model fitting, but use truncated distributions for model checking.”

3.3. Calculating raw residuals

Using the above methods, we have N_S simulated outcomes for each censored outcome. Sets of N_S raw residuals for these censored outcomes are then calculated in an intuitive manner as

where is the fitted value for the ith observation from the original regression shown in Table 2.

Residuals for the other, observed outcomes are obtained in the usual way as

This means that the noncensored outcome data continue to provide their usual residuals, found using survreg. However, the censored observations provide a distribution of residuals that we can describe using the vector for each censored outcome. Histograms and other summaries of these vectors can then be included in standard residual plots, as we show in the next section. We will examine in the discussion the advantages and disadvantages of our use of instead of the pseudo outcomes , in the definitions of the residuals, but for now note that the main reason for this choice is that it results in a single residual for the observed outcome data.

3.4. Calculating standardized residuals

Standardized residuals may be produced by dividing all the and by , where N is the sample size and p is the number of covariates used (including an intercept term, where present in the model). This means that, in large samples, the standardized residuals should resemble a standard normal, rather than a normal distribution with variance not equal to one. We suggest that standardizing in this way is useful for model checking because we then have a very simple reference distribution. However, this has the potential disadvantage of losing the scale on which the outcome is measured, which might inhibit the interpretation of residuals in some situations.

We propose standardizing residuals by dividing by , rather than the maximum likelihood estimate , because survreg does not provide the conventional estimate of σ that results from using ordinary least squares when no data are censored. Our proposal means that conventional standardized residuals are obtained when no outcome data are censored; it is highly desirable that methods with censored data simplify to standard methods when no data are censored. However, the distinction between dividing by and will be unimportant in situations where the sample size is reasonably large.

3.5. Calculating studentized residuals

Standard linear regression theory describes how to further studentize residuals (Armitage and Colton, 2005), where the impact of the observations’ leverages on the standardized residuals’ variances are taken into account. The leverages are a function of the design matrix, and so depend on covariate values, rather than the outcome data. Standard theory shows how the variance of the standardized residuals can depend a great deal on the leverages, particularly in situations where some observations possess much greater leverage than others. In general, the variance of the standardized residuals (Section 3.4) is slightly too small to be compared to a standard normal distribution.

The process of studentizing scales this “leverage effect” on the distribution of the residuals. However, the theory that justifies this process relies on having fully observed the outcome data—that is, having no censored outcomes. At best it is not obvious how to studentize residuals where some censoring has occurred. Hence, we do not provide a concrete proposal for studentizing our residuals in this article and instead leave this as a possible avenue for future work.

Despite this, we wish to emphasize a few points. First of all, in large samples containing no observations with grossly large leverages, the effect of further studentizing our standardized residuals will be negligible. Hence, in the vast majority of applications, the omission of studentizing will also be negligible. Second, in situations where the omission of studentizing is thought to be potentially more serious, the simulated outcomes for the censored data could be used to provide multiply imputed datasets where complete data techniques, including studentizing residuals, could be used. We address this possibility in the next subsection and in the discussion. Finally, our computer program provides the leverages that result from treating the censored data as if observed (and taking any value, as mentioned above, the leverages do not depend on the outcome data). Although these leverages only strictly apply in the absence of censoring, their values give an indication of when the omission of studentizing may be more serious: If any leverages are very much larger than the rest, then this should be acknowledged when interpreting the standardized residuals.

3.6. Comparison to multiple imputation

Multiple imputation is a technique for dealing with missing data, to make use of data that may otherwise be excluded from analysis. However, the concept of censored data is closely related that of missing data, and indeed such data can be multiply imputed (Royston, 2007; StataCorp, 2013). In multiple imputation, every missing value is replaced by a simulated value (Morris et al., 2014; White et al., 2011). This imputation process is repeated m times. The analysis model is then fitted to each of the resulting m imputed datasets, creating multiple estimates of each parameter. These multiple estimates are pooled using Rubin’s Rules (Rubin, 1987), and standard errors that reflect the uncertainty regarding the missing data are obtained.

Our methods, as in conventional multiple imputation procedures, take into account all parameter uncertainty and are based on maximum likelihood. Furthermore, we also effectively produce multiply imputed datasets, because each of the N_S simulated outcomes for each censored value could be used to produce an imputed dataset. Hence, if we used a standard linear regression model as our analysis model, and combined the results from the simulated datasets using Rubin’s Rules, we would recover (approximately) the inferences shown for the original data shown in Table 2. These observations show that what we propose is very similar in concept to multiple imputation. We however have no need to use imputation to fit the analysis model, so we do not use our procedure to make primary inferences, but we instead effectively use multiply imputed datasets for model checking.

We return to the possibility of fully using multiple imputation (i.e., to use multiple imputation to make the primary inferences) in the discussion.

4. Results

This section presents the results of applying our methodology to the COPD trial data described in Section 2. As explained in the previous section, the vectors of simulated describe the distribution of residuals for each censored observation i. Histograms of each set of simulated residuals are displayed in the residual plot. This shows the full distribution of the censored residuals. By default, this option is not invoked in the R function that accompanies the article, censplot (see the online supplementary material), as clarity can be diminished in datasets with many censored outcomes.

Plots are shown using the default approach for taking into account parameter uncertainty (Section 3.1.1.) in Fig. 2a, and then using the alternative approach based on nonparametric bootstrapping (Section 3.1.2) in Fig. 2b, using N_S = 1, 000 simulations. The residuals have been standardized as described in Section 3.4. The residuals are plotted against fitted values by default, but one may also plot them against any complete covariate from the original dataset, or by the order in which they were collected in the case that the data are time-dependent.

Figure 2. Residual plot from COPD trial using the same data as in Fig. 1, but now applying our method. The location of expected values of censored outcomes is highlighted, and shows that the fit to the censored data may be poorer than Fig. 1 suggests.

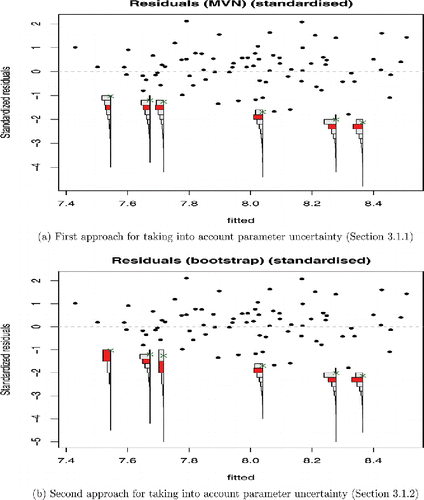
Numerical summaries for the simulated residuals for each censored outcome are shown in Table 3, calculated using the following methods: Calculating residuals by treating the censoring value as if it were the observed value (the standard output of survreg), and using our two approaches for taking into account parameter uncertainty. Figure 2a and 2b shows that both alternatives for taking into account parameter uncertainty produce very similar results for this example.

Table 3. COPD trial dataset: Summary of residuals based on censoring outcome , that is, survreg output; multivariate normal sampling; and bootstrapping approaches.

	Residuals and fitted values
Fitted values	7.72	7.54	7.67	8.37	8.04	8.28
survreg	−0.94	−0.77	−0.89	−1.59	−1.26	−1.50
MVN approach (IQR)	−1.60 (−1.91, −1.41)	−1.43 (−1.75, −1.18)	−1.56 (−1.89, −1.36)	−2.38 (−2.63, −2.22)	−1.97 (−2.26, −1.81)	−2.27 (−2.51, −2.11)
Bootstrap approach (IQR)	−1.59 (−1.91, −1.39)	−1.38 (−1.68, −1.18)	−1.52 (−1.79, −1.33)	−2.34 (−2.56, −2.21)	−1.96 (−2.23, −1.79)	−2.25 (−2.51, −2.11)

It can be seen in Fig. 2a and 2b that, in this case, calculating residuals using censoring value as if it were the observed value results in conservative residuals. This is because here, the true value of a censored outcome is at most the limit of detection. Thus, calculating residuals based on this value will result in the smallest possible residuals. Hence, our method for plotting residuals is superior to survreg on its own, as our method plots the expected value of each censored outcome, rather than the most conservative estimate.

Both approaches for taking into account the parameter uncertainty give similar results for this example. However, the degree of censoring in this dataset is small (Table 1), so our motivating dataset does not present a very considerable challenge for our methods. Nevertheless, Fig. 2a and 2b provides no evidence that the model assumptions are violated, and the random scatter in these figures suggests that the homoscedasticity assumption is reasonable. In addition, a QQ plot to check the normality assumption is recommended. The approaches are compared again using two more challenging simulated datasets in the online supplementary materials, where the effect of greater proportions and different types of censored data are explored.

5. Discussion

The examination of residual plots to informally assess the assumptions made by a regression model is important whether or not some outcome data are censored. We acknowledge that producing residual plots is just one technique for checking model assumptions, and that a common use of such plots is to check for a linear trend and homoscedasticity. Further diagnostic checks are highly advisable in applied work, and in particular QQ plots are very useful for investigating potential deviations from the normality assumptions made by standard linear models. The best way to produce QQ plots when some outcome data are censored is an interesting avenue for further work. We have presented a method for producing more appropriate residual plots where some or all outcome data are censored. This is because our approach produces distributions of residuals for outcomes that are not observed exactly due to censoring. We have shown the resulting residual plots for data from a trial for COPD treatment, and include a number of simulated datasets in the supplementary materials that accompany this article, which collectively address a variety of types and proportions of censored outcome data. In situations where there is no censoring, our procedure produces the types of residuals that are familiar to those using ordinary least-square routines to fit linear regression models.

The function written to create such plots, censplot and its associated plotting function, are also provided in the supplementary materials. A limitation of our program is that it is coded for use with only normally distributed outcome data. The command’s functionality could be extended to handle the other distributions that are possible when using survreg however, and this could form the subject of future work.

We standardize the residuals by default, but there is currently no option included to studentize the residuals. This is because studentized residuals are calculated using leverage statistics, whose formal theory relies on the absence of censored outcomes. It is therefore unclear how to studentize residuals when some outcome data are censored. Rather than attempt to studentize our residuals, we instead present the leverages as output to allow the user to further informally assess whether the lack of studentizing is likely to be a serious concern; we suspect that in most cases it will not be.

We have emphasized the connection between our approach and multiple imputation. However, since our analysis model can be fitted to censored outcome data using standard software, there is no need to resort to using multiple imputation here. Despite this, by conceptualizing our approach as a type of multiple imputation procedure, an alternative but closely related idea is to use standard complete case diagnostic methods on each of the multiply imputed datasets that can be produced using our method. Using standard model diagnostics for all imputed datasets in the context of multiple imputation is often recommended (Abayomi et al., 2008) and the same idea could be also used here. These standard diagnostic methods include producing studentized residuals, and so this resolves the difficulty we have encountered in studentizing our residuals. This idea also possesses other advantages: For example, as the residuals for each imputed dataset have the usual desirable properties (for instance, they sum to zero), the resulting residuals across all imputed datasets also have these properties. Conceptualizing our approach as a multiple imputation procedure therefore motivates using , instead of the pseudo outcomes , in the definition of the residuals.

We however prefer to define in the calculation of residuals, which instead motivates our approach. This is because our definition of a residual provides the usual, and single, residual for uncensored data, as provided in standard survreg output. The multiple imputation conceptualization instead provides multiple residuals for both censored and uncensored data, which can be presented as either separate residual plots for each imputed dataset or as a distribution of residuals for all observations on a single plot. In our opinion this unnecessarily complicates matters and does not provide what the applied statistician is likely to desire, which is a single residual plot similar to the one shown in Fig. 1, but where the observed data provide a single residual obtained in the usual way and where the uncertainty in the censored data is shown.

However, the disadvantages of our approach are that our residuals have not been shown to possess the usual standard properties and we have failed to provide a way to studentize residuals.

To summarize, we feel that we have provided an improvement on the current residual diagnostics for censored data. By displaying a distribution of residuals for censored outcomes on our residual plots, but retaining the usual residuals for uncensored outcomes, our plots are easily interpreted and enable applied statisticians to better assess whether standard linear models are appropriate for their datasets where some or all outcome data are censored.

Acknowledgments

The authors are grateful to the COPD research group at Imperial College London, headed by Jadwiga Wedzicha, for allowing us to use their data from the COPD trial. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health. The authors also thank the anonymous reviewer for a number of helpful suggestions, in particular regarding the importance of QQ plots.

Funding

This article presents independent research funded by the National Institute for Health Research (NIHR) under the Programme Grants for Applied Research programme (RP-PG-0109-10056).

Supplementary materials

• Plotting simulated data, R code details: Examples of censplot where the data are right- and interval-censored, and have a high proportion of censoring. Details of the more esoteric arguments of the function censplot. (PDF file)

• Full R code, producing simulated data: Full R code for censplot, along with code necessary to reproduce the simulated data used in Section 1.1.1 of the simulated data file. (PDF file)