Precipitation downscaling in Canadian Prairie Provinces using the LARS-WG and GLM approaches

Abstract

Two stochastic precipitation simulation models, namely the Long Ashton Research Station weather generator (LARS-WG) and a Generalized Linear Model-based weather generator (GLM-WG), are evaluated for downscaling daily precipitation at four selected locations (Banff, Calgary, Saskatoon and Winnipeg) in the Canadian Prairies. These weather generators model precipitation occurrence and amount components separately. Large-scale climate variables (including mean temperature, sea level pressure and relative humidity, derived from National Centers for Environmental Prediction reanalysis data) and observed precipitation records are used to calibrate and validate GLM-WG, while only observed precipitation records are used to calibrate and validate LARS-WG. A comparison of common statistical properties (i.e. annual/monthly means, variability of daily and monthly precipitation and monthly proportion of dry days) and characteristics of drought and extreme precipitation events derived from simulated and observed daily precipitation for the calibration (1961–1990) and validation (1991–2003) periods shows that both weather generators are able to simulate most of the statistical properties of the historical precipitation records, but GLM-WG appears to perform better than LARS-WG for simulating precipitation extremes and temporal variability of drought severity indices. For developing projected changes to precipitation characteristics, a change factor approach based on Canadian Global Climate Model (CGCM) simulated current (1961–1990) and future (2071–2100) period precipitation is used for driving simulations of LARS-WG, while for driving GLM-WG simulations, large-scale predictor variables derived from CGCM current and future period outputs are used. Results of both weather generators suggest significant increases to the mean annual precipitation for the 2080s. Changes to selected return levels of annual daily precipitation extremes are found to be both location- and generator-dependent, with highly significant increases noted for Banff with LARS-WG and for both Banff and Calgary with GLM-WG. Overall, 5- and 10-yr return levels are associated with increases (with the exception of Winnipeg) while 30- and 50-yr return levels are associated with site-dependent increases or decreases. A simple precipitation-based drought severity index suggests decreases in drought severity for the 2080s.

Abstract

Deux modèles stochastiques de simulation de la précipitation, notamment LARS-WG et un générateur de conditions météorologiques basé sur un modèle linéaire généralisé (GLM-WG), sont évalués pour la mise à l'échelle (downscaling) des précipitations journalières à quatre endroits sélectionnés (Banff, Calgary, Saskatoon et Winnipeg) dans les Prairies canadiennes. Ces générateurs de conditions météorologiques modélisent séparément les composantes de l’occurrence et du montant des précipitations. Des variables climatiques à grande échelle (y compris la température moyenne, la pression au niveau de la mer et l'humidité relative, provenant de centres nationaux de données de réanalyse de prévision environnementale) et des données de précipitations observées sont utilisées pour calibrer et valider le GLM-WG, tandis que des données de précipitations observées seulement sont utilisées pour calibrer et valider LARS-WG. Une comparaison des propriétés statistiques communes (ç-à-d les moyennes annuelles/mensuelles, la variabilité des précipitations journalières et mensuelles et la proportion mensuelle de jours secs) et des caractéristiques des événements de sécheresse et de précipitations extrêmes provenant de précipitations journalières simulées et observées pour les périodes de calibrage (1961-1990) et de validation (1991-2003) montrent que les deux générateurs de conditions météorologiques sont capables de simuler la plupart des propriétés statistiques des données historiques de précipitation, mais il semble que le GLM-WG simule mieux les extrêmes de précipitation et la variabilité temporelle des indices de sévérité de la sécheresse que le LARS-WG. Pour développer des projections des changements des caractéristiques des précipitations, une approche du facteur de changement climatique basée sur la précipitation simulée par le modèle canadien de climat global (CGCM) pour la période courante (1961-1990) et la période future (2071-2100) est utilisée pour les simulations du LARS-WG, tandis que pour les simulations du GLM-WG, des variables prédictives de grande échelle, provenant des sorties du CGCM pour les périodes courante et future, sont utilisées. Les résultats des deux générateurs de conditions météorologiques indiquent une augmentation significative de la moyenne des précipitations annuelles pour les années 2080. Les changements aux périodes de retour sélectionnées des extrêmes annuels de précipitations journalières sont trouvés être, à la fois, dépendants de l'emplacement et du générateur, avec des augmentations très significatives notées pour Banff avec le LARS-WG et pour les deux, Banff et Calgary, avec le GLM-WG. Globalement, des valeurs de retour de 5- et 10-ans sont associées à une augmentation (à l'exception de Winnipeg), tandis que les valeurs de retour de 30- et 50-ans sont associées à une augmentation ou diminution dépendamment du site. Un simple indice de la gravité de la sécheresse, basé sur la précipitation, suggère la diminution de la sévérité de la sécheresse pour les années 2080.

Introduction

Long-term changes or shifts in the historical climate are projected for different parts of the world on the basis of transient climate change simulations performed with Global Climate Models (GCMs) under anthropogenic forcing (Intergovernmental Panel on Climate Change [IPCC] 2007). Despite rapid ongoing developments in the models, direct use of GCM simulated precipitation for impact studies at fine spatial and temporal resolutions is still in question due to various model limitations (e.g. Hughes et al. 1993; Wilby et al. 2004; Wheater 2006; Meehl et al. 2007). To address such limitations, downscaling approaches are widely used to simulate time series of precipitation for climate change impact studies at local and regional scales (e.g. Fowler et al. 2007; Maraun et al. 2010; Mladjic et al. 2011; Poitras et al. 2011). These approaches can broadly be classified into two main families, i.e. dynamical and statistical downscaling (e.g. Giorgi and Mearns 1991; Wilby and Wigley 1997; Maraun et al. 2010).

In dynamical downscaling, Regional Climate Models (RCMs) driven by outputs from GCMs are used to study climate change and variability (Giorgi and Mearns 1999). RCMs, due to their higher spatial resolution compared to that of the GCMs, represent precipitation extremes better, as demonstrated in a number of recent studies (e.g. Seth et al. 2007; Prömmel et al. 2010; Di Luca et al. 2012). Although RCMs are expected to improve the signal-to-noise ratio of precipitation extremes (e.g. Kendon et al. 2010), there are still several limitations. For instance, despite being more efficient than the driving GCMs, RCMs are still computationally expensive (e.g. Mearns et al. 2003). Therefore, multiple simulations from RCMs for uncertainty analysis are still challenging. Moreover, RCMs are likely to inherit some of the biases of the driving GCMs (Durman et al. 2001).

As an alternative to dynamical downscaling, the statistical downscaling approach is used to address discrepancies between coarse-scale GCM outputs and local-scale observations, based on empirical relationships between observations and large-scale GCM features (e.g. Christensen et al. 2008). Thus, the accuracy of this approach depends directly on the credibility of the GCM to model large-scale features. This methodology has the advantages of being inexpensive and computationally simple. In addition, some variants, such as the GLM approach discussed below, can provide an analytical capability with which to evaluate the explanatory power of different GCM output variables, and hence enable selection of more robust driving variables than GCM-simulated precipitation. Some statistical downscaling approaches can also produce stochastic simulation ensembles that allow some quantification of uncertainty in the projected climate change signal, which is an important issue (e.g. Maraun et al. 2010; Chun 2011). Among others, Wilby and Wigley (1997) and Maraun et al. (2010) provide classification of statistical downscaling approaches. These approaches can be classified into three main categories, i.e. regression methods or transfer functions, weather typing and weather generators. Transfer functions are based on direct quantitative relationships between predictand and predictors through regression-like methods, while weather typing approaches involve grouping of atmospheric circulation patterns in relation to local climatic variables. Weather generators consist of several continuous or categorical empirical relationships that depend on large-scale atmospheric features for deriving their parameters. A common assumption to all statistical downscaling methods is that the physical relationships underlying the statistical relationships identified over a reference historical period remain valid for the future period (Wilby et al. 2004; Vrac et al. 2007). The current study concerns only the use of weather generators. Originally developed for stochastic simulation of long sequences of weather variables (e.g. temperature and precipitation) using information from short observed samples (e.g. Richardson and Wright 1984; Racsko et al. 1991), weather generators are becoming popular for downscaling current and future period weather variables for evaluating site-specific climate variability and its impact on environment and society (e.g. Semenov et al. 1998; Jones et al. 2009).

In the Canadian context, there have been some attempts to use weather generators for modelling precipitation (e.g. Qian et al. 2004). However, studies of their use to assess multi-scale precipitation characteristics under climate scenarios are limited, particularly for the Canadian Prairies. This part of Canada is of significant importance to the Canadian economy from the viewpoint of its agricultural production and natural resources and has often faced competing water demands for domestic, industrial and agricultural usage. It has also experienced extreme floods and several extensive and persistent droughts. Therefore, the results of the study, particularly of future projections of climate variability, should be helpful in guiding improved adaptation and management decisions.

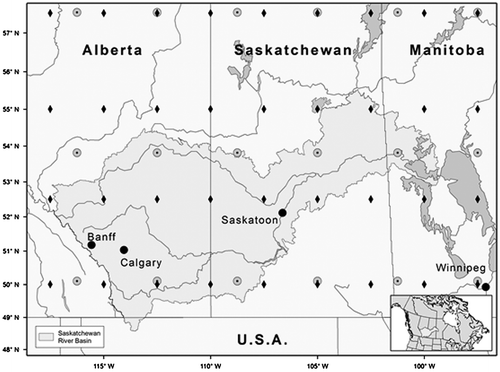
In this study, two widely used stochastic weather generators are employed to simulate daily precipitation series to assess climate variability and change at four typical prairie locations (i.e. Banff, Calgary, Saskatoon and Winnipeg; Figure 1) at various time scales. The weather generators used are LARS-WG, developed at the UK Long Ashton Research Station (Semenov and Stratonovitch 2010), and a Generalized Linear Model (GLM) based approach, proposed by Chandler and Wheater (2002). LARS-WG was initially proposed for generating weather sequences (e.g. temperature and precipitation series) for agricultural studies (Racsko et al. 1991; Semenov and Barrow 1997). Some recent studies (e.g. Zhang et al. 2011) have employed this weather generator for climate change assessment, while others have used it for assessing the performance of modified weather generators. LARS-WG is generally well suited for various climatic regions (e.g. Qian et al. 2008).

Figure 1 Canadian Prairie Provinces with the four selected study sites (Banff, Calgary, Saskatoon and Winnipeg), overlain by National Centers for Environmental Prediction (NCEP; black diamonds) and Canadian Global Climate Model (CGCM; grey circles with black centres) grid cells. Inset shows the location of the study area in North America.

Using the GLM framework, Chandler and Wheater (2002) proposed a stochastic precipitation modelling approach that can incorporate indices of large-scale, low-frequency climate patterns (such as the North Atlantic Oscillation) based on a two-stage precipitation model of Coe and Stern (1982). This GLM approach has been used to assess possible impacts of climate variability for various climatic regions ranging from semi-arid (Mirshahi et al. 2008) to temperate (Chandler and Wheater 2002), and for assessment of flood and drought risk in the UK (Chun et al. 2012). Many precipitation modelling algorithms, such as Markov chain models of different orders (e.g. Richardson and Wright 1984; Stöckle et al. 1998; McKague et al. 2003), can be considered as special cases of the more versatile GLM approach (Yang et al. 2005). Herein, this approach is referred to as GLM-WG (Generalized Linear Model-based weather generator) for simplicity and ease of presentation.

This paper is arranged as follows: data and methods are described in the next section, and detailed results of the study ranging from calibration and verification of the selected weather generators to their intercomparison based on ensembles of simulations are given. In the last section of the paper, conclusions and discussion of the implications of the results obtained, as well as potential further developments of the two weather generators, are presented.

Data and methodology

Study area and data

As mentioned in the introduction, the focus of the present study is on the southern Canadian Prairies. Figure 1 shows a map of the study area and the location of the four prairie sites selected for the study (Table 1). Three of the four sites (i.e. Banff, Calgary and Saskatoon) are located in the Saskatchewan River Basin, which forms the basis of a much larger effort focused on climate change and future water security in this river basin. These, together with the availability of relatively complete long-term instrumental records, were important factors in the selection of sites. Daily precipitation records were obtained from the Canadian Daily Climate Data (CDCD) portal (www.climate.weatheroffice.gc.ca) for the 1961 to 2003 period. For Banff, precipitation records are available from two stations, 3050520 and 3050519, for the 1961–1994 and 1995–2003 periods, respectively. However, the two stations have relatively different annual precipitation totals (see Table 1). Therefore, only station 3050520 for the period between 1961 and 1994 is used for the model formation at Banff (See the section on Model calibration, validation and performance assessment for more details).

Table 1. Information about meteorological stations used in the study.

Station name (identification number)	Longitude	Latitude	Elevation	Data period	Annual precipitation (mm)
	(Decimal degrees)	(Decimal degrees)	(m)
Banff CS (519)	–115.6	51.2	1397	1995–2003	328
Banff (520)	–115.6	51.2	1384	1961–1994	468
Calgary (1093)	–114.0	51.1	1084	1961–2003	407
Saskatoon (7120)	–106.7	52.2	504	1961–2003	352
Winnipeg (3222)	–97.2	49.9	239	1961–2003	520

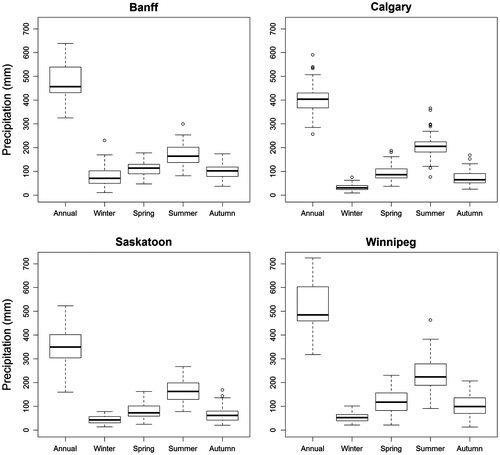
For an overview, boxplots of annual and seasonal precipitation totals obtained from the 1961–2003 period are shown in Figure 2. These sites have a similar seasonal pattern of precipitation, with wet summer months (June, July and August) and relatively dry winter months (December, January and February). On average, both spring (March, April and May) and autumn (September, October and November) receive more precipitation than winter but less than summer. Of the four sites, Saskatoon receives the least amount of precipitation on an annual time scale. Regarding the possible climate drivers of precipitation, Bonsal (2011) has presented an analysis in the Prairies region containing the four studied sites.

Figure 2 Boxplots of annual (January to December) and winter (December, January and February), spring (March, April and May), summer (June, July and August) and autumn (September, October and November) precipitation observed at Banff, Calgary, Saskatoon and Winnipeg. The boxes correspond to the interquartile range (IQR), the line in the middle of the box to the median value and the whiskers to either the maximum value or to 1.5 times the IQR. Outliers that lie outside the 1.5 times IQR range are shown using circles.

Gridded values of large-scale climate variables from National Centers for Environmental Prediction (NCEP) reanalysis data (Kalnay et al. 1996) are used to drive GLM-WG simulations for calibration and verification periods. The NCEP outputs are available at 2.5-degree latitude (90N–90S) 2.5-degree longitude (0E–357.5E) global grids. Although there are 17 pressure levels ranging from 1000 to 10 hPa, not all variables are available at all levels. Generally, reanalysis data products are obtained through assimilating diverse data types including data from land surface, ship, satellite and other sources. Details of the NCEP data assimilation approach can be found in Kalnay et al. (1996). The NCEP large-scale variables considered in this study include mean sea level pressure (SLP), mean temperature (T) and relative humidity (RH). The same large-scale climate variables derived from CGCM outputs are used for developing projected changes to precipitation characteristics (discussed later). The CGCM outputs are available on a spatial grid with 96 longitudinal and 48 latitudinal cells which are approximately 3.75 degrees 3.75 degrees. Similar to the NECP outputs, 17 pressure levels from 1000 to 10 hPa are considered in the CGCM. Details of the model and available outputs are available in Flato and Boer (2001). As most of the NCEP and CGCM outputs at different pressure levels are found strongly related at the four selected sites, near the surface outputs are used in the study for detailed analysis.

Many previous studies (e.g. Hughes et al. 1993; Leith 2005), motivated by the assumption that GCMs simulate large-scale atmospheric circulation better than the local-scale climate variables, have adopted this approach. Two simulations of the CGCM are considered: one is for the 1961–1990 historical reference period, that uses the 20C3M scenario, and the other corresponds to 2071–2100, that uses the IPCC Special Report on Emissions Scenarios (SRES) A1B scenario (Flato and Boer 2001; Nakicenovic et al. 2000). Unlike GLM-WG, LARS-WG requires only observed precipitation records for its calibration and verification, and it uses a “change-factor” approach for developing projected changes to precipitation characteristics. The change factors are derived on the basis of the ratios of the monthly mean values of precipitation characteristics (e.g. mean precipitation amount and mean lengths of wet and dry spells) from the reference and future period climate model simulations.

Stochastic precipitation models

LARS-WG

Due to its flexible structure, LARS-WG is available in a number of different structural forms (Semenov and Stratonovitch 2010). In general, the generator simulates precipitation series from semi-empirical distributions of wet and dry spells and precipitation amounts. These semi-empirical distributions are developed from historical records using a fixed number of bins and represent a discretized form of the observed probability distribution (Semenov and Barrow 2002). The length of a wet day sequence (the definition of a wet day is discussed later in another subsection) is randomly sampled from the semi-empirical distribution on the basis of the proportion of events falling in each bin, assuming a uniform distribution for each bin. The same procedure is followed for sampling dry day sequences. Transition from a wet (dry) day sequence to dry (wet) day sequence is controlled by the observed proportion of wet/dry days. For a given wet day, the precipitation amount is generated from the same semi-empirical distribution of precipitation for a particular month, but independent of the length of the wet day sequence and/or independent of the amount of precipitation on previous days (Semenov and Barrow 2002). Similar to the sampling of wet and dry day sequences, the proportion of events in each bin of the semi-empirical distribution of precipitation amount is used as the selection probability for each of the considered bins.

GLM-WG

The GLM-WG framework is based on modelling precipitation occurrence and precipitation amount processes (Chandler and Wheater 2002). The occurrence process is modelled using a logistic regression as:(1)

where is the probability of precipitation occurrence for the ith day, is a transposed predictor vector and is a coefficient vector. The sizes of predictor and coefficient vectors depend on the number of parameters in the model (Table 2).

Table 2. Identified Generalized Linear Model-based weather generator (GLM-WG) structures for four studied sites. I[Y(t–1)>0] is an indicator function for precipitation occurrence on previous day. ln[1+Y(t–1)] represents log transformed previous day precipitation.

Precipitation occurrence model components	Banff	Calgary	Saskatoon	Winnipeg
Precipitation occurrence model components	Banff	Calgary	Saskatoon	Winnipeg
Constant	Y	Y	Y	Y
Sea level pressure (SLP)	Y	Y	Y	Y
Temperature (T)	Y	Y	Y	Y
Relative humidity (RH)	Y	Y	Y
I[Y(t–1)>0]	Y	Y	Y	Y
Daily seasonal effect, cosine component (cos)	Y	Y	Y	Y
Daily seasonal effect, sine component (sin)	Y	Y	Y	Y
2-way interaction: SLP and cos	Y
2-way interaction: SLP and sin	Y
2-way interaction: T and cos		Y
2-way interaction: T and sin		Y
2-way interaction: T and winter months index			Y
2-way interaction: T and spring months index			Y
Number of parameters	9	9	9	6
Precipitation amounts model components	Banff	Calgary	Saskatoon	Winnipeg
Constant	Y	Y	Y	Y
Sea level pressure (SLP)	Y		Y	Y
Temperature (T)		Y
Relative humidity (RH)		Y
ln[1+Y(t–1)]	Y	Y	Y	Y
Daily seasonal effect, cosine component	Y	Y	Y	Y
Daily seasonal effect, sine component	Y	Y	Y	Y
Winter months index		Y
Summer months index		Y
2-way interaction: T and spring months index	Y
Dispersion parameter	Y	Y	Y	Y
Number of parameters	7	9	6	6

Y: means the component included in the model structure.

The expected daily precipitation amount on a wet day i () is modelled using a gamma distribution with a constant dispersion parameter (ν) and a log link function:(2)

where is a transposed predictor vector and γ is a coefficient vector. The predictor vectors and consist of large-scale climate predictors and other variables, representative of seasonal fluctuations, and their interactions. Thus, in contrast to LARS-WG, GLM-WG simulates precipitation based on driving climate states at a specific time at a specific location.

Although GLM-WG has been used in Europe (e.g. Chandler and Wheater 2002; Yang et al. 2005), Africa (Kenabatho et al. 2008), Asia (Mirshahi et al. 2008), Australia (Frost 2007) and South America (Furrer and Katz 2007) to study climate variability, it has not been fully examined in North America.

Model calibration, validation and performance assessment

Both weather generators require site-specific calibration. Observed precipitation data from 1961–1990 are used for calibration and those from 1991–2003 for validation. Based on the results of the Wilcoxon rank sum test, the medians of the annual total precipitation distributions for all four sites are not significantly different for the validation and calibration periods. In a similar manner, the Kolmogorov Smirnov (KS) tests are performed on monthly basis. Generally, the results of the KS tests are not found significant for summer and autumn months, but are found significant for some winter (a dry period) and spring (that represents dry to wet transition period) months. For practical purposes, we assume that the calibration and validation period time series of precipitation have stable descriptive statistics (i.e. stationarity on the annual scale), despite few significant differences noticed at the monthly scale.

For calibrating LARS-WG, semi-empirical distributions of wet and dry day sequences are developed for the 1961–1990 period using a fixed number of bins (i.e. 23) for each month of the year. Similarly, semi-empirical distributions of precipitation amount are also developed for each month. These distributions are used to randomly generate wet and dry day sequences and precipitation amount on each wet day, following the procedure described above. For validating LARS-WG, simulated sequences of precipitation for the validation period (1991–2003) are generated using semi-empirical distributions from the calibration period (1961–1990). Additional discussion on this subject is provided later.

For calibrating GLM-WG, in addition to the set of large-scale climate predictors (i.e. SLP, T and RH), a simple Fourier representation of the annual cycle at the daily timescale is considered to capture seasonality in the precipitation occurrence and amount models. Additional interaction terms between large-scale predictors and cyclic terms are also considered. A previous day precipitation state indicator (I[Y(t–1)>0]) is included to capture short-term persistence in the precipitation occurrence process; inclusion of too many higher-order dependence terms can lead to over-dispersion problems that damp down extremes and interannual variability (e.g. Katz and Parlange 1998). Each of the candidate predictors (i.e. SLP, T, RH, zonal wind, meridional wind, wind speed, daily seasonal effects, previous day’s precipitation and various interaction terms) is screened using the likelihood ratio test (Chandler 2006) and abiding by the principle of parsimony in choosing an appropriate model structure. Large-scale predictor variables from NCEP reanalysis are standardized using 1961–1990 period mean and standard deviation before implementing the predictor screening following procedures from Leith (2005). One of the attractive advantages to using the standardized climate variables is that the bias between reanalysis data and climate model outputs can be alleviated to some extent (Leith 2005).

Each of the two weather generators is calibrated over the 1961–1990 period. The calibrated weather generators are used to simulate 100 precipitation series for the entire 1961–2003 period. From these simulations, subsamples for the 1991–2003 period are used for validation. This implies observational stationarity, which is less stringent an assumption for GLM-WG compared to LARS-WG. Recognizing that this strategy favours GLM-WG in validation, an alternate evaluation of LARS-WG is also performed by estimating its parameters solely from the precipitation observations for the validation period.

Performance assessment of the calibrated weather generators is carried out by comparing various statistics derived from simulation ensembles with those derived from observed records. Six statistics including mean, variance and autocorrelation of daily precipitation sequences, mean and variance of monthly and yearly accumulations and proportion of dry days (PDD) are considered.

In addition to the above-mentioned statistics, observed and simulated distributions of annual daily precipitation extremes and precipitation-based indices of drought patterns are also assessed. Gumbel probability plots are used to compare observed and simulated annual daily precipitation extremes. A Drought Severity Index (DSI) proposed by Phillips and McGregor (1998) is used to compare characteristics of observed and simulated drought patterns. Droughts lasting for at least three months and longer are evaluated using DSI3 values. Though DSI is commonly used in Europe to characterize drought patterns (e.g. Chun et al. 2012), its applications in Canada are limited, but starting to emerge (PaiMazumder et al. 2012). A DSIn series represents accumulated n monthly precipitation deficit (i.e. the cumulated amount below the n monthly average) as a fraction of the mean annual precipitation. For this study, DSI3 represents the accumulated 3-monthly precipitation deficit with respect to the mean annual precipitation over the 1961 to 1990 period. According to Phillips and McGregor (1998) and PaiMazumder et al. (2012), a drought event occurs when DSI exceeds 10 (i.e. when the accumulated precipitation deficit is greater than 10% of the mean annual precipitation). Based on the studies for the UK (Phillips and McGregor 1998; Chun et al. 2013), more than 95% of the observed DSI3 values were less than 25 and the highest values were usually around 50.

Projected changes to precipitation characteristics

For simulating precipitation under climate scenarios, LARS-WG adopts a “change factor” method (e.g. Semenov and Barrow 1997; Semenov and Stratonovitch 2010). Statistics of CGCM-simulated precipitation for reference and future climate are used to construct change factors, which are then used to perturb historical observations that constitute the weather generator’s parameters in the form of semi-empirical distributions. As a result, a LARS-WG-simulated yearly series for a future time horizon does not correspond to a specific year in the historical period. For the case of GLM-WG, calibrated models of occurrence and amount processes are used to simulate precipitation sequences for current and future periods using respective large-scale predictors from the CGCM.

Projected changes to annual/seasonal precipitation totals, 5-, 10-, 30- and 50-year return levels of annual daily precipitation extremes and drought severity indices are assessed by comparing current and future period simulation ensembles for each of the two weather generators separately. For both current and future periods, each considered statistic (e.g. 10-year return level of annual daily precipitation) is obtained from 100 simulated samples. The mean/median values from the simulated sets of statistics for current and future periods are used to study relative projected change, while the entire sets of simulated statistics are used to analyse statistical significance of the projected change using the rank sum test (Wilcoxon 1945).

Other considerations

Another important point of concern is the selection of a suitable threshold for defining precipitation events. According to Yang et al. (2006), selection of a suitable threshold can remove trace values and resolve problems of data inconsistency, but loss of information may become a concern in the case of high thresholds. Although a higher threshold (e.g. 1 mm which is recommended by the World Meteorological Organization for a day to be a wet day; Tank et al. 2009) can improve accuracy of the occurrence model in GLM-WG, it causes under-dispersion in the amounts model and can lead to poor results for precipitation extremes. Since simulating precipitation extremes is an important feature of a weather generator, a 0.2-mm threshold is used for defining a wet day, after examining thresholds between 0.2 and 1 mm. For performing a test of significance for changes in various characteristics of precipitation (e.g. selected return levels of annual maximum daily precipitation), the 5% significance level is used throughout the paper. Detailed results are presented only for Saskatoon and a summary of the results is provided for the other three sites (i.e. Banff, Calgary and Winnipeg). Where appropriate, results for all four sites are presented to support overall conclusions.

Results

Calibration, validation and performance evaluation of LARS-WG and GLM-WG

Both weather generators are calibrated following the procedures described in the methodology section. For LARS-WG, this procedure is fairly straightforward, while that for GLM-WG requires detailed discussion. Identified structures of occurrence and amount models are summarized in Table 2. From the set of large-scale climate predictors, SLP and T are found to be significant variables for precipitation occurrence model at all sites. Except for Winnipeg, RH is also found to be an important predictor variable for precipitation occurrence at the other three sites. A possible reason that the relative humidity variable has less explained power at Winnipeg compared to the other sites is that the distribution of relative humidity is rather more uniform across the entire year. For the occurrence models, Fourier representation of the annual cycle at the daily timescale and previous day precipitation state indicator are found to be indispensable predictors. Additional interactions between SLP and cyclic terms for Banff, T and cyclic terms for Calgary, and T and seasonal indices for Saskatoon are found to be influential secondary predictors.

Compared to the occurrence models, the precipitation amounts models are generally simpler and have lesser or equal numbers of predictor variables. As for the occurrence models, Fourier representation of the annual cycle is necessary to characterize the temporal structure of the amount models. In addition, the amount of the previous day’s precipitation (ln[1+Y(t-1)]) is used. For Calgary, the amounts model requires further indices for winter and summer months to capture seasonality. The models for Saskatoon and Winnipeg include SLP, while the model for Calgary includes RH and T as external driving variables. For Banff, the model includes SLP and spring temperature (i.e. two way interactions of T and spring months’ index). The more complicated structure of the model for Calgary, which requires a larger number of parameters, may be due to dynamic local seasonal climate processes such as the Chinook. Overall, the number of GLM-WG parameters is less than 20 (see Table 2), which is also less than the number of parameters (more than 100) required for LARS-WG. In general, parametric approaches are usually parsimonious because the modelled distributions are summarized in terms of a few statistics, whereas semi-parametric approaches need more parameters in order to capture various features of the empirical distributions.

In addition to likelihood tests, optimality of identified GLM-WG structures was also ensured using residual analysis as proposed in Chandler and Wheater (1998a, 1998b). Such diagnostics (results are not shown) were performed for each of the four sites and for each of the occurrence and amount models separately. Based on this analysis, the identified model structures reported in Table 2 were found adequate.

Daily statistics

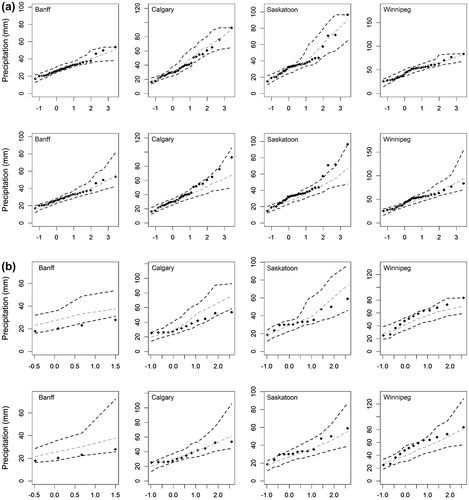
To evaluate the performance of the weather generators, quantile-quantile (Q-Q) plots are often used to compare simulated and observed distributions of variables of interest (e.g. Qian et al. 2008). Such plots for LARS-WG and GLM-WG simulated daily precipitation amount are shown in Figure 3. If the points of a Q-Q plot align along a 1:1 diagonal line, the simulated distribution is deemed to be consistent with the observed distribution. Overall, the results of Figure 3 suggest that both weather generators are able to simulate observed precipitation for both calibration and verification periods. This figure also suggests that daily extremes may have reduced from larger (in the calibration period) to smaller values (in the verification period) at Banff, Calgary and Saskatoon. There may be differences in the daily precipitation characteristics between the calibration and verification periods (i.e. lack of stationarity). One possible explanation of this change in the extreme behavior is that the verification period is much shorter than the calibration period and that may not be enough to capture fully variability in extremes. Figure 8 (presented later in this section) provides a better comparison of extremes.

Figure 3 Quantile-quantile (Q-Q) plots of observed and simulated daily precipitation for the (a) calibration and (b) verification periods. Diagonal line represents perfect match. LARS-WG is the Long Ashton Research Station weather generator, and GLM-WG is the Generalized Linear Model-based weather generator.

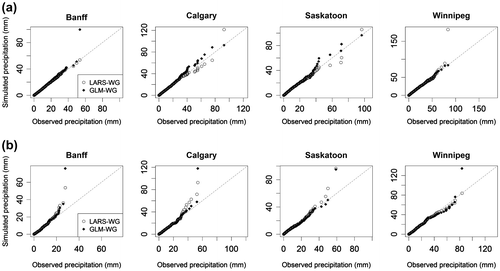
A closer look at the plots (Figure 3) suggests that both generators produce more heavy precipitation events than those present in the historical records. This tendency is relatively more obvious for GLM-WG than LARS-WG. For the latter generator, this behavior could be explained on the basis of the last bin of the semi-empirical distribution containing a higher proportion of larger daily precipitation values not actually observed. For the former generator, this behavior could be due to the reason that it is a parametric approach that may simulate much larger values than actually observed.

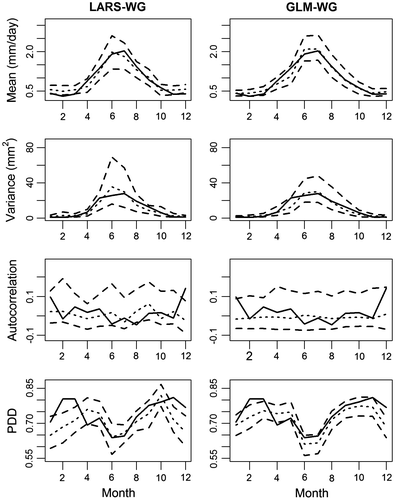
Plots of mean, variance and lag-1 correlation of observed and simulated daily precipitation values and proportion of observed and simulated dry days for each month of the year for the calibration period are shown in Figure 4 for Saskatoon. Generally observed statistics lie within the 95% confidence band derived from 100 simulated samples. However, certain discrepancies can be noted. For example, both weather generators are unable to reproduce lag-1 correlations for July. Apparently, the missed lag-1 autocorrelation is related to inadequate capture of summer convective precipitation in the Prairies, for which the two generators may need to be improved. Overall, mean and variability of daily precipitation values are generally well simulated. However, slightly worse performance is noticed for winter and spring seasons. The proportion of dry days is poorly estimated for most of the winter, spring and fall months by both weather generators. Similar plots for the verification period shown in Figure 5 suggest that the performance of both weather generators is comparable to that for the calibration period. The PDD values for some winter and spring months lie outside the confidence bands in Figure 5. This behavior could be attributed to lack of stationarity in seasonal patterns of precipitation in calibration and verification periods noted earlier at the monthly scale. In summary, the results of calibration and verification for Banff, Calgary and Winnipeg are similar to those for Saskatoon except that both generators perform poorly in simulating lag-1 correlation for February.

Figure 4 Comparison of observed (solid lines) and ensemble averaged simulated (small dashed lines) values of mean, variance, first autocorrelation and proportion of dry days (PDD) derived from daily precipitation sequences for Saskatoon for the calibration period. Upper and lower large dashed lines correspond to 2.5^th and 97.5^th quantiles, respectively. LARS-WG is the Long Ashton Research Station weather generator, and GLM-WG is the Generalized Linear Model-based weather generator.

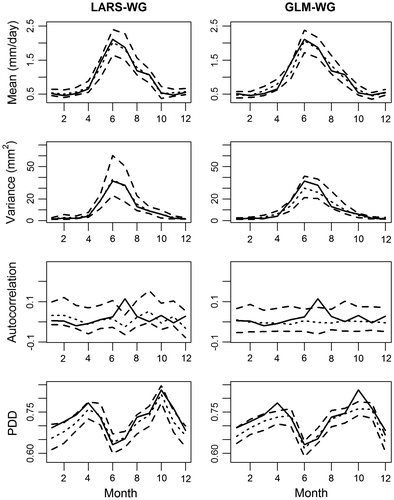
Figure 5 Comparison of observed (solid lines) and ensemble averaged simulated (small dashed lines) values of mean, variance, first autocorrelation and proportion of dry days (PDD) derived from daily precipitation sequences for Saskatoon for the verification period. Upper and lower large dashed lines correspond to 2.5^th and 97.5^th quantiles, respectively. LARS-WG is the Long Ashton Research Station weather generator, and GLM-WG is the Generalized Linear Model-based weather generator.

Aggregated statistics

Monthly and annual statistics are also important aspects of the performance of weather generators (e.g. Jones et al. 2009). Plots of mean and variance of observed and simulated monthly precipitation for the calibration period are shown in Figure 6a for Saskatoon. These results are obtained from 100 simulated 30-year series. Both weather generators perform reasonably well in simulating mean and variance of monthly precipitation for the calibration period but perform relatively poorly in simulating variance of monthly precipitation for some of the winter and spring months. The performance of GLM-WG is not as good as that of LARS-WG in simulating variance of monthly precipitation, generally resulting in less variable monthly precipitation. For the verification period, results of a similar evaluation are shown in Figure 6b for Saskatoon. Generally, these results are consistent with those for the calibration period, except that the discrepancy between observed and simulated variance of monthly precipitation is more obvious for spring months. Similar behavior was noted for the other three sites. Overall, the precipitation variance for winter and spring months is challenging for both generators to simulate.

Figure 6 Comparison of observed (solid lines) and ensemble averaged simulated (small dashed lines) values of mean and variance of monthly precipitation for Saskatoon for the (a) calibration and (b) verification periods. Upper and lower large dashed lines correspond to 2.5^th and 97.5^th quantiles, respectively. LARS-WG is the Long Ashton Research Station weather generator, and GLM-WG is the Generalized Linear Model-based weather generator.

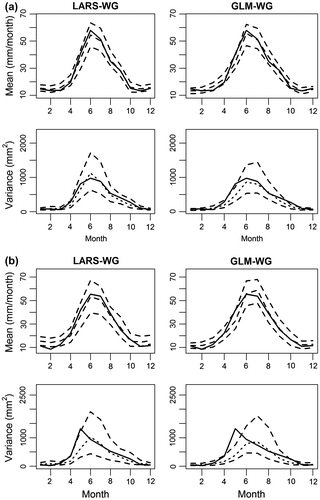
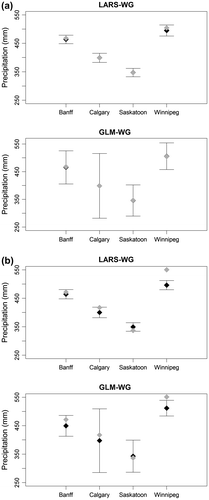
Figure 7 shows observed mean annual precipitation in comparison to both LARS-WG and GLM-WG simulations, along with 95% confidence bands. Although the observed and ensemble-averaged simulated mean annual precipitation values agree with each other for all four sites, the variability in the GLM-WG simulated annual precipitation is considerably larger compared to that of the LARS-WG simulated annual precipitation. This behavior is particularly obvious for Calgary (see Figure 7). For the verification period, both generators apparently perform well for Banff, Calgary and Saskatoon but not for Winnipeg. The poor performance for Winnipeg in the verification period requires additional investigation.

Figure 7 Observed (black dots) and ensemble averaged simulated (grey dots) mean annual precipitation along with the 95% confidence bands derived from 100 simulated precipitation series. LARS-WG is the Long Ashton Research Station weather generator, and GLM-WG is the Generalized Linear Model-based weather generator.

Precipitation extremes and drought indices

Since precipitation-related extremes impact human society in various ways, it is important to analyse how well a weather generator is able to simulate observed distributions of extremes. Figure 8a shows Gumbel plots of observed and simulated annual daily extremes for all four sites for the calibration period. There are clear differences between the LARS-WG and GLM-WG simulations. For LARS-WG, there are no extremes that are higher than the largest historical extremes. As a consequence, the LARS-WG simulations appear to level off around the largest historical extremes. Such a behavior is expected since LARS-WG uses semi-empirical distributions of daily precipitation values. In contrast, GLM-WG is able to produce precipitation extremes in a reasonable manner and with a more natural-looking spread. Although the GLM-WG can in principle generate physically-questionable high precipitation values (e.g. Chun 2011), the simulations in this study did not experience this problem. Thus, the parametric approach appears to be more suitable for precipitation modelling at the four studied sites. Results for the verification period shown in Figure 8b generally support these conclusions. However, because of the limited amount of observed data for Banff for the verification period, only limited evaluation is possible for this site, and therefore concrete conclusions cannot be drawn.

Figure 8 Gumbel probability plots of observed (black dots) and ensemble averaged simulated (grey lines) annual daily precipitation extremes for the (a) calibration and (b) verification periods. Upper and lower dashed lines correspond to 2.5^th and 97.5^th simulated quantiles, respectively. LARS-WG is the Long Ashton Research Station weather generator, and GLM-WG is the Generalized Linear Model-based weather generator.

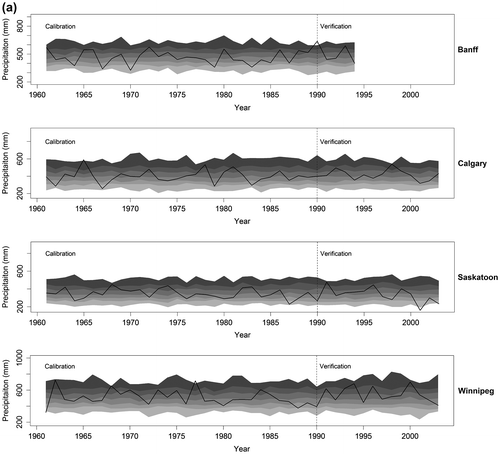
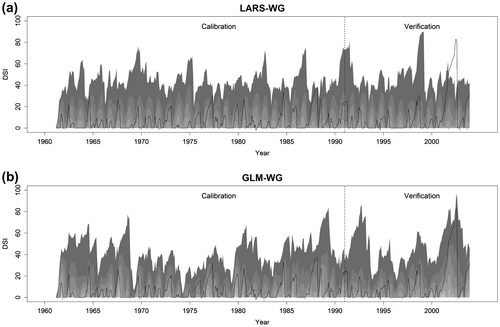
Since drought patterns evolve over time, it is important to assess how well the two weather generators are able to simulate the temporal behavior of monthly and/or annual precipitation before discussing DSI results. Observed and simulated annual precipitation totals along with 5th, 25th, 50th, 75th, and 95th quantile values obtained from an ensemble of 100 simulations are shown in Figure 9 for all four sites for both calibration and verification periods. The LARS-WG simulated values do not vary over time as much as those simulated by GLM-WG. As a consequence, interannual variations are more obvious in GLM-WG simulations. The main reason could be that the GLM-WG simulations instantaneously respond to the influence of external driving climate variables (i.e. SLP, T and RH). At the monthly time scale, almost the same temporal differences were noticed between the LARS-WG and GLM-WG simulated precipitation series (results are not shown).

Figure 9 Time series plots of observed (black solid line) and (a) the Long Ashton Research Station weather generator (LARS-WG) and (b) the Generalized Linear Model-based weather generator (GLM-WG) simulated (greyscale bands) annual precipitation for the calibration and verification periods. For simulated precipitation, mean and 0–5, 5–25, 25–50, 50–75, and 75–95 and 95–100th quantile intervals (from light to dark grey) derived from 100 simulated samples are shown.

In Figure 10, the temporal evolution of observed and simulated values of DSI3 is shown for Saskatoon for both calibration and verification periods. Generally, the observed values of DSI3 lie within the simulated envelope of DSI3 (i.e. 5th and 95th quantile values) for both generators; the temporal patterns of DSI3 are relatively invariant over the calibration period compared to the patterns simulated by GLM-WG. For the validation period, LARS-WG simulated drought patterns also exhibit considerably less variability over time compared to the case of GLM-WG. As a consequence, LARS-WG is not able to capture 2001–2004 drought and GLM-WG is able to do so because the DSI3 values for the 2001 to 2004 period lie within the 99th percentile of the simulated distribution of DSI3. Moreover, higher values of simulated DSI3 by GLM-WG for the 1960s and late 1980s correspond well to Canadian Prairie droughts of the twentieth century, identified in previous studies (e.g. Bonsal and Wheaton 2005; Bonsal et al. 2011). The results of Figure 10 elaborate further the importance of interannual and interseasonal variability in simulated precipitation and suggest that the GLM-WG could be a useful tool for drought assessment and management related applications.

Figure 10 Plots of observed and simulated values of Drought Severity Index (DSI3) for droughts lasting for at least 3 months at Saskatoon. Greyscale bands (from light to dark grey) correspond to 0–5, 5-25, 25–50, 75–95 and 95–100th quantiles intervals derived from the simulated ensemble. LARS-WG is the Long Ashton Research Station weather generator, and GLM-WG is the Generalized Linear Model-based weather generator.

Finally, we present a summary of the evaluation of LARS-WG simulations when this generator is calibrated using the validation period observed precipitation data. In this case, LARS-WG uses more information from the validation period observations than GLM-WG. Interestingly, the LARS-WG results are not very different from the results presented above under the assumption of observational stationarity. However, the second set of results performs better in Q-Q plots and monthly statistics comparisons. Concerning comparison of extremes, the GLM-WG does a better job compared to both types of validation of LARS-WG, i.e. (1) LARS-WG cannot generate extreme values larger than the historically observed and (2) LARS-WG cannot capture drought timings satisfactorily, although it produces more severe droughts in the second validation method.

Projected changes

After investigating the performance of the two weather generators through various diagnostics at multiple temporal scales, the calibrated weather generators are used to study projected changes to precipitation characteristics for the 2080s (2071–2100) with respect to 1970s (1961–1990). In this respect, it is useful to investigate first the differences between the distributions of large-scale climate variables (i.e. T, SLP and RH) for the current and future climate. Figure 11 shows the distributions of large-scale climate variables obtained from NCEP reanalysis data and CGCM current and future period outputs for Banff, Calgary, Saskatoon and Winnipeg. Overall, the distributions of CGCM climate variables match well those derived from NCEP reanalysis data for the current period. It is interesting to notice that the future distributions of SLP and RH are not much different from those of the current period. However, distributions of T have shifted to the right, which suggests that T will contribute significantly in driving future period precipitation series using GLM-WG.

Figure 11 Probability density functions of the standardized large-scale climate variables (SLP, T and RH) derived from Canadian Global Climate Model (CGCM) outputs for current (1961–1990) (grey solid lines) and future (2071–2100) (grey dashed lines) periods. Probability density functions of the same variables derived from National Centers for Environmental Prediction (NCEP) reanalysis data (black lines) for the current (1961–1990) period are also shown. Plots from the first to fourth rows correspond to Banff, Calgary, Saskatoon and Winnipeg, respectively.

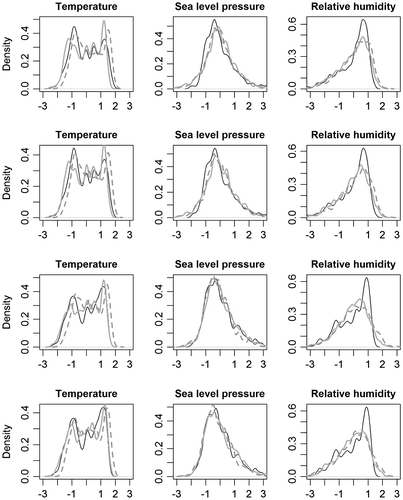
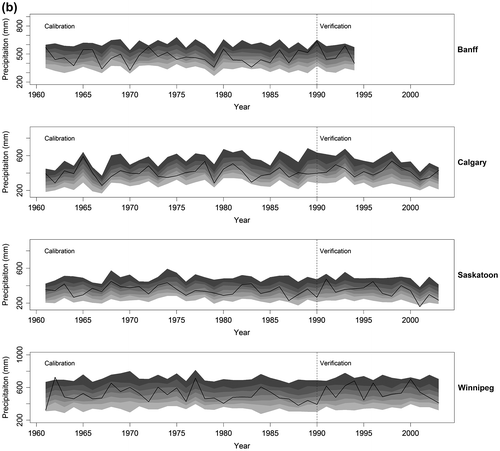
Figure 12 shows LARS-WG and GLM-WG downscaled annual precipitation for the 2080s. Similar to the results shown in Figure 9, LARS-WG simulations lack interannual variability. In comparison, the interannual variability signal is clearly visible in the case of the GLM-WG simulations. Compared to an observed median annual precipitation of ∼340 mm for Saskatoon for the 1961–1990 reference period, LARS-WG (GLM-WG) simulation for the 2080s is about 400 mm (390 mm). This result suggests that Saskatoon will get wetter on average although the lowest simulated 2080s annual total precipitation is less than 200 mm.

Figure 12 Downscaled annual precipitation for 2080s using the Long Ashton Research Station weather generator (LARS-WG) and the Generalized Linear Model-based weather generator (GLM-WG) for Saskatoon. Greyscale bands (from light to dark grey) correspond to 0–5, 5–25, 25–50, 50–75 and 95–100th quantile intervals of the simulated ensemble.

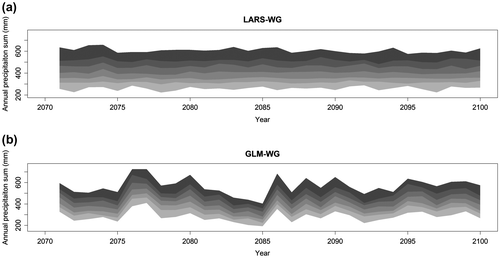
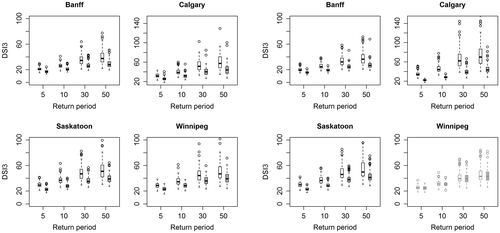
Figure 13 presents boxplots of 5-, 10-, 30- and 50-year return levels of simulated annual daily precipitation extremes for current (1961–1990) and future (2071–2100) periods. The range of percentage change in return levels varies from –6 to 15% for LARS-WG and from –2 to 52% for GLM-WG. Negative changes are generally found for the 50-yr return level, except for Winnipeg, where all changes are negative. In general, the changes to return levels are not only site-dependent but also depend on the choice of weather generator and on the return period. Based on the results of the Wilcoxon rank sum test, LARS-WG shows significant changes (mainly increases) for nearly all four selected return levels for Banff, but non-significant changes for Calgary. For Saskatoon, increases in return levels are found significant only for 5- and 10-yr return periods (5-, 10- and 30-yr for Winnipeg). Compared to this, GLM-WG shows significant increases to all return levels for Banff and Calgary and to those corresponding to small return periods (5- and 10-yr) for Saskatoon. For Winnipeg, none of the changes (mostly decreases) are found to be statistically significant. Overall, none of the negative changes (mostly for 30- and 50-yr return levels) are found to be statistically significant.

Figure 13 Boxplots of 5-, 10-, 30- and 50-year return levels of annual daily precipitation extremes for the 1961–1990 current (white box) and 2071–2100 future (grey box) periods for the Long Ashton Research Station weather generator (LARS-WG; left four panels) and Generalized Linear Model-based weather generator (GLM-WG; right four panels). Statistically significant (insignificant) differences in return levels are shown in black (grey). The boxes correspond to the interquartile range (IQR), the line in the middle of the box to the median value and the whiskers to either the maximum value or to 1.5 times the IQR. Outliers that lie outside the 1.5 times IQR range are shown using circles.

Finally, Figure 14 presents 5-, 10-, 30- and 50-year return levels of DSI3 for current (1961–1990) and future (2071–2100) periods. In general, GLM-WG future DSI series exhibit higher interannual variability than the LARS-WG series, which is expected on the basis of the results shown in Figure 10. Both weather generators suggest negative changes to all four selected return levels of DSI3 for all four sites, meaning reduced risk of precipitation drought in the future. The Wilcoxon rank sum test indicates that decreases in DSI3 return values are statistically significant for Banff, Calgary and Saskatoon but not for Winnipeg. It should be noted that DSI3 is based exclusively on precipitation amounts, whereas future agricultural droughts are also driven by increased evapotranspiration due to higher temperatures (Dai 2011). Therefore, significant decreases to DSI3 should be interpreted with caution. Future work should investigate changes to frequency and severity of droughts with the consideration of changes to temperature regimes as well.

Figure 14 Boxplots of 5-, 10-, 30- and 50-year return levels of annual maximum Drought Severity Index (DSI3) for droughts lasting for at least 3 months for the 1961–1990 current (white box) and 2071–2100 future (grey box) periods for the Long Ashton Research Station weather generator (LARS-WG; left four panels) and Generalized Linear Model-based weather generator (GLM-WG; right four panels). Statistically significant (insignificant) differences in return levels of drought indices are shown in black (grey). The boxes correspond to the interquartile range (IQR), the line in the middle of the box to the median value and the whiskers to either the maximum value or to 1.5 times the IQR. Outliers that lie outside the 1.5 times IQR range are shown using circles.

Discussion and conclusions

Weather generators are useful tools for simulating multiple time series of precipitation that can be used for many practical applications, including flood and drought risk assessment, developing reservoir operation and management strategies and driving agricultural decision support systems for optimal management of resources. The use of weather generators has recently increased substantially, particularly for downscaling GCM outputs at specific sites of interest to generate probabilistic climate change projections. In this study, two weather generators, namely LARS-WG and GLM-WG, are used for downscaling daily precipitation using CGCM simulated climate variables for current (1961–1990) and future (2071–2100) time periods at four selected sites (Banff, Calgary, Saskatoon and Winnipeg) in the southern Canadian Prairies. The precipitation modelling and downscaling ability of both weather generators has been assessed at multiple time scales, ranging from daily and monthly to annual aggregations, using commonly used statistics of precipitation amounts, distributions of precipitation extremes and patterns of precipitation-based drought severity indices.

On the basis of comparison of selected statistics of simulated and observed monthly and annual precipitation totals, it is found that both weather generators perform almost equally well. However, when annual daily extremes and temporal evolution of drought severity indices are investigated, GLM-WG performs relatively better than LARS-WG in simulating interannual variability observed in drought indices and in capturing the extreme upper tail of the distribution of observed extremes. This behavior is partly attributed to large-scale climate information used for driving GLM-WG simulations.

According to the results obtained with LARS-WG (GLM-WG), annual average precipitation is projected to increase by 12% (16%) at Banff, 10% (62%) at Calgary, 18% (19%) at Saskatoon and 14% (3%) at Winnipeg for the 2080s (1971–2100) with respect to the 1970s (1961–1990). Generally, the directions of change of the annual average precipitation from the two generators are consistent and positive for all sites. However, the annual change simulated by GLM-WG is more variable from one site to the other (3–62%). The large change for Calgary appears to be an outlier in comparison with the other sites and needs further investigation before these results can be recommended for application. For annual daily precipitation extremes, it is found that changes to 5-, 10-, 30- and 50-year return levels are not only site-dependent but also depend on the choice of the weather generator. For example, for nearly all selected return levels, LARS-WG suggests significant increases at Banff, and non-significant increases at Calgary, while GLM-WG suggests significant increases at both Banff and Calgary. Generally, changes (mostly increases) to short return period (i.e. 5- and 10-year) return levels are found statistically significant more often than changes (increases or decreases) to higher return period (i.e. 30- and 50-year) return levels. One possible reason could be that a 30-year simulation is not long enough to detect changes in return levels corresponding to higher return periods which are generally associated with large uncertainties.

Projected changes to precipitation-based drought severity for the four selected sites suggest that the southern Canadian Prairies will perhaps experience less severe droughts in the future. However, future agricultural droughts would also be impacted by increases in temperature and hence increases in evapotranspiration. Therefore, these results should only be viewed as informative in relation to the ability of weather generators to downscale drought-related variables.

The above projected changes to selected characteristics of precipitation for the 2080s should be interpreted with caution since these projections are based on many assumptions. For example, these include the ability of the CGCM to simulate future precipitation and large-scale circulation patterns as well as the ability of the stochastic weather generators to downscale current and future period precipitation at selected sites. In addition, as a generally perceived weakness of the statistical downscaling approach, the validity and robustness of the weather generators’ parameters outside their calibration domains (e.g. Wilby et al. 2004) is another critical concern to be borne in mind.

As many of the large-scale climate variables could be correlated, identified structures of precipitation occurrence and amount processes in GLM-WG can only be considered as locally valid. However, it is important to note that the framework of GLM-WG is particularly useful for exploring relationships between large-scale climate variables and local-scale precipitation processes as well as for performing various sensitivity analyses. For example, for the identification of GLM-WG structures, zonal and meridional winds and climate variables at different pressure levels were also considered as possible driving variables in this study. However, precipitation response to wind was found erratic and highly correlated with SLP. Also, the climate variables at different pressure levels do not provide much additional information as they are highly correlated with the near surface variables (c.f. Widmann et al. 2003). Therefore, GLM-WG structures use only near surface climate variables (i.e. T, SLP and RH).

Although the final model structures for Banff, Calgary, Saskatoon and Winnipeg are slightly different, GLM-WG provides lower precipitation for higher SLP and lower RH. Compared to this, interpretation of the GLM-WG relationship with temperature and precipitation is relatively complicated. For higher temperature, the probability of precipitation occurrence is lower but the expected amount of precipitation is higher. Overall, only T, SLP and RH fields are considered for the GLM-WG precipitation simulation because these fields are expected to be more robust predictor variables. Although the NCEP or CGCM precipitation is not considered as a predictor variable in this study as in Widmann et al. (2003), it would be interesting to investigate how well the NCEP and CGCM is able to capture the physical processes involved in summer convective storms in another study. Also, it would be interesting to investigate spatial variability of CGCM and NCEP precipitation fields over the study area in the future. Further sensitivity studies on how local precipitation processes are related to regional temperature patterns within the GLM-WG framework would be worthwhile to explore.

Despite only daily precipitation series at individual sites investigated in this study, the GLM-WG framework can readily be extended to model precipitation series at multiple sites simultaneously (following Yang et al. 2005). For the LARS-WG case, an interpolation can be applied to site-specific simulations to produce spatial patterns of precipitation (Semenov and Brooks 1999). Even though long simultaneous precipitation measurements are rarely available, multisite precipitation modelling and downscaling is an interesting area for further research. Another interesting area of study for the application of weather generators is downscaling of sub-daily precipitation, because of the sensitivity of many urban drainage systems to sub-daily precipitation extremes. By using a Poisson cluster model, the GLM-WG simulated daily precipitation can be further disaggregated into hourly or six-hourly precipitation (e.g. Segond et al. 2006), or to finer time-scales using scaling properties (Gires et al. 2012). The Poisson cluster model could also be useful for disaggregating LARS-WG simulated daily precipitation series at sub-daily time scales, but further work is needed and will be pursued in future to explore these possibilities.

Climate variables from only one GCM are analyzed to investigate future climate variability in southern Canadian Prairies. As climate change projections vary from one GCM to another, a similar analysis of downscaling precipitation using climate variables from multiple GCMs under multiple greenhouse gas emission scenarios would be useful in producing a more robust climate change signal. Additional simulations from the CGCM would also help address the uncertainty issue in the future climate for the Canadian Prairies.

Acknowledgements

The authors would like to thank M. Semenov for providing necessary information for using LARS-WG, and Heather Wilson from the Global Institute for Water Security for providing geographic information system (GIS) support. The first author is funded by the post-doctoral fellowship from the Global Institute for Water Security, and he would like to thank A. Barr and B. Bonsal from Environment Canada for discussion on the Canadian Prairies climate and drought. The authors would like to thank two anonymous referees for their thoughtful comments that helped improve the overall merit of the paper.