Numerical modelling in support of a conceptual model for groundwater flow and geochemical evolution in the southern Outaouais Region, Quebec, Canada

Abstract

A two-dimensional vertical-section numerical model for groundwater flow and transport using age, tritium and chloride was used to help validate a conceptual model of geochemical evolution within a representative regional-scale hydrogeological system in the Outaouais Region, Quebec, Canada. The flow system includes up to 30 m of Quaternary sediments and marine clays overlying fractured silicate rock of the Canadian Shield. Calibration of the regional flow model using observed piezometric levels and tritium concentrations showed that shallow groundwater flow is dominated by local flow systems limited to 30–40 m depth, 1–5 km long, and with groundwater residence times of 10–50 years. Intermediate systems, on the order of 5–15 km long, are less extensive than initially thought and are characterised by maximum depths of about 100 m and residence times of 200–6000 years. A model-calibrated hydraulic conductivity of 8 × 10⁻⁵ m.s⁻¹ was required in the upper 50 m of the fractured bedrock. The active flow zone was inferred to extend to depths of about 100–150 m, with any deeper regional flow essentially negligible. Differences between tritium-based ages and simulated mean residence times were attributed to mixing of groundwater in open boreholes. Concentrations of ⁴He could be explained by diffusive transport from deeper and older groundwater, exacerbated by sampling. With new insight from the numerical modelling, the conceptual flow model has been updated to now include only a weak component of regional flow combined with significant local- and intermediate-scale flow systems connected to the upper fractured bedrock. The simulated flow system is also consistent with the geochemical evolution of the region, which is dominated by young Ca-HCO₃-type waters in the unconfined aquifer and by older Cl⁻ signatures from the remnant Champlain Sea seawater.

Un modèle numérique en deux dimensions vertical d’écoulement et de transport a été utilisé afin d’aider à la validation d’un modèle conceptuel d’évolution géochimique au sein d’un système hydrogéologique régional représentatif de la région de l’Outaouais, Québec, Canada. Le système d’écoulement inclut jusqu’à 30 m de sédiments du Quaternaire et d’argiles marines déposés sur le socle rocheux silicaté et fracturé du Bouclier Canadien. La calibration du modèle d’écoulement régional basée sur les données de piézométrie et complétées par les teneurs en tritium a montré que les systèmes d’écoulement sont dominés par des systèmes locaux limités aux 30–40 premiers mètres de profondeur et avec des âges de l’eau de 10 à 50 ans. Les systèmes intermédiaires, de l’ordre de 2–5 km de long, sont moins étendus qu’initialement pensé et sont caractérisés par une profondeur d’environ 100 m et des âges entre 200 et 6000 ans. Une conductivité hydraulique élevée (8 × 10⁻⁵ m.s⁻¹, élevée par rapport aux données de terrain), dans les 50 premiers mètres de roc fracturé, a permis d’expliquer la piézométrie et les concentrations en tritium observées. La zone active d’écoulement du modèle calibré a une profondeur d’environ 100–150 m et il n’y a pas d’écoulement au-delà de cette profondeur. Les différences entre le tritium et les temps de résidences moyens modélisés et ceux des échantillons sont dues au mélange dans des puits ouverts aggravés par l’échantillonnage. Les concentrations en ⁴He sont dues à la diffusion à partir d’eaux souterraines plus âgées, exacerbées par l’échantillonnage. Le modèle conceptuel d’écoulement supporté par le modèle numérique a été actualisé pour maintenant inclure une faible composante d’écoulement régional combinée avec d’importants systèmes d’écoulements locaux et intermédiaires, et connectés à la partie supérieure fracturée du roc. Le système d’écoulement simulé est cohérent avec le modèle d’évolution géochimique de la région, dominé par des eaux de type Ca-HCO₃ dans l’aquifère libre et par des signatures de restes de la Mer de Champlain.

Introduction

Like many fractured bedrock environments, the Canadian Shield is characterised by a complex geological structure including a variable lithology and mineralogy, as well as by complex faults and fractures (Farvolden et al. 1988). Understanding groundwater flow patterns and geochemical evolution can therefore be challenging in these environments. In the Outaouais Region (southern Quebec, Canada; Figure 1), even the recent geological history is complex, and includes invasion and retreat of the Champlain Sea following the last glaciation, which has had lasting effects on the geochemical evolution of groundwater. With increasing stresses on shallow groundwater resources in the region due to a rapidly growing population, water supply is becoming more reliant on the fractured bedrock. Excluding the city of Gatineau, which contains 2/3 of the regional population and which relies mainly on surface water, 91% of the remaining population uses groundwater as their main drinking water supply (Comeau et al. 2013). A better understanding of these resources is important for future development, and for groundwater protection and sustainability.

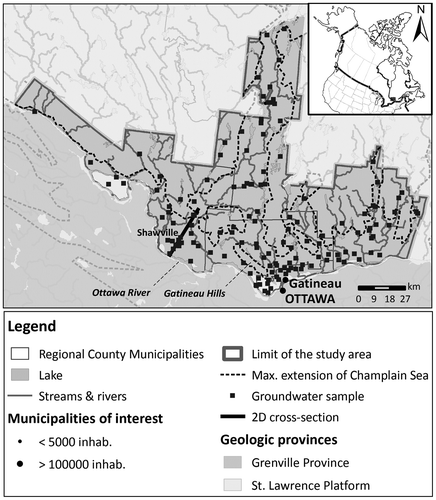
Figure 1. Location of the study area and highlights of the two-dimensional cross-section, including the maximum extent of the Champlain Sea (data from Comeau et al. 2013).

A conceptual model for groundwater flow and geochemical evolution was recently proposed by Montcoudiol et al. (2015) for the southern Outaouais Region along a two-dimensional (2D) cross-section, as shown in Figure 2. As part of their paper, Montcoudiol et al. (2015) used major ion concentrations to identify a chemical zonation of groundwater (Figure 2), which was based on a regional-scale study presented in Montcoudiol et al. (2014) and Comeau et al. (2013). The main geochemical processes inferred to be responsible for this zonation were the dissolution of silicates (mainly anorthite, CaAl₂Si₂O₈) in the unconfined (up-gradient) part of the aquifer, mixing with fossil waters from the Champlain Sea invasion, and cation exchange in the confined part, as well as mixing between recently infiltrated and older water in the down-gradient unconfined part (as identified in Figure 2). This hypothesis is tested in the current paper.

Figure 2. Conceptual hydrogeological model along the selected two-dimensional cross-section perpendicular to the Ottawa River at far right (Montcoudiol et al. 2015).

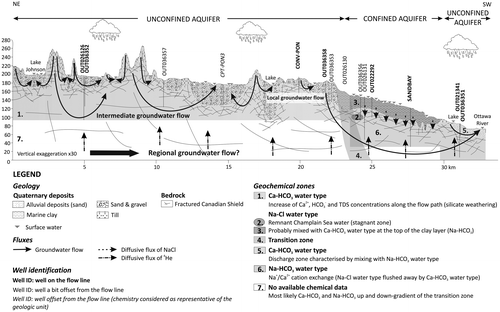
Remnant seawater from the Champlain Sea invasion was confirmed by field data, and evidence of mixing was found between a tritium-rich water component and an older helium-rich component. Montcoudiol et al. (2015) also showed that the hydrochemical system is dynamic and still evolving from induced changes since the last glaciation. Although their conceptual model was developed from detailed field data which yielded much insight into the long-term groundwater flow dynamics and geochemical evolution, several questions remain.

One key question concerns the context of local, intermediate and regional flow systems (Tóth 1999) in the case of this specific Outaouais flow system and in the more general context of similar settings in southern Quebec and elsewhere within the Canadian Shield. It is still unclear, for example, whether a regional flow component exists at the Outaouais site. Groundwater flow simulations by Sykes et al. (2009) in typical Canadian Shield geological settings suggest that, assuming an anisotropy of K_x/K_z = 0.1, flow in deep rock is a subdued reflection of the topography rather than being part of a regional component. Gleeson and Manning (2008) also showed that regional flow decreases with lower relief, although this hypothesis has to be tested in the Outaouais case in which the horizontal conductivity is assumed to be greater than the vertical.

In this paper, a 2D vertical-section numerical model for groundwater flow and transport using tritium, chloride and age is developed in order to help validate the conceptual model of Montcoudiol et al. (2015), and to help explain the geochemical evolution of groundwater within the bedrock of the Grenville geologic province (Outaouais Region, Quebec). The flow model was designed in part to help provide insight into the local and intermediate flow systems and to determine their relative importance with respect to groundwater geochemical evolution. The tritium transport model is used to support the flow model calibration.

The impact of the Champlain Sea invasion is then assessed by simulating chloride intrusion from the ancient seawater boundary and marine clay into the confined aquifer. Mean groundwater age, including the effect of age dispersion, is also simulated to help interpret geochemical evolution, with simulated ages compared to ages inferred from the observed tritium and ¹⁴C data. This is the first detailed quantitative study of relationships between groundwater flow, groundwater age, and geochemical evolution in the context of Quaternary aquifers overlying fractured rock of the Canadian Shield.

Study area and geological history of the region

The study area is located in the southwestern part of the Outaouais Region, in southern Québec, Canada (Figure 1). The modelling is applied to a conceptual model proposed by Montcoudiol et al. (2015) which was developed based on interpreting groundwater chemical data along the 2D cross-section identified in Figure 1. The cross-section is located along the dominant groundwater flow direction, extending approximately 30 km from the Gatineau Hills in the northeast to the Ottawa River in the southwest, passing through the township of Shawville.

The geological history of the region and the resulting distribution of Quaternary deposits within the Outaouais study area were presented by Montcoudiol et al. (2014). A brief review of the geological history is presented herein with a particular focus on the site geology and hydrogeology, and its immediate surroundings.

Along the cross-section (Figure 2), the underlying bedrock is part of the Grenville Province of the Canadian Shield, dating from the Proterozoic (Precambrian). The cross-section passes through two principal types of rocks: non-carbonated metamorphic rocks (gneiss and paragneiss) in the northeast and calco-silicate rocks (marble) to the southwest (towards the Ottawa River). The bedrock is characterised by a high degree of stress-induced fracturing in the upper 50–60 m (Sterckx 2013), which has likely produced extensive preferential flow paths.

Unconsolidated deposits left prior to the last glaciation have not been found in the study area, likely due to erosion by the many glacial–deglacial cycles during the Quaternary period (Daigneault et al. 2012). During the last glaciation, abrasion of the bedrock and ice movement deposited a discontinuous layer of till directly overlying the bedrock, while during the last deglaciation, freshwater fluvio-glacial sediments were deposited in the lower valleys. The Ottawa River valley (including lower reaches of secondary river valleys) was then invaded by the Champlain Sea about 12,000 years ago (Parent and Occhietti 1988), which left marine clays on top of the fluvio-glacial sediments (if they had not already been eroded). Due to isostatic rebound, the Champlain Sea progressively left the region about 10,000 years ago, leaving behind deltaic, littoral and pre-littoral sediments. Along the main rivers, this sequence is buried by ancient and more recent alluvium (Comeau et al. 2013).

Numerical modelling

Simulation approach

A four-step modelling approach is adopted in this study, incorporating groundwater flow, tritium and chloride transport, and mean groundwater age (Figure 3). The first step was to reproduce the current flow conditions, calibrating the model with available hydraulic head data. Since the hydraulic conductivities could not be uniquely calibrated based on observed head data alone (due in part to the sparse available data which were not fully representative of the aquifer conditions), the calibration is improved in Step 2 by simulating the recent tritium distribution throughout the entire aquifer. Using the tritium concentrations in precipitation from the nearby Ottawa meteorological station as a transient surface boundary condition, the theoretical tritium distribution at the sampling date (2012) was compared to the tritium concentrations measured in the groundwater samples and final adjustments made to the hydraulic conductivity field. Step 3 involved simulating the transport and evolution of chloride (as an ideal tracer) following intrusion of water from the Champlain Sea into the aquifer, followed by groundwater freshening after the retreat of the sea, and continuing up to present-day conditions. The aim of this simulation was to explain the current chloride distribution in the aquifer. In Step 4, the steady-state mean groundwater age distribution is simulated under current flow conditions and checked against the tritium and ¹⁴C isotope data.

Figure 3. Sequential modelling strategy: (a) Step 1: steady-state flow model, (b) Step 2: calibration of the flow model using tritium, (c) Step 3: simulation of chloride transport from the Champlain Sea invasion, and (d) Step 4: groundwater age model. For simplicity, the inclined bottom boundary is not shown here. Fixed heads, representing surface water, are shown as small triangles on the water table.

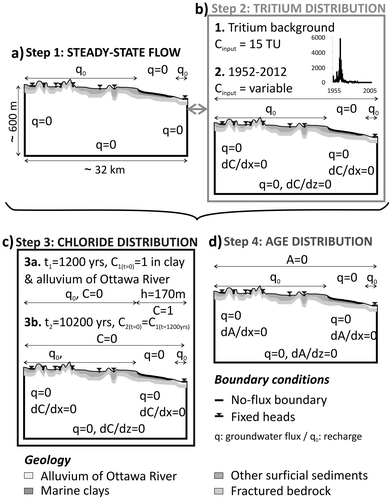
The same 2D vertical domain (including the hydrostratigraphy), which follows the conceptual model of Figure 2, is used for all simulations; only the governing equations and boundary conditions are changed. An identical spatial discretisation was used in all simulations. Considering the regional scale of the model domain (about 32 km) and the lack of data pertaining to the distribution and characteristics of fractures, an equivalent porous medium (EPM) approach was applied in all cases. All simulations were performed with the FLONET/TR2 model. Details on the numerical implementation of the flow and transport equations can be found in Molson and Frind (2014) and are summarised in Appendix 1.

Groundwater flow model

Model domain and flow boundary conditions

The FLONET model domain is 32.5 km long and varies in depth between 550 and 600 m from the ground surface to the bottom boundary. The up-gradient left boundary is located in the Gatineau Hills and corresponds to a surface water divide. The right (down-gradient) boundary is located at the centre of the Ottawa River, which acts as the major discharge zone for the entire Outaouais Region. These two boundaries are both set as symmetry (no-flow) boundaries.

The bottom boundary was assumed impermeable (Figure 3a), and assigned a slope similar to the average topographic gradient, varying from 354 to 505 m below sea level. A preliminary 10-km-deep model (not shown), assuming a uniform hydraulic conductivity of 1 × 10⁻⁹ m.s⁻¹ below the base of a 100-m-deep fractured zone, showed that essentially all groundwater flowed within the shallow Quaternary sediments and upper fractured bedrock zone, with only 0.01% of the total infiltration reaching depths of 350 m below sea level. Moreover, at these depths, higher density saline groundwater would further inhibit deeper flow systems (Normani et al. 2009; Sykes et al. 2009).

The top boundary of the flow model corresponds to the water table which was initially positioned to correspond with the surface topography, then was allowed to deform during the simulation to its equilibrium position. Topographic elevations (from 268 m asl to 72 m asl) were extracted from a digital elevation model (DEM) with a resolution of 10 m (Comeau et al. 2013). A recharge (Type 2) condition was applied across the top boundary except for surface water bodies which were represented using fixed heads (Type 1) and at the surface of the confining clay layer (treated as a no-flow boundary) (Figure 3a). The applied recharge flux was equivalent to 30% of the total annual precipitation. Indeed, using the model HELP^® (Hydrologic Evaluation of Landfill Performance; Schroeder and Ammon 1994), Comeau et al. (2013) found that in the Outaouais Region, an average of 30% of the precipitation infiltrates as recharge to the aquifers. Observed data from the Shawville meteorological station (station ID 7038040; Environment Canada 2013) from 1948 to 2012 showed an average annual precipitation rate of about 839 mm.yr⁻¹; thus, a constant recharge rate of 252 mm.yr⁻¹ was assigned in the model.

Model discretisation

The 2D vertical section was discretised with elements every 10 m in the horizontal direction. Vertically, the entire section was divided into nine hydrostratigraphic layers – the bottom two layers represent the upper fractured and deeper unfractured bedrock, while the top seven represent the unconsolidated Quaternary sediments (Table 1). Each hydrostratigraphic layer was discretised vertically into several grid element layers ranging in thickness from 15 m at the bottom to 0.5 m at the top (Figure 4b and Table 1). The topmost element layer (which follows the water table) is used as a high-K recharge spreading layer that redistributes recharge away from low-conductivity zones and avoids the development of ponding conditions (Beckers and Frind 2000). To accommodate the free water table, the grid is allowed to deform vertically (Molson and Frind 2014). The global mesh is composed of 6514 × 87 (= 566,718) triangular elements in the horizontal and vertical dimensions, respectively.

Table 1. Description of the hydrostratigraphic units and their hydraulic properties.

Stratigraphic unit	Vertical discretisation (No. of grid layers)	Hydraulic conductivity (m.s^−1)*	Porosity [−]
Recharge spreading layer (RSL)	1	1×10^−5	0.30
Alluvium	2	1×10^−4 [5×10^−4]	0.35
Deltaic sediments	4	1×10^−4 [2×10^−4]	0.30
Littoral sediments	1	3×10^−4	0.35
Marine clays	4	1×10^−10	0.50 [0.65]
Fluvio-glacial sediments	4	3×10^−4 [1×10^−4]	0.25
Till	1	8×10^−5	0.15
Shallow bedrock (fractured)	8	1×10^−6 [8×10^−5] (top 50 m)	0.03
Deep bedrock (less fractured and/or unfractured)	42	1×10^−7 (40–50 m thick)	0.02
			0.01
		1×10^−8 (50–60 m thick)	0.01
			0.01
		1×10^−10 (60–70 m thick)
		1×10^−12 (to bottom)
Transport parameters: αLH = 20 m; αLV = 2 m and αTH = αTV = 0.01 m

^* Initial estimated K values are from Comeau et al. (2013).

[−]: final calibrated values of hydraulic conductivities and porosity.

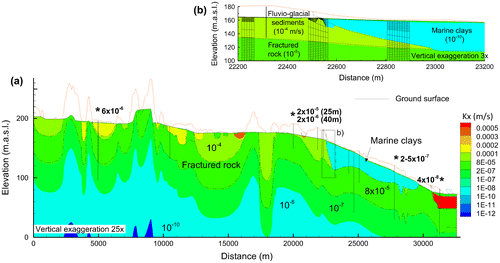
Figure 4. Simulation domain showing: (a) distribution of hydraulic conductivities along the two-dimensional cross-section, and (b) selected mesh detail in three areas near the fluvio-glacial sediment-clay interface. The vertical bars represent the wells shown in Figure 2. Asterisks identify wells where hydraulic conductivities (shown in bold) were calculated from hydraulic testing. For clarity, the full depth of 550 to 600 m is not shown. K distribution is shown for Step 3b (following seawater retreat; K for Step 3a – during seawater intrusion – was identical but had low-K marine clay instead of the high-K alluvium near the far right boundary).

Hydraulic properties

Comeau et al. (2013) compiled and validated more than 2000 hydraulic tests within the top 150 m of unconsolidated sediments and fractured bedrock throughout the Outaouais regional study area (average hydraulic conductivities for each hydrostratigraphic unit are provided in Table 1). Attribution of hydraulic conductivities in the Quaternary sediments is based on the geological cross-section of Figure 2 and data from Comeau et al. (2013) (Figure 4a). Since the hydraulic conductivity of the clay proposed by Comeau et al. (2013) appeared to be too high (2 × 10⁻⁷ m.s⁻¹) compared to published values for the Champlain Sea clays (Table 2), a conductivity of 1 × 10⁻¹⁰ m.s⁻¹ was applied.

Table 2. Literature review of measured hydraulic conductivities and porosities of Champlain Sea clay deposits.

Reference	Hydraulic conductivity (m.s^−1)	Porosity [−]
Tavenas et al. (1983)	1×10^−11 – 1×10^−10
Leroueil et al. (1988)	1×10^−9 – 5×10^−9
Desaulniers and Cherry (1989)	7.5×10^−11 – 4.9×10^−10	0.64
Lapierre et al. (1990)	~1×10^−9
O'Shaughnessy and Garga (1994) and Garga and O’Shaughnessy (1994)	8×10^−10 – 2×10^−9	0.5
Leroueil et al. (2003)	~1×10^−9
Marques et al. (2004)	~1×10^−9
Duhaime et al. (2013)	3×10^−11 – 5×10^−9

Hydraulic conductivities in the top 50 m of bedrock (assumed highly fractured) and in the underlying 100 m (assumed much less fractured) were assigned based on air-pressure slug tests in 3-m packed intervals (wells CONV-PON and SANDBAY, the latter showing uniform conductivity with depth; Figure 2) and on pumping tests (wells OUT036352 and OUT21341; Figure 2), which yielded hydraulic conductivities between 2 × 10⁻⁵ and 3 × 10⁻⁸ m.s⁻¹ (Figure 4a). These values correspond well to the range for Canadian Shield fractured bedrock observed at the regional scale (Sterckx 2013), where wells have been drilled to a maximum bedrock depth of 150 m. This range of hydraulic conductivities was applied assuming an exponential decrease with depth (Figure 4a), which matches the observed distribution of K values and is commonly observed in crystalline bedrock (Maréchal 1998). Below 150 m, the bedrock is considered to be much less permeable, with hydraulic conductivities decreasing from 10⁻¹⁰ to 10⁻¹² m.s⁻¹, again assuming an exponential decrease with depth (Table 1; Farvolden et al. 1988; Maréchal 1998).

Fractured silicate rock is generally anisotropic, characterised by sub-horizontal fractures with ratios of horizontal to vertical hydraulic conductivities of K_x/K_z ranging from 1 to 10 (Farvolden et al. 1988; Gleeson 2009; Lachassagne et al. 2011). Without any further data on anisotropy at the Outaouais site, a conservative anisotropy factor of 5 (K_x/K_z = 5) was applied for the entire bedrock unit. The Quaternary deposits were considered isotropic. This issue is further addressed in the Discussion section.

Since measured porosities were not available, values compiled by Fetter (2001) were applied (Table 1). The clay porosity was later adjusted during calibration to 0.65 which is similar to the mean porosity of similar clays measured by Desaulniers and Cherry (1989).

Chloride transport model: Two-step modelling strategy

Chloride evolution in the 2D section (Step 3, Figure 3c) was simulated in two sub-steps, in which a change in boundary conditions was invoked between Step 3a representing flooding by saltwater of the Champlain Sea (applying a constant seawater elevation over the affected area) and Step 3b following seawater retreat (applying recharge across the top surface). A change in hydraulic conductivity near the far right boundary was also invoked to account for the replacement of marine clay by river alluvium sediments. Thus, only the hydraulic conductivity distribution and boundary conditions were changed between sub-steps, and the simulated chloride concentrations at the end of Step 3a were used as the initial condition for Step 3b.

Step 3a: Champlain Sea invasion

Step 3a was simulated to represent the approximately 1200-year period of saltwater invasion from the Champlain Sea (Catto et al. 1981). The clay layer left by the Champlain Sea was assumed to have been rapidly deposited, and its pore water was assumed to be initially saturated with seawater (Figure 3c; Desaulniers and Cherry 1989). During the Champlain Sea invasion (Step 3a), alluvium from the Ottawa River was not yet present; thus, the hydraulic conductivity in this area (which was needed for Step 3b) was assigned the hydraulic conductivity of clay, which is considered justified as marine clay lenses have been discovered in boreholes drilled along the Ottawa River (MDDEFP 2012). An initial normalised chloride concentration of C/C₀ = 1 was imposed as the initial condition in all clay units. The rest of the domain had an initial concentration of 0 (Figure 3c).

The transport model in this study did not include density-driven flow since (1) horizontal flow gradients dominate throughout the system, especially following retreat of the Champlain Sea; and (2) water from the Champlain Sea, being far from the ocean and at this late stage of inundation, was considered to be diluted marine water with a significant proportion of ice-melt (fresh) water. Analyses of clay pore water by Catto et al. (1981), for example, in the area of Chalk River (~100 km upstream of Shawville on the Ottawa River) revealed Champlain Sea salinities between 12 and 16 g.L⁻¹, similar to the maximum concentration measured by Cloutier et al. (2010) in marine clays from the Montreal area, about 200 km downstream. Others have found similar salinities, including Desaulniers and Cherry (1989) in marine clays near Montreal, and Quigley et al. (1983) in clays between Ottawa and Montreal. It is likely that the salinity was higher in the deep water body of the central Champlain Sea but became more diluted during later stages of the invasion and along its long arms which extended inland (Torrance 1988).

Deep, brackish formation water was also not included in the model. The depth of the interface between fresh water and brackish groundwater in Canadian Shield areas has been observed to vary from 200 m (Frape and Fritz 1987) to 650 m (Frape et al. 1984). Salinity in the Canadian Shield generally does not exceed 1000 mg.L⁻¹ at depths of less than 500 m (Farvolden et al. 1988; Gascoyne and Kamineni 1994). Furthermore, at the nearby Chalk River nuclear facility, where extensive investigations have been carried out for siting nuclear fuel repositories, groundwater Total Dissolved Solids (TDS) content does not exceed 700 mg.L⁻¹ at a depth of 400 m. An initial concentration of 0 was therefore assigned throughout the bedrock where the average TDS content would only be about 5% of the Champlain Sea concentration.

The extent of the top seawater boundary condition was based on Barnett (1988) who found evidence for Champlain Sea elevations of 170 m asl in the Renfrew area, which faces Shawville on the opposite bank of the Ottawa River. This elevation also corresponds to the maximum elevation of the clay layer on the 2D cross-section. Along the same boundary surface, a Cauchy (Type 3) transport boundary condition (Molson and Frind 2014) was set with a normalised chloride concentration of C/C₀ = 1 (Figure 3d). In the valleys within the northern (up-gradient) part of the cross-section, some clay deposits were also found, suggesting that the Champlain Sea probably reached even higher elevations but likely lasted a shorter time, and thus would have had less impact on the hydrochemistry. It was also assumed that the transitional period from one hydraulic regime to another was short and that the flow system responded immediately to these changes.

The duration of marine transgression varied within the basin, depending on the distance from the mouth of the St. Lawrence River. The study area is located in an extreme northwestern arm of the Champlain Sea, where the ice cover lasted longer, and where seawater invasion occurred relatively later (Catto et al. 1981). Two events of marine transgression have been identified in the nearby region of Renfrew. The first event lasted less than 200 years, between 12,150 and 12,000 years BP, after which the Champlain Sea retreated in step with a new advance of the ice sheet for about 1000 years. The second phase of the Champlain Sea lasted about 1200 years, from the ice retreat 11,400 years BP to the withdrawal of the sea at about 10,200 years BP due to isostatic rebound (Catto et al. 1981). For modelling purposes, the first phase is considered negligible and only the second phase is simulated, representing 1200 years of seawater intrusion (Figure 3d).

Step 3b: Champlain Sea retreat

Similar to the assumption of rapid marine transgression, seawater retreat and flow system response is also assumed to be rapid. After the retreat of the Champlain Sea about 10,200 years ago (Catto et al. 1982), the flow systems (including boundary conditions) were assumed to be similar to those of today, even though the Ottawa River valley has had its current shape for only about the last 8000 years (Catto et al. 1982; Teller 1990). Isostatic rebound is not taken into account by the model although groundwater systems are dynamic and are still evolving as a result of the Laurentide Ice Sheet melting (Lemieux et al. 2008; Sykes et al. 2009). In Step 3b, following seawater retreat, the clay layer within 2.5 km of the Ottawa River, which was initially present in Step 3a, is replaced by permeable river alluvium (K = 5 × 10⁻⁴ m.s⁻¹; Figure 4).

In Step 3b, a Cauchy condition is again applied at the top boundary, but with a chloride concentration set to 0 representing low chloride content in rainwater. The initial condition in the domain corresponds to the final chloride distribution from the previous (Step 3a) model. The Step 3b chloride transport model is run for 10,200 years (Figure 3d).

Groundwater age model: Initial and boundary conditions

The TR2 transport module of FLONET/TR2 was subsequently applied to simulate mean steady-state groundwater residence times (advective-dispersive ages), according to Equation (4) in Appendix I. In the age simulation, all nodes corresponding to recharge at the top surface are assigned as Type 1 fixed age boundaries (A = 0 years) while all other boundaries are assigned zero age-gradient conditions with the initial age set at 0 throughout the domain (Figure 3d). All other parameters (dispersivities, diffusion coefficient, retardation factor and decay constant) remain the same as for the transport of chloride.

Modelling results

Calibration of the flow model: Hydraulic heads and tritium

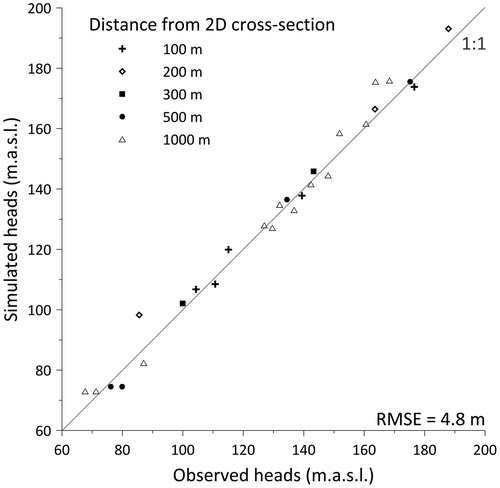
Calibration of the hydraulic conductivity in the flow model was first completed using only the hydraulic head data (Figure 5). The observed head data set includes 27 wells within 1 km of the 2D cross-section, which were validated at the regional scale (for errors, anomalous data, etc.) by Comeau et al. (2013). Most measurements (15/27) were taken in wells located in the confined bedrock aquifer. The few measurements (7/27) taken from the unconfined bedrock aquifer are located in the valleys of the higher topographic regions. The remaining head measurements (5/27) were taken in the unconfined aquifer near the Ottawa River.

Figure 5. Calibration results: simulated vs. observed heads. Note: RMSE - Root Mean Squared Error.

As pointed out by Ophori (1999), calibration to hydraulic heads alone is non-unique based on uncertain combinations of recharge and hydraulic conductivity (K). To improve the calibration, the flow model was also checked by comparing simulated and observed tritium distributions. The initial simulated tritium concentrations based on the head-calibrated flow model showed a relatively poor fit with essentially no tritium predicted for the shallow bedrock. A final re-calibration of K was therefore performed with insights from the observed tritium distribution, whose concentrations are more sensitive to changes in the hydraulic parameters, especially the hydraulic conductivity of the shallow bedrock. This additional step also helped improve the calibration to the hydraulic heads, the final hydraulic conductivity values being significantly higher than the initial estimate (Table 1).

Tritium concentrations were available for 12 wells (Montcoudiol et al. 2015) along the 2D cross-section (Figure 2). Although the decrease in tritium activity due to migration time within the unsaturated zone is not taken into account in the model, the water table is relatively shallow in most parts of the aquifer (except in the topographic highs); thus, travel times through the unsaturated zone would be short relative to the total residence time and this limitation would therefore not significantly affect the results.

The initial conditions for the transient tritium simulation from 1953–2012 were based on a simulated steady-state tritium distribution assuming the current-condition flow field, and a constant Type-1 concentration of 15 Tritium Units (TU) across the water table (Clark and Fritz 1997). Tritium concentrations measured on a monthly basis at the Ottawa meteorological station (World Meteorological Organization [WMO] code 7162800; IAEA/WMO 2011) were then used as the top boundary condition from 1953 to 2012 (Figure 3b). A few missing data points were replaced by the average value between the closest measurement times. The series ends in 2007. From this last measurement to the sampling date, an average value of 15 TU was applied, similar to the background value (which also corresponds to the average value of the two final years of measurements).

The flow model calibration to hydraulic heads (Figure 5) showed that irrespective of the transverse distance of the observation wells from the 2D cross-section, the deviation from the 1:1 best-fit line was minimal, which confirms that the 2D cross-section indeed closely follows a regional flow line and thus a 2D vertical model is considered an acceptable simplification. The root mean squared error (RMSE) is less than 5 m, with calculated heads on average 1.2 m greater than those measured (Figure 5). In the unconfined aquifer, the water table is below the ground surface (up to 60 m deep) whereas the confined aquifer is partly under artesian conditions (up to 3.7 m above ground). Artesian conditions were confirmed by a flowing well at one of the sampled wells.

Test simulations showed that when the shallow bedrock K was too low, the simulated tritium would remain only in the Quaternary sediments. In the final calibrated model, with a higher hydraulic conductivity of 8 × 10⁻⁵ m.s⁻¹ in the shallow bedrock, a more reasonable RMSE value of 6.1 TU was obtained. However, the simulated concentrations were still almost systematically under-estimated compared to tritium contents measured in the field (Table 3).

Table 3. Comparison between observed and simulated tritium concentrations.

Well ID	Measured tritium (TU)	Simulated tritium (TU)
OUT036352	16.9	9.9
OUT036357	14.9	12.4
CONV-PON	18.8	12.5
OUT036358*	20.7	9.3
OUT036353*	15.1	9.2
OUT036356	< 0.8	11.8
SANDBAY	10.9	11.8
OUT021341	9.8	11.5
OUT036351*	17.5	12.2

Note:

^* Wells in Quaternary sediments with no information on the screen location, for which simulated concentrations assume a screened interval 5 m long at the bottom of the well.

Since the model did not simulate the decay of tritium due to increased travel time through the unsaturated zone, over-estimated tritium concentrations were expected. Different hypotheses can be proposed to explain the discrepancies. First, a greater proportion of water sampled from the bedrock wells would likely have originated from fracture zones, whereas the model-based concentrations in the bedrock wells were averaged over the length of the open borehole. The equivalent porous medium approach used in the model would also tend to decrease the tritium compared to tritium migration through discrete fractures. Furthermore, in the five bedrock wells cased through the overlying Quaternary deposits (other than those through marine clay), leakage from shallow (younger) groundwater might be expected since the shallow bedrock is fractured. For wells in the Quaternary deposits, the location of the well screen was not known, but for simplicity the well was considered screened over the bottom 5 m.

Simulated flow systems

The simulated steady-state groundwater flow system and advective (particle-track) travel times (residence times from recharge to discharge) along selected streamlines are shown in Figure 6. Flow system depths and the extent of intermediate flow systems are controlled by the hydraulic K distribution, topography and by surface water bodies which act as discharge zones (Figure 6a). Local flow systems (on horizontal scales of ~1–5 km) are located in the first 50 m below ground surface. All intermediate systems (~5–15 km) reach the base of the model but flow rates are essentially negligible at these depths (evident from the exponential decrease in streamfunction contour levels with depth). The simulation showed no evidence of regional groundwater flow at scales greater than 15 km.

Figure 6. Simulated flow system showing: (a) steady-state flow lines, and (b) detail of flow systems in the unconfined aquifer, including total residence times from recharge to discharge, shown on corresponding streamlines (streamlines are identified by streamfunction contours in m².s⁻¹, e.g. 1E-06; residence times are shown in years, in bold text, e.g. 3 years). For clarity, the full depth of 550 to 600 m is not shown.

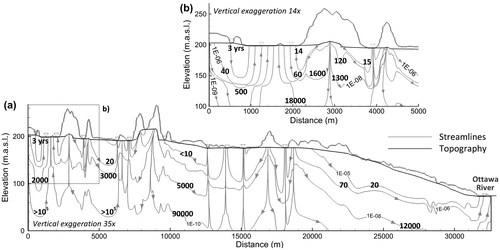
Due to the rapid decrease of hydraulic conductivity in the bedrock at depths greater than 150–200 m, maximum particle tracking-based groundwater residence times are on the order of hundreds of thousands of years. Detail shown in Figure 6b reveals primarily short residence times (< 100 years) in the first tens of metres of depth, within the Quaternary sediments. Residence times are longer for groundwater infiltrating from high-elevation rock outcrop areas, with flow paths controlled by the layer geometry. Groundwater discharging to the central discharge zones of large surface-water bodies has originated from deeper flow paths and has longer mean residence times (up to 18,000 years) compared to groundwater discharging into small rivers, especially below Lake Johnson (at kilometres 1–2). In the confined aquifer (Figure 6c), groundwater flows most rapidly in the upper fractured part of the bedrock, with groundwater residence times of less than 100 years.

In recharge and discharge zones, the decreasing hydraulic conductivity with depth has induced significant variations in the hydraulic heads. Below discharge areas, hydraulic heads are relatively constant in the first 200 m and increase between 0.5 and 1 m over the remaining model depth (with a vertical hydraulic gradient ∇h of 1.4 to 2.9 × 10⁻³ m.m⁻¹, Figure A1a and Figure A1e in Appendix II), whereas they decrease by 6 m over the same depths below recharge zones (∇h = −1.1 × 10⁻² m.m⁻¹, Figure A1b). In the clay layer overlying the up-gradient part of the confined aquifer (Figure A1c), hydraulic heads increase with depth in the clay and in the upper part of the bedrock, and decrease with depth into the deeper bedrock (−2 × 10⁻³ m.m⁻¹). In the down-gradient part of the confined aquifer, hydraulic heads are higher in the deep bedrock (Figure A1d) than in the fractured bedrock. Artesian conditions therefore prevail in the up-gradient part of the confined aquifer while fluxes are downward farther down-gradient.

Analysis of vertical flux variations with depth (not shown) reveals that 99% of the total recharge remains within the first 100–200 m of the water table (depending on the position along the cross-section), which corresponds to the Quaternary deposits and the shallow fractured bedrock (K = 8 × 10⁻⁵ m.s⁻¹; Table 1). In recharge areas where hydraulic gradients are high but hydraulic conductivities are low (e.g. thin layers of Quaternary deposits or outcropping bedrock), groundwater fluxes remain low. Maximum fluxes are found in the fluvio-glacial sediments. Although the depth of the active flow zone is conditioned by the thickness of the most permeable layer of bedrock, these results are in agreement with observations made in similar settings of the Canadian Shield (Farvolden et al. 1988; Gascoyne 2004; Manning and Caine 2007).

Simulated chloride distribution

The simulated chloride distribution at the end of the Champlain Sea invasion 10,200 years ago (end of Step 3a) and its current expected distribution (end of Step 3b) are shown in Figure 7a and ^{Figure 7}c, respectively. Figure 7b represents an intermediate time 800 years after the retreat of the Champlain Sea.

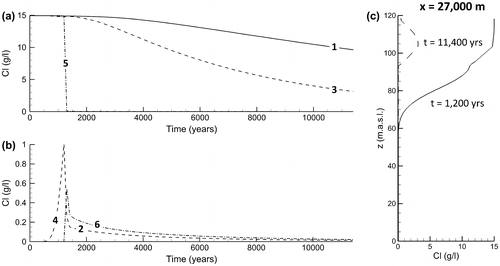
Figure 7. Simulated chloride distribution from t = 0, representing the start of the Champlain Sea invasion, showing (a) Step 3a: Simulated Cl after 1200 years of seawater invasion (about 10,200 years ago); (b) intermediate step at t = 2000 years (800 years after seawater retreat); and (c) Step 3b: current conditions 11,400 years after the start of sea invasion (10,200 years since seawater retreat). Selected streamlines are also shown (with 10× less groundwater flux in each successively deeper streamtube. Points 2, 4 and 5 are located on the same streamline which passes through the confined aquifer. Vertical exaggeration is 45×. For clarity, only the local area impacted by the seawater is shown. Concentrations are based on a maximum seawater concentration of 15 g.L⁻¹ (Catto et al. 1981). Blanked areas represent concentrations < 250 mg.L⁻¹ (drinking water standard in Canada). See Figure A2 for concentration breakthrough curves at selected points 1–6.

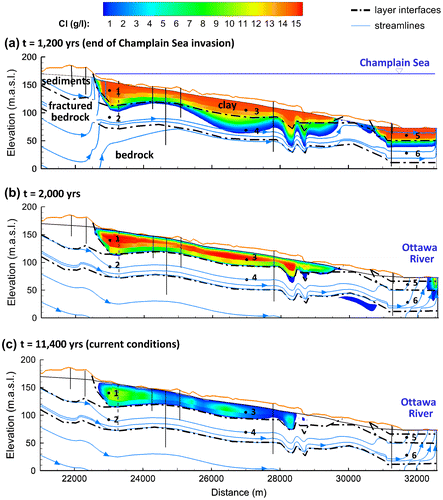
Due to the constant sea level of 170 m elevation imposed in Step 3a, velocities in the upper fractured part of the bedrock are 100 times less than under current conditions, and mean residence times are longer. The flow patterns are also different from the current conditions. Most water which has infiltrated up-gradient of the clay layer discharges just before the aquifer becomes confined. Groundwater flowing within the confined fractured bedrock aquifer recharges from further up-gradient. Two distinct discharge areas can be identified: one where the till currently outcrops (ca. km 30) and one at the far down-gradient end of the 2D cross-section. At the end of the Champlain Sea invasion (Figure 7a), chloride from the marine clay begins diffusing downwards into the shallow fractured bedrock aquifer which is recharged by chloride-free rainwater. Once in the bedrock, chloride is transported rapidly down-gradient. A gap in the simulated chloride plume is seen at kilometre 30, where a preferential discharge zone has formed due to more permeable overburden.

Chloride concentrations in the clay are still elevated 800 years following seawater retreat (Figure 7b), whereas all chloride in the aquifer has been flushed away by freshwater recharging in the unconfined part. Velocities below the centre of the Ottawa River are slower and chloride is still found in significant concentrations.

The chloride distribution 10,200 years following seawater retreat (Figure 7c) shows that most of the initial chloride in the bedrock aquifer has been flushed away (where concentrations are less than 1000 mg.L⁻¹), with most of the residual chloride still found in the marine clay. Maximum chloride concentrations in the clay remain about 11,000 mg.L⁻¹, similar to the original assumed seawater concentrations. This behaviour is consistent with a theoretical case described by Atteia et al. (2005) who show diffusion from a seawater-saturated aquitard into a confined freshwater aquifer. The results are also generally consistent with the observed chloride concentrations in most of the sampled wells and with investigations in similar marine clays presented, for example, by Cloutier et al. (2010) and Desaulniers and Cherry (1989). Some differences were observed, however, in concentrations below 1000 mg.L⁻¹. Sample OUT036356 in the confined aquifer, for example, had a Na–Cl water type (Figure 2) and the highest chloride concentration (around 350 mg.L⁻¹), whereas the corresponding simulated concentration was much lower (6 mg.L⁻¹). Calculated concentrations for wells OUT026131 and OUT022292 are 10 times lower than those measured in the corresponding samples, whereas they are on the same order of magnitude for the SANDBAY well (15 mg.L⁻¹ for calculated and observed values) and for well OUT21341 (15 mg.L⁻¹ calculated vs. 12 mg.L⁻¹ observed). Differences could be simply due to heterogeneities in the fractured bedrock, which would also explain why the observed concentration in sample OUT036356 was higher compared to the others, if this sample was located in a less permeable zone. In the field, chloride concentrations above the drinking water standard of 250 mg.L⁻¹ are currently found only in the clay layer. Concentrations are below this limit in the aquifer where chloride has been flushed by fresh water.

Simulated chloride concentrations over time are shown in Figure A2a and A2b of Appendix II at three different sites in the overburden (points 1 and 3 in the clay and 5 in the alluvium) and three in the confined fractured bedrock aquifer (points 2, 4 and 6; see locations in Figure 7). During invasion of the Champlain Sea, the clay remains saturated in chloride (points 1 and 3) while chloride in the fractured bedrock aquifer at point 4 gradually increases. Chloride concentrations in the up- and down-gradient parts of the bedrock aquifer (points 2 and 6) remain near zero.

Following seawater retreat, the breakthrough curves in the clay follow a slow diffusion-controlled decline, while points 4 and 6 in the fractured bedrock (now under the new hydraulic regime with higher flow gradients) are rapidly flushed by fresh water (Figure A2a). Below the Ottawa River, the initial chloride in the alluvium (point 5) is also quickly removed. Under the higher flow gradients, chloride migrating through the upper fractured bedrock had also penetrated into the deeper unfractured bedrock, reaching a depth of 100 m at kilometre 31, about 200–300 years after the Champlain Sea retreat. Thus, low-concentration chloride signals are seen at the base of the bedrock aquifer at points 4 and 6 (Figure A2b), which are only slowly decreasing because of low velocities below the Ottawa River and slow back-diffusion from the deeper rock.

Over the 10,200-year simulation time after seawater retreat, chloride has also diffused upwards at the surface of the clay over a thickness of about 5 m (Figure A2c), resulting in similar profiles to those described by O’Shaughnessy and Garga (1994). Diffusion towards the bottom of the clay layer (Figure A2c) is similar to observations by Torrance (1979) for other sites in the Ottawa region. Artesian conditions can also play a role in the leaching of marine clays (Torrance 1979; Rankka et al. 2004).

Age distribution

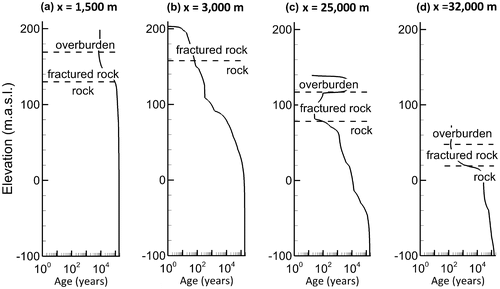
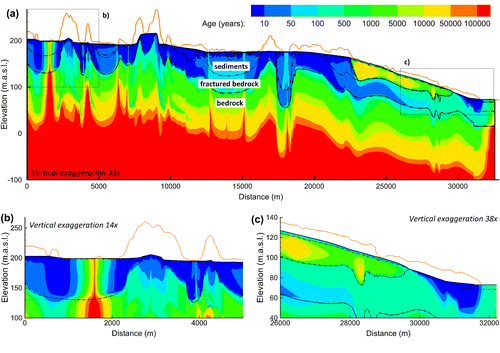
The age model was run for 100,000 years, which was sufficient to reach steady state within the first 200 m of depth (Figure 8a). Mean residence times in the Quaternary deposits were less than 100 years, and they were less than 10 years in the Ottawa River alluvium. Age contours are controlled by the flow system and by dispersion, with generally increasing ages with depth. An important exception is below the clay layer where younger, more recently recharged water can be found in the confined aquifer below the older water trapped in the clay. At depths greater than about 150 m, groundwater is more than 50,000 years old due to very low-flow conditions and limited mixing. Typical age profiles at different locations in the aquifer can be found in Figure A3. Under large surface-water bodies, for example under Lake Johnson at kilometre 2, (Figures 8b and A3a^{Figure 8}) or below the Ottawa River (Figures 8c and A3d^{Figure 8}), ages rapidly increase with depth due to the low hydraulic gradients and low groundwater velocities. Ages greater than 1000 years are evident in the unfractured bedrock with low hydraulic conductivities (with K ≤ 10⁻⁷ m.s⁻¹). Marine clays are characterised by ages greater than 20,000 years, whereas groundwater in the underlying higher K fractured bedrock layer is younger due to rapid displacement of groundwater from the nearest recharge zone (Figure 8c and A3c^{Figure 8}). In the unconfined aquifer, the maximum advective-dispersive ages are similar to the advective-based residence times (Figure 6), whereas in the confined aquifer, mixing of older water into younger water results in much higher advective-dispersive ages.

Figure 8. Simulated steady-state mean groundwater ages, showing (a) the two-dimensional cross-section to a depth of −100 m asl, (b) age detail in the upgradient part of the unconfined aquifer, and (c) age detail in the confined aquifer with overburden and rock interfaces shown for reference (dashed lines).

Discussion and validation of the conceptual model

Model sensitivity

Anisotropy

Little information is available on the bedrock anisotropy in this study area, although fractures are known to exist (as shown by the packer test results in well CONV-PON; Figure 4). In another part of the Grenville Province of the Canadian Shield, Lavigne et al. (2010) considered the Precambrian basement isotropic at depths below 200 m, although this was not based on literature or field data. At the Whiteshell Research Area (Superior Province of the Canadian Shield, southern Manitoba, Canada), Ophori et al. (1996) and Sykes et al. (2009) accounted for vertical fractures by applying an anisotropy factor of K_x/K_z = 0.1 to a depth of 300 m. Below this depth, the bedrock was considered isotropic. Additional simulations of the Outaouais flow system (not shown) showed that anisotropy has relatively little impact on the distribution of local and intermediate flow systems since the bulk hydraulic conductivity decreases so rapidly with depth.

Hydraulic and transport properties

The simulated tritium distribution was much more sensitive to the hydraulic conductivity of the bedrock than to the Quaternary deposits, which are on average only about 20 m thick with relatively high hydraulic conductivities, allowing rapid migration of tritium toward the bottom of these layers. Transport through the fractured bedrock was thus the main control on tritium behaviour, because of the bedrock’s relatively lower K, and because of the longer spatial scales for the local flow systems which were on the order of 1 to 5 km. This behaviour also reflects the hydraulic link between the Quaternary sediments and the fractured bedrock.

The sensitivity of tritium transport to changes in recharge rates was also tested (using 10, 20 and 35% of total precipitation). Simulated tritium concentrations showed only minor changes within the range of uncertainty in recharge compared to changes in the bedrock hydraulic conductivities. A lower longitudinal dispersivity of α_LH = 10 m (compared to the base case of α_LH = 20 m) showed a slightly less extended but more concentrated tritium plume (especially in zones of high velocities). Excessively high dispersivities tended to homogenise and decrease the tritium concentrations, which also did not reflect the observations.

Chloride transport scenarios

The chloride transport simulation assumed a single 1200-year Champlain Sea invasion, and neglected an inferred initial 200-year invasion. Within a reasonable uncertainty of ±200 years, errors in assuming a shorter 1200-year duration would appear to have a limited effect on the final results since the simulated chloride plume had almost reached steady state within 1200 years following seawater invasion, while most chloride had been flushed away within a few hundred years after its retreat. Thus, a possible 200-year invasion episode followed by 1000 years of ice advance before the major invasion of 1200 years most likely would not have changed the final result.

The impact of the maximum estimated elevation reached by the Champlain Sea (170 m asl), which corresponded to the maximum elevation of the clay layer, was also of interest, in particular since some marine clays had been found at higher elevations of around 180 m asl, notably in the unconfined part of the aquifer (at kilometres 14–15). In a subsequent simulation (not shown), a higher fixed head of 180 m was applied in all areas less than 180 m in elevation, again with a fixed concentration of C/C₀ = 1 allowing intrusion of salt water. Assuming the same invasion duration of 1200 years, chloride was again rapidly flushed away after the Champlain Sea retreat, indicating results were not sensitive to the intrusion duration.

The progressive sedimentation of marine clays and sea level rise were not tested in this study but they would be expected to have some impact on the flow patterns and on the chloride plume development. It would be of interest to model more realistic scenarios to justify the simplifications and compare simulated current chloride plumes.

The modelling results suggest that seawater intrusion into the deeper unfractured bedrock did not occur during the Champlain Sea invasion (Figure 7a). Following seawater retreat, the simulated chloride plume does penetrate the upper part of the less fractured bedrock but remains for less than 1000 years (Figure 7b) as it is slowly replaced by fresh water. At the end of the simulation, the chloride concentrations in this part of the bedrock aquifer have decreased to about 10–15 mg.L⁻¹.

A similar conceptual model was proposed by Aquilina et al. (2015) in which saline groundwater in a basement aquifer in France was quickly replaced by mobile fresh water but remained in the deeper bedrock. In this case, the study area is located in an arm of the Champlain Sea where the seawater was diluted (15,000 mg.L⁻¹) and the invasion episode was short. Intrusion of seawater into the deeper bedrock was likely limited at the Outaouais site and became slowly diluted after the Champlain Sea retreat. However, no samples from the deeper bedrock in this area are available to validate this hypothesis.

Comparison of ages

Most of the bedrock boreholes pass through different groundwater age layers (Figure 9). As explained in Montcoudiol et al. (2015), the groundwater samples show evidence of both low mean residence times (where tritium was detected) and higher mean residence times (accumulation of ⁴He). For the four boreholes sampled for noble gases (Montcoudiol et al. 2015), it appears that the average (relatively young) age is not consistent with the high concentrations of ⁴He but rather reflects the maximum age of the groundwater component flowing through the open borehole, which seems to be a better indicator. For example, CONV-PON has the lowest concentration of ⁴He and has the smallest simulated age range (from 11 to 23 years along the open borehole; Figure 9c). On the other hand, OUT036356 does not show evidence of tritium and has calculated ages varying from 580 to 900 years (Figure 9f). Finally, wells OUT036357 and OUT021341 present the highest ⁴He concentrations as well as the largest simulated age range, from 6 to 1430 and from 1 to 1530 years, respectively (Figure 9b and ^{Figure 9}i), with detected concentrations of tritium.

Figure 9. Simulated advective-dispersive groundwater age and tritium profiles for selected wells: (a) OUT036352, (b) OUT036357, (c) CONV-PON, (d) OUT036358, (e) OUT036353, (f) OUT036356, (g) SANDBAY, (h) OUT036351 and (i) OUT021341. The simulated ages and tritium concentrations represent average nodal values based on the open borehole length for bedrock wells, and the entire well length for wells in Quaternary sediments for which the location of the screen is unknown. ¹⁴C ages are expressed as percentage of modern carbon (pmC).

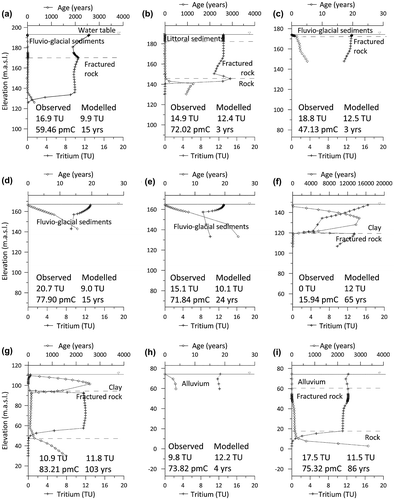
Interpretation of tritium (and other species) should be treated with caution, however, since most of the wells are located in areas where the flow is assumed to be sub-horizontal and mixing would occur as a result of sampling in open boreholes. Areas of natural flow mixing also occur near the discharge zones, as in bedrock well OUT021341 close to the Ottawa River. Generally, vertical profiles, from the ground surface to the bottom of the wells, show tritium concentrations close to present atmospheric levels near the surface (Figure 9). Since atmospheric tritium has been almost constant over the last approximately 10 years, tritium that infiltrated into the first few metres during this period has already been partly degraded and concentrations are thus less than the current atmospheric tritium levels. Concentrations then increase with depth, corresponding to what is left of the historic tritium peak, and are still higher than the current levels. At deeper depths, tritium is absent and is representative of levels which had recharged before the bomb testing peak and which have been decaying for several decades.

Observed ¹⁴C measurements for each well are also given in Figure 9. The modelling results show that the ¹⁴C concentrations cannot be used for assessing mean groundwater residence times as they are not correlated to simulated ages. They rather reflect processes occurring in the unsaturated and saturated zones, as discussed in Montcoudiol et al. (2015). Only the ¹⁴C age calculated for sample OUT036356 (the only sample to have undergone some decay; see Montcoudiol et al. 2015) can be compared with the modelling results. The simulated age is lower than the estimated ¹⁴C age and lower than the age suggested by the chemical data. As mentioned before, chloride simulations suggested that sample OUT036356 comes from a well which is probably located within a less permeable zone where ages are higher than those calculated by the model.

Note that simulated groundwater ages greater than the depositional age of their host formations (e.g. ages of 20,000 years for the marine clays) are not inconsistent; this simply reflects the theoretical mean steady-state age which would be reached (e.g. in the future) under uniform conditions.

Validation of the conceptual model

The updated conceptual model with the interpreted flow systems and groundwater residence times is shown in Figure 10. A major change to the original conceptual model was the removal of a regional flow component. In general, local flow systems had already been well identified, but intermediate flow systems are now thought to be laterally less extensive and also deeper, extending the modelling results from Sykes et al. (2009) and Ophori et al. (1996) to a different set of conditions in the Canadian Shield, while regional-scale flow remains negligible. Topography and surface water bodies also exercise a more important control than initially thought, as most areas of local topographic minima (corresponding to streams, lakes and rivers) are locations of strongly focussed discharge.

Figure 10. Final revised conceptual model, showing flow directions and total residence times from recharge to discharge zones along selected conceptual flow lines.

In this new conceptual model, vertical flow gradients in the confined aquifer have now been clarified. Specifically, the confined aquifer is now divided into two parts, with the up-gradient area (from km 23 to 24) characterised by upward vertical flow gradients (referred to previously as flowing artesian) whereas the down-gradient part has downward vertical flow gradients. These findings need to be verified against more detailed and reliable data (only one artesian well was found in this part of the confined aquifer). Regardless of the flow gradient directions, groundwater flow is very slow in the clay where chloride transport is dominated by downward diffusion into the fractured bedrock, where it becomes diluted due to rapidly flowing fresh water. Some upward diffusion towards surface fresh water is also suggested.

The simulated lateral extents of the intermediate flow systems have been reduced in the new conceptual model, which affects how the chemistry data should be interpreted. All samples were originally believed to have been taken along a flow line from an intermediate flow system extending along most of the 2D cross-section and were assumed to represent the geochemical evolution of groundwater. Although this is true in the confined part, all samples taken in the up-gradient unconfined bedrock are now presumed to belong to different flow systems, reflecting their own geochemical evolution depending on their mean residence times. Samples OUT036358 and OUT036353, located in highly conductive fluvio-glacial sediments, show significant rock–water interactions compared to samples from the unconfined bedrock (Montcoudiol et al. 2015). While these sediments result from glacial erosion and have similar mineral chemistry to the bedrock, the higher mineralisation of the samples could be explained by their proximity to the underlying marble bedrock (Montcoudiol et al. 2015).

Local flow systems are characterised by very short residence times of less than 50 years, which explains the occurrence of tritium in most samples from the unconfined aquifer. Fast simulated flow conditions in the unconfined bedrock aquifer are consistent with the observed chemical composition of groundwater, which shows limited interaction between groundwater and rock. The high chloride concentration in sample OUT036356 cannot be accurately simulated and likely reflects unresolved heterogeneities and less permeable zones, also suggested by the low ¹⁴C activity. Except for this sample, ¹⁴C contents cannot be interpreted because in addition to radioactive decay, they are adversely affected by chemical reactions occurring in the unsaturated and saturated zones (Montcoudiol et al. 2015) which are not taken into account in the model. Finally, old groundwater is found at intermediate depths (about 150–200 m) from which diffusion of ⁴He could explain the high concentrations of this element measured in some samples (Andrews 1987).

Modelling approach and limitations

The 2D models developed here are relatively simple with respect to the complexity of the real system and the chronology of past events. For example, groundwater ages were simulated over a 100,000-year period assuming no changes in flow conditions. While model sensitivity tests showed that the simplifications applied to represent the Champlain Sea invasion (sea level rise, rate of clay sedimentation and uplift) did not have a significant impact on the final results representing current conditions, the system response time to these major system changes was not tested. Groundwater ages, for example, especially in the Quaternary sediments and fractured bedrock where residence times are short, would likely be affected by uplift, which is a slow process occurring over 10,000 years. The rate of clay sedimentation and sea level rise would also likely have some impact on the chloride and age distribution, since the flow velocities become negligible under hydrostatic conditions below the seawater. However, the speed at which the confined aquifer recovered from the retreat of the Champlain Sea, from one extreme to the other, is probably the main factor controlling the extent of the current chloride plume.

As expected, the distribution of the hydraulic conductivities at depth exerts an important control on the flow systems, which affects both the extent and depth of the tritium and chloride plumes and the age distribution. Because of its added sensitivity to the flow field, transport modelling thus appears to be a good means to improve the flow model calibration. The tritium simulation, for example, showed that the hydraulic conductivities had to be high in the upper part of the bedrock to allow sufficient penetration of the tritium, which would explain the observed tritium concentrations well above the detection limits in the unconfined bedrock wells.

Evidence of such highly conductive bedrock zones was demonstrated by Sterckx (2013) in his analysis of aquifer transmissivities calculated from hydraulic tests. Furthermore, hydraulic packer tests carried out in two wells along the cross-section (CONV-PON and SANDBAY) responded completely differently, with the SANDBAY well being tight all along the open borehole, whereas well CONV-PON was characterised by a highly conductive zone at depths between 20 and 25 m. Packer test results suggested hydraulic conductivities on the order of 10⁻⁵ m.s⁻¹ at this location, which is similar to the model-calibrated value.

Conclusions and perspectives

Four sequential numerical modelling approaches (for groundwater flow, and transport of tritium, chloride and age) were developed to support a 2D vertical-plane conceptual hydrogeochemical model along a 32-km flow path representative of the western Outaouais area, Quebec, Canada. Calibration of the flow model was augmented using tritium which appeared to be most sensitive to the hydraulic conductivity of the upper fractured bedrock, which was calibrated to 8×10⁻⁵ m.s⁻¹. This is relatively high for bedrock but consistent with discrete hydraulic conductivities measured using packer tests and specific capacity tests in other regional wells, and supports the conclusion of Sterckx (2013) that the upper part of the bedrock is densely fractured.

The flow simulation showed negligible regional flow at scales > 15–30 km, which is a real-case confirmation of the conclusions drawn by Gleeson and Manning (2008) for a synthetic low-relief model. The simulated intermediate systems, on scales of 5–15 km, are likely less laterally extensive than proposed in the original conceptual model. Therefore, only those water samples taken just up-gradient of the confined aquifer and those from the confined aquifer likely lie along the same flow path. Samples from different locations within the unconfined bedrock aquifer likely belong to different intermediate flow systems. This conclusion is consistent with the interpretation by Montcoudiol et al. (2015), with the slight adaptation that the samples are now interpreted to lie along somewhat less extensive flow systems, but separate systems nevertheless. Their relatively similar chemistry, which suggests limited water–rock contact time (Montcoudiol et al. 2015), is the result of similar mean residence times on the order of hundreds of years within these different intermediate flow systems.

Local flow system depths predicted by the model appear limited to the first 40 m, and mainly lie within the Quaternary sediment layers and the first tens of metres of bedrock in outcropping areas. These local flow systems are characterised in the model by scales of 1–5 km and by residence times of a few tens of years or less, explaining the occurrence of tritium. The active flow zone appears to extend only into the first 100–150 m, with almost stagnant conditions below this depth (residence times > 10⁵ years). The model suggests old groundwater should often be found at relatively shallow depths (excluding recharge zones) from which diffusion of ⁴He can explain the high concentrations found in the samples.

The simulations support the conceptual model that the Champlain Sea invasion caused diluted seawater to migrate into the hydraulically connected Quaternary deposits and fractured upper bedrock aquifer system, but due to short mean residence times of less than 1000 years, all chloride has since been flushed from the active flow system. Current residual chloride concentrations likely result from slow diffusion out of the clay layer and subsequent mixing with up-gradient groundwater. High chloride concentrations in sample OUT036356 are probably indicative of heterogeneities and less conductive areas as commonly found in fractured bedrock but which are not resolved in the current model.

Relatively short residence times and a predominance of local flow systems suggest a relatively vulnerable aquifer system, even within the shallow confined fractured bedrock where in direct contact with the unconfined aquifer. Relatively rapid infiltration from surface contaminants, for example agricultural fertilisers, could therefore be a risk to local water supply wells. Nevertheless, water supplies within the conductive Quaternary aquifers have good potential for providing additional high-quality potable water as outlined in Montcoudiol et al. (2014). Although the apparently highly fractured shallow bedrock appears sufficient for meeting local household water supplies, the storage volumes would still be limited, restricting more intense development of the resource.

The numerical flow and transport modelling has provided much insight into the hydrogeological system; however, improvements could be made through the collection of additional data, specifically in the clays and within the fractured bedrock. Tracer tests would be very useful to independently constrain flow velocities. A more complete validation of the conceptual model would also require geochemical modelling which at this scale would need additional simplifications. For example, one approach could focus on silicate weathering along a flow line or on cation exchange in the confined aquifer. These approaches will be considered in future work.

Acknowledgements

This project was funded primarily by the Quebec Ministry of Sustainable Development, Environment, and the Fight against Climate Change (MDDELCC), with contributions from the following Regional Partners: l’Agence de Traitement de l’Information Numérique de l’Outaouais (L’ATINO), WESA Enviro-Eau, Regional County Municipalities (Collines de l’Outaouais, Vallée de la Gatineau, Pontiac and Papineau), the City of Gatineau, Regional Watershed Organisations (ABV des 7, COBALI and OBV-RPNS), and the Regional Council for Environment and Sustainable Development in Outaouais (CREDDO). We also acknowledge research support from the Natural Sciences and Engineering Research Council of Canada (NSERC) and from a Canada Research Chair in Quantitative Hydrogeology of Fractured Porous Media held by the second author. We thank P. Therrien of Université Laval who provided invaluable computer technical support. Finally, we would like to thank CWRJ Co-editor Jim Buttle, Clément Roques (ETH Zurich), and an anonymous reviewer for their helpful comments.

Appendix 1.

Governing equations of the numerical models

Groundwater flow

The flow system representing the conceptual model was simulated using the FLONET/TR2 model (Molson and Frind 2014) which uses the dual formulation for flow in terms of hydraulic potentials Φ [L] and stream functions ψ [L².T⁻¹], assuming 2D steady-state, isothermal and uniform density conditions, as defined by Equation (1) and Equation (2), respectively:

(1)

(2)

where x and y are the horizontal and vertical coordinate directions, respectively [L], and K_xx and K_yy are the principal components of the hydraulic conductivity tensor [L.T⁻¹].

Element-based groundwater velocities for the transport simulations are calculated in FLONET/TR2 based on the simulated stream functions. These velocities are used to calculate advective groundwater ages based on particle tracking using a fourth-order Runge–Kutta integration scheme within Tecplot (©Tecplot Inc. 2014). A full advective-dispersive age transport simulation is presented later in the paper. The flow field is assumed at steady state for all simulations.

Tritium and chloride

Tritium and chloride transport is simulated using the TR2 module within FLONET/TR2 which solves the 2D advective-dispersive mass transport equation (Equation 3):

(3)

where D_ij is the hydrodynamic dispersion tensor [L².T⁻¹], R is the retardation factor [−], c is the tritium or chloride concentration [M.L⁻³], x_i are the spatial coordinates [L], v_i is the average linear flow velocity [L.T⁻¹], λ is the first-order decay rate [T⁻¹] and t is the time [T].

For tritium, a retardation factor of R = 1 and a linear decay rate of λ = 1.53 × 10⁻⁴ d⁻¹ were applied, where the decay rate corresponds to a half-life of 12.43 years (Clark and Fritz 1997). For chloride, which is non-reactive, λ = 0 and R = 1. The effective molecular diffusion coefficient for tritium was 1 × 10⁻¹⁰ m².s⁻¹, and for chloride it was 2 × 10⁻¹⁰ m².s⁻¹ (Quigley et al. 1983; Desaulniers and Cherry 1989).

The dispersion tensor D_ij in Equation (3) is defined using the four-component dispersivity formulation of Lichtner et al. (2002), which uses two principal longitudinal dispersivities (α_LH, α_LV) and two principal transverse dispersivities (α_TH, α_TV), for the horizontal and vertical directions, respectively. In all transport simulations, the longitudinal horizontal dispersivity for the domain (α_LH = 20 m) was estimated using the relationships developed by Gelhar et al. (1992), based on the system scale of 32 km. The longitudinal vertical dispersivity (α_LV) was set at 2 m (10 × less than α_LH) while the two transverse dispersivities were set at 0.01 m (same order of magnitude as applied at similar scales by Bester et al. (2006). See Molson and Frind (2014) for the full dispersion tensor formulation, including diffusion.

The tritium and chloride transport simulations assume steady-state flow conditions and dilute water. Density effects are not considered. The time step was 10 days, which meets the Courant stability criterion.

Groundwater mean age

Advective-dispersive mean groundwater ages were computed to complement the advective ages as the former include full mixing between different age groundwaters, and are therefore more realistic than advective travel times. A similar equation to Equation (3) is solved for mean groundwater age (Equation 4):

(4)

where A is groundwater age (T) relative to a recharge age of 0 days, and where the + 1 term represents a growth of age at a rate of 1 day/day. The dispersion tensor and dispersivities are defined identically as in the tritium and chloride simulations. A molecular diffusion coefficient of 1 × 10⁻¹⁰ m².s⁻¹ was assumed. The approach accounts for advective-dispersive age mixing along and across flow lines.

Appendix 2.

Additional figures

^{Figure A1Figure A2Figure A3}

Figure A1. Simulated hydraulic head profiles within the two-dimensional cross-section in different hydrogeological settings: (a) discharge zone under Lake Johnson, (b) recharge zone, (c) artesian conditions, (d) non-artesian conditions in the confined aquifer, and (e) discharge zone under the Ottawa River.

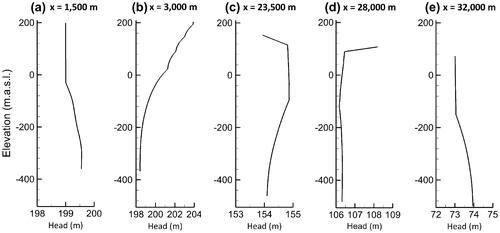
Figure A2. Simulated chloride variations over time at different points in the model showing response and decay since flooding (t = 0) and retreat (t = 1200 years) of the Champlain Sea: (a) chloride response within the overburden (points 1 and 3 in the marine clay, point 5 in the alluvium), (b) response within the bedrock (points 2, 4 and 5 are located along the same flow line), and (c) chloride variations over depth at 1200 and 11,400 years at x = 27,000 m (passing through points 2 and 5). See Figure 7 for point locations.

Figure A3. Simulated age profiles along the two-dimensional cross-section in different hydrogeological settings: (a) in a discharge zone under Lake Johnson, (b) in a recharge zone, (c) in the confined aquifer, and (d) in the discharge zone below the Ottawa River.