Modelling Temperature, Currents and Stratification in Placentia Bay

Abstract

Placentia Bay is an important spawning and nursery ground for Atlantic Cod (Gadus morhua) and a vital shipping corridor for Newfoundland industry, but our ability to forecast the bay circulation is limited. In this study, a three-dimensional (3-D) circulation model based on a finite-volume coastal ocean model (FVCOM) was developed in 1999 to simulate temperature, currents and stratification. The model is forced at the lateral open boundaries with five leading tidal constituents and non-tidal sea surface elevation and at the surface with wind and heat flux. The open boundary temperature, salinity and non-tidal sea levels are derived from a larger-scale shelf model. Simulated tides agree well with tide-gauge data, with a root sum square (RSS) error of 4.6 cm for the elevations of the five tidal constituents and a relative root mean square (RMS) error of 37% for M₂ tidal currents. The modelled temperature has RMS errors of 1°–2°C. The non-tidal currents show reasonable agreement with moored measurements. The model realistically simulates many features of the bay that may affect early life stages of fish, including the evolution of stratification from spring to fall, the cyclonic circulation in the outer bay and late-spring upwelling on the western side of the outer bay.

RÉSUMÉ [Traduit par la rédaction] La baie Placentia est une frayère et une aire de croissance importantes pour la morue (Gadus morhua) ainsi qu'une voie de circulation vitale pour l'industrie à Terre-Neuve, mais notre capacité à prévoir la circulation dans la baie est limitée. Dans notre étude, nous avons élaboré un modèle de circulation en trois dimensions en nous fondant sur un modèle d'océanologie côtière à volumes finis (FVCOM) afin de simuler la température, les courants et la stratification en 1999. Le modèle est forcé aux limites ouvertes latérales avec cinq grandes composantes de la marée et l'élévation de la surface libre de la mer non soumise aux marées et à la surface avec le vent et le flux thermique. La température aux limites ouvertes, la salinité et les niveaux de la mer non soumis aux marées ont été établis à partir d'un modèle du plateau continental à grande échelle. Les simulations de marée concordent bien avec les données recueillies à l'aide de marégraphes, avec une erreur quadratique moyenne (RSS) de 4,6 cm pour les élévations des cinq composantes de la marée et une erreur quadratique moyenne relative (RMS) de 37% pour les courants de marée M₂. La température obtenue à l'aide du modèle présente des erreurs RMS de 1° à 2°C. Les courants sans marée concordent raisonnablement bien avec les mesures obtenues au moyen d'instruments amarrés. Le modèle simule de façon réaliste beaucoup de caractéristiques de la baie qui se répercutent sans doute sur les premiers stades de la vie du poisson, notamment l'évolution de la stratification du printemps à l'automne, la circulation cyclonique dans l'avant-baie et la remontée d'eau froide à la fin du printemps sur la rive ouest de l'avant-baie.

Keywords:

• circulation
• temperature
• stratification
• numerical modelling
• FVCOM
• Placentia Bay

1 Introduction

Placentia Bay is located on the south side of the island of Newfoundland and is bordered by the Burin Peninsula to the west and the Avalon Peninsula to the east (Fig. 1). It is about 130 km long along the bay and about 100 km wide across the mouth of the bay. There is pronounced variability in the bottom topography. At the head of the bay, channels that are hundreds of metres deep are subdivided by elongated islands. Winds are predominantly from the southwest and west from spring until fall and from the northwest and west in winter. There are frequent extratropical storms in winter and spring and occasional tropical storms in summer and fall. The mean ocean circulation is generally cyclonic into the bay on the eastern side and out on the western side.

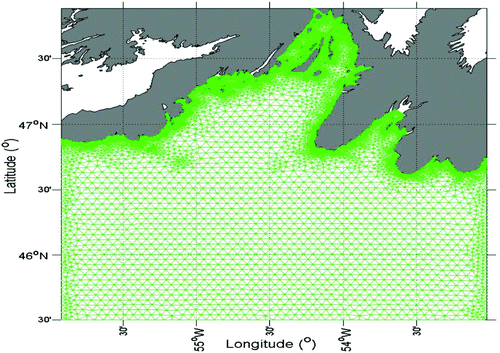
Fig. 1 Map of model domain showing the major locations and features, bathymetry (in metres). The thick red lines indicate transects where the model volume transports are calculated. A is Merasheen Island; B is Red Island and C is Long Island. D is one of the two tide-gauge stations (red dots).

There are important fisheries in the bay, especially for Atlantic Cod (Gadus morhua), which has received considerable interest because of its ecological sensitivity and economic importance (Bradbury et al., 2000). In the coastal embayments of Newfoundland, such as Placentia Bay, currents are less influenced by the cold Labrador Current and more by local processes, such as wind forcing (deYoung et al., 1993) which can contribute to both transport and vertical mixing, thereby influencing the abundance and distribution of larval fish (Pepin et al., 1995).

Over the past two decades, in situ observations have been made in Placentia Bay in support of broader oceanographic studies (Hart et al., 1999; Schillinger et al., 2000) to improve our knowledge of the mean and seasonal circulation and temperature variability. It is not practical, however, to use field observations to examine the physical factors affecting fisheries ecosystems directly. Thus, we require a three-dimensional (3-D) circulation model to understand the detailed and dynamical oceanography of Placentia Bay. Although several different regional models have been used to hindcast and forecast the tidal currents and shelf circulation for the Newfoundland and Labrador shelf and slope region, which includes Placentia Bay (Greenberg and Petrie, 1988; Tang et al., 1996; Han, 2000, 2005; Han et al., 2008, 2011), they all have insufficient horizontal resolution for Placentia Bay and, thus, offer little insight into the detailed circulation of the bay, particularly given the topographic complexity at the head of the bay. Therefore, a high-resolution 3-D numerical model focused on the Placentia Bay region is warranted.

In this paper, we will describe the first application of a 3-D, high-resolution, unstructured-grid, finite-volume coastal ocean model (FVCOM; Chen et al., 2003) to Placentia Bay. The advantage of an FVCOM in simulating the physical environment in coastal and embayment areas has been well demonstrated in other studies (e.g., Huang et al., 2008; Foreman et al., 2009, 2012). Its unstructured grid in the horizontal is highly suitable for the complex coastal boundary and bathymetry of Placentia Bay. Our main objectives are to establish and validate the model results against independent observational data including mooring data and tide-gauge data and to examine key circulation features as well as the stratification and mixed-layer depth.

2 Model configuration

a FVCOM Model (Version 2.6)

Combining the advantages of both horizontal grid flexibility and computational efficiency, the FVCOM model used in this study integrates independent variables through individual control volumes and is solved numerically by flux through the volume boundaries to guarantee the horizontal conservation of mass and momentum (Chen et al., 2003, 2006a, 2006b). A time-splitting method is used for computational efficiency including an internal mode and an external mode constrained by its Courant-Friedrichs-Levy (CFL) condition. Unlike a finite difference model, a second-order accurate upwind scheme, based on piecewise linear reconstruction of a dynamic variable, is implemented for the spatial flux calculation for variable values (Hubbard, 1999; Kobayashi et al., 1999). A sigma coordinate is chosen to resolve the topography better. For a more accurate estimation of sea level, currents, and salinity and temperature fluxes, all variables except currents are placed at nodes; currents are placed at centroids.

b Model Domain

The model domain is 53°W to 56°W and 45.5°N to 47.8°N (Fig. 1). The geometry of the domain features some offshore banks (Green Bank, Whale Bank, St. Pierre Bank) and channels (such as Haddock Channel). The shoreline of the bay is made up of relatively steep cliffs and has many inlets. Three islands are located in upper Placentia Bay, the largest being Merasheen and the other two being Red Island and Long Island. The outer bay is 200 m deep at the centre of the mouth, while much of the remainder of the outer bay is typically 100 m deep. The average depth of the bay is approximately 125 m although there are several 400 m deep channels that run along the longitudinal axis of the inner bay. The model bathymetry is mainly derived from the multibeam bathymetry of the Canadian Hydrographic Service. The bathymetry has been smoothed to minimize the pressure gradient errors (Mellor et al., 1993). The governing equations of the model are solved on an unstructured triangular grid whose spacing is largest (3–5 km) along the open boundary and smallest (100 m) along the coastline (Fig. 2). There are 20 unequally spaced layers in the vertical, with higher resolution near the surface and bottom to better resolve the shear current and thermodynamic process there. For example, the vertical spacing is approximately 0.25 m near the sea surface and bottom at a location with a water depth of 100 m.

Fig. 2 The horizontal grid used in the numerical model.

The model equations are solved with an integration time step of 1 s for the external mode and an internal to external mode ratio of 10. The model is integrated from 1 April to 30 November 1999. Harmonic analysis of the model output from 20 April to 30 November is carried out to separate tidal elevations and currents from non-tidal components.

A volume preserving technique is used to smooth the bottom bathymetry. The technique limits the depth slope within each triangle (Foreman et al., 2009). A maximum element slope of 0.1 was recommended for FVCOM (Chen et al., 2004). One problem is that without sufficient smoothing of the bathymetry there is an exaggeration of temperature mixing in regions with steep bottom topography. We used a maximum slope of 0.4 to retain relatively accurate bathymetry and inhibit excessive mixing in the vertical.

c Model Forcing and Initial Conditions

The model is forced by winds and heat fluxes at the sea surface, tidal and non-tidal sea levels, and temperature and salinity at the lateral open boundaries. We used a spatially uniform wind stress over the entire computational domain. Hourly wind speed and direction data collected at Argentia were applied from 1 April to 30 November 1999. Heat fluxes, including shortwave radiation, longwave radiation, latent heat flux and sensible heat flux, were calculated based on Environment Canada's meteorological observations at Argentia and the spatially variable sea surface temperature from a monthly-mean temperature climatology (Geshelin et al., 1999). The surface shortwave heat flux was calculated using the relationships of Curry and Webster (1998). A revised equation from Li et al. (2006) was used to calculate the albedo, including the white cap effect (Monahan and MacNiocaill, 1986); modified code from the Tropical Ocean and the Global Atmospheric Program (TOGA)-Coupled Ocean Atmospheric Response Experiment (COARE) (Fairall et al., 1996) was used to calculate the sensible and latent heat fluxes. The formulation of Fung et al. (1984) was used to estimate longwave radiation based on Geshelin et al.’s (1999) sea surface temperature and the observed air temperature, dewpoint temperature, cloud cover and wind speed. Then net heat flux was calculated from these four heat flux components.

Five leading semi-diurnal (M₂, S₂ and N₂) and diurnal (K₁ and O₁) constituents and non-tidal sea levels at the lateral open boundaries were obtained from a large model of the Newfoundland Shelf (Han et al., 2011) and specified along the open boundary. The temperature and salinity along the open boundaries were specified in the same way. Note that this shelf model reproduces tidal elevation accurately and the temperature, salinity, and volume transport of the inshore Labrador Current well (Han et al., 2011). Results from the Newfoundland Shelf model were interpolated to provide temperature and salinity along the boundary in order to avoid underestimating seasonal and daily changes in the hydrographic conditions. However, to maintain temperature and salinity conservation, this condition was used only when the boundary flux was directed into the domain. Thus, a temperature or salinity jump easily emerges because of the changing wind stress on the volume flux. To capture this jump efficiently, we used the Flux Corrected Transport (FCT) scheme which is basically a conservative shock-capture scheme.

The sea level and velocity were initialized with the results of the large-scale Newfoundland Shelf model (Han et al., 2011) throughout the computational domain to reduce the ramp-up time. The initial temperature and salinity conditions were generated from the historical monthly-mean temperature and salinity data (Geshelin et al., 1999) at standard z-levels. The monthly-mean temperature and salinity data were used instead of the results from the Newfoundland Shelf model because the depth of the shelf model is much shallower than the depth used in the Placentia Bay domain. Because the initial velocity and sea level provided by the Han et al. (2011) model does not match the initial temperature and salinity fields exactly, we allowed the model to spin up for 19 days. Separate monthly climatology runs indicate the model can reach a dynamic equilibrium state in 10 days.

Because there is no significant river runoff into Placentia Bay, the present model did not include the freshwater input from the river runoff. The surface salinity was restored to the monthly-mean climatology of Geshelin et al. (1999) with a time scale of five days.

d Data for Comparison

In situ observations were used to validate model results. They included de-tided water levels at Argentia (Fig. 1), tidal elevations at Argentia and another location (D in Fig. 1), and temperature and currents at mooring sites M1–M4 (see Fig. 1 for locations) at 20-minute intervals between 20 April and 20 June 1999 (Hart et al., 1999). Currents at 20 m and 55 m (45 m for M4) except for M3 at 55 m were available for comparison. Satellite images in late April and mid-June 1999 were obtained from the National Oceanic and Atmospheric Administration (NOAA, 2011) for comparison with the model surface temperature pattern. Salinity data for M1–M4 were not used because of data quality issues with the current meters. Han et al. (2011) showed that the accuracy of the shelf model is better than 0.5 (practical salinity scale used). The present bay model is expected to have a similar accuracy for salinity, except in a few localized areas close to a river mouth.

3 Model validation

a Comparison of Observed and Calculated Tidal Elevation and Currents

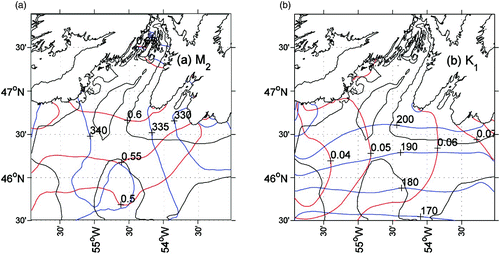
Harmonic analysis was used to process the model output from 20 April to 30 November 1999. Figure 3 shows the co-amplitude and co-phase charts of the computed tidal constituents for M₂ and K₁. The M₂ tide propagates from the Avalon Channel westward through the model domain and northward toward the head of the bay, with a maximum amplitude of 70 cm. The S₂ and N₂ constituents (not shown) have similar spatial patterns but with amplitudes four to five times smaller, which is consistent with other studies of the semi-diurnal tidal constituents along the inner Newfoundland Shelf (Han, 2000; Han et al., 2010). The K₁ diurnal constituent is much smaller than the M₂ tide. The co-amplitude increases from the outside to the inside of the bay, consistent with an amphidromic point in the Laurentian Channel (Han et al., 1996) west of the model domain.

Fig. 3 (a) M₂ and (b) K₁ co-amplitude (red, in metres) and co-phase (blue, in degrees) charts. The 100 m and 200 m isobaths are displayed as black lines.

To establish a quantitative measure of model and data agreement, we used two indices:

1.	The root mean square (RMS) difference; and
2.	The absolute error () and the relative error (), where , L is the number of observations, AMP is the amplitude, ϕ is the phase, subscripts o and m represent the observations and model, respectively.

These statistics for model tidal elevation and observations at coastal tide gauges are given in Table 1. For these two coastal sites, the RMS amplitude difference is approximately 2 cm. The RMS phase difference is below 6° for the semi-diurnal and diurnal constituents except K₁. The absolute error accounts for the discrepancies in both amplitude and phase with observations. The error for the five constituents is approximately 2 cm. The semi-diurnal constituents have smaller relative errors than the diurnal constituents. The root sum square absolute error for the five constituents is 4.6 cm, indicating good agreement between the model tidal elevation and the tide-gauge data.

Table 1. Summary and statistics for observed and computed semi-diurnal and diurnal tidal elevations at two coastal tide-gauge stations. AO is the observed amplitude. PO is the observed phase. AMO is the amplitude difference of observed and model results. PMO is the phase difference of observed and model results. See Fig. 1 for the location of the tide gauges.

Sites	AO (cm)	PO (°C)	AMO (cm)	PMO (°)	RMS amplitude difference (cm)	RMS phase difference (°)	absErr (cm)	relErr
M2
D	67	334.4	−1.7	−1.2	2.6	1.9	2.3	3.3%
Argentia	69	338.8	−3.2	2.3
S2
D	19	14.0	−1.8	−2.2	2.3	4.6	2.1	10.8%
Argentia	20	15.8	−3.6	6.2
N2
D	13	321.5	−0.2	−7.5	1.4	5.4	1.3	9.4%
Argentia	15	324.1	−2.0	−1.1
K1
D	9	179.7	−3.6	26.8	2.8	24.4	2.7	33.8%
Argentia	7	183.2	−1.8	21.8
O1
D	8	170.8	−3.6	0.5	4.2	3.6	2.9	34.9%
Argentia	9	165.4	−4.7	5.0

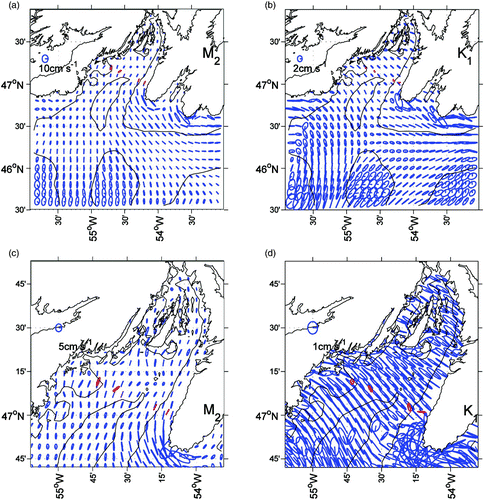
The computed M₂ and K₁ tidal current ellipses at the sea surface layer (σ = 0.0025) are shown in Fig. 4. For M₂, a nearly rectilinear tidal flow (10 cm s⁻¹) dominates the Avalon Channel and along the coast of the Avalon Peninsula. In the outer bay, the tidal flow has a magnitude of 3–5 cm s⁻¹. The tidal current at the head of bay is weaker except near the coast. Relatively strong tidal currents occur on the outer shallow banks with amplitudes approaching 10 cm s⁻¹. The S₂ and N₂ surface tidal currents (not shown) have spatial patterns similar to the M₂ tidal constituent but with smaller magnitudes. The computed K₁ tidal current at the sea surface is relatively weak compared to the M₂ tidal current. The K₁ tidal current exhibits a zonal rectilinear flow pattern in the east and a meridional flow pattern in the west. A southeastward flow dominates the centre of the bay with a maximum of approximately 6 cm s⁻¹ over the outer shelf banks. The general surface current features in the present model are consistent with previous model results (Han, 2000; Han et al., 2010). The relative absolute error of the modelled M₂ current is 41% and 33% for eastward and northward components, respectively.

Fig. 4 Near-surface (a) M₂ and (b) K₁ tidal current ellipses for the entire model domain, with corresponding close-ups (c) and (d) for the bay area. The 100 m and 200 m isobaths are displayed as black lines. Observations are in red. Note that the scales are different among the panels.

b Comparison of Observed and Modelled Water Levels and Currents

To eliminate inertial oscillations, a 36-hour low-pass filter is used to process the water level and current data. Model water level at the Argentia station (Fig. 1) is compared with tide-gauge observations. The variability in sea level at this station is influenced by the wind and transport from offshore.

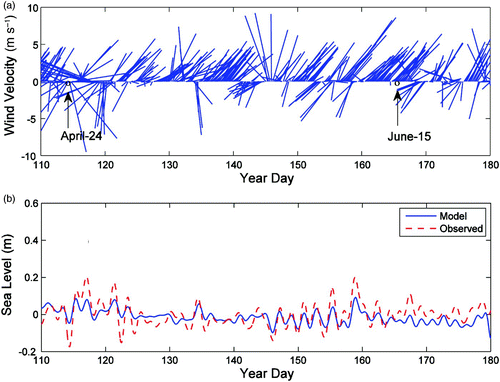
A time series comparison between the hourly observed and simulated sea level is shown in Fig. 5. We also plot the 5-hour averaged wind velocity vectors from hourly wind data used to force the model (Fig. 5a). The inverse barometric effect based on the atmospheric pressure data at St. John's Airport (note that there are no data available from Argentia for this time) has been removed from the tide-gauge data to enable comparison with the modelled sea level. There is fair agreement in both amplitude and phase, with the best agreement in amplitude occurring when the wind is strong. The sub-tidal sea level variations and their correlation with wind velocity vectors can be seen. From days 110–120, when the wind is upwelling-favourable at first, the sea level decreases to approximately −0.2 m; later when the wind changes to downwelling-favourable, the sea level increases to 0.2 m. The present model qualitatively reproduces this pattern.

Fig. 5 (a) Wind speed and direction and (b) low-pass (36-hour) filtered sea level anomalies at Argentia from April to June 1999.

Quantitative comparisons are also made using low-pass filtered times series. By using the RMS difference and

where Var is the variance, ζ is the sea level and o and m represent observation and model, respectively, statistics are calculated to determine the model's ability to reproduce the observations. The RMS difference between the observed and modelled sea level is 5.2 cm and γ² is 0.58 which demonstrates good agreement between the modelled and observed sea level. Some of the difference can be attributed to the use of air pressure data at St. John's instead of Argentia for the correction of the inverse barometric effect.

Currents are rotated to bay-coordinates for a better comparison. The along-bay component is defined to be 45° counterclockwise from the east while the cross-bay component is rotated by 45° from the east. Two components of velocity for the model and the observations are shown in Fig. 6 at 20 m and 55 m (45 m for M4). From the model, we sample the low-pass filtered current data at the σ-layer and interpolate it onto the depth of the observed data sample because the model employs a σ-coordinate in the vertical. Figure 6 shows that the alongshore component speeds at these four stations are approximately 20 cm s⁻¹, much stronger than the cross-shore component which is approximately 10 cm s⁻¹. Furthermore, the alongshore component speed decreases slightly with depth. To establish the quantitative measurement of the agreement between the modelled and observed values for current, we calculate the RMS difference, velocity difference ratio (VDR) and speed difference ratio (SDR) indices

where V is the velocity vector and the subscripts o and m represent the observed and modelled values, respectively. The VDR index represents a relative error that takes into account the modelled and observed values in both magnitude and direction. We define good agreement as a VDR less than 0.5. The VDR values (Table 2) indicate that the agreement at 20 m is good for M2 and M3 and fair for M4; the agreement at 55 m is fair for M2 and poor in all other instances. The maximum RMS difference can reach 10 cm s⁻¹ with a VDR of 1.1 at 20 m for M1. M1 is close to the western coast, where heavy smoothing was applied to the bottom bathymetry and the flow is more likely to be influenced by the inner bay as a result of the mean cyclonic circulation in Placentia Bay (Schillinger et al., 2000). The poorer results at M1 are caused, in part, by the heavy smoothing of the bathymetry and insufficient resolution of the inner bay.

Fig. 6 Time series (36 h low-pass filtered) of observed (red) and modelled (blue) along-bay (U) and cross-bay (V) currents at (a) 20 m for M1, M2, M3 and M4 and (b) at 55 m for M1 and M2 and 40 m for M4.

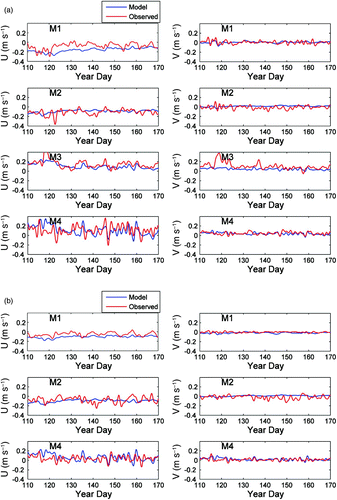
Table 2. Current statistics: along-bay and cross-bay RMS current differences (m s⁻¹), VDR, and SDR at 20 m and 55 m (45 m for M4). See Fig. 1 at M1, M2, M3 and M4.

	20 m				55 m
	Along-bay, RMS	Cross-bay, RMS	VDR	SDR	Along-bay, RMS	Cross-bay, RMS	VDR	SDR
M1	0.10	0.03	1.00	0.73	0.06	0.02	1.13	0.89
M2	0.06	0.04	0.34	0.22	0.07	0.04	0.65	0.34
M3	0.07	0.09	0.31	0.24	–	–	–	–
M4	0.12	0.03	0.65	0.50	0.07	0.02	1.35	0.91

c Comparison of Observed and Modelled Temperature

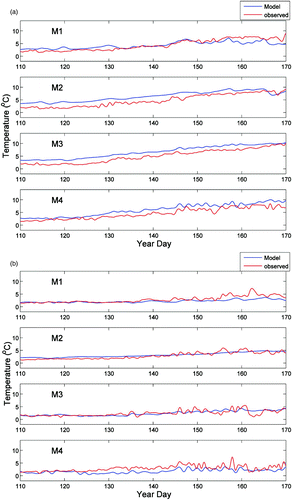
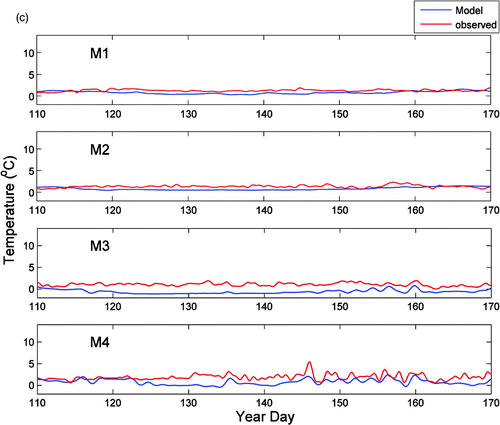
Both modelled and observed temperatures are shown in Fig. 7, for M1–M4 at 10 m, 30 m and 55 m (45 m for M4). The model results correctly reproduce the seasonal temperature variability in the upper layer of the water column as well as the surface heating and vertical mixing. At 10 m, the ocean temperature increases from 2°C in April to 8°C in late June in response to solar heating and is highly variable at synoptic scales as a result of wind forcing. In contrast, the temperature at depths greater than 30 m shows much less variability. Overall the model results agree well with seasonal observations in the upper water column. The largest hourly difference between observed and computed temperatures is about 4°C. Averaged over 24 hours, the difference is reduced to 2.6°C.

Fig. 7 Observed (red) and modelled (blue) low-pass filtered temperature time series (a) at 10 m, (b) at 30 m, and (c) at 55 m (45 m for M4).

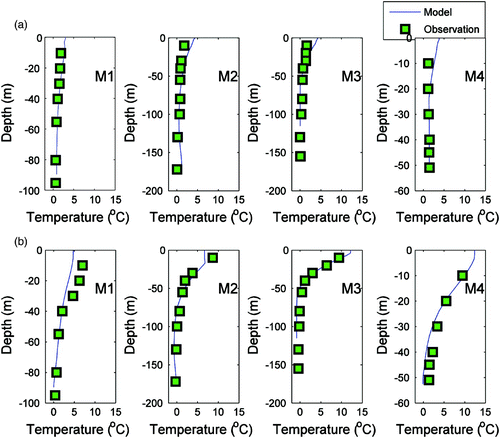
Figure 8 shows the comparison of the vertical temperature profile between the model results and the observations on 24 April and 15 June 1999, respectively. The model results generally agree well with the observed data. In particular, there is good agreement for the formation of the thermocline from early to late spring. In April, the temperature is more uniform in the vertical with the surface temperature below 5°C. In June, with increasing temperatures in the top 50 m, the thermocline layer can be clearly observed, and the surface temperature differs among the different sites. At M4 and M3, surface temperatures are 5°C higher than at M2 because of the coastal upwelling on the west side of the bay forced by northeastward winds (see Section 4a for further discussion).

Fig. 8 Comparison of the vertical temperature profile between the model results and observations at M1, M2, M4 and M4 on (a) 24 April and (b) 15 June 1999.

Quantitative comparisons for time series temperatures are made and summarized in Tables 3–5, respectively, for low-pass filtered temperature time series using the same filter for sea level and currents. The RMS difference, γ² (defined similarly to that for the sea level) and correlation coefficients are used to quantify the agreement between the observed and modelled results. Considering the seasonal trend and notable synoptic variability in the upper ocean, we define the agreement to be good when the RMS difference is less than 1.5°C and γ² is less than 0.5 at 10 m. Considering the small variation in temperature in deeper water, we only calculate the RMS difference to determine the bias of the mode results against the observed value at 30 m and deeper. This difference is then treated only as an indicator to determine if the agreement is good (less than 1) or not.

Table 3. Statistics for the comparison of the10 m modelled and observed temperatures at M1, M2, M3 and M4. See Fig. 1 for the locations of M1, M2, M3 and M4.

Location	RMS difference (°C)	γ^2	Correlation coefficient
M1	1.22	0.32	0.87
M2	1.79	0.55	0.94
M3	1.73	0.44	0.98
M4	1.58	0.57	0.95

Table 4. Statistics for the comparison of the 30 m modelled and observed temperatures at M1, M2, M3 and M4. See Fig. 1 for the locations of M1, M2, M3 and M4.

Location	RMS difference (°C)	γ^2	Correlation coefficient
M1	1.07	0.72	0.83
M2	0.67	0.27	0.90
M3	0.74	0.49	0.72
M4	1.45	1.72	0.59

Table 5. RMS temperature difference between the observed and simulated values at 55 m (45 m at M4). See Fig. 1 for the locations of M1, M2, M3 and M4.

Location	RMS difference (°C)
M1	0.62
M2	0.70
M3	1.74
M4	1.38

As can be seen (Tables 3–5), the RMS difference in the upper 30 m is less than 1.5°C and γ² is below 1 except for M2 at 10 m and M4 at 10 and 30 m; this indicates good agreement over most of the observed points. The correlation coefficient between the modelled and observed temperature at these depths is approximately 0.9 with a high correlation of 0.98 for M3 at 10 m. The deeper water temperature statistics reveal that the RMS difference ranges from 0.62° to 1.74°C which is a relatively good comparison. The temperature comparison demonstrates overall good agreement between the observed and modelled results. The fair agreement at different depths and locations suggests that our model has reasonable skill in simulating the temperature variation in Placentia Bay.

4 Circulation and stratification

a Circulation Pattern and Evolution

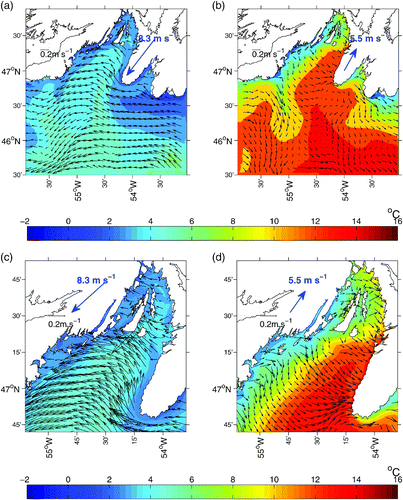
The model reproduces two distinct surface circulation modes that reveal the differences in wind directions from April to June (Fig. 9). At 1800 utc 24 April, the surface current was directed westward along the coast in response to the northerly winds (Fig. 9a). The cyclonic circulation pattern is well defined in the outer area of Placentia Bay. At 0000 utc 15 June (Fig. 9b), the dominant offshore surface flow over the model domain was generated by the strong southwesterly winds.

Fig. 9 Model surface circulation and temperature (°C) fields at (a) 1800 24 April and (b) 0000 15 June 1999. The corresponding close-ups for the bay area are shown in (c) and (d). The magnitude and direction of the wind (blue arrow) are also shown.

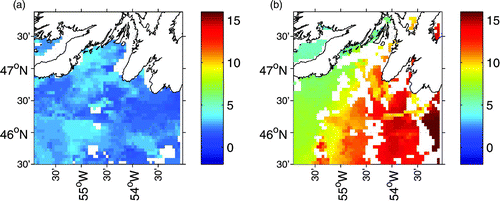
The simulated surface temperatures from Placentia Bay were consistent with the general circulation patterns. In April, the lower temperature water spread westward along the coast (Fig. 9a). The surface Ekman transport advected the cold water along the coast, some of which steered into Placentia Bay and flowed out along the west coast following the cyclonic circulation. In contrast, in June, the wind-induced coastal upwelling pumped low temperature water from a deeper layer up to the surface on the west coast of the bay (Fig. 9b). The offshore transport of low temperature water was most notable near 47°N where a pool of low temperature water is observed. As the cold water spread southeastward, a cold-water front formed and, consequently, a zone with a horizontal gradient of 9°C over 100 km developed between the warm and cold water. As a result of the southwesterly winds, surface temperature along the east coast warmed up. These model temperature patterns are supported by satellite observations (Fig. 10). Nevertheless, the model seems to overestimate the strength of upwelling in the vertical and the temperature gradient across the western bay (Figs 9b and 10b). Note that the satellite observations represent the skin temperature while the model temperature is from the top level of the model, slightly beneath the surface (varying from 0.88 to 1.20 m). Also, because of data scarcity, the satellite results are a 5-day composite; therefore, the timing of the satellite and model results is not exactly the same.

Fig. 10 Five-day satellite SST (°C) images from NOAA during late April (22–26 April) and mid-June (15–19 June) 1999.

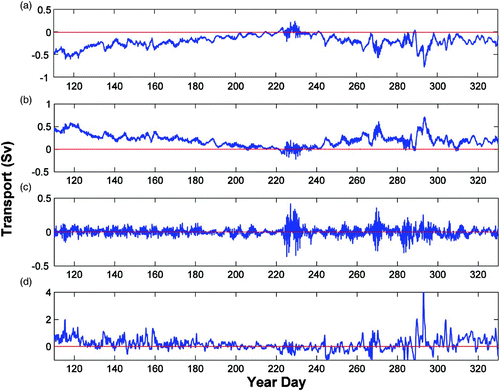
The model transport associated with the partial cyclonic gyre in the outer area of Placentia Bay generally decreases from spring to summer and increases towards fall, with some substantial changes at synoptic time scales (Fig. 11). The mean transport for days 110–330 is about 0.22 Sv (where 1 Sv = 10⁶ m³ s⁻¹). The transport decrease and increase in the outer bay gyre correspond well with the model transport through the Avalon Channel (see Fig. 1 for location) associated with the inshore Labrador Current. The model mean transport for this period is 0.25 Sv through the channel. The model result suggests that about 88% of the available inshore Labrador Current enters the outer area of Placentia Bay. The model mean transport for the validation period (days 110–180) is 0.34 Sv through the Avalon Channel with a standard deviation of 0.36 Sv, consistent with an observation-based estimated mean of 0.39 Sv (Greenberg and Petrie, 1988).

Fig. 11 Modelled transport through (a) western and (b) eastern Placentia Bay at 47°N and (c) the net transport (positive northward). The modelled transport across the Avalon Channel (from the coast to the 90 m isobath on the offshore side of the channel), is also shown in (d) (positive westward). The zero line (red) is also depicted. See Fig. 1 for the location of the transects.

b Evolution of Stratification and Mixed-Layer Depth

The model simulations provide a detailed representation of the seasonal and spatial evolution of stratification and mixed-layer depth during the spring and fall of 1999. The seasonal development of stratification can be affected by the heat flux, with a steady trend from spring to summer. The mixed-layer depth shallows as the stratification increases. Spatially, the wind-driven turbulence can interrupt the strong stratification and penetrate more deeply in some areas. In the fall, the reduced heat flux and increased wind mixing break down the stratification, and the water column becomes well mixed again.

To assess the strength of stratification and mixed-layer depth quantitatively, the Richardson number (Ri), buoyancy frequency (N) and the Levitus (1982) criterion based on the 0.125 sigma-t change from the surface density are used. The critical Ri is usually taken as 0.25. When Ri exceeds 0.25, the turbulence is suppressed. For Ri >1, the stratification is generally considered stable (Silva et al., 1999; Galperin et al., 2007). Time series of depth-averaged (0–10 m) N ² and Ri values at M1 (for the western bay) and M4 (for the eastern bay) are shown in Fig. 12. Both of these parameters show the seasonal change in water column stratification and mixing in response to solar heating and wind forcing. During April, Ri at the two points is below the critical value of 0.25 most of the time. The water column stratification is weak and can be frequently disturbed as indicated by the N ² time series plots. During May and June, N ² time series plots at the two locations show an increasing trend corresponding to increased stratification as a result of increasing shortwave radiation incident at the surface. However, at M1, N ² becomes low during days 130–140, days 145–155 and days 160–170 which also corresponds to a low value in the Ri time series. This is mainly associated with upwelling on the west coast induced by the dominant southwesterly winds. In summer, the stratification pattern is similar to that in late spring. In fall the stratification weakens again at both locations.

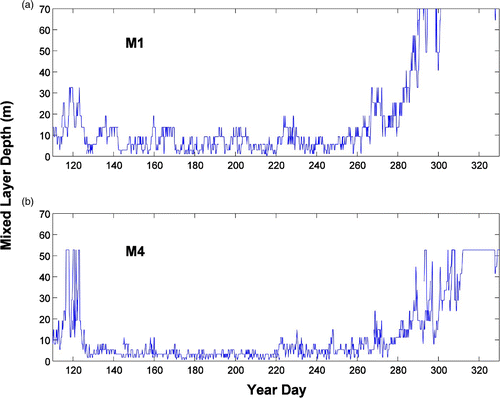
Fig. 12 Depth-averaged (0–10 m) buoyancy frequency squared N ² and Richardson number (Ri) at (a) M1 and (b) M4 for April–November 1999. In the plots of the Ri time series, the two red lines denote Ri = 1 and Ri = 0.25.

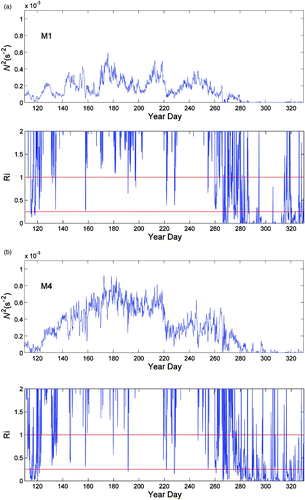
To further elucidate the above phenomenon, the mixed-layer depth at these two locations is also calculated (Fig. 13). During early spring, the mixed layer is deep when the stratification is weak, but during late spring, the mixed-layer depth shallows to approximately 6 m as the stratification becomes strong (Fig. 13; M4). For M1, on the other hand, the mixed-layer depth is approximately 12 m most of the time. In summer, the depth of the mixed layer remains shallow. In fall, the mixed-layer depth deepens at both locations. These seasonal and spatial patterns are consistent with the plot of the Ri time series (Fig. 12).

Fig. 13 Mixed-layer depth for (a) M1 and (b) M4.

We chose the 10 m averages because the summer stratification between M1 and M4 can be well contrasted. The 20 m averages were also examined, supporting the conclusions derived from the 10 m averages, although there are some quantitative differences.

c Implications for Cod Larval Transport and Growth

For Atlantic cod, evidence is increasing that spawning occurs in multiple coastal areas around Newfoundland (Smedbol et al., 1998; Lawson and Rose, 2000). Compared with offshore habitats, coastal spawning may lead to increased survival because of higher growth rates (Frank and Leggett, 1982; Taggart and Leggett, 1987; Pepin et al., 1995). As a result, following the right site hypothesis proposed by deYoung and Rose (1993) for Atlantic cod, Placentia Bay is one of the few areas in Atlantic Canada where spawner biomass and, therefore, egg and larval supplies are reasonably healthy.

The spatially different stratification reproduced by the present FVCOM model could have important implications for the habitat of cod spawning place and egg movements in Placentia Bay. Bradbury et al. (2000) observed stage I eggs concentrated at three places located in the eastern, western and inner bay (Fig. 1, Perch Rock, Oderin Bank, Bar Haven) during April and May corresponding to the peak spawning areas. They also found that late-stage eggs were abundant on the western side of the bay during June when larval densities were still highest. The movement and abundant distribution of eggs may be attributed to the circulation pattern and stratification evolution. During April, most early-stage eggs were located in the inner and eastern parts of the bay (M4). Because of the cyclonic mean circulation around Placentia Bay, eggs gradually moved to the inner and western parts of the bay to have the longest time for safe development. During early summer, when the bay was highly stratified, the western bay (M1) was characterized by upwelling with relatively weaker stratification. Elevated chlorophyll-a and zooplankton may have occurred over these areas providing abundant nutrition for late-stage eggs and larvae. The deeper mixed-layer depth in the western bay may also provide a better temperature environment for larvae.

5 Conclusions

We have developed a 3-D FVCOM circulation model for Placentia Bay, which is forced at the lateral open boundaries with five leading tidal constituents and non-tidal sea levels and at the surface with wind and heat flux. The model is used to simulate circulation variability in the spring and fall of 1999 and the model results are compared with observations from April to June. Overall, the model simulates the tidal elevations, currents, non-tidal circulation and temperature well.

The five tidal constituents from the model results compare well with the tide-gauge data, with an RMS error of 4.6 cm. The dominant M₂ tidal currents are well reproduced with a relative RMS error of 37%.

The simulated cyclonic bay circulation patterns agree well with field measurements (Hart et al., 1999). The model correctly reproduces the upwelling process caused by the southwesterly winds. At synoptic time scales, the model currents are in fair or good agreement with observations at 20 m with VDR values less than 0.65 except at M1 (where VDR is 1).

The temperature and stratification evolutions in spring 1999 are well simulated by the model. The modelled temperatures show good agreement with the observations at synoptic scales, with RMS errors of 1°–2°C. Stratification, occasionally interrupted by wind and mixing, was initiated in April in response to solar heating, subsequently enhanced in May and June and weakened again during fall. The spatial differences in stratification are also captured by the model. The model realistically reproduces the upwelling along the west coast of the bay in response to strong southwesterly winds. This upwelling and related mixing provides an important mechanism for nutrient supply from the deep water to the surface, influencing primary productivity and conditions for plankton and fish larvae in the bay.

The present model may be improved in several different ways. The horizontal resolution for the inner bay could be increased to resolve narrow channels better and to mitigate the requirement to smooth the bathymetry. Freshwater input at the head of the inner bay could be added. Spatially variable wind and heat-flux forcing could be used but would require the installation of meteorological stations around Placentia Bay. The more realistic offshore open boundary forcing could be implemented as better large-scale shelf model results become available.

Acknowledgements

This work was partially funded by ArcticNet, a Network of Centres of Excellence of Canada; the Centre for Ocean Model Development and Application, Fisheries and Oceans Canada; the Canadian Space Agency Government Related Initiatives Program; and the Natural Sciences and Engineering Research council (NSERC). GH received travel funds from the Program for Aquaculture Regulatory Reseach. Useful comments were received from two anonymous reviewers.