Homothetic Efficiency: Theory and Applications

Abstract

We provide a nonparametric revealed preference approach to demand analysis based on homothetic efficiency. Homotheticity is widely assumed (often implicitly) because it is a convenient and often useful restriction. However, this assumption is rarely tested, and data rarely satisfy testable conditions. To overcome this, we provide a way to estimate homothetic efficiency of consumption choices. The method provides considerably higher discriminatory power against random behavior than the commonly used Afriat efficiency. We use experimental and household survey data to illustrate how our approach is useful for different empirical applications and can provide greater predictive success.

KEY WORDS:

• Homotheticity
• Nonparametric analysis
• Revealed preference
• Test power
• Utility maximization.

1. INTRODUCTION

Homotheticity of consumer preferences is an important and useful concept in both theoretical and empirical work. If a consumer’s preferences are homothetic, we can deduce his entire preference relation from a single indifference set. Furthermore, testing data for homothetic utility maximization can provide substantially stronger discriminatory power against the alternative hypothesis than testing for utility maximization alone.

Homotheticity has important implications in many different fields. For example, it is important for the construction of superlative index numbers (Diewert 1976). In particular, by assuming homotheticity, superlative price indices are independent of the consumer’s standard of living (i.e., utility level). Thus, such indices are independent of the reference quantity base and therefore representative for any welfare level. Statistical agencies construct consumer price indices (CPI) from superlative price indices to provide measures of inflation in the economy. Other fields in which homotheticity plays an important role include the aggregation of consumer demand and the existence of “community indifference curves,” the modeling of separable preference structures and two-stage budgeting, and it is also a common assumption in the international trade literature.

This article provides measures of the homothetic efficiency of a dataset using a revealed preference approach. We introduce the homothetic efficiency index (HEI), which is a homothetic analogue to the well-known Afriat efficiency index (AEI) and can be interpreted as a measure of wasted income. The HEI generalizes the index proposed by Heufer (2013) for the case with only two goods. Just as the AEI, the HEI only reflects the least efficient choice in a dataset. Therefore, to have a more detailed and robust data analysis, we extend this measure by introducing the more disaggregated homothetic efficiency vector (HEV), which provides efficiency indices for each observed choice. We provide a strong theoretical justification for using the HEI and HEV based on the concept of vector-rationalization recently introduced by Halevy, Persitz, and Zrill (2015).

The revealed preference approach was originally developed by Samuelson (1938), but the contributions of Varian (1982, 1983) were responsible for spurring its use and initiated a substantial applied literature. Varian’s generalized axiom of revealed preference (GARP) is widely used to test data for consistency with utility maximization. Varian (1983) was the first to provide tests for homotheticity and separability. Since then, contributions analyzing revealed preference methods for separability, such as Swofford and Whitney (1987, 1988, 1994) and Cherchye et al. (2015), and homotheticity, such as Knoblauch (1993), Liu and Wong (2000), and Heufer (2013), have appeared. However, there remains considerable potential for revealed preference techniques for conditions that extend beyond simple utility maximization. Actual consumption data often violate certain conditions. For homotheticity, Alston et al. (1990) and Serletis and Rangel-Ruiz (2005) found that Varian’s condition is violated at every observation. This finding might explain why tests for homotheticity seem to have grown less in popularity than they could have: as opposed to tests for utility maximization, there was no way to measure the extent of these violations. Approaches that measure this extent should therefore be very useful.

As recently documented by Hands (2016), Paul Samuelson often referred to models that used the assumption of homotheticity or other, similarly strong assumptions as “Santa Claus economics.” Throughout the present article, we adopt the interpretation that homotheticity is indeed a very strong and possibly unrealistic assumption but that it can sometimes provide a good approximation of true preferences. For example, researchers who need the assumption (e.g., for the construction of index numbers) can use our techniques to measure how well a homothetic utility function approximates reality and, if the approximation is close enough, use the result to justify it.

The contribution of Heufer (2013) is only applicable to two-dimensional experimental data. Field and survey data such as household expenditure panel data typically have more than two goods. Testing typical expenditure data for consistency with utility maximization can entail a problem: as price changes between periods are usually small and income increases over time, budgets are often completely contained in other budgets. This can lead to very low test power. For example, Varian (1982) reported that for the data he used, many budgets are contained in the budget of the next period, which implies low test power; see also Bronars (1987) for an analysis of the same data. For household demand, where income changes are usually relatively small, it is plausible to assume that demand is homothetic, and therefore, it is reasonable to test for consistency with homothetic utility maximization, which can lead to considerably higher test power. As budgets do not have to intersect when demand is assumed to increase proportionally, a test for homotheticity can be useful even for Varian’s (1982) dataset with zero test power for utility maximization.

Varian’s (1983) homothetic axiom of revealed preference (HARP) can be easily tested with a set of price-quantity data. It is a necessary and sufficient condition for consistency with homothetic utility maximization and therefore characterizes the hypothesis of homothetic preferences. However, it is a binary test: the data either satisfy HARP or do not. When HARP is violated, the measures introduced here show how close the data come to being consistent with HARP. Both the HEI and the HEV provide the minimal adjustments required to make a dataset consistent with homothetic utility maximization. Our measures allow us to go further than merely rejecting HARP by quantifying and interpreting the extent of the inconsistency.

A related approach was proposed by Blundell, Browning, and Crawford (2003). They suggested combining revealed preference conditions with expansion paths that are nonparametrically estimated using pooled household data. However, their procedure differs from ours in some important respects. First, while their procedure is designed for household panel data, our approach lends itself to panel as well as experimental data. Second, our methods can be meaningfully applied to datasets with any number of observations and are therefore applicable to each individual household in the panel. This allows us to avoid any preference homogeneity assumptions across households and, consequently, optimally exploits the structure of household panel data.

Given the widespread assumption of homotheticity—which is often not even explicitly discussed—it should be tested whenever possible, but it rarely is. Our contribution makes it easy for researchers to determine how consistent their data are with homotheticity. Our efficiency index allows us to separate the cases in which the assumption is justified from those in which it is not.

To illustrate and motivate the methods proposed in this article, we apply them to two datasets. The first application is to a panel of expenditures on nondurable consumption categories for 3,134 Spanish households. These survey data were previously analyzed by Browning and Collado (2001), Crawford (2010), and Cherchye et al. (2015) in different contexts. The second application is to data from an experimental dictator game conducted by Fisman, Kariv, and Markovits (2007). As a means of analyzing the survey and experimental data, we implement an idea proposed by Beatty and Crawford (2011) that combines efficiency and power into a single measure, called predictive success.

Our main results can be summarized as follows. (i) Efficiency can be very high for HARP, thus providing motivation for researchers who rely on the assumption of homothetic preferences. (ii) For consumer choice data, HARP has considerably higher discriminatory power against irrational behavior than does GARP. (iii) Adjusting expenditures for homothetic efficiency can have negligible effects on power. Thus, HARP can have substantially higher power than GARP even when expenditures are adjusted for efficiency. (iv) Based on the measure of predictive success, homotheticity is a better model than utility maximization alone for demand behavior of households in our survey data application.

The remainder of the article is organized as follows. Section 2 addresses utility maximization, while Section 3 addresses homothetic utility maximization; they are organized in parallel. Section 2.1 recalls Afriat’s theorem on rationalization by a utility function, while Section 3.1 defines homotheticity and recalls Varian’s (1983) theorem on rationalization by a homothetic utility function. Section 2.2 discusses efficiency measures and the Afriat efficiency index, while Section 3.2 introduces the first new measure, the homothetic efficiency index, and discusses its properties and implications. Section 2.3 discusses a more disaggregate efficiency measure, called the Varian efficiency vector, while Section 3.3 introduces a corresponding measure for homothetic efficiency, called the homothetic efficiency vector. Section 3.4 introduces and discusses a measure of misspecification that measures how much additional adjustment is necessary to make the data fit homothetic utility maximization after accounting for violations of utility maximization. Section 4 uses two datasets to apply the proposed methods. Section 5 concludes. The Appendix contains all proofs.

2. UTILITY MAXIMIZATION AND EFFICIENCY

2.1. Utility Maximization

We use the following notation: For all $\mathbf{x},\mathbf{y}\in {\mathbb{R}}^L$, x≧y if x_i ⩾ y_i for all i = 1, …, L; x ⩾ y if x≧y and x ≠ y; and x > y if x_i > y_i for all i = 1, …, L. We denote ${\mathbb{R}}_{+}^L=\{\mathbf{x}\in {\mathbb{R}}^L:\mathbf{x}\geqq (0,\dots ,0)\}$ and ${\mathbb{R}}_{++}^L=\{\mathbf{x}\in {\mathbb{R}}^L:\mathbf{x}>(0,\dots ,0)\}$. The commodity space is ${\mathbb{R}}_{+}^L$, and the price space is ${\mathbb{R}}_{++}^L$, where L ⩾ 2 is the number of different commodities. A (competitive) budget set is defined as $B^i=B\left({\mathbf{p}}^i\right)=\{\mathbf{x}\in {\mathbb{R}}_{+}^L:{\mathbf{p}}^i{\mathbf{x}}^i\le 1\}$, where ${\mathbf{p}}^i={(p_1^i,\dots ,p_L^i)}^{\text{'}}\in {\mathbb{R}}_{++}^L$ is the price vector, and income is normalized to 1. A demand function $D:{\mathbb{R}}_{++}^L\times {\mathbb{R}}_{++}\to {\mathbb{R}}_{+}^L$ of a consumer assigns to each budget set the commodity bundle chosen by the consumer. Unless otherwise noted, we assume that demand is exhaustive (i.e., pⁱxⁱ = 1). We also assume that the only observables of the model are N ⩾ 1 different budgets and the corresponding demand of a consumer. The entire set of observations on a consumer is denoted Ω = {(xⁱ, pⁱ)}^N_{i = 1}.

The bundle xⁱ is directly revealed preferred to a bundle x, written ${\mathbf{x}}^i{\text{R}}^0\mathbf{x}$, if pⁱxⁱ ⩾ pⁱx; it is strictly directly revealed preferred to x, written ${\mathbf{x}}^i{\text{P}}^0\mathbf{x}$, if pⁱxⁱ > pⁱx; and it is revealed preferred to x, written ${\mathbf{x}}^i\text{R}\mathbf{x}$, if $\text{R}$ is the transitive closure of ${\text{R}}^0$, that is, if there exists a sequence x^j, …, x^k, such that ${\mathbf{x}}^i{\text{R}}^0{\mathbf{x}}^j{\text{R}}^0\dots {\mathbf{x}}^k{\text{R}}^0\mathbf{x}$. The bundle xⁱ is strictly revealed preferred to x, written ${\mathbf{x}}^i\text{P}\mathbf{x}$, if ${\mathbf{x}}^i\text{R}{\mathbf{x}}^j{\text{P}}^0{\mathbf{x}}^k\text{R}\mathbf{x}$ for some j, k = 1, …, N.

A set of observations Ω satisfies the generalized axiom of revealed preference (GARP) if for all i, j = 1, …, N, it holds that $\left[\text{not}{\mathbf{x}}^i{\text{P}}^0{\mathbf{x}}^j\right]\text{whenever}{\mathbf{x}}^j\text{R}{\mathbf{x}}^i.$ We say that a utility function $u:{\mathbb{R}}_{+}^L\to \mathbb{R}$ rationalizes a set of observations Ω if u(xⁱ) ⩾ u(y) whenever ${\mathbf{x}}^i{\text{R}}^0\mathbf{y}$. Let $\mathcal{U}$ denote the set of all continuous, non-satiated, monotonic, and concave utility functions. GARP is easily testable and a necessary and sufficient condition for utility maximization, as Theorem 1 (Afriat’s theorem) shows.

Theorem 1 (Afriat 1967; Diewert 1973; Varian 1982).

The following conditions are equivalent:

1.	the set of observations Ω satisfies GARP;
2.	there exist numbers Ui, λi > 0 such that Ui ⩽ Uj + λjpj(xi − xj) for all i, j = 1, …, N;
3.	there exists a $u\in \mathcal{U}$ that rationalizes the set of observations Ω.

2.2. The Afriat Efficiency Index

When a set of observations does not satisfy GARP, it is interesting to obtain a measure of how severe the violation is. One of the most popular measures of the severity of a violation is the Afriat efficiency index (AEI) proposed by Afriat (1972), also called the critical cost efficiency index (CCEI). Define, for some e ∈ [0, 1], the relation ${\text{R}}^0\left(e\right)$ as ${\mathbf{x}}^i{\text{R}}^0\left(e\right)\mathbf{x}$ if e pⁱxⁱ ⩾ pⁱx, and let $\text{R}\left(e\right)$ be the transitive closure of ${\text{R}}^0\left(e\right)$; furthermore, define the relation ${\text{P}}^0\left(e\right)$ as e pⁱxⁱ > pⁱx. With these concepts, we can define a new version of GARP, called GARP(e).

Definition 1.

A set of observations Ω satisfies GARP(e) for some e ∈ (0, 1] if for all i, j = 1, …, N, it holds that $\left[\text{not}{\mathbf{x}}^i{\text{P}}^0\left(e\right){\mathbf{x}}^j\right]\text{whenever}{\mathbf{x}}^j\text{R}\left(e\right){\mathbf{x}}^i.$

Definition 2.

For a set of observations Ω, the Afriat efficiency index (AEI) is the greatest number e such that Ω satisfies $\text{GARP}\left(e\right)$.

The AEI is a measure of wasted income: if a consumer has an AEI of e < 1, then he could have obtained the same level of utility by spending only a fraction of e of what he actually spent to obtain this level. One way to compute it is to use a binary search algorithm as described by Varian (1990).

For the rationalization results in both this section and the next, we will make use of a concept called e-rationalization and, later, v-rationalization. This concept has recently been introduced by Halevy, Persitz, and Zrill (2015).

Definition 3.

A utility function $u\in \mathcal{U}$ e-rationalizes a set of observations Ω if u(xⁱ) ⩾ u(y) whenever ${\mathbf{x}}^i{\text{R}}^0\left(e\right)\mathbf{y}$.

For e close to 1, a utility function that e-rationalizes a set of data still comes close to explaining the observed choices. It provides a good motivation and justification to compute and report the AEI and our new homothetic efficiency index in the next section.

Theorem 2.

The following conditions are equivalent:

1.	the set of observations Ω satisfies GARP(e);
2.	there exist numbers Ui, λi > 0 such that Ui ⩽ Uj + λjpj(xi/e − xj) for all i, j = 1, …, N;
3.	there exists a $u\in \mathcal{U}$ that e-rationalizes the set of observations Ω.

Theorem 2 is a special case of Theorem 3. We therefore only provide a proof of Theorem 3 in the Appendix. In the inequalities of Theorem 2, the only change relative to the inequalities in Theorem 1 is the addition of e, which relaxes the constraints. In that sense, we can also interpret the AEI as an adjustment to the data that is necessary to make the data fit the utility maximization model.

Reporting the AEI has become standard in empirical studies, particularly experimental studies. See, for example, Sippel (1997), Mattei (2000), Harbaugh, Krause, and Berry (2001), Andreoni and Miller (2002), Février and Visser (2004), Choi et al. (2007b), Fisman, Kariv, and Markovits (2007), Dickinson (2009), and Camille et al. (2011). A common alternative to the AEI is the Houtman–Maks-Index (Houtman and Maks 1985), which is based on the maximal subset of a set of choices consistent with GARP; for a computationally feasible approach to compute this index, see Heufer and Hjertstrand (2015). Fleissig and Whitney (2005) showed how to statistically test violations of the Afriat inequalities. Echenique, Lee, and Shum (2011) provided a new measure based on a money pump argument, and Dean and Martin (2015) provided a new measure based on the minimum cost of breaking all cycles or money pumps. Apesteguia and Ballester (2015) provided a measure based on welfare loss.

2.3. The Varian Efficiency Vector

The AEI does not provide information about which observed choices are causing the violation of GARP. To obtain such information, we first consider a generalization of GARP(e):

Definition 4.

A set of observations Ω satisfies GARP(v) for some v ∈ (0, 1]^N if for all i, j = 1, …, N, it holds that $\left[\text{not}{\mathbf{x}}^i{\text{P}}^0\left(v_i\right){\mathbf{x}}^j\right]\text{whenever}{\mathbf{x}}^j\text{R}\left(v_j\right){\mathbf{x}}^i.$

Such a vector v can be a more disaggregated measure of efficiency. Varian (1993) defined one such measure, the violation index $\bar{\mathbf{v}}=(v_1,\dots ,v_N)$ with ${\bar{v}}_i={min}_{\{j:{\mathbf{x}}^j\text{R}{\mathbf{x}}^i\}}{\mathbf{p}}^i{\mathbf{x}}^j.$ If the data satisfy GARP, then ${\bar{v}}_i=1$ for all i. Otherwise, ${\bar{v}}_i<1$ for some i, and this provides information regarding which xⁱ are problematic.

Proposition 1 (Varian 1993).

A set of observations Ω satisfies GARP($\bar{\mathbf{v}}$).

Varian (1993) also noted that the vector $\bar{\mathbf{v}}$ does not, in general, give the minimum perturbation of budgets required. He provides an improved violation index that is computed by an iterative algorithm. See also Cox (1997) for a discussion of the improved violation index. The “exact” efficiency indices can be computed from the inequalities (1(1) $$\begin{array}{c}\hfill V^i\ge V^j\text{whenever}{v}_i{\mathbf{p}}^i{\mathbf{x}}^i\ge {\mathbf{p}}^i{\mathbf{x}}^j,\text{and}\end{array}$$(1) ) and (2(2) $$\begin{array}{c}\hfill V^i>V^j\text{whenever}{v}_i{\mathbf{p}}^i{\mathbf{x}}^i>{\mathbf{p}}^i{\mathbf{x}}^j.\end{array}$$(2) ) below by using a simple mixed integer programming problem. To formulate this procedure, we initially make use of the fact that GARP(v) is equivalent to the following inequalities: (1) $$\begin{array}{c}\hfill V^i\ge V^j\text{whenever}{v}_i{\mathbf{p}}^i{\mathbf{x}}^i\ge {\mathbf{p}}^i{\mathbf{x}}^j,\text{and}\end{array}$$(1) (2) $$\begin{array}{c}\hfill V^i>V^j\text{whenever}{v}_i{\mathbf{p}}^i{\mathbf{x}}^i>{\mathbf{p}}^i{\mathbf{x}}^j.\end{array}$$(2)

See Cherchye et al. (2015) for a similar approach in the context of testing for weak separability of the utility function. The inequalities in Equations (1(1) $$\begin{array}{c}\hfill V^i\ge V^j\text{whenever}{v}_i{\mathbf{p}}^i{\mathbf{x}}^i\ge {\mathbf{p}}^i{\mathbf{x}}^j,\text{and}\end{array}$$(1) ) and (2(2) $$\begin{array}{c}\hfill V^i>V^j\text{whenever}{v}_i{\mathbf{p}}^i{\mathbf{x}}^i>{\mathbf{p}}^i{\mathbf{x}}^j.\end{array}$$(2) ) are equivalent to the existence of numbers Vⁱ and X^ij such that, for all observations i, j = 1, …, N, (c.i) $$\begin{array}{c}\hfill V^i-V^j<X^{ij},\end{array}$$(c.i) (c.ii) $$\begin{array}{c}\hfill (X^{ij}-1)\le V^i-V^j,\end{array}$$(c.ii) (c.iii) $$\begin{array}{c}\hfill v_i{\mathbf{p}}^i{\mathbf{x}}^i-{\mathbf{p}}^i{\mathbf{x}}^j<X^{ij}{A}^i,\end{array}$$(c.iii) (c.iv) $$\begin{array}{c}\hfill (X^{ij}-1)A^j\le {\mathbf{p}}^j{\mathbf{x}}^i-v_j{\mathbf{p}}^j{\mathbf{x}}^j,\end{array}$$(c.iv) (c.v) $$\begin{array}{c}\hfill 0\le V^i<1,\end{array}$$(c.v) (c.vi) $$\begin{array}{c}\hfill X^{ij}\in \{0,1\},\end{array}$$(c.vi) where Aⁱ > pⁱxⁱ is a fixed number. We suggest calculating the efficiency indices v by solving the following mixed integer linear programming problem (MILP; this type of approach was introduced to the revealed preference literature by Cherchye et al. 2008) with respect to Vⁱ, X^ij and v_i: (3) $$\begin{array}{c}\hfill min\sum _{i=1}^N(1-v_i)\text{subject}\text{to}\text{(c.i)--(c.vi)}\text{and}\mathbf{v}\in {(0,1]}^N.\end{array}$$(3)

Since any solution to an MILP problem is a global solution, this problem is guaranteed to find a global optimum (in the L1-norm) in the efficiency indices v. We can now formally define a vector efficiency index.

Definition 5.

For a set of observations Ω, a Varian efficiency vector (VEV) is a vector $\tilde{\mathbf{v}}$ such that Ω satisfies GARP$\left(\tilde{\mathbf{v}}\right)$ and there does not exist ${\mathbf{v}}^{\text{'}}\ge \tilde{\mathbf{v}}$ such that Ω satisfies GARP(v′).

When v is computed using the above MILP-approach, it will be a VEV.

The next definition generalizes e-rationalization introduced in Definition 3.

Definition 6.

A utility function $u\in \mathcal{U}$ v-rationalizes a set of observations Ω if u(xⁱ) ⩾ u(y) whenever ${\mathbf{x}}^i{\text{R}}^0\left(h_i\right)\mathbf{y}$.

Theorem 3.

The following conditions are equivalent:

1.	the set of observations Ω satisfies GARP(v);
2.	there exist numbers Ui, λi > 0 such that Ui ⩽ Uj + λjpj(xi/vj − xj) for all i, j = 1, …, N;
3.	there exists a $u\in \mathcal{U}$ that v-rationalizes the set of observations Ω.

Theorem 3 follows from Theorem 1 in Halevy, Persitz, and Zrill (2015). As their theorem does not contain our condition 2 (it can be constructed from the details of their proof), we include a brief proof of our Theorem 3 in the Appendix. Note that the change to the inequalities in Theorem 3 compared to the inequalities in Theorem 2 consists in replacing the blanket adjustment e with an individual adjustment per observation.

3. HOMOTHETIC EFFICIENCY

3.1. Homothetic Utility Maximization

Homotheticity is a restriction on preferences. We say that a utility function is homothetic if it is a positive monotonic transformation of a linearly homogeneous utility function; that is, if u(x) > u(y), then u(αx) > u(αy) for all α > 0. Varian (1983) provided the following axiom, which he shows is equivalent to homothetic rationalization (Theorem 4).

Definition 7 (Varian 1983).

A set of observations Ω satisfies the homothetic axiom of revealed preference (HARP) if for all distinct choices of indices i, j, …, ℓ, it holds that (pⁱx^j)(p^jx^k)⋅⋅⋅(p^ℓxⁱ) ⩾ 1.

Theorem 4 (Varian 1983).

The following conditions are equivalent:

1.	the set of observations Ω satisfies HARP;
2.	there exist numbers Ui such that Ui ⩽ Ujpjxi for all i, j = 1, …, N;
3.	there exists a homothetic $u\in \mathcal{U}$ that rationalizes the set of observations Ω.

We can always assume that a homothetic utility function u is homogeneous of degree 1 such that u(αx) = αu(x). Thus, a homothetic utility maximizer who consumes xⁱ at pⁱ will consume αxⁱ if prices remain constant but his income is multiplied by α. Recall that we normalized prices such that income at the observed consumption is always 1 (i.e., pⁱxⁱ = 1), which implies that α can be interpreted as income. As Varian (1983) explained, “the U_i’s can be interpreted as utility levels and the λⁱ’s can be interpreted as marginal utilities of income at the various levels of observed consumption.” Together, this implies that a homothetic utility maximizer’s marginal utility of income at xⁱ is ∂u(αxⁱ)/∂α = Uⁱ, in which case Uⁱ is equal to λⁱ.

Setting Uⁱ = λⁱ in the inequalities in condition 2 of Theorem 1 gives us Uⁱ ⩽ U^j + U^jp^j(xⁱ − x^j), and with pⁱxⁱ = 1, we obtain Uⁱ ⩽ U^jp^jxⁱ, which are the inequalities in condition 2 of Theorem 4. This relationship has already been identified by Diewert (1973) and was explored in greater detail by Varian (1983).

3.2. The Homothetic Efficiency Index

The challenge ^{Figure 1}is now to define an appropriate measure of homothetic efficiency that corresponds to the AEI and allows the same or a similar interpretation. A straightforward idea would be to multiply the right-hand side in the condition for HARP in Definition 7 by some e ∈ (0, 1], but this is problematic.

Suppose that we have a set Ω = {(xⁱ, pⁱ)}²_{i = 1}, with p¹x² = 8/5 and p²x¹ = 2/5, such that HARP is violated. As (8/5)(2/5) = 16/25, we might want to simply multiply the right-hand side of HARP by 16/25 and call this the homothetic efficiency. However, suppose that the same consumer faces the same two budgets again (observed as p³ and p⁴) and repeats the choices (observed as x³ and x⁴). Then, (p¹x²)(p²x³)(p³x⁴)(p⁴x¹) = 256/625, and homothetic efficiency would be reduced, even though the lower bound of wasted income did not increase. Repeating this ad infinitum, the efficiency would drop to zero, even though the consumer clearly enjoys a good amount of utility. Thus, we need to account for the number of choices that go into the left-hand side of HARP. We therefore suggest using the following axiom, called HARP(e), which takes into account the number of scalars that are multiplied.

Definition 8.

A set of observations Ω satisfies HARP(e) for some e ∈ (0, 1] if for all distinct choices of indices i, j, k, …, ℓ, it holds that $$\left(\frac{{\mathbf{p}}^i{\mathbf{x}}^j}{e}\right)\left(\frac{{\mathbf{p}}^j{\mathbf{x}}^k}{e}\right)\cdots \left(\frac{{\mathbf{p}}^{\ell }{\mathbf{x}}^i}{e}\right)\ge 1.$$

Theorem 5 confirms that this definition is a good analog for GARP(e).

As an illustration, consider the situation in Figure 1(a), which shows two observations. The dashed line shows the boundary of the shifted budget B¹ that contains x². The intersection of the dashed line and the ray through the origin and x¹, shown as λx¹, gives the demand on the shifted budget if preferences are homothetic. Here, λ is equal to p¹x². Clearly, if the dashed budget were observed and λx¹ were chosen, it would be revealed preferred to x². However, as λx¹ is in the interior of budget B², x² is strictly revealed preferred to λx¹; thus, HARP is violated.

Figure 1. (a) and (b) An illustration of HARP(e) and the homothetic efficiency index (HEI). The example uses x¹ = (2, 4), p¹ = (1/10, 1/5), x² = (8, 4), and p² = (1/10, 1/20). The greatest e for which $\text{HARP}\left(e\right)$ is satisfied is 4/5. (c) The choices x¹ and x² violate GARP. If x¹ is replaced by x′¹, the AEI will decrease. (d) The choices x¹ and x² violate HARP but not GARP. If x¹ is replaced by x′¹, the HEI will decrease.

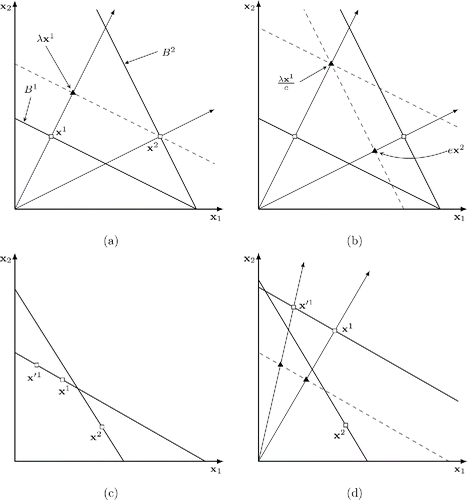
Figure 1(b) shows that if x¹ is scaled upward by a factor equal to λ/e, we find that while x² is still strictly revealed preferred to it—${\mathbf{x}}^2{\text{P}}^0(\lambda {\mathbf{x}}^1/e)$—it is not strictly revealed preferred at efficiency level e—$\left[\text{not}{\mathbf{x}}^2{\text{P}}^0\left(e\right)(\lambda {\mathbf{x}}^1/e)\right]$. This is the smallest e for which ex² is not strictly revealed preferred to λx¹/e and is indeed the smallest e for which HARP(e) is satisfied.

Given HARP(e), we propose the following definition, which is analogous to that of the AEI:

Definition 9.

For a set of observations Ω, the homothetic efficiency index (HEI) is the greatest e ∈ (0, 1] such that Ω satisfies HARP(e).

Note that the HEI cannot increase as the number of observations increases; it can only decrease as more observations are added. This is because the HEI is the minimum over all simple cycles in the data (such as going from xⁱ to itself in the definition of HARP(e)). The cycle that determined the old minimum remains in the data as more observations are added. The HEI can be computed with the same algorithm used for calculating the AEI (simply exchange GARP(e) for HARP(e) in the algorithm) and can be reported as a summary statistic.

Analogous to Theorem 2, the following theorem shows that HARP(e) is necessary and sufficient for homothetic e-rationalization. It serves as our main justification for the definition of the HEI.

Theorem 5.

For any e ∈ (0, 1] the following conditions are equivalent:

1.	the set of observations Ω satisfies HARP(e);
2.	there exist numbers Ui such that Ui ⩽ Ujpjxi/e for i, j = 1, …, N;
3.	there exists a homothetic $u\in \mathcal{U}$ that e-rationalizes the set of observations Ω.

Theorem 5 is a special case of Theorem 6. We therefore only provide a proof of Theorem 6 in the Appendix. Theorem 5 also shows why we can still interpret the HEI as a measure of wasted income, just as the AEI. Suppose that a homothetic utility function u e-rationalizes Ω, but u(y) > u(xⁱ) despite that ${\mathbf{x}}^i\text{R}\mathbf{y}$. This contradiction of the ranking of bundles by u with $\text{R}$ disappears if we assume that the consumer wasted a fraction e of his income because, by e-rationalization, we must have ${\mathbf{x}}^i\text{R}\left(e\right)\mathbf{y}$.

We again observe that the addition of e to the inequalities in Theorem 5 provides a less stringent version of the inequalities in Theorem 4. Thus, as we can interpret the AEI as an adjustment to the data that is necessary to make them fit the utility maximization model, we can interpret the HEI as an adjustment necessary to make them fit the homothetic utility maximization model.

Beyond the findings in Theorem 5, it is interesting to consider other properties of the HEI. Jerison and Jerison (2012) listed six desirable properties for measures of inconsistency. Let us define $1-\text{AEI}$ ($1-\text{HEI}$) as the measures of inconsistency with (homothetic) utility maximization corresponding to the respective efficiency measures. Both these measures satisfy all six properties: both are (a) “well defined for any demand set;” are (b) zero when GARP (HARP) is satisfied and positive otherwise; (c) “increase (or at least do not decrease) when inconsistency seems clearly to increase;” are (d) a “continuous function of prices and quantities demanded;” are (e) “independent of commodity units;” and are (f) “unaffected by changes in prices and incomes that leave all budget sets and consumption choices unchanged.”

Jerison and Jerison (2012) noted that these conditions hold for the AEI. It can be relatively easily verified that the conditions also hold for the HEI. Property (a) holds because e can be set to be arbitrarily close to zero for HARP(e), and (b) holds because the HEI is equal to 1 if HARP is satisfied and less than 1 otherwise. Definition 8 demonstrates that (d) holds because the value of the greatest e for which the inequalities hold must change continuously in changes of the values of the pⁱx^j, p^jx^k, …. Properties (e) and (f) are automatically satisfied given our normalization in Section 2.1, but it can be easily verified that they also hold for a nonnormalized version.

For property (c), Jerison and Jerison (2012) provided a figure, the relevant part of which is reproduced in Figure 1(c). They state that an inconsistency measure should increase when x¹ is replaced by x′¹, which is the case for both the measures based on the AEI and the HEI. In addition, Figure 1(d) illustrates that this is still the case for the HEI when one of the budgets and the choices are scaled up such that the GARP violation is resolved and only the HARP violation remains.

3.3. The Homothetic Efficiency Vector

Similar to the case of the AEI, the HEI is only a lower bound on homothetic efficiency. A homothetic efficiency vector that provides information about how much each budget has to be perturbed to achieve a meaningful kind of consistency while keeping the perturbations minimal would be informative and useful for applied work. We suggest the following straightforward generalization of HARP(e).

Definition 10.

A set of observations Ω satisfies HARP(h) for some h = (h₁, …, h_N) ∈ (0, 1]^N if for all i, j = 1, …, N, it holds that (4) $$\begin{array}{c}\hfill \left(\frac{{\mathbf{p}}^i{\mathbf{x}}^j}{h_i}\right)\left(\frac{{\mathbf{p}}^j{\mathbf{x}}^k}{h_j}\right)\cdots \left(\frac{{\mathbf{p}}^{\ell }{\mathbf{x}}^i}{h_{\ell }}\right)\ge 1.\end{array}$$(4)

Analogous to Theorem 3, the following theorem shows that HARP(h) is necessary and sufficient for homothetic v-rationalization, or h-rationalization as we call it here.

Theorem 6.

For any h = (h₁, …, h_N) ∈ (0, 1]^N, the following conditions are equivalent:

1.	the set of observations Ω satisfies HARP(h);
2.	there exist numbers Ui such that for i, j = 1, …, N (5) $$\begin{array}{c}\hfill U^i\le U^j{\mathbf{p}}^j{\mathbf{x}}^i/h_j;\end{array}$$(5)
3.	there exists a homothetic $u\in \mathcal{U}$ that h-rationalizes the set of observations Ω.

The proof of Theorem 6 can be found in the Appendix. Given HARP(h), we propose the following definition, which is analogous to that of the VEV:

Definition 11.

For a set of observations Ω, a homothetic efficiency vector (HEV) is a vector h such that Ω satisfies HARP(h) and there does not exist a h′ ⩾ h such that Ω satisfies HARP(h′).

The problem with computing a vector h with maximal values is that “breaking cycles” is not as easy as in the standard case in Varian (1993). It is not feasible to consider breaking “homothetically revealed preference cycles.” This would amount to solving the NP-hard problem of finding a simple shortest path in a weighted complete graph (i.e., a path that visits each vertex at most once, except for the first vertex if the path is a cycle). The complexity of this endeavor quickly approaches a level that makes computation infeasible. However, it is possible to compute a first-order approximation of the HEV in polynomial time. To see how, we define κ_i = log (h_i) for all i = 1, …, N and note that a first-order Taylor expansion of log (h_i) about point 1 yields log (h_i) ≃ −(1 − h_i), such that (6) $$\begin{array}{ccc}\hfill argmax\sum _{i=1}^N{\kappa }_i& =& argmax\sum _{i=1}^{N}log\left(h_i\right)\simeq argmax\sum _{i=1}^N-(1-h_i)\hfill \\ & =& argmin\sum _{i=1}^N(1-h_i).\hfill \end{array}$$(6) The left-hand side of the inequalities in Equation (5(5) $$\begin{array}{c}\hfill U^i\le U^j{\mathbf{p}}^j{\mathbf{x}}^i/h_j;\end{array}$$(5) ) is positive, implying that they can be equivalently rewritten as follows (by log-linearization): (7) $$\begin{array}{c}\hfill {\kappa }_j+u^i-u^j\le log\left({\mathbf{p}}^j{\mathbf{x}}^i\right),\end{array}$$(7) for all i, j = 1, …, N, where uⁱ = log (Uⁱ) and κ_j = log (h_j). Consider the following linear program (solved with respect to κ_i ∈ ( − ∞, 0] and uⁱ ∈ ( − ∞, ∞) for all i = 1, …, N): (8) $$\begin{array}{c}\hfill max\sum _{i=1}^N{\kappa }_i\text{subject}\text{to}\text{Equation}\text{(7)},\end{array}$$(8) and define the optimal solutions from this problem as ${\widehat{\kappa }}_i$ for all i = 1, …, N. Given the Taylor approximation in Equation (6(6) $$\begin{array}{ccc}\hfill argmax\sum _{i=1}^N{\kappa }_i& =& argmax\sum _{i=1}^{N}log\left(h_i\right)\simeq argmax\sum _{i=1}^N-(1-h_i)\hfill \\ & =& argmin\sum _{i=1}^N(1-h_i).\hfill \end{array}$$(6) ), the set of numbers ${\widehat{h}}_i=exp\left({\widehat{\kappa }}_i\right)$ is a first-order approximation to the HEV (in the L1-norm).

Since ∑^N_{i = 1}log (h_i) is a monotonic log-transformation of ∏^N_{i = 1}h_i, the linear problem in Equation (8(8) $$\begin{array}{c}\hfill max\sum _{i=1}^N{\kappa }_i\text{subject}\text{to}\text{Equation}\text{(7)},\end{array}$$(8) ) is equivalent to solving (9) $$\begin{array}{c}\hfill max\prod _{i=1}^N{h}_i\text{subject}\text{to}\text{Equation}\text{(5)}.\end{array}$$(9) This shows that the problem in Equation (8(8) $$\begin{array}{c}\hfill max\sum _{i=1}^N{\kappa }_i\text{subject}\text{to}\text{Equation}\text{(7)},\end{array}$$(8) ) does not compute the set of indices closest to the unit vector in a “true” norm. However, solving the problem in Equation (8(8) $$\begin{array}{c}\hfill max\sum _{i=1}^N{\kappa }_i\text{subject}\text{to}\text{Equation}\text{(7)},\end{array}$$(8) ) has several advantages over, for example, computing the HEV in the Minkowski norm, which would amount to solving the following problem: $min{\left({\sum }_{i=1}^N{(1-h_i)}^{\phi }\right)}^{1/\phi }$ subject to Equation (5(5) $$\begin{array}{c}\hfill U^i\le U^j{\mathbf{p}}^j{\mathbf{x}}^i/h_j;\end{array}$$(5) ) for some ϕ ⩾ 1 (the L1-norm corresponds to setting ϕ = 1). First, it is a computationally tractable procedure for large datasets since it can be solved with elementary linear programming techniques, that is, in polynomial time (which is not the case for any optimization problem based on, e.g. the Minkowski norm).

Second, because the Taylor approximation is taken about point 1, a strong theoretical justification for using the first-order approximation is that it should perform very well when the “true” HEV is close to the unit vector. The empirical applications in Section 4 show that homothetic efficiency is indeed close to the unit vector in many cases. Thus, we expect the linear problem in Equation (8(8) $$\begin{array}{c}\hfill max\sum _{i=1}^N{\kappa }_i\text{subject}\text{to}\text{Equation}\text{(7)},\end{array}$$(8) ) to provide a good approximation of the HEV. Third, rephrasing a potentially intractable problem based on a first-order approximation is a commonly used procedure to find maximal elements in constrained optimization problems.

3.4. Missoptimization and Misspecification

As argued above, efficiency measures can be interpreted as the minimal adjustment necessary to make the data fit a particular model. As homotheticity imposes stronger restrictions on demand than utility maximization, adjustment by the HEI and HEV already accounts for any deviation from utility maximization. Indeed, let e^A be the AEI and e^H the HEI, and we must have e^H ⩽ e^A, and therefore, the data will always satisfy GARP(e^H).

To learn something about the additional requirement imposed by homotheticity, it would be useful to have a measure that only takes into account the additional inefficiency due to the assumption of homotheticity, that is, a measure that controls for the inefficiency already contained in the data due to the violation of GARP. That would provide us with measures of missoptimization and new measures of misspecification, which tells us how well the data fit the specific assumption of homotheticity after accounting for missoptimization.

Using the results of Theorem 2, the AEI can be computed by setting up a linear program to maximize e subject to the existence of numbers Uⁱ, λⁱ > 0 such that Uⁱ ⩽ U^j + λ^jp^j(xⁱ/e − x^j). Analogously, the HEI can be computed by setting up a linear program to maximize e subject to the existence of numbers Uⁱ such that Uⁱ ⩽ U^jp^jxⁱ/e. Recall that we obtain the latter set of inequalities in the same way as the AEI by setting Uⁱ = λⁱ and using the normalization pⁱxⁱ = 1.

As we know by the AEI that there exist numbers Uⁱ, λⁱ > 0 such that Uⁱ ⩽ U^j + λ^jp^j(xⁱ/e^A − x^j), we suggest using these adjusted inequalities and imposing the homotheticity restrictions Uⁱ = λⁱ on them. Thus, we obtain Uⁱ ⩽ U^j + U^jp^jxⁱ/e^A − U^jp^jx^j, and with the normalization pⁱxⁱ = 1, this reduces to Uⁱ ⩽ U^jp^jxⁱ/e^A. We can then proceed to add a second index in the same way as we added the original homothetic efficiency index, that is, we can maximize ${\tilde{e}}^H$ subject to the existence of numbers Uⁱ such that $U^i\le \left(U^j{\mathbf{p}}^j{\mathbf{x}}^i\right)/\left({\tilde{e}}^H{e}^A\right)$. This is equivalent to finding the greatest ${\tilde{e}}^H$ such that HARP$\left({\tilde{e}}^H{e}^A\right)$ is satisfied.

It is easy to see that this procedure will set ${\tilde{e}}^H=e^H/e^A$ (i.e., the original HEI divided by the original AEI). Thus ${\tilde{e}}^H$ is the additional adjustment required to make data that have already been adjusted to fit the utility maximization model also fit the homothetic utility maximization model. We can then interpret 1 − e^H/e^A as a measure of misspecification (or additional inefficiency). Interestingly, 1 − e^H/e^A can be written as (e^A − e^H)/e^A, that is, the difference between the AEI and the HEI normalized by the AEI. The same concept can be applied to the vector efficiencies.

Definition 12.

The misspecification index (MSI) is the normalized difference between the AEI e^A and the HEI e^H: $$\text{MSI}=\frac{e^A-e^H}{e^A}.$$The MSI based on vector efficiency (MSIV) is the average normalized difference between individual entries of the VEV v = (v₁, …, v_N) and the HEV h = (h₁, …, h_N): $$\text{MSIV}=\frac{1}{N}\sum _{i=1}^N\frac{v_i-h_i}{v_i}.$$

Similar to the AEI and HEI, there is no natural acceptable ^{Table 1}value for the misspecification index. Perhaps Varian’s (1993) possibly tongue-in-cheek suggestion of using an AEI of 0.95 as the critical value—“for sentimental reasons”—is not a bad idea, and analogously, we suggest using an MSI and MSIV of 0.05 as a focal point. In any case, the measures will provide the researcher with information about the (relative) performance of different models. We will report results for both the MSI and the MSIV for the two different datasets we analyze in Section 4.

4. APPLICATIONS

Our aim with this empirical exercise is to show that homothetic efficiency can be high for consumer choice data and that data that are adjusted by the HEV or HEI can have much higher discriminatory power against random behavior than data adjusted by the VEV or AEI. This is particularly true for the survey dataset we analyze in Section 4.1. However, our results from the experimental data in Section 4.2 are less unequivocal. While homothetic utility maximization is a good approximation for some subjects, others exhibit choices that are arguably too far removed from homotheticity to apply the model of homothetic utility maximization. This demonstrates the importance of testing for homotheticity and computing homothetic efficiency before estimating homothetic utility functions.

4.1. Survey Data: Household Expenditures

We illustrate our methods using data from the Spanish Continuous Family Expenditure Survey (Encuesta Continua de Presupuestos Familiares, abbreviated ECPF). These data were obtained from Crawford (2010) and come from a quarterly budget survey, over the period 1985–1997, that interviews Spanish households about their consumption expenditures for up to a maximum of eight consecutive quarters. See also Browning and Collado (2001) for a detailed discussion of the data. We use a subsample of couples with and without children, where the husband is employed full-time and the wife is out of the labor force. We focus exclusively on consumption expenditures on nondurable consumption categories. Overall, we use data containing 21,866 observations on 3134 households.

We begin the analysis by calculating the AEI, HEI, VEV, and HEV for each household. The HEV is computed by solving the linear problem in Equation (8(8) $$\begin{array}{c}\hfill max\sum _{i=1}^N{\kappa }_i\text{subject}\text{to}\text{Equation}\text{(7)},\end{array}$$(8) ). To facilitate comparison with the VEV, we calculated the VEV by slightly modifying the problem in Equation (3(3) $$\begin{array}{c}\hfill min\sum _{i=1}^N(1-v_i)\text{subject}\text{to}\text{(c.i)--(c.vi)}\text{and}\mathbf{v}\in {(0,1]}^N.\end{array}$$(3) ). This corresponds to how the HEV is computed and is achieved by first log-linearizing the constraints (c.i(c.i) $$\begin{array}{c}\hfill V^i-V^j<X^{ij},\end{array}$$(c.i) )–(c.vi(c.vi) $$\begin{array}{c}\hfill X^{ij}\in \{0,1\},\end{array}$$(c.vi) ) and then maximizing ${\sum }_{i=1}^N{\tilde{v}}_i$, where ${\tilde{v}}_i=log\left(v_i\right)$. We also computed the VEV in the L1-norm by solving the problem in Equation (3(3) $$\begin{array}{c}\hfill min\sum _{i=1}^N(1-v_i)\text{subject}\text{to}\text{(c.i)--(c.vi)}\text{and}\mathbf{v}\in {(0,1]}^N.\end{array}$$(3) ). Interestingly, we obtained practically identical solutions, which suggests that log-linearization provides a very good approximation (see the discussion in Section 3.3).

The results are presented in Table 1, where each row reports the mean, minimum, the first, second (median) and third quartiles and the maximum calculated across all households. The entries for the VEV and HEV in the third and fourth rows are averages across all households. For example, to obtain the entry “min,” we first computed min {v₁, …, v_N} and min {h₁, …, h_N} for each household and then calculated the mean of these values over all households.

Table 1. Efficiency and misspecification measures (ECPF)

Measure	Mean	Min	First quartile	Median	Third quartile	Max
AEI	0.9998	0.9698	1.0000	1.0000	1.0000	1.0000
HEI	0.9917	0.9518	0.9890	0.9936	0.9965	1.0000
VEV	1.0000	0.9998	1.0000	1.0000	1.0000	1.0000
HEV	0.9960	0.9865	0.9936	0.9978	0.9996	1.0000
MSI	0.0081	0.0000	0.0034	0.0062	0.0107	0.0482
MSIV	0.0040	0.0000	0.0019	0.0033	0.0053	0.0243

As can be seen, homothetic efficiency is very close to utility maximization efficiency. For example, the mean across all observations and households of the HEV is 0.9960 (compared to the 1.0000 for the VEV). The same table also reports the misspecification measures MSI and MSIV described in Section 3.4. Evidently, the additional adjustment necessary to make the data fit the homothetic model is very limited, which is unsurprising given the very high levels of homothetic efficiency. Based on the measures reported in Table 1, we can conclude that homothetic utility maximization performs very well.

The next consideration is test power. The standard approach to calculating the power of revealed preference tests is based on Bronars (1987). We follow Bronars’ approach and generate many random choice sets that are uniformly distributed on the budget sets and compute the fraction of sets that either violate GARP or HARP, which we refer to as the power of GARP and HARP, respectively.

To analyze the loss in power for expenditure-adjusted data, we employ the following three-step procedure: (i) we compute the efficiency index using the observed data; then, (ii) we generate random datasets using Bronars’ approach; and, finally, (iii) we calculate the fraction of sets violating GARP or HARP, where expenditures are adjusted for efficiency. More precisely, we deflate expenditures by the efficiency index computed in the first step when testing whether the randomly generated datasets satisfy GARP or HARP. Repeating the three-step procedure for all four efficiency indices AEI, VEV, HEI, and HEV allows us to compare the loss in discriminatory power across the indices and to analyze the potential loss in power from adjusting expenditures by efficiency.

Table 2 reports the power of GARP and HARP depending on how expenditures are adjusted. As discussed in the introduction, allowing for deviations from 100% efficiency often leads to a loss in power, which may render the analysis practically meaningless. As seen from Table 2, this concern is clearly warranted for utility maximization alone. Indeed, the first, third, and fifth rows show that utility maximization alone barely has any power against uniformly random behavior (the power for the average household is less than 9%) This means that GARP is essentially unable to reject random consumption behavior. In contrast, the second, fourth, and sixth rows show that HARP has substantially more power against uniformly random behavior. Although there is a loss in power for HARP for some households when expenditures are adjusted by the HEV, 50% of the households nevertheless have a power of at least 73%. Notably, the sixth row shows that the loss in power for HARP is negligible when adjusting expenditures by the HEV. More precisely, adjusting income by the HEV has little effect on power, which rather forcefully addresses the concern that adjusting expenditures by efficiency in revealed preference testing renders the analysis meaningless.

Table 2. Power for GARP and HARP (ECPF)

	Expenditures
Axiom	adjusted	Mean	Min	First quartile	Median	Third quartile	Max
GARP	No	0.0886	0.0000	0.0000	0.0300	0.1600	0.6700
HARP	No	0.9997	0.9800	1.0000	1.0000	1.0000	1.0000
GARP	AEI	0.0854	0.0000	0.0000	0.0200	0.1600	0.6400
HARP	HEI	0.6329	0.0000	0.3600	0.7300	0.9300	1.0000
GARP	VEV	0.0872	0.0000	0.0000	0.0300	0.1600	0.6400
HARP	HEV	0.9748	0.2100	0.9700	0.9900	1.0000	1.0000

The main conclusions that can be drawn from our results thus far are as follows, (i) The consumption choices of the households are very close to satisfying homothetic preferences (i.e., the households have high homothetic efficiency, and the misspecification is low), and (ii) homotheticity can have much higher discriminatory power against random behavior than utility maximization alone. In fact, the vast majority of households have very high power against random behavior even when expenditures are adjusted by homothetic efficiency.

However, this is a sequential analysis and, as such, fails to give any indication of the trade-off between efficiency and power. Beatty and Crawford (2011) and Heufer (2012) suggested combining efficiency and power into a single measure based on the idea of predictive success originally advanced by Selten (1991) (see also Heufer (2008) for an early application of the trade-off approach to compare two different efficiency indices). Beatty and Crawford’s (2011) measure is computed as the difference between the pass rate and one minus the power. The outcome of this measure is a value between negative one and one. Negative values would suggest that the model fails to describe the preferences of the household: the model does not pass the revealed preference axiom and provides low discriminatory power against random behavior. In contrast, a high and positive predictive success indicates a potentially useful model: it passes the revealed preference axiom and has high power against random behavior.

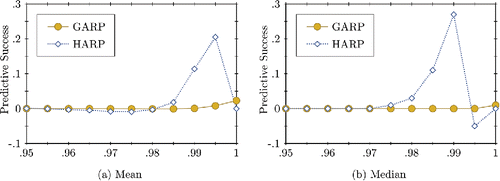
Following Beatty and Crawford (2011) and Heufer (2012), we can use the predictive success to find the optimal level of efficiency across the households as follows. For a given efficiency level e, first calculate HARP(e), which gives the pass rate (either zero or one). Second, calculate the power using HARP(e). Doing so for an arbitrarily fine grid gives the predictive success at each efficiency level. The optimal efficiency level is the one that produces the highest predictive success. Figure 2 presents the results from this analysis. Figure 2(a) shows the average predictive success across all households for each efficiency level in the grid. As seen from this plot, GARP obtains a maximal predictive success very close to zero at an efficiency level of one. One interpretation of this is that the theory of utility maximization performs about as well as a theory that explains consumer demand as purely random behavior. The results for HARP are quite different. We find that the maximal average predictive success across households is 0.22 obtained at an efficiency level of 0.995. Thus, according to these results, homothetic utility maximization provides a considerably better fit to the data than utility maximization alone at an efficiency level only slightly below one. The results for the median of the predictive success across all households shown in Figure 2(b) are even more favorable to homothetic utility maximization. In this case, the predictive success is essentially zero for GARP at all efficiency levels but close to 0.3 at an efficiency level of 0.99 for HARP.

Figure 2. Measure of predictive success across all households for each efficiency level in the grid (ECPF).

4.2. Experimental Data: Preferences for Giving

Fisman, Kariv, and Markovits (2007, FKM) analyzed data obtained in a laboratory experiment. They employed the same setup as Andreoni and Miller (2002, AM), that is, a generalized dictator game in which one subject (the dictator) allocates token endowments between himself and an anonymous other subject with different transfer rates. The payoffs of the dictator and the beneficiary are interpreted as two distinct goods and the transfer rates are interpreted as the price ratio. In both papers, the authors estimate CES utility functions, and thus, they implicitly maintain the hypothesis that choices are homothetic. Testing how “close” the choices are to homotheticity is therefore important and should be conducted at least as a pretest to screen out particularly inefficient choices.

Heufer (2013) computed a simple two-dimensional version of homothetic efficiency for both the FKM and the AM data. We only focus on the FKM data here, as they contain 50 choices per subject as opposed to 8 in the AM data. Note that subjects were not required to spend their entire endowment, and a few subjects occasionally chose bundles somewhat below the budget line. One subject made several choices far below the budget line, leading to an AEI and HEI of approximately 0.1, which caused convergence problems for the computation of the VEV. We therefore decided to exclude that subject from the analysis. The results for our measures are presented in Table 3.

Table 3. Efficiency and misspecification measures (FKM)

Measure	Mean	Min	First quartile	Median	Third quartile	Max
AEI	0.8971	0.2717	0.8721	0.9566	0.9823	0.9972
HEI	0.8279	0.2534	0.7810	0.8809	0.9553	0.9874
VEV	0.9887	0.8820	0.9892	0.9980	0.9998	1.0000
HEV	0.9617	0.7814	0.9525	0.9773	0.9878	0.9982
MSI	0.0848	0.0032	0.0288	0.0564	0.1062	0.4312
MSIV	0.0279	0.0028	0.0112	0.0206	0.0373	0.1198

Regarding the first two rows, we find that the AEI is noticeably higher than the HEI for most subjects. However, as discussed above, the AEI and HEI are summary statistics and may be uninformative in describing the entire distribution of the indices. The third and fourth rows of Table 3, which provide the results for the VEV and HEV, offer a different picture. These results suggest that homothetic efficiency is close to utility maximization. In particular, the HEV displays the same pattern as the VEV. They are both characterized by one or a few observations with lower values, while the remaining values in the vector are very close to one.

Table 3 also reports the misspecification measures. If we accept the value of 0.05 suggested in Section 3.4 as the threshold, we find that based on the MSI, slightly less than half of all subjects fit the homothetic utility maximization model well. Again, the picture given by the vector-based MSIV is different; it suggests that more than 75% of all subjects fit the homothetic utility maximization model well.

Table 4 reports the power of GARP and HARP. The results, in particular for GARP, are very different from the results for the ECPF data in Table 2. For the experimental data, the test power for most subjects is very high, while for the household survey data, the test power for GARP is low enough to prevent a meaningful test for utility maximization. As the subjects made choices on 50 budgets, this finding is perhaps unsurprising. Thus, imposing additional restrictions on utility, such as homotheticity, may not be essential for an informative analysis.

Table 4. Power for GARP and HARP (FKM)

	Expenditures
Axiom	adjusted	Mean	Min	First quartile	Median	Third quartile	Max
GARP	No	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
HARP	No	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
GARP	AEI	0.9659	0.4500	1.0000	1.0000	1.0000	1.0000
HARP	HEI	0.9847	0.4700	1.0000	1.0000	1.0000	1.0000
GARP	VEV	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
HARP	HEV	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

With little to no difference in test power between GARP and HARP, and the fact that homothetic efficiency can never be higher than Afriat efficiency, we cannot expect the predictive success of the homothetic model to be superior. Figure 3(a) shows that for the average subject, the predictive success of the homothetic utility maximization model is lower for all efficiency levels below one. Figure 3(b) shows that up until an efficiency level of 0.86, the median predictive success is slightly higher for HARP, but it drops to zero at a level of 0.89, while the predictive success of GARP is 1 for levels between 0.87 and 0.95, after which it drops to zero. This drop to zero occurs because less than half of subjects have an HEI greater than 0.89, or an AEI greater than 0.96.

Figure 3. Measure of predictive success across all subjects for each efficiency level in the grid (FKM).

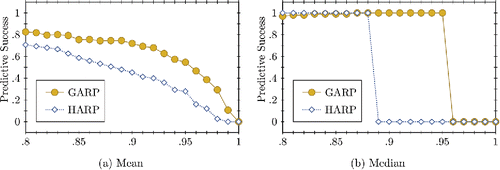
The conclusions we can draw from the analysis of the experimental data are not as unambiguous as those from the household survey data. Approximately, 50%–75% of the subjects have rather high homothetic efficiency levels and low misspecification values. For these subjects, the measures we have introduced indicate no problems with estimating a homothetic utility function. However, this also means that assuming homothetic preferences and estimating CES utility functions may be problematic for the remaining subjects. Imposing homotheticity on the data to have a model with higher test power seems unnecessary for this dataset, and from the perspective of predictive success, the model of utility maximization alone performs slightly better.

We can think of at least two potential reasons for the differences between the survey and experimental data. First, social preferences are likely to be more context specific (see, e.g., Eckel and Grossman 1996), and different wealth levels can be considered a context. Our findings are in line with the results reported by Heufer (2013), who found that many subjects in Fisman, Kariv, and Markovits (2007) deviate substantially from homotheticity. This deviation is more pronounced than in the experiment by Choi et al. (2007a), which uses a similar methodology but is about risk aversion.

Second, Fisman, Kariv, and Markovits (2007) selected normalized prices that vary substantially—they were between 1/50 and 1/100. This resulted in stark differences in the wealth levels between budgets. However, prices and expenditures varied very little in the survey data, which is natural given that prices for everyday goods and income levels do not typically change substantially. It is plausible for such data that after a small increase in income, a household will not drastically reallocate relative expenditures.

5. CONCLUSION

Consumer choice data often violate homothetic utility maximization. In such cases, it would be interesting to know how closely the data approach homothetic utility maximization. For this purpose, we introduced a nonparametric approach to estimating homothetic efficiency of demand data by generalizing Heufer’s (2013) method. We introduced the homothetic efficiency index (HEI) and the homothetic efficiency vector (HEV), which are analogous to the Afriat efficiency index (AEI) and Varian’s improved violation index or Varian efficiency vector (VEV). As with the AEI, the HEI can be interpreted as a measure of wasted income. As a nonparametric approach, our method does not rely on any specific form of a utility function.

Both the HEI and the HEV can be used to adjust data by deflating expenditures to reconstruct bounds on preferred and worse sets. This is motivated by a concept called e- and h-rationalization, which was recently introduced by Halevy, Persitz, and Zrill (2015): for efficiency close to 100%, there still exists a utility function that adequately explains the data as the result of homothetic utility maximization with only minor deviation.

We applied the method to two datasets. The application demonstrates how a dataset that has very low power against the alternative hypothesis of random behavior can still be useful when testing for the stronger condition of homothetic utility maximization. Using the measure of predictive success applied to household survey data, we find that homothetic utility maximization can be considerably more successful in explaining the demand behavior for efficiency levels close to one. However, this is not the case for all types of datasets. For data from a laboratory experiment that already had high test power, the model of utility maximization alone performs slightly better from the perspective of predictive success.

The approach can also be translated to production analysis. Hanoch and Rothschild (1972) and Varian (1984) already described nonparametric ways to test production for homotheticity. As homotheticity of production is assumed in many applications, a nonparametric test that provides a measure of homothetic efficiency independent of a specific production function should at the very least be a useful screening device and robustness check before parameters of a homothetic production function are estimated.

We expect that our results will help to analyze experimental, survey, and field data. It will be worthwhile to test the assumption of homotheticity before estimating homothetic utility functions, to quantify the extent of the violation of homotheticity, and to obtain high test power against the alternative hypothesis of random behavior.

Supplementary Materials

A zip file containing all necessary Matlab codes to replicate the empirical applications is available online.

ACKNOWLEDGMENTS

Access to data collected by Raymond Fisman, Shachar Kariv, and Daniel Markovits is gratefully acknowledged. Thanks to an associate editor, the editor, and Linda Hirt-Schierbaum for helpful comments. Thanks to two anonymous referees for comments and suggestions that greatly improved the article.

APPENDIX A: PROOFS

Proof of Theorem 3.

The equivalence of (1) and (3) is part of Theorem 1 by Halevy, Persitz, and Zrill (2015). The inequalities of condition (2) can be constructed from the details of their proof. In particular, they showed that GARP(v) implies the existence of a function f(x) = min _i{fⁱ + λⁱzⁱ(x)} with λⁱ > 0 and f(xⁱ) ⩾ fⁱ. They then defined zⁱ(x) = pⁱx/v_i − pⁱxⁱ if x ≠ xⁱ and zⁱ(x) = 0 otherwise and show that with this zⁱ(x), f(x) v-rationalizes Ω. By the definition of f, we then have f(x) ⩽ fⁱ + λⁱpⁱ(x/v_i − xⁱ) for all i. With zⁱ(xⁱ) = 0 we have f(xⁱ) ⩽ fⁱ, and together with f(xⁱ) ⩾ fⁱ this implies f(xⁱ) = fⁱ. With fⁱ = Uⁱ, this function can be constructed using the numbers from our condition 2, and as it rationalizes Ω, condition (2) implies (3). Furthermore, if the function exists, the numbers in the inequalities can be taken from the function. As GARP(v) ensures the existence of the function, condition (1) implies (2), which completes the proof.

Proof of Theorem 6.

• (1) ⇒ (2): The proof follows Varian (1983) with some adjustments. Parts of it are necessary for the next step, which is why a brief version is included here. Assume HARP(h) holds. Define (A.1) $$\begin{array}{ccc}\hfill U^i& =& \underset{\{j,k,\dots ,m,i\}}{min}\left\{\left(\frac{{\mathbf{p}}^j{\mathbf{x}}^k}{h_j}\right)\left(\frac{{\mathbf{p}}^k{\mathbf{x}}^{\ell }}{h_k}\right)\cdots \left(\frac{{\mathbf{p}}^m{\mathbf{x}}^i}{h_m}\right)\right\}.\hfill \end{array}$$(A.1) Let $$\begin{array}{ccc}\hfill U^i& =& \left(\frac{{\mathbf{p}}^j{\mathbf{x}}^k}{h_j}\right)\left(\frac{{\mathbf{p}}^k{\mathbf{x}}^{\ell }}{h_k}\right)\cdots \left(\frac{{\mathbf{p}}^m{\mathbf{x}}^i}{h_m}\right)\hfill \\ \hfill U^j& =& \left(\frac{{\mathbf{p}}^n{\mathbf{x}}^o}{h_n}\right)\left(\frac{{\mathbf{p}}^o{\mathbf{x}}^q}{h_o}\right)\cdots \left(\frac{{\mathbf{p}}^r{\mathbf{x}}^j}{h_r}\right).\hfill \end{array}$$Then $$\begin{array}{ccc}\hfill U^i& =& \left(\frac{{\mathbf{p}}^j{\mathbf{x}}^k}{h_j}\right)\left(\frac{{\mathbf{p}}^k{\mathbf{x}}^{\ell }}{h_k}\right)\cdots \left(\frac{{\mathbf{p}}^m{\mathbf{x}}^i}{h_m}\right)\hfill \\ & \le & \left(\frac{{\mathbf{p}}^n{\mathbf{x}}^o}{h_n}\right)\left(\frac{{\mathbf{p}}^o{\mathbf{x}}^q}{h_o}\right)\cdots \left(\frac{{\mathbf{p}}^r{\mathbf{x}}^j}{h_r}\right)\left(\frac{{\mathbf{p}}^j{\mathbf{x}}^i}{h_j}\right)\hfill \\ & =& U^j{\mathbf{p}}^j{\mathbf{x}}^i/h_j.\hfill \end{array}$$

• (2) ⇒ (3): Define U(x) = min _j{U^jp^jx/h_j} with the U^j defined as in the previous step of the proof. It can be easily verified that $U\in \mathcal{U}$ and that U is homothetic; what remains to be shown is that U e-rationalizes Ω. By the definition of the Uⁱ, it follows that U(xⁱ) = Uⁱpⁱxⁱ/h_i, and with pⁱxⁱ = 1 we obtain U(xⁱ) = Uⁱ/h_i and with h_i ⩽ 1 we obtain Uⁱ ⩽ U(xⁱ). Suppose ${\mathbf{x}}^i{\text{R}}^0\left(h_i\right)\mathbf{y}$. Then h_ipⁱxⁱ ⩾ pⁱx and with pⁱxⁱ = 1 we obtain h_i ⩾ pⁱx. By definition of U(x), U(x) ⩽ Uⁱpⁱx/h_i, and with h_i ⩾ pⁱx we obtain U(x) ⩽ Uⁱ. It follows that U(x) ⩽ Uⁱ ⩽ U(xⁱ) and thus U(x) rationalizes Ω.

• (3) ⇒ (1): This part follows from Varian (1983) with minor obvious adjustments.