Exact and approximate algorithms for part-machine clustering based on a relationship between interval graphs and Robinson matrices

Abstract

An important manufacturing cell formation problem requires permutations of the rows (parts) and columns (machines) of a part-machine incidence matrix such that the reordered matrix exhibits a block-diagonal form. Numerous objective criteria and algorithms have been proposed for this problem. In this paper, a new perspective is offered that is based on the relationship between the consecutive ones property associated with interval graphs and Robinson structure within symmetric matrices. This perspective enables the cell formation problem to be decomposed into two permutation subproblems (one for rows and one for columns) that can be solved optimally using dynamic programming or a branch-and-bound algorithm for matrices of nontrivial size. A simulated annealing heuristic is offered for larger problem instances. Results pertaining to the application of the proposed methods for a number of problems from the literature are presented.

Keywords:

• Facility layout
• cellular manufacturing
• interval graphs
• Robinson matrix
• dynamic programming
• branch and bound

1. Introduction

Group technology provides a framework for accommodating a diverse collection of products and activities associated with a manufacturing process. An especially noteworthy application of group technology is cellular manufacturing, which requires the identification of families of parts that are assigned to production cells consisting of groups of machines. The cell formation problem is a well-studied problem in the operations research and industrial engineering literature and encompasses a variety of issues that have been outlined carefully in a comprehensive review by Selim et al. (1998). As observed by Shargal et al. (1995), an important initial step in the design of a cellular manufacturing system is the clustering of the part-machine matrix that contains important processing information within the system.

In this paper, we focus on the problem of inducing a block-diagonal form for binary part-machine matrices. A value of “one” (“zero”) in a part-machine matrix indicates that the part associated with the row requires (does not require) processing on the machine corresponding to the column. A block-diagonal form is established by permuting the rows and columns of the part-machine matrix such that the “ones” in the matrix group together along the diagonal. Shargal et al. (1995) indicate that methods for permuting part-machine matrices are typically based on one of three models: (i) minimum spanning trees (McCauley, 1972); (ii) the traveling salesman problem (Askin et al., 1991); and (iii) the linear placement problem (Suryanarayanan et al., 1991). Each of these methods attempts to produce a block-diagonal form via the independent establishment of permutations for parts and machines and the subsequent blending of these permutations.

Our goal in this paper is to present an alternative method for obtaining a block-diagonal form that is based on the consecutive ones property associated with interval graphs and the corresponding relationship to Robinson matrices. Accordingly, our approach is based on the pioneering work of Fulkerson and Gross (1965) and Kendall (1969) which, to the best of our knowledge, has not previously been addressed in the cell formation literature. A graph G = (V, E), with vertex set V and edge set E, is an interval graph if an interval (Δ v) on the real number line can be generated for each vertex, v ∈ V, such that the condition {u, v}∉ E ↔ Δ u ∩ Δ v = ø holds. Fulkerson and Gross (1965) proved that consecutive ones in the columns of the incidence matrix corresponding to G = (V, E) is a necessary and sufficient condition for a graph to be an interval graph. Kendall (1969) subsequently showed that if a matrix possesses consecutive ones in all columns, then the product of that matrix with its transpose must exhibit a perfect Robinson structure, whereby elements of the matrix are “never increasing” when moving away from the main diagonal in any direction (Robinson, 1951).

Why are the consecutive ones property and Robinson matrices relevant to cell formation? The importance of the consecutive ones property stems from the well-established practice of permuting the rows and columns of the part-machine matrix to obtain a block-diagonal form (Shargal et al., 1995; Crama and Oosten, 1996; Sarker and Khan, 2001). A block-diagonal form is characterized by cells that consist primarily of ones along the main diagonal and primarily of zeros away from the main diagonal. The ones that appear outside the blocks along the main diagonal are termed “exceptional elements”, and such elements correspond to bottleneck machines and exceptional parts (Malakooti and Yang, 2002). Likewise, the occurrence of zeros within the blocks along the main diagonal produces an adverse effect on machine utilization within the corresponding cell (Chandrasekharan and Rajagopalan, 1986). The consecutive ones property is in accordance with the goal of block-diagonal form, minimization of exceptional parts, and maximization of machine utilization. If each block along the main diagonal consists of consecutive ones in all rows and columns of the block, and if there are no ones outside the block (i.e., consecutive zeros outside the main diagonal blocks), then the objectives of minimizing exceptional elements and maximizing utilization are satisfied perfectly. Further support of the importance of the consecutive ones property to cell formation is offered by the fact that all of the clustering efficiency measures for block-diagonal form used by Shargal et al. (1995) during their search for algorithms for part-machine clustering are based principally on counts of adjacent ones (and sometimes adjacent zeros) within rows and columns.

The relevance of the consecutive ones property to block-diagonal form and part-machine clustering establishes one aspect of the motivation for our paper. The fact that a permuted part-machine matrix with consecutive ones in all rows and columns must yield part and machine similarity matrices with a perfect Robinson structure provides the remainder of the motivation. Our premise is that permuting the part and machine similarity matrices to have at least an approximate Robinson structure will have a propensity to yield a reordered part-machine matrix with large bands of consecutive ones and block-diagonal form. We develop some effective criteria for producing a Robinson structure and demonstrate that exact procedures based on dynamic programming and a branch-and-bound algorithm are feasible for problems of nontrivial size. For larger part-machine matrices, we develop a simulated annealing heuristic. We apply these methods to a number of part-machine matrices in the published literature.

In Section 2 of this paper, we more formally describe the relationship between the consecutive ones property and Robinson matrices. An illustrative example is also presented in Section 2. Section 3 describes the dynamic programming, branch and bound, and simulated annealing methods used to obtain permutations for parts and machines based on a Robinson structure. Computational results for problems in the cell formation literature are reported in Section 4, and the paper concludes with a brief summary in Section 5.

2. The consecutive ones property and Robinson matrices

2.1. Basic definitions

We define A = [a _ij ] as an n × m incidence matrix for n parts and m machines, where a _ij = 1 if part i requires processing on machine j (for 1 ≤ slanti ≤ slantn and 1 ≤ slantj ≤ slantm). The n × n matrix AA ^T is a symmetric similarity matrix for parts, where an element in row i and column i′ of the matrix represents the number of machines that parts i and i′ have in common. Similarly, the m × m matrix A ^T A is a symmetric similarity matrix for machines, where an element in row j and column j′ of the matrix represents the number of parts that machines j and j′ have in common.

We denote φ = (φ (1), φ (2),…, φ (n)) as a permutation of the n parts such that φ (k) is the part in position k of the permutation. An n × n permutation matrix for parts, Λ = [λ _ij ], is constructed from φ by defining, for 1 ≤ slanti ≤ slantn, λ _{iφ (i)} = 1 and λ _ij = 0 for 1 ≤ slantj ≠ φ (i) ≤ slantn. The set of all n¡ permutations of parts is represented as Φ (φ ∈ Φ). We define γ = (γ (1), γ (2), …, γ (m)) as a permutation of the m machines such that γ (k) is the machine in position k of the permutation. An m × m permutation matrix for machines, Ω = [ω _ij ], is constructed from γ by defining, for 1 ≤ slanti ≤ slantm, ω _{iγ (i)} = 1 and ω _ij = 0 for 1 ≤ slantj ≠ γ (i) ≤ slantm. The set of all m¡ permutations of machines is represented as Γ (γ ∈ Γ). With these definitions in place, a permutation of the original part-machine matrix, A, based on φ and γ can be concisely represented as ΛAΩ ^T . The correspondingly permuted part and machine similarity matrices are Λ (AA ^T ) Λ ^T and Ω (A ^T A) Ω ^T , respectively.

2.2. A numerical example

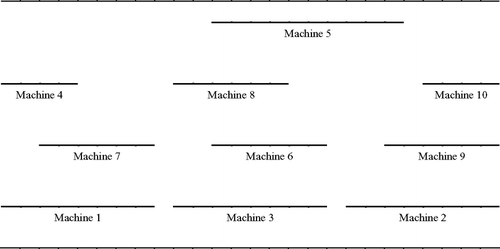
Consider the 12 × 10 part-machine matrix displayed in Fig. 1(a), and the permutations φ = (5, 1, 6, 10, 7, 8, 11, 2, 4, 9, 3, 12) and γ = (4, 1, 7, 8, 3, 6, 5, 2, 9, 10). For the moment, we will ignore how these permutations were obtained and focus solely on their results. The reordered part-machine matrix, ΛAΩ ^T , based on these permutations is shown in Fig. 1(b). The permuted matrix exhibits a block-diagonal form with ones grouping along the main diagonal. Moreover, within each row and column of the permuted matrix, the ones are consecutive. This consecutivity property ensures that interval assignments can be produced for both parts and machines. To illustrate, Fig. 2 displays an interval assignment for machines. Notice that the interval for each machine overlaps only with the intervals for machines that produce some of the same parts. For example, the interval for machine 5 only overlaps with the intervals of machines for which it has at least one part in common (machines 8, 3, 6, 2, and 9). Figure 1(c) represents the permuted part similarity matrix, Λ (AA ^T ) Λ ^T . We observe that this matrix has a perfect Robinson structure because the elements never increase when moving away from the main diagonal within any row or column. This same property holds for the permuted machine similarity matrix, Ω (A ^T A) Ω ^T , in Fig. 1(d).

Fig. 1 A numerical example to illustrate the relationship between the consecutive ones property of the part-machine matrix and the Robinson structure of the part and machine similarity matrices: (a) the raw matrix, A; (b) the permuted matrix, ΛAΩ ^T ; (c) the permuted part matrix, Λ (AA ^T ) Λ ^T ; and (d) the permuted machine matrix, Ω(A ^T A) Ω ^T .

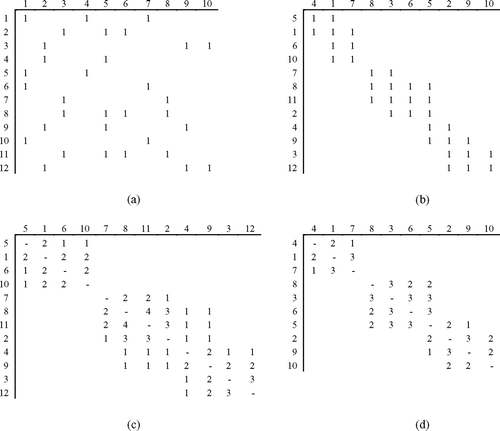
Fig. 2 An interval assignment for machines associated with the optimally permuted part-machine matrix in Fig. 1(b).

The example in (Fig. 1a, Fig. 1b, Fig. 1c, Fig. 1d) establishes the premise of our proposed method. If we can obtain permutations of the rows and columns of the part-machine matrix such that the reordered matrix exhibits the consecutive ones property in all rows and columns, then, based on the classic result reported in Kendall (1969), the correspondingly permuted part and machine similarity matrices will have a perfect Robinson structure. Although the converse of Kendall's theorem is not always true, permutation of the part and machine similarity matrices into a Robinson structure should provide a strong propensity for the correspondingly reordered part-machine matrix to exhibit the consecutive ones property and block-diagonal form.

In practice, achieving consecutive ones in all rows and columns and a perfect Robinson structure for the part and machine similarity matrices is likely unattainable. In other words, there is no permutation of parts and machines that will provide a perfect Robinson structure for the respective similarity matrices. Nevertheless, if we can permute the similarity matrices to realize an approximate Robinson structure, then this should tend to produce a block-diagonal form in the part-machine matrix. In the next section, we present several optimization criteria that might be useful for approximating a Robinson structure.

2.3. Optimization criteria for an approximate Robinson structure

There are a host of possible criteria that can be devised to approximate a Robinson structure within a reordered similarity matrix. One option is to use the linear placement problem described by Suryanarayanan et al. (1991) and Shargal et al. (1995). We adapt two within-row and column gradient criteria used by Brusco and Stahl (2005, Ch. 9) within the context of an anti-Robinson structure (i.e., never decreasing elements when moving away from the main diagonal within a row or column) in applied data analysis. Without loss of applicability, we display these criteria within the context of permuting the similarity matrix for parts, P = AA ^T . The linear placement model, under the assumption of equal distances between positions in the sequence (d _kl = d _lk = l − k for 1 ≤ slantk < l ≤ slantn), is as follows:

The second criterion is an unweighted within-row-and-column gradient index:

where

The third criterion is the weighted within-row-and-column gradient index:

or

The linear placement criterion, f ₁(φ), attempts to place similar parts close to one another and the imposed penalties are a function of the distances between positions in the sequence. The indices f ₂(φ) and f ₃(φ) both use two terms above the main diagonal of the reordered matrix. (Because P is symmetric, consideration of the below diagonal terms is redundant.) The first term in f ₂(φ) and f ₃(φ) measures whether or not a Robinson structure is present in row h above the main diagonal, whereas the second term determines the appropriateness of the structure in column l above the diagonal The two indices differ in that f ₃(φ) assigns more credit to concordance with a Robinson structure and a greater penalty to discordance with a Robinson structure.

Based on our preliminary experiments, we concluded that f ₃(φ) generally produces a slightly better block-diagonal structure than f ₂(φ). This finding is likely attributable to the fact that f ₃(φ) penalizes egregious violations of a Robinson structure more harshly than f ₂(φ). For example, assume that elements of “one” and “five” were observed within a row (above the main diagonal) in a reordered matrix, and that the five is to the right of the one. This violation of the Robinson structure would be penalized a value of “−1” using f ₂(φ), which measures only consistency or inconsistency with the structure. In contrast, a penalty of “1 – 5 = −4” would be realized with f ₃(φ), which captures the seriousness of the violation. We have observed that the optimal part-machine permutations for f ₁(φ) and f ₃(φ) were identical in most cases and, therefore, do not advocate one criterion over the other with respect to performance. However, with respect to computational efficiency of the exact algorithms (particularly, the branch-and-bound algorithm), optimal permutations were typically obtained in much less time for f ₃(φ) relative to f ₁(φ). For this reason, the remainder of our paper focuses on the f ₃(φ) index and we refer to the problem posed by Equation (4) as the Robinson Permutation Problem (RPP).

3. Solution procedures

3.1. A dynamic programming algorithm

The dynamic programming approach for the RPP is comparable to implementations for several problems pertaining to row layout (Picard and Queyranne, 1981; Kouvelis et al., 1995; Brusco, 2004). We provide a sufficient description of the dynamic programming method as related to our implementation for the RPP. We employ the following notation:

S	=	the set of indices for parts {1, 2, …, n}.
θ	=	the power set of S, i.e., the set of all subsets of S.
θ k	=	the set of all subsets in θ that have exactly k part indices.
S k	=	S k ∈ θ k is an arbitrary subset from θ k . In other words, S k represents one of the n¡/(k¡(n − k)¡) subsets of size k contained in θ k . We delineate S k i (for all i∈ S k ) as S k with the further condition that part i is placed last in any partial sequence of the parts in S k .
F(S k i )	=	the contribution to the RPP index that is accumulated from placing part i in the last position of the sequence for subset S k .
F* (S k )	=	the best possible RPP index that can be achieved for subset S k .
τ* (S k )	=	the part that should be placed last in the partial sequence of the objects in S k to produce the best possible RPP index value, F* (S k ).

The stages of the dynamic programming algorithm are characterized by the subset sizes. In the first stage, we indicate that the contribution to the RPP objective function is zero for all n subsets of size 1:

The recursion equations for stages 2 ≤ slantk ≤ slantn are established as

The values of F* (S _k ) and τ* (S _k ) are stored in 2 ⁿ -dimensional vectors and accessed using a binary representation of the subset. The optimal permutation is acquired by backtracking from the final subset in stage n, which is S _n = S, using the stored values τ* (S _k ) for 1 ≤ slantk ≤ slantn. As noted by Brusco (2004), the principal limitation of the dynamic programming approach is the computer memory required to store the F* (S _k ) and τ* (S _k ) values. For current microcomputer platforms, memory constraints preclude optimal solutions for n ≈ 27 or greater. A small numerical demonstration of the dynamic programming algorithm is provided in the Appendix.

3.2. A branch-and-bound algorithm

Branch-and-bound methods have also proven effective for permutation problems (Brusco, 2004; Brusco and Stahl, 2005, Chs. 7–11). We have designed a branch-and-bound procedure for the RPP that can facilitate optimal solutions for problems with n = 35 or more objects. We begin by obtaining a lower bound for f ₃(φ) using 20 restarts of a pairwise interchange heuristic similar to the CRAFT heuristic (Armour and Buffa, 1963) for the quadratic assignment problem. Each restart uses a different, randomly generated, initial permutation. The best solution found across the 20 restarts provides an initial incumbent solution, φ_B, and corresponding lower bound, f _LB. The steps of the branch-and-bound algorithm are as follows:

• Step 0. Set t = 1, φ (t) = 1, and φ (k) = 0 for 2 ≤ slantk ≤ slantn. Obtain φ_B and f _LB using a pairwise interchange heuristic. Compute the following three-dimensional array, Y = [y _ijl ]: y _ijl = (p _ij + p _jl − 2p _il ) for 1 ≤ slanti ≠ j ≠ l ≤ slantn.

• Step 1. Set t = t + 1.

• Step 2. Set φ (t) = φ (t) + 1.

• Step 3. If φ (t) = φ (k) for any k = 1, …, t−1, then go to Step 2.

• Step 4. If φ (t) = 2 and φ (k) ≠ 1 for any k = 1, …, t −1, then go to Step 2.

• Step 5. If t = 1 and φ (t) > n, then return best solution and Stop.

• Step 6. If t > 1 and φ (t) > n, go to Step 11.

• Step 7. If t = n−1, then go to Step 8. Otherwise go to Step 9.

• Step 8. Compute f ₃(φ) for the complete sequence. If f ₃(φ) > f _LB, then set f _LB = f ₃(φ) and φ_B = φ. Go to Step 2.

• Step 9. Conduct tests for insertion of the part in position t to position s. Define η _t as the subset of parts assigned to the first t positions and perform the following test for t − 1 ≥ slants ≥ slant 1:

  If Equation (10) is satisfied for t −1 ≥ slants ≥ slant 1, then go on to Step 10, otherwise go to Step 2.

• Step 10. Conduct the bound test to determine whether the current partial permutation can lead to a value of f ₃(φ) > f _LB upon its completion.

  If Equation (11) is satisfied, go to Step 1, otherwise go to Step 2.

• Step 11. Perform depth retraction by setting φ (t) = 0 and t = t −1. Go to Step 2.

The branch-and-bound procedure constructs partial sequences by assigning parts to positions indexed by the pointer, t. Partial sequences are pruned if a part has already been assigned to a previous position in the sequence (Step 3), or if part 2 is assigned prior to part 1 in the sequence (Step 4). The latter pruning rule prevents evaluation of sequences that are the reverse order of other sequences where part 1 precedes part 2. The most important pruning rules are those in Steps 9 and 10. Step 9 prunes the partial solution if the relocation of the part in position t to an earlier position in the permutation, s, (1 ≤ slants ≤ slantt−1) will lead to a better RPP criterion value. The bound test in Step 10 enacts a pruning operation if it is determined that pursuit of the partial sequence cannot ultimately lead to a complete permutation with an RPP criterion value greater than the current bound. All permutations have been implicitly or explicitly evaluated if t = 1 and φ (t) > n at Step 5, which results in termination of the algorithm. The computation time associated with the branch-and-bound algorithm tends to become excessive for n > 35.

3.3. A simulated annealing heuristic

Although exact methods, such as dynamic programming and branch-and-bound algorithms, are capable of providing guaranteed optimal solutions to RPP instances of nontrivial size, they are not computationally feasible for some of the larger part-machine matrices encountered in the empirical literature. Therefore, we also developed a simulated annealing heuristic for the RPP that is capable of accommodating larger test problems. The structure of the simulated annealing heuristic is closely related to those designed for related permutation problems (Heragu and Alfa, 1992; Brusco and Stahl, 2000), and the selection of algorithm parameters (cooling factor, temperature length, etc) were based on previous research as well as our own experimentation. The pseudocode for the simulated annealing heuristic is displayed in Fig. 3.

Fig. 3 Pseudocode for the simulated annealing heuristic.

3.4. Partitioning the reordered matrix

It is important to clarify that the dynamic programming, branch-and-bound and simulated annealing algorithms for RPP are designed for seriating the rows and columns of the part-machine matrix, not partitioning them. Accordingly, our methods are designed in the spirit of the Bond Energy Algorithm (BEA) (McCormick et al., 1972). The BEA is a classic seriation procedure that spans several literature bases, and has served as the impetus for subsequent refinements in the cell formation context (Askin et al., 1991; Shargal et al., 1995). The goodness-of-fit associated with a seriation procedure can be assessed using clustering efficiency measures such as those offered by Shargal et al. (1995). However, as noted by Crama and Oosten (1996), a seriation procedure does not establish a partition of parts and machines. Shargal et al. (1995), for example, visually established blocks from the reordered matrix.

Although visual selection of blocks based on the permuted matrix is perfectly viable, we have written a computer program for partitioning the reordered part-machine matrix produced by our RPP algorithms. The program allows the user to specify the desired number of blocks, b, and then uses a simple exchange algorithm to move parts and machines from one block to another while preserving the order of parts and machines obtained by our permutation methods. The objective criterion of the partitioning program that we selected is to maximize the modified grouping efficiency index originally proposed by Kumar and Chandrasekharan (1990), and also employed by Crama and Oosten (1996). The index is computed as follows:

where e is the number of operations (ones appearing in A), e _O is the number of exceptional elements (ones appearing outside the blocks along the main diagonal), and e _V is the number of voids (zeros appearing inside the blocks along the main diagonal). The algorithm could be modified, however, for a myriad of other clustering efficiency measures (see Sarker and Mondal (1999) and Sarker and Khan (2001) for reviews).

4. Computational results

We applied the dynamic programming, branch-and-bound and simulated annealing algorithms to the example data set in Fig. 1(a), as well as a number of cell formation problems from the research literature. The test problems from the literature include: (i) the 10 × 15 matrix presented by Chan and Milner (1983); (ii) the 19 × 12 matrix presented by Askin et al. (1991); (iii) the 19 × 12 matrix presented by Vakharia and Wemmerlöv's (1990); (iv) the 20 × 8 matrix presented by King and Nakornchai (1982); (v) the 11 × 22 matrix and the 10 × 15 matrix presented by Seifoddini (1988); (vi) the 23 × 20 matrix presented by Groover (1987); (vii) the 16 × 30 matrix (problem 1) presented by Boctor (1991); (viii) the 35 × 20 matrix presented by Carrie (1973); (ix) the 35 × 20 matrix presented by Boe and Cheng (1991); (x) the 40 × 24 matrix (problem 2) presented by Chandrasekharan and Rajagopalan (1989); and (xi) the 41 × 30 matrix presented by Kumar and Vanelli (1987).

A summary of results for each test problem is provided in Table 1. The results include the total CPU time required to obtain the RPP permutations using dynamic programming, branch-and-bound and simulated annealing algorithms. In addition, we report the total Jaccard index (Anderberg, 1973, Ch. 4) for the optimally permuted part-machine matrices. The Jaccard index, which was recognized as an especially effective measure of clustering efficiency by Shargal et al. (1995), is computed for rows as follows:

where

The total Jaccard index is the sum of the row and column Jaccard indices. We also report, for each problem, the number of blocks, b, and modified grouping efficiency index, α . These results were obtained from the partitioning algorithm described in Section 3.4.

Table 1 Performance of dynamic programming (DP), branch and bound (BB), and simulated annealing (SA) for selected cell formation problems*

			CPU Time;
Source matrix	Size	Density	DP	BB	SA	JI	b	α
Figure 1(a) example	12 × 10	0.275	0.01	0.02	1.18	15.25	3	0.738 10
Chan and Milner (1983)	10 × 15	0.327	0.06	0.12	1.56	23.17	3	0.800 00
Askin et al. (1991)	19 × 12	0.329	2.07	0.12	2.54	27.87	4	0.537 74
Vakharia and Wemmerlöv (1990)	19 × 12	0.325	2.10	0.12	2.52	28.21	3	0.515 46
King and Nakornchai (1982)	20 × 8	0.381	4.94	0.34	2.39	32.74	3	0.852 46
Seifoddini (1988)	11 × 22	0.314	26.99	5.64	3.20	33.94	3	0.666 67
Groover (1987)	23 × 20	0.246	66.70	59.46	4.97	29.58	6	0.424 05
Boctor (1991)	16 × 30	0.252	—	103.88	7.09	34.72	4	0.477 01
Carrie (1973)	35 × 20	0.194	—	18.56	11.61	63.06	4	0.747 19
Boe and Cheng (1991)	35 × 20	0.219	—	6690.34	11.64	46.11	7	0.526 88
Chandrasekharan and Rajagopalan (1989)	40 × 24	0.135	—	41 263.15	12.06	66.56	8	0.821 43
Kumar and Vannelli (1987)	41 × 30	0.104	—	79 160.96	14.73	44.76	9	0.500 00

The CPU times for both the dynamic programming and branch-and-bound algorithm are quite modest for all test problems where both dimensions of the matrix are 20 or fewer. The dynamic programming approach was faster than the branch-and-bound algorithm for the two smallest matrices, but required more CPU time for all remaining test problems where comparisons were possible. Dynamic programming was computationally infeasible for the last five test problems in Table 1 because of computer memory limitations.

Although space limitations prevent the display of the RPP optimally permuted part-machine matrices for each of the test problems, we believe that closer inspection of at least one matrix is warranted. (Figure 4a, Figure 4b, Figure 4c, Figure 4d) presents the results for the Chan–Milner matrix in a structure similar to that of (Fig. 1a, Fig. 1b, Fig. 1c, Fig. 1d). The raw matrix is shown in Fig. 4(a) and the RPP optimally permuted matrix is shown in Fig. 4(b). The optimally permuted matrix exhibits a strong block-diagonal structure, and there are only a few violations of the consecutive ones property in the rows and columns of Fig. 4(b). Accordingly, Fig. 4(c) and Fig. 4(d) exhibit a strong, although not perfect, Robinson structure. For example, consider the row for machine 1 in Fig. 4(d). When moving to the right in this row, away from the main diagonal, there is an increase from two to three when proceeding from column 4 to column 6.

Fig. 4 (a) A part-machine matrix from Chan and Milner (1983), A; (b) an optimal Robinson permutation of that matrix, ΛAΩ ^T ; (c) an optimal permutation of the part similarity matrix, Λ (AA ^T ) Λ ^T ; and (d) an optimal permulation of the machine similarity matrix, Ω (A ^T A) Ω ^T .

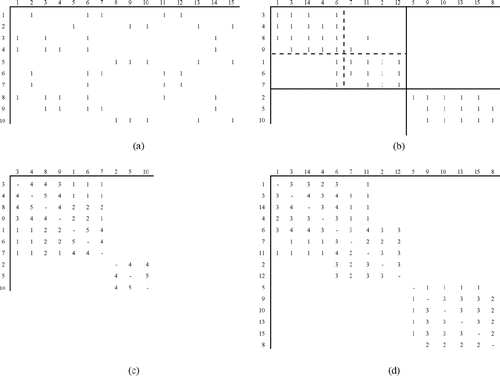
The block-diagonal form of Fig. 4(b) provides a visual representation that can be used to select partitions of part and machine indices, which enables the creation of cells. We display our partitioning program results for the matrix in Fig. 4(b) for the b = 2 and b = 3 blocks. For example, consider the two-block partition that we have shown in Fig. 4(b) with solid lines. The upper-left cell is comprised of parts {3, 4, 8, 9, 1, 6, 7} and machines {1, 3, 14, 4, 6, 7, 11, 2, 12}. The bottom-right cell consists of parts {2, 5, 10} and machines {5, 9, 10, 13, 15, 8}. This solution, which yields α = 0.605, has the desired property of no exceptional elements. However, the proportion of voids might be too large to enable a desired level of machine utilization. To improve machine utilization, a decision-maker might consider the three-block partition obtained by splitting the upper-left cell into two cells, as we have shown in Fig. 4(b) with dashed lines. This solution has only six voids and, therefore, enables greater machine utilization. The price paid for the increase in machine utilization is five exceptional elements (i.e., note the five ones outside the boundaries of the dashed lines). Nevertheless, the grouping efficiency of the three-block solution is α = 0.800, which is clearly superior to the corresponding index for b = 2.

One of the most interesting aspects of Table 1 is a comparison of the results for Carrie's matrix relative to those for the Boe–Cheng matrix. These two matrices have the same dimensions and nearly the same density. In fact, the Boe–Cheng matrix is a perturbed version of Carrie's matrix. The branch-and-bound algorithm provided optimal RPP part-machine permutations for both matrices; however, the differences in required computation time were enormous. For Carrie's matrix, which has a strong block-diagonal form resulting from optimal RPP permutation, the optimal permuted matrix was obtained in 18.56 seconds. Although the optimal RPP part-machine permutation for the Boe–Cheng matrix also has a block-diagonal form, it is not as strong as the form for Carrie's matrix. The required computation time for the Boe–Cheng matrix was 6690.34 seconds, more than 350 times that required for Carrie's matrix.

The Jaccard indices for the Carrie and Boe–Cheng RPP permuted matrices also provide explanation for the marked difference in CPU times, with the total Jaccard index for Carrie's matrix being more than 36% greater than the corresponding index for the Boe–Cheng. Although the computation time for the Boe–Cheng matrix seems excessive, it should be remembered that the solution procedure is solving a permutation problem for a 35 × 35 matrix as part of this process, which permits a solution space of 35¡/2 = 5.166 × 10³⁹ permutations. In this light, the solution time of just under 2 hours does not seem to be an especially unreasonable consumption of resources. In addition, it is reassuring to observe that the simulated annealing algorithm obtains the optimal solution to the RPP in under 8 seconds. Similar results were realized for the two largest part-machine matrices in Table 1. The branch-and-bound algorithm obtained optimal RPP permutations for the Chandrasekharan–Rajagopalan 40 × 24 matrix and the Kumar–Vanelli 41 × 30 matrix in roughly 11.5 and 22 hours, respectively. However, the simulated annealing heuristic matched these optimal RPP solutions in 12.06 and 14.73 seconds, respectively.

5. Conclusions

The intended primary contribution of our paper was to position the part-machine clustering problem in cell formation within the context of the consecutive ones property and its relationship to interval graphs and Robinson matrices, which to our knowledge is unprecedented in the literature. At the same time, we recognized that it was not sufficient to link cell formation to Robinson matrices without providing any computational tools for fitting Robinson structure so as to establish block-diagonal form in the part-machine matrix. For this reason, we offered a secondary contribution that focused on the use of dynamic programming, branch-and-bound, and simulated annealing methods for obtaining Robinson-based permutation of matrices. Dynamic programming and the branch-and-bound algorithm have the advantage of guaranteeing an optimal solution for the selected RPP criterion. Our computational results show that both of these exact methods are effective for establishing block-diagonal patterning, within a reasonable time frame, for many part-machine matrices from the literature. However, even the more scalable of the procedures, the branch-and-bound algorithm, can require excessive amounts of computation time for matrices where one of the dimensions exceeds 35.

Our simulated annealing heuristic does not verify optimality, but can handle larger matrices. Other metaheuristics such as tabu search, genetic algorithms, and variable neighborhood search may also prove useful for larger instances of the RPP. Fortunately, the cell formation literature already contains a number of contributions using these methods (Shargal et al., 1995; Onwubolu and Mutingi, 2001; Lei and Wu, 2005) and adaptation for RPP should be relatively straightforward. A perhaps more challenging, but no less important extension would be the development and testing of multicriterion cell formation approaches (see, for example, Malakooti and Yang (2002)) that incorporate Robinson indices as part of the objective function.

Appendix A numerical illustration of the dynamic programming algorithm

Consider the 3 × 4 part-machine matrix, A, and part-similarity matrix, P shown in Fig. A1.

• Stage 1 (initialize for recursion, k = 1).

• F*(S ₁ = {1}) = 0 and τ *(S ₁ = {1}) = 1,

• F*(S ₁ = {2}) = 0 and τ *(S ₁ = {2}) = 2,

• F*(S ₁ = {3}) = 0 and τ *(S ₁ = {3}) = 3.

• Stage 2 ( k = 2):

• F(S ₂ ¹ = {1,2}) = F*(S ₁ = {2}) + p ₂₁+ p ₁₃− 2p ₂₃ = 0 + 0 + 1 − 2(1) = −1.

• F(S ₂ ² = {1,2}) = F*(S ₁ = {1}) + p ₁₂+ p ₂₃− 2p ₁₃ = 0 + 0 + 1 − 2(1) = −1.

• F(S ₂ ¹ = {1,3}) = F*(S ₁ = {3}) + p ₃₁+ p ₁₂− 2p ₃₂ = 0 + 1 + 0 − 2(1) = −1.

• F(S ₂ ³ = {1,3}) = F*(S ₁ = {1}) + p ₁₃+ p ₃₂− 2p ₁₂ = 0 + 1 + 1 − 2(0) = 2.

• F(S ₂ ² = {2,3}) = F*(S ₁ = {3}) + p ₃₂+ p ₂₁− 2p ₃₁ = 0 + 1 + 0 − 2(1) = −1.

• F(S ₂ ³ = {2,3}) = F*(S ₁ = {2}) + p ₂₃+ p ₃₁− 2p ₂₁ = 0 + 1 + 1 − 2(0) = 2.

• F*(S ₂ = {1,2}) = max (F(S ₂ ¹ = {1,2}), F(S ₂ ² = {1,2})) = −1 and τ*(S ₂ = {1,2}) = 1 or 2,

• F*(S ₂ = {1,3}) = max (F(S ₂ ¹ = {1,3}), F(S ₂ ³ = {1,3})) = 2 and τ*(S ₂ = {1,3}) = 3, F*(S ₂ = {2,3}) = max (F(S ₂ ² = {2,3}), F(S ₂ ³ = {2,3})) = 2 and τ*(S ₂ = {2,3}) = 3.

• Stage 3 ( k = 3):

• F(S ₃ ¹ = {1,2,3}) = F*(S ₂ = {2,3}) = 2,

• F(S ₃ ² = {1,2,3}) = F*(S ₂ = {1,3}) = 2,

• F(S ₃ ³ = {1,2,3}) = F*(S ₂ = {1,2}) = −1,

• F*(S ₃ = {1,2,3}) = max (F(S ₃ ¹ = {1,2,3}), F(S ₃ ² = {1,2,3}), F(S ₃ ³ = {1,2,3})) = 2. and τ *(S ₃ = {1,2}) = 1 or 2.

To find the optimum we can place either part 1 or part 2 last in the sequence and backtrack. Backtracking from part 1 at Stage 3, we proceed to F*(S ₂ = {2,3}) in Stage 2 and remove part 3, then we move to F*(S ₁ = {2}) at Stage 1 and remove part 2. This yields the sequence 2-3-1. If we backtrack from part 2 at Stage 3, we obtain the reverse of the 2-3-1 sequence (i.e., 1-3-2). Both sequences are optimal because of the symmetry of P. Both permutations yield a perfect Robinson structure in P.

Fig. A1 The part-machine matrix A and the part similarity matrix P.

Biographies

Michael J. Brusco is the Synovus Professor of Marketing and Operations Research at Florida State University. His research focuses on the development of optimal and heuristic solution procedures for combinatorial optimization problems related to scheduling, location, layout, and data analysis. He is a past member of the Board of Directors for the Classification Society of North America, and currently serves on the Editorial Board of the Journal of Classification.

Douglas Steinley is an Assistant Professor of Psychological Sciences at the University of Missouri-Columbia. His research focuses on general multivariate statistical procedures, with emphasis on combinatorial optimization as related to exploratory data analysis. He is a member of the Board of Directors for the Classification Society of North America and currently is the Book Review Editor for the Journal of Classification.

Notes

*CPU times in seconds are for a 3.4 GHz, Pentium PC with 1GB of RAM (dynamic programming was infeasible when one of the matrix dimensions exceeded 26). The density is the proportion of ones in the matrix. The JI column contains the total Jaccard index (sum of row and column Jaccard indices). The b and α columns contain the number of blocks and the modified grouping index, respectively, after applying the partitioning algorithm.