Sequencing with limited flexibility

Abstract

We consider the problem of resequencing a set of prearranged jobs when there is limited resequencing flexibility and sequence-dependent changeover costs. Resequencing flexibility is limited by how far forward or backward a job can shift in the sequence relative to its original position. We show how the problem can be solved using dynamic programming in polynomial time with respect to the number of jobs. We also show how the same solution approach can be extended to problems where sequencing constraints are job specific and to problems where job features, which determine changeover costs, are jointly determined with the job sequence. We provide an integer programming formulation to the resequencing problem whose linear programming relaxation offers a useful lower bound. We also describe a family of decomposition heuristics that are easy to customize to provide desired levels of solution quality and solution time. We document the quality of the lower bound from the linear programming relaxation and the upper bound from the heuristic using numerical results. We also provide numerical results to support managerial insights regarding the value of flexibility. We show that the value of flexibility is of the diminishing kind with most of the benefit realized with relatively limited flexibility. We also show that a balanced allocation of flexibility among forward and backward position shifting is superior to an unbalanced one. More significantly, we show that forward and backward position shifting flexibility are complements with the value of one increasing in the amount of the other. Finally, we apply our solution approach to a real-world case from the automotive industry.

Keywords:

• Sequencing
• feature assignment
• flexibility
• traveling salesman problem
• automotive industry

1. Introduction

Consider the following examples.

Example 1: Consider a vehicle resequencing problem typical in many automotive assembly lines where vehicles on a moving line must be rearranged once they emerge from one department and enter a new one. For example, vehicles leaving the body shop are usually resequenced prior to entering the paint shop in order to minimize the number of paint color changeovers. The resequencing is typically carried out by temporarily pulling vehicles off the line and reinserting them later to form a new sequence (Lahmar et al., 2003). The number of vehicles that can be simultaneously pulled off is limited by the number of available offline buffers. In turn, this limits the maximum number of positions a vehicle can shift forward relative to its position in the original sequence. The length of time a vehicle can remain off the line can also be limited by scheduling constraints, such as a time window within which a vehicle must be ready for shipment, or by process requirements, such as a maximum amount of time allowed between two successive operations, e.g., a vehicle must be painted within a few minutes of receiving a chemical pretreatment. In either case, this limits the number of positions a vehicle can shift backward relative to its position in the original sequence.

Example 2: Consider an aircraft sequencing problem, where a traffic controller must decide on a landing sequence for a set of airplanes waiting to land. The airplanes belong to different categories such as wide-body jets, medium-sized jets, and small airplanes. The time between consecutive landings must be greater than a minimum separation time that depends on the type of planes involved and the sequence in which they land. For example the separation time between the landing of a wide-body jet, which generates substantial turbulence, and a small commuter airplane is larger than the separation time between a wide-body jet and a medium-sized jet. In determining a landing sequence for a set of incoming airplanes, the air traffic controller typically attempts to minimize the total waiting time for all the airplanes without excessively delaying any individual one (Psaraftis, 1980; Beasley et al., 2000). In turn, this often translates into a constraint on the maximum number of positions an aircraft could be shifted either backward or forward relative to its initial arrival position (Psaraftis, 1980)

Example 3: Consider a vehicle routing problem where requests for distinct point-to-point transportation arrive dynamically. The dispatcher resequences these requests periodically to minimize the total distance traveled while adhering to a policy of not excessively delaying any individual request. For example, the dispatcher may be required to limit the number of slots a request could be moved up or down the waiting list.

These three distinct examples have several features in common. All three involve: (i) the rearranging of an initial sequence; (ii) the desire to minimize the sum of sequence-dependent costs; and (iii) constraints on the number of positions a job can shift forward (forward position-shifting constraints) or backward (backward position-shifting constraints) relative to its position in the original sequence. We refer to problems with these three features as resequencing problems with limited flexibility and sequence-dependent costs. Instances of this problem are numerous and arise in various settings in manufacturing, transportation, and service systems. However, despite its prevalence, the problem has received a relatively limited consideration in the literature.

The earliest paper to consider a resequencing problem with position-shifting constraints appears to be due to Dear (1976). He considers an aircraft sequencing problem with constraints on position shifting with a single parameter K, a maximum on the number of positions a job can shift either forward or backward. He does not offer a specific solution method but instead solves the problem via full enumeration. Psaraftis (1980) addresses a similar problem but in a more general setting, consisting of n job types and n _i (i = 1, …, n) jobs of each type. He proposes a dynamic programming algorithm that he shows to be linear in n _i but exponential in n.

Balas (1999) describes a class of constrained Traveling Salesman Problems (TSPs) that he shows to be solvable in linear time in the number of jobs. One of these problems corresponds to the one addressed by Psaraftis when n _i = 1. Lahmar et al. (2003) describe a resequencing problem motivated by the automotive industry with a single position-shifting constraint parameter, K, where K is the maximum number of positions a job can shift forward relative to its original position. They also solve for the resequencing problem via a decomposition heuristic.

Resequencing with constraints and sequence-dependent costs is also related to the bandwidth-limited TSP, in which the relative position of each pair of jobs in the final sequence is determined by the jobs' relative position in an initial sequence (Lawler et al., 1985) and the time-dependent TSP, in which the sequence-dependent costs also depend on the position of the jobs in the sequence (Picard and Queyranne, 1978). Other versions of the TSP that are related include the TSP with time windows, which can also be transformed into a TSP with job-dependent position windows (Balas and Simonetti, 2000).

In this paper, we consider a set of resequencing problems with two asymmetric position-shifting parameters, K ₁ and K ₂, that can assume any value in the range zero to n −1. We show that the problem can be solved using dynamic programming in a time that is polynomial in the number of jobs for fixed K ₁ and K ₂, and further specify the computational complexity for several special cases. We show how the same solution approach can be extended to problems where sequencing constraints are job specific and to problems where job features, which determine changeover costs, are jointly determined with the job sequence. We present an integer programming formulation of the problem, the linear programming relaxation of which can be used as a lower bound. We also provide an easy to compute upper bound and show how it can be used as the basis for a heuristic. We also describe a family of decomposition heuristics that are easy to customize to provide desired levels of solution quality and solution time. We provide computational results documenting the quality of the lower bound and the heuristic solution. We also present numerical results that support managerial insights regarding the value of resequencing flexibility. In particular, we show that the marginal benefit from resequencing flexibility is diminishing and that symmetric flexibility (K ₁ = K ₂ = k) is superior to asymmetric flexibility (K ₁ + K ₂ = 2k but K ₁ ≠ K ₂). More significantly, we show that forward and backward position shifting flexibility are complements with the value from higher K ₁ increasing in K ₂ and vice versa.

The organization of this paper is as follows. In Section 2, we formulate the problem, describe our solution procedure, and present several computational complexity results. We also describe extensions to the original problem to include job-dependent sequencing constraints and the joint allocation of job feature and job sequencing. In Section 3, we present the integer programming formulation and the corresponding linear programming relaxation. In Section 4, we describe the decomposition heuristic solution. In Section 5, we provide numerical results and discuss managerial insights. In Section 6, we apply our solution procedure to a real-world case from the automotive industry. In Section 7, we offer a summary and concluding comments.

2. Problem formulation and solution procedure

The resequencing problem with position-shifting constraints can be stated as follows. Given an initial ordering σ = (1,…, n) of n jobs, find a minimum-cost permutation π of σ, satisfying:

where π is defined as a one-to-one mapping from each job (denoted by its position in σ) to its position in the final ordering such that π(i) represents the position of job i in the final sequence, and K ₁, K ₂ are positive integers. The conditions in Equation (1) guarantee that the maximum number of positions a job could be shifted forward is K ₁ and the maximum number of positions a job could be shifted backward is K ₂. We refer to Equation (1-i) as the forward position-shifting constraint and Equation (1-ii) as the backward position-shifting constraint. Figure 1 and Figure 2 illustrate feasible and infeasible sequences for both forward and backward position-shifting constraints. The cost of each permutation is determined by the cost matrix c = [c _ij ], where c _ij is the cost if job i is immediately succeeded by job j.

Fig. 1 Feasible and infeasible (π(6)+K ₁ = 3+2 ≥ 6) forward position-shifting scenarios for n = 8 and K ₁ = 2.

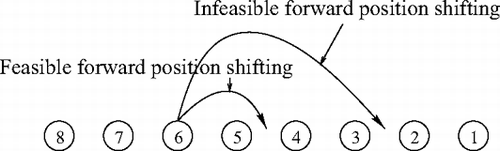
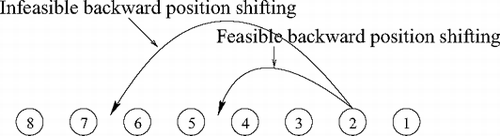
Fig. 2 Feasible and infeasible (π(2)−K ₂ = 7−3 ≤ 2) backward position-shifting scenarios for n = 8 and K ₂ = 3.

Our problem can be viewed as a TSP with side constraints. In fact, when K ₁ and K ₂ are both larger or equal to n−1, our problem reduces to the unconstrained TSP. In that case, constraints (1) become redundant and jobs can be ordered in any sequence that minimizes the total cost. On the other hand, when K ₁ or K ₂ = 0, resequencing is not allowed. Thus, in this paper, we focus on cases where at least one of the K _i parameters is in the range one to n−2. Special cases of interest include 0 < K ₁ < n−1 and K ₂ = n −1 for which forward shifting is unconstrained and 0 < K ₂ < n−1 and K ₁ = n −1 for which backward shifting is unconstrained.

Similar to the TSP, our problem can be defined on a graph G = (N,A) with arc costs c _ij for all arcs (i,j) ∈ A. Our objective is then to find a Hamiltonian cycle on G subject to constraints (1). In what follows, we take this graph-theoretic view. In particular, we let G′ = (N′,A′) be a multi-stage directed graph constructed from G with n+2 stages of nodes, one stage for each of the n positions in a tour with the dummy job 0 appearing at the beginning and end of the tour as source node s and sink node t in the graph. Every stage h includes a set of nodes corresponding to feasible partial ordering σ in which the first h jobs are fixed. Thus, the number of jobs sequenced in a certain stage corresponds to the stage itself.

We define (M,h,i) to be the node corresponding to the state where jobs in subset M ⊂ N (|M| = h−1 ∀ h) are assigned positions 1 through h−1 and job i assigned position h. For the unconstrained TSP, the cost of an optimal tour segment including subset M and job i in position h+1 can then be calculated recursively as follows:

The above Dynamic Programming (DP) formulation for sequencing problems is not new; see for example the classic paper by Held and Karp (1962) for similar formulations. Let B _h (M,i) = {j:j ∉ M ∪ {i}, h+1+K ₁ ≥ j} be the set of possible successor jobs to job i, at position h+1 such that conditions (1-i) are satisfied, and S(M,h,i) and P(M,h,i) to be the set of successor and predecessor nodes to node (M,h,i) respectively. Both sets of nodes can be defined as

Each node in stage h is linked to all nodes in its successor set at stage h+1 and all nodes in its predecessor set at stage h−1. Since M ∪ {i}∪ B _h (M,i) = {1,2, …, h+K ₁,h+K ₁+1}, it is sufficient to represent each node (M,h,i) in the auxiliary graph by the set {i,B _h (M,i)}. That is, once the exact set of candidate successor jobs is known, the set of visited jobs can be identified and vice versa. Also, each path between source node s and sink node t gives a feasible solution to the problem.

The DP cost recursion equation can hence be rewritten as

Before we show how a similar DP formulation can be used to solve the general version of the resequencing problem with constraints, we consider first the case of unconstrained backward shifting (0 < K ₁ < n−1 and K ₂ = n−1). Let us distinguish two types of stages in G′; stages of type I and type II. A stage h is called of type I when 0 < h ≤ n−K ₁ and of type II if h > n−K ₁. Then we can show the following result.

Lemma 1 For the resequencing problem with K ₁ < n−1, and K ₂ = n−1, the set S(M,h,i) of successor nodes to node (M,h,i) includes K ₁+1 nodes when h−1 is a stage of type I and n−h nodes when h−1 is a stage of type II.

Proof. For h+K ₁ ≤ n, M ∪ {i}∪ B _h (M,i) = {1,2, …, h+K ₁,h+K ₁+1}. Therefore, |B _h (M,i)| = K ₁+1. For h+K ₁ > n−1, M ∪ {i}∪ B _h (M,i) = {1,2, …, n} and |B _h (M,i)| = n−h. Since the number of nodes in stage h+1 that succeed node (M,h,i) corresponds to the number of jobs at position h+1 that could possibly succeed job i, then:

Lemma 1 implies that in all stages h such that h+1 ≤ n−K ₁, there are K ₁+1 arcs emanating from each node, while in all stages h such that h+1 > n−K ₁, there are n−h such arcs.

Proposition 1 The number of nodes at a stage h in the graph G′ is

Proof. Suppose that h is a stage of type I with nodes (M,h,i). The unordered set M is composed of h−1 jobs that are chosen from the first h−1+K ₁ jobs. Job i can be chosen from the set that includes the remaining K ₁ jobs and job h+K ₁. The product of both combinations gives:

If h is a stage of type II (h > n−K ₁) with nodes (M,h,i), the unordered set M is composed of h−1 jobs that are chosen from all n jobs (because h−1+K ₁ > n−1). Job i can be chosen from the set of remaining unassigned n−h+1 jobs. The product of both combinations gives.

We are now ready to state the main result for this section. The proof can be found in the Appendix.

Theorem 1. The above DP algorithm can solve for the resequencing problem with parameters 0 < K ₁ < n−1 and K ₂ = n−1 in polynomial time with respect to the number of jobs. The complexity of the algorithm increases exponentially with respect to K ₁. For the case of K ₁ = 1 and K ₂ = n−1, the computational complexity is of order O(n ²).

The result in Theorem 1 makes intuitive sense. We expect computational effort to be affected primarily by the sequencing flexibility that arises from higher values of K ₁. This is consistent with results observed in other contexts where sequencing flexibility is constrained. For example, Monma and Potts (1989) show that for batch scheduling problems with setup times, computational complexity increases exponentially in the number of batches but polynomially in the number of jobs.

The case of unconstrained forward shifting (K ₁ = n−1 and 0 < K ₂ < n−1) is identical to the previous one. Moreover, with a relabeling of the positions of the jobs in the original sequence from {1, 2, …, n} to {n, n−1, …, 1} and the parameters K ₁ into K ₂ (and vice versa), the “problem with unconstrained forward shifting” transforms into a “problem with unconstrained backward shifting”. In fact, as shown in the following lemma, this equivalence extends to problems with arbitrary values of K ₁ and K ₂.

Lemma 2. Consider a resequencing problem P with cost matrix [c _ij ] and parameters K ₁ = k ₁ and K ₂ = k ₂. Consider also problem with cost matrix [ _ij ] = c _{(n−j+1),(n−i+1)} and parameters K ₁ = k ₂ and K ₂ = k ₁. Given that problem P has initial sequence {1, 2, …, n} and has initial sequence {n, n−1, …, 1}, both problems are equivalent and result in the same optimal solution.

Proof. Let job i in problem P have final position π(i). Then, in problem , job i has initial position δ(i) = n+1−i and final position (δ(i)) = n+1−π(i). By definition of , we have:

or equivalently

which corresponds to the conditions (1) with K ₁ = k ₁ and K ₂ = k ₂.

Lemma 2 implies that problem P with constraints (1) and parameters K ₁ = k ₁ and K ₂ = k ₂ can be transformed into problem with parameters K ₁ = k ₂ and K ₂ = k ₁. Similarly, any problem with forward position-shifting constraints can be transformed into a problem with backward position-shifting constraints.

2.1. The constrained forward and backward position-shifting case

We refer to the case where 0 < K ₁ < n−1 and 0 < K ₂ < n−1 as the constrained forward and backward position-shifting case.

Theorem 2. The resequencing problem with parameters 0 < K ₁ < n−1 and 0 < K ₂ < n−1 can be solved in polynomial time with respect to the number of jobs.

Proof. The proof follows from the fact that the special cases described above are problems with larger state spaces and, therefore, computationally harder. The DP algorithm for these special cases can be adapted to solve the constrained case by, for example, assigning a dummy large cost to any arc incident to an infeasible node. Alternatively, we may eliminate at a preprocessing stage all infeasible states.

In the remainder of this section we show how these infeasible states can be identified and evaluate the impact of their elimination on the complexity of the problem.

Definition 1. A node (M,h+1,i) in stage h+1 is infeasible if it cannot be reached from any node (M\{i},h,i′) in stage h without violating the sequencing constraints π(i)−K ₂ ≤ i.

In view of the above definition, any set B _h (M,i) that contains job j such that j ∉ M ∪{i} and h+1−K ₂ > j is not considered. Hence, for some stages, all states are still feasible, whereas others have fewer states, and consequently, some paths through G′ become infeasible. Let G”(N”,A”) be the resulting graph after eliminating infeasible nodes from graph G′. Then, the following proposition allows us to calculate the total number of states in graph G”.

Proposition 2. For graph G”, the number of nodes V _h (K ₁,K ₂) is given by

Proof. Similar to G′ (where K ₂ = n−1 and 0 < K ₁ < n−1), G” is constructed such that condition π(i)+K ₁ ≥ i is always satisfied.

For cases (i) and (ii), h ≤ K ₂, the position of any job i in position h is π(i) ≤ K ₂ ≤ i+K ₂ which always satisfies condition (1-ii). Thus, the number of nodes in any stage h ≤ K ₂ of graph G′ is similar to that in stages of type I in G” for case (i) and to that in stages of type II for case (ii).

For case (iii), using Lemma 2, this case can be seen as the reverse of case (i). Thus, substituting K ₁ by K ₂ and h−1 by n−h gives the expression in (iii).

For case (iv), since each node (M,h,i) can be represented by the combination of job i and the set B _h (M,i), the total number of nodes can be obtained by first calculating the number of sets B _h (M,i). A job i at position h must belong to the set {h−K ₂, …,h+K ₁} which has cardinality K ₁+K ₂+1. The set of successor jobs B _h (M,i) contains K ₁+1 jobs among the set {h−K ₂+1, …,h+K ₁+1}. Let us distinguish between the following three cases: i = h−K ₂, i = h+K ₁, and h−K ₂ < i < h+K ₂. For i = h−K ₂, jobs h+K ₁ and h+K ₁+1 must belong to the set B _h (M,i) thus the total number of sets B _h (M,i) is equal to

For i = h+K ₁, job h+K ₁ cannot belong to the set B _h (M,i) while job h+K ₁+1 is always included. Thus, the total number of sets B _h (M,i) is equal to

For h−K ₂ < i < h+K ₂, jobs h+K ₁ and h+K ₁+1 must belong to the set B _h (M,i) thus the total number of sets B _h (M,i) is equal to

Summing all possibilities, we find

The results of Proposition 2 allow us to further characterize the complexity of two important special cases, 0 < K ₁ + K ₂ < n−1 and K ₁ = K ₂.

2.2. The case of 0 < K ₁ + K ₂ < n−1

In many practical applications, the parameters K ₁ and K ₂ are small relative to n – see the discussion in Section 5. Therefore, the case of 0 < K ₁+K ₂ < n−1 is of interest. Because in this case, more nodes are infeasible, it is also more tractable. The following theorem further specifies the complexity of this case (the proof is included in the Appendix).

Theorem 3. The resequencing problem with parameters K ₁ and K ₂, where K ₁+K ₂ < n−1 has a complexity of

2.3. The case of symmetric resequencing flexibility (K ₁ = K ₂)

In this section, we consider the case where both parameters K ₁ and K ₂ are equal (K ₁ = K ₂ = k) and 2k < n−1. This is the case treated by Balas (1999) and the complexity result we obtain here confirms Theorem 3 in Balas (1999). This symmetric case is of interest since it provides an upper bound on the computational complexity of related problems with asymmetric flexibility where K ₁ + K ₂ = 2k but K ₁ ≠ K ₂.

Theorem 4. The resequencing problem with K ₁ = K ₂ = k has complexity of order O(nk ^3/22^2k−1).

Proof. Using the bounds found for the asymmetric case, we have:

For the symmetric case, the above bound on the number of arcs in graph G” can be rewritten as

where the last inequality follows from Stirling's approximation. Thus, the complexity of the problem is of maximum order of O(nk ^3/22^2k−1).

Theorem 5. The resequencing problem with K ₁ and K ₂ has complexity of order O(n(K ₁+K ₂)^3/22^{(K ₁+K ₂−5/2)}).

Proof. Recall from the proof of Theorem 3 in the Appendix that:

Note that

Consider a positive integer k such that K ₁+K ₂ = 2k (a similar analysis applies if K ₁+K ₂ = 2k +1, we can then rewrite B1+B3 as

and since

and K ₁ K ₂ ≤ K ² we have

Substituting K ₁+K ₂ by 2k in B2, we get:

Summing all expressions, we have:

which is similar to the bound in Theorem 4. Substituting back (K ₁+K ₂)/2 for k, we can see that the complexity of a resequencing problem with K ₁ and K ₂ is bounded by a polynomial function of order of O(n(K ₁+K ₂)^3/22^{(K ₁+K ₂−5/2)}).

2.4. Resequencing with job-dependent constraints

We have so far considered resequencing problems with uniform position-shifting constraints. However, in certain applications, it may be necessary to assign different constraints to different jobs. For example, different jobs may have different priorities or different deadlines and may not tolerate the same amount of forward and backward shifting. Incorporating job-dependent constraints is not difficult. We replace the uniform constraints in Equation (1) by the following job-specific constraint for each job i:

The same DP approach can be adapted to solve the problem. First we construct the modified graph G” such that:

We then eliminate all nodes (M,h,i) in graph G” whose corresponding B _h (M,i) includes jobs that violate constraints (4). The complexity of such problems clearly depends on the specific constraint parameters of each job. However, the complexity is bounded by a function of the order of O(nm ²(max _i {K ₁(i)}+max _i {K ₂(i)})^3/22(max _i {K ₁(i)}+max _i {K ₂(i)}−5/2)).

2.5. The joint sequencing and feature assignment problem

In certain applications, the cost c _ij of switching from job i to job j is determined by the features assigned to jobs iand j. For example, in the automotive industry, depending on customer order preferences, each type of vehicle body can be painted with a variety of colors. To mitigate the impacts of cancellations and changeover costs, it is common to postpone the final assignment of paint colors to vehicle bodies until the painting stage. In this vehicle resequencing problem, changeover costs in the paint shop area are determined by the colors that have been assigned to the vehicles. Hence, it is desirable to jointly carry out the feature assignment and the resequencing of jobs to minimize the total changeover cost.

Let the matrix a = [a _il ] represent the set of feasible assignments of features to jobs, with a _il = 1 if vehicle i can be assigned feature l and a _il = 0 otherwise, with i = 1, 2, …, n and l = 1, 2, …, m. Also let the matrix c = [c _ll′] be a cost matrix, where c _ll′ represents the cost incurred if a job with feature l immediately follows a job with feature l′. Given an initial sequence of jobs, the joint feature assignment and resequencing problem seeks to simultaneously determine: (i) an assignment of features to jobs; and (ii) a final sequence of jobs subject to forward and backward position-shifting constraints and to feature assignment feasibility.

The approach used to solve the resequencing problem can be extended to solve the joint feature assignment and resequencing problem. In particular, let G ⁽³⁾ denote a graph composed of nodes (M,h,i,l) representing the jobs assigned to positions 1 through h−1, the job i at position h, and the feature l assigned to job i. To model feature assignment, each node in the previous graph G” is duplicated into a maximum of m nodes (nodes that correspond to jobs with an infeasible feature are deleted). The maximum number of nodes in any stage h is the product of m and the corresponding number of nodes at stage h in G”. The arcs connecting the nodes of jobs that can be sequenced in consecutive positions will have a cost representing the cost of switching between the assigned features. Clearly, the number of arcs in G ⁽³⁾ is bounded by the number of arcs in G” multiplied by m ² (the maximum number of arcs between each consecutive job couple). Thus, the complexity of the joint problem is still polynomial in the number of jobs. These results are summarized below.

Theorem 6. The complexity of the joint feature assignment and resequencing problem with m features, n jobs, and constraint parameters K ₁ and K ₂ is polynomial in n and m. For K ₁+K ₂ < n−1, complexity is of order O(nm ²(K ₁+K ₂)^3/22^{(K ₁+K ₂−5/2)}).

Note that for a fixed sequence, the feature assignment problem can be formulated as a shortest path problem in a staged directed network and can be solved via DP using an algorithm of complexity of order O(nm ²). This of course coincides with the complexity specified in Theorem 4 with parameters K ₁ = K ₂ = 0 (|Ω(0,0)| ≤ nm ²).

3. An integer programming formulation

In this section, we present an Integer Programming (IP) formulation to the resequencing problem. The IP formulation yields via its Linear Programming (LP) relaxation an easy to compute lower bound. This lower bound can be useful in benchmarking heuristic solutions when the optimal cost is too expensive to compute (see Section 4). The lower bound can also be useful in alternative exact solution procedures, such as branch and bound. For practitioners, having an IP formulation is desirable since it allows the direct use of a general purpose commercial IP solver and can also provide more flexibility in including additional constraints.

The resequencing problem with constraint parameters K ₁ and K ₂ can be formulated as an IP as follows.

subject to

The decision variables y _ijh take a value of one when job i is assigned position h and job j is assigned position h+1 and zero otherwise. The objective function (5) represents the total changeover cost incurred by the job sequence. Constraints (6) and (7) ensure that dummy job 0 is assigned position 0 and that the succeeding job is at position 1. Constraints (8) ensure that there is a unique cycle of jobs and that there is a successor and a predecessor for each job. Constraints (9) ensure that the last job is succeeded by dummy job n+1 and is assigned position n. Constraints (10) guarantee that only one job is assigned to each position in the sequence and that each position has only one job assigned to it. Constraints (11) guarantee that the resequencing constraints are satisfied, while constraints (12) ensure the integrality of the assignment variables.

The LP relaxation of the above problem provides a lower bound on the optimal cost. This lower bound can be further tightened by introducing the following additional constraints (a valid cut):

An IP formulation can also be obtained for the joint resequencing and feature assignment problem described in Section 3. Let variables x _ilh take a value of one if job i is assigned feature l (among a maximum of m features) and position h and zero otherwise. We redefine variables y _ijh as follows. Consider variables y _ll'h that take a value of one if a switchover cost from feature l to l′ is incurred at position h and zero otherwise. Then, the joint resequencing and feature assignment problem can be formulated as follows:

subject to

where a _il is a parameter defined as

Constraints (15) and (16) ensure that for each job, only a single position is assigned and that each position is assigned to a single job. Constraints (17) ensure that dummy job 0 is assigned position 0 and dummy feature 0. Constraints (18) and constraints (19) ensure that a switchover cost from feature l to l′ is incurred at position h only if the job at that position h has feature l′ and the job at position h+1 has feature l. Constraints (20) guarantee that conditions (1) are met, while constraints (21) ensure that only feasible features are assigned.

4. A heuristic procedure

Although the resequencing problem can be solved exactly in polynomial time with respect to n, the complexity of the algorithm is exponential in K ₁ and K ₂. Therefore, when K ₁ or K ₂ is large, there can be a need for a heuristic procedure that identifies good feasible solutions quickly. This is particularly the case in settings where resequencing must be done in real time. A heuristic solution also provides an upper bound on the optimal solution, which along with the lower bound from the LP relaxation of the IP formulation can serve as the basis for a branch-and-bound algorithm.

In this section, we describe a family of heuristics that can be easily customized to yield solutions within desired ranges of solution time and solution quality. The heuristics take advantage of the fact that an optimal solution to a resequencing problem with parameters K ₁ = k ₁′ and K ₂ = k ₂′ is feasible to a resequencing problem with parameters K ₁ = k ₁ and K ₂ = k ₂ when k ₁′ ≤ k ₁ and k ₂′ ≤ k ₂, a result that follows from the fact that smaller values of K ₁ and K ₂ correspond to more constrained versions of the problem. Hence, solving a problem with smaller values for K ₁ and K ₂ provides a heuristic solution to a problem with larger values for the same parameters. The heuristics also take advantage of the fact that, under suitable conditions, solving iteratively a series of problems with smaller values for K ₁ and K ₂, such that the optimal solution of one problem serves as the starting sequence to the next one, also leads to a solution feasible for a problem with larger values of K ₁ and K ₂. In the following proposition, we describe conditions under which the result holds.

Proposition 3. The solution to a series of b resequencing problems with parameters (K ₁,K ₂) = (k _1,1, k _2,1), (k _1,2,k _2,2),…, and (k _1,b ,k _2,b ), such that the starting sequence to the jth problem (with parameters (k _1,j ,k _2,j )) is the optimal solution to the (j−1)th problem, is feasible to a resequencing problem with parameters K ₁ and K ₂ if ∑ _{j = 1} ^b k _1,j ≤ K ₁ and ∑ _{j = 1} ^b k _2,j ≤ K ₂.

Proof. Let π^(j)(i) denote the position of job i after the jth iteration so that π^(j)(i) = π^(j)(π^(j−1)(i)). Any solution to the first iteration satisfies the condition i−K ₁ ≤ i−k _1,1 ≤ π⁽¹⁾(i) ≤ i+k _2,1 ≤ i+K ₂. Any solution to the second iteration satisfies π⁽¹⁾(i)−k _2,1 ≤ π⁽²⁾(i) ≤ π⁽¹⁾(i)+k _2,2. However, since i−K ₁ ≤ i−k _1,1−k _1,2 ≤ π⁽¹⁾(i) − k _1,2 and π⁽¹⁾(i)+ k _2,2 ≤ i+k _2,1+k _2,2 ≤ i+K ₂, we have i−K ₁ ≤ π⁽²⁾(i) ≤ i+K ₂. In a similar fashion, we can show by induction that the solution after the jth iteration satisfies i−K ₁ ≤ i−∑ _{l = 1} ^j k _1,l ≤ π^(j)(i) ≤ i+∑ _{l = 1} ^j k _2,l ≤ i+K ₂. Therefore, the solution obtained after the bth iteration is feasible for the resequencing problem with parameters K ₁ and K ₂.

Proposition 3 characterizes a family of heuristics that yield feasible solutions to a resequencing problem with parameters (K ₁, K ₂), with solution quality and time depending on the choice of b, the number of subproblems that are iteratively solved, and the parameters (k _1,j , k _2,j ) of the subproblem solved in each iteration j. For example, choosing b = 1, k _1,1 = K ₁ and k _2,2 = K ₂ corresponds to solving the original problem exactly and without decomposition. On the other hand, setting b = min (K ₁, K ₂) and (k _1,j = k _2,j ) = 1 corresponds to solving b subproblems where forward and backward position shifting are each limited to one in each iteration. The former yields superior solution quality while the latter is computationally easier to solve – computational time is linear in b and n. Between these two extreme cases, there is a wide range of choices for b and (k _1,j ,k _2,j ). In general, given that solution time is linear in the number of iterations but exponential in the constraint parameters at each iteration, it is computationally easier to solve many subproblems with small values for the constraint parameters than a few subproblems with large values for the constraints parameters.

In the numerical results we report in Section 5, we restrict ourselves to the class of heuristics with only two parameters b and k such as that K ₁ = bk + r ₁ and K ₂ = bk + r ₂, where b, k, r ₁ and r ₂ are positive integers with r ₁ < k and r ₂ < k. We then solve iteratively a series of b resequencing problems with parameters (k, k) followed by a problem with parameters (r ₁, r ₂). This simple parametrization allows one to easily increase the accuracy or decrease solution time by only manipulating k and b.

The solution obtained from these heuristics can be improved by noting that position-shifting constraints could be applied independently to each job (see Section 3). This is important since in the solution different jobs would have shifted a different number of positions in either direction. Applying a uniform constraint parameter to all jobs may no longer be feasible. Therefore, for each job i with position π_H(i) in the heuristic solution, we can associate a job specific constraint parameter K ₁(i) such that K ₁(i) ≤ k ₁−i+π_H(i) and K ₂(i) ≤ k ₂+i−π_H(i). We can then solve the resequencing problem with these job-dependent constraint parameters. The solution time and quality would of course depend on our choice of K ₁(i) and K ₂(i), with larger values increasing the solution time but leading to a higher solution quality. Setting the parameters K ₁(i) = min {k−i+π_H(i),k} and K ₂(i) = min {k+i−π_H(i),k} guarantees that the computational complexity of each iteration does not exceed that of the decomposition procedure iteration. In Section 5, we provide numerical results that illustrate the benefits from this procedure. In the following proposition, we formally show that solving the resequencing problem with job-dependent constraints yields solutions that are feasible to the original problem.

Proposition 4. Consider problem P with initial ordering σ = (1,2, …,n) and constraint parameters K ₁ and K ₂. Consider also problem P _H with initial ordering σ _H feasible in P given by mapping π _H of σ and constraint parameters K ₁(i) = k ₁−i+π _H (i) and K ₂(i) = k ₂+i−π _H (i). Then, any solution feasible in P _H is also feasible in P.

proof. Let π′ be a mapping of σ_H that gives a feasible permutation in P _H. Then π_H(i) − K ₁(i) ≤ π′(i) ≤ π_H(i) + K ₂(i). Substituting the value of K ₁(i) and K ₂(i) leads to π_H(i)−[k ₁−i+π_H(i)] ≤ π′(i) ≤ π_H(i)+[k ₂+i−π_H(i)], which simplifies as i−k ₁ ≤ π′(i) ≤ i+k ₂. Therefore, any feasible solution in P _H is also feasible in P.

5. Numerical Study

The objective of this numerical study is to investigate: (i) the effect of the parameters K ₁ and K ₂ on the optimal solution; (ii) the quality of the lower bounds obtained from the LP relaxation; and (iii) the quality of the solution obtained from the decomposition heuristic.

5.1. The value of resequencing flexibility

In many applications, the amount of resequencing flexibility that can be afforded is limited. For example, in the vehicle resequencing problem, flexibility is achieved by investing in expensive “pull-off tables” used to pull a vehicle from a moving assembly line, temporarily store it, and then later insert it back into the line. In the aircraft scheduling problem, various rules prevent air traffic controllers from excessively delaying an aircraft or letting it jump too far ahead of others. Increased flexibility also carries a computational cost. Problems with less-restrictive resequencing constraints are harder to solve. Hence, there can be both an economic and computational need to limit the amount of resequencing flexibility. The question that then arises is how much performance is foregone by limiting this flexibility. Also, if only a limited amount of flexibility can be afforded, how should it be distributed among forward and backward position shifting.

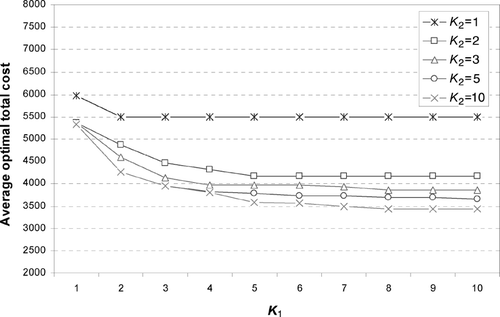
In this section we shed some light on the above two questions. In particular, we examine the effect of increasing either K ₁ or K ₂ on the optimal cost. We also examine the effect of choosing K ₁ and K ₂ when K ₁ + K ₂ = 2k, where k is a fixed constant. To this end, we carried out a series of numerical experiments with varying cost structures, varying the number of jobs, and varying the values of K ₁ and K ₂. Representative results are shown in Fig. 3 for a system with n = 30 and changeover costs randomly drawn from three different uniform distributions, U(0,500), U(100,400) and U(200,300). The results are shown for K ₂ = n−1 and K ₁ ranging from one to n−1, with K ₁ = n−1 representing the case of full flexibility. Figure 3 shows the percentage cost difference between the optimal costs for K ₁ = k ₁ and K ₁ = n−1. This percentage measures the amount of performance foregone by not having full flexibility.

Fig. 3. Percentage difference between the optimal cost for a problem with limited flexibility, K ₁ < n−1, and K ₂ = n−1, and the one for a problem with full flexibility, K ₁ = K ₂ = n−1 (percentage difference is defined as γ = 100×(|z*_{(K 1 = k 1,K 2 = n−1)}− z*_{(K 1 = n−1,K 2 = n−1)}|/(z*_{(K 1 = 1,K 2 = n−1)}−z*_{(K 1 = n−1,K 1 = n−1)}))).

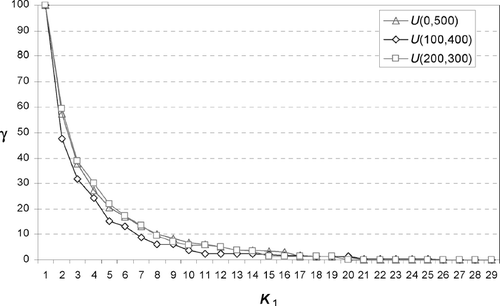
The results show that the effect of flexibility diminishes rapidly with most of the benefits of full flexibility achieved with relatively modest levels of flexibility. For instance, a 40 to 50% drop in total cost is observed when K ₁ is increased from one to two. The decrease is less than 20% when we increase K ₁ from two to three. The decrease is even smaller for additional increases in K ₁. Hence, the results suggest that when flexibility is expensive, a small amount of flexibility would be optimal and rarely would full flexibility be justified.

To examine the effect of flexibility allocation, we compare different scenarios where the total amount of flexibility is fixed, that is K ₁ + K ₂ = 2k, where k is constant and then vary the values of K ₁ and K ₂. Figure 4 shows the percentage difference in the optimal costs between each allocation and the symmetric allocation corresponding to K ₁ = K ₂ = k. The changeover costs are drawn randomly from a uniform distribution U(100, 400). As we can see, symmetric allocations are generally more desirable than less symmetric ones, especially when the overall flexibility is limited. This does make intuitive sense since both forward and backward flexibility exhibit diminishing returns.

Fig. 4 Average percentage difference between the optimal costs of problems with (K ₁ = K ₂ = k) and problems with (K ₁ = k±δ,K ₂ = k∓δ) for δ ∈ {−4, …,0,…,4} and k = 1,…,10 for five problem instances with n = 30 and a cost matrix with U(100,400) (percentage difference defined as γ′ = 100×(|z*_(k,k)−z*_{(k±δ,k∓δ)}|/z*_(k,k))).

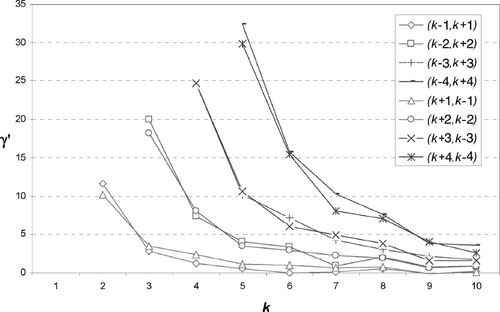
We also examine the effect of varying one type of flexibility while keeping the other one constant. For example, in Fig. 5 we show results where we vary K ₁ for different levels of K ₂. The results suggest that K ₁ and K ₂ are complements, with the benefit from higher K ₁ greater when K ₂ is larger. For each value of K ₂, increasing K ₁ far beyond K ₂ tends to yield relatively little benefit. These results suggest that increasing one type of flexibility when the other is limited is generally not very helpful.

Fig. 5 Combined effect of K ₁ and K ₂ on the average optimal total cost for five problem instances with n = 30 and a cost matrix with U(100,400).

5.2. The quality of the heuristic solution

To illustrate the quality of the solution obtained from the heuristic, we generated several hundred sample problems with varying cost structures, values of K ₁ and K ₂, and number of jobs. Representative results are shown in Fig. 6, Fig. 7, Fig. 8, Fig. 9. The examples shown are for a system with n = 30, K ₁ = 1, …, 29, and K ₂ = n−1. The performance of the heuristic is reported for values of k = 1, 2, 5, and 10. For each pair K ₁ and k we solve a series of b subproblems such that k = ⌊ K ₁/b ⌋ followed by a subproblem with parameter K ₁−bk (if K ₁≠ bk). We then apply the improvement heuristic to the resulting sequence. For each value of K ₁, we also solve the problem optimally and obtain the percentage cost difference between the heuristic and the optimal solution.

Fig. 6 Average percentage difference between the optimal cost and the heuristic solution cost for five problem instances with n = 30 and a cost matrix with U(200,300).

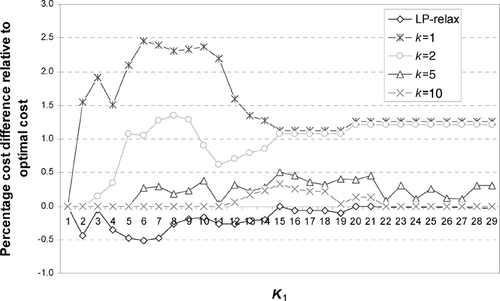
Fig. 7 Average percentage difference between the optimal cost and the heuristic solution cost for five problem instances with n = 30 for a cost matrix with U(100,400).

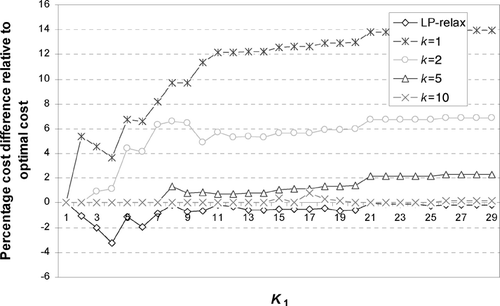
Fig. 8 Average percentage difference between the optimal cost and the heuristic solution cost for ten problem instances with n = 30 for a cost matrix with |i−j|× U(10,40).

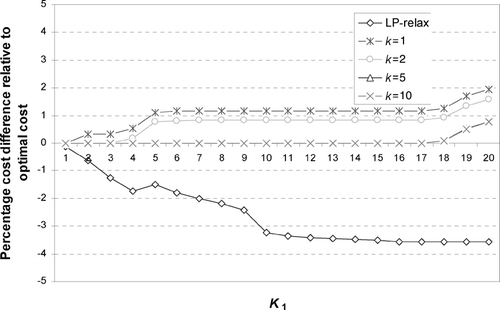
Fig. 9 Average percentage difference between optimal cost and heuristic solution cost for ten problem instances with n = 30 for a cost matrix with (30−|i−j|)× U(10,40).

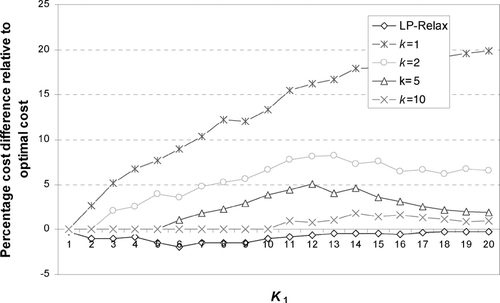
We considered scenarios with different cost structures. In the scenarios shown in Fig. 6 and Fig. 7, we generated the elements of the cost matrix randomly using uniform distributions U(200, 300) and U(100, 400) to reflect cost structures with different levels of variability. As it can be seen, the quality of the heuristic solution is generally encouraging. For example, for K ₁ = 10 and k = 2, the percentage difference between the heuristic cost and the optimal cost is less than 0.5 for U(200, 300) and less than 6% for U(100, 400). As it might be expected, the performance of the heuristic does deteriorate with higher variability in changeover costs. For instance, for the U(100, 400) case, the differences between the heuristic cost and the optimal cost are as high as 14% for k = 1. The impact of higher variability can be mitigated by increasing k. For example, increasing k from one to two reduces the maximum percentage difference from 14% to less than 7%. Sample results that compare the optimal solution, the decomposition heuristic solution, and the heuristic improvement solution are shown in Table 1. As we can see, the impact of the improvement heuristic is relatively limited. In general, applying the decomposition heuristic alone tends to be sufficient.

Table 1 Percentage difference ((Opt Sol.− LP-relax) × 100/LP-relax) between the optimal cost, the heuristic solution cost and the improvement heuristic solution cost (n = 30, K ₁ = 4, K ₂ = 29, U(100, 400)).

		Decomposition heuristic		Improvement heuristic
K 1	Optimal solution	Solution	Percentage difference (%)	Solution	Percentage difference (%)
1	5339	5339	0.00	5339	0.00
2	4260	4260	0.00	4260	0.00
3	3935	3935	0.00	3935	0.00
4	3779	3779	0.00	3779	0.00
5	3589	3704	3.20	3616	0.75
6	3549	3590	1.16	3587	1.07
7	3457	3560	2.98	3560	2.98
8	3404	3457	1.56	3449	1.32
9	3404	3457	1.56	3431	0.79
10	3355	3447	2.74	3416	1.82
11	3329	3397	2.04	3383	1.62
12	3329	3397	2.04	3352	0.69
13	3327	3397	2.10	3352	0.75
14	3327	3397	2.10	3352	0.75
15	3317	3397	2.41	3352	1.06
16	3315	3352	1.12	3352	1.12

In the scenarios shown in Fig. 8 and Fig. 9, we generated the changeover costs such that there is correlation, either positive or negative, between the initial positions of jobs and the changeover costs between these jobs. To induce positive correlation, we generated changeover costs between jobs that have positions i and j in the initial sequence according to the formula c _ij = |i−j|X where X is generated randomly from a uniform distribution U(10, 40). In this case, jobs that are located in neighboring positions in the original sequence tend to have small corresponding changeover costs. To induce negative correlation, we generated changeover costs between jobs that have positions i and j in the initial sequence according to the formula c _ij = (n−|i−j|)X where X is generated again randomly from a uniform distribution U(10, 40). In this case, jobs that are located in neighboring positions in the original sequence tend to have large corresponding changeover costs. The numerical results show that the heuristic performs significantly better in the first case (see Fig. 8 and Fig. 9). For instance, in the first case, the difference between the heuristic and the optimal solution does not exceed 2% and the heuristic reaches optimality for many problem instances; while for the second case there can be a significant difference between the heuristic cost and the optimal cost. This result is mainly due to the local search nature of the heuristic. Since low costs between closely positioned jobs make it undesirable to move jobs too far from their original position, the heuristic is capable of identifying efficient solutions quickly even for small values of k.

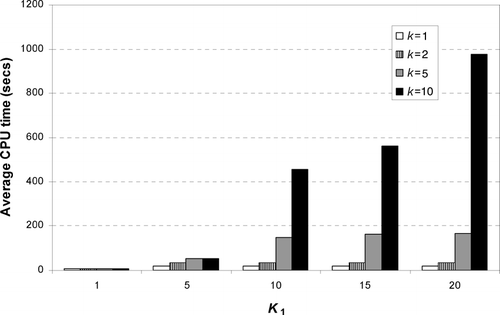
All the computational results show that solving problems with larger values of k and smaller values of b is generally preferable to larger values of b and smaller values of k. Of course the latter involves a larger local search space and is therefore computationally more expensive. Figure 10 illustrates how computational effort increases with k for different values of K ₁. For example, for problem instances with K ₁ = 20, the average CPU time for the heuristic increases from 165 seconds for k = 5 to 975 seconds for k = 10. This increase in CPU time is accompanied with an improvement, albeit more modest, in the solution quality (see Fig. 8). Hence, within the family of heuristics defined by k and b, there is a quality-computational effort tradeoff.

Fig. 10 Comparison of average CPU time for different values of k for five problem instances with n = 30 for a cost matrix with |i−j|× U(10,40).

5.3. The quality of the lower bound

We tested the quality of the lower bound obtained from the LP relaxation using the same data used to test the quality of the heuristic. Sample results are shown in Fig. 6, Fig. 7, Fig. 8, Fig. 9. We also tested the effectiveness of the additional valid constraints in tightening the lower bound (See Table 2). The lower bound from the LP relaxation with and without the valid cut is tight. The additional constraints do help in further tightening this lower bound.

Table 2 Percentage difference ((Opt Sol.− LP-relax) × 100/LP-relax) between optimal solution and linear programming relaxation solution with and without the valid inequality (n = 30, U(0, 500))

		LP relaxation		LP relaxation with valid inequality
K 1	Optimal solution	Solution	Percentage difference (%)	Solution	Percentage difference(%)
1	4005	4005.00	0.00	4005.00	0.00
2	2607	2580.29	1.03	2505.85	4.04
3	1966	1901.53	3.39	1845.64	6.52
4	1619	1528.30	5.93	1475.92	9.69
5	1393	1321.38	5.42	1277.52	9.04
6	1278	1169.67	9.26	1156.21	10.53
7	1151	1076.13	6.96	1065.47	8.03
8	1053	1012.78	3.97	1000.17	5.28
9	1001	949.25	5.45	938.01	6.72
10	947	902.00	4.99	892.63	6.09
11	919	866.58	6.05	855.89	7.37
12	889	833.36	6.68	827.22	7.47
13	844	807.77	4.49	804.41	4.92
14	844	778.49	8.41	777.06	8.61
15	827	763.77	8.28	761.64	8.58
16	824	749.49	9.94	748.43	10.10
17	767	735.78	4.24	735.78	4.24
18	767	728.24	5.32	727.78	5.39
19	767	719.35	6.62	719.35	6.62
20	759	715.67	6.05	715.61	6.06
21	726	713.33	1.78	713.33	1.78
22	726	704.83	3.00	704.83	3.00
23	726	704.35	3.07	703.98	3.13
24	726	704.20	3.10	703.88	3.14
25	726	704.20	3.10	703.88	3.14
26	726	704.20	3.10	703.88	3.14
27	721	701.92	2.72	701.61	2.76
28	721	701.92	2.72	701.61	2.76
29	721	701.92	2.72	701.56	2.77

6. An example application

In this section, we present results obtained by applying our solution approach to a real-world example using actual data obtained from the Ford Motor Company. The problem we consider is the one described in Section 1 (example 1). The problem consists of resequencing vehicles in an automated assembly line once they emerge from the body shop and prior to entering the paint shop. Vehicles can be resequenced using pull-off buffers that can temporarily pull a vehicle from the line and then reinsert it at a later time. This resequencing flexibility is limited by the number of pull-off tables and by the allowable time a vehicle can remain pulled from the line. Because pull-off tables are expensive to implement and operate, only a few are usually available.

In the paint area, vehicles undergo a series of painting operations. If two consecutive vehicles are painted different colors, a significant changeover cost is incurred since the current paint must be flushed out and disposed of, and paint nozzles must be thoroughly washed and cleaned with solvents. The changeover cost is primarily determined by the volume of paint that must be purged from an intermediate pipe that connects the paint nozzle to the paint tanks. Although the volume of paint that is purged is always the same (approximately 1 gallon), the cost of different paints can vary widely. In the plant we observed, color costs range from $27 per gallon (basic black) to $122 per gallon (bright amber); see Table 3. This makes it desirable to form large blocks of the expensive colors while possibly incurring the cost of more frequent color changeovers of the cheaper ones. Note that the cost of changing colors is not sequence dependent (e.g., the cost of going from darker to lighter colors is not more expensive than going from lighter to darker colors). New paint technology has recently removed this dependency. The flexibility in what color a particular vehicle can be painted is determined by current demand requirement and available vehicle body type. Therefore, the set of feasible colors (features) for two consecutive vehicles can vary significantly.

Table 3 Cost per gallon for different paint colors

Color	Price ($/gallon)
Ebony	26.94
Oxford white	33.06
Med platinium	39.64
Wedge blue	51.75
Harvest gold	60.94
Bright atlantic	66.60
Amazon green	73.04
Toreader red	75.36
Vermilion	77.83
Jalapeno green	95.46
Bright amber	121.92

Although a typical plant may produce several hundred vehicles per day, only a small block of vehicles (15 in one of the plants we observed) are considered for resequencing at a time. This is due to the difficulty in predicting too far in advance the input sequence to the paint area. This means that resequencing and color assignment have to be carried out successively for one block of vehicles at a time. Each block is associated with a color-assignment matrix that indicates the set of feasible colors for each vehicle in the block. The color-assignment matrix usually reflects the current product mix (i.e., current demand for combinations of body style and color). Since any feasible color could theoretically be selected during the painting process, this may create imbalances in the product mix. However, these imbalances are short lived, since they are taken into account when updating the color-assignment matrix for subsequent blocks. In other words, an overproduction of a particular “body style/color” combination will eliminate this combination from consideration in future periods. Since the plant produces several hundred vehicles per day and each body style/color combination has a demand significantly greater than the number of vehicles in one block, the mix of colors produced is generally balanced with the demand for these colors at the end of the day.

Clearly, the problem is an example of the joint resequencing and feature assignment problem we discussed in Section 2.5. Using production and cost data collected from Ford, we applied our DP approach to obtain the optimal solution and the optimal cost. A goal of this numerical study is to examine the benefit of having one or more pull-off tables in the paint shop area. This is important since the investment cost of each pull-off table can be significant (in the order of several hundred thousand dollars). Pull-off tables are not used in some plants because the resulting savings are not believed to be sufficient to justify their cost.

Our computational results are shown in Fig. 11 and Fig. 12. The data tested cover 13 days worth of production of over 8000 vehicles. Table 4 shows the number of vehicles produced in each day. The data collected specifies the sequence of vehicles as they leave the body shop area and the set of feasible paint colors associated with each vehicle at that time. In Fig. 11, we show results where we solve a joint resequencing and color assignment problem involving the total number of vehicles for each day. The block of vehicles considered for resequencing consists of the entire set of vehicles from that day (in Fig. 12, we examine the impact of using smaller and uniform block sizes). Figure 11 shows the percentage decrease in total cost relative to a system with no resequencing but where colors are assigned optimally (i.e., we solve only for the feature assignment problem by setting K ₁ = K ₂ = 0). Results are provided for four different levels of K ₁ and K ₂, where in our setting K ₁ represents the number of pull-off tables and K ₂ the maximum time a vehicle can remain pulled (in a paced assembly line, this corresponds to the maximum number of equally spaced vehicles that are allowed to pass the pulled vehicle). As we can see, depending on K ₂, the cost savings can be significant even with a single pull-off table. For example, for K ₁ = 1 and K ₂ = 4, the cost saving is in excess of 34%. Assuming that approximately a gallon of paint is flushed with each changeover, this translates into a saving of approximately $1100 000 per year per paint line. Consistent with our results in previous sections, the value of flexibility exhibits diminishing returns with most of the cost reduction achieved with only one or two pull-off tables.

Fig. 11 Impact of resequencing flexibility on the total cost (average percentage for 13 production days).

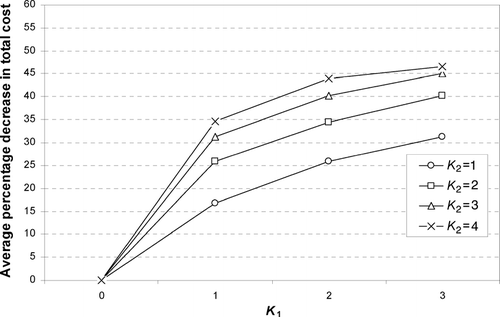
Table 4 Daily production requirements for a 13-day period sample

	Day
	1	2	3	4	5	6	7	8	9	10	11	12	13
Number of vehicles (n)	204	884	837	696	770	852	832	826	142	734	803	687	116

Fig. 12 Impact of the block size on the total cost for K ₁ = 2 (average cost for 13 production days).

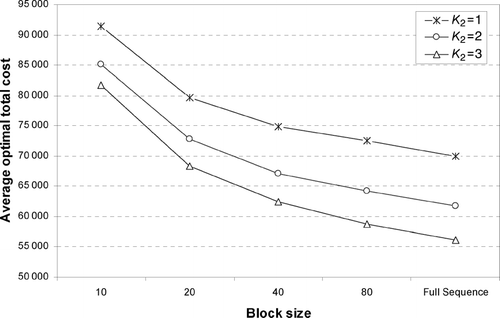
In Fig. 12, we compare the impact of the size of the block of vehicles which are considered for resequencing at a time. Specifically, we divide the original sequence of vehicles for each day into a sequence of uniform blocks ranging from ten to 80 each. We then solve a series of joint resequencing and color assignment problems for each block separately (in doing so, we keep track of the last color used by each block since it determines the changeover cost for the block that follows it). We also obtain the optimal cost for the extreme case of a single block consisting of all vehicles in 1 day, which provides us with a benchmark against which smaller block sizes can be compared. Figure 12 shows the cumulative total cost for the 13 production days for different block sizes, including a block size (indicated by “full sequence” in the graph) that corresponds to the full production sequence in each day. As we can see, there is a significant improvement in going from a block of size ten to one of 20. However, there is relatively little additional cost reduction with further increases in the block size. This seems to support the current practice where block sizes tend to be relatively small in most plants.

The results from Fig. 11 and Fig. 12 are good news for automotive companies, such as Ford. The benefits of resequencing flexibility may be possible to realize relatively cheaply, with a limited investment in pull-off tables, and by considering only small blocks of vehicles at a time. The ability to consider only small sequences of vehicles at a time is particularly important since resequencing decisions are carried out in real time, with a short window for deciding for each incoming block which vehicle should be pulled and what colors the vehicles should be painted.

7. Conclusions

In this paper, we have addressed the problem of resequencing a set of prearranged jobs when there is limited flexibility on the number of positions a job can move forward or backward relative to its original position. We showed how the problem can be effectively solved using DP. In particular, we showed that the computational complexity is linear in the number of jobs for problems with forward and backward position-shifting constraints and polynomial for problems with only one type of constraint. However, the complexity of the algorithm increases exponentially in the constraint parameters. We discussed two important extensions of the model to include: (i) job-dependent sequencing constraints; and (ii) the joint determination of job features and job sequences. We showed how these problems can be formulated as integer programs, whose LP relaxations offer useful lower bounds. We introduced a family of heuristics that are easy to customize to yield desired levels of solution quality and solution time. We also provided numerical results to document the quality of the lower bound and the heuristic solution. We used numerical results to reveal that the value of flexibility is of a diminishing kind with most of the benefits realized with relatively little flexibility. We found that symmetric flexibility (equal forward and backward position shifting flexibility) is generally more desirable than asymmetric flexibility. More importantly, we showed that forward and backward flexibility are complements with the benefits derived from one increasing in the amount of the other. We also applied our solution approach to a real-world case where the resequencing and feature assignment problems are solved simultaneously.

There are several promising avenues for future research. In many applications, higher sequencing flexibility requires additional investments in hardware or software. It would be useful to let the parameters K ₁ and K ₂ be decision variables and to explicitly include the costs of K ₁ and K ₂ in the objective function. Also, in many applications, the performance criterion may be other than the reduction of changeover costs. For example, we may wish to minimize delay-related measures such as flow time, lateness, or tardiness. It would be valuable to see the extent to which the results of this paper can be adapted to problems with different objective functions.

Appendix

Proof of Theorem 1. The DP algorithm corresponds to finding a shortest s−t path in graph G′. Its complexity is equal to the number of feasible arcs. Using Proposition 1, it is easy to calculate the number of all arcs in G′, denoted |Ω(K ₁,K ₂)| where in our case K ₂ = n−1, as the product of the number of nodes and the associated number of their outgoing arcs as follows:

where A1 is the number of arcs between stages 1 and n−K ₁ of type I, A2 is the number of arcs between the last stage of type I (n−K ₁) and the first stage of type II (n−K ₁+1), and A3 is the sum of arcs between stages n−K ₁+1 and n−1 of type II. Substituting K ₁ by one in the above expression, the number of arcs |Ω(1,n−1)| = 2(n−1)² which implies that the problem is of the order O(n ²). To show that the complexity of the problem increases exponentially with K ₁, we develop upper and lower bounds on the number of arcs in graph G′. A1 can be rewritten as

where the second equality follows from the fact that

Using the fact that

where e = exp (1), then A1 can be bounded as follows:

To complete the proof, we provide upper bounds for A3:

which can be rewritten as

Summing the upper bounds on all expressions leads to

This proves that |Ω(K ₁,n−1)| can be bounded by a function that increases polynomially with the number of jobs n, but exponentially with parameter K ₁.

Proof of Theorem 3. We distinguish between different types of stages h in G ⁽³⁾: (i) h < K ₂; (ii) h > n−K ₁; and (iii) K ₂ ≤ h ≤ n−K ₁.

For h < K ₂, similar to graph G”, the number of arcs that emanate from each node is K ₁+1. Similarly, for h > n−K ₁, the number of arcs that emanate from each node is K ₂+1. For K ₂ ≤ h ≤ n−K ₁, the number of nodes is the same in each stage. Given that the maximum number of arcs that emanate from each node in each stage is K ₁+1 and the maximum number of arcs that are incident to each is K ₂+1, the maximum number of arcs between two consecutive stages is bounded by min (K ₁,K ₂)+1.

An upper bound on the total number of arcs can be found as follows:

The term B1 can be rewritten as follows:

and therefore an upper bound on B1 can be written as

Similarly, an upper bound on the term B3 is given by

Also, an upper bound on B2 is given by

Summing all expressions, we obtain:

Hence, the problem has a complexity of

Biographies

Maher Lahmar received B.S. and M.S. degrees in Industrial Engineering from Bilkent University, Turkey, and a Ph.D. in Industrial Engineering from the University of Minnesota. He is currently an Assistant Professor of Industrial Engineering at the University of Houston and Director of the Enterprise Logistics Laboratory. His research interests are in the areas of manufacturing systems, facility planning, production and inventory control, and supply chain management. He serves on the Texas Department of Transportation (TexDOT) Technical Assistance Panel (TAP) for the Research Management Committee (RMC2). He is also a member of IIE, INFORMS, and IEEE.

Saif Benjaafar is a Professor of Industrial & Systems Engineering at the University of Minnesota where he is also Director of the Industrial & Systems Engineering Division and Director of the Center for Supply Chain Research. He was a Distinguished Senior Visiting Scientist at Honeywell Laboratories, a Visiting Professor at Ecole Centrale Paris and Hong Kong University of Science and Technology, and a Visiting Fellow at the Logistics Institute at National University of Singapore and at Katholieke Universiteit Leuven, Belgium. He Holds Ph.D. and M.S. degrees from Purdue University and a BS degree from the University of Texas at Austin. His research interests include manufacturing and service operations, production and inventory systems, and supply chain management. He serves on the Editorial Board of several journals including IIE Transactions, NRL, POM, and IEEE Transactions, among others.

Acknowledgement

This research is supported by grants from the National Science Foundation and the Air Force Office of Scientific Research.