A model-based clustering approach to the recognition of the spatial defect patterns produced during semiconductor fabrication

Abstract

Defects on semiconductor wafers tend to cluster and the spatial defect patterns of these defect clusters contain valuable information about potential problems in the manufacturing processes. This study proposes a model-based clustering algorithm for automatic spatial defect recognition on semiconductor wafers. A mixture model is proposed to model the distributions of defects on wafer surfaces. The proposed algorithm can find the number of defect clusters and identify the pattern of each cluster automatically. It is capable of detecting defect clusters with linear patterns, curvilinear patterns and ellipsoidal patterns. Promising results have been obtained from simulation studies.

Keywords:

• Model-based clustering
• mixture model
• pattern recognition

1. Introduction

The fabrication of Integrated Circuits (ICs) is a complex and costly process that involves hundreds of steps. Defects generated during these manufacturing steps not only lower the manufacturing yield but also cause potential reliability problems. Because a high yield and reliability are essential to successful IC fabrication, prompt identification of the root causes of defects as well as their early elimination is critical (Kuo et al., 1998; Kuo and Kim, 1999).

Defects on semiconductor wafers are not uniformly distributed; instead, they tend to cluster. A defect cluster is defined as an aggregation of defects that are generated from the same defect generation mechanism. Spatial defect pattern recognition is to detect the existence, shape, location and orientation of the defect clusters. The spatial defect patterns are thought to result from the superposition of both global defect patterns and local defect patterns (Hwang and Kuo, 2007). Global defects are generated by random causes, such as particles in clean rooms, thermal variations in annealing processes and variations in deposition and etching processes, etc. Local defects are created by assignable causes, such as human mistakes, particles from equipment and chemical stains, etc. Random causes create defects all over the wafer surfaces, which are expensive to remove, while assignable causes generate defects in clusters. Each local defect cluster can be categorized, according to its spatial pattern, into its defect generation cause. For example, a cluster with a curvilinear shape is probably caused by a material handling scratch (Hwang and Kuo, 2007). Most yield/reliability improvement efforts are focused on finding and removing assignable causes. Because the spatial patterns of local defect clusters contain useful information about their defect generation mechanisms, methods that can detect local defect clusters and identify their spatial patterns are needed.

Traditionally, the detection of spatial defect patterns on semiconductor wafers depends on manual reviews by human experts. Although manual inspection is accurate for finding the causes of the defects, it is very slow. It may take as long as several hours to examine one wafer. In addition, inspectors are unable to concentrate for long time periods due to mental fatigue. Automated defect scanning, on the other hand, uses laser light to scan wafer surfaces to identify the locations and relative sizes of defects. This method is fast enough to scan a wafer in several minutes. The purpose of our study is to develop an automatic method that takes as input the defect data generated by automated defect scanning tools, and then groups the defects into clusters and determines the pattern of each cluster.

There are many studies on defect pattern recognition in semiconductor fabrication. Some examples are listed here. Gleason et al. (1998) employ an automated clustering algorithm using artificial intelligence. Chen and Liu (2000) use neural networks for pattern recognition. Shankar and Zhong (2005) detect defect patterns using fuzzy logic. Wang et al. (2006) propose a hybrid clustering method to simultaneously recognize both convex and non-convex patterns. Hwang and Kuo (2007) propose a two-step method using model-based clustering. Compared to other approaches, model-based clustering has the following advantages: (i) it is flexible enough that no training data are needed for new defect patterns to be easily detected; and (ii) the clustering results can be used for yield estimation and prediction via advanced yield models based on spatial point processes (Hwang, 2004).

In model-based clustering, the observations are considered to be generated from mixture distributions, and generally clustering with multivariate normal distributions with (optional) random background noise (or “clutter”) is studied. However, defect clusters with curvilinear patterns are observed on wafers and global defects may not be homogeneous for some manufacturing processes. Hwang and Kuo (2007) propose the use of spatial non-homogeneous Poisson processes, bivariate normal distributions and principal curves to model the distributions of global defects, the distributions of local defects in clusters with ellipsoidal patterns and the distributions of local defects in clusters with curvilinear patterns, respectively. In the first step of their algorithm, they cluster the defects assuming that all of the local defect clusters are modeled by bivariate normal distributions. They also determine the number of clusters in this step using the Bayesian Information Criterion (BIC) (Schwarz, 1978). In the second step, they cluster the defects assuming that all of the local defect clusters are modeled by principal curves. By comparing the log-likelihood values of each cluster for the two steps, they are able to identify whether or not a cluster has a curvilinear pattern. Their algorithm, however, tends to overestimate the number of defect clusters when curvilinear defect clusters are present on the wafer surfaces because they estimate the number of clusters in the first step assuming bivariate normal distributions for all the local defect clusters. Their algorithm does not identify the linear clusters. In addition, the computational time of the two-step algorithm is high.

In this study, we extend the work of Hwang and Kuo (2007) to overcome the shortcomings mentioned above. A new mixture model is proposed to model the distribution of defects on the wafers. This model is capable of modeling the existence on the same wafer surface of clusters with curvilinear patterns, linear patterns and ellipsoidal patterns. A one-step algorithm, based on the CEM (Classification-Expectation-Maximization) algorithm for parameter estimation and the BIC for model selection, is developed. Promising results are obtained from simulation studies. The clustering results provide valuable information for yield and reliability improvement.

The rest of the paper is organized as follows. Section 2 discusses the new mixture model proposed to describe the distributions of defects on the wafers. Section 3 describes the clustering algorithm. Simulation studies are presented in Section 4, and Section 5 concludes the paper.

2. Model-based clustering

Our focus in this study is on classifying defects into clusters and identifying the pattern of each cluster. Global defects generated from random causes occur all over the wafer surface and are considered to form a global defect cluster. Local defects generated by assignable causes tend to cluster and different defect generation mechanisms generate different defect patterns accordingly. The purpose of this study is to discriminate the defects created by assignable causes and to find the characteristics of the resulting clusters using model-based clustering.

2.1. Mixture model

Banfield and Raftery (1993) propose a method for model-based clustering of d-dimensional data based on a mixture of multivariate normal distributions. Background noises, if they exist, are assumed to be homogeneous and a spatial homogeneous Poisson process is used to to represent the noises. That is, the observations are assumed to follow a mixture distribution:

where s denotes the location of an observation and the model parameters are θ = (p, θ ₀, θ ₁, …, θ _G ). Herein, G is the number of mixture components, excluding the clutter. The mixing proportions p = (p ₀,p ₁, …, p _G ) satisfy p _k ≥ 0, k = 0, …, G, and ∑ _{k = 0} ^G p _k = 1. The zeroth component corresponds to the background noise, and f ₀ (s|θ₀) is the density of the spatial homogeneous Poisson process. f _k (s| θ _k ), k = 1, …, G represent the probability density functions of the multivariate normal distributions. Banfield and Raftery (1993) develop a clustering method aimed at maximizing the classified likelihood:

where the γ _i are the indexing values for classification, such that γ _i = k if the ith observation belongs to the kth component. E _k = {s _i :γ _i = k,i = 1, …, n} is the set of observations in the kth component of the mixture, and n is the total number of observations. The model-based clustering approach described above has been widely applied in many disciplines. For example, Campbell et al. (1997) apply it to find textile flaws and Dasgupta and Raftery (1998) use it for minefield detection.

The mixture model (1), however, has two limitations, which make it unsuitable for defect pattern recognition in semiconductor fabrication. First, the background noises, if they exist, are assumed to be homogeneous, but the global defects on the wafers may be non-homogeneous for some fabrication processes. Second, the distributions of observations in all the mixture components are assumed to follow multivariate normal distributions, but the defect distributions in clusters with curvilinear patterns may not be well modeled by multivariate normal distributions. In order to overcome these two limitations, a new mixture model is proposed to describe the distributions of defects on the wafers:

In this new model, the distributions of defects in the local defect clusters are modeled by either bivariate normal distributions or principal curves. If a local defect cluster has an ellipsoidal or a linear pattern, the bivariate normal distribution is used to model the distribution of defects in that cluster. On the other hand, the principal curve is used to model the distribution of defects in a cluster with a curvilinear pattern. The distribution of global defects is modeled by a spatial non-homogeneous Poisson process. Note that the spatial homogeneous Poisson process can be considered as a special case of the spatial non-homogeneous Poisson process. Thus, using the spatial non-homogeneous Poisson process does not exclude the situations in which the global defects are uniformly distributed. In the new mixture model, f ₀ (s| θ ₀), f _k,BVN(s| θ _k,BVN) and f _k,PC(s| θ _k,PC) are the density functions of the spatial non-homogeneous Poisson process, the bivariate normal distribution and the principal curve, respectively.

Note that new pattern identification parameters, u _k ,k = 1, …, G, are introduced in the new mixture model (3). The pattern identification parameters satisfy:

The patterns of the local defect clusters can be identified by estimating the pattern identification parameters.

2.2. Bivariate normal distributions

The distribution of local defects in a cluster with an ellipsoidal pattern or a linear pattern is modeled by the bivariate normal distribution. The probability density function of the bivariate normal distribution is

Herein, θ _k,BVN = ( μ _k , Σ _k ), where μ _k is the mean vector determining the location of the cluster and Σ _k is the variance-covariance matrix. The variance-covariance matrix is a symmetric, positive definite matrix that contains information about shape, size and orientation of the cluster (Bensmail et al., 1997).

The variance-covariance matrix can be decomposed as Σ _k = D _k A _k D _k ^T, where A _k is a diagonal matrix of eigenvalues and D _k is an orthogonal matrix consisting of the eigenvectors. For a cluster with an ellipsoidal pattern, the diagonal elements of A _k , i.e., the eigenvalues of Σ _k , are of similar magnitude, whereas a cluster appears to be a linear line if one eigenvalue is much smaller than the other one.

2.3. Principal curves

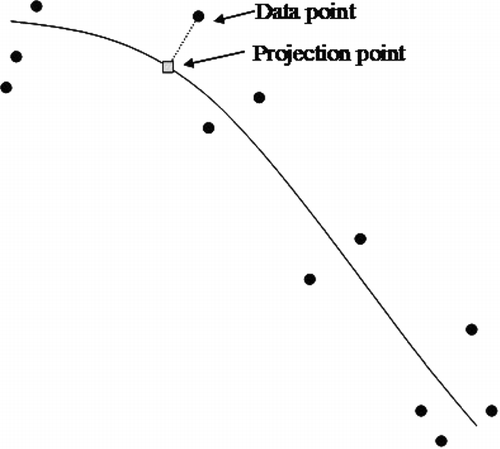
The distribution of local defects in a cluster with a curvilinear pattern is modeled by the principal curve. Principal curves were introduced by Hastie and Stuetzle (1989) and applied in a clustering context by Banfield and Raftery (1992), Stanford and Raftery (2000) and Hwang and Kuo (2007). Figure 1 shows a simple example of the principal curve.

Fig. 1 An example of the principal curve.

The principal curve is a one-dimensional curve that passes through d-dimensional data. The one-dimensional curve in d-dimensional space ℜ ^d is defined as a vector function f(δ) of a single scalar variable δ and δ provides an ordering along the curve (Hastie and Stuetzle, 1989). Consider a data set s consisting of n observations in ℜ ^d , f is the principal curve of s if

where the projection index δ _f :ℜ ^d → ℜ is defined as

Herein, the projection index δ _f (s) of s is the value of δ for which f(δ) is the projection point of s on the curve, i.e., the closest point on the curve from the data point s.

The principal curve of data s of size n is found using the following algorithm (Hastie and Stuetzle, 1989).

	Initialization:
	Find f 0(δ) = +bδ, where b is the first principal component of s.
	Repeat:
	Find δ f i (s j ),j = 1, …, n.
	Find f (i + 1)(δ).
	Until | d i + 1− d i | is less than a criterion, where d i = ∑ j = 1 n | |s j − f i (δ f i (s j ))| |2.

The principal curve of s is obtained by the iterative steps of finding a curve, f(δ), and the projection index of each data point, δ _f ⁱ (s _j ), j = 1, …, n. The algorithm stops when there is little improvement in the sum of squared distances between the data points and the curve.

The density of the principal curve is written as (Stanford and Raftery, 2000)

where ‖s−f(δ _k )‖ is the Euclidean distance from the point s to its projection point, f(δ _k ), on the curve. The scalar parameter ν _k is the length of the principal curve, and the scalar parameter σ _k is the variance of the distances from the data points to the curve.

2.4. Spatial non-homogeneous Poisson process

The distribution of global defects is modeled by the spatial non-homogeneous Poisson process. The properties of the spatial non-homogeneous Poisson process are described by its intensity function, which governs the likelihood of an observation occurring at a location s. Consider the spatial non-homogeneous Poisson process that models the global defect distribution on a wafer surface, D ∈ ℜ²,{N(D):| D| ≥ 0}. Herein, N(D) is the number of defects on D. The intensity function at location s∈ D, λ (s| θ ₀), is defined as λ (s| θ ₀) = lim _{|d s|→ 0} E[N(d s)]|d s|, where E[N(d s)] is the expected number of defects on an infinitesimal region around s, Ds (Diggle, 1983). In this study, we assume a quadratic intensity function, namely:

where r is the distance from a defect at location s to the center of the wafer and the parameters θ ₀ = α = (α₁,α₂,α₃). The quadratic intensity function (4) is used because studies based on actual data have suggested that the defect density near the edge (outer region) is higher than the defect density near the center (inner region) (Hansen and Thyregod, 1998).

The density of the spatial non-homogeneous Poisson process is (Diggle, 1983):

Estimates of the parameters, α can be obtained by maximizing the likelihood function (Daley and Vere-Jones, 1988):

where n ₀ is the number of global defects.

3. Clustering algorithm

In the previous section, we discussed the new mixture distribution proposed to model the defect distributions on wafer surfaces. In this section, we consider the problem of estimating the unknown model parameters p ₀, …, p _G , u ₁, …, u _G and θ ₀, …, θ _G . The number of local defect clusters, G, also needs to be estimated. In this study, we use the CEM algorithm for parameter estimation and the BIC for model selection.

3.1. CEM algorithm for clustering

Let us introduce latent variables z _i = (z _i0, z _i1, …, z _iG ), i = 1, …, n, which satisfy:

It is assumed that z _i follows an identical and independent multinomial distribution of a single trial with parameters (p ₀,p ₁, …, p _G ). The indexing values for classification, the γ _i in the classification likelihood function (2), satisfy γ _i = k if z _ik = 1. In the parameter estimation, the z _i are regarded as missing data. The complete data are considered to be (s _i ,z _i ).

Assuming the number of the local defect clusters G is fixed, the following iterative steps are applied to estimate the model parameters.

At the mth iteration:

	Step 1. E-step Compute (m) given (m − 1), (m − 1) and (m − 1): where the superscripts (m − 1) and (m) indicate estimates of the previous iteration and the current iteration, respectively. denotes the maximum likelihood estimate of θ .
	Step 2. C-step Partition the defects into clusters according to (m). Then γ i (m) = k if ik (m) = i (m)),i = 1, …, n.
	Step 3. M-step 3.1 Compute the estimate (m): where n k is the number of defects in the kth cluster. 3.2. Compute the estimates k (m)and Σ k (m), k = 1, …, G: 3.3. Compute the estimate (m), which maximizes the likelihood of the spatial non-homogeneous Poisson process given by Equation (5). 3.4. Compute the estimates k (m) and σ k (m),k = 1, …, G: Find the principal curve for the defects of each local cluster using the algorithm described in Section 2.3. Compute the distance between each defect in the cluster and the principal curve. ν k (m)is the length of the principal curve and σ k (m) is the variance of the distances from the defects to the principal curve. 3.5. Compute the estimates k (m),k = 1, …,G: For each local defect cluster, calculate ∏ i:γ i = k f k.BVN(s i | μ k (m), Σ k (m)) and ∏ i:γ i = k f k,PC (s i | ν k (m+ 1), σ k (m + 1)), the likelihood values assuming the bivariate normal distribution and the principal curve, respectively. The pattern that yields the higher likelihood is assigned to the cluster.

Steps 1–3 are repeated until convergence criteria are satisfied.

It is necessary to distinguish the linear clusters from the ellipsoidal clusters. In order to do so, we compute the eigenvalues of Σ _k for all clusters with u _k = 1. If for a cluster, one eigenvalue of its variance-covariance matrix is much smaller than the other one, it will be identified as a linear cluster. In this study, a cluster is identified as a linear cluster if one eigenvalue of its variance-covariance matrix is less than 5% in magnitude than the other eigenvalue.

3.2. Number of clusters

Finding the number of clusters is a crucial part of a model-based clustering analysis. There are many criteria proposed in the literature for model selection, such as information complexity (Bozdogan, 1993) and the BIC, etc. In this study, we choose the BIC as our model selection criterion because it is very simple and has been widely supported in the model-based clustering literature (e.g., Dasgupta and Raftery (1998) and Hwang and Kuo (2007)).

The BIC is approximated as (Schwarz, 1978):

where ℓ _G (s|) is the maximized log-likelihood of the model with G local defect clusters; m _G is the total number of independent parameters in the model with G local defect clusters. The second term is the penalty for using more complicated models. The BIC balances the fit of a model and its complexity. Hwang and Kuo (2007) propose to select the number of local clusters that yields the first local maximum of the approximated BIC. This approach, however, often overestimates the number of defect clusters, especially when clusters with curvilinear patterns present on the wafers. In this study, we modify their model selection criterion and propose two model selection rules. There are G local defect clusters if: (i) G local defect clusters yield the first local maximum of the approximated BIC, i.e., BIC _{G − 1} < BIC _G ≥ BIC _{G + 1}; or (ii) BIC _{G + 1} > BIC _G and | (BIC _{G + 1}− BIC _G )/BIC _G | < α. Herein, BIC _G denotes the approximated BIC value according to the model with G local defect clusters. The second model selection rule can be interpreted as follows: if increasing the number of local clusters from G to G + 1 does not improve the approximated BIC value significantly, the number of clusters will be selected as G. Currently, choosing a proper value for α is empirical. A value too high or too low may cause underestimation or overestimation of the number of clusters. In practice, one may need to analyze some “pilot” or “trial” wafers to find an optimal value. In this study, we choose α = 10% empirically.

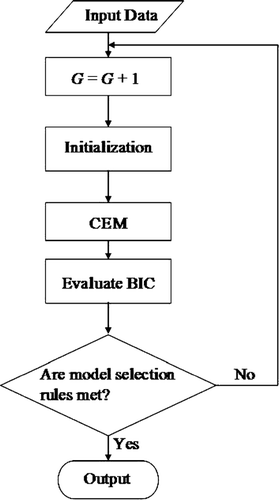
Figure 2 presents the flow-chart of the clustering algorithm using the CEM and the BIC. The algorithm has a loop with respect to the number of local defect clusters. Within that loop, the k-means clustering algorithm is applied to provide an initial clustering of the defects.

Fig. 2 Flowchart of the clustering algorithm.

4. Simulation

This section presents the clustering results obtained when the algorithm is applied to two simulated cases. In the simulation studies, the diameter of the wafers is 20 cm. The global defects are simulated from the spatial non-homogeneous Poisson process using a thinning method (Diggle, 1983). The intensity function used in the global defect generation is quadratic, that is

In both simulation cases, the coefficients, the a variables are assumed to be independent and to follow a left-truncated normal distribution with mean μ, standard deviation σ and left truncation point k:

where φ and Φ are the probability density function and the cumulative density function of the standard normal distribution, respectively. In this paper, the truncation point is set to zero to guarantee non-negativity of the coefficients. The mean vector and the standard deviation vector are set to be (μ _{a 1} , μ _{a 2} , μ _{a 3} ) = (50, 20, 3) and (σ _{a 1} , σ _{a 2} , σ _{a 3} ) = (20, 10, 2), respectively.

The local defects in a cluster with a curvilinear pattern are generated from the assumption that the defects are distributed uniformly along and about an arc. The local defects in a cluster with an ellipsoidal pattern are created by sampling from the bivariate normal distributions with random variance-covariance matrices. Each local defect cluster has 100 local defects.

The algorithm is coded using MATLAB and executed on a computer with Pentium 4 3.0 GHz CPU and 1024 Mb RAM. The computational times are calculated using the cputime function in MATLAB. In order to measure the performance of the clustering algorithm, we define the misclassification rate as

In simulation case 1, defect patterns on ten wafers are simulated. Figure 3(a) shows three representative patterns. Two local defect clusters, one with a curvilinear pattern and one with an ellipsoidal pattern, are generated on each wafer. The mean vector of the bivariate normal distribution, which is used to generate the ellipsoidal cluster, is assumed to be random in the rectangular region {(x,y): − 4 < x < − 2, − 4 < y < − 2}, where (0, 0) is the center of the wafer. The local cluster with the curvilinear pattern is randomly generated in the region {(x,y):y > 0}. Note that the two local clusters generated in this case are always separated, that is, they are not closely adjacent or overlapped. The clustering algorithm successfully finds the correct number of local defect clusters and identifies the correct pattern for each local cluster for all ten wafers. Figure 3(b) displays the clustering results for the three representative wafers.

Fig. 3 Three representative patterns of simulation case 1: (a) original defect patterns; and (b) clustering results.

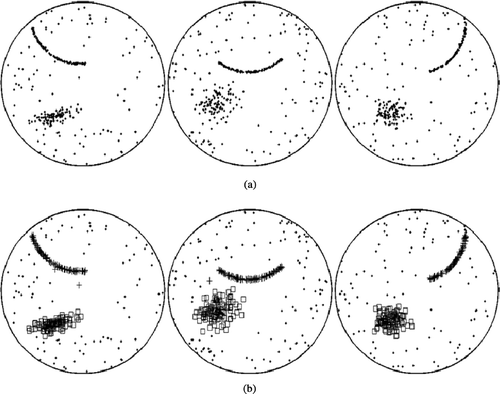
In simulation case 2, we also generate defect patterns on ten wafers. On each wafer, two local defect clusters, one with a curvilinear pattern and one with an ellipsoidal pattern, are closely adjacent or overlapped. Three representative wafers are shown in Fig. 4(a). The two local defect clusters on the first wafer are closely adjacent but not overlapped; the two local clusters on the second wafer are slightly overlapped while the two on the third wafer are highly overlapped. Figure 4(b) presents the clustering results of the algorithm applied to the three representative wafers. For all ten wafers, the clustering algorithm finds the correct number of local defect patterns. For the first two wafers shown in Fig. 4(a), the algorithm identifies the correct pattern for each local defect cluster, while for the third wafer, the algorithm assigns an ellipsoidal pattern and a linear pattern to the two local defect clusters, respectively. This indicates a limitation of the algorithm proposed in this paper. Since the proposed clustering approach clusters the defects only according to their spatial locations, it may not perform well when two or more defect clusters are highly overlapped.

Fig. 4 Three representative patterns of simulation case 2: (a) original defect patterns; and (b) clustering results.

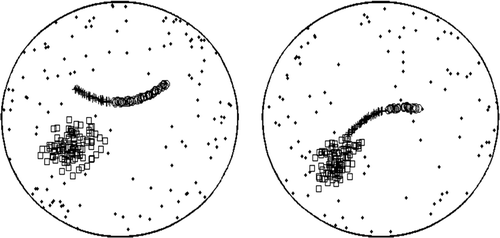
For the purpose of comparison, the two-step algorithm developed by Hwang and Kuo (2007) is applied to analyze the wafers of these two cases. The two-step algorithm overestimates the number of clusters for all of the ten wafers in case 1 and six of the ten wafers in case 2. It tends to partition a curvilinear cluster into two or more pieces and model each piece by a bivariate normal distribution or a principal curve. Figure 5 shows typical clustering results of the two-step algorithm applied to the two cases.

Fig. 5 Typical clustering results using the two-step algorithm.

Table 1 summarizes the averaged computational times and the averaged misclassification rates of the new algorithm and the averaged computational times of the two-step algorithm applied to the two simulation cases. As seen from the table, the algorithm is able to analyze one wafer within about 75 seconds. The two-step algorithm, however, needs about 547 seconds to analyze one wafer. When the local defect clusters are separated, the proposed algorithm has a very high accuracy. As the distance between the two local clusters decreases, the accuracy of the new algorithm decreases. However, most of the local defects are identified by the new algorithm. Note that the misclassification rate of the two-step algorithm is not calculated because the two-step algorithm overestimates the number of defect clusters for most of the wafers and there is not a proper way to compute the misclassification rate when the estimated number of clusters is not correct.

Table 1 Summary of the performance of the clustering algorithms

	Averaged computational time (seconds)
Case	New algorithm	Two-step algorithm	Averaged misclassification rate using the new algorithm (%)
1	74.5	546.7	3.4
2	71.2	522.4	15.4

5. Conclusions

This paper proposes an automatic method for defect pattern recognition via model-based clustering for semiconductor fabrication process control. A mixture model is proposed to model the distribution of defects on semiconductor wafers. The proposed mixture model uses the spatial non-homogeneous Poisson process to model distribution global defects generated by assignable causes. The distributions of local defects are modeled by either the bivariate normal distribution or the principal curve. A clustering algorithm using the CEM for parameter estimation and the BIC for model selection is developed. Simulation studies prove that the new algorithm is fast and that it performs well. The clustering results will not only help the manufacturer monitor the manufacturing process but also provide valuable information for yield estimation.

Biographies

Tao Yuan received a Bachelor of Engineering degree in Thermal Engineering at Tsinghua University, Beijing, China in 2000, and a Master of Science degree in Aerospace Engineering and a Master of Engineering degree in Industrial Engineering at Texas A&M University, College Station, in 2003 and 2004, respectively. He is currently pursuing a Ph.D. degree in Industrial and Information Engineering at the University of Tennessee, Knoxville. His research interests are in statistical yield/reliability analysis of micro-/nano-electronics.

Way Kuo is University Distinguished Professor and Dean of Engineering at the University of Tennessee. Previously, he was with Texas A&M University and Bell Labs. He is an elected member of the US National Academy of Engineering, Academia Sinica, Taiwan and the International Academy for Quality. He has co-authored five textbooks and currently serves as Editor of IEEE Transactions on Reliability. He is a Fellow of IIE, ASQ, INFORMS, IEEE and the National Quality Institute.

Acknowledgements

The authors would like to thank the referees for valuable comments. The research is partially supported by NSF project DMI-0429176.