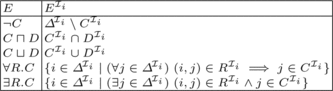AUGMENTING SUBSUMPTION PROPAGATION IN DISTRIBUTED DESCRIPTION LOGICS

Abstract

Distributed description logics (DDL) enable reasoning with multiple ontologies interconnected by directional semantic mapping, called bridge rules. Bridge rules map concepts of a source ontology into concepts of a target ontology. Concept subsumptions of the source ontology can be propagated according to a propagation pattern expressed by means of bridge rules into concept subsumptions of the target ontology. In the basic formulation of DDL, such a propagation is mostly limited to cases when pairs of ontologies are directly linked by means of bridge rules. However, when more than two ontologies are involved, one would expect that subsumption propagates along chains of ontologies linked by bridge rules, but the semantics of DDL is too weak to support this behavior. In a recent study, an adjusted semantics for DDL that supports subsumption propagation through chains of bridge rules has been introduced. This study makes use of a so-called compositional consistency requirement that has been employed before in package-based description logics. While the results concerning subsumption propagation under the adjusted semantics are encouraging, there are important drawbacks. In this article we take a wider perspective, and propose a study of several different alternative extensions of the DDL semantics. For each of them we study the formal properties, and we select the one that, according to our analysis, constitutes a good compromise, and for this case we provide a sound and complete tableaux decision procedure.

INTRODUCTION

Distributed description logics (DDL) have been introduced by Borgida and Serafini (2003) and consecutively developed by further research (Serafini, Borgida, and Tamilin, 2005; Serafini and Tamilin, 2006; Ghidini et al., 2007). Distributed description logics are intended especially to enable reasoning over systems of multiple ontologies connected by directional semantic mapping, built upon the formal, logical, and well-established framework of description logics (DL) (Baader et al., 2003) and the local model semantics (Ghidini and Giunchiglia, 2001). Distributed description logics capture the idea of importing and reusing concepts between several heterogeneous ontologies. This idea combines well with the basic assumption of the semantic web that no central ontology but rather many ontologies with redundant knowledge will exist (Berners-Lee, Hendler, and Lassila, 2001).

In DL, a knowledge base, also called an ontology, contains a set of terminological axioms that assert relation upon concepts. For instance, with subsumption axioms we assert that some particular concept is a subconcept of another concept. While the ontology contains a set of axioms that record selected relations between concepts directly, using the logical semantics of DL some more relations are possibly implied. These relations may then be queried by the user. Say, if we assert directly that C is a subconcept of D and D in turn is a subconcept of E, this implies also that C is a subconcept of E. This relation is called subsumption: if C is a subconcept of D, we say that C is subsumed by D.

Distributed description logics enrich DL with new kinds of axioms, called bridge rules. Bridge rules represent a semantic mapping between ontologies in a formal fashion. With bridge rules one is able to assert that some concept C, local to ontology 𝒯₁, is related to some other concept D, local to 𝒯₂. ¹ While technically this relation is not exactly equivalent to the subsumption present inside the local ontologies, with bridge rules we also indicate either a subconcept or a superconcept relation. Moreover, bridge rules are directed, and hence if there is a bridge rule with direction from 𝒯₁ to 𝒯₂, then 𝒯₂ reuses knowledge from 𝒯₁, but not necessarily the other way around. Semantic mapping encoded in bridge rules enables for knowledge reuse between local ontologies in a DDL knowledge base via the effect called subsumption propagation.

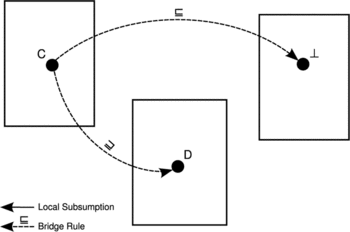
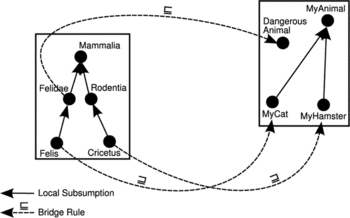
Consider the example depicted in Figure 1. Let the ontology on the right be our local backyard ontology. In this ontology, we maintain knowledge about all animals in our backyard. Instead of complex modeling of all relations between our animals, we reuse a far more complex ontology that contains classification of all animal species. We map MyCat to genus Felis, and we also create the concept DangerousAnimal and map it to Felidae, the family of all cats, since we also keep a hamster and we know that all cats hunt hamsters for food. Thanks to the semantics of DDL we are now able to derive that MyCat is a subconcept of DangerousAnimal, even if this relation is not derived in the original backyard ontology locally. We say that the subsumption between Felisand Felidae has propagated to the backyard ontology thanks to the mapping. Please also note that the direction of the mapping is from the species ontology to the backyard ontology, as we only intend to reuse the knowledge of the species ontology within the backyard ontology and not the other way around. The mapping depicted on Figure 1 does not affect the knowledge within the species ontology in any way.

FIGURE 1 A simple DDL knowledge base with bridge rules. In this knowledge base it always holds that MyCat is a subconcept of DangerousAnimal, even if this fact is not explicitly recorded.

Subsumption propagation has been described as desired and one of the main features of DDL and it has been studied (Borgida and Serafini, 2003; Serafini and Tamilin, 2004; Homola, 2007). Homola (2008) argues that the original semantics of DDL behaves counterintuitively in certain cases and proposes an adjustment to the semantics in order to cope with this issue.

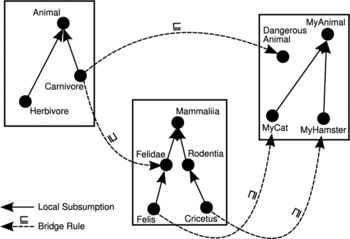
For illustration, consider Figure 2 which extends the previously discussed example depicted in Figure 1. In this case, the situation is more complex. We no longer map between concepts Felidae and DangerousAnimal, but instead these two concepts are connected indirectly via the concept Carnivore from yet another ontology. This third ontology deals with animal behavior in contrast with the species ontology that merely provides classification. In case there are such ontologies available, we suggest that this way of modelling is even more natural. As in the previously mentioned example, again we would expect to derive that MyCat is a subconcept of DangerousAnimal within the backyard ontology. This relation, however, is not derived under the original DDL semantics. In the example from Figure 2 there is a so-called chain of bridge rules. The onto-bridge rule between concepts Carnivore and Felidae and the other one between Felis and MyCat form a chain, as Felis is a subconcept of Felidae in the classification ontology. Similar chains are also possible with into-bridge rules. The adjusted semantics of Homola (2008) allows subsumption propagation along such chains of bridge rules and hence the subsumption between MyCat and DangerousAnimal is entailed under this semantics.

FIGURE 2 An example of complex concept mapping between three ontologies. In this case, the query whether MyCat is a subconcept of DangerousAnimal is not true under the original DDL semantics.

In this article we take steps forward in order to develop a distributed tableaux reasoning algorithm that would decide satisfiability of concepts and subsumption with respect to the adjusted semantics. The algorithm that is introduced in this article handles chaining onto-bridge rules correctly, but it is unable to cope with chaining into-bridge rules. We provide precise characterization of the semantics that the algorithm actually implements. The algorithm works with acyclic DDL knowledge bases build on top of 𝒜ℒ𝒞 as the local language. As in the case of the tableaux algorithm which is known for the original semantics (Serafini et al., 2005), the algorithm is truly distributed and it permits the scenario where every local ontology is governed by an autonomous reasoning service and these services communicate by passing queries. The local reasoner that has started the computation collects all the answers and makes the decision at the end. Besides the fact that each algorithm works under a different semantics, the main distinguishing feature of the newly introduced algorithm is that communication between local reasoners is divided into multiple messages. We believe that such behavior may serve as a base for more fine-grained optimization in the future.

DISTRIBUTED DESCRIPTION LOGICS

Distributed description logics rely on DL (Baader et al., 2003) as for the representation language of the local knowledge bases. Description logics provide a well-established ontological representation language with formal semantics and with reasoning tasks and associated computational issues well understood. In the following, we briefly introduce the 𝒜ℒ𝒞 DL in order to build on top of it later in the article.

A DL knowledge base typically consists of a TBox and an ABox. The TBox contains terminological knowledge, that is, definitions of concepts and their relations (i.e., subsumption axioms). The ABox contains knowledge about individuals, their relations, and their membership in concepts. In this work, we concentrate above all on the terminological part of the knowledge and hence we will only work with TBoxes below. We will denote TBoxes with 𝒯 _i because we deal with several ontologies. Assume that i is an index from some finite index set I. Each TBox is a set of subsumption axioms called general concept inclusions (GCI), each of the form i: C⊑D, where C and D are concepts. Concepts are either atomic or complex. Atomic concepts have no further structure. Complex concepts are composed from atomic concepts and roles using some of the DL concept constructors. For a list of constructors and their meaning, see Figure 3.

FIGURE 3 Complex concepts in 𝒜ℒ𝒞 and their semantics.

The semantics of DL is model-theoretic. Each ontology 𝒯 _i is assigned an interpretation ℐ _i consisting of a domain Δ^{ℐ _i} and an interpretation function ·^{ℐ _i} which interprets each concept C by C ^{ℐ _i}  ⊆ Δ^{ℐ _i} . Each role R is interpreted by R ^{ℐ _i}  ⊆ Δ^{ℐ _i}  × Δ^{ℐ _i} . Complex concepts must satisfy further semantic constraints (see Figure 3). There are also two special concepts ⊥ and ⊤. The bottom concept (⊥) is always interpreted by ⊥^{ℐ _i}  = ∅ and the top concept (⊤) is always interpreted by ⊤^{ℐ _i}  = Δ^{ℐ _i} , but they are formally defined as syntactic sugar: ⊥ stands for E ⊓ ¬ E and ⊤ stands for E ⊔ ¬ E, for some new concept name E.

A GCI axiom i: C⊑D, is satisfied by ℐ _i whenever C ^{ℐ _i}  ⊆ D ^{ℐ _i} . An interpretation ℐ _i is a model of 𝒯 _i if it satisfies all GCI in 𝒯 _i . A concept C is satisfiable, if there exists an interpretation ℐ _i such that C ^{ℐ _i} is nonempty. In addition, C is satisfiable with respect to a TBox 𝒯 _i if there exists an interpretation ℐ _i with C ^{ℐ _i}  ≠ ∅ that is a model of 𝒯 _i . And, subsumption i: C⊑D is entailed by 𝒯 _i if C ^{ℐ _i}  ⊆ D ^{ℐ _i} holds in all models of 𝒯 _i . Satisfiability of concepts and subsumption entailment are standard decision problems that are investigated in each DL.

Two concepts C and D are equivalent if in each interpretation ℐ _i we have C ^{ℐ _i}  = D ^{ℐ _i} . A concept C is in negation normal form (NNF) if negation (¬) only appears in C directly in front of atomic concepts. For each concept, an equivalent concept in NNF exists (Baader et al., 2003), we denote the NNF of C by nnf(C). For a more detailed introduction to DL, please refer to the work of Baader et al. (2003) and Horrocks, Sattler, and Tobies (1999).

A DDL knowledge base, commonly dubbed distributed TBox 𝔗, includes a set of local TBoxes each over its own DL language and a set of bridge rules 𝔅 that provide mappings between these local TBoxes. The local languages are commonly required to be under 𝒮ℋℐ𝒬 (Horrocks et al., 1999) as it is not trivial to extend DDL with nominals (Serafini et al., 2005). In this work, we will stay under 𝒜ℒ𝒞, which is a sublanguage of 𝒮ℋℐ𝒬. The formal definition is as follows.

Definition 1

Assume a nonempty index set I, a set of concept names and a set of role names . A distributed TBox is a pair 𝔗 = ⟨{𝒯 _i } _i∈I , 𝔅⟩ such that:

1. Each local TBox 𝒯 _i is a collection of 𝒜ℒ𝒞 GCI axioms over N_{C i} and N_{R i} . Each GCI is of the form:

2. The set of bridge rules 𝔅 divides into sets of bridge rules . Each 𝔅 _ij is a collection of bridge rules in direction from 𝒯 _i to 𝒯 _j which are of two forms, into-bridge rules and onto-bridge rules (in the respective order):

As we will see below, while bridge rules are not semantically equivalent to subsumption axioms (GCI), they also work with the notions of subconcept and superconcept. Intuitively speaking, into-bridge rules cause the mapped image of the source concept to always stay inside the target concept, so hence their name. Conversely, onto-bridge rules cause that the target concept is always inside the mapped image of the source concept. As previously mentioned, the direction of bridge rules matters and hence 𝔅 _ij and 𝔅 _ji are possibly and expectedly distinct. The bridge graph G_𝔗 = ⟨V, E⟩ of a distributed TBox 𝔗 is defined as follows: V = I and ⟨i, j⟩ ∈ E if 𝔅 _ij  ≠ ∅. We say that 𝔗 is acyclic if G_𝔗 is acyclic.

Given a TBox 𝒯, a hole is an interpretation ℐ^ε = ⟨∅, ·^ε⟩ with empty domain. Holes are used for fighting propagation of inconsistency. We use the most recent definition, introduced by Serafini et al. (2005). A distributed interpretation ℑ = ⟨{ℐ _i } _i∈I , {r _ij } _{i, j∈I, i≠j} ⟩ of a distributed TBox 𝔗 consists of a set of local interpretations {ℐ _i } _i∈I and a set of domain relations {r _ij } _{i, j∈I, i≠j} . For each i ∈ I, either ℐ _i  = (Δ^{ℐ _i} , ·^{ℐ _i} ) is an interpretation of the local TBox 𝒯 _i or ℐ _i  = ℐ^ε is a hole. Each domain relation r _ij is a subset of Δ^{ℐ _i}  × Δ^{ℐ _j} . We denote by r _ij (d) the set {d′ | ⟨d, d′⟩ ∈ r _ij } and by r _ij (D) the set .

Definition 2

For every i and j, a distributed interpretation ℑ satisfies the elements of a distributed TBox 𝔗 (denoted by ℑ⊧_ε ·) according to the following clauses:

1. ℑ⊧_ε i: C⊑D if ℐ _i ⊧i: C⊑D;

2. ℑ⊧_ε𝒯 _i if ℑ⊧_ε i: C⊑D for each i: C⊑D ∈ 𝒯 _i ;

3. if r _ij (C ^{ℐ _i} ) ⊆ G ^{ℐ _j} ;

4. if r _ij (C ^{ℐ _i} ) ⊇ G ^{ℐ _j} ;

5. ℑ⊧_ε𝔅 if ℑ satisfies all bridge rules in 𝔅;

6. ℑ⊧_ε𝔗 if ℑ⊧_ε𝔅 and ℑ⊧_ε𝒯 _i for each i.

If ℑ⊧_ε𝔗 then we also say that ℑ is a (distributed) model of 𝔗.

The two standard decision problems in DL—satisfiability of concepts and entailment of subsumption also play a prominent rôle in the context of DDL. Formally, the decision problems are defined as follows.

Definition 3

Given a distributed TBox 𝔗, an i-local concept C is satisfiable with respect to 𝔗 if there exists a distributed model ℑ of 𝔗 such that C ^{ℐ _i}  ≠ ∅.

Definition 4

Given a distributed TBox 𝔗 and two i-local concepts C and D, it is said that C is subsumed by D with respect to 𝔗 if C ^{ℐ _i}  ⊆ D ^{ℐ _i} in every distributed model ℑ of 𝔗. We also sometimes say that the subsumption formula i: C⊑D is entailed by 𝔗 and denote this by 𝔗⊧_ε i: C⊑D.

It is a well-known result that, in most DL, subsumption and (un)satisfiability are interreducible (Baader et al., 2003). It follows rather straightforward, that this reduction is also valid for DDL, as follows in Theorem 1.

Theorem 1

Assume a distributed TBox 𝔗 and two i-local concepts C and D. 𝔗⊧_ε i: C⊑D if and only if the concept ¬ C ⊓ D is unsatisfiable with respect to 𝔗. Also, C is satisfiable with respect to 𝔗 if and only if the subsumption formula i: C⊑ ⊥ is not entailed by 𝔗.

In the literature, several properties have been identified as desired for a logic of modular and distributed ontologies (Loebe, 2006). In context of DDL, three particular properties are considered as desiderata. These are (intuitively explained):

• monotonicity: addition of new knowledge does not affect the previously entailed knowledge;

• directionality: some local ontology 𝒯 _i possibly affects another local ontology 𝒯 _j , only if they are connected by a directed path of bridge rules starting from T _i and eventually reaching T _j ;

• local inconsistency: if one local ontology is inconsistent this does not necessarily cause the inconsistence of the whole distributed ontology; instead the local inconsistency should be dealt with allowing only minimal necessary damage.

These properties have been formalized in the context of DDL in the literature and it was proven that they hold for the original DDL semantics (Borgida and Serafini, 2003; Serafini and Tamilin, 2004; Serafini et al., 2005). In any extension of the DDL semantic, it is desirable to maintain these three properties, if possible. The properties are formalized as follows.

Definition 5 (Monotonicity)

The monotonicity property is satisfied whenever in every distributed TBox 𝔗 it holds that

Directionality states that there should also be no back-flow of information against the direction of bridge rules. That is, if 𝒯 _i and 𝒯 _j are not connected by any directed path of bridge rules (in direction from i to j) then 𝒯 _i does not affect 𝒯 _j , which means that removal of 𝒯 _i should have no effect in 𝒯 _j .

Definition 6 (Directionality)

The directionality property is satisfied whenever in every distributed TBox 𝔗 with index set I and bridge graph G_𝔗 for every i, j ∈ I, i ≠ j it holds that if there is no directed path between i to j in G_𝔗, then

where 𝔗⁻ⁱ is obtained by removing 𝒯 _i , 𝔅 _ik , and 𝔅 _li from 𝔗 for each k, l ∈ I.

The local inconsistency property states that even if some of the local TBoxes happen to be inconsistent, the inconsistency does not necessarily spread and pollute the whole distributed ontology. There are more options how to formalize such a property and several formalizations occur in the literature (Borgida and Serafini, 2003; Serafini and Tamilin, 2004; Serafini et al., 2005). We use the most recent definition by Serafini et al. (2005), which is rather technical but in fact describes very well the exact extent of inconsistency propagation that occurs under the original DDL semantics.

The limited amount of inconsistency propagation that occurs in DDL is justified by the following observation. If some local TBox 𝒯 _i is inconsistent, then the only admissible local interpretation is a hole. This affects onto-bridge rules outgoing from 𝒯 _i – the only admissible local interpretation for every j-concept D that is a target of an onto-bridge rule outgoing from 𝒯 _i is the empty set (i.e., D ^{ℐ _j}  = ∅ in each distributed model ℑ of 𝔗).

We will use some auxiliary notation. Let ⊧_d be a kind of entailment just as ⊧_ε only that it does not allow holes in local interpretations. ² Given J ⊆ I, 𝔗(ε _J ) is obtained from 𝔗 by removing each 𝒯 _j such that j ∈ J, and adding to each 𝒯 _i , i ∈ I∖J.

Definition 7 (Local inconsistency)

The local inconsistency property is satisfied whenever in each distributed TBox 𝔗 the following holds: 𝔗⊧_ε i: C⊑D if and only if for any J ⊆ I, not containing i, 𝔗(ε _J )⊧_d i: C⊑D.

The mechanism of knowledge reuse within DDL ontologies is formally characterized by the notion called subsumption propagation. Intuitively, subsumption propagates from one local ontology where it follows from the local knowledge to some another ontology that is connected by bridge rules. For an example, recall the distributed ontology depicted in Figure 1. Here, the biological classification ontology on the left locally entails Felis ⊑ Felidae. Thanks to a pair of bridge rules, this subsumption is propagated into the backyard ontology on the right and MyCat ⊑ DangerousAnimal is distributively entailed.

This subsumption propagation scenario is only a very basic one. The subsumption propagation property has been formulated in a more general setting. One such formulation appears in the work of Serafini and Tamilin (2004). Here subsumption is propagated between G and the union H ₁ ⊔…⊔ H _n , given a locally entailed subsumption A⊑B ₁ ⊔…⊔ B _n in a neighboring local ontology and a sufficient number of bridge rules. This exact form of the property, formulated in the form of an inference rule in Theorem 2, is somewhat important for the original DDL framework: it provides the grounds for the distributed reasoning algorithm introduced by Serafini and Tamilin (2004).

Theorem 2 (Subsumption propagation)

Given a distributed TBox 𝔗 with an index set ℐ, two local TBoxes 𝒯 _i and 𝒯 _j , i, j ∈ I, i-local concepts A, B ₁,…, B _n and j-local concepts G, H ₁,…, H _n , for some n > 0, the following inference rule is valid:

Study of subsumption propagation in more complex cases also appears in the literature (Serafini et al., 2005; Homola, 2007). These cases are not as interesting for this study, since they do not extend the case in that particular aspect that only two local ontologies which are directly connected with bridge rules are studied. In this work we concentrate on indirectly connected ontologies, a case with which, as we will see later, the original semantics is not completely able to cope.

IMPROVING SUBSUMPTION PROPAGATION

As outlined in the introduction with the example of Figure 2, the subsumption propagation pattern in the original DDL is, in some cases, not as strong as one would desire. In a recent article, Homola (2008) proposes a way to adjust the semantics of DDL in order to improve subsumption propagation in the cases when local ontologies are only connected indirectly. Here we provide a more systematic analysis of the possible improvements, and for one of them we extend the distributed tableaux algorithm for DDL described by Serafini et al. (2005).

This work is concerned with remote ontologies. The basic intuition behind this notion is of two local ontologies within a distributed system, which are not connected directly by a single bridge rule. Since we are interested in subsumption propagation between remote ontologies we further refine this notion considering the following two aspects. First, we are only interested in cases when these ontologies are in fact connected by some directed path of bridge rules; this is due to the directionality desideratum which allows no knowledge reuse if this is not the case. Second, even if two ontologies are connected directly, we must still also consider the remote connections between them, that is, paths of bridge rules spanning across multiple ontologies.

The characteristic pattern of interest, when dealing with remote ontologies is characterized by the notion of chain of bridge rules. Chain of bridge rules is a directed path of bridge rules that combine together with respect to subconcept-superconcept relations.

Definition 8

Let 𝔗 be distributed TBox with an index set I. A chain of bridge rules is either a directed path of into-bridge rules

of length n > 0 such that for each 1 < i < n we have 𝔗⊧_ε i: D _i ⊑C _i (into-chain); or a directed path of onto-bridge rules

of length n > 0 such that for each 1 < i < n we have 𝔗⊧_ε i: C _i ⊑D _i (onto-chain).

While there is no notion of bridge rules composition or bridge rules inference in the literature, and also in this work we do not intend to introduce this kind of reasoning with bridge rules formally, we will use the notion of bridge rules composition as a metaphor in what follows. The point is that the desired extent of subsumption propagation according to our intuitions is characterized by a hypothetical semantics in which each chain of bridge rules between C of 𝒯 _i and D of 𝒯 _j has the power equal to a single bridge rule between these two concepts. In the basic case, this propagation pattern is characterized by the following composition of bridge rules:

Semantically, these two composition rules correspond to the following two conditions (in the respective order):

Since the above two conditions must hold for any interpretation of A, B, and C, then they correspond to the following inclusions between domain relations:

Notice that when any two of i, j, and k are equal, the above properties include r _ii for some i ∈ I which is not defined in a DDL. So we suppose that the above properties hold only in the case when i, j, and k are three mutually distinct indices. Our investigation proceeds with studying the properties of an amended semantics of DDL which obeys restrictions (5) and (6).

Definition 9

Given a distributed interpretation ℑ with domain relation r, we say that r (and also ℑ) satisfies compositional consistency if for any three mutually distinct indices i, j, k ∈ I we have r _ij ○ r _jk  = r _ik .

Now the adjusted semantics is simply obtained from the original DDL semantics by allowing only distributed interpretations that satisfy compositional consistency. In accordance, we often use the wording “DDL under compositional consistency” when referring to this semantics.

The adjusted semantics actually extends the original one, in the sense that if some subsumption formula Φ is entailed by a distributed TBox 𝔗 in the original semantics, then it is also entailed by 𝔗 under compositional consistency. The only difference is that in the adjusted semantics possibly some more subsumption formulae are entailed in addition. This is formally stated in the following theorem (for a proof please refer to Homola (2008)).

Theorem 3

Given a distributed TBox 𝔗 and a subsumption formula Φ, if 𝔗⊧_εΦ according to the original semantics, then 𝔗⊧_εΦ also holds in DDL under compositional consistency.

To demonstrate the mechanism of improved subsumption propagation within the adjusted semantics, let us revisit the example from Figure 2 formally.

Example 1

1. Recall the example depicted in Figure 2. Let us simplify the notation by renaming the concepts as follows: C: = MyCat, D: = DangerousAnimal, E: = Felis, F: = Felidae, G: = Carnivore. Remaining concepts are of no interest (see Figure 4). Assume the index set I = {b, c, y}, where b represents the behavior ontology (on the left), c represents the classification ontology (in the middle), and y represents the backyard ontology (on the right). There are various axioms in 𝔗 = ⟨{𝒯 _b , 𝒯 _c , 𝒯 _y ,}, 𝔅⟩ but of the GCI only c: E⊑F, actually matters to us, and there are three bridge rules in 𝔅:

FIGURE 4 Renaming of concepts from Figure 2 employed in Example 1. The three local ontologies are referred to as 𝒯 _b —behavior ontology, 𝒯 _c —classification ontology, and 𝒯 _y —backyard ontology.

We query whether it holds that 𝔗⊧_ε y: C⊑D. Assume a distributed interpretation ℑ. Let us first assume that ℑ contains no hole. From Definition 2 we get r _cy (E ^{ℐ _c} ) ⊇ C ^{ℐ _y} . We also have r _bc (G ^{ℐ _b} ) ⊇ F ^{ℐ _c} , but since r _cy (·) is a mapping we get that r _cy (r _bc (G ^{ℐ _b} )) ⊇ r _cy (F ^{ℐ _c} ). And from compositional consistency we get that r _cy (r _bc (G ^{ℐ _b} )) = r _by (G ^{ℐ _b} ) implies r _by (G ^{ℐ _b} ) ⊇ r _cy (F ^{ℐ _c} ). From the GCI c: E⊑F we get F ^{ℐ _c}  ⊇ E ^{ℐ _c} and from properties of mapping we again get r _cy (F ^{ℐ _c} ) ⊇ r _cy (E ^{ℐ _c} ). Putting this all together we derive:

and that amounts to r _by (G ^{ℐ _b} ) ⊇ C ^{ℐ _y} . On the other hand, from the into-bridge rule between 𝒯 _b and 𝒯 _y we derive r _by (G ^{ℐ _b} ) ⊆ D ^{ℐ _y} , and so we finally get C ^{ℐ _y}  ⊆ D ^{ℐ _y} .

For the case with holes assume for instance that ℐ _b  = ℐ^ε. In that case G ^{ℐ _b}  = ∅. Thanks to the constraint generated by bridge rules and the GCI we easily derive that also F ^{ℐ _c}  = ∅, E ^{ℐ _c}  = ∅, and also C ^{ℐ _y}  = ∅. In such a case, however, C ^{ℐ _y}  ⊆ D ^{ℐ _y} holds trivially. If we substitute other local interpretations for holes, we get the very same result analogously.

Summing up, in every model of 𝔗, we have C ^{ℐ _y}  ⊆ D ^{ℐ _y} and hence 𝔗⊧_ε y: C⊑D. Recall that we have actually used the compositional consistency requirement in our argumentation. Without it we would not be able to establish the result: we would not be able to prove that r _by (G ^{ℐ _b} ) ⊇ r _cy (F ^{ℐ _c} ). In fact, the original DDL semantics allows models that violate this inclusion and hence 𝔗⊧_ε y: C⊑D does not hold under the original semantics.

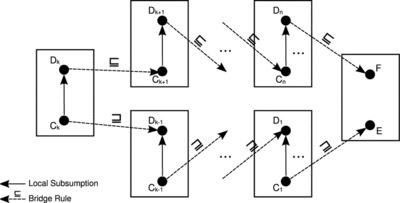
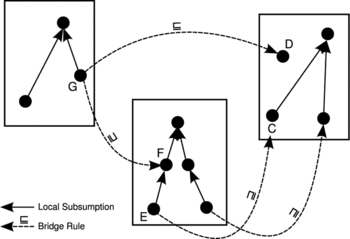
Theorem 4 provides a more general characterization of cases when subsumption propagates to remote ontologies. This characterization generalizes the setting from Figures 2-4. For a proof, refer again to the work of Homola (2008).

Theorem 4

Given a distributed TBox, as illustrated in Figure 5, with an index set I and a set of bridge rules 𝔅, that features n + 1 local TBoxes 𝒯₀, 𝒯₁,…, 𝒯 _n with concepts E, F ∈ 𝒯₀, and C _i , D _i ∈ 𝒯 _i , for 1 ≤ i ≤ n, and k with 1 ≤ k ≤ n such that:

1. 𝔗⊧_ε i: C _i ⊑D _i , for 1 ≤ i ≤ n,

2. , for 1 ≤ i < k,

3. , for k ≤ i < n,

4. and .

FIGURE 5 Depiction of the distributed TBox from Theorem 4.

In DDL under compositional consistency, it follows that 𝔗⊧_ε0: E⊑F.

In a nutshell, Theorem 4 basically says that the effect of bridge rules is now transitive, and hence subsumption propagates even between remote ontologies within the system. Since we deliberately did not formally introduce the notion bridge rules inference, as it is not the primary subject of this article, relying only on the current DDL notation this must be formulated in a rather complex fashion. If such a notion is introduced by future research, the theorem may be reformulated in a more elegant way.

As a counterpart of the positive effects of the newly introduced semantics, we also observe some undesired side effects. In particular, the full compositionality of domain relation spoils the directionality and the local inconsistency properties.

Example 2

Consider the following distributed TBox 𝔗 with the index set I = {1, 2, 3}, such that 𝒯₁ = ∅, 𝒯₂ = ∅, 𝒯₃ = ∅ and two bridge rules .

Under the semantics with compositional consistency, it follows that 𝔗⊧_ε3: D⊑ ⊥. There is no directed path from 𝒯₁ to 𝒯₃. If 𝔗 satisfies the directionality property, it should be possible to remove 𝒯₁ form 𝔗 without losing any of the entailed subsumptions. But this is not the case since 𝔗⁻¹⊭_ε3: D⊑ ⊥. The proof that 𝔗⊧_ε3: D⊑ ⊥ is as follows:

1. 𝔗⊧_ε3: D⊑ ⊥ because by the second bridge rule, r ₂₃(C ^ℐ₂ ) ⊇ D ^ℐ₃ and C ^ℐ₂  = ∅, as we will prove.

2. Assume r ₂₃(C ^ℐ₂ ) ≠ ∅.

3. Hence there are x ∈ C ^ℐ₂ and y ∈ Δ^ℐ₃ such that y ∈ r ₂₃(x).

4. Now from compositional consistency, there must be z ∈ Δ^ℐ₁ such that z ∈ r ₂₁(x) and y ∈ r ₁₃(z).

5. But from the first bridge rule we now get z ∈ ⊥^ℐ₁ which is a contradiction, as x ∈ C ^ℐ₂ , z ∈ r ₂₁(x) and r ₂₁(C ^ℐ₂ ) ⊆ ⊥^ℐ₁ .

Example 3

Consider distributed TBox 𝔗 with index set I = {1, 2, 3} and a set of bridge rules 𝔅, such that 𝒯₁ = {⊤ ⊑ ⊥}, 𝒯₂ = ∅, 𝒯₃ = ∅ which only contains one bridge rule

Since 𝒯₁ is inconsistent, the only admissible local interpretation is a hole. Similarly as in the example above, r ₂₃ = ∅, because otherwise Δ^ℐ₁ would be nonempty. Hence, 𝔗⊧_ε3: D⊑ ⊥. If local inconsistency would hold, then for each J ⊆ I, 3 ∉ J we must have 𝔗(ε _J )⊧_d3: D⊑ ⊥. For J = {1} this does not hold, however, as we will show. In this case 𝔗(ε _J ) = ⟨{𝒯₂, 𝒯₃}, 𝔅⟩. Consider the d-interpretation ℑ with Δ^ℐ₂  = C ^ℐ₂  = {x}, Δ^ℐ₃  = D ^ℐ₃  = {y}, r ₂₃ = {⟨x, y⟩} and r ₃₂ = ∅. Clearly, ℑ is a d-model of 𝔗(ε _J ), computational consistency is satisfied by r, and indeed ℑ⊭_d3: D⊑ ⊥ since D ^ℐ₃  ≠ ∅.

As shown by Examples 2–3, important properties of the original DDL semantics are violated under the compositional consistency requirement. Willing to preserve these properties, most notably directionality, we have two possible directions: first option is to drop condition (5) completely; the other option is to restrict the applicability of property (5) to the case in which (i, j) and (j, k) are links of the bridge graph. In the following two sections we analyze both these options.

DDL Under the Transitivity Condition

From Examples 2–3, we conclude that the compositional consistency requirement is perhaps too strong. It implies all the constraints that are necessary in order to increase subsumption propagation in the amount we have described as desired, but it also implies further consequences that are possibly destructive as we have seen in the examples. In the following, we study a relaxed version of the compositional consistency condition, which basically is just transitivity of the domain relation in distributed models. We will show that subsumption propagation is more limited under this weaker condition, but on the other hand, this semantics satisfies the desiderata postulated for DDL including directionality and the guarded inconsistency propagation. In addition, we will be able to introduce a distributed tableaux reasoning algorithm that decides satisfiability for this semantics later. Formally, the weaker condition is defined as follows.

Definition 10

Given a distributed interpretation ℑ with domain relation r, we say that r (and also ℑ) satisfies the transitivity condition if for any three mutually distinct indices i, j, k ∈ I we have r _ij ○ r _jk  ⊆ r _ik .

Apparently, a distributed interpretation satisfies the transitivity condition if and only if its domain relation is transitive. The semantics obtained by allowing only distributed interpretations that satisfy the transitivity condition is hence called DDL under transitivity or DDL with transitive domain relation. The first observation for the new semantics is that the proposition of Theorem 4 does not hold any more if we relax from compositional consistency to transitivity. We demonstrate this problem by an example.

Example 4

Consider a distributed TBox 𝔗 with three local TBoxes 𝒯₁, 𝒯₂, and 𝒯₃, with local concepts C ₁, D ₁ in 𝒯₁, E ₂ in 𝒯₂, and F ₃ in 𝒯₃, and with bridge rules:

This distributed TBox is clearly a very simple instance of the setting assumed by Theorem 4. According to this theorem, we should be able to derive 𝔗⊧_d1: C ₁⊑D ₁. This is not true, however, as a distributed model of 𝔗 exists in which . This distributed model ℑ has three local domains Δ^ℐ₁  = {c ₁, d ₁}, Δ^ℐ₂  = {e ₂} and Δ^ℐ₃  = {f ₃}. Local concepts are interpreted as follows: , , , and . Finally, the domain relation is the following: r ₂₁ = {⟨e ₂, c ₁⟩, ⟨e ₂, d ₁⟩}, r ₂₃ = {⟨e ₂, f ₃⟩}, r ₃₁ = {⟨f ₃, d ₁⟩}, r ₁₂ = r ₃₂ = r ₁₃ = ∅. It is easily verified that r is transitive; hence the transitivity condition is satisfied, and hence Theorem 4 does not stand if compositional consistency is relaxed to transitivity. At the same time, this example does not invalidate Theorem 4 under compositional consistency, as the stronger condition is not satisfied by ℑ because r ₂₁(e ₂) = {c ₁, d ₁} ⊈ {d ₁} = r ₃₁(r ₂₃(e ₂)).

So we see that DDL with transitive domain relation has problems with “chaining” into-bridge rules. Luckily enough of the problem does not affect chaining onto-bridge rules—if we analyze Example 1 we will see that transitivity is enough to guarantee the two chaining onto-bridge rules in this example to propagate the subsumption relationship as expected. This observation holds in general and is formally established by Theorem 5. This theorem is a weaker version of Theorem 4 and it provides a characterization of the semantics of DDL under the transitivity condition.

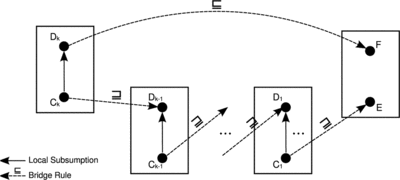
Theorem 5

Given a distributed TBox, as illustrated in Figure 7, with an index set I and a set of bridge rules 𝔅, that features k + 1 local TBoxes 𝒯₀, 𝒯₁,…, 𝒯 _k with concepts E, F ∈ 𝒯₀, and C _i , D _i ∈ 𝒯 _i , for 1 ≤ i ≤ k, such that:

1. 𝔗⊧_ε i: C _i ⊑D _i , for 1 ≤ i ≤ k,

2. , for 1 ≤ i < k,

3. and .

FIGURE 6 Depiction of the distributed TBox from Example 2.

FIGURE 7 Depiction of the distributed TBox from Theorem 5.

In DDL under the transitivity condition it follows that 𝔗⊧_ε0: E⊑F.

Proof

The theorem is proved by the following chain of inclusions:

Inclusion 3 is a direct consequence of the into-bridge rule . As for Inclusion 2, 𝔗⊧_d k: C _k ⊑D _k implies and since r _k0(·) we also have . Inclusion 1 divides into

Both these inclusions ought to be proven by mathematical induction. The first inclusion is proven by induction on k, base case is . This is a direct consequence of the onto-bridge rule . In the induction step, by the induction hypothesis we have . From the assumptions of the theorem we derive

The composition of mappings r ₁₀(r ₂₁(…r _k−1k−2(·)…)) is a mapping, and so . Together with the induction hypothesis this amounts to the inclusion we wanted to prove.

As for the second inclusion, we shall prove a slightly more general proposition:

where 0 ≤ n ≤ k − 2. The inclusion we ought to prove is then derived by setting n = 0. The proposition is proved by mathematical induction on k − n. As for the base case consider k − n = 2, and so n = k − 2. That means we have to show , which holds because ℑ satisfies transitivity. The induction step is for k − n = j > 2, and so n = k − j. From the induction hypothesis we get . And since r _n+1n (·) is a mapping, we also get . Once again, since ℑ satisfies the transitivity condition we have . By combining the last two inclusions we directly get

By setting n = 0 we derive the inclusion we wanted to prove, and hence the theorem.

And so we see that this weaker semantics only partially solves the problem of lacking subsumption propagation between remote ontologies. Subsumption propagates along chains of onto-bridge rules, but it fails to propagate along chains of into-bridge rules. On the other hand, compared to the stronger semantics, it satisfies the requirements that have been placed on DDL (Borgida and Serafini, 2003; Serafini et al., 2005), as we formally demonstrate later.

Theorem 6

The monotonicity property is satisfied in DDL under transitivity.

Proof

Given 𝒯 _i ∈ 𝔗 and C, D ∈ 𝒯 _i such that 𝒯 _i ⊧_ε C⊑D, only models of 𝒯 _i and ℐ^ε are allowed in the ℐ _i slot of any distributed model ℑ of 𝔗. Since in each of these C⊑D holds, we get 𝔗⊧_ε i: C⊑D directly from the definition.

While monotonicity is a rather trivial property that expectedly holds also for this semantics, recall that the stronger semantics we have presented in the previous section do not satisfy directionality, as we have shown. Fortunately the semantics of DDL under transitivity behaves more reasonably—directionality is satisfied—as we formally prove later.

Theorem 7

The directionality property is satisfied in DDL under transitivity.

Proof

Given a distributed TBox 𝔗, we shall prove that if there is no directed path from i to j in G_𝔗, then

where 𝔗⁻¹ is obtained by removing 𝒯 _i , 𝔅 _ik , and 𝔅 _li from 𝔗 for each k, l ∈ I, k, l ≠ i.

If part. By contradiction. Assume that 𝔗⁻ⁱ ⊧_ε j: C⊑D and 𝔗⊭_ε j: C⊑D. If 𝔗⊭_ε j: C⊑D then there is a distributed model ℑ of 𝔗 in which C ^{ℐ _j}  ⊈ D ^{ℐ _j} . Let ℑ⁻ⁱ be obtained from ℑ by removing ℐ _i and r _ik and r _ki for all k ≠ i. Since ℑ is a model of 𝔗, ℑ⁻ⁱ is a model of 𝔗⁻ⁱ (this follows directly from the construction). However and and hence . This implies that 𝔗⁻ⁱ ⊭_ε j: C⊑D but we have assumed the contrary.

Only-if part. By contradiction. Assume that 𝔗⊧_ε j: C⊑D and 𝔗⁻ⁱ ⊭_ε j: C⊑D. If 𝔗⁻ⁱ ⊭_ε j: C⊑D, there is a distributed model ℑ⁻ⁱ of 𝔗⁻ⁱ in which . Let J ⊂ I be the set of nodes reachable from i by some directed path in G_𝔗. Let ℑ be the following distributed interpretation of 𝔗:

1. for each m ∈ I∖J;

2. 2. ℐ _m  = ℐ^ε for each m ∈ J;

3. if m, n ∈ I∖J;

4. r _mn  = ∅ if either m ∈ J or n ∈ J.

We now show that ℑ is a distributed model of 𝔗. In order to demonstrate this, we need to show that local axioms and bridge rules of 𝔗 are satisfied by ℑ, and that the domain relation of ℑ is transitive.

Local axioms. For any m ∈ I, each local GCI axiom φ =m: G⊑H must be satisfied by ℐ _m . If m ∈ J then ℐ _m is a hole, which satisfies any local CGI axiom, and hence it also satisfies φ. If m ∈ I∖J then , which satisfies φ because ℑ⁻ⁱ is a distributed model of 𝔗⁻ⁱ and φ occurs in since .

Bridge rules. Given m, n ∈ I and a bridge rule b that maps from m: G to n: H, we must show that b is satisfied by ℑ. We distinguish between several cases. First, if m, n ∉ J, then b is satisfied by ℑ because , , and b is satisfied by ℑ⁻ⁱ . The case when m ∈ J and n ∈ I∖J is impossible, because there is a bridge rule from m to n and hence if m belongs to J, n must also belong to J. In all remaining cases n ∈ J. In this case it follows that r _mn (G ^{ℐ _m} ) = ∅ and H ^{ℐ _n}  = ∅, because r _mn  = ∅ and ℐ _n is a hole. In such a case however ℑ satisfies φ.

Transitivity. We have to show for any three mutually distinct indices k, m, n ∈ I that r _km ○ r _mn  ⊆ r _kn . If none of k, m, n belongs to J, then the fact that , , and implies r _km ○ r _mn  ⊆ r _kn . If at least one of k, m and n belongs to J, then either r _km or r _mn is equal to ∅, which implies that r _km ○ r _mn  = ∅ ⊆ r _kn .

And so we have shown that ℑ is a distributed model of 𝔗. However, since there is no directed path from i to j in G_𝔗, it follows that j ∉ J and hence and hence C ^{ℐ _j}  ⊈ D ^{ℐ _j} . This in turn implies that 𝔗⊭_ε j: C⊑D, but we have assumed the contrary.

Another property that is broken by the stronger semantics is the local inconsistency property. It turns out that this problem is indeed caused by the intricate implications of computational consistency and when we only require transitivity, the property holds.

Theorem 8

The local inconsistency property is satisfied in DDL under transitivity.

Proof

Given a distributed TBox 𝔗 over an index set I, and given some i ∈ I, a subsumption formula φ =i: C⊑D, we ought to prove the equivalence:

If part. Suppose by contradiction that for all subsets J of I such that i ∉ J, 𝔗(ε _J )⊧_dφ and 𝔗⊭_εφ. In that case there is an ε-model ℑ¹ of 𝔗 in which . Since this is an ε-model, some of its local interpretations are possibly holes. Let J be the set of all indices in I that hold a hole as local interpretation, i.e., . As ℑ¹⊭_εφ we have i ∉ J, because otherwise ℐ _i  = ℐ^ε and hole entails any formula including φ. Let ℑ² be the distributed interpretation obtained by cutting the holes off from ℑ¹, i.e., ℑ² has I∖J as its index set, for each j ∈ I∖J and for any j, k ∈ I∖J. We will now show that ℑ² is a d-model of 𝔗(ε _J ).

1. Indeed ℑ² is a d-interpretation, because it does not contain holes any more.

2. Given any j ∈ I∖J and any j-local GCI ψ, either ψ also belongs to 𝒯 _j of 𝔗 and hence it is satisfied by since ℑ¹ satisfies 𝒯 _j , or by construction of 𝔗(ε _J ) ψ =j: D⊑ ⊥ and there is some bridge rule in 𝔗 with k ∈ J. Since b is satisfied by ℑ¹ and we have and hence ψ is satisfied.

3. Also each bridge of 𝔗(ε _J ) rule, say b between 𝒯 _j and 𝒯 _k , j, k ∈ I∖J, is satisfied by ℑ² since b also appears in 𝔗 and , , and ℑ¹ satisfies b.

4. Moreover, ℑ² satisfies transitivity because ℑ¹ does and for any j, k ∈ I∖J.

Hence we have found a contradiction because 𝔗(ε _J ) ought to entail φ but it does not, since ℑ² is a model of 𝔗(ε _J ) in which (because , and ).

Only-if part. Suppose by contradiction that 𝔗⊧_εφ and there is J ⊆ I, not containing i, such that 𝔗(ε _J )⊭_dφ. In this case there must be a d-model of 𝔗(ε _J ), say ℑ¹ such that . Let us construct a distributed interpretation ℑ², starting from ℑ¹ and adding hole into each slot j ∈ J, i.e., for each j ∈ I∖J and for each j ∈ J. Moreover, for any pair of indices j, k ∈ I we set if both i, j ∈ I∖J and otherwise. We now prove that ℑ² is an ε-model of 𝔗.

1. Obviously ℑ² is an ε-interpretation of 𝔗.

2. Each local GCI ψ in 𝔗 is satisfied, as if ψ ∈ 𝒯 _j , j ∈ I∖J then ψ also appears in 𝔗(ε _J ) and since we have entails ψ. If ψ ∈ 𝒯 _k , k ∈ J then ψ is satisfied since is a hole.

3. Let b be a bridge rule directed from 𝒯 _j and 𝒯 _k , j, k ∈ I that maps between j: C and k: D. If both j, k ∈ I∖J then b is satisfied because it is satisfied by ℑ¹ and we have , , . If both j, k ∈ J than b is satisfied because , and . If j ∈ I∖J and k ∈ J than b is satisfied because and . If j ∈ J and k ∈ I∖J and then b is satisfied because which surely is a subset of . The last case occurs when j ∈ J, k ∈ I∖J and . In this case b is also satisfied because by construction the local GCI k: D⊑ ⊥ belongs to 𝔗(ε _J ) and hence which surely is a subset of .

4. Finally, we show that the domain relation r ² is transitive, that is, for any three mutually distinct k, m, n ∈ I it holds that . If none of k, m, n belongs to J that this holds because , , , and r ¹ is transitive. Thanks to the construction of ℑ² however, in any other case either (if k ∈ J or m ∈ J) or (if m ∈ J or n ∈ J). Hence in all these cases transitivity trivially holds, since .

And so we have just shown that ℑ² is an ε-model of 𝔗. Now we again reach contradiction, as we have assumed that 𝔗 entails φ but (because , and ).

And so we have shown that in the semantics of DDL under transitivity the level of subsumption propagation between remote ontologies is limited to propagation along chaining onto-bridge rules in scenarios that instantiate Theorem 5. Propagation of subsumption along chaining into-bridge rules is not granted, but all desiderata postulated for DDL, including directionality and local inconsistency are satisfied.

DDL with Restricted Compositionality

We will now follow the other approach that we have outlined. In this approach we keep both restrictions (5) and (6), but we try to apply them more cautiously. This approach is motivated by the following example.

Example 5

Consider a distributed TBox 𝔗 which contains local ontologies about cats 𝒯 _c , music 𝒯 _m , botany 𝒯 _b , and another one about fruit 𝒯 _f . Suppose that there is some knowledge encoded within each of them and they are all consistent. There are also some bridge rules between 𝒯 _b and 𝒯 _f for instance:

In contrast the two local ontologies 𝒯 _c and 𝒯 _t are completely isolated. Let ℑ be a model of 𝔗 in which Berry ^{ℐ _f} is nonempty and hence there are some x ∈ Berry ^{ℐ _b} , y ∈ Berry ^{ℐ _f} such that (x, y) ∈ r _bf . So far this situation is perfectly natural. However, compositional consistency requires existence of z ₁ ∈ Δ^{ℐ _c} and z ₂ ∈ Δ^{ℐ _m} such that (x, z ₁) ∈ r _bc , (z ₁, y) ∈ r _cf , (x, z ₂) ∈ r _bm and (z ₂, y) ∈ r _mf . In turn, (x, z ₁) ∈ r _bc implies existence of (x, w ₁) ∈ r _bm , (w ₁, z ₁) ∈ r _mc , (x, w ₂) ∈ r _bf and (w ₂, z ₁) ∈ r _fc , etc. As we can see, even if local TBoxes 𝒯 _c and 𝒯 _m are totally unrelated, compositional consistency implies existence of elements in ℐ _c and ℐ _m and generates many r-connections between these elements and elements of the other local TBoxes. Such behavior is indeed rather strange and as we have seen it even causes trouble in the sense that some important DDL properties are violated.

From the example above we conjecture that compositional consistency is perhaps a stronger condition than we really need in order to support subsumption propagation. It does the job, as established by Theorem 4, but in addition, it has undesirable side effects. In this case, we try to weaken the condition as follows. Given a distributed TBox and a distributed interpretation over some index set I, we do not require compositional consistency to hold for every i, j, k ∈ I, but only when local TBoxes 𝒯 _i , 𝒯 _j , and 𝒯 _k are actually connected with bridge rules. The relaxed version of the restriction is as follows.

Definition 11

Given a distributed TBox 𝔗 with an index set I and bridge graph G_𝔗, let ℑ be a distributed interpretation of 𝔗 with domain relation r, we say that r (and also ℑ) satisfies restricted compositional consistency (also restricted compositionality) if for any three mutually distinct indices i, j, k ∈ I such that there is a directed path from i to j and another one from j to k in G_𝔗 we have r _ij ○ r _jk  = r _ik .

The semantics of DDL under this condition is called DDL under restricted compositionality. This restriction is reasonable in the sense that the proposition of Theorem 4 holds even in this relaxed case. In other words, subsumption does propagate along both: chains of into- and chains of onto-bridge rules. This is verified by inspection of the proof given by Homola (2008): compositional consistency is only applied in this proof in cases which are covered also by the weaker version. Also directionality is satisfied under this semantics.

Theorem 9

The directionality property is satisfied in DDL under restricted compositionality.

Proof

Given a distributed TBox 𝔗 we shall prove that if there is no directed path from i to j in G_𝔗, then

where 𝔗⁻¹ is obtained by removing 𝒯 _i , 𝔅 _ik , and 𝔅 _li from 𝔗 for each k, l ∈ I, k, l ≠ i.

If part. By contradiction. Assume that 𝔗⁻ⁱ ⊧_ε j: C⊑D and 𝔗⊭_ε j: C⊑D. If 𝔗⊭_ε j: C⊑D then there is a distributed model ℑ of 𝔗 in which C ^{ℐ _j}  ⊈ D ^{ℐ _j} . Let ℑ⁻ⁱ be obtained from ℑ by removing ℐ _i and r _ik and r _ki for all k ≠ i. Since ℑ is a model of 𝔗, ℑ⁻ⁱ is a model of 𝔗⁻ⁱ (this follows directly from the construction). However and and hence . This implies that 𝔗⁻ⁱ ⊭_ε j: C⊑D but we have assumed the contrary.

Only-if part. By contradiction. Assume that 𝔗⊧_ε j: C⊑D and 𝔗⁻ⁱ ⊭_ε j: C⊑D. If 𝔗⁻ⁱ ⊭_ε j: C⊑D, there is a distributed model ℑ⁻ⁱ of 𝔗⁻ⁱ in which . Let J ⊂ I be the set of nodes reachable from i by some directed path in G_𝔗. Let ℑ be the following distributed interpretation of 𝔗:

1. for each m ∈ I∖J;

2. ℐ _m  = ℐ^ε for each m ∈ J;

3. if m, n ∈ I∖J;

4. r _mn  = ∅ if either m ∈ J or n ∈ J.

We now show that ℑ is a distributed model of 𝔗. In order to demonstrate this, we need to show that local axioms and bridge rules of 𝔗 are satisfied by ℑ, and that the domain relation of ℑ satisfies the restricted compositionality condition.

Local axioms. For any m ∈ I, each local GCI axiom φ =m: G⊑H must be satisfied by ℐ _m . If m ∈ J then ℐ _m is a hole, which satisfies any local CGI axiom, and hence it also satisfies φ. If m ∈ I∖J then , which satisfies φ because ℑ⁻ⁱ is a distributed model of 𝔗⁻ⁱ and φ occurs in since .

Bridge rules. Given m, n ∈ I and a bridge rule b that maps from m: G to n: H, we must show that b is satisfied by ℑ. We distinguish between several cases. First, if m, n ∉ J, then b is satisfied by ℑ because , , and b is satisfied by ℑ⁻ⁱ . The case when m ∈ J and n ∈ I∖J is impossible, because there is a bridge rule from m to n and hence if m belongs to J, n must also belong to J. In all remaining cases n ∈ J. In this case it follows that r _mn (G ^{ℐ _m} ) = ∅ and H ^{ℐ _n}  = ∅, because r _mn  = ∅ and ℐ _n is a hole. In such a case however ℑ satisfies φ.

Restricted compositionality. Let k, m, n ∈ I be three mutually distinct indices such that there exists a directed path from k to m in G_𝔗 and another one from m and n. We must now show that r _km ○ r _mn  = r _kn . If none of k, m, n belongs to J, then the fact that , , and implies that r _km ○ r _mn  = r _kn . If k ∈ J, then the fact that r _km  = ∅ and r _kn  = ∅ implies that r _km ○ r _mn  = r _kn . If m ∈ J then necessarily also n ∈ J since there is a directed path between these two nodes in G_𝔗. But n ∈ J implies that r _mn  = r _kn  = ∅, thus implying r _km ○ r _mn  = r _kn . Finally if n ∈ J then again r _mn  = r _kn  = ∅, and so r _km ○ r _mn  = r _kn .

And so we have shown that ℑ is a distributed model of 𝔗. However, since there is no directed path from i to j in G_𝔗, it follows that j ∉ J and hence and hence C ^{ℐ _j}  ⊈ D ^{ℐ _j} . This in turn implies that 𝔗⊭_ε j: C⊑D, but we have assumed the contrary.

And so we have shown that this restricted form of compositional consistency does not break directionality. Unfortunately, there are still some undesired effects that this restriction poses on the semantics as demonstrated by the example below.

Example 6

Consider distributed a TBox 𝔗 with index set I = {1, 2, 3} and a set of bridge rules 𝔅, such that 𝒯₁ = {⊤ ⊑ ⊥}, 𝒯₂ = ∅, 𝒯₃ = ∅ which contains bridge rules:

Since 𝒯₁ is inconsistent, the only admissible interpretation is a hole, and so due to compositional consistency, even in the restricted case, r ₂₃ = ∅. Hence 𝔗⊧_ε3: D⊑ ⊥. If local inconsistency would hold, then for each J ⊆ I, 3 ∉ J we must have 𝔗(ε _J )⊧_d3: D⊑ ⊥. Similarly, as in Example 3, for J = {1} this does not hold, as 𝔗(ε _J ) admits a d-model ℑ with Δ^ℐ₂  = C ^ℐ₂  = {x}, Δ^ℐ₃  = D ^ℐ₃  = {y}, r ₂₃ = {⟨x, y⟩} and r ₃₂ = ∅, for which ℑ⊭_d3: D⊑ ⊥ since D ^ℐ₃  ≠ ∅.

In this section we have examined and evaluated the approach of applying the compositional consistency restriction in DDL in order to improve subsumption propagation (Homola, 2008). We have shown that while subsumption propagation is indeed improved, there are also undesirable consequences of such an approach: the directionality and the local inconsistency properties are violated. In order to retain directionality we have verified two options. First, falling back from computational consistency to transitivity which amounts to less subsumption propagation but all desired properties of DDL are retained. And second, applying compositional consistency more cautiously, only if the local ontologies that are involved are connected by some directed path of bridge rules. The second approach provides just the same level of subsumption propagation as the semantics under unrestricted compositionality and also retains directionality but as we have just seen it still violates the local inconsistency property.

Summing up, with respect to the current state of the art, the semantics of DDL with transitive domain relation provides a reasonable compromise. It ensures subsumption propagation along chaining onto-bridge rules in scenarios that instantiate Theorem 5. Propagation of subsumption under chaining into-bridge rules is not granted, but all desiderata postulated for DDL, including transitivity and localized inconsistency, are satisfied. In the next section we take a look at reasoning with this semantics.

DISTRIBUTED TABLEAUX ALGORITHM FOR TRANSITIVE DDL

In this section, we introduce a distributed tableaux algorithm for deciding satisfiability of concepts with respect to an acyclic distributed TBox for DDL over 𝒜ℒ𝒞 under the transitivity requirement. As much as in the original algorithm (Serafini et al., 2005), also in our approach, local reasoners are run independently. We keep precise track of the domain relation r however, and the communication between local reasoners is divided into multiple queries. Hence, while the original algorithm can be seen as working with autonomous local tableaux by passing queries, our algorithm can be seen as working with a truly distributed tableau.

Definition 12

Assume a distributed TBox 𝔗 = ⟨{𝒯 _i } _i∈I , ℬ⟩ over 𝒜ℒ𝒞 with index set I, concept names and role names . Let CC _i be the set of all (atomic and complex) concepts over N_{C i} and N_{R i} in negation normal form. A distributed completion tree ³ T = {T _i } _i∈I is a set of labeled trees T _i  = ⟨V _i , E _i , ℒ _i , r _i ⟩, such that for each i ∈ I:

1. the trees {⟨V _i , E _i ⟩} _i∈I are mutually disjoint;

2. the labeling function ℒ _i labels each node x ∈ V _i with ℒ _i (x) ⊆ 2^{CC _i} and each edge ⟨x, y⟩ ∈ E _i with ℒ _i (⟨x, y⟩) ∈N_{R i} ;

3. the labeling function r _i labels each node x ∈ V _i with a set of references to its r-images r _i (x) ⊆ {j: y | j ∈ I ∧ y ∈ V _j }.

During the run of the tableaux algorithm, tableaux expansion rules are applied on the completion tree and the tree is expanded by each rule application. If no more rules are applicable, we say that the completion tree is complete. There is a clash in the completion tree T if for some x ∈ V _i and for some C ∈ N_{C i} we have {C, ¬ C} ⊆ ℒ _i (x). If there is no clash in T then we say that T is clash-free. In order to assure termination we use the standard subset blocking technique that is common for 𝒜ℒ𝒞. Given a distributed completion tree T = {T _i } _i∈I , a node x ∈ V _i is blocked, if it has an ancestor y ∈ V _i such that ℒ _i (x) ⊆ ℒ _i (y). In such a case we also say that x is blocked by y. A node y ∈ V _i is said to be an R-successor of x ∈ V _i , if ⟨x, y⟩ ∈ E _i and ℒ _i (⟨x, y⟩) = R.

The distributed tableaux algorithm for deciding satisfiability of concepts with respect to a distributed TBox takes a distributed TBox 𝔗, a concept C in NNF and i ∈ I as its inputs. The algorithm then continues in three steps:

1. Initialization. Create a new completion tree T = {T _j } _j∈I such that T _j  = ⟨{s ₀}, ∅, {s ₀ → {C}}, ∅⟩ for j = i and T _j  = ⟨∅, ∅, ∅, ∅⟩ for j ≠ i.

2. Tableau expansion. Apply the tableaux expansion rules of Figure 8 exhaustively.

3. Answer. If none of the tableaux expansion rules in Figure 8 are applicable any longer (i.e., the completion tree is now complete), answer “C is satisfiable” if a clash-free completion tree has been constructed. Answer “C is unsatisfiable” otherwise.

FIGURE 8 Tableaux expansion rules for DDL over 𝒜ℒ𝒞 under the transitivity requirement. First five rules are standard 𝒜ℒ𝒞 tableaux rules. Note that the ⊔ -rule is nondeterministic. The final two rules are new and are triggered by bridge rules.

Below we present a formal correctness proof for the newly introduced algorithm. The proof is based on the classic proof for 𝒜ℒ𝒞 as in fact the only new thing to prove here is that the algorithm uses the -rule and the -rule to combine several autonomous local 𝒜ℒ𝒞 reasoners correctly. The proof is done in three parts. We first prove termination: on every input the algorithm always terminates and never ends up in an infinite loop; then soundness: if the algorithm answers that C is satisfiable with respect to 𝔗 for some i-local concept C and a distributed TBox 𝔗, then there actually exists some model of 𝔗 that supports this; and finally we prove completeness: for every concept C that is satisfiable with respect to 𝔗, the algorithm indeed gives a correct answer.

Theorem 10

Given a distributed TBox 𝔗 over 𝒜ℒ𝒞 with acyclic bridge graph G_𝔗 and an i-local concept C on the input, the distributed tableaux algorithm for deciding satisfiability of concepts with respect to a distributed TBox over 𝒜ℒ𝒞 for DDL with transitive domain relation always terminates and it is sound and complete.

Proof

Termination. Given a distributed TBox 𝔗 with local TBox 𝒯 _i and an i-local concept C, we ought to prove that the algorithm, once started with 𝔗, C, and i on input, eventually terminates. The algorithm initializes the completion tree to T = {T _j } _j∈I such that T _j  = ⟨{s ₀}, ∅, {s ₀ → {C}}, ∅⟩ for j = i and T _j  = ⟨∅, ∅, ∅, ∅⟩ for j ≠ i. The computation then continues by expanding T _i . If there are no onto-bridge rules ingoing into 𝒯 _i the algorithm eventually terminates thanks to subset blocking, this result is known for 𝒜ℒ𝒞. If there are some ingoing onto-bridge rules, then possibly in some x ∈ V _i such that C ∈ ℒ _i (x) and C appears on a right-hand side of an onto-bridge rule, say , the -rule is applied and computation is triggered in T _k . By structural induction we assume that this computation eventually terminates (the length of the longest incoming path of onto-bridge rules decreased for 𝒯 _k compared to 𝒯 _i , and all such paths are finite because of acyclicity). During this process we possibly get some new concepts in ℒ _i (x) that are introduced thanks to incoming into-bridge rules that trigger the -rule—but only finitely many. The computation now continues in x and its descendants and possibly the -rule is triggered again in some y ∈ V _i , a descendant of x. But thanks to subset blocking, this happens only finitely many times. Hence the algorithm eventually terminates.

Soundness. Now that we know that the algorithm terminates, we shall prove that if it answers “C is satisfiable” on input 𝔗, C, and i, then it also holds that C is satisfiable in 𝒯 _i with respect to 𝔗, that is we must show that in such a case there exists a distributed model ℑ of 𝔗 such that C ^{ℐ _i}  ≠ ∅. Given 𝔗, C, and i and let T be the complete and clash-free completion tree that the algorithm has constructed to support the decision. Let us construct the distributed interpretation ℑ as follows:

1. Let Δ^{ℐ _i}  = V _i , for each i ∈ I.

2. Let x ∈ A ^{ℐ _i} , for each atomic concept A ∈ ℒ _i (x), for each x ∈ V _i and each i ∈ I.

3. Let ⟨x, y⟩ ∈ R ^{ℐ _i} for each ⟨x, y⟩ ∈ E _i such that ℒ _i (⟨x, y⟩) = R, for each i ∈ I, if y is not blocked.

4. Let ⟨x, z⟩ ∈ R ^{ℐ _i} for each ⟨x, y⟩ ∈ E _i such that ℒ _i (⟨x, y⟩) = R, for each i ∈ I, in case that y is blocked by z.

5. Let rij(x) = y for each x ∈ V _i and for each j: y ∈ r _i (x).

Please observe that if computation was never triggered within some T _j of T during the run of the algorithm, then ℐ _j  = ℐ^ε. It remains to show that ℑ is in fact a model of 𝔗 and C ^{ℐ _i}  ≠ ∅. We will first prove the following proposition:

Given any i ∈ I, for each E ∈ ℒ _i (x) (i.e., also for complex concepts) we have x ∈ E ^{ℐ _i} .

This is proven by induction on the structure of E. We need to consider the following cases:

1. E is atomic. We know that x ∈ E ^{ℐ _i} from the construction.

2. E = ¬ E ₁, E ₁ atomic. Since T is clash-free, E ₁ ∉ ℒ _i (x) and by construction . In that case, however, .

3. E = E ₁ ⊓ E ₂. Since T is complete, the ⊓ -rule is not applicable and hence also E ₁ ∈ ℒ _i (x) and E ₂ ∈ ℒ _i (x). By induction, we now have that and and hence also x ∈ E ^{ℐ _i} .

4. E = E ₁ ⊔ E ₂. Since T is complete, the ⊔ -rule is not applicable and hence either E ₁ ∈ ℒ _i (x) or E ₂ ∈ ℒ _i (x). By induction we now either have or we have . In either case however also x ∈ E ^{ℐ _i} .

5. E = ∃ R·E ₁. Since T is complete, the ∃ -rule is not applicable and hence there must be y ∈ V _i , an R-successor of x such that E ₁ ∈ ℒ _i (y). By induction and by construction of ℑ ⟨x, y⟩ ∈ R ^{ℐ _i} . But that means that x ∈ E ^{ℐ _i} .

6. E = ∀ R·E ₁. Since T is complete, the ∀ -rule is not applicable and hence for every y ∈ V _i , an R-successor of x, we have E ₁ ∈ ℒ _i (y). By induction and by construction of ℑ ⟨x, y⟩ ∈ R ^{ℐ _i} . But that means that x ∈ E ^{ℐ _i} .

Thus we have verified that the local interpretation ℐ _i is indeed an 𝒜ℒ𝒞 interpretation and that C has an instance in this interpretation (since C ∈ ℒ _i (s ₀)). In addition we have in fact also proven that each i-local GCI axiom E ₁⊑E ₂ is satisfied by ℐ _i —from the completeness of T, nnf(¬ E ₁ ⊔ E ₂) ∈ x, for each x ∈ V _i , and hence . It follows that implies .

It remains to show that ℑ is indeed a distributed model of 𝔗 in the adjusted semantics. First, all the bridge rules must be satisfied. Given an onto-bridge rule , we ought to show that . So let , that is x ∈ V _l and E ₂ ∈ ℒ _l (x). But T is complete, -rule is not applicable, and hence there must be y ∈ V _k with E ₁ ∈ ℒ _k (y) and l: x ∈ r _k (y). That means, however, that and ⟨x, y⟩ ∈ r _kl , and so . Therefore, the bridge rule is satisfied by ℑ.

Given an into-bridge rule , we ought to show that . Let . Then there is y ∈ V _k such that l: x ∈ r _l (y). But since T is complete, it must be the case that E ₂ ∈ ℒ _l (x) and hence . Therefore the bridge rule is satisfied by ℑ.

The last thing in order to verify that ℑ is indeed a model of 𝔗 is to show that ℑ satisfies the transitivity requirement. We ought to show that for each k, l, m ∈ I, if y ∈ r _kl (x) and z ∈ r _lm (y) then also z ∈ r _km (x). Given the two assumptions we know by construction that l: y ∈ r _k (x) and m: z ∈ r _l (y). That means that x ∈ V _k was initialized after several “chained” applications of the -rule starting from y ∈ V _l and y in turn after several “chained” -rule applications starting from z ∈ V _m . In that case, however, r _l (y) ⊆ r _k (x). Hence m: z ∈ r _k (x) and so z ∈ r _km (x).

And thus ℑ is a distributed model of 𝔗 that satisfies the transitivity condition and C ^{ℐ _i}  ≠ ∅ —in other words, C is satisfiable in 𝒯 _i with respect to 𝔗.

Completeness. Given 𝔗 with index set I, a concept C and i ∈ I such that C is satisfiable in 𝒯 _i with respect to 𝔗, we shall prove that the algorithm answers “C is satisfiable,” if run on input 𝔗, C, and i. Let ℑ be a distributed model of 𝔗 with C ^{ℐ _i}  ≠ ∅, we know that one must exist. We will simulate the run of the algorithm. During the initialization T _i is set to ⟨{s ₀}, ∅, {s ₀ → {C}}, ∅⟩ and all the other T _j , i ≠ j, are set to ⟨∅, ∅, ∅, ∅⟩. There is no clash in T. We will show by induction (on the number of tableau expansion steps) that after each tableau expansion step the completion tree T is expanded in such a way that no clash is introduced. In order to demonstrate this, we inductively construct an auxiliary mapping to track the relation between ℑ and T. This mapping will keep the property (*):

Let x be an arbitrary member of C ^{ℐ _i} , place π(s ₀) = x. So, if a tableaux expansion rule is triggered in some x ∈ V _i of the clash-free completion tree T (from induction hypothesis), we consider several cases, based on the kind of rule that was triggered:

1. ⊓-rule is triggered in x because E ₁ ⊓ E ₂ ∈ ℒ _i (x). Then by induction hypothesis . In that case also and , and hence the property (*) is maintained after the algorithm adds E ₁ and E ₂ to ℒ _i (x).

2. ⊔-rule is triggered in x because E ₁ ⊔ E ₂ ∈ ℒ _i (x). Then by induction hypothesis . In that case, however, either or . Without loss of generality, let it be the case that . Without loss of generality, we assume that the algorithm adds E ₁ to ℒ _i (x), as a nondeterministic decision takes place. Hence, the property (*) is maintained after this step.

3. ∃-rule is triggered in x because it has an R-successor y, and ∃ R·E ₁ ∈ ℒ _i (x). Then π(x) ∈ ∃ R ·E ₁ ^{ℐ _i} and so there is some y′ ∈ Δ^{ℐ _i} such that and ⟨π(x), y′⟩ inR ^{ℐ _i} . When the algorithm generates a new node y in this step we set π(y) = y′ and the property (*) is maintained.

4. ∀-rule is triggered in x because it has an R-successor y, and ∀ RRE ₁ ∈ ℒ _i (x), as a consequence E ₁ is added to ℒ _i (y). We know that y was created by an application of the ∃ -rule and hence π(y) is an R-successor of x in ℐ _i . But ℐ _i is a model of 𝒯 _i and hence π(y) ∈ y ^{ℐ _i} since from induction hypothesis we know that . Hence (*) is maintained after this step.

5. 𝒯-rule is triggered in x, resulting to adding nnf(¬ E ₁ ⊔ E ₂) into ℒ _i (x). Then (*) is maintained as ℐ _i is a model of 𝒯 _i and so it holds that π(x) ∈ (nnf(¬ E ₁ ⊔ E ₂))^{ℐ _i} .

6. -rule is triggered in x because E ₂ ∈ ℒ _i (x) and . From induction hypothesis, , and hence π(x) ∈ r _ji (y′) for some . Set π(y) = y′ for the node y that is newly created in V _i as the result of this expansion step. The label ℒ _j (y) has been set to E ₁ but since then (*) is maintained.

7. -rule is triggered in x because of E ₁ ∈ ℒ _i (x), j: y ∈ r _i (x) and , resulting to adding E ₂ into ℒ _j (y). From induction hypothesis have . Observe that the definition of -rule and the inductive construction of π(·) in previous steps also assure that j: y ∈ r _i (x) implies π(y) ∈ r _ij (π(x)). This is because initialization of new y ∈ V _j always follows incoming r-edge and r is transitive because of computational consistency. It follows that , since ℑ is a distributed model of 𝔗 and the bridge rule assures this. Hence (*) is maintained even after this step.

We already know that the algorithm always terminates. Once this happens, it follows that T is now complete, because no rule is applicable, and clash-free, because the property (*) is maintained all the way up to this point. Hence the algorithm answers “C is satisfiable” and hence the theorem.

The algorithm for the original DDL semantics of Serafini et al. (2005) is obviously truly distributed in the sense that it supports a scenario in which several autonomous reasoning services run independently, one for each local ontology, and communicate by passing queries. While this is also the case for the newly introduced algorithm, it is not necessarily that obvious. In order to clarify this, we provide a message protocol that handles -rule and -rule execution in a truly distributed fashion, and it also collects the information that the completion tree is complete within the reasoner that has initialized the computation. The algorithm employs three kinds of messages querySat(x, r, C), answerSat(x, C, answer), and pushConcept(x, C). In the message-based version, the algorithm starts by initializing the local completion tree T _j when asked for satisfiability of some j-local concept C with respect to 𝔗. More local completion trees are initialized during the runtime by passing a querySat(x, r, C) message every time the -rule is fired. When -rule is fired, the consequences of the into-bridge rule are propagated by passing a pushConcept(x, C) message. Once a local completion tree T _k is complete this is announced by passing a answerSat(x, C, answer) message to the local reasoner that has triggered the computation in 𝒯 _k . Detailed specification of the protocol messages is given in Figure 9.

FIGURE 9 The message protocol for the newly introduced distributed tableaux algorithm. For each kind of message we specify when the message is sent from some local reasoning service T _j and also what happens when the message is received in some local reasoning service T _j (T _j is always the local reasoning service). An auxiliary data structure S _j is introduced in each T _j in order to track messages that have been sent in order to assure termination.

RELATED WORK

A distributed tableaux reasoning algorithm for the original semantics of DDL has been introduced by Serafini and Tamilin (2005) and Serafini et al. (2005), and implemented in the system DRAGO. ⁴ This algorithm is based on a fix-point characterization of the original DDL semantics. Given a set of bridge rules 𝔅 _ij between 𝒯 _i and 𝒯 _j , define the operator 𝔅 _ij (·) as follows:

Consequently, another operator denoted by 𝔅, is defined:

As showed by Serafini et al. (2005), the 𝔅 operator always has a fix-point 𝔅*(𝔗) when repeatedly applied on a distributed TBox 𝔗. Moreover, 𝔗⊧_ε i: φ if and only if the ith component TBox of 𝔅*(𝔗) locally entails φ. Consequently, the standard 𝒮ℋℐ𝒬 tableaux reasoning algorithm (Horrocks et al., 1999) is used with one additional bridge rule (see Figure 10). The unsatisfiability check called by 𝔅 _ij -rule is done by running the same algorithm again for the i-concept that is being checked. Compared to the algorithm introduced in this article, this algorithm does not keep track of the domain relation r and does not in fact construct a true distributed tableau that would correspond to a particular distributed model of the input concept. Instead, it cleverly uses the fix-point characterization and constructs multiple local tableaux in order to guarantee the existence of such a model. Most prominently, all consequences that are added to the triggering node if the unsatisfiability check is successful are estimated prior to the unsatisfiability check is executed. In contrast, in our approach computation in remote ontology is triggered by one message and consequences are announced back to the triggering node once they are computed, possibly by several independent messages. We believe that keeping precise track of all model structures, including the domain relation and dividing the communication into more fine-grained messages may provide better grounds for future optimization. In a sense we may conclude that in the way how calls are made to the remote tableaux, the original algorithm by Serafini et al. (2005) resembles more a black box approach, whereas the newly introduced algorithm is more like a glass box approach. Another significant difference between the two algorithms is that unlike the newly introduced algorithm, the original one is able to handle cyclic bridge rules; a blocking strategy that is employed to achieve this was described by Tamilin (2007, Sect. 5.3.4, p. 91). Finally, it is worth noting that the newly introduced algorithm is easily adjusted to correspond to the original DDL semantics (by setting r _i (y) to {j: x} and not to {j: x} ∪ r _j (x) in the -rule).

FIGURE 10 The tableaux expansion rule used in the original DDL algorithm (Serafini and Tamilin, 2005).

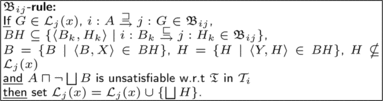
Another distributed ontology framework is called ℰ-connections (Cuenca Grau, Parsia, and Sirin, 2004). Here, interontology roles (called links) are employed instead of concept mapping. A dedicated set of symbols ε _ij is used for (directed) links between 𝒯 _i and 𝒯 _j . Links are then used in existential and value restrictions, and complex concepts involving links are formed (for instance, the i-concept ∀ E.C is composed using the link E ∈ ε _ij and the j-concept C). Semantically, a combined interpretation consists of local interpretations ℐ _i with nonempty domains Δ^{ℐ _i} and each link E ∈ ε _ij is interpreted by E ^ℐ ⊆ Δ^{ℐ _i}  × Δ^{ℐ _j} . Reasoning support for ℰ-connections is provided by extending the tableaux reasoning algorithm for 𝒮ℋℐℱ(D). The two tableaux rules that are essential to handle links are depicted in Figure 11. There is a notable correspondence between the ∃ _link -rule and our -rule and also between the ∀ _link -rule and our -rule. This is not that surprising, given the known correspondence between DDL and ℰ-connections (Kutz, Lutz, Wolter, and Zakharyaschev, 2004). Given the nature of ℰ-connections the ∀ _link -rule works exactly the other way around, compared to our -rule, and in this respect the instantiation of a j-tree by one application of the ∃ _link -rule and possibly multiple applications of the ∀ _link -rule resembles an unsatisfiability check call from the 𝔅 _ij -rule of the original DDL algorithm. Remarkably, the exact mechanism how this happens within the ℰ-connections algorithm seems to be more transparent and prone to optimization. The algorithm introduced in this article in addition keeps track on the domain relation, which is needed to handle subsumption propagation along chains of bridge rules. There is no domain relation within ℰ-connections, and hence no need for such a feature.

FIGURE 11 The tableaux expansion rules of the algorithm for ℰ-connections (Cuenca Grau et al., 2004).

Yet another point of view on distributed ontologies is offered by package-based description logics, or P-DL (Bao, Caragea, and Honavar, 2006). In P-DL, the intuition of importing is pursued: every concept name belongs to some local ontology, but can be also imported to and used by other ontologies in the system. The P-DL semantics uses domain relations. In contrast to other approaches, only one-to-one domain relations are allowed and also compositional consistency (that we have borrowed and applied on DDL) is required. Local domains in P-DL semantics are viewed as partially overlapping, and not disjoint. As a result, some of the problems known for DDL, such as restricted knowledge propagation between remote ontologies, which we also address in this article, are not an issue for P-DL according to Bao et al. (2006). On the other hand, in P-DL, reasoning over a distributed ontology is always equivalent to reasoning over the union of local ontologies, which is not a goal of DDL. The distributed tableaux algorithm for P-DL is introduced by Bao et al. (2006). It uses 𝒜ℒ𝒞 as local language and requires acyclic importing relation. It uses message-based protocol, similar to ours, and keeps track of the domain relation. Since imported concepts may appear anywhere in the importing ontology, messages are invoked directly from the adjusted 𝒜ℒ𝒞-tableaux rules.

A completely different approach to distributed ontology reasoning is taken by Schlicht and Stuckenschmidt (2008), where distributed reasoning algorithm based on resolution techniques is introduced. Yet another distributed ontology framework called integrated distributed description logics (IDDL) is introduced by Zimmermann (2007), a reasoning algorithm based on reduction to multiple DL knowledge bases that are checked for consistency independently, and described by Zimmermann and Le Duc (2008).

CONCLUSION

In this article we have studied subsumption propagation in DDL. We point out that subsumption propagation is not sufficient in cases where local ontologies are only connected indirectly by a chain of bridge rules. This can be seen as a completion of the earlier work of Homola (2008). After an analysis of the properties that are (not) enjoyed by the different alternatives, we found that the most appropriate extension is the one that satisfies the so-called transitivity condition. For this extension we develop a distributed tableaux reasoning algorithm that decides satisfiability of concepts and subsumption with respect to the adjusted semantics. The algorithm that is introduced in this article handles chaining onto-bridge rules correctly, but is unable to cope with chaining into-bridge rules.

As in the case of the tableaux algorithm that is known for the original semantics (Serafini et al., 2005), the newly introduced algorithm is also fully distributed and it permits the scenario where every local ontology is governed by an autonomous reasoning service and these services communicate by passing queries. The local reasoner that has started the computation collects all the answers and makes the final decision at the end. To demonstrate this fact more clearly, we have provided a message-based protocol for the algorithm. Besides the fact that each of these algorithms works under a different semantics, the main distinguishing feature of the newly introduced algorithm is that communication between local reasoners is divided into multiple messages. Computation is sparked in a remote reasoner at some point and both reasoners continue to run independently. If subsumption propagation is proven by the remote reasoner, the local reasoner is acknowledged by a message. We believe that such behavior may serve as a base for more fine-grained optimization in the future.

The two most prominent open issues put forward by this article are: extending the algorithm so that it would handle DDL under compositional consistency to the full extent, that is, also dealing with chaining into-bridge rules; and, extending the algorithm towards more expressive DL, since the current version only supports 𝒜ℒ𝒞 as the local representation language and requires acyclic concept mapping. Computational handling of distributed knowledge bases in which the concept mapping is not necessarily acyclic is an interesting problem. Remaining research problems that are closely related to this work include practical evaluation of the algorithm by implementation, complexity analysis for the decision problems, and combining, within a unified framework, the current approach with that of Homola (2007), which has addressed the problem of interaction between bridge-rules in DDL.

This work was supported from projects VEGA nos. 1/0173/03 and 1/0719/09 awarded by Slovak Ministry of Education and Slovak Academy of Sciences and also from the project no. UK/365/2008 awarded by Comenius University. The authors would like to thank Ján Kl’uka and Michaela Danišová.

Notes

Even if the DDL framework has been extended for representing mappings between roles and also so-called heterogeneous mappings (i.e., mappings between concepts and roles) (Ghidini, Serafini, and Tessaris, 2007), in this article we restrict to the case of mapping between concepts.

Let also any distributed interpretation that does not contain holes be called a d-interpretation and also let each d-interpretation that is a distributed model of 𝔗 be called a d-model of 𝔗. In order to make the distinction explicit, we will also use the terms ε-interpretation and ε-model in order to indicate that holes may be present.

We prefer the usual naming, and we use the name distributed completion tree even if it is technically no longer a tree but rather a forest, that is, a graph composed of several isolated independently rooted trees.

DRAGO Reasoner homepage: http://drago.itc.it/