MODEL-CHECKING ALTERNATING-TIME TEMPORAL LOGIC WITH STRATEGIES BASED ON COMMON KNOWLEDGE IS UNDECIDABLE

Abstract

We present a semantics for the Alternating-time Temporal Logic (ATL) with imperfect information, in which the participants in a coalition choose their strategies such that each agent's choice is the same in all states that form the common knowledge for the coaltion. We show that ATL with this semantics has an undecidable model-checking problem if the semantics is also synchronous and the agents have perfect recall.

INTRODUCTION

Alternating-time Temporal Logic (ATL) (Alur, Henzinger, and Kupferman 1998; 2002) is a modal logic that generalizes CTL. It is defined over concurrent game structures with one or more players. A formula in ATL expresses that a coalition A of agents can cooperate to ensure that the formula φ holds.

Different semantics have been given for the cooperation modalities, depending on whether the knowledge that each agent has of the current state of the game is complete or not (i.e., semantics with complete, resp. incomplete information), whether agents can use knowledge of the past game states when deciding on their next move (i.e., semantics based on perfect, resp. imperfect recall), and whether the agents in the coaltion are aware of their possibility to enforce their goal, or they must be told so (i.e., de re vs. de dicto semantics; Jamroga and van der Hoek, 2004). Other variants of the semantics of ATL are studied (e.g., Schobbens, 2004; Jamroga and Agotnes, 2007); see also Bulling, Dix, and Jamroga (2010) for a recent survey on the topic.

In this article we study a variation of the semantics for ATL, in which agents in coalitions choose their strategies based on the common knowledge, available inside the coalition, of the system history. More precisely, when an agent chooses her next move, she uses not only the information she observes of the system history, but also the knowledge she has about the knowledge of the other agents in the coalition, and the knowledge she has about the knowledge the other agents have about their knowledge, and so forth. This is a variation of the AT L _iR logic studied in Schobbens, (2004), see also Jamroga and van der Hoek (2004) and Bulling, Dix, and Jamroga (2010). However, in our semantics, all the agents in a coalition utilize the same information about the system state: the common knowledge, for that coalition, of the system state. This is where our semantics differs from that in Schobbens (2004), Jamroga and van der Hoek (2004), and Bulling, Dix, and Jamroga (2010), where the information which is used by each agent in a coalition depends only on her individual knowledge of the system state, and thus might be different for two distinct agents in the same coalition. Our semantics is therefore closer to that studied in Dima, Enea, and Guelev, (2010), where the strategies used by the agents of a coalition are based on the distributed knowledge inside the coalition.

Group strategies based on common knowledge have the following property: after the strategy is fixed and shared among the agents in the coalition, at each subsequent time instant, each agent knows exactly the sequence of actions that any other agent in the coalition has issued up to that instant. This means that if, for example, for trust purposes, agent Alice wants to check whether agent Bob in the same coalition has applied the appropriate sequence of actions that he was supposed to, and this is checked by verifying Bob's log, the access that Alice gets to Bob's log does not give her any extra information about Bob's local state at any moment, besides the information that Alice already had when the coalition was created and the joint strategy was fixed. If strategies based on individual knowledge were used within coalitions, then such a scenario would lead to an information leak because, when Alice gets informed about the actual sequence of actions taken by Bob, she might deduce some information about Bob's initial local state, because Bob's strategy might differ when applied in distinct states that are identically observed by Alice.

In this article we concentrate on the simplest setting of ATL with strategies based on common knowledge and do not model the trust part of the above scenario. The main result of our article is that, for ATL with common-knowledge strategies, the model-checking problem is undecidable. Our proof is an adaptation of van der Meyden (1998) and Shilov and Garanina (2002), where it is shown that the model-checking problem is undecidable for CTL with common knowledge, with a synchronous and perfect recall semantics; see also van der Meyden and Shilov (1999). Note that the results from the cited papers cannot be used directly because the common knowledge operator cannot be straightforwardly expressed in ATL with our semantics. The only connection is the following: For systems in which agents have a single choice in each state, is equivalent with C _A □φ, where C _A is the common knowledge operator for the group A.

The rest of the article is organized as follows: in the next section we recall the game arenas framework for interpreting ATL and present the three variants of group strategies that can be used for interpreting the coalition operators: individual strategies, strategies based on distributed knowledge, and strategies based on common knowledge, and we give the relationship among the three types of strategies. In the third section we recall the semantics of ATL and introduce the new semantics based on group strategies with common knowledge. The fourth section contains our undecidability proof. The final section offers our conclusions.

BACKGROUND

In this section we give some basic definitions and fix some notations. We recall here the notations for game arenas with emphasis on the equivalence relations. We present the three types of strategies: group strategies based on individual knowledge, group strategies based on distributed knowledge, and group strategies based on common knowledge, and we discuss the relationships among them.

Definition 1

A game arena Γ = (Ag, Q, (Q _a ) _a ∈ Ag , Q _e , (C _a ) _a ∈ Ag , δ, λ, Q ₀) is a tuple where

	Ag is a finite set whose elements are called agents; subsets A ⊆ Ag are called coalitions.
	Q a is a finite set of local states for agent a, and Q e is a finite set of environment states.
	Q =  a ∈ Ag Q a  × Q e is the set of global states.
	C a is a finite set of actions available to agent a. We denote by C A the set of actions available for the coalition A, C A  =  a ∈ A C a , and C = C Ag .
	δ ⊆ Q × C × Q is the transition relation.
	Q 0 ⊆ Q is the set of initial states.
	Π is the set of atomic propositions and λ: Q → 2Π is the state-labeling function, associating with each state q ∈ Q the set of atomic propositions which hold in q.

We write for a transition (q, c, q′) ∈ δ. Also, given a global state q, we denote q| _a its a-component and call it the a -projection of q.

A run ρ is a (finite or infinite) sequence of transitions agreeing on intermediate states, i.e., . The length of a run ρ, denoted |ρ|, is the number of its transitions, η, in the case of finite runs, or ∞ for infinite runs. A run ρ is initialized if q ₀ ∈ Q ₀.

We denote by Runs ^f (Γ) the set of finite initialized runs and by Runs ^ω(Γ) the set of infinite initialized runs of Γ. When the game arena is understood from the context, we only use the notations Runs ^f , resp. Runs ^ω. ρ[i] denotes the state on i-th position in the run ρ, and ρ[0 … i] denotes the prefix of ρ of length i, for all i, 0 ≤ i ≤ |ρ|. Note that, if ρ ∈ Runs ^f (Γ) or ρ ∈ Runs ^ω(Γ), then we have ρ[0 … i] ∈ Runs ^f (Γ), for all i, 0 ≤ i < |ρ|.

Two states are observationally equivalent for agent a if the same atomic propositions observable by agent a have the same truth values in both states. Denote this relation for states ∼ _a , ∼ _a  ⊆ Q × Q. Thus, formally,

We extend the relation ∼ _a for finite runs in the following way: given two runs of equal length, ,

The distributed knowledge equivalence relation is an extension of this relation to coalitions that are “willing to exchange” information about their local states. On states, the distributed knowledge relation inside the set of agents (coalition) A is defined as follows:

This relation is then extended straightforwardly on runs as follows: given two runs of equal length, ,

The common knowledge equivalence relation on states is a different extension of the observability relations ∼ _a to coalitions in which agents are “not willing to share” the information about their local state with the other agents in the coalition. This relation is denoted by and is formally defined as follows:

Note that when for all coalitions A ⊆ Ag, the system is equivalent to a system with complete information.

can be extended on runs in the following way:

Definition 2

(Dima, Enea, and Guelev, 2010) A strategy with distributed knowledge (or dk-strategy for short) for a set of agents (coalition) A is any mapping .

An individual strategy for an agent a is a strategy for the set of agents { a }.

We write Σ _dk (A, Γ) for the set of all strategies of coalition A in game arena Γ. Given a dk-strategy σ ∈ Σ _dk (A, Γ), we define the projection on agent a ∈ A of σ as the mapping with for all .

Furthermore, Σ _ind (A, Γ) denotes the set of tuples of individual strategies for agents in A, i.e.,

In the sequel the term ind-strategy for a coalition A denotes a tuple of individual strategies, one for each agent in A. In an ind-strategy, each agent plans his future actions based solely on his information about the system state, without any other interaction with the other agents or reference to the knowledge the other agents have about the current state.

Note that in a strategy with distributed knowledge for a coalition with at least two agents, the agents' actions depend on the common observations of all agents in the coalition. Therefore, implementing such strategies requires some type of communication among agents. One of the suggested communication patterns in Dima, Enea, and Guelev (2010) is the use of an “arbiter” that gathers the information about the local states of each agent in the coalition and then issues to each agent its action according to the dk-strategy under play. The more classical notion of coalition in Jamroga and van der Hoek (2004) and Bulling, Dix, and Jamroga (2010) is to consider that a coalition acts together simply when each agent in the coalition follows an individual strategy for his play.

Definitions 3

A strategy with common-knowledge (or ck-strategy for short) for a set of agents A is a mapping .

We write Σ _ck (A, Γ) for the set of all strategies of coalition A in game arena Γ.

A ck-strategy maps each history of common-knowledge observations for coalition A to a tuple of actions for the given coalition. The intuition is that each agent chooses the same action for histories (i.e., sequences of observations) that might be different according to their individual knowledge, but are considered identical with respect to the common knowledge of the group A.

Similarly with the case of dk-strategies, we define the projection on agent a ∈ A of a ck-strategy σ ∈ Σ _ck (A, Γ) as the mapping with σ| _a (α) = σ(α)| _a for all .

A dk-strategy σ is compatible with a run if for all i ≤ |ρ|,

Similarly, a ck-strategy σ is compatible with ρ if for all i ≤ |ρ|,

Remark 1

In many practical situations, it is more convenient to define the local states of the agents by means of some subsets of atomic propositions Π _a  ⊆ Π, which are assumed to be observable to agent a, subsets might not be pairwise disjoint. In this framework, the labeling of any two global states q, q′ whose a-projection is the same, i.e., , has the property that . Then, for each global state q, we identify, by abuse of notation, the local state of a in q (i.e., q| _a ) with λ(q) ∩ Π _a .

For a given set of agents A ⊆ Ag, we denote Π _A  = ∪ _a ∈ A Π _a . We also denote the function defined by λ _A (q) = λ(q) ∩ Π _A , and, by abuse of notation, we write λ _a for λ_{a}. Note also that, within this framework, a dk-strategy is a mapping .

We will utilize this variant of game arenas in the third section of this work.

The following results are obtained directly from the definitions:

Proposition 1

The following strict inclusions hold:

SYNTAX AND SEMANTICS OF ATL AND

We recall here the syntax of ATL and present the three variants of its semantics, corresponding to the utilization of ind-strategies, dk-strategies or ck-strategies for interpreting coalition operators.

The syntax of ATL is defined by the following grammar:

where p ∈ Π and A ⊆ Ag.

Formulas of the type read as “coalition A can enforce φ”. The operator ⟨⟨·⟩⟩ is a path quantifier and (“next”), (“until”), (“weak until”) are temporal operators.

The usual derived operators can be obtained as follows:

Formulas of the type [[A]]φ read as “coalition A cannot avoid” φ.

ATL is interpreted over concurrent game structures. Three different interpretations can be given, according to the possibility given to coalitions to utilize ind-strategies, dk-strategies or ck-strategies. We denote the three variants of semantics.

Formally, given a game structure Γ, an infinite run ρ ∈ Runs ^ω (Γ), a point , we put:

	– if p ∈ λ(ρ[i]) for any α ∈ {ind, ck, dk}.
	– , again for any α ∈ {ind, ck, dk}.
	– , for any α ∈ {ind, ck, dk}.
	– if there exists σ ∈ Σ ind (A, Γ) such that for all runs ρ′ that are compatible with σ and satisfy ;
	– if there exists σ ∈ Σ ind (A, Γ) such that for all runs ρ′ that are compatible with σ and satisfy , there exists j ≥ i such that for all ;
	– , if there exists σ ∈ Σ ind (A, Γ) such that for all runs ρ′ that are compatible with σ and satisfy , there exists j ≥ i such that for all , for all .

For the case of , the semantics of the coalition operators must be rewritten as follow:

	– if there exists σ ∈ Σ ck (A, Γ) such that for all runs ρ′ that are compatible with σ and satisfy ;
	– if there exists σ ∈ Σ ck (A, Γ) such that for all runs ρ′ that are compatible with σ and satisfy , there exists j ≥ i such that for all ;
	– if there exists σ ∈ Σ ck (A, Γ) such that for all runs ρ′ that are compatible with σ and satisfy , there exists j ≥ i such that for all , for all .

Finally, the semantics is defined similarly with , with the difference that all references to are replaced with references to ∼ _A , and each quantification over strategies is restricted to elements from Σ _ck (A, Γ).

We say that a formula φ is satisfied in the game arena Γ, written for all ρ ∈ Runs ^ω(Γ).

We note that the usual notation ATL denotes the logic in which the semantics is given by . Also, in Dima, Enea, and Guelev (2010), denotes the logic in which the semantics is given by . This is a modification of the ATL logic with operators of the type ⟨⟨A⟩⟩ _D(A) from Jamroga and van der Hoek (2004), by ensuring that strategies are not only feasible when the coalition is created, but also during the whole existence of the coalition. A similar relationship can be observed between the semantics and the operators of the type ⟨⟨A⟩⟩ _C(A) from Jamroga and van der Hoek (2004).

In the balance of the paper, denotes the logic whose semantics is given by .

UNDECIDABILITY OF THE MODEL-CHECKING PROBLEM FOR

In this section we present our undecidability result for the model-checking problem in . The problem statement is the following:

Problem 1

(The Model-Checking Problem for ) Given a game arena Γ and an formula φ, decide whether .

Theorem 1

The model-checking problem for is undecidable.

Proof

We reduce the Halting problem for Turing machines that start with an empty tape to the model-checking problem for . The proof is structured as follows: first we present how to encode a Turing machine into a game arena, second we explain how the transitions are simulated in the model, and then we prove the correctness of the theorem statement.

Without loss of generality we restrict the Halting problem to Turing machines satisfying the following properties:

1.	They never write a blank symbol.
2.	They have a single initial state, denoted q 0.
3.	During a computation the machines never return to the initial state q 0.
4.	They halt when they reach a final state, i.e., there are no transitions leaving a final state.

The construction is similar to van der Meyden (1998) and Shilov and Garanina (2002), see also van der Meyden and Shilov (1999). In van der Meyden (1998) asynchrony is used to “guess” the amount of space required by the computation. Instead of asynchrony, we shall use temporal operators to describe an arbitrary long but finite computation.

Intuitively, we encode the configurations of the Turing machine and the transitions between the configurations as runs in the game arena. The runs consist of states that encode the contents of the tape cells and the positions of the R/W head. Some extra bits of information are needed, such as the fact that some state represents a cell that is at the left (or the right) of the head position, or that some states represent the transition that is applied on a tape cell, encoding both the previous and/or the next tape symbol for that transition and the direction in which the head moves after taking the transision.

Also, some states represent the left and right limit of the tape space. We use a special state marking the right limit as a guess of the amount of space that is needed for simulating a Turing machine that halts when starting with an empty tape.

The transitions between configurations of the Turing machine are also encoded as runs in the game arena. Then, the observability relation of one agent in the arena is utilized for connecting a run encoding a configuration with a run encoding a transition between configurations, which is then connected with the run encoding the next configuration with the aid of the observability relation of the second agent.

Finally, checking that the constructed game arena can simulate a halting run of the given Turing machine is done by checking the satisfiability of a reachability formula, saying that the two agents in the game cannot avoid (in the sense of choosing some strategy with common knowledge that applies to any identically observable history) the situation in that the game reaches some state that signals that the Turing machine halts.

Formally, for a Turing machine M = ⟨Q ^M , Γ ^M , β, Σ ^M , δ ^M , q ₀, F ^M ⟩ we construct a game arena denoted Γ = (Ag, Q, (Q _a ) _a ∈ Ag , (C _a ) _a ∈ Ag , δ, λ, Q ₀) for two agents, in which the set of global states is:

(The local states will be defined by identifying which sets of the atomic propositions that can be seen by each agent, as in Remark 1 above.)

The sets of states are four copies of the set of states of M. The states in Σ ^M• = {s ^• | s ∈ Σ ^M , s ≠ β} correspond to the symbols preceding the head. The states in ^•Σ ^M  = {^• s | s ∈ Σ ^M } correspond to the symbols that follow the head. The blank symbol can never appear on the tape segment at the left of the head because we have only Turing machines that do not write blank symbols. We shall call the states in overlined states. We shall use them to encode final configurations. The state is used to enforce the system to have an initial configuration. In a run, this state will always follow the state ⟨β, q ₀⟩, where q ₀ is the initial state. We use the tuples in (Σ ^M  × Q ^M  × Σ ^M  × {left, right} × {prev, next}) to encode transitions of the Turing machine. The labels left, right indicate whether the head will move to the left or, respectively, to the right, and the labels prev and next mark the previous position of the head, respectively the next position where the head is moving.

The symbols in the last line of Equation (5) represent delimiters in order to assure that the machine does not move its head off the “guessed” space. In a run, the state ε _L will encode the left margin of the tape and the state ε _R , the right margin. Likewise, are delimiters corresponding to the initial and, respectively, to the final configuration.

The set of initial states is and the set of actions consists of a singleton set C ₁ = C ₂ = C = {act}.

The transition relation is given by the following rules:

	– Transitions that encode a sequence of symbols on the machine's tape are the following: for all .
	– A state in the set Σ M  × Q M is preceded by the states in Σ M• and followed by states in •Σ M ; this is modeled by the following transitions: for all , for all q ∈ Q M  ∖ (F M  ∪ {q 0}), , and .
	– The same rule applies for the final configuration: for all , for all q f  ∈ F M , , .
	– In a run encoding a transition we mark the position where the head was and the position where the head is moving. If the head moves to left then for all symbols and for all states q p , q n  ∈ Q M  ∖ (F M  ∪ {q 0}) for which (s n , q n , L) ∈ δ M (s p , q p ) holds, ,
	– When the head moves to right we have ⟨s p , q p , right, prev⟩ ∈ δ, ⟨s p , q p , right, prev⟩⟨s n , q n , right, next⟩ ∈ δ, for all symbols and for all states q p , q n  ∈ Q M  ∖ (F M  ∪ {q 0}) for which (s n , q n , R) ∈ δ M (s p , q p ) holds.
	– No transition leading to the initial state is permitted. Instead, from the initial state we can pass into any other symbol: ε L s • ∈ δ, ε L ⟨s, q⟩ ∈ δ. In a run encoding a transition the next state will be the leftmost encoding the transition: ε L ⟨s, q, right, prev⟩ ∈ δ, ε L ⟨s, q, left, next⟩ ∈ δ.
	– A dual situation holds for the final state, ε R : for all symbols s ∈ Σ M , and for all states q ∈ Q M , • s ε R  ∈ δ, ⟨s, q⟩ε R  ∈ δ, ⟨s, q, right, next⟩ε R  ∈ δ, ⟨s, q, left, prev⟩ε R  ∈ δ.
	– The same rules apply for the runs encoding the final configuration. In this situation the head must be on a final state: , , for all symbols s ∈ Σ M , s ≠ β and for all final states q f  ∈ F M ;
	– , ⟨s, q f ⟩, for all s ∈ Σ M and for all q f  ∈ F M ;
	– In the initial run the head is on the first position and encodes the initial configuration, the empty tape. ⟨β, q 0⟩ ∈ δ. In order to force the game arena to encode the initial configuration we distinguish between β and . will only follow an initial state. , , ;
	– Once the final state is reached it is never left: ε R ε R , , ;
	– Finally, nothing else belongs to δ.

The set of atomic propositions is

The valuation function is defined by the following rules:

Propositions p ₁, p ₂, p ₃ ∈ Π are interpreted to false in any other state.

The extra propositions are used for clarifying the observability relation for each agent, namely, for all s ∈ Σ ^M and q ∈ Q ^M :

	– for all
	– for all
	– for all
	– for all
	– for both i = 1, 2.

As above, the extra propositions are interpreted as false in any other state.

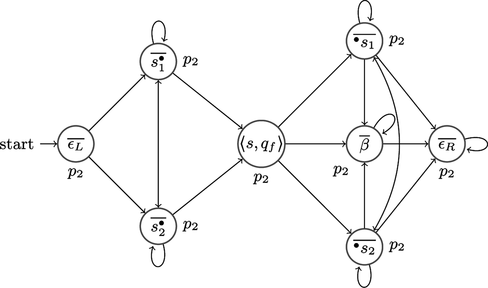
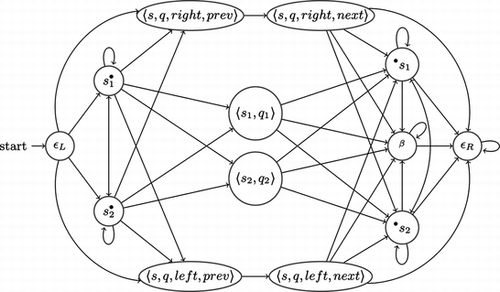
Figures 1, 2, and 3 offer a graphical representation of the encoding of a Turing machine. In Figure 1 we represent the part of the game arena accepting runs that encode the initial configuration. The automaton in Figure 2 accepts runs that encode intermediate configurations and, respectively, in Figure 3, final configurations. Any run ρ ∈ Run s ^f (Γ) ∪ Run s ^ω(Γ) is uniquely accepted by one of the three parts of the game arena.

FIGURE 1 The initial configuration.

FIGURE 2 An intermediate configuration (only the states corresponding with two symbols from Σ ^M are represented here).

FIGURE 3 The final configuration.

Next we describe the way configurations of the Turing machine are encoded as runs in the game arena. We denote a configuration of the Turing machine as a word over the alphabet Σ ^M  ∪ (Σ ^M  × Q ^M ) where a character of Σ ^M  × Q ^M appears only once. Hence the set of configurations is .

In the game arena we have two types of run: runs that encode configurations and the runs that encode transitions.

A configuration cnfg = s ₁⋯s _i − 1⟨s _i , q⟩s _i + 1⋯s _n is encoded by a run . There are infinitely many runs that encode one configuration, in this case, all runs that start with the state sequence . An initial configuration is encoded by all runs that start with . Respectively, a final configuration cnf g _f  = s ₁⋯s _k − 1⟨s _k , q _f ⟩s _k + 1⋯s _n is encoded by all the runs starting with the overlined state sequence , for m ∈ ℕ, m ≠ ∞.

The other type of run that may occur in Γ encodes transitions. For two configurations

connected by a transition in which the R/W head of the Turing machine goes right, that is, for some , the transition coding run associated to the transition is the following run in Γ:

Similarly, when and for , the transition coding run for the transition is defined as follows:

Before showing the proof for correctness we offer some helpful properties of the system presented above.

Considering the valuation function, the following properties hold in our model:

Proposition 2

If ρ₁ and ρ₂ are two runs in the game arena Γ, then ρ₁ ∼ ₁ρ₂ iff ρ₁ = ρ₂ or ρ₁ encodes a configuration cnfg and ρ₂ encodes a transition coding run cnfg .

Proof

The implication from right to left follows directly from the notation of transition coding runs and the definition of the labeling function λ₁. In order to prove the implication from left to right, we shall verify whether we have another run different from the mentioned ones, ∼₁ equivalent with ρ₁.

Consider and ρ₂ = x _L x ₁…x _n x _R . Consider . The case when the head moves to right is similar. Suppose that ρ₁ ∼ ₁ρ₂, ρ₁ ≠ ρ₂ and ρ₁ encodes a configuration cnf g ₁ and there is no configuration cnf g ₂ in the Turing machine M such that ρ₂ = (cnf g ₁ ⊢ cnf g ₂).

We consider only initialized runs, thus the initial state . Because a run contains followed by ⟨β, q ₀⟩ and followed by ⟨s, q _f ⟩, we have x _L  = ε _L . Following the same idea, we observe that x _R  = ε _R for a finite configuration. Using the definition of λ₁ and λ₂ and the fact that x if and only if x = ⟨s _j + 1, q″, left, prev⟩, it follows that for all j, 1 ≤ j ≤ i − 2 we have . Hence we have for j, i + 1 ≤ j ≤ n.

Furthermore, we have that only for . We can eliminate the overlined states because an overlined state follows only another overlined state or a state containing q _f , q _f  ∈ F ^M . We also eliminate the states of the type ⟨s _i − 1, q, right, next⟩ because these states follow only , for . Now, because only and belong to δ, we have either and x _i  = ⟨s _i , q⟩, or and x _i  = ⟨s _i , q, left, prev⟩.

Because none of the observationally equivalent states can form a correct initialized run, we have proved that ρ₁ ∼ ₁ρ₂ implies ρ₁ = ρ₂ or ρ₁ encodes a configuration cnfg and ρ₂ encodes a transition coding run .

Proposition 3

If ρ₁ and ρ₂ are two runs in the game arena Γ, then ρ₁ ∼ ₂ρ₂ iff ρ₁ = ρ₂ or ρ₁ encodes a configuration cnfg and ρ₂ encodes a transition coding run .

Proof

The proof is similar to the one used for Proposition 2.

Putting together Proposition 2 and Proposition 3 we obtain the following property:

Proposition 4

For each computation in the Turing machine M, , where cnfg and are instantaneous configurations of M, iff there exist runs in the game arena Γ that encode cnfg and, respectively, , such that and .

Proof

The proof is constructed by following a series of equivalences. In the Turing machine M having the computation means that there exist a natural number m, the length of the computation, and m configurations denoted cnf g ₀, cnf g ₁, …, cnf g _m such that . We write this .

From Proposition 2 and Proposition 3 it follows that for two instantaneous configurations of the Turing machine M, cnf g _i and cnf g _i + 1, we have cnf g _i  ⇒ _M cnf g _i + 1 iff there exist ρ _i , ρ _i + 1 two runs that encode cnf g _i and, respectively, cnf g _i + 1 in the game arena Γ such that |ρ _i | = |ρ _i + 1| ≥ |cnfg _i | and ρ _i  ∼ ₁(cnfg _i ⊢cnf g _i + 1) ∼ ₂ ρ _i + 1, for all i natural numbers. By fixing the length of the runs and configurations to the “guessed” value or the length of we can write that . According to our definition of λ₁ and λ₂, we have now .

Note that the reflexive transitive closure of ⇒ _M leads to the complete proof. Hence, iff and .

We now turn to the proof of the theorem. We prove in the rest of this section that iff the the Turing machine M halts when starting with the empty tape.

In order to prove the implication from left to right we state that starting with the empty tape, machine M halts. This means that there exists n ∈ , there exists i ∈ , 1 ≤ i ≤ n and there exists a finite sequence of configurations , where cnf g ₀ = ⟨β, q ₀⟩β ^n − 1 is an initial configuration, cnf g _f  = s ₁…s _k − 1⟨s _k , q _f ⟩s _k + 1…s _n is a final configuration for some s ₁,…, s _k − 1 ∈ Σ ^M  ∖ {β} and s _k + 1,…, s _n  ∈ Σ ^M , 0 ≤ k ≤ n. Consider the length of the computation to be f, f ∈ . By Proposition 4 we can also consider that in the game arena Γ there exists a finite sequence of runs ρ₀, ρ₁,…, ρ _f and such that

We consider a game arena with a single action. Therefore there is only one corresponding final run ρ _f , reachable from ρ₀, and, furthermore, the proposition p ₃ is visible in the n-th state, of ρ _f . We therefore conclude that the formula holds in the game arena Γ.

In order to prove the implication from right to left we show that for any run satisfying the formula , there exists an initial run equivalent with ρ.

If , then in the game arena there exists a run and there exist n ∈  and i ∈ , 1 ≤ i ≤ n such that

This means that there exists k ∈ , a sequence of k runs ρ₀,…, ρ _k such that .

Following Proposition 3, there exists a sequence of configurations in the Turing machine corresponding to the runs ρ₁, ρ₂…ρ _k such that

where cnf g ₀ is an initial configuration and

for some i, is a final configuration.

Hence, the machine M halts when starting with an empty tape.

CONCLUSION

We have presented a semantics for the coalition operators of ATL in which the agents utilize, in their strategies, the same action in states that lie in the same common-knowledge observability for the coalition in which they participate. We have shown that the model-checking problem is undecidable for , a result inspired from the techniques used in Fagin et al., (2004); van der Mayden (1998) van der Mayden and Shilov (1999) and Shilov and Garanina (2002).

It would be interesting to investigate the possibility to generalize the decidability results on model-checking temporal epistemic logics with common knowledge (van Benthem and Pacuit 2006; Lomuscio and Penczek 2007) to the setting presented here.