SCALED SELF-ORGANIZING MAP – HIDDEN MARKOV MODEL ARCHITECTURE FOR BIOLOGICAL SEQUENCE CLUSTERING

Abstract

The self-organizing hidden Markov model map (SOHMMM) introduces a hybrid integration of the self-organizing map (SOM) and the hidden Markov model (HMM). Its scaled, online gradient descent unsupervised learning algorithm is an amalgam of the SOM unsupervised training and the HMM reparameterized forward-backward techniques. In essence, with each neuron of the SOHMMM lattice, an HMM is associated. The image of an input sequence on the SOHMMM mesh is defined as the location of the best matching reference HMM. Model tuning and adaptation can take place directly from raw data, within an automated context. The SOHMMM can accommodate and analyze deoxyribonucleic acid, ribonucleic acid, protein chain molecules, and generic sequences of high dimensionality and variable lengths encoded directly in nonnumerical/symbolic alphabets. Furthermore, the SOHMMM is capable of integrating and exploiting latent information hidden in the spatiotemporal dependencies/correlations of sequences’ elements.

INTRODUCTION

Machine learning presupposes that available information can be cast into sets of numerical and symbolical values. Subsequent tasks and procedures, such as modeling and analysis, are carried out by incorporating and processing the resulting numerical/symbolical data. It is a common practice to encode explicitly each piece of meaningful/useful information, something that includes intrinsic time and space dependencies. Consequently, a considerable number of machine learning approaches assumes that the ordering of the datasets’ elements does not carry any information (viz. the relative positioning and arrangement of each vector's elements are arbitrary). In certain cases, however, this is not accurate; space ordering of vectors’ elements (i.e., which element comes first, second, etc.) or, equivalently, time arrangement (i.e., which elements precede and which follow) is significant and, more important perhaps, is an additional source of information. Thus, machine learning approaches employed for biological sequence analysis and similar tasks should be in position to capture and exploit such latent information.

We are currently witnessing an exponential growth of linear descriptions of protein, deoxyribonucleic acid (DNA) and ribonucleic acid (RNA) chain molecules requiring automated analysis. Thus, the application range of computational/statistical/machine learning techniques for modeling and studying biological molecules is continually expanding (Mount 2004). Whereas the goal of biological sequence analysis often is to study a particular sequence, its molecular structure and function, the analysis typically proceeds through the study of an ensemble of sequences consisting of its different versions in different species or even, in the case of polymorphisms, different versions in the same species. Because nucleotide or amino acid sequences with a given function or structure, in general, will differ and be uncertain, sequence models must be probabilistic (Baldi and Brunak 2001). Models stemming from the computational intelligence research field such as neural networks (NNs), hidden Markov models (HMMs) and Bayesian networks can be employed in domains characterized by the presence of large numbers of (possibly noisy or incomplete) data, variable sequence patterns, and complex structures.

Clustering (Xu and Wunsch 2005; Du 2010) is one standard method that can create higher abstractions (symbolisms) from raw data automatically; another alternative method is to project high-dimensional data as points on a low-dimensional display. Because the self-organizing map (SOM) is a combination of these two methods, it has great capabilities as a clustering, dimensionality reduction, and data visualization algorithm (Kohonen 2001; Seiffert and Jain 2002; Kraaijveld, Mao, and Jain 1995; Ultsch 2003; Brugger, Bogdan, and Rosenstiel 2008; Tasdemir and Merenyi 2009; Tasdemir 2010).

HMMs come with a solid statistical foundation and with theoretically verified learning algorithms (Koski 2001; Baldi and Brunak 2001). HMMs’ architecture and probabilistic foundations prove useful for capturing and deciphering the latent information hidden in the spatial structure and linear aspects of chain molecules and for analyzing the sequential pattern of monomers in sequences. HMMs, when applied properly, work very well in practice, hence, their wide range of applications (Durbin et al. 1998; Mount 2004) includes gene parsing/recognition, (periodical) pattern discovery, motifs, multiple alignments, and functional sites.

The self-organizing hidden Markov model map (SOHMMM) is an integration of the SOM and the HMM techniques. The SOHMMM's core consists of a novel unified/hybrid SOM-HMM algorithm. The proposed model carries out probabilistic sequence analysis with little—or even complete—absence of prior knowledge; therefore, it can have various applications in clustering, dimensionality reduction, and visualization of large-scale sequence spaces and in sequence discrimination, search, and classification. In our previously published reports (Ferles and Stafylopatis 2008a; Ferles and Stafylopatis 2008b; Ferles, Siolas, and Stafylopatis 2011) the theory of the SOHMMM framework has been briefly presented and the behavior of the model has been investigated roughly through experiments. Specifically, the experimental methodologies that have been followed, based on artificial sequence data (Ferles and Stafylopatis 2008b) and protein sequences (Ferles and Stafylopatis 2008a; Ferles, Siolas, and Stafylopatis 2011), suggest a primordial attempt for studying and analyzing characteristic aspects of the SOHMMM.

The current self-contained treatment analyzes the SOHMMM in depth and in detail (from the most primary concepts to the rather elaborate ones). A determinant new component is the novel scaled online unsupervised learning algorithm that is in position to model sequences of arbitrary large lengths. The devised learning methodology is a significant/marked improvement on its previous nonscaled counterparts (Ferles and Stafylopatis 2008a; Ferles and Stafylopatis 2008b). Furthermore, extensive analytical proofs are given for both the scaling and the unsupervised learning algorithms, whereas, in our previous publications (Ferles and Stafylopatis 2008a; Ferles and Stafylopatis 2008b; Ferles, Siolas, and Stafylopatis 2011), these were missing. Moreover, in the present study, issues regarding the realization of the SOHMMM algorithm are being addressed systematically/methodically. Last, assiduous experiments have been conducted in order to test/verify/prove the SOHMMM's effectiveness and efficiency in a more practical sense. Consequently, all the reported qualitative and quantitative results reveal the characteristics, performance, and capabilities of the improved scaled SOHMMM algorithm.

The rest of this article is organized as follows: the next section contains a review of several spatiotemporal unsupervised self-organizing networks and SOM-HMM combinations existing in the literature. The theory of HMMs is briefly presented in “Self-Organizing Hidden Markov Model Map”; also, the basis of online gradient descent for reparameterized HMMs is set. Moreover, the section contains a complete and thorough overview of the SOHMMM prototype from an architectural and algorithmic standpoint. “Scaled Online Unsupervised Learning Algorithm” commences with an extensive analysis of the scaling procedure wherein the resultant adaptations/modifications (in the primary SOHMMM framework) are pinpointed. This section is concluded with the presentation of the scaled online unsupervised learning algorithm. Qualitative and quantitative experimental (comparative) results and application issues are discussed in “Experiments.” Finally, “Conclusions” synopsizes the paper.

RELATED WORK

Various models have been proposed that extend the SOM, by recurrent dynamics and/or recursive connections, for processing sequential data. The sequential activation retention and decay network (James and Miikkulainen 1994) is a feature map architecture that creates distributed response patterns (representations) for different sequences of vectors. The extended Kohonen feature map (Hoekstra and Drossaers 1993) equips the SOM with internal connections from each neuron to all other neurons. The temporal Kohonen map (Chappell and Taylor 1993) transforms the neurons in such a way that these act as leaky integrators. The recurrent SOM (Varsta, Heikkonen, and Millan 1997; Koskela et al. 1998) uses a similar dynamic recurrent structure with the difference that leaky integrators are moved from output units to inputs. The recursive SOM (Voegtlin 2002) is a modified SOM in which time representation, which is implicit and self-referent, is implemented by homogeneous feed-forward and feed-backward connections that describe activities or learning rules. The merge SOM context (Strickert and Hammer 2004) refers to a fusion of arbitrary lattice topologies with a learning architecture that implements a compact back reference to the previous winner.

The SOM for structured data (Hagenbuchner, Sperduti, and Tsoi 2003; Sperduti 2001) suggests a recursive mechanism capable of exploiting information conveyed in the input directed acyclic graphs (DAGs) and information encoded in the DAG topology. The approach in Hagenbuchner, Sperduti, and Tsoi (2005) is effective in diversifying the mapping of vertices and substructures according to the context in which they occur inside a tree. An empirical comparison of these recursive models is presented in Vanco and Farkas (2010). In the general framework of Hammer and colleagues (2004), a uniform formulation is obtained that allows the investigation of possible learning algorithms and theoretical properties of several approaches combining the SOM with recurrent techniques.

The self-organizing mixture model (Verbeek, Vlassis, and Krose 2005) introduces an expectation-maximization (E-M) algorithm that yields topology-preserving maps based on probabilistic mixture models. The approach in Lebbah, Rogovschi, and Bennani (2007) is a special case of the previous model because it proposes a Bernoulli probabilistic SOM able to handle binary data. Soft topographic vector quantization (Graepel, Burger, and Obermayer 1998) employs deterministic annealing on different cost/error functions for the generation of topographic mappings. In Heskes (2001), the relation between SOMs and mixture modeling is investigated. The goal of the generalized taxonomy (Barreto, Araujo, and Kremer 2003) is to provide a nonlinear generative framework for describing unsupervised spatiotemporal networks, making it easier to compare and contrast their representational and operational characteristics.

All SOM variants are in position to process sequences and/or trees encoded numerically (viz. continuous/real or discrete/binary values). Processing of symbolic sequences is carried out after an intermediate preprocessing stage (i.e., after transforming symbolic sequences to numerical data spaces). Some approaches use orthogonal encoding (Strickert and Hammer 2004; Lebbah, Rogovschi, and Bennani 2007; Somervuo 2004). This sparse encoding scheme has the advantage of not introducing any algebraic correlations between the symbols but suffers from the disadvantage of increasing substantially the length of biological sequences (e.g., by a factor of 20 in the case of proteins).

The techniques (Kohonen and Somervuo 2002; Kohonen and Somervuo 1998) combine the concept of the generalized median with the batch computation of the SOM. Their computing relies on data described by predetermined (dis)similarities (for instance, weighted Levenshtein or local feature distances). A drawback of the dissimilarity SOM (DSOM) is that the training phase's computational complexity behaves quadratically with respect to the number of input data. In Conan-Guez, Rossi, and Gollib (2006) several modifications of the basic DSOM algorithm are proposed, which allow a much faster implementation. Another drawback of the DSOM, and in general of median clustering, is that it restricts prototype locations to the data space such that a severe loss of accuracy can be expected. This problem has been identified in Hammer and colleagues (2007), and also in Hammer and Hasenfuss (2010), where a different approach is followed.

In the literature, a number of attempts have been made to combine HMMs and NNs to form hybrid models that combine the expressive power of artificial NNs with the sequential time series aspect of HMMs. The approach in Baldi and Chauvin (1996) suggests a class of hybrid architectures wherein the HMM and NN components are trained inseparably. In these architectures, the NN component is used to reparameterize and tune the HMM component. There are also certain techniques based on scenarios involving SOM and HMM modules (see, for instance, Kang et al. 2007; Recanati, Rogovschi, and Bennani 2007; Tsuruta et al. 2003; Kurimo and Somervuo 1996; Kurimo 1997; Kurimo and Torkkola 1992; Somervuo 2000; Minamino, Aoyama, and Shimomura 2005; Rogovschi, Lebbah, and Bennani 2010). The training procedures of the two subunits are nearly always disjoint and are carried out independently. These approaches can be categorized in two classes. The first class contains the methods in which an SOM is used as a front-end processor (e.g., vector quantization, preprocessing, feature extraction) for the inputs of an HMM, whereas the second class consists of the models that place the SOM on top of the HMM. A type of composite HMM (Krogh et al. 1994) is implemented by training several HMM components in parallel. The Baum–Welch learning algorithm is utilized for partitioning the sequences of a single protein family into clusters (subfamilies) of similar sequences.

SELF-ORGANIZING HIDDEN MARKOV MODEL MAP

Hidden Markov Model

In essence, an HMM is a stochastic process generated by two interwoven probabilistic mechanisms, an underlying one (i.e., hidden) and an observable one (which produces the symbolic sequences). Thereinafter, we may denote each individual HMM as λ = (A, B, π), where A, B and π are the transition, emission, and initial state probability stochastic matrices, respectively.

Let be a homogeneous Markov chain, where each random variable q _t assumes a value in the state space S = {s ₁, s ₂, …, s _N }. The conditional stationary probabilities are denoted as

and are arranged in the transition stochastic matrix A = {a _ij }. Let be a random process defined over the finite space V = {v ₁, v ₂, …, v _M }, where, in general, M ≠ N. The processes and are related by the conditional probability distributions

and are organized into the emission stochastic matrix B = {b _j (k)}. The initial state probability distribution π = {π _j } is defined as

Suppose O = o ₁ o ₂ … o _T is an observation sequence in which each observation o _t assumes a value from V. Consider the forward variable α _t (i) as the joint probability of the observation sequence up to time t ≤ T and of the hidden Markov chain being in state s _i at time t, given the model λ:

A recursive solution for α _t (i) is the following:

Also, consider the backward variable β _t (i) as the probability of the observation sequence from time t + 1 till the end T conditioned on the hidden Markov chain being in the state s _i at time t, given the model λ:

Again, we can solve for β _t (i) recursively as follows:

In certain cases, the emission probabilities’ indexes are denoted as o _t and not as k. This interchange is made whenever the exact observation symbols are insignificant for the formulation under consideration, whereas these values are considered to be given and specific.

The resulting forward-backward algorithm provides a computationally efficient solution to the scoring problem for an HMM (Koski 2001). It allows the evaluation of the probability of O conditioned on model λ, so that the computational requirement is linear to the observation sequence length

It should be noted that 1 ≤ t ≤ T; consequently we have T ways for computing P(O|λ).

Bayesian Inference and Gradient Descent for HMMs

The Bayes theorem can be utilized for parameterizing/tuning an HMM λ from a corpus of data O:

where the posterior P(λ|O) represents the updated belief in the probability that HMM λ is correct, given that we have observed the dataset O. The term P(O|λ) is the probability of observing data O given model λ and is referred to as the likelihood. The prior P(λ) represents the estimate of the probability that HMM λ is correct before we have obtained any data. The probability of observing dataset O independently from the model λ is denoted as P(O). For technical reasons, probabilities can be very small. The solution is to work with the corresponding logarithms so that

From an optimization standpoint, the prior plays the role of a regularizer, that is, of an additional penalty term that can be used to enforce additional constraints. Note that the term P(O) plays the role of a normalizing constant that does not depend on the HMM's parameters and is therefore irrelevant for the optimization. The objective is to approximate the best HMM within a class, that is, to find the set of parameters that maximize the posterior. If the prior is uniform over all HMMs considered (which is usually the case), then the problem reduces to finding the maximum of P(O|λ), or equivalently logP(O|λ); this procedure is referred to as maximum likelihood (ML) estimation.

Frequently, the function being optimized is complex and its modes cannot be solved analytically. The solution is to resort to iterative and/or stochastic methods, such as gradient descent or simulated annealing. The present study's objective is to approximate the best possible model λ(x) that maximizes the posterior logP(λ(x)|O), or equivalently, the likelihood logP(O|λ(x)). Because the likelihood function is differentiable, its maxima can be estimated by using gradient descent (Jang, Sun, and Mizutani 1997; Baldi 1995). An algorithm for stochastic gradient descent on the likelihood, with x as the parameter to be estimated (viz. with respect to x), can be derived by using the rule

where η is the learning rate, which is appropriately adjusted during the learning process. Moreover, there exist well-known guarantees for the convergence of a stochastic gradient descent if the learning rate η fulfills certain properties (Kuan and Hornik 1991; Kushner and Clark 1978).

Notice that the contribution of each sequence must be weighted by the inverse of its likelihood. This may seem a little paradoxical at first sight but is easily understood. If the HMM assigns a small likelihood to a given observation sequence, the HMM is not performing properly on that sequence, and therefore, the corresponding error signal should be high.

In general, the algorithm introduced above should be useful in situations in which smoothness and/or online learning are important (Baldi and Chauvin 1994). These could include large models with many parameters and relatively scarce data, which may be more prone to overfitting; local optima trapping and other pathological behaviors when trained with discontinuous or batch rules; analog physical implementations in which only continuous learning rules can be realized; all situations where the storage of examples for batch learning is not desirable.

When the gradient descent principle is applied to complex models, it requires the propagation of information “backward,” as in the case of the forward-backward algorithm for HMMs. The gradient descent equations, with respect to the likelihood, can be derived directly by exploiting a normalized exponential reparameterization:

with w _ij , r _jt , u _j as the new variables (Baldi and Chauvin 1994). The partial derivatives of the likelihood that are required for the stochastic gradient descent algorithm are contained in the first appendix (alongside their analytic/algebraic proofs).

The employed reparameterization has three main advantages: first, adjustment of the new variables automatically preserves standard stochastic constraints; second, transition, emission and initial state probability distributions can never reach the absorbing value 0; third, in the case of online learning, abrupt jumps in parameter space are avoided. As a result of these advantages, the above reparameterization overcomes certain drawbacks of the Baum–Welch algorithm and of similar E-M methods (Baum 1972). Under certain circumstances, the Baum–Welch algorithm turns out to be problematic (Koski 2001). Especially in the case of a single training sequence, at each iteration, the algorithm resets a transition or emission probability to its expected frequency. Consequently, it is clear that the Baum–Welch algorithm can lead to discontinuous jumps in parameter space; as a result, the procedure is not suitable for online learning, in other words, for application after each training example. Another limitation of the Baum–Welch algorithm is that zero probabilities are absorbing: once a transition or emission probability is set to 0, it is never used again and thereafter remains equal to 0.

Basic SOHMMM

There are two opposing tendencies in the self-organizing process. First, the set of reference patterns tends to describe the density function of the input data. Second, local interactions between processing neurons tend to preserve continuity in the low-dimensional lattice of outputs. A result of these opposing tensions is that the reference pattern distribution, tending to approximate a smooth hypersurface, also seeks an optimal orientation and form in the output space that best imitates the overall structure of the input data distributions. The primal prerequisite for realizing this type of reference pattern distribution is the existence of a series of such adaptable reference patterns. Although the expressive power and model-fitting properties of a single HMM are unquestionable, the implementation of reference pattern distributions requires collections of HMMs. Subsequently, each individual HMM that comprises these ensembles is adjusted appropriately in such a way that the produced mapping is ordered, descriptive, and representative of the input data distribution.

The SOHMMM implements a nonlinear, ordered, smooth mapping of observation sequence data onto the reference patterns of a regular, low-dimensional array. In its basic form it produces a probability distribution graph of input data that summarizes the HMMs’ distributions on observation sequence space. It converts the nonlinear statistical relationships between sequence data into simple geometric relationships of their image points on a low-dimensional display, usually a regular two-dimensional grid of nodes. Because the SOHMMM thereby compresses information, preserving the most important topological and statistical relationships of the primary data elements on the display, it may also be thought to produce some kind of abstraction. These characteristics—abstraction, dimensionality reduction and visualization in synergy with clustering—can be utilized in a number of sequence data analysis tasks.

More specifically, SOHMMM's mapping is implemented in the following way, which closely resembles the two aforementioned tendencies. Each reference pattern (neuron) e in the SOHMMM array consists of an HMM λ _e , also called reference HMM. In total there are E neurons. The lattice type of the array can be defined to be rectangular, hexagonal, or even irregular. For instance, Figure 1 depicts a two-dimensional hexagonal array of nodes, in which each is associated to a reference HMM λ _e . Because the SOHMMM is conceptualized as a self-organizing methodology, its algorithmic realization fuses the corresponding competition and cooperation processes. The leading partial process, viz. competition, finds the neuron with the best match (usually referred to as the “winner”), whereas the following partial process, viz. cooperation, improves the match in the neighboring neurons located in the vicinity of the winner.

FIGURE 1 SOHMMM lattice alongside an example of topological neighborhood (y₁<y₂). Each four-vertex graph represents a reference HMM neuron.

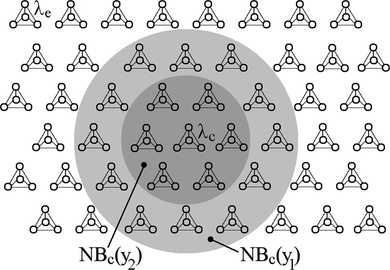
First, assume O = o ₁ o ₂...o _T is an input observation sequence. This input observation sequence O is connected to all HMMs in parallel.

Competition

Considering the probabilities of O given each λ _e (likelihoods), the image of the input observation sequence O on the SOHMMM array is defined as the array element yielding the maximum likelihood, viz. the position of the best match identifies with the location of the highest response. Subsequently, the input is mapped onto this location, as in a set of decoders. Thus, the definition of the best matching HMM (indicated by the subscript c), in other words, the HMM corresponding to the maximum likelihood, is

Cooperation

Let NB _c be the neighborhood set around the model λ _c , which matches best with O; NB _c consists of all neurons up to a certain radius on the grid from neuron c. During the process in which the nonlinear projection is formed, those HMMs that are topologically close according a certain geometric distance (viz. all HMMs within NB _c ) will activate each other to gain some knowledge from the given input O. Actually, we attempt to optimize the parameters of every λ _e  ∈ NB _c in order to best describe how a given observation comes about. This will result in a local relaxation or smoothing effect on the parameters of HMMs in this neighborhood, which, in continued learning, leads to global ordering.

Learning within the SOHMMM framework is achieved by following a hybrid approach that integrates the original incremental SOM training algorithm and the stochastic gradient descent. Therefore, an algorithm for adjusting the HMMs’ parameters can be derived by using the three propositions in the first appendix and Equation (13). The resulting SOHMMM online gradient descent unsupervised learning algorithm is an iterative procedure in which the parameters of interest, namely , and , are adjusted according to the following rules:

The indicator function is defined as

Variable y ≥ 0 is an integer, the discrete time coordinate. The function η(y) plays the role of a scalar learning rate factor (0 < η(y) < 1) and, usually, is decreasing monotonically in time. In the relaxation process, the function h _ce (y) has a very central role because it acts as the neighborhood function, a smoothing kernel defined over the lattice points. For efficiency, it is necessary that h _ce (y) → 0 when y → ∞. Usually h _ce (y) = h(∥δ _c −δ _e ∥, y) where δ _c , δ _e ∈ ℜ ² are the location vectors of HMMs λ _c and λ _e on the array. With increasing ∥δ _c −δ _e ∥ the function h _ce  → 0. The width and form of h _ce define the stiffness of the elastic surface to be fitted to the input data.

At this point, it should be noted that the SOHMMM's learning algorithm is clearly online, and, as such, it is closer to the Bayesian spirit of updating one's belief as data become available. More important, perhaps, learning after the presentation of each sample introduces a degree of stochasticity that may be useful in exploring the space of solutions and averting the phenomenon of trapping in local optima (Bishop 1995; Jang, Sun, and Mizutani 1997).

The SOHMMM online gradient descent unsupervised learning algorithm, detailed in this section, is representative of many alternative forms and obviously can give rise to a number of variants and different implementations, for example, a learning algorithm with a momentum term for regulating the influence of the previous gradient descent direction, a slightly different determination of the winner node, and a type of stochastic gradient descent on an energy-cost function in accordance with the variation proposed in Heskes (1996; 1999). Even devising a batch counterpart is a quite straightforward procedure. The outcome of this procedure would be learning rules (incorporating information from all available sequences) consisting of summations over all online learning equations (which correspond to each individual sequence).

SCALED ONLINE UNSUPERVISED LEARNING ALGORITHM

The present section (in conjunction with the corresponding appendix) contains not only the definitions/formulations of the scaling methodology but, more importantly, highlights the series of overall adaptations, modifications, and alternations that are carried out on the SOHMMM prototype.

Scaling Procedure

In the general case, the probabilities P (o ₁ o ₂ … o _t |λ) are typically very small, because they are equal to the product of many transition and emission probabilities, each less than 1. It can be seen that as t starts to increase, each term of a _t (i) starts to head exponentially to zero. For sufficiently large t (e.g., 100 or more) the dynamic range of the a _t (i) computation will exceed the precision range of essentially any machine, even in double precision. The same applies to the backward variables β _t (i), because as t decreases they also tend to zero exponentially fast. Consequently, during the implementation of the SOHMMM algorithm and in particular of the forward and backward procedures, one has to deal with precision issues. A scaling procedure, where forward and backward variables are scaled during the propagation (by a suitable coefficient that is independent of i and depends only on t) is mandatory for avoiding underflow.

The exact formulas for scaling the forward and backward variables are given along the lines described in Rabiner (1989). Typically, they are defined as

and

A recursive solution for the scaled forward variable is the following:

where the scaling coefficient s c _t is defined as

Next, we compute the scaled backward variable from the backward recursion. The only difference is the use of the same scaling factors for each time t. Because each scaling factor effectively restores the magnitude of the forward variables, and the backward variables are comparable to them, using the same scaling coefficients is an effective way of constraining the additional computation cost. Moreover, the scaling of the forward and backward variables is defined in a complementary way so that the learning equations remain essentially invariant under scaling. A recursive solution for the scaled backward variable is the following:

Thus, by induction we get

where a _t (i) and β _t (i) are the forward and backward variables computed according to the forward-backward algorithm.

The first significant change that incurs because of the scaling refers to the procedure for computing the likelihood. Initially, we can notice that by using the evaluation formula (10) for t = T, and Equation (33) we get

also, by using Equations (27) and (28) we have

Consequently, the likelihood with respect to the scaled forward/backward variables can be computed by using Equations (35) and (36):

or equivalently

Thus, the log-likelihood can be computed instead of the likelihood; because as it has been analyzed previously, it would be out of the machine precision bounds, anyway.

The second significant effect the scaling procedure has on the SOHMMM is with regard to the online gradient descent learning rules. The integration of Equations (18)–(20) with the three propositions in the second appendix brings forth a learning algorithm for adjusting the SOHMMM's parameters, which, in parallel, keeps the computation within precision range.

It should be obvious that the scaling procedure need not be applied at every time instant t but can be performed whenever desired or necessary (e.g., to prevent underflow). If scaling is not performed at some instant t, the scaling coefficients s c _t are set to 1 at that time, and all the conditions discussed above are then met.

Algorithmic Implementation

Initially, let OS = {O ⁽¹⁾, O ⁽²⁾, …, O ^(D)} be a set of D observation sequences, where is the dth observation sequence which consists of T _d symbols.

The SOHMMM consists of E HMMs arranged onto a two-dimensional hexagonal lattice. For visual inspection, the hexagonal lattice is to be preferred, because it does not favor horizontal and vertical directions as much as the rectangular array. In theory, it is preferable that the lattice edges impose an oblong form of the map because the elastic network must be oriented and stabilized along these two dimensions.

In the present approach, during the ordering phase of the SOHMMM's scaled online unsupervised learning algorithm, a Gaussian neighborhood function is utilized

where the parameter σ(y) defines the width of the kernel and is some monotonically decreasing function of time. Frequently, the function's standard deviation starts with a value of the same magnitude as half the largest dimension of the lattice and decreases to one map unit at the end of the phase. The learning rate factor decreases monotonically, starting with reasonably high values (close to unity) and, at the end, attaining values smaller by one (or more) orders of magnitude. Afterward, during the fine adjustment (tuning phase), the width of the neighborhood remains fixed and N B _c contains the nearest neighbors of HMM λ _c on the lattice. The learning rate is determined by a function inversely proportional to y.

A generic formulation of SOHMMM's scaled online gradient descent unsupervised training algorithm is the following:

EXPERIMENTS

Globin Protein Family

For this set of experiments the focus will be on globins. Globins form a well-known family of heme-containing proteins that reversibly bind oxygen and are involved in its storage and transport. The globin protein family is a large family that is composed of subfamilies. From crystallographic studies, all globins have similar overall three-dimensional structures but widely divergent sequences. The globin sequences used here were extracted from the iProClass protein knowledgebase (iProClass 2011), a database that provides extensive information integration of over 90 biological databases. In total, 560 proteins belonging to the three major globin subfamilies were retrieved (namely hemoglobin α-chains, hemoglobin β-chains, and myoglobins). The resulting globin dataset's composition is 194 α-globins, 216 β-globins, and 150 myoglobins. Consequently, for all the following experiments, the 20-letter amino acid alphabet of proteins should be considered.

Primary Investigation

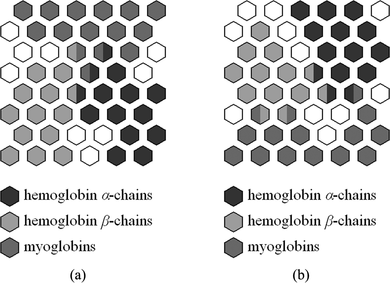
The first series of experiments was performed by using the whole globin protein dataset. The SOHMMM employs a rectangular 6 × 8 array of 48 HMM neurons. Initially, in order to test (roughly) SOHMMM's capabilities and performance, several experiments, with various learning rate and monotonically decreasing neighborhood functions, were conducted. The usual standard selection for these functions (which is common for many SOM approaches) yielded satisfactory results. Consequently, the learning rate was defined as an exponentially decreasing function between 1.0 and 0.1, whereas the neighborhood kernels’ standard deviations started with a value equal to half the largest dimension in the lattice and decreased linearly to one map unit. Also, the maximum total duration of both the ordering and tuning phases was set to five epochs. In the present study, the mean value of accurately clustered globin sequences is employed as a statistical performance measure. In other words, class information that is excluded from training will be used to perform a posterior evaluation of the representation and generalization capabilities of the trained model. An estimate of this measure, averaged on 50 replications of identical experiments, is 95.31 ± 0.57%. Equivalently, the stratified ten-fold cross-validation methodology on all 560 globins yields 95.23 ± 0.61%. Figure 2(a) depicts a representative outcome after the execution of the SOHMMM online unsupervised learning algorithm. The SOHMMM seems to succeed in capturing the important statistical properties of globins, and in managing to divide the training dataset into three clusters of similar globin sequences. The examination of the illustrated results confirms that these clusters, which are formed during an automated unsupervised procedure, are distinct and coherent with well-defined boundaries. 185 hemoglobin α-chains, 205 hemoglobin β-chains, and 143 myoglobins are assigned to HMMs that form the clusters of their respective globin subfamilies. Thus, the vast majority of protein sequences is correctly clustered by being associated to HMMs that represent certain domains of the protein subfamilies’ spaces. Only a few protein sequences (27, strictly speaking) are assigned to HMMs lying at the boundaries of the clusters. These HMMs demonstrate a tendency to represent globins belonging to two different protein subfamilies, thus obstructing the accurate clustering of specific protein sequences. Nevertheless, such phenomena should be considered justifiable and expected from the moment the SOHMMM produces a smooth mapping of the protein subfamilies on a low-dimensional display (in the form of adjacent clusters), and the HMMs under consideration are located at the boundaries of the three clusters.

FIGURE 2 The SOHMMM lattice wherein each hexagon represents an HMM neuron. (a) The SOHMMM for the protein training set that incorporates all 560 globins. (b) The SOHMMM after the completion of the training process, in which only 225 globins (selected at random) have been used. In (a) and (b), HMMs corresponding to sequences from each one of the three globin subfamilies are differentiated by distinct gray-scale shades.

Experiments were conducted to study/analyze in which way and to what extent the SOHMMM's behavior and performance are affected by the duration of the training phase and the size of the lattice. The learning rate and neighborhood kernels were tuned according to the adjustment schemes followed in all previous experiments (because such an approach always works quite well in practice).

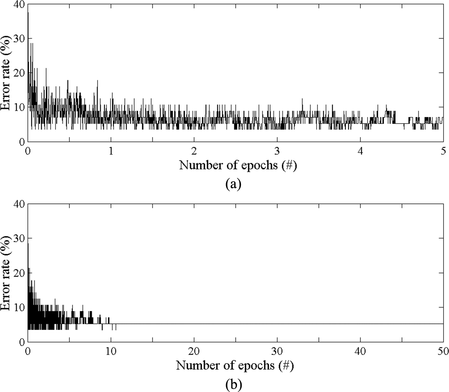
A representative scenario of a training phase (corresponding to a 6 × 8 SOHMMM lattice) lasting ten times more epochs than previously is illustrated in Figure 3. Based on this, certain remarks can be made starting from the evident observation that most learning is completed within the first few epochs, after which the SOHMMM goes through a fine-tuning stage. These findings are analogous to the ordering and tuning phases that are integrated into the model's unsupervised learning algorithm. Moreover, one can notice that the average error rate actually decreases, rapidly at the beginning and gradually at the end, despite the fact that training is based on maximizing the likelihood, which does not incorporate any kind of class information or domain knowledge. Thus, we can defensibly claim that, as long as category assignments are in accordance with the underlying attributes and structure of the data at hand, the SOHMMM produces rather accurate results. In addition, the fact that at the end of the first five epochs the SOHMMM has already reached good levels of performance (which is only slightly improved during the remaining epochs) further supports the statement that even short training periods prove sufficient. Partially, this is due to the proven learning algorithm that generates probabilistic modules (i.e., the SOHMMM neurons), which exploit all provided information in a more efficient manner, at least when compared with other (usually heuristic) deterministic vector-based methodologies. Also, after certain oscillations at the very beginning of the training phase, the SOHMMM converges to an optimum, demonstrating stability along the way, whereas, at the end, fluctuations are practically diminished, at least for the problem under consideration.

FIGURE 3 Error-epoch trajectories for training of the SOHMMM on globin protein sequence data. Plot (a) shows a zoomed portion from point 1 to 5 of the epoch series.

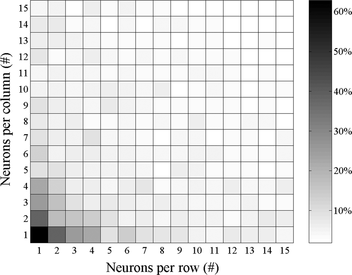
The graph in Figure 4 depicts the results of a stratified ten-fold cross-validation methodology when applied to a variety of SOHMMM array dimensionalities. A first key observation to be made is that there is a broad spectrum of lattice sizes that yield satisfying results. Consequently, reasonable variations in the array size have a small impact on SOHMMM's performance. This relative robustness against certain free parameters (i.e., neurons per row/column) is a desired characteristic for an unsupervised method because accurate values cannot be obtained if class information is unknown or missing. The only pitfall that must be avoided is utilizing degenerate SOHMMM lattices (e.g., 1 × 1). Obviously, a limited number of HMMs are not in position to model all data or clusters; as a result, certain attributes and relations are misrepresented; in such cases, erroneous states prevail and performance deterioration is inevitable. On the contrary, it is apparent that increasing the size of SOHMMM arrays that already work well is not a wise practice, because one can hardly trace a gain in terms of performance, and computational robustness is compromised.

FIGURE 4 Average error rate percentages for various sizes of the SOHMMM lattice.

Limited Number of Training Data

The second series of experiments was conducted by using an SOHMMM completely similar to the one used initially in the previous experimental investigation (namely a 6 × 8 SOHMMM lattice). The training set consisted of 75 protein sequences picked at random from each of the three main protein subfamilies, summing up to a total of 225 protein sequences. The remaining 335 globins were withheld in order to study and test the SOHMMM on sequence data not used during the training process. Figure 2(b) illustrates the results of a representative scenario after the completion of both the ordering and tuning phases. The previous analysis and remarks regarding the formed clusters apply almost unaltered to this case, too. The qualitative properties of both SOHMMMs are similar; minor differences, which relate to the positioning, shape, and size of the respective three clusters, are insignificant aftereffects of random initialization and of different sequence presentation order. A valid quantitative comparison of the first and second series of experiments should take into consideration the response of the model to all 560 protein sequences (both those used for training the SOHMMM and those not used for training). In this representative case, 183 hemoglobin α-chains, 204 hemoglobin β-chains, and 141 myoglobins are assigned correctly to their respective protein subfamilies, whereas the mean value of accurately clustered globins is calculated as 94.47 ± 0.59% (averaged on 50 replications of identical experiments). These results prove inferior, because the percentage of correctly clustered globins slightly drops, followed by an increase in the percentage of proteins associated with HMMs that describe globins of two different subfamilies. Such an outcome is justifiable by the fact that fewer globin sequences (less than half of the available) obviously contain less information, thus, the resulting SOHMMM reflects the limited and fragmentary nature of the supplied information.

Discussion

The experimental setup based on the globin protein family establishes certain properties of the SOHMMM and confirms some of its advantages. Because digital symbol sequences are representative descriptions of protein chain molecules, they also exhibit the same length diversity as their biological counterparts. Evidently, the SOHMMM devises a mechanism for handling such discrete symbol sequential data (of variable lengths) written in alphabets of arbitrary cardinalities, such as the 20-letter amino acid alphabet of proteins. Also, the SOHMMM is able to access and exploit the latent information hidden in the spatial dependencies/correlations of protein chain molecules. The exact values of the training parameters (albeit inaccurate and sketchy) do not seem to affect the SOHMMM's efficiency and robustness. As has been shown, rough estimates of these parameters (i.e., array size, learning rate factor, and neighborhood function) prove more than adequate. Moreover, even a small number of training cycles (five epochs at maximum) is usually sufficient to ensure stability and convergence.

By implementing the self-organization and competitive strategies, the SOHMMM manages, in certain cases, to contrive higher abstractions (symbolisms) that build on the probabilistic attributes of topologically neighboring HMMs. The SOHMMM approach seems able to capture the statistical properties of the globin protein family by covering a larger set of distributions and, consequently, by expressing relations inaccessible to single uncorrelated HMMs. Thus, it accomplished the tasks of identifying the three major globin subfamilies and of partitioning all protein sequences into the three clusters that represented these subfamilies. A matter of significant value is that both tasks have been carried out along a straightforward process of learning from protein chain molecules, without requiring any kind of prior or posterior knowledge. Even in the case of the reduced protein training set (second series of experiments) the results were slightly inferior. The SOHMMM reached a generalization level that eliminated overtraining phenomena and, at the same time, clustered accurately the landslide of globins that had been used for training and testing. In this case, the SOHMMM appears to be rather independent of the number of input protein sequences, something that became evident from the fact that less than half of the available globins sufficed to form the final model. However, it must be noted that the minimum necessary number of input sequences is highly problem dependent, because it is determined by the complexity and nature of the problem and by how descriptive are the inputs of the overall sequence space.

One of the SOHMMM's main objectives is to produce simplified descriptions and summaries of sequence datasets. As has been shown, it projects globin subfamilies (which are high-dimensional complex sequence data) as points on a two-dimensional display. These projections represent the input protein sequences in a lower-dimensional space in such a way that clusters and relations between globins are preserved as faithfully as possible. In addition, each cluster's constituent HMMs develop into decoders of their respective protein sequence domains, and these decoders are formed onto the SOHMMM lattice in a systematic order. The globins that are assigned to a SOHMMM neuron are actually described by a probabilistic model in a process resembling dimensionality reduction. Finally, an issue of significant importance is that, once an SOHMMM has been successfully derived from a family of protein sequences, all HMM nodes can be labeled according to the assigned proteins’ categories or annotate information (in a process resembling calibration), as in Figure 2(b). Because the best matching neuron of any given unknown protein chain molecule can be computed, this protein can be classified as belonging to the cluster represented by the labeled HMM node. Processes based on this strategy can be used in discrimination tests, database searches, and classification problems. If well-established class-specific training sets for protein families were available, SOHMMMs could be derived (based on them) and, subsequently, be employed for similarity searches across protein databases. Inter alia, the second series of experiments demonstrates an exemplar classification task, according to which each of the 335 globins, not used for training, was classified as belonging to the cluster/subfamily represented by the labeled HMM neuron that returned the highest probability.

Qualitative Comparative Results

An attempt to automatically discover subfamilies of globins using a competitive learning approach is described by Krogh and colleagues (1994). The proposed methodology yields a composite HMM consisting of component HMMs. Eventually, each individual cluster is represented by a single component HMM. Seven nonempty clusters representing protein sequences from known globin subfamilies were constructed. Four of the clusters contained varied sequences, which belonged to different globin subfamilies or to specific organisms. The entire number of α-globins, β-globins, and myoglobins was distributed into the remaining three (largest) clusters. Cluster 1 contained almost exclusively alpha, α-type, and α-like globins. Nearly all beta, β-type, and β-like globins were included in cluster 2. Finally, the subfamily of myoglobins was assigned to cluster 3. In essence, these results are in agreement with the findings of the two series of experiments. Such unified unsupervised learning HMM hybrid approaches are able to discriminate and, subsequently, cluster the three major globin subfamilies correctly.

Quantitative Comparative Results

The third series of experiments involves a 6 × 4 SOHMMM grid; all other (network and training) parameters are identical to those employed in the previous two globin experimental schemes. In the literature, 226 globins (belonging to five protein classes) are used as a benchmark for evaluating the performance of several neural gas (NG) and SOM algorithms (Hammer and Hasenfuss 2007; Hammer et al. 2007; Hammer and Hasenfuss 2010). The results displayed in Table 1 are obtained from a repeated stratified ten-fold cross-validation averaged over 100 repetitions and have been retrieved from the respective reports. All devised models (except the SOHMMM) are especially designed for handling relational data (such as pairwise similarities/dissimilarities derived from alignments of biological sequences).

TABLE 1 Average Accuracy Percentages

Model	Overall
SOHMMM	94.93 ± 0.62
Supervised Relational Batch NG	94.4 ± 1.3
Relational Batch NG	91.9 ± 1.6
Supervised Relational SOM	91.5
Supervised Relational Hyperbolic SOM	91.5
Deterministic Annealing	90.7 ± 0.8
Supervised Median Batch NG	89.4
Supervised Relational k-Means	88.2
Relational k-Means	88.0
Median Batch NG	76.3
Median k-Means	76.1

A first observation regarding the experimental results is that the SOHMMM performs well in terms of classification accuracy, marginally outperforming the other approaches. However, one should note that this result is achieved through a direct unsupervised learning methodology without utilizing any kind of either class information or any type of elaborate distances (which must be predetermined by experts). Per contra, all other algorithms that score above 91% exploit both protein class information and predetermined evolutionary distances (which are based on prior knowledge or domain information).

A plausible explanation of the effectiveness of the proposed method could be its capability to tackle symbolic sequences directly and systematically within a proven probabilistic framework. The SOHMMM manages, to a certain extent, to capture and decipher information hidden in the proteins’ amino acid compositions and information distributed across the spatial correlations of the protein monomers (which usually remain inaccessible or unexploited). For instance, all other reported approaches handle nonnumerical sequences by resorting to the solution of pairwise distances and generalized medians; this leads to a considerable loss of information.

In many applications, it does not suffice that an algorithm just detects a biological signal; it should also provide the means to interpret its solution in order to gain biological insight and extract biologically relevant knowledge about the sequence analysis problem at hand. Each SOHMMM neuron (which is associated with a cluster) is a source of information in the sense that it can be used for studying the profile and statistical properties of the proteins that are being represented by the corresponding HMM (Durbin et al. 1998; Mount 2004). Within this scope, the results of the remaining algorithms suggest a clustering of predefined similarities (which is not associated to a prototype or to a statistical model), and hence, they leave narrow margins for subsequent investigations and further sequence analysis.

Last, another advantage of the SOHMMM, compared with the methodologies based on relational data, regards its computational efficiency. Each single training step of the SOHMMM scaled online unsupervised learning algorithm necessitates calculations, under the condition that T _d  ≫ N and T _d  ≫ M (only degenerate models do not meet these two conditions). Consequently, the total execution time of the training phase scales linearly with respect to the overall number of employed training sequences. On the contrary, the computational complexity for training relational models scales quadratically also with respect to the number of training sequences. Despite the fact that faster implementations have been proposed (Conan-Guez, Rossi, and Gollib 2006), the quadratic nature of relational algorithms cannot be avoided, essentially because rational data are intrinsically described by a quadratic number of pairwise similarities.

CONCLUSIONS

The SOHMMM introduces a hybrid framework that integrates the SOM and the HMM principles. Conclusively, to a lesser or greater extent, the SOHMMM approach:

1.	is based on a firm probabilistic basis;
2.	devises a scaled online gradient descent unsupervised learning algorithm;
3.	employs an HMM likelihood function during the competition phase, whereas during the cooperation phase, follows a hybrid approach by combining the stochastic gradient descent and the scaled forward-backward algorithms;
4.	is in position to analyze (directly) sequences derived from biological chain molecules (e.g., linear descriptions of proteins and genes);
5.	can capture and exploit the latent information hidden in the spatial structure and linear aspects of such molecules;
6.	can accommodate and handle nonnumerical/symbolic sequences of high dimensionality and/or widely variable lengths;
7.	covers an extended set of distributions that represent the input sequence space in a more faithful manner;
8.	integrates the clustering, dimensionality reduction and visualization disciplines in a unified scheme;
9.	provides procedures for sequence discrimination, search, and classification.

In spite of its capabilities, the SOHMMM can suffer in particular from two weaknesses, which are inherited from its constituent HMMs. First, HMMs for chain molecules often have a large number of unstructured parameters; thus, a high amount of meaningful and descriptive (of the sequence space under consideration) biological sequences is mandatory. This problem aggravates when only a few sequences are available in a family, not an uncommon situation in early stages of genome projects or in certain cases of gene and protein groups. Second, first-order HMMs are limited by their first-order Markov property: they cannot express dependencies between hidden states; in other words, they are based on the (arbitrary) assumption that the conditional probability of a current event given the past history depends only on the immediate past and not on the remote past. Proteins fold into complex three-dimensional shapes determining their function. Subtle, long-range correlations in their chains may exist; these are accessible to higher-order HMMs and most times are missed by any first-order HMM. Therefore, the SOHMMM fails to capture such correlations. Nevertheless, we must not overlook the fact that a major difficulty with higher-order HMMs is the exponential growth of free parameters and of the corresponding computational cost.

Notes

Classification results of the SOHMMM, supervised relational SOMs, (relational) NG variants, and k-means on the globin protein family.

APPENDIX A

The propositions referenced in the main text are presented next. Because of space limitations, certain analytical proofs have been omitted. Nevertheless, the exact mathematical proofs of Propositions 1, 3 (Lemmas 1, 3) are similar to those of Proposition 2 (Lemma 2), which is detailed below.

Lemma 1:

Proposition 1:

Lemma 2:

Proof

By using the evaluation formula (10) for t = T and the forward recursion (6) for α _T (j), we get

We differentiate partially (A4) with respect to b _x (y), to obtain

Moreover, the use of the forward recursion (6) in the first term yields

Hence, we need to calculate only the second term on the right-hand side. The task is accomplished for the benefit of our purposes by using the forward recursion (6) once more

By performing the differentiation we obtain

Insertion of these partial derivatives into the second term of (A6) gives

We now compute the values of each of the two terms on the right-hand side of (A10). First, by interchanging the order of summations in the first term of (A10) and, subsequently, by using the backward (9) and the forward (6) recursions, we obtain

Second, by interchanging the order of summations in the second term of (A10) and, subsequently, by using the backward recursion (9), we obtain

With the use of (A10), (A11), and (A12), we have rewritten the right-hand side of (A6) as

The double sum is seen to be exactly of the same form as that obtained in (A6). Hence, we may continue the differentiation of and reorganize the resulting expressions exactly in the same manner as above. As a result of (5), we get

but, by the backward recursion (9) and from (5), it follows that

Consequently, by (A13) and (A15), we see that when going downward, the differentiation stops at the point where appears, because is the last remaining expression that might contain a b _x (y) term. As a result we have

As a result of the expression I{o _l  = y|λ}, the only nonzero terms of the above summation are those for which the rule o _l  = v _y stands true. So, an equivalent expression to (A16) is

Thus, (A3) has been proved.

Proposition 2:

Proof

Using the chain rule on the left-hand side of (A18), we get

From the normalized exponential reparameterizations (14)–(16), it follows that the partial derivatives of the emission parameters b _j (t) are

By applying (A20), (A21), and (A3), the right-hand side of (A19) yields

By interchanging the order of summations in the second term of (A22), we get

Each symbol ο _l of an observation sequence O, assumes a single value from V (one out of the M possible values v _m ); consequently, the summation over the indicator function yields

Insertion of the expression (A23) and of the equality (A24) into (A22) yields

Thus, (A18) has been proved.

Lemma 3:

Proposition 3:

APPENDIX B

The analytic mathematical proofs of Propositions 1, 3 are similar to that of Proposition 2, which is detailed next.

Proposition 1:

Proposition 2:

Proof

By using (33) and (34) in the left-hand side of (B2), we get

where the last equality follows from (37). Thus, (B2) has been proved.

Proposition 3: